Алгебра 9 класс мордкович номер: ГДЗ по алгебре 9 класс: Мордкович. Решебник задачника.

Помогите найти двузначное число! № 7.9 Алгебра 9 класс Мордкович – Рамблер/класс

Помогите найти двузначное число! № 7.9 Алгебра 9 класс Мордкович – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

Какое двузначное число в 4 раза больше суммы своих цифр и в 3 раза больше произведения цифр?

 

ответы

Пусть ab — искомое 2-значное число, тогда:

Решениями полученной системы является пара чисел (0; 0), (2; 4), но поскольку число 0 не принято считать двузначным, то ответом задачи является число 24.

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

ЕГЭ

10 класс

11 класс

Химия

похожие вопросы 5

Домашняя контрольная работа № 3 Вариант 2 10. При каких значениях р уравнение… Мордкович 8 класс алгебра

10. При каких значениях р уравнение  -х 2 + 6х — 2 = р:
а)    не имеет корней;
б)    имеет один корень; (Подробнее…)

ГДЗМордкович А.Г.Алгебра8 класс

Когда скорость изменения функции будет наибольшей или наименьшей? Алгебра 10-11 класс Колмогоров Упр 308

 Совсем я в точных науках не сильна) Кто поможет?) Найдите значения аргумента из промежутка [-2; 5], при которых скорость изменения (Подробнее…)

ГДЗ11 классКолмогоров А. Н.Алгебра

Васильевых. 50 вариантов ответов по русскому языку. Вариант 31 ч.2 Задание 13 ОГЭ Русский язык 9 класс Однородное подчинение придаточных

     Среди предложений    21-29:  
      (21) И Митрофанов услышал в этом смехе и прощение себе, и даже какое-то (Подробнее…)

ГДЗРусский языкОГЭ9 классВасильевых И.П.

16. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)… Цыбулько И. П. Русский язык ЕГЭ-2017 ГДЗ. Вариант 13.

16.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)

в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)

ГДЗЕГЭРусский языкЦыбулько И.П.

ЕГЭ-2017 Цыбулько И. П. Русский язык ГДЗ. Вариант 13. 18. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)…

18.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)

ГДЗЕГЭРусский языкЦыбулько И.П.

График уравнения на координатной плоскости. Построение графиков онлайн. Тема: Системы уравнений

Пусть дано уравнение с двумя переменными F(x; y) . Вы уже научились решать такие уравнения аналитически. Множество решений таких уравнений также можно представить в виде графика.

Графиком уравнения F(x; y) называется множество точек координатной плоскости xOy, координаты которых удовлетворяют уравнению.

Чтобы построить уравнение с двумя переменными, сначала выразите переменную y через переменную x в уравнении.

Наверняка вы уже умеете строить различные графики уравнений с двумя переменными: ax + b = c — прямая, yx = k — гипербола, (x — a) 2 + (y — b) 2 \ u003d R 2 — окружность, радиус которой равен R, а центр находится в точке O(a; b).

Пример 1

Постройте уравнение x 2 — 9y 2 = 0.

Решение.

Разложим на множители левую часть уравнения.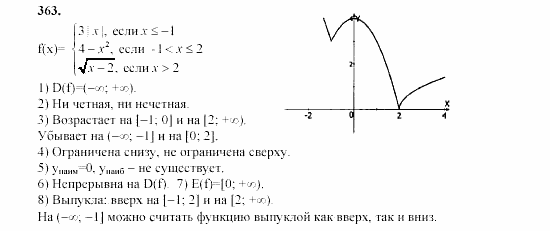

(х — 3у)(х + 3у) = 0, т. е. у = х/3 или у = -х/3.

Ответ: рисунок 1.

Особое место занимает задание фигур на плоскости уравнениями, содержащими знак модуля, на чем мы остановимся подробнее. Рассмотрим этапы построения уравнений вида |y| = f(x) и |y| = |f(x)|.

Первое уравнение эквивалентно системе

(f(x) ≥ 0,
(y = f(x) или y = -f(x)).

То есть его график состоит из графиков двух функций : y = f(x) и y = -f(x), где f(x) ≥ 0,

Для построения графика второго уравнения строятся графики двух функций: y = f(x) и y = -f(x).

Пример 2

Постройте уравнение |y| = 2 + х.

Решение.

Данное уравнение эквивалентно системе

(x + 2 ≥ 0,
(y = x + 2 или y = -x — 2).

Строим множество точек.

Ответ: рис. 2.

Пример 3

Постройте уравнение |y – x| = 1.

Решение.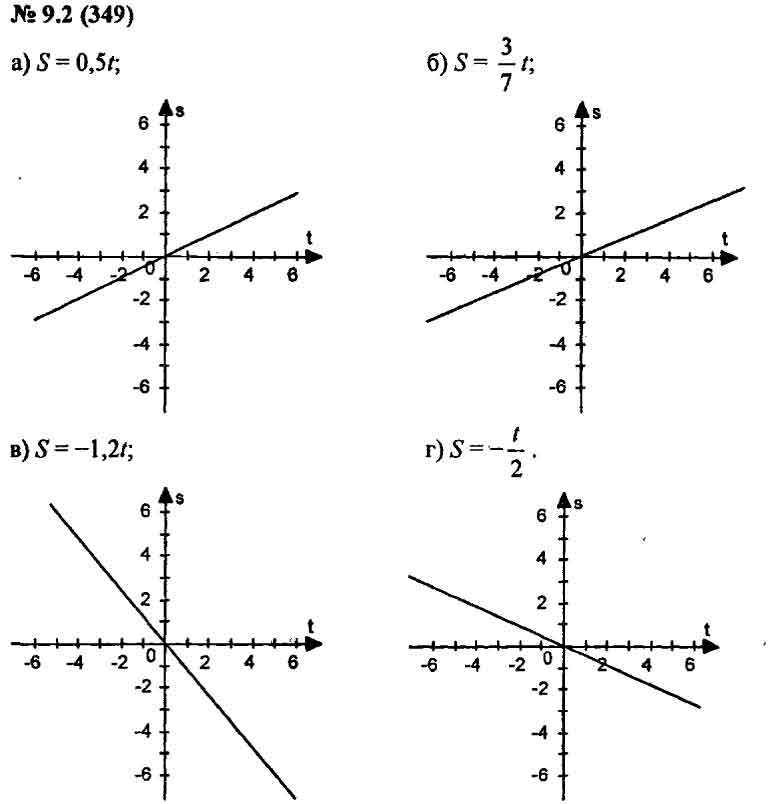

Если y ≥ x, то y = x + 1, если y ≤ x, то y = x — 1.

Ответ: рисунок 3.

При построении графиков уравнений, содержащих переменную под знаком модуля, удобно и рационально использовать метод площадей , основанный на разбиении координатной плоскости на части, в которых каждое подмодульное выражение сохраняет свой знак.

Пример 4

Постройте уравнение x + |x| + у + |у| = 2.

Решение.

В этом примере знак каждого выражения подмодуля зависит от квадранта координат.

1) В первой координатной четверти x ≥ 0 и y ≥ 0. После расширения модуля данное уравнение будет иметь вид:

2x + 2y = 2, а после упрощения x + y = 1.

2) Во второй четверти, где х

3) В третьем квартале х

4) В четвертом квартале при x ≥ 0 и y

Построим это уравнение в четвертях.

Ответ: рисунок 4.

Пример 5

Нарисуйте набор точек, координаты которых удовлетворяют равенству |x – 1| + |у – 1| = 1.

Решение.

Нули подмодульных выражений x = 1 и y = 1 разбивают координатную плоскость на четыре области. Разобьём модули по регионам. Представим это в виде таблицы.

Регион	Знак выражения подмодуля	Полученное уравнение после расширения модуля
я	х ≥ 1 и у ≥ 1	х + у = 3
II	х	-х+у=1
III	х	х + у = 1
IV	х ≥ 1 и у	х – у = 1

Ответ: рисунок 5.

На координатной плоскости можно указать цифры и неравенства .

График неравенства с двумя переменными представляет собой множество всех точек координатной плоскости, координаты которых являются решениями этого неравенства.

Рассмотрим алгоритм построения модели решения неравенства с двумя переменными :

1. Запишите уравнение, соответствующее неравенству.
2. Постройте уравнение из шага 1.
3. Выберите произвольную точку в одной из полуплоскостей. Проверить, удовлетворяют ли координаты выбранной точки заданному неравенству.
4. Изобразите графически множество всех решений неравенства.

Рассмотрим прежде всего неравенство ax + bx + c > 0. Уравнение ax + bx + c = 0 определяет прямую, делящую плоскость на две полуплоскости. В каждом из них функция f(x) = ax + bx + c знакосохраняющая. Для определения этого знака достаточно взять любую точку, принадлежащую полуплоскости, и вычислить значение функции в этой точке. Если знак функции совпадает со знаком неравенства, то эта полуплоскость будет решением неравенства.

Рассмотрим примеры графических решений наиболее распространенных неравенств с двумя переменными.

1) ax + bx + c ≥ 0. Рисунок 6 .

2) |х| ≤ а, а > 0, Рисунок 7 .

3) x 2 + y 2 ≤ a, a > 0. Рисунок 8 .

4) г ≥ х2. Рисунок 9

5) xy ≤ 1. Рис. 10.

Если у вас есть вопросы или вы хотите попрактиковаться в моделировании множеств всех решений неравенств с двумя переменными с помощью математического моделирования, вы можете бесплатный 25-минутный урок с онлайн-репетитором после регистрации. Для дальнейшей работы с преподавателем у вас будет возможность выбрать подходящий вам тарифный план.

Есть вопросы? Не умеете рисовать фигуру на координатной плоскости?
Чтобы получить помощь репетитора — зарегистрируйтесь.
Первый урок бесплатно!

сайта, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Линейное уравнение с двумя переменными — это любое уравнение, имеющее следующую форму:

a*x + b*y =c . Здесь x и y — две переменные, a,b,c — некоторые числа.

Решением линейного уравнения a*x + b*y = c, является любая пара чисел (x, y), которая удовлетворяет этому уравнению, то есть превращает уравнение с переменными x и y в правильное числовое равенство.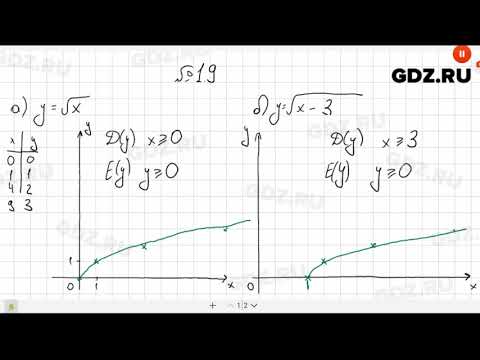 Линейное уравнение имеет бесконечное число решений.

Если каждую пару чисел, являющихся решением линейного уравнения с двумя переменными, представить на координатной плоскости в виде точек, то все эти точки образуют график линейного уравнения с двумя переменными. Наши значения x и y будут служить координатами точек. В этом случае значение x будет абсциссой, а значение y будет ординатой.

График линейного уравнения с двумя переменными

График линейного уравнения с двумя переменными – это множество всех возможных точек координатной плоскости, координаты которых будут решениями этого линейного уравнения. Нетрудно догадаться, что график будет представлять собой прямую линию. Поэтому такие уравнения называются линейными.

Алгоритм построения

Алгоритм построения линейного уравнения с двумя переменными.

1. Начертите оси координат, подпишите их и отметьте шкалу единиц измерения.

2. В линейном уравнении положим x = 0 и решим полученное уравнение относительно y. Отметьте полученную точку на графике.

3. В линейном уравнении возьмите число 0 в качестве y и решите полученное уравнение относительно x. Отметьте полученную точку на графике

4. При необходимости возьмите произвольное значение x и решите полученное уравнение относительно y. Отметьте полученную точку на графике.

5. Соединить полученные точки, продолжить по ним график. Подпишите получившуюся строку.

Пример: Постройте уравнение 3*x — 2*y =6;

Положим х=0, тогда — 2*y=6; у=-3;

Положим y=0, тогда 3*x = 6; х=2;

Отмечаем полученные точки на графике, проводим через них прямую и подписываем. Посмотрите на картинку ниже, график должен выглядеть так.

В этом уроке мы более подробно рассмотрим построение уравнений. Для начала вспомним, что такое рациональное уравнение и множество его решений, образующих график уравнения. Давайте подробнее рассмотрим график линейного уравнения и свойства линейной функции, научимся читать графики. Далее рассмотрим график квадратного уравнения и свойства квадратичной функции. Рассмотрим гиперболическую функцию, ее график и график уравнения окружности. Далее переходим к построению и изучению множества графов.

Тема: Системы уравнений

Урок: Графики уравнений

Рассматриваем рациональное уравнение вида и системы рациональных уравнений вида

Мы говорили, что каждое уравнение в этой системе имеет свой график , если конечно нет решений уравнений. Мы рассмотрели несколько графиков различных уравнений.

Теперь систематически рассмотрим каждое из известных нам уравнений, т.е. сделаем обзор по графики уравнений .

1. Линейное уравнение с двумя переменными

x, y — до первой степени; а,б,в — конкретные числа.

Пример:

График этого уравнения представляет собой прямую линию.

Действовали эквивалентными преобразованиями — оставили y на месте, все остальное перенесли на другую сторону с противоположными знаками. Исходное и полученное уравнения эквивалентны, т. е. имеют один и тот же набор решений. Мы можем построить график этого уравнения, и способ его построения следующий: находим точки пересечения с осями координат и строим по ним прямую.

В данном случае

Зная график уравнения, мы можем многое сказать о решениях исходного уравнения, а именно: если если

Эта функция возрастает, т.е. при увеличении x увеличивается y. Мы получили два частных решения, но как записать множество всех решений?

Если у точки есть абсцисса х, то ордината этой точки

Итак числа

У нас было уравнение, мы построили график, мы нашли решения. Набор всех пар — сколько их? Бесчисленное количество.

Это рациональное уравнение

Найдем y, эквивалентными преобразованиями получим

Зададим и получим квадратичную функцию, график ее известен.

Пример: Постройте рациональное уравнение.

График представляет собой параболу, ветви направлены вверх.

Найдем корни уравнения:

Схематично изобразим график ( Рис. 2).

С помощью графика мы получаем всевозможную информацию как о функции, так и о решениях рационального уравнения. Мы определили интервалы знакопостоянства, теперь найдем координаты вершины параболы.

Уравнение имеет бесконечное число решений, т.е. бесчисленное множество пар, удовлетворяющих уравнению, но все А каким может быть х? Любой!

Если мы зададим любой x, то получим точку

Решением исходного уравнения является набор пар

3. Постройте уравнение

Вам нужно выразить y. Рассмотрим два варианта.

График функции представляет собой гиперболу, функция не определена для

Функция уменьшается.

Если взять точку с абсциссой, то ее ордината будет равна

Решением исходного уравнения является множество пар

Построенная гипербола может быть смещена относительно осей координат.

Например, график функции — тоже гипербола — будет сдвинут на единицу вверх по оси Y.

4. Уравнение окружности

Это рациональное уравнение с двумя переменными. Множество решений — это точки окружности. Радиус центральной точки равен R (рис. 4).

Рассмотрим конкретные примеры.

а.

Приводим уравнение к стандартному виду уравнения окружности, для этого выбираем полный квадрат суммы:

— получили уравнение окружности с центром в .

Построим график уравнения (рис. 5).

б. Уравнение графика

Напомним, что произведение равно нулю тогда и только тогда, когда один из сомножителей равен нулю, а второй существует.

График заданного уравнения состоит из множества графиков первого и второго уравнений, т.е. двух прямых.

Построим (рис. 6).

Построим график функции Прямая проходит через точку (0;-1). Но как оно пройдет — увеличится или уменьшится? Определить это нам поможет угловой коэффициент, коэффициент при х, он отрицательный, значит функция убывающая. Найдите точку пересечения с осью быка, это точка (-1;0).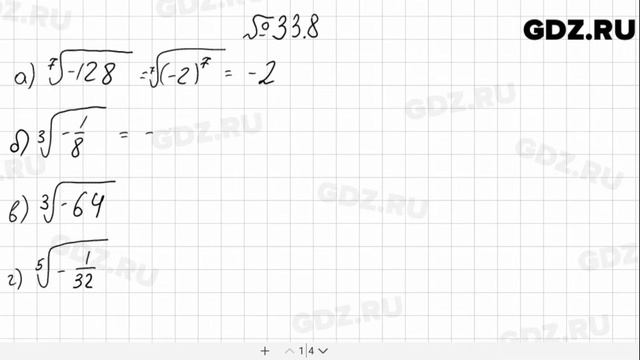

Аналогично строим график второго уравнения. Прямая проходит через точку (0; 1), но увеличивается, так как наклон положительный.

Координаты всех точек двух построенных прямых являются решением уравнения.

Итак, мы разобрали графики важнейших рациональных уравнений, они будут использованы как в графическом методе, так и при иллюстрации других методов решения систем уравнений.

1. Мордкович А.Г. и др. Алгебра 9класс: учеб. Для общеобразовательных учреждений. — 4-е изд. — М.: Мнемозина, 2002. — 192 с.: ил.

2. Мордкович А.Г. и соавт. Алгебра 9 класс: Рабочая тетрадь для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М.: Мнемозина, 2002. — 143 с.: ил.

3. Ю. Н. Макарычев, Алгебра. 9 класс: учеб. для учащихся общеобразовательных школ. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 7-е изд., испр. и доп. — М.: Мнемозина, 2008.

4. Алимов Ш.А., Колягин Ю. М., Сидоров Ю.В. Алгебра. 9 класс 16 изд. — М., 2011. — 287 с.

5. Мордкович А.Г. Алгебра. 9 класс В 14 ч. Часть 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 12-е изд., стер. — М.: 2010. — 224 с.: ил.

6. Алгебра. 9 класс В 2 часа. Часть 2. Задание для студентов общеобразовательных учреждений / А. Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина и др.; Эд. А. Г. Мордкович. — 12-е изд., испр. — М.: 2010. — 223 с.: ил.

1. Раздел College.ru по математике ().

2. Интернет-проект «Задачи» ().

3. Образовательный портал «РАЗРЕШУ УСЛОВИЯ» ().

1. Мордкович А.Г. и соавт. Алгебра 9 класс: Рабочая тетрадь для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М.: Мнемозина, 2002. — 143 с.: ил. № 95-102.

Прямоугольная система координат представляет собой пару перпендикулярных линий координат, называемых осями координат, расположенных так, что они пересекаются в начале координат.

Обозначение осей координат буквами x и y общепринято, но буквы могут быть любыми. Если используются буквы x и y, то плоскость называется xy-plane . В разных приложениях могут использоваться буквы, отличные от x и y, и, как показано на рисунках ниже, существует uv-плоскостей и ts-плоскостей .

Упорядоченная пара

Под упорядоченной парой действительных чисел мы подразумеваем два действительных числа в определенном порядке. Каждую точку P на координатной плоскости можно связать с уникальной упорядоченной парой действительных чисел, проведя через точку P две линии, одну перпендикулярную оси x, а другую перпендикулярную оси y.

Например, если взять (a,b)=(4,3), то на координатной полосе

Построить точку P(a,b) означает определить точку с координатами (a,b) на координатная плоскость. Например, на рисунке ниже нанесены различные точки.

В прямоугольной системе координат оси координат делят плоскость на четыре области, называемые квадрантами. Они нумеруются против часовой стрелки римскими цифрами, как показано на рисунке.

Определение графика

расписание уравнение с двумя переменными x и y, представляет собой множество точек на плоскости xy, координаты которых входят в множество решений этого уравнения

Пример: нарисуйте график y = x 2

Поскольку 1/ x не определено, когда x=0, мы можем построить только точки, для которых x ≠ 0

Пример: найти все пересечения с осями
(a) 3x + 2y = 6
(b) x = y 2 -2y
(c) y = 1/x

Пусть y = 0, тогда 3x = 6 или x = 2

— искомая точка пересечения оси x.

Установив, что x=0, находим, что точкой пересечения оси y является точка y=3.

Таким образом, вы можете решить уравнение (b), а решения для (c) приведены ниже не пересекается с осью y

Пусть x = 0

y = 1/0 => y также не определено, => нет пересечения с осью y

На рисунке ниже точки (x,y ), (-x,y),(x,-y) и (-x,-y) представляют углы прямоугольника.

График симметричен относительно оси x, если для каждой точки (x,y) графика точка (x,-y) также является точкой графика.

График симметричен относительно оси y, если для каждой точки графика (x,y) точка (-x,y) также принадлежит графику.

График симметричен относительно центра координат, если для каждой точки (x,y) графика точка (-x,-y) также принадлежит этому графику.

Определение:

График функции на координатной плоскости определяется как график уравнения y = f(x)

График f(x) = x + 2

Пример 2. График f(x) = |x|

График совпадает с линией y = x for x > 0 и со строкой y = -x

для x

график f(x) = -x

Объединив эти два графика, мы получим

график f(x) = |x|

Пример 3 Участок

t(x) = (x 2 — 4) / (x — 2) =

= ((x — 2)(x + 2)/(x — 2)) =

= (x + 2) x ≠ 2

Следовательно, эту функцию можно записать в виде

y = x + 2 x ≠ 2

График h(x)= x 2 — 4 или x — 2

график y = x + 2 x ≠ 2

Пример 4 График

Графики функций со смещением

Предположим, что известен график функции f(x)

Тогда можно найти графики

y = f(x) + c — график функции f(x), сдвинутый

ВВЕРХ на c значений

y = f(x) — c — график функции f(x), сдвинутый на

ВНИЗ на значения c

y = f(x + c) — график функции f(x), сдвинутый на

ВЛЕВО по значениям c

y = f(x — c) — график функции f(x), перемещенный

Справа по значениям c

Пример 5.