Задание по алгебре 8 класс миндюк: ГДЗ по Алгебре 8 класс: Макарычев и Миндюк (Решебник)

Содержание

ГДЗ по алгебре 8 класс Макарычев, Миндюк решебник с ответами к задачам

8класс

Рациональные дроби.

Рациональные дроби. (Упражнения с 1 по 262)

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 Контрольные вопросы и задания; 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 Контрольные вопросы и задания; 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 Контрольные вопросы и задания; 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 231 232 233 234 235 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262

Квадратные корни.

Квадратные корни. (Упражнения с 263 по 511)

263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 Контрольные вопросы и задания; 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 360 361 362 363 364 365 366 367 368 Контрольные вопросы и задания; 369 370 371 372 373 374 375 376 377 378 379 380 381 382 383 384 385 386 387 388 389 390 391 392 393 394 395 396 397 398 399 400 401 402 403 404 405 406 Контрольные вопросы и задания; 407 408 409 410 411 412 413 414 415 416 417 418 419 420 421 422 423 424 425 426 427 428 429 430 431 432 433 434 435 436 437 438 439 440 441 442 443 Контрольные вопросы и задания; 444 445 446 447 448 449 450 451 452 453 454 455 456 457 458 459 460 461 462 463 464 465 466 467 468 469 470 471 472 473 474 475 476 477 478 479 480 481 482 483 484 485 486 487 488 489 490 491 492 493 494 495 496 497 498 499 500 501 502 503 504 505 506 507 508 509 510 511

Квадратные уравнения.

Квадратные уравнения. (Упражнения с 512 по 723)

512 513 514 515 516 517 519 520 521 522 523 524 525 526 527 528 529 530 531 532 533 534 535 536 537 538 539 540 541 542 543 544 545 546 547 548 549 550 551 552 553 554 555 556 557 558 559 560 561 562 563 564 565 566 567 568 569 570 571 572 573 574 575 576 577 578 579 580 581 582 583 584 585 586 587 588 589 590 591 592 593 594 595 596 597 598 599 Контрольные вопросы и задания; 600 601 602 603 604 605 606 607 608 609 610 611 612 613 614 615 616 617 618 619 620 621 622 623 624 625 626 627 628 629 630 631 632 633 634 635 636 637 638 639 Контрольные вопросы и задания; 640 641 642 643 644 645 646 647 648 649 650 651 652 653 654 655 656 657 658 659 660 661 662 663 664 665 666 667 668 669 670 671 672 673 674 675 676 677 678 679 680 681 682 683 684 685 686 687 688 689 690 691 692 693 694 695 696 697 698 699 700 701 702 703 704 705 706 707 708 709 710 711 712 713 714 715 716 717 718 719 720 721 722 723

Неравенства.

Неравенства. (Упражнения с 724 по 963)

724 725 726 727 728 729 730 731 732 733 734 735 736 737 738 739 740 741 742 743 744 745 746 747 748 749 750 751 752 753 754 755 756 757 758 759 760 761 762 763 764 765 766 767 768 769 770 771 772 773 774 775 776 777 778 779 780 781 782 783 784 785 786 787 788 789 790 791 792 793 794 795 796 797 798 Контрольные вопросы и задания; 799 800 801 802 803 804 805 806 807 808 809 810 811 812 813 814 815 816 817 818 819 820 821 822 823 824 825 826 827 828 829 830 831 832 833 834 835 836 837 838 839 840 841 842 843 844 845 846 847 848 849 850 851 852 853 854 855 856 857 858 859 860 861 862 863 864 865 866 867 868 869 870 871 872 873 874 875 876 877 878 879 880 881 882 883 884 885 886 887 888 889 890 891 892 893 894 895 896 897 898 899 900 901 902 903 904 Контрольные вопросы и задания; 905 906 907 908 909 910 911 912 913 914 915 916 917 918 919 920 921 922 923 924 925 926 927 928 929 930 931 932 933 934 935 936 937 938 939 940 941 942 943 944 945 946 947 948 949 950 951 952 953 954 955 956 957 958 959 960 961 962 963

Степень с целым показателем.

Степень с целым показателем. Элементы статистики. (Упражнения с 964 по 1078)

964 965 966 967 968 969 970 971 972 973 974 975 976 977 978 979 980 981 982 983 984 985 986 987 988 989 990 991 992 993 994 995 996 997 998 999 1000 1001 1002 1003 1004 1005 1006 1007 1008 1009 1010 1011 1012 1013 1014 1015 1016 1017 1018 1019 1020 1021 1022 1023 1024 1025 1026 1027 Контрольные вопросы и задания; 1028 1029 1030 1031 1032 1033 1034 1035 1036 1037 1038 1039 1040 1041 1042 1043 1044 1045 1046 1047 1048 1049 1050 1051 1052 1053 1054 1055 1056 1057 1058 1059 1060 1061 Контрольные вопросы и задания; 1062 1063 1064 1065 1066 1067 1068 1069 1070 1071 1072 1073 1074 1075 1076 1077 1078

Дополнительные упражнения.

Дополнительные упражнения. (Упражнения с 1079 по 1105)

1079 1080 1081 1082 1083 1084 1085 1086 1087 1088 1089 1090 1091 1092 1093 1094 1095 1096 1097 1098 1099 1100 1101 1102 1103 1104 1105

Задачи повышенной трудности.

Задачи повышенной трудности. (Упражнения с 1106 по 1153)

1106 1107 1108 1109 1110 1111 1112 1113 1114 1115 1116 1117 1118 1119 1120 1121 1122 1123 1124 1125 1126 1127 1128 1129 1130 1131 1132 1133 1134 1135 1136 1137 1138 1139 1140 1141 1142 1143 1144 1145 1146 1147 1148 1149 1150 1151 1152 1153

ГДЗ по Алгебре 8 класс Макарычев, Миндюк Учебник

Авторы: Макарычев Ю. Н., Миндюк Н. Г., Нешков К. И., Суворова С. Б.

Издательство: Просвещение

Тип: Учебник

ГДЗ по Алгебре 8 класс Макарычев – это пособие, которое создано в помощь ученикам в изучении такого нелегкого предмета. Математика всегда вызывает наибольшие трудности в учебном году, ведь не каждый ученик обладает подходящим складом ума, и не каждый учитель способен хорошо объяснить трудную тему.

Решебник по алгебре 8 класс содержит в себе материал, который поможет ученику восполнить пробелы в изучении данного предмета, подготовиться к контрольным работам и ОГЭ по учебнику 8 класс Миндюк. Также восьмиклассник всегда сможет проверить уже сделанные домашние задания и исправить допущенные ошибки при их выполнении.

Номера упражнений

1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192939495969798991001011021031041051061071081091101111121131141151161171181191201211221231241251261271281291301311321331341351361371381391401411421431441451461471481491501511521531541551561571581591601611621631641651661671681691701711721731741751761771781791801811821831841851861871881891901911921931941951961971981992002012022032042052062072082092102112122132142152162172182192202212222232242252262272282292302312322332342352362372382392402412422432442452462472482492502512522532542552562572582592602612622632642652662672682692702712722732742752762772782792802812822832842852862872882892902912922932942952962972982993003013023033043053063073083093103113123133143153163173183193203213223233243253263273283293303313323333343353363373383393403413423433443453463473483493503513523533543553563573583593603613623633643653663673683693703713723733743753763773783793803813823833843853863873883893903913923933943953963973983994004014024034044054064074084094104114124134144154164174184194204214224234244254264274284294304314324334344354364374384394404414424434444454464474484494504514524534544554564574584594604614624634644654664674684694704714724734744754764774784794804814824834844854864874884894904914924934944954964974984995005015025035045055065075085095105115125135145155165175185195205215225235245255265275285295305315325335345355365375385395405415425435445455465475485495505515525535545555565575585595605615625635645655665675685695705715725735745755765775785795805815825835845855865875885895905915925935945955965975985996006016026036046056066076086096106116126136146156166176186196206216226236246256266276286296306316326336346356366376386396406416426436446456466476486496506516526536546556566576586596606616626636646656666676686696706716726736746756766776786796806816826836846856866876886896906916926936946956966976986997007017027037047057067077087097107117127137147157167177187197207217227237247257267277287297307317327337347357367377387397407417427437447457467477487497507517527537547557567577587597607617627637647657667677687697707717727737747757767777787797807817827837847857867877887897907917927937947957967977987998008018028038048058068078088098108118128138148158168178188198208218228238248258268278288298308318328338348358368378388398408418428438448458468478488498508518528538548558568578588598608618628638648658668678688698708718728738748758768778788798808818828838848858868878888898908918928938948958968978988999009019029039049059069079089099109119129139149159169179189199209219229239249259269279289299309319329339349359369379389399409419429439449459469479489499509519529539549559569579589599609619629639649659669679689699709719729739749759769779789799809819829839849859869879889899909919929939949959969979989991000100110021003100410051006100710081009101010111012101310141015101610171018101910201021102210231024102510261027102810291030103110321033103410351036103710381039104010411042104310441045104610471048104910501051105210531054105510561057105810591060106110621063106410651066106710681069107010711072107310741075107610771078107910801081108210831084108510861087108810891090109110921093109410951096109710981099110011011102110311041105110611071108110911101111111211131114111511161117111811191120112111221123112411251126112711281129113011311132113311341135113611371138113911401141114211431144114511461147114811491150115111521153

Контрольные вопросы и задания

§1§2§3§4§5§6§7§8§9§10§11§12§13

Решебник по алгебре 8 класс Макарычева – ответы к учебнику

ГДЗ к обновленному учебнику был подготовлен для помощи школьникам, которые найдут ответы алгебра 8 класс, просто выбрав нужный номер упражнения, что позволит легко сориентироваться.

С помощью учебника 8 класс Миндюк учащиеся познакомятся с рациональными выражениями, иррациональными числами, арифметическими квадратными корнями, степени с отрицательным показателем, научатся решать квадратные и дробно-рациональные уравнения, линейные неравенства и их системы, строить графики функций и выполнять их преобразования и многое другое. Освоить все темы нереально, каждый второй школьник обращается за помощью к репетиторам, услуги которых сейчас стоят дорого.

В учебнике присутствует больше 1000 заданий, которые предстоит решать школьникам на протяжении всего учебного года. Ученики и так испытывают большую нагрузку по всем предметам. Ничего плохого не случится, если ребенок несколько раз в году решит отдохнуть и просто спишет домашнее задание. Отдыхать и разгружать мозг тоже очень важно, особенно в подростковом возрасте!

В случае, если вы не успели подготовиться к урокам по разным причинам, решебник подойдет для быстрого списывания перед уроком алгебры. Можно пользоваться ГДЗ по математике даже на уроке, ведь все ответы доступны и в мобильной версии сайта. Но не злоупотребляйте этим, ведь знания также важны, как и хорошие отметки!

Знания математики помогут при изучении геометрии, физики, химии и других школьных предметов. А особенно станут полезны во взрослой жизни и при поступлении в высшие учебные заведения. Поэтому важно уже в 8 классе разобраться с существующими проблемами, а не сталкиваться с трудностями дальше.

Особенно полезно ГДЗ для выполнения задач на смекалку. Проблемные, исследовательские задачи не по силам решать всем, но с помощью решебника можно разобраться с ними и не получить плохую отметку от придирчивого учителя.

В этом учебном году детям предстоит узнать много нового, полезного и интересно, приобрести важные навыки. Все это необходимо для успешного обучения в школе, для сдачи экзамена по алгебре в 9 классе. Те операции, которым вы научитесь на уроках алгебры, будут помогать успешно изучать и другие учебные дисциплины.

Надеемся, что работа с пособием будет для вас интересной и полезной, позволит увидеть алгебру не только как учебный школьный предмет, но и как средство самовоспитания, развития своих способностей, поможет рассматривать математику как часть общечеловеческой культуры.

Это самый свежий сборник с новыми заданиями Макарычев, Миндюк, который составлялся квалифицированными специалистами. Ответы по алгебре свободно доступны для любого желающего. Можно смотреть решения с компьютера, планшета или смартфона в любое время.

Если вам помог наш сайт, то обязательно оставляйте комментарии. Возможно ваши замечания, будут полезны другим школьникам. А если вы нашли ошибку в наших решениях, что маловероятно, то мы обязательно ее исправим!

Алгебра является одним из основных предметов школьного курса, во время прохождения которого происходит усвоение информации, которая обязательно пригодится при сдаче основного государственного экзамена. Это очень важные знания, которые должны стать первоначальной базой, для наложения материала из остальных наук.

Значение курса алгебры

Взаимосвязь предметов делает значение математических вычислений достаточно существенной. Без математики невозможно стать успешным в усвоении остального школьного курса. ГДЗ алгебра Макарычев поможет разобраться с представляемыми данными и устранить пробелы в знаниях, которые могут появиться в процессе систематического недопонимания основных моментов. Можно выделить несколько пунктов, которые наглядно показывают значимость пособия домашняя работа по алгебре 8 класс Макарычев:

подробное описание каждого этапа решения задания;
наличие необходимых пояснений, которые помогут учащемуся самостоятельно разобраться с возникшими вопросами;
четкая систематизация материала;
возможность предварительной подготовки к будущим занятиям.

Работая с домашняя работа по алгебре.8 класс Макарычев у ребенка появляется возможность усвоить знания в максимальной степени, которую он не сможет достичь в процессе школьного урока.

Структура учебника

Для того, чтобы учащийся смог легко разобраться с материалом, который размещен в учебнике, он составлен специальным образом:

все задания одинаковой тематики размещены в одном разделе;
задания располагаются в зависимости от сложности по принципу от простого к сложному;
имеются дополнительные материалы для более четкого понимания темы.

С помощью домашняя работа по алгебре Макарычев 8 класс можно самостоятельно подготовится к экзамену, так как в любое время можно обратиться к материалу, который уже был давно пройден и с легкостью актуализировать знания. Это существенно сэкономит средства, которые могли быть потрачены на репетитора.

Обучение алгебре очень важно не пропустить даже самых незначительных данных. Все темы гдз алгебра Макарычев являются очень важными и дают существенную помощь в получении образования в целом. Не зря говорят, что математика является царицей наук. Действительно, на ней базируются все остальные школьные предметы, в которых необходимы точные вычисления: химия, физика, биология. При недостаточном уровне знаний просто невозможно успешно освоить школьный курс обучения на высоком уровне.

ГДЗ Алгебра 8 класс Макарычев, Миндюк, Нешков

Алгебра 8 класс
Тип пособия: Учебник
Авторы: Макарычев, Миндюк, Нешков
Издательство: «Просвещение»

Контрольные вопросы и задания

§1§2§3§4§5§6§7§8§9§10§11§12§13

Задания из учебника

Контрольные вопросы и задания: §1

Условие

Решебник №1

Решебник №2

Особенности изучения алгебры

Алгебра — точная наука, которая не терпит никаких отклонений или недомолвок.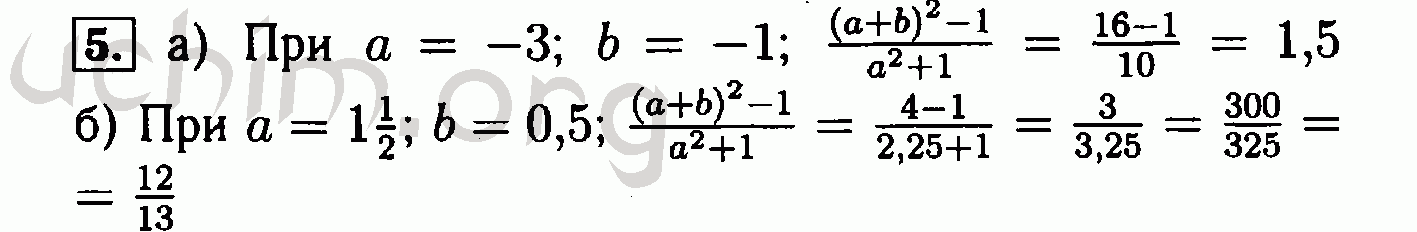 Еще ученые древности восхищались строгостью математических вычислений, которые можно при помощи нее построить. С тех пор практически ничего не изменилось. Конечно, были сделаны новые открытия, созданы формулы, но сама структура этого предмета осталась прежней. Причем довольно давно замечено, что любовь к этой дисциплине либо возникает сразу же, либо не появляется вовсе. Поэтому школьники в наши дни делятся на два типа — одни понимают и легко ориентируются в алгебраических нюансах, другие же со скрипом осваивают то, что преподают в школе.

В восьмом классе ученикам предстоит узнать и изучить еще более трудные темы:

рациональные дроби;
квадратные корни и уравнения;
неравенства;
степени с целым показателем;

элементы статистики.

Каждый из этих разделов включает в себя множество параграфов, которые помогают их полноценно раскрыть. Поэтому любое отвлечение или пропуск занятий грозят перерасти в серьезные пробелы в знаниях. Но это вовсе не означает что нужно заранее смириться с неудачей и пассивно плыть по течению.

Конечно, если у ребенка не наблюдается математических способностей, то навряд ли он станет отличником по данному предмету. Тем не менее можно все же поддерживать успеваемость на достаточно высоком уровне. Но для этого надо, чтобы подросток понимал что именно, и зачем он делает. В этом может помочь решебник к пособию «Алгебра 8 класс Учебник Макарычев, Миндюк, Нешков (Просвещение)», где очень лаконично и доступно изложена вся необходимая информация по курсу этого года.

Состав решебника

В сборнике содержится более 1150 упражнений, которые рассчитаны на тренировку соответствующих навыков у учеников. Обширные ответы по каждому

номеру помогут вникнуть в принцип выполнения заданий и понять как применяются полученные знания на практике. На нашем сайте представлено «ГДЗ по алгебре 8 класс Макарычев», которыми можно воспользоваться онлайн.

Это тем более удобно, что современные ученики привыкли искать большую часть информации в интернете, а не в библиотеке. Практически у каждого сейчас есть телефон или планшет, с помощью которого легко открыть решебник. Удобная навигация мгновенно отправит пользователя к нужному номеру.

Кроме того, на страницах данного издания, подростки найдут:

развернутые ответы на все задания;
подробные варианты решений;
дополнительные комментарии по особо сложным упражнениям.

В решебнике школьники найдут того помощника, которого им зачастую не хватает при выполнении домашних заданий. Родителям больше не придется беспокоиться о том, где найти для любимого чада хорошего репетитора.

На что рассчитан ГДЗ

В случае когда тема осталась недопонятой, очень сложно решить необходимую задачу. Перечитывая же самостоятельно теорию далеко не все восьмиклассники поймут для чего и на что рассчитаны формулы и уравнения. Поэтому многие пользуются моментом и начинают списывать готовое д/з у своих одноклассников, либо из ГДЗ. Конечно, это может выручить раз, два, на крайний случай три. Но ввиду того, что сейчас в школах проверочные работы проводятся чуть ли не после каждой темы, то можно «засыпаться» при решении задач, ведь учащиеся просто не будут знать сам принцип действий.

Решебник в первую очередь является средством самоконтроля, который позволяет определять уровень своих знаний и корректировать его в зависимости от ситуации. В качестве шпаргалки он не принесет успехов в учебе и может лишь усугубить ситуацию, потому что чем дольше школьники списывают, тем больше реальных познаний и навыков они упускают.

Поэтому стоит пересилить себя и начать использовать решебник по назначению — как методическое пособие в учебе. Только в этом случае можно рассчитывать на полноценные знания по такому сложному предмету, как алгебра. Конечно, по началу школьникам может показаться трудным просматривать и тщательно изучать информацию. Но со временем это войдет в привычку и будет отнимать всего несколько минут.

Для чего предназначен решебник

Решебник к пособию «Алгебра 8 класс Учебник Макарычев» поможет:

Проверить д/з, оценить его правильность.
Легко выявить ошибки, исправить их.
Потренироваться в решении аналогичных примеров, чтобы закрепить результат.
Хорошо запомнить алгоритмы решений.

Можно быстро и без проблем повторить необходимые темы перед контрольной, чтобы освежить свои знания и правильно все написать. Кроме того, ГДЗ позволяет самостоятельно восполнить те пробелы, которые образовались из-за невнимательности или в силу внешних факторов (например, пропуск занятий из-за болезни).

Стоит ли использовать ГДЗ

Применять решебник или нет — этот выбор должен сделать каждый самостоятельно. Но стоит учитывать и то, что многие школьники, которые уже по нему занимаются, не испытывают проблем с учебой, получают только положительные оценки и могут спокойно ответить на любой неожиданный вопрос учителя. ГДЗ по алгебре 8 класс Учебник Макарычев, Миндюк, Нешков (Просвещение) составлен опытными преподавателями, которые не один год обучали детей алгебре. Именно поэтому все ответы и решения представлены в предельно доступном виде. Даже сильно отставшие от программы учащиеся без труда разберутся во всех хитросплетениях этой науки.

Не стоит надеяться на то, что знания придут сами по себе. Если ребята хотят преуспевать в этой области, то придется приложить усилия. А это значит, что все заданные упражнения они должны выполнять самостоятельно, и только после этого заглядывать на страницы сборника. Если все сделано правильно, то значит тема усвоена хорошо. А вот при возникновении ошибок, стоит выяснить по какой именно причине те возникли, тщательно проработать каждый момент и закрепить результат путем выполнения нескольких аналогичных номеров. Не стоит игнорировать эти аспекты, ведь совсем скоро предстоит сдавать ОГЭ, где будут очень важны полученные ранее знания и навыки.

ГДЗ решебник по алгебре 8 класс Макарычев, Миндюк, Нешков Учебник Просвещение

Алгебра 8 класс

Тип пособия: Учебник

Авторы: Макарычев, Миндюк, Нешков

Издательство: «Просвещение»

Науку, которая изучает величины и действия над ними называют алгеброй. Это один из древнейших разделов математики. Она очень важна как для развития общества, так и для отдельно взятого индивидуума. Её знания необходимы практически во всех сферах деятельности. Экономика, строительство, наука и многое другое, где алгебраические знания являются основой. В рамках школьной программы математику начинают изучать с первого класса и на протяжении всего процесса обучения совершенствуют свои навыки и умения вплоть до выпуска.

Чему научат уроки алгебры

Учебный курс восьмого класса направлен на изучение рациональных дробей, числовых неравенств, а также ребята познакомятся со свойствами квадратного корня и действиями над ним. Осваивая предмет они научатся:

Правильно использовать алгебраические термины и понятия.
При помощи уравнений решать задачи.
Пользоваться изученными формулами.
Строить графики квадратичной функции.
Применять на практике изученный материал.

Основная цель дисциплины научить школьника логически мыслить, рассуждать, делать выводы, анализировать и находить закономерности.

Неоценимая помощь решебника

Алгебра – это один из сложных предметов. Многие ученики не совсем успешно усваивают учебный материал. Допускаемые ошибки, непонимание, пробелы в знаниях, все это негативно отражается на оценках и успеваемости. Хорошим помощником в такой ситуации станет «ГДЗ по Алгебре 8 класс Учебник Макарычев, Миндюк, Нешков (Просвещение)». Сборник содержит правильные и подробно расписанные онлайн-ответы. Они представлены абсолютно ко всем номерам упражнений учебника. С их помощью ученик сможет не только проверить правильное выполнение домашней работы, но и:

понять ход решения задач и уравнений;
разобраться со сложной темой и понять суть вопроса;
сэкономить своё время и силы на поиск необходимой информации;
заранее подготовиться к предстоящему уроку.

Решебник даст возможность подтянуть знания и оценки в самые кратчайшие сроки. Регулярное использование ГДЗ только положительным образом отразится на успеваемости, к тому же школьник всегда будет подготовлен к любой самостоятельной работе.

Краткая характеристика ученика

Хорошим пособием для получения качественных знаний по предмету является учебник по алгебре за 8 класс авторы Макарычев, Миндюк. Материал пособия расписан понятным и доступным языком, даны подробные инструкции с примерами к особо сложным заданиям. Определения и формулы выделены отдельным шрифтом, а наличие дополнительной информации способствует лучшему усвоению дисциплины.

Задания из учебника

Контрольные вопросы и задания

§1§2§3§4§5§6§7§8§9§10§11§12§13

Задания из учебника: 1

Видеорешение

ГДЗ по алгебре 8 класс Макарычев, Миндюк (Учебник)

Решебник по алгебре 8 класс Макарычев – то, в чем нуждается каждый школьник, который испытывает трудности в учебе. Это самый лёгкий способ выучить уроки. Так как математика — один из сложных учебных предметов, не всем детям даётся легко. К её выполнению нужно подойти со всей серьёзностью. Школьная программа отличается своей повышенной сложностью, так и нагрузка по д/з часто превышает силы учащихся. Школьники не могут сосредоточиться на одном предмете, так как присутствуют ещё дисциплины. К выполнению уроков по точной науке, нужно подойти со всей серьёзностью, что бы в дальнейшем не возникало недопониманий и неправильного восприятия материала.

Какую помощь может оказать гдз по алгебре восьмой класс Макарычев учебник

В пособие содержится тридцать пять глав, которые поделены на тематические параграфы. Все номера содержат полные ответы, поэтому можно в один момент проверить правильность выполнения домашней работы. Помимо этого, сборник по алгебре за восьмой класс, авторы: Макарычев Ю. Н., Миндюк Н. Г., Нешков К. И., Суворова С. Б. посодействует:

оперативно и комфортно найти информацию с помощью табличного указателя;
научиться самостоятельности, так как ученики могут сами выполнить упражнения и проверить себя;
быстро найти ответ, так как ГДЗ находятся в онлайн-доступе.

Здесь можно найти ответы на то, что такое одночлен и многочлен. Увидишь, как правильно изображаются графики функций. Узнаешь, когда применяются формулы сокращенного умножения. Научишься выполнять действия с квадратными корнями и решать квадратные уравнения. Благодаря этому решебнику время, отведенное на уроки, во много раз сокращается. Имея это пособие, возрастает вера в собственные знания. Оно имеет, наряду с краткими ответами, более расширенное пояснение к наиболее сложным заданиям. Поэтому, если вдумчиво переписывать, обязательно разберешься и запомнишь, то, что тебе было не понятно на уроке. Если есть под рукой этот умк, то это гарантия верного выполнения дом. задания и хорошая подготовка к проверочным работам.

Ответы из решебника

Упражнения

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 360 361 362 363 364 365 366 367 368 369 370 371 372 373 374 375 376 377 378 379 380 381 382 383 384 385 386 387 388 389 390 391 392 393 394 395 396 397 398 399 400 401 402 403 404 405 406 407 408 409 410 411 412 413 414 415 416 417 418 419 420 421 422 423 424 425 426 427 428 429 430 431 432 433 434 435 436 437 438 439 440 441 442 443 444 445 446 447 448 449 450 451 452 453 454 455 456 457 458 459 460 461 462 463 464 465 466 467 468 469 470 471 472 473 474 475 476 477 478 479 480 481 482 483 484 485 486 487 488 489 490 491 492 493 494 495 496 497 498 499 500 501 502 503 504 505 506 507 508 509 510 511 512 513 514 515 516 517 518 519 520 521 522 523 524 525 526 527 528 529 530 531 532 533 534 535 536 537 538 539 540 541 542 543 544 545 546 547 548 549 550 551 552 553 554 555 556 557 558 559 560 561 562 563 564 565 566 567 568 569 570 571 572 573 574 575 576 577 578 579 580 581 582 583 584 585 586 587 588 589 590 591 592 593 594 595 596 597 598 599 600 601 602 603 604 605 606 607 608 609 610 611 612 613 614 615 616 617 618 619 620 621 622 623 624 625 626 627 628 629 630 631 632 633 634 635 636 637 638 639 640 641 642 643 644 645 646 647 648 649 650 651 652 653 654 655 656 657 658 659 660 661 662 663 664 665 666 667 668 669 670 671 672 673 674 675 676 677 678 679 680 681 682 683 684 685 686 687 688 689 690 691 692 693 694 695 696 697 698 699 700 701 702 703 704 705 706 707 708 709 710 711 712 713 714 715 716 717 718 719 720 721 722 723 724 725 726 727 728 729 730 731 732 733 734 735 736 737 738 739 740 741 742 743 744 745 746 747 748 749 750 751 752 753 754 755 756 757 758 759 760 761 762 763 764 765 766 767 768 769 770 771 772 773 774 775 776 777 778 779 780 781 782 783 784 785 786 787 788 789 790 791 792 793 794 795 796 797 798 799 800 801 802 803 804 805 806 807 808 809 810 811 812 813 814 815 816 817 818 819 820 821 822 823 824 825 826 827 828 829 830 831 832 833 834 835 836 837 838 839 840 841 842 843 844 845 846 847 848 849 850 851 852 853 854 855 856 857 858 859 860 861 862 863 864 865 866 867 868 869 870 871 872 873 874 875 876 877 878 879 880 881 882 883 884 885 886 887 888 889 890 891 892 893 894 895 896 897 898 899 900 901 902 903 904 905 906 907 908 909 910 911 912 913 914 915 916 917 918 919 920 921 922 923 924 925 926 927 928 929 930 931 932 933 934 935 936 937 938 939 940 941 942 943 944 945 946 947 948 949 950 951 952 953 954 955 956 957 958 959 960 961 962 963 964 965 966 967 968 969 970 971 972 973 974 975 976 977 978 979 980 981 982 983 984 985 986 987 988 989 990 991 992 993 994 995 996 997 998 999 1000 1001 1002 1003 1004 1005 1006 1007 1008 1009 1010 1011 1012 1013 1014 1015 1016 1017 1018 1019 1020 1021 1022 1023 1024 1025 1026 1027 1028 1029 1030 1031 1032 1033 1034 1035 1036 1037 1038 1039 1040 1041 1042 1043 1044 1045 1046 1047 1048 1049 1050 1051 1052 1053 1054 1055 1056 1057 1058 1059 1060 1061 1062 1063 1064 1065 1066 1067 1068 1069 1070 1071 1072 1073 1074 1075 1076 1077 1078 1079 1080 1081 1082 1083 1084 1085 1086 1087 1088 1089 1090 1091 1092 1093 1094 1095 1096 1097 1098 1099 1100 1101 1102 1103 1104 1105 1106 1107 1108 1109 1110 1111 1112 1113 1114 1115 1116 1117 1118 1119 1120 1121 1122 1123 1124 1125 1126 1127 1128 1129 1130 1131 1132 1133 1134 1135 1136 1137 1138 1139 1140 1141 1142 1143 1144 1145 1146 1147 1148 1149 1150 1151 1152 1153

Контрольные работы

1 2 3 4 5 6 7 8 9 10 11 12 13

В изучении наиболее тяжелой является царица наук. Вскоре всем обучающимся предстоит сдавать ОГЭ и ЕГЭ. Математика входит в обязательный предмет, который необходимо сдавать. Не у всех учеников математический склад ума, для некоторых она вызывает немалый страх. Приближается сложный период, когда на горизонте замаячат первые серьезные экзамены, и каждый уважающий себя школьник, обязан подготовиться к ним основательно. Сделать это эффективно посодействуют специальные доп. данные, которые любезно предоставят образовательные учреждения. И не думайте, что на восьмой ступени образования начинать готовиться еще рано. Кто-то практикует прокрастинацию и оставляет все на последний год, однако это огромная ошибка, которая чревата неприятностями. Ведь девятиклассники должны еще подготовить выступление, наряд и то, как они будут праздновать выпускной. Для некоторых эти 9 месяцев последние в школьных стенах, они обязаны будут определиться с будущим местом обучения, выбрать колледж, техникум, а значит, профессию. Такое решение принять очень трудно, так как оно повлияет на всю жизнь и карьеру. В связи с этим заниматься и тренироваться по самым главным и основным дисциплинам. А с этим поможет представленный далее онлайн-решебник.

Какую пользу можно извлечь из справочника с ответами по алгебре 8 класс Макарычев

Но можно ли ученику схитрить таким образом, чтобы не пришлось сутками смотреть в оригинальный печатный учебник или искать в интернете или куче других книг достоверную информацию? Ответ на такой вопрос очень прост: вам достаточно только открыть сборник, после чего можно уверенно заявлять о том, что никакие поиски правильных номеров, а также непосредственно сами решения задачек вам больше не страшны. В действительности школьное издание — это хорошее средство для углублений своих знаний, но иногда приходит время и для того, чтобы попросту использовать решебник для максимального ускорения выполнения упр-ий. Список многочисленных плюсов:

постоянный онлайн-доступ на компьютеры, смартфоны, планшеты и другие устройства;
дополнительные исчерпывающие и детальные пояснения, которые составляли профессиональные методисты с большим опытом;
справочные материалы;
круглосуточная доступность благодаря онлайн-режиму.

Содержание гдз по алгебре для 8 класса, авторы: Макарычев Ю., Миндюк Г., Нешков К. И., Суворова С. Б.

Учебно-методический комплекс включает параграфы и главы, рекомендованные к освоению на конкретном этапе:

Различные действия с рациональными дробями.
Квадратные корни, уравнения.
Числовые неравенства, системы.
Статистика, комбинаторика, вероятность.

по алгебре 8 класс Макарычев, Миндюк | ответы на 5

Решебник алгебра 8 кл

Чтобы успеть своевременно и качественно подготовиться к экзамену, который предстоит в следующем, выпускном классе, многие восьмиклассники приступают к самостоятельному изучению предмета. В этом им сможет помочь по алгебре за 8 класс Макарычев — в том случае, если грамотно и эффективно организовать занятия. Желательно запланировать на них не менее часа в день, занимаясь ежедневно. И стараться не допускать длительных, превышающих 10-14 дней, пропусков в подготовке. В противном случае это может привести к забыванию значительной части изученной информации. А последующее форсированное наверстывание материала вызовет усталость и спад интереса к изучаемому предмету.

Кто и почему использует сборники с ответами в процессе обучения?

Среди тех, кто часто или даже на постоянной основе применяет Правильные решения по алгебре 8 класс Макарычева — такие категории пользователей:

Явные плюсы применения онлайн справочника по алгебре за 8 класс (автор Макарычев)

Хотя и сегодня не все согласны с тем, что еуроки — полезный и нужный ресурс, его сторонники обращают внимание на такие плюсы этой информации:

Изучая сборники готовых ответов, разрабатывая и внедряя собственные схемы работы с ним, восьмиклассники учатся планировать, ценить свое время, оперативно находить и применять информацию. Это пригодится подросткам и в настоящем, и в будущем, не только в школе, но и впоследствии, после ее окончания.

В этом им сможет помочь по алгебре за 8 класс Макарычев — в том случае, если грамотно и эффективно организовать занятия.

Www. euroki. org

08.07.2018 9:39:32

2018-07-08 09:39:32

Источники:

Https://www. euroki. org/gdz/ru/algebra/8_klass/reshebnik-po-algebre-8-klass-makarychev-fgos-931

по алгебре 8 класс Макарычев, Миндюк учебник Решебник » /> » /> .keyword { color: red; }

Решебник алгебра 8 кл

Если ваш ребенок получает двойки и тройки по контрольным работам и тестам, если каждое упражнение, заданное на дом превращает жизнь семьи в тяжелое испытание, настало время признаться – школьнику нужна помощь в виде онлайн-решебника по алгебре авторов: Макарычев, Миндюк, Нешков, Суворова. Такая ситуация знакома многим семьям, и далеко не всегда виновником является сам ученик. Большинство детей от природы любознательны и умны, однако имеют разный темп усвоения материала, виды памяти и способность концентрироваться.

Препятствиями к хорошему усвоению рабочей программы по ФГОС могут стать:

слишком большое количество учеников в коллективе; неопытность педагога, его предвзятость или неумение донести тему; отсутствие дисциплины на занятиях; ограниченность времени на разбор теоретического материала.

Однако далеко не у всех семей есть средства на репетиторов или возможность сменить преподавателя, перейдя в другой коллектив или школу. Не все родители способны помочь своим детям с решением заданий до правильного ответа, так как сами давно забыли школьную программу, не имеют педагогических наклонностей, терпения или времени. Что же делать?

Лучший помощник – это для 8 класс Макарычева, Миндюка, Нешкова

Объясните школьнику, как необходимо пользоваться сборником готовых домашних заданий:

Сначала следует самостоятельно решить задачку и сверить итог с верным ответом в конце учебника. При несовпадении результата повторите теоретический материал, изученный в ходе классной работы. Затем найдите номер упражнения в онлайн-решебнике и посмотрите правильный алгоритм выполнения, найдите свою ошибку. Закройте пособие и снова решите упражнение сами, опираясь на увиденный пример.

Поступая так, ребенок получит ощутимую пользу, усвоит верные алгоритмы выполнения задач, почувствует уверенность в собственных силах, а значит, вскоре сможет обходиться без использования сборников , написанного Макарычевым.

Задания

Авторы Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков и С. Б. Суворова разработали учебно-методический комплекс для восьмиклассников по алгебре. Подготовкой к печати и распространением учебных пособия занимается издательство «Просвещение» с 2015 года. Актуальной на данный момент является версия 2019 года. Она и представлена на страницах нашего приложения.

Как Макарычева и Миндюка упрощают подготовку к урокам алгебры?

Чтобы успевать по данной дисциплине и в дневнике приносить домой исключительно отличные и хорошие отметки, необходимо приучить себя тратить какое-то количество времени на самообразование. Недостаточно усердно работать только на уроке, еще нужно уделять время выполнению упражнений, которые задаются учителем на дом. Тренировка практических умений и навыков лежит в основе приобретения надежного образования, которое будет служить гражданину верой и правдой на протяжении всей его сознательной жизни. В зависимости от врожденных способностей к точным наукам у разных школьников прогресс в этой области требует различных временных инвестиций.

Дополнительную тренировку, а также соответствующую методическую поддержку может обеспечить онлайн-решебник по алгебре авторами: Макарычев, Миндюк, Нешков, Суворова. Он имеет целый ряд преимуществ перед альтернативными пособиями, например:

можно также использовать при индивидуальных занятиях с репетитором или при подготовке домашней работы под контролем взрослого члена семьи.

Рабочая программа по алгебре за 8 класс с решебником Макарычева

Качественное образование в школе обеспечивает высокие баллы на выпускном экзамене и отсутствие проблем при дальнейшем обучении, где бы последнее ни происходило. Следующие параграфы являются наиболее важными для восьмиклассника:

Благодаря качественно подобранным номерам и примерам, решебник сослужит отличную пользу при подготовке к контрольным, самостоятельным, диагностическим работам, а также тестам. Сборник отлично подходит для упорядоченного повторения ранее пройденного материала, например, при тренировке сдачи ОГЭ.

Задания

Содержание задач полностью соответствуют федеральному государственному стандарту образования ФГОС, на основании которого разрабатываются и обновляются рабочие программы для средних школ;.

Gdz. ru

04.03.2018 15:39:40

2018-03-04 15:39:40

Источники:

Https://gdz. ru/class-8/algebra/makarychev-8/

по Алгебре 8 класс: Макарычев. Подробный решебник учебника. » /> » /> .keyword { color: red; }

Решебник алгебра 8 кл

Издание: Алгебра. 8 класс. учебник для общеобразовательных организаций Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова — Просвещение, 2013-2022г.

Готовое домашнее задание () по алгебре для 8 класса от Макарычева Ю. Н. с алгоритмом решения примеров и задач, различными вариантами ответов, пояснениями к упражнениям повышенного уровня сложности. Решебник актуален для учебников 2013-2022 года.

Поиск в решебнике

Структура решебника

Номера заданий

Готовые домашние задания для 8 класса по алгебре Макарычева

Пособие с пояснениями от Ответкина – это не просто краткие материалы для списывания, но надежный помощник восьмиклассника. С его помощью школьник сможет разобраться с трудными темами, понять алгоритм выполнения той или иной задачи, проверить правильность собственных ответов. Ученику не придется краснеть от вопроса учителя: «Каким образом ты получил эти цифры?». Он сможет показать подробное решение примера, объяснить, почему использовал тот или иной метод, опираясь на материалы решебника.

Наш сайт пользуется спросом не только у школьников, но и у их родителей. Многие из них уже забыли учебную программу по алгебре за 8 класс, но хотят проверять правильность домашнего задания своего ребенка.

В чем преимущества от Ответкина?

Проверенные и актуальные данные

Подробные комментарии.

Экономия средств

Только конкретная информация.

Удобство пользования сайтом

Главная задача Ответкина – приучить школьников к самостоятельности, дать им возможность понять предмет, поднять свою успеваемость на бесплатной основе.

Уникальные подробные решения с пояснениями Ответкина

Школьную программу по алгебре за 8 класс нельзя назвать легкой. Знакомство с иррациональными числами, преобразованием дробей, статистикой, способами решения квадратных и дробных рациональных уравнений – часто заводят восьмиклассников в тупик. Стоит ученику пропустить несколько уроков, быть невнимательным при изучении новой темы и он уже не сможет без чьей-либо помощи нагнать материал.

Перед родителями встает проблема: где искать репетиторов, как выбрать хорошего преподавателя, который точно поможет ребенку? Требуется время, чтобы далеко ездить к учителю и деньги на оплату дополнительных занятий. Но Ответкин предлагает лучшую альтернативу дорогим курсам и репетиторам. С помощью нашего сайта школьники смогут быстро исправить свои оценки, самостоятельно разобраться в сложных темах.

Почему родители предпочитают Ответкина вместо репетиторов?

Простое и быстрое решение проблемы. Отпадают сложности с поиском учителя, который действительно знает свой предмет и умеет объяснять материал в доступной форме. Не нужно тратить время на дорогу туда и обратно, расходовать деньги. Родительский контроль. Репетитор встречается с учеником максимум 2-3 раза в неделю. Но родители, получив доступ к готовым домашним заданиям, могут сами контролировать своего ребенка, проверять его тетрадь каждый день. Развитие самостоятельности. При правильном использовании решебника школьник приучает себя к самостоятельности: проверяет правильность выполнения домашнего задания, проводит работу над ошибками, разбирается с непонятными моментами. Круглосуточный доступК . С окончанием занятий на помощь учителя рассчитывать не приходится, но наш сайт выручает учащихся в любое время суток. Чтобы узнать правильное решение даже не обязательно находиться за компьютером, зайти на Ответкин можно с любого смартфона.

Наши решебники с алгоритмом выполнения заданий не имеют аналогов. В сравнении с ними даже видео ответы оставляют желать лучшего. Как правило, спикер монотонно говорит около 10 минут, по сути, пересказывая краткое решение. Но он не объясняет важные нюансы в упражнении, не погружается в теорию, которая помогла бы лучше усвоить новую тему.

Как пользоваться сайтом и открыть ответ с комментарием?

Устройство нашего сайта простое и понятное. Им с легкостью могут пользоваться как школьники, так и их родители. Для быстрой навигации по порталу краткие ответы записаны на белом фоне, а подробные на цветном. Если пользователь хочет увидеть алгоритм решения задачи — он открывает комментарии, которые выделены цветом.

Незарегистрированным пользователям доступны только короткие ответы для записи в тетрадь. Подробный алгоритм выполнения задачи и комментарии откроются после авторизации.

Зарегистрироваться на Ответкине можно двумя способами:

Способ 1 – через социальные сети. Нажмите рядом с кнопкой «Войти» значок гугл аккаунта, Вконтакте или любой другой. Подтвердите вход, согласитесь с правилами пользования сайтом. Автоматически у вас создается аккаунт, в который вы сможете заходить через социальную сеть. Способ 2 – с использованием почтового ящика. Введите в поле «E-mail» точный адрес вашей почты. Ожидайте ссылки, нажав на которую вы активизируете свой аккаунт и сможете беспрепятственно пользоваться сайтом.

После регистрации вы получите доступ в ваш личный кабинет. Здесь вы сможете поменять пароль и, при желании, подписаться на рассылку с сайта. В личном кабинете каждому пользователю предоставлена бесплатная подписка. Это значит, что на бесплатной основе вы сможете открыть 3 ответа в сутки с подробными комментариями и пояснениями. Каждое из открывшихся решений можно просматривать много раз, оно будет храниться в истории личного кабинета в течение 24 часов. Там же будет указано, сколько еще времени доступно данное задание.

Если есть необходимость в просмотре большего количества ответов в день – нужно приобрети ежемесячную платную подписку. Стоимость ее символическая, все тарифы можно увидеть внутри личного кабинета. При оформлении платной подписки в вашем профиле также исчезнет реклама.

Решебник алгебры восьмого класса к учебнику Макарычева, Миндюка, Нешкова и Суворова

Учебное пособие с подробными ответами и комментариями за 8 класс составлено на основе учебника Макарычева 2013 года. Он соответствует ФГОС, является частью трехлетнего курса алгебры в общеобразовательных школах Российской Федерации. Все номера готовых домашних заданий совпадают с нумерацией учебника.

Содержание алгебры восьмого класса включает 43 темы, 13 параграфов и 5 глав. Система упражнений в каждом пункте построена на пошаговом усложнении трудности задач — от самых простых примеров к более сложным. В качестве основных и дополнительных заданий есть нестандартные, они размещены в рубрике «Для тех, кто хочет знать больше». Учебник содержит немало номеров, где школьники должны перейти от описания реальной ситуации к уравнению. Это дает им начальный опыт в использовании способов наглядного представления данных.

Решебник от Ответкина по алгебре 8 класса помогает с изучением следующих тем и математических определений:

Рациональные дроби и действия над ними: сложение, вычитание, умножение, деление, возведение в степень. Сложение и вычитание дробей с разными и одинаковыми знаменателями. Сокращение дробей. Квадратные корни и их свойства. Нахождение примерных значений квадратного корня. Преобразование выражений, содержащих квадратный корень. Вынесение множителя за и под знак квадратного корня. Нахождение квадратного корня из дроби, степени, произведения. Преобразование двойных радикалов. Квадратные уравнения и решение задач с их помощью. Теорема Виета. Дробные рациональные уравнения и задачи с ними. Уравнения с параметром. Числовые неравенства, их свойства, сумма и разность числовых неравенств. Числовые промежутки. Погрешность. Точность приближения. Доказательства неравенств. Степень и ее свойства. Степени с целым показателем и с целым отрицательным показателем. Стандартный вид числа. Начальное представление о статистике. Сбор статистических данных и их группировка. Наглядность статистической информации. Среднее квадратичное отклонение. Дисперсия.

Мы надеемся, что с помощью Ответкина восьмиклассники смогут решить свои проблемы с успеваемостью по алгебре, понять и даже полюбить этот непростой предмет. Надежный советчик в виде нашего сайта поможет разобраться в пропущенных темах, дойти до 9 класса без пробелов в математических знаниях.

Там же будет указано, сколько еще времени доступно данное задание.

Otvetkin. info

18.09.2019 13:34:05

2019-09-18 13:34:05

Источники:

Https://otvetkin. info/reshebniki/8-klass/algebra/makarychev

Заблаговременная подготовка – залог успеха

ГДЗ по алгебре за 8 класс Макарычев Ю.Н. книга-решение, практическое пособие, содержащее готовые ответы на задачи и примеры второй части одноименного учебника, составленного коллективом российских авторов: Ю. Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворов.

Готовые ответы из решения по алгебре 8 класса от Макарычева — помощь в изучении предмета

Современные программы для изучения такой сложной дисциплины как алгебра очень насыщены. Это создает трудности для родителей, которым трудно контролировать своих детей. Сами восьмиклассники не всегда успевают разобраться в механизме решения примера на уроке, что мешает им эффективно выполнять задание. домашнее задание.

Помощь в приобретении навыков решения алгебраических задач и уравнений может оказать решатель по алгебре для 8 класса Макарычев Ю.Н. Он содержит не только готовые ответы, но и подробный алгоритм их получения расчетным или аналитическим путем.

На нашем сайте представлены максимально удобные варианты использования готовых домашних заданий:

Здесь сосредоточены самые актуальные версии Решебников для основных учебников школьного курса;
Найти нужный ответ можно с помощью механизма быстрого поиска, указав в строке либо номер задачи, либо выдержку из ее условия;
Воспользоваться ресурсом можно с любого электронного гаджета — компьютера, планшета, смартфона.

Кроме того, мы предлагаем пользователям для каждой задачи несколько решений из разных решений, что повышает качество домашней работы.

ГДЗ для Макарычева Ю.Н. и Миндюка Н.Г. — основа для изучения алгебры в 8 9 классе0005

Готовые ответы решателя, представленные на нашем сайте, соответствуют по номерам учебнику практических задач по алгебре для восьмиклассников, изданному в 2013 году.

Книга состоит из пяти теоретических глав, подкрепленных упражнениями: и свойства рациональных дробей;

Правила действий с квадратными корнями;

Квадратные уравнения и порядок их решения;

Алгоритм решения неравенств и их свойства;

Степени с целочисленными показателями и элементами статистики.

В качестве приложений учебник содержит задания повышенной сложности, исторические факты и основные правила алгебры для 7 класса.

Наш сайт поможет школьникам выполнить домашнее задание по учебнику алгебры для 8 класса Мордокович Ю. Н. А родители смогут эффективно контролировать успеваемость своих детей.

Алгебра 8 класс

Макарычев, Миндюк, Нешков

Образование

В восьмом классе текучесть школьной программы становится еще больше. Дополнительные уроки, д/с и ответственность иногда сильно выматывают, что может снизить уровень внимания, вызвать раздражение. В этот период очень важно не пропустить ни одной темы из курса алгебры. Потому что не поняв одной мысли, можно упасть в пучину непонимания, что приведет только к плохим результатам обучения. Особое внимание следует уделить таким темам, как «Квадратные уравнения» и «Целые степени». Отличная поддержка в этом будет оказана Решебник к учебнику «Алгебра 8 класс» Макарычев, Миндюк, Нешков.

Что включено.

В этом сборнике вы найдете упражнения по пяти главам, которые входят в школьную программу. Помимо ГДЗ по алгебре Макарычева 8 класса содержит различные исторические факты об этой науке и основные правила, изложенные в удобном контексте. В качестве дополнительных предусмотрены задания с высоким уровнем сложности и детальным разбором каждого из них.

Нужен ли резольвер.

Может стать настоящей палочкой-выручалочкой для контроля правильности выполненной д/з. Снова обращаться к книге Решебник к учебнику «Алгебра 8 класс» Макарычева крайне внимательно, так как он рассчитан на помощь. Рано или поздно преподаватель заметит, что ученик списывает, не утруждая себя запоминанием материала, и тогда успеваемость может быстро скатиться вниз.

«Образование», 2013

Решебник по алгебре за 8 класс Макарычев Ю.Н. представляет собой сборник готовых домашних заданий, составленный на основе учебника, рекомендованного Министерством образования в качестве учебного пособия для 8 классов общеобразовательных школ, который был сформирован группой ученых — Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворов.

ГДЗ по алгебре 8 класс: Макарычев, Миндюк, Нешков, Феоктистов

ГДЗ по алгебре за 8 класс Макарычев не следует рассматривать как основание для списывания. По сути, это возможность проверить правильность домашнего задания или разобраться в алгоритме решения сложных примеров и задач.

Если родители стремятся контролировать успеваемость своих детей, то им тоже стоит воспользоваться Решебником — здесь можно найти не только итоговые ответы, но и комментарии по их выполнению.

Удобнее всего пользоваться решебником на базе нашего сайта, который:

предоставляет бесплатный и неограниченный доступ к готовым ответам по теме с телефона, планшета или ноутбука;
позволяет найти задачу по ее номеру, указанному в таблице;
представляет самые последние версии решебников.

При решении математических примеров на нашем сайте вы также можете воспользоваться специальными сервисами — для вычисления площади треугольника, деления и умножения на столбик, решения квадратных уравнений.

Для отдельных вариантов заданий дается несколько решений, что позволяет глубже разобраться в вопросе решения примера или задачи.

Решебник по алгебре 8 класс Макарычева Ю.Н. — задачник из учебника 2013-2017

Учащиеся 8-х классов большинства общеобразовательных школ РФ пользуются задачником по алгебре Ю.Н. Макарычевой как основу для закрепления полученных на уроках знаний.

Практическое пособие издано в 2013 году. В нем отражены такие ключевые вопросы алгебры, как:

понятие, свойства и действия с рациональными дробями и квадратными корнями;
решение квадратных уравнений и неравенств;
целых степеней и основная статистика.

В практикум также входит комплекс задач повышенной сложности, факты из истории науки, а также основные правила алгебры 7 класса в краткой форме.

Отрицательные корни квадратного уравнения. Квадратные уравнения. Решение полных квадратных уравнений

Некоторые задачи по математике требуют умения вычислять значение квадратного корня. К таким задачам относится решение уравнений второго порядка. В этой статье мы представляем эффективный метод вычисления квадратных корней и применяем его при работе с формулами корней квадратного уравнения.

Что такое квадратный корень?

В математике этому понятию соответствует символ √. Исторические данные говорят о том, что впервые его стали применять примерно в первой половине 16 века в Германии (первая немецкая работа по алгебре Кристофа Рудольфа). Ученые считают, что этот символ представляет собой преобразованную латинскую букву r (основание основания означает «корень» на латыни).

Корень любого числа равен такому значению, квадрат которого соответствует корневому выражению. На языке математики это определение будет выглядеть так: √x = y, если y 2 = x.

Корень положительного числа (x > 0) также является положительным числом (y > 0), но если взять корень отрицательного числа (x

Вот два простых примера:

√9 = 3 так как 3 2 = 9, √(-9) = 3i так как i 2 = -1

Итерационная формула Герона для нахождения значений квадратных корней

Приведенные примеры очень просты, и вычисление корней в них не составляет труда. Трудности начинают появляться уже при нахождении значений корней для любой величины, которая не может быть представлена в виде квадрата натурального числа, например √10, √11, √12, √13, не говоря уже о том, что на практике это необходимо найти корни для нецелых чисел: например, √(12,15), √(8,5) и так далее.

Во всех вышеперечисленных случаях следует использовать специальный метод вычисления квадратного корня. В настоящее время известно несколько таких методов: например, разложение в ряд Тейлора, деление на столбец и некоторые другие. Из всех известных методов, пожалуй, наиболее простым и эффективным является использование итерационной формулы Герона, известной также как вавилонский метод определения квадратных корней (есть сведения, что древние вавилоняне применяли ее в своих практических расчетах).

Пусть необходимо определить значение √x. Формула для нахождения квадратного корня выглядит следующим образом:

a n+1 = 1/2(an +x/an n), где lim n->∞ (an) => x.

Расшифруем эту математическую запись. Для вычисления √x следует взять некоторое число a 0 (оно может быть произвольным, однако для быстрого получения результата следует выбрать его так, чтобы (a 0) 2 было как можно ближе к x. Затем подставить его в указанной формуле вычисления квадратного корня и получить новое число 1, которое уже будет ближе к искомому значению. После этого необходимо подставить 1 в выражение и получить 2. Эту процедуру следует повторять до тех пор, пока достигается требуемая точность

Пример применения итерационной формулы Герона

Для многих алгоритм получения квадратного корня из заданного числа может показаться достаточно сложным и запутанным, но на деле все оказывается гораздо проще, так как эта формула очень быстро сходится ( особенно если выбрано хорошее число 0).

Приведем простой пример: необходимо вычислить √11. Выбираем а 0 = 3, так как 3 2 = 9, что ближе к 11, чем 4 2 = 16. Подставляя в формулу, получаем:

а 1 = 1/2 (3 + 11/3) = 3,333333;

а 2 = 1/2 (3,33333 + 11/3,33333) = 3,316668;

а 3 = 1/2 (3,316668 + 11/3,316668) = 3,31662.

Продолжать вычисления нет смысла, так как мы обнаружили, что 2 и 3 начинают различаться только в 5-м знаке после запятой. Таким образом, достаточно было применить формулу всего 2 раза, чтобы вычислить √11 с точностью 0,0001.

В настоящее время для вычисления корней широко используются калькуляторы и компьютеры, однако полезно запомнить отмеченную формулу, чтобы иметь возможность вручную вычислить их точное значение.

Уравнения второго порядка

Понимание того, что такое квадратный корень, и умение его вычислять используется при решении квадратных уравнений. Эти уравнения представляют собой равенства с одним неизвестным, общий вид которых показан на рисунке ниже.

Здесь c, b и a — некоторые числа, причем a не должно быть равно нулю, а значения c и b могут быть совершенно произвольными, в том числе и равными нулю.

Любые значения x, удовлетворяющие указанному на рисунке равенству, называются его корнями (это понятие не следует путать с квадратным корнем √). Так как рассматриваемое уравнение имеет 2-й порядок (х 2), то корней для него не может быть больше, чем два числа. Далее в статье мы рассмотрим, как найти эти корни.

Нахождение корней квадратного уравнения (формулы)

Этот метод решения рассматриваемого типа равенств также называют универсальным, или методом через дискриминант. Его можно применять к любым квадратным уравнениям. Формула для дискриминанта и корней квадратного уравнения выглядит следующим образом:

Из нее видно, что корни зависят от значения каждого из трех коэффициентов уравнения. Причем вычисление х 1 отличается от вычисления х 2 только знаком перед квадратным корнем. Подкоренное выражение, равное b 2 — 4ac, есть не что иное, как дискриминант рассматриваемого равенства. Дискриминант в формуле для корней квадратного уравнения играет важную роль, поскольку определяет количество и тип решений. Так, если он равен нулю, то решение будет только одно, если положительное, то уравнение имеет два действительных корня, и, наконец, отрицательный дискриминант приводит к двум комплексным корням х 1 и х 2.

Теорема Виета или некоторые свойства корней уравнений второго порядка

В конце XVI века один из основоположников современной алгебры, француз, изучая уравнения второго порядка, смог получить свойства ее корнеплоды. Математически их можно записать так:

х 1 + х 2 = -б/а и х 1 * х 2 = с/а.

Оба равенства могут быть легко получены каждым; для этого нужно только произвести соответствующие математические операции с корнями, полученными по формуле с дискриминантом.

Совокупность этих двух выражений по праву можно назвать второй формулой корней квадратного уравнения, позволяющей угадывать его решения без использования дискриминанта. Здесь следует отметить, что хотя оба выражения справедливы всегда, использовать их для решения уравнения удобно только в том случае, если оно может быть факторизовано.

Задача на закрепление полученных знаний

Решим математическую задачу, в которой продемонстрируем все приемы, рассмотренные в статье. Условия задачи таковы: нужно найти два числа, у которых произведение равно -13, а сумма равна 4.

Это условие сразу напоминает теорему Виета, по формулам суммы квадратных корней и их произведения запишем:

х 1 + х 2 = -b/a = 4;

х 1 * х 2 = с/а = -13.

Предположим, что a = 1, тогда b = -4 и c = -13. Эти коэффициенты позволяют составить уравнение второго порядка:

х 2 — 4х — 13 = 0.

Используем формулу с дискриминантом, получаем следующие корни:

х 1,2 = (4 ± √D) /2, D = 16 — 4 * 1 * (-13) = 68,

То есть задача сводилась к нахождению числа √68. Обратите внимание, что 68 = 4 * 17, тогда, используя свойство квадратного корня, мы получаем: √68 = 2√17.

Теперь используем рассмотренную формулу квадратного корня: а 0 = 4, тогда:

а 1 = 1/2 (4 + 17/4) = 4,125;

а 2 = 1/2 (4,125 + 17/4,125) = 4,1231.

Нет необходимости вычислять 3, потому что найденные значения отличаются всего на 0,02. Таким образом, √68 = 8,246. Подставив его в формулу для х 1,2, получим:

х 1 = (4 + 8,246)/2 = 6,123 и х 2 = (4 — 8,246)/2 = -2,123.

Как видите, сумма найденных чисел действительно равна 4, но если найти их произведение, то оно будет равно -12,999, что удовлетворяет условию задачи с точностью до 0,001.

Библиографическое описание: Гасанов А. Р., Курамшин А. А., Ельков А. А., Шильненков Н. В., Уланов Д. Д., Шмелева О. В. Методы решения квадратных уравнений // Молодой ученый. 2016. №6.1. С. 17-20..02.2019).

Наш проект посвящен способам решения квадратных уравнений. Цель проекта: научиться решать квадратные уравнения способами, не входящими в школьную программу. Задача: найти все возможные способы решения квадратных уравнений и научиться пользоваться ими самостоятельно и познакомить с этими методами одноклассников.

Что такое «квадратные уравнения»?

Квадратное уравнение — уравнение вида ось 2 + bx + c = 0 , где a , b , c — некоторые числа ( a ≠ 0 ), x — неизвестно.

Числа a, b, c называются коэффициентами квадратного уравнения.

а называется первым коэффициентом;
b называется вторым коэффициентом;
c — свободный член.

А кто первым «изобрел» квадратные уравнения?

Некоторые алгебраические методы решения линейных и квадратных уравнений были известны еще 4000 лет назад в Древнем Вавилоне. Найденные древние вавилонские глиняные таблички, датированные где-то между 1800 и 1600 годами до нашей эры, являются самым ранним свидетельством изучения квадратных уравнений. В этих же табличках приведены методы решения некоторых типов квадратных уравнений.

Необходимость решения уравнений не только первой, но и второй степени в древности была вызвана необходимостью решения задач, связанных с нахождением участков земель и земляных работ военного характера, а также развитием астрономия и собственно математика.

Правило решения этих уравнений, изложенное в вавилонских текстах, по существу совпадает с современным, но неизвестно, как вавилоняне пришли к этому правилу. Почти все клинописные тексты, найденные до сих пор, дают только задачи с решениями, изложенными в виде рецептов, без указания того, как они были найдены. Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствует понятие отрицательного числа и общие методы решения квадратных уравнений.

Вавилонские математики примерно 4 века до н.э. использовал метод дополнений к квадратам для решения уравнений с положительными корнями. Около 300 г. до н.э. Евклид предложил более общий геометрический метод решения. Первым математиком, который нашел решения уравнения с отрицательными корнями в виде алгебраической формулы, был индийский ученый. Брахмагупта (Индия, 7 век нашей эры).

Брахмагупта изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме:

ax2 + bx = c, a>0

В этом уравнении коэффициенты могут быть отрицательными. Правление Брахмагупты по существу совпадает с нашим.

В Индии публичные соревнования по решению сложных задач были обычным явлением. В одной из старых индийских книг о таких состязаниях сказано следующее: «Как солнце своим блеском затмит звезды, так ученый человек затмит славу на публичных собраниях, предлагая и решая алгебраические задачи». Задания часто были облечены в стихотворную форму.

В алгебраическом трактате Аль-Хорезми дана классификация линейных и квадратных уравнений. Автор перечисляет 6 типов уравнений, выражая их следующим образом:

1) «Квадраты равны корням», т. е. ах2 = Ьх.

2) «Квадраты равны числу», т.е. ах2 = с.

3) «Корни равны числу», т.е. ах2 = с.

4) «Квадраты и числа равны корням», т.е. ax2 + c = bx.

5) «Квадраты и корни равны числу», т. е. ax2 + bx = c.

6) «Корни и числа равны квадратам», т.е. bx + c == ax2.

Для Аль-Хорезми, который избегал использования отрицательных чисел, члены каждого из этих уравнений являются сложениями, а не вычитаниями. При этом уравнения, не имеющие положительных решений, заведомо не учитываются. Автор излагает методы решения этих уравнений, используя методы аль-джабра и аль-мукабала. Его решение, конечно, не совсем совпадает с нашим. Не говоря уже о том, что оно чисто риторическое, следует отметить, например, что при решении неполного квадратного уравнения первого рода Аль-Хорезми, как и все математики до XVII века, не учитывает нуль решение, наверное, потому что в конкретных практических задачах это не имеет значения. При решении полных квадратных уравнений Аль-Хорезми излагает правила их решения на конкретных числовых примерах, а затем их геометрические доказательства.

Формы для решения квадратных уравнений по модели Аль-Хорезми в Европе впервые были описаны в «Книге счетов», написанной в 1202 году. Итальянский математик Леонард Фибоначчи . Автор самостоятельно разработал несколько новых алгебраических примеров решения задач и первым в Европе подошел к введению отрицательных чисел.

Эта книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задания из этой книги были перенесены почти во все европейские учебники XIV-XVII вв. Общее правило решения квадратных уравнений, приведенных к единому каноническому виду x2 + bx = c со всеми возможными сочетаниями знаков и коэффициентов b, c, было сформулировано в Европе в 1544 г. М. Штифель.

У Виеты есть общий вывод формулы для решения квадратного уравнения, но Виета распознал только положительные корни. Итальянские математики Тарталья, Кардано, Бомбелли в числе первых в 16 в. учитывать, кроме положительных, и отрицательные корни. Лишь в XVII в. благодаря работам Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений приобретает современный вид.

Рассмотрим несколько способов решения квадратных уравнений.

Стандартные способы решения квадратных уравнений из школьной программы:

Факторизация левой части уравнения.
Метод выбора полного квадрата.
Решение квадратных уравнений по формуле.
Графическое решение квадратного уравнения.
Решение уравнений с помощью теоремы Виета.

Остановимся подробнее на решении редуцированных и нередуцированных квадратных уравнений с помощью теоремы Виета.

Напомним, что для решения заданных квадратных уравнений достаточно найти два числа, произведение которых равно свободному члену, а сумма равна второму коэффициенту с обратным знаком.

Пример. х 2 -5x+6=0

Вам нужно найти числа, произведение которых равно 6, а сумма равна 5. Эти числа будут 3 и 2.

Ответ: x 1 =2, х 2 =3.

Но вы можете использовать этот метод для уравнений с первым коэффициентом, не равным единице.

Пример. 3x 2 +2x-5=0

Возьмем первый коэффициент и умножим его на свободный член: x 2 +2x-15=0

Корнями этого уравнения будут числа, произведение которых равно — 15, а сумма равна — 2. Это числа 5 и 3. Чтобы найти корни исходного уравнения, делим полученные корни на первый коэффициент.

Ответ: х 1 =-5/3, х 2 =1

6. Решение уравнений методом «переноса».

Рассмотрим квадратное уравнение ax 2 + bx + c = 0, где a≠0.

Умножив обе его части на а, получим уравнение а 2 х 2 + абх + ас = 0.

Пусть ах = у, откуда х = у/а; то приходим к уравнению y 2 + by + ac = 0, которое эквивалентно данному. Находим его корни в точках 1 и 2, используя теорему Виета.

Наконец, мы получаем x 1 = y 1 /a и x 2 = y 2 /a.

При этом методе коэффициент а умножается на свободный член, как бы «переносится» на него, поэтому он называется «переносным» методом. Этот метод используется, когда легко найти корни уравнения с помощью теоремы Виета и, что особенно важно, когда дискриминант является точным квадратом.

Пример. 2x 2 — 11x + 15 = 0.

«Перенесем» коэффициент 2 в свободный член и, сделав замену, получим уравнение y 2 — 11y + 30 = 0.

Согласно обратной теореме Виета

y 1 = 5, х 1 = 5/2, х 1 = 2,5; у 2 = 6, х 2 = 6/2, х 2 = 3.

Ответ: х 1 =2,5; Х 2 = 3.

7. Свойства коэффициентов квадратного уравнения.

Пусть задано квадратное уравнение ax 2 + bx + c = 0, a ≠ 0.

1. Если а + b + с = 0 (т.е. сумма коэффициентов уравнения равна нулю), то х 1 = 1.

2. Если а — b + с = 0, или b = a + c, тогда x 1 = — 1.

Пример. 345x 2 — 137х — 208 = 0.

Так как а + b + с = 0 (345 — 137 — 208 = 0), то х 1 = 1, х 2 = -208/345.

Ответ: х 1 =1; Х 2 = -208/345 .

Пример. 132x 2 + 247х + 115 = 0

Так как a-b + c = 0 (132 — 247 + 115 = 0), то х 1 = — 1, х 2 = — 115/132

2 9 Ответ: х

1 = — 1; Х 2 =- 115/132

Существуют и другие свойства коэффициентов квадратного уравнения. но их использование сложнее.

8. Решение квадратных уравнений с помощью номограммы.

Рис. 1. Номограмма

Это старый и ныне забытый метод решения квадратных уравнений, помещенный на с. 83 сборника: Брадис В.М. Четырехзначные математические таблицы. — М., Просвещение, 1990.

Таблица XXII. Номограмма для решения уравнения z2 + pz + q = 0 . Эта номограмма позволяет, не решая квадратного уравнения, определить корни уравнения по его коэффициентам.

Криволинейный масштаб номограммы строится по формулам (рис. 1):

Принимая OS = p, ED = q, OE = a (все в см), из рис. 1 подобие треугольников САН и ВПР получаем пропорцию

откуда после подстановок и упрощений следует уравнение z 2 + pz + q = 0, и буква z означает метку любой точки на кривой шкале.

Рис. 2 Решение квадратного уравнения с помощью номограммы

Примеры.

1) Для уравнения z 2 — 9z + 8 = 0 номограмма дает корни z 1 = 8,0 и z 2 = 1,0

Ответ: 8,0; 1.0.

2) Решить уравнение по номограмме

2z 2 — 9z + 2 = 0.

Коэффициенты этого уравнения делим на 2, получаем уравнение z 2 — 4,5z + 1 = 0.

Номограмма дает корни z 1 = 4 и z 2 = 0,5.

Ответ: 4; 0,5.

9. Геометрический метод решения квадратных уравнений.

Пример. Х 2 + 10x = 39.

В оригинале эта задача формулируется так: «Квадрат и десять корней равны 39».

Рассмотрим квадрат со стороной х, на его сторонах построены прямоугольники так, что другая сторона каждого из них равна 2,5, следовательно, площадь каждого равна 2,5х. Полученную фигуру затем дополняют новым квадратом ABCD, достраивая по углам четыре равных квадрата, сторона каждого из которых равна 2,5, а площадь равна 6,25

Рис. 3 Графический способ решения уравнения х 2 + 10х = 39

Площадь S квадрата ABCD можно представить в виде суммы площадей: исходного квадрата х 2, четырех прямоугольников (4 ∙ 2,5х = 10х) и четырех присоединенных квадратов (6,25∙4=25), т.е. S = х 2 + 10х = 25. Заменив х 2 + 10х на число 39, получим, что S = 39 + 25 = 64, откуда следует, что сторона квадрат ABCD, т.е. отрезок AB=8. Для искомой стороны x исходного квадрата получаем

10. Решение уравнений по теореме Безу.

Теорема Безу. Остаток после деления многочлена P(x) на двучлен x — α равен P(α) (то есть значению P(x) при x = α).

Если число α является корнем многочлена P(x), то этот многочлен делится на x -α без остатка.

Пример. х²-4х+3=0

Р(х)= х²-4х+3, α: ±1,±3, α=1, 1-4+3=0. Разделите P(x) на (x-1): (x²-4x+3)/(x-1)=x-3

x²-4x+3=(x-1)(x-3), (x-1)(x-3)=0

x-1=0; х=1 или х-3=0, х=3; Ответ: х 1 =2, х 2 =3.

Заключение: Умение быстро и рационально решать квадратные уравнения просто необходимо для решения более сложных уравнений, например дробно-рациональных уравнений, уравнений высших степеней, биквадратных уравнений, а в старших классах тригонометрических, показательных и логарифмических уравнений . Изучив все найденные способы решения квадратных уравнений, можно посоветовать одноклассникам, помимо стандартных способов, решать методом переноса (6) и решать уравнения по свойству коэффициентов (7), так как они более доступны для понимания .

Литература:

Брадис В.М. Четырехзначные математические таблицы. — М., Просвещение, 1990.
Алгебра 8 класс: учебник для 8 класса. общеобразовательных учреждений Макарычев Ю.В. Н., Миндюк Н. Г., Нешков К. И., Суворова С. Б. изд. С. А. Теляковского 15-е изд., перераб. — М.: Просвещение, 2015
https://en.wikipedia.org/wiki/%D0%9A%D0%B2%D0%B0%D0%B4%D1%80%D0%B0%D1%82%D0%BD%D0%BE% D0 %B5_%D1%83%D1%80%D0%B0%D0%B2%D0%BD%D0%B5%D0%BD%D0%B8%D0%B5
Глейзер Г.И. История математики в школе. Руководство для учителей. / Ред. В.Н. Моложе. — М.: Просвещение, 1964.

Квадратное уравнение — решить легко! *Далее по тексту «КУ». Друзья, казалось бы, в математике это может быть проще, чем решение такого уравнения. Но что-то мне подсказывало, что у многих с ним проблемы. Решил посмотреть, сколько показов выдает Яндекс по запросу в месяц. Вот что получилось, посмотрите:

Что это значит? Это значит, что эту информацию ищут около 70 000 человек в месяц, и это лето, а что будет в течение учебного года — запросов будет в два раза больше. Это и неудивительно, ведь эту информацию ищут те парни и девушки, которые давно закончили школу и готовятся к экзамену, а также стараются освежить в памяти школьники.

Несмотря на то, что существует множество сайтов, рассказывающих, как решить это уравнение, я решил тоже внести свою лепту и опубликовать материал. Во-первых, я хочу, чтобы посетители приходили на мой сайт по этому запросу; во-вторых, в других статьях, когда речь пойдет о «КУ», я буду давать ссылку на эту статью; в-третьих, о его решении я расскажу немного больше, чем обычно изложено на других сайтах. Давайте начнем! Содержание статьи:

Квадратное уравнение представляет собой уравнение вида:

где коэффициенты a, b и с произвольными числами, где a≠0.

В школьном курсе материал подается в следующей форме — условно сделано разделение уравнений на три класса:

1. Имеют два корня.

2. * Имеют только один корень.

3. Не имеют корней. Здесь стоит отметить, что они не имеют настоящих корней

Как вычисляются корни? Просто!

Вычисляем дискриминант. Под этим «ужасным» словом скрывается очень простая формула:

Корневые формулы следующие:

*Эти формулы нужно знать наизусть.

Можно сразу записать и решить:

Пример:

1. Если D > 0, то уравнение имеет два корня.

2. Если D = 0, то уравнение имеет один корень.

3. Если Д

Посмотрим на уравнение:

По этому поводу, когда дискриминант равен нулю, школьный курс говорит, что получается один корень, здесь он равен девяти. Верно, но…

Это представление несколько неверно. На самом деле корней два. Да-да, не удивляйтесь, получается два равных корня, а если быть математически точным, то в ответ надо написать два корня:

х 1 = 3 х 2 = 3

Но это так — а небольшое отступление. В школе можно записать и сказать, что корень только один.

Теперь следующий пример:

Как известно, корень из отрицательного числа не извлекается, поэтому решения в данном случае нет.

Вот и весь процесс принятия решения.

Квадратичная функция.

Вот как решение выглядит геометрически. Это крайне важно понимать (в дальнейшем, в одной из статей, мы подробно разберем решение квадратного неравенства).

Это функция вида:

где x и y — переменные

a, b, c — заданные числа, где a ≠ 0

График представляет собой параболу:

То есть получается, что решая квадратное уравнение с «y» равным нулю, мы находим точки пересечения параболы с осью x. Таких точек может быть две (дискриминант положительный), одна (дискриминант равен нулю) или ни одной (дискриминант отрицательный). Подробнее о квадратичной функции Вы можете прочитать в статье Инны Фельдман.

Рассмотрим примеры:

Пример 1: Принять решение 2x 2 +8 х –192=0

а=2 б=8 с= -192

Д = б 2 –4ас = 8 2 –4∙2∙(–192) = 64+1536 = 1600

Ответ: х 1 = 8 х 2 = -12

* Можно было сразу разделить левую и правую части уравнения на 2, то есть упростить его. Расчеты станут проще.

Пример 2: Принять решение x2 –22 х+121 = 0

а=1 б=-22 с=121

D = b 2 –4ac =(–22) 2 –4∙1∙121 = 484–484 = 0

Получили, что х 1 = 11 и х 2 = 11

В ответе допустимо написать х = 11.

Ответ: х = 11

Пример 3: Решить 2 х 2 –8 х + 72 = 0

а=1 б= -8 с=72

D = b 2 –4ac =(–8) 2 –4∙1∙72 = 64–288 = –224

Дискриминант отрицательный, решения в действительных числах нет.

Ответ: нет решения

Дискриминант отрицательный. Есть решение!

Здесь речь пойдет о решении уравнения в случае, когда получен отрицательный дискриминант. Вы знаете что-нибудь о комплексных числах? Я не буду здесь подробно останавливаться на том, почему и где они возникли и какова их конкретная роль и необходимость в математике, это тема для большой отдельной статьи.

Понятие комплексного числа.

Немного теории.

Комплексное число z — это число вида

г = а + би

где a и b — действительные числа, i — так называемая мнимая единица.

а+би — это ЕДИНОЕ ЧИСЛО, а не дополнение.

Мнимая единица равна корню минус один:

Теперь рассмотрим уравнение:

Получите два сопряженных корня.

Неполное квадратное уравнение.

Рассмотрим частные случаи, это когда коэффициент «b» или «c» равен нулю (или оба равны нулю). Они легко решаются без каких-либо дискриминантов.

Случай 1. Коэффициент b = 0.

Уравнение принимает вид:

Преобразуем:

Пример:

4x 2 -16 = 0 => 4x 2 =16 => x 2 = 4 = > x 1 = 2 x 2 = -2

Случай 2. Коэффициент c = 0.

Уравнение принимает вид:

Преобразование, факторизация:

*Произведение равно нулю, когда хотя бы один из множителей равен нулю.

Пример:

9x 2 –45x = 0 => 9x (x–5) =0 => x = 0 или x–5 =0

x 1 = 0 x 2 = 5

Случай 3. Коэффициенты b = 0 и c = 0.

Здесь видно, что решением уравнения всегда будет x = 0.

Полезные свойства и закономерности коэффициентов.

Есть свойства, позволяющие решать уравнения с большими коэффициентами.

а х 2 + бх + с =0 равенство

и + b + c = 0, тогда

— если для коэффициентов уравнения a x 2 + бх + с =0 равенство

а + с = б , , затем

Эти свойства помогают решать уравнения определенного типа.

Пример 1: 5001 х 2 –4995 х – 6=0

Сумма коэффициентов 5001+( – 4995)+( – 6) = 0, поэтому

Пример 2: 2501 х 2 +2507 х +6=0

Равенство а + с = б , означает

Закономерности коэффициентов.

1. Если в уравнении ах 2 + bx + с = 0 коэффициент «b» равен (а 2 +1), а коэффициент «с» численно равен коэффициенту «а», то его корни равны

ах 2 + (а 2 +1) ∙ х + а = 0 => х 1 = -а х 2 = -1 / а.

Пример. Рассмотрим уравнение 6х 2 +37х+6 = 0.

х 1 = -6 х 2 = -1/6.

2. Если в уравнении ах 2 — bx + с = 0 коэффициент «b» равен (а 2 +1), а коэффициент «с» численно равен коэффициенту «а», то его корни составляют

ах 2 — (а 2 + 1) ∙ х + а = 0 => х 1 = а х 2 = 1 / а.

Пример. Рассмотрим уравнение 15x 2 –226x +15 = 0.

x 1 = 15 x 2 = 1/15.

3. Если в уравнении ах 2 + bx — c = 0 коэффициент «b» равно (a 2 – 1), а коэффициент «с» численно равен коэффициенту «а» , , то его корни равны

ах 2 + (а 2 -1) ∙ х — а = 0 => х 1 = — а х 2 = 1 / а.

Пример. Рассмотрим уравнение 17х 2 + 288х — 17 = 0.

х 1 = — 17 х 2 = 1/17.

4. Если в уравнении ах 2 — bx — с = 0 коэффициент «b» равен (а 2 — 1), а коэффициент с численно равен коэффициенту «а», то его корни

ах 2 — (а 2 -1) ∙ х — а = 0 => х 1 = а х 2 = — 1 / а.

Пример. Рассмотрим уравнение 10х2 — 99х -10 = 0.

х 1 = 10 х 2 = — 1/10

Теорема Виета.

Теорема Виета названа в честь известного французского математика Франсуа Виета. Используя теорему Виета, можно выразить сумму и произведение корней произвольного КУ через его коэффициенты.

45 = 1∙45 45 = 3∙15 45 = 5∙9.

В сумме число 14 дает только 5 и 9. Это корни. При определенной сноровке, используя представленную теорему, можно решать многие квадратные уравнения сразу устно.

Теорема Виета, кроме того. удобно тем, что после решения квадратного уравнения обычным способом (через дискриминант) можно проверить полученные корни. Я рекомендую делать это постоянно.

МЕТОД ПЕРЕНОСА

При этом методе коэффициент «а» умножается на свободный член, как бы «переносится» на него, поэтому он и называется способ передачи. Этот метод используется, когда легко найти корни уравнения с помощью теоремы Виета и, что особенно важно, когда дискриминант является точным квадратом.

Если a a ± b+c ≠ 0, то используется метод переноса, например:

2 X 2 – 11 x+ 5 = 0 (1) => X 2 90 – 11 х+ 10 = 0 (2)

По теореме Виета в уравнении (2) легко определить, что х 1 = 10 х 2 = 1

Полученные корни уравнения нужно разделить на 2 (так как двойку «выкинули» из х 2), получаем

х 1 = 5 х 2 = 0,5.

В чем причина? Посмотрите, что происходит.

Дискриминанты уравнений (1) и (2) равны:

Если смотреть в корни уравнений, то получаются только разные знаменатели, а результат зависит именно от коэффициента при х 2:

Второй (модифицированный) корень в 2 раза больше.

Следовательно, делим результат на 2.

*Если выпадает тройка, то делим результат на 3 и так далее.

Ответ: х 1 = 5 х 2 = 0,5

кв.ур-т.е. и экзамен.

Скажу кратко о его важности — ВЫ ДОЛЖНЫ УМЕТЬ РЕШАТЬ быстро и не задумываясь, нужно знать наизусть формулы корней и дискриминанта. Многие задания, входящие в состав заданий ЕГЭ, сводятся к решению квадратного уравнения (в том числе и геометрического).

Что стоит отметить!

1. Форма уравнения может быть «неявной». Например, возможен следующий ввод:

15+ 9x 2 — 45x = 0 или 15x+42+9x 2 — 45x=0 или 15 -5x+10x 2 = 0.

Вам необходимо привести его к эталону форме (чтобы не запутаться при решении).

2. Помните, что x — неизвестная величина и ее можно обозначать любой другой буквой — t, q, p, h и другими.

Просто. По формулам и понятным простым правилам. На первом этапе

необходимо привести данное уравнение к стандартному виду, т.е. к виду:

Если уравнение уже дано вам в таком виде, то первый этап делать не нужно. Самое главное правильно

определить все коэффициенты a , b и c .

Формула для нахождения корней квадратного уравнения.

Выражение под знаком корня называется Дискриминант . Как видите, чтобы найти x, мы

используем только a, b и c . Тех. шансы из квадратного уравнения . Просто аккуратно подставьте

значения a, b и c в эту формулу и посчитайте. Замените на их знака!

Например, , в уравнении:

a =1; б = 3; с = -4.

Подставляем значения и пишем:

Пример почти решен:

Это ответ.

Наиболее распространенными ошибками является путаница со знаками значений a, b и с . Вернее, с подстановкой

отрицательных значений в формулу вычисления корней. Здесь подробная формула сохраняет

с конкретными числами. Если есть проблемы с расчетами, сделайте это!

Предположим, нам нужно решить следующий пример:

Здесь a = -6; б = -5; с = -1

Расписываем все подробно, внимательно, ничего не пропуская со всеми знаками и скобками:

Часто квадратные уравнения выглядят несколько иначе. Например, так:

Теперь обратите внимание на практические приемы, которые резко уменьшают количество ошибок.

Первый прием . Не ленись до решив квадратное уравнение приведем его к стандартной форме.

Что это значит?

Предположим, после любых преобразований у вас получилось следующее уравнение:

Не спешите писать формулу корней! Вы почти наверняка перепутаете шансы a, b и c.

Правильно постройте пример. Сначала х в квадрате, потом без квадрата, потом свободный член. Вот так:

Избавьтесь от минуса. Как? Нам нужно умножить все уравнение на -1. Получаем:

А теперь можно смело записывать формулу корней, вычислять дискриминант и завершать пример.

Решайте сами. У вас должны получиться корни 2 и -1.

Второй прием. Проверьте свои корни! По теореме Виета .

Для решения заданных квадратных уравнений, т.е. если коэффициент

x2+bx+c=0,

, то x 1 x 2 =c

x1 +x2 =− b

Для полного квадратного уравнения, в котором a≠1 :

x 2 + b x+ c = 90,222 9

разделить все уравнение на a:

→ →

где х 1 и х 2 — корни уравнения.

Приемная третья . Если в вашем уравнении есть дробные коэффициенты, избавьтесь от дробей! Умножить

уравнение на общий знаменатель.

Заключение. Практические советы:

1. Перед решением приводим квадратное уравнение к стандартному виду, строим его правильно .

2. Если перед иксом в квадрате стоит отрицательный коэффициент, устраняем его, умножая все

уравнения на -1.

3. Если коэффициенты дробные, дроби исключаем, умножая все уравнение на соответствующие 92+b*x+c=0, где x- переменная, a,b,c – константы; а0 . Задача состоит в том, чтобы найти корни уравнения.

Геометрический смысл квадратного уравнения

График функции, представленной квадратным уравнением, представляет собой параболу. Решениями (корнями) квадратного уравнения являются точки пересечения параболы с осью x. Отсюда следует, что возможны три случая:
1) парабола не имеет точек пересечения с осью x. Это означает, что он находится в верхней плоскости ветвями вверх или в нижней плоскости ветвями вниз. В таких случаях квадратное уравнение не имеет действительных корней (имеет два комплексных корня).

2) парабола имеет одну точку пересечения с осью Ох. Такая точка называется вершиной параболы, и квадратное уравнение в ней приобретает свое минимальное или максимальное значение. В этом случае квадратное уравнение имеет один действительный корень (или два одинаковых корня).

3) Последний случай на практике более интересен — есть две точки пересечения параболы с осью абсцисс. Это означает, что существует два действительных корня уравнения.

На основе анализа коэффициентов при степенях переменных можно сделать интересные выводы о расположении параболы.

1) Если коэффициент а больше нуля, то парабола направлена вверх, если отрицательный — ветви параболы направлены вниз.

2) Если коэффициент b больше нуля, то вершина параболы лежит в левой полуплоскости, если принимает отрицательное значение, то в правой. 92 в обе части и выполняем преобразование

Отсюда находим

Формула дискриминанта и корни квадратного уравнения

Дискриминант — это значение подкоренного выражения. Если оно положительное, то уравнение имеет два действительных корня, вычисляемых по формуле При дискриминанте, равном нулю, квадратное уравнение имеет одно решение (два совпадающих корня), которые легко получить из приведенной выше формулы для D=0. Когда дискриминант отрицателен, действительных корней уравнения нет. Однако для изучения решений квадратного уравнения в комплексной плоскости их значение вычисляется по формуле

Теорема Виета

Рассмотрим два корня квадратного уравнения и на их основе построим квадратное уравнение. Из обозначений легко следует сама теорема Виета: если мы имеем квадратное уравнение вида то сумма его корней равна коэффициенту p, взятому с обратным знаком, а произведение корней уравнения равно к свободному члену q. Формула вышеизложенного будет иметь вид Если константа а в классическом уравнении отлична от нуля, то нужно разделить на нее все уравнение, а затем применить теорему Виета. 92-26x+120=0 .

Решение: Запишите коэффициенты и подставьте в дискриминантную формулу

Корень этого значения равен 14, его легко найти с помощью калькулятора, или запомнить при частом использовании, однако для удобства в конце В статье я приведу вам список квадратов чисел, которые часто можно встретить в таких задачах.
Найденное значение подставляем в формулу корня

и получаем

Задание 2. решаем уравнение

2×2+x-3=0.

Решение: Имеем полное квадратное уравнение, выписываем коэффициенты и находим дискриминант

Используя известные формулы, находим корни квадратного уравнения

Задача 3. решить уравнение

9×2 -12x+4=0.

Решение: У нас есть полное квадратное уравнение. Определить дискриминант

Мы получили случай, когда корни совпадают. Находим значения корней по формуле 92+х-6=0 .

Решение: В случаях, когда имеются малые коэффициенты при x, целесообразно применять теорему Виета. По его условию получаем два уравнения

Из второго условия получаем, что произведение должно быть равно -6. Это означает, что один из корней отрицательный. У нас есть следующая возможная пара решений (-3;2), (3;-2) . С учетом первого условия отбрасываем вторую пару решений.
Корни уравнения равны

Задача 5. Найдите длины сторон прямоугольника, если его периметр равен 18 см, а площадь 77 см 2.

Решение: Половина периметра прямоугольника равна сумме прилежащих сторон. Обозначим х — большую сторону, тогда 18-х — меньшую сторону. Площадь прямоугольника равна произведению этих длин:
х(18х)=77;
или
х 2 -18х + 77 = 0.
Находим дискриминант уравнения

Вычисляем корни уравнения

Если а х=11, то 18х=7, верно и наоборот (если х= 7, то 21-х=9).

Задача 6. Разложить на множители квадратное уравнение 10x 2 -11x+3=0.

Решение: Вычислить корни уравнения, для этого находим дискриминант

Подставляем найденное значение в формулу корней и вычисляем

Применяем формулу разложения квадратного уравнения по корням

Разложение скобки, мы получаем тождество.

Квадратное уравнение с параметром

Пример 1. При каких значениях параметра а уравнение (а-3) х 2 + (3-а) х-1/4 = 0 имеет один корень?

Решение: Прямая подстановка значения a=3 показывает, что оно не имеет решения. Далее воспользуемся тем, что при нулевом дискриминанте уравнение имеет один корень кратности 2. Выпишем дискриминант

упростим его и приравняем нулю

Получили квадратное уравнение относительно параметра а, решение которой легко получить с помощью теоремы Виета. Сумма корней равна 7, а их произведение равно 12. Простым перебором устанавливаем, что числа 3,4 будут корнями уравнения. Так как решение а=3 мы уже отвергли в начале расчетов, то единственно правильным будет — а=4. Таким образом, при a = 4 уравнение имеет один корень. 92+(2a+6)x-3a-9=0 имеет более одного корня?

Решение: Рассмотрим сначала особые точки, ими будут значения a=0 и a=-3. Когда a=0, уравнение упростится до вида 6x-9=0; x=3/2 и будет один корень. Для a= -3 мы получаем тождество 0=0 .
Вычислить дискриминант

и найти значения а, при которых он положителен

Из первого условия получаем а>3. Для второго находим дискриминант и корни уравнения

Определим интервалы, в которых функция принимает положительные значения. Подставляя точку a=0 получаем 3>0 . Итак, вне интервала (-3; 1/3) функция отрицательна. Не забудьте точку a=0, которую следует исключить, так как в исходном уравнении один корень.
В результате получаем два интервала, удовлетворяющих условию задачи

Подобных задач на практике будет много, попробуйте разобраться с задачами самостоятельно и не забывайте учитывать взаимоисключающие условия. Изучите хорошо формулы решения квадратных уравнений, они довольно часто нужны при расчетах в различных задачах и науках.

определение, примеры. Примеры тождественно равных друг другу выражений

Получив представление о тождествах, логично перейти к знакомству с . В этой статье мы ответим на вопрос, что такое тождественно равные выражения, а также на примерах разберемся, какие выражения тождественно равны, а какие нет.

Навигация по страницам.

Что такое тождественно равные выражения?

Определение тождественно равных выражений дается параллельно с определением тождества. Это происходит на уроке алгебры в 7 классе. В учебнике по алгебре для 7 классов автор Ю. Н. Макарычев приводит следующую формулировку:

Определение.

— это выражения, значения которых равны при любых значениях входящих в них переменных. Числовые выражения, соответствующие одинаковым значениям, также называются тождественно равными.

Это определение используется до класса 8, оно справедливо для целочисленных выражений, так как они имеют смысл при любых значениях входящих в них переменных. А в 8 классе уточняется определение тождественно равных выражений. Поясним, с чем это связано.

В 8 классе начинается изучение других видов выражений, которые, в отличие от целочисленных выражений, могут не иметь смысла для некоторых значений переменных. Это заставляет ввести определения допустимых и недопустимых значений переменных, а также диапазона допустимых значений ОДВ переменной и, как следствие, уточнить определение тождественно равных выражений.

Определение.

Два выражения, значения которых равны при всех допустимых значениях их переменных, называются тождественно равные выражения . Два числовых выражения, имеющие одинаковое значение, также называются тождественно равными.

В этом определении тождественно равных выражений стоит уточнить смысл фразы «для всех допустимых значений входящих в них переменных». Под ним подразумеваются все такие значения переменных, для которых одновременно имеют смысл оба тождественно равных выражения. Эта идея будет разъяснена в следующем разделе на примерах.

Определение тождественно равных выражений в учебнике А. Г. Мордковича дано несколько иначе:

Определение.

Идентичные равные выражения — это выражения слева и справа от тождества.

По смыслу это и предыдущее определения совпадают.

Примеры тождественно равных выражений

Определения, введенные в предыдущем подразделе, позволяют привести примера тождественно равных выражений .

Начнем с тождественно равных числовых выражений. Числовые выражения 1+2 и 2+1 тождественно равны, потому что они соответствуют равным значениям 3 и 3. Выражения 5 и 30:6 также тождественно равны, как и выражения (2 2) 3 и 2 6 (значения последних выражений равны благодаря ). Но числовые выражения 3+2 и 3−2 не тождественно равны, так как они соответствуют значениям 5 и 1 соответственно, но они не равны.

Теперь приведем примеры тождественно равных выражений с переменными. Это выражения a+b и b+a . Действительно, при любых значениях переменных a и b записанные выражения принимают одни и те же значения (что следует из цифр). Например, с a=1 и b=2 мы имеем a+b=1+2=3 и b+a=2+1=3 . При любых других значениях переменных a и b мы также получим равные значения этих выражений. Выражения 0·x·y·z и 0 также тождественно равны при любых значениях переменных x, y и z. Но выражения 2 х и 3 х не тождественно равны, так как, например, при х=1 их значения не равны. Действительно, при x=1 выражение 2 x равно 2 1=2 , а выражение 3 x равно 3 1=3 .

Когда области допустимых значений переменных в выражениях совпадают, как, например, в выражениях а+1 и 1+а , или а б 0 и 0 , или и , и значения этих выражений равны равны для всех значений переменных из этих областей, то здесь все ясно — эти выражения тождественно равны для всех допустимых значений переменных, входящих в них. Итак, a+1≡1+a для любого a , выражения a b 0 и 0 тождественно равны при любых значениях переменных a и b , а выражения и тождественно равны при всех x из ; изд. С. А. Теляковский. — 17-е изд. — М. : Просвещение, 2008. — 240 с. : больной. — ИСБН 978-5-09-019315-3.

Алгебра: учебник на 8 кл. общеобразовательные учреждения / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; изд. С. А. Теляковский. — 16-е изд. — М. : Просвещение, 2008. — 271 с. : больной. — ISBN 978-5-09-019243-9.

Мордкович А. Г. Алгебра. 7-й класс. В 14 ч. Ч. 1. Учебник для студентов общеобразовательных учреждений / А. Г. Мордкович. — 17-е изд.

, доп. – М.: Мнемозина, 2013. – 175 с.: ил. ISBN 978-5-346-02432-3.

Обе части которого являются тождественно равными выражениями. Тождества делятся на буквы и цифры.

Тождественные выражения

Два алгебраических выражения называются тождественными (или тождественно равными ), если при любых числовых значениях букв они имеют одинаковое числовое значение. Это, например, выражения:

х (5 + х ) и 5 х + х 2

Оба представленных выражения при любом значении x будут равны между собой, поэтому их можно назвать тождественными или тождественно равными.

Числовые выражения, равные друг другу, также можно назвать идентичными. Например:

20 — 8 и 10 + 2

Тождества букв и чисел

Тождества букв есть равенство, справедливое для любых значений входящих в него букв. Другими словами, такое равенство, при котором обе части являются тождественно равными выражениями, например:

( a + b ) m = am + bm
( a + b ) 2 = a 2 + 2 ab + b 2

Числовой идентификатор — это равенство, содержащее только числа, выраженные цифрами, в котором обе части имеют одинаковое числовое значение. Например:

4 + 5 + 2 = 3 + 8
5 (4 + 6) = 50

Тождественные преобразования выражений

Все алгебраические операции представляют собой преобразование одного алгебраического выражения в другое, идентичное первому.

При вычислении значения выражения, раскрытии скобок, вынесении общего множителя за скобки и в ряде других случаев одни выражения заменяются другими, тождественно равными им. Замена одного выражения другим, тождественно равным ему, называется тождественным преобразованием выражения или просто преобразованием выражения . Все преобразования выражений выполняются на основе свойств операций над числами.

Рассмотрим тождественное преобразование выражения на примере выноса общего множителя за скобки:

10 х — 7 х + 3 х = (10 — 7 + 3) х = 6 x

Рассмотрим два равенства:

1. a 12 * a 3 = a 7 * a 8

Это равенство выполняется для любого значения переменной a. Диапазоном допустимых значений для этого равенства будет весь набор действительных чисел.

2. а 12: а 3 = а 2 * а 7 .

Это неравенство будет выполняться для всех значений переменной а, кроме а равного нулю. Диапазоном допустимых значений этого неравенства будет весь набор действительных чисел, кроме нуля.

О каждом из этих равенств можно утверждать, что оно будет верным при любых допустимых значениях переменных а. Такие уравнения в математике называются тождествами .

Понятие тождества

Тождество есть равенство, истинное при любых допустимых значениях переменных. Если в это равенство вместо переменных подставить какие-либо допустимые значения, то должно получиться правильное числовое равенство.

Стоит отметить, что истинные числовые равенства также являются тождествами. Тождества, например, будут свойствами действий над числами.

3. а + b = b + а;

4. а + (б + в) = (а + б) + в;

6. а*(б*с) = (а*б)*с;

7. а*(б + с) = а*б + а*с;

11. а*(-1) = -а.

Если два выражения для любых допустимых переменных соответственно равны, то такие выражения называются тождественно равными . Ниже приведены несколько примеров тождественно равных выражений: 92*b) и -a 3 *b 2 ;

3. ((x 3 *x 8)/x) и x 10 .

Мы всегда можем заменить одно выражение любым другим выражением, тождественно равным первому. Такая замена будет тождественной трансформацией.

Примеры тождеств

Пример 1: Имеют ли место следующие равенства тождеств:

1. а + 5 = 5 + а;

2. а*(-б) = -а*б;

3. 3*а*3*б = 9*а*б;

Не все приведенные выше выражения будут тождествами. Из этих равенств только 1,2 и 3 равенства являются тождествами. Какие бы числа мы в них не подставляли, вместо переменных a и b мы все равно получаем правильные числовые равенства.

Но 4 равенство больше не тождество. Потому что не для всех допустимых значений это равенство будет выполняться. Например, при значениях a = 5 и b = 2 вы получите следующий результат:

Это равенство неверно, так как число 3 не равно числу -3.

Разобравшись с понятием тождеств, можно перейти к изучению тождественно равных выражений. Цель этой статьи — объяснить, что это такое, и показать на примерах, какие выражения будут тождественно равны другим.

Тождественно равные выражения: определение

Понятие тождественно равных выражений обычно изучается вместе с самим понятием тождества в рамках школьного курса алгебры. Вот основное определение, взятое из одного учебника:

Определение 1

тождественно равны друг другу будут такие выражения, значения которых будут одинаковыми для любых возможных значений переменных, входящих в их число. сочинение.

Также тождественно равными считаются такие числовые выражения, которые будут соответствовать одинаковым значениям.

Это достаточно широкое определение, которое будет верным для всех целочисленных выражений, смысл которых не меняется при изменении значений переменных. Однако позже возникает необходимость уточнить это определение, поскольку помимо целых чисел существуют и другие виды выражений, которые не будут иметь смысла с некоторыми переменными. Отсюда возникает понятие допустимости и недопустимости тех или иных значений переменных, а также необходимость определения диапазона допустимых значений. Сформулируем уточненное определение.

Определение 2

Идентичные равные выражения — это те выражения, значения которых равны друг другу при любых допустимых значениях переменных, входящих в их состав. Числовые выражения будут тождественно равны друг другу при условии, что значения совпадают.

Фраза «при любых допустимых значениях переменных» указывает на все те значения переменных, при которых оба выражения будут иметь смысл. Мы поясним это положение позже, когда приведем примеры тождественно равных выражений.

Можно также указать следующее определение:

Определение 3

Идентичные равные выражения — это выражения, расположенные в одном и том же идентификаторе слева и справа.

Примеры выражений, тождественно равных друг другу

Используя определения, данные выше, рассмотрим несколько примеров таких выражений.

Начнем с числовых выражений.

Пример 1

Таким образом, 2 + 4 и 4 + 2 будут тождественно равны друг другу, так как их результаты будут равны (6 и 6).

Пример 2

Точно так же тождественно равны выражения 3 и 30: 10 , (2 2) 3 и 2 6 (для вычисления значения последнего выражения нужно знать свойства степени) .

Пример 3

Но выражения 4 — 2 и 9 — 1 не будут равны, так как их значения различны.

Перейдем к примерам литеральных выражений. A + b и b + a будут тождественно равны, и это не зависит от значений переменных (равенство выражений в данном случае определяется коммутативным свойством сложения).

Пример 4

Например, если a равно 4, а b равно 5, результаты останутся теми же.

Другой пример тождественно равных выражений с буквами: 0 · x · y · z и 0 . Какими бы ни были значения переменных в этом случае, при умножении на 0 они дадут 0. Неравные выражения — это 6 x и 8 x, потому что они не будут равны ни для какого x.

В том случае, если диапазоны допустимых значений переменных будут совпадать, например, в выражениях а + 6 и 6 + а или а b 0 и 0, или х 4 и х, и значения сами выражения будут равны для любых переменных, то такие выражения считаются тождественно равными. Итак, a + 8 = 8 + a для любого значения a, и a · b · 0 тоже = 0, так как при умножении любого числа на 0 получается 0. Выражения x 4 и x будут тождественно равны для любого x из интервал [ 0 , + ∞) .

Но область допустимого значения в одном выражении может отличаться от области действия другого.

Пример 5

Например, возьмем два выражения: x — 1 и x — 1 · x x . Для первого из них диапазоном допустимых значений х будет все множество действительных чисел, а для второго множество всех действительных чисел, кроме нуля, потому что тогда в знаменателе мы получим 0, а такое деление не определено. Эти два выражения имеют общий диапазон, образованный пересечением двух отдельных диапазонов. Можно сделать вывод, что оба выражения x — 1 · x x и x — 1 будут иметь смысл при любых действительных значениях переменных, кроме 0 .

Основное свойство дроби также позволяет нам заключить, что x-1 x x и x-1 будут равны для любого x, отличного от 0. Это означает, что эти выражения будут тождественно равны друг другу в общем диапазоне допустимых значений, и при любом вещественном x нельзя говорить об тождественном равенстве.

Если заменить одно выражение другим, тождественно равным ему, то этот процесс называется тождественным преобразованием. Это понятие очень важно, и мы подробно поговорим о нем в отдельной статье.

Если вы заметили ошибку в тексте, выделите ее и нажмите Ctrl+Enter

Два выражения называются тождественно равными в наборе, если они имеют смысл в этом наборе и все их соответствующие значения равны.

Равенство, в котором левая и правая части являются тождественно равными выражениями, называется тождеством.

Замена одного выражения другим, тождественно равным ему на данном множестве, называется идентичное преобразование выражения.

Задание. Найти область выражения.

Решение. Так как выражение является дробью, то для нахождения его области действия нужно найти те значения переменной X , у которых знаменатель равен нулю, и исключить их. Решая уравнение X 2 — 9 = 0, находим, что X = -3 и X = 3. Следовательно, область определения этого выражения состоит из всех чисел, кроме -3 и 3. Если обозначить это к X , то мы можем написать:

X = (-¥; -3) È (-3; 3) È (3; +¥).

Задача. Являются ли выражения и X — 2 тождественно равными: а) на множестве R ; б) на множестве ненулевых целых чисел?

Решение. а) на множестве R эти выражения не тождественно равны, так как при X = 0 выражение не имеет значения, а выражение X — 2 имеет значение -2.

б) На множестве целых чисел, отличных от нуля, эти выражения тождественно равны, так как = .

Задача. При каких значениях X следующие равенства являются тождествами:

а) ; б) .

Решение. а) Равенство есть тождество, если ;

б) Равенство есть тождество, если .

Какой пример рационального использования. Рациональные числа, определение, примеры

Природопользование — Это деятельность человеческого общества, направленная на использование.

Выделяют рациональное и нерациональное природопользование.

Экологическое управление Эрани

Эранский экологический менеджмент — Это система рационального природопользования, при которой легкодоступные природные ресурсы используются не в полной мере, что приводит к быстрому истощению ресурсов. При этом производится большое количество отходов и сильно загрязняется окружающая среда.

Внутреннее природопользование характерно для хозяйства, развивающегося за счет нового строительства, освоения новых земель, использования природных ресурсов, увеличения численности занятых. Такое хозяйство сначала приносит хорошие результаты при относительно низком научно-техническом уровне производства, но быстро приводит к уменьшению природных и трудовых ресурсов.

Рациональное природопользование

— Это система природопользования, при которой полностью используются извлекаемые природные ресурсы, обеспечивается восстановление возобновляемых природных ресурсов, полностью и многократно используется продукция (т.е. безотходное производство), что позволяет значительно снизить загрязнение окружающей среды .

Рациональное природопользование характерно для интенсивного хозяйства, которое развивается на основе достижений научно-технического прогресса и хорошей организации труда при высокой производительности труда. Пример рационального природопользования Возможно безотходное производство, при котором полностью используются отходы, в результате чего снижается расход сырья и минимизируется загрязнение окружающей среды.

Одним из видов безотходного производства является многократное использование в технологическом процессе Воды, забираемые из рек, озер, бурения скважин и т.п. Используемая вода очищается и вновь участвует в производственном процессе.

Система мероприятий, направленных на поддержание взаимодействия между деятельностью человека и окружающей средой, называется охраной природы. Охрана окружающей среды представляет собой комплекс различных мероприятий, направленных на обеспечение функционирования природных систем. Рациональное природопользование предполагает обеспечение экономного использования природных ресурсов и условий существования человечества.

В систему особо охраняемых природных территорий входят заповедники, национальные парки, заказники, памятники природы. Инструментом наблюдения за состоянием биосферы является система экологического мониторинга — система непрерывных наблюдений за состоянием природной среды в результате хозяйственной деятельности человека.

Охрана природы и рациональное природопользование

В процессе становления науки экологии произошло смешение понятий, определяющее сущность этой науки вообще и структуру экологического цикла наук в частности. Экология стала интерпретировать как науку об охране, так и о рациональном использовании природы. Автоматически все, что связано с природной средой, стало называться окружающей средой, в том числе охрана природы и охрана окружающей среды.

При этом два последних понятия были искусственно смешаны и в настоящее время рассматриваются в комплексе. По конечным целям охрана природы и охрана окружающей среды близки друг к другу, но все же не тождественны.

Охрана природы Направлен в первую очередь на поддержание рационального взаимодействия деятельности человека и окружающей среды в целях сохранения и восстановления природных ресурсов и предотвращения вредного влияния результатов хозяйственной деятельности на природу и здоровье человека.

Охрана окружающей среды Основное внимание уделяется потребностям человека. Это комплекс различных мероприятий (административно-хозяйственных, технологических, правовых, общественных и др.), направленных на обеспечение функционирования природных систем, необходимых для сохранения здоровья и благополучия человека.

Природопользование направлено на удовлетворение потребностей человека за счет рационального использования природных ресурсов и природных условий.

Природопользование — Рассматривается в комплексе совокупность воздействий человечества на географическую оболочку Земли, совокупность всех форм эксплуатации природных ресурсов. Задачи природопользования сводятся к разработке общих принципов осуществления деятельности человека, связанной либо с непосредственным использованием природы и ее ресурсов, либо с воздействиями на нее.

Принципы рационального природопользования

Практическое применение экологических знаний проявляется прежде всего в решении экологических проблем. Только экология как наука может создать научную базу для эксплуатации природных ресурсов. Внимание экологии в первую очередь направлено на закономерности, лежащие в основе естественных природных процессов.

Рациональное природопользование Предполагает экономное использование природных ресурсов и условий с учетом интересов будущих поколений людей. Она направлена на обеспечение условий для существования человечества и получения материальных благ, на максимальное использование каждого природно-территориального комплекса, на предотвращение или существенное снижение возможного вредного воздействия производственных процессов или иных видов человеческой деятельности, на сохранение и приумножение продуктивность природы, сохранение ее эстетической функции, обеспечение и регулирование хозяйственного освоения ее ресурсов с учетом сохранения здоровья людей.

В противовес рациональному Эранному рациональному природопользованию Влияет на снижение качества, расточительство и истощение природных ресурсов, подрыв реабилитационных сил природы, загрязнение окружающей среды, снижение ее оздоровительных и эстетических достоинств. Это приводит к ухудшению состояния природной среды и не обеспечивает сохранение природно-ресурсного потенциала.

Использование окружающей среды включает:

добычу и переработку природных ресурсов, их охрану, возобновление или воспроизводство;
использование и охрана естественной среды жизнедеятельности человека;
сохранение, восстановление и рациональное изменение экологического равновесия природных систем;
регулирование воспроизводства человека и количества людей.

Охрана природы, рациональное использование и воспроизводство природных ресурсов – общечеловеческая задача, участвовать в решении которой должен каждый живущий на планете.

Экологическая деятельность направлена главным образом на сохранение разнообразия форм жизни на земле. Сочетание видов живых организмов на нашей планете создает особую основу жизни, которая называется Генофонд. Это понятие шире, чем просто совокупность живых существ. Он включает не только проявленные, но и потенциальные наследственные отложения каждого вида. Мы еще не все знаем о перспективах использования того или иного типа. Существование какого-то тела, казалось бы, ненужного, в будущем может оказаться не только полезным, но и, может быть, спасительным для человечества.

Основной задачей охраны природы является не защита каких-то видов растений или животных от угрозы исчезновения, а сочетание высокого уровня продуктивности с сохранением в биосфере широкой сети очагов генетического разнообразия. Биологическое разнообразие фауны и флоры обеспечивает нормальный круговорот веществ, устойчивое функционирование экосистем. Если человечество сможет решить эту важную экологическую задачу, в будущем можно рассчитывать на производство новых продуктов питания, лекарств, сырья для промышленности.

Проблема сохранения биологического разнообразия живых организмов на планете в настоящее время является наиболее острой и значимой для человечества. От того, как будет решена эта проблема, будет зависеть возможность сохранения жизни на Земле и самого человечества как части биосферы.

Являясь частью природы, человек на протяжении многих веков использовал ее дары для развития технологий и на благо человеческой цивилизации, нанося при этом колоссальный и непоправимый ущерб окружающему пространству. Современные факты ученых говорят о том, что пора задуматься о разумном использовании природы, ведь бездумное растрата земных ресурсов может привести к необратимой экологической катастрофе.

В контакте с

Система рационального природопользования

Современная система рационального природопользования представляет собой целостную структуру, охватывающую все сферы деятельности человека на современном этапе, в том числе общественное потребление природных ресурсов.

Наука рассматривает природопользование как совокупность мероприятий по рациональному использованию природных ресурсов, направленных не только на переработку, но и на восстановление с помощью усовершенствованных методов и технологий. Кроме того, это дисциплина, дающая теоретические знания и практические навыки для сохранения и приумножения природного разнообразия и богатства всего мирового пространства.

Классификация природных ресурсов

По происхождению природные ресурсы делятся на:

Производственное использование выделено:

Мировой земельный фонд.
Лесной фонд — часть земельного фонда, на которой произрастают деревья, кустарники, травы.
Гидроресурсы – это энергетические и ископаемые озера, реки, моря, океаны.

По степени утомления:

Рациональное и нерациональное природопользование

Рациональное природопользование – непрерывное воздействие человека на окружающее пространство, где он может управлять взаимоотношениями с природой на основе ее сохранения и защиты от нежелательные последствия в процессе своей деятельности.

Признаки рационального природопользования:

Восстановление и воспроизводство природных ресурсов.
Охрана земли, воды, животного и растительного мира.
Бережное извлечение минералов и безвредная обработка.
Сохранение природной среды для жизни человека, животных и растений.
Поддержание экологического баланса природной системы.
Регулирование рождаемости и населения.

Рациональное природопользование предполагает взаимодействие всей природной системы на основе соблюдения законов экологии, рационализации в использовании, сохранении и приумножении имеющихся ресурсов. Сущность природопользования основана на первичных закономерностях взаимного синтеза различных природных систем. Таким образом, при рациональном природопользовании осуществляется анализ биосистемы, ее бережная эксплуатация, охрана и воспроизводство с учетом не только текущих, но и перспективных интересов развития отраслей народного хозяйства и сохранения здоровья людей.

Примеры рационального природопользования:

Современное состояние природопользования свидетельствует о неравномерном подходе, который приводит к нарушению экологического баланса и очень сильно восстанавливается от антропогенного воздействия. Кроме того, экстенсивная эксплуатация на базе старых технологий привела к тому, что окружающая среда находится в загрязненном и угнетенном состоянии.

Признаки нерационального природопользования:

Примеров нерационального природопользования, которое, к сожалению, преобладает в хозяйственной деятельности и характерно для интенсивного производства, достаточно много.

Примеры нерационального природопользования:

Нарезное земледелие, дезинтеграция склонов на холмах, что приводит к образованию оврагов, эрозии почв и разрушению плодородного слоя Земли (гумуса).
Изменить гидрологический режим.
Лесоразведение, Разрушение заповедных территорий, избыточный выпас скота.
СБРОС ПРОМЫВКИ I. Сточных вод В реках, озерах, море.
Загрязнение атмосферы химическими веществами.
Уничтожение ценных видов растений, животных и рыб.
Открытый способ добычи.

Принципы рационального природопользования

Деятельность человека в рамках поиска путей рационального использования природных богатств и повышения методов экологической безопасности основывается на следующих принципах:

Пути реализации принципов

На современном этапе многие страны реализуют политические программы и проекты в сфере применения рациональных методов использования природных ресурсов, которые касаются:

Кроме того, в рамках отдельного государства ведется работа по разработке и реализации региональных планов и мероприятий по охране окружающей среды, и в этой сфере должны осуществляться государственные и общественные организации. Данные мероприятия позволят:

обеспечить населению экологически чистый труд на производстве;
создать здоровую среду для жителей городов и сел;
уменьшить опасное воздействие природных катаклизмов и катастроф;
сохранить экосистему в неблагополучных регионах;
внедряют современные технологии для обеспечения экологических норм;
регулируют акты природоохранного законодательства.

Проблема рационального использования природных ресурсов гораздо шире и сложнее, чем может показаться на первый взгляд. Необходимо помнить, что в природе все тесно взаимосвязано и ни один компонент не может существовать изолированно друг от друга.

Ущерб, нанесенный многовековой хозяйственной деятельностью, исправится только в том случае, если общество осознает решение проблем глобальной экологической ситуации. И это каждодневная работа для отдельной личности, государства и мирового сообщества.

Кроме того, прежде чем вести биологический предмет, необходимо досконально изучить всю сельскохозяйственную систему, освоить знания и понять суть ее существования. И только ориентируясь по ее законам и ее законам, человек сможет рационально использовать все ее блага и ресурсы, а также приумножать и сохранять для будущего поколения людей.

В этой статье мы начнем изучение рациональных чисел . Здесь мы дадим определение рациональных чисел, дадим необходимые пояснения и приведем примеры рациональных чисел. После этого мы сосредоточимся на том, как определить, является ли это число рациональным или нет.

Навигация по странице.

Определение и примеры рациональных чисел

Сейчас мы дадим несколько определений рациональных чисел. Несмотря на различия в формулировках, все эти определения имеют единый смысл: рациональные числа сочетаются с целыми и дробными числами, подобно тому как целые числа объединяют натуральные числа с противоположными им числами и числом ноль. Другими словами, рациональные числа обобщают целые и дробные числа.

Начнем с S. определения рациональных чисел которые воспринимаются наиболее естественно.

Из озвученного определения следует, что рациональным числом является:

Любое натуральное число N. Действительно, любое натуральное число можно представить в виде обыкновенной дроби, например, 3 = 3/1.
Любое целое число, в частности, количество нулей. На самом деле любое целое число можно записать либо в виде положительной обыкновенной дроби, либо в виде отрицательной обыкновенной дроби, либо в виде нуля. Например, 26 = 26/1,.
Любая обыкновенная дробь (положительная или отрицательная). Это прямо подтверждается определением рациональных чисел.
Любое смешанное число. Действительно, всегда можно представить смешанное число в виде неправильной обыкновенной дроби. Например, и.
Любая конечная десятичная дробь или бесконечная периодическая дробь. Это связано с тем, что указанные десятичные дроби переводятся в обыкновенные дроби. Например, и 0, (3) = 1/3.

Также ясно, что любая бесконечная непериодическая десятичная дробь не является рациональным числом, так как не может быть представлена в виде обыкновенной дроби.

Теперь мы можем легко привести примера рациональных чисел . Числа 4, 903, 100 321 являются рациональными числами, так как они натуральные. Целые числа 58, -72, 0, -833 333 333 также являются примерами рациональных чисел. Обыкновенные дроби 4/9, 99/3 также являются примерами рациональных чисел. Рациональные числа — это числа.

Из приведенных выше примеров видно, что существуют также положительные и отрицательные рациональные числа, а рациональное число ноль не является ни положительным, ни отрицательным.

Озвученное выше определение рациональных чисел можно сформулировать короче.

Определение.

Рациональные числа Называют числа, которые можно записать в виде дробей Z/N, где Z — целое число, а N — натуральное число.

Докажем, что это определение рациональных чисел эквивалентно предыдущему определению. Мы знаем, что можно считать дробь знаком деления, тогда из свойств деления целых чисел и правил деления целых чисел следует справедливость следующих равенств. Таким образом, это доказательство.

Приведем примеры рациональных чисел на основе этого определения. Числа -5, 0, 3 и являются рациональными числами, так как их можно записать в виде дробей с целым числителем и натуральным знаменателем вида и соответственно.

Определение рациональных чисел можно дать в следующей формулировке.

Определение.

Рациональные числа — Это числа, которые можно записать в виде конечной или бесконечной периодической десятичной дроби.

Это определение также эквивалентно первому определению, поскольку каждой обыкновенной дроби соответствует конечная или периодическая десятичная дробь и обратно, а любое целое число можно сравнить с десятичной дробью с нулями после запятой.

Например, числа 5, 0, -13 являются примерами рациональных чисел, так как их можно записать в виде следующих десятичных дробей 5,0, 0,0, -13,0, 0,8 и -7, (18).

Закончим теорию этого абзаца следующими утверждениями:

целые и дробные числа (положительные и отрицательные) составляют множество рациональных чисел;
каждое рациональное число можно представить в виде дроби с целым числом и натуральным знаменателем, и каждая такая дробь является некоторым рациональным числом;
каждое рациональное число может быть представлено в виде конечной или бесконечной периодической десятичной дроби, и каждая такая дробь является некоторым рациональным числом.

Является ли это число рациональным?

В предыдущем пункте мы выяснили, что любое натуральное число, любое целое число, любая обыкновенная дробь, любое смешанное число, любая конечная десятичная дробь, а также любая периодическая десятичная дробь является рациональным числом. Это знание позволяет нам «узнавать» рациональные числа из множества записанных чисел.

А как быть, если число задано в виде некоторого, или как и т.п., как ответить на вопрос, рационально ли это число? Во многих случаях ответить на него очень сложно. Уточняем некоторые направления движения мысли.

Если число задано в виде числового выражения, которое содержит только рациональные числа и знаки арифметического действия (+, -, · и :), значением этого выражения является рациональное число. Это следует из того, как определяются действия с рациональными числами. Например, проделав все действия в выражении, мы получим рациональное число 18.

Иногда после упрощения выражений и более сложных видов можно определить, рационально ли заданное число.

Пойдем дальше. Число 2 является рациональным числом, поскольку рационально любое натуральное число. Что насчет номера? Это рационально? Получается, что нет — это не рациональное число, это иррациональное число (доказательство этого факта методом от противного приведено в учебнике по алгебре для 8 класса, указанном ниже в списке литературы). Доказано также, что квадратный корень из натурального числа является рациональным числом только в тех случаях, когда число является полным квадратом некоторого натурального числа под корнем. Например, оба — рациональные числа, так как 81=92 и 1,024 = 32 2, а числа и не рациональны, так как числа 7 и 199 не являются полными квадратами натуральных чисел.

А число рациональное или нет? В этом случае легко заметить, что, следовательно, данное число рационально. Является ли число рациональным? Доказано, что корень K-й степени из целого числа является рациональным числом только тогда, когда число под знаком корня является степенью некоторого целого числа. Следовательно, оно не является рациональным числом, так как не существует целого числа, пятая степень которого равна 121.

Метод антинасти позволяет доказать, что логарифмы некоторых чисел по тем или иным причинам не являются рациональными числами. Например, мы доказываем, что не является рациональным числом.

Предположим противное, то есть предполагается, что — рациональное число и его можно записать в виде обыкновенной дроби M/N. Тогда приведите следующие равенства:. Последнее равенство невозможно, так как в левой части это нечетное число 5 N, а в правой части — четное число 2 m. Следовательно, наше предположение неверно, следовательно, не является рациональным числом.

В заключение стоит отметить, что при выяснении рациональности или иррациональности цифр следует воздерживаться от устойчивых выводов.

Например, не следует сразу утверждать, что произведение иррациональных чисел π и E является иррациональным числом, оно «как бы очевидно», но не доказано. При этом возникает вопрос: «А с чего бы произведением быть рациональное число»? А почему бы и нет, ведь можно привести пример иррациональных чисел, произведение которых дает рациональное число:.

Также неизвестно, являются ли числа и многие другие числа рациональными или нет. Например, есть иррациональные числа, иррациональная степень которых есть рациональное число. Для иллюстрации приведем степени типа, основанием степени и показателем являются не рациональные числа, а , а 3 — рациональное число.

Библиография.

Математика. 6 класс: учёба. Для общего образования. учреждения / [Н. Я. Виленкин и др.] — 22-е изд., Акт. — М.: Мнемозина, 2008. — 288 с.: ил. ISBN 978-5-346-00897-2.
Алгебра: исследования. За 8 кл. общее образование. учреждения / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворов]; Эд. С. А. Теликовский. — 16-е изд. — М.: Просвещение, 2008. — 271 с. : ИЛ. — ISBN 978-5-09-019243-9.
Гусев В. А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): учеб. выгода. — м.; Выше. Шк., 1984. — 351 с., ил.

Человечество издавна удовлетворяет свои потребности в еде, тепле, отдыхе за счет природных ресурсов. В ряде случаев наша деятельность наносит непоправимый вред окружающей среде. Поэтому мы должны рационально использовать природные ресурсы.

Это позволит экономически и обоснованно потреблять те дары, которые дарит нам наша планета. Рациональное природопользование, примеры которого позволят вам углубиться в этот вопрос, требует детального рассмотрения.

Понятие природопользования

Прежде чем рассматривать примеры рационального и нерационального природопользования, необходимо дать определение этому понятию. Есть две основные интерпретации.

Первое определение рассматривает природопользование как систему разумного потребления ресурсов, которая снижает скорость переработки, позволяет природе восстанавливаться. При этом подразумевается, что человек не ущемляет себя в использовании даров окружающей среды, а совершенствует технологию, позволяющую в полной мере использовать каждый природный ресурс.

Второе определение утверждает, что экологический менеджмент является теоретической дисциплиной, рассматривающей пути повышения рациональности использования имеющихся ресурсов. Эта наука ищет возможность оптимизации этого вопроса.

КЛАССИФИКАЦИЯ РЕСУРСОВ

Рациональное природопользование, примеры которого следует рассмотреть более подробно, требует продуманного использования ресурсов. Надо понимать, что под ними подразумевается. Природные ресурсы не создаются человеком, а применяются к нему.

Эти средства классифицируются по разным признакам. По направлению использования различают производственные, рекреационные, лечебные, научные и другие ресурсы. Также существует разделение на возобновляемые и невозобновляемые группы. К первой категории относятся энергия ветра, солнца, воды Мирового океана и др.

Природные ископаемые невозобновляемы. Прежде всего, это следует отнести к нефти, газу, углю и другим видам топливного сырья.

Эти подходы к группировке условны. Ведь даже энергия Солнца когда-то будет нам недоступна. Через огромное количество лет наша звезда погаснет.

Виды природных ресурсов

Существующие природные ресурсы принято разделять на несколько групп. Их нужно рассматривать больше. Во-первых, в современном мире широко используются водные ресурсы. Мы их потребляем, используем в технических целях. Необходимо поддерживать чистоту этих ресурсов, не нарушая исконные места обитания подводных представителей флоры и фауны.

Второй важной группой являются земельные ресурсы. Примером рационального природопользования является диспенсер, например, природных ландшафтов под культурами, которые после своего выращивания не накладывают почву.

Также К. природные ресурсы Ввод полезных ископаемых, леса, флоры и фауны. Энергетические ресурсы очень важны для нас.

Признаки рациональности

Рассматривая сегодняшние действия человека, такие как промышленное производство, сельское хозяйство, туризм, изменение природных ландшафтов, иногда сложно однозначно сказать, что из перечисленного является примером рационального природопользования. Ведь деятельность человека влияет на нашу окружающую среду.

Рациональное природопользование называют наиболее гармоничным взаимодействием нас с миром. Это понятие имеет несколько характерных черт.

Использование даров природы рационально, если человек в процессе своей деятельности применяет новые технологии, а также интенсивные подходы к производству. Для этого внедряются методы безотходного производства новой продукции, а также автоматизируются все технологические процессы.

Такой подход к ведению бизнеса характерен для развитых стран мира. Они служат примером для многих других государств.

Эраннский экологический менеджмент

Примеры рационального использования окружающей среды сегодня можно найти повсюду. Но есть и противоположный подход к управлению экономикой. Характеризуется массой негативных явлений, представляющих собой опасную тенденцию как для страны-производителя, так и для всего мира.

Нерациональное использование природных ресурсов характеризуется как неразумное, хищническое потребление. При этом люди не думают о последствиях таких своих действий. Иррациональный подход также имеет свои особенности. Прежде всего, это экстенсивный подход к ведению хозяйственной деятельности. При этом применяются устаревшие технологии и методы производства.

Такие циклы нелогичны, не продуманы до конца. Результат — много отходов. Некоторые из них наносят вред окружающей среде, здоровью людей и даже приводят к гибели целых видов живых существ.

Вечный экологический менеджмент ведет человечество в пропасть, экологический кризис. Такой подход к бизнесу характерен для стран Латинской Америки, Азии и Восточной Европы.

Основные примеры

Существует несколько основных видов деятельности, которые можно однозначно отнести к определенной группе использования ресурсов окружающей среды. Примером рационального природопользования является использование безотходных технологий производства. С этой целью создают предприятия замкнутого или полного цикла переработки.

При этом важно постоянно совершенствовать технику, подходы в изготовлении изделий. Одним из основных примеров также может быть создание ООПТ, где активно проводятся мероприятия по охране и восстановлению флоры, фауны.

Деятельность человека лишает мест обитания многие виды животных и растений. Изменения иногда настолько сильны, что их практически невозможно повернуть. Также примером рационального природопользования является восстановление участков разработки природных полезных ископаемых, создание природных ландшафтов.

Общепринятые принципы

В мире принята общая система, в которой признаются уместными национальные принципы рационального использования окружающей среды. Они не должны наносить непоправимый ущерб окружающей среде. Это главный принцип, ставящий интересы природы выше экономической выгоды.

Разработал несколько принципов, которые могут служить примером рационального природопользования. Является ли мошенничество с болотами, бездумная вырубка леса, уничтожение редких видов животных, согласно этим постулатам, настоящим преступлением? Конечно! Люди должны научиться потреблять минимальное количество ресурсов.

Пути улучшения положения

Рассматривая рациональное природопользование, примеры которого были приведены выше, следует сказать о реальных методах его улучшения. Они успешно применяются во всем мире. В первую очередь финансируются предприятия, ведущие исследования в области повышения полноты освоения природных ресурсов.

Также внедряются методы продуманного размещения производства в каждой конкретно взятой экологической зоне. Производственные циклы меняются, чтобы уменьшить количество отходов. С учетом особенностей региона определяется экономическая специализация предприятий, разрабатываются природоохранные мероприятия.

Также с учетом особенностей экологической обстановки осуществляется контроль и мониторинг последствий того или иного вида деятельности человека. Мировое сообщество столкнулось с необходимостью внедрения новейших технологий, экологических мероприятий по сохранению экологических характеристик среды, в которой может существовать человечество. Ведь до точки невозврата, когда восстановить прежние природные условия будет невозможно, нам всего несколько шагов.

Примеры мирового сообщества

Мировым примером рационального природопользования является организация хозяйственной деятельности Новой Зеландии. Эта страна полностью перешла на неисчерпаемые источники энергии, установив приоритетное значение охраняемых территорий.

Это лидер в области экологического туризма. Леса в этой стране остаются неизменными, их рубят, а охота здесь категорически запрещена. Многие экономически развитые страны также постепенно переходят на энергию Солнца и Ветра. Каждое государство обязуется применять методы, повышающие рациональность природопользования.

Рассмотрев рациональное природопользование, примеры которого были представлены выше, можно понять его важность. Будущее всего человечества зависит от нашего отношения к миру. Ученые утверждают, что экологическая катастрофа уже близка. Мировое сообщество обязано принять все меры для улучшения организации хозяйственной деятельности, производимой человеком.

Международные договоры, соглашения и конвенции в области природопользования и охраны окружающей среды, участником которых является Россия, традиционно являются источниками национального экологического права. Более того, это особый источник права. Его правила имеют приоритет перед нормами, предусмотренными национальным законодательством. В каждом законе Российской Федерации содержится формула: если установлены иные правила Российской Федерации, чем предусмотренные законом правила Международного договора, применяются правила Международного договора. Придание договору особой роли обусловлено необходимостью поддержания и обеспечения правопорядка в мире в сфере общества и природы. Россия является участником более 70 многосторонних международных договоров, соглашений и конвенций.

г) прекращение обработки истощенных земель.

1. Безопасность жизнедеятельности. / Ред. С.В. Белова. — М.: Высшая школа, 1999.
2. Лотоса В.Е. Технологии базовых отраслей природопользования.
No related posts.

ГДЗ по алгебре 8 класс Макарычев, Миндюк решебник с ответами к задачам

ГДЗ по Алгебре 8 класс Макарычев, Миндюк Учебник

Решебник по алгебре 8 класс Макарычева – ответы к учебнику

Значение курса алгебры

Структура учебника

ГДЗ Алгебра 8 класс Макарычев, Миндюк, Нешков

Контрольные вопросы и задания

Задания из учебника

Похожие ГДЗ Алгебра 8 класс

Контрольные вопросы и задания: §1

Условие

Решебник №1

Решебник №2

Особенности изучения алгебры

Состав решебника

На что рассчитан ГДЗ

Для чего предназначен решебник

Стоит ли использовать ГДЗ

ГДЗ решебник по алгебре 8 класс Макарычев, Миндюк, Нешков Учебник Просвещение

Чему научат уроки алгебры

Неоценимая помощь решебника

Краткая характеристика ученика

Задания из учебника

Контрольные вопросы и задания

Похожие ГДЗ Алгебра 8 класс

Задания из учебника: 1

Видеорешение

ГДЗ по алгебре 8 класс Макарычев, Миндюк (Учебник)

Какую помощь может оказать гдз по алгебре восьмой класс Макарычев учебник

Упражнения

Контрольные работы

Какую пользу можно извлечь из справочника с ответами по алгебре 8 класс Макарычев

Содержание гдз по алгебре для 8 класса, авторы: Макарычев Ю., Миндюк Г., Нешков К. И., Суворова С. Б.

по алгебре 8 класс Макарычев, Миндюк | ответы на 5

Кто и почему использует сборники с ответами в процессе обучения?

Явные плюсы применения онлайн справочника по алгебре за 8 класс (автор Макарычев)

Источники:

Лучший помощник – это для 8 класс Макарычева, Миндюка, Нешкова

Задания

Как Макарычева и Миндюка упрощают подготовку к урокам алгебры?

Рабочая программа по алгебре за 8 класс с решебником Макарычева

Задания

Источники:

Структура решебника

Номера заданий

Готовые домашние задания для 8 класса по алгебре Макарычева

В чем преимущества от Ответкина?

Уникальные подробные решения с пояснениями Ответкина

Почему родители предпочитают Ответкина вместо репетиторов?

Как пользоваться сайтом и открыть ответ с комментарием?

Решебник алгебры восьмого класса к учебнику Макарычева, Миндюка, Нешкова и Суворова

Источники:

Заблаговременная подготовка – залог успеха

Готовые ответы из решения по алгебре 8 класса от Макарычева — помощь в изучении предмета

ГДЗ для Макарычева Ю.Н. и Миндюка Н.Г. — основа для изучения алгебры в 8 9 классе0005

Что включено.

Нужен ли резольвер.

ГДЗ по алгебре 8 класс: Макарычев, Миндюк, Нешков, Феоктистов

Решебник по алгебре 8 класс Макарычева Ю.Н. — задачник из учебника 2013-2017

Отрицательные корни квадратного уравнения. Квадратные уравнения. Решение полных квадратных уравнений

Что такое квадратный корень?

Итерационная формула Герона для нахождения значений квадратных корней

Пример применения итерационной формулы Герона

Уравнения второго порядка

Нахождение корней квадратного уравнения (формулы)

Теорема Виета или некоторые свойства корней уравнений второго порядка

Задача на закрепление полученных знаний

2 9 Ответ: х

Геометрический смысл квадратного уравнения

Формула дискриминанта и корни квадратного уравнения

Теорема Виета

Квадратное уравнение с параметром

определение, примеры. Примеры тождественно равных друг другу выражений

Что такое тождественно равные выражения?

Примеры тождественно равных выражений

Тождественные выражения

Тождества букв и чисел

Тождественные преобразования выражений

Понятие тождества

Примеры тождеств