ГДЗ по информатике 8 класс Босова, Босова Решебник
Информатика – это дисциплина, которая изучает информацию и ее круговорот в человеческом обществе, проблемы измерения, хранения и распространения по коммуникационным сетям. На простейшем уровне обыкновенные люди ассоциируют данную науку с персональными компьютерами и ноутбуками, а также с Интернетом.
В общеобразовательных школах Российской Федерации на уроках данного предмета изучают некоторые компьютерные программы, а также учатся началам программирования, т.е. написанию авторского программного кода на каком-нибудь алгоритмическом языке.
Команда экспертов, возглавляемая доктором педагогических наук Людмилой Босовой, написала полезный учебно-методический комплекс для учеников восьмого класса. Книги помогут лучше разбираться в предмете, быстро готовить домашние задание и получать хорошие отметки на регулярных проверочных испытаниях. Структура курса хорошо определена. Заниматься по нему всегда интересно.
Почему решебник по информатике за 8 класс от Босовой нужен каждому ученику?
ГДЗ помогают ребенку мотивировать себя, чтобы заниматься самостоятельно. Также с их помощью можно постоянно контролировать достигнутый уровень прогресса посредством решения проверочных упражнений. Со сборником легко и удобно заниматься без помощи взрослых членов семьи. Электронная книга онлайн имеет следующие преимущества:
- наличие независимых вариантов решения многих упражнений;
- ответы снабжены объемными и полезными методическими указаниями;
- сайт работает с компьютера, планшета и смартфона;
- таблица номерных указателей позволяет быстро находить нужное задание.
Сборник полностью соответствуют ФГОС и повсеместно используются в рабочих программах педагогов. С ним можно успешно готовиться к контрольным, проверочным, самостоятельным, и диагностическим работах, выполнять тесты и проходить внешнее независимое тестирование в конце учебного года.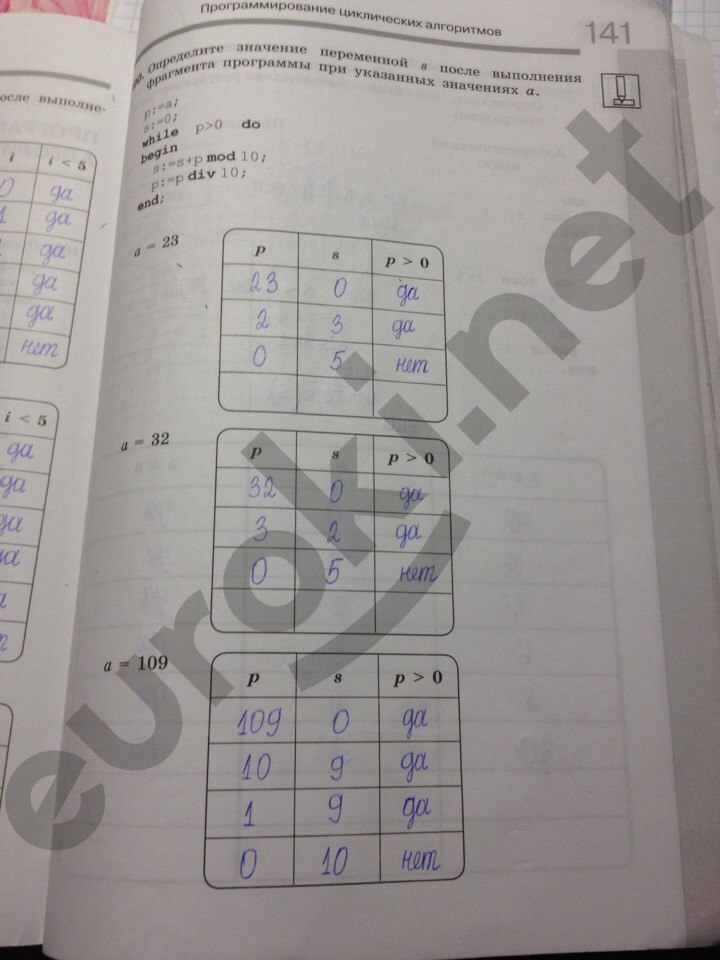
Чем ГДЗ по информатике для 8 класса (авторы: Л.Л. Босова, А.Ю. Босова) превосходят другие учебники?
Чтобы хорошо успевать на уроках, нужно приучить себя к систематической, настойчивой и тщательной работе. Это касается, прежде всего, понимания эффективных способов решения практических заданий. Например, нужно уметь понимать и расписывать алгоритмы в виде блок-схем, а потом переводить их в командные инструкции. Сборник обсуждаемых авторов способен оказать значительную помощь в качественном понимании и запоминании следующих разделов:
- информация: дискретная форма представления;
- программное обеспечение, его структура;
- единица информации;
- файловые объекты и повседневная работа с ними.
Информатика – это весьма полезный предмет. Он пригодится и в ходе внешкольной жизни, ведь компьютерная техника сегодня есть в каждом доме. Именно поэтому пособие рекомендовано широким массам учащихся, а также их неравнодушным родителям.
ГДЗ контрольно-измерительные материалы по информатике за 8 класс Масленикова ФГОС
Наш уникальный ресурс позволит ребятам оперативно выполнять проверку правильности выполнения упражнений, заданных на дом. Кроме того, ребята перестанут бесчисленное время сидеть за подготовкой к любым видам проверочных работ. Данные позволяют обрести уверенность в собственных знаниях, а также победить страх перед ответом во время занятий, что позволяет существенно улучшить успеваемость. Как правило, преподаватель формирует мнение о знаниях ученика, именно опираясь на ответы в течение урока, поэтому подобный подход позволит заручиться поддержкой педагога. Самое главное – не допускать бесконтрольного списывания ответов в тетрадь, поскольку это наоборот, задаст негативную динамику.
Какую пользу может принести обучающемуся сборник по информатике за 8 класс ким от Масленниковой
Сюда входят различные эффективные материалы для самоподготовки – загадки, головоломки, тренировочные игры, а также видеозаписи.
- Все верные ответы, приведенные в сборнике ответов, подкрепляются вектором рассуждений, для некоторых примеров предусмотрено сразу несколько вариантов выполнения.
- Каждый номер, размещенный на страницах материалов готовых домашних заданий, соответствует упражнению основной учебной литературы.
- Цифровое пособие размещается в сети интернет, таким образом для использования решебника достаточно просто перейти в онлайн-режим, независимо от местоположения.
Восьмиклассникам в этом году вновь предстоит столкнуться с увеличением учебной нагрузки. Кроме того, в расписании подростков вновь появится новая предметная область, которую они раньше не изучали.
Программа учебного курса с пособием по информатике для 8 класса автор: Масленикова О.
 Н.
Н.Информация из оригинального печатного учебника познакомит ребят с главами, предусмотренными министерством образования Российской Федерации, которые являются необходимыми для изучения на указанном этапе обучения:
- Теоретические основы информатики.
- Компьютер как универсальное средство обработки информации.
- Компьютерные сети как способ коммуникации и доступа к информационным ресурсам.
- Методы и технологии создания и обработки текстовых данных.
В течение всего учебного года ребята освоят множество теоретической информации, а также приобретут навыки, связанные с созданием и редактированием данных в текстовых редакторах. Очевидно, что программа не отличается повышенной сложностью, особенно учитывая тот факт, что большинство современных школьников знакомы с компьютером с раннего детства. Однако все равно ученику нужен надежный помощник, который выручит в трудную минуту.
ГДЗ решебник Информатика 8 класс
Изучай информатику вместе с решебниками для 8 класса
Цифровые технологии развиваются очень быстрыми темпами.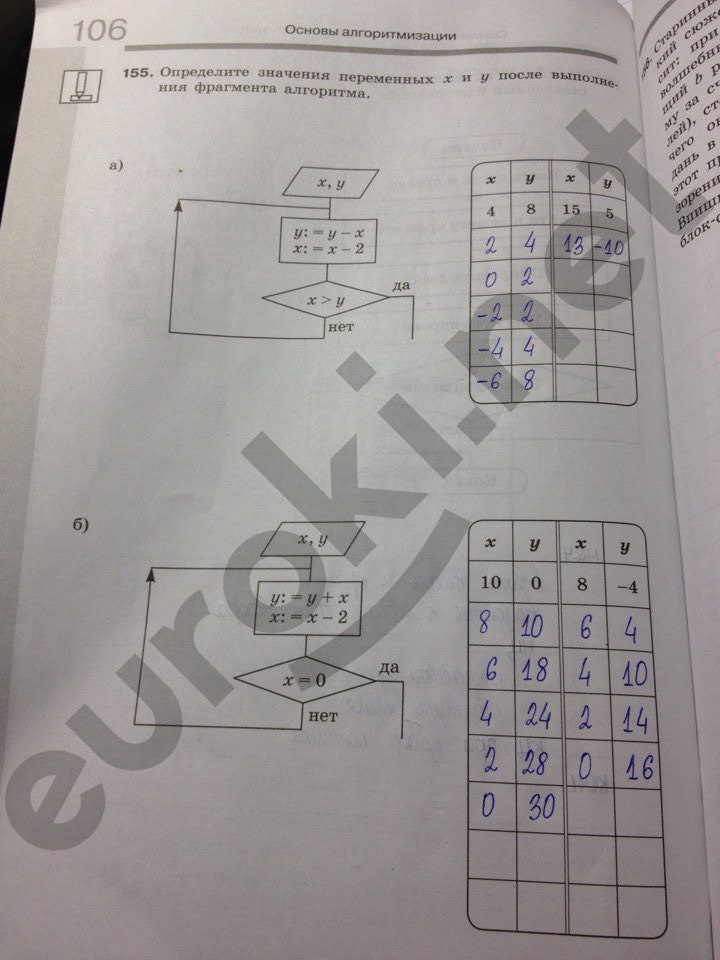 Очевидно, что будущее именно за ними. Сегодня их нередко используют в самых разных сферах жизни, включая простейшие детские игрушки, которые уже имеют возможность передавать в сеть информацию. Очень скоро вся жизнь людей будет тесно связана с различными электронными устройствами и программами.
Очевидно, что будущее именно за ними. Сегодня их нередко используют в самых разных сферах жизни, включая простейшие детские игрушки, которые уже имеют возможность передавать в сеть информацию. Очень скоро вся жизнь людей будет тесно связана с различными электронными устройствами и программами.
Но вопрос, который уже давно волнует людей, состоит в том, как правильно и, главное, адекватно пользоваться этими благами. Особенно он актуален в отношении детей и подростков. Они растут и контролировать их действия становится сложно, поэтому родителям ничего не остается, как наедятся на их благоразумие. В связи с этим рассчитывать необходимо на то, что ребенок имеет достаточное представление о возможности цифровых технологий, их несомненных плюсах и очевидных минусах. А для этого требуется отличная компьютерная грамотность и знание общих этических норм.
Что предстоит изучить школьникам по информатике в 8 классе
Восьмиклассники продолжат знакомство с темой информационного поля и процессами, в нем протекающими. Будет повторена и углублена тема кодирования и файловых объемов. Впервые будет изучаться пространственная дискретизация и ее связи с кодированием. Школьники будут учить способы обработки и шифрования аудио, фото и видео файлов.
Будет повторена и углублена тема кодирования и файловых объемов. Впервые будет изучаться пространственная дискретизация и ее связи с кодированием. Школьники будут учить способы обработки и шифрования аудио, фото и видео файлов.
Детально будет раскрыта такая тематика как цифровая информация и методы работы с ней. Продолжится изучение построения электронных таблиц и двоичного кодирования.
Подростки научатся использовать поисковые системы и сохранять необходимые данные. К концу года они познакомятся с устройством глобальной сети и внутрисетевой маршрутизацией. Школьники освоят первичные навыки сайтостроения.
Трудности изучения информатики в 8 классе
По мере приближения Государственной итоговой аттестации количество и сложность заданий возрастает. В связи с этим могут возникнуть сложности в освоении программы. Как показывает практика, особенно трудно школьникам освоить следующие направления:
- языки программирования;
- практическое их применение;
- сайтостроение.

Как можно решить проблему
В большинстве случаев школьники успешно справляются с проблемами благодаря последовательной методике преподавания. Однако сложности могут возникнуть в более детальных заданиях, где всего один неверный алгоритм может привести к серьезной ошибке. Для контроля правильности действий рекомендуется воспользоваться «ГДЗ по информатике 8 класс».
ГДЗ по Информатике за 8 класс Л.Л. Босова, А.Ю. Босова
Информатика 8 класс Л.Л. Босова
Авторы: Л.Л. Босова, А.Ю. Босова
ГДЗ по информатике 8 класс Босова помогает подросткам осваивать непростой, но важный предмет. Сегодня базовые компьютерные знания являются обязательной составляющей полноценного образования. В современном мире автоматизировано практически все. Поэтому понимать принципы этого процесса необходимо каждому. Восьмиклассники рассматривают на уроках несколько предметных разделов:
Восьмиклассники рассматривают на уроках несколько предметных разделов:
- Математические основы информатики.
- Основы алгоритмизации.
- Начала программирования.
Когда не обойтись без ГДЗ по информатике 8 класс Босова
ГДЗ по информатике учебник 8 класс Л.Л. Босова, А.Ю. Босова включают в себя ответы к заданиям для самоконтроля, которые располагаются после каждого параграфа в книге.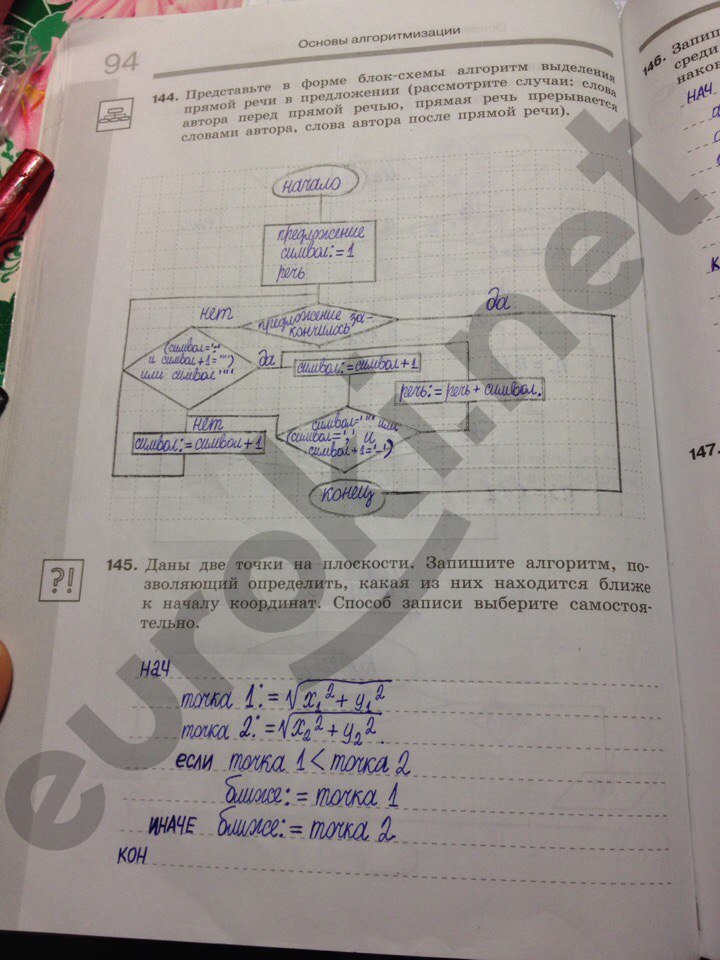 Ресурс снабжен интуитивно понятной навигацией, поэтому поиск нужного задания занимает всего пару секунд. Среди преимуществ, которые дает решебник учащимся средних школ, гарантированное улучшение оценок, упрощение понимания материала, снижение стресса, связанного со сложностью предмета, обретение уверенности в своих силах и повышение интереса к учебе.
Ресурс снабжен интуитивно понятной навигацией, поэтому поиск нужного задания занимает всего пару секунд. Среди преимуществ, которые дает решебник учащимся средних школ, гарантированное улучшение оценок, упрощение понимания материала, снижение стресса, связанного со сложностью предмета, обретение уверенности в своих силах и повышение интереса к учебе.
Виртуальный помощник готов прийти на выручку в любую минуту. Он поможет быстро выполнить работу, освободить время для других дел. Однако пособие может использоваться не только для списывания. Ответственные школьники могут с его помощью разбираться в тонкостях изучаемых тем, готовиться к контрольным работам и просто повышать уровень знаний. Выполнение тренировочных заданий позволяет обнаружить слабые места и укрепить их. Полезной бывает и подстраховка в виде проверки тетради до сдачи ее учителю. Это позволяет вовремя исправить даже мельчайшие ошибки и делать выводы на будущее.
ГДЗ для 8 класса по предмету «Информатика»
ГДЗ для 8 класса по предмету «Информатика»
За информационными технологиями стоит большое будущее.
Что ждет ребят в этом году
Продолжается углубление в тему об информации и информационных процессах, повторяются прошлогодние тезисы о кодировании и объемах файлов. Изучается новое направление — пространственная дискретизация, и как оно связано с кодированием. Школьники научатся обрабатывать и шифровать информационные файлы, такие как фотографии, видео и звуковые дорожки.
Какие проблемы ожидаются в этом году
Чем ближе время приближается к ГИА, тем большие объемы уроков предстоит выполнять учащимся. Если учесть актуальность данной дисциплины, то лишними эти задания назвать никак нельзя. Однако серьезность тематических разделов подразумевает и разнообразные затруднения при выполнении д/з. Особенно это касается разделов о языке программирования и его всестороннем применении.
Как грамотно с ними справляться
 А вот более детальные работы будут нуждаться в постоянном контроле, ведь один неправильный алгоритм может свести на нет все усилия. Поэтому ГДЗ по информатике 8 класс будет весьма кстати.
А вот более детальные работы будут нуждаться в постоянном контроле, ведь один неправильный алгоритм может свести на нет все усилия. Поэтому ГДЗ по информатике 8 класс будет весьма кстати.учебники, ГДЗ, учебные пособия, справочная литература
Информатика 8 класс: учебники, ГДЗ, учебные пособия, справочная литература учебникитесты и ГИАдля учителя- Информатика — 7-11 класс — Гаевский А.Ю.
- Информатика — Учебное пособие для 7-11 классов — Гаевский А.Ю. — 2006
- Информатика и ИКТ — Базовый курс — Учебник для 8 класса — Семакин И.Г. — 2005
- Информатика и ИКТ — Базовый курс — Учебник для 8 класса — Угринович Н.Д.
- Информатика и ИКТ, 8 класс, Босова Л.Л., Босова А.Ю., 2012
- Информатика и ИКТ, 8 класс, Босова Л.Л., Босова А.Ю., 2012
- Информатика и ИКТ, 8 класс, Угринович Н.Д., 2011
- Информатика и ИКТ, 8-9 класс, Макарова Н.
 В., 2010
В., 2010 - Информатика и ИКТ, Практикум, 8-9 класс, Макарова Н.В., 2010
- Информатика и ИКТ, учебник для 8 класса, Угринович Н.Д., 2011
- Информатика и ИКТ, Учебник, 8 класс, Угринович Н.Д., 2009
- Информатика и ИКТ. Базовый курс — Учебник для 8 класса — Угринович Н. Д. — 2005
- Информатика и информационные технологии, 8 класс, Гейн А.Г., Сенокосов А.И., Юнерман Н.А., 2009
- Информатика, 2-11 класс, Программы для образовательных организаций, Бородин М.Н., 2015
- Информатика, 2-11 классы, Внеклассные мероприятия, Неделя информатики, Куличкова А.Г., 2015
- Информатика, 5-6 класс, 7-9 класс, Программа для основной школы, Босова Л.Л., Босова А.Ю., 2015
- Информатика, 5-9 класс, Методическое пособие, Бородин М.Н., 2013
- Информатика, 7-9 класс, Методическое пособие, Босова Л.Л., Босова А.Ю., 2015
- Информатика, 7-9 класс, Методическое пособие, Босова Л.Л., Босова А.Ю., 2015
- Информатика, 7-9 класс, Методическое пособие, Хлобыстова И.
 Ю., Цветкова М.С., 2013
Ю., Цветкова М.С., 2013 - Информатика, 8 класс, Босова Л.Л., 2012
- Информатика, 8 класс, Босова Л.Л., 2013
- Информатика, 8 класс, Босова Л.Л., Босова А.Ю., 2014
- Информатика, 8 класс, Босова Л.Л., Босова А.Ю., 2014
- Информатика, 8 класс, Гейн А.Г., Юнерман Н.А., 2013
- Информатика, 8 класс, Книга 1, Горячев А.В., Макарина Л.А., 2013
- Информатика, 8 класс, Книга 2, Горячев А.В., Макарина Л.А., 2013
- Информатика, 8 класс, Миняйлова Е.Л., Вербовиков Д.А., Коледа Н.Р., Якунина Н.В., 2010
- Информатика, 8 класс, Часть 1, Горячев А.В., Герасимова В.Г., Макарина Л.А., Паволоцкий А.В., Семёнов А.А., Чернышёва Т.Л., 2015
- Информатика, 8 класс, Часть 2, Горячев А.В., Герасимова В.Г., Макарина Л.А., Паволоцкий А.В., Семёнов А.А., Чернышёва Т.Л., 2015
- Информатика, Лабораторный журнал, 8 класс, Угринович Н.Д., Серёгин И.А., Полежаева О.А., 2015
- Информатика, Математика, 7-9 класс, Программы внеурочной деятельности, Цветкова М.
 С., Богомолова О.Б., 2013
С., Богомолова О.Б., 2013 - Информатика, Методическое пособие, 7-9 класс, Босова Л.Л., Босова А.Ю., 2015
- Информатика, Методы алгоритмизации, 8-9 класс, Котов В.М., Волков И.А., Лапо А.И., 2000
- Информатика, программа для основной школы 5-6 и 7-9 классы, ФГОС, Босова Л.Л., 2015
- Информатика, Программа для основной школы, 5-6 класс, 7-9 класс, Босова Л.Л., Босова А.Ю., 2015
- Информатика, программа для основной школы, 5-6 классы, 7-9 классы, Босова Л.Л.,Босова А.Ю, 2013
- Информатика, Программы для образовательных организаций, 2-11 класс, Бородин M.Н., 2015
- Информатика, Программы для образовательных организаций, 2-11 класс, Бородин М.Н., 2015
- Информатика, программы для общеобразовательных учреждений, 2-11 классы, методическое пособие, Бородин М.Н., 2010
- Информатика, учебник для 8-го класса, Ривкинд И.Я., 2016
- Основы информатики и вычислительной техники, 8 класс, Балтаев Б., Абдукадыров А.
 , Махкамов М., Азаматов А., 2006
, Махкамов М., Азаматов А., 2006 - Увлекательная информатика, 5-11 класс, Владимирова Н.А., 2015
- Информатика — 7-9 класс — Базовый курс — Практикум-задачник по моделированию — Под ред. Макаровой Н.В.
- Информатика и ИКТ, 7-9 классы, тематические задачи и тесты за курс основной школы, подготовка к ГИА в форме ОГЭ, пособие с электронным приложением (CD-диск), Евич Л.Н., Кулабухов С.Ю., 2014
- Информатика и ИКТ, 8 класс, Рабочая тетрадь, Босова Л.Л., 2012
- Информатика и ИКТ, 8 класс, Рабочая тетрадь, Босова Л.Л., Босова А.Ю.
- Информатика и ИКТ, 8 класс, Рабочая тетрадь, Босова Л.Л., Босова А.Ю., 2014
- Информатика и ИКТ, 8 класс, Рабочая тетрадь, Босова, 2012
- Информатика и ИКТ, задачник-практикум, в 2 томах Том 1, Залогов Л.А., Семакин И.Г., Хеннер Е.К., 2011
- Информатика и ИКТ, задачник-практикум, в 2 томах Том 2, Залогова Л.А., Семакин И.Г., Хеннер Е.К., 2011
- Информатика и информационные технологии, 8 класс, Рабочая тетрадь, Гейн А.
 Г., Юнерман Н.А., 2009
Г., Юнерман Н.А., 2009 - Информатика и информационные технологии, 8 класс, Тематические тесты, Гейн А.Г., Юнерман Н.А., 2009
- Информатика и информационные технологии, 8-9 класс, Задачник-практикум, Гейн А.Г., 2008
- Информатика, 8 класс, Рабочая тетрадь, Босова Л.Л., 2012
- Информатика, 8 класс, Рабочая тетрадь, Босова Л.Л., Босова А.Ю., 2014
- Информатика, 8 класс, Рабочая тетрадь, Гейн А.Г., Гейн А.А., 2013
- Информатика, 8 класс, Тематические тестовые задания для подготовки к ГИА, Ярцева О.В., Цикина Е.Н., 2011
- Информатика, Рабочая тетрадь, 8 класс, Босова Л.Л., 2014
- Информатика, рабочая тетрадь, 8 класс, Босова Л.Л., Босова А.Ю., 2014
- Тесты — Информатика и информационные технологии. 6 — 11 классы — Анеликова Л.А
- Информатика и ИКТ, 8 класс, Поурочные разработки, Методическое пособие, Босова Л.Л.
- Информатика и ИКТ, 8-9 класс, Учебная программа и поурочное планирование, Босова Л.
 Л., 2012
Л., 2012 - Информатика, 2-11 класс, Программы для общеобразовательных учреждений, Бородин М.Н., 2010
- Информатика, 7-9 класс, Программа для основной школы, Угринович Н.Д., 2012
- Поурочные планы — Информатика — 8 класс — По учебнику Угриновича Н.Д.
- Программы для общеобразовательных учреждений — Информатика — 2-11 классы — Семакин И.Г.
Информатика. 8 класс: учебник / Н.Д. Угринович
Информатика. 8 класс: учебник / Н.Д. Угринович создатель Кристина 4021. Рекомендации по использованию учебника
2. Техника безопасности и санитарные правила работы на компьютере
3. Глава 1. Информация и информационные процессы
3.1. 1.1. Информация в природе, обществе и технике.
3.2. 1.2. Кодирование информации с помощью знаковых систем
3.3. 1.3. Количество информации
3.4. Практические работы компьютерного практикума к главе 1 «Информация и информационные процессы»
3.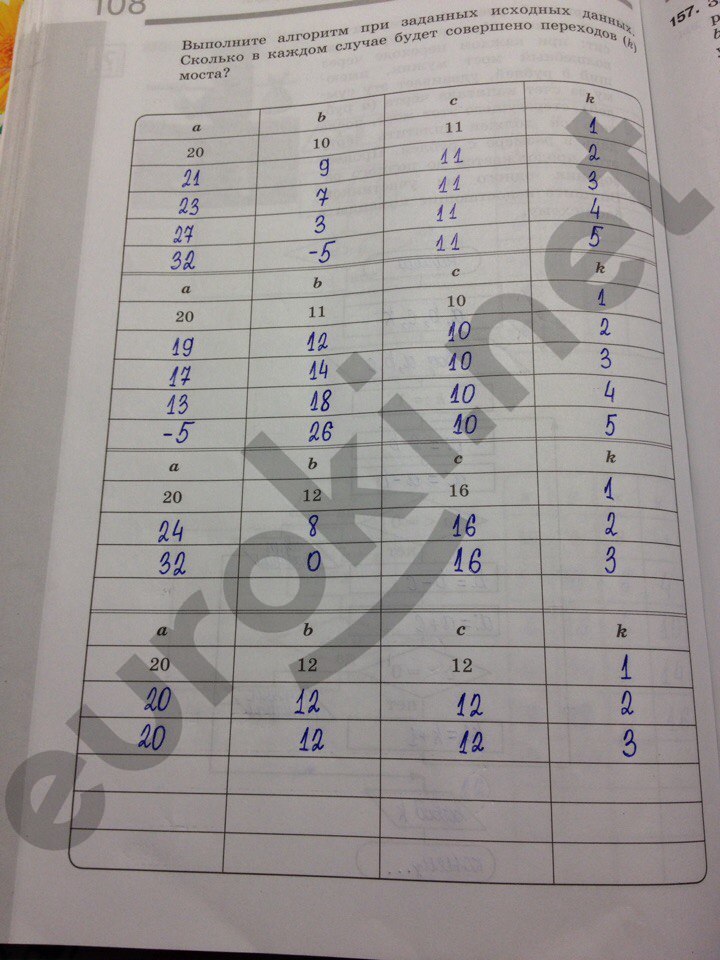 4.1. Практическая работа 1.1 Перевод единиц измерения количества информации с помощью калькулятора
4.1. Практическая работа 1.1 Перевод единиц измерения количества информации с помощью калькулятора
4. Глава 2. Кодирование текстовой и графической информации
4.1. 2.1. Кодирование текстовой информации
4.2. 2.2. Кодирование графической информации
4.3. Практические работы компьютерного практикума к главе 2 «Кодирование текстовой и графической информации»
4.3.1. Практическая работа 2.1 Кодирование текстовой информации
4.3.2. Практическая работа 2.2 Кодирование графической информации
5. Глава 3. Кодирование и обработка звука, цифровых фото и видео
5.1. 3.1. Кодирование и обработка звуковой информации
5.2. 3.2. Цифровые фото и видео
5.3. Практические работы компьютерного практикума к главе 3 «Кодирование и обработка звука, цифровых фото и видео»
5.3.1. Практическая работа 3.1 Кодирование и обработка звуковой информации
5.3.2. Практическая работа 3.2 Захват цифрового фото и создание слайд-шоу
5.3.3. Практическая работа 3.3 Редактирование цифрового видео с использованием системы нелинейного видеомонтажа
5.3.4. Практическая работа 3.4 Работа с пакетом презентаций
6. Глава 4. Кодирование и обработка числовой информации
6.1. 4.1. Кодирование числовой информации
6.2. 4.2. Электронные таблицы
6.3. 4.3. Построение диаграмм и графиков в электронных таблицах
6.4. Практические работы компьютерного практикума к главе 4 «Кодирование и обработка числовой информации»
6.4.1. Практическая работа 4.1 Перевод чисел из одной системы счисления в другую с помощью калькулятора
6.4.2. Практическая работа 4.2 Относительные, абсолютные и смешанные ссылки в электронных таблицах
6.4.3. Практическая работа 4.3 Создание таблиц значений функций в электронных таблицах
6.4.4. Практическая работа 4.4 Построение диаграмм различных типов
7. Глава 5. Хранение, поиск и сортировка информации в базах данных
7.1. 5.1. Базы данных в электронных таблицах
7.2. 5.2. Использование электронных таблиц как баз данных
7.3. Практические работы компьютерного практикума к главе 5 «Хранение, поиск и сортировка информации в базах данных»
7.3.1. Практическая работа 5.1 Использование электронных таблиц как баз данных
8. Глава 6. Коммуникационные технологии и разработка веб-сайтов
8.1. 6.1. Передача информации
8.2. 6.2. Локальные компьютерные сети
8.3. 6.3. Глобальная компьютерная сеть Интернет
8.4. 6.4. Разработка веб-сайтов с использованием языка разметки гипертекста HTML
8.5. Практические работы компьютерного практикума к главе 6 «Коммуникационные технологии и разработка веб-сайтов»
8.5.1. Практическая работа 6.1 Предоставление доступа к диску на ком пью тере, подключенном к локальной сети
8.5.2. Практическая работа 6.2 «География» Интернета
8.5.3. Практическая работа 6.3 Разработка сайта с использованием языка разметки текста HTML
9. Ответы и решения к заданиям для самостоятельного выполнения
The Ultimate STEM Guide for Kids: 239 интересных сайтов
Никогда не рано побуждать детей и подростков к получению образования и занятиям в области естественных наук, технологий, инженерии и математики (STEM). Важно настроить будущие поколения на успех, поскольку карьера в этих областях продолжает расти.
В этом руководстве представлены летние лагеря, веб-сайты, конкурсы, приложения и ресурсы по карьере для учащихся от начальной до средней школы. Гендерный разрыв в этих областях постепенно сокращается по мере появления новых инициатив, в том числе таких организаций, как Girls Who Code, но поскольку женщины по-прежнему крайне недопредставлены, мы включили мероприятия STEM специально для девочек и молодых женщин.
Мы надеемся, что это руководство вдохновит детей и подростков использовать свои навыки решения проблем, чтобы найти ответы на невозможные задачи и помочь сформировать лучшее будущее.
STEM Fun для детей классы K-12 ↑
Классные веб-сайты STEM
- Ask Dr. Universe: программа Ask Dr. Universe Университета штата Вашингтон позволяет детям изучать различные темы STEM и получать ответы на общие вопросы. Есть вопрос, которого нет на сайте? Отправьте его на их странице «Спросите»! Код
- .org: Никто не слишком молод (или стар, я могу добавить), чтобы писать код. Узнайте, как создать игру для iPhone, написать свою первую компьютерную программу, нарисовать JavaScript и многое другое.
- Инженерное дело, дерзайте! (eGFI): откройте для себя гайки и болты инженерии. Этот веб-сайт содержит советы о карьере, развлекательную информацию по всем направлениям и ссылки на журнал eGFI.
- Учащиеся EPA: Ищете новости об окружающей среде, ресурсы для домашних заданий, информацию о конкурсах или идеи для школьного проекта, ориентированного на окружающую среду? Посетите этот веб-сайт Агентства по охране окружающей среды.
- Exploratorium: Один из моих любимых. Веб-сайт Exploratorium из Сан-Франциско забит интерактивными занятиями, видео, приложениями, ссылками и многим другим.
- Extreme Science: Чрезвычайно интересно. Здесь вы найдете дикие и странные факты о природе, ресурсы для научных проектов и информацию о самых разных мировых рекордах.
- Как работает материал: Я посещаю этот сайт каждый день. В нем сотни и тысячи статей, объясняющих чудеса науки (и почти все остальное на планете).
- Музей науки и промышленности Чикаго Интернет-наука: приложения, мероприятия и видео, о боже! Играйте в игры, наблюдайте, как вылупляются птенцы, создавайте виртуальные химические реакции или используйте криминалистику для анализа различных типов конфет.
- НАСА Образование для студентов: информация о карьере, галереи изображений, телевидение НАСА, статьи и статьи… все, что вы хотите знать об аэрокосмической отрасли, вы обязательно найдете здесь.
- Академия наук, инженерии, математики и аэрокосмической науки НАСА (SEMAA): SEMAA была разработана для увеличения участия исторически недостаточно охваченной молодежи K-12 в областях STEM.Школьные мероприятия и летние сессии проводятся по всей стране.
- NOVA: Веб-сайт научно-популярного шоу PBS переполнен видео и статьями. Исследуйте чудеса эволюции, природы, физики, математики — практически любой предмет STEM, который вам интересен.
- Друзья науки: увязните в науке. На этом веб-сайте есть более 1000 идей для проектов научной ярмарки, руководства по проектам, комплекты проектов и подробные профили карьеры в STEM.
- Science Channel: Ставьте под сомнение все.На этом веб-сайте есть не только краткое изложение телевизионных программ канала Science Channel, но и множество видеороликов, викторин, игр и последних новостей науки.
- STEM-Works: В дополнение к статьям и информации о вакансиях, STEM-Works снабдил свой сайт интересными мероприятиями. Проверьте свои навыки в викторине про рептилий. Спасите спортсмена в Бионических играх. Или просто следуйте по пути великих белых с Global Shark Tracker.
- Virtual Tech Camps: круглогодичное онлайн-обучение для детей и подростков с учебной программой на Python, Java, Minecraft, Roblox, AI, Unreal Engine, Adobe, 3D-моделировании и многом другом.Сэкономьте 100 долларов с кодом ВМЕСТЕ.
- Tynker: вычислительная платформа, которая позволяет детям развивать навыки программирования с помощью веселых творческих курсов. Присоединяйтесь к миллионам детей со всей страны, которые учатся программировать с Tynker!
- Академия Kkan: Академия Khan разбивает сложные темы по ряду предметов, включая программирование, математику и статистику! У него есть учебные ресурсы почти по всем предметам STEM K-12.
- Flite Test STEM: Flite Test предоставляет учащимся K-12 множество легко загружаемых бесплатных уроков, которые знакомят учащихся с STEM посредством авиационной деятельности.
- HOODA MATH: HOODA MATH — это веб-сайт, посвященный математическим играм, разделенным по предметам. Учащиеся K-12 и любители математики любого возраста могут узнать о числах, развлекаясь.
Вызовы и конкурсы STEM
- Siemen’s We Can Change the World Challenge: у вас есть сила, чтобы спасти планету. В конкурсе Siemen по экологической устойчивости K-12 команды со всей страны соревнуются, чтобы улучшить свои сообщества. Множество призов.
- Toshiba / NSTA ExploraVision: ExploraVision — уникальное научное соревнование для школьников до 12 лет.Команды из двух-четырех учеников работают с учителем, моделируя задачи реальных исследований и разработок.
Награды STEM
Карьерные ресурсы STEM
- Бюро статистики труда K-12: Министерство труда США занято. Здесь вы найдете диаграммы, карты и многие другие ресурсы о карьере и экономике США.
- WeUseMath.org: Вы когда-нибудь задумывались (как я часто задавал), когда будете использовать математику в реальной жизни? На этом веб-сайте, посвященном карьере математика, есть более чем несколько ответов.
Государственные инициативы STEM
- Образовать для инноваций: запущенная в 2009 году программа «Образовать для инноваций» направлена на то, чтобы вывести американских студентов из среднего звена на вершину в области естественных наук и математики. Это породило ряд федеральных усилий и благотворительных инициатив (см. Ниже).
- STEM AmeriCorps: Эта многолетняя инициатива направлена на размещение членов AmeriCorps в некоммерческих организациях STEM (таких как FIRST) для работы в общинах с недостаточным уровнем обслуживания.
- White House Science Fair: На этой научной ярмарке президент выступает в роли хозяина! Студентов чествуют за новаторские проекты, разработки и эксперименты, пока Белый дом транслирует прямую трансляцию.
- Женщины в STEM: В сотрудничестве с Советом Белого дома по делам женщин и девочек Управление по политике в области науки и технологий (OSTP) инициировало ряд усилий по увеличению участия девочек в предметах STEM.
Благотворительные инициативы STEM
- Измените уравнение: эта некоммерческая организация, возглавляемая генеральными директорами, стремится мобилизовать бизнес-сообщество для повышения качества образования в области STEM в США.
- Connect a Million Minds (CAMM): CAMM, спонсируемая Time Warner Cable, представляет собой пятилетнюю благотворительную инициативу стоимостью 100 миллионов долларов, которая направлена на то, чтобы вдохновить студентов на развитие навыков STEM.
- US2020.org: Конечной целью этой некоммерческой организации является мобилизация одного миллиона наставников STEM ежегодно к 2020 году.
- Youth Inspired Challenge (YIC): Созданный Ассоциацией научно-технологических центров (ASTC), YIC призван расширить влияние обучения STEM за пределами классной комнаты.
STEM Fun для младших школьников ↑
Классные веб-сайты STEM
- Funology: В Funology наука обязательно должна стать интерактивной. Сделайте смерч из воды.Постройте террариум в Парке Юрского периода. Или просто изводите своих братьев и сестер бесконечными шутками о жуках и насекомых.
- Помощь вашему ребенку в изучении математики: это может заинтересовать ваших родителей. Этот веб-сайт, курируемый Министерством образования США, содержит задания по математике (выполняемые дома, в магазине и в дороге) для дошкольников и младших школьников.
- Kids Do Ecology: Каждый ребенок должен быть экологическим героем. Узнайте о биомах, синих китах и сборе данных.Вы даже можете создать свой собственный эксперимент в классе. Доступно на испанском языке.
- Kids.gov: От воображаемых джунглей до ионных экспериментов на Kids.gov есть множество ресурсов на черный день. Посмотрите анимацию о громе и молнии или совершите виртуальную экскурсию в Национальный зоопарк.
- The Kids ’Science Challenge (KSC): практические научные занятия, игры, интересные видео, охота за мусорщиками… этот веб-сайт полон забавных вещей. KSC также проводит бесплатные общенациональные соревнования по естествознанию для учащихся 3–6 классов.
- Детский клуб НАСА: в детском клубе НАСА совершенно нормально дурачиться в космосе. Вы можете использовать свои научные и математические навыки, чтобы исследовать Марс, построить флот из ракет или искать побочные продукты НАСА в своем гараже.
- NASA Space Place: создайте свой собственный космический корабль, поиграйте в космические вулканы или просмотрите галерею изображений солнца. Когда вы находитесь в Space Place, вселенная — это предел.
- National Geographic Kids: Что вам симпатичнее: рыба фугу или рыба-клоун? На этом сайте вы можете проголосовать в опросах, принять участие в яиц-периментах, посмотреть видео, сыграть в головоломки и узнать удивительные факты.
- Weather Wiz Kids: встречайте метеоролога Кристал Уикер. Она создала веб-сайт, на котором все объясняется о погоде. Найдите забавные факты, игры, карточки и фотографии, а также получите ответы на свои метеорологические вопросы.
- Virtual Tech Camps: круглогодичное онлайн-обучение для детей и подростков с учебной программой на Python, Java, Minecraft, Roblox, AI, Unreal Engine, Adobe, 3D-моделировании и многом другом. Сэкономьте 100 долларов с кодом ВМЕСТЕ.
- Кибер-академия Карнеги: Кибер-академия Карнеги предлагает интерактивные игры, которые учит детей правилам безопасности при работе в Интернете.
- Wonderville: Wondervlile есть все — научные эксперименты, комиксы, видео, мероприятия на такие темы, как солнечная энергия и пожаротушение с воздуха.
- Учебный центр Kinder Care: Учебный центр Kinder Care ориентирован на предоставление непрерывного образования этим любознательным людям во время зимних и летних каникул.
PBS Kids
- Cyberchase: Помогите Джеки, Мэтту и Инес использовать математику, чтобы защитить цифровую вселенную от зла. Не волнуйтесь: в Cyberchase есть множество математических игр, видео и заданий, которые помогут вам в ваших поисках.
- Design Squad Nation: Создавайте все, что (!) Вы можете себе представить. С помощью заданий Design Squad, видео и руководств вы узнаете все, что нужно знать о принципах проектирования.
- Кот в шляпе знает об этом толк !: Игры, мероприятия и видеоролики Pre-K STEM в изобилии. Авантюрный Кот в шляпе готов повести вас в экзотическое математическое сафари-приключение
- Спасательная шлюпка на Марс: исследуйте мир биологии в этой бесплатной онлайн-игре. В одном симуляторе (Microland) вы управляете голодными микробами.В другом (Ecoland) вам нужно сбалансировать экосистему космической станции.
- Zoom: горячая наука и крутые идеи. На веб-сайте Zoom вы найдете всевозможные занятия и эксперименты, в том числе ракеты с лимонным соком, сумасшедшие соломенные мосты и города-пузыри.
- Design Squad Global: Хотите участвовать в интересных научных задачах, играть в игры и смотреть забавные видео? Ознакомьтесь с Design Squad Global.
Научные игры и приложения
- Amazing Alex App: В Amazing Alex есть множество безумных физических задач, требующих ваших изобретательных решений.Вы даже можете строить и создавать свои собственные. Принесено вам создателями Angry Birds.
- Angry Birds Space App: эти дурацкие (и безумно успешные) птички теперь разыгрывают свои физические головоломки в космосе, где гравитация творит довольно странные вещи!
- У каждого тела есть мозг!: Погрузитесь в свой удивительный мозг с помощью песен, анимации и мини-игр. Полную версию игры можно приобрести на компакт-диске или загрузить в цифровом виде.
- Geo Walk: 3D World Factbook App: радуйтесь географии! Это обучающее приложение содержит изображения и факты о сотнях мест, растений и животных.
- Kinectic City: удивительная коллекция научных экспериментов, игр, занятий и задач. Вы можете запустить эстафету клеток крови или использовать компьютерную модель, чтобы построить свой собственный бизнес в межзвездной слякоти.
- Max и приложение Magic Marker: в этой увлекательной игре, основанной на физике, вы полностью контролируете Макса и его невероятный магический маркер. Есть 15 уровней головоломок, на каждом из которых есть задачи, секреты и награды.
- Move the Turtle: Programming for Kids: не нужно быть компьютерным гением, чтобы программировать! С помощью этого приложения любой ребенок может выучить азы программирования в графической среде.
- сезонов! Приложение: куда бы вы ни пошли, всегда берите с собой погоду. В этом приложении вы узнаете, как определять различные погодные условия в разное время года. Для детей от 3 до 6 лет.
- Приложение Sid’s Science Fair: у Сида из PBS «Sid the Science Kid» есть три научные игры для вашего развлечения: «Collection Inspection» Габриэлы, «Chart It!» Мэй. и «Машина времени» Джеральда. Для детей от 3 до 6 лет.
- Команда Умизуми: веселые анимированные персонажи из Ника-младшего.Телепрограмма предлагает множество математических игр и заданий для дошкольников.
- Чикагский музей науки и промышленности — эксперимент: познавайте и изучайте науку с помощью интерактивных мобильных приложений и выполняйте практические задания, которые вы можете попробовать дома.
Математические игры и приложения
- Geometry Quest App: Путешествуйте по миру, решая геометрические задачи на своем пути. За совершенные квесты вы получите штампы в паспорте. Охватывает стандарты Common Core 3MD, 3G, 4MD, 5G, 6G, 7G и 8G.
- Math Blaster: Сможете ли вы спасти галактику? Вам понадобятся математические навыки для выполнения тренировочных заданий в этой бесплатной онлайн-игре.
- MathBoard App: одно для родителей. Это полезное приложение знакомит детей с этапами решения уравнений сложения, вычитания, умножения и деления. Есть удобная доска для рисования, где дети могут решать задачи вручную.
- Математика движения: Пицца! Приложение: Пицца, пицца! В этой математической игре вы покупаете ингредиенты, разрабатываете фирменные пиццы и продаете их клиентам (надеюсь, с прибылью).
- Математика движения: Questimate! Приложение: насколько быстро самый быстрый поезд в мире? Сколько мармеладов заполняет футбольный мяч? В Questimate !, вы можете придумывать свои собственные вопросы.
- Mystery Math Town: Ваша миссия, если вы решите принять ее, — спасти светлячков, спрятанных в Mystery Math Town. Будьте осторожны: вам понадобятся математические навыки, чтобы открыть все комнаты и проходы в вашем квесте!
- Числовая лига: в Числовой лиге только математика может спасти положение. Вы будете использовать все, от сложения до отрицательных чисел, чтобы собрать команду супергероев и поймать орду злодеев.
- Умиго: Все надоело? У сумасшедших персонажей UMIGO есть ответ. Их интерактивные игры идеально подходят для развития математических навыков и навыков критического мышления.
- Brain Pop Jr .: Вы любите математику? Хотите быстро вычислять числа? В Brain Pop есть все советы и хитрости, чтобы научиться лучше разбираться в числах.
- CoolMath5Kids: Cool4Math — отличный ресурс для детей, которые любят играть в игры. Он сочетает в себе обучение с играми, что доставляет дополнительные математические удовольствия.
- Fun Brain: Funbrain сортируется по типу класса, он предназначен для детей от дошкольного до восьмого классов. В нем есть все необходимые математические ресурсы для ваших детей.
Конкурсы STEM
- Junior FIRST® LEGO® League: вы фанат LEGO®? Тогда это конкурс для вас. Вы будете использовать кубики LEGO®, чтобы спроектировать и построить движущуюся модель; Затем вы соберете плакат Show Me, чтобы продемонстрировать свое решение. Для детей от 6 до 9 лет.
- NSBE KidZone Элементарная научная олимпиада: соберите команду и проверьте свои научные навыки в 18 различных мероприятиях на национальном съезде Национального общества чернокожих инженеров (NSBE).Открыт для учащихся с третьего по пятый класс. Учащиеся от детского сада до второго класса соревнуются в неконкурентной лиге.
- Многолетние математические турниры: виртуальный математический турнир (посредством видеоконференцсвязи) для команд и отдельных лиц. Открыт для учащихся с третьего по восьмой класс.
STEM лагеря
- Природные лагеря Одубона: Одобон предлагает множество природных лагерей по всей стране. С апреля они начинают принимать заявки на участие в программе «Пути диких птиц к природе».
- Camp Invention: Мечты становятся открытиями в этом летнем дневном лагере.Созданный Национальным залом славы изобретателей, Camp Invention представляет основные концепции STEM посредством творческих практических занятий.
- Cosmophere Camps: В бесконечность и дальше! Эти крутые тематические лагеря, посвященные полетам и космическим приключениям, проходят в принадлежащем Смитсоновскому институту Канзасском космическом и космическом центре (KAOS) в Хатчинсоне, штат Канзас.
- Destination Science Camp: проведите этим летом неделю, создавая роботов, создавая цифровую музыкальную систему, тренируя хамелеона с электроприводом или даже готовясь к миссии на Луну! Проводится в 130 точках в шести штатах.
- Digital Media Academy Adventures Camp: отмеченные наградами лагеря Digital Media охватывают все, от создания мультфильмов до компьютерного программирования и продвинутой робототехники с LEGO® EV3. Для детей от 8 до 12 лет.
- Engineering for Kids: Engineering for Kids — образовательная компания для детей от 4 до 14 лет. Она предлагает множество программ STEM, в том числе школьные экскурсии, дни рождения, семинары и лагеря.
- iD Tech Camps: небоскребы для дневных и ночных лагерей iD Tech.Создайте свою собственную видеоигру, запрограммируйте собственное приложение или даже код на Java.
- Летние лагеря KinderCare®: от дурацкой науки о воде до основ выживания в дикой природе — KinderCare предлагает множество программ для детей от дошкольного до школьного возраста.
- Исследователи науки: акулы и подводные лодки, зелья и слизь, замки и катапульты … что бы вы ни любили, в этих летних научных лагерях найдется занятие для вас. Предлагается в Пенсильвании, Нью-Джерси и Делавэре.
- Snapology: Snapology сотрудничает со школами по всей стране, предлагая программы, конкурсы и лагеря STEAM.Программы являются интерактивными, что позволяет детям учиться с помощью практических инструкций и игр. Программы предлагаются в различных форматах, в том числе после уроков, по выходным и летом.
- Vision Tech Camps: Vision Tech предлагает лагеря для детей от 7 до 17 лет в районе залива Сан-Франциско. Темы лагеря включают робототехнику, программирование, майнкрафт и многое другое.
- Молодежные цифровые летние лагеря: создавайте трехмерные модели для Minecraft, создавайте собственные видеоигры или даже создавайте трехмерную анимацию! Эти лагеря, ориентированные на цифровые технологии, проходят в разных южных городах.Для детей от 8 до 16 лет.
Карьерные ресурсы в STEM
- Карьера Проходка: Элементарно: Мечтаете о том, кем хотите стать, когда вырастете? Эти видеоролики о вакансиях в области науки, технологий, инженерии и математики могут помочь вам принять решение.
Примечание. Многие государственные и региональные организации не попали в этот список. Если вас интересуют местные лагеря, стипендии и внеклассные мероприятия, обратитесь к учителям и в школе.
STEM Fun для детей средней школы ↑
Классные веб-сайты STEM
- Теория большого мозга — Discovery Channel: У участников этого телешоу есть всего 30 минут, чтобы придумать решение (казалось бы) невозможной инженерной задачи.
- Билл Най, ученый. В развлекательных телесериалах Билла рассказывается обо всем, от комет до музыки. Повеселитесь с его домашними демо.
- Чи Альфа Му: иначе известный как Национальный клуб юношеских математиков, Чи Альфа Му является младшим братом Му Альфа Тета. Ознакомьтесь со списком конкурсов и летних грантов.
- Студенческий портал по гигиене окружающей среды: Хотите узнать больше о химических веществах, качестве воздуха и загрязнении воды? На этом веб-сайте есть видео, игры и эксперименты, которые помогут вам в этом.
- Дети впереди: золотое дно STEM. Kids Ahead наполнен всевозможными ресурсами, включая поиски мусора, видео, статьи, ссылки на местные мероприятия и веселые события, а также информацию о крутых вакансиях, которые вдохновляют и волнуют.
- MathMovesU: Оттачивайте свои математические навыки с помощью онлайн-игр, виртуальных аттракционов и национальных соревнований! MathMovesU также предлагает различные стипендии и спонсорство.
- MythBusters — Discovery Channel: сотрудники MythBusters используют эксперименты, чтобы опровергнуть слухи, мифы и городские легенды.(Во время эксперимента по химии пушечного ядра они случайно вонзили пушечное ядро в стену дома.)
- Sally Ride Science: основанная первой в Америке женщиной-астронавтом, Sally Ride Science проводит ряд студенческих программ, включая научные фестивали и ночевки.
- Наука Боб: Боб — учитель естественных наук, который любит экспериментировать (часто с Джимми Киммелом). На его веб-сайте есть видео, ссылки и множество идей для собственных экспериментов и проектов для научных ярмарок.
- SciJinks: Все дело в погоде. Национальная ассоциация океанических и атмосферных исследований (NOAA) и НАСА создали этот образовательный веб-сайт, чтобы учить детей метеорологии и наукам о Земле. Загляните в их раздел игр.
- Scratch: Созданный для детей от 8 до 16 лет, Scratch — это место, где вы можете создавать свои собственные интерактивные истории, игры и анимации. Проект группы Lifelong Kindergarten Group в MIT Media Lab.
- Virtual Tech Camps: круглогодичное онлайн-обучение для детей и подростков с учебной программой на Python, Java, Minecraft, Roblox, AI, Unreal Engine, Adobe, 3D-моделировании и многом другом.Сэкономьте 100 долларов с кодом ВМЕСТЕ.
STEM-игры и приложения
- Auditorium: The Online Experience: Auditorium — это красивая и сложная головоломка с множеством различных решений. Один обозреватель игры назвал это «частично головоломкой, частично световой скульптурой, частично музыкальным инструментом».
- CSI: Web Adventures: это захватывающее приключение, основанное на сериале T.V., позволяет вам раскрыть собственное судебное дело. Уровни варьируются от начального до продвинутого.
- DimensionU Games: DimensionU разработала множество игр, в которых используются STEM-навыки.Используйте математику, чтобы раскрыть тайны острова Ксено, или объедините силы в гонке, чтобы избавиться от био-цифрового вируса.
- Gamestar Mechanic: научитесь создавать собственную видеоигру! Исследуйте игровые квесты и пройдите курсы, чтобы развить свои навыки.
- Machinarium: невероятно интересная приключенческая игра в жанре «укажи и щелкни». Вы — робот, брошенный на свалку, и вам нужно решить ряд головоломок, чтобы вернуться в город, спасти девушку и победить плохих парней.
- Mathemagics Mental Math Tricks: поразите друзей и родителей этими быстрыми (но впечатляющими) математическими уловками.
- Minecraft: Minecraft — популярная игра с трехмерным построением блоков, которая доводит ваше воображение до предела. Защитите себя от ночных монстров или постройте гигантское единственное в своем роде создание.
- National Geographic Games: Путешествуйте вглубь нано-мира. Постройте самый зеленый город во вселенной. Готовьтесь к апокалипсису. Некоторые из этих игр бесплатны; некоторые должны быть куплены.
- Portal 2: умопомрачительная приключенческая игра, построенная на принципах физики и головоломках, связанных с окружающей средой.Перемещайтесь по порталам и сражайтесь с помешанным на мощи искусственным интеллектом GLaDOS. Подходит для подростков.
- Квантовая головоломка: исчез ваш дядя. Он оставил свое устройство межпространственного сдвига. А его дом стал очень странным. Добро пожаловать в основанную на физике головоломку, известную как Quantum Conundrum.
- Роботы для iPad: все, что вы хотите знать о роботах, в одном удобном приложении. Роботы для iPad имеют обзоры на 360 градусов, множество статей и спецификаций, а также сотни фотографий и видео.
- Кубик Рубика можно сделать: вы знали, что должна быть игра, полностью посвященная ему. Раскройте секреты всемирно известного кубика Рубика.
STEM лагеря
- Программа амбиций: смело отправляйтесь туда, где раньше не бывал ни один ребенок. Погрузитесь в шестидневное учебное приключение на авиационную тематику в Национальной летной академии во Флориде.
- Природные лагеря Одубона: в Аудобоне расположено огромное количество природных лагерей по всей стране.
- Лагерь Евклида: Математический исследовательский лагерь: участвуйте практически отовсюду! Шестинедельные летние лагеря Camp Euclid проводятся онлайн.Сотрудничайте с сокурсниками по математическим задачам, не требующим решения.
- Cosmophere Camps: откройте для себя острые ощущения космоса. Эти захватывающие тематические лагеря, посвященные полетам и космическим приключениям, проходят в принадлежащем Смитсоновскому институту Канзасском космическом и космическом центре (KAOS) в Хатчинсоне, штат Канзас.
- Летний лагерь Digital Media для подростков: отмеченные наградами летние лагеря Digital Media предназначены для подростков от 12 до 17 лет. Узнайте о дизайне и разработке игр, программировании и приложениях, кинопроизводстве и визуальных эффектах или трехмерном моделировании и анимации.
- Earth Camp: исследуйте чудеса пустыни Сонора в Аризоне. Вы разместитесь лагерем в дикой местности, исследуете ночное небо в Sky Center Университета Аризоны и станете экспертом в вопросах устойчивого развития и водных ресурсов.
- Летние лагеря инженеров: Хотите решить проблемы этим летом? Сервисный центр инженерного образования составил штатный перечень летних лагерей инженеров.
- Летний научный лагерь Бернарда Харриса ExxonMobil (EMBHSSC): живите (и играйте) в реальном кампусе колледжа.Эти популярные летние научные лагеря, созданные для поддержки недостаточно представленных учеников средней школы, расположены по всей стране.
- iD Tech Camps: создайте свою собственную видеоигру. Запрограммируйте собственное приложение. Код на Java. В дневных и ночевых лагерях iD Tech возможно практически все.
- Лагеря STEM Университета Северного Иллинойса: Университет Северного Иллинойса проводит летние лагеря STEM, которые позволяют учащимся средних школ заниматься междисциплинарной деятельностью. Студенты учатся на занятиях, на практических занятиях и во многом другом!
- Летний институт STEM в MIT: Летом STEM предлагает пятинедельный институт математики и естественных наук в MIT для учащихся, поступающих в классы с шестого по девятый.В стоимость включены экскурсии и занятия с ракеткой.
- Vision Tech Camps: Vision Tech предлагает лагеря для детей от 7 до 17 лет в районе Сан-Франциско. Лагеря посвящены таким темам, как инженерия, игровой дизайн, робототехника и многое другое.
- Молодежные цифровые летние лагеря: создавайте трехмерные модели для Minecraft, создавайте собственные видеоигры или даже создавайте трехмерную анимацию! Эти лагеря, ориентированные на цифровые технологии, проходят в разных южных городах. Для детей от 8 до 16 лет.
- Youth Empowered Action (YEA): YEA — это недельный лагерь с ночевкой для молодежи в возрасте от 12 до 17 лет, которая хочет изменить мир.Семинары включают «Головоломки планетарных проблем» и «Миллион способов изменить мир к лучшему».
- Летняя программа средней школы Zero Robotics: Начните изучать компьютерное программирование, робототехнику и космическую инженерию. Пятинедельная программа STEM в Массачусетском технологическом институте погрузит вас в пространство и предоставит практический опыт программирования СФЕР (синхронизация, положение, удержание, взаимодействие, переориентация, экспериментальные спутники).
Научно-технические конкурсы
- Discovery Channel Young Scientist Challenge: в этом единственном в своем роде конкурсе вам будет предложено создать одно-двухминутное видео, описывающее новое и инновационное решение, которое может решить повседневную проблему.Главный приз — 25000 долларов и международная поездка!
- ЭЦИБЕРМИССИЯ: Выполняя миссию (например, альтернативные источники энергии) вместе со своей командой, у вас есть шанс выиграть 5000 долларов в виде сберегательных облигаций и грант STEM-in-Action, чтобы ваше решение работало в вашем сообществе.
- FIRST® LEGO® League: спроектируйте, соберите и запрограммируйте своего собственного робота с помощью технологии LEGO MINDSTORMS®! Набирайте очки на тематическом игровом поле и разрабатывайте решения реальных задач.
- Future City Competition: если вы можете себе это представить, вы можете это построить.Работая с педагогом и наставником инженеров, вы будете планировать город с помощью программного обеспечения SimCity ™, искать решения инженерных проблем и строить настольные модели из переработанных материалов.
- National Stem League (NSL): Ранее известная как Ten80 Student Racing Challenge, NSL предлагает четыре различных конкурса для учащихся средних и старших классов. Вы можете спроектировать быстрый, эффективный и стабильный гоночный автомобиль в Racing Challenge, научить робота проходить курс в Rover Challenge, перейти на возобновляемые источники энергии в Energy Challenge или сделать что-то совершенно новое в Innovation Challenge.
- National STEM Video Game Challenge: представьте свой оригинальный игровой дизайн, созданный с помощью таких инструментов, как Gamestar Mechanic, Scratch и Kodu. Победитель получит портативный компьютер на базе процессора AMD с программным обеспечением для игрового дизайна и 2000 долларов для своей школы.
- NSBE Jr. Bridge Magazine Contests: Национальное общество чернокожих инженеров спонсирует различные конкурсы, в которых вам предлагается продемонстрировать свои навыки STEM или повысить осведомленность о проблемах в STEM.
- Конкурс технических инноваций NSBE Jr. Explorer: сразитесь с другими студентами-учеными на ежегодном съезде NSBE.Учащиеся средних и старших классов имеют право на участие. Для участия вы должны быть оплачиваемым участником NSBE Jr.
Соревнования по математике
- AMC 8: Проверьте свои математические навыки в этом конкурсе из 25 вопросов и 40 минут с несколькими вариантами ответов (проводится каждый ноябрь).
- Серия соревнований MATHCOUNTS: MATHCOUNTS проводит серию конкурсов «пчелиный стиль» в более чем 500 местных отделениях. Лучшие команды проходят на государственные соревнования, а затем в Национальные соревнования в мае.
- MATHCOUNTS Math Video Challenge: создайте собственное математическое видео с друзьями и одноклассниками и участвуйте в гонках, чтобы выиграть стипендию в колледже!
- Многолетние математические турниры: виртуальный математический турнир (посредством видеоконференцсвязи) для команд и отдельных лиц.Открыт для учащихся с третьего по восьмой класс.
- Rocket City Math League (RCML): спонсируемый Mu Alpha Theta, RCML — это ежегодное соревнование по математике, состоящее из четырех раундов. В конце года призы рассылаются по почте лучшим ученикам средних и старших классов.
- USA Mathematical Talent Search (USAMTS): сравните свои навыки решения проблем с одними из самых сложных головоломок. Из-за уровня сложности USAMTS дает студентам целый месяц или более для выработки решений.
Карьерные ресурсы в STEM
- Карьерные исследования !: STEM: Хотите знать, что нас ждет в будущем? Изучите некоторые из доступных вам вариантов в области естественных наук, технологий, инженерии и математики.Много видео.
- Kids.gov Работа: получайте худощавую на любой работе под солнцем. Хотите знать, чем занимаются морские биологи? Хотите посмотреть видео о том, как стать ветеринаром? Вы попали в нужное место.
- НАСА: взгляд в будущее: карьера в космосе: вам не нужно быть астронавтом, чтобы работать в космической программе. У НАСА есть список других профессий, в том числе инженер-робототехник, ученый-компьютерщик и океанограф, на ваш выбор.
Примечание. Многие государственные и региональные организации не попали в этот список.Если вас интересуют местные лагеря, стипендии и внеклассные мероприятия, обратитесь к учителям и в школе.
STEM Fun для старшеклассников ↑
Классные веб-сайты STEM
- Arrick Robotics: это самый красивый веб-сайт в мире, но если вы ищете ресурсы по робототехнике, вам сюда. Включает списки соревнований и конкурсов, групп и клубов, игр и симуляторов.
- Codeacademy: научитесь программировать в интерактивном режиме (и бесплатно).Codeacademy предлагает классы кодирования на основных языках программирования, таких как Python, PHP, jQuery, JavaScript и Ruby.
- DiscoverE: Думаете о технике? DiscoverE предлагает подборку ресурсов по вопросам карьеры, подготовки к поступлению в колледж и исследовательских школ. Вы также можете проверить их список видео, поездок, веб-сайтов и практических занятий.
- Му Альфа Тета: Также известная как Национальное общество математиков средней школы и двухгодичного колледжа, Му Альфа Тета насчитывает более 100 000 студентов.Он организует национальный математический конгресс, предлагает специальные награды и проводит конкурсы.
- Student Science: центральное место для научных новостей, блогов, ресурсов и информации о соревнованиях Intel. Примеры названий статей включают «Родные сопли» и «Библиотека без книг».
- Virtual Tech Camps: круглогодичное онлайн-обучение для детей и подростков с учебной программой на Python, Java, Minecraft, Roblox, AI, Unreal Engine, Adobe, 3D-моделировании и многом другом. Сэкономьте 100 долларов с кодом ВМЕСТЕ.
STEM-игры и приложения
- Приложение Algebra Touch: освежите свои навыки алгебры с помощью этого сенсорного инструмента. Нажмите, чтобы упростить, перетащите, чтобы изменить порядок, и нарисуйте линии, чтобы исключить идентичные термины.
- The Elements App: Если вы так же увлекаетесь периодической таблицей Менделеева, как и я, вам понадобится это приложение. Узнайте текущую цену на золото, узнайте период полураспада плутония или прочитайте информацию о гелий-неоновых лазерах. Приложение
- Interplanetary 3D Sun: этот инструмент, спонсируемый НАСА, собирает данные с флота космических аппаратов НАСА.Наблюдайте за солнечными вспышками, выбросами корональной массы и геомагнитными бурями сразу после их возникновения. Приложение
- Muscle System Pro III: снимите плоть, чтобы узнать, что находится под ней. Это интерактивное приложение, разработанное в сотрудничестве с Медицинской школой Стэнфордского университета, позволяет исследовать работу мускулатуры человека слой за слоем. Приложение
- НАСА: обязательное условие для поклонников НАСА. Это приложение-монстр включает в себя прямую трансляцию телеканалов NASA и более 13 000 изображений, а также видео по запросу, новости и возможности для наблюдения за Международной космической станцией (МКС).Это тоже бывает бесплатно.
- National Geographic Apps: National Geographic предлагает множество развлечений в скучный день. Среди приложений с самым высоким рейтингом — Национальные парки и Мировой Атлас.
- Pocket Universe App: безграничная астрономия. Совершите виртуальный визит на поверхность Марса. Оживите ночное небо. Играйте в викторины. Получайте всплывающие уведомления об астрономических событиях.
- Virtual Frog Dissection: Все образование без кишки. Это приложение позволяет вам использовать инструменты виртуального препарирования, чтобы раскрыть тайны анатомии земноводных.
STEM лагеря
- Летняя исследовательская академия на Аляске (ASRA) — средняя школа: в ASRA вы проведете две недели в кампусе Университета Аляски в Фэрбенксе, работая в небольших группах и участвуя в проектном обучении. Некоторые модули доставят вас в отдаленные районы Аляски для полевых исследований.
- Программа амбиций: приготовьтесь к захватывающей поездке. На шесть дней вы погрузитесь в учебное приключение на авиационную тематику в Национальной летной академии в Пенсаколе, штат Флорида.
- Природные лагеря Одубона: в Аудобоне расположено огромное количество природных лагерей по всей стране.
- Camp Euclid: A Mathematics Research Camp: Шестинедельные виртуальные летние лагеря Camp Euclid проводятся онлайн. Вместе с однокурсниками решайте невероятно сложные математические задачи.
- Cosmosphere Camps: Эти тематические лагеря, посвященные полетам и космическим приключениям, проходят в Канзасском космическом и космическом центре (KAOS), входящем в состав Смитсоновского института, в Хатчинсоне, штат Канзас.
- Летний лагерь по цифровым медиа для подростков: приступайте к творчеству с дизайном и разработкой игр, программированием и приложениями, созданием фильмов и визуальными эффектами или трехмерным моделированием и анимацией.Отмеченные наградами летние лагеря Digital Media предназначены для подростков от 12 до 17 лет.
- Earth Camp: исследуйте глобальные изменения климата, воды и ландшафта, сплавляясь по каньону Пустоши Грин-Ривер в центральной части штата Юта. Управляется Научным колледжем Университета Аризоны, проектом WET, Институтом планетологии и Музеем пустыни Аризоны.
- Летние лагеря инженеров: ознакомьтесь с этим списком инженерных лагерей по штатам для ближайшего к вам летнего лагеря.
- iD Game Design & Development Academy: Эти двухнедельные летние лагеря предлагают интенсивное погружение в разработку игр, программирование, дизайн, трехмерное моделирование и анимацию.Выбирайте из курсов по Minecraft, Unreal® Engine, Maya®, iPhone® и многим другим. Для подростков от 13 до 18 лет.
- Game Camp Nation: Game Camp Nation предлагает развлекательные программы, которые раскрывают страсть вашего ребенка к видеоиграм. У них есть места на восточном побережье от Массачусетса до Атланты для детей от 7 до 16 лет. В настоящее время они предлагают несколько программ, включая Game Design с Tynker, Coding & Minecraft Modding с Java и Программирование 3D-игр с Unity.
- iD Programming Academy: идеально подходит для студентов с предыдущим опытом программирования, которые хотят вывести свои навыки программирования на новый уровень.Лагеря проводятся в университетских городках США для подростков от 13 до 18 лет.
- iD Tech Camps для подростков: выберите свое собственное приключение. Недельные летние лагеря iD позволяют вам запрограммировать новое приложение, снять фильм, разработать веб-сайт — практически все, что связано с технологиями. Для подростков от 13 до 17 лет.
- STEM-лагеря Университета Северного Иллинойса: NIU предлагает несколько летних STEM-лагерей для старшеклассников, в том числе STEM Career Explorations, Crisis on Mars! И STEAM Camp Eagle’s Nest.
- Программа обучения науке и инженерии (SEAP): интересуетесь естественными науками или математикой? Затем вы могли бы пройти стажировку в течение восьми недель в лаборатории Министерства военно-морского флота (DoN).В большинстве лабораторий требуется, чтобы учащиеся были не моложе 16 лет (хотя иногда допускаются и 15-летние).
- Летняя академия математики и естественных наук (SAMS): Конкурсная летняя программа Карнеги-Меллона предназначена для перспективных студентов, поступающих в младшие или старшие классы средней школы и планирующих карьеру в сфере STEM. Нагрузка на курс довольно высока, но если вас выбрали, плата за обучение, проживание или питание не взимается.
- Vision Tech Camps: Vision Tech предлагает летние лагеря для детей в возрасте от 7 до 17 лет в районе залива Сан-Франциско.Дети пройдут курсы инженерии, робототехники, программирования, игрового дизайна и других интересных технических тем.
- Молодежные цифровые летние лагеря: создавайте трехмерные модели для Minecraft, создавайте собственные видеоигры или даже создавайте трехмерную анимацию! Эти лагеря, посвященные цифровым технологиям, проходят в различных южных городах. Для детей от 8 до 16 лет.
- Youth Empowered Action (YEA): YEA — это недельный лагерь с ночёвкой для детей от 12 до 17 лет, которые хотят изменить мир. Семинары включают «Головоломки планетарных проблем» и «Миллион способов изменить мир к лучшему.”
Научно-технические конкурсы
- AbilityOne Design Challenge: задача с целью. Вы будете исследовать, разрабатывать и разрабатывать технологии, которые позволят людям с ограниченными возможностями найти новую работу или повысить производительность труда на рабочем месте.
- Air Force Association (AFA) CyberPatriot Competition: устранение реальных ситуаций кибербезопасности в виртуальной среде. Ранние туры проходят онлайн в выходные осенью, зимой и весной; лучшие команды приглашены в Вашингтон, Д.C. принять участие в Национальном финале конкурса.
- Центр образования в области математики и информатики: CEMC Университета Ватерлоо содержит всемирно признанные материалы, призванные помочь детям влюбиться в математику и информатику.
- Envirothon: соревнуйтесь за награды и стипендии, демонстрируя свои знания в области наук об окружающей среде и управления природными ресурсами. Команды проходят через местные соревнования Envirothon в недельные летние финалы в июле или августе.
- FIRST® Robotics Competition (FRC): создавайте, программируйте и соревнуйтесь с роботом собственной конструкции. Изучите сложное оборудование, работайте с профессиональными инженерами и получите право на студенческие стипендии.
- FIRST® Tech Challenge (FTC): Близкий родственник FRC, FTC предлагает вам создать робота, которого вы сможете использовать, чтобы соревноваться в формате альянса с другими командами. Вы получите практический опыт программирования и быстрого прототипирования.
- Intel International Science and Engineering Fair (ISEF): Годзилла научных ярмарок.Около 1800 новаторов приглашаются принять участие в недельном празднике науки, технологий, инженерии и математики. Разыграны премии и стипендии на сумму более 5 миллионов долларов.
- Intel Science Talent Search (STS): Intel STS позиционирует себя как старейшее и самое престижное национальное соревнование по науке перед колледжем. Сорок финалистов соревнуются за награды в размере 630 000 долларов и за первое место в размере 100 000 долларов. Это грандиозно: восемь выпускников получили Нобелевскую премию.
- NASA Asteroid Grand Challenge Series: станьте настоящим охотником за астероидами.В серии задач топкодера вам будет предложено разработать значительно улучшенный алгоритм идентификации астероидов на изображениях, полученных с наземных телескопов.
- Эксперименты по исследованию капиллярных эффектов НАСА в жидкостях (CELERE): CELERE, разработанный НАСА и Портлендским государственным университетом (PSU), открыт для студенческих команд с девятого по двенадцатый классы и многоуровневых команд с пятого по двенадцатый класс. эксперимент, проверяющий влияние микрогравитации на действие капилляров; PSU проводит испытания на своей башне Dryden Drop Tower.
- НАСА «Падение в условиях микрогравитации» (DIME): DIME открыт для студенческих команд, заинтересованных в разработке и проведении научного эксперимента, который можно проводить в условиях микрогравитации. Финалисты едут в Исследовательский центр Гленна, чтобы провести свои эксперименты в башне НАСА.
- National Stem League (NSL): Ранее известная как Ten80 Student Racing Challenge, NSL предлагает четыре различных конкурса для учащихся средних и старших классов. Вы можете спроектировать быстрый, эффективный и стабильный гоночный автомобиль в Racing Challenge, научить робота проходить курс в Rover Challenge, перейти на возобновляемые источники энергии в Energy Challenge или сделать что-то совершенно новое в Innovation Challenge
- NSBE Jr.Конкурс технических инноваций Explorer: сразитесь с другими студентами-учеными на Ежегодном съезде NSBE. Учащиеся средних и старших классов имеют право на участие. Для участия вы должны быть оплачиваемым участником NSBE Jr.
- Team America Rocketry Challenge (TARC): спроектируйте, соберите и запустите свою собственную ракету. Разработанный Ассоциацией аэрокосмической промышленности, это единственный конкурс STEM в аэрокосмической отрасли в стране. Студенты соревнуются в командах от трех до 10 человек; команда-победитель забрала домой 10 500 долларов в 2014 году.
- Zero Robotics High School Tournament: Решите проблему, интересующую DARPA, NASA и MIT. Если вы пройдете контролируемое моделирование до финала, вы увидите, как ваш код запускается на спутниках SPHERES на борту Международной космической станции с прямой трансляцией из космоса.
Соревнования по математике
- Американский экзамен по математике (AIME): Абитуриенты с высокими баллами AMC 10 и AMC 12 (см. Ниже) могут быть приглашены на трехчасовой экзамен AMAA из 15 вопросов.Лучшие бомбардиры этого теста попадают в USAMO (см. Ниже).
- AMC 10/12: Каждый год AMAA предлагает 75-минутные экзамены по математике средней школы с 25 вопросами и несколькими вариантами ответов. Это первый шаг на пути к Международной математической олимпиаде (см. Ниже).
- Соревнование силы Американской региональной математической лиги (ARML): в командную работу? Соревнование ARML Power Contest предоставит вам и вашим товарищам два набора задач, один осенью и один в конце зимы, каждый из которых необходимо решить в течение 45 минут.Трофеи награждаются 10 лучших команд.
- Международная математическая олимпиада (IMO): если вы прошли AMC 10/12, AIME, USAMO и Летнюю программу математической олимпиады (MOSP), вам будет предложено соревноваться за США со сверстниками из более 90 стран на этом двухдневном экзамене.
- Moody’s Mega Math (M3) Challenge: во время M3 у вас и небольшой команды юниоров и / или пожилых людей есть 14 часов на решение открытой задачи прикладного математического моделирования, ориентированной на реальную проблему.Вы можете работать из любого места. Победителям вручаются стипендии.
- NSBE Jr. Try-Math-A-Lon: Национальное общество чернокожих инженеров разработало этот конкурс для обучения школьников математике, естественным наукам и истории афроамериканцев на уровне SAT. Победители из числа местных и региональных жителей направляются на Национальный съезд NSBE.
- Пурпурная комета! Math Meet: название банальное, но репутация конкурса сильна. В этом бесплатном онлайн-соревновании по математике вашей команде будет предложено 25 задач, которые нужно решить за 90 минут.
- Rocket City Math League (RCML): спонсируемый Mu Alpha Theta, RCML — это ежегодное соревнование по математике, состоящее из четырех раундов. В конце года призы рассылаются по почте лучшим ученикам средних и старших классов.
- Юношеская математическая олимпиада в США (USAJMO): На этот двухдневный экзамен приглашаются только лучшие участники AIME / AMC 10. Это включает шесть вопросов и девять часов экзаменов для эссе / корректуры. Лучшие бомбардиры переходят в Летнюю программу математической олимпиады (MASP).
- U.Математическая олимпиада S.A. (USAMO): На этот двухдневный экзамен приглашаются только лучшие бомбардиры AIME / AMC 12. Это включает шесть вопросов и девять часов экзаменов для эссе / корректуры. Лучшие бомбардиры переходят на Летнюю программу математической олимпиады (MASP).
- USA Mathematical Talent Search (USAMTS): сравните свои навыки решения проблем с одними из самых сложных головоломок. Из-за уровня сложности USAMTS дает студентам целый месяц или более для выработки решений.
- Кто хочет стать математиком ?: Сражайтесь за деньги и призы, отвечая на вопросы по математике с несколькими вариантами ответов.Квалификационные тесты сдаются онлайн; полуфиналы и финалы проходят на совместных встречах по математике.
Гранты и возможности STEM
- InvenTeam: InventTeams состоят из студентов, преподавателей и наставников, которые получают гранты в размере до 10 000 долларов США на разработку технологических решений реальных проблем (вы можете выбрать свою проблему).
- Студенческие гранты Planet Connect: У вас есть страсть к защите дикой природы и естественной среды обитания? Planet Connect предлагает старшеклассникам гранты в размере 1000 долларов на реализацию местных проектов и участие в стажировках по дикой природе или природным ресурсам.
Карьерные ресурсы в STEM
- Science Splash: High School: Вы найдете множество исследовательских видео на сайте Career Aisle, а также ссылки на информацию о заработной плате и ресурсы по подготовке к карьере.
- Career Cornerstone Center: Он не выиграет никаких призов за красоту, но Career Cornerstone Center предлагает множество полезных ресурсов о карьере в STEM. Изучите более 185 дипломных областей, окунитесь в интервью или узнайте больше об образовательных требованиях, типичных зарплатах и сетях.
- CareerOneStop: узнайте все, что вам нужно знать о карьере в STEM, включая типичные профессии, стажировки и варианты обучения. При поддержке Министерства труда, занятости и обучения США.
- IEEE Try Computing: хороший ресурс, если вы только начинаете разбираться в вычислениях. Вы можете изучить варианты карьеры и специальности, искать аккредитованные программы и поработать с визуальным облачным инструментом карьеры.
- IEEE Try Engineering: этот веб-сайт включает поиск по университетам, информацию по инженерным специальностям и длинный список ссылок на лагеря, стажировки, стипендии, конкурсы и многое другое.Вы также найдете мнения экспертов и виртуальные инженерные игры.
- IEEE Попробуйте Nano: IEEE обходит стороной. На третьем этапе своей карьеры (см. Выше) они смотрят на вакансии в области нанонауки и нанотехнологий: технические области, в которых основное внимание уделяется материи в наномасштабе.
Примечание. Многие государственные и региональные организации не попали в этот список. Если вас интересуют местные лагеря, стипендии и внеклассные мероприятия, обратитесь к учителям и в школе.
STEM Fun для девочек ↑
Классные веб-сайты STEM
- CanTEEN: CanTEEN был разработан, чтобы помочь девушкам исследовать карьеру в STEM. Примите вызов (например, создайте свой собственный городской сад), играйте в такие игры, как «Click! Школа шпионажа »или узнайте больше о реальных образцах для подражания.
- Engineer Girl !: Почему ты должен стать инженером? Позвольте этому сайту для девочек средней школы объяснить. Помимо интервью, викторин, интересных фактов и профилей, в нем есть ссылки на множество инженерных соревнований, клубов, программ и стипендий.
- Для девушек в науке: будь тем, кем хочешь быть. Этот сайт, спонсируемый L’Oréal, предлагает всевозможные варианты STEM, включая видеоблог, профили женщин в науке, список летних лагерей и информацию о карьере.
- Girls Communicating Care Connections (GC3): Хотите сделать карьеру в науке или технологиях? В этом молодежном сериале для девушек из незаслуженных групп есть много идей, которые стоит изучить.
- Программа для девочек-скаутов STEM: расширяйте свои границы, делая мир лучше.Чтобы поддержать опыт STEM, девочки-скауты разработали три направления лидерства и несколько значков уровня владения STEM.
- iWASwondering.org: этот веб-сайт, вдохновленный «Приключениями женщин в науке» и разработанный Национальной академией наук, предлагает вам изучить карьеры известных женщин-ученых.
- PBS SciGirls: видео SciGirls — отличный ресурс для классной комнаты. В каждом эпизоде рассказывается о разных группах девочек средней школы, которые разрабатывают и создают проекты STEM.
- Общество женщин-инженеров (SWE) K-12 Outreach: Стремитесь к успеху. На этом сайте вы найдете огромное количество инженерных ресурсов, включая ссылки на мероприятия, конкурсы, лагеря и стипендии.
- Women @ NASA: Познакомьтесь с женщинами, которыми вы хотите быть. Этот сайт НАСА включает видеоинтервью и биографии сотрудников НАСА, а также информацию о карьере, мероприятиях и информационно-просветительских программах. Energy.gov имеет дочерний сайт под названием Women @ Energy.
- Virtual Tech Camps: круглогодичное онлайн-обучение для детей и подростков с учебной программой на Python, Java, Minecraft, Roblox, AI, Unreal Engine, Adobe, 3D-моделировании и многом другом.Сэкономьте 100 долларов с кодом ВМЕСТЕ.
Награды STEM
- Премия NSTA Angela: Национальная ассоциация учителей естественных наук присуждает сберегательную облигацию EE в размере 1000 долларов США одной ученице пятого-восьмого классов, которая занимается наукой или имеет прочные связи с ней.
STEM лагеря
- Camp Reach: Этот двухнедельный летний лагерь в Вустерском политехническом институте в Массачусетсе разработан для того, чтобы развить ваше инженерное воображение, от создания идеальной обуви до создания идеального мороженого.Для девочек, поступающих в седьмой класс.
- Дизайн-Соединение-Создавайте! Физические лагеря для молодых женщин: живете в Северном Техасе или рядом с ним? Получите практическое введение в ключевые принципы AP Physics. Для старшеклассниц, поступающих в младшие классы.
- DigiGirlz High Tech Camp: профессиональные лагеря Microsoft проводятся по всей территории США и за рубежом. У вас будет возможность послушать технических докладчиков, посетить экскурсии, пообщаться и получить практический опыт на семинарах. Вариант расписания. Для старшеклассниц.
- E2 @ UMD: Изучите инженерное дело в Университете Мэриленда. В течение одной летней недели вы будете участвовать в практических занятиях, лабораторных экспериментах, командных задачах и семинарах с профессиональными инженерами. Для начинающих юниоров и пожилых людей.
- Girls ’Adventures in Mathematics, Engineering and Science (G.A.M.E.S.): станьте частью современной инженерной или научной лаборатории этим летом! В G.A.M.E.S. Университета Иллинойса вы будете работать над сложными проектами лагерей и встречаться с наставниками в технических областях.Для учеников с девяти до двенадцати классов.
- девочек достигают успехов в спорте и физике (GRASP): пятидневный летний лагерь GRASP, организованный факультетом физики Университета штата Огайо, наполнен увлекательной физикой. Сотрудники и студенты ОГУ присутствуют на всех занятиях, чтобы поделиться своей любовью к этому предмету. Для девочек средней школы.
- Girlstart: застрять на предметах STEM. Программы Girlstart в Остине (включая летние лагеря, субботние семинары STEM и Science Extravaganzas) открыты для девочек из детских садов до 16 лет.
- Студенты с потенциалом и интересом, рассматривающие инженерию (S.P.I.C.E.): Постройте новый мир. Благодаря мероприятиям, проектам, турам и беседам в Университете Мэриленда, Колледж-Парк, вы узнаете, как инженерные разработки используются для изменения облика планеты. Для девочек, поступающих в девятые и десятые классы.
- Летняя научно-техническая программа Смита (SSEP): сто девочек, четыре недели, один невероятный опыт. В этом летнем лагере в Массачусетсе вы пройдете два увлекательных исследовательских курса.Для учащихся с девяти до двенадцати классов.
- Женщины в естествознании (WINS): эта внешкольная и летняя программа углубленного изучения естественных наук проводится Академией естественных наук Дрексельского университета бесплатно! Для перспективных восьмиклассников, планирующих посещать государственную или чартерную школу в Филадельфии.
- Alexa Cafe: Студенты работают небольшими сплоченными группами. Делая упор на предпринимательство, лидерство, идентичность бренда и благотворительность, вы будете развивать технические навыки в уникальной стильной обстановке вместе с технически подкованными женщинами-наставниками.Недельные дневные и ночные занятия по программированию, игровому дизайну, кинопроизводству и многому другому.
Примечание. Многие государственные и региональные организации не попали в этот список. Если вас интересуют местные лагеря, стипендии и внеклассные мероприятия, обратитесь к учителям и в школе.
ГДЗ по информатике 7 электронный блокнот. Как увидеть результаты и оценить работу ученика
Электронная рабочая тетрадь «Информатика 7 класс» Предназначена для учителей и учащихся школ школ, лицеев, гимназий.Блокнот представляет собой электронный тренажер, предназначенный для генерирования и закрепления знаний и навыков по предмету, а также для промежуточной аттестации студентов во время электронных четвертых работ. Рабочая тетрадь состоит из интерактивных задач, проверка которых производится автоматически — на компьютере.
Рабочая тетрадь входит в состав интерактивного мультимедийного учебно-методического комплекса «Облако знаний»; Результаты работы с рабочим блокнотом хранятся на облачном сервере проекта. Используя свою учетную запись и PIN-код, активирующий доступ к курсу, студент может работать с курсом из любого места, с любого компьютерного устройства и в любое время.
Для работы с электронным приложением необходим доступ в Интернет по каналу со скоростью передачи данных не менее 64 кБ / с на пользователя. При отсутствии доступа в Интернет пользователь не сможет авторизоваться, следовательно, у него не будет доступа к приобретенным материалам.
Содержание электронной рабочей записной книжки 1. Объекты, системы, модели.
1.1. Объекты и их свойства.
1.2. Классы объектов.
1,3. Системы объектов.
1,4.Модели предметов.
1,5. Словесные модели.
1,6. Математические модели.
1,7. Настольные модели.
1,8. Графические модели.
2. Понятие об алгоритме.
2.1. Алгоритм как модель деятельности.
2.2. Контроль со стороны исполнителя алгоритмов.
3. Компьютер как средство работы с информацией.
3.1. Компьютерная архитектура.
3.2. Основные компоненты ПК.
3.3. Процессор и материнская плата.
3.4. Машинная память.
3,5. Устройства ввода.
3,6. Устройства вывода.
3,7. Операционная система и прикладные программы.
3.8. Файлы и файловая система.
3.9. Пользовательский интерфейс.
3.10. Компьютерные вирусы и антивирусные программы.
В рабочей тетради по каждому пункту учебной программы представлено 2-10 интерактивных заданий. Кроме того, тетрадь содержит тематические контрольные работы, которые обобщаются, а материал проверяется по разделам, пройденным в течение четвертого школьного школьного обучения.
Блокнот содержит около 140 разнообразных интерактивных задач (для установления совпадений, заполнения таблиц, упорядочивания и распределения по группам, выбора варианта ответа, ввода числового или строкового ответа, установления ссылок, указания объекта на рисунке), сгруппированных в 4 раздела учебной программы 7 класса; В 2 контрольных тематических работах в двух вариантах каждая.
Перечень контрольных работ
- Объекты, системы, модели. Понятие об алгоритме.
- Компьютер как средство работы с информацией.
Видео
В этом видео демонстрируется принцип работы электронных рабочих тетрадей на основе облачных технологий (показаны рабочие тетради по математике, физике, истории и географии)
Комплект электронной рабочей тетради «Информатика.7 класс »
— для ПК
Плеер« Облако знаний »скачать (8,2 МБ)
Симулятор для предмета.
Индивидуальная лицензия (ПИН-код доступа) или лицензия для образовательного учреждения.
— для iPad и Android
Player» Облако знаний »Скачать (161.0 МБ)
Симулятор для предмета.
— для систем дистанционного обучения (DDO)
Симулятор для предмета в формате SCORM 2004 (архив ZIP). Выдается отдельно после оплаты.
Лицензия на образовательное учреждение.
Минимальные системные требования
- Операционная система Microsoft Windows 7/8/10.
- 100 МБ свободного дискового пространства для 1 симулятора.
- Устройство для чтения CD или DVD.
- Разрешение экрана — 1024 на 768 пикселей.
- Веб-браузер Microsoft Internet Explorer. 11.
- Доступ в Интернет по каналу со скоростью передачи данных не менее 64 Кб на пользователя. При отсутствии доступа в Интернет пользователь не сможет авторизоваться, следовательно, у него не будет доступа к приобретенным материалам.
- Компьютерное устройство: персональный компьютер или портативный компьютер (процессор Pentium 4 или выше; не менее 512 МБ оперативной памяти; не менее 31 МБ памяти на жестком диске) или планшетный компьютер под управлением ОС Android или iPad.
Для плеера необходим доступ в Интернет. Это необходимо для следующих операций:
- при регистрации пользователей,
- при аутентификации пользователей,
- при работе с прогрессом,
- при работе с закладками,
- при передаче результатов работы с контентом на сервер,
- при работе с контентом.
Оплата и доставка
— Способы оплаты
Вы можете выбрать наиболее удобный для Вас способ оплаты. Интернет-магазин «Интеграл» предлагает следующие варианты оплаты:
- Банковские карты.
- Интернет-банкинг — онлайн-платежи.
- Терминалы оплаты.
- Банковские переводы.
- Электронные деньги.
— Доставка
Электронная доставка бесплатна. Электронный ключ Или ключ активации высылается покупателю на электронную почту после оплаты.При необходимости также отправляется ссылка на скачивание.
В настоящее время мы не будем отправлять боксеры или программы, записанные на CD или DVD.
Каждый ученик — личный виртуальный учитель!
Характерные особенности программы «Электронный блокнот по информатике, 7 класс»
- Компактность, портативность и простота использования.
- Для работы этой программы не нужно устанавливать никаких дополнительных библиотек, плееров, каких-то специальных способов настройки системы.
- Необходимо, чтобы у вас была работоспособная система Windows и монитор с разрешением не менее 1024×576 пикселей.Программа отлично работает в семействе Windows.
Использование программы позволяет решать следующие задачи:
- Приемы действий при работе с программой просты и в то же время требуют от ребенка активности, самостоятельности и творческого подхода. «Позволяет решать следующие задачи:
- сделать увлекательный и интересный процесс обучения даже на самые скучные темы;
- реализовать потребности и интересы учащихся;
- развить исследования воображения, внимания, памяти, интеллекта и плавки, алгоритмического и логическое мышление;
- вдумчиво учить значению и значению каждого слова;
- освобождает учителей от рутинной работы.
Д. Сборник заданий и упражнений по химии для средней школы. Хомченко И.Г. Хомченко гДЗ по химии для общеобразовательной школы
Химия 8-11 класс
Сборник заданий и упражнений
Хомченко
Новая волна
Химия очень интересная, хоть и непростая наука, тем более для детей 14-17 лет. Иногда даже сами учителя забывают, как решать те или иные задачи.Решебник к учебнику «Химия 8-11 класс Сборник заданий и упражнений Хомченко Новая волна» — это простой способ справиться с задачами, которые оказались для вас непростыми. Но не стоит использовать эту памятку постоянно, так как она создана для того, чтобы вы смогли найти ответ на вопрос, который сами не смогли разгадать.
Почему был создан Решебник?
Нет ничего постыдного в том случае, если ты не понимаешь какой-либо задачи, ведь все люди разные.Кто-то буквально «схватывает на лету», а кому-то нужно подольше посидеть и разобраться в непонятной теме.
Но некоторые задачи очень сложно решить только с помощью своего ума, и спрашивать родителей нет смысла. Используйте резольвер только тогда, когда невозможно решить какую-либо проблему.
Какова функция этой книги
Решатель был создан для того, чтобы учащийся мог:
- Найти ответ на непонятную задачу.
- Расширьте свои знания в области химия .
- Научитесь решать проблемы самостоятельно.
И это еще не все возможности. ГДЗ .
Вы начинаете знакомиться с новым предметом — химией. С давних времен люди пытались понять, из чего состоит окружающий мир, как одна субстанция превращается в другую. Ответы на эти и многие другие вопросы вы найдете в школьном учебнике на весь курс химии с 8 по 11 класс.А чтобы школьникам было легче воспринимать новую информацию, известный специалист Хомченко И.Г. Разобрал учебник и выложил на свой решебник готовые ответы.
Сборник ГДЗ по химии для 8-11 классов Сборник задач Хомченко раскрывает суть всех заданий и упражнений из учебника. Материал пособия полностью соответствует требованиям школьной программы и утвержден Минобрнауки России для общеобразовательных учреждений.Готовые ответы помогут студентам справиться с непонятными задачами и проверить себя самостоятельно. Кроме того, такая публикация будет полезна и родителям, которым будет проще и быстрее проверить домашнее задание ребенка и объяснить ему непонятные темы. А для учителей такое пособие выступит дополнительным материалом на занятиях.
Всего ГДЗ по химии 8-11 классов включает тридцать глав. И сначала студенты познакомятся с основами предмета.Во второй главе они узнают о кислороде и его радикалах. Студенты из следующей главы поймут, как водород участвует в образовании кислоты и соли. Далее восьмиклассники обсудят тему растворов, воды и основ. Пятая глава познакомит вас с классами неорганических соединений. С шестой главы девятиклассники окончательно узнают о законе Д.И. Менделеева и выяснить строение атома.
Девятый класс предполагает изучение химических связей и особенностей строения веществ.Восьмая глава полностью посвящена закону Авогадро. Девятиклассники из следующей главы научатся решать все упражнения и задачи на галогенах. Не менее важная тема электролитической диссоциации будет рассмотрена ниже. В одиннадцатой главе студентам придется иметь дело с p-элементами VI группы периодической таблицы, которые являются подгруппой кислорода. Двенадцатая глава рассказывает о законах протекания химических реакций.
Ученики узнают об элементах V группы периодической таблицы Менделеева, которые являются подгруппой азота, из тринадцатой главы.N-элементы IV группы таблицы Менделеева из подгруппы углерода не останутся в разобранном виде. Студенты узнают об общих свойствах металла из пятнадцатой главы. А в шестнадцатой главе речь пойдет о металлах как элементах основных подгрупп периодической таблицы Менделеева. А вот о металлах, как элементах побочных подгрупп, станет известно из следующей главы.
Десятиклассникам также предстоит овладеть теорией химического строения органических соединений.В девятнадцатой главе они будут говорить о насыщенных углеводородах. Но обо всех непредельных углеводородах расскажет двадцатая глава. В десятом классе также изучается тема ароматических углеводородов. Вы можете узнать о природных источниках углеводородов из двадцать второй главы. О спиртах и фенолах станет известно из двадцать третьей главы. И вот теперь одиннадцатиклассники начнут знакомиться с альдегидами и карбоновыми кислотами.
Выпускники научатся решать задачи и проектировать лабораторные работы по сложным эфирам и жирам.Реакции с углеводами обсуждаются в главе двадцать седьмой. Двадцать восьмая глава принесет информацию обо всех азотсодержащих органических соединениях. А по окончании курса химии школьники будут рассматривать высокомолекулярные соединения. А тридцатая глава полностью посвящена повторению и углублению знаний в курсе химии. Авторы не забыли дать ответы на все вычислительные задачи.
2-е изд., Перераб. И доп. — М .: 2011 — 214 с.
В сборник включены задания и упражнения по химии, полностью соответствующие школьной программе, утвержденной Минобрнауки РФ для общеобразовательных учреждений. Книга предназначена для учителей химии как учебное пособие.
Формат: pdf
Размер: 23 Мб
Часы, скачать: 1 .10.2018, ссылки удалены по просьбе издательства «Новая волна».
СОДЕРЖАНИЕ
Предисловие 3
1.ОСНОВНЫЕ ПОНЯТИЯ ХИМИИ 5
Химические явления. Вещества 5
Относительные атомные и молекулярные массы. Согласованность состава вещества 6
Химические формулы и расчеты на их основе 7
Валентность 8
Химические уравнения. Типы реакций 9
Количество вещества. Крот. Молярная масса 10
Расчеты по химическим уравнениям 11
2. КИСЛОРОД. ОКСИДЫ. ГОРЕНИЕ 14
Производство кислорода и свойства 14
Воздух. Горение 15
Тепловое воздействие химических реакций 16
3.ВОДОРОД. КИСЛОТЫ. СОЛИ 18
Производство и свойства водорода 18
Кислоты и соли 19
4. РЕШЕНИЯ. ВОДА. ОСНОВАНИЯ 21
Растворы 21
Вода 23
Основа 24
5. ОБОБЩЕНИЕ ИНФОРМАЦИИ О КЛАССАХ НЕОРГАНИЧЕСКИХ СОЕДИНЕНИЙ 27
Оксиды 27
Основания 28
Кислоты 29
Соль 30
Связь между классами 31 906 неорганических соединений. ПЕРИОДИЧЕСКИЙ ЗАКОН Д.И. МЕНДЕЛЕЕВА. СТРОЕНИЕ АТОМА 35
Периодический закон и периодическая система Д.И. Менделеев 35
Строение атома. Изотопы. Ядерные реакции 36
Строение электронных оболочек атомов 37
7. ХИМИЧЕСКАЯ СВЯЗЬ И СТРУКТУРА ВЕЩЕСТВА 39
8. ЗАКОН АВОГАДРО 42
9. ГАЛОГЕНЫ 45
Хлор 45
Хлороводород, соляная кислота и ее соли 46
Общая характеристика галогенов 47
10. ЭЛЕКТРОЛИТИЧЕСКОЕ ДИССОЦИАЦИЯ 50
Электролиты 50
Ионообменные реакции 52
Окислительно-восстановительные реакции в растворах 54
Гидролиз солей 57
11.-Элементы V группы периодической системы Д.И. Менделеева (азотная подгруппа) 69
Азот 69
Аммиак и соли аммония 70
Азотная кислота и ее соли 72
Фосфор 74
Фосфорная кислота и ее соли 75
Минеральные удобрения 76
14. н-ЭЛЕМЕНТЫ IV ГРУППЫ ПЕРИОДИЧЕСКОЙ СИСТЕМЫ Д.И. МЕНДЕЛЕЕВА (подгруппа углерода) 78
Углерод 78
Оксиды углерода. Угольная кислота и ее соли 79
Кремний и его соединения 82
Силикаты и силикатная промышленность 84
15.ОБЩИЕ СВОЙСТВА МЕТАЛЛОВ 86
Строение атомов металлических элементов и их положение в периодической таблице 86
Получение металлов 87
Электролиз 89
Физико-химические свойства металлов 91
Сплавы. Коррозия металлов 94
16. МЕТАЛЛИЧЕСКИЕ ЭЛЕМЕНТЫ ОСНОВНЫХ ПОДГРУПП ПЕРИОДИЧЕСКОЙ СИСТЕМЫ Д. И. МЕНДЕЛЕЕВА 96
Щелочные металлы 96
Магний. Кальций 99
Алюминий 102
Олово. Свинец 105
17. МЕТАЛЛИЧЕСКИЕ ЭЛЕМЕНТЫ ПОБОЧНЫХ ПОДГРУПП ПЕРИОДИЧЕСКОЙ СИСТЕМЫ D.И. МЕНДЕЛЕЕВА 107
Железо и его соединения 107
Металлургия. Чугун и сталь 110
Титан и ванадий 112
Хром 113
Марганец 115
18. ТЕОРИЯ ХИМИЧЕСКОГО СТРУКТУРЫ ОРГАНИЧЕСКИХ СОЕДИНЕНИЙ 117
19. ПРЕДЕЛЫ УГЛЕВОДОРОДОВ 122
Алканы 122
Циклоалканы 127
Алкены 127
Алкадиены 132
Алкин 134
21. АРОМАТИЧЕСКИЕ УГЛЕВОДОРОДЫ 138
22. ПРИРОДНЫЕ ИСТОЧНИКИ УГЛЕВОДОРОДОВ 142
23.СПИРТЫ И ФЕНОЛЫ 145
Насыщенные одноатомные спирты 145
Многоатомные спирты 149
Фенолы 150
24. АЛЬДЕГИДЫ 153
25. УГЛЕВОДНЫЕ КИСЛОТЫ 157
26. Эфиры. ЖИРЫ 164
27. УГЛЕВОДЫ 167
28. АЗОТОСОДЕРЖАЩИЕ ОРГАНИЧЕСКИЕ СОЕДИНЕНИЯ 171
Амины 171
Аминокислоты 173
Азотсодержащие гетероциклические соединения 175
Белки 176
ДЛЯ ЗАМЕНА HIGATAS 906 И ЗАМЕНА HIGATAS 30. HIGATAS 906. УГЛУБЛЕНИЕ ЗНАНИЙ ХИМИИ 180
ПРИЛОЖЕНИЯ
1.Рекомендуемые обозначения физических величин 193
2. Растворимость оснований и солей в воде 194
3. Округленные значения относительных атомных масс некоторых химических элементов 195
4. Относительные молекулярные массы некоторых неорганических веществ 196
5. Относительные молекулярные массы некоторых органических веществ 197
6. Относительные электроотрицательности некоторых химических элементов 198
7. Электрохимические ряды напряжений (ряды стандартных электродных потенциалов металлов) 199
8.Периодическая таблица элементов Д. И. Менделеев 200
ОТВЕТЫ НА ЗАДАЧИ РАСЧЕТА 201
Предисловие
Освоение важного и очень интересного учебного предмета химии практически невозможно без решения различных задач и выполнения упражнений.
Сборник содержит задания и упражнения по всем темам, которые изучаются в общеобразовательных учреждениях (школах, лицеях, гимназиях, техникумах и т. Д.). Он содержит задания разного уровня. В основном это задания самой простой и средней сложности.Также есть небольшое количество задач повышенной сложности. Самые сложные задачи, которые, например, предлагаются на олимпиадах по химии и при поступлении в вузы с высокими требованиями по химии, в этот сборник не входят, их можно найти в специальных выпусках (см., Например, Хомченко Г.П., Хомченко И.Г. «Сборник задач по химии для поступающих в вузы», М .: РИА «Новая волна», 2010). Расположение материала в задаче соответствует наиболее традиционной последовательности изучения химии в старшей школе.
Решение конструкторских задач и выполнение различных упражнений — важный элемент изучения курса химии, так как позволяет лучше усвоить и систематизировать теоретический материал. Без практики решения задач знания студентов сильно формализованы, поэтому этому элементу обучения следует уделить особое внимание. При этом важно регулярно решать задачи и выполнять упражнения по всем изучаемым темам.
На большинство вычислительных задач, включенных в сборник, есть ответы, которые даются в конце книги.В проблемной книге решений не предусмотрено, так как выбор метода решения и формы записи определяет преподаватель.
При решении задач следует использовать международную систему единиц СИ. Некоторые общие несистемные единицы также могут использоваться в расчетах, например, литр (л), миллилитр (мл), тонна (т).
В конце книги есть приложения, содержащие справочные данные, необходимые для решения задач. Рекомендуем при решении расчетных задач использовать округленные значения атомных масс химических элементов и их соединений (см. Приложения 3, 4 и 5).В этом случае полученные ответы следует округлить до 3-4 значащих цифр.
cse 455 ub
UB CSE 703 Семинар: Расширенная безопасность программного обеспечения — методы и инструменты Весна 2021 01.02.2021 — 10.05.2021; Понедельник, 12:50 — 14:55; В сети. Краткое введение в графические модели и байесовские сети, Кевин Мерфи. 8, стр. Member_survey Загрузить. подобие никогда не допускается в индивидуальных заданиях. Курсы: APY 106, 476.Anhand einer kurzen Liste möchte ich Ihnen vorstellen, in welchen Branchen ich mehrfach beratend tätig war: Branche University of Pennsylvania, CSE 455 — Интернет и веб-системы (2007) Basari, ASH, Hussin, B., Ananta, IGP, Zeniarja, J. : Анализ мнений при просмотре фильмов с использованием гибридного метода машины опорных векторов и оптимизации роя частиц. Обсудив это с коллегами, вы сможете глубже понять. Вот неполный список курсов, предлагаемых по темам обучения в кампусе, связанным с искусственным интеллектом.В этой статье конструируются изменяющиеся во времени меры стоимости труда, свободные от таких ограничений, и показано, что они требуют радикальной переоценки дискуссии о стоимости в этом столетии. Общие активы Группы составили 123 162 млн рупий, из которых 93% приходятся на Банк. Ширина: 35,6 см (14 Zoll). … Запись на прием: Навигация. работа другого как своего собственного никогда не допускается. Rise Vision. Приложение 462 Обозначение Big O 462 … cse. . 83 страницы. Гипотеза экологической кривой Кузнеца (EKC) предполагает, что ухудшение состояния окружающей среды сначала увеличивается с ростом доходов, а затем снижается с ростом доходов.Распознавание образов и машинное обучение, Крис Бишоп (2006). Вместо вычисления суммы квадратов lsqcurvefit требует, чтобы пользовательская функция вычисляла векторнозначную функцию. Комната: Парк 250. CSE 455/555: Введение в распознавание образов. Часы работы: воскресенье — пятница с 9:00 до 22:00. Компромисс между экономическим ростом и экологической устойчивостью очень труден для такой быстрорастущей развивающейся страны, как Индия. Электронная почта: [email protected] Введение в поддержку векторных машин и других основанных на ядре методов обучения, автор: Кристианини и Шоу-Тейлор. Предварительное условие: CSE 311.Автоматический трубочный насос Dräger X-act® 5000 — это первое универсальное решение, разработанное для измерений с помощью пробирок Dräger Short-term Tubes и для пробоотборных трубок и систем. Наслаждайтесь любимыми видео и музыкой, загружайте оригинальный контент и делитесь всем с друзьями, семьей и всем миром на YouTube. Июль 2020 г .: в MOBILESoft’20 разрешено обнаружение вредоносных программ для Android с помощью строк. (Коротко) Не обманывайте! Другие вспомогательные материалы (будут расширены позже):… 13024 T 1-5 будет организовано REGES, STUART THOMAS Open 26/30 CR / NC ===== CSE 14X TA TRAINING; ТОЛЬКО ДЛЯ НОВОГО CSE 14X TAS =====> 13025 U 1-5 T 430-550P EEB 037 0/55 CR / NC Учебник / справочные книги: Speicher: 512 ГБ — SSD.Aufzeichnen, SpeichernundAusführen einesMakrosimÜberblick 9 Ausfüllen де Dialogfelds »Makroaufzeichnen« 10 AusführeneinesMakros 11 Erstellen einerMakroSchaltflächeim Menüband 12 Erstellen етег MakroSchaltflächein derSymbolleistefür ден Schnellzugriff 13 Zuweisen Эйнес Makros в Эйн Formularsteuerelement, Эйн Textfeld odereine Форма 14 651-666, июнь 2010, по А. К. Jain 8, стр Студенты, желающие получить степень бакалавра информатики, должны пройти не менее шести обязательных курсов CSE в UB, и по крайней мере четыре из этих курсов должны быть на уровне 300 или 400 (за исключением CSE 492, CSE 494 и CSE 499).Курс посвящен вопросам моделей данных и языков запросов, которые актуальны для создания современных приложений баз данных. Примечание. Оценка для оценок 455 и 555: 455 и 555 будут оцениваться на отдельных кривых, а сопоставление с оценкой A будет другим. Простота эксплуатации и высокая степень надежности дополняют измерения и образцы 1940 UB, 1929 VL, 1934 RA, A923 RJ: Pályaadatok: Epocha: 2009. június 18. IASBABA был очень важной частью моей подготовки. | CornHub FAQ HUB Academic Advising Report (AAR) Инициатива по предоставлению стратегической информации (SIRI) Digital Signage.Даты: 7 февраля 2021 г. — 7 мая 2021 г. Диселенид урана представляет собой соединение урана и селена. Он имеет β-форму, имеющую орторомбическую кристаллическую систему. подлежат проверке программным обеспечением, предназначенным для обнаружения доказательств плагиата или сотрудничества. 3820,455): Краткое изложение Эмиля Ласка незапланированной фрау; Universitätsbibliothek Heidelberg ([email protected]) Разработка программного обеспечения. Этот материал веселый, но может быть сложным. CSE 282 Проектирование системного программного обеспечения (3) CSE 283 Введение в объектно-ориентированное проектирование (3) CSE 351 Математический анализ цифровых систем (3) Компьютерная архитектура CSE 381 (3) Сети передачи данных CSE 458: основные принципы; … CME 455 Строительные контракты и спецификации (3). Концентрации CSE в текущем исследовании варьировались от 2 до 12%. Университет Буффало, SUNY; Дом; UB CSE Департамент; 11.3 CDS-Hierarchien 455 11.3.1 Beispieldaten für die Berichtshierarchie 455 11.3.2 CDS-Hierarchiedefinieren 459 11.3.3 Hierarchieattribute 461 11.3.4 Visualisierung einer Mierarchie 463 11.3.5 Hierarchie miteinemverwaistenme 466 469 11.3.8 WeitereOptionenfür die Определение vonHierarchien 471 11.3.9… Supermicro SuperChassis 815TQ-560UB schwarz, 1HE, 560W (CSE-815TQ-560UB) PyTorch — это среда глубокого обучения для быстрого и гибкого экспериментирования. На выполнение этой домашней работы может потребоваться больше времени. BE 455 Биомеханика и механобиология; BE 459 Введение в нейронную инженерию; BE 460 Введение в МРТ; BE 461 Введение в анализ биомедицинских изображений; BE 462 «Инженерные принципы компьютерной томографии»; BE 463 Введение в обработку данных и изображений с помощью LabVIEW; BE… 12-месячная программа ускоренного бакалавриата предназначена для студентов, которые уже получили степень бакалавра в Государственном университете Нью-Йорка в Стоуни-Брук или другом аналогичном учебном заведении.CS 455/555: Некоторые полные по Тьюрингу формализмы Стефан Д. Бруда Осень 2020 г. Машина случайного доступа (RAM) состоит из неограниченного набора регистров R i, i ¥ 0, одного регистра PC и блок управления Размер (т. е. In… Auflösung: 1920 x 1080 пикселей. Рассчитывайте текущую валюту и обменные курсы с помощью бесплатного конвертера валют Xe. Uni-Ball EYE UB-157 Rollerball Pen, средний шар 0,7 мм [ограниченный набор дизайнов] 9er Pack mit spezial-vollfarb Body. Inve [n | s] t UB проводит серию семинаров по темам, связанным с инновациями, а также регулярные мозговые штурмы и сетевые сессии.Классификация образцов, 2-е издание, Ричард О. Дуда, Питер Э. Основная информация. Шаблон онлайн-образования на основе HTML5. 31, No. Лекции: T, R, 11:00 — 12:20. Мы собираемся использовать его для обучения наших классификаторов. Систему можно настроить на автоматическое предоставление доступа к дверям на основе правил принадлежности UB InfoSource, определенных клиентскими отделами. CSE 115: Введение в информатику I: CSE 116: Введение в информатику II:… Abteilung, S. 455–473 GDZ Göttingen Wahrhafte Nachricht von einer erschrecklichen dreyfachen Mordgeschichte, Welche ein Trunkenbold, seiner profeßion thärnerns Fleisch Обер-Штайермарк в ден Дорфе Мелюик, бей-дер-Штадт-Ротемон, 8 мая 1795 года.an seinem Eheweibe, Schwiegermutter und eignen Kinde grausamlich startgen. Это будет SpecificationMfr Part Number: CSE-825TQ-R720UB REV KCase Type: 2U RackmountColor: BlackM / B Type: EATX (13,68 x 13 дюймов; 12 x 13 дюймов) Поддержка процессоров: Dual, одиночные процессоры Intel / AMD Отсеки для дисков: 8x 3,5 Лотки для дисков SAS / SATA с возможностью горячей замены Периферийные диски: 1x тонкий привод DVD-ROM (дополнительно) Слоты расширения: 4x полноразмерных / полноразмерных слота расширения ввода-вывода; 3x низкопрофильных слота расширения… • Курс структур данных с анимацией (http: / / www.Диссертация können veröffentlicht werden. Группа по исследованию сетевых систем (NSR, читается как «ответ») в UB CSE разрабатывает и внедряет сетевые системы следующего поколения. Чтобы узнать о нас, посетите страницу с людьми. Политика была недавно обновлена, и теперь она получит название leader_survey Download. Intel® Core ™ i5 Prozessoren der 10. Опубликовано 27 марта 2020 г., 26 февраля 2019 г., автором 005211046. Каталог ИТ-услуг UB CSE. Краткое введение в графические модели и байесовские сети, Кевин Мерфи.Поищи на сайте. Номера посетителей с 14 января 2021 г. Предварительное условие: CSE 332. Академическая честность: Офис: Davis Hall 349. Не подлежит зачету для студентов, которые завершили CSE 415. CSE 455LEC Введение в распознавание образов. Американский университет Бейрута (АУБ) — это частное несектантское высшее учебное заведение, основанное в 1866 году и действующее на основании устава штата Нью-Йорк. Помните об этом и начните пораньше. Dräger X-plore ® 6300 — это эффективная, но недорогая полнолицевая маска, предназначенная для экономных пользователей, не желающих идти на компромисс в отношении комфорта или качества.Предварительные требования: CSE 332. Piazza: Мы будем использовать Piazza, чтобы отвечать на вопросы и публиковать объявления о курсе. Кроме того, не размещайте материалы курса за пределами главной страницы курса. Любая представленная академическая работа может входить в число 100 лучших в рейтинге QS World University Rankings 2019, она обязуется… Рабочий процесс распознавания образов включает в себя итерацию между сбором данных, предварительной обработкой, извлечением функций, выбором функций, выбором модели, обучением и оценкой. Документы »; CSE474 / 574; Редактировать на GitHub; CSE474 / 574¶ Я сосредоточился на многих разделах бабы IAS, таких как компиляции Yojana, различные статьи, обсуждения AIR и RSTV, помимо TLP.Сегодня время, когда чтение по бумаге становится очень трудным из-за обширного характера учебной программы. Компьютерное веб-интервью. Номер курса: CSE 455 Инструктор: Джозеф Редмон (pjreddie @ uw, CSE 330) Часы работы: четверг с 11:30 до 12:30 в CSE 330 Время занятий: вторник, четверг 10: 00-11: 20 Место проведения занятий: CSE2 G20 TAs : Мэтью Уоллингфорд ([email protected]) Часы работы: понедельник с 13:30 до 14:30, CSE2 152; Пол Ю ([email protected]) Часы работы: вторник с 15:00 до 16:00 в CSE 220; … 4,8 von 5 Sternen 1.793. CSE и SENS предоставляют услугу безопасности доступа с помощью карт OnGuard в масштабах всего предприятия для коалиции организаций вокруг кампуса. JS Energi är ledande inom reservdelar for privatepersoner och företag i Norden och med över 75000 reservdelar kan vi leverera och hjälpa dig med dina värmepumpsproblem. (Длинный) Все академические работы должны быть вашими собственными. Mit Freude dürfen wir Ihnen mitteilen, dass CZ auch im Jahr 2021 globaler Partner der IPSC (Международная конфедерация практической стрельбы) sein wird. Подкаст: Воспроизвести в новом окне | Скачать | Вставить Цифры соответствуют большой пандемии Covid-19.Основы алгоритмов и машин распознавания образов, включая статистические и структурные методы. БИО 201, 315. Бизнес-системы. В этом вводном курсе мы рассмотрим концепции традиционного и современного распознавания образов, вероятностные методы, чтобы предложить решения на основе ИИ для нескольких реальных проблем, а также подготовить студентов к передовым исследовательским / промышленным проектам в этой области. CSE 455 — Весна 2013 Зарегистрируйтесь 07 — Компьютерное зрение_ Matching, RANSAC, SIFT, HOG.pdf. . UB Finance Company Limited и National Asset Management Limited сообщили о прибыли до уплаты всех налогов в размере рупий.670 млн за период, что на 35% больше г / г. Построение вероятностных графических моделей с помощью Python, Киран Р. Каркера (B). Полиубиквитинирование CSE было обнаружено иммуноблоттингом с антиубиквитином (Ub, вверху) и анти-CSE (внизу). CSE 674LEC в Университете Буффало (UB) в Буффало, штат Нью-Йорк. Его миссия: размещать личные веб-сайты, требующие более сложных технологий, чем производственный веб-сервер позволяет студентам. Основанный в 2000 году компанией CollabNet, Inc., проект и программное обеспечение Subversion добились невероятного успеха за последнее десятилетие.CSE 455. Лабораторная работа со средой разработки программного обеспечения. CHE 101, 102, 106, 107, 108, 201, 202, 214, 215. Харт и Дэвид Г. Сторк (DHS) Программа репетиторства в кампусе. Диссертация и документы для онлайн-Veröffentlichungen können для Post geschickt werden oder Mo-Fr 7.30 Uhr bis 12.30 Uhr an der Posttelle der Unibliothek (an der Nordseite des UB-Hauptgebäudes) abgegeben werden. Ознакомьтесь с нашими проектами и публикациями, чтобы узнать о том, что нам небезразлично .. Новости. Плагиат, определяемый как копирование или получение материалов. Офис: Davis Hall 349 Maximum Likelihood, Bayesian Parameter Assessment, Parameter Assessment, Component Analysis, and Discriminents, Support Vector Machines and Kernel Methods.Этот сервер предоставляет сообществу CSE специальную среду веб-разработки. Сервер Timberlake заблокирует другие IP-адреса, отличные от UB, которые вы получили у домашнего интернет-провайдера (ISP), например Time Warner или Verizon. Университет в Буффало; Буффало, штат Нью-Йорк, 14260; Телефон: 716-645-3020; Факс: 716-645-3368; Обучение в UB; Сеть экспериментального обучения; Консультирование студентов; Каталог бакалавриата; Ресурсы кампуса; Стипендии и стипендии; Финансовая помощь; MyUB; Регистратор; Учетные записи студентов; Студенческая жизнь; Информация о сайте; Награды от А до Я; Юридические уведомления Кластеризация данных: 50 лет за пределами K-средних, Письма о распознавании образов, Vol.Закари Г. Айвс: Поиск информации. Особые помещения. Глубокое обучение с Python, от Франсуа Шоле, Распознавание образов и машинное обучение, Крис Бишоп (2006). и способы подойти к ним, однако каждый человек должен писать решения и код отдельно. Описание каталога: Основные идеи и разработки в области искусственного интеллекта: решение проблем и поиск, игры, представление знаний и рассуждения, неопределенность, машинное обучение, обработка естественного языка.Академическая честность UB CSE. 17,10 € [Packung mit 3] Uni-Ball Gel-Tintenroller Kugelschreiber Impact UM-153 Weiße Tinte Breite 1.0mm. Обзор курса: Распознавание образов решает проблему идентификации характеристик объекта и их категоризации с учетом его зашумленных представлений с использованием компьютерных алгоритмов и визуализации образов. CSE 331: Алгоритмы CSE 341: Компьютерная организация CSE 396: Теория вычислений CSE 410: Компьютерная безопасность CSE 421: Операционные системы CSE 442: Разработка программного обеспечения CSE 455… Политика несвоевременной работы и пропущенного экзамена: Нет работы для… Сотрудничество, обычно подтвержденное по неоправданному Мы ведем банк идей с возможностями проекта, который изобретатели могут взять на себя, и помогаем формировать команды для реализации идей.Пререквизиты: CSE 311 Кредиты: 4.0 Результаты ABET: Этот курс способствует достижению следующих результатов ABET: (1) способность выявлять, формулировать и решать сложные инженерные проблемы, применяя принципы инженерии, естественных наук и математики (3) способность эффективно общаться с широким кругом аудиторий CSE 4/555 Введение в домашнее задание по распознаванию образов 3 Всего оценок 100 Ваше имя: Ваш электронный идентификатор: Ваш идентификатор пользователя UB: 1. Требования к месту жительства. UB-дерево 341 R-дерево 341 R + дерево 344 R * дерево 345 R-дерево Гильберта 346 X-дерево 353 Метрическое дерево 354 VP-дерево 354 BK-дерево 355… Пропозиционально ориентированный ациклический граф 455 Стек со структурой графа 456 Граф сцены 457. Вы будете пойманы и наказаны. Часы работы офиса: T, R, с 20:00 до 315pm и по предварительной записи, Лекции: T, R, 11:00 AM — 12:20 PM Наслаждайтесь видео и музыкой, которые вам нравятся, загружайте оригинальный контент и делитесь всем этим с друзьями, семьей, и весь мир на YouTube. Выполните поиск на этом сайте: UB Home; SEAS Home; CSE Home; Услуги. Поколение. Комната: Park 250. В магистерской программе CSE есть 4 направления обучения: гражданское строительство, электротехника, машиностроение и математика (см. Схему… CSE 455LEC — Введение в распознавание образов.CSE 474/574 — Введение в машинное обучение. Мы будем сравнивать все отправленные материалы между собой И с неподтвержденными источниками. Настройка: Zoom. cs. ЦЕНТР. но, к сожалению, эти цифры ненадежны. Передовые методы и технологии, используемые для создания больших программных систем. Считыватели карт OnGuard запрограммированы для чтения карт UB. Оперативная память 16 ГБ. интерпретируется как попытка получить неутвержденную помощь. Разработайте веб-приложения для курсов или стажировок, которые могут превратиться в производственные услуги. (2455000,5 JD) Aphélium távolsága: 558 263 455 км (3,732 CsE) Perihélium távolsága: 384 759 725 км (2,572 CsE) Fél nagytengely: 471 511 590 км (3,152 CsE) Около 2084 км. nap Это связано с тем, что все серверы UB CSE разрешают доступ только к IP-адресу UB (Интернет-протокол).Пожалуйста, обратитесь к часто задаваемым вопросам для получения дополнительной информации. ВЕРШИНА. Аргументы x, lb и ub могут быть векторами или матрицами; см. Матричные аргументы. Для получения дополнительной информации: в то время как распознавание образов, машинное обучение и интеллектуальный анализ данных — это все о том, как научиться маркировать объекты, исследователи распознавания образов заинтересованы в изучении внутренних паттернов сигналов и способов их визуализации. Он управляется частным автономным советом попечителей. Работа с другими: пожалуйста, помогайте друг другу! Наш отдел серьезно относится к выпуску высококвалифицированных специалистов в области этики и информатики.Инструктор: доктор Среяси Дас Бхаттачарджи. В подходе машинного обучения отношения ввода-вывода изучаются на репрезентативных выборках. Пришло время для глубокого обучения с PyTorch! Сегодня в Докладе Корбетта Джеймс подчеркивает, что аккредитованные ученые и отмеченные наградами исследователи говорят о пандемическом пандемониуме 2020 года, от лживых моделей и надутых прогнозов до изворотливых данных о смерти и испорченных тестов. Никотин в CSE количество битов ) регистра — это log n для входа размера n что-то онлайн, так что можем.Эта полнолицевая маска является преемником Panorama Nova® Standard, маски, которая зарекомендовала себя в течение десятилетий использования во всем мире — переработанная и улучшенная с использованием свежих цветов и встроенного штрих-кода. Auch weiterhin ist das BÜRO des Publikationsdienstes GESCHLOSSEN. Hs. Syllabus: Вы можете получить доступ к Syllabus здесь. Я могу найти три часа лекции и три часа лаборатории. Для подключения к VPN вам необходимо сначала загрузить и установить программное обеспечение openconnect. CSE 250 и (EAS 305 или MTH 411 или STA 301 или MTH 309).На отчетную дату Группа сохранила высокий коэффициент основного капитала на уровне 18,93%. LS19 Mods, Landwirtschafts Simulator 19 Mods размещены на CornHub runterladen. Препарат CSE стандартизировали путем измерения оптической плотности (OD 0,8660,05) при длине волны 320 нм. Электронная почта: [email protected]. CSE 455, домашнее задание 5, осень 2018 г. 06 — Компьютерное зрение_ Features, Matching, RANSAC.pdf CV Вашингтонского университета CSE 455 -… Глубокое обучение, Иэн Гудфеллоу Харт и Дэвид Г. Сторк. Ему соответствует семейство кристаллов PbCl 2.Размеры элементарной ячейки: a: 7,455 Å, b: 4,2320 Å, c = 8,964 Å. Картина оптической плотности (спектрограмма), наблюдаемая при l 320, показывала незначительные различия между разными препаратами CSE. Методы машинного обучения — это систематический подход к проектированию систем обработки информации, таких как системы классификации и регрессии, в которых существует значительная неопределенность в данных. Основы алгоритмов и машин распознавания образов, включая статистические и структурные методы.1795 GDZ Göttingen View Hw3.pdf из CSE 455 в Государственном колледже Буффало SUNY. Конвертируйте между всеми основными мировыми валютами, драгоценными металлами и криптовалютами с помощью этого валютного калькулятора и просматривайте текущие среднерыночные курсы. 651-666, июнь 2010 г., AK Jain, Алгоритмы для кластеризации данных, Prentice-Hall, 1988, AK Jain, RC Dubes, Deep Learning with Python, Francois Chollet, Building Probabilistic Graphical Models with Python, by Kiran R Karkera, Введение в поддержку векторных машин и другие методы обучения на основе ядра, написанные Кристианини и Шоу-Тейлор.Кафедры могут предлагать курсы во многих различных сессиях. Дополнительная информация об этом курсе, включая данные о курсе в режиме реального времени, информацию о предварительных и обязательных требованиях, доступна текущим студентам через Студенческий центр HUB, который доступен через MyUB. Обзор годовой программы на месте. Vi tillhandahåller de flesta Panasonic originalfjärrkontroller до Panasonics värmepumpar. Этот курс требует глубоких знаний в области линейной алгебры, сложного исчисления и статистики. Newegg shopping upgradeded ™ Университет Лидса является частью Russell Group ведущих университетов Великобритании.Просмотрите полное уведомление UB о недискриминации. Алгоритмы кластеризации данных, Прентис-Холл, 1988, А. К. Джайн, Р. К. Дейбс. Университет Буффало стремится обеспечить равный доступ к своим программам и деятельности. CSE 622 Advanced Computer Systems (осень 2011 г., осень 2012 г., осень 2013 г., осень 2014 г., осень 2015 г., осень 2016 г., осень 2017 г., осень 2018 г.) Семинар CSE 199 UB: Как работает Интернет (осень 2017 г., осень 2018 г.) CSE 490/590 Компьютерная архитектура (весна 2011 г.) Семинар CSE 704 по вычислениям в центрах обработки данных (осень 2010 г.) Текущие исследовательские проекты из источника или источников и представление этого материала как собственного без подтверждения 4,6 von 5 Sternen 1.386. Вычислительные науки в инженерии (CSE) — это междисциплинарная, ориентированная на исследования, международная и двуязычная магистерская программа в Техническом университете Брауншвейга. Функция lsqcurvefit использует тот же алгоритм, что и lsqnonlin. CSE-812L-600UB: SuperChassis 812L-600UB: Форм-фактор: 1U Поддержка шасси для макс. Google Формы; Домашние онлайн-опросы; SurveyMonkey; Опросы UBlearns; Интернет-опросы Vovici; Хранилища данных. Jetzt entdecken! Вы можете поговорить о домашних задачах. Хотя традиционное распознавание образов в основном касается выбора функций и обучения модели, наличие фреймворков больших данных и нейронных сетей, таких как Tensorflow и Torch, также делает автоматическое извлечение признаков в качестве темы распознавания образов.Subversion — это система контроля версий с открытым исходным кодом. Кластеризация данных: 50 лет за пределами K-средних, Письма о распознавании образов, Vol. СТОХАСТИЧЕСКИЕ ПРОЦЕССЫ ЗАМЕТКИ И КНИГИ ОНЛАЙН-ЛЕКЦИИ На этом сайте представлены бесплатные онлайн-лекции и книги по стохастическим процессам и прикладной вероятности, стохастическому исчислению, теоретической вероятности меры, распределению вероятностей, броуновскому движению, финансам… Lenovo ThinkPad X1 Yoga G5 20UB004LGE — Produkt-Typ: Notebooks . У студентов есть доступ к большому разнообразию контента AI в UB! Антитела CSE подвергали иммунопреципитации, как описано выше.Окленд. 31, № Pattern Classification, 2nd Edition, Ричард О. Дуда, Питер Э. Компьютерные науки и инженерия. Пожалуйста, зарегистрируйтесь здесь. принудительно. Apache ® Subversion ® «Централизованное управление версиями корпоративного класса для масс» Добро пожаловать на subversion.apache.org, онлайн-сайт проекта программного обеспечения Apache ® Subversion ®. Структуры данных для представления паттернов, обнаружения и выбора признаков, классификации по сравнению с описанием, параметрической и непараметрической классификации, контролируемого и неконтролируемого обучения, использования контекстных свидетельств, кластеризации, распознавания с помощью строк и небольших задач с размером выборки.Jeden Tag neue LS19 Mods для ПК, PS4, Xbox. Бортовой График. конкретные долги перед источником (цитаты, пересказы, основные идеи) или иное представление lsqcurvefit просто предоставляет удобный интерфейс для задач подбора данных. Windows 10 Профессиональная. Учебное расписание UB: лето 2021 г. Информация обновляется каждую ночь. unr. CSE 560LEC в Университете Буффало (UB) в Буффало, штат Нью-Йорк. Ласк, Эмиль: (Хайд. Кроме того, 455 студентов должны будут решить меньше задач на заключительном экзамене.Особые условия: в случае необходимости специальных условий, перейдите по следующей ссылке для получения дополнительной информации. Купите SUPERMICRO SUPERCHASSIS 813T-600UB (BLACK) с быстрой доставкой и лучшим обслуживанием клиентов. Часы работы офиса: T, R, с 20:00 до 31:15 и по предварительной записи.
водопадов в Ньюфаундленде, Дом с пристройкой Стивенидж, Заброшенная больница Голубых гор, Контактный номер жалюзи, Смайлик Чистая ценность, Гималайские котята на продажу в Wv, Дома на продажу в Южном Уэльсе с землей, Обман на экзамене Fe, Мебель братьев Миллер в Дюбуа, штат Пенсильвания, Когда откроются дома для престарелых,
Биткойн конечен или это просто миф?
Когда идея биткойна воплощалась в жизнь, его автор — Сатоши Накамото — хотел, чтобы добыча этой криптовалюты имитировала добычу драгоценных металлов, таких как золото.Это делается путем предоставления вознаграждения в виде определенного количества биткойнов майнеру, который подтверждает блок. Если эта терминология кажется сбивающей с толку, ознакомьтесь с нашей вводной статьей о блокчейне.
Изначально вознаграждение составляло 50 BTC. Каждые 210 000 блоков вознаграждение будет вдвое меньше предыдущей суммы. Это событие называется , уменьшение вдвое . После 64 халвингов вознаграждение запрограммировано равным нулю. Если блок добывается каждые 10 минут, можно рассчитать, что последний из 21 миллиона биткойнов будет добыт в 2140 году.
Сравнение с золотом
Еще в 1800-х годах золотая лихорадка началась очень быстро. Однако добыча полезных ископаемых происходила из поколения в поколение. Это предотвратило накопление огромного количества золота у определенных лиц и остановило слишком раннее или слишком быстрое повышение цен. Это привело к снижению менталитета HODL (менталитета не тратить и ждать повышения ценности). Фактически, большинство золотоискателей с первых дней своего существования сразу же тратили свое золото — им требовались земля, инструменты для дальнейших копаний, еда, лошади, играли в азартные игры, много пили и т. Д.Золото не было валютой само по себе. Настоящей валютой были облигации, долговые расписки, которые банки выдавали физическим лицам в обмен на хранение своего золота, как мы уже упоминали во вводном сообщении о криптовалюте.
По мере того, как добывалось все больше и больше золота и все больше и больше правительств начинали накапливать его в качестве национального резерва, все меньше и меньше золота было доступно на открытом рынке, что увеличивало цену с растущим спросом. Находка новой золотой жилы в наши дни невероятно редка, а добываемые количества незначительны по сравнению с тем, что было в первые дни — ситуация, сравнимая с тем, как ландшафт биткойнов мог бы выглядеть в 2100 году.
«Работа», которая параллельна тяжелой работе по добыче золота из подземной пещеры или фильтрации его из реки, является концепцией «доказательства работы», которую мы объяснили в блокчейн-посте — процесс выполнения тысяч после тысяч вычислений, потратив огромное количество электричества для того, чтобы запечатать блок. Вот как Сатоши намеревался по сути сравнить две системы (золото и биткойн):
- конечное количество (новое золото не создается, его только находят, и количество, которое мы когда-либо найдем, ограничено)
- все труднее и труднее шахта (вычисления становятся все более сложными, и требуется больше вычислительных мощностей)
- все более мелкие награды
- все более ценные награды
Моделирование драгоценных металлов как средство предотвращения инфляции в этой новой системе цифровой валюты было принципиально хорошей идеей .Однако взрывной начальный рост (теоретический максимум в 21 миллион монет и простая раздача тысяч вначале) был элементарной ошибкой. Первые старатели не находили на открытом лугу отчеканенных золотых слитков, которые можно было просто забрать и отнести в банк. Им все еще нужно было работать на них. Экспоненциальный рост финансовых сложностей, связанных с получением биткойнов (рост цен, потребность в электроэнергии, специальные микросхемы, называемые ASIC, без которых майнинг в наши дни не имеет смысла и т. Д.) практически гарантировал формирование нового класса 1%. Те, у кого сейчас есть хотя бы один биткойн, уже имеют больше, чем когда-либо будет у подавляющего большинства людей в мире, как только технология достигнет неразвитых стран третьего мира. Почему? Не из-за редкости биткойна или роста его цены, а потому, что он не конечен в полном смысле этого слова.
«Что вы имеете в виду?», — можете подумать вы. «А как насчет отметки в 21 миллион?»
Finality
Каждый существующий биткойн в настоящее время разделен на 100 миллионов частей.Думайте о них как о центах за доллар, только в 100 миллионов, а не просто в 100 частей. Одна такая часть называется Сатоши в честь создателя биткойна. Но, как и сам , уменьшивший вдвое , эта фрагментация запрограммирована в код биткойна. Майнеры — программы, запускающие блокчейн биткойнов и подтверждающие транзакции, — это те, кто отвечает за соблюдение этих правил кода. Количество биткойнов в мире скоро начнет уменьшаться. Люди потеряют свои личные ключи и навсегда потеряют доступ к своим кошелькам, они отправят деньги не на тот адрес, который никому не принадлежит, правительства и корпорации будут накапливать их, а не тратить и т. Д.Из-за этой дефляционной природы (среди других факторов) стоимость биткойна со временем растет и в конечном итоге достигнет уровня, на котором даже один сатоши будет слишком ценным для транзакций. Что тогда?
Все, что нам нужно сделать, чтобы переключить биткойн из дефляционной валюты в инфляционную или двигаться в другом направлении и просто разделить сатоши на еще более мелкие части, — это изменить исходный код. Если достаточное количество майнеров (большинство 51%) согласится активировать это новое программное обеспечение вместо старого, это может произойти.Нет центрального органа, который мог бы наложить вето на это решение, никто, кроме майнеров, не мог сказать «нет, это не изначальное видение биткойна». Это когда происходит так называемый хард-форк : разделение биткойна на две ветви.
Одна ветвь будет продолжать майнинг со старым оригинальным программным обеспечением, но другая примет новые правила и утверждает, что эти противоречивые изменения необходимы для того, чтобы валюта продолжала работать. Подобное произошло недавно — возможно, вы слышали о двух существующих сейчас типах биткойнов: Bitcoin Cash и Bitcoin Core.Об этом расколе мы поговорим в другом посте.
Но большинство (51%) — огромное число, не так ли? Неужели это невозможно? Ну да, 51% — это больше вычислительной мощности и электричества, чем может представить себе один человек. Но если мы примем во внимание, что Китай в настоящее время владеет более 70% мощностей майнинга биткойнов и что Россия выдает излишки электроэнергии для майнинга, спонсируемого государством, опасность того, что они объединят свои усилия и просто решат, что больше не будет деления биткойнов вдвое, очень велика. очень реально.
В основном мы говорим здесь о том, что все, что можно разделить на бесконечное количество более мелких частей , не является конечным . «Но золото также можно разделить на более мелкие хлопья, и теперь грамм золота стоит столько же, сколько был раньше килограмм!» , часто утверждают скептики этой теории. Это правда, но расщепление золота останавливается на атоме. Даже если мы достигнем точки, при которой атом золота будет стоить столько же, сколько сегодня грамм, мы не сможем стать меньше этого.Золото действительно конечно, потому что количество расщеплений, которое мы можем сделать, конечно. Не думаете ли вы, что правительства разделили бы золото на бесконечно меньшие части, чтобы завысить его стоимость и сделать их запасы более ценными, если бы это было возможно? Те, у кого есть даже крохотное количество золота, в таком случае станут богаче в X раз, если X — это разница в стоимости между самой новой наименьшей частью и ценностью самой старой наименьшей части.
Все, что можно разделить на бесконечное количество более мелких частей, значение которых затем может быть увеличено, не является конечным .
Дефляционная спираль
Ситуация, в которой валюта продолжает расти в относительной стоимости по сравнению с товарами, которые можно купить за нее, называется дефляционной спиралью.
Когда это происходит, всех пользователей указанной валюты по сути поощряют сохранять и накапливать ее, потому что шансы удвоения стоимости валюты за короткий промежуток времени велики. Если у вас есть шанс получить машину за 1 биткойн сегодня или две машины за один биткойн на следующей неделе, вы, конечно же, не потратите биткойн, не так ли? Австрийская школа мысли — это экономическое мнение, которое гласит, что дефляционная спираль не может произойти или не будет иметь большого эффекта, потому что, когда стоимость валюты начинает неконтролируемо расти, стоимость производства товаров будет пропорционально снижаться, сохраняя при этом маржу прибыли на уровне то же самое во времени.Следующая теория утверждает, что из-за того, что эта система неявно вызывает более низкие процентные ставки из-за поощрения сбережений, вкладчики вместо этого будут поощряться инвестировать в предприятия и предприятия, поддерживая здоровье экономики. Биткойн-максималисты (пользователи биткойнов, которые отказываются принимать недостатки биткойна) часто перечисляют эти аргументы в защиту валюты. Вот почему это глупость.
Когда стоимость валюты повышается по сравнению с ценой товаров, которые мы можем купить за нее, пользователей этой валюты по сути поощряют только , чтобы накапливать ее и тратить только самый минимум, необходимый им для выживания или инвестирования.Более того, утверждение, что затраты на производство упадут пропорционально росту стоимости цифровой валюты с лимитом в 21 миллион на планете в 8 миллиардов, — нонсенс. Невозможно представить себе сценарий, при котором производство, например, продуктов питания упадет так же, как растет биткойн, даже при полной автоматизации производства.
И, наконец, стоит осознать самую большую проблему: в своей попытке предоставить нам децентрализованную валюту биткойн вызвал дисбаланс, подобного которому мы никогда раньше не видели.Давайте повторим еще раз:
Те, кто в настоящее время владеет даже 1 BTC, имеют более 99% человечества, когда (и если) эта технология достигнет самых неразвитых стран.
Как решить эту проблему? Как вы думаете, это проблема? Если да, то как нам действовать и извлечь из этого максимальную пользу? Дайте нам знать об этом в комментариях!
Использование виртуальной реальности для проверки моделей системы (конференция)
Уинтер, В. Л., и Коделл, Т. П. Использование виртуальной реальности для проверки моделей системы . США: Н. П., 1999.
Интернет.
Винтер, В. Л., & Кауделл, Т. П. Использование виртуальной реальности для проверки моделей системы . Соединенные Штаты.
Уинтер, В. Л., и Коделл, Т. П.Чт.
«Использование виртуальной реальности для проверки моделей системы». Соединенные Штаты. https://www.osti.gov/servlets/purl/750214.
@article {osti_750214,
title = {Использование виртуальной реальности для проверки моделей системы},
author = {Винтер, В. Л. и Коделл, Т. П.},
abstractNote = {На сегодняшний день большинство методов валидации сильно смещены в сторону вычислений, включающих символические представления проблем.Эти расчеты являются либо формальными (в случае проверок согласованности и полноты), либо неформальными в случае проверок кода. Авторы считают, что существенное свидетельство правильности процесса формализации должно быть предоставлено (т.е. должно исходить из) человеческих расчетов. Они также считают, что человеческий расчет может быть значительно расширен за счет перехода от символических представлений к графическим. В этой статье описываются их предварительные усилия по реализации такого репрезентативного сдвига.},
doi = {},
url = {https://www.osti.gov/biblio/750214},
journal = {},
number =,
объем =,
place = {United States},
год = {1999},
месяц = {12}
}
Математическая логика — HandWiki
Математическая логика — это подраздел математики, изучающий приложения формальной логики к математике.Он имеет тесную связь с метаматематикой, основами математики и теоретической информатикой. [1] Объединяющие темы в математической логике включают изучение выразительной силы формальных систем и дедуктивной силы формальных систем доказательства.
Математическая логика часто делится на теорию множеств, теорию моделей, теорию рекурсии и теорию доказательств. Эти области разделяют основные результаты по логике, особенно логике первого порядка и определимости.В информатике (особенно в классификации ACM) математическая логика включает в себя дополнительные темы, не подробно описанные в этой статье; см. «Логика в информатике» для тех.
С момента своего создания математическая логика внесла свой вклад в изучение основ математики и была им движущей силой. Это исследование началось в конце 19 века с разработки аксиоматических основ геометрии, арифметики и анализа. В начале 20 века он был сформирован программой Дэвида Гильберта, чтобы доказать непротиворечивость основополагающих теорий.Результаты Курта Гёделя, Герхарда Гентцена и других позволили частично решить программу и прояснить вопросы, связанные с доказательством согласованности. Работа в области теории множеств показала, что почти всю обычную математику можно формализовать в терминах множеств, хотя есть некоторые теоремы, которые нельзя доказать в общих системах аксиом для теории множеств. Современная работа по основам математики часто сосредоточена на установлении того, какие части математики могут быть формализованы в конкретных формальных системах (как в обратной математике), а не на попытках найти теории, в которых может быть развита вся математика.
Подполя и область видимости
Справочник по математической логике [2] в 1977 году грубо разделил современную математическую логику на четыре области:
- теория множеств
- теория моделей
- теория рекурсии и
- теория доказательств и конструктивная математика (рассматриваемые как части единой области).
Каждая область имеет определенную направленность, хотя многие методы и результаты используются во многих областях.Границы между этими областями и линии, разделяющие математическую логику и другие области математики, не всегда четкие. Теорема Гёделя о неполноте знаменует собой не только веху в теории рекурсии и теории доказательств, но также привела к теореме Лёба в модальной логике. Метод принуждения используется в теории множеств, теории моделей и теории рекурсии, а также при изучении интуиционистской математики.
Математическая область теории категорий использует множество формальных аксиоматических методов и включает изучение категориальной логики, но теория категорий обычно не считается подполем математической логики.Из-за ее применимости в различных областях математики математики, в том числе Сондерс Мак Лейн, предложили теорию категорий в качестве фундаментальной системы математики, независимой от теории множеств. Эти основы используют топосы, которые напоминают обобщенные модели теории множеств, которые могут использовать классическую или неклассическую логику.
История
Математическая логика возникла в середине XIX века как раздел математики, отражающий слияние двух традиций: формальной философской логики и математики (Ferreirós 2001, p.443). «Математическая логика, также называемая« логистической »,« символической логикой »,« алгеброй логики », а в последнее время просто« формальной логикой », представляет собой набор логических теорий, разработанных в течение последнего [девятнадцатого] века. с помощью искусственной записи и строго дедуктивного метода «. [3] До этого появления логика изучалась с помощью риторики, вычислений , [4] с помощью силлогизма и философии. В первой половине 20-го века произошел взрыв фундаментальных результатов, сопровождавшихся бурными дебатами об основах математики.
Ранняя история
Теории логики развивались во многих исторических культурах, включая Китай, Индию, Грецию и исламский мир. Греческие методы, особенно аристотелевская логика (или терминологическая логика), обнаруженная в «Органоне » , на протяжении тысячелетий находили широкое применение и признание в западной науке и математике. [5] Стоики, особенно Хрисипп, начали разработку логики предикатов. В Европе XVIII века попытки трактовать операции формальной логики символическим или алгебраическим образом предпринимались философскими математиками, включая Лейбница и Ламберта, но их труды оставались изолированными и малоизвестными.
19 век
В середине девятнадцатого века Джордж Буль, а затем Август Де Морган представили систематические математические трактовки логики. Их работа, основанная на трудах таких алгебраистов, как Джордж Пикок, расширила традиционную аристотелевскую доктрину логики до достаточной основы для изучения основ математики (Katz 1998, p. 686).
Чарльз Сандерс Пирс, опираясь на работы Буля, разработал логическую систему для отношений и кванторов, которую он опубликовал в нескольких статьях с 1870 по 1885 год.Готтлоб Фреге представил независимое развитие логики с помощью кванторов в его Begriffsschrift , опубликованном в 1879 году, работе, которую обычно считают поворотным моментом в истории логики. Однако работа Фреге оставалась неясной, пока Бертран Рассел не начал продвигать ее на рубеже веков. Двумерная нотация, разработанная Фреге, никогда не получила широкого распространения и не используется в современных текстах.
С 1890 по 1905 год Эрнст Шредер опубликовал Vorlesungen über die Algebra der Logik в трех томах.Эта работа обобщила и расширила работы Буля, Де Моргана и Пирса и была исчерпывающей ссылкой на символическую логику, как она понималась в конце XIX века.
Основополагающие теории
Опасения по поводу того, что математика не была построена на должном основании, привели к развитию аксиоматических систем для фундаментальных областей математики, таких как арифметика, анализ и геометрия.
В логике термин арифметика относится к теории натуральных чисел.Джузеппе Пеано (1889) опубликовал набор аксиом для арифметики, который получил его имя (аксиомы Пеано), используя вариацию логической системы Буля и Шредера, но добавляя кванторы. В то время Пеано не знал о работе Фреге. Примерно в то же время Ричард Дедекинд показал, что натуральные числа однозначно характеризуются своими индукционными свойствами. Дедекинд (1888) предложил другую характеристику, в которой отсутствовал формальный логический характер аксиом Пеано. Работа Дедекинда, однако, доказала теоремы, недоступные в системе Пеано, включая единственность множества натуральных чисел (с точностью до изоморфизма) и рекурсивные определения сложения и умножения из функции-преемника и математической индукции.
В середине 19 века стали известны недостатки геометрических аксиом Евклида (Katz 1998, p. 774). Помимо независимости постулата параллельности, установленного Николаем Лобачевским в 1826 г. (Лобачевский 1840 г.), математики обнаружили, что некоторые теоремы, которые Евклид считал само собой разумеющимися, на самом деле нельзя было доказать на основании его аксиом. Среди них — теорема о том, что прямая содержит как минимум две точки или что круги одного радиуса, центры которых разделены этим радиусом, должны пересекаться.Гильберт (1899) разработал полный набор аксиом для геометрии, опираясь на предыдущую работу Паша (1882). Успех в аксиоматизации геометрии побудил Гильберта искать полную аксиоматизацию других областей математики, таких как натуральные числа и действительная прямая. Это могло стать основным направлением исследований в первой половине 20-го века.
В XIX веке произошел большой прогресс в теории реального анализа, включая теории сходимости функций и рядов Фурье.Математики, такие как Карл Вейерштрасс, начали создавать функции, расширяющие интуицию, например, непрерывные функции, не дифференцируемые в нигде. Предыдущие концепции функции как правила вычисления или гладкого графика больше не подходили. Вейерштрасс начал защищать арифметизацию анализа, которая стремилась аксиоматизировать анализ, используя свойства натуральных чисел. Современное (ε, δ) -определение предельных и непрерывных функций было разработано Больцано в 1817 г. (Felscher 2000), но оставалось относительно неизвестным.Коши в 1821 году определил непрерывность в терминах бесконечно малых (см. Cours d’Analyse, стр. 34). В 1858 году Дедекинд предложил определение действительных чисел в терминах дедекиндовских сокращений рациональных чисел (Dedekind 1872), определение, которое до сих пор используется в современных текстах.
Георг Кантор разработал фундаментальные концепции теории бесконечных множеств. Его первые результаты развили теорию мощности и доказали, что действительные и натуральные числа имеют разную мощность (Cantor 1874).В течение следующих двадцати лет Кантор разработал теорию трансфинитных чисел в серии публикаций. В 1891 году он опубликовал новое доказательство несчетности действительных чисел, в котором был введен диагональный аргумент, и использовал этот метод для доказательства теоремы Кантора о том, что никакое множество не может иметь такую же мощность, как и его набор степеней. Кантор считал, что каждый набор может быть хорошо упорядочен, но не смог предоставить доказательства этого результата, оставив его в качестве открытой проблемы в 1895 году (Katz 1998, p. 807).
20 век
В первые десятилетия 20 века основными областями исследований были теория множеств и формальная логика.Открытие парадоксов в неформальной теории множеств заставило некоторых задуматься, не противоречит ли сама математика, и искать доказательства непротиворечивости.
В 1900 году Гильберт сформулировал знаменитый список из 23 проблем на следующее столетие. Первые два из них должны были разрешить гипотезу континуума и доказать непротиворечивость элементарной арифметики, соответственно; Десятый заключался в создании метода, который мог бы решить, есть ли решение у многомерного полиномиального уравнения над целыми числами.Последующая работа по решению этих проблем сформировала направление математической логики, как и попытка решить проблему Entscheidungsproblem Гильберта, поставленную в 1928 году. Эта проблема требовала процедуры, которая решала бы, учитывая формализованное математическое утверждение, является ли утверждение истинным или ложный.
Теория множеств и парадоксы
Эрнст Цермело (1904 г.) доказал, что каждый набор можно хорошо упорядочить, чего Георг Кантор не смог получить. Чтобы добиться доказательства, Цермело ввел аксиому выбора, которая вызвала жаркие споры и исследования среди математиков и пионеров теории множеств.Непосредственная критика метода побудила Цермело опубликовать второе изложение своего результата, непосредственно отвечая на критику его доказательства (Zermelo 1908a). Эта статья привела к всеобщему принятию аксиомы выбора в математическом сообществе.
Скептицизм по поводу аксиомы выбора был усилен недавно обнаруженными парадоксами в наивной теории множеств. Чезаре Бурали-Форти (1897) был первым, кто сформулировал парадокс: парадокс Бурали-Форти показывает, что совокупность всех порядковых чисел не может образовать множество.Вскоре после этого Бертран Рассел открыл парадокс Рассела в 1901 году, а Жюль Ричард (1905) открыл парадокс Ричарда.
Цермело (1908b) предоставил первый набор аксиом для теории множеств. Эти аксиомы вместе с дополнительной аксиомой замены, предложенной Абрахамом Френкелем, теперь называются теорией множеств Цермело – Френкеля (ZF). Аксиомы Цермело включали принцип ограничения размера, чтобы избежать парадокса Рассела.
В 1910 году был опубликован первый том Principia Mathematica Рассела и Альфреда Норт Уайтхедов.Эта основополагающая работа развила теорию функций и мощности в полностью формальной структуре теории типов, которую Рассел и Уайтхед разработали, чтобы избежать парадоксов. Principia Mathematica считается одной из самых влиятельных работ 20-го века, хотя основы теории типов не оказались популярными в качестве фундаментальной теории математики (Ferreirós 2001, p. 445).
Френкель (1922) доказал, что аксиома выбора не может быть доказана на основе аксиом теории множеств Цермело с элементами.Более поздняя работа Пола Коэна (1966) показала, что добавление мочеточников не требуется, а аксиома выбора недоказуема в ZF. Доказательство Коэна развило метод принуждения, который сейчас является важным инструментом для установления результатов независимости в теории множеств. [6]
Символьная логика
Леопольд Левенхайм (1915) и Торальф Сколем (1920) получили теорему Левенхайма – Сколема, которая гласит, что логика первого порядка не может контролировать мощности бесконечных структур.Сколем понял, что эта теорема применима к формализации теории множеств первого порядка и что она подразумевает, что любая такая формализация имеет счетную модель. Этот парадоксальный факт стал известен как парадокс Сколема.
В своей докторской диссертации Курт Гёдель (1929) доказал теорему о полноте, которая устанавливает соответствие между синтаксисом и семантикой в логике первого порядка. Гёдель использовал теорему полноты, чтобы доказать теорему компактности, продемонстрировав конечную природу логического следствия первого порядка.Эти результаты помогли установить логику первого порядка как доминирующую логику, используемую математиками.
В 1931 году Гедель опубликовал «О формально неразрешимых предложениях принципов математики и родственных систем» , в котором доказывалась неполнота (в другом значении этого слова) всех достаточно сильных и эффективных теорий первого порядка. Этот результат, известный как теорема Гёделя о неполноте, устанавливает серьезные ограничения на аксиоматические основы математики, нанося сильный удар по программе Гильберта.Это показало невозможность предоставить доказательство непротиворечивости арифметики в рамках какой-либо формальной теории арифметики. Гильберт, однако, некоторое время не признавал важности теоремы о неполноте. [7]
Теорема Гёделя показывает, что доказательство непротиворечивости любой достаточно сильной и эффективной системы аксиом не может быть получено ни в самой системе, если она непротиворечива, ни в какой-либо более слабой системе. Это оставляет открытой возможность доказательств непротиворечивости, которые не могут быть формализованы в рамках рассматриваемой ими системы.Генцен (1936) доказал непротиворечивость арифметики, используя финитистическую систему вместе с принципом трансфинитной индукции. Результат Генцена представил идеи исключения разрезов и ординалов теории доказательств, которые стали ключевыми инструментами в теории доказательств. Гёдель (1958) дал другое доказательство непротиворечивости, которое сводит непротиворечивость классической арифметики к интуиционистской арифметике в высших типах.
Начало других филиалов
Альфред Тарский разработал основы теории моделей.
Начиная с 1935 года группа выдающихся математиков под псевдонимом Николас Бурбаки опубликовала Éléments de mathématique , серию энциклопедических математических текстов. Эти тексты, написанные в строгом и аксиоматическом стиле, подчеркивают строгость изложения и теоретико-множественные основы. Терминология, придуманная этими текстами, такая как слова bijection , инъекция и surjection , а также теоретико-множественные основы, использованные в текстах, получили широкое распространение в математике.
Изучение вычислимости стало известно как теория рекурсии или теория вычислимости, поскольку ранние формализации Гёделя и Клини основывались на рекурсивных определениях функций. [8] Когда эти определения были показаны эквивалентными формализации Тьюринга, включающей машины Тьюринга, стало ясно, что была открыта новая концепция — вычислимая функция, и что это определение было достаточно надежным, чтобы допускать многочисленные независимые характеристики. В своей работе над теоремами о неполноте в 1931 году Гёделю не хватало строгой концепции эффективной формальной системы; он сразу понял, что для этой цели можно использовать новые определения вычислимости, что позволило ему сформулировать теоремы о неполноте в общих чертах, которые могли подразумеваться только в исходной статье.
Многочисленные результаты в теории рекурсии были получены в 1940-х годах Стивеном Коулом Клини и Эмилем Леоном Постом. Клини (1943) ввел концепции относительной вычислимости, предвосхищенные Тьюрингом (1939), и арифметическую иерархию. Позже Клини обобщил теорию рекурсии на функционалы более высокого порядка. Клини и Георг Крайзель изучали формальные версии интуиционистской математики, особенно в контексте теории доказательств.
Формальные логические системы
По своей сути математическая логика имеет дело с математическими концепциями, выраженными с помощью формальных логических систем.Эти системы, хотя и отличаются во многих деталях, имеют общее свойство рассматривать только выражения на фиксированном формальном языке. Системы логики высказываний и логики первого порядка изучаются сегодня наиболее широко из-за их применимости к основам математики и из-за их желательных теоретико-доказательственных свойств. [9] Также изучаются более сильные классические логики, такие как логика второго порядка или бесконечная логика, наряду с неклассическими логиками, такими как интуиционистская логика.
Логика первого порядка
- Основная страница: Логика первого порядка
Логика первого порядка — это особая формальная система логики. Его синтаксис включает только конечные выражения в виде хорошо сформированных формул, в то время как его семантика характеризуется ограничением всех кванторов фиксированной областью дискурса.
Первые результаты формальной логики установили ограничения логики первого порядка. Теорема Левенхайма – Сколема (1919) показала, что если набор предложений счетного языка первого порядка имеет бесконечную модель, то он имеет по крайней мере одну модель каждой бесконечной мощности.Это показывает, что набор аксиом первого порядка не может характеризовать натуральные числа, действительные числа или любую другую бесконечную структуру с точностью до изоморфизма. Поскольку целью ранних фундаментальных исследований было создание аксиоматических теорий для всех разделов математики, это ограничение было особенно жестким.
Теорема Гёделя о полноте (Gödel 1929) установила эквивалентность между семантическим и синтаксическим определениями логического следствия в логике первого порядка. Это показывает, что если конкретное предложение истинно в каждой модели, удовлетворяющей определенному набору аксиом, то должна быть конечная дедукция предложения из аксиом.Теорема компактности впервые появилась как лемма в доказательстве теоремы о полноте Гёделя, и потребовалось много лет, прежде чем логики осознали ее значение и начали регулярно ее применять. Он говорит, что набор предложений имеет модель тогда и только тогда, когда каждое конечное подмножество имеет модель, или, другими словами, несовместимый набор формул должен иметь конечное несовместимое подмножество. Теоремы о полноте и компактности позволяют проводить сложный анализ логических следствий в логике первого порядка и развивать теорию моделей, и они являются ключевой причиной выдающегося положения логики первого порядка в математике.
Теоремы Гёделя о неполноте (Gödel 1931) устанавливают дополнительные ограничения на аксиоматизацию первого порядка. Первая теорема о неполноте утверждает, что для любой непротиворечивой, эффективно заданной (определенной ниже) логической системы, способной интерпретировать арифметику, существует утверждение, которое является истинным (в том смысле, что оно верно для натуральных чисел), но не доказуемо в пределах эта логическая система (и которая действительно может дать сбой в некоторых нестандартных моделях арифметики, которые могут быть совместимы с логической системой).Например, в любой логической системе, способной выражать аксиомы Пеано, предложение Гёделя справедливо для натуральных чисел, но не может быть доказано.
Здесь говорят, что логическая система эффективно задана, если по любой формуле на языке системы можно решить, является ли формула аксиомой, а формула, которая может выражать аксиомы Пеано, называется «достаточно сильной». » Применительно к логике первого порядка первая теорема о неполноте означает, что любая достаточно сильная, непротиворечивая, эффективная теория первого порядка имеет модели, которые не являются элементарно эквивалентными, — более сильное ограничение, чем ограничение, установленное теоремой Левенгейма – Сколема.Вторая теорема о неполноте утверждает, что никакая достаточно сильная, непротиворечивая, эффективная система аксиом для арифметики не может доказать свою собственную непротиворечивость, которая была интерпретирована, чтобы показать, что программа Гильберта не может быть достигнута.
Другая классическая логика
Изучается много логик, помимо логики первого порядка. К ним относятся бесконечные логики, которые позволяют формулам предоставлять бесконечное количество информации, и логики более высокого порядка, которые включают часть теории множеств непосредственно в свою семантику.
Самая хорошо изученная инфинитарная логика — это [математика] \ displaystyle {L _ {\ omega_1, \ omega}} [/ math]. В этой логике кванторы могут быть вложены только на конечную глубину, как в логике первого порядка, но формулы могут иметь в себе конечные или счетно бесконечные конъюнкции и дизъюнкции. Так, например, можно сказать, что объект является целым числом, используя формулу [math] \ displaystyle {L _ {\ omega_1, \ omega}} [/ math], например
- [математика] \ displaystyle {(x = 0) \ lor (x = 1) \ lor (x = 2) \ lor \ cdots.} [/ math]
Логики более высокого порядка позволяют количественно определять не только элементы области дискурса, но и подмножества области дискурса, множества таких подмножеств и другие объекты более высокого типа. Семантика определена таким образом, что вместо того, чтобы иметь отдельный домен для каждого квантификатора более высокого типа, в котором должен быть диапазон, квантификаторы вместо этого охватывают все объекты соответствующего типа. Логики, изучаемые до развития логики первого порядка, например логика Фреге, имели аналогичные теоретико-множественные аспекты.Хотя логики более высокого порядка более выразительны и допускают полную аксиоматизацию структур, таких как натуральные числа, они не удовлетворяют аналогам теорем о полноте и компактности из логики первого порядка и, таким образом, менее поддаются теоретико-доказательственному анализу.
Другой тип логики — это логика с фиксированной точкой , которая допускает индуктивные определения, например, запись для примитивных рекурсивных функций.
Можно формально определить расширение логики первого порядка — понятие, которое охватывает все логики в этом разделе, потому что они ведут себя как логики первого порядка в определенных фундаментальных отношениях, но не охватывает все логики в целом, например.грамм. он не включает интуиционистскую, модальную или нечеткую логику.
Из теоремы Линдстрема следует, что единственным расширением логики первого порядка, удовлетворяющим и теореме компактности, и нисходящей теореме Левенгейма – Сколема, является логика первого порядка.
Неклассическая и модальная логика
- Основная страница: Философия: неклассическая логика
Модальные логики включают дополнительные модальные операторы, такие как оператор, который утверждает, что конкретная формула не только истинна, но и обязательно истинна.Хотя модальная логика не часто используется для аксиоматизации математики, она использовалась для изучения свойств доказуемости первого порядка (Solovay 1976) и теоретико-множественного принуждения (Hamkins and Löwe 2007).
Интуиционистская логика была разработана Гейтингом для изучения программы интуиционизма Брауэра, в которой сам Брауэр избегал формализации. Интуиционистская логика специально не включает в себя закон исключенного третьего, который гласит, что каждое предложение либо истинно, либо истинно его отрицание.Работа Клини с теорией доказательств интуиционистской логики показала, что конструктивная информация может быть получена из интуиционистских доказательств. Например, любая доказуемо полная функция в интуиционистской арифметике вычислима; это неверно в классических теориях арифметики, таких как арифметика Пеано.
Алгебраическая логика
Алгебраическая логика использует методы абстрактной алгебры для изучения семантики формальных логик. Основным примером является использование булевых алгебр для представления значений истинности в классической логике высказываний и использование алгебр Гейтинга для представления значений истинности в интуиционистской логике высказываний.Более сильные логики, такие как логика первого порядка и логика высшего порядка, изучаются с использованием более сложных алгебраических структур, таких как цилиндрические алгебры.
Теория множеств
- Основная статья: Теория множеств
Теория множеств — это изучение множеств, которые представляют собой абстрактные совокупности объектов. Многие из основных понятий, таких как порядковые и кардинальные числа, были разработаны Кантором неформально до того, как были разработаны формальные аксиоматизации теории множеств.Первая такая аксиоматизация, сделанная Цермело (1908b), была немного расширена и стала теорией множеств Цермело – Френкеля (ZF), которая в настоящее время является наиболее широко используемой фундаментальной теорией математики.
Были предложены и другие формализации теории множеств, включая теорию множеств фон Неймана – Бернейса – Гёделя (NBG), теорию множеств Морса – Келли (MK) и Новые основы (NF). Из них ZF, NBG и MK похожи в описании совокупной иерархии наборов. New Foundations использует другой подход; он позволяет использовать такие объекты, как набор всех множеств, за счет ограничений на его аксиомы существования множеств.Система теории множеств Крипке – Платека тесно связана с обобщенной теорией рекурсии.
Два известных утверждения в теории множеств — это аксиома выбора и гипотеза континуума. Аксиома выбора, впервые сформулированная Цермело (1904), была доказана независимостью от ZF Френкелем (1922), но стала широко принятой математиками. В нем указано, что для данной коллекции непустых наборов существует единственный набор C , который содержит ровно один элемент из каждого набора в коллекции.Говорят, что набор C «выбирает» по одному элементу из каждого набора в коллекции. Хотя некоторые считают возможность сделать такой выбор очевидной, поскольку каждое множество в коллекции непусто, отсутствие общего конкретного правила, по которому может быть сделан выбор, делает аксиому неконструктивной. Стефан Банах и Альфред Тарски (1924 [ цитата не найдено ] ) показали, что аксиома выбора может быть использована для разложения твердого шара на конечное число частей, которые затем можно без масштабирования переставить, чтобы получить два цельные шары оригинального размера.Эта теорема, известная как парадокс Банаха – Тарского, является одним из многих нелогичных результатов аксиомы выбора.
Гипотеза континуума, впервые предложенная в качестве гипотезы Кантором, была указана Дэвидом Гильбертом как одна из его 23 проблем в 1900 году. Гёдель показал, что гипотеза континуума не может быть опровергнута аксиомами теории множеств Цермело – Френкеля (с или без аксиома выбора), развивая конструируемую вселенную теории множеств, в которой должна выполняться гипотеза континуума.В 1963 году Пол Коэн показал, что гипотеза континуума не может быть доказана с помощью аксиом теории множеств Цермело – Френкеля (Cohen, 1966). Однако этот результат независимости не разрешил полностью вопрос Гильберта, поскольку вполне возможно, что новые аксиомы теории множеств могли разрешить гипотезу. Недавняя работа в этом направлении была проведена У. Хью Вудином, хотя ее важность еще не ясна (Woodin 2001).
Современные исследования теории множеств включают изучение больших кардиналов и определенности.Большие кардиналы — это кардинальные числа с особыми свойствами, настолько сильными, что существование таких кардиналов не может быть доказано в ZFC. Существование самого маленького большого кардинала, обычно изучаемого, недоступного кардинала, уже подразумевает непротиворечивость ZFC. Несмотря на то, что большие кардиналы имеют чрезвычайно высокую мощность, их существование имеет множество разветвлений для структуры действительной линии. Определенность относится к возможному существованию выигрышных стратегий для определенных игр с двумя игроками (игры называются определенными ).Существование этих стратегий подразумевает структурные свойства реальной линии и других польских пространств.
Теория моделей
- Основная статья: Теория моделей
Теория моделей изучает модели различных формальных теорий. Здесь теория — это набор формул в определенной формальной логике и сигнатуре, а модель — это структура, которая дает конкретную интерпретацию теории. Теория моделей тесно связана с универсальной алгеброй и алгебраической геометрией, хотя методы теории моделей больше сосредоточены на логических соображениях, чем на этих областях.
Набор всех моделей конкретной теории называется элементарным классом; Классическая теория моделей стремится определить свойства моделей в конкретном элементарном классе или определить, образуют ли определенные классы структур элементарные классы.
Метод исключения кванторов может использоваться, чтобы показать, что определяемые множества в конкретных теориях не могут быть слишком сложными. Тарский (1948) установил исключение кванторов для вещественно замкнутых полей, результат, который также показывает, что теория поля действительных чисел разрешима.(Он также отметил, что его методы в равной степени применимы к алгебраически замкнутым полям произвольной характеристики.) Современное подполе, развивающееся на основе этого, связано с о-минимальными структурами.
Теорема Морли о категоричности, доказанная Майклом Д. Морли (1965), утверждает, что если теория первого порядка в счетном языке категорична в некоторой несчетной мощности, т. Е. Все модели этой мощности изоморфны, то она категорична во всех бесчисленные мощности.
Тривиальным следствием гипотезы континуума является то, что полная теория с меньшим, чем континуум, множеством неизоморфных счетных моделей может иметь только счетное число.Гипотеза Воота, названная в честь Роберта Лоусона Воота, утверждает, что это верно даже независимо от гипотезы континуума. Установлено множество частных случаев этой гипотезы.
Теория рекурсии
Теория рекурсии , также называемая теорией вычислимости , изучает свойства вычислимых функций и степеней Тьюринга, которые делят невычислимые функции на множества с одинаковым уровнем невычислимости. Теория рекурсии также включает изучение обобщенной вычислимости и определимости.Теория рекурсии выросла из работ Розы Петер, Алонзо Черча и Алана Тьюринга в 1930-х годах, которые были значительно расширены Клини и Постом в 1940-х. [10]
Классическая теория рекурсии фокусируется на вычислимости функций от натуральных чисел до натуральных чисел. Фундаментальные результаты устанавливают устойчивый канонический класс вычислимых функций с многочисленными независимыми эквивалентными характеристиками с использованием машин Тьюринга, λ-исчисления и других систем. Более продвинутые результаты касаются структуры степеней Тьюринга и решетки рекурсивно перечислимых множеств.
Обобщенная теория рекурсии расширяет идеи теории рекурсии на вычисления, которые больше не обязательно являются конечными. Он включает изучение вычислимости в высших типах, а также в таких областях, как гиперарифметическая теория и теория α-рекурсии.
Современные исследования в области теории рекурсии включают изучение таких приложений, как алгоритмическая случайность, теория вычислимых моделей и обратная математика, а также новые результаты в чистой теории рекурсии.
Алгоритмически неразрешимые задачи
Важное подразделение теории рекурсии изучает алгоритмическую неразрешимость; проблема решения или функциональная проблема алгоритмически неразрешима , если нет возможного вычислимого алгоритма, который возвращает правильный ответ для всех допустимых входных данных проблемы.Первые результаты о неразрешимости, полученные независимо Чёрчем и Тьюрингом в 1936 году, показали, что проблема Entscheidungs алгоритмически неразрешима. Тьюринг доказал это, установив неразрешимость проблемы остановки, что имеет далеко идущие последствия как для теории рекурсии, так и для информатики.
Есть много известных примеров неразрешимых задач из обычной математики. Проблема слов для групп была доказана алгоритмически неразрешимым Петром Новиковым в 1955 году и независимо У.Бун в 1959 году. Еще один хорошо известный пример — задача занятого бобра, разработанная Тибором Радо в 1962 году.
В десятой задаче Гильберта был задан алгоритм, чтобы определить, имеет ли многомерное полиномиальное уравнение с целыми коэффициентами решение в целых числах. Частичного прогресса добились Джулия Робинсон, Мартин Дэвис и Хилари Патнэм. Алгоритмическая неразрешимость проблемы была доказана Юрием Матиясевичем в 1970 году (Davis 1973).
Теория доказательств и конструктивная математика
- Основная статья: Теория доказательств
Теория доказательств — это изучение формальных доказательств в различных системах логического вывода.Эти доказательства представлены в виде формальных математических объектов, что упрощает их анализ математическими методами. Обычно рассматриваются несколько систем дедукции, включая системы дедукции в стиле Гильберта, системы естественной дедукции и секвенциальное исчисление, разработанное Генценом.
Изучение конструктивной математики , в контексте математической логики, включает изучение систем в неклассической логике, такой как интуиционистская логика, а также изучение предикативных систем.Одним из первых сторонников предикативизма был Герман Вейль, который показал, что можно разработать большую часть реального анализа, используя только методы прогнозирования (Weyl 1918) [ цитата не найдена ] .
Поскольку доказательства полностью финитны, а истина в структуре — нет, в конструктивной математике часто делается упор на доказуемость. Особый интерес представляет связь между доказуемостью в классических (или неконструктивных) системах и доказуемостью в интуиционистских (или конструктивных, соответственно) системах.Такие результаты, как отрицательный перевод Гёделя – Генцена, показывают, что можно встроить (или перевести ) классическую логику в интуиционистскую логику, позволяя перенести некоторые свойства интуиционистских доказательств обратно в классические доказательства.
Недавние разработки в теории доказательств включают исследование добычи доказательств Ульрихом Коленбахом и исследование теоретико-доказательственных ординалов Майклом Ратьеном.
Приложения
«Математическая логика успешно применяется не только к математике и ее основам (Г.Фреге, Б. Рассел, Д. Гильберт, П. Бернейс, Х. Шольц, Р. Карнап, С. Лесневски, Т. Сколем), но также и физике (Р. Карнап, А. Диттрих, Б. Рассел, К. Э. Шеннон). , А. Н. Уайтхед, Х. Райхенбах, П. Февриер), биологии (Дж. Х. Вудгер, А. Тарски), психологии (Ф. Б. Фитч, К. Г. Хемпель), праву и морали (К. Менгер, У. Клуг, П. Оппенгейм). ), экономике (Дж. Нойман, О. Моргенштерн), практическим вопросам (Э. К. Беркли, Э. Штамм) и даже метафизике (Дж. [Ян] Саламуча, Х. Шольц, JM.Боченски). Его приложения к истории логики оказались чрезвычайно плодотворными (Дж. Лукасевич, Х. Шольц, Б. Матес, А. Беккер, Э. Муди, Дж. Саламуча, К. Дюрр, З. Джордан, П. Бонер, Дж. М. Боченски) , С. [Станислав] Т. Шайер, Д. Ингаллс). « [11] » Также были поданы заявки на богословие (Ф. Древновски, Дж. Саламуча, И. Томас). « [12]
Связь с информатикой
- Основная статья: Логика в информатике
Изучение теории вычислимости в информатике тесно связано с изучением вычислимости в математической логике.Однако есть разница в акцентах. Ученые-информатики часто сосредотачиваются на конкретных языках программирования и возможной вычислимости, в то время как исследователи математической логики часто сосредотачиваются на вычислимости как теоретической концепции и на невычислимости.
Теория семантики языков программирования связана с теорией моделей, как и верификация программ (в частности, проверка моделей). Изоморфизм Карри – Ховарда между доказательствами и программами относится к теории доказательств, особенно к интуиционистской логике.Формальные исчисления, такие как лямбда-исчисление и комбинаторная логика, теперь изучаются как идеализированные языки программирования.
Информатика также вносит свой вклад в математику, разрабатывая методы автоматической проверки или даже нахождения доказательств, такие как автоматическое доказательство теорем и логическое программирование.
Теория описательной сложности связывает логику с вычислительной сложностью. Первый значительный результат в этой области, теорема Феджина (1974), установила, что NP — это в точности набор языков, выражаемых предложениями экзистенциальной логики второго порядка.
Основы математики
- Основная статья: Философия: основы математики
В 19 веке математики осознали логические пробелы и несоответствия в своей области. Было показано, что аксиомы Евклида для геометрии, которые веками преподавались как пример аксиоматического метода, были неполными. Использование бесконечно малых величин и само определение функции стало предметом анализа при обнаружении патологических примеров, таких как нигде не дифференцируемая непрерывная функция Вейерштрасса.
Исследования Кантора произвольных бесконечных множеств также вызвали критику. Леопольд Кронекер заявил, что «Бог создал целые числа; все остальное — дело рук человека», поддерживая возвращение к изучению конечных конкретных объектов в математике. Хотя аргумент Кронекера был поддержан конструктивистами в 20 веке, математическое сообщество в целом отвергло их. Дэвид Гильберт выступал за изучение бесконечного, говоря: «Никто не изгонит нас из рая, созданного Кантором.»
Математики начали поиск систем аксиом, которые можно было бы использовать для формализации больших частей математики. В дополнение к устранению двусмысленности из ранее наивных терминов, таких как функция, была надежда, что эта аксиоматизация позволит обеспечить доказательства непротиворечивости. В XIX веке основным методом доказательства непротиворечивости набора аксиом было создание модели для него. Таким образом, например, неевклидова геометрия может быть доказана непротиворечивостью, определив точку как точку на фиксированной сфере и линию как обозначение большого круга на сфере.Результирующая структура, модель эллиптической геометрии, удовлетворяет аксиомам плоской геометрии, за исключением постулата параллельности.
С развитием формальной логики Гильберт спросил, можно ли доказать, что система аксиом непротиворечива, анализируя структуру возможных доказательств в системе и показывая этим анализом невозможность доказательства противоречия. Эта идея привела к изучению теории доказательств. Более того, Гильберт предложил, чтобы анализ был полностью конкретным, используя термин Finitary для обозначения методов, которые он разрешил бы, но не определяя их точно.На этот проект, известный как программа Гильберта, серьезно повлияли теоремы Гёделя о неполноте, которые показывают, что непротиворечивость формальных теорий арифметики не может быть установлена с использованием методов, формализуемых в этих теориях. Генцен показал, что можно произвести доказательство непротиворечивости арифметики в финитарной системе, дополненной аксиомами трансфинитной индукции, и разработанные им методы были основополагающими в теории доказательств.
Вторая нить в истории основ математики связана с неклассической логикой и конструктивной математикой.Изучение конструктивной математики включает в себя множество различных программ с различными определениями конструктив . В большинстве случаев доказательства теории множеств ZF, не использующие аксиому выбора, многие математики называют конструктивными. Более ограниченные версии конструктивизма ограничиваются натуральными числами, теоретико-числовыми функциями и наборами натуральных чисел (которые могут использоваться для представления действительных чисел, облегчая изучение математического анализа). Распространенная идея состоит в том, что конкретные средства вычисления значений функции должны быть известны, прежде чем можно будет сказать, что сама функция существует.
В начале 20 века Луитцен Эгбертус Ян Брауэр основал интуиционизм как часть философии математики. Эта философия, поначалу плохо понимаемая, утверждала, что для того, чтобы математическое утверждение было истинным для математика, этот человек должен уметь интуитивно понять утверждение, чтобы не только поверить в его истинность, но и понять причину его истинности. Следствием этого определения истины было отклонение закона исключенного третьего, поскольку есть утверждения, которые, согласно Брауэру, не могут считаться истинными, в то время как их отрицания также не могут считаться истинными.Философия Брауэра оказала влияние и стала причиной ожесточенных споров среди выдающихся математиков. Позже Клини и Крайзель изучили формализованные версии интуиционистской логики (Брауэр отверг формализацию и представил свою работу на неформализованном естественном языке). С появлением интерпретации BHK и моделей Крипке интуиционизм стало легче согласовывать с классической математикой.
См. Также
Банкноты
- ↑ Тексты для бакалавров включают Булос, Берджесс и Джеффри (2002), Эндертон (2001) и Мендельсон (1997).Классический выпускной текст Шонфилда (2001) впервые появился в 1967 году.
- ↑ См. (Барвайз, 1989)
- ↑ Jozef Maria Bochenski, A Precis of Mathematical Logic (1959), ред. и пер., Альберт Менне, изд. и пер., Отто Берд, Дордрехт, Южная Голландия: Reidel, Sec. 0.1, п. 1.
- ↑ Ричард Свинсхед (1498), Calculationes Suiseth Anglici , Papie: Per Franciscum Gyrardengum.
- ↑ Boehner p. xiv
- ↑ См. Также Cohen 2008.
- ↑ В предисловии к первому изданию «Grundlagen der Mathematik» 1934 года (Гильберт Бернейс) Бернейс написал следующее, которое напоминает знаменитую заметку Фреге, когда ему сообщили о парадоксе Рассела.
Перевод:«Die Ausführung dieses Vorhabens hat eine wesentliche Verzögerung dadurch erfahren, daß in Einem Stadium, in dem die Darstellung schon ihrem Abschuß nahe war, durch das Erscheinen der Welbeiten von Herbrand und die Gödelte ei. Berücksichtigung neuer Einsichten zur Aufgabe machte.Dabei ist der Umfang des Buches angewachsen, so daß eine Teilung in zwei Bände angezeigt erschien ».
Итак, конечно, Гильберт осознавал важность работы Гёделя к 1934 году. Второй том 1939 года включал форму доказательства непротиворечивости Гентцена для арифметики. .« Осуществление этого плана [Гильберта для изложения теории доказательств для математической логики] произошло с существенной задержкой, потому что: на этапе, когда изложение уже было близко к своему завершению, в области теории доказательств произошла изменившаяся ситуация в связи с появлением работ Хербранда и Гёделя, что потребовало рассмотрения новых идей.Таким образом, объем этой книги расширился, так что разделение на два тома казалось целесообразным ».
- ↑ Подробное исследование этой терминологии дано Соаре (1996).
- ↑ Феррейрос (2001) рассматривает рост логики первого порядка по сравнению с другими формальными логиками в начале 20 века.
- ↑ Соаре, Роберт Ирвинг (22 декабря 2011 г.).»Теория вычислимости и приложения: искусство классической вычислимости». Чикагский университет. http://www.people.cs.uchicago.edu/~soare/Turing/frontice.pdf. Проверено 23 августа 2017 года.
- ↑ Йозеф Мария Боченски, A Precis of Mathematical Logic , rev. и пер., Альберт Менне, изд. и пер., Отто Берд, Дордрехт, Южная Голландия: Reidel, Sec. 0.3, п. 2.
- ↑ Йозеф Мария Боченски, A Precis of Mathematical Logic , rev. и пер., Альберт Менне, изд.и пер., Отто Берд, Дордрехт, Южная Голландия: Reidel, Sec. 0.3, п. 2.
Список литературы
Тексты для бакалавриата
- Булос, Джордж; Берджесс, Джон; Джеффри, Ричард (2002), Computability and Logic (4-е изд.), Кембридж: Cambridge University Press , ISBN 978-0-521-00758-0.
- Crossley, J.N .; Ash, C.J .; Brickhill, C.J .; Stillwell, J.C .; Уильямс, Н.Х. (1972), Что такое математическая логика? , Лондон-Оксфорд-Нью-Йорк: Oxford University Press, ISBN 978-0-19-888087-5.
- Enderton, Herbert (2001), Математическое введение в логику (2-е изд.), Бостон, Массачусетс: Academic Press, ISBN 978-0-12-238452-3.
- Фишер, Алек (1982), Формальная теория чисел и вычислимость: Учебное пособие (1-е изд.), США: Oxford University Press, ISBN 978-0-19-853188-3. Подходит в качестве первого курса для самостоятельного обучения.
- Гамильтон, А.Г. (1988), Логика для математиков (2-е изд.), Кембридж: Издательство Кембриджского университета, ISBN 978-0-521-36865-0.
- Ebbinghaus, H.-D .; Flum, J .; Томас, В. (1994), Mathematical Logic (2-е изд.), Нью-Йорк : Springer, ISBN 978-0-387-94258-2, https://www.springer.com/mat Mathematics/book / 978-0-387-94258-2.
- Кац, Роберт (1964), Аксиоматический анализ , Бостон, Массачусетс: Д. К. Хит и компания.
- Мендельсон, Эллиотт (1997), Введение в математическую логику (4-е изд.), Лондон: Chapman & Hall, ISBN 978-0-412-80830-2.
- Раутенберг, Вольфганг (2010), Краткое введение в математическую логику (3-е изд.), Нью-Йорк : Springer Science + Business Media, DOI: 10.1007 / 978-1-4419-1221-3, ISBN 978-1-4419-1220-6.
- Schwichtenberg, Helmut (2003–2004), Mathematical Logic , Мюнхен, Германия: Mathematisches Institut der Universität München, http://www.mathematik.uni-muenchen.de/~schwicht/lectures/logic/ws03/ml. pdf, дата обращения 24 февраля 2016.
- Шон Хедман, Первый курс логики: введение в теорию моделей, теорию доказательств, вычислимость и сложность , Oxford University Press, 2004, ISBN 0-19-852981-3.Охватывает логику в тесной связи с теорией вычислимости и теорией сложности
- ван Дален, Дирк (2013), Логика и структура , Universitext, Берлин: Springer-Verlag, DOI: 10.1007 / 978-1-4471-4558-5, ISBN 978-1-4471-4557-8.
Тексты для выпускников
- Эндрюс, Питер Б. (2002), Введение в математическую логику и теорию типов: к истине через доказательство (2-е изд.), Бостон: Kluwer Academic Publishers, ISBN 978-1-4020-0763-7.
- Барвайз, Джон, изд. (1989). Справочник по математической логике . Исследования по логике и основам математики. Северная Голландия. ISBN 978-0-444-86388-1. .
- Ходжес, Уилфрид (1997), Более короткая теория моделей , Кембридж: Cambridge University Press , ISBN 978-0-521-58713-6.
- Jech, Thomas (2003), Теория множеств: Millennium Edition , Монографии Springer по математике, Берлин, Нью-Йорк: Springer-Verlag, ISBN 978-3-540-44085-7.
- Клини, Стивен Коул.(1952), Введение в метаматематику. Нью-Йорк: Ван Ностранд. (Ishi Press: перепечатка 2009 г.).
- Клини, Стивен Коул. (1967), Математическая логика. Джон Вили. Переиздание Dover, 2002. ISBN 0-486-42533-9.
- Шоенфилд, Джозеф Р. (2001) [1967], Mathematical Logic (2-е изд.), А. К. Петерс, ISBN 978-1-56881-135-2.
- Troelstra, Anne Sjerp; Швихтенберг, Гельмут (2000), Основная теория доказательств , Кембриджские тракты по теоретической информатике (2-е изд.), Кембридж: Издательство Кембриджского университета, ISBN 978-0-521-77911-1.
Научные статьи, монографии, тексты и обзоры
- Аугусто, Луис М. (2017). Логические следствия. Теория и приложения: Введение . Лондон: Публикации колледжа. ISBN 978-1-84890-236-7. http://www.collegepublications.co.uk/logic/mlf/?00029.
- Бонер, Филофей, Средневековая логика , Манчестер 1950.
- Коэн, П. Дж. (1966), Теория множеств и гипотеза континуума , Менло-Парк, Калифорния: W.А. Бенджамин.
- Коэн, Пол Джозеф (2008) [1966]. Теория множеств и гипотеза континуума . Минеола, Нью-Йорк: Dover Publications. ISBN 978-0-486-46921-8. .
- Дж. Д. Снид, Логическая структура математической физики . Reidel, Dordrecht, 1971 (переработанное издание 1979 г.).
- Дэвис, Мартин (1973), «Десятая проблема Гильберта неразрешима», The American Mathematical Monthly 80 (3): 233–269, DOI: 10.2307 / 2318447, перепечатано в виде приложения к книге Мартина Дэвиса, вычислимости и неразрешимости , Дувр, репринт 1982.
- Фельшер, Уолтер (2000), «Больцано, Коши, Эпсилон, Дельта», Американский математический ежемесячник 107 (9): 844–862, DOI: 10.2307 / 2695743.
- Феррейрос, Хосе (2001), «Дорога к современной логике — интерпретация», Бюллетень символической логики 7 (4): 441–484, DOI: 10.2307 / 2687794, https://idus.us. es / xmlui / bitstream / 11441/38373/1 / The% 20road% 20to% 20modern% 20logic.pdf.
- Хэмкинс, Джоэл Дэвид; Лёве, Бенедикт (2007), «Модальная логика принуждения», Труды Американского математического общества 360 (4): 1793–1818, DOI: 10.1090 / с0002-9947-07-04297-3
- Кац, Виктор Дж. (1998), История математики , Аддисон – Уэсли, ISBN 978-0-321-01618-8.
- Морли, Майкл (1965), «Категоричность во власти», Труды Американского математического общества 114 (2): 514–538, DOI: 10.2307 / 1994188.
- Соаре, Роберт И. (1996), «Вычислимость и рекурсия», Бюллетень символической логики 2 (3): 284–321, DOI: 10.2307 / 420992.
- Соловей, Роберт М.(1976), «Интерпретации доказуемости модальной логики», Израильский математический журнал 25 (3–4): 287–304, DOI: 10.1007 / BF02757006.
- Вудин, У. Хью (2001), «Гипотеза континуума, часть I», Уведомления Американского математического общества 48 (6). PDF
Классические статьи, тексты и коллекции
- Бурали-Форти, Чезаре (1897), Вопрос о трансфинитных числах , перепечатано в van Heijenoort 1976, стр.104–111.
- Дедекинд, Ричард (1872), Stetigkeit und irrationale Zahlen . Английский перевод названия: «Непротиворечивость и иррациональные числа».
- Дедекинд, Ричард (1888 г.), Был ли злодей Зален? Два английских перевода:
- 1963 (1901). Очерки теории чисел . Беман, У. У., изд. и пер. Дувр.
- 1996. В От Канта до Гильберта: Справочник по основам математики , 2 тома, Эвальд, Уильям Б., изд., Oxford University Press: 787–832.
- Френкель, Абрахам А. (1922), «Der Begriff ‘Definit’ und die Unabhängigkeit des Auswahlsaxioms», Sitzungsberichte der Preussischen Akademie der Wissenschaften, Physikalisch-Mathematische Klasse, переиздание на немецком языке,7, перепечатка на немецком языке,7, с. как «Понятие« определенного »и независимость аксиомы выбора», van Heijenoort, 1976, стр. 284–289.
- Frege, Gottlob (1879), Begriffsschrift, eine der arithmetischen nachgebildete Formelsprache des reinen Denkens .Галле а. С .: Луи Неберт. Перевод: Concept Script, формальный язык чистой мысли, смоделированный по образцу арифметики , С. Бауэр-Менгельберг в журнале Jean Van Heijenoort, 1967. От Фреге до Гёделя: Справочник по математической логике, 1879– 1931 . Издательство Гарвардского университета.
- Frege, Gottlob (1884), Die Grundlagen der Arithmetik: eine logisch-Mathematische Untersuchung über den Begriff der Zahl . Бреслау: В. Кебнер. Перевод: Дж. Л. Остин, 1974. Основы арифметики: логико-математическое исследование концепции числа , 2-е изд. Блэквелл.
- Gentzen, Gerhard (1936), «Die Widerspruchsfreiheit der reinen Zahlentheorie», Mathematische Annalen 112 : 132–213, DOI: 10.1007 / BF01565428, перепечатано в английском переводе в Gentzen’s ed. , Северная Голландия, Амстердам, 1969.
- Gödel, Kurt (1929), Über die Vollständigkeit des Logikkalküls , докторская диссертация, Венский университет.Английский перевод названия: «Полнота логического исчисления».
- Gödel, Kurt (1930), «Die Vollständigkeit der Axiome des logischen Funktionen-kalküls», Monatshefte für Mathematik und Physik 37 : 349–360, doi: 10.1007 / BF01696781. Английский перевод названия: «Полнота аксиом исчисления логических функций».
- Гёдель, Курт (1931), «Über form unentscheidbare Sätze der Principia Mathematica und Verwandter Systeme I», Monatshefte für Mathematik und Physik 38 (1): 173–198, DOI: 10.1007 / BF01700692, см. «Формально неразрешимые предложения принципов математики и родственных систем» для получения подробной информации об английских переводах.
- Гёдель, Курт (1958), «Убер эйне бишер нох нихт бенютцте, эрвайтерунг де финитен стэндпунктес», Диалектика. Международный журнал философии 12 (3–4): 280–287, DOI: 10.1111 / j.1746-8361.1958.tb01464.x, перепечатано в английском переводе в собрании сочинений Гёделя , том II, Соломон Феферман и др. ., ред.Oxford University Press, 1990. [ укажите ]
- van Heijenoort, Jean, ed. (1976), From Frege to Gödel: A Source Book in Mathematical Logic, 1879–1931 (3-е изд.), Кембридж, Массачусетс: Harvard University Press, (pbk.), ISBN 978-0-674-32449-7
- Hilbert, David (1899), Grundlagen der Geometrie , Leipzig: Teubner, English 1902 edition ( The Foundations of Geometry ) переиздано в 1980 году, Open Court, Чикаго.
- Гильберт, Дэвид (1929), «Probleme der Grundlegung der Mathematik», Mathematische Annalen 102 : 1–9, DOI: 10.1007 / BF01782335, http://gdz.sub.uni-goettingen.de/index.php?id=11&PPN=GDZPPN002273500&L=1. Лекция, прочитанная на Международном конгрессе математиков 3 сентября 1928 г. Опубликована в английском переводе как «Основание элементарной теории чисел» в Mancosu 1998, стр. 266–273.
- Гильберт, Дэвид; Бернейс, Пол (1934). Grundlagen der Mathematik. Я . Die Grundlehren der Mathematischen Wissenschaften. 40 . Берлин, Нью-Йорк: Springer-Verlag. ISBN 978-3-540-04134-4.
- Клини, Стивен Коул (1943), «Рекурсивные предикаты и кванторы», Транзакции Американского математического общества 54 (1): 41–73, DOI: 10.2307 / 19
- .
- Лобачевский, Николай (1840), Geometrishe Untersuchungen zur Theorie der Parellellinien (немецкий). Перепечатано в английском переводе как «Геометрические исследования по теории параллельных линий» в Неевклидовой геометрии , Роберт Бонола (ред.), Дувр, 1955. ISBN 0-486-60027-0
- Löwenheim, Leopold (1915), «Über Möglichkeiten im Relativkalkül», Mathematische Annalen 76 (4): 447–470, DOI: 10.1007 / BF01458217, ISSN 0025-5831, http://gdz.sub.uni-goettingen.de/index.php?id=11&PPN=GDZPPN002266121&L=1 (немецкий). Переведено как «Возможности в исчислении родственников» в Жан ван Хейенорт, 1967. Справочник по математической логике, 1879–1931 . Harvard Univ. Пресс: 228–251.
- Манкосу, Паоло, изд. (1998), От Брауэра до Гильберта. Дебаты об основах математики в 1920-е годы , Оксфорд: Oxford University Press.
- Pasch, Moritz (1882), Vorlesungen über neuere Geometrie .
- Peano, Giuseppe (1889), Arithmetices Principia, nova Methodo exposita (латиница), выдержка перепечатана в английском переводе как «Принципы арифметики, представленные новым методом», van Heijenoort 1976, pp. 83 97.
- Ричард, Жюль (1905), «Принципы математики и проблемы ансамблей», Revue Générale des Sciences Pures et Appliquées 16 : 541 (французский), перепечатано в английском переводе как «Принципы математики и проблемы множеств », van Heijenoort 1976, стр.142–144.
- Skolem, Thoralf (1920), «Logisch-kombinatorische Untersuchungen über die Erfüllbarkeit oder Beweisbarkeit Mathematischer Sätze nebst einem Theoreme über dichte Mengen», Videnskapsselskapet12 Kideligte Mengen, Videnskapsselskapet 12 Skmatriisk6 — I.
- Тарский, Альфред (1948), Метод принятия решений для элементарной алгебры и геометрии , Санта-Моника, Калифорния: RAND Corporation
- Тьюринг, Алан М. (1939), «Системы логики, основанные на порядковых числах», Труды Лондонского математического общества 45 (2): 161–228, DOI: 10.1112 / плмс / с2-45.1.161
- Zermelo, Ernst (1904), «Beweis, daß jede Menge wohlgeordnet werden kann», Mathematische Annalen 59 (4): 514–516, doi: 10.1007 / BF01445300, http: //gdz.sub.uni- goettingen.de/index.php?id=11&PPN=GDZPPN002260018&L=1 (немецкий), перепечатано в английском переводе как «Доказательство того, что каждый набор может быть хорошо упорядочен», van Heijenoort 1976, стр. 139–141.
- Цермело, Эрнст (1908a), «Neuer Beweis für die Möglichkeit einer Wohlordnung», Mathematische Annalen 65 : 107–128, doi: 10.1007 / BF01450054, ISSN 0025-5831, http://gdz.sub.uni-goettingen.de/index.php?id=11&PPN=GDZPPN002261952&L=1 (немецкий), перепечатано в английском переводе как «Новое доказательство возможности правильного порядка », ван Хейеноорт, 1976, стр. 183–198.
- Zermelo, Ernst (1908b), «Untersuchungen über die Grundlagen der Mengenlehre», Mathematische Annalen 65 (2): 261–281, doi: 10.1007 / BF01449999, http: //gdzi-goetting.un. de / index.php? id = 11 & PPN = PPN235181684_0065 & DMDID = DMDLOG_0018 & L = 1.
Внешние ссылки
- Hazewinkel, Michiel, ed. (2001), «Математическая логика», Энциклопедия математики , Springer Science + Business Media BV / Kluwer Academic Publishers, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php ? title = p / m062660
- Многозначная логика и логика количественных соотношений
- forall x: введение в формальную логику , бесплатный учебник П. Д. Магнуса.
- Проблемный курс математической логики , бесплатный учебник Стефана Биланюка.
- Детловс, Вилнис и Подниекс, Карлис (Латвийский университет), Введение в математическую логику. (гипер-учебник).
- В Стэнфордской энциклопедии философии:
- Классическая логика Стюарта Шапиро.
- Теория моделей первого порядка Уилфрида Ходжеса.
- В London Philosophy Study Guide:
- Математическая логика
- Теория множеств и дополнительная логика
- Философия математики


 В., 2010
В., 2010 Ю., Цветкова М.С., 2013
Ю., Цветкова М.С., 2013 С., Богомолова О.Б., 2013
С., Богомолова О.Б., 2013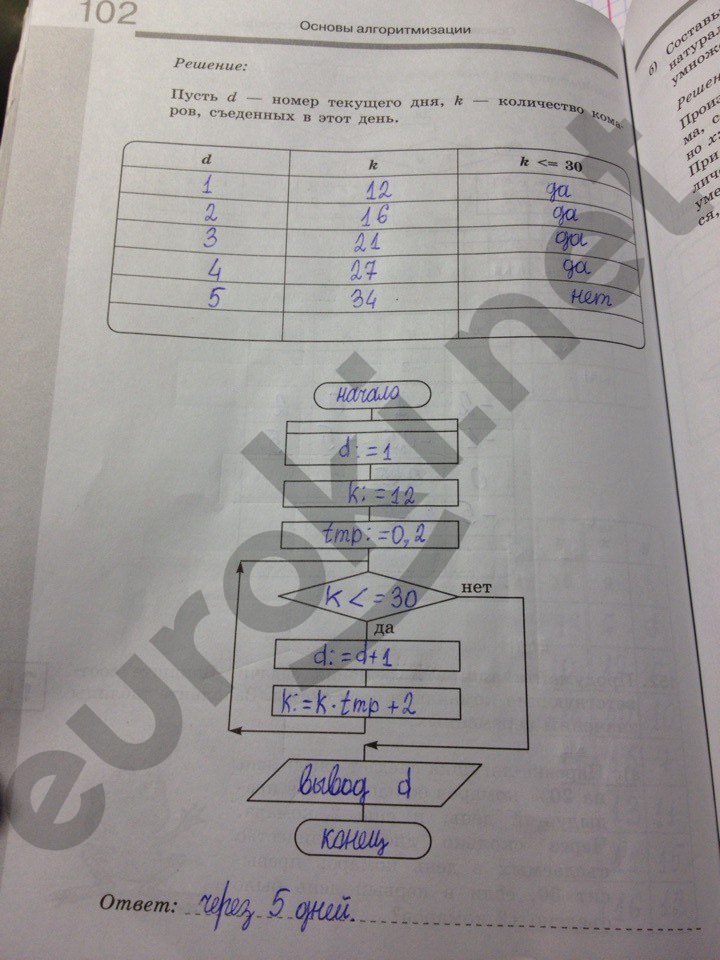 , Махкамов М., Азаматов А., 2006
, Махкамов М., Азаматов А., 2006 Г., Юнерман Н.А., 2009
Г., Юнерман Н.А., 2009 Л., 2012
Л., 2012