Решение задач по геометрии 8 класс онлайн: Решение задач по геометрии, 8 класс, К учебнику по геометрии за 7-9 класс, Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Юдина И.И., Позняк Э.Г., 2005

Практика. Решение задач 8 класс онлайн-подготовка на Ростелеком Лицей

Центральный и вписанный углы

 

Вспомним определение и свойства центрального и вписанного углов (см. рис. 1): центральный угол – это угол, вершина которого совпадает с центром окружности; вписанный угол – это угол, вершина которого принадлежит окружности.

 

Рис. 1. Центральный угол  и вписанный угол

При этомвписанный угол равен половине градусной меры дуги окружности, на которую он опирается, а центральный угол равен этой дуге:

Одним из следствий является то, что два вписанных угла, опирающихся на одну дугу (или одну хорду), равны друг другу (см. рис. 2).

Рис. 2. Вписанные углы , опирающиеся на одну дугу

 

Угол, вершина которого лежит внутри окружности

 

 

А как обстоит дело с остальными углами, опирающимися на дугу, но вершина которых не лежит ни на окружности, ни в ее центре?

 

Понятно, что в этом случае вершина лежит либо внутри окружности (см. рис. 3), либо снаружи (см. рис. 4).

Рис. 3. Вершина угла лежит внутри окружности

Рис. 4. Вершина угла лежит вне окружности

Рассмотрим случай, когда вершина лежит внутри окружности. Угол  опирается на дугу  (см. рис. 5).

Рис. 5. Угол  опирается на дугу

Интуитивно понятно, что угол больше вписанного, опирающегося на ту же самую дугу. Продлим стороны угла  и  до пересечения с окружностью (см. рис. 6) и попробуем выразить сам угол через величины дуг, на которые разбита окружность.

Рис. 6. Стороны угла  и  продлили до пересечения с окружностью

Наш угол является внешним для треугольника . А раз так, то он равен сумме двух внутренних углов, не смежных с ним (см. рис. 7):

Рис. 7. Угол , являющийся внешним для треугольника , равен сумме двух внутренних углов, не смежных с ним

Но углы  и  уже являются вписанными, а значит, каждый из них равен половине дуги, на которую опирается:

Уберем лишнее с рисунка (см. рис. 8).

Рис. 8. Угол  равен полусумме дуг  и

Итак: если через точку внутри окружности проведены две секущие, то угол между ними равен полусумме дуг, на которые опираются сам угол и ему вертикальный.

Легко проверить, что это выполняется и для центрального, и для вписанного углов (как для предельных случаев). Т. е. мы обобщили теорему о центральном и вписанном угле (как раньше обобщили теорему Пифагора теоремой косинусов).

Второй случай, когда вершина угла лежит вне окружности, а стороны угла пересекают эту окружность. Попробуйте самостоятельно изобразить этот случай и выразить величину угла через дуги, на которые окружность поделилась сторонами угла. А решение можно посмотреть ниже.

---

 

Угол, вершина которого лежит вне окружности

Итак, постановка задачи: через точку, лежащую вне окружности, проходят две секущие (см. рис. 9). Выразить величину угла через полученные дуги окружности.

Рис. 9. Через точку, лежащую вне окружности, проходят две секущие

Посмотрим на две дуги, которые лежат внутри угла : дуги  и .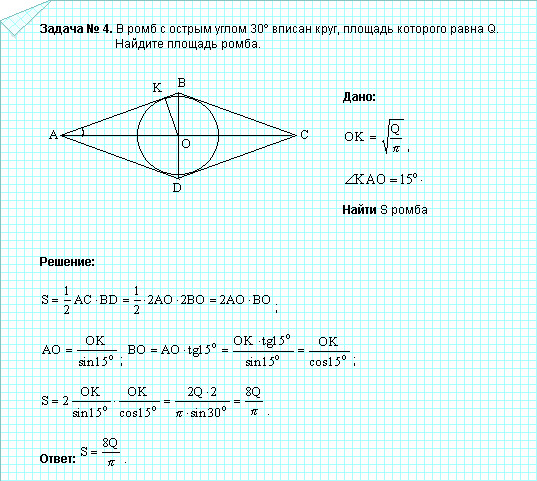 Мы знаем, как выразить через дуги вписанные углы, которые на них опираются. Поэтому попробуем выразить угол  через вписанные углы. Для этого соединим точки  и . Получим два вписанных угла  и  (см. рис. 10).

Рис. 10. Соединили точки  и , получили два вписанных угла  и

Угол  опирается на дугу , угол  опирается на дугу . Эти углы равны половине соответствующих дуг. И при этом исследуемый угол  выражается через эти два угла.

В самом деле, угол  является внешним для треугольника , значит:

Тогда:

Вспомним теперь, что эти углы равны половинам своих дуг:

Таким образом, угол  равен полуразности дуг, заключенных внутри угла.

---

 

 

Свойство вписанного четырехугольника

 

 

При изучении новых объектов мы обычно формулируем два типа утверждений: свойства (то, что мы всегда можем сказать об этом объекте) и признаки (благодаря чему мы можем узнать именно этот объект).

 

Например: у каждой лошади есть голова. Это свойство лошадей или их необходимый признак. Но назвать признаком наличие головы нельзя: она есть у людей, у собак и т. д.

Умение читать книги – достаточный признак человека (если кто-то умеет читать, то это точно человек). Если признак работает в обе стороны, то он так и называется – необходимым и достаточным. Молния – необходимый и достаточный признак грозы (если гроза, то обязательно есть молния, но если видим молнию, значит, точно гроза).

Итак, ранее мы убедились, что, в отличие от треугольников, далеко не все четырехугольники можно вписать в окружность (и, соответственно, любой четырехугольник можно вписать в окружность). Например, квадрат можно вписать в окружность, а ромб, не являющийся квадратом, нельзя.

Оказалось, что можно сформулировать признаки вписанного и описанного четырехугольников (т. е. то свойство, которым обладают только такие четырехугольники и не обладают остальные).

Свойство вписанного четырехугольника: если четырехугольник вписан в окружность, то суммы противоположных углов в нем равны  (см. рис. 11).

Рис. 11. Если четырехугольник вписан в окружность, то суммы противоположных углов в нем равны

 

Признак вписанного четырехугольника

 

 

Доказать это свойство оказалось несложно (Окружность и многоугольники). Но оно не поможет нам, если мы не докажем, что у любого другого не вписанного четырехугольника суммы противоположных углов не равны . Вспомните пример с лошадью: отсутствие головы точно говорит нам, что данный объект не лошадь, но вот ее наличие еще ничего не говорит.

 

Итак, в свое время мы доказали свойство, а обратное утверждение приняли на веру. Сейчас у нас есть все инструменты, чтобы вернуться и доказать признак вписанного четырехугольника.

Теорема

Если в четырехугольнике сумма противоположных углов равна , то он вписанный (вокруг него можно описать окружность).

Доказательство

Рассмотрим четырехугольник , у которого углы  и  в сумме равны  (см. рис. 12).

Рис. 12. Четырехугольник , где сумма углов  и  равна

Вокруг любого треугольника можно описать окружность. Опишем ее вокруг треугольника  (см. рис. 13) и докажем, что она пройдет обязательно и через точку .

Рис. 13. Вокруг треугольника  описана окружность

Будем доказывать методом от противного. Предположим, что окружность не проходит через точку . Тогда точка  может оказаться внутри или вне окружности.

Рассмотрим случай, когда она находится внутри (см. рис. 13).

Рис. 13. Точка  находится внутри окружности

Продлим стороны до пересечения с окружностью:

Но тогда он больше, чем просто половина дуги :

При этом угол  вписанный и равен половине дуги, на которую опирается:

Если к обеим частям неравенства прибавить равные выражения, то получим эквивалентное неравенство:

Таким образом:

Но это противоречит условию. Таким образом, точка  не может лежать внутри окружности.

Самостоятельно рассмотрите случай, когда точка  лежит вне окружности, и докажите, что это невозможно. Там рассуждения совершенно аналогичны (изменится только знак неравенства).

Доказано.

Итак, равенство суммы противоположных углов  является теперь необходимым и достаточным признаком вписанного четырехугольника.

 

Нахождение значений тригонометрических функций

 

 

Мы с вами успели убедиться, что тригонометрические функции очень удобный инструмент для решения геометрических задач. Во многом это связано с тем, что значение тригонометрической функции зависит только от величины угла и не зависит от типа треугольника.

 

В произвольном треугольнике есть три угла и для каждого угла можно посчитать значение синуса, косинуса, тангенса и котангенса (или указать, что тангенс не определен – для прямого угла).

Мы нашли значения тригонометрических функций для некоторых углов. Обычно их сводят в такую таблицу (см. рис. 15).

Рис. 15. Таблица значений основных тригонометрических функций

Запоминать ее не обязательно (хотя при решении большого количества задач вы это сделаете непроизвольно), лучше помнить, как можно их получить (Тригонометрические функции произвольных углов. Теоремы синусов и косинусов).

Значения разных тригонометрических функций для одного угла связаны между собой основными тригонометрическими тождествами:

Зная значение одной тригонометрической функции угла, можно найти все остальные.

 

Задача 1. Найти неизвестные тригонометрические функции угла, если:

Решение

Можно, конечно, найти угол, зная, что угол лежит в интервале от  до , а его косинус равен  (см. рис. 16).

Рис. 16. Иллюстрация к задаче 1

Зная определение тригонометрической функции (косинус – абсцисса соответствующей точки на окружности) (см. рис. 17), несложно получить, что:

Т. е. .

Рис. 17. Иллюстрация к задаче 1

Но мы рассмотрим общий способ, ведь нам не обязательно «повезет» с табличным значением тригонометрической функции.

Чтобы найти синус, зная, косинус, воспользуемся тождеством, которое их связывает, а именно:

Выразим из него синус:

Мы получили два возможных значения синуса. Как быть? Если бы у нас не было больше никакой информации об угле, то на этом нам бы пришлось остановиться. Действительно, при данном значении косинуса у синуса может быть два значения (вертикальная прямая пересекает окружность в двух точках с противоположными ординатами) (см. рис. 18).

Рис. 18. Иллюстрация к задаче 1

Но у нас есть дополнительная информация: угол лежит в четвертой четверти (см. рис. 19).

Рис. 19. Иллюстрация к задаче 1

В этой четверти у всех точек окружности ордината отрицательная, значит, синус будет иметь знак «минус»:

Осталось найти тангенс и котангенс, зная синус и косинус:

Ответ: .

Обратите внимание: если бы в условии речь шла об угле треугольника, то мы бы сами ограничили величину угла: , и сказали бы, что т. к. его косинус положительный, то угол лежит в первой четверти (тогда и все остальные тригонометрические функции данного угла были бы положительными).

 

Задача 2. Найти неизвестные тригонометрические функции угла, если:

Решение

Мы знаем, что, по определению, синус угла – это ордината соответствующей точки окружности. Видим, что окружность пересекается горизонтальной прямой  в двух точках (см. рис. 20).

Рис. 20. Иллюстрация к задаче 2

Значит, условию  соответствуют два угла:  в первой четверти и  во второй (больше никакой информации об угле, в отличие от предыдущей задачи, нет).

Соответственно, у нас будут два разных значения косинуса. По рисунку видно, что по модулю эти значения равны и отличаются только знаком (см. рис. 21).

Рис. 21. Иллюстрация к задаче 2

Снова воспользуемся основным тригонометрическим тождеством:

Тогда:

В такой постановке мы бы должны были получить и два возможных значения тангенса и котангенса (с точностью до знака). Давайте добавим информацию о величине угла, чтобы получить однозначный ответ: пусть  (или, по-другому, угол находится во второй четверти).

Косинус, который ему соответствует, имеет знак «минус» (т. к. абсциссы точек окружности во второй четверти отрицательные):

Осталось найти тангенс и котангенс:

Ответ: .

 

Теоремы синусов и косинусов

 

 

Кроме непосредственно тригонометрических функций, у нас есть еще два очень мощных инструмента, которые помогают нам находить недостающие элементы треугольников: теорема синусов и теорема косинусов. Вспомним обе теоремы.

 

Теорема синусов: отношение сторон к синусам противолежащих углов постоянно для данного треугольника и равно диаметру описанной окружности:

Возьмем первую часть этого утверждения:

Зная три элемента в этой пропорции, мы можем найти четвертый.

Например, если мы знаем две стороны и один противолежащий угол, то можем найти второй угол:

Или знаем одну сторону и два угла, найдем вторую сторону:

Теорема косинусов: квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:

С помощью этой теоремы мы находим третью сторону, если знаем две стороны и угол между ними. Или, зная три стороны, можно найти каждый угол, точнее – его косинус.

Задача 3. Выяснить тип треугольника (остроугольный, прямоугольный, тупоугольный), если его стороны равны:

Решение

Тип треугольника определяется его наибольшим углом, а наибольший угол лежит напротив наибольшей стороны (см. рис. 22). Зная три стороны, мы можем найти угол, используя теорему косинусов.

Рис. 22. Иллюстрация к задаче 3

1. Стороны треугольника равны , значит, наибольший угол лежит напротив стороны . По теореме косинусов имеем:

Выразим косинус:

Косинус положительный, соответствующий ему угол треугольника может быть только острым (у тупых углов косинус отрицательный – соответствующие им точки окружности расположены во второй четверти) (см. рис. 23). Т. е. наибольший угол треугольника острый, остальные тем более острые. Треугольник остроугольный.

Рис. 23. Иллюстрация к задаче 3

Остальные два случая решаются аналогично. Выполните их самостоятельно. У вас должно получиться, что во втором случае косинус наибольшего треугольника равен  (треугольник прямоугольный), а в третьем – косинус угла отрицательный (треугольник тупоугольный).

Ответ: остроугольный, прямоугольный, тупоугольный.

 

Свойство биссектрисы угла треугольника

 

 

Биссектриса делит угол пополам – это ее определение. Но, оказывается, противоположную сторону треугольника она тоже делит всегда не пополам, но в определенном соотношении.

 

Биссектриса  треугольника  делит противоположную сторону на два отрезка. Обозначим их как  и  (см. рис. 24). Углы , и, конечно, .

Рис. 24. Биссектриса  треугольника  делит противоположную сторону на отрезки  и

Кроме того, углы  и  смежные (см. рис. 25):

Рис. 25. Смежные углы  и

Но у таких углов синусы тоже равны (в самом деле, на единичной окружности двум таким углам соответствует одно и то же значение синуса) (см.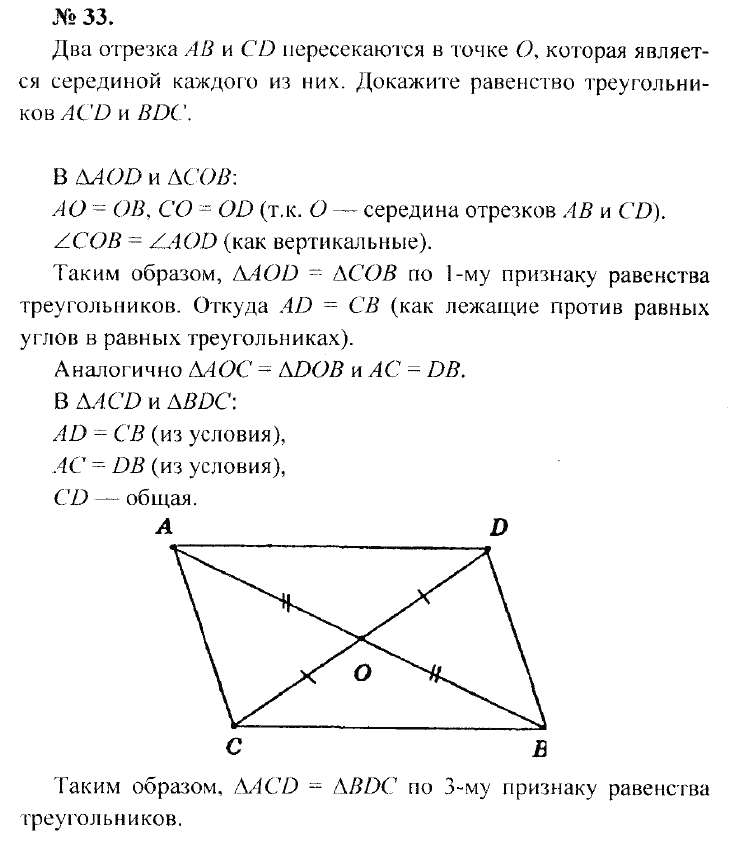 рис. 26).

Рис. 26. На единичной окружности углам  и  соответствует одно и то же значение синуса

Тогда имеем:

Применим к двум треугольникам теоремы синусов. Для треугольника  имеем:

Для треугольника  имеем:

Но правые части в обеих пропорциях равны, следовательно, равны и левые:

Или:

Таким образом, мы доказали, что биссектриса угла треугольника делит его противоположную сторону на отрезки, пропорциональные прилежащим сторонам. Этот факт сам по себе полезный инструмент, который мы будем использовать для решения различных задач.

 

Решение практической задачи с использованием теоремы синусов

 

 

Задача 4. На горе находится башня, высота которой равна  м. Некоторый предмет  у подножия горы наблюдают сначала с вершины  башни под углом  к горизонту, а потом с ее основания  под углом . Найдите высоту  горы (см. рис. 27).

 

 

Рис. 27. Иллюстрация к задаче 4

Решение.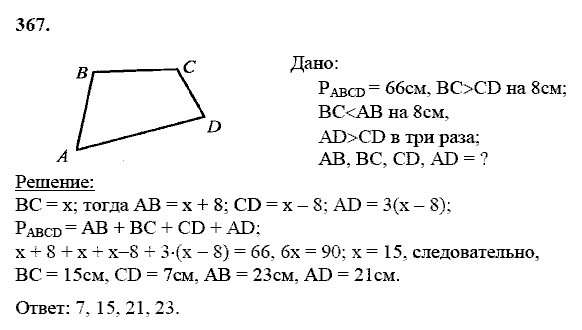

Рассмотрим прямоугольный треугольник  (см. рис. 28):

Рис. 28. Иллюстрация к задаче 4

Тогда:

Теперь рассмотрим треугольник . В нем мы знаем:

Тогда:

Используем теорему синусов:

 м

Ответ:  м.

Чтобы потренироваться использовать рассмотренные инструменты для решения других задач, используйте наши тренажеры и тесты. Чем больше вы практикуетесь, тем легче вам будет «увидеть», какой инструмент лучше всего применить для решения той или иной задачи и как именно это сделать.

 

Список литературы

1. Александров А.Д., Вернер А.Л., Рыжик В.И. Геометрия, 8 класс. Учебник. – М.: «Просвещение», 2018.
2. Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В./Под ред. Садовничего В.А. Геометрия, 8 класс. Учебник. – М.: «Просвещение», 2018.
3. Мерзляк А.Г., Полонский В.Б., Якир М.С., Геометрия. 8 класс. Учебник. – М.: издательский центр «ВЕНТАНА-ГРАФ», 2018.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал tmath.ru (Источник)
2. Интернет-портал cleverstudents.ru (Источник)
3. Интернет-портал схемо.рф (Источник)

 

Домашнее задание

1. Доказать, что если в параллелограмм можно вписать окружность и можно описать около него окружность, то этот параллелограмм – квадрат.
2. Найти угол между лучом  и положительной полуосью , если точка  имеет координаты .
3. В равнобедренной трапеции меньшее основание равно боковой стороне, большее основание равно  см, а угол при основании равен . Найти периметр трапеции.

 

Для 8 класса «Решение задач ПОДОБИЕ ТРЕУГОЛЬНИКОВ» (геометрия) (32 слайда)

Слайд 1

Решение задач на готовых чертежах. Подобные треугольники.
Геометрия. 8 класс.
Пономарева Юлия Васильевна, учитель математики МБОУ Каменно-Балковская СОШ

Слайд 2

8
9
10
11
12
14
15
16
17
18
20
21
22
23
24
30
29
28
27
26
1
2
3
4
5
6
13
19
25
7

Слайд 3

1.
Найти:
Дано:
А
B
D
16
30
С
20

Слайд 4

2.
Дано:
Найти:
А
D
14
20
С
21
B

Слайд 5

3.
Дано:
Найти:
А
B
D
4,5
С
13,5

Слайд 6

4.
Дано:
Найти:
А
D
4
С
6
B

Слайд 7

5.
Дано:
Найти:
А
B
C
M
K
N
6
5
7

Слайд 8

6.
Дано:
Найти:
А
B
C
N
5
M
2

Слайд 9

7.
Найти:
Дано:
А
B
C
D
O
K

Слайд 10

8.
Найти:
Дано:
А
B1
А1
А2
А3
А4
B2
B3
B4

Слайд 11

9.
Дано:
Найти:
А
C
B
D
8
4

Слайд 12

10.
Дано:
Найти:
А
C
B
D
8
4

Слайд 13

11.
Найти:
Дано:
А
B
C
N
M
K

Слайд 14

12.
Найти:
Дано:
А
B
C
N
M
K

Слайд 15

13.
Найти:
Дано:
А
B
N
M
K
C

Слайд 16

14.
Дано:
Найти:
А
B
N
M
P
C
Подсказка.
х

Слайд 17

15.
Дано:
Найти:
А
B
M
С
N
К
6
4
12
15

Слайд 18

16.
Дано:
Найти:
А
B
E
D
15
C
10
8
x
x+6

Слайд 19

17.
Дано:
Найти:
4
5
a
b
x
2x + 3
y
y — 1

Слайд 20

18.
Дано:
Найти:
А
B
C
16
D
4

Слайд 21

19.
Найти:
Дано:
А
B
C
8
D
О
6
5
10

Слайд 22

20.
Найти:
Дано:
А
B
C
D
6
K
E
1
9

Слайд 23

21.
Найти:
Дано:
А
C
D
5
В
M
8
3,9
3,6

Слайд 24

22.
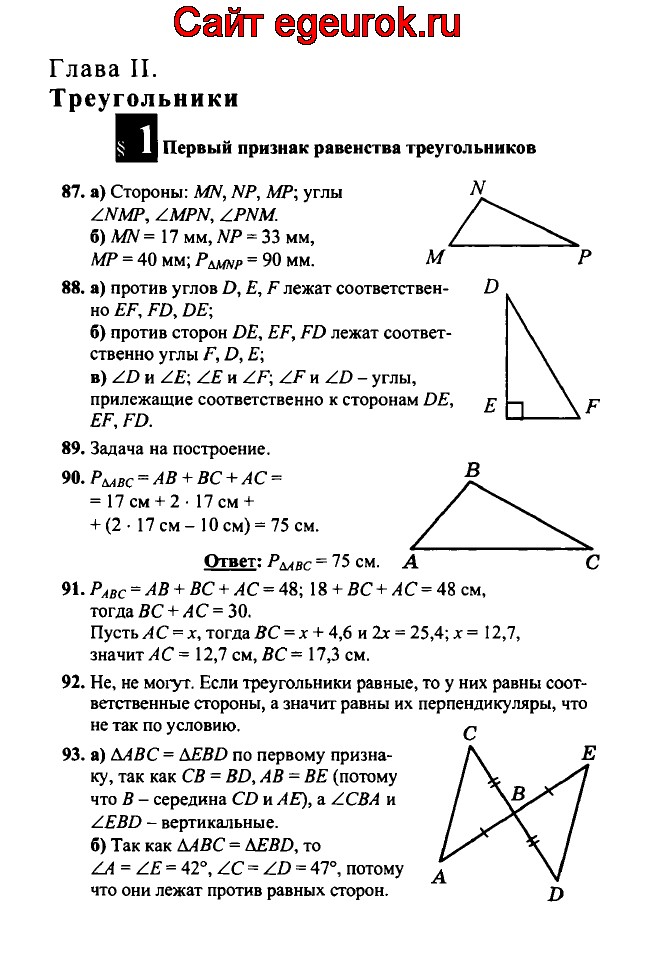
Найти:
Дано:
А
B
C
M
N

Слайд 25

23.
Найти:
Дано:
А
C
B
F
E

Слайд 26

24.
Найти:
Дано:
А
D
1
B
2
C
3

Слайд 27

25.
Найти:
Дано:
А1
C
B1
А
B
C1
710
10
2a
3a
2b
3b
?

Слайд 28

26.
Найти:
Дано:
А1
C
B1
А
C1
800
10a
5a
14b
7b
?
B
12c
6c
400
?

Слайд 29

27.
Найти:
Дано:
А
B
N
M
15
C
10
8
3
4

Слайд 30

28.
Найти:
Дано:
А
B
C
D
15
4
12
O
5

Слайд 31

29.
Найти:
Дано:
А
B
C
M
N
10
4
5
6

Слайд 32

30.
Найти:
Дано:
А
B
N
M
C
20

Искусство решения проблем

Искусство решения проблем размещает эту AoPSWiki, а также многие другие онлайн-ресурсы для учащихся, интересующихся математическими соревнованиями. Посмотрите на AoPSWiki. Отдельные статьи часто содержат примеры проблем и решений для многих уровней решения проблем. Многие также имеют ссылки на книги, веб-сайты и другие ресурсы, имеющие отношение к теме.

• Учебники по математике
• Математические форумы
• Веб-сайты по математике

Содержание

• 1 Видео с кратким руководством Введение в AMC
• 2 обучающих сайта
• 3 Интуитивные олимпиадные решения
• 4 бесплатных курса математики
• 5 Список ресурсов
• 6 математических конкурсов
• 7 задач по математике
  • 7.1 Книги задач
  • 7.2 Проблемы в сети
    • 7.2.1 Вводные средства решения проблем
    • 7.2.2 Решатели проблем среднего уровня
    • 7.2.3 Решатели олимпиадных задач
• 8 Артикул
• 9 Огромный список ссылок
  • 9.1 Рекомендации по курсу AoPS
  • 9.2 AMC 8 Подготовка
    • 9. 2.1 Проблемы
  • 9.3 AMC 10/12 Подготовка
    • 9.3.1 Проблемы
  • 9.4 Подготовка AIME
    • 9.4.1 Проблемы
  • 9.5 Начало подготовки к Олимпиаде
    • 9.5.1 Связка общих ссылок
    • 9.5.2 Проблемы
  • 9.6 Средняя/продвинутая подготовка к Олимпиаде
    • 9.6.1 Проблемы
  • 9.7 Ссылки на книги:
    • 9.7.1 Олимпиадный уровень
      • 9.7.1.1 Бесплатно
      • 9.7.1.2 Не бесплатно
  • 9.8 Наборы задач
• 10 См. также

Видео с кратким руководством Введение в AMC

Краткий видео обзор AMC и AIME.

Учебные веб-сайты

• Тренажер задач AMC: https://amctrainer.com/play
• Генератор задач и программа для чтения вики AoPS: https://vqbc.github.io/tribun/
• конкурсы mathRanks: https://mathranks.net/

Интуитивные олимпиадные решения

https://www. imomath.xyz/

Размещены интуитивно понятные решения проблем IMO, которые помогают читателю понять, *как* думать о решении самостоятельно, а не просто запоминать трюк в решении. Более миллиона просмотров, очень широкое распространение.

Бесплатные курсы по математике

Введение в теорию чисел: https://thepuzzlr.com/math-courses

Бесплатный учебный курс AMC 8, охватывающий все основные понятия: https://thepuzzlr.com/courses/amc-8-bootcamp/

Бесплатный курс AMC 10: https://thepuzzlr.com/courses/amc-10-crash-course/

Список ресурсов

Все необходимое для AMC 8: https://thepuzzlr.com/courses/amc-8-bootcamp/

Все необходимое для AMC 10: https://thepuzzlr.com/courses/amc-10-crash-course/

Занятия по математике

• В школе «Искусство решения задач» проводятся занятия, пользующиеся популярностью среди самых успевающих учащихся в США. Серия задач AoPS.

Математические конкурсные задачи

Сборники задач

Многие математические конкурсы продают книги прошлых конкурсов и решения. Эти книги могут стать отличным дополнительным материалом для энергичных студентов, изучающих математику.

• В ARML есть четыре сборника задач, охватывающих большинство соревнований ARML, а также некоторые соревнования NYSML. Однако, как правило, их трудно найти. Кое-что можно заказать здесь.
• книг MOEMS доступны здесь, в AoPS.
• книг по MATHCOUNTS доступны здесь, в AoPS.
• книг AMC доступны здесь, в AoPS.
• Книги Конкурса Мандельброта доступны здесь, в AoPS.

Онлайн-задачи

Art of Problem Solving поддерживает очень большую базу данных задач по математике. Многие веб-сайты математических конкурсов содержат архивы прошлых задач. Список соревнований по математике ведет к ссылкам на многие из этих домашних страниц соревнований. Вот несколько примеров:

Вводные решения задач

• Mu Alpha Theta.org размещает прошлые конкурсные задачи.
• Noetic Learning Challenge Math — Решение задач для одаренных учащихся начальной школы.
• Страница MathCounts Drills Элиаса Сааба.
• Список всех соревнований MathCounts с 2000 по 2017 год.
• Домашняя страница олимпиады по математике в средней школе штата Алабама.
• Южноафриканская олимпиада по математике включает многолетние прошлые задачи с решениями.
• Beestar.org — Еженедельные задачи по решению задач и рейтинг почетных списков, классы 1–8

Решатели задач среднего уровня

• Задачи и решения математических конкурсов AoPS
• Прошлые проблемы USAMTS можно найти на домашней странице USAMTS.
• Еженедельные математические задачи Иваны Александровой для старшеклассников содержат хорошие задачи, которые заставят вас задуматься и научат вас новым навыкам и материалам
• Сайт Kalva — один из лучших ресурсов по математическим задачам на планете. (В настоящее время не в сети. Зеркало можно найти на этой странице)
• Задачи прошлой математической олимпиады Колорадо (CMO) можно найти на домашней странице CMO.
• Прошлые задачи Международного поиска математических талантов (IMTS) можно найти здесь
• Brilliant — это веб-сайт, на котором можно решать задачи, чтобы набирать очки и переходить на более высокие уровни.
• Clevermath Аналогичен предыдущему

Решатели олимпиадных задач

• Математические задачи и решения AoPS
• Math and CS Research — это издание по математике и информатике, содержащее статьи и наборы задач по широкому кругу тем.
• Прошлые проблемы USAMTS можно найти на домашней странице USAMTS.
• Сайт Kalva — один из лучших ресурсов по математическим задачам на планете. (В настоящее время не в сети, но доступно несколько зеркал, например здесь.)
• Математические головоломки Ника — Сложные задачи с подсказками и решениями.
• Канадская математическая олимпиада проводится здесь Канадским математическим обществом.
• Задачи Всесоюзных математических олимпиад 1961-1986 гг. — Задач много, решений нет. [Сайт больше не существует. Сайт заменен веб-захватом]
• Прошлые задачи Международного поиска математических талантов (IMTS) можно найти здесь
• Olympiad Math Madness — Стопки сложных задач, без решений. [Сайт больше не существует. Сайт заменен веб-захватом]

Статьи

• Тайм-менеджмент
• Плюсы и минусы математических соревнований Ричарда Рущика.
• Создание позитивной культуры ожиданий в математическом образовании от лауреата премии Sister Scholastica Дэррила Хилла.
• «Хватит совершать глупые ошибки» Ричарда Рущика.
• Какие вопросы действительно глупые вопросы? Ричард Рущик.
• Обучение через обучение
• Как написать математическое решение Ричарда Ручика и Мэтью Кроуфорда.
• Неравенство доктора Киран Кедлая
• Олимпиадное неравенство Томаса Дж. Милдорфа
• Теория чисел Олимпиады: абстрактная перспектива Томаса Дж. Милдорфа
• Теория чисел Наоки Сато
• Теория чисел Олимпиады через сложные задачи Джастина Стивенса
• Барицентрические координаты в олимпийской геометрии Макса Шиндлера и Эвана Чена
• Подъем экспоненты (LTE) Амира Хоссейна Парварди
• УФ-метод Матиаса Бэка Тейса Кнудсена
• Китайская теорема об остатках Эвана Чена
• Contest Reflections by Wanlin Li

Огромный список ссылок

Рекомендации по курсу AoPS

• Рекомендации по курсу «Искусство решения проблем»
• Вы все еще не можете выбрать курс? Перейдите по ссылке выше и нажмите , свяжитесь с нами в нижней части раздела «Карта курса», чтобы запросить личные рекомендации!

AMC 8 Подготовка

Проблемы

AMC 8 Проблемы в разделе ресурсов

Проблема и решения: AMC 8 Проблемы в вики AoPS

Подготовка к AMC 10/12

Чем поможет подготовка к AIME Оценка AMC 10/12

Какой класс выбрать?

AMC 10 для практики AMC 12

Подготовка АМС

AMC 10/12 Подготовка

AIME/AMC 10 Перекрытие и подготовка

Как подготовиться к amc10 и aime?

Подготовка к AMC 10?

Проблемы

AMC 10 Проблемы в разделе Ресурсы

Проблемы AMC 10 в AoPS Wiki

AMC 12 Проблемы в разделе ресурсов

AHSME (старый AMC 12) Проблемы в AoPS Wiki

Проблемы AMC 12 в AoPS Wiki

Подготовка к AIME

Подготовка к поступлению в USAMO

Как подготовиться к AIME

Подготовка к AIME

Использование вопросов, не относящихся к AIME, для подготовки к AIME

Лучшие книги для подготовки к AIME?

Как улучшить оценку AIME, чтобы сделать JMO?

Подготовка к AIME и USAMO

Проблемы

Проблемы AIME в разделе ресурсов

Проблемы AIME в AoPS Wiki

Задачи AIME, отсортированные по сложности

Начальная подготовка к Олимпиаде

• Общий
• Общий
• Как подготовиться к USAJMO?
• USAMO проблемы с подготовкой/выполнением
• Простые олимпиады для практики USAJMO?
• Для USAMO: ACoPS или Engel?
• Олимпиадные задачи — как подготовиться
• Подготовка к USAMO/Олимпиадам: с чего начать?
• Подготовка к USAJMO

Набор общих ссылок

• Подготовка к USAMO
• Подготовка USAMO
• USAMO
• Приготовление Усамо
• Подготовка USAMO
• Обратный отсчет до USAMO
• Подготовка USAMO
• Подготовка USAJMO
• Подготовка USAMO
• Подготовка USAJMO
• Как подготовиться к USAMO/Making Red MOP
• Жесткая подготовка
• Подготовка USAMO и JMO
• ПОДГОТОВКА USAMO
• Новичок в USAMO
• Что мне делать?
• Улучшить до уровня USAMO и IMO
• Подготовка к США(J)MO
• соревнование по математике/советы, как стать лучше
• Подготовка к Олимпиаде
• Подготовка к Олимпиаде
• Подготовка USAJMO
• Правильное обучение
• Что ведет к успеху

Проблемы

• USAJMO Проблемы в разделе ресурсов
• Проблемы USAJMO в AoPS Wiki
• Проблемы USAMO в разделе ресурсов
• Задачи USAMO в AoPS Wiki

Средняя/продвинутая подготовка к олимпиаде

Задачи

• Практическая олимпиада 1
• Практическая Олимпиада 2
• Тренировочная Олимпиада 3
• Практические решения олимпиады
• Проблемы USAMO в разделе ресурсов
• Проблемы USAMO в AoPS Wiki
• Проблемы ИМО в разделе ресурсов
• Проблемы IMO в AoPS Wiki

Ссылки на книги:

Олимпиадный уровень

Бесплатно

• Леммы в олимпиадной статье по геометрии
• Плоская геометрия
• Эван Чен OTIS-Выдержки
• Основы олимпиадной теории чисел
• Теория чисел Олимпиады через сложные задачи
• Современная олимпиадная теория чисел

Not Free

• Плоская евклидова геометрия: теория и проблемы
• Евклидова геометрия в математических олимпиадах
• Комплексные числа и геометрия
• Геометрия комплексных чисел
• Комплексные числа от А до … Я
• 103 Задачи по тригонометрии: из тренинга группы ИМО США
• Введение в диофантовы уравнения: проблемный подход
• Введение в теорию чисел и неравенства
• 104 Задачи по теории чисел: из тренинга группы ИМО США
• 102 Комбинаторные задачи
• Путь к комбинаторике для студентов: стратегии подсчета
• -fkmr1 Математические олимпиады США 1972-1986 Задачи и решения
• Искусство и ремесло решения проблем
• Стратегии решения проблем

Наборы задач

• Сборник прошлых статей в формате PDF
• Практические задачи со всего мира
• Общие задачи по олимпиадной математике
• Набор задач условной вероятности
• 31 Олимпиадные задачи по вероятностному методу
• 567 Красивое и жесткое неравенство
• Неравенства
• 100 полиномиальных задач
• Задачи тригонометрии
• Общие все уровни
• Теория чисел
• Олимпиадные задачи
• 33 функциональных уравнения
• Проблемы индукции
• Индукционные решения
• 260 задач по геометрии
• 150 задач по геометрии
• 50 задач на диофантовы уравнения
• 60 задач по геометрии
• 116 Проблемы
• Алгебраические неравенства
• 100 задач по комбинаторике
• 100 проблем
• Теория чисел
• Геометрия
• Общий
• 100 задач по теории чисел
• 100 задач на функциональные уравнения
• Начальный/промежуточный счет и вероятность
• 40 функциональных уравнений
• 100 геометрических неравенств
• 10 забавных нетрадиционных задач 🙂
• 169 функциональных уравнений
• Геометрия треугольника
• Вероятность
• Алгебра
• Теория чисел
• Круговая геометрия
• Другая геометрия

Рейтинг всех олимпиад (уровень сложности)

См.

также

• Список математических олимпиад
• Стипендии по математике
• Научные конкурсы
• Соревнования по информатике
• Как подготовить

© 2022 ООО «АоПС Инкорпорейтед»

Неверное имя пользователя

Войти в АоПС

Имя пользователя:

Пароль:

Оставаться в системе

Как решить проблемы с геометрией с участием прямоугольников и треугольников

Ключевые члены

O Точка

O Линия

O СЕГМЕНТ

O RAY

O ENGLAN0003

o Area

o Square

o Triangle

 

Objectives

 

o Get familiar with some fundamental geometric figures

o Calculate the perimeter and area of ​​a rectangle

o Derive a formula for the площадь треугольника

 

Геометрия изучает точки, линии, формы, углы и отношения между ними. Мы рассмотрим некоторые простые формы, такие как треугольники и прямоугольники, и обсудим, как вычислить некоторые их свойства.

 

Элементы геометрии

 

Прежде чем рассматривать некоторые более сложные фигуры, мы должны иметь представление об определенных терминах, которые используются при изучении геометрии. Несколько основных геометрических понятий включают точки, линии и углы. Точка , по сути, является местоположением — ее часто представляют с помощью маленькой точки, и она представляет собой местоположение в пространстве и не имеет ни длины, ни ширины, ни глубины. Несколько точек показаны ниже.

 

 

 

Линия в геометрии имеет почти те же характеристики, что и в реальной жизни (и в алгебре). Геометрическая линия прямая и бесконечно простирается в противоположных направлениях. Если две прямые пересекаются в одной точке, то говорят, что они пересекаются на 90 623. Пример строки показан ниже; обратите внимание, что на концах линии есть стрелки, указывающие на то, что линия продолжается бесконечно.

 

Конечная часть линии называется сегмент линии. Отрезки линий имеют длины, которые являются конечными (ограниченными) числами, в отличие от линий, длина которых бесконечна (неограничена). Отрезок линии показан ниже; концы отрезка показаны точками.

 

Луч — это часть линии только с одной конечной точкой, как показано ниже. Его длина по-прежнему бесконечна, но у него есть один опознаваемый конец.

 

 

Когда две прямые, отрезки, лучи или их комбинации пересекаются, они образуют угол. Пример угла показан ниже.

 

 

Углы можно измерять в градусах (°) в диапазоне от 0° до 360°. Некоторые примеры угловых измерений показаны ниже.

 

 

Используя эти основные геометрические термины и фигуры, мы можем теперь перейти к изучению некоторых более сложных фигур.

 

Прямоугольники

 

Прямоугольник представляет собой особый вид замкнутой геометрической фигуры с четырьмя сторонами; пример прямоугольника показан ниже.

 

 

Прямоугольники можно описать двумя их измерениями: длиной (которую мы можем обозначить как l ) и шириной (которую мы можем обозначить как w ). Противоположные стороны прямоугольника равны по длине, а все «внутренние» углы равны 90°; таким образом, мы можем нарисовать прямоугольник, как показано ниже.

 

 

Одной из характеристик прямоугольников, которую мы можем легко вычислить, является его периметр, который представляет собой сумму длин всех сторон. Периметр P — следующее:

P = L + W + L + W

Мы можем упростить это выражение, преобразуя добавление подобных терминов в умножение:

9069 P = ulactration:

9069 P =.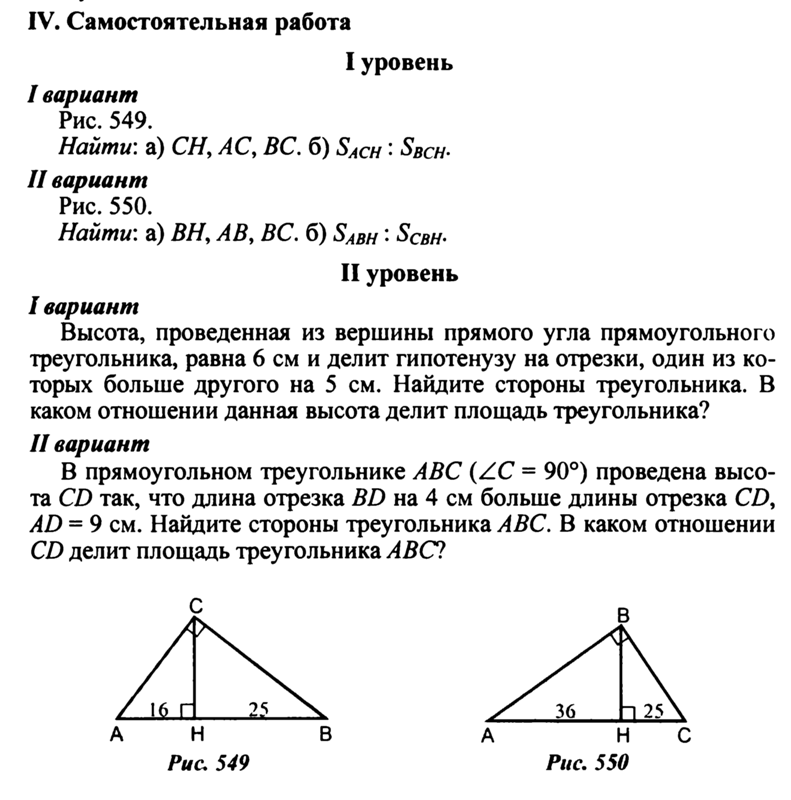 l + l + w + w

P = 2 l + 2 w

 

Например, рассмотрим прямоугольник ниже.

 

 

Поскольку противоположные стороны равны по длине, у прямоугольника есть две стороны длиной 6 единиц и две стороны длиной 3 единицы. Таким образом, периметр будет следующим:

 

 

Хотите узнать больше? Почему бы не пройти онлайн-курс Pre-Algebra?

Периметр 18 единиц. (Обратите внимание, что «единицей» могут быть дюймы, футы, метры или любой другой тип измерения длины. Если единица измерения указана, используйте эту конкретную единицу; в противном случае достаточно общего термина «единицы».)

 

Практическая задача : Вычислите периметр прямоугольника ниже. Все измерения указаны в футах.

 

 

Решение : Напомним, что противоположные стороны прямоугольника равны по длине. Таким образом, этот прямоугольник имеет две стороны длиной 10 футов и две стороны длиной 2 фута. Тогда периметр P будет следующим:

 

 

В качестве альтернативы мы могли бы просто использовать формулу, полученную выше.

 

 

 

Практическая задача : Некоторый прямоугольник имеет периметр 50 метров и длину 14 метров. Какова его ширина?

 

Решение : Мы можем решить эту задачу, внимательно изучив представленную информацию и применяя то, что мы знаем о решении уравнений. Мы знаем, прежде всего, что периметр P прямоугольника подчиняется следующей формуле, где l — длина, а w это ширина.

 

Постановка задачи говорит нам, каков периметр ( P ), а также какова длина ( l ). Давайте введем эти значения в приведенное выше уравнение, а затем максимально упростим результат.

 

 

Чтобы найти ширину прямоугольника, нам нужно найти только w , используя тот же подход, который мы использовали при решении линейных уравнений.

 

 

Thus, the width of the rectangle is 11 meters. Давайте проверим этот результат, чтобы убедиться, что он работает. Из условия задачи мы знаем, что длина прямоугольника равна 14 метрам.

 

 

Таким образом, ответ подтверждается.

 

 

Мы также можем вычислить площадь прямоугольника, которая является мерой того, сколько места он занимает. Рассмотрим прямоугольник шириной 4 единицы и длиной 2 единицы.

 

 

Разделим каждую сторону на сегменты длиной 1, как показано ниже.

 

 

Теперь, используя эти деления, мы нарисуем сетку, которая разделит прямоугольник.

 

 

Обратите внимание, что сетка разделена на более мелкие области, каждая сторона которых имеет длину 1 единицу.

 

Каждая из этих меньших областей представляет собой квадрат (прямоугольник, длина и ширина которого равны) со сторонами длины 1. Определим одну из этих областей как 1 квадратную единицу — квадрат, размеры которого (длина и ширина) равны 1 единице. Теперь обратите внимание, что прямоугольник имеет в общей сложности 8 квадратных единиц, которые разделены на два ряда по четыре или четыре ряда по два (в зависимости от того, как вы смотрите на диаграмму). Но вычислить количество объектов (в данном случае квадратных единиц) в строках и столбцах можно путем умножения: обратите внимание, что количество квадратных единиц в прямоугольнике — это просто произведение длины и ширины.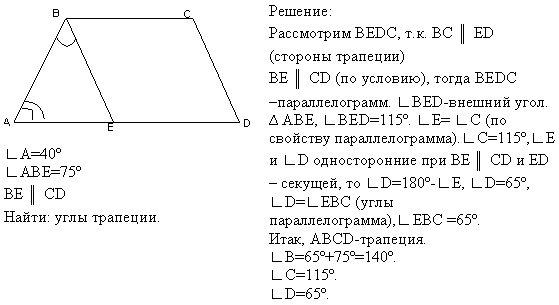 Таким образом, площадь A прямоугольника длиной l и шириной w является произведением l и w:

 

 

Эта формула применима к любому прямоугольнику, независимо от длины его сторон. (То есть длины могут быть целыми положительными, дробными, десятичными, рациональными или иррациональными числами.)

 

Например, предположим, что у нас есть прямоугольник длиной 5 дюймов и шириной 3 дюйма, как показано ниже.

 

Наша цель состоит в том, чтобы вычислить, сколько квадратов со стороной в 1 дюйм может поместиться в этот прямоугольник. Результатом будет общая площадь прямоугольника. Располагая квадраты краем к краю, мы можем разместить пять из них поперек прямоугольника и три по прямоугольнику.

 

 

Из диаграммы видно, что в прямоугольник можно поместить 15 квадратов размером в один квадратный дюйм. Таким образом, прямоугольник имеет площадь 15 квадратных дюймов. Конечно, на это указывает и формула:

 

 

 

Практическая задача : Вычислите площадь прямоугольника шириной 32 дюйма и длиной 3,2 дюйма.

 

Решение : Формула площади прямоугольника применяется независимо от используемых чисел (конечно, если они положительные). Таким образом, давайте просто воспользуемся формулой для площади A:

 

 

 

Треугольники

 

Мы также можем рассмотреть некоторые характеристики другой распространенной геометрической фигуры: треугольника. Треугольник — замкнутая геометрическая фигура с тремя сторонами; примеры треугольников показаны ниже.

 

 

Периметр треугольника вычисляется почти так же, как периметр прямоугольника: просто сложите длины сторон треугольника (в этом случае у фигуры только три стороны, и эти стороны могут быть разной длины). Однако рассчитать площадь несколько сложнее. Для прямоугольников мы смогли увидеть площадь просто как ряды и столбцы квадратов. Из-за формы треугольника мы не можем аккуратно вписать в него квадраты.

 

 

Мы должны использовать несколько иной подход к нахождению площади треугольника. Давайте рассмотрим общий треугольник, показанный ниже; этот треугольник не имеет особых свойств.

 

 

Теперь определим два характерных размера этого (или любого) треугольника: длину основания (обозначим b ) и высоту (обозначим h ). Основание — это просто длина стороны «на земле» или внизу фигуры. Тогда высота является максимальным расстоянием, на которое треугольник достигает «над землей».

 

 

Площадь треугольника равна A. Если бы у нас было два таких треугольника совершенно одинаковой формы, общая площадь двух треугольников тогда была бы 2 A.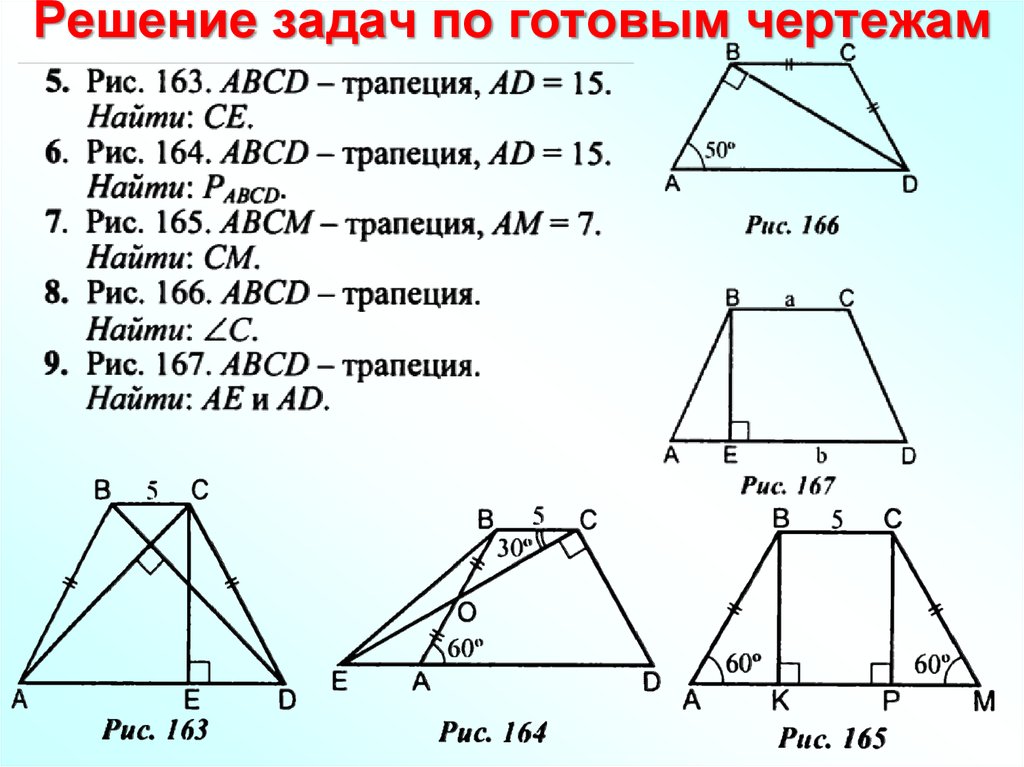 Давайте воспользуемся этим фактом. попытаться построить более знакомую фигуру.

 

 

Сначала разрежем один из треугольников по высоте.

 

 

Обратите внимание, что оба разделенных треугольника имеют высоту ч 90 672 (как мы определили для исходного треугольника) и что их основания равны 90 669 х 90 672 и 90 669 у, 90 672, где 90 669 х + у 90 672 равно 90 669 b. Мы не знаем, что такое х и х , но поскольку мы разрезали треугольник, мы знаем, что эти два основания должны в сумме давать основание исходного треугольника. Теперь давайте попробуем переставить части так, чтобы получился прямоугольник!

 

Теперь рассмотрим характеристики этой новой фигуры (помните, ее площадь 2 A, , где A — площадь исходного треугольника).

 

 

Фигура представляет собой прямоугольник — обратите внимание, что противоположные стороны равны по длине (помните, что x + y = b ). Но мы знаем, как вычислить площадь прямоугольника: это просто произведение длины и ширины (в данном случае 90 669 b 90 672 и 90 669 h 90 672). Однако эта общая площадь равна 90 669, удвоенной по 90 672 площади исходного треугольника. Таким образом, произведение b и h равно 2 A.

 

 

Изучая линейные уравнения для конкретной переменной, мы научились решать их. В этом случае мы можем выделить A , умножив обе части выражения на .

Таким образом, мы получили формулу площади треугольника. Этот вывод, хотя и не показан в полной математической строгости, дает правильную формулу площади для всех треугольников, а не только для показанного выше. Процесс расчета высоты ч треугольника может быть несколько сложным, но если вы знаете основание и высоту, вы теперь можете вычислить площадь треугольника.

 

 

Практическая задача : Вычислите площадь приведенного ниже треугольника.