-
Школьный помощник
- математика 5 класс
- математика 6 класс
- алгебра 8 класс
- геометрия 7 класс
- русский язык 5 класс
- русский язык 6 класс
- русский язык 7 класс
- математика
- алгебра
- геометрия
- русский язык
«»
следующая предыдущая вернуться на предыдущую страницуТакой страницы нет !!!
- Популярные запросы
- Обстоятельство
- Дополнение
- Определение
- Деление дробей
- Математика 6 класс
- Русский язык 7 класс
- Русский язык 6 класс
- Алгебра 8 класс
- Математика 5 класс
- Алгебра 7 класс
- Русский язык 5 класс
- Наименьшее общее кратное
- Наибольший общий делитель.
 Взаимно простые числа
Взаимно простые числа - Буквы о и а в корнях -кос- / -кас-; -гор- / — гар-; -клан- / -клон-; -зар- / -зор-
- Буквы о и а в корнях -кос- / -кас-; -гор- / — гар-; -клан- / -клон-; -зар- / -зор-
- Окружность и круг
- Доли. Обыкновенные дроби
- Деление и дроби
- Квадратный корень из неотрицательного числа
- Антонимы. Синонимы
- Десятичная запись дробных чисел
- Буквы о – а в корнях -лаг- / -лож-, -рос- / -раст- (-ращ-)
Алгебра, 8 класс: уроки, тесты, задания
Алгебраические дроби. Арифметические операции над алгебраическими дробями
-
Понятие алгебраической дроби
-
Применение основного свойства алгебраической дроби
-
Как складывать и вычитать алгебраические дроби с равными знаменателями
-
Как складывать и вычитать алгебраические дроби с разными знаменателями
-
Как умножать, делить и возводить в степень алгебраические дроби
-
Упрощение рациональных выражений
-
Решение рациональных уравнений
Квадратичная функция y = kx².
 Функция y = k/x
Функция y = k/x
-
Квадратичная функция y = kx² и её свойства. Парабола
-
Функция y = k/x и её свойства. Гипербола
-
Как построить график функции у = f(x + l)
-
Как построить график функции у = f(x) + m
-
Как построить график функции y = f(x + l) + m
-
Квадратичная функция y = ax² + bx + c
-
Решение квадратных уравнений с помощью графиков функций
Функция квадратного корня y = √x
-
Понятие квадратного корня
-
Функция квадратного корня y = √x, её свойства и график
-
Множество рациональных чисел
-
Базовые свойства квадратных корней
-
Преобразование иррациональных выражений
Квадратные уравнения
-
Какие бывают квадратные уравнения
-
Способы решения квадратных уравнений
-
Решение рационального уравнения, сводящегося к квадратному
-
Использование рациональных уравнений для решения задач
-
Упрощённая формула для решения квадратного уравнения
-
Применение теоремы Виета
-
Решение иррационального уравнения, сводящегося к квадратному
Действительные числа
-
Множества натуральных чисел, целых чисел, рациональных чисел
-
Понятие иррационального числа
-
Множество действительных чисел и её геометрическая модель
-
Модуль действительного числа и его геометрический смысл
-
Приближённые значения по недостатку (по избытку)
-
Понятие степени с отрицательным целым показателем
-
Стандартный вид положительного числа
Неравенства
-
Понятие числовых промежутков
-
Свойства числовых неравенств.
 Свойства неравенств одинакового смысла
Свойства неравенств одинакового смысла
-
Как решать линейное неравенство
-
Методы решения квадратных неравенств
-
Понятие монотонности функции. Исследование функций на монотонность
Международная оценка образовательных достижений учащихся (PISA)
ГДЗ по алгебре 8 класс (решебники)
Где Гдз • Решебники • 8 класс • АлгебраГДЗ по алгебре для 8 класса – многочисленные онлайн-сборники, которые включают в себя решенные задачки и примеры по предмету, составленные на основе основных российских учебников для средних школ.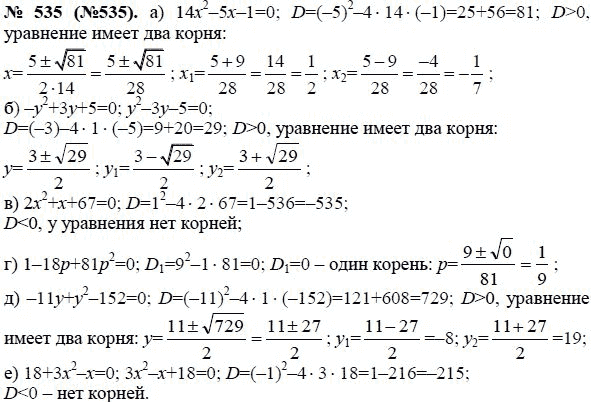 Они помогают восьмиклассникам научиться применять на практике правила, теоремы и формулы.
Они помогают восьмиклассникам научиться применять на практике правила, теоремы и формулы.
Авторы: Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова
Годы: 2013-2018
Авторы: А.Г. Мордкович
Годы: 2010-2013
Решебники помогают понять алгебру 8 класса
В школьных учебниках, как правило, приведены теоремы и формулы, а также несколько простых образцов их применения на практике. Многим ребятам на базе этого материала сложно усвоить непростые темы по алгебре и успевать по предмету.
Стоит ли родителям сразу искать школьнику репетитора, если он испытывает трудности с выполнением домашней работы. Вопрос можно решить проще и эффективнее: воспользоваться ГДЗ по алгебре за 8 класс. Это практическое пособие позволяет разобраться в выполнении упражнений по широкому кругу тем:
- квадратичная функция и функция у=К/х;
- решение квадратных уравнений и теорема Виета;
- свойства иррациональных уравнений и неравенств;
- преобразование рациональных выражений и свойства квадратного корня.

На базе онлайн-сборников ученики могут проверять свою домашнюю работу, устранять пробелы в знаниях за предыдущие годы изучения математики, разбираться самостоятельно в сложных задачках, а также готовиться к итоговой аттестации.
Родители ребят, благодаря решебникам по алгебре для 8 класса, могут не только обойтись без репетиторов, но и самостоятельно контролировать успеваемость своих детей.
Сайт ГДЕ ГДЗ – почему онлайн-решебники удобнее бумажных аналогов?
Чтобы найти ответ на задачку или пример в традиционном сборнике потребуется немало времени для пролистывания книги. В онлайн-решебнике все иначе: достаточно кликнуть номер задания в таблице и получить готовый ответ с подробным алгоритмом решения.
На сайте ГДЕ ГДЗ сосредоточены все самые свежие версии решебников, которые составлены на базе последних изданий учебников по алгебре с учетом текущих требований с учетом текущих стандартов оформления задач Министерства Образования России.
В чем преимущества сайта ГдеГдз.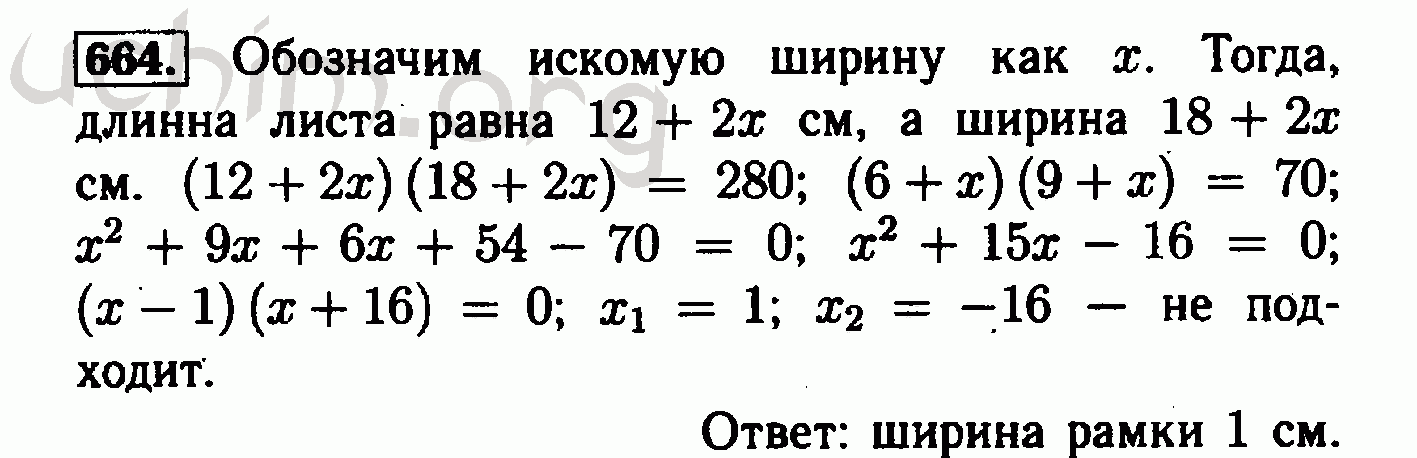 Ру?
Ру?
- возможность использования материала с любого устройства, благодаря адаптивному дизайну ресурса;
- отсутствие сообщений на весь экран и видеороликов, которые обязательны к просмотру.
Школьники и их родители могут использовать ГдеГдз.Ру в любое время суток, бесплатно и без регистрации. Переадресация на сторонние сайт при этом не происходит: все ответы и решения хранятся в базе нашего ресурса.
Автор учебников по математике Нина Тарасенкова: Итоги ВНО — результат кризиса всей системы образования
Пороговый балл теста внешнего оценивания по математике не преодолели более 31% участников – разбираемся вместе с экспертом, почему «дебют» получился провальным.
Программу урезали на треть
Внешнее независимое оценивание закончилось, а недоумение тех, кто учил, и досада тех, кто учился, еще не улеглись. Учителя весь учебный год взывали, призывали и «стимулировали» грядущим обязательным тестированием, родители искали лучших репетиторов и платили им соответствующие деньги, дети напрягались – кто как мог и хотел. А результат – плачевный.
А результат – плачевный.
Разные эксперты называют разные причины этого фиаско: от пресловутой дистанционки и неподъемной тяжести программы до сокращения количества уроков и гуманитаризации образования. Профессор Черкасского национального университета им. Богдана Хмельницкого Нина Тарасенкова, по учебникам которой учатся школьники от 5-го до 11-го класса, уверена, что все гораздо глубже и серьезнее.
|
— Шок от результатов ВНО у нас практически каждый год, в этом году он наибольший, потому что на уровень «стандарт» добавились гуманитарные классы, профтехобразование, где математика практически не изучалась, — говорит Нина Тарасенкова. — Поражают цифры: на математику профильного уровня зарегистрировались почти 292 тысячи учеников, а явились 245 тысяч – 83,9%. Хотя им математика была нужна для поступления. А на уровень «стандарт» зарегистрировались чуть больше 77 тысяч, пришли чуть больше 9 тысяч – то есть испугались «вусмерть»?
— Поражают цифры: на математику профильного уровня зарегистрировались почти 292 тысячи учеников, а явились 245 тысяч – 83,9%. Хотя им математика была нужна для поступления. А на уровень «стандарт» зарегистрировались чуть больше 77 тысяч, пришли чуть больше 9 тысяч – то есть испугались «вусмерть»?
При этом эксперты уверены: тест был совсем не сложным и хорошо структурированным. В некоторых заданиях в решении было 2-3 шага, то есть они были элементарными. Более серьезные задачи были интересные, но не запредельные. И при этом 31% не преодолели даже порог «сдал/не сдал». Почему? Нина Анатольевна считает, что сложившаяся ситуация закономерна и создана последними 30 годами.
— Система образования в Украине в целом пришла в кризисное состояние, — уверена ученая. — Введенную систему ВНО можно только приветствовать, но нужно разводить элитную математику и массовую, об этом мы уже говорили с разработчиками ВНО. Массовая математика необходима, но она у нас сейчас на уровне, урезанном на треть от той программы, которая была 30 лет назад.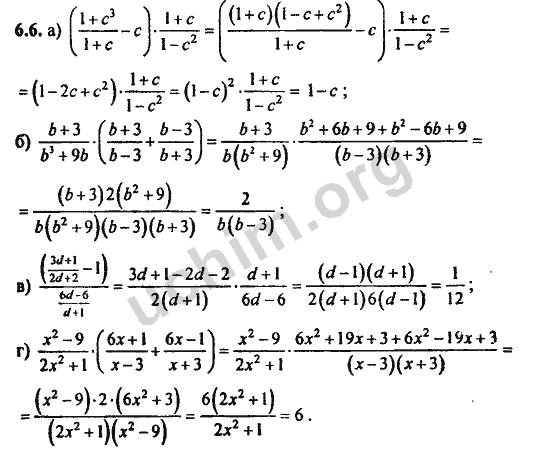 Я, как один из авторов школьных программ по математике начиная с 2011 года, могу сказать, что за этот период объем курса сократился значительно. И несмотря на это, у нас резко падает результативность обучения. Особенно в последние 5-7 лет, когда диджитализация выросла везде и во всем.
Я, как один из авторов школьных программ по математике начиная с 2011 года, могу сказать, что за этот период объем курса сократился значительно. И несмотря на это, у нас резко падает результативность обучения. Особенно в последние 5-7 лет, когда диджитализация выросла везде и во всем.
И «возвращение» выпускного экзамена педагог называет большой победой, поскольку отсутствие внешнего контроля приводит к тому, что можно снизить требования, имитировать обучение и изучение. И именно это сейчас и происходит, а «верхушка айсберга» — низкие результаты ВНО. Нина Тарасенкова называет три основные ошибки в процессе обучения.
Ошибка № 1. Создание когнитивного диссонанса в первые минуты урока
Правое и левое полушарие нашего мозга работают по абсолютно разным принципам. Правое отвечает за образную графическую информацию и работает по принципу фотографа – «снимает» то, что видит, а потом только рассматривает детали. Левое работает по принципу аналитика и строителя, составляя общую картину из деталей.
Возможности правого полушария даны нам от рождения, и, по данным физиологов, до 15-16-летнего возраста на любой когнитивный раздражитель первым реагирует правое полушарие. Когнитивный раздражитель – это слово, рисунок, текст, действие. И когда правое понимает, что текст не для него, включается левое полушарие. И на этом строятся одни из самых серьезных ошибок на уроках математики.
Наша школа – вербальная, так заложено, что первым было слово. Учитель приходит в класс и говорит: «Сегодня мы будем изучать ромб как разновидность параллелограмма». И в этот момент на этот когнитивный раздражитель реагирует правое полушарие, которому нет работы, и оно футболит мяч на поле левого полушария. В это время учитель подходит к доске, рисует ромб и показывает отличия параллелограмма и ромба. И в момент, когда включилось левое полушарие, у нас идут картинки. То есть на первых же минутах урока мы создали когнитивный диссонанс, и ответ мозга будет: «Ой, это не для меня!», и дальше все просто «закрывается».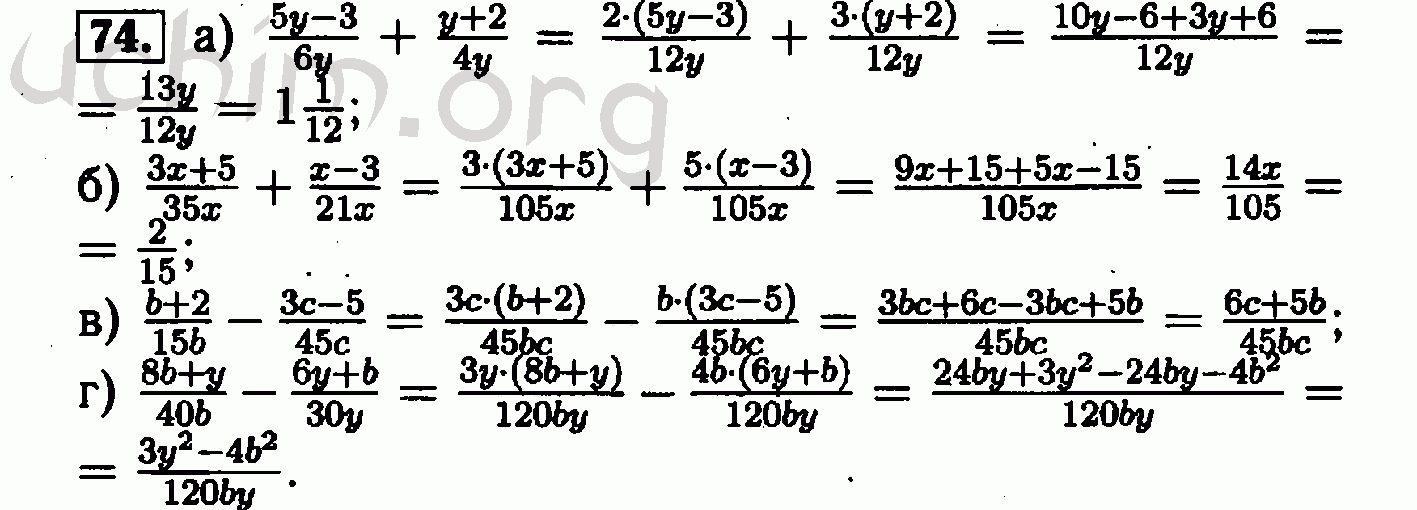 А ученик начинает имитировать обучение: делает вид, что слушает, делает вид, что выполняет задания, а сам куда-то подсматривает, ищет подсказки. Он – имитатор, в него ничего не заходит, он «в домике». А каким может быть результат обучения, если не произошло восприятия и осмысления информации? Никаким.
А ученик начинает имитировать обучение: делает вид, что слушает, делает вид, что выполняет задания, а сам куда-то подсматривает, ищет подсказки. Он – имитатор, в него ничего не заходит, он «в домике». А каким может быть результат обучения, если не произошло восприятия и осмысления информации? Никаким.
Ошибка № 2. Несоблюдение закономерностей усвоения материала
У психолога Льва Выготского есть гениальная идея о зонах развития человека. По природе у нас познавательное отношение к миру, но познавательный процесс может происходить случайно, а может – не случайно, для этого и происходит обучение. А в нем есть свои закономерности, и, если их не соблюдать, результат получится стихийный.
Нарушение закономерностей организации усвоения – это вторая причина низких результатов. Даже если мы «растрясли» учеников, заставили их что-то воспринимать, но в этот открытый сосуд мы вливаем неправильно, на выходе будет неправильный результат.
Выготский выделил две принципиальные зоны развития ученика, ребенка:
- это зона актуального развития, то, что ученик может уверенно делать сам;
-
и зона ближайшего развития – то, что он сможет делать с помощью другого – внешних носителей, учителя, но сам может ошибаться.

Как все происходит: мы начинаем обучение в зоне доступного, но еще не освоенного. Мы в ней тренируем и тренируем, пока это не переходит в умения и навыки, и тогда зона актуального развития пополняется новым опытом. То есть какую-то часть программы мы должны отрабатывать в зоне ближайшего развития до уровня самостоятельности и переходить к следующему материалу.
А мы правильно начинаем работу в зоне ближайшего развития, но не доводим этот фрагмент опыта до самостоятельности, он не переходит в зону актуального развития. И поэтому следующий кусок учебного материала строится на песке, у него нет базы.
Когда-то у нас были школьные переводные экзамены, и это было правильно, потому что заставляли хоть слабого, хоть сильного ученика «переварить» все по-новому. Готовясь и осознавая свою ответственность за экзамен, дети еще раз проводили работу в зоне актуального развития. И это выводило знания на какой-то допустимый уровень, на котором можно было дальше строить что-то новое. А у нас все образование – карточный домик. Поэтому никакие супер-репетиторы даже за два года ничего не сделают. Сломана старая гумбольтовская немецкая система, производной от которой было советское образование. И сейчас мы пожинаем плоды этого.
А у нас все образование – карточный домик. Поэтому никакие супер-репетиторы даже за два года ничего не сделают. Сломана старая гумбольтовская немецкая система, производной от которой было советское образование. И сейчас мы пожинаем плоды этого.
Ошибка № 3. Развлечение впереди обучения
|
Диджитализация, возможность использования гаджетов, дистанционное обучение привело к тому, что мы ринулись осваивать интерактивные средства обучения для того, чтобы развлечь учеников. Завлечь их использованием того, что им интересно. Идея правильная, но получается «телега впереди коня». Определяющим в обучении является содержательность образования.
Идея правильная, но получается «телега впереди коня». Определяющим в обучении является содержательность образования.
В математике есть три вида объектов усвоения: математические понятия (логарифмы, уравнения в алгебре, треугольник, плоскость – в геометрии), факты (аксиомы, теоремы, формулы) и способы действий (правила, алгоритмы, некоторые из которых нужно даже вербально заучить). И каждый вид объектов усвоения – это отдельная форма мышления. Мы гонимся за красивостями и нарушаем закономерности формирования этих объектов усвоения. Если они не проведены на уроке в полном объеме, знания будут ущербными.
Побороть страх успехом
|
Конечно, по-настоящему математику любят немногие, а некоторые даже откровенно побаиваются. Отсюда «другой склад ума» и «не всем это дано». Страх перед математикой блокирует механизмы памяти, и ребенок «закрывается», поскольку у него формируется установка «мне это недоступно», «я этого никогда не пойму». Как только мелькнула такая мысль – до такого ученика уже не достучаться.
«Растопить» это нельзя никакими словами, только через реальный успех. Дать ему элементарное упражнение, с которым он справится, а вы его на этом успехе подогреете: «Молодец, ты же можешь!». Ощущение успеха на уровне наркотической зависимости, это наша жизненная потребность. К сожалению, на уроках не получается создавать такие ощущения у учеников из-за целого ряда факторов.
КСТАТИ
Почему школьники не смогли воспользоваться формулами
В этом году на ВНО был дан перечень формул – такого никогда не было. Можно было подсмотреть, использовать, но результат – ах! И дело не во внешних носителях и не в перегрузке памяти. В процессе обучения отсутствует целенаправленное обучение распознаванию формул. Быстренько вкидываются новые формулировки и решаются задачи на тренировку формулы – и это все правильно.
Можно было подсмотреть, использовать, но результат – ах! И дело не во внешних носителях и не в перегрузке памяти. В процессе обучения отсутствует целенаправленное обучение распознаванию формул. Быстренько вкидываются новые формулировки и решаются задачи на тренировку формулы – и это все правильно.
Но без набитой руки невозможно решать более сложные задачи. Это как сесть за руль машины и уметь только читать правила дорожного движения, а потом подъехать к светофору и судорожно искать, что делать в этой ситуации. Вот это сейчас и происходит в школьной математике.
У нас сейчас есть правило «не перегружать ученика», то есть дети не заучивают. Но математика – такая хитрая штука, где все заучивается, если делать однотипные упражнения. А времени не хватает.
ЧТО ДЕЛАТЬ
Увеличить количество часов
Четыре, а то и три часа математики в неделю – это катастрофа. Уроки должны быть каждый день, и лучше бы не по одному. В новой украинской школе дают возможность 5 часов математики, для углубленного изучения можно выбрать 6. А шесть часов нужно, чтобы нормально усвоить и получить базовые навыки. И чем слабее ученик, тем ему больше нужно этих тренировочных простых упражнений, чтобы он набил руку и научился делать хоть что-то сам. А для этого нужно не 4 часа в неделю, а 6.
В новой украинской школе дают возможность 5 часов математики, для углубленного изучения можно выбрать 6. А шесть часов нужно, чтобы нормально усвоить и получить базовые навыки. И чем слабее ученик, тем ему больше нужно этих тренировочных простых упражнений, чтобы он набил руку и научился делать хоть что-то сам. А для этого нужно не 4 часа в неделю, а 6.
Не относиться к образованию как к сфере услуг
Повседневным лозунгом для всех должен стать «Я хочу знать». Не «вложите в меня», а «я хочу научиться». Мы должны переломить эту ситуацию с введением термина «образовательные услуги», потому что и родители, и дети стали относиться к образованию как к сфере услуг.
Ничего не может происходить без усилий, и учение – это переход из зоны актуального в зону ближайшего, укрепление и движение дальше. Хорошо, когда есть внутренняя потребность в движении к новому, но если ее нет, геймификация обучения математике не спасет. Нужно подталкивать, и лучшим средством является ситуация успеха. Здесь, кстати, важна и нужна и поддержка со стороны родителей.
Здесь, кстати, важна и нужна и поддержка со стороны родителей.
Вернуть учителей к истокам методики преподавания математики
Тем закономерностям формирования математических понятий, фактов и способов действий, которые и составляют образование, нужно в полной мере учить на уроках. Если этого не делать в школе, мы и дальше будем терять результаты. А у нас зачастую именно на этом экономится время, чтобы решить еще 2-3 задачи. Нарушение методических схем введения объектов усвоения – одна из страшных ошибок.
Не увлекаться игровыми формами
Учитель придумывает отличный сюжет и вплетает в него новый математический материал, урок проходит «на ура». На следующий день ученики помнят сюжет, эмоции, а математики не помнят вовсе. И эта та самая телега впереди коня: мы подбираем содержание под правила игры, и ничего не срабатывает. Сюжет должен притягиваться к содержательной основе, а не наоборот.
Не делить математику на элитную и массовую уже в 5-м классе
Это противоречит психофизиологии: дети развиваются в этом возрасте очень по-разному, поэтому нельзя утверждать, что этот ребенок готов воспринимать элитную математику, а этот – нет. Так можно потерять тех учеников, которые бы развились позднее. Сейчас официально в Украине углубленное изучение математики разрешено с 8-го класса, и на этой позиции нужно оставаться.
Так можно потерять тех учеников, которые бы развились позднее. Сейчас официально в Украине углубленное изучение математики разрешено с 8-го класса, и на этой позиции нужно оставаться.
ДОСЬЕ
Нина Анатольевна Тарасенкова – профессор, доктор педагогических наук, заведующая кафедрой математики и методики обучения математики Черкасского национального университета им. Хмельницкого. Автор более 500 научных работ, учебников, одна из разработчиков школьных программ по математике 2005 г., 2011-2013 гг., 2015 г., 2017г. Создатель школьных учебников «Математика» (5, 6, 10 класс), «Геометрия» (7, 8, 9, 10,11 класс), «Алгебра» (7-9 класс) и дидактического сопровождения к ним – более 90 пособий в соавторстве.
P.S
Изучением плачевных результатов теперь будут заниматься специалисты Центра оценивания качества образования, разработчики тестов, методисты. Будут анализировать и работы учеников, чтобы понять, где «спотыкались». Из того что рассказывают дети и родители, понятно, что практически никто не тратил время на решение несложных задач, где 1-3 шага, – просто угадывали ответы и на этом теряли баллы. Ну и плюс невнимательность.
Из того что рассказывают дети и родители, понятно, что практически никто не тратил время на решение несложных задач, где 1-3 шага, – просто угадывали ответы и на этом теряли баллы. Ну и плюс невнимательность.
Обязательное ВНО по математике никто не отменит, как рассчитывают многие. А вот часов, может, и добавят, надеются педагоги. Нам без нее все равно никуда, ведь она «ум в порядок приводит», учит мыслить свернутыми структурами и действовать в жестких правилах. А этот навык экстраполируется на все сферы жизни. И математика нужна не для того, чтобы уметь строить графики функций, а чтобы устанавливать причинно-следственные связи и выводить следствие из данных. А это все есть в наших повседневных жизненных ситуациях.
ЧИТАЙТЕ ТАКЖЕ
M / J Grade 8 Pre-Algebra — 1205070
Домик на дереве Хейли: похожие треугольники и наклон: Узнайте, как похожие прямоугольные треугольники могут показать одинаковый уклон между любыми двумя разными точками на не вертикальной линии, когда вы помогаете Хейли построить лестницу к ее дому на дереве в этом интерактивном руководстве.
Тип: Оригинальное учебное пособие для учащихся
Математические модели и социальное дистанцирование:Узнайте, как математические модели могут показать, почему социальное дистанцирование во время эпидемии или пандемии важно, в этом интерактивном руководстве.
Тип: Оригинальное учебное пособие для учащихся
Построение функций с двух точек зрения: В этом интерактивном руководстве научитесь создавать функцию для моделирования линейной зависимости между двумя величинами и определять наклон и точку пересечения по оси Y с учетом двух точек, которые представляют функцию.
Тип: Оригинальное учебное пособие для учащихся
Многоступенчатые уравнения: часть 5 Сколько решений ?:Узнайте, как уравнения могут иметь одно решение, без решения или бесконечно много решений в этом интерактивном руководстве.
Это пятая часть из пяти в серии о решении многошаговых уравнений.
- Щелкните , чтобы открыть Часть 1: Объединение терминов «Нравится»
- Щелкните ЗДЕСЬ , чтобы открыть Часть 2: Распределительное свойство
- Щелкните ЗДЕСЬ , чтобы открыть Часть 3: Переменные на обеих сторонах
- Щелкните ЗДЕСЬ , чтобы открыть Часть 4: Собираем все вместе
- [ТЕКУЩИЙ РУКОВОДСТВО] Часть 5: Сколько решений?
Тип: Оригинальное учебное пособие для учащихся
Многоступенчатые уравнения: часть 4 Собираем все вместе: Изучите альтернативные методы решения многоступенчатых уравнений в этом интерактивном руководстве.
Это пятая часть из пяти в серии о решении многошаговых уравнений.
- Щелкните , чтобы открыть Часть 1: Объединение терминов «Нравится»
- Щелкните ЗДЕСЬ , чтобы открыть Часть 2: Распределительное свойство
- Щелкните ЗДЕСЬ , чтобы открыть Часть 3: Переменные на обеих сторонах
- [ТЕКУЩЕЕ РУКОВОДСТВО] Часть 4: Собираем все вместе
- Щелкните ЗДЕСЬ , чтобы открыть Часть 5: Сколько решений?
Тип: Оригинальное учебное пособие для учащихся
Объем сферического пузырькового чая: Из этого интерактивного руководства вы узнаете, как рассчитать объем сфер, узнав, как они делают Bubble Tea.
Тип: Оригинальное учебное пособие для учащихся
Многоступенчатые уравнения: Часть 3 Переменные с обеих сторон:Узнайте, как решать многоступенчатые уравнения, которые содержат переменные с обеих сторон уравнения, в этом интерактивном руководстве.
Это пятая часть из пяти в серии о решении многошаговых уравнений.
- Щелкните ЗДЕСЬ , чтобы открыть Часть 1: Объединение терминов «Нравится»
- Щелкните ЗДЕСЬ , чтобы открыть Часть 2: Распределительное свойство
- [ТЕКУЩЕЕ РУКОВОДСТВО] Часть 3: Переменные на обеих сторонах
- Щелкните ЗДЕСЬ , чтобы открыть Часть 4: Собираем все вместе
- Щелкните ЗДЕСЬ , чтобы открыть Часть 5: Сколько решений?
Тип: Оригинальное учебное пособие для учащихся
Многоступенчатые уравнения: Часть 2 Распределительное свойство: Узнайте, как решать многоступенчатые уравнения с помощью свойства распределения в этом интерактивном руководстве.
Это вторая часть из пяти в серии о решении многоступенчатых уравнений.
- Щелкните , чтобы открыть Часть 1: Объединение терминов «Нравится»
- [ТЕКУЩЕЕ РУКОВОДСТВО] Часть 2: Распределительная собственность
- Щелкните ЗДЕСЬ , чтобы открыть Часть 3: Переменные на обеих сторонах
- Щелкните ЗДЕСЬ , чтобы открыть Часть 4: Собираем все вместе
- Щелкните ЗДЕСЬ , чтобы открыть Часть 5: Сколько решений?
Тип: Оригинальное учебное пособие для учащихся
Круиз по функциям:Путешествуйте вместе, узнавая, как качественно описывать функции в этом интерактивном руководстве.
Тип: Оригинальное учебное пособие для учащихся
Многоступенчатые уравнения: Часть 1 Объединение одинаковых терминов: Узнайте, как решать многоступенчатые уравнения, содержащие похожие термины, в этом интерактивном руководстве.
Это первая часть из пяти в серии, посвященной решению многоступенчатых уравнений.
- [ТЕКУЩЕЕ РУКОВОДСТВО] Часть 1. Объединение терминов «Нравится»
- Щелкните , чтобы открыть Часть 2: Распределительное свойство
- Щелкните ЗДЕСЬ , чтобы открыть Часть 3: Переменные на обеих сторонах
- Щелкните ЗДЕСЬ , чтобы открыть Часть 4: Собираем все вместе
- Щелкните ЗДЕСЬ , чтобы открыть Часть 5: Сколько решений?
Тип: Оригинальное учебное пособие для учащихся
Функции, сладкие функции: Посмотрите, как приятно определять наклон линейных функций и сравнивать их в этом интерактивном руководстве. Определите и сравните наклон или скорость изменения, используя словесные описания, таблицы значений, уравнения и графические формы.
Определите и сравните наклон или скорость изменения, используя словесные описания, таблицы значений, уравнения и графические формы.
Тип: Оригинальное учебное пособие для учащихся
Лето развлечений:Развлекайтесь с функциями! Узнайте, как определять линейные и нелинейные функции в этом интерактивном руководстве.
Тип: Оригинальное учебное пособие для учащихся
Управляется функциями: Узнайте, как определить, является ли связь функцией, в этом интерактивном руководстве, в котором показаны входные и выходные данные, уравнения, графики и словесные описания.
Тип: Оригинальное учебное пособие для учащихся
Понятие движения, часть 3 — Средняя скорость:Опишите среднюю скорость багги для дюн, используя кинематику в этом интерактивном руководстве.Вы рассчитаете смещение и среднюю скорость, создадите и проанализируете график рассеяния скорости в зависимости от времени и свяжете среднюю скорость с наклоном графика рассеяния положения и времени.
Это часть 3 из 3 из серии, которая отражает практические занятия, основанные на запросах, из наших популярных семинаров.
- Щелкните, чтобы открыть «Понятие движения», часть 1 — Измерения времени
- Щелкните ЗДЕСЬ, чтобы открыть «Понятие движения», часть 2 — Позиция и время
Тип: Оригинальное учебное пособие для учащихся
Понятие движения, часть 2 — Положение против времени: Продолжить изучение кинематики для описания линейного движения, сосредоточив внимание на измерениях положения и времени из испытания движения в части 1. В этом интерактивном руководстве вы определите измерения местоположения с помощью искровой ленты, проанализируете диаграмму рассеяния данных местоположения-времени, вычислите и интерпретируете наклон на графике местоположения-времени и сделаете выводы о средней скорости багги для дюн
В этом интерактивном руководстве вы определите измерения местоположения с помощью искровой ленты, проанализируете диаграмму рассеяния данных местоположения-времени, вычислите и интерпретируете наклон на графике местоположения-времени и сделаете выводы о средней скорости багги для дюн
Тип: Оригинальное учебное пособие для учащихся
Диаграммы рассеяния. Часть 6: Использование линейных моделей:Узнайте, как использовать уравнение линейной линии тренда для интерполяции и экстраполяции двумерных данных, построенных на диаграмме рассеяния.В этом интерактивном руководстве вы увидите полезность линий тренда и то, как они используются.
Это 6-я часть серии из 6. Щелкните ниже, чтобы открыть другие руководства из этой серии.
Тип: Оригинальное учебное пособие для учащихся
Диаграммы рассеяния. Часть 5: Интерпретация уравнения линии тренда.Узнайте, как интерпретировать наклон и точку пересечения по оси Y линейной линии тренда, когда двумерные данные нанесены на диаграмму рассеяния в этом интерактивном руководстве.
Это 5-я часть серии из 6. Щелкните ниже, чтобы открыть другие руководства из этой серии.
Тип: Оригинальное учебное пособие для учащихся
Диаграммы рассеяния, часть 4: Уравнение линии тренда:Узнайте, как написать уравнение линейной линии тренда, подогнанной к двумерным данным на диаграмме рассеяния, в этом интерактивном руководстве.
Это четвертая часть серии из 6. Щелкните ниже, чтобы открыть другие руководства из этой серии.
Тип: Оригинальное учебное пособие для учащихся
Диаграммы рассеяния, часть 3: Линии тренда:Изучите неформальную подгонку линии тренда к данным, изображенным на диаграмме рассеяния, в этом интерактивном онлайн-руководстве.
Это часть 3 из 6 частей. Щелкните ниже, чтобы открыть другие руководства из этой серии.
Тип: Оригинальное учебное пособие для учащихся
Диаграммы рассеяния, часть 1: построение графиков:Узнайте, как построить двумерные данные на диаграмме рассеяния в этом интерактивном руководстве.
Это первая часть из 6 серий. Щелкните ниже, чтобы открыть другие руководства из этой серии.
Тип: Оригинальное учебное пособие для учащихся
Преобразования дома:Научитесь описывать последовательность преобразований, в результате которых получаются похожие фигуры. Это интерактивное руководство позволит вам попрактиковаться в поворотах, переводах, отражениях и растяжениях.
Тип: Оригинальное учебное пособие для учащихся
Изменить возраст вождения ?:Узнайте, как оценить обоснованность аргументов нескольких выступающих, когда они обсуждают, следует ли повышать возраст вождения с 16 до 18 или даже выше, с помощью этого интерактивного руководства.
Тип: Оригинальное учебное пособие для учащихся
Куда делись все скраб-сойки ?:Изучите ограничивающие факторы экосистемы Флориды и опишите, как эти ограничивающие факторы влияют на одно коренное население — Флоридскую скраб-сойку — с помощью этого интерактивного учебного пособия.
Тип: Оригинальное учебное пособие для учащихся
По горячим следам:Изучите, как температура влияет на скорость химических реакций, в этом интерактивном руководстве.
Тип: Оригинальное учебное пособие для учащихся
Да или нет ГМО ?:Узнайте, что такое генная инженерия и некоторые применения этой технологии.В этом интерактивном руководстве вы получите представление о некоторых преимуществах и потенциальных недостатках генной инженерии. В конечном итоге вы сможете критически относиться к генной инженерии и написать аргумент, описывающий вашу собственную точку зрения на ее влияние.
Тип: Оригинальное учебное пособие для учащихся
Построение линейных функций из таблиц:Научитесь создавать линейные функции из таблиц, содержащих наборы данных, которые связаны друг с другом особым образом, по мере того, как вы завершите это интерактивное руководство.
Тип: Оригинальное учебное пособие для учащихся
Образцы плитки I: восьмиугольники и квадраты:В этом задании ученикам дается узор плитки, состоящий из равных правильных восьмиугольников и квадратов.Их просят определить меру внутреннего угла восьмиугольника и проверить атрибуты квадрата.
Тип: Задача по решению проблем
Разбиение шестиугольника:Цель этого задания — найти способ разложить правильный шестиугольник на конгруэнтные фигуры.Это задумано как учебное задание, которое дает студентам возможность попрактиковаться в работе с преобразованиями.
Тип: Задача по решению проблем
Пенни в рай:Цель этого задания — дать учащимся контекст для исследования больших чисел и измерений.Студенты должны плавно переводить единицы с очень большими числами, чтобы успешно выполнить эту задачу. Общее количество монет, отчеканенных за один год или за последнее столетие, феноменально велико, и его трудно понять. Один из способов оценить, насколько велико это число, — это рассмотреть, как далеко достигли бы все эти пенни, если бы мы могли сложить их один на другой: это еще одно феноменально большое число, но то, насколько оно велико, может стать неожиданностью. .
Тип: Задача по решению проблем
Прибыль DVD, Вариант 1:В этом задании учащихся просят определить цену за единицу продукта при двух различных обстоятельствах.Их также просят обобщить стоимость производства x единиц в каждом случае.
Тип: Задача по решению проблем
Очки:В этом ресурсе учащиеся определяют объемы трех стаканов для питья разной формы.Им потребуются предварительные знания формул объема для цилиндров, конусов и сфер, а также опыт решения уравнений, упрощения квадратных корней и применения теоремы Пифагора.
Тип: Задача по решению проблем
Как погода?:Это задание можно использовать в качестве быстрой оценки, чтобы увидеть, могут ли учащиеся разобраться в графике в контексте реальной ситуации.Студенты также должны обратить внимание на шкалу на вертикальной оси, чтобы найти правильное соответствие. Первый и третий графики на первый взгляд выглядят очень похожими, но значения функций сильно различаются, поскольку шкалы на вертикальных осях сильно различаются. Задача также может быть использована для создания группового обсуждения интерпретации функций, заданных графами.
Тип: Задача по решению проблем
Интерпретация графика:Цель этого задания — помочь студентам научиться читать информацию о функции из ее графика, попросив их показать часть графика, которая демонстрирует определенное свойство функции.Задача может быть использована для дальнейшего обучения пониманию функций или в качестве инструмента оценки, с оговоркой, что это требует некоторого творческого подхода, чтобы решить, как лучше всего проиллюстрировать некоторые из утверждений.
Тип: Задача по решению проблем
Купон или скидка:В этом задании ученикам предлагается реальная проблема, связанная с ценой продаваемого товара.Чтобы ответить на вопрос, учащиеся должны представить проблему, указав переменную и связанные с ней величины, а затем написать и решить уравнение.
Тип: Задача по решению проблем
Паста из киноа 1:В этом задании учащимся предлагается найти количество двух ингредиентов в смеси для макарон.Задача предоставляет всю информацию, необходимую для решения проблемы путем постановки двух линейных уравнений с двумя неизвестными. Эта последовательность задач помогает различать ожидания 8-го класса и старшей школы, связанные с системами линейных уравнений.
Тип: Задача по решению проблем
Решение уравнений:В этом упражнении студента просят решить множество уравнений (одно решение, бесконечные решения, нет решения) традиционным алгебраическим способом и использовать изображения балансировочных весов, чтобы показать процесс решения.
Тип: Задача по решению проблем
Тарифы на сотовый телефон:Это задание представляет собой реальную задачу, требующую от студентов написать линейные уравнения для моделирования различных планов сотового телефона. Рассмотрение графиков линий в контексте планов сотовых телефонов позволяет студентам связать значения точек пересечения двух линий с одновременным решением двух линейных уравнений.Студенты должны найти решение алгебраически для выполнения задачи.
Тип: Задача по решению проблем
Знак решений:Можно много сказать о решении уравнения, не решая его, просто глядя на структуру и операции, составляющие уравнение.Это упражнение переключает внимание с знакомой проблемы «поиска решения» на размышления о том, что на самом деле означает, что число является решением уравнения.
Тип: Задача по решению проблем
Две строки:В этой задаче нам дается график из двух линий, включающий координаты точки пересечения и координаты двух вертикальных пересечений, и запрашиваются соответствующие уравнения линий.Это очень простая задача, которая соединяет графики, уравнения, решения и точки пересечения.
Тип: Задача по решению проблем
У кого лучшая работа ?:В этом задании студенту предлагается построить график и сравнить две пропорциональные зависимости и интерпретировать удельную ставку как наклон графика.
Тип: Задача по решению проблем
Кофе за фунт:В этом примере учащиеся ответят на вопросы о цене за единицу кофе, построят график информации и объяснят значение наклона в данном контексте.
Тип: Задача по решению проблем
Велосипедная гонка:Цель этого задания состоит в том, чтобы учащиеся интерпретировали два графика расстояние-время в контексте велогонки. У этого есть два основных математических аспекта: интерпретация того, что означает конкретная точка на графике с точки зрения контекста, и понимание того, что «крутизна» графика что-то говорит нам о том, насколько быстро движутся велосипедисты.
Тип: Задача по решению проблем
Лисицы и кролики:Эта задача подчеркивает важность предложения «каждый вход имеет ровно один выход» в определении функции, которое нарушается в таблице значений двух совокупностей.Примечательно, что, поскольку данные представляют собой набор пар ввода-вывода, словесного описания функции не дается, поэтому часть задачи заключается в обработке того, как будет выглядеть «форма правила» предлагаемых функций.
Тип: Задача по решению проблем
Правила функции:В эту задачу можно играть как в игру, в которой учащиеся должны угадать правило, а инструктор дает все больше и больше пар входных выходов.Указания только трех пар вход-выход может быть недостаточно, чтобы прояснить правило. Преподаватели могут рассмотреть возможность изменения входных данных, например, во второй таблице, чтобы обеспечить нецелочисленные записи. Хороший вариант игры — попросить учеников, которые думают, что они нашли правило, поставляют пары вход-выход, а учителя подтверждают или отрицают их правоту. Вербализация правила требует точности языка. Эту задачу можно использовать, чтобы представить идею функции как правила, которое назначает уникальный выход каждому входу.
Тип: Задача по решению проблем
Введение в линейные функции:Это задание позволяет учащимся изучить различия между линейными и нелинейными функциями. В отличие от двух, он усиливает свойства линейных функций.
Тип: Задача по решению проблем
Моделирование с помощью линейной функции:Основная цель этого задания — выявить распространенные заблуждения, которые возникают, когда учащиеся пытаются моделировать ситуации с помощью линейных функций.Эта задача, будучи множественным выбором, также может служить в качестве быстрой оценки, чтобы оценить понимание классом моделирования с линейными функциями.
Тип: Задача по решению проблем
Приливы:Это простая задача по интерпретации графика функции с точки зрения взаимосвязи между величинами, которые он представляет.
Тип: Задача по решению проблем
Езда по библиотеке:В этом задании учащиеся рисуют графики двух функций из словесных описаний. Обе функции описывают одну и ту же ситуацию, но изменение точки зрения наблюдателя меняется, когда функция имеет нулевое выходное значение.Этот небольшой поворот заставляет студентов тщательно обдумать интерпретацию зависимой переменной. Эту задачу можно использовать по-разному: Для создания обсуждения в классе графического представления. В качестве быстрой оценки построения графиков, например, во время разминки класса. Чтобы вовлечь студентов в обсуждение в малых группах.
Тип: Задача по решению проблем
Вычисление квадратного корня из 2:Это задание предназначено для учебных целей, чтобы учащиеся могли научиться и уверенно пользоваться калькулятором и понять, что он может, а что нет.Эта задача дает возможность поработать над понятием разряда (в частях [b] и [c]), а также понять часть аргумента, почему квадратный корень из 2 не является рациональным числом.
Тип: Задача по решению проблем
Сравнение снежных конусов:Учащиеся просто узнают о сходстве в этом классе, поэтому они могут не осознавать, что это необходимо в данном контексте.Учителя должны быть готовы оказать поддержку учащимся, которые борются с этой частью задания. Чтобы упростить задачу, учитель может просто сказать ученикам, что, исходя из наклона чашки с усеченным конусом, весь конус будет иметь высоту 14 дюймов, а отрезанная часть — 10 дюймов. (См. Объяснение в решении.) Стоит обсудить части (c) и (e). Процентное увеличение для снежных шишек меньше, чем для соков. Снежные конусы имеют объем, равный объему сока, плюс объем купола, который одинаков в обоих случаях.Добавление одного и того же числа к двум числам в соотношении всегда будет приближать их отношение к единице, что в данном случае означает, что соотношение — и, следовательно, процентное увеличение — будет меньше.
Тип: Задача по решению проблем
Конгруэнтные сегменты:Первый опыт трансформаций студентов, скорее всего, будет связан с определенными формами, такими как треугольники, четырехугольники, круги и фигуры с симметрией.Демонстрация последовательности преобразований, которая показывает, что два общих линейных сегмента одинаковой длины совпадают, — это хороший способ для учащихся начать думать о преобразованиях в более широком смысле.
Тип: Задача по решению проблем
Конгруэнтные треугольники:Это задание преследует две цели: во-первых, научить учащихся понимать жесткие движения в контексте демонстрации конгруэнтности.Во-вторых, знания учащихся об размышлениях уточняются за счет рассмотрения понятия ориентации в части (b). Каждый раз, когда плоскость отражается относительно линии, это меняет на противоположные понятия «по часовой стрелке» и «против часовой стрелки».
Тип: Задача по решению проблем
Отражая отражения:В этом материале учащиеся экспериментируют с последовательными отражениями треугольника в координатной плоскости.
Тип: Задача по решению проблем
Оценка квадратного корня:По определению, квадратный корень из числа n — это число, возведенное в квадрат, чтобы получить n . Цель этого задания — научить учащихся использовать значение квадратного корня, чтобы найти десятичное приближение квадратного корня из неквадратного целого числа.Студентам может потребоваться руководство, чтобы подумать о том, как подойти к задаче.
Тип: Задача по решению проблем
Отражение точки:Цель этого задания — применить отражение к одной точке. Стандарт просит студентов применять жесткие движения к линиям, отрезкам и углам.Хотя в этой задаче отражение применяется только к одной точке, она имеет высокий когнитивный спрос, если учащихся просят представить картинку. Это потому, что координаты точки (1000,2012) очень большие. Если ученики попытаются нанести эту точку и линию отражения на обычную координатную сетку xy, то либо график будет слишком большим, либо точка будет лежать так близко к линии отражения, что неясно, лежит она или нет. в этой строке. Хорошая картинка требует тщательного выбора подходящего участка на плоскости и соответствующих надписей.Более того, отражения линий, сегментов линий и углов обнаруживаются путем отражения отдельных точек.
Тип: Задача по решению проблем
Отражение прямоугольника по диагонали:Задача предназначена для учебных целей и предполагает, что учащиеся знают свойства жестких преобразований, описанных в.Обратите внимание, что вершины рассматриваемых прямоугольников не попадают точно в точки пересечения горизонтальных и вертикальных линий сетки. Это означает, что учащимся необходимо приблизиться, и это создает дополнительную проблему. Проблема также в том, что сетки нарисованы так, что они выровнены по диагонали прямоугольников, а не по вертикали и горизонтали страницы. Однако такой выбор сетки также упрощает рассуждения об отражениях, если они понимают описания жестких движений, указанные в MAFS.8.G.1.3.
Тип: Задача по решению проблем
Скоростной спуск:Эта задача особенно хорошо подходит для учебных целей. Учащимся будет полезно обсудить в классе наклон, точку пересечения по оси y, точку пересечения по оси x и значение ограниченной области для более точной интерпретации того, что моделирует уравнение.
Тип: Задача по решению проблем
Найдите угол:Используйте неформальные аргументы, чтобы установить факты о сумме углов и внешнем угле треугольников, об углах, образованных, когда параллельные прямые пересекаются трансверсалью, и о критерии подобия треугольников угол-угол.
Тип: Задача по решению проблем
Найдите недостающий угол:Эта задача дает нам возможность увидеть, как со временем созревают математические идеи, заложенные в стандарты и кластеры. Задание «Использует факты о дополнительных, дополнительных, вертикальных и смежных углах в многоэтапной задаче для написания и решения простых уравнений для неизвестного угла на фигуре ()», за исключением того, что оно требует, чтобы учащиеся знали, кроме того, кое-что о параллельные линии, которые ученики не увидят до 8-го класса.В результате эта задача особенно хорошо иллюстрирует связи между соответствующими стандартами на разных уровнях обучения.
Тип: Задача по решению проблем
Вазы для цветов:Цель этого задания — дать студентам возможность попрактиковаться в работе с формулами объема цилиндров, конусов и сфер в увлекательном контексте, который дает возможность придать смысл ответам.
Тип: Задача по решению проблем
Это прямоугольник ?:Цель этого задания — предоставить студентам возможность применить широкий спектр идей из геометрии и алгебры, чтобы показать, что данный четырехугольник является прямоугольником.Здесь очень важен творческий подход, поскольку единственная информация — это декартовы координаты вершин четырехугольника. Использование этой информации для демонстрации того, что четыре угла являются прямыми углами, потребует некоторых вспомогательных построений. Студентам потребуется достаточно времени, а по некоторым из методов, описанных ниже, — руководство. Награда за тщательное выполнение этой задачи должна оправдывать затраченные усилия, поскольку дает студентам возможность увидеть несколько геометрических и алгебраических построений, объединенных для достижения общей цели.Учитель может пожелать, чтобы учащиеся сначала провели мозговой штурм по методам демонстрации того, что четырехугольник является прямоугольником (перед тем, как представить им явные координаты прямоугольника для этой задачи): в идеале они могут затем разделиться на группы и сразу же приступить к работе после того, как представят координаты четырехугольника для этой задачи.
Тип: Задача по решению проблем
Определение рациональных чисел:Задача предполагает, что учащиеся могут выразить данную повторяющуюся десятичную дробь в виде дроби.Учителя, которым нужно заполнить эти базовые знания, могут рассмотреть связанную задачу «8.NS Преобразование десятичных представлений рациональных чисел в дробные представления».
Тип: Задача по решению проблем
Иррациональные числа на числовой прямой:Когда учащиеся наносят иррациональные числа на числовую линию, это помогает укрепить идею о том, что они вписываются в систему счисления, которая включает более знакомые целые и рациональные числа.Сейчас хорошее время для учителей, чтобы начать использовать термин «действительная числовая линия», чтобы подчеркнуть тот факт, что числовая система, представленная числовой линией, является действительными числами. Когда ученики начинают изучать комплексные числа в старшей школе, они сталкиваются с числами, которые не находятся на прямой числовой прямой (а фактически находятся на «числовой плоскости»). Эту задачу можно использовать для оценивания или, если немного доработать, можно использовать в учебных целях.
Тип: Задача по решению проблем
Доставка овсяных хлопьев:Студенты должны подумать о различных способах размещения цилиндрических контейнеров в прямоугольной коробке.В процессе обучения учащиеся должны понимать, что, хотя некоторые настройки могут показаться разными, в результате получается коробка с одинаковым объемом. Кроме того, учащиеся должны прийти к осознанию (посредством обсуждения и / или вопросов), что толщина картонной коробки очень мала и не окажет существенного влияния на расчеты.
Тип: Задача по решению проблем
Образцы плитки II: шестиугольники:Это задание идеально подходит для учебных целей, когда студенты могут не торопиться и разработать несколько стандартов математической практики, поскольку математическое содержание напрямую связано с содержанием стандарта по суммам углов в треугольниках, но несколько превосходит его.Тщательный анализ углов требует от учащихся построения обоснованных аргументов (MAFS.K12.MP.3.1) с использованием абстрактных и количественных рассуждений (MAFS.K12.MP.2.1). Создание рисунка в части (c) помогает учащимся определить общий математический аргумент, повторяющийся несколько раз (MAFS.K12.MP.8.1). Если учащиеся используют блоки шаблонов для развития интуиции при разложении шестиугольника на треугольники, то это также пример MAFS.K12.MP.5.1.
Тип: Задача по решению проблем
Соответствие треугольника координатам:В этом материале учащиеся решат, как использовать преобразования в координатной плоскости, чтобы перевести треугольник в конгруэнтный треугольник.Включены исследовательские примеры, чтобы побудить к аналитическому мышлению.
Тип: Задача по решению проблем
Сравнение рациональных и иррациональных чисел:Студентам дается пара цифр. Их просят определить, какой из них больше, а затем обосновать свой ответ.Используемые числа — это рациональные числа и обычные иррациональные числа, такие как p и квадратные корни. Эту задачу можно использовать для построения или оценки начального понимания рациональных приближений иррациональных чисел.
Тип: Задача по решению проблем
Музыка и спорт:В этом задании учащемуся предлагается собрать данные о том, играют ли одноклассники на каком-либо инструменте и / или занимаются ли они спортом, суммировать данные в таблице и решить, существует ли связь между занятиями спортом и игрой на музыкальном инструменте.Наконец, студента просят создать график, чтобы отобразить любую связь между переменными.
Тип: Задача по решению проблем
Какой твой любимый урок?:Учащимся предлагается изучить данные, представленные в формате таблицы, а затем вычислить процентное соотношение строк или столбцов и сформулировать вывод о значении данных.Любой расчет подходит для решения, поскольку нет четкой взаимосвязи между переменными. Видит ли учащийся сильную ассоциацию или нет, менее важно, чем то, правильно ли использует его или ее ответ данные и демонстрирует понимание того, что ассоциация означает, что распределение любимого предмета различно для учеников 7 и 8 классов.
Тип: Задача по решению проблем
Текстовые сообщения и оценки I:Учащимся предлагается изучить диаграмму рассеяния, а затем интерпретировать ее значение.Учащиеся должны определить форму взаимосвязи (линейная, изогнутая и т. Д.), Направление или корреляция (положительная или отрицательная), любые конкретные выбросы, силу взаимосвязи между двумя переменными и любые другие соответствующие наблюдения.
Тип: Задача по решению проблем
Аэропорты США:В этом ресурсе двумерные данные реального мира отображаются в виде точечной диаграммы.Предоставляется уравнение линейной функции, моделирующей взаимосвязь между двумя переменными, и оно изображено на диаграмме рассеяния. Студентов просят использовать модель для интерпретации данных и делать прогнозы.
Тип: Задача по решению проблем
Сравнение скоростей в графиках и уравнениях:Это задание дает учащимся возможность рассуждать о графиках, наклонах и показателях без шкалы на осях или уравнения для представления графиков.Учащиеся, которые предпочитают работать с конкретными числами, могут написать шкалу на осях, чтобы помочь им начать работу.
Тип: Задача по решению проблем
Скорость в зависимости от расстояния:В этом задании учащиеся интерпретируют два графика, которые выглядят одинаково, но показывают очень разные величины.Первый график дает информацию о том, насколько быстро движется автомобиль, а второй график дает информацию о положении автомобиля. Эта задача хорошо подходит для проведения обсуждения в классе или небольшой группе. Учащиеся узнают, что графики рассказывают истории и что их нужно интерпретировать, тщательно обдумывая отображаемые количества.
Тип: Задача по решению проблем
Мусор США, версия 1:В этой задаче правило функции более концептуально.Мы присваиваем году (входу) общее количество мусора, произведенного в этом году (соответствующий выход). Даже если бы мы не знали точное количество мусора за год, ясно, что в одном году не будет производиться два разных количества мусора. Таким образом, это имеет смысл как «правило», даже несмотря на то, что нет никакого алгоритмического способа определить выход для данного входа, кроме как искать его в таблице.
Тип: Задача по решению проблем
Продажа мазута в убыток:Задача представляет собой задачу моделирования, которая связана с финансовыми решениями, с которыми обычно сталкиваются предприятия, а именно с балансом между поддержанием запасов и привлечением краткосрочного капитала для инвестиций или реинвестирования в развитие бизнеса.
Тип: Задача по решению проблем
Курица и стейк, Вариант 1:В этом задании по решению задач студентам предлагается применить свое понимание линейных соотношений для определения количества курицы и стейка, необходимого для барбекю, что будет включать в себя создание уравнения, рисование графика и интерпретацию того и другого.Этот ресурс также включает комментарии по согласованию стандартов и аннотированные решения.
Тип: Задача по решению проблем
Кими и Джордан:Студентов просят составить и изобразить линейные уравнения, чтобы сравнить сбережения двух человек.Назначение таблицы в (а) — помочь студентам заполнить (б), заметив регулярность в повторяющихся рассуждениях, необходимых для заполнения таблицы (Стандарт для математической практики).
Тип: Задача по решению проблем
Персики и сливы:В этом задании учащимся предлагается поразмышлять об относительной стоимости фунта двух фруктов, не зная, какова стоимость.Учащиеся, которым это сложно, могут добавить шкалу к графику и рассуждать о значениях упорядоченных пар. Сравнение двух подходов в ходе обсуждения в классе может быть полезным способом помочь учащимся разобраться в уклоне.
Тип: Задача по решению проблем
Видео трансляция:Создайте функцию для моделирования линейной зависимости между двумя величинами.Определите скорость изменения и начальное значение функции из описания взаимосвязи или из двух значений (x, y), включая чтение их из таблицы или графика. Интерпретируйте скорость изменения и начальное значение линейной функции в терминах моделируемой ситуации, а также в терминах ее графика или таблицы значений.
Тип: Задача по решению проблем
Бег по футбольному полю:Студентам необходимо подумать о том, как они могут использовать теорему Пифагора для определения расстояний, пройденных Беном Ватсоном и Чемпом Бейли.Здесь следует сосредоточиться не на том, кто пробежал большее расстояние, а на том, чтобы увидеть, как построить прямоугольные треугольники, чтобы применить теорему Пифагора к этой проблеме. Студенты должны использовать свои навыки измерения и делать разумные оценки, чтобы строить треугольники и правильно применять теорему.
Тип: Задача по решению проблем
Курица и стейк, Вариант 2:В этом задании по решению задач студентам предлагается применить свое понимание линейных соотношений для определения количества курицы и стейка, необходимого для барбекю, что будет включать в себя создание уравнения, рисование графика и интерпретацию того и другого.Этот ресурс также включает комментарии по согласованию стандартов и аннотированные решения.
Тип: Задача по решению проблем
Расстояние по каналу:В этом задании по решению проблем учащимся предлагается найти линейную функцию, которая моделирует что-то в реальном мире.После нахождения уравнения линейной зависимости между глубиной воды и расстоянием через канал, учащиеся должны озвучить значение уклона и пересечения линии в контексте этой ситуации. Также включены комментарии по согласованию стандартов и иллюстрированные решения.
Тип: Задача по решению проблем
Уравнения линий:Это задание просит учащегося понять взаимосвязь между наклоном и изменениями значений x и y линейной функции.
Тип: Задача по решению проблем
Найдите изменение:В этом упражнении учащимся предлагается распознать взаимосвязь между наклоном и разницей значений x- и y- линейной функции.Помогите учащимся укрепить свое понимание линейных функций и подтолкнуть их к более свободным рассуждениям о наклонах и пересечениях по оси Y. Эта задача также дала разумную отправную точку для обсуждения формы линейного уравнения с точкой наклона.
Тип: Задача по решению проблем
Ремонт печи:Студентам предлагается написать уравнения для моделирования затрат на ремонт трех разных компаний и определить условия, при которых каждая компания будет наименее затратной.Это задание можно использовать как для оценки понимания учащимися систем линейных уравнений, так и для стимулирования обсуждения и размышления учащихся, которые позволят более прочно закрепить эти концепции. Решение может быть найдено несколькими способами, включая графический или алгебраический подход.
Тип: Задача по решению проблем
Гигантбургеры:Студента просят выполнить операции с числами, выраженными в научных обозначениях, чтобы решить, действительно ли 7% американцев действительно едят в Giantburger каждый день.
Тип: Задача по решению проблем
Расширение определений экспонент, вариант 1:Это учебное задание, предназначенное для обсуждения значения отрицательных целочисленных показателей. Хотя некоторым ученикам это может быть незнакомо, для них полезно усвоить условное обозначение, что отрицательное время — это просто любое время до t = 0.
Тип: Задача по решению проблем
Сколько решений ?:Учащемуся дается уравнение 5x-2y = 3 и просят, если возможно, написать второе линейное уравнение, создающее системы, приводящие к одному, двум, бесконечным и никаким решениям.
Тип: Задача по решению проблем
Идет дождь!!! (Сравните площади протертых лобовых стекол):В этом задании по решению проблем ученикам предлагается определить, позволяют ли дворники на автомобиле или грузовике лучше видеть водителю большую площадь.Чтобы решить эту проблему, учащиеся должны применить теорему Пифагора и свою способность находить области кругов и параллелограммов, чтобы найти ответ. Обязательно нажимайте ссылки на оранжевой полосе вверху страницы, чтобы получить дополнительную информацию о задаче. Из рисунка NCTM: Это! Математические задачи для семей.
Тип: Задача по решению проблем
Доказательство совпадающих углов:В этом учебном пособии учащихся просят доказать, что два угла совпадают, если им предоставлена ограниченная информация.Перед просмотром этого видео учащиеся должны иметь основу из параллельных линий, поперечных сечений и треугольников.
Тип: Учебное пособие
Объем конуса:В этом видео объясняется формула объема конуса и применяется формула для решения проблемы.
Тип: Учебное пособие
Формула расстояния и теорема Пифагора:Из этого туториала Вы узнаете, как найти расстояние между линиями с помощью теоремы Пифагора.В этом видео показана связь между формулой расстояния и теоремой Пифагора.
Тип: Учебное пособие
Сумма мер доказательства треугольников:Это видео демонстрирует сумму углов в треугольнике.Это видео полезно как для студентов, изучающих алгебру и геометрию.
Тип: Учебное пособие
Метод замены:В этом видео показано, как решить систему уравнений с помощью метода подстановки.
Тип: Учебное пособие
Распознавание линейных функций:В этом видео вы определите, является ли ситуация линейной или нелинейной, путем определения скорости изменения между координатами.Вы сможете проверить свою работу, построив график заданных координат.
Тип: Учебное пособие
Сравнение линейных функций на графике:В этом руководстве студенты будут сравнивать линейные функции на графике. Студенты должны понимать наклон и скорость изменения, прежде чем просматривать это руководство.
Тип: Учебное пособие
Сравните линейные функции из таблицы и графика:В этом руководстве показано, как сравнить линейные функции, представленные как в таблице, так и на графике. Перед просмотром этого видео учащиеся должны иметь представление о скорости изменений.
Тип: Учебное пособие
Сравнение линейных функций:Учащиеся сравнивают линейные функции, представленные на графике и в таблице. Перед просмотром этого учебного пособия учащиеся должны хорошо понимать скорость изменений.
Тип: Учебное пособие
Линейная функция: трата денег:В этом руководстве вы попрактикуетесь в использовании уравнения в форме пересечения наклона для нахождения координат, а затем нанесете на график координаты, чтобы предсказать ответ на проблему.
Тип: Учебное пособие
Интерпретация линейных графиков:В этом руководстве вы рассмотрите несколько реальных примеров линейных графиков и интерпретируете взаимосвязь между двумя переменными.
Тип: Учебное пособие
Построение линейного уравнения с помощью таблицы:Студенты узнают, как построить линейное уравнение с помощью таблицы.Студентам не нужно будет строить графики из формы с пересечением наклона, хотя они будут преобразовывать уравнение из стандартной формы в форму с пересечением наклона перед созданием таблицы.
Тип: Учебное пособие
Использование формы наклона-пересечения линии:В этом видео вы попрактикуетесь в написании уравнений линий в форме пересечения наклона из графиков.Затем вы попрактикуетесь в построении линий из уравнений в форме пересечения наклона.
Тип: Учебное пособие
Нахождение наклона из двух упорядоченных пар:В этом руководстве показан пример нахождения наклона между двумя упорядоченными парами.Наклон представлен как подъем / спуск, изменение y, деленное на изменение x, а также как m.
Тип: Учебное пособие
Как приблизительно вычислить квадратные корни:В этом видео вы попрактикуетесь в приближении квадратных корней из чисел, не являющихся точными квадратами.Вы найдете идеальный квадрат внизу и вверху, чтобы приблизительно определить значение квадратного корня между двумя целыми числами.
Тип: Учебное пособие
Классифицирующие числа:В этом руководстве вы попрактикуетесь в классификации чисел как целых, целых, рациональных и иррациональных чисел.
Тип: Учебное пособие
Отрицательные показатели:Этот учебник показывает студентам правило отрицательных показателей.Учащиеся увидят, используя переменные, шаблон для отрицательных показателей.
Тип: Учебное пособие
Отрицательные показатели:В этом руководстве студенты узнают об отрицательных показателях степени.Особое внимание уделяется умножению на обратную величину.
Тип: Учебное пособие
Нахождение кубических корней:Узнайте, как найти кубический корень из -512 с помощью разложения на простые множители.
Тип: Учебное пособие
Введение в кубические корни:Студенты узнают, что такое кубические корни и как их найти. Студенты также узнают, как найти кубический корень отрицательного числа.
Тип: Учебное пособие
Введение в квадратные корни:Учащиеся узнают о символе квадратного корня (главный корень) и о том, что значит найти квадратный корень.Студенты также узнают, как решать простые уравнения с квадратным корнем.
Тип: Учебное пособие
Экспоненты с отрицательным основанием:В этом руководстве вы примените то, что вы знаете об умножении отрицательных чисел, чтобы определить, как влияют отрицательные основания с показателями и какие паттерны развиваются.
Тип: Учебное пособие
Проблема слова линейного уравнения:Узнайте, как решить проблему со словами, написав уравнение для моделирования ситуации. В этом видео мы используем линейное уравнение 210 (t-5) = 41790.
Тип: Учебное пособие
Решение уравнений: проблема со словом:В этом учебном пособии показана задача со словами, в которой учащиеся найдут размеры сада, учитывая только его периметр.Учащиеся создадут уравнение для решения.
Тип: Учебное пособие
Двухступенчатые уравнения:Студенты будут практиковать двухшаговые уравнения, некоторые из которых требуют объединения одинаковых терминов и использования свойства распределения.
Тип: Учебное пособие
Решение двухэтапных уравнений:В этом видео показано, как решить двухшаговое уравнение.Он начинается с концепции равенства: то, что делается с одной стороной уравнения, должно быть сделано с другой стороной уравнения.
Тип: Учебное пособие
Линейные уравнения:Этот учебник поможет вам изучить наклоны линий и увидеть, как наклон представлен на осях x-y.
Тип: Учебное пособие
Показатели и степени:В этом руководстве рассматривается концепция степеней и степеней и рассказывается, как оценивать степени с отрицательными знаками.
Тип: Учебное пособие
Мощность энергетического имущества:В этом руководстве показано, как использовать мощность степенного свойства как с числами, так и с переменными.
Тип: Учебное пособие
Линейные уравнения:Уравнения вида y = mx описывают прямые в декартовой плоскости, которые проходят через начало координат. Тот факт, что многие функции линейны при рассмотрении в мелком масштабе, важен в таких областях математики, как исчисление.
Тип: Учебное пособие
Решение многоступенчатых уравнений:В этом коротком видеоролике объясняется, как решать многоступенчатые уравнения с переменными с обеих сторон и почему необходимо выполнять одни и те же шаги с обеих сторон уравнения.
Тип: Учебное пособие
Возведение экспоненциальных выражений в степень:Если термин, возведенный в степень, заключен в круглые скобки, а затем возведен в другую степень, это выражение можно упростить, используя правила умножения степени.
Тип: Учебное пособие
Повышение качества продуктов и удельного веса:Любое выражение, состоящее из членов умножения и деления, можно заключить в круглые скобки и возвести в степень. Затем это можно упростить, используя правила умножения показателей.
Тип: Учебное пособие
Диаграммы разброса:Диаграммы рассеяния используются для визуализации взаимосвязи между двумя количественными переменными в бинарном отношении. Например, тенденции во взаимосвязи между ростом и весом группы людей можно изобразить и проанализировать с помощью диаграммы рассеяния.
Тип: Учебное пособие
Решение несовместимых или зависимых систем:Решая систему линейных уравнений относительно x и y с одним решением, мы получаем уникальную пару значений для x и y. Но что происходит, когда вы пытаетесь решить систему без решений или с бесконечным количеством решений?
Тип: Учебное пособие
Форма пересечения склона:Линейные уравнения вида y = mx + b могут описывать любую невертикальную линию в декартовой плоскости.Константа m определяет наклон линии, а константа b определяет точку пересечения y и, следовательно, вертикальное положение линии.
Тип: Учебное пособие
Научная нотация:Научная нотация используется для удобной записи чисел, для представления которых требуется много цифр.В этом руководстве объясняется, как преобразовать стандартную нотацию в научную.
Тип: Учебное пособие
Линейные уравнения с одной переменной:Этот урок знакомит учащихся с линейными уравнениями с одной переменной, показывает, как их решать, используя свойства равенств сложения, вычитания, умножения и деления, и позволяет учащимся определить, является ли значение решением, существует ли бесконечно много решений или вообще нет решения.Сайт содержит объяснение уравнений и линейных уравнений, как решать уравнения в целом, а также стратегию решения линейных уравнений. Урок также объясняет противоречие (уравнение без решения) и тождество (уравнение с бесконечными решениями). В конце есть пять практических задач, чтобы студенты могли проверить свои знания со ссылками на ответы и объяснениями, как эти ответы были найдены. Также указаны дополнительные ресурсы.
Тип: Учебное пособие
Основные аддитивные цвета:Этот ресурс помогает пользователю изучить три основных цвета, которые имеют фундаментальное значение для человеческого зрения, изучить различные цвета в видимом спектре, наблюдать получающиеся цвета при добавлении двух цветов и узнать, что такое белый свет.Комбинация текста и виртуального манипулятора позволяет пользователю исследовать эти концепции разными способами.
Тип: Учебное пособие
Основные субтрактивные цвета:Пользователь изучит три основных субтрактивных цвета в видимом спектре, исследует результирующие цвета, когда два субтрактивных цвета взаимодействуют друг с другом, и изучит формирование черного цвета.
Тип: Учебное пособие
Преобразование единиц скорости:На этом уроке учащиеся будут просматривать видеоролик Khan Academy, в котором будет показано, как преобразовывать коэффициенты с использованием единиц скорости.
Тип: Учебное пособие
Ползунок наклона:В этом упражнении учащиеся настраивают ползунки, которые регулируют коэффициенты и константы линейной функции, и исследуют, как их изменения влияют на график.Уравнение линии может иметь форму пересечения уклона или стандартную форму. Это задание позволяет учащимся изучить линейные уравнения, уклоны и точки пересечения по оси Y, а также их визуальное представление на графике. Это упражнение включает в себя дополнительные материалы, в том числе справочную информацию по затронутым темам, описание того, как использовать приложение, и вопросы исследования для использования с java-апплетом.
Тип: виртуальный манипулятор
Линейная функциональная машина:В этом упражнении учащиеся подставляют значения в независимую переменную, чтобы увидеть, каковы выходные данные для этой функции.Затем на основе этой информации они должны определить коэффициент (наклон) и константу (пересечение оси y) для линейной функции. Это упражнение позволяет студентам изучить линейные функции и то, какие входные значения полезны при определении правила линейной функции. Это упражнение включает в себя дополнительные материалы, в том числе справочную информацию по затронутым темам, описание того, как использовать приложение, и вопросы исследования для использования с апплетом Java.
Тип: виртуальный манипулятор
Графические линии:Позволяет учащимся получить доступ к декартовой системе координат, в которой можно построить график линейных уравнений и наблюдать за деталями линии и наклона.
Тип: виртуальный манипулятор
Информационный буклет:С помощью этого виртуального манипулятора учащиеся могут построить график функции и набора упорядоченных пар на одной и той же координатной плоскости. Константы, коэффициенты и показатели можно регулировать с помощью ползунков, чтобы учащийся мог исследовать влияние на график при изменении параметров функции.Студенты также могут проверить отклонение данных от функции. Это упражнение включает в себя дополнительные материалы, в том числе справочную информацию по затронутым темам, описание того, как использовать приложение, и вопросы исследования для использования с java-апплетом.
Тип: виртуальный манипулятор
Функциональный флаер:В этом онлайн-инструменте учащиеся вводят функцию для создания графика, на котором константы, коэффициенты и показатели можно регулировать с помощью ползунков.Этот инструмент позволяет учащимся изучать графики функций и то, как изменение чисел в функции влияет на график. Используя вкладки в верхней части страницы, вы также можете получить доступ к дополнительным материалам, включая справочную информацию о затронутых темах, описание того, как использовать приложение, и вопросы исследования для использования с java-апплетом.
Тип: виртуальный манипулятор
Advanced Data Grapher:Это онлайн-утилита для построения графиков, которую можно использовать для создания коробчатых диаграмм, пузырьковых диаграмм, диаграмм рассеяния, гистограмм и диаграмм типа «стержень-лист».
Тип: виртуальный манипулятор
Number Cruncher:В этом упражнении учащиеся вводят вводимые данные в функциональную машину. Затем, исследуя выходные данные, они должны определить, какую функцию выполняет машина.Это упражнение позволяет учащимся изучить функции и какие входные данные наиболее полезны для определения правила функции. Это упражнение включает в себя дополнительные материалы, в том числе справочную информацию по затронутым темам, описание того, как использовать приложение, и вопросы исследования для использования с java-апплетом.
Тип: виртуальный манипулятор
Подгонка кривой:С помощью мыши учащиеся будут перетаскивать точки данных (со своими планками ошибок) и мгновенно наблюдать за формой наиболее подходящей полиномиальной кривой.Студенты могут выбрать тип соответствия: линейный, квадратичный, кубический или четвертичный. Может отображаться наилучшая или регулируемая посадка.
Тип: виртуальный манипулятор
График уравнений:Это интерактивное моделирование исследует построение графиков линейных и квадратных уравнений.Пользователям предоставляется возможность определять и изменять коэффициенты и константы, чтобы наблюдать результирующие изменения на графике (ах).
Тип: виртуальный манипулятор
Линия Best Fit:Это средство манипуляции позволяет пользователю ввести несколько координат на сетке, оценить линию наилучшего соответствия, а затем определить уравнение для линии наилучшего соответствия.
Тип: виртуальный манипулятор
Вращение точки:Этот виртуальный манипулятор представляет собой интерактивное визуальное представление вращения точки вокруг начала системы координат. Исходную точку можно перетаскивать в разные положения, а угол поворота можно изменять с шагом 90 °.
Тип: виртуальный манипулятор
РешенияNCERT для математики 8-го класса, глава 9 в формате PDF на 2021-2022 гг.
Решения NCERT для класса 8 по математике Глава 9
Класс 8 по математике Глава 9 все решения для упражнений
| Класс: 8 | по математике |
| Глава 9: |
NCERT Solutions для класса 8
Математика для класса 8 Глава 9 Решения
Математика для класса 8 Глава 9 Алгебраические выражения и идентичности Все упражнения на английском и хинди среднего языках приведены ниже для загрузки в формате PDF.Все решения выполнены правильно с учетом последней программы CBSE Syllabus 2021-22 гг.
8 Математика Глава 9 Решения на английском языке Средний
8 Математика Глава 9 Решения на хинди Средний
Класс 8 Математика Упражнение 9.1 Решения в видео
Класс 8 Математика Решения на видео Упражнение по математике для 8-го класса 9.1 ПояснениеУпражнение по математике для 8-го класса 9.2 Решения на видео
Упражнение по математике для 8-го класса 9.2 Решение Упражнение по математике для класса 8 9.2 ОбъяснениеУпражнение по математике для класса 8 9.3 Решения на видео
Упражнение по математике для класса 8 9.3 Решения в видео Упражнение по математике для класса 8 9.3 ОбъяснениеМатематическое упражнение для класса 8
Упражнение по математике для класса 8 9.4 Решение Упражнение по математике для класса 8 9.4 ПояснениеУпражнение по математике для класса 9.5 Решения на видео
Упражнение по математике для 8-го класса 9.2]= 6400 — 4
= 6396
В главе 9 «Алгебраические выражения и тождества» мы должны узнать о таких фундаментальных терминах, как множители, коэффициенты, моном, бином, бином, трехчлен и все другие полиномы, как и в других полиномах, в алгебраических терминах. выражение, сложения и вычитания выражений, оставляя похожие термины в сторону. Умножение двух или трех одночленов и умножение одночлена или двучлена на многочлен. Упрощение различных многочленов с использованием различных тождеств.Ниже приведены некоторые стандартные идентификаторы:
1. (a — b) ² = a² — 2ab + b²
2. (a + b) ² = a² + 2ab + b²
3. (a + b) (a — b) ) = a² — b²
Знаете ли вы?
Чтобы факторизовать или упростить любое алгебраическое выражение, требуются общие тождества. Принятие общего помогает сделать множители выражений и упростить множители двух. Чтобы понять алгебраическое выражение в простейшей форме, мы должны помнить почти все тождества.
Извините! — Страница не найдена
Пока мы разбираемся, возможно, поможет одна из ссылок ниже.
Дом Назад- Класс
- Онлайн-тесты
- Ускоренный онлайн-курс JEE
- Двухлетний курс для JEE 2021
- Класс
- Онлайн-курс NEET
- Серия онлайн-тестов
- Фонд Калифорнии
- CA Средний
- CA Финал
- Программа CS
- Класс
- Серия испытаний
- Книги и материалы
- Тестовый зал
- Умный взломщик BBA
- Обучение в классе
- Онлайн-коучинг
- Серия испытаний
- Умный взломщик IPM
- Книги и материалы
- GD-PI
- CBSE, класс 8
- CBSE, класс 9
- CBSE, класс 10
- CBSE, класс 11
- CBSE, класс 12
- Обучение в классе
- Онлайн-классы CAT
- Серия испытаний CAT
- MBA Жилой
- Умный взломщик CAT
- Книги и материалы
- Онлайн-классы без CAT
- Серия испытаний без CAT
- Тестовый зал
- GD-PI
- Обучение в классе
- Серия испытаний
- Интервью с Civils
- Класс
- Онлайн-классы
- Серия испытаний SSC
- Переписка
- Практические тесты
- Электронные книги SSC
- SSC JE Study Package
- Класс
- RBI класс B
- Банковский тест серии
- Переписка
- Банковские электронные книги
- Банк ПДП
- Онлайн-коучинг
- Обучение в классе
- Серия испытаний
- Книги и материалы
- Класс
- Программа моста GRE
- GMAT Онлайн-коучинг
- Консультации при приеме
- GMAT Обучение в классе
- Стажировка
- Корпоративные программы
- Студенты колледжа
- Рабочие специалисты
- Колледжи
- Школы
Математика для 8 классов — Sirius Education Solutions
Обновлен с большей практикой STAAR!
8 класс Математика
STAAR Подготовка и практика
8 класс по математике обеспечивает систематический и всесторонний охват 13 TEKS готовности, которые составляют 60-65% теста STAAR.Каждый урок содержит пошаговые интерактивные примеры, инструкции по решению тестовых вопросов STAAR и обширную практику STAAR с более чем 490 вопросами и более чем 290 уникальными типами задач. В программе:
- Успех поддержки: Одна или несколько страниц тестовых заданий STAAR для каждого из 27 вспомогательных TEKS
- Совокупный обзор: Смешанный обзор готовности TEKS
- Стратегии сдачи теста STAAR: Интерактивный урок с 3 ключевые стратегии
- Графические калькуляторы: Интерактивный урок о том, когда и как использовать графический калькулятор для теста STAAR
- Great Griddables: Интерактивный урок о том, как заполнить сетки свободного отклика, чтобы избежать небрежных ошибок
- Глоссарий: Основные термины, которые должны будут знать учащиеся
8-й класс Математика для учителя №
Этот полноцветный TE с спиральным переплетом предоставляет полные решения для каждого элемента практики STAAR и примечания на полях для учителей / репетиторов.В Руководстве по заданиям показан порядок возрастания сложности, и каждый вопрос включает название проблемы, процесс TEKS и уровень DOK.
Также доступны…
Зингер по математике для 8-го класса: ответы на самые пропущенные задания теста STAAR
Zingers помогает всем учащимся научиться решать самые сложные тестовые задания. Zinger легко внедряется в различных условиях и обеспечивает комплексные инструкции и практику, а также позволяет учащимся правильно отвечать на сложные вопросы.Используйте Zinger для разминки, разминки и интенсивной подготовки непосредственно перед тестом STAAR.
Практические тесты по математике для 8 класса
Предоставляет два отдельных полноразмерных буклета с тестами — Форма A и Форма B — которые соответствуют плану и опубликованным тестам STAAR. Также включены листы с ответами учащихся (пузырьковые листы) и версия для учителя с полными решениями для каждого элемента теста, чтобы учителя могли дать учащимся содержательные отзывы.
SE: G8MSE, 236 стр .; TE: G8MTE, 208 стр .; Практические тесты: G8MPT; Зингеры: G8MZ
Сопутствующие товары
целей 8-го класса — проект Connected Mathematics
Goals 8 класса — Connected Mathematics Project Переключить специальные возможности- Дом
- Математика
- Математические цели по единицам
- Цели 8-го класса
Мышление с помощью математических моделей
Линейные и нелинейные отношения:
Распознавайте и моделируйте закономерности в двумерных данных.- Представляйте шаблоны данных с помощью графиков, таблиц, описаний слов и алгебраических выражений
- Изучить природу линейных функций в контексте
- Используйте математические модели, чтобы ответить на вопросы о линейных отношениях
- Записывать линейные функции на основе словесной, числовой или графической информации
- Анализировать и решать линейные уравнения
- Модельные ситуации с неравенством, выраженным как «максимум» и «как минимум»
- Изучить природу обратной вариации в контекстах
- Используйте математические модели, чтобы ответить на вопросы об обратных зависимостях вариации
- Сравнить обратную зависимость вариации с линейной зависимостью
Анализ данных:
Измерьте разброс данных и силу связи в двумерных данных.- Используйте данные для прогнозов
- Подгоните линию к данным, которые показывают линейный тренд, и измерьте точность подбора
- Анализировать графики разброса двумерных данных для определения силы линейной связи между двумя переменными
- Неформально используйте коэффициенты корреляции для описания силы линейной связи, проиллюстрированной диаграммами разброса
- Используйте стандартное отклонение для измерения изменчивости в одномерном распределении
- Различать категориальные и числовые переменные
- Используйте двусторонние таблицы и анализ частот ячеек и относительных частот, чтобы решить, связаны ли две переменные
В поисках Пифагора
Теорема Пифагора:
Поймите и примените теорему Пифагора.- Разработайте стратегии для определения расстояния между двумя точками на координатной сетке
- Объясните доказательство теоремы Пифагора
- Используйте теорему Пифагора и ее обратную теорему для решения множества задач
- Используйте теорему Пифагора, чтобы найти уравнение круга с центром в начале координат
Действительные числа:
Поймите, что набор действительных чисел состоит из рациональных и иррациональных чисел.- Интерпретация квадратных корней и кубических корней из чисел, используя соответствующие геометрические представления
- Отнесите площадь квадрата к длине стороны квадрата
- Оценить значения квадратных корней
- Оценить значения кубических корней
- Соотнесите объем куба с длиной ребра куба
- Сравните числа, которые могут быть представлены как дроби (рациональные числа), с числами, которые не могут быть представлены как дроби (иррациональные числа), и поймите, что набор действительных чисел состоит из рациональных и иррациональных чисел
- Представлять рациональные числа в виде дробей и завершающих десятичных знаков или повторяющихся десятичных знаков
- Признать, что иррациональные числа не могут быть представлены в виде дробей и представляют собой неповторяющиеся десятичные дроби
- Признайте, что квадратный корень из целого числа, не являющегося квадратом, является иррациональным
- Найдите иррациональные числа на числовой строке
- Использование и понимание свойств рациональных и иррациональных чисел
Рост, рост, рост
Экспоненциальные функции:
Изучите проблемные ситуации, в которых две или более переменных имеют экспоненциальную связь друг с другом.- Определите ситуации, которые можно смоделировать с помощью экспоненциальной функции
- Определите характер изменения (фактор роста / спада) между двумя переменными, которые представляют экспоненциальную функцию в ситуации, таблице, графике или уравнении
- Представьте экспоненциальную функцию таблицей, графиком или уравнением
- Установите связи между схемами изменения в таблице, графике и уравнении экспоненциальной функции
- Сравните скорость роста / спада и коэффициент роста / спада для экспоненциальной функции и узнайте роль, которую каждый играет в экспоненциальной ситуации
- Определите коэффициент роста / спада и начальное значение в проблемных ситуациях, в таблицах, графиках и уравнениях, которые представляют экспоненциальные функции
- Определите, представляет ли экспоненциальная функция модель роста (увеличения) или убывания (убывания) с помощью уравнения, таблицы или графика, представляющего экспоненциальную функцию
- Определите значения независимых и зависимых переменных из таблицы, графика или уравнения экспоненциальной функции
- Используйте экспоненциальное уравнение для описания графика и таблицы экспоненциальной функции
- Предсказать точку пересечения оси Y из уравнения, графика или таблицы, представляющей экспоненциальную функцию
- Интерпретировать информацию о том, что точка пересечения оси Y экспоненциальной функции представляет
- Определите влияние фактора роста и начального значения экспоненциальной функции на график функции
- Решайте задачи об экспоненциальном росте и затухании в различных предметных областях, включая науку и бизнес, используя уравнение, таблицу или график
- Обратите внимание, что одно экспоненциальное уравнение может моделировать разные контексты
- Сравните экспоненциальные и линейные функции
Эквивалентность:
Развивайте понимание эквивалентных экспоненциальных выражений.- Написать и интерпретировать экспоненциальные выражения, которые представляют зависимую переменную в экспоненциальной функции
- Разработайте правила работы с рациональными показателями и объясните, почему они работают
- Записывать, интерпретировать и оперировать числовыми выражениями в экспоненциальном представлении
- ритуал и интерпретировал эквивалентные выражения, используя правила для экспонент и операций
- Решать задачи, связанные с показателями, включая научную нотацию
Бабочки, вертушки и обои
Преобразования:
Опишите типы преобразований, которые связывают точки движениями отражений, вращений и перемещений; и методы идентификации и создания симметричных плоских фигур.- Распознать свойства преобразований отражения, поворота и смещения
- Изучите методы использования преобразований жесткого движения для создания симметричных конструкций
- Использовать правила координат для основных преобразований жесткого движения
Конгруэнтность и сходство:
Поймите соответствие и сходство и исследуйте необходимые и достаточные условия для установления конгруэнтных и похожих форм.- Признать, что две фигуры совпадают, если одна получена из другой последовательностью преобразований отражения, вращения и / или переноса
- Признать, что две фигуры похожи, если одна может быть получена из другой последовательностью отражений, вращений, перемещений и / или растяжений
- Используйте преобразования, чтобы описать последовательность, которая демонстрирует соответствие между фигурами
- Используйте преобразования, чтобы изучить минимальные условия измерения для установления соответствия треугольников
- Используйте преобразования, чтобы изучить минимальные условия измерения для установления подобия треугольников
- Связать свойства углов, образованных параллельными прямыми и поперечными линиями, и сумму углов в любом треугольнике со свойствами преобразований
- Использование свойств совпадающих и подобных треугольников для решения задач о формах и размерах
Скажи это символами
Эквивалентность:
Развивайте понимание эквивалентных выражений и уравнений.- Модельные ситуации с символическими высказываниями
- Распознавать, когда два или более символических утверждения представляют один и тот же контекст
- Используйте свойства действительных чисел, например распределительное свойство для записи эквивалентных выражений
- Определить, эквивалентны ли различные символьные выражения математически
- Интерпретировать эквивалентные выражения информации, представленные в данном контексте
- Определить, какое эквивалентное выражение или уравнение использовать для ответа на конкретные вопросы или принятия решений
- Опишите взаимосвязь между объемами цилиндров, конусов и сфер, имеющих одинаковую высоту и радиус, с помощью алгебраических уравнений
- Решите линейные уравнения в скобках
- Определите, имеет ли уравнение конечное число, бесконечное число или полное отсутствие решений
- Развивайте понимание и некоторую беглость с помощью факторизации квадратичных выражений
- Решите квадратные уравнения, разложив на множители
- Уметь узнавать, как и когда использовать символы для отображения взаимосвязей, обобщений и доказательств
Функции:
Развивайте понимание конкретных функций, таких как линейные, экспоненциальные и квадратичные функции.- Развивать навыки определения и представления отношений, выраженных в проблемных контекстах с соответствующими функциями, и использовать эти отношения для решения проблемы
- Проанализировать уравнения, чтобы определить закономерности изменений в таблицах и графиках, которые представляет уравнение
- Свяжите части символьного утверждения или выражения с базовыми свойствами отношения и с контекстом проблемы
- Определите характеристики графика (точки пересечения, максимумы и минимумы, форму и т. Д.)) уравнения, глядя на его символическое представление
Это в системе
Linear Equations:
Развивайте понимание линейных уравнений и систем линейных уравнений.- Распознать линейные уравнения с двумя переменными в стандартной форме, Ax + By = C
- Признайте, что линейное уравнение в форме Ax + By = C имеет бесконечно много решений ( x , y ), и график этих решений всегда представляет собой прямую линию
- Признайте, что форма линейных уравнений Ax + By = C эквивалентна форме y = mx + b для линейных уравнений
- Продолжить развитие навыков решения линейного уравнения с двумя переменными графическими и алгебраическими методами
- Признать, что решение системы линейных уравнений — это нахождение значений переменных, которые будут одновременно удовлетворять всем уравнениям в системе
- Развить навыки решения систем линейных уравнений графическими и алгебраическими методами, в частности:
- Графические решения отдельных уравнений
- Запись уравнений системы в эквиваленте y = mx + b form
- Использование линейных комбинаций уравнений системы для исключения одной переменной
- Признать, что системы линейных уравнений в for могут иметь
- Ровно одно решение, представленное точкой (точками) пересечения линий, представленных уравнениями;
- Бесконечно много решений, представленных одной линией, представляющей каждое уравнение; или
- Нет решений, что представлено двумя параллельными линиями
- Стратегический выбор графических и символьных методов для использования в конкретной системе линейных уравнений
- Овладеть навыками работы с символами при решении систем линейных уравнений
- Решите простую систему, состоящую из линейного уравнения и квадратного уравнения с двумя переменными, символически и графически
- Решать задачи, связанные с системами линейных уравнений
Linear Inequalities:
Развивайте понимание графических и символических методов решения линейных неравенств с одной и двумя переменными.- Распознавать различия между строгим <и инклюзивным ≤ неравенством
- Продолжить развитие навыков решения линейного неравенства двух переменных графическими и алгебраическими методами
- Умение решать системы линейных неравенств графическими и символическими методами, в частности:
- Построение графика решений каждого отдельного неравенства и нахождение области возможных точек, удовлетворяющих обоим неравенствам
- Решая неравенства, чтобы найти пары чисел, удовлетворяющие обоим неравенствам
- Стратегический выбор из графических и символических методов, которые следует использовать для конкретной системы линейных неравенств
NCERT для математики класса 8 Глава 9 Алгебраические выражения и идентичности
Подпишитесь на обновленияПолучить здесь NCERT Solutions for Class 8 Maths Chapter 9 .Эти решения NCERT для 8-го класса математики включают подробные ответы на все вопросы главы 9 — Алгебраические выражения и идентичности , приведенные в книге NCERT , которая предписана для 8-го класса в школах.
Ресурс: Решения Национального совета образовательных исследований и обучения (NCERT)
Класс: 8-й класс
Предмет: математика
Глава: Глава 9 — Алгебраические выражения и идентичности
Решения NCERT для математики 8 класса Глава 9 Алгебраические выражения и идентичности
Подписаться на последние обновления
Выберите StateAndaman & NicobarAndhra PradeshArunachal PradeshAssamBiharChandigarhChhattisgarhDadra & Нагар HaveliDaman & DiuDelhiGoaGujaratHaryanaHimachal PradeshJammu & KashmirJharkhandKarnatakaKeralaLadakhLakshadweepMadhya PradeshMaharashtraManipurMeghalayaMizoramNagalandOdishaPuducherryPunjabRajasthanSikkimTamil NaduTelanganaTripuraUttar PradeshUttarakhandWest Бенгальский
Математика класса VIII Глава 9 Алгебраические выражения и тождества Решение NCERT приведено ниже.
| «Предыдущее | Следующая » |
Решения NCERT для математики класса 8 Все главы
- Подписка на обновления
Стипендия в размере 15 лакхов
Последний срок: Прием в BVP Pune 2021
- Глава 1 Рациональные числа
- Глава 2 Линейные уравнения с одной переменной
- Глава 3 Что такое четырехугольники
- Глава 4 Практическая геометрия
- Глава 5 Обработка данных
- Глава 6 Квадраты и квадратные корни
- Глава 7 Кубики и кубические корни
- Глава 8 Сравнение количеств
- Глава 9 Алгебраические выражения и тождества
- Глава 10 Визуализация твердых форм
- Глава 11 Измерение
- Глава 12 Показатели и полномочия
- Глава 13 Прямые и обратные пропорции
- Глава 14 Факторизация
- Глава 15 Введение в графики
- Глава 16 Игра с числами
Мы надеемся, что наши решения NCERT для математики 8 класса помогли вам в учебе! Если вам понравились наши решения NCERT для математики 8-го класса, поделитесь этим постом.
Решения NCERT для всех субъектов класса 8
| Математика | Английский |
| Наука | Хинди |
| Социальные науки | Санскрит |
Математические решения для 8-го класса
Чтобы получать оповещения об экзаменах и вакансиях в правительстве Индии в кратчайшие сроки, присоединяйтесь к нашему каналу Telegram.
Теги: Алгебраические выражения и идентичности Решения NCERT Решения CBSE по математике класса 8 Решения по математике CBSE класса VII Решения ICBSE класса 8 Ответы по математике CBSEРешения по математике класса 8Книжные решения по классу VIIIFee Решения NCERTМатематика Решения NCERT Класс 8Решения NCERTКниги NCERT Решения NCERT для класса 8 Решения NCERT для классов Решения NCERT для класса 8 Решения NCERT для классов Решения NCERT 8 MathsNCERT Решения для математики 8-го класса Глава 9 .
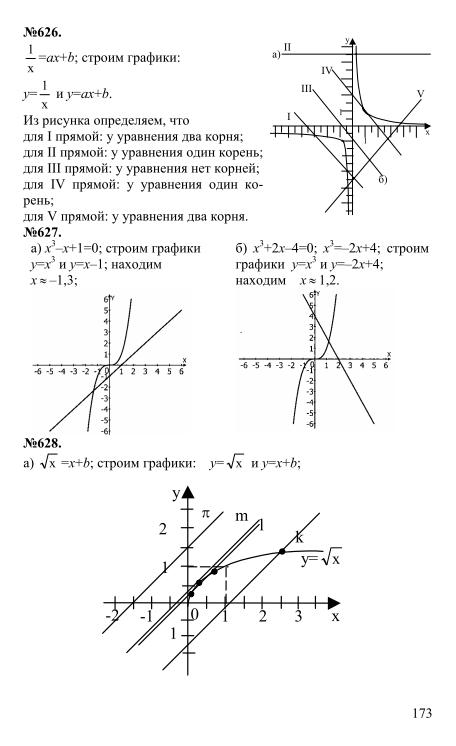 Взаимно простые числа
Взаимно простые числа Свойства неравенств одинакового смысла
Свойства неравенств одинакового смысла


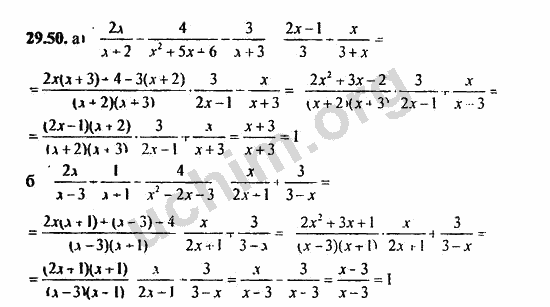 Выход – подбадривать ребенка. Фото: скриншот
Выход – подбадривать ребенка. Фото: скриншот