Конспект «Краткий курс геометрии 8 класс»
«Краткий курс геометрии 8 класс»
«Краткий курс геометрии 8 класс» — это краткие теоретические сведения по курсу геометрии за 8 класс (определения, теоремы, основные свойства). Цитаты взяты в учебных целях из пособия «Геометрия: задачи на готовых чертежах для подготовки к ОГЭ и ЕГЭ (базовый уровень): 8 класс / Э.Н.Бабаян. — Ростов н/Д: Феникс.
Планиметрия
☑ 1. Многоугольник
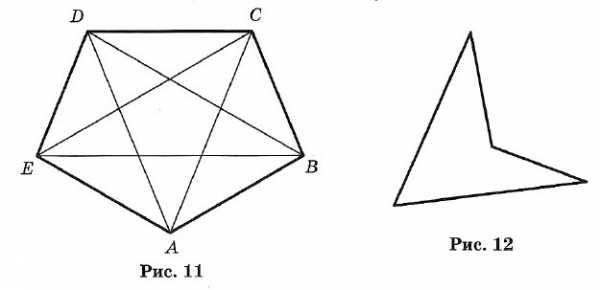
ABCDE — пятиугольник (рис. 11). Точки А, В, С, D, Е — вершины многоугольника; ∠A, ∠B, ∠C, ∠D, ∠E — углы; АВ, ВС, CD и т. д. — стороны; отрезки АС, AD, BE, BD, СЕ — диагонали; Р = АВ + ВС + … + ЕА — периметр многоугольника.
Многоугольник называется выпуклым (см. рис. 11), если он целиком расположен по одну сторону от каждой прямой, проходящей через две его соседние вершины. В противном случае многоугольник называется невыпуклым (рис. 12).
Свойства
1. Сумма внутренних углов произвольного n-угольника равна 180° • (n — 2).
3. В выпуклом n-угольнике из каждой вершины можно провести (n — 3) диагоналей, которые разбивают n-угольник на (n — 2) треугольников.
4. В выпуклом n-угольнике число диагоналей равно n(n — 3)/2.
☑ 2. Правильные многоугольники
Выпуклый многоугольник, у которого равны все углы и стороны, называется правильным.
Свойства
1. Каждый угол правильного n-угольника равен аn = 180°(n — 2)/n
2. Около правильного n-угольника можно описать окружность, и притом только одну.
3. В правильный n-угольник можно вписать окружность, и притом только одну.
4. Окружность, вписанная в правильный n-угольник, касается всех сторон n-угольника в их серединах.
5. Центр окружности, описанной около правильного n-угольника, совпадает с центром окружности, вписанной в тот же n-угольник.
6. Длина стороны правильного n-угольника, вписанного в окружность радиуса R, равна а = 2R sin(180°/n).
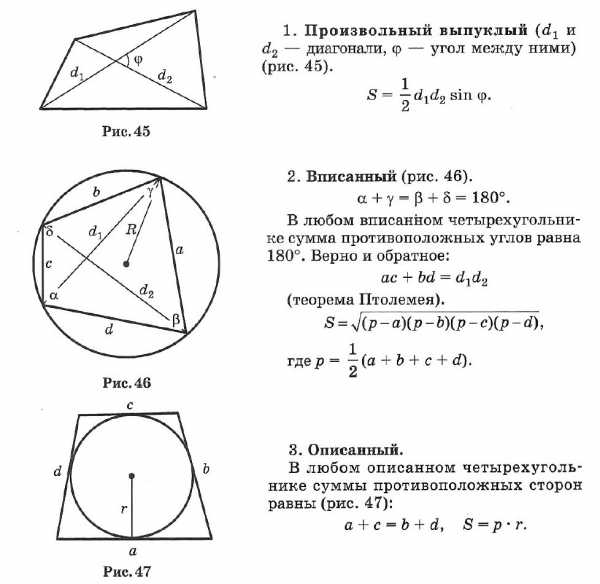
☑ 3. Четырехугольник
☑ 4. Параллелограмм
Признаки параллелограмма (рис. 48)
- Если в четырехугольнике две стороны равны и параллельны (АВ = DC, АВ || CD), то такой четырехугольник — параллелограмм.
- Если в четырехугольнике противоположные стороны попарно равны (АВ = DC, AD = DC), то такой четырехугольник — параллелограмм.
- Если в четырехугольнике противоположные углы попарно равны (∠A = ∠C; ∠B = ∠D), то такой четырехугольник — параллелограмм.
- Если в четырехугольнике диагонали пересекаются и в точке пересечения делятся пополам, то такой четырехугольник — параллелограмм.
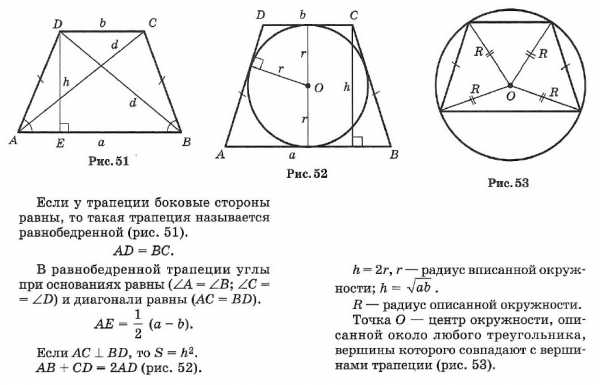
☑ 5. Трапеция

Равнобедренная трапеция

Прямоугольная трапеция
☑ 6. Прямоугольник
☑ 7. Ромб

☑ 8. Квадрат
☑ 9. Теорема Чевы
☑ 10. Теорема Менедая
☑ 11. Теорема синусов
☑ 12. Теорема косинусов
☑ 13. Площадь треугольника

☑ 14. Площадь многоугольников
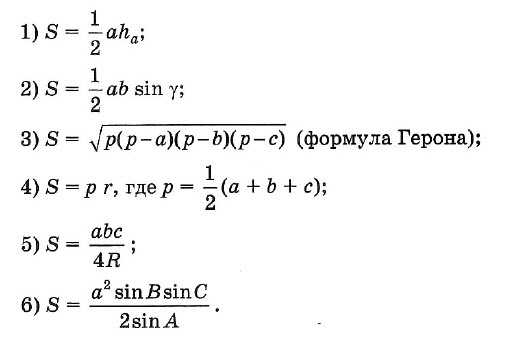
☑ 15. Равносторонний (правильный) треугольник

☑ 16. Подобные треугольники
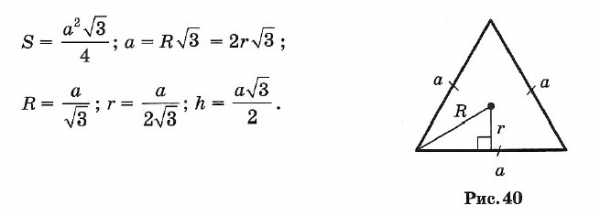
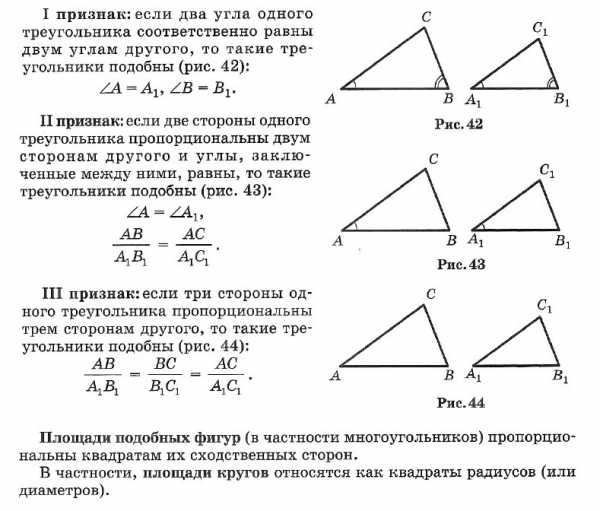
☑ 17. Признаки подобия треугольников
☑ 18. Окружность
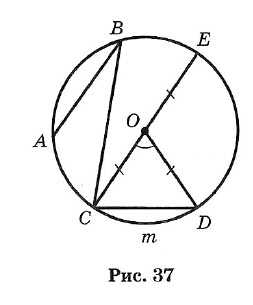
 Окружностью называется геометрическое место точек плоскости, равноудаленных от одной ее точки (центра) (рис. 37).
Окружностью называется геометрическое место точек плоскости, равноудаленных от одной ее точки (центра) (рис. 37).
На рисунке ОС = ОЕ = OD = R.
Часть окружности (например, CmD) называется дугой.
Отрезок, соединяющий две точки окружности, называется хордой, а хорда, проходящая через центр, — диаметром.
АВ, ВС, CD и СЕ — хорды окружности. СЕ — наибольшая из хорд — диаметр.
Обозначение: d или D. D = 2R.
Часть плоскости, ограниченная окружностью, называется кругом.
Часть круга, ограниченная дугой (CmD) и стягивающей ее хордой (CD), называется сегментом.
Часть круга, ограниченная двумя радиусами и дугой, называется сектором.
Угол, образованный двумя радиусами, называется центральным (∠COD на рис. 37).
Угол, у которого вершина лежит на окружности, а стороны являются хордами, называется вписанным (например, ∠ABC).
☑ 19. Свойства касательных к окружности
Угол, образованный двумя касательными (СА и СВ), исходящими из одной точки, называется описанным (∠ACB на рис. 38).
2. Две касательные, проведенные к окружности из одной точки, равны, и центр окружности лежит на биссектрисе угла между ними.
☑ 20. Окружность и треугольник
1. Около всякого треугольника можно описать окружность; центром окружности является точка пересечения перпендикуляров, проведенных к сторонам через их середины (рис. 39).
2. Во всякий треугольник можно вписать окружность; центром окружности является точка пересечения биссектрис (рис. 40).
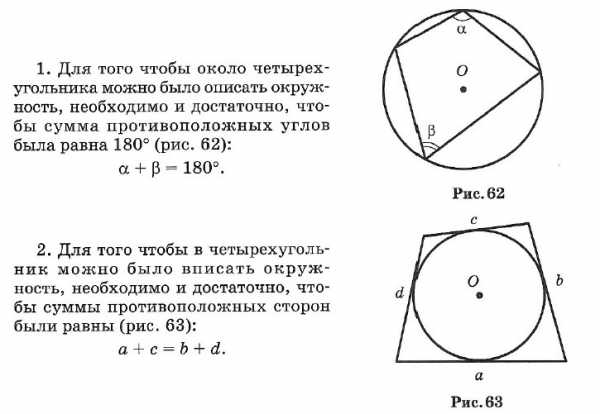
☑ 21. Окружность и четырехугольник
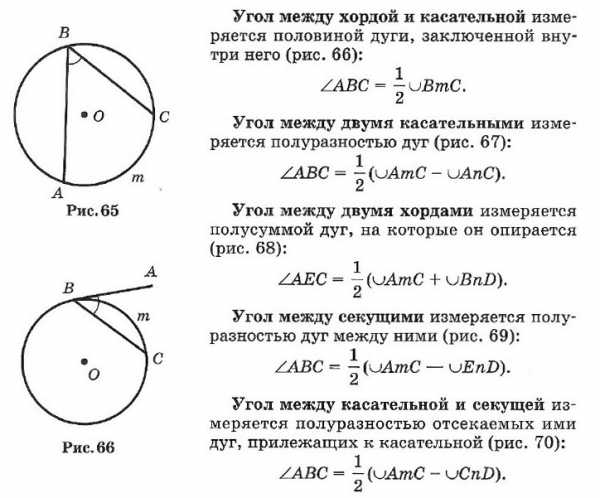
☑ 22. Углы и окружность

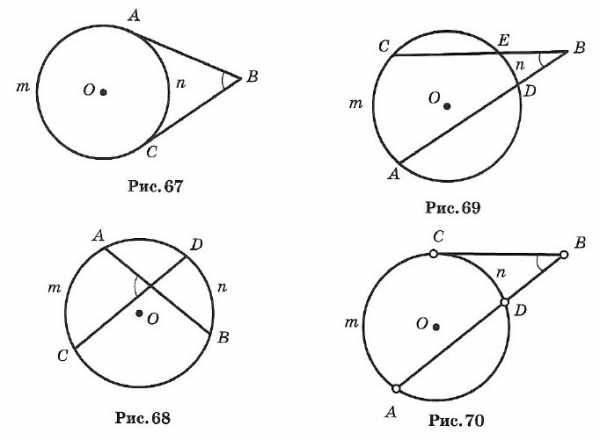
☑ 23. Метрические соотношения в окружности
☑ 24. Длина окружности. Площадь круга и его частей
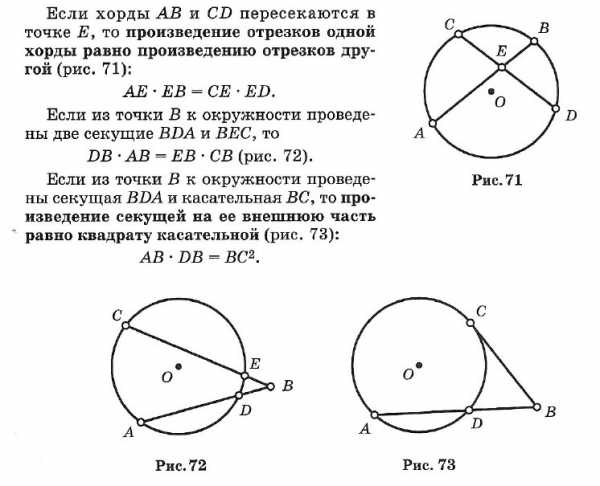
☑ 25. Уравнение окружности

Вы смотрели «Краткий курс геометрии 8 класс» — все определения, теоремы и основные свойства из Геометрии за 8 класс. Выберите дальнейшие действия:
uchitel.pro
Решение базовых задач. Видеоурок. Геометрия 8 Класс
В ходе данного урока мы рассмотрим решение базовых задач с применением теоремы Пифагора, научимся находить стороны прямоугольного треугольника и доказывать, что данный треугольник является (либо не является) прямоугольным.
Найти гипотенузу прямоугольного треугольника с катетами и .
Дано: ; . , .
Найти: .
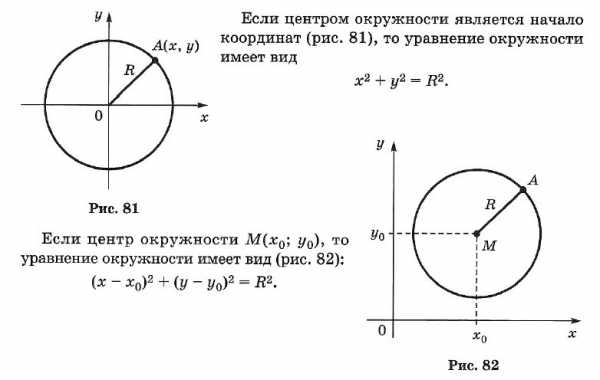
Рис. 1. Прямоугольный треугольник
Решение
Поскольку – прямоугольный, можем воспользоваться теоремой Пифагора.
Так как существует вариант, что , то берем во внимание, что длина стороны – число положительное.
Ответ: .
Является ли прямоугольным треугольник со сторонами , , ?
Дано: . , , .
Определить: – прямоугольный треугольник?
Решение
Обратим внимание, что если является прямоугольным, то прямой угол будет самым большим углом этого треугольника. А значит, напротив него будет лежать самая большая сторона. А сторона, которая лежит напротив большого угла называется гипотенузой. Допустим, что – гипотенуза. И пусть предположительно прямоугольный. Тогда сможем применить теорему Пифагора.
25 = 4 + 16
25 ¹ 20
А это значит, что не является прямоугольным.
Ответ: не является прямоугольным.
На рис. 2 на клетчатой бумаге поставлены точки , и (в узлах сетки). Найдите длины отрезков , и и определите, является ли прямоугольным треугольник .
Рис. 2. Точки , и
Решение
Две клеточки – 1 единица измерения.
По условию задачи, нет прямоугольного треугольника. Но на клетчатой бумаге есть маленькие квадратики, а у них – прямых угла. Этим и воспользуемся, сделав сами прямоугольный треугольник.a) Проведем по вертикали вверх от точки линию до пересечения с горизонтальной линией от точки , отметим пересечение (рис. 3) – получим прямоугольный треугольник . – гипотенуза. По теореме Пифагора, .
Рис. 3. Построение точки
Так как рисунок выполнен на клеточной бумаге, то мы можем просто посчитать длину сторон . ; .
Аналогично найдем через пересечения вертикали от точки и горизонтали от точки , обозначив (рис. 4).
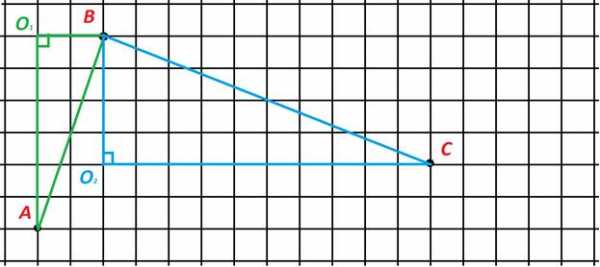
Рис. 4. Построение точки
Запишем для , по теореме Пифагора, .
Также найдем .
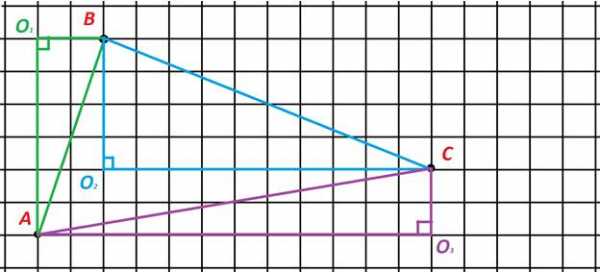
Рис. 5. Построение отрезка
Для : .
Б) – прямоугольный?
, ,
Найдем наибольшую сторону. Это сторона . Предположим, что – прямоугольный. – гипотенуза. Тогда, по теореме Пифагора, .
37 = 29 + 10
37 ¹ 39
Таким образом, – не прямоугольный.
Ответ: , , , – не прямоугольный.
Вывод
На данном уроке мы рассмотрели решение базовых задач с использованием теоремы Пифагора.
Список рекомендованной литературы
- Александров А.Д. и др. Геометрия, 8 класс. – М.: Просвещение, 2006.
- Учебник “Геометрия, 7-9”, авт. Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.
- Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрия, 8 класс. – М.: Просвещение, 2011.
- Мерзляк А.Г., Полонский В.Б., Якир С.М. Геометрия, 8 класс. – М.: ВЕНТАНА-ГРАФ, 2009.
Рекомендованные ссылки на ресурсы сети Интернет
- Festival.1september.ru (Источник).
- Festival.1september.ru (Источник).
- 5klass.net (Источник).
Рекомендованное домашнее задание
- Найти гипотенузу , если , – катеты, см, см.
- Необходимо обнести забором участок, имеющий форму прямоугольного треугольника с катетами м и м. Как найти длину этой изгороди?
interneturok.ru
ГДЗ и решебники Геометрия 8 класс
Геометрия является одним из самых сложных дисциплин в школе. Домашняя подготовка к данному уроку занимает массу времени. Если для учеников, которым легко даются точные науки, геометрия – не проблема, то другим школьникам дисциплина невероятно трудна и непонятна. Получается, что из-за оценок по этому предмету страдает вся успеваемость. Но решебник по геометрии, 8 класс, поможет справиться с данной проблемой. Сверяя полученные ответы и пользуясь типичным алгоритмом решений заданий, точная наука вас больше не будет страшить.
Решебник, геометрия, 8 класс – удобный поиск и моментальный доступ
Все ГДЗ, которые находятся на сайте отличаются проверенными данными и достоверными решениями. Возможность ошибки сразу исключается, поэтому за правильный ответ задачи вы можете быть уверены.
Годовые домашние задания просты в использовании. Достаточно найти решебник с нужным автором, затем зайти в темы, параграфы и выбрать конкретный номер задания. Это занимает минимальное количество времени. Достаточно несколько движений руки и вы уже списываете готовое решение.
Онлайн-решебник позволяет использовать пособие не только дома за компьютером, но также на уроке или на перемене в мобильной версии. Типовые задачи позволяют запомнить порядок действий упражнений и применять их во время работы в классе. Поверьте, что решебник обязательно даст положительные результаты в нелегкой учебе школьника.
Решебник по геометрии 8 помогает закрепить знания
Если вы думаете, что пособие предназначено только для автоматического списывания решений, то слишком ошибаетесь. Грамотное использование ребешника позволяет укреплять пройденный материал с помощью выполнения типичных заданий. Ученик сможет самостоятельно делать задания, опираясь на помощника в виде решебника. Уверенность в правильности домашних заданий помогает ребенку почувствовать себя знающим в данной дисциплине.
Каким образом происходит контроль знаний с помощью ГДЗ?
- Вы сможете всегда проверить правильность выполнения домашнего задания благодаря ГДЗ 8, геометрия.
- Будут исключены недочеты и маленькие ошибки, так как правильный алгоритм действий всегда перед вами.
- Если возникнет затруднительная или спорная ситуация в решении, то всегда можно заглянуть в ГДЗ.
Таким образом, ответ на любую задачу по геометрии для восьмого класса будет при вас.
Геометрия, 8 класс, решебник — понятен детям и взрослым
Благодаря готовым домашним заданиям родители могут контролировать своих детей. Как это происходит? Попросите своего ребенка выполнить домашнюю работу, а затем проверьте правильность по решебнику. Если подростку трудно это сделать, то помогите ему, используя подсказки-пособия.
Совместное выполнение домашней работы не только вас сблизит с ребенком, но также повлияет на его успеваемость в школе. Если вы доверяете своему сыну или дочке, то позвольте ему использовать самостоятельно ГДЗ. Сознательный ребенок не будет решения бездумно списывать, а разберется в алгоритме действий.
www.obozrevatel.com
ГДЗ по Геометрии 8 класс от гдзометр
- 1 Класс
- Математика
- Русский язык
- Английский язык
- Информатика
- Литература
- Человек и мир
- Окружающий мир
- Музыка
- 2 Класс
- Математика
- Русский язык
- Белорусский язык
- Английский язык
- Информатика
- Немецкий язык
- Литература
- Человек и мир
- Окружающий мир
- Музыка
- Технология
- 3 Класс
- Математика
- Русский язык
- Белорусский язык
- Английский язык
- Информатика
- Немецкий язык
- Литература
- Человек и мир
- Окружающий мир
- Музыка
- Испанский язык
- 4 Класс
- Математика
- Русский язык
- Белорусский язык
- Английский язык
- Информатика
- Немецкий язык
- Литература
- Человек и мир
- Окружающий мир
- Музыка
- Испанский язык
- 5 Класс
- Математика
- Русский язык
- Белорусский язык
- Английский язык
- Физика
- Биология
- Информатика
- У
gdzometr.com
ГДЗ по геометрии 8 класс
Геометрия 8 класс. Л.С.Атанасян
Автор: Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. Домашняя работа по геометрии за 8 класс.
Учебник: К учебнику «Геометрия, 7-9 класс». Учебник для общеобразовательных учреждений.
Издательство: М.: Просвещение, 2003-2012 год.
Ответы на вопросы к учебнику Л.С.Атанасян
Выберите из задачника номер упражнения, чтобы просмотреть решение.Глава V. Четырехугольники
§ 1. Многоугольники
§ 2. Параллелограм и трапеция
§ 3. Прямоугольник, ромб, квадрат
Глава VI. Площадь
§ 1. Площадь многоугольника
§ 2. Площади параллелограма, прямоугльника и трапеции
§ 3. Теорема Пифагора
Глава VII. Подобные треугольники
§ 1. Определение подобных треугольников
§ 2. Признаки подобия треугольников
§ 3. Применения подобия к доказательству теорем и решению задач
§ 4. Соотношения между сторонами и углами прямоугольного треугольника
Глава VIII. Окружность
§ 1. Касательные окружности
§ 2. Центральные и вписанные углы
§ 3. Четыре замечательные точки треугольника
§ 4. Вписанная и описанная окружности
Глава IX. Векторы
§ 1. Понятие вектора
§ 2. Сложение и вычитание векторов
§ 3. Умножение вектора на число. Применение векторов к решению задач
Учебник по геометрии Л.С. Атанасяна, крупнейшего отечественного математика, внесшего огромный вклад с советскую и российскую науку, давно стал настоящей классикой. В нем доступно и информативно излагается материал, предлагаются к решению задачи различной степени сложности. Занимаясь по нему системно, восьмиклассники с успехом осваивают премудрости подобия треугольников или же применения вектора для решения задач. Однако определенному проценту школьников изучение геометрии в 8 классе дается с трудом. Этому есть объективные причины. Возможно, был плохо усвоен материал предыдущего года или проявлено недобросовестное отношение к самостоятельным занятиям. Возможно и банальное – школьник является очевидным гуманитарием, которому любые точные науки в тягость.
Однако учиться надо и делать это нужно качественно, ведь учебный год закончится прохождением ГИА, куда геометрия входит в обязательном порядке. Предлагаем вниманию восьмиклассников онлайн решебник по геометрии 8 класса к учебнику Л.С. Атанасяна. Воспользовавшись им, можно еще раз изучить пройденный в классе материал, подробно рассмотреть разобранные на уроке задания, попробовать самостоятельно решить аналогичные.
Решебник – отличное сочетание теоретического и практического материала. На примере разбора задач можно проследить основной алгоритм из решения, опробовать его при работе над домашними упражнениями. На примере предлагаемых чертежей и схем можно понять логику построения изображений геометрических фигур и соотношений предметов, увидеть, что нужно и важно учитывать при решении тех или иных стереометрических задач.
Решебник станет «палочкой-выручалочкой» и для родителей. Давно позабыв премудрости геометрии, родным восьмиклассника фактически приходится изучать материал заново. Помочь в этом смогут ГДЗ. Контроль со стороны взрослых зачастую необходим, чтобы дети не просто списывали готовые решения, а попытались продумать, как был получен тот или иной ответ, какие были использованы методы и закономерности.
Незаменимыми ГДЗ по геометрии за 8 класс станут и при подготовке к ЕГЭ. Можно будет вернуться к пройденному материалу, еще раз уточнить забытые или непонятые детали, что поможет увеличить шансы на успешную сдачу единого государственного экзамена.
www.ggdz.ru


