Номер 415 — ГДЗ по Геометрии для 7-9 класса Учебник Атанасян, Позняк, Кадомцев, Бутузов (решебник)
Номер 415 — ГДЗ по Геометрии для 7-9 класса Учебник Атанасян, Позняк, Кадомцев, Бутузов (решебник) — GDZwowПерейти к содержанию
Search for:
Авторы: Атанасян Л. С., Позняк Э. Г., Кадомцев С. Б., Бутузов В.Ф.
Издательство: Просвещение
Тип: Учебник
Номера
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091929394959697989910010110210310410510610710810911011111211311411511611711811912012112212312412512612712812913013113213313413513613713813914014114214314414514614714814915015115215315415515615715815916016116216316416516616716816917017117217317417517617717817918018118218318418518618718818919019119219319419519619719819920020120220320420520620720820921021121221321421521621721821922022122222322422522622722822923023123223323423523623723823924024124224324424524624724824925025125225325425525625725825926026126226326426526626726826927027127227327427527627727827928028128228328428528628728828929029129229329429529629729829930030130230330430530630730830931031131231331431531631731831932032132232332432532632732832933033133233333433533633733833934034134234334434534634734834935035135235335435535635735835936036136236336436536636736836937037137237337437537637737837938038138238338438538638738838939039139239339439539639739839940040140240340440540640740840941041141241341441541641741841942042142242342442542642742842943043143243343443543643743843944044144244344444544644744844945045145245345445545645745845946046146246346446546646746846947047147247347447547647747847948048148248348448548648748848949049149249349449549649749849950050150250350450550650750850951051151251351451551651751851952052152252352452552652752852953053153253353453553653753853954054154254354454554654754854955055155255355455555655755855956056156256356456556656756856957057157257357457557657757857958058158258358458558658758858959059159259359459559659759859960060160260360460560660760860961061161261361461561661761861962062162262362462562662762862963063163263363463563663763863964064164264364464564664764864965065165265365465565665765865966066166266366466566666766866967067167267367467567667767867968068168268368468568668768868969069169269369469569669769869970070170270370470570670770870971071171271371471571671771871972072172272372472572672772872973073173273373473573673773873974074174274374474574674774874975075175275375475575675775875976076176276376476576676776876977077177277377477577677777877978078178278378478578678778878979079179279379479579679779879980080180280380480580680780880981081181281381481581681781881982082182282382482582682782882983083183283383483583683783883984084184284384484584684784884985085185285385485585685785885986086186286386486586686786886987087187287387487587687787887988088188288388488588688788888989089189289389489589689789889990090190290390490590690790890991091191291391491591691791891992092192292392492592692792892993093193293393493593693793893994094194294394494594694794894995095195295395495595695795895996096196296396496596696796896997097197297397497597697797897998098198298398498598698798898999099199299399499599699799899910001001100210031004100510061007100810091010101110121013101410151016101710181019102010211022102310241025102610271028102910301031103210331034103510361037103810391040104110421043104410451046104710481049105010511052105310541055105610571058105910601061106210631064106510661067106810691070107110721073107410751076107710781079108010811082108310841085108610871088108910901091109210931094109510961097109810991100110111021103110411051106110711081109111011111112111311141115111611171118111911201121112211231124112511261127112811291130113111321133113411351136113711381139114011411142114311441145114611471148114911501151115211531154115511561157115811591160116111621163116411651166116711681169117011711172117311741175117611771178117911801181118211831184118511861187118811891190119111921193119411951196119711981199120012011202120312041205120612071208120912101211121212131214121512161217121812191220122112221223122412251226122712281229123012311232123312341235123612371238123912401241124212431244124512461247124812491250125112521253125412551256125712581259126012611262126312641265126612671268126912701271127212731274127512761277127812791280128112821283128412851286128712881289129012911292129312941295129612971298129913001301130213031304130513061307130813091310
Вопросы для повторения
Глава 1
123456789101112131415161718192021
Глава 2
123456789101112131415161718192021
Глава 3
123456789101112131415
Глава 4
1234567891011121314151617181920
Глава 5
1234567891011121314151617181920
Глава 6
12345678910
Глава 7
123456789101112131415161718
Глава 8
1234567891011121314151617181920212223242526
Глава 9
1234567891011121314151617181920
Глава 10
123456789101112131415161718192021
Глава 11
123456789101112131415161718192021
Глава 12
123456789101112
Глава 13
1234567891011121314151617
Глава 14
1234567891011121314151617181920212223242526
Adblockdetector
Геометрия 8 класс Атанасян Задачи 399-423
Упражнения 399 — 423 из учебника «Геометрия 8 класс.
УМК Атанасян» с ответами и решениями. Глава 5. Четырёхугольники. § 3. Прямоугольник, ромб, квадрат (46. Прямоугольник. 47. Ромб и квадрат. 48. Осевая и центральная симметрии). Геометрия 8 класс Атанасян Задачи 399-423 + ОТВЕТЫ.
Вернуться в ОГЛАВЛЕНИЕ учебника
Нажмите на спойлер, чтобы посмотреть ответ на задание.
Задача № 399. □ Докажите, что параллелограмм, один из углов которого прямой, является прямоугольником.
Смотреть решение задачи № 399
Задача № 400. □ Докажите, что если в четырёхугольнике все углы прямые, то четырёхугольник — прямоугольник.
Смотреть решение задачи № 400
Задача № 401. Найдите периметр прямоугольника ABCD, если биссектриса угла А делит сторону: а) ВС на отрезки 45,6 см и 7,85 см; б) DC на отрезки 2,7 дм и 4,5 дм.
Смотреть решение задачи № 401
Задача № 402. □ Диагонали прямоугольника ABCD пересекаются в точке О. Докажите, что треугольники AOD и АОВ равнобедренные.
Смотреть решение задачи № 402
Задача № 403. В прямоугольнике ABCD диагонали пересекаются в точке О. Найдите периметр треугольника АОВ, если ∠CAD = 30°, АС = 12 см.
Смотреть решение задачи № 403
Задача № 404. □ Докажите, что медиана прямоугольного треугольника, проведённая к гипотенузе, равна половине гипотенузы.
Смотреть решение задачи № 404
Задача № 405. □ В ромбе одна из диагоналей равна стороне. Найдите: а) углы ромба; б) углы, которые диагонали ромба образуют с его сторонами.
Смотреть решение задачи № 405
Задача № 406. Найдите периметр ромба ABCD, в котором ∠B = 60°, АС= 10,5 см.
Смотреть решение задачи № 406
Задача № 407. Найдите углы, которые образуют диагонали ромба с его сторонами, если один из углов ромба равен 45°.
Смотреть решение задачи № 407
Задача № 408. Докажите, что параллелограмм является ромбом, если: а) его диагонали взаимно перпендикулярны; б) диагональ делит его угол пополам.
Смотреть решение задачи № 408
Задача № 409. □ Докажите, что ромб, у которого один угол прямой, является квадратом.
Смотреть решение задачи № 409
Задача № 410. □ Является ли четырёхугольник квадратом, если его диагонали: а) равны и взаимно перпендикулярны; б) взаимно перпендикулярны и имеют общую середину; в) равны, взаимно перпендикулярны и имеют общую середину?
Смотреть решение задачи № 410
Задача № 411. □ В прямоугольном треугольнике проведена биссектриса прямого угла. Через точку пересечения этой биссектрисы с гипотенузой проведены прямые, параллельные катетам. Докажите, что полученный четырёхугольник — квадрат.
Смотреть решение задачи № 411
Задача № 412.
Смотреть решение задачи № 412
Задача № 413.
□ Постройте прямоугольник: а) по двум смежным сторонам; б) по стороне и диагонали; в) по диагонали и углу между диагоналями.
Смотреть решение задачи № 413
Задача № 414. □ Постройте ромб: а) по двум диагоналям; б) по стороне и углу.
Смотреть решение задачи № 414
Задача № 415. □ Постройте квадрат: а) по стороне; б) по диагонали.
Смотреть решение задачи № 415
Задача № 416. □ Даны две точки А и В, симметричные относительно некоторой прямой, и точка М. Постройте точку, симметричную точке М относительно той же прямой.
Смотреть решение задачи № 416
Задача № 417.
Сколько осей симметрии имеет: а) отрезок; б) прямая; в) луч?Смотреть решение задачи № 417
Задача № 418. Какие из следующих букв имеют ось симметрии: А, Б, Г, Е, О, F ?
Смотреть решение задачи № 418
Задача № 419. □ Докажите, что прямая, проходящая через середины противоположных сторон прямоугольника, является его осью симметрии.
Смотреть решение задачи № 419
Задача № 420. □ Докажите, что прямая, содержащая биссектрису равнобедренного треугольника, проведённую к основанию, является осью симметрии треугольника.
Смотреть решение задачи № 420
Задача № 421. □ Даны точки А, В и М. Постройте точку, симметричную точке М относительно середины отрезка АВ.
Смотреть решение задачи № 421
Задача № 422. Имеют ли центр симметрии: а) отрезок; б) луч; в) пара пересекающихся прямых; г) квадрат?
Смотреть решение задачи № 422
Задача № 423. Какие из следующих букв имеют центр симметрии: А, О, М, X, К?
Смотреть решение задачи № 423
Вы смотрели: Упражнения из учебника «Геометрия 8 класс. УМК Атанасян» с ответами и решениями. Глава 5. Четырёхугольники. § 3. Прямоугольник, ромб, квадрат. Геометрия 8 класс Атанасян Задачи 399-423 + ОТВЕТЫ.
Вернуться в ОГЛАВЛЕНИЕ учебника
Просмотров: 6 258
Делители числа 415 — Найти простые факторизации/множители числа 415 , 415 — самый большой коэффициент.
Парные множители числа 415 равны (1, 415), (5, 83), а его простые множители равны 5 × 83.- Все множители числа 415: 1, 5, 83 и 415
- Отрицательные коэффициенты 415: -1, -5, -83 и -415
- Простые множители числа 415: 5, 83
- Факторизация числа 415: 5 1 × 83 1
- Сумма коэффициентов 415: 504
| 1. | Какие множители числа 415? |
| 2. | Коэффициенты 415 с помощью простой факторизации |
| 3. | Коэффициенты 415 в парах |
| 4. | Часто задаваемые вопросы о факторах 415 |
Что такое множители числа 415?
Множители 415 — это пары тех чисел, произведение которых дает 415. Эти множители являются либо простыми, либо составными числами.
Как найти делители числа 415?
Чтобы найти делители числа 415, нам нужно найти список чисел, на которые число 415 делится без остатка.
- 415/83 = 5; следовательно, 83 — это множитель 415, а 5 — тоже множитель 415.
- 415/1 = 415; следовательно, 1 является коэффициентом 415, а 415 также является коэффициентом 415.
Точно так же мы можем найти и другие факторы. Следовательно, множители числа 415 равны 1, 5, 83, 415.
☛ Также проверьте:
- Факторы 78 — Делители 78 равны 1, 2, 3, 6, 13, 26, 39, 78
- Коэффициенты 180 — Коэффициенты 180 равны 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 30, 36, 45, 60, 90, 180
- Множители 11 — Множители 11 равны 1, 11
- Множители 28 — Множители 28 равны 1, 2, 4, 7, 14, 28
- Факторы 9 — Делители 9 равны 1, 3, 9
Коэффициенты 415 с помощью простой факторизации
Число 415 составное, поэтому оно имеет простые делители.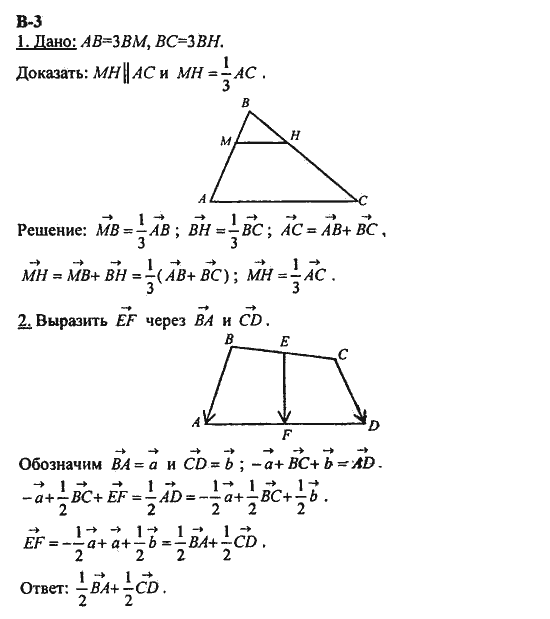
Теперь давайте научимся вычислять простые множители числа 415.
Первый шаг — разделить число 415 на наименьший простой множитель, здесь это 5. Продолжаем делить, пока не получится ненулевой остаток.
- 415 ÷ 5 = 83
Дальнейшее деление 83 на 5 дает ненулевой остаток. Поэтому мы останавливаем процесс и продолжаем делить число 83 на следующий наименьший простой множитель. В конце концов мы останавливаемся, если следующего простого множителя не существует или когда мы не можем дальше делить.
Итак, разложение числа 415 на простые множители можно записать как 5 1 × 83 1 , где 5, 83 — простые числа.
Делители 415 в парах
Парные множители 415 — это пары чисел, которые при умножении дают произведение 415. Парные множители числа 415:
- 1 × 4155
- 5 × 83 = (5, 83)
Отрицательные парные множители числа 415:
- -1 × -415 = (-1, -415)
- -5 × -83 = (-5, -83)
ПРИМЕЧАНИЕ: Если (a, b) является парным множителем числа, то (b, a) также является парным множителем этого числа.
Коэффициенты 415 решенных примеров
Пример 1: Сколько множителей существует для числа 415?
Решение:
Делители числа 415 равны 1, 5, 83, 415. Следовательно, число 415 имеет 4 делителя.
Пример 2. Найдите наименьшее общее кратное (НОК) и наибольший общий делитель (НОД) чисел 415 и 408.
Решение:
Множители числа 415 равны 1, 5, 83, 415, а числа 408 равны 1, 2, 3, 4, 6, 8, 12, 17, 24, 34, 51, 68, 102, 136, 204, 408.
Следовательно, наименьшее общее кратное (НОК) чисел 415 и 408 равно 169320, а наибольший общий делитель (НОД) чисел 415 и 408 равен 1.
Пример 3. Найдите, являются ли 1, 5 и 350 делителями 415.
Решение:
При делении 415 на 350 остается остаток. Следовательно, число 350 не является делителем 415. Все числа, кроме 350, являются делителями 415.
Пример 4. Найдите произведение всех простых делителей числа 415.
Решение:
Поскольку простые делители числа 415 равны 5, 83. Следовательно, произведение простых делителей = 5 × 83 = 415
перейти к слайдуперейти к слайдуперейти к слайдуперейти к слайду
Готовы увидеть мир глазами математика?
Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Записаться на бесплатный пробный урок
перейти к слайдуперейти к слайдуперейти к слайдуперейти к слайдуперейти к слайду
Часто задаваемые вопросы о факторах 415
Что такое факторы 415?
Множители числа 415 равны 1, 5, 83, 415, а его отрицательные множители равны -1, -5, -83, -415.
Какова сумма всех множителей числа 415?
Все множители числа 415 равны 1, 5, 83, 415 и, следовательно, сумма всех этих множителей равна 1 + 5 + 83 + 415 = 504
Каковы простые делители числа 415?
Простые делители числа 415 равны 5, 83.