Сведения об общеобразовательной организации
Сведения об общеобразовательной организацииЦвет:C C C
Изображения Вкл. Выкл.
Обычная версия сайта
- Телефон доверия: 8 800 200-01-22
Ошибка 404
К сожалению запрашиваемая страница не найдена.
Но вы можете воспользоваться поиском или картой сайта ниже
|
|
Урок по геометрии 8 класс
Эпиграф урока:
Геометрия является самым могущественным
средством для изощрения наших умственных способностей и даёт возможность
правильно мыслить и рассуждать.
Г. Галилей.
«Природа говорит языком математики: буквы этого языка — … математические фигуры»
Г. Галилей.
Галиле́о Галиле́й — итальянский физик, механик, астроном, философ и математик, оказавший значительное влияние на науку своего времени. Он первым использовал телескоп для наблюдения небесных тел и сделал ряд выдающихся астрономических открытий. Галилей — основатель экспериментальной физики. Эксперимента́льная фи́зика — способ познания природы, заключающийся в изучении природных явлений в специально приготовленных условиях.
Ребята, посмотрите на доску. На ней представлены фигуры. Как можно назвать все эти фигуры? Откройте тетради и запишите дату и тему сегодняшнего урока: “Четырёхугольники”.
Обобщающий урок по геометрии «Четырехугольники». 8-й класс
Тема урока «Решение задач по теме: «Четырёхугольники»
Тип урока Урок обобщения и систематизации
Цели
Предметные:
систематизировать знания о четырёхугольниках: параллелограмм, трапеция, ромб,
прямоугольник, квадрат.
Личностные: развивать навыки самостоятельной работы, эмоциональной сферы, анализа своей работы.
Метапредметные: умение самостоятельно определять цели своего обучения,
ставить и формулировать для себя новые задачи в учёбе и познавательной деятельности.
Планируемые результаты учащийся научится решать задачи разного уровня сложности на применение свойств и признаков четырёхугольников из материалов ГИА.
Основные понятия Параллелограмм, его определение, свойства и признаки;
трапеция, её определение и свойства;
прямоугольник, ромб, квадрат и их свойства.
Задачи:
ü вооружение учащихся системой знаний по теме “Четырехугольники”;
ü формирование навыков самостоятельной работы, работы в малых группах;
ü подготовка
учащихся к ГИА.
План урока.
1.Организационный момент.
2.Повторение (фронтальный опрос).
3.Математический диктант.
4. Закончите предложение, либо впишите пропущенные слова.
3. Теоретическая самостоятельная работа.
4.Кроссворд
5.Физминутка-релаксация.
6. Решение задач по готовым чертежам.
7.Теоретический тест.
8. Подведение итогов урока
.
Оборудование: компьютер, проектор, презентация.
Ход урока
1. Организационный момент. Вступительное слово учителя.
На доске записано: эпиграф
1.Повторение.
Фронтальное обсуждение схемы. Почему на схеме верхний четырёхугольник изображён таким странным: ни равных сторон, ни равных углов у него нет?
Ответ. В определении четырёхугольника ничего не сказано о равенстве сторон или углов.
Вопрос. О чем говорят стрелки, проведенные от верхнего четырехугольника?
Ответ.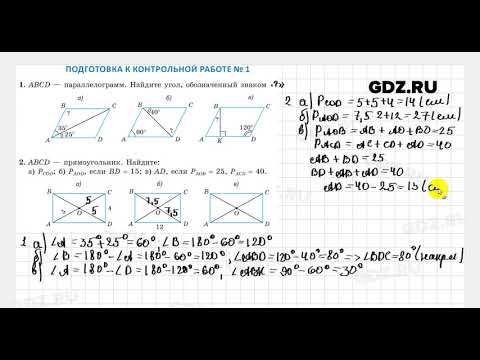
Среди четырехугольников можно выделить
особые, которые имеют больше характерных признаков, чем все остальные. Это
параллелограмм и трапеция.
Вопрос.
Что означают стрелки, идущие от параллелограмма и трапеции?
Ответ. Среди параллелограммов существуют такие, которые обладают дополнительными свойствами. Это – ромб, прямоугольник и квадрат. Также, среди трапеций существуют те, которые обладают дополнительными свойствами. Это – равнобедренная трапеция и прямоугольная трапеция.
Вопрос. Дайте определение параллелограмма. Какими свойствами обладает параллелограмм?
Вопрос. Что вы знаете об углах параллелограмма, прилежащих к одной стороне и о диагонали?
Вопрос. Дайте определение ромба. Каким особым свойством обладает ромб?
Вопрос. Дайте определение прямоугольника. Назовите особое свойство прямоугольника.
Вопрос. Какая фигура объединяет в себе все свойства параллелограмма, прямоугольника, ромба?
Вопрос.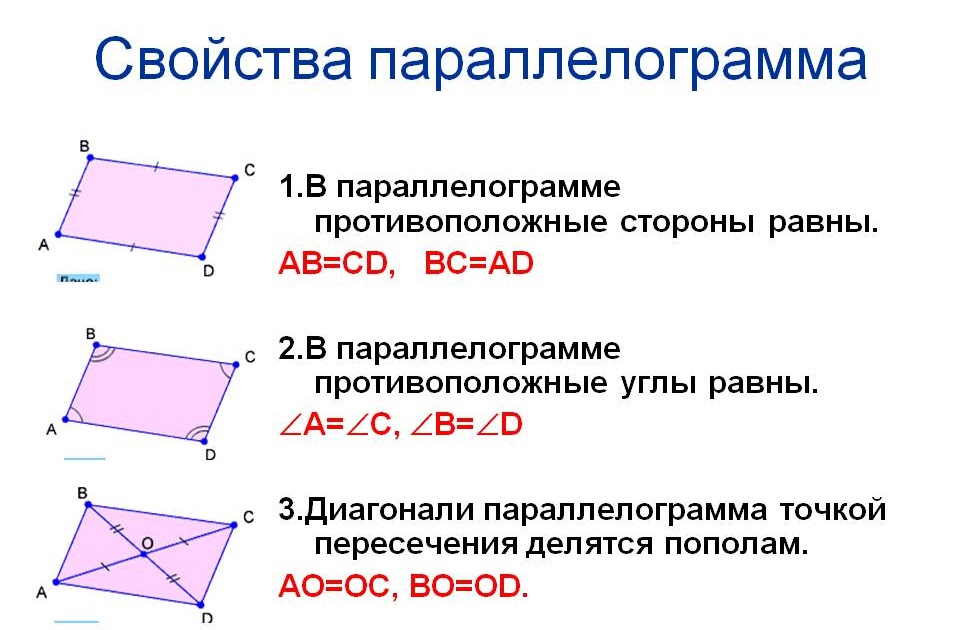
Дайте определение трапеции. Какие виды
трапеции вы знаете. Дайте их определения.
2. Фронтальный опрос. Математический диктант. Отвечая на вопросы диктанта, пишем ответ – номер фигуры, обладающей данным свойством.
На слайде изображены фигуры: ромб, прямоугольник, трапеция, параллелограмм, квадрат.
Обучающиеся называют номер той фигуры, которая обладает названным свойством.
1. Имеет равные диагонали. (прямоугольник, квадрат)
2. Имеет равные противоположные углы.(параллелограмм)
3. Имеет перпендикулярные диагонали. (ромб, квадрат)
4. Имеет равные противоположные стороны. (параллелограмм)
5. Углы, прилежащие к одной стороне, в сумме составляют 180°.
6. Диагонали являются биссектрисами углов. (ромб)
7. Сумма всех углов равна 360°. (четырехугольник)
Историческая справка.
Параллелограмм – от греч.
слов
“параллелос” — тот, что идет рядом, и “грамма” — черта;
Прямоугольник – параллелограмм с прямыми углами;
Ромб – от лат. слова “ромбус” — волчок, юла;
Квадрат – от лат. слова “квадратус” — четырехугольный;
Трапеция – от лат. слова “трапезиум” — столик.
Закончите предложение, либо впишите пропущенные слова. 1. Параллелограмм — это четырёхугольник, у которого противолежащие стороны ______________________________________________. 2. Диагонали параллелограмма пересекаются и ____________________________________. 3. У параллелограмма противоположные стороны и противоположные углы ____________. 4. Прямоугольник — _____________________, у которого все углы_____________________. 5.Диагонали прямоугольника_____________________________. 6. Ромб — это__________________, у которого все
стороны______________. 7. Диагонали ромба пересекаются под___________________________. 8.Диагонали ромба являются_________________________________________________. 9. Квадрат — это_______________________, у которого все стороны______________________. 10. У квадрата все углы_________, диагонали квадрата пересекаются__________________, 11.Диагонали квадрата являются______________________________________________. |
Теоретическая самостоятельная работа.
| Параллело- | Прямо- | Ромб | Квадрат |
Противолежащие стороны параллельны и равны |
|
|
|
|
Все стороны равны |
|
|
|
|
Противолежащие углы равны, сумма соседних углов равна 180 |
|
|
|
|
Все углы прямые. |
|
|
|
|
Диагонали пересекаются и точкой пересечения делятся пополам |
|
|
|
|
Диагонали равны |
|
|
|
|
Диагонали взаимно перпендикулярны и являются биссектрисами его углов |
|
|
|
|
| Паралле- | Прямо- | Ромб | Квадрат |
Противолежащие стороны параллельны и равны | + | + | + | + |
Все стороны равны | — | — | + | + |
Противолежащие углы равны, сумма соседних углов равна 180 | + | + | + | + |
Все углы прямые. | — | + | — | + |
Диагонали пересекаются и точкой пересечения делятся пополам | + | + | + | + |
Диагонали равны | — | + | — | + |
Диагонали взаимно перпендикулярны и являются биссектрисами его углов | — | — | + | + |
Сказка-вопрос.
Собрались все четырёхугольники
на лесной поляне и стали обсуждать вопрос о выборе своего короля. Долго спорили
и никак не могли прийти к единому мнению. И вот один старый параллелограмм
сказал: «Давайте отправимся все в царство четырёхугольников.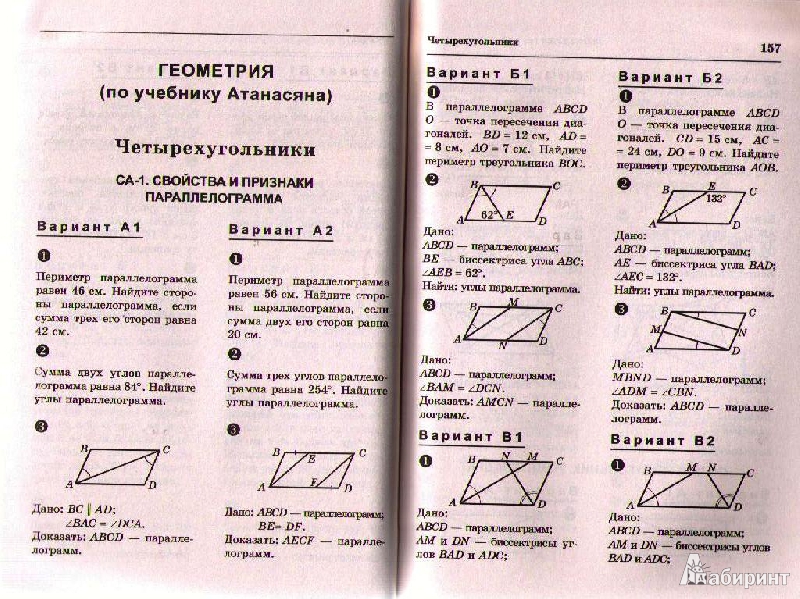
Кто первым придёт,
тот и будет королём». Все согласились. Рано утром отправились все в далёкое
путешествие. На пути им повстречалась река, которая сказала: «Переплывут меня
только те, у кого диагонали пересекаются и точкой пересечения делятся пополам».
Часть четырёхугольников осталась на берегу, остальные отправились дальше. На
пути встретилась высокая гора, которая сказала, что даст пройти только тем, у
кого диагонали равны. Несколько путешественников осталось у горы, остальные
продолжили путь. Дошли до большого обрыва, где был узкий мост. Мост сказал, что
пропустит тех, у кого диагонали пересекаются под прямым углом. По мосту прошёл
только один четырёхугольник, который первым добрался до царства и был
провозглашён королём. Вопросы:
1.Кто стал королём?
2.Кто первым вышел из соревнования?
3.Кто был основным соперником?
Ответы:
1 – Квадрат.
2 — Произвольный четырехугольник и трапеция.
3 – Прямоугольник.
Комплекс упражнений для глаз:
1)
вертикальные движения глаз вверх – вниз;
2) горизонтальное вправо – влево;
3) вращение глазами по часовой стрелке и против;
4) закрыть глаза и представить по очереди цвета радуги как можно отчетливее;
5) на доске начерчены кривые (спираль, окружность, ломаная)и четырехугольники ;
предлагается глазами “нарисовать” эти фигуры несколько раз в одном, а затем в
другом направлении.
Аристотель говорил: «Ум заключается не только в знании, но и в умении приложить знание на деле».
4.Решение задач на готовых чертежах
Ребятам предлагается решить задачи на готовых чертежах.
|
| |||
Дано: ОКМN прямо угольник, КМО = 20° Найти: KOM, OMN и MON. | Дано: АВСD – прямоугольник ВD = 12 см Найти: АС | Дано: АВСD – прямоугольник, РABCD= 48 см, АВ в 2 раза меньше ВС. Найти: стороны АВСD . |
Ребятам
предлагается решить задачи на готовых чертежах.
|
| |||||||||
Дано: ОМNК – ромб МОN = 65. Найти углы ромба. | Дано: АВСD – ромб ВАС = 60, АС = 7см Найти: АВ. | Дано: четырёхугольник АВСD ВС = АD, ВСAD, РАВСD = 36 см ВАС = САD. Найти стороны АВСD. Ребятам предлагается решить задачи на готовых чертежах.
|
Тест.
1. Четырёхугольник, у которого только две стороны параллельны
- ромб
- трапеция
- квадрат
- прямоугольник
Верный — 2
2. Трапеция, у которой один из углов равен 90 градусов, называется
- равнобедренной
- остроугольной
- тупоугольной
- прямоугольной
Верный — 4
3. Любой ромб является:
- квадратом
- прямоугольником
- параллелограммом
- трапецией
Верный — 3
4.
Если в параллелограмме диагонали перпендикулярны, то этот
параллелограмм:
- ромб
- квадрат
- прямоугольник
- нет правильного ответа
Верный — 1
5. Любой прямоугольник является:
- ромбом
- квадратом
- параллелограммом
- нет правильного ответа
Верный — 3
6. Если в четырёхугольнике диагонали перпендикулярны, то этот четырёхугольник:
- ромб
- квадрат
- прямоугольник
- нет правильного ответа
Верный — 4
7. Диагонали четырёхугольника в точке пересечения делятся пополам. Одна из его сторон равна 4 см. Чему равна противолежащая сторона?
- 2 см
- 8 см
- 4 см
- 6 см
Верный — 3
8.
Сумма двух углов параллелограмма равна 100 градусов, найдите
углы параллелограмма.
- 40, 140
- 80, 100
- 50, 130
- 40, 60
Верный — 3
9. Сумма углов выпуклого четырёхугольника равна:
- 180
- 360
- 540
- 2160
Верный — 2
10. Квадрат — это…
- параллелограмм с равными сторонами
- параллелограмм с равными углами
- прямоугольник, у которого все стороны равны
- нет правильного ответа
Верный — 3
11. У этого четырёхугольника диагонали всегда равны?
- трапеция
- прямоугольник
- ромб
- параллелограмм
Верный — 2
12. В равнобедренной трапеции один из углов равен 110 градусов.
найдите все углы.
- 55, 55, 125, 125
- 180, 70, 180, 70
- 70, 110, 70, 110
- нет верного ответа
Верный — 3
13. Какое из утверждений неверное?
- У прямоугольника углы — прямые
- у ромба все стороны равны
- у квадрата диагонали взаимно перпендикулярны
- у трапеции стороны попарно параллельны
Верный — 4
14. Найдите периметр ромба, если один из его углов равен 60 градусов, а меньшая диагональ равна 12 см.
- 48 см
- 36 см
- 24 см
- 72 см
Верный — 1
15. Какое утверждение неверно:
- квадрат — одновременно параллелограмм и прямоугольник
- угол между стороной и диагональю квадрата равен 45 град.
- диагонали квадрата взаимно перпендикулярны
- существует квадрат, который не является ромбом
Верный — 4
(Слайд 2).
Загадки 1 команде:
1.И у меня равны диагонали,
Хочу сказать я, хоть меня не называли.
И хоть я не зовусь квадратом,
Он мне приходится родным братом.(Квадрат).
2.Хоть стороны мои
Попарно и равны, и параллельны,
Всё ж я в печали, что не равны мои диагонали,
Да и углы они не делят пополам.
Но всё ж, скажи, дружок, кто я? (Параллелограмм).
Загадки 2 команде:
1.Знаете ли вы меня
Хочу проверить,
Любую площадь я могу измерить,
Ведь у меня четыре стороны
И все они между собой равны.
И у меня равны диагонали,
Углы мне они делят пополам, и ими
На части равные разбит я сам. (Прямоугольник)
2.Мои, хотя и не равны диагонали,
По значимости всем я уступлю едва ли.
Ведь под прямым углом они пересекаются,
И каждый угол делят пополам,
И очень важная
фигура я, скажу я вам.
(Ромб).
III. Историческая справка (домашнее задание).
открытых учебников | Siyavula
Загрузите наши открытые учебники в различных форматах, чтобы использовать их так, как вам удобно. Нажмите на обложку каждой книги, чтобы увидеть доступные для загрузки файлы на английском и африкаанс. Лучше, чем просто бесплатные, эти книги также имеют открытую лицензию! См. различные открытые лицензии для каждой загрузки и пояснения к лицензиям в нижней части страницы.
Математика
- Читать онлайн
Учебники
Английский
- 7A PDF (CC-BY-ND)
- 7B PDF (CC-BY-ND)
Африкаанс
- 7A PDF (CC-BY-ND)
- 7B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- 8A PDF (CC-BY-ND)
- 8B PDF (CC-BY-ND)
Африкаанс
- 8A PDF (CC-BY-ND)
- 8B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- 9A PDF (CC-BY-ND)
- 9B PDF (CC-BY-ND)
Африкаанс
- 9A PDF (CC-BY-ND)
- 9B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
Наука
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 7А
- PDF (CC-BY-ND)
Класс 7Б
- PDF (CC-BY-ND)
Африкаанс
Граад 7А
- PDF (CC-BY-ND)
Граад 7Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 8А
- PDF (CC-BY-ND)
Класс 8Б
- PDF (CC-BY-ND)
Африкаанс
Граад 8А
- PDF (CC-BY-ND)
Граад 8Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 9А
- PDF (CC-BY-ND)
Класс 9Б
- PDF (CC-BY-ND)
Африкаанс
Граад 9А
- PDF (CC-BY-ND)
Граад 9Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 4А
- PDF (CC-BY-ND)
Класс 4Б
- PDF (CC-BY-ND)
Африкаанс
Граад 4А
- PDF (CC-BY-ND)
Граад 4Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 5А
- PDF (CC-BY-ND)
Класс 5Б
- PDF (CC-BY-ND)
Африкаанс
Граад 5А
- PDF (CC-BY-ND)
Граад 5Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 6А
- PDF (CC-BY-ND)
Класс 6Б
- PDF (CC-BY-ND)
Африкаанс
Граад 6А
- PDF (CC-BY-ND)
Граад 6Б
- PDF (CC-BY-ND)
Лицензирование наших книг
Эти книги не только бесплатны, но и имеют открытую лицензию! Один и тот же контент, но разные версии (фирменные или нет) имеют разные лицензии, как объяснено:
CC-BY-ND (фирменные версии)
Вам разрешается и поощряется свободное копирование этих версий.
Вы можете копировать, распечатывать и распространять их столько раз, сколько захотите. Вы можете загрузить их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственное ограничение заключается в том, что вы не можете каким-либо образом адаптировать или изменять эти версии учебников, их содержание или обложки, поскольку они содержат соответствующие бренды Siyavula, логотипы спонсоров и одобрены Департаментом базового образования. Для получения дополнительной информации посетите сайт Creative Commons Attribution-NoDerivs 3.0 Unported.
Узнайте больше о спонсорстве и партнерстве с другими, которые сделали возможным выпуск каждого из открытых учебников.
CC-BY (версии без торговой марки)
Эти версии одного и того же контента без торговой марки доступны для вас, чтобы вы могли делиться ими, адаптировать, преобразовывать, изменять или развивать их любым способом, при этом единственным требованием является предоставление соответствующей ссылки на Siyavula.
Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.
Рабочая тетрадь по геометрии серии 100+™ для 8–10 классов, электронная книга
Серия 100+™
Загляни внутрь
Серия 100+™
- 128 страниц
- 8–10 классы / 13–16 лет
В настоящее время: $12,99
Описание
Серия 100+ «Геометрия» предлагает углубленную практику и повторение сложных математических тем средней школы, таких как повороты, отражения и преобразования; соответствие и сходство; функции синуса и косинуса.