ГДЗ: Алгебра 8 класс Ершова, Голобородько
C-1. Часть А (стр. 6)
Вариант 1 Вариант 2C-1. Часть Б (стр. 6-7)
Вариант 1 Вариант 2C-1. Часть В (стр. 7-8)
Вариант 1 Вариант 2C-2. Часть А (стр. 8)
Вариант 1 Вариант 2C-2. Часть Б (стр. 9)
Вариант 1 Вариант 2C-2. Часть В (стр. 9-10)
Вариант 1 Вариант 2C-3. Часть А (стр. 14-15)
Вариант 1 Вариант 2C-3. Часть Б (стр. 15)
Вариант 1 Вариант 2C-3. Часть В (стр. 16)
Вариант 1 Вариант 2C-4. Часть А (стр. 17)
Вариант 1 Вариант 2C-4. Часть Б (стр. 17)
Вариант 1 Вариант 2C-4. Часть В (стр. 17-18)
Вариант 1 Вариант 2C-5. (стр. 18-19)
Вариант 1 Вариант 2C-6. Часть А (стр. 20)
Вариант 1 Вариант 2C-6. Часть Б (стр. 20-21)
Вариант 1 Вариант 2C-6. Часть В (стр. 21-22)
Вариант 1 Вариант 2C-7. Часть А (стр. 25-26)
Вариант 1 Вариант 2C-7. Часть Б (стр. 26-27)
Вариант 1 Вариант 2C-7. Часть В (стр.
 27-28)Вариант 1 Вариант 2
27-28)Вариант 1 Вариант 2C-8. Часть А (стр. 28-29)
Вариант 1 Вариант 2C-8. Часть Б (стр. 29-30)
Вариант 1 Вариант 2C-8. Часть В (стр. 30-31)
Вариант 1 Вариант 2C-9. Часть А (стр. 31-32)
Вариант 1 Вариант 2C-9. Часть Б (стр. 32-33)
Вариант 1 Вариант 2C-9. Часть В (стр. 33)
Вариант 1 Вариант 2C-10. Часть А (стр. 38)
Вариант 1 Вариант 2C-10. Часть Б (стр. 38-39)
Вариант 1 Вариант 2C-10. Часть В (стр. 39-40)
Вариант 1 Вариант 2C-11. Часть А (стр. 40-41)
Вариант 1 Вариант 2C-11. Часть Б (стр. 41)
Вариант 1 Вариант 2C-11. Часть В (стр. 41-42)
Вариант 1 Вариант 2C-12. (стр. 42-44)
Вариант 1 Вариант 2C-13. Часть А (стр. 48)
Вариант 1 Вариант 2C-13. Часть Б (стр. 48)
Вариант 1 Вариант 2C-13. Часть В (стр. 49)
Вариант 1 Вариант 2C-14. Часть А (стр. 49)
Вариант 1 Вариант 2C-14. Часть Б (стр. 50)
Вариант 1 Вариант 2C-14. Часть В (стр.
 50)Вариант 1 Вариант 2
50)Вариант 1 Вариант 2C-15. Часть А (стр. 51)
Вариант 1 Вариант 2C-15. Часть Б (стр. 51-52)
Вариант 1 Вариант 2C-15. Часть В (стр. 52)
Вариант 1 Вариант 2C-17. Часть А (стр. 58)
Вариант 1 Вариант 2C-17. Часть Б (стр. 58)
Вариант 1 Вариант 2C-17. Часть В (стр.58-59)
Вариант 1 Вариант 2C-18. Часть А (стр. 59)
Вариант 1 Вариант 2C-18. Часть Б (стр. 60)
Вариант 1 Вариант 2C-18. Часть В (стр. 60-61)
Вариант 1 Вариант 2C-19. Часть А (стр. 65)
Вариант 1 Вариант 2C-19. Часть Б (стр. 65-66)
Вариант 1 Вариант 2C-19. Часть В (стр. 66-67)
Вариант 1 Вариант 2C-20. Часть А (стр. 71)
Вариант 1 Вариант 2C-20. Часть Б (стр. 72)
Вариант 1 Вариант 2C-20. Часть В (стр. 72-73)
Вариант 1 Вариант 2C-21. Часть А (стр. 73-74)
Вариант 1 Вариант 2C-21. Часть Б (стр. 74)
Вариант 1 Вариант 2C-21. Часть В (стр. 75)
Вариант 1 Вариант 2C-23. Часть А (стр.
 81)Вариант 1 Вариант 2
81)Вариант 1 Вариант 2C-23. Часть Б (стр. 82)
Вариант 1 Вариант 2C-23. Часть В (стр. 82-83)
Вариант 1 Вариант 2CА-1. Часть А (стр. 156)
Вариант 1 Вариант 2CА-1. Часть Б (стр. 157)
Вариант 1 Вариант 2CА-1. Часть В (стр. 157-158)
Вариант 1 Вариант 2CА-2. Часть А (стр. 158-159)
Вариант 1 Вариант 2CА-2. Часть Б (стр. 159-160)
Вариант 1 Вариант 2CА-2. Часть В (стр. 160)
Вариант 1 Вариант 2CА-4. Часть А (стр. 165)
Вариант 1 Вариант 2CА-4. Часть Б (стр. 165-166)
Вариант 1 Вариант 2CА-4. Часть В (стр. 166)
Вариант 1 Вариант 2CА-5. Часть А (стр. 167)
Вариант 1 Вариант 2CА-5. Часть Б (стр. 167-168)
Вариант 1 Вариант 2CА-5. Часть В (стр. 168)
Вариант 1 Вариант 2CА-6. Часть А (стр. 168-169)
Вариант 1 Вариант 2CА-6. Часть Б (стр. 169)
Вариант 1 Вариант 2CА-6. Часть В (стр. 169-170)
Вариант 1 Вариант 2CА-7. Часть А (стр. 170)
Вариант 1 Вариант 2CА-7.
 Часть Б (стр. 171)Вариант 1 Вариант 2
Часть Б (стр. 171)Вариант 1 Вариант 2CА-7. Часть В (стр. 171-172)
Вариант 1 Вариант 2CА-8. (стр. 172-173)
Вариант 1CА-9. Часть А (стр. 176)
Вариант 1 Вариант 2CА-9. Часть Б (стр. 177)
Вариант 1 Вариант 2CА-9. Часть В (стр. 177-178)
Вариант 1 Вариант 2CА-10. Часть А (стр. 178-179)
Вариант 1 Вариант 2CА-10. Часть Б (стр. 179-180)
Вариант 1 Вариант 2CА-10. Часть В (стр. 180-181)
Вариант 1 Вариант 2CА-11. Часть А (стр. 183-184)
Вариант 1 Вариант 2CА-11. Часть Б (стр. 184-185)
Вариант 1 Вариант 2CА-11. Часть В (стр. 185)
Вариант 1 Вариант 2CА-12. Часть А (стр. 186)
Вариант 1 Вариант 2CА-12. Часть Б (стр. 186-187)
Вариант 1 Вариант 2CА-12. Часть В (стр. 187)
Вариант 1 Вариант 2CА-14. Часть А (стр. 192)
Вариант 1 Вариант 2CА-14. Часть Б (стр. 192-193)
Вариант 1 Вариант 2CА-14. Часть В (стр. 193-194)
Вариант 1 Вариант 2CА-15. Часть А (стр.
 194)Вариант 1 Вариант 2
194)Вариант 1 Вариант 2CА-15. Часть Б (стр. 195)
Вариант 1 Вариант 2CА-15. Часть В (стр. 195-196)
Вариант 1 Вариант 2CА-16. Часть А (стр. 196-197)
Вариант 1 Вариант 2CА-16. Часть Б (стр. 197-198)
Вариант 1 Вариант 2CА-16. Часть В (стр. 198)
Вариант 1 Вариант 2CА-17. Часть А (стр. 199)
Вариант 1 Вариант 2CА-17. Часть Б (стр. 199-200)
Вариант 1 Вариант 2CА-17. Часть В (стр. 200-201)
Вариант 1 Вариант 2CА-19. Часть А (стр. 205)
Вариант 1 Вариант 2CА-19. Часть Б (стр. 205-206)
Вариант 1 Вариант 2CА-19. Часть В (стр. 206-207)
Вариант 1 Вариант 2CА-20. Часть А (стр. 207)
Вариант 1 Вариант 2CА-20. Часть Б (стр. 208)
Вариант 1 Вариант 2CА-20. Часть В (стр. 208-209)
Вариант 1 Вариант 2CА-21. Часть А (стр. 209)
Вариант 1 Вариант 2CА-21. Часть Б (стр. 209-210)
Вариант 1 Вариант 2CА-21. Часть В (стр. 210)
Вариант 1 Вариант 2CА-22. (стр. 211-212)
Вариант 1 Вариант 2CП-1.
 Часть А (стр. 92)Вариант 1 Вариант 2
Часть А (стр. 92)Вариант 1 Вариант 2СП-1. Часть Б (стр. 93)
Вариант 1 Вариант 2СП-1. Часть В (стр. 94)
Вариант 1 Вариант 2СП-2. Часть А (стр. 94-95)
Вариант 1 Вариант 2СП-2. Часть Б (стр. 95-96)
Вариант 1 Вариант 2СП-2. Часть В (стр. 96)
Вариант 1 Вариант 2СП-3. Часть А (стр. 99)
Вариант 1 Вариант 2СП-3. Часть Б (стр. 100)
Вариант 1 Вариант 2СП-3. Часть В (стр. 100-101)
Вариант 1 Вариант 2СП-4. Часть А (стр. 101-102)
Вариант 1 Вариант 2СП-4. Часть Б (стр. 102-103)
Вариант 1 Вариант 2СП-4. Часть В (стр. 103)
Вариант 1 Вариант 2СП-5. (стр. 104-105)
Вариант 1 Вариант 2СП-6. Часть А (стр. 108)
Вариант 1 Вариант 2СП-6. Часть Б (стр. 108-109)
Вариант 1 Вариант 2СП-6. Часть В (стр. 109)
Вариант 1 Вариант 2СП-7. Часть А (стр. 110)
Вариант 1 Вариант 2СП-7. Часть Б (стр. 110-111)
Вариант 1 Вариант 2СП-7. Часть В (стр. 111-112)
Вариант 1 Вариант 2СП-8.
 Часть А (стр. 112)Вариант 1 Вариант 2
Часть А (стр. 112)Вариант 1 Вариант 2СП-8. Часть Б (стр. 113)
Вариант 1 Вариант 2СП-8. Часть В (стр. 113-114)
Вариант 1 Вариант 2СП-9. (стр. 114-115)
Вариант 1 Вариант 2СП-10. Часть А (стр. 117-118)
Вариант 1 Вариант 2СП-10. Часть Б (стр. 118-119)
Вариант 1 Вариант 2СП-10. Часть В (стр. 119-120)
Вариант 1 Вариант 2СП-11. Часть А (стр. 120-121)
Вариант 1 Вариант 2СП-11. Часть Б (стр. 121)
Вариант 1 Вариант 2СП-11. Часть В (стр. 121-122)
Вариант 1 Вариант 2СП-12. Часть А (стр. 125)
Вариант 1 Вариант 2СП-12. Часть Б (стр. 125-126)
Вариант 1 Вариант 2СП-12. Часть В (стр. 126-127)
Вариант 1 Вариант 2СП-13. Часть А (стр. 127)
Вариант 1 Вариант 2СП-13. Часть Б (стр. 128)
Вариант 1 Вариант 2СП-13. Часть В (стр. 128-129)
Вариант 1 Вариант 2СП-14. (стр. 129-130)
Вариант 1 Вариант 2СП-15. Часть А (стр. 134)
Вариант 1 Вариант 2СП-15. Часть Б (стр.
 134-135)Вариант 1 Вариант 2
134-135)Вариант 1 Вариант 2СП-15. Часть В (стр. 135-136)
Вариант 1 Вариант 2СП-16. Часть А (стр. 136-137)
Вариант 1 Вариант 2СП-16. Часть Б (стр. 137)
Вариант 1 Вариант 2СП-16. Часть В (стр. 138)
Вариант 1 Вариант 2СП-17. Часть А (стр. 139)
Вариант 1 Вариант 2СП-17. Часть Б (стр. 139-140)
Вариант 1 Вариант 2СП-17. Часть В (стр. 140-141)
Вариант 1 Вариант 2СП-18. Часть А (стр. 141)
Вариант 1 Вариант 2СП-18. Часть Б (стр. 142)
Вариант 1 Вариант 2СП-18. Часть В (стр. 142-143)
Вариант 1 Вариант 2СП-19. Часть А (стр. 143-144)
Вариант 1 Вариант 2СП-19. Часть Б (стр. 144-145)
Вариант 1 Вариант 2СП-19. Часть В (стр. 145-146)
Вариант 1 Вариант 2СП-20. Часть А (стр. 146-147)
Вариант 1 Вариант 2СП-20. Часть Б (стр. 147)
Вариант 1 Вариант 2СП-20. Часть В (стр. 148)
Вариант 1 Вариант 2СП-21. (стр. 149-150)
Вариант 1 Вариант 2К-1. Часть А (стр.
 10-11)Вариант 1 Вариант 2
10-11)Вариант 1 Вариант 2К-1. Часть Б (стр. 11-12)
Вариант 1 Вариант 2К-1. Часть В (стр. 13-14)
Вариант 1 Вариант 2К-2. Часть А (стр. 22-23)
Вариант 1 Вариант 2К-2. Часть Б (стр. 23)
Вариант 1 Вариант 2К-2. Часть В (стр. 24)
Вариант 1 Вариант 2К-3. Часть А (стр. 34-35)
Вариант 1 Вариант 2К-3. Часть Б (стр. 35-36)
Вариант 1 Вариант 2К-3. Часть В (стр. 36-37)
Вариант 1 Вариант 2К-4. Часть А (стр. 44-45)
Вариант 1 Вариант 2К-4. Часть Б (стр. 45-46)
Вариант 1 Вариант 2К-4. Часть В (стр. 46-47)
Вариант 1 Вариант 2К-5. Часть А (стр. 55)
Вариант 1 Вариант 2К-5. Часть Б (стр. 56)
Вариант 1 Вариант 2К-5. Часть В (стр. 57)
Вариант 1 Вариант 2К-6. Часть А (стр. 61-62)
Вариант 1 Вариант 2К-6. Часть Б (стр. 62-63)
Вариант 1 Вариант 2К-6. Часть В (стр. 63-64)
Вариант 1 Вариант 2К-7. Часть А (стр. 67-68)
Вариант 1 Вариант 2К-7. Часть Б (стр.
 68-69)Вариант 1 Вариант 2
68-69)Вариант 1 Вариант 2К-7. Часть В (стр. 70-71)
Вариант 1 Вариант 2К-8. Часть А (стр. 77-78)
Вариант 1 Вариант 2К-8. Часть Б (стр. 78-79)
Вариант 1 Вариант 2К-8. Часть В (стр. 79-80)
Вариант 1 Вариант 2К-9. Часть А (стр. 83-84)
Вариант 1 Вариант 2К-9. Часть Б (стр. 84-85)
Вариант 1 Вариант 2К-9. Часть В (стр. 86-87)
Вариант 1 Вариант 2К-10. Часть А (стр. 87-88)
Вариант 1 Вариант 2К-10. Часть Б (стр. 88-89)
Вариант 1 Вариант 2К-10. Часть В (стр. 89-90)
Вариант 1 Вариант 2КA-1. Часть А (стр. 162)
Вариант 1 Вариант 2КA-1. Часть Б (стр. 163)
Вариант 1 Вариант 2КA-1. Часть В (стр. 163-164)
Вариант 1 Вариант 2КA-2. Часть А (стр. 173-174)
Вариант 1 Вариант 2КA-2. Часть Б (стр. 174)
Вариант 1 Вариант 2КA-2. Часть В (стр. 174-175)
Вариант 1 Вариант 2КA-3. Часть А (стр. 181)
Вариант 1 Вариант 2КА-3. Часть Б (стр. 182)
Вариант 1 Вариант 2КA-3.
 Часть В (стр. 182-183)Вариант 1 Вариант 2
Часть В (стр. 182-183)Вариант 1 Вариант 2КА-4. Часть А (стр. 189-190)
Вариант 1 Вариант 2КА-4. Часть Б (стр. 190-191)
Вариант 1 Вариант 2КA-4. Часть В (стр. 191)
Вариант 1 Вариант 2КА-5. Часть А (стр. 202-203)
Вариант 1 Вариант 2КА-5. Часть Б (стр. 203)
Вариант 1 Вариант 2КA-5. Часть В (стр. 204)
Вариант 1 Вариант 2КА-6. Часть А (стр. 212-213)
Вариант 1 Вариант 2КА-6. Часть Б (стр. 213)
Вариант 1 Вариант 2КA-6. Часть В (стр. 213-214)
Вариант 1 Вариант 2КА-7. Часть А (стр. 214-215)
Вариант 1 Вариант 2КА-7. Часть Б (стр. 215)
Вариант 1 Вариант 2КA-7. Часть В (стр. 216)
Вариант 1 Вариант 2КП-1. Часть А (стр. 96-97)
Вариант 1 Вариант 2КП-1. Часть Б (стр. 97-98)
Вариант 1 Вариант 2КП-1. Часть В (стр. 98)
Вариант 1 Вариант 2КП-2. Часть А (стр. 105)
Вариант 1 Вариант 2КП-2. Часть Б (стр. 106)
Вариант 1 Вариант 2КП-2. Часть В (стр. 106-107)
Вариант 1 Вариант 2КП-3.
 Часть А (стр. 115)Вариант 1 Вариант 2
Часть А (стр. 115)Вариант 1 Вариант 2КП-3. Часть Б (стр. 116)
Вариант 1 Вариант 2КП-3. Часть В (стр. 116-117)
Вариант 1 Вариант 2КП-4. Часть А (стр. 122-123)
Вариант 1 Вариант 2КП-4. Часть Б (стр. 123)
Вариант 1 Вариант 2КП-4. Часть В (стр. 124)
Вариант 1 Вариант 2КП-5. Часть А (стр. 131)
Вариант 1 Вариант 2КП-5. Часть Б (стр. 131-132)
Вариант 1 Вариант 2КП-5. Часть В (стр. 132-133)
Вариант 1 Вариант 2КП-6. Часть А (стр. 150-151)
Вариант 1 Вариант 2КП-6. Часть Б (стр. 151-152)
Вариант 1 Вариант 2КП-6. Часть В (стр. 152-153)
Вариант 1 Вариант 2КП-7. Часть А (стр. 153-154)
Вариант 1 Вариант 2КП-7. Часть Б (стр. 154)
Вариант 1 Вариант 2КП-7. Часть В (стр. 155)
Вариант 1 Вариант 2ГДЗ по Алгебре для 8 класса Г.В. Дорофеев, С.Б. Суворова, Е.А. Бунимович, Л.В. Кузнецова, С.С. Минаева, Л.О. Рослова на 5
Авторы: Г.В. Дорофеев, С.Б. Суворова, Е. А. Бунимович, Л.В. Кузнецова, С.С. Минаева, Л.О. Рослова.
А. Бунимович, Л.В. Кузнецова, С.С. Минаева, Л.О. Рослова.
Издательство: Просвещение 2014
«ГДЗ по алгебре 8 класс Дорофеев, Суворова, Бунимович, Кузнецова, Минаева, Рослова (Просвещение)» было разработано лучшими педагогами страны, которые придерживались современной методики обучения с целью создать качественное полезное пособие. Оно поможет справиться с трудностями всем школьникам. В решебнике подростки найдут то, благодаря чему им удастся успешно освоить этот курс.
Уроки алгебры
В новом учебном году на занятиях учащиеся 8 классов познакомятся, а дома будут более детально разбирать следующие параграфы учебника:
- Сложение и вычитание алгебраических дробей с разными знаменателями.
- Рациональные уравнения.
- Понятие квадратного корня.
- Возведение алгебраической дроби в степень.
- Квадратные уравнения.

- Степень с отрицательным показателем.
Учителя стараются максимально подробно объяснить теоретическую часть материала. Но времени катастрофически не хватает, чтобы как следует поработать с каждым школьником индивидуально. Подросткам приходится разбираться во всем самостоятельно. Чтобы ребята не окружали себя большим количеством справочников и не тратили много времени на выполнение домашних заданий, им рекомендуется начать практиковаться вместе с данным пособием формата ГДЗ, которое было выпущено издательством «Просвещение».
Для чего нужен онлайн-решебник по алгебре для 8 класса от Дорофеева
О пользе данного справочника многие знают не понаслышке. Некоторые ребята с его помощью сумели даже полюбить этот непростой предмет, хотя раньше отдавали предпочтение изучению гуманитарных наук. Они постепенно начали разбираться в теоретических вопросах и в том, как решаются уравнения и другие задания. Подростки перестали пропускать занятия по неуважительным причинам и начали активно работать в классе.
- – разобраться в условии задания;
- – понять принцип решения того или иного номера;
- – подсмотреть верный ответ на какой-либо вопрос;
- – проверить себя;
- – навсегда устранить часто-повторяющиеся ошибки.
А самое главное заключается в том, что информация в «ГДЗ по алгебре за 8 класс Дорофеев Г. В., Суворова С. Б., Бунимович Е. А., Кузнецова Л. В., Минаева С. С., Рослова Л. О (Просвещение)»
NCERT Solutions for Class 8 Math Chapter 11
- Решения НЦЭРТ
- Класс 8
- Математика
- измерение
Математика NCERT 8 класс, Глава 11: Измерение . В этой главе подробно объясняются все понятия периметра и площади других плоских фигур, таких как четырехугольников . Кроме того, акцент будет сделан на концепции площади поверхности и объема твердых тел , таких как куб, прямоугольный параллелепипед, и цилиндр. Первая половина главы посвящена следующим темам:
В этой главе подробно объясняются все понятия периметра и площади других плоских фигур, таких как четырехугольников . Кроме того, акцент будет сделан на концепции площади поверхности и объема твердых тел , таких как куб, прямоугольный параллелепипед, и цилиндр. Первая половина главы посвящена следующим темам:
- Площадь трапеции
- Площадь общего четырехугольника: площадь специальных четырехугольников вкратце обсуждаются в этом разделе.
Обычный четырехугольник можно разделить на два треугольника, проведя одну из его диагоналей.
- Площадь ромба
- Площадь многоугольника
Нерешенные вопросы по вышеприведенным темам даны в первых двух упражнениях.
Во второй половине главы Твердые формы , такие как куб, прямоугольный параллелепипед и цилиндр

- Цилиндр имеет конгруэнтных круговых граней , которые параллельны друг другу. Когда отрезок линии , соединяющий центр круговых граней , является перпендикулярным основанию , тогда такие цилиндров известны как прямых круговых цилиндров.
После этого учащиеся будут проинформированы о площади поверхности куба, прямоугольного параллелепипеда, и цилиндра.
Также объясняется концепция общей площади поверхности и площади боковой поверхности .
- Боковые стенки (грани, исключая верхнюю и нижнюю) составляют площадь боковой поверхности прямоугольного параллелепипеда.
Объем куба , кубоид, и цилиндр также объясняется в следующем разделе на кратком примере и дополняется соответствующей необходимой диаграммой.
- Пространство, занимаемое трехмерным объектом , называется его объемом
Концепция Объем и емкость объясняется на решенных примерах.
(a) Объем относится к объему пространства , занимаемому объектом.
(b) Вместимость относится к количеству, которое вмещает контейнер.
Оценку этих понятий можно выполнить, решив упражнения 11.3 и 11.4.
Решенные примеры рассматриваются в главе, чтобы учащиеся поняли каждую тему кристально ясно. Эта глава основана на формулах, поэтому требует понимания концепции и применения формул. Нужно быть осторожным в применении правильной формулы везде, где это необходимо.
Страница № 171:
Вопрос 1:
Квадратное и прямоугольное поля с размерами, указанными на рисунке, имеют одинаковый периметр. Какое поле имеет большую площадь?
Какое поле имеет большую площадь?
Ответ:
Периметр квадрата = 4 (сторона квадрата) = 4 (60 м) = 240 м
Периметр прямоугольника = 2 (длина + ширина)
= 2 (80 м + ширина)
= 160 м + 2 × ширина
Известно, что периметр квадрата и прямоугольника одинаковы.
160 м + 2 × Ширина = 240 м
Ширина прямоугольника = = 40 м
Площадь квадрата = (Сторона) 2 = (60 м) 2 = 3600 м 2
Площадь прямоугольника = длина × ширина = (80 × 40) м 2 = 3200 м 2
Таким образом, площадь квадратного поля больше площади прямоугольного поля.
Видео Решение для измерения (Страница: 171 , Q.No.: 1)
Решение NCERT для класса 8 по математике — измерение 171 , Вопрос 1
Страница № 171:
Вопрос 2:
Миссис Кошик имеет квадратный участок с размерами, показанными на следующем рисунке. Она хочет построить дом посреди участка. Вокруг дома разбит сад. Найдите общие затраты на создание сада вокруг дома из расчета 55 рупий за м 9 .0156 2 .
Вокруг дома разбит сад. Найдите общие затраты на создание сада вокруг дома из расчета 55 рупий за м 9 .0156 2 .
Ответ:
Площадь квадратного участка = (25 м) 2 = 625 м 2
Площадь дома = (15 м) × (20 м) =300 м Площадь оставшейся части = Площадь квадратного участка − Площадь дома = 625 м 2 − 300 м 2 = 325 м 2 Стоимость обустройства сада вокруг дома составляет 55 рупий. за м 2 . Общая стоимость обустройства сада площадью 325 м 2 = рупий (55 × 325) = 17 875 рупий Форма сада прямоугольная в середине и полукруглая на концах, как показано на диаграмме. Найдите площадь и периметр сада [Длина прямоугольника 20 − (3,5 + 3,5) метра] Длина прямоугольника = [20 − (3,5 + 3,5)] метра = 13 м Окружность 1 полукруглой детали = π r Окружность обеих полукруглых частей = (2 × 11) м = 22 м Периметр сада = AB + Длина обеих полукруглых частей BC и DA + CD = 13 м + 22 м + 13 м = 48 м Площадь сада = площадь прямоугольника + 2 × площадь полукруглой области NCERT Решение для 8 класса по математике — измерение 171 , Вопрос 3 A
напольная плитка имеет форму параллелограмма с основанием 24 см. Площадь параллелограмма =
Основание × высота Следовательно, площадь одной плитки
= 24 см × 10 см = 240 см 2 Необходимое количество
плитки = =
45000 плиток Таким образом, 45000 плиток
требуется для покрытия пола площадью 1080 м 2 . Муравей двигается вокруг нескольких кусочков еды разной формы, разбросанных по полу. Для получения какого куска еды муравью потребуется больше времени? Помните, что длину окружности можно получить, используя выражение c = 2 πr , где r — радиус окружности. (a)Radius ( r ) of semi-circular part = Perimeter of the given figure = 2. (b)Radius ( r ) полукруглой части = Периметр данной фигуры = 1,5 см + 2,8 см + 1,5 см + π (1,4 см) (c) Радиус ( r ) полукруглой части = Периметр фигуры (с) = 2 см + π r + 2 см Таким образом, муравью придется дольше ходить за кусочком еды (b), потому что периметр фигуры, заданной в варианте (b), больше всех.
7 2 Номер страницы 171:
Вопрос 3:
Ответ:
№: 3)
Страница № 171:
Вопрос 4:
 и соответствующая высота 10 см. Сколько таких плиток
требуется для покрытия пола площадью 1080 м 2 ?
(При необходимости вы можете разделить плитки любым способом, которым вы хотите заполнить
вверх по углам).
и соответствующая высота 10 см. Сколько таких плиток
требуется для покрытия пола площадью 1080 м 2 ?
(При необходимости вы можете разделить плитки любым способом, которым вы хотите заполнить
вверх по углам). Ответ:
Страница № 171:
Вопрос 5:
Answer:
 8 cm + π r
8 cm + π r
Видео Решение для измерения (Страница: 171 , Q.No.: 5)
Решение NCERT для математики класса 8 — измерение 171 , Вопрос 5
Страница № 177:
Вопрос 1 :
Форма верхней поверхности стола — трапеция. Найдите его площадь, если его параллельные стороны равны 1 м и 1,2 м, а расстояние между ними по перпендикуляру 0,8 м.
E
Ответ:
Площадь трапеции = (Сумма параллельных сторон) × (Расстояния между параллельными сторонами)
Видео Решение для измерения (Страница: 177, Q.
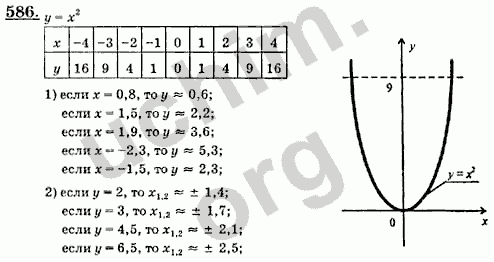 №: 1)
№: 1)NCERT Решение для 8 класса по математике — измерение 177, Вопрос 1
Страница № 178:
Вопрос 2:
площадь трапеции 34 см 2 а длина одной из параллельных сторон равна 10 см, а ее высота составляет 4 см. Найдите длину другой параллельной стороны.
Ответ:
Известно, что площадь трапеции = 34 см 2 и высота = 4 см
Пусть длина одной параллельная сторона a . Мы знаем, что
Площадь трапеции = (Сумма параллельных сторон) × (Расстояния между параллельными сторонами)
Таким образом, длина другая параллельная сторона равна 7 см.
Страница № 178:
Вопрос 3:
Длина ограждения поле в форме трапеции ABCD равно 120 м. Если BC = 48 м, CD = 17 м и AD = 40 м, найдите площадь этого поля. Сторона АВ перпендикулярна параллельные стороны AD и BC.
Ответ:
Длина забора трапеция ABCD = AB + BC + CD + DA
120 м = AB + 48 м + 17 м + 40 м
АВ = 120 м — 105 m = 15 м
Площадь поля ABCD
Страница № 178:
Вопрос 4:
Диагональ
поле в форме четырехугольника равно 24 м, а перпендикуляры опущены на
от остальных противоположных вершин 8 м и 13 м. Найди
площадь поля.
Найди
площадь поля.
Ответ:
Дано, что
Длина диагонали, d = 24 м
Длина перпендикуляры, h 1 и h 2 , от противоположных вершин до диагонали составляют ч 1 = 8 м и ч 2 = 13 м
Площадь четырехугольник
Таким образом, площадь поле 252 м 2 .
Страница № 178:
Вопрос 5:
Диагонали ромба равны 7,5 см и 12 см. Найдите его площадь.
Ответ:
Площадь ромба = (Товар его диагоналей)
Следовательно, площадь данного ромба
=
= 45 см 2
Страница № 178:
Вопрос 6:
Найдите площадь ромба со стороной 5 см и высотой 4,8 см. Найдите длину другой диагонали, если длина одной из ее диагоналей равна 8 см.
Ответ:
Пусть длина другой диагонали ромба равна х .
Ромб — частный случай параллелограмма.
Площадь параллелограмма равна произведению его основания на высоту.
Таким образом, площадь данного ромба = Основание × Высота = 5 см × 4,8 см = 24 см 2
другая диагональ ромба равна 6 см.
Видео Решение для измерения (Страница: 178 , Q.No.: 6)
Решение NCERT для 8 класса по математике — измерение 178 , Вопрос 6
Страница № 178:
Вопрос 7:
Пол здания состоит из 3000 плиток, которые представляют собой ромбы имеет форму и каждая из его диагоналей имеет длину 45 см и 30 см. Находить общая стоимость шлифовки пола, если стоимость за м 2 4 рупии.
Ответ:
Площадь ромба = (Товар его диагоналей)
Площадь каждой плитки
= 675 см 2
Площадь 3000 плиток = (675 × 3000) см 2 = 2025000 см 2 = 202,5 м 2
Стоимость полировки 4 рупии за м 2 .
Стоимость полировки 202,5 м 2 площадь = рупий (4 × 202,5) = 810
Таким образом, стоимость полировки пола составляет 810 рупий.
Страница № 178:
Вопрос 8:
Мохан хочет купить поле в форме трапеции. Его сторона вдоль реки параллельна и вдвое больше стороны вдоль дороги. Площадь этого месторождения составляет 10500 м 9 .0156 2 и расстояние по перпендикуляру между двумя параллельными сторонами равно 100 м, найдите длину стороны вдоль реки.
Ответ:
Пусть длина поля вдоль дороги л м. Отсюда длина поля по реке составит 2 l м.
Площадь трапеции = (Сумма параллельных сторон) (Расстояние между параллельными сторонами)
Таким образом, длина поля вдоль реки = (2 × 70) м = 140 м
Видео Решение для измерения (Страница: 178 , Q.No.: 8)
Решение NCERT для класса 8 по математике — измерение 178 , Вопрос 8
Страница № 178:
Вопрос 9:
Верх
поверхность приподнятой платформы имеет форму правильного восьмиугольника
показано на рисунке. Найдите площадь восьмиугольной поверхности.
Ответ:
Сторона правильного восьмиугольника = 5 см
Площадь трапеции ABCH = Площадь трапеции DEFG
Площадь прямоугольника HGDC = 11 × 5 = 55 м 2
Площадь восьмиугольника = Площадь трапеции ABCH + площадь трапеции DEFG
+ Площадь прямоугольника HGDC
= 32 м 2 + 32 м 2 + 55 м 2 = 119 м 2
Страница № 178:
Вопрос 10:
Существует пятиугольник Парк в форме, как показано на рисунке.
Для нахождения его площади Джиоти и Кавита поделили его двумя разными способами.
Найти площадь этого парка с использованием обоих способов. Можете ли вы предложить другой способ нахождения его площади?
Ответ:
Путь Джиоти площадь нахождения выглядит следующим образом.
Площадь пятиугольника = 2 (Площадь трапеции ABCF)
= 337,5 м 2
Путь Кавиты
площадь нахождения выглядит следующим образом.
Площадь пятиугольника = Площадь ΔABE + Площадь квадрата БКДЕ
Страница № 178:
Вопрос 11:
Схема соседней фоторамки имеет внешние размеры = 24 см × 28 см и внутренние размеры 16 см × 20 см. Найдите площадь каждой части рамы, если ширина каждой части одинакова.
Ответ:
При этом ширина каждой секции одинакова. Следовательно,
IB = BJ = CK = CL = DM = DN = AO = AP
IL = IB + BC + CL
28 = IB + 20 + CL
IB + CL = 28 см − 20 см = 8 см
IB = CL = 4 см
Отсюда IB = BJ = CK = CL = DM = DN = AO = AP = 4 см
Площадь сечения BEFC = Площадь сечения DGHA
Площадь сечения ABEH = Площадь сечения CDGF
⇒ Площадь сечения ABEH = Площадь сечения CDGF
= 1216+244=80 см2
Страница № 186:
Вопрос 1:
Имеются две прямоугольные коробки, как показано на соседнем рисунке. Для изготовления какой коробки требуется меньше материала?
Ответ:
Мы знаем, что
Общая площадь поверхности куба = 2 ( lh + bh + lb )
Общая площадь поверхности куба = 6 (
Общая площадь прямоугольного параллелепипеда (a) = [2{(60) (40) + (40) (50) + (50) (60)}] см 2
= [2(2400 + 2000) + 3000)] см 2
= (2 × 7400) см 2
= 14800 см 2
Общая площадь поверхности куба (b) = 6 (50 см) 2 = 15000 см 2
Таким образом, кубовидная коробка (а) потребует меньшего количества материала.
Видео Решение для измерения (Страница: 186 , Q.No.: 1)
Решение NCERT для класса 8 по математике — измерение 186 , Вопрос 1
Страница № 186:
Вопрос 2:
А чемодан с размерами 80 см × 48 см × 24 см должен быть покрытые брезентовой тканью. Сколько метров брезента шириной 96 см требуется, чтобы покрыть 100 таких чемоданов?
Ответ:
Общая площадь чемодан = 2[(80) (48) + (48) (24) + (24) (80)]
= 2[3840 + 1152 + 1920]
= 13824 см 2
Общая площадь 100 чемоданов = (13824 × 100) см 2 = 1382400 см 2
Требуемый брезент = Длина × Ширина
1382400 см 2 = Длина × 96 см
Длина = = 14400 см = 144 м
Таким образом, 144 м брезента требуется, чтобы покрыть 100 чемоданов.
Страница № 186:
Вопрос 3:
Найти сторона куба, площадь поверхности которого 600 см 2 .
Ответ:
Учитывая, что поверхность площадь куба = 600 см 2
Пусть длина каждого
сторона куба l .
Площадь поверхности куба = 6 (сбоку) 2
600 см 2 = 6 л 2
л 2 = 100 см 2
l = 10 см
Таким образом, сторона куб равен 10 см.
Страница № 186:
Вопрос 4:
Рухсар нарисовал вне шкафа измерения 1 м × 2 м × 1,5 м. Как сколько площади поверхности она покроет, если закрасит все, кроме дна кабинета?
Ответ:
Длина ( l ) шкаф = 2 м
Ширина ( b ) шкаф = 1 м
Высота ( h ) шкаф = 1,5 м
Площадь шкафа что было окрашено = 2 ч ( л + б ) + фунт
= [2 × 1,5 × (2 + 1) + (2) (1)] м 2
= [3(3) + 2] м 2
= (9 + 2) м 2
= 11 м 2
Страница № 186:
Вопрос 5:
Дэниел красит стены и потолок прямоугольного зала красками.
длина, ширина и высота 15 м, 10 м и 7 м соответственно. Из
каждая банка краски 100 м 2 площади окрашены. Сколько банок
краски ей понадобится, чтобы покрасить комнату?
Из
каждая банка краски 100 м 2 площади окрашены. Сколько банок
краски ей понадобится, чтобы покрасить комнату?
Ответ:
Учитывая, что
Длина ( l ) = 15 м, ширина ( b ) = 10 м, высота ( h ) = 7 м
Площадь зала под покраску = Площадь стены + Площадь пола потолок
= 2 ч ( л + b ) + фунт
= [2(7) (15 + 10) + 15 × 10] м 2 9000 ) + 150] м 2
= 500 м 2
Дано, что 100 м 2 площади можно покрасить из каждого Можно.
Количество банок, необходимых для покраски площади 500 м 2
=
Следовательно, для покраски стен и потолка кубический зал.
Страница № 186:
Вопрос 6:
Опишите, как эти два фигуры справа похожи и чем они отличаются. Какая коробка имеет большую площадь боковой поверхности?
Ответ:
Сходство между обоими
цифры в том, что оба имеют одинаковую высоту.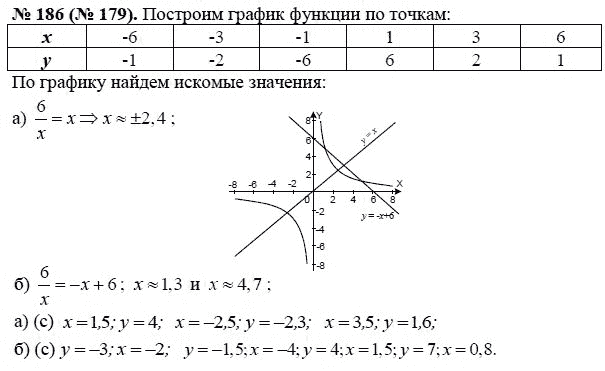
Разница между две фигуры в том, что одна — цилиндр, а другая — куб.
Площадь боковой поверхности куб = 4 л 2 = 4 (7 см) 2 = 196 см 2
Площадь боковой поверхности цилиндр = 2π rh см 2 = 154 см 2
Следовательно, куб имеет большая площадь боковой поверхности.
Страница № 186:
Вопрос 7:
A закрытый цилиндрический резервуар радиусом 7 м и высотой 3 м изготовлен из лист металла. Сколько листов металла требуется?
Ответ:
Общая площадь цилиндр = 2π r ( r + ч )
м 2
= 440 м 2
Таким образом, 440 м 2 нужен лист металла.
Страница № 186:
Вопрос 8:
площадь боковой поверхности полого цилиндра 4224 см 2 . Его разрезали по высоте и образовали прямоугольный лист шириной 33 см. Найдите периметр прямоугольного листа?
Ответ:
Полый цилиндр
разрезать по высоте, чтобы получился прямоугольный лист.
Площадь цилиндра = Площадь из прямоугольного листа
4224 см 2 = 33 см × длина
Таким образом, длина прямоугольный лист 128 см.
Периметр прямоугольный лист = 2 (Длина + Ширина)
= [2 (128 + 33)] см
= (2 × 161) см
= 322 см
Страница № 186:
Вопрос 9:
Дорожный каток совершает 750 полных оборотов, чтобы проехать один раз и выровнять дорогу. Найдите площадь дороги, если диаметр дорожного катка 84 см, а длина 1 м.
Ответ:
За один оборот ролик покроет площадь, равную площади его боковой поверхности.
Таким образом, за 1 оборот площадь пройденной дороги = 2π rh
За 750 оборотов пройдена площадь дороги
=
= 1980 м 2
Видео Решение 6 P
, Q.No.: 9)
Решение NCERT для класса 8 по математике — измерение 186 , Вопрос 9
Номер страницы 186:
Вопрос 10:
Компания упаковывает свои
сухое молоко в цилиндрической емкости, основание которой имеет диаметр 14
см и высотой 20 см. Компания размещает этикетку вокруг поверхности
емкость (как показано на рисунке). Если этикетка находится на расстоянии 2 см от
сверху и снизу, какова площадь этикетки.
Компания размещает этикетку вокруг поверхности
емкость (как показано на рисунке). Если этикетка находится на расстоянии 2 см от
сверху и снизу, какова площадь этикетки.
Ответ:
Высота этикетки = 20 см − 2 см − 2 см = 16 см
Радиус этикетки
Этикетка в форме цилиндр, радиус и высота которого равны 7 см и 16 см.
Площадь этикетки = 2π (Радиус) (Высота)
Страница № 191:
Вопрос 1:
Дан цилиндрический танк, в каком положении вы найдете площадь поверхности и в каком объем ситуации.
(а) Чтобы узнать, сколько может держать
(b) Номер цемента мешки, необходимые для его штукатурки
(c) Найдите количество меньших баков, которые можно наполнить водой из Это.
Ответ:
(a) В этой ситуации мы найдем объем.
(b) В этой ситуации найдем площадь поверхности.
(c) В этой ситуации мы найдем объем.
Страница № 191:
Вопрос 2:
Диаметр цилиндра A
7 см, а высота 14 см. Диаметр цилиндра В равен 14 см и
высота 7см. Не производя расчетов, можете ли вы предположить, чьи
объем больше? Проверьте это, найдя объем обоих
цилиндры. Проверьте, не имеет ли цилиндр большего объема также
площадь поверхности больше?
Диаметр цилиндра В равен 14 см и
высота 7см. Не производя расчетов, можете ли вы предположить, чьи
объем больше? Проверьте это, найдя объем обоих
цилиндры. Проверьте, не имеет ли цилиндр большего объема также
площадь поверхности больше?
Ответ:
Высоты и диаметры этих цилиндров А и В равны поменяны местами.
Мы это знаем,
Объем цилиндра
Если меры r и h совпадают, то цилиндр большего радиуса будет имеют большую площадь.
Радиус цилиндра A = см
Радиус цилиндра B = см = 7 см
По радиусу цилиндр В больше, поэтому объем цилиндра В будет больше.
Давайте проверим это по расчет объема обоих цилиндров.
Объем цилиндра A
Объем цилиндра B
Объем цилиндра B больше.
Площадь поверхности цилиндр А
Площадь поверхности цилиндр В
Таким образом, площадь поверхности
цилиндра B также больше, чем площадь поверхности цилиндра A.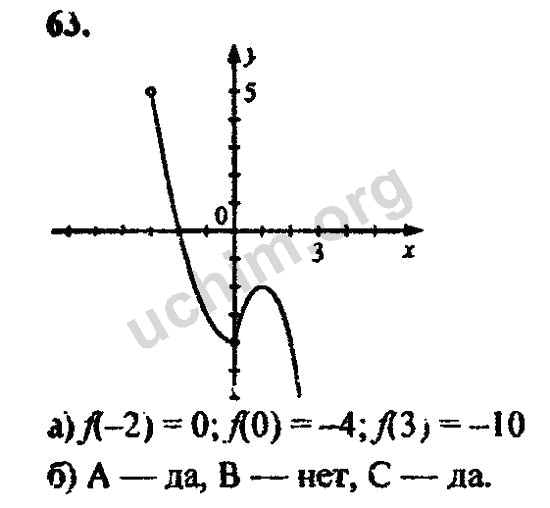
Страница № 191:
Вопрос 3:
Найти высота прямоугольного параллелепипеда, площадь основания которого равна 180 см 2 и объем 900 см 3 ?
Ответ:
Площадь основания прямоугольного параллелепипеда = Длина × Ширина = 180 см 2
Объем прямоугольного параллелепипеда = Длина × Ширина × Высота
900 см 3 = 180 см 2 × Высота
Таким образом, высота куб 5 см.
Страница № 191:
Вопрос 4:
A кубоид имеет размеры 60 см × 54 см × 30 см. Как много в данный прямоугольный параллелепипед можно поместить маленькие кубики со стороной 6 см?
Ответ:
Объем параллелепипеда = 60 см × 54 см × 30 см = 97200 см 3
Сторона куба = 6 см
Объем куба = (6) 3 см 3 = 216 см 3
Необходимое количество кубики =
Таким образом, можно получить 450 кубов.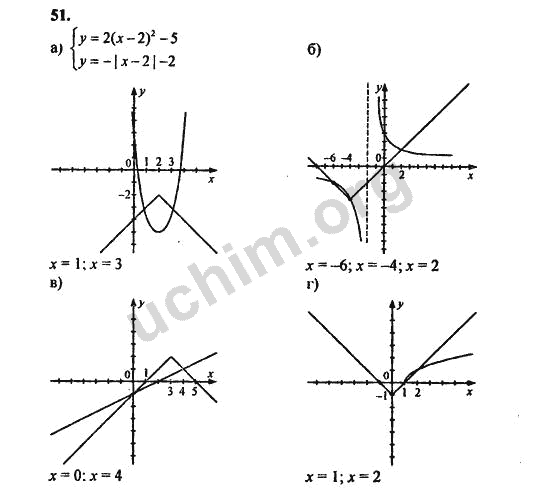 помещается в данный кубоид.
помещается в данный кубоид.
Страница № 191:
Вопрос 5:
Найти высота цилиндра объемом 1,54 м 3 а диаметр основания 140 см?
Ответ:
Диаметр основания = 140 см
Радиус ( r ) из база
Объем цилиндра
Таким образом, высота цилиндр 1м.
Страница № 191:
Вопрос 6:
Молочная цистерна имеет форму цилиндра радиусом 1,5 м и длиной 7 м. Найдите количество молока в литрах, которое можно хранить в баке?
Ответ:
Радиус цилиндра = 1,5 м
Длина цилиндра = 7 м
Объем цилиндра
1 м 3 = 1000 л
Необходимое количество = (49,5 × 1000) л = 49500 л
Таким образом, в баке может храниться 49500 л молока.
Видеорешение для измерения (Страница: 191 , Q.No.: 6)
Решение NCERT для математики класса 8 — измерение 191 , Вопрос 6
Страница № 191 :
Вопрос 7:
Если каждое ребро куба удваивается,
(i) сколько раз будет площадь его поверхности увеличилась?
(ii) как во сколько раз увеличится его объем?
Ответ:
(i) Пусть изначально
ребра куба быть l .
Начальный площадь поверхности = 6 л 2
Если каждое ребро куба удваивается, тогда получается 2 l .
Новый площадь поверхности = 6(2 л ) 2 = 24 л 2 = 4 × 6 л 2
Понятно, площадь поверхности увеличится в 4 раза.
(ii) Начальный объем куб = л 3
Когда каждое ребро куба удваивается, получается 2 l .
Новый объем = (2 л ) 3 = 8 л 3 = 8 × л 3
Понятно, объем куба увеличится в 8 раз.
Страница № 192:
Вопрос 8:
Вода выливается в кубический резервуар со скоростью 60 литров в минуту. Если объем резервуара 108 м 3 , найдите количество часов, которое потребуется для заполнения резервуара.
Ответ:
Объем кубовидного резервуара = 108 м 3 = (108 × 1000) л = 108000 л
Дано, что вода выливается со скоростью 60 л в минуту.
То есть (60 × 60) L = 3600 л в час
Необходимое количество часов = 30 часов
Таким образом, наполнение резервуара займет 30 часов.
Видеорешение для измерения (Страница: 192 , Q.No.: 8)
Решение NCERT для класса 8 по математике — измерение 192 , вопрос 8
Как комбинировать множества с объединениями, пересечениями и дополнениями
Автор: Мэри Джейн Стерлинг и
Обновлено : 26-03-2016
Линейная алгебра для чайников
Исследовать книгу Купить на Amazon
Наборы элементов можно комбинировать или изменять с помощью операций над наборами. Подобно сложению или вычитанию действительных чисел, операции над множествами строго определены, чтобы что-то делать с задействованными множествами. Операции над множествами — это объединение, пересечение и дополнение:
Объединение двух наборов A и B запрашивает все элементы наборов A и B — все вместе (без повторения каких-либо общих элементов).

Пересечение двух наборов A и B запрашивает все элементы, которые имеют общие элементы A и B . Если два множества не имеют ничего общего, то ваш ответ — 9.0231 пустой набор или нулевой набор .
дополнение набора A запрашивает все элементы, которые не не в наборе, но находятся в универсальном наборе. Универсальный набор — это все, что рассматривается в данный момент. Например, если вы работаете с наборами, содержащими буквы английского алфавита, универсальный набор состоит из 26 букв.
Примеры вопросов
Даны наборы A = {2, 4, 6, 8}, B = {4, 8, 16, 24, 32}, C = {3, 6, 9, 12, 15 , 18, 21}, а универсальный набор —
Объединение A и B состоит из всех элементов A и B , поэтому
Обратите внимание, что цифры 4 и 8 не повторяются.
 Пересечение A и B состоит из всех общих элементов двух наборов, поэтому
Пересечение A и B состоит из всех общих элементов двух наборов, поэтомуПересечение B и C — это все элементы, которые являются общими для двух наборов, но эти два набора не имеют ничего общего, поэтому
Комплектация набора C состоит из всего, что есть в универсальном наборе , а не в наборе C , поэтому
Учитывая наборы D = {0, 1, 2, 3, 4}, E = {0, 2, 6, 10}, F = {1, 3, 6, 10}, и U = {0, 1, 2, 3, … , 10}, найти наборы
Скобки в этих задачах с операциями над множествами работают так же, как скобки в алгебраических выражениях — сначала вы выполняете то, что находится внутри скобок. Чтобы найти дополнение пересечения множеств D и F , сначала нужно найти пересечение D и F = {1, 3}; затем, вернувшись к универсальному набору U , вы найдете дополнение:
Дополнением является все , кроме 1 и 3 на пересечении. Чтобы найти пересечение двух объединений, сначала найдите два объединения: объединение D и E = {0, 1, 2, 3, 4, 6, 10} и объединение E и Ф = {0, 1, 2, 3, 6, 10}. Вы записываете пересечение — что общего между двумя результатами — как
Чтобы найти пересечение двух объединений, сначала найдите два объединения: объединение D и E = {0, 1, 2, 3, 4, 6, 10} и объединение E и Ф = {0, 1, 2, 3, 6, 10}. Вы записываете пересечение — что общего между двумя результатами — как
Практические вопросы
1 .Для множеств A = {0, 2, 4, 6, 8, …, 20}, B = {0, 5, 10, 15, 20}, C = {7, 11, 17} и универсальный набор U = {0, 1, 2, 3, 4, …, 20 }, найти пересечение A и B .
2 .Для множеств A = {0, 2, 4, 6, 8, …, 20}, B = {0, 5, 10, 15, 20}, C = { 7, 11, 17} и универсальный набор U = {0, 1, 2, 3, 4, … , 20}, найти объединение A и B .
Ниже приведены ответы на практические вопросы:
Ответ: {0, 10, 20}.
В наборах A и B используются только эти три элемента.
Ответ: {0, 2, 4, 5, 6, 8, 10, 12, 14, 15, 16, 18, 20}.