Алгебра 7. Карточки-задания | Учебно-методический материал по алгебре (7 класс):
Тема. «Значение числового выражения» (1 уровень) Алгебра – 7
Найти значение числового выражения
1) , 2) ,
3) , 4) .
Тема. «Значение числового выражения» (2 уровень) Алгебра – 7
Найти значение числового выражения
1) , 2) ,
3) , 4) .
Тема. «Значение числового выражения» (2 уровень) Алгебра – 7
Вычислить:
- сумму квадратов чисел 3,1 и 2,9;
- квадрат разности чисел 5,3 и -4,7;
- куб суммы чисел 1,37 и -1,35.
Тема. «Значение числового выражения» (3 уровень) Алгебра – 7
Вычислить:
1) , 2) ,
3) , 4) .
……………………………………………………………………………………………………. .
.
Тема. «Алгебраические выражения» (1 уровень) Алгебра – 7
Найти значение выражения:
1) при ;
2) при ;
3) при ;
4) при .
Тема. «Алгебраические выражения» (2 уровень) Алгебра – 7
Найти значение выражения:
1) при и ; и ;
2) при и ; и .
Тема. «Алгебраические выражения» (2 уровень) Алгебра – 7
Найти значение выражения:
1) при и ; и ;
2) при и ; .
Тема. «Алгебраические выражения» (3 уровень) Алгебра – 7
Найти значение выражения:
1) при и ;
2) при и .
………………………………………………………………………………………………………
Тема. «Свойства арифметических действий» (1 уровень) Алгебра – 7
Вычислить наиболее рациональным способом:
1) ;
2) .
Тема. «Свойства арифметических действий» (2 уровень) Алгебра – 7
Вычислить наиболее рациональным способом:
1) 2)
3) 4) .
Тема. «Свойства арифметических действий» (2 уровень) Алгебра – 7
Найти значение выражения, используя распределительное свойство умножения:
1) , 2) , 3) , 4) .
Тема. «Свойства арифметических действий» (3 уровень) Алгебра – 7
Разберите, как выполнено умножение:
.
Используя данный прием, выполните вычисления:
1) , 2) , 3) ,
4) , 5) , 6) .
………………………………………………………………………………………………………
Тема. «Правила раскрытия скобок» (1 уровень) Алгебра – 7
Раскрыть скобки:
1) , 2) ,
3) , 4) ,
5) , 6) ,
7) , 8) .
Тема. «Правила раскрытия скобок» (1 уровень) Алгебра – 7
Раскрыть скобки и привести подобные слагаемые:
1) , 2) , 3) , 4) ,
5) , 6) ,
7) , 8) .
Тема. «Правила раскрытия скобок» (2 уровень) Алгебра – 7
Упростить выражение:
1) , 2) ,
3) , 4) ,
5) , 6) ,
7) , 8) .
Тема. «Правила раскрытия скобок» (3 уровень) Алгебра – 7
Раскрыть скобки и упростить:
1) , 2) ,
3) , 4) .
Тема. «Правила раскрытия скобок» (3 уровень) Алгебра – 7
Найти значение выражения:
1) при ;
2) при ;
3) при ;
4) при .
………………………………………………………………………………………………………
Тема. «Решение уравнений» (1 уровень) Алгебра – 7, § 2.
Решить уравнение:
1) , 2) ,
3) , 4) ,
5) , 6) .
Тема. «Решение уравнений» (1 уровень) Алгебра – 7, § 2.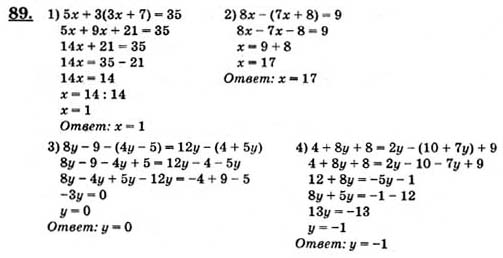
Решить уравнение:
1) , 2) ,
3) , 4)
Тема. «Решение уравнений» (2 уровень) Алгебра – 7, § 2.
Решить уравнение:
1) , 2) ,
3) , 4) .
Тема. «Решение уравнений» (3 уровень) Алгебра – 7, § 2.
Решить уравнение:
1) ,
2) ,
3) ,
4).
Тема. «Решение уравнений» (3 уровень) Алгебра – 7, § 2.
При каком значении а:
1) значение выражения равно значению выражения ;
2) значение выражения в три раза больше значения выражения ;
3) значение выражения в два раза меньше значения выражения ;
4) значение выражения на 5 больше значения выражения ;
5) разность выражений и равна 36?
……………………………………………………………………………………………………. ..
..
Тема «Решение задач с помощью уравнений» (2 уровень) Алгебра – 7, § 3.
1) Двое рабочих изготовили 657 деталей, причем первый изготовил на 63 детали больше второго. Сколько деталей изготовил каждый?
2) Папе и дедушке вместе 111 лет. Сколько лет каждому, если папа в 2 раза моложе дедушки?
Тема «Решение задач с помощью уравнений» (3 уровень) Алгебра – 7, § 3.
1) За 3 ч мотоциклист проезжает то же расстояние, что велосипедист за 5 ч. Скорость мотоциклиста на 12 км/ч больше скорости велосипедиста. Определите скорость каждого.
2) На двух садовых участках 84 яблони. Если с одного из них пересадить на другой 1 яблоню, то на нем станет в 3 раза больше яблонь, чем останется на другом. Сколько яблонь на каждом участке?
…………………………………………………………………………………………………….
Тема «Свойства степени с натуральным показателем» (1 уровень) Алгебра – 7, § 6.
1) Возвести в степень произведение:
а) , б) в) , г) .
2) Вычислить значение выражения, используя свойство степени произведения:
а) б) , в) , г) .
Тема «Свойства степени с натуральным показателем» (2 уровень) Алгебра – 7, § 6
1) Выполнить возведение в степень:
а) , б) , в) , г) .
2) Упростить выражение:
а) , б) , в) , г) ,
д) , е) , ж) , з) .
Тема «Свойства степени с натуральным показателем» (3 уровень) Алгебра – 7, § 6
Найти значение выражения, используя свойства степеней:
1) , 2) . 3) , 4) ,
5) , 6) , 7) , 8) .
……………………………………………………………………………………………………..
Тема «Стандартный вид одночлена» (1 уровень) Алгебра – 7, § 7.
№1. Выполнить умножение:
1) , 2) , 3) ,
4) , 5) , 6) .
№2. Перемножить одночлены:
1) ,
2) .
Тема «Стандартный вид одночлена» (1 уровень) Алгебра – 7, § 7.
Выполнить возведение одночлена в степень:
1) , 2) , 3) , 4) ,
5) , 6) , 7) , 8) .
Тема «Стандартный вид одночлена» (2 уровень) Алгебра – 7, § 7.
Упростить выражение:
1) , 2) , 3) ,
4) , 5) , 6).
Тема «Стандартный вид одночлена» (3 уровень) Алгебра – 7, § 7.
Представить в виде одночлена стандартного вида:
1) , 2) ,
3) , 4) .
…………………………………………………………………………………………………….
Тема «Приведение подобных членов» (1 уровень) Алгебра – 7
Привести подобные члены:
1) , 2) ,
3) , 4) ,
5) , 6) .
Тема «Приведение подобных членов» (2 уровень) Алгебра – 7
Упростить выражение и найти его значение:
1) при ,
2) при ,
3) при .
……………………………………………………………………………………………………..
Тема «Сложение и вычитание многочленов» (1 уровень) Алгебра – 7, § 9
Составить сумму и разность многочленов и привести к стандартному виду:
1) и , 2) и ,
3) и , 4) и ,
5) и , 6) и .
Тема «Сложение и вычитание многочленов» (2 уровень) Алгебра – 7, § 9
Упростить выражение:
1) , 2) ,
3) , 4) .
…………………………………………………………………………………………………….
Тема «Умножение одночлена на многочлен» (1 уровень) Алгебра – 7, § 10
Выполнить умножение:
1) , 2) , 3) , 4) ,
5) , 6) , 7) ,
8) , 9) , 10) .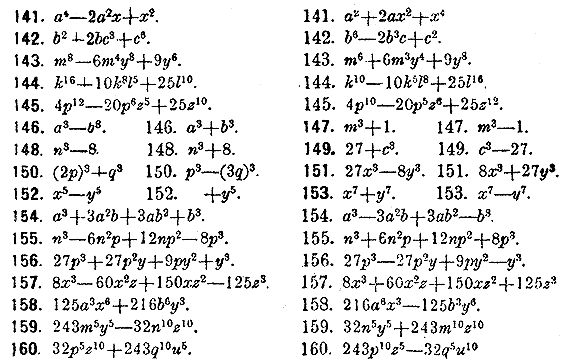
Тема «Умножение одночлена на многочлен» (2 уровень) Алгебра – 7, § 10
Упростить выражение:
1) , 2) , 3) ,
4) , 5) , 6) .
Тема «Умножение одночлена на многочлен» (2 уровень) Алгебра – 7, § 10
Упростить выражение:
1) , 2) ,
3) , 4) .
Тема «Умножение одночлена на многочлен» (3 уровень) Алгебра – 7, § 10
Упростить выражение и найти его значение:
1) при ,
2) при .
…………………………………………………………………………………………………….
Тема «Умножение многочленов» (1 уровень) Алгебра – 7, § 11
Выполнить умножение:
1) , 2) ,
3) , 4) ,
5) , 6) .
Тема «Умножение многочленов» (2 уровень) Алгебра – 7, § 11
Выполнить умножение:
1) , 2) ,
3) , 4) ,
5) , 6) .
Тема «Умножение многочленов» (3 уровень) Алгебра – 7, § 11
Выполнить умножение:
1) , 2) ,
3) , 4) ,
5) , 6) .
………………………………………………………………………………………………………
Тема «Вынесение общего множителя за скобки» (1 уровень) Алгебра – 7, § 12
Вынести общий множитель за скобки:
1) , 2) ,
3) , 4) ,
5) , 6) ,
7) , 8) .
Тема «Вынесение общего множителя за скобки» (1 уровень) Алгебра – 7, § 12
Вынести общий множитель за скобки:
1) , 2) ,
3) , 4) ,
5) , 6) ,
7) , 8) .
Тема «Вынесение общего множителя за скобки» (2 уровень) Алгебра – 7, § 12
Вынести общий множитель за скобки:
1) ,
2) ,
3) ,
4) ,
5) .
……………………………………………………………………………………………………. .
.
Тема «Способ группировки» (1 уровень) Алгебра – 7, § 20.
Вынести общий множитель за скобки:
1) , 2) ,
3) , 4) ,
5) , 6) .
Тема «Способ группировки» (2 уровень) Алгебра – 7, § 13
Разложите на множители:
1) , 2) ,
3) , 4) ,
5) , 6) .
Тема «Способ группировки» (3 уровень) Алгебра – 7, § 13
№1. Разложите на множители:
1) ,
2) ,
3) ,
4)
№2. Разберите, как выполнено разложение на множители многочлена ;
= .
Разложите на множители:
а) ; б) .
……………………………………………………………………………………………………..
Тема «Разность квадратов» (1 уровень) Алгебра – 7, § 15
Выполнить умножение:
1) , 2) ,
3) , 4) ,
5) , 6) ,
7) , 8) .
Тема «Разность квадратов» (2 уровень) Алгебра – 7, § 15
Выполнить умножение:
1) , 2) ,
3) , 4) ,
5) , 6) .
Тема «Разность квадратов» (3 уровень) Алгебра – 7, § 15
Выполнить умножение:
1) , 2) ,
3) , 4) ,
5) , 6) ,
7) .
……………………………………………………………………………………………………
Тема «Квадрат суммы. Квадрат разности» (1 уровень) Алгебра – 7, § 16
Выполнить преобразования по соответствующей формуле:
1) , 2) , 3) ,
4) , 5) , 6) ,
7) , 8) , 9) ,
10) , 11) , 12) .
………………………………………………………………………………………………
Алгебраические дроби
1 вариант
Выполнить действия
1) , 2) , 3) , 4),
5) :, 6) : , 7) : , 8) : ,
9) : , 10) , 11) , 12) : 6а,
13) : (), 14) ,
15) : , 16) : .
2 вариант
Выполнить действия
1) , 2) , 3) , 4),
5) :, 6) : , 7) : , 8) : ,
9) : , 10) , 11) , 12) : 6а,
13) : (), 14) ,
15) : , 16) : .
3 вариант
Выполнить действия
1) , 2) , 3) , 4),
5) :, 6) : , 7) : , 8) : ,
9) : , 10) , 11) , 12) : 6а,
13) : (), 14) ,
15) : , 16) : .
вариант | II | вариант | |
№ задания | Номер правильного ответа/ответ | № задания | Номер правильного ответа/ответ |
I | часть | I | часть |
1 | 3 | 1 | 1 |
2 | 1 | 2 | 4 |
3 | 4 | 3 | 1 |
4 | 1 | 4 | 2 |
5 | 2 | 5 | 3 |
6 | 4 | 6 | 1 |
7 | 4 | 7 | 2 |
8 | 3 | 8 | 3 |
II | часть | II | часть |
1 | при х=-5 | 1 | при х=4 |
2 | х=-7 | 2 | х=-9,5 |
3 | b=19 | 3 | b=3 |
4 | 60 | 4 | 100 |
5 | 6 | 5 | 1 |
Математические задания и игры для 7-го класса
Как математические игры и занятия повышают уровень знаний учащихся 7-го класса
Математические игры и занятия могут быть отличным средством, дополняющим и поддерживающим обучение математике. Использование математических игр в классе позволяет учащимся практиковать математику не только весело, но и эффективно. Ученики любят игры, потому что они увлекательны и увлекательны, а учителя любят игры, потому что они помогают учащимся практиковать то, чему они научились.
Учащиеся 7 класса развивают навыки абстрактного и количественного мышления и узнают о важности использования репрезентативных выборок для построения выводов. Они изучают соотношения, чертежи в масштабе, рациональные и отрицательные числа, а также способы графического отображения пропорциональных отношений. Решению реальных задач (включая такие объекты, как треугольники, четырехугольники и многоугольники) и практике расчета процентов и скидок помогают занятия, использующие различные модели.
Они изучают соотношения, чертежи в масштабе, рациональные и отрицательные числа, а также способы графического отображения пропорциональных отношений. Решению реальных задач (включая такие объекты, как треугольники, четырехугольники и многоугольники) и практике расчета процентов и скидок помогают занятия, использующие различные модели.
для десятичных дробей
Физические и визуальные модели десятичных дробей трудно расширить более чем на несколько позиций, потому что размер модели резко меняется при перемещении с места на место. Просмотр десятичных дробей как суммы дробей дает учащимся другой способ думать о десятичных дробях.
Напишите на доске 237,9036 в стандартной десятичной форме и в виде суммы произведений.
Затем нарисуйте числовую линию, как показано ниже. Используйте стрелку, чтобы обозначить каждую цифру числа, написанного на доске. По мере того, как вы «выстраиваете» число, учащиеся могут видеть, как относительно мало цифра в каждом дополнительном десятичном разряде влияет на размер десятичной дроби.
По мере того, как вы «выстраиваете» число, учащиеся могут видеть, как относительно мало цифра в каждом дополнительном десятичном разряде влияет на размер десятичной дроби.
Начните с первых двух цифр: 2 3 _ . _ _ _ _
Обратите внимание, что даже если бы цифра десятков была 9 (максимально возможная), число не достигло бы 300. Напишите следующую цифру и нарисуйте ее стрелку: 2 3 7 . _ _ _ _
Обратите внимание, что даже если бы цифра единиц была 9 (наибольшая возможная), число не достигло бы 240. Продолжайте со следующей цифрой: 2 3 7 . 9 _ _ _
Обратите внимание, что хотя десятые доли равны 9 (максимальное возможное число), число не достигает 238. стрелка не может быть длиннее, чем стрелка перед ней.
Стратегии исследования
- Понять Спросите: «Если бы я продолжал рисовать стрелки, какой длины была бы стрелка для цифры «3» в тысячном разряде? Как это соотносится со стрелкой для «3» в разряде десятков?» Было бы слишком мало, чтобы увидеть.
 Потребовалось бы 10 000 из них от начала до конца, чтобы длина стрелки равнялась цифре «3» в разряде десятков.
Потребовалось бы 10 000 из них от начала до конца, чтобы длина стрелки равнялась цифре «3» в разряде десятков. - Оцените На доске напишите 1234 и 0,1234 . Спросите: «Как в каждом числе объединенное значение последних трех цифр соотносится со значением первой цифры?» В обоих случаях сумма цифр 2, 3 и 4 меньше 9.0076 1 ⁄ 4 значение первой цифры.
для деления на дроби
Напишите на доске 8 •
3 ⁄ 4 . Затем, как показано ниже, используйте графическую или физическую модель площади, чтобы показать, что умножение на 3 ⁄ 4 равносильно умножению на 3 и последующему делению на 4.
Since the fraction bar represents division, another way to think about 3 ⁄ 4 is 3 ÷ 4.
Think of multiplying by the fraction 3 ⁄ 4 как две операции с целыми числами:
Поскольку деление является обратным или обратным умножению, вы можете делить, используя противоположные операции, как мы использовали для умножения.
Подумайте о делят на фракцию 3 ⁄ 4 в виде двух операций с целыми числами:
40004, так как умножение на 4, а затем делится на 3, так же, как на умножение на 4. ⁄ 3 , чтобы разделить на 3 ⁄ 4 , можно умножить на 4 ⁄ 3 .
Стратегии исследования
- Анализ Предложите учащимся еще раз просмотреть последний шаг и отметить порядок: умножьте, затем разделите. Спросите: «Почему порядок двух операций не влияет на результат?» Если учащиеся думают о делении на 3 как об умножении на 1 ⁄ 3 , они могут указать коммутативное свойство умножения.

- Применить Спросите: «Когда одна дробь делится на другую дробь, имеет ли значение, какая дробь превращается в обратную? Используйте пример для объяснения». Да, это важно, потому что деление не коммутативно. Например, рассмотрим 1 ⁄ 2 ÷ 1 ⁄ 4 . Изменение 1 ⁄ 2 на 2 ⁄ 1 и умножение не дает правильного частного: 2 ⁄ 1 • 1
для уклона
Чтобы привлечь внимание учащихся к тому, как поведение функции отражается в форме ее графика, используйте модель, которая не использует числа и представляет различные типы наклонов.

Сравните эти модели, каждая из которых имеет свой тип шага или наклона, как показано ниже. Подчеркните, что наклон представляет собой отношение, которое связывает вертикальное изменение, подъем , или y , к горизонтальному изменению, пробег , или x . Обратите внимание, что три модели вверху показывают положительный рост слева направо, отражая положительное изменение в и .
Используйте тот же подход для моделей, которые показывают функции, которые «падают» слева направо, представляя отрицательный наклон, в котором изменение y отрицательно.
Стратегии запросов
- Понимание Скажите: «Представьте функцию, представленную моделью справа в верхнем ряду. Если х увеличить с 3 до 7, как приблизительно изменится и ? «Можете ли вы сказать, каким будет начальное и конечное значение и ? Почему или почему нет?» Около половины из 4 или 2; Нет.
 Модель не показывает значения x и y , а только относительные изменения x и y ; тем не менее, вы сможете определить, изображена ли функция на координатной плоскости.
Модель не показывает значения x и y , а только относительные изменения x и y ; тем не менее, вы сможете определить, изображена ли функция на координатной плоскости. - Подать заявку Объясните, что магазин продает подержанные компакт-диски по 2,25 доллара за штуку. Спросите: «Какая из 6 вышеперечисленных моделей лучше всего отражает зависимость общей стоимости от количества купленных компакт-дисков? Объяснять.» Модель в середине верхнего ряда; для каждой единицы справа пробег — количество купленных компакт-дисков — рост, или увеличение доллара, составляет около 2,25 единиц. Изменение подъема больше, чем изменение пробега.
для длины-площади-объема
Создайте графическое изображение, чтобы показать взаимосвязь между длиной, площадью и объемом.
1. Начните с единичного куба. Постройте два других куба, у одного длина ребра в два раза больше, а у другого длина ребра в три раза больше, чем у исходного куба.
Начните с единичного куба. Постройте два других куба, у одного длина ребра в два раза больше, а у другого длина ребра в три раза больше, чем у исходного куба.
2. Разберите каждый больший куб на единичные квадраты и сложите каждую группу так, чтобы получилась полоса, показывающая общее количество единичных квадратов и кубов. Это создает тройную гистограмму, как показано ниже.
3. Используя разные цвета для каждого из них, нарисуйте линию или кривую через верхнюю часть длины каждого ребра, верхнюю часть полос площади и верхнюю часть полос громкости.
Стратегии исследования
- Оценка Спросите: «Если вы сделаете каждое ребро куба в 10 раз длиннее, что произойдет с площадью поверхности и что произойдет с объемом? Площадь поверхности увеличится в 100 раз, а объем увеличится в 1000 раз.
- Применить Спросите: «Если щенок за год вырастет в два раза выше, что, по вашему мнению, произойдет с его весом? Почему?» Щенок будет весить примерно в 8 раз больше, потому что его объем будет примерно в 8 раз больше.

для среднего и медианного значения
Используйте гистограмму данных, чтобы проиллюстрировать разницу между
средним и медианным .- Начните с графика, подобного приведенному ниже, на котором показаны голы, забитые в 11 футбольных матчах.
- Затем отобразите данные в порядке от наименьшего к наибольшему. На перестроенном графике отобразите медиану и среднее значение, как показано.
Стратегии исследования
- Анализ Спросите: «Почему среднее значение этих данных больше медианы?» Обсудите, как каждая мера описывает средний балл . Учащиеся должны увидеть, что четыре результативные игры показывают среднее значение, а не медиану. Если бы в каждой из этих результативных игр было забито на два гола меньше, медиана осталась бы прежней, но среднее значение было бы меньше.

- Вычислить Напишите или просто произнесите следующее утверждение: В общем, если вы найдете, насколько далеко каждое значение данных от среднего, сумма различий выше среднего равна сумме ниже. Предложите учащимся использовать модель, чтобы решить, верно ли утверждение и почему. Утверждение верно. На модели суммы разностей обозначены красной и зеленой областями. Зеленая область выше среднего соответствует красной области ниже среднего.
для умножения многочленов
На рисунках ниже показано, как частичные произведения, полученные при умножении полиномов, аналогичны произведениям, полученным при умножении чисел.
Пример с числами: Умножить 4 × 357.
Пример с полиномами: 3 0 Умножить0017 x ( x 2 + 2 x — 6)
Стратегии запросов
- Analyze на плате.

- Применить Напишите 5 b ( a + b + c ) на доске. Спросите: «Будет ли этот продукт содержать термин 5 ab 2 c ? Почему или почему нет?» Нет. Термин 5b умножается на a , на b и на c , в результате чего получается 3 непохожих термина, ни один из которых не содержит все 3 переменные a , b и c . .
для процентного изменения
Используйте визуальные модели и вырезки, чтобы подчеркнуть, как процентное увеличение или уменьшение описывает размер изменения по отношению к исходной сумме.

Используйте аналогичную процедуру для моделирования процентного уменьшения на 25%.
Стратегии запросов
- Подать заявку Спросите: «На сколько процентов увеличится цена билета на бейсбольный матч, если она удвоится? А если утроится? Объяснять.» Когда что-то удваивается, сумма увеличения равна исходной сумме, поэтому процентное увеличение составляет 100%. Когда что-то увеличивается втрое, увеличение в два раза превышает первоначальную сумму, поэтому процентное увеличение составляет 200%.
- Проанализируйте Попросите учащихся объяснить, чем отличаются два приведенных ниже утверждения. В каждом случае попросите их указать процент увеличения.
- Цена бензина на этой неделе составляет 120% от цены прошлой недели.
- Цена на бензин выросла на 120% с прошлой недели.
- Оператор A сравнивает новую цену со старой ценой, оператор B сравнивает изменение со старой ценой.
 Утверждение A описывает увеличение на 20 %, а B описывает увеличение на 120 % — в 6 раз больше, чем увеличение в первом утверждении!
Утверждение A описывает увеличение на 20 %, а B описывает увеличение на 120 % — в 6 раз больше, чем увеличение в первом утверждении!
для отношения периметр-площадь
Постройте график, чтобы показать отношения между длиной стороны, периметром и площадью.
1. Начните с квадрата и постройте три других, больших квадрата со сторонами, длина которых в два, три и четыре раза превышает длину стороны исходного квадрата.
2. Разберите каждый больший квадрат на единичные квадраты и сложите единичные квадраты, чтобы построить гистограмму.
3 Нарисуйте линию рядом с каждой стопкой единичных квадратов, чтобы показать общую длину стороны или периметр каждого построенного квадрата.
4. Проведите линию через вершины стержней периметра и кривую через вершины площадных стержней.
Стратегии исследования
- Применить Спросите: «Если каждую сторону квадрата увеличить в 10 раз, что произойдет с периметром и что произойдет с площадью? Периметр будет в 10 раз больше, а площадь в 100 раз больше.
- Оценить Спросите: «Если удвоить размеры треугольника, что произойдет с площадью? Почему? Площадь увеличилась вчетверо. Возможное объяснение: и основание, и высота удваиваются. Когда вы умножаете их, чтобы найти площадь, вы получаете площадь в четыре раза больше.
для вероятности
Используйте прямоугольник, чтобы показать, почему произведение
1 ⁄ 6 × 1 ⁄ 6 можно использовать, чтобы найти вероятность выпадения 5, а затем еще 5, когда куб с числами 1–6 выбрасывается дважды. 1. Разделите прямоугольник на 6 равных частей, чтобы показать, сколько раз, по вашему мнению, выпадет каждое число на кубике с числами от 1 до 6 при многократном бросании кубика.
Заштрихуйте секцию «5». Выразите число дробью: 1 ⁄ 6 .
2. Разделите секцию «5» на 6 равных частей, чтобы показать, сколько раз после выпадения 5 будет выпадать каждое число.
Заштрихуйте подраздел «5». Выразите число дробью: 1 ⁄ 6 . Умножьте две дроби.
Стратегии исследования
- Понять Обратите внимание учащихся на заштрихованные подразделы в секции «5» прямоугольника справа. Спросите: «Что будет представлять нижний подраздел? Почему 6 подразделов равны?» Доля раз, когда вы ожидаете выбросить сначала 5, а затем 6; При любом броске каждое число имеет равные шансы выпасть.
- Создать Предложите учащимся с помощью круга построить площадную модель вероятности выпадения трех решек при подбрасывании правильной монеты. Модели должны выглядеть примерно так, как показано ниже.
для пропорций
Геометрическая модель пропорций использует преимущества знакомства учащихся с аналогиями и другими моделями, включающими геометрические фигуры.

- Разместите 3 физические модели или чертежи геометрических фигур в стандартном формате пропорций. Попросите учащихся поместить, нарисовать или описать фигуру, которая принадлежит пустому месту.
- Попросите добровольца переставить фигуры, чтобы создать другую визуальную пропорцию.
Возможные варианты:
- Чтобы более точно связать эту визуальную модель с числовыми пропорциями, используйте квадраты и треугольники, разделенные на конгруэнтные части.
Стратегии запросов
- Понять Отобразите эти два визуальных соотношения со знаком вопроса между ними. Спросите: «Это правильная пропорция? Почему или почему нет?» Нет, пропорции не те. Один показывает отношение «маленькое к большому», а другой — отношение «большое к малому».
- Оценить Спросите: «Когда фотографию увеличивают пропорционально, какое соотношение остается неизменным?» Любые отношения двух соответствующих расстояний, например, отношение длины к ширине.

для связанных углов
Используйте физические модели, чтобы показать, как могут изменяться углы, когда соотношение между ними остается постоянным.
Модель углов поперечной
Вырежьте 3 полоски картона и соедините их с помощью застежек, чтобы сформировать поперечную. Поверните поперечную, как показано на рисунке (остальные полосы остаются параллельными).
По мере изменения размера углов сосредоточьте внимание учащихся на парах углов, которые остаются равными, и на парах, которые остаются дополнительными.
Модель углов параллелограмма
Используйте 4 полосы и застежки, чтобы сформировать прямоугольник. Поверните пару противоположных сторон, как показано. . .
… для создания непрямоугольного параллелограмма. По мере того, как углы меняются в размерах, сосредоточьте внимание учащихся на парах углов, которые остаются дополнительными и равными. Укажите, как уменьшение одного угла равно увеличению другого угла.
По мере того, как углы меняются в размерах, сосредоточьте внимание учащихся на парах углов, которые остаются дополнительными и равными. Укажите, как уменьшение одного угла равно увеличению другого угла.
Стратегии исследования
- Создать Предложите учащимся нарисовать схему поперечной, пересекающей три параллельных прямых, образующих 12 непрямых углов. Попросите учащихся отметить наборы углов, которые всегда равны. Ученики должны обозначить конгруэнтными все тупые углы, а также все острые углы.
- Анализ Обратите внимание на модель параллелограмма. Обратите внимание, что в качестве меры угла A уменьшается, мера угла B увеличивается на такую же величину. Спросите: «Что это говорит вам о сумме четырех внутренних углов параллелограмма?» Общая мера 4 углов должна быть 360°, такая же, как сумма для прямоугольника, потому что любое уменьшение одного угла компенсируется эквивалентным увеличением другого.

для решения уравнений
Предметы, размещенные на чашах весов, отталкиваются под действием силы своего веса. Таким образом, положительные количества и сложение можно представить на модели весов, просто размещая предметы или рисуя фигуры на чашах. Отрицательные числа и вычитание могут быть представлены противоположностью нисходящей силы, восходящей силы — например, силы, которую кто-то выталкивает из-под одной из кастрюль.
Пример: Решить 3 x − 5 = 7
Стратегии исследования
- Оценить Спросите: «Почему имеет смысл показывать отрицательное число как силу, толкающую вверх?» Отрицательная величина противоположна соответствующему положительному числу; сила, толкающая вверх, противоположна силе, толкающей вниз.
- Применить Напишите на доске 2 x + 3= 7.
 Спросите: «Как бы вы использовали модель баланса для решения этого уравнения?» На левой сковороде есть 2 коробки с пометкой «x» и 3 единицы измерения. На правом поддоне ничего нет, но рука под ним давит вверх с силой 7.
Спросите: «Как бы вы использовали модель баланса для решения этого уравнения?» На левой сковороде есть 2 коробки с пометкой «x» и 3 единицы измерения. На правом поддоне ничего нет, но рука под ним давит вверх с силой 7.
для решения неравенств
Неравенство типа 4
< 6 можно изобразить на числовой прямой. Учитывая два действительных числа, меньшее число всегда будет слева на числовой прямой.Покажите два числа на числовой строке и приведите примеры прибавления одной и той же суммы к двум числам.
Обратите внимание, что в каждом случае суммы идут в том же порядке. Красная точка все еще находится слева от синей точки.
Используйте аналогичную модель, чтобы показать, что вычитание той же суммы из исходных чисел также не меняет порядок.
Затем используйте модель, чтобы продемонстрировать, что происходит, когда два числа умножаются (или делятся) на одну и ту же положительную величину. Опять порядок не меняется.
Опять порядок не меняется.
Наконец, используйте модель, чтобы показать, что умножение (или деление) на отрицательное число не меняет порядок. Обратите внимание, что красная и синяя точки меняются местами. Знак неравенства нужно поменять местами, чтобы предложение осталось верным.
Стратегии исследования
- Понять Спросите: «Как бы вы объяснили, почему знак неравенства должен меняться на противоположный при умножении обеих частей неравенства на отрицательное число, но не при сложении отрицательного числа? к обеим сторонам неравенства?» Учащиеся могут использовать числовую прямую, чтобы показать, что умножение на отрицательное число меняет порядок произведений в числовой строке.
- Применить На доске написать –3 x < 6. Спросите: «Если вы разделите обе части на 3, нужно ли поменять знак отношения?» «Что, если на следующем шаге вы умножите обе части на –1?» нет; да.

для отрицательных чисел
Модели могут помочь учащимся понять целые числа ниже нуля, но ни одна модель не работает идеально во всех случаях
1 . Монеты или двухцветные жетоны особенно полезны, чтобы помочь учащимся понять разницу между отрицательные количества и вычитание .Пусть одна сторона монеты или жетона представляет 1, а другая сторона -1.
Используйте модель, чтобы показать различные значения знака минус в числовом выражении.
Пример: Упростить −|−6 − (−2)|
Итак, −|−6 − (−2)| = −4.
Стратегии исследования
- Обобщить Спросите: «Каковы два способа использования знака минус и чем они отличаются?» Учащиеся должны различать вычесть , что означает отнять или найти разность, и взять противоположное , что означает найти обратную добавку.

- Анализ Напишите на доске −(−5 − 5) . Спросите: «Что означает каждый знак минус в этом выражении?» Попросите учащихся упростить выражение. Первое означает обратное — (-5 — 5) . Второе означает, что принимает противоположность 5 . Третий означает вычесть 5 . Результат 10.
1 Fuson, Wearne, Hiebert, Murray, Human, Olivier, Carpenter, and Fennema, 1997; Hiebert, Carpenter, Fennema, Fuson, Wearne, Murray, Olivier, and Human, 1997 Цитируется в Adding it Up
Рабочие листы по математике для 7-го класса в формате pdf, математические задачи для 7-го класса
Метрическая система США
Попрактикуйтесь в метрической системе США с помощью этого бесплатного печатного листа по математике.
Распечатать здесь >>>
Шаблоны десятичных чисел
Практикуйте шаблоны десятичных чисел с помощью этого бесплатного печатного листа по математике.
Распечатать здесь >>>
Комбинации смешанных десятичных чисел2
Потренируйтесь в составлении смешанных десятичных чисел2 с помощью этого бесплатного печатного листа по математике.
Распечатать здесь >>>
Комбинации смешанных десятичных чисел
Попрактикуйтесь в построении смешанных десятичных чисел с помощью этого бесплатного печатного листа по математике.
Распечатать здесь >>>
Стороны треугольника по теореме Пифагора 1
Практикуйте теорему Пифагора 1 о сторонах треугольника с помощью этого бесплатного печатного листа по математике.
Распечатать здесь >>>
Стороны треугольника по теореме Пифагора 2
Практикуйте теорему Пифагора 2 о сторонах треугольника с помощью этого бесплатного печатного листа по математике.
Распечатать здесь >>>
Стороны треугольника Теорема Пифагора 3
Попрактикуйтесь в теореме Пифагора 3 о сторонах треугольника с помощью этого бесплатного распечатываемого листа по математике.
Распечатать здесь >>>
Стороны треугольника по теореме Пифагора 4
Попрактикуйтесь в теореме 4 по теореме Пифагора о сторонах треугольника с помощью этого бесплатного печатного листа по математике.
Распечатать здесь >>>
Рабочие листы по математике для 7-го класса — помогите учащимся не отставать от более напряженного расписания, так как они могут легко преуспеть в математике; не отставая из-за сильного давления. В это время ученикам обычно от 12 до 13 лет, и в математике они начинают изучать алгебру и геометрию. В течение этого года, когда учащихся привлекают к изучению алгебры и геометрии, они должны иметь четкое представление об основных понятиях и уметь решать основные уравнения. Это включает в себя одношаговое решение проблем «X». 7-й класс считается критическим годом в обучении, так как содержание, которое они охватят в этом году, будет продолжаться в течение всего школьного времени. Именно поэтому мы предоставили вам рабочие листы, которые помогут вам усовершенствовать свои основы и помогут вам глубже понять более сложные уравнения. В наших рабочих листах мы упомянули задачи, относящиеся к учебной программе, которую вы будете изучать в этом году в школе. С помощью наших пошаговых рабочих листов для 7-го класса вы сможете решать математические задачи чрезвычайно обширным образом. Что поможет вам развить свои навыки и одновременно уверенность в себе; поскольку чем лучше вы справитесь с этим, тем увереннее вы будете браться за следующую задачу. В этих рабочих листах 7-го класса вы будете охватывать десятичные числа и проценты, навыки, основанные на алгебре, и навыки, основанные на геометрии. Предоставление вам возможности сохранить ваши старые и новые навыки нетронутыми и в хорошей форме. Рабочие листы — отличный способ учиться, поскольку они предлагают учащимся независимость; и они свободны от границ. Наши рабочие листы разработаны таким образом, чтобы вы не чувствовали, что все еще выполняете школьную работу, мы по-разному проверяем ваши навыки и методы; они помогут вам развивать новые навыки, оттачивая предыдущие.
В наших рабочих листах мы упомянули задачи, относящиеся к учебной программе, которую вы будете изучать в этом году в школе. С помощью наших пошаговых рабочих листов для 7-го класса вы сможете решать математические задачи чрезвычайно обширным образом. Что поможет вам развить свои навыки и одновременно уверенность в себе; поскольку чем лучше вы справитесь с этим, тем увереннее вы будете браться за следующую задачу. В этих рабочих листах 7-го класса вы будете охватывать десятичные числа и проценты, навыки, основанные на алгебре, и навыки, основанные на геометрии. Предоставление вам возможности сохранить ваши старые и новые навыки нетронутыми и в хорошей форме. Рабочие листы — отличный способ учиться, поскольку они предлагают учащимся независимость; и они свободны от границ. Наши рабочие листы разработаны таким образом, чтобы вы не чувствовали, что все еще выполняете школьную работу, мы по-разному проверяем ваши навыки и методы; они помогут вам развивать новые навыки, оттачивая предыдущие.
Седьмой класс открывает новую захватывающую главу в математическом путешествии вашего ученика. Хотя многие важные понятия, с которыми они столкнулись во второй половине начальной школы, будут включены в освещение этого года, они также будут ходить по изрядной части незнакомой территории. В течение следующих нескольких месяцев ваш ученик вступит в эпоху алгебры.
Перспектива изучения математики в средней школе может показаться пугающей для многих учащихся. Однако при достаточном обучении и практике они могут легко справиться с математическими заданиями 7-го класса. Вооружите своих детей практическими ноу-хау в понимании и решении математических задач с помощью наших рабочих листов на Математические задачи 7-го класса .
Год начнется с подведения итогов предыдущих тем. Ваш ребенок будет добавлять факториалы в свой репертуар теории чисел. Они также будут классифицировать и манипулировать целыми числами, а также отображать их на числовых линиях.
Дальнейшее увеличение сложности задач с дробями и десятичными числами можно найти в 7 классе. Они будут выполнять действия над положительными и отрицательными дробями.
Они будут выполнять действия над положительными и отрицательными дробями.
Их обсуждение показателей степени будет сопровождаться концепцией квадратных корней и интернализацией квадратных корней для обычных полных квадратов.
Как и в 6-м классе, в этом году будет представлен ряд простых, но практически ценных тем, состоящих из соотношений и пропорций, ставок и процентов. В основном они будут решаться с помощью текстовых задач и включать в себя проблемы реального мира. Продолжая изучение практических навыков, в 7 классе также обычно обсуждают финансовую математику — например, учатся различать лучшие купоны или распродажи, скидки, а также простые и сложные проценты.
В первой половине этого года может быть несколько задач со словами, чтобы еще больше отточить навыки критического мышления вашего ребенка.
Обратите внимание, что вашему ребенку может потребоваться научный калькулятор или телефон для выполнения длинных арифметических и геометрических последовательностей.
Со временем ваши дети столкнутся с самой значимой новой темой года — алгебраическими выражениями. Они будут иметь дело с различными типами переменных выражений. Некоторые будут содержать до трех операций. Крайне важно, чтобы они научились упрощать эти выражения для последующих тем. Значительная часть года будет посвящена решению проблем неравенства.
Они будут иметь дело с различными типами переменных выражений. Некоторые будут содержать до трех операций. Крайне важно, чтобы они научились упрощать эти выражения для последующих тем. Значительная часть года будет посвящена решению проблем неравенства.
По мере освоения работы с переменными учащиеся перейдут к линейным функциям, вычислению наклонов и отсутствующих координат, а также графическому отображению данных.
Они также будут использовать свои новообретенные алгебраические навыки в геометрии для нахождения отсутствующих углов и идентификации различных пар углов. В целом геометрия будет довольно заметной, включая такие темы, как внутренние и центральные углы, сечения трехмерных фигур, получение площадей и периметров составных фигур и преобразования. На этом этапе также будет введена квинтэссенция теоремы Пифагора.
Если вы учитель или родитель, обучающийся на дому, вы, вероятно, можете подтвердить, насколько утомительной может быть подготовка учебных материалов, таких как викторины и контрольные работы.


 Представьте в виде степени с основанием 5 число 1254
Представьте в виде степени с основанием 5 число 1254 Значение выражения 5в — 3с при в= и с=- равно:
Значение выражения 5в — 3с при в= и с=- равно: Какая из данных функций не является линейной?
Какая из данных функций не является линейной?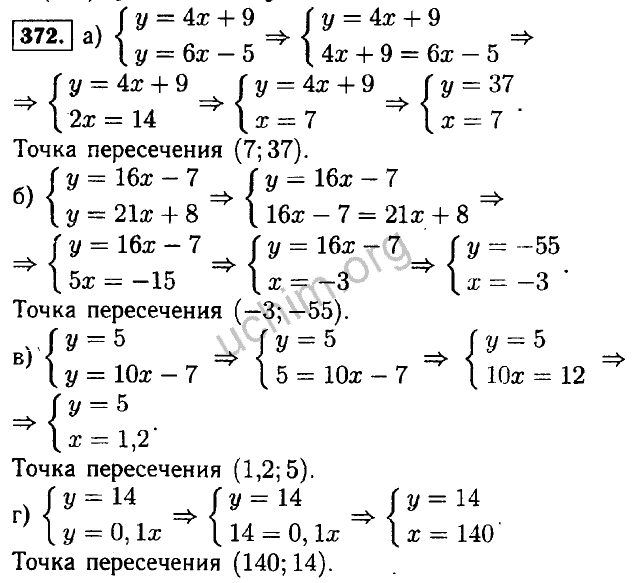
 Потребовалось бы 10 000 из них от начала до конца, чтобы длина стрелки равнялась цифре «3» в разряде десятков.
Потребовалось бы 10 000 из них от начала до конца, чтобы длина стрелки равнялась цифре «3» в разряде десятков.
 Модель не показывает значения x и y , а только относительные изменения x и y ; тем не менее, вы сможете определить, изображена ли функция на координатной плоскости.
Модель не показывает значения x и y , а только относительные изменения x и y ; тем не менее, вы сможете определить, изображена ли функция на координатной плоскости.
 Утверждение A описывает увеличение на 20 %, а B описывает увеличение на 120 % — в 6 раз больше, чем увеличение в первом утверждении!
Утверждение A описывает увеличение на 20 %, а B описывает увеличение на 120 % — в 6 раз больше, чем увеличение в первом утверждении!
 Спросите: «Как бы вы использовали модель баланса для решения этого уравнения?» На левой сковороде есть 2 коробки с пометкой «x» и 3 единицы измерения. На правом поддоне ничего нет, но рука под ним давит вверх с силой 7.
Спросите: «Как бы вы использовали модель баланса для решения этого уравнения?» На левой сковороде есть 2 коробки с пометкой «x» и 3 единицы измерения. На правом поддоне ничего нет, но рука под ним давит вверх с силой 7.
