Вопросы по алгебре 7 класс с ответами: Тесты по алгебре (7 класс), контрольные работы по вариантам с ответами онлайн

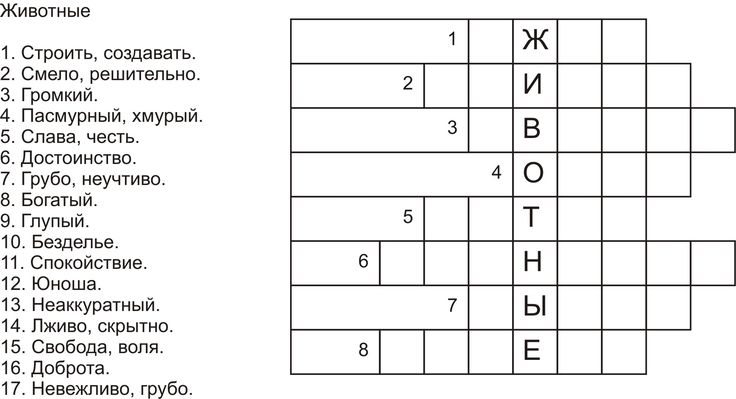
Одночлены 7 класс с ответами

Тесты по алгебре 7 класс. Тема: «Одночлены»

Правильный вариант ответа отмечен знаком +

1. Как будет выглядеть одночлен 4a³b² × 2ab³ в упрощенном виде?

a. 8a⁴b⁵ +

b. 6a³b⁶ -

c. 6a⁴b⁵ -

d. 8a³b⁶ -

2. 2y³z + 6y³z = …

a. 12y³z -

b. 8y⁶z² -

c. 12y⁹z -

d. 8y³z +

3. Какой вид имеет одночлен, если первым в нем идет числовой множитель, а затем произведение одинаковых степеней переменных в виде одной степени?

a. нестандартный -

b. обычный —

c. стандартный +

d. необычный -

4. Что такое степень одночлена?

a. разность показателей степеней всех переменных -

b. сумма показателей степеней всех переменных +

c. произведение показателей степеней всех переменных -

d. частное показателей степеней всех переменных -

5. Какой коэффициент имеет одночлен 6x²yz⁴?

a. 6 +

b. 2 -

c. 1 -

d. 4 -

6. Чему равно буквенное значение в примере 5a × 3a⁴b²?

a. a⁴b² -

b. a⁵b² +

c. ab⁷ -

d. a⁷b -

7. Какими одночленами являются одночлены 6m²n⁷ и 2m²n⁷?

a. подобными +

b. аналогичными -

c. похожими -

d. двойниками -

8. Как называется числовой множитель одночлена стандартного вида?

a. параметр одночлена -

b. коэффициент одночлена +

c. величин одночлена -

d. показатель одночлена -

9. Какую степень имеет одночлен 7?

a. четверной -

b. единичной -

c. тройной -

d. нулевой +

тест 10. Как называются многочлены 3xy³ и -3xy³?

a. противоположными +

b. разными -

c. непохожими -

d. отличающимися -

11. 7xa² × 4x = …

a. 11xa² -

b. 28xa² -

c. 28x²y² +

d. 11x²y² -

12. Какую степень имеет одночлен 8d²sp⁴?

a. 8 -

b. 7 +

c. 15 -

d. 6 -

13. Какой пример не является одночленом?

a. 2xy² -

b. 10 -

c. mn + 3 +

d. 5e²f -

14. Чему равна степень одночлена, не содержащего переменных?

a. 0 +

b. 1 -

c. 2 -

d. 3 -

15. 2z⁴ × … = 16z⁴y²

a. 14y² -

b. 8y² +

c. 14zy -

d. 8zy² -

16. Какое арифметическое действие используется при работе со степенями?

a. сложение +

b. умножение -

c. вычитание -

d. деление -

17. Чему будет равен коэффициент одночлена 3a

5b³ × 4ab⁶?

a. 7 -

b. 15 -

c. 90 -

d. 12 +

18. Какой коэффициент у одночлена -3a³b³?

a. -3 +

b. 3 -

c. 9 -

d.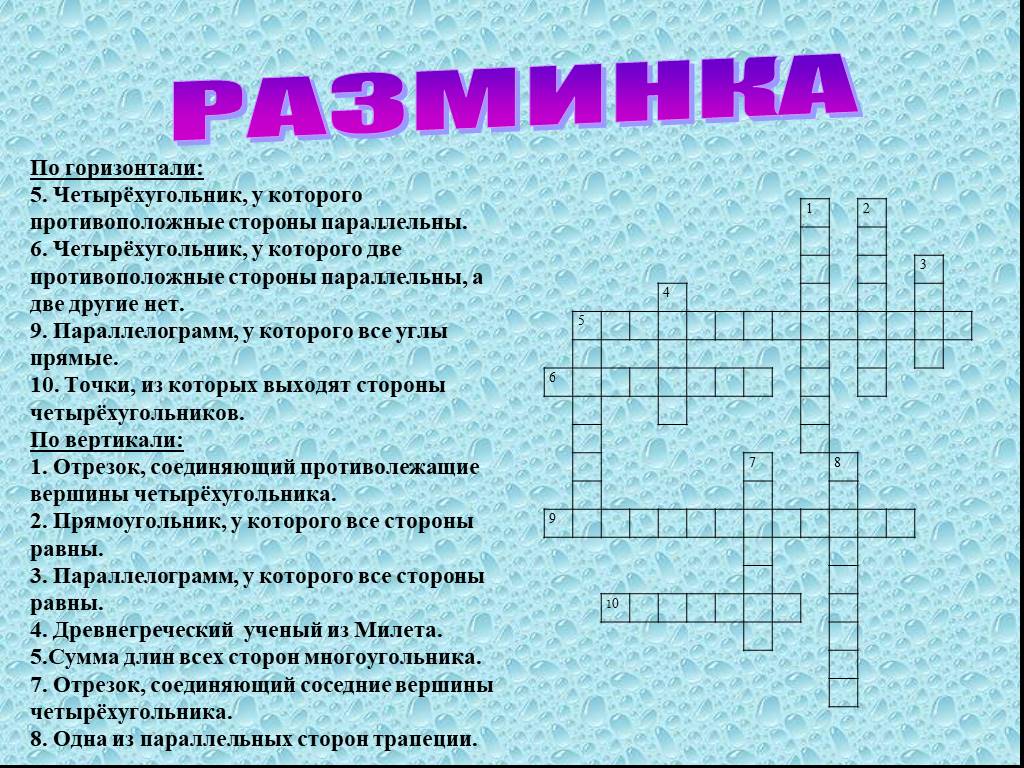 6 -

19. Какой из вариантов является одночленом?

a. y/3 -

b. 4z⁵ — 2 -

c. 6x³y² +

d. 3m + 3n -

тест-20. Вася и Миша собрали 10 кг клубники. Вася собрал в 4 раза больше клубники, чем Миша? Как записать в виде одночлена результат сбора ягод Васи?

a. 4x +

b. x -

c. 4x + x -

d. 4/x -

21. … × 5pt³ = 10p³t³

a. 5p³

-

b. 2p² +

c. 5p² -

d. 2p³ -

22. Как представить в виде степени y⁸ × y⁴?

a. y¹² +

b. y⁴ -

c. y³² -

d. y² -

23. Как называется свойство множества, в котором при умножении одночлена на одночлен результатом является одночлен?

a. замкнутостью относительно операции умножения +

b. открытостью относительно операции умножения -

c. ограниченностью относительно операции умножения -

d. бесконечностью относительно операции умножения -

24. Чему равен коэффициент одночлена в примере 0,4x² × 3y × 6z⁴?

a. 9,4 -

b. 7 -

c. 8 -

d. 7,2 +

25. Чему равна степень одночлена m⁷m⁹?

a. 16 +

b. -2 -

c. 63 -

d. 7/9 -

26. 8u⁹t × 2t³ = …

a. 10u⁹t³ -

b. 6ut¹² -

c. 16u⁹t⁴ +

d. 10ut²⁷ -

27. Как переводится английское слово «monomial»?

a. одночлен +

b. дробь -

c. натуральное число -

d. многочлен -

28. Какой буквой обозначается коэффициент одночлена?

a. m -

b. k +

c. o -

d. p -

29. (2xy)³= …

a. 8x⁴y⁴ -

b. 6x

4y⁴ -

c. 8x3y³ +

d. 6x³y³ -

тест_30. Какой результат будет после раскрытия скобок (6y)²?

a. 36y² +

b. 12y³ -

c. 36y³ -

d. 12y² —

Итоговый тест по алгебре за курс 7 класса

Итоговый тест по алгебре за 7 класс

Часть 1.

При выполнении заданий с выбором ответа обведите номер выбранного ответа в работе. Если Вы обвели не тот номер, то зачеркните обведённый номер крестиком и затем обведите номер нового ответа.

А1. Упростите выражение -4m + 9n — 7m — 2n.

1. -3m + 11n

2. -3m + 7n

3. 11m + 7n

4. -11m + 7n

A2. Решите уравнение 10у – 13,5 = 2у — 37,5.

1. 6,375

2. 3

3. -3

4. 4

A3. Упростите выражение с⁷ : c⁴ ∙ c.

1. c⁵

2. c⁶

3. c⁴

4. c¹²

A4. Выполните умножение (3a — b)(2b — 4a).

1. -12a² – 10ab – 2b²

2. -12a² + 10ab – 2b²

3. 6ab – 2b²

4. 6ab – 4b

A5. Преобразуйте в многочлен (4х – 5у)².

1. 16х² – 20ху + 25у²

2. 16х² — 40ху + 25у²

3. 4х² – 25у²

4. 16х² – 25у²

A6. Упростите выражение -3а⁷b²∙(5a³)².

1. 15a¹³b²

2. -15a¹²b²

3. 75a¹²b²

4. -75a¹³b²

A7. Найдите значение выражения (-1)³ – (-2)³ + 5² – 7².

1. 83

2. 33

3. -16

4. -17

А8. Представьте выражение в виде квадрата двучлена 4у² — 12у + 9.

1. (4у — 3)²

2. (2у — 9)²

3. 2у — 3²

4. (2у — 3)²

А9. Выразите у через х в выражении -5х + у = -17.

1. У = 17 + 5х

2. У = -5х + 17

3. У = -17 + 5х

4. У = 17 — 5х

А10. Прямая пропорциональность задана формулой у=х. Укажите значение у, соответствующее х = -12.

1. 4

2. -4

3. 36

4. -36

А11. Какое значение принимает сумма х + у, если х = -2,6; y = -4,4?

1. -1,8

2. 1,8

3. 7

4. -7

А12. Раскройте скобки и приведите подобные слагаемые (2,7х — 15) – (3,1х — 14).

1. 2,7х — 9

2. -0,4х — 9

3. 5,8х — 1

4. -0,4х — 1

А13. Найдите значение выражения 2,7 — 49 : (-7).

1. 9,7

2. 4,3

3. -4,3

4. -9,7

А14. Составьте выражение по условию задачи: «Турист шел со скоростью b км/ч. Какое расстояние он пройдет за 8 часов?».

1. 8 — b

2. 8 + b

3. 8b

4. 8 : b

А15. В одной системе координат заданы графики функций у = 2х – 4 и у = -3. Определите координаты точки их пересечения.

1. (1,5; -3)

2. (1,5; 1)

3. (0,5; -3)

4. (-0,5; -3)

А16. Найдите координаты точки пересечения графика функции с осью абсцисс.

1. (4; 0)

2. (0; 4)

3. (8; 0)

4. (16; 0)

А17. Вычислите .

1. 3²

2. 3³

3. 81

4. 3⁴

А18. Через какую точку проходит график функции у = 3х + 5?

1. (2; -3)

2. (1; -2)

3. (2; 11)

4. (-2; 11)

А19. Приведите одночлен к стандартному виду 5х⁵у∙0,3ху³.

1. 15х⁶ у⁴

2. 1,5х⁵ у³

3. 1,5х⁶ у⁴

4. 1,5ху

А20.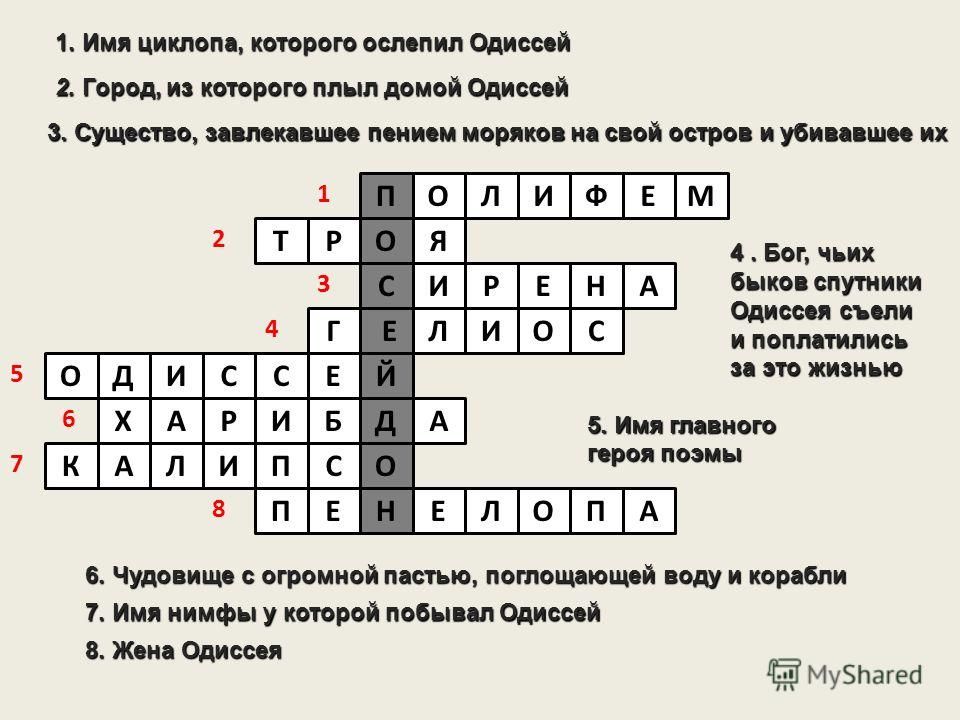 Вынесите общий множитель за скобку 12ху – 4у².

1. 4(3ху – 4у)

2. 4у(х — у)

3. у(12х — 4)

4. 4у(3х — у)

А21. Разложите на множители а(у — 5) – b(y — 5).

1. (a — b)(y — 5)

2. (a + b)(y — 5)

3. (y — 5) ∙ a

4. (y — 5) ∙ b

А22. При всех значениях а значение выражения 2а(а — 18) + 3(а² + 12а) – 5а² + 3 равно:

1. 3

2. -3

3. 2a + 3

4. a + 3

А23. Выполните умножение дробей:

1. 2,5

2. 0,4

3. 1

4. -1

Часть 2.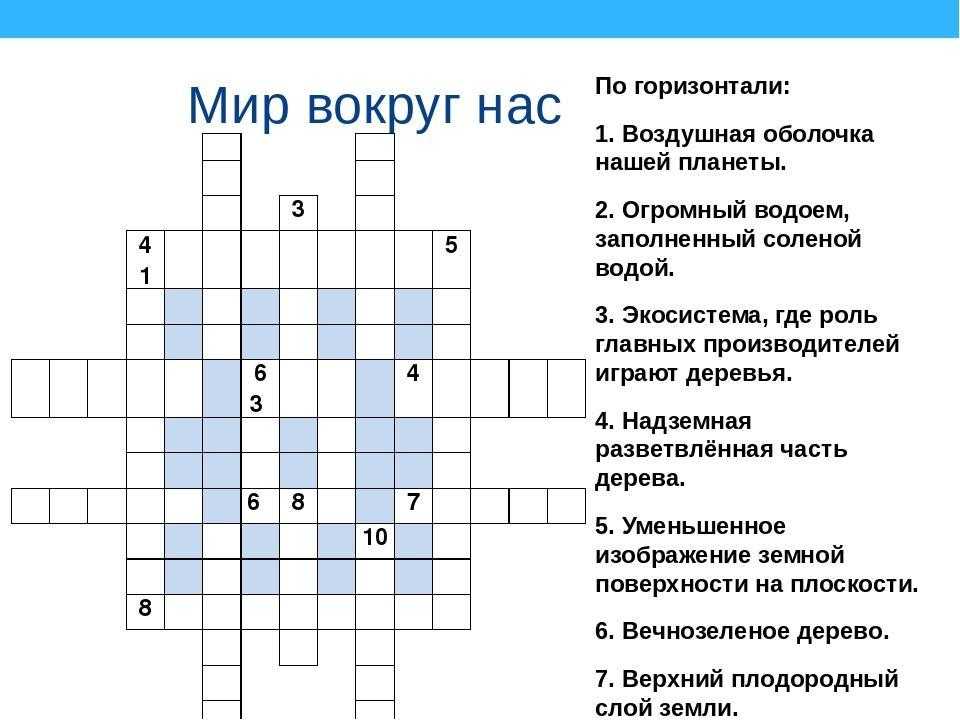

Полученный ответ на задание записывается в отведённом для этого месте. В заданиях «решите уравнение» в ответе указывайте только числа, являющиеся корнями уравнения. Если ответ содержит несколько чисел, разделяйте их точкой с запятой (;) и записывайте числа в порядке возрастания. Если ответом является обыкновенная дробь, то переведите ее в десятичную дробь и запишите в ответ десятичную дробь. В задаче в ответ запишите только число (наименования указывать не надо). В системах уравнений ответ запишите в виде точки.

В случае записи неверного ответа зачеркните его и запишите рядом новый.

B1. Решите уравнение 8у – (3у + 19) = -3(2у — 1).

Ответ:____________________________________

B2. Решите уравнение 5х² – 4х = 0.

Ответ:____________________________________

В3. Решите уравнение

Ответ:____________________________________

В4.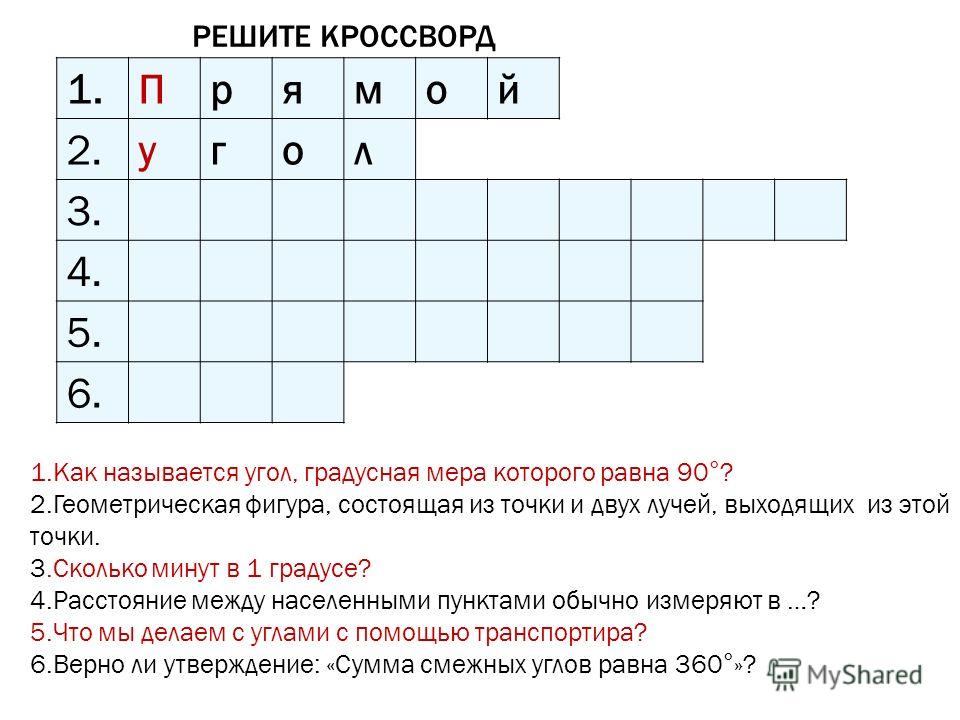 Упростите выражение .

Ответ:____________________________________

В5. Решите задачу:

В трех мешках 114 кг сахара. В первом на 16 кг меньше, чем во втором, а в третьем на 2 кг меньше, чем во втором. Сколько килограммов сахара во втором мешке?

Ответ:____________________________________

В6. Решите систему уравнений .

Ответ:____________________________________

В7. Сколько различных трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, если цифры в числе не повторяются.

Ответ:____________________________________

10 Наиболее распространенные общие базовые вопросы по математике в 7-м классе

Родители учащихся 7-го класса должны знать, что важно использовать практические вопросы по таким предметам, как математика. Таким образом, если ваши учащиеся хорошо изучили материалы теста Common Core Math для 7-го класса, теперь они могут использовать вопросы Common Core Math для 7-го класса в этой статье для дальнейшей практики.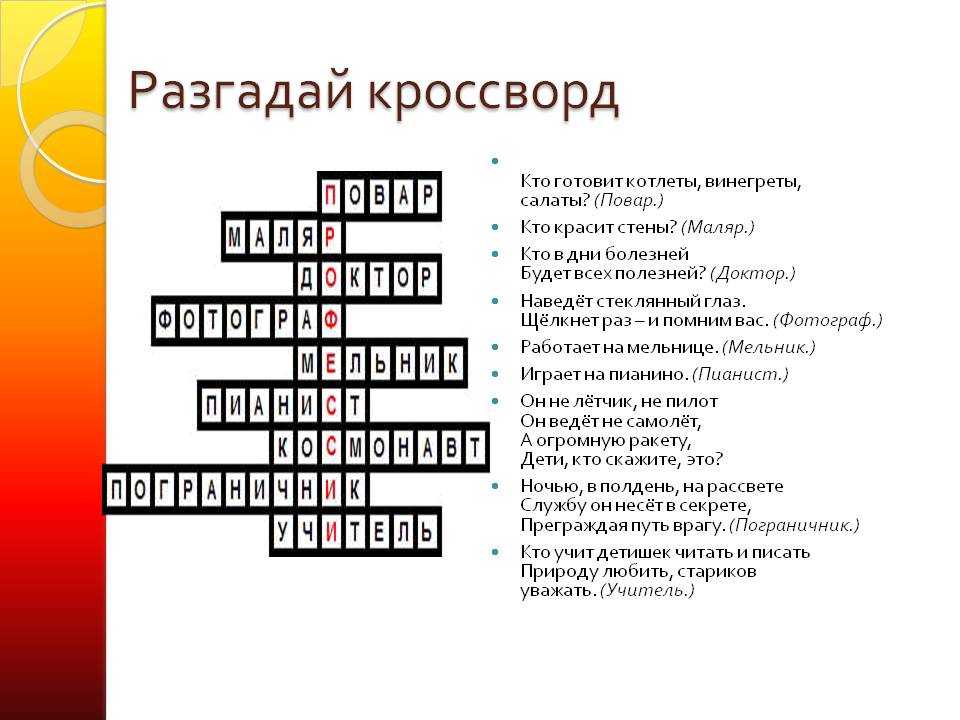 Уверяем вас, что в этой статье мы подготовили 10 лучших практических вопросов по общей основной математике для 7-го класса для учащихся 7-го класса. Ответы на эти вопросы подробно описаны, чтобы учащиеся также ознакомились с тем, как решать вопросы.

Не забудьте перейти по некоторым связанным ссылкам в нижней части этого поста, чтобы получить лучшее представление о том, какие вопросы по математике нужно учащимся практиковать.

Абсолютно лучшая книга для достижения отличных результатов по общей базовой математике для 7-го класса

10 Образец общих основных практических вопросов по математике для 7-го класса

1- Каково среднее значение этих чисел? \(2, 28, 28, 19, 67, 44, 35\)

А. 19

Б. 28

В. 44

Г. 35

2- На прошлой неделе 24 000 болельщиков посетили футбольный матч. На этой неделе в три раза больше людей купили билеты, но одна шестая из них аннулировала свои билеты. Сколько участников на этой неделе?

A. 48000

B. 54000

C. 60000

D. 72000

3- Следующие трапеции подобны. Каково значение \(x\)?

A. 7

B. 8

C. 18

D. 45

4- Если \(x=- 8\), какое уравнение верно?

А. \(х(2х-4)=120\)

Б. \(8 (4-х)=96\)

С.\( 2 (4х+6)=79\)

Г. \(6х-2=-46\)

5- В мешочке с шариками \(\frac{1}{3}\) черные, \(\frac{1}{6}\) белые, \(\frac{1}{4}\) красные а остальные 12 синие. Сколько шаров белых?

A. 8

B. 12

C. 16

D. 24

6- Лодка плывет 40 миль на юг, а затем 30 миль на восток. На каком расстоянии находится лодка от начальной точки?

А. 45

Б. 50

В. 60

D. 70

7- София купила диван за 530,40 долларов. Цена дивана обычно составляет 624 доллара. Какой процент скидки получила София на диван?

А. \(12\%\)

Б. \(15\%\)

В. \(20\%\)

Г. \(25\%\)

8- Оценка у Эммы было вдвое меньше, чем у Авы, а у Мии было вдвое больше, чем у Авы. Если оценка Мии была 60, то какова оценка Эммы?

А. 12

Б. 15

В. 20

Г. 30

9- В мешке 18 мячей: два зеленых, пять черных, восемь синих, коричневый, красный и один белый. Если из мешка наугад вынуть 17 шаров, какова вероятность того, что вынут коричневый шар?

A. \(\frac{1}{9}\)

B. \(\frac{1}{6}\)

C. \(\frac{16}{17}\)

D. \(\frac{17}{18}\)

10- Веревка весит 600 грамм на метр длины. Каков вес в килограммах 12,2 метра этой веревки? (1 килограмм = 1000 граммов)

A. 0,0732

B. 0,732

C. 7,32

D. 7320

Лучший 7-й класс для математической подготовки к 2022

Ответы:

1- B
Напишите цифры в порядок в заказе. :
\(2, 19, 28, 28, 35, 44, 67\)
Поскольку у нас есть 7 чисел (7 нечетно), то медианой является число в середине, равное 28.

2- C
Три раза по 24 000 равно 72 000. Одна шестая из них аннулировала свои билеты.
Одна шестая от 72 000 равна 12 000 \((\frac{1}{6}) × 72000 = 12000\).
60 000 \(72 000 – 12 000 = 60 000\) болельщиков на этой неделе

3- A
Чтобы найти значение \(x\), нужно иметь отношение.
\(\frac{45}{40}=\frac{2x+4}{16}⇒ 40(2x+4)=45×16 ⇒ x=7\)

4- C
\(8 (4-(-8))=96\)

5- A
\(\frac{1}{3}x + \frac{1}{6}x + \frac{1}{4} x + 12= x\)
\((\frac{1}{3} + \frac{1}{6} + \frac{1}{4}) x+ 12= x\)
\((\frac {9}{12})x+ 12 = x\)
\(x = 48\)
В мешочке с маленькими шариками \(\frac{1}{6}\) белые, тогда: \(\frac{48 {6} = 8\) 92 ⇒ c = 50\)

7- B
Вопрос в следующем: 530,40 сколько процентов от 624?
Используйте формулу процентов:
\(часть = \доля{процентов}{100}× целое\)
\(530,40= \фрак{процентов}{100}× 624 ⇒ 530,40 = \фрак{процентов ×624}{100} ⇒53040 = проценты ×624\)
\(⇒проценты = \frac{53040}{624}= 85\)
530,40 равно \(85 \%\) от 624. Следовательно, скидка составляет: \(100\% – 85\% = 15\%\)

8- B
Если оценка Мии была 60, то оценка Авы равна 30. Поскольку оценка Эммы была вдвое меньше, чем у Авы, следовательно, оценка Эмме 15.

9- D
Если из мешка наугад вынуть 17 шаров, в мешке останется один шар.
Вероятность выбора коричневого шара равна 1 из 18. Следовательно, вероятность не выбрать коричневый шар составляет 17 из 18, и такая же вероятность не выбрать коричневый шар после удаления 17 шаров.

10- C
Вес 12,2 метра этой веревки равен: \(12,2 × 600 \пробел г = 7320 \пробел г\)
\(1\пробел кг = 1000 \пробел г\) следовательно,
\( 7320 \пробел г ÷ 1000 = 7,32 \пробел кг\)

Ищете лучший ресурс, который поможет вам успешно сдать тест по общей базовой математике в 7 классе?

Лучшие книги для учащихся 7-го класса Common Core Тест по математике

Реза

Реза — опытный преподаватель математики и эксперт по подготовке к экзаменам, который обучает многих учеников с 2008 года. поднять свои баллы по стандартизированным тестам и поступить в колледжи своей мечты. Он работает со студентами индивидуально и в группах, ведет как живые, так и онлайн-курсы по математике, а также математическую часть стандартизированных тестов. Он предлагает индивидуальный индивидуальный план обучения и индивидуальное внимание, которое меняет отношение учащихся к математике.

3 месяца назад

15 вопросов по алгебре и практических задач (KS3, KS4, GCSE)

В вопросах по алгебре используются буквы или символы для представления неизвестных значений или значений, которые могут изменяться. Здесь вы найдете 15 вопросов по алгебре, чтобы проверить свои знания и показать вам различные способы использования алгебры для решения задачи на поиск неизвестного значения или для обобщения.

В дополнение к обучению по математике для выпускных экзаменов по математике мы предоставляем дополнительную поддержку средним школам бесплатно для пересмотра GCSE по математике для экзаменов GCSE 2022, включая:
— прошлые работы GCSE по математике
— рабочие листы GCSE по математике
— вопросы по математике GCSE
— контрольный список GCSE по математике

Алгебра в KS3 и KS4

Есть много тем и методов внутри алгебры. В KS3 мы учимся писать и обрабатывать основные алгебраические выражения и линейные уравнения. В KS4 мы развиваем эти методы, чтобы позволить нам иметь дело с более сложными алгебраическими задачами, например, с квадратными уравнениями или системой уравнений.

Как решать алгебраические вопросы

Когда вам предлагают решить алгебраическую задачу, важно установить, что вас просят сделать. Вот некоторые из ключевых терминов вместе с тем, что они означают:

• Решите уравнение – узнайте значение неизвестного
• Подставить — поместите полученные значения в алгебраическое выражение
• Упростите — соберите вместе похожие термины, чтобы выражение или уравнение выглядело проще
• Раскрыть скобки – умножить скобки
• Факториз – заключить в скобки
• Сделать х субъектом – переписать уравнение в виде х =…..

Помните, при работе с алгеброй мы все равно должны применять БОДМАС/БИДМАС. то есть скобки, индексы (степени, показатели степени, квадратные корни), деление, умножение, сложение, вычитание.

При работе с алгебраическими выражениями и уравнениями мы должны тщательно продумать, какие операции следует выполнять в первую очередь.

Загрузите рабочий лист 15 вопросов по алгебре и практических задач (KS3 и KS4)

Помогите своим ученикам подготовиться к выпускным экзаменам по математике с помощью этого бесплатного рабочего листа по алгебре, содержащего 15 вопросов и ответов с несколькими вариантами ответов.

Алгебра в KS2

Идеи написания и упрощения выражений, решения уравнений и подстановок введены в KS2. Вот несколько примеров вопросов по алгебре KS2:

Вопросы по алгебре KS2

2 плитки шоколада будут стоить 2 партии c или 2c, а 2 напитка будут стоить 2 партии d или 2d.

Нам нужно собрать вместе подобные термины, так что 4m + 2m = 6m и 5 – 1 = 4 (обратите внимание на отрицательное значение).

Вопросы по алгебре KS3

В KS3 мы изучаем различные методы алгебры, чтобы отвечать на вопросы по алгебре и практиковаться в решении задач по алгебре.

К ним относятся:

• Упрощение алгебраических выражений
• Расширяющие скобки и факторинг
• Составление алгебраических уравнений из текстовых задач
• Решение алгебраических уравнений и неравенств
• Подстановка в выражения
• Изменение субъекта уравнения
• Работа с реальными графиками и линейными графиками
• Последовательности

Слайд, помогающий учащимся разобраться с уравнением прямой из онлайн-интервенции Third Space Learning.

Вопросы по алгебре KS3: основы алгебры

12a+5b

В этом вопросе n равно 7, поэтому мы можем подставить 7 в формулу.

 

Плата = 20 фунтов стерлингов + 4 × 7 92 — 6х\\ \end{выровнено}

 

В качестве альтернативы, если мы разложим 4x − 6, мы получим 2(2x − 3), что означает, что стороны могут быть равны 2 и 2x − 3.

C=\frac{5(F-32)}{9}

C=\frac{5F-32}{9}

C=\frac{5F}{9}-32

C=5F-\frac{32}{9}

\begin{align} F&=\frac{9C}{5}+32 \hspace{3cm} &\text{вычесть 32}\\\\ F-32&=\frac{9C}{5} &\text{умножить на 5}\\\\ 5(F-32)&=9C &\text{разделить на 9}\\\\ \frac{5(F-32)}{9}&=C \end{выровнено} 9{\ круг} .

Чтобы решить это, нам нужно написать уравнение.

 

Пусть сейчас возраст Джейми равен x . Тогда возраст отца Джейми в 4 раза больше.

 

Через 14 лет возраст Джейми будет x + 14, а возраст отца Джейми будет 4x + 14 .

 

Поскольку мы знаем, что возраст отца Джейми будет в два раза больше возраста Джейми, мы можем записать

 

4x+14=2(x+14)

 

Теперь у нас есть уравнение, которое мы можем решить.

 

\begin{выровнено} 4x+14&=2(x+14) \hspace{3cm} &\text{раскрыть скобки}\\ 4x+14&=2x+28 \hspace{3cm} &\text{вычесть 2x}\\ 2x+14&=28\hspace{3cm} &\text{вычесть 14}\\ 2x&=14 \hspace{3cm} &\text{раскрыть скобки}\\ х&=7 \hпробел{3см} \end{выровнено}

 

Сейчас Джейми 7 лет, то есть его отцу 28 лет. Сумма их возрастов равна 35 .

Вопросы по алгебре KS3: графики

y=2x-1

y=2x+1

y=4x-2

y=2x+5

В точке (2, 5) x равно 2, а y равно 5. Мы можем проверить, какое уравнение работает, если подставить эти значения:

 

\begin{выровнено} y&=2x−1 \quad \quad \quad 5=2×2−1 \quad \quad \text{False}\\ y&=2x+1 \quad \quad 5=2×2+1 \quad \quad \text{True}\\ y&=4x−2 \quad \quad \quad 5=4×2−2 \quad \quad \text{False}\\ y&=2x+5 \quad \quad 5=2×2+5 \quad \quad \text{False} \end{выровнено}

Вопросы по алгебре KS4

Алгебра широко изучается в программе GCSE и IGCSE.

В KS4 мы опираемся на методы, изученные в KS3. Темы включают:

• Расширение и факторизация многочленов
• Решение квадратных уравнений
• Решение одновременных уравнений
• Неравенства
• Алгебраические дроби
• Дальнейшая работа над графиками
• Функции

Один из слайдов GCSE по алгебре, посвященный онлайн-вмешательству Third Space Learning, который помогает учащимся с помощью факторизации квадратичных вычислений. 92+4х+3

Вопросы по алгебре KS4: составление и решение уравнений

Площадь треугольника равна area = \frac{1}{2} × b × h.

 

Если мы заполним то, что знаем, получим:

 

\begin{выровнено} 24&=\frac{1}{2}\times 6 \times (3x-1) \hspace{3cm} &\text{simplify}\\\\ 24&=3(3x-1) &\text{умножить скобки}\\\\ 24&=9x-3 &\text{добавить 3}\\\\ 27&=9x &\text{разделить на 9}\\\\ х&=3 \end{выровнено}

  9{2}+2x-15&=0 &\text{факторизация}\\\\ (x+5)(x-3)&=0 &\text{решить}\\\\ &x=-5 \text{ или } x=3 \end{выровнено}

Мы можем написать одновременные уравнения, чтобы решить это.

 

2a+3c=48 (уравнение 1)
3a+c=44 (уравнение 2)

 

Умножьте уравнение 2 на 3, чтобы сделать коэффициенты при c равными: 9a+3c=132 (уравнение 03)

 

Вычесть уравнение 1 из уравнения 3:
7a= 84
a=12

 

Подставьте a в уравнение 3:
3×12+c=44
36+c=44
c=8

 

8 фунтов стерлингов.

Вопросы по алгебре KS4: графики

3y=x+7

y=2x-2

y=\frac{1}{2}x-9

2y=3x+8

Две прямые параллельны , их градиент должен быть равен.

 

Если мы переставим 2y=x+7 так, чтобы y стало субъектом, мы получим y=\frac{1}{2}x+\frac{7}{2}. 92+1 \end{выровнено}

 

Минимальное значение 1. Это происходит, когда (x+2) равно 0.

y=5x+5

y=3x+4

y=\frac{-3}{4}x+ 3

y=\frac{-3}{4}x+\frac{21}{4}

Чтобы определить градиент линии, нам нужно определить градиент нормали.

 

Мы знаем, что нормаль проходит через точки (0, 0) и (3, 4), поэтому мы можем вычислить градиент: \frac{4-0}{3-0}=\frac{4}{ 3}.

 

Градиент касательной будет равен \frac{-3}{4}.

 

Теперь мы можем использовать y=mx+c . Мы знаем, что касательная проходит через точку (3, 4) и что ее градиент равен \frac{-3}{4} .

 

Поэтому

 

\begin{выровнено} 4&=\frac{-3}{4} \times 3 +c\\\\ 4&=\frac{-9}{4}+c\\\\ 4+\frac{9}{4}&=c\\\\ \фракция{25}{4}&=с \end{выровнено}

 

y=\frac{-3}{4}x+\frac{25}{4} \text{ или } 4y=-3x+25

Ищете дополнительные вопросы и ресурсы по алгебре?

Бесплатная библиотека ресурсов по математике GCSE от Third Space Learning содержит подробные уроки с пошаговыми инструкциями по решению задач по алгебре, а также рабочие листы с практическими вопросами по алгебре и другими экзаменационными вопросами GCSE.