Степень с натуральным показателем 7 класс самостоятельная: Самостоятельная работа «Свойства степени с натуральным показателем» 7 класс (УМК А.Г. Мерзляк)

Самостоятельная работа Свойства степени с натуральным показателем.

1 в	2 в	в	в
А) (а5 )2 а5	А) (х3)2 х4	А) (в3 )2 в9	А) (с4)2 с2
Б) (а2 а5)2	Б) (х3 х5)4	Б) (в2 в5)2	Б) (с3 с5)4
В) а4 (а4)4	В) х3 (х3)3	В) в4 (в4)4	В) с3 (с3)3
Г) (а а7)7	Г) (х х5)5	Г) (в в7)7	Г) (с с5)5
Д) у12 : (у6)2	Д) с10 : (с2)5	Д) с18 : (с6)3	Д) а15 : (а3)5
Е) (у4)5 : (у4)2	Е) (с3)7 : (с3)6	Е) (с4)5 : (с4)2	Е) (а3)7 : (а3)6
Ж) (у у2)3 : (у у3)2	Ж) (с2 с)3 : (с3 с)2	Ж) (с с2)3 : (с с3)2	Ж) (а2 а)3 : (а3 а)2
Вычислите З) 37 (32)3 : 310 И) 0,25 55 К) 94 : 37 Л) 1012 26 56	Вычислите З) 28 (2 3)2 : 212 И) 0,253 43 К) 162 : 25 Л) 310 710 218	Вычислите З) 34 (32)3 : 37 И) 0,27 57 К) 95 : 39 Л) 1011 2 5 55	Вычислите З) 210 (2 3)2 : 214 И) 0,53 43 К) 163 : 27 Л) 315 715 2113
1 в	2 в	в	в
А) (а5 )2 а5	А) (х3)2 х4	А) (в5 )2 в5	А) (с3)2 с4
Б) (а2 а5)2	Б) (х3 х5)4	Б) (в2 в5)2	Б) (с3 с5)4
В) а4 (а4)4	В) х3 (х3)3	В) в4 (в4)4	В) с3 (с3)3
Г) (а а7)7	Г) (х х5)5	Г) (в в7)7	Г) (с с5)5
Д) у12 : (у6)2	Д) с10 : (с2)5	Д) с12 : (с6)2	Д) а10 : (а2)5
Е) (у4)5 : (у4)2	Е) (с3)7 : (с3)6	Е) (с4)5 : (с4)2	Е) (а3)7 : (а3)6
Ж) (у у2)3 : (у у3)2	Ж) (с2 с)3 : (с3 с)2	Ж) (с с2)3 : (с с3)2	Ж) (а2 а)3 : (а3 а)2
Вычислите З) 37 (32)3 : 310 И) 0,25 55 К) 94 : 37 Л) 1012 26 56	Вычислите З) 28 (2 3)2 : 212 И) 0,253 43 К) 162 : 25 Л) 310 710 218	Вычислите З) 34 (32)3 : 37 И) 0,27 57 К) 95 : 39 Л) 1011 2 5 55	Вычислите З) 210 (2 3)2 : 214 И) 0,53 43 К) 163 : 27 Л) 315 715 2113
1 в	2 в	в	в
А) (а5 )2 а5	А) (х3)2 х4	А) (в5 )2 в5	А) (с3)2 с4
Б) (а2 а5)2	Б) (х3 х5)4	Б) (в2 в5)2	Б) (с3 с5)4
В) а4 (а4)4	В) х3 (х3)3	В) в4 (в4)4	В) с3 (с3)3
Г) (а а7)7	Г) (х х5)5	Г) (в в7)7	Г) (с с5)5
Д) у12 : (у6)2	Д) с10 : (с2)5	Д) с12 : (с6)2	Д) а10 : (а2)5
Е) (у4)5 : (у4)2	Е) (с3)7 : (с3)6	Е) (с4)5 : (с4)2	Е) (а3)7 : (а3)6
Ж) (у у2)3 : (у у3)2	Ж) (с2 с)3 : (с3 с)2	Ж) (с с2)3 : (с с3)2	Ж) (а2 а)3 : (а3 а)2
Вычислите З) 37 (32)3 : 310 И) 0,25 55 К) 94 : 37 Л) 1012 26 56	Вычислите З) 28 (2 3)2 : 212 И) 0,253 43 К) 162 : 25 Л) 310 710 218	Вычислите З) 34 (32)3 : 37 И) 0,27 57 К) 95 : 39 Л) 1011 2 5 55	Вычислите З) 210 (2 3)2 : 214 И) 0,53 43 К) 163 : 27 Л) 315 715 2113

Самостоятельные работы по теме » Степень с натуральным показателем» | Учебно-методический материал по алгебре (7 класс) по теме:

Самостоятельная работа по теме « Степень с натуральным показателем»

Вариант – 1

1. Представьте в виде квадрата или куба число:

а) 9; б) 6,25; в) .                   (3 балла)

2. Сравните значение выражения с нулём:

а) (-11)9 (-11)8; б) (-14)25:(-14)8. (2 балла)

3. Среди выражений (-Х)2, -(-Х)2, -(-Х2) укажите те, которые тождественно                                                                                                      равны Х2.                                      (2 балла)

4. Замените * таким выражением, чтобы выполнялось равенство:

а) (*)5=Х20; б) (*)3 с8=с20; в) а3 *=а10; г) а12:*=а6; д) (с5)*=с15. (5баллов)

5. Найдите ошибку!

а) 5 5 5 5=45; б) 71=1; в) 23 27=221; г) 23+27=210; д) (2Х)3=2Х3. (5баллов)

Вариант – 2

1. Представьте в виде квадрата или куба число:

а) -27; б) 0,064; в) . (3 балла)

2. Сравните значение выражения с нулём:

а) (-6)4 (-6)10; б) (-6)12:64.        (2 балла)

3. Среди выражений (-Х)3, -(-Х)3, -(-Х3) укажите те, которые тождественно                                                                                                      равны Х3.                                   (2 балла)                                         

4. Замените * таким выражением, чтобы выполнялось равенство:

                а) (*)7=Х21; б) у7 (у2)4=(*)5; в) * а=а2; г) *:у5=у6; д) (Х10)*=1.

                                                            (5баллов)

5. Найдите ошибку!

а) (-3)3=-9; б) 00=1; в) 23 27=410; г) 230:210=23; д) (а3)2=а9.

                                                             (5баллов

А-7; § 6

2 Самостоятельная работа

«Свойства степени с натуральным показателем»

I – уровень

Вариант 1

1. Записать произведение в виде степени:

а) х10∙х2∙х,

б) 23∙4∙28.

2. Произвести указанные действия:

а) (а5)2:(а3)2,

б) .

3. Вычислить:

а) ,

б) ,

в) .

А-7; § 6

2 Самостоятельная работа

«Свойства степени с натуральным показателем»

I – уровень

Вариант 2

1. Записать произведение в виде степени:

а) а∙а5∙а15,

б) 9∙33∙311.

2. Произвести указанные действия:

а) (у7)3:(у4)4,

б) .

3. Вычислить:

а) ,

б) ,

в) .

А-7; § 6

2 Самостоятельная работа

«Свойства степени с натуральным показателем»

II – уровень

Вариант 3

1. Записать произведение в виде степени:

а) (х3)4∙(х2)3:(х5)3,

б) 27∙163∙82.

2. Произвести указанные действия:

а) ,

б) .

3. Вычислить:

а) ,

б) ,

в) 3∙26-8∙43+5∙82.

А-7; § 6

2 Самостоятельная работа

«Свойства степени с натуральным показателем»

II – уровень

Вариант 4

1. Записать произведение в виде степени:

а) (у10)6:(у5)5∙(у3)2,

б) 273∙36∙814.

2. Произвести указанные действия:

а) ,

б) .

3. Вычислить:

а) ,

б) ,

в) 4∙36-11∙272+7∙93.

А-7; § 6

2 Самостоятельная работа

«Свойства степени с натуральным показателем»

III – уровень

Вариант 5

1. Записать произведение в виде степени:

а) 816:2434∙276:96,

б) 23n-1∙4n+2:8n-3.

2. Вычислить:

а) ,

б) .

3. Решить уравнения:

а) 97х+1=812х+4,

б) .

А-7; § 6

2 Самостоятельная работа

«Свойства степени с натуральным показателем»

III – уровень

Вариант 6

1. Записать произведение в виде степени:

а) 89:163∙1283:642,

б) 27n-2∙243n+1:9n+3.

2. Вычислить:

а) ,

б) .

3. Решить уравнения:

а) 253х-6=125х+5,

б) .

А-7; § 6

2 Самостоятельная работа

«Свойства степени с натуральным показателем»

IV – уровень

Вариант 7

1. Записать произведение в виде степени:

а) (164)5:2564∙(642)4:1286,

б) 95n+3∙273n+1:812n-5.

2. Решить уравнения:

а) ,

б) (253х-3)2=27х:33.

3. Вычислить:

а) ,

б) .

4. Доказать:

(87-218) делиться на 7.

А-7; § 6

2 Самостоятельная работа

«Свойства степени с натуральным показателем»

IV – уровень

1. Записать произведение в виде степени:

а) (2433)5:(812)4∙278:(93)2,

б) 643n+3:32n+7∙162n-9.

2. Решить уравнения:

а) ,

б) 16х∙3=32х∙4.

3. Вычислить:

а) ,

б) .

4. Доказать:

(7910+799∙11) делиться на 30.

А – 7; § 6

Карточка № 1

Произведение		(-х) (-х) (-х) (-х) (-х)		(2х) (2х) (2х) (2х)		(-5Х) (-5Х) (-5Х) (-5Х) (-5Х) (-5Х)
Степень	Х7		Х		(х+2)2
Значение выражения при х=-1

		(-0,3)		а2	а4у3
Показатель		3		3	2		4
Степень	Х6		(а+в)4

*	Х8	Х14
Х3
Х5
:	С2	С6
С8
С18

(*)*	5	2
а3
в2
Х	(…)3	(…)2
(…)2	Х7
(…)3		Х27

А -7; § 6

Карточка № 2

Возведите отрицательное число (-2) в степень Х. Заполните таблицу.

Проведите аналогичное исследование для положительного числа 3. Заполните таблицу.

Сформулируйте вывод об изменении значений дробей с отрицательным и положительным основаниями в зависимости от четности показателя.

        А -7; § 6

Карточка № 2

Возведите отрицательное число (-2) в степень Х. Заполните таблицу.

Проведите аналогичное исследование для положительного числа 3. Заполните таблицу.

Сформулируйте вывод об изменении значений дробей с отрицательным и положительным основаниями в зависимости от четности показателя.

А-7; § 6

1 Самостоятельная работа

«Степень с натуральным показателем»

I – уровень

Вариант 1

1. Записать произведение в виде произведения степеней

5∙5∙5∙5∙а∙а∙а.

2. Вычислить:

а) (-3)4,

б) 52∙23,

в) .

3. Записать числа в стандартном виде:

а) 3053,

б)50,25.

А-7; § 6

1 Самостоятельная работа

«Степень с натуральным показателем»

I – уровень

Вариант 2

1. Записать произведение в виде произведения степеней

в∙в∙в∙в∙7∙7∙7∙7∙7.

2. Вычислить:

а) (-2)5,

б) 53∙22,

в) .

3. Записать числа в стандартном виде:

а) 205,7,

б) 35100.

А-7; § 6

1 Самостоятельная работа

«Степень с натуральным показателем»

II – уровень

Вариант 3

1. Записать произведение в виде произведения степеней

3а∙9∙а∙а∙27.

2. Вычислить:

а) 54,

б) (-2)3∙112,

в) .

3. Записать числа в стандартном виде:

а) 525000202,

б) 93,53.

А-7; § 6

1 Самостоятельная работа

«Степень с натуральным показателем»

II – уровень

Вариант 4

1. Записать произведение в виде произведения степеней

b∙b∙4∙2∙b∙16∙b.

2. Вычислить:

а) (-4)4,

б) 72∙53,

в) .

3. Записать числа в стандартном виде:

а) 112,35,

б) 39444005.

1 Самостоятельная работа

«Степень с натуральным показателем»

III – уровень

Вариант 5

1.  Вычислить:

а),

б),

2. Представить числа в виде квадрата или куба:

а) 0,008,

б) 216,

в) .

3. Сравните числа:

а) (-5,2)3 и (-2,4)2,

б) -7,12 и -5,92

А-7; § 6

1 Самостоятельная работа

«Степень с натуральным показателем»

III – уровень

Вариант 6

1.  Вычислить:

а),

б),

2. Представить числа в виде квадрата или куба:

а) 0,0625,

б) ,

в) 343.

3. Сравните числа:

а) (-2,4)4 и (-5,2)3,

б) -6,82 и -5,72

1 Самостоятельная работа

«Степень с натуральным показателем»

IV – уровень

Вариант 7

1.  . Записать произведение в виде произведения степеней

x3∙23∙x∙8∙x2∙128,

2. Представить число в виде произведения степеней простых чисел:

а) 18∙20∙22,

б) 243∙15∙125.

3. Какой цифрой заканчивается значение выражения:

а) 155 + 135+75,

б) 2123 +3223 +1423?

А-7; § 6

1 Самостоятельная работа

«Степень с натуральным показателем»

IV – уровень

Вариант 8

1.  . Записать произведение в виде произведения степеней

81∙у∙у4∙27∙у2∙92,

2. Представить число в виде произведения степеней простых чисел:

а) 14∙15∙16,

б) 343∙14∙63.

3. Какой цифрой заканчивается значение выражения:

а) 164 + 244+324,

б) 1521 +1921 +2721?

Степень с натуральным показателем

Вариант А 1

1. Выполните действия:

а) 5∙23-32;

б) -10+(-1)3.

2. Найдите значение выражения

-х5 при х=-2.

3. Упростите выражения:

а) с4∙с7:с9;

б) (а4)3∙а;

в) (-2х)4.

4. Вычислите, используя свойства степени:

а) 203∙ 0,53;

б) .

5. Представьте в виде степени с основанием у:

((у2)3)4.

Степень с натуральным показателем

Вариант А 2

1. Выполните действия:

а)62-3∙23;

б)( -1)3-10.

2. Найдите значение выражения

-х3 при х=-3.

3. Упростите выражения:

а) с18:с15∙с2;

б) (а2)5:а;

в) (-7х)2.

4. Вычислите, используя свойства степени:

а) 0,252∙ 1002;

б) .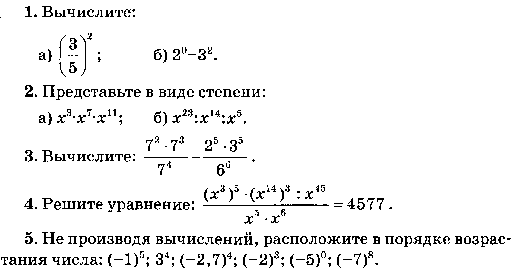

5. Представьте в виде степени с основанием у:

((у3)4)5.

Степень с натуральным показателем

Вариант Б 1

1. Выполните действия:

а) 0,2∙(-5)2-16∙;

б)(-0,5)3-0,50.

2. Найдите значение выражения

3-х3 при х=-1.

3. Упростите выражения:

а) (с4)2∙с3;

б);

в) (-3ав)3.

4. Вычислите, используя свойства степени:

а) 0,42∙ 2502;

б) .

5. Представьте в виде степени с основанием у:

(((-у)3)2)4.

Степень с натуральным показателем

Вариант Б 2

1. Выполните действия:

а) 81∙-0,05∙(-10)2;

б)(-0,2)0-0,23.

2. Найдите значение выражения

1-х5 при х=-1.

3. Упростите выражения:

а) (с5)3∙с4;

б);

в) (-2ав)4.

4. Вычислите, используя свойства степени:

а) 1,254∙ 84;

б) .

5. Представьте в виде степени с основанием у:

(((-у)2)3)4.

Степень с натуральным показателем

Вариант В 1

1. Выполните действия:

а) -42∙;

б)+(-3)3.

2. Найдите значение выражения

16-0,5х5 при х=-2.

3. Упростите выражения:

а);

б);

в) (-3авс)3.

4. Вычислите, используя свойства степени:

а) 1,15∙;

б) .

5. Представьте в виде степени с основанием у:

(уn+5)2:((-у2)3)2.

Степень с натуральным показателем

Вариант В 2

1. Выполните действия:

а) ;

б)+(-2)3.

2. Найдите значение выражения

1-при х=-3.

3. Упростите выражения:

а);

б);

в) (-5авс)3.

4. Вычислите, используя свойства степени:

а) 2,37∙;

б) .

5. Представьте в виде степени с основанием у:    (уn-4)5∙((-у4)2)3.

А-7; § 6

Самостоятельная работа по теме «Свойства степени» 7класс

Алгебра, 7 класс.

Самостоятельная работа по теме

Степень с натуральным показателем.

1 вариант.

Уровень 3.

3²; 5³; 12²; (-4)²; (-7)³; 2⁸; (-3)⁵

Уровень 2.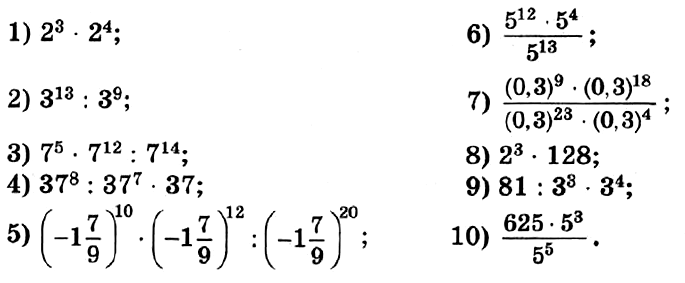

8³; 23²; 0,1²; (-0,6)³; (-2,5)²; (-2)⁴

Уровень 1.

0,2²; (-0,9)³; (-7,5)²; ; 4³+8²; (-2)⁵+3⁵

Алгебра, 7 класс.

Самостоятельная работа по теме

Степень с натуральным показателем.

2 вариант.

Уровень 3.

4²; 6³; 13²; (-9)²; (-2)³; 2⁷; (-3)⁶

Уровень 2.

7³; 48²; 0,2²; (-0,5)³; (-4,1)²; (-2)⁵

Уровень 1.

0,3²; (-0,8)³; (-6,2)²; ; 4²+7³; (-2)⁷+3⁸

Алгебра, 7 класс.

Самостоятельная работа по теме

Степень с натуральным показателем.

3 вариант.

Уровень 3.

5²; 7³; 14²; (-3)²; (-8)³; 2⁶; (-3)⁷

Уровень 2.

6³; 54²; 0,3²; (-0,4)³; (-9,2)²; (-2)⁶

Уровень 1.

0,4²; (-0,7)³; (-5,1)²; ; 6³+8²; (-2)⁸+3⁴

Алгебра, 7 класс.

Самостоятельная работа по теме

Степень с натуральным показателем.

4 вариант.

Уровень 3.

6²; 4³; 15²; (-2)²; (-9)³; 2⁵; (-3)⁸

Уровень 2.

5³; 31²; 0,4²; (-0,2)³; (-3,5)²; (-2)⁷

Уровень 1.

0,5²; (-0,6)³; (-4,2)²; ; 4³+5²; (-2)⁵+3⁷

Алгебра, 7 класс.

Самостоятельная работа по теме

Степень с натуральным показателем.

5 вариант.

Уровень 3.

7²; 3³; 16²; (-5)²; (-4)³; 2⁴; (-3)⁹

Уровень 2.

9³; 82²

; 0,5²; (-0,1)³; (-3,4)²; (-2)⁸

Уровень 1.

0,6²; (-0,5)³; (-3,7)²; ; 3²+8³; (-2)⁷+3¹⁰

Алгебра, 7 класс.

Самостоятельная работа по теме

Степень с натуральным показателем.

6 вариант.

Уровень 3.

8²; 2³; 17²; (-6)²; (-5)³; 2⁹; (-3)⁴

Уровень 2.

4³; 94²; 0,6²; (-0,7)³; (-8,)²; (-2)⁹

Уровень 1.

0,7²; (-0,4)³; (-2,3)²; ; 2³+7²; (-2)⁵+3⁹

Контрольная работа «Степень с натуральным показателем. Одночлен» 7 класс

Степень с натуральным показателем. Одночлен.

В а р и а н т А – 1 К – 4

1. Вычислите: а)

б) в)

2. Выполните действия:

3. Постройте график функции . Определите по графику значение у при х = -2.

4. Упростите выражения: а)

б) в)

5. Используя свойство степени, найдите значение выражения:

В а р и а н т А – 2 К – 4 Вычислите: а) б) в) Выполните действия: Постройте график функции . Определите по графику значение у при х = 2. Упростите выражения: а) б) в) 5. Используя свойство степени, найдите значение выражения: .
Дополнительно: Вычислите: , если .	Дополнительно: Вычислите: , если .
В а р и а н т В – 1 К – 4 Вычислите: а) б) в) Выполните действия: а) б) в) Постройте график функции ; определите по графику значение х, соответствующее значению Упростите выражения: а) б) в) 5. Используя свойства степени, найдите значение выражения: .	В а р и а н т В – 2 К – 4 Вычислите: а) б) в) Выполните действия: а) б) в) Постройте график функции ; определите по графику значение х, соответствующее значению Упростите выражения: а) б) в) 5. Используя свойства степени, найдите значение выражения: .
Дополнительно: Вычислите: , если	Дополнительно: Вычислите: , если

Решебник (ГДЗ) самостоятельные работы по алгебре 7 класс Александрова

С-1. Числовые выражения:

Вариант 1 Вариант 2 Вариант 3 Вариант 4

С-2. Алгебраические выражения:

Вариант 1 Вариант 2 Вариант 3 Вариант 4

С-3. Что такое математический язык:

Вариант 1 Вариант 2 Вариант 3 Вариант 4

С-4. Что такое математическая модель:

Вариант 1 Вариант 2 Вариант 3 Вариант 4

С-5. Линейное уравнение с одной переменной:

Вариант 1 Вариант 2 Вариант 3 Вариант 4

С-6.

Координатная прямая:

Вариант 1 Вариант 2 Вариант 3 Вариант 4

С-7 Координатная плоскость:

Вариант 1 Вариант 2 Вариант 3 Вариант 4

С-8. Линейное уравнение с двумя переменными и его график:

Вариант 1 Вариант 2 Вариант 3 Вариант 4

С-9. Линейная функция и её график:

Вариант 1 Вариант 2 Вариант 3 Вариант 4

С-10. Линейная функция и её график:

Вариант 1 Вариант 2 Вариант 3 Вариант 4

С-11. Линейная функция y=kx:

Вариант 1 Вариант 2 Вариант 3 Вариант 4

С-12. Основные понятия:

Вариант 1 Вариант 2 Вариант 3 Вариант 4

С-13. Метод подстановки:

Вариант 1 Вариант 2 Вариант 3 Вариант 4

С-14.

Метод подстановки:

Вариант 1 Вариант 2 Вариант 3 Вариант 4

С-15. Метод алгебраического сложения:

Вариант 1 Вариант 2 Вариант 3 Вариант 4

С-16. Метод алгебраического сложения:

Вариант 1 Вариант 2 Вариант 3 Вариант 4

С-17. Системы двух линейных уравнений с двумя переменными:

Вариант 1 Вариант 2 Вариант 3 Вариант 4

С-18. Определение степени с натуральным показателем:

Вариант 1 Вариант 2 Вариант 3 Вариант 4

С-19. Таблица основных степеней:

Вариант 1 Вариант 2 Вариант 3 Вариант 4

С-20. Свойства степени с натуральным показателем:

Вариант 1 Вариант 2 Вариант 3 Вариант 4

С-21. Умножение и деление степеней с одинаковыми показателями:

Вариант 1 Вариант 2 Вариант 3 Вариант 4

С-22.

Стандартный вид одночлена. Сложение и вычитание одночленов:

Вариант 1 Вариант 2 Вариант 3 Вариант 4

С-23. Сложение и вычитание одночленов:

Вариант 1 Вариант 2 Вариант 3 Вариант 4

С-24. Умножение одночленов. Возведение одночлена в натуральную степень:

Вариант 1 Вариант 2 Вариант 3 Вариант 4

С-25. Деление одночлена на одночлен:

Вариант 1 Вариант 2 Вариант 3 Вариант 4

С-26. Основные понятия:

Вариант 1 Вариант 2 Вариант 3 Вариант 4

С-27. Сложение и вычитание многочленов:

Вариант 1 Вариант 2 Вариант 3 Вариант 4

С-28. Умножение многочлена на одночлен:

Вариант 1 Вариант 2 Вариант 3 Вариант 4

С-29. Умножение многочлена на одночлен:

Вариант 1 Вариант 2 Вариант 3 Вариант 4

С-30.

Умножение многочлена на многочлен:

Вариант 1 Вариант 2 Вариант 3 Вариант 4

С-31. Формулы сокращенного умножения. Квадрат двучлена:

Вариант 1 Вариант 2 Вариант 3 Вариант 4

С-32. Формулы сокращенного умножения. Разность квадратов :

Вариант 1 Вариант 2 Вариант 3 Вариант 4

С-33. Формулы сокращенного умножения. Сумма и разность кубов:

Вариант 1 Вариант 2 Вариант 3 Вариант 4

С-34. Вынесение общего множителя за скобки:

Вариант 1 Вариант 2 Вариант 3 Вариант 4

С-35. Способ группировки:

Вариант 1 Вариант 2 Вариант 3 Вариант 4

С-36. Разность квадратов:

Вариант 1 Вариант 2 Вариант 3 Вариант 4

С-37. Сумма и разность кубов:

Вариант 1 Вариант 2 Вариант 3 Вариант 4

С-38.

Квадрат двучлена:

Вариант 1 Вариант 2 Вариант 3 Вариант 4

С-39. Разложение многочленов на множители с помощью комбинации различных приемов:

Вариант 1 Вариант 2 Вариант 3 Вариант 4

С-40. Сокращение алгебраических дробей:

Вариант 1 Вариант 2 Вариант 3 Вариант 4

С-42. Графическое решение уравнений:

Вариант 1 Вариант 2 Вариант 3 Вариант 4

С-43. Что означает в математике запись y=f(x):

Вариант 1 Вариант 2 Вариант 3 Вариант 4

С-44. Итоговое повторение:

Вариант 1 Вариант 2 Вариант 3 Вариант 4

С-41. Функция y=x2 и её график:

Вариант 1 Вариант 2 Вариант 3 Вариант 4

ГДЗ Алгебра 7 класс Попов, Мордкович

Решебник к учебнику «Алгебра 7 класс Тетрадь для самостоятельных и контрольных работ Попов, Мордкович, Экзамен» — это пособие, в котором можно найти решение и ответы ко всем номерам книги. Оно поможет в выполнении домашнего задания ученикам и в проверке работ преподавателям. Родители часто используют его как подсказку, когда нет времени на то, чтобы вникать в материал, изучаемый по алгебре.

Преимущества решебника

ГДЗ (готовые домашние задания) четко структурированы. Вы с легкостью найдете нужный материал. Как и учебник по алгебре, решебник состоит из 8 разделов:

• Математический язык и модель;
• Линейная функция;
• Системы двух линейных уравнений;
• Степень и свойства натурального показателя;
• Одночлены;
• Многочлены;
• Разложение на множители;
• Функция.

Структура ГДЗ

К каждой теме дается несколько самостоятельных и одна контрольная работа. Самостоятельные работы идут в 2 вариантах, контрольные – в 4. Первые задания соответствуют базовым знаниям и даются в виде тестирования. Ученикам предлагается выбрать только положительный или отрицательный ответ без объяснений действия. Поэтому в ГДЗ ответы к таким номерам даны только в виде «да» и «нет». Остальные упражнения предполагают более развернутого решения. В ГДЗ четко прописаны все действия и дан развернутый ответ.

Как пользоваться

На нашем сайте размещена онлайн-версия пособия. Вам необходимо выбрать раздел, вариант и номер задания. Все упражнения решены математиками, поэтому ответы корректны. ГДЗ используют для подготовки домашнего задания, отработки навыков дома и проверки выполненных номеров. Старайтесь только сверяться с ответами и исправлять их в случае необходимости. Так вы сможете выявить, с каким материалом у вас возникли трудности и проработать его еще раз. Обычное списывание не приведет к желаемому результату.

Свойства степени с натуральным показателем. Алгебра, 7 класс: уроки, тесты, задания.

1.	Умножение степеней Сложность: лёгкое	1
2.	Степень в степени Сложность: лёгкое	1
3.	Возведение степени в степень (буквы) Сложность: лёгкое	2
4.	Степень в степени (основание) Сложность: лёгкое	2
5.	Степень в степени (показатель степени) Сложность: лёгкое	2
6.	Произведение трёх степеней Сложность: лёгкое	2
7.	Произведение степеней (основание — бином) Сложность: лёгкое	1
8.	Частное трёх степеней Сложность: лёгкое	2
9.	Произведение степеней с одинаковыми основаниями (буквы) Сложность: лёгкое	3
10.	Произведение двух степеней (числа) Сложность: лёгкое	2
11.	Частное двух степеней (отрицательное основание) Сложность: лёгкое	2
12.	Возведение степени в степень (числа) Сложность: лёгкое	2
13.	Частное двух степеней (дробь) Сложность: лёгкое	3
14.	Частное двух степеней (отрицательные смешанные числа) Сложность: лёгкое	1
15.	Произведение степеней с одним основанием (числа) Сложность: среднее	3
16.	Произведение отрицательных и противоположных степеней Сложность: среднее	5
17.	Уравнение (частное степеней, целые числа) Сложность: среднее	3
18.	Дробь (буквы) Сложность: среднее	2
19.	Произведение степени и степени в степени Сложность: среднее	2
20.	Деление и умножение степеней Сложность: среднее	3
21.	Произведение двух дробей Сложность: среднее	2
22.	Произведение степеней в степени Сложность: среднее	3
23.	Частное степени в степени и степени Сложность: среднее	2
24.	Умножение и деление степеней Сложность: среднее	1
25.	Вычисление выражения со степенями Сложность: среднее	1

Индикаторы общей кислотной основы

| Наука

Обновлено 1 марта 2020 г.

Розанн Козловски

Рецензент: Лана Бандойм, Б.С.

Кислотные и щелочные индикаторы используются в химии для определения pH вещества. Они меняют цвет в зависимости от того, добавлены ли они к кислоте, основанию или нейтральному веществу. Большинство индикаторов являются слабыми кислотами и реагируют на изменение концентрации ионов водорода.

Шкала pH и индикаторы кислоты и щелочи

Диапазон pH составляет от 0 до 14, где 7 является нейтральным.PH выше 7 указывает на основание, а значение ниже 7 указывает на кислоту. Шкала pH является логарифмической, и при изменении каждого отдельного числа на шкале происходит десятикратное изменение кислотности и щелочности (основности).

Кислотные и щелочные индикаторы чувствительны к изменению pH или, точнее, к изменению концентрации ионов водорода , H ⁺ в растворе.

Большинство кислотных и основных индикаторов представляют собой большие органические молекулы, которые содержат чередующиеся двойные и одинарные углерод-углеродные связи. В основных растворах индикаторы кислоты и основания становятся ионами, теряя ионы водорода из своего химического состава, обычно из группы ОН. Это изменяет структуру молекулы, заставляя индикаторы поглощать свет с разной длиной волны и менять цвет.

Типы индикаторов

Многие типы индикаторов работают со всей шкалой pH. Важно выбрать тот, который соответствует рассматриваемому диапазону pH. Ниже приведены несколько общих индикаторов.

Лакмусовая бумага

Одним из распространенных индикаторов кислот и оснований является лакмусовая бумага, созданная путем обработки фильтровальной бумаги красителем, полученным из лишайников.Раствор, нанесенный на лакмусовую бумагу, либо сохранит цвет лакмусовой бумаги, либо изменит его.

Красная лакмусовая кислота — слабая дипротонная кислота; он может отдавать два атома водорода. При pH ниже 4,5 красная лакмусовая бумажка остается красной, но становится синей в основе. При pH выше 8,3 синяя лакмусовая бумажка остается синей, но становится красной в кислоте.

Лакмусовая бумажка не способна определять значение pH, только различает кислоты и основания . Нейтральная лакмусовая бумага фиолетового цвета.

Индикатор фенолфталеина

Индикатор фенолфталеина представляет собой слабую кислоту, имеющую две разные структуры в зависимости от того, находится ли она в щелочном (розовом) или кислотном (бесцветном) растворе.Раствор щелочного металла поглощает свет в видимом спектре света, и человеческий глаз воспринимает изменение цвета на розовый при уровне pH 8,2, продолжающееся ярким пурпурным при pH 10 и выше.

Фенолфталеин обычно используется в качестве индикатора в экспериментах по кислотно-щелочному титрованию в химической лаборатории. Раствор известной концентрации осторожно добавляют к раствору неизвестной концентрации и индикатора фенолфталеина. Когда раствор превращается из бесцветного в розовый (или наоборот), это означает, что титр , или точка нейтрализации достигнуты, и можно рассчитать неизвестную концентрацию.

Индикатор бромтимолового синего

Бромтимоловый синий, слабая кислота, чаще всего используется в качестве индикатора для относительно нейтральных растворов — слабых кислот и оснований. Диапазон pH составляет от 6 до 7,6. Раствор кажется желтым до pH 6, в нейтральном растворе он становится зеленым, и становится синим в щелочных растворах с pH выше 7,6.

В лаборатории бромтимоловый синий часто используется в качестве красителя для биологических препаратов , для тестирования фотосинтеза и может использоваться для определения pH в плавательных бассейнах.

Индикатор метилового красного

В качестве индикатора кислоты и основания метиловый красный становится красным в кислых растворах при pH 4,4 и ниже и становится желтым при достижении pH 6,2. Между этими конечными значениями цвета, в диапазоне pH от 4,4 до 6,2, цвет оранжевый.

Метиловый красный может использоваться как индикатор кислоты и основания в лаборатории и как азокраситель, самая большая группа синтетических красителей , обычно используемых для обработки текстильных изделий.

Универсальный индикатор

Универсальный индикатор — это раствор, содержащий смесь индикаторов, часто фенолфталеина, метилового красного и бромтимолового синего.Определение приблизительного pH достигается добавлением в раствор нескольких капель универсального индикатора.

Красный означает сильную кислоту в диапазоне pH от 1 до 4, тогда как слабая кислота имеет оранжевый оттенок. В нейтральном растворе цвет становится желто-зеленым. Пурпурный цвет указывает на сильное основание, pH выше 11, тогда как слабые основания имеют голубоватый оттенок.

Как сделать индикатор pH из капусты — Научные проекты

Артикул:

НАЖМИТЕ ЗДЕСЬ, если хотите узнать, почему краснокочанная капуста меняет цвет.
Хотите узнать еще больше о pH?

Вот сайт, который дает хорошее общее объяснение pH:

http://pc65.frontier.osrhe.edu/hs/science/cph.htm

А вот действительно хорошее руководство по pH:

http://www. science.ubc.ca/~chem/tutorials/pH/launch.html

Книги с сопутствующими материалами:

Бат, Джон Б. и Мэйберри, Салли К. Кухонная химия, Карсон-Деллоса, 1994.

Пошаговая серия учебных пособий, содержащих простые научные эксперименты, для детей от детского сада до шестиклассников.

Chem Fax, Flinn Scientific, 1990. Это отличный источник демонстраций для учителей и занятий в классе для студентов.

Гарднер, Роберт. Научные проекты о кухонной химии, Enslow, 1999. Содержит идеи для научных проектов с использованием различных продуктов питания или других материалов, найденных на кухне.

Herron, Frank, Sarquis, J., Sarquis, M., Schrader, and Kulka, Chemistry, D.C. Heath and Company, 1996. Этот уникальный учебник включает макро- и микролабораторные исследования в каждую из глав.В книге также есть много разделов «Потребительская химия».

Хиллман, Ховард. Наука о кухне: Руководство к знанию того, как и почему для развлечения и успеха на кухне, Houghton Mifflin, 1989. Очень приятная и легкая для чтения книга, которая отвечает на многие общие вопросы, касающиеся науки о еде и кулинарии.

ЛеМэй, Билл, Роббли и Брауэр. Химия: Связь с нашим изменяющимся миром, Prentice Hall, 1996. Эта книга используется во многих средних школах в качестве учебника общей химии для первого года обучения.Содержит около тридцати упражнений «Химия в действии», которые соотносят концепции химии с реальным миром.

Лешниг, Луи В. Простые химические эксперименты с повседневными материалами, Стерлинг, 1995. Эта книга идеально подходит для учащихся начальной и средней школы, но многие упражнения также можно использовать на уровне средней школы для демонстрации конкретной концепции.

Манделл, Мюриэль. Простые эксперименты на кухне: изучение науки с повседневной едой, Стерлинг, 1994. Отличная книга, полная идей для обучения многим научным концепциям с использованием пищевых продуктов.

МакГи, Гарольд. On Food and Cooking: The Science and Lore Of The Kitchen, Simon and Schuster, 1984. Отличный справочник, посвященный науке о еде и кулинарии. Включает много исторической и справочной информации о большинстве пищевых продуктов.

МакГи, Гарольд. Любопытный повар: больше кухонной науки и знаний, Macmillan, 1990. Это вторая из двух книг, написанных автором. В этой книге он пытается ответить на другие вопросы, касающиеся еды и приготовления пищи. Она написана в форме рассказа и содержит меньше исторической информации, чем первая книга.

Филлипс, Джон С., Виктор Строзак и Шерил Уилстром. Chemistry: Concepts and Applicatons, Glencoe / McGraw-Hill, 1997. Учебник по общей химии, содержащий «MiniLabs» и «ChemLabs» в каждой главе.

Уилбрахам, Стейли и Матта. Chemistry, Addison-Wesley, 1997. Это учебник, который в настоящее время используется государственными школами Питтсбурга для всех классов общей химии, а также для школьных классов химии. Он содержит множество простых заданий, разделы, посвященные бытовой химии, и другие полезные темы.Очень хорошо написанный текст, который легко понять учащимся.

Уильямс, Тэмми К. Научные эксперименты, химия и физика, Mark Twain Media, 1995. Научные эксперименты, написанные специально для учеников средней школы, которые можно легко адаптировать к любой программе средней школы.

Зумдал, Стивен С. Вводная химия: фонд, Д. К. Хит, 1996. Учебник для старшеклассников. Каждая глава содержит интересные разделы «Химия в фокусе».

8.1 — Тест хи-квадрат на независимость

Как мы проверяем независимость двух категориальных переменных? Это будет сделано с использованием критерия независимости хи-квадрат.

Как и во всех предыдущих статистических тестах, нам необходимо определить нулевую и альтернативную гипотезы. Кроме того, как мы узнали, нулевая гипотеза считается истинной до тех пор, пока у нас не будет доказательств, опровергающих ее. В этом уроке нас интересует исследование того, связаны ли две категориальные переменные или связаны (т.э., иждивенец). Следовательно, пока у нас не будет доказательств, позволяющих предположить, что это так, мы должны предполагать, что это не так. Это мотивация гипотезы для теста независимости хи-квадрат:

• \ (H_0 \): в генеральной совокупности две категориальные переменные независимы.
• \ (H_a \): В совокупности две категориальные переменные являются зависимыми.

Примечание! Есть несколько способов сформулировать эти гипотезы. Вместо использования слов «независимый» и «зависимый» можно было бы сказать «нет никакой связи между двумя категориальными переменными» по сравнению с тем, что существует связь между двумя категориальными переменными.«Или» нет связи между двумя категориальными переменными »или« существует связь между двумя переменными ». Важная часть состоит в том, что нулевая гипотеза относится к двум категориальным переменным, которые не связаны между собой, в то время как альтернатива пытается показать, что они связаны.

После того, как мы собрали наши данные, мы суммируем данные в двусторонней таблице непредвиденных обстоятельств. Эта таблица представляет собой наблюдаемые подсчеты и называется таблицей наблюдаемых отсчетов или просто таблицей наблюдаемых .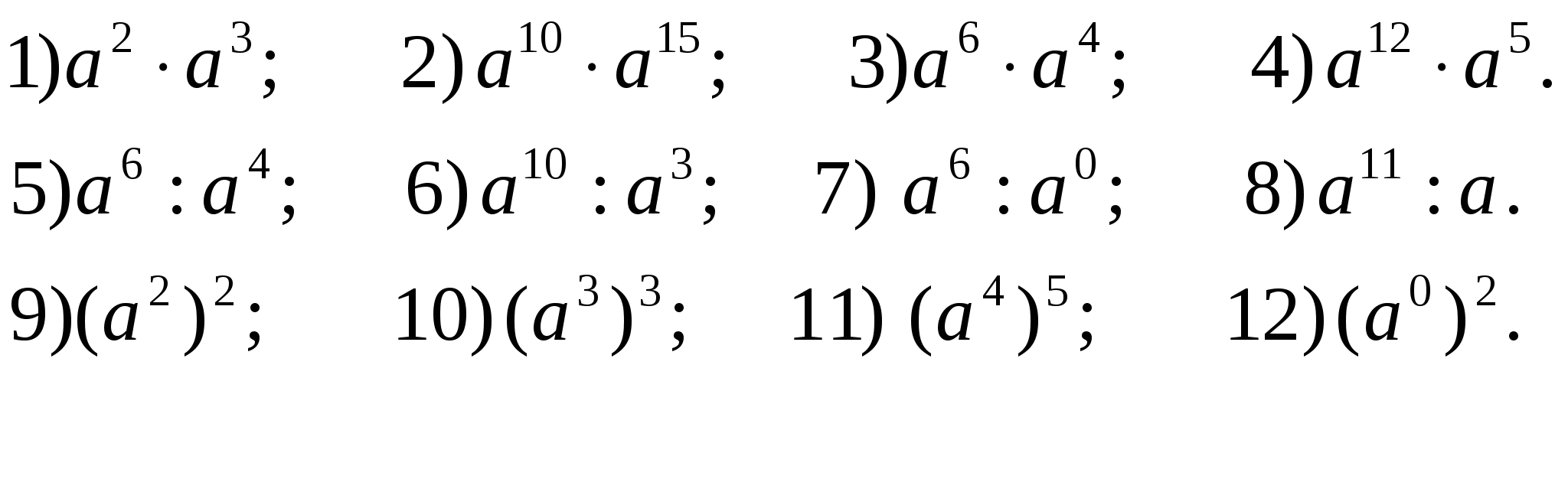 В таблице непредвиденных обстоятельств на вводной странице этого урока представлены наблюдаемые подсчеты партийной принадлежности и мнения опрошенных.

Возникает вопрос: «Как бы выглядела эта таблица, если бы две переменные не были связаны?» То есть, при нулевой гипотезе о том, что две переменные независимы, как мы ожидаем, что наши данные будут выглядеть?

Рассмотрим следующую таблицу:

	Успех	Отказ	Всего
Группа 1	A	B	A + B
Группа 2	С	D	К + Д
Итого	А + С	B + D	A + B + C + D

Общее количество равно \ (A + B + C + D \).Давайте сосредоточимся на одной ячейке, скажем, Группа 1 и Успех с наблюдаемым счетчиком A. 2} \ end {align}

Если мы рассматриваем счетчики вместо вероятностей, то мы получаем счет, умножая вероятность на общее количество.2} \ right) (A + B + C + D) \\ [10pt] & = \ mathbf {\ dfrac {(A + B) (A + C)} {A + B + C + D}} \ end {align}

Это число , которое мы ожидаем от , чтобы увидеть, были ли две переменные независимыми (т.е. предполагая, что нулевая гипотеза верна).

Ожидаемое количество ячеек

Ожидаемое количество для каждой ячейки при нулевой гипотезе:

\ (E = \ dfrac {\ text {(итого по строке)} (\ text {column total})} {\ text {общий размер выборки}} \)

Центр отчетов

Рейтинги соответствия и удобства использования присваиваются на основе оценки материалов по ряду критериев и индикаторы с рецензентами, предоставляющими подтверждающие доказательства для определения и обоснования каждого присужденного балла.

Для ELA и математика, рейтинги совмещения представляют собой степень соответствия материалов ожиданиям, частично соответствия ожиданиям или не соответствуют ожиданиям в отношении соответствия стандартам подготовки к колледжу и карьере, включая все стандарты присутствуют и рассматриваются с должной глубиной, чтобы помочь студентам в освоении навыков и знания, необходимые для подготовки к поступлению в колледж и карьере.

Для науки рейтинги соответствия представляют собой степень, в которой материалы соответствуют ожиданиям, частично соответствуют ожиданиям или не соответствуют ожиданиям в отношении соответствия научным стандартам нового поколения, включая все стандарты присутствуют и рассматриваются с должной глубиной, чтобы помочь студентам в освоении навыков и знания, необходимые для подготовки к поступлению в колледж и карьере.

Для всех областей содержимого рейтинги юзабилити представляют собой степень соответствия материалов ожиданиям, частичного соответствия ожиданиям или не соответствуют ожиданиям в отношении эффективных практик (как указано в инструменте оценки) для использования и дизайн, планирование и обучение учителей, оценка, дифференцированное обучение и эффективное использование технологий.

Математика К-8

• Фокус и согласованность — 14 возможных точек

  • 12–14 баллов: оправдывает ожидания

  • 8–11 баллов: частично соответствует ожиданиям

  • Ниже 8 баллов: не оправдывает ожиданий

• Строгость и математическая практика — 18 возможных баллов

  • 16-18 баллов: оправдывает ожидания

  • 11–15 баллов: частично соответствует ожиданиям

  • Ниже 11 баллов: не оправдывает ожиданий

• Поддержка с инструкциями и удобство использования — 38 возможных баллов

  • 31–38 баллов: оправдывает ожидания

  • 23-30 баллов: частично соответствует ожиданиям

  • Ниже 23: не оправдывает ожиданий

Математическая средняя школа

• F ocus и Coherence — 18 возможных точек

  • 14–18 баллов: оправдывает ожидания

  • 10-13 баллов: частично оправдывает ожидания

  • Ниже 10 баллов: не оправдывает ожиданий

• Строгость и математическая практика — 16 возможных баллов

  • 14–16 баллов: оправдывает ожидания

  • 10-13 баллов: частично оправдывает ожидания

  • Ниже 10 баллов: не оправдывает ожиданий

• Поддержка с инструкциями и удобство использования — 36 возможных баллов

  • 30-36 баллов: оправдывает ожидания

  • 22-29 баллов: частично соответствует ожиданиям

  • Ниже 22: не оправдывает ожиданий

ELA К-2

• Сложность и качество текста — 58 возможных баллов

  • 52-58 баллов: оправдывает ожидания

  • 28-51 балл: частично соответствует ожиданиям

  • Ниже 28 баллов: не оправдывает ожиданий

• Развитие знаний с помощью текстов, словарного запаса и задач — 32 возможных балла

  • 28-32 балла: оправдать ожидания

  • 16-27 баллов: частично соответствует ожиданиям

  • Ниже 16 баллов: не оправдывает ожиданий

• Поддержка с инструкциями и удобство использования — 34 возможных балла

  • 30-34 балла: соответствует ожиданиям

  • 24–29 баллов: частично соответствует ожиданиям

  • Ниже 24 баллов: не оправдывает ожиданий

ELA 3-5

• Сложность и качество текста — 42 возможных балла

  • 37-42 балла: оправдывает ожидания

  • 21–36 баллов: частично соответствует ожиданиям

  • Ниже 21 балла: не оправдывает ожиданий

• Развитие знаний с помощью текстов, словарного запаса и задач — 32 возможных балла

  • 28-32 балла: оправдать ожидания

  • 16-27 баллов: частично соответствует ожиданиям

  • Ниже 16 баллов: не оправдывает ожиданий

• Поддержка с инструкциями и удобство использования — 34 возможных балла

  • 30-34 балла: соответствует ожиданиям

  • 24–29 баллов: частично соответствует ожиданиям

  • Ниже 24 баллов: не оправдывает ожиданий

ELA 6-8

• Сложность и качество текста — 36 возможных баллов

  • 32–36 баллов: соответствует ожиданиям

  • 18–31 балл: частично соответствует ожиданиям

  • Ниже 18 баллов: не оправдывает ожиданий

• Развитие знаний с помощью текстов, словарного запаса и задач — 32 возможных балла

  • 28-32 балла: оправдать ожидания

  • 16-27 баллов: частично соответствует ожиданиям

  • Ниже 16 баллов: не оправдывает ожиданий

• Поддержка с инструкциями и удобство использования — 34 возможных балла

  • 30-34 балла: соответствует ожиданиям

  • 24-29 баллов: частично соответствует ожиданиям

  • Ниже 24 баллов: не оправдывает ожиданий

Средняя школа ELA

• Сложность и качество текста — 32 возможных балла
  

  • 28-32 балла: соответствует ожиданиям

  • 16-27 баллов: частично соответствует ожиданиям

  • Ниже 16 баллов: не оправдывает ожиданий

• Развитие знаний с помощью текстов, словарного запаса и задач — 32 возможных балла
  

  • 28-32 балла: оправдать ожидания

  • 16-27 баллов: частично соответствует ожиданиям

  • Ниже 16 баллов: не оправдывает ожиданий

• Поддержка с инструкциями и удобство использования — 34 возможных балла
  

  • 30-34 балла: соответствует ожиданиям

  • 24-29 баллов: частично соответствует ожиданиям

  • Ниже 24 баллов: не оправдывает ожиданий

Средняя школа естественных наук

• Предназначен для NGSS — 26 возможных точек

  • 22-26 баллов: оправдывает ожидания

  • 13–21 балл: частично соответствует ожиданиям

  • Ниже 13 баллов: не оправдывает ожиданий

    
    

• Согласованность и объем — 56 возможных точек

  • 48-56 баллов: соответствует ожиданиям

  • 30–47 баллов: частично соответствует ожиданиям

  • Ниже 30 баллов: не оправдывает ожиданий

    
    

• Поддержка с инструкциями и удобство использования — 54 возможных балла

  • 46-54 балла: оправдывает ожидания

  • 29–45 баллов: частично соответствует ожиданиям

  • Ниже 29 баллов: не оправдывает ожиданий

Центр отчетов

Рейтинги соответствия и удобства использования присваиваются на основе оценки материалов по ряду критериев и индикаторы с рецензентами, предоставляющими подтверждающие доказательства для определения и обоснования каждого присужденного балла.

Для ELA и математика, рейтинги совмещения представляют собой степень соответствия материалов ожиданиям, частично соответствия ожиданиям или не соответствуют ожиданиям в отношении соответствия стандартам подготовки к колледжу и карьере, включая все стандарты присутствуют и рассматриваются с должной глубиной, чтобы помочь студентам в освоении навыков и знания, необходимые для подготовки к поступлению в колледж и карьере.

Для науки рейтинги соответствия представляют собой степень, в которой материалы соответствуют ожиданиям, частично соответствуют ожиданиям или не соответствуют ожиданиям в отношении соответствия научным стандартам нового поколения, включая все стандарты присутствуют и рассматриваются с должной глубиной, чтобы помочь студентам в освоении навыков и знания, необходимые для подготовки к поступлению в колледж и карьере.

Для всех областей содержимого рейтинги юзабилити представляют собой степень соответствия материалов ожиданиям, частичного соответствия ожиданиям или не соответствуют ожиданиям в отношении эффективных практик (как указано в инструменте оценки) для использования и дизайн, планирование и обучение учителей, оценка, дифференцированное обучение и эффективное использование технологий.

Математика К-8

• Фокус и согласованность — 14 возможных точек

  • 12–14 баллов: оправдывает ожидания

  • 8–11 баллов: частично соответствует ожиданиям

  • Ниже 8 баллов: не оправдывает ожиданий

• Строгость и математическая практика — 18 возможных баллов

  • 16-18 баллов: оправдывает ожидания

  • 11–15 баллов: частично соответствует ожиданиям

  • Ниже 11 баллов: не оправдывает ожиданий

• Поддержка с инструкциями и удобство использования — 38 возможных баллов

  • 31–38 баллов: оправдывает ожидания

  • 23-30 баллов: частично соответствует ожиданиям

  • Ниже 23: не оправдывает ожиданий

Математическая средняя школа

• F ocus и Coherence — 18 возможных точек

  • 14–18 баллов: оправдывает ожидания

  • 10-13 баллов: частично оправдывает ожидания

  • Ниже 10 баллов: не оправдывает ожиданий

• Строгость и математическая практика — 16 возможных баллов

  • 14–16 баллов: оправдывает ожидания

  • 10-13 баллов: частично оправдывает ожидания

  • Ниже 10 баллов: не оправдывает ожиданий

• Поддержка с инструкциями и удобство использования — 36 возможных баллов

  • 30-36 баллов: оправдывает ожидания

  • 22-29 баллов: частично соответствует ожиданиям

  • Ниже 22: не оправдывает ожиданий

ELA К-2

• Сложность и качество текста — 58 возможных баллов

  • 52-58 баллов: оправдывает ожидания

  • 28-51 балл: частично соответствует ожиданиям

  • Ниже 28 баллов: не оправдывает ожиданий

• Развитие знаний с помощью текстов, словарного запаса и задач — 32 возможных балла

  • 28-32 балла: оправдать ожидания

  • 16-27 баллов: частично соответствует ожиданиям

  • Ниже 16 баллов: не оправдывает ожиданий

• Поддержка с инструкциями и удобство использования — 34 возможных балла

  • 30-34 балла: соответствует ожиданиям

  • 24-29 баллов: частично соответствует ожиданиям

  • Ниже 24 баллов: не оправдывает ожиданий

ELA 3-5

• Сложность и качество текста — 42 возможных балла

  • 37-42 балла: оправдывает ожидания

  • 21–36 баллов: частично соответствует ожиданиям

  • Ниже 21 балла: не оправдывает ожиданий

• Развитие знаний с помощью текстов, словарного запаса и задач — 32 возможных балла

  • 28-32 балла: оправдать ожидания

  • 16-27 баллов: частично соответствует ожиданиям

  • Ниже 16 баллов: не оправдывает ожиданий

• Поддержка с инструкциями и удобство использования — 34 возможных балла

  • 30-34 балла: соответствует ожиданиям

  • 24-29 баллов: частично соответствует ожиданиям

  • Ниже 24 баллов: не оправдывает ожиданий

ELA 6-8

• Сложность и качество текста — 36 возможных баллов

  • 32–36 баллов: соответствует ожиданиям

  • 18–31 балл: частично соответствует ожиданиям

  • Ниже 18 баллов: не оправдывает ожиданий

• Развитие знаний с помощью текстов, словарного запаса и задач — 32 возможных балла

  • 28-32 балла: оправдать ожидания

  • 16-27 баллов: частично соответствует ожиданиям

  • Ниже 16 баллов: не оправдывает ожиданий

• Поддержка с инструкциями и удобство использования — 34 возможных балла

  • 30-34 балла: соответствует ожиданиям

  • 24-29 баллов: частично соответствует ожиданиям

  • Ниже 24 баллов: не оправдывает ожиданий

Средняя школа ELA

• Сложность и качество текста — 32 возможных балла
  

  • 28-32 балла: соответствует ожиданиям

  • 16-27 баллов: частично соответствует ожиданиям

  • Ниже 16 баллов: не оправдывает ожиданий

• Развитие знаний с помощью текстов, словарного запаса и задач — 32 возможных балла
  

  • 28-32 балла: оправдать ожидания

  • 16-27 баллов: частично соответствует ожиданиям

  • Ниже 16 баллов: не оправдывает ожиданий

• Поддержка с инструкциями и удобство использования — 34 возможных балла
  

  • 30-34 балла: соответствует ожиданиям

  • 24-29 баллов: частично соответствует ожиданиям

  • Ниже 24 баллов: не оправдывает ожиданий

Средняя школа естественных наук

• Предназначен для NGSS — 26 возможных точек

  • 22-26 баллов: оправдывает ожидания

  • 13–21 балл: частично соответствует ожиданиям

  • Ниже 13 баллов: не оправдывает ожиданий

    
    

• Согласованность и объем — 56 возможных точек

  • 48-56 баллов: соответствует ожиданиям

  • 30–47 баллов: частично соответствует ожиданиям

  • Ниже 30 баллов: не оправдывает ожиданий

    
    

• Поддержка с инструкциями и удобство использования — 54 возможных балла

  • 46-54 балла: оправдывает ожидания

  • 29–45 баллов: частично соответствует ожиданиям

  • Ниже 29 баллов: не оправдывает ожиданий

Химия капусты — поиск кислот и оснований

Ключевые концепции
Химия
Кислоты
Базы
Свет

Введение
Вы, возможно, проводили эксперименты с хорошо обозначенными кислотами и основаниями в школе, но задумывались ли вы когда-нибудь о том, является ли определенный продукт питания или химическое вещество в доме кислотой или основанием? Вы можете узнать это, используя краснокочанную капусту для приготовления индикаторного раствора.

Когда два или более ингредиента полностью растворяются друг в друге, у вас есть решение. Например, при смешивании соли с водой получается прозрачный раствор, хотя соль есть и раствор имеет соленый вкус. При смешивании с водой химическое вещество «жертвует» заряженную частицу (называемую ионом) раствору — в данном случае ион водорода — или «принимает» один из них, определяет, будет ли это раствор кислотным или основным. Индикатор меняет цвет при воздействии такой смеси в зависимости от того, является ли раствор кислотным или основным.

Фон
Кислоты — это растворы, которые теряют ионы водорода и обычно имеют кислый вкус. Кислоты, такие как соки цитрусовых и домашний уксус, являются очень распространенными бытовыми растворами. Основания — это растворы, которые вытягивают ионы водорода из раствора на себя, «принимают» их и обычно кажутся скользкими. Основания имеют множество практических применений. Например, «антациды», такие как TUMS, используются для снижения кислотности в желудке. Другие основы делают полезные бытовые чистящие средства.

Чтобы определить, является ли что-то кислотой или основанием, вы можете использовать химическое вещество, называемое индикатором. Индикатор меняет цвет при попадании кислоты или основания. Есть много разных типов индикаторов, одни из которых являются жидкостями, а другие сконцентрированы на маленьких полосках лакмусовой бумаги. Индикаторы могут быть извлечены из множества различных источников, включая пигмент многих растений. Например, краснокочанная капуста содержит молекулу индикаторного пигмента, называемого флавином, который представляет собой тип молекулы, называемый антоцианом.В очень кислых растворах антоциановый цвет приобретает красный цвет, в нейтральных — лиловый, а в щелочных растворах — зеленовато-желтый. Следовательно, цвет, который меняет раствор антоциана, можно использовать для определения pH раствора — показателя того, насколько щелочной или кислый раствор является.

Материалы
• Маленькая красная капуста
• Кастрюля с кипятком
• Фильтр
• Две большие миски или горшки
• Терка
• Дозатор столовой
• Большая ложка (по желанию)
• Три или более маленьких белых бумажных стаканчика (также подойдут маленькие белые бумажные стаканы или посуда)
• Очки или другие защитные очки
• Лимонный или лаймовый сок
• Уксус
• Чистящее средство на основе отбеливателя
• Другие продукты для тестирования, такие как прозрачная содовая, раствор пищевой соды, яичные белки, помидоры, творог (по желанию)

Подготовка
• Натереть небольшую красную капусту на терке. Если вы не хотите тереть всю капусту на терке, достаточно натереть половину кочанной капусты. Переложите мелко натертую на терке капусту в большую миску или кастрюлю.
• Вскипятите кастрюлю с водой. Будьте осторожны при обращении с кипящей водой. Налейте кипяток в миску с капустной мякотью, пока вода не покроет капусту.
• Оставьте капустную смесь настаиваться, периодически помешивая, пока жидкость не станет комнатной температуры. Это должно занять не менее получаса. Жидкость станет красной или пурпурно-красной.
• Поместите ситечко на другую большую миску или кастрюлю и вылейте капустную смесь через ситечко, чтобы удалить мякоть капусты. Нажмите на мякоть в ситечке, например, большой ложкой, чтобы выжать из мякоти больше жидкости.
• Теперь в миске должна быть только жидкость фиолетового или синего цвета. Это будет ваш индикаторный раствор, который вы будете использовать для проверки pH различных жидкостей.
• Детям следует носить защитные очки или другие защитные очки, а взрослым следует соблюдать осторожность и соблюдать осторожность при обращении с отбеливателем и уксусом, поскольку они могут вызвать раздражение глаз и кожи.

Порядок действий
• Наполните небольшой белый бумажный стаканчик, стакан или белую посуду одной столовой ложкой раствора индикатора капусты. Какого цвета ваш индикаторный раствор?
• Добавляйте в индикаторный раствор капли сока лимона или лайма до тех пор, пока раствор не изменится в цвете. Аккуратно перемешайте раствор и убедитесь, что цвет не изменился. Какого цвета стал раствор?
• Цвет раствора будет меняться в зависимости от его pH: красный цвет означает, что pH равен 2; Фиолетовый означает pH 4; Фиолетовый означает pH 6; Синий означает pH 8; Сине-зеленый означает pH 10; Зеленовато-желтый означает pH 12.
• Каков pH раствора сока лимона или лайма в зависимости от его цвета?
• В другой небольшой белый бумажный стаканчик добавьте одну столовую ложку исходного раствора индикатора капусты. Добавьте капли уксуса, пока раствор не изменит цвет. Какого цвета стал раствор уксуса? Каков pH раствора?
• В третий маленький белый бумажный стаканчик добавьте одну столовую ложку исходного раствора индикатора капусты. Обращаясь с ним осторожно, добавляйте капли отбеливающего чистящего средства до тех пор, пока раствор не изменит цвет. Какого цвета стал отбеливающий раствор и что это говорит о его pH?
• Если вы хотите проверить pH других продуктов, снова добавьте одну столовую ложку исходного раствора индикатора капусты в маленький белый бумажный стаканчик и добавляйте капли пищи, пока не увидите, как раствор меняет цвет. Если продукт не в жидкой форме, раздавите его или растворите в небольшом количестве воды, прежде чем добавлять в индикаторный раствор. Какого цвета стал раствор и что это говорит о его pH?
• Extra: Есть и другие овощи и фрукты, которые также можно использовать для создания индикаторов pH: красный лук, кожура яблок, черника, кожица винограда и сливы. Какие различные источники пигмента дают наилучшие показатели?
• Extra: Вы можете использовать индикаторное решение для написания секретных сообщений. Просто используйте лимонный сок полной крепости, чтобы написать невидимое сообщение на бумаге, и дайте ему высохнуть. Чтобы раскрыть сообщение, нарисуйте индикатор капусты по бумаге кистью.

Наблюдения и результаты
Изменился ли цвет индикаторного раствора, когда вы добавили сок лайма или лимона, уксус и отбеливатель? Указывает ли цвет раствора, что сок лайма или лимона и уксус были кислыми (имели более низкий pH) и что отбеливатель был основным (с более высоким pH)?

Раствор с pH от 5 до 7 является нейтральным, 8 или выше — это основание, а 4 или ниже — кислота.Сок лайма, лимонный сок и уксус являются кислотами, поэтому они должны были сделать индикаторный раствор красным или пурпурным. Отбеливатель — сильная основа, поэтому он должен был придать раствору индикатора зеленовато-желтый цвет.

Насколько щелочной или кислый раствор будет, зависит от количества в нем ионов водорода. Основной раствор принимает ионы водорода (или отдает электронные пары как ионы гидроксида), тогда как кислый раствор отдает ионы водорода (или принимает электронные пары). Индикатор, как антоцианин, реагирует на уровни ионов водорода в растворе.Антоцианин и другие биологические пигменты поглощают свет определенных длин волн и отражают другие, и именно отраженный свет, который мы видим, придает им определенный цвет. В зависимости от уровня ионов водорода в растворе индикаторный пигмент подвергается химической реакции, которая изменяет его химическую структуру, заставляя его отражать свет с другой длиной волны и тем самым менять цвет.

Очистка
Разбавьте раствор отбеливателя водой, прежде чем слить его в канализацию.(Не забывайте надевать очки, когда делаете это.)

Больше для изучения
«Эксперименты с кислотами и основаниями» из Fun Science Gallery
«Кислоты и основания повсюду» от Rader’s Chem4Kids.com
«Кислоты, основания и шкала pH» от Science Buddies
» Химия капусты »от Science Buddies

Это задание предоставлено вам в сотрудничестве с Science Buddies

Ключ к мотивации студентов

Эймс, К. (1992). Классы, цели, структуры и мотивация студентов. Журнал педагогической психологии, 84 , 261-271.

APA Рабочая группа Совета по делам образования (1997, ноябрь). Психологические принципы, ориентированные на учащихся: основы школьной реформы и модернизации . Вашингтон, округ Колумбия: Американская психологическая ассоциация.

Бандура, А. (1977). Самоэффективность: к объединяющей теории изменения поведения. Психологический обзор, 84 , 191-215.

Бандура. А. (1993). Воспринимаемая самоэффективность в когнитивном развитии и функционировании. Психолог-педагог, 28 , 149-167.

Бандура, А. (1997). Самоэффективность: осуществление контроля . Нью-Йорк: Фриман.

Барнетт, В. С. (1996). Жизни на волоске: анализ выгод и затрат для возраста 27 лет в рамках дошкольной программы High / Scope Perry (Монографии фонда High / Scope Educational Research Foundation, 11). Ипсиланти, Мичиган: High / Scope Press.

Бауманн, Дж. Ф., Зейферт-Кесселл, Н., и Джонс, Л. А. (1992). Влияние обучения мыслям вслух на способности учащихся начальной школы контролировать понимание прочитанного. Journal of Reading Behavior, 24 (2), 143-172.

Биб-Франкенбергер, М., Босиан, К. М., Макмиллан, Д. Л., и Грешем, Ф. М. (2004). Сортировка второклассников: отличие оставшихся от продвинутых. Журнал педагогической психологии, 96 (2), 204-215.

Борковский, Я.Дж., Карр М., Реллингер Э. и Прессли М. (1990). Саморегулируемое познание: взаимозависимость метапознания, атрибуции и самооценки. В Б. Ф. Джонс и Л. Идол (ред.), Измерения мышления и когнитивного обучения . Хиллсдейл, Нью-Джерси: Lawrence Erlbaum Associates, Inc.

Сечи, С. Дж., И Папьерно, П. Б. (2005). Риторика и реальность сокращения разрыва: когда «неимущие» выигрывают, а «имущие» — еще больше. Американский психолог, 60 (2), 149-160.

Cervone, D., Shadel, W.G., Smith, R.E., & Fiori, M. (2006). Саморегуляция и наука о личности: Ответ на комментарии. Прикладная психология: международный обзор , 55 (3), 470-488.

Комбс, А. У. (1962). Перцептивный взгляд на адекватную личность. В A. W. Combs (Ed.), 1962 Ежегодник ASCD, Восприятие, поведение, становление: новое направление в образовании (стр. 50-64). Александрия, Вирджиния: Ассоциация по надзору и разработке учебных программ.

Коннелл, Дж. П., и Веллборн, Дж. Г. (1991). Компетентность, автономия и взаимосвязь: мотивационный анализ процессов само-системы. В М. Р. Гуннаре и Л. А. Сроуфе (ред.), Самостоятельные процессы в развитии: Миннесотский симпозиум по детской психологии, 23 , 43-77. Чикаго: Издательство Чикагского университета.

d’Ailly, H. (2003). Автономия детей и воспринимаемый контроль в обучении: модель мотивации и достижений на Тайване. Журнал педагогической психологии, 95 (1), 84-96.

d’Ailly, H. (2004). Роль выбора в обучении детей: отличительные культурные и гендерные различия в эффективности, заинтересованности и усилиях. Canadian Journal of Behavioral Science, 36 (1), 17-29.

Деци, Э. Л., и Райан, Р. М. (1985). Внутренняя мотивация и самоопределение в поведении человека . Нью-Йорк: Пленум.

Деци, Э. Л., и Райан, Р. М. (2002). Обзор теории самоопределения: организменная диалектическая перспектива.В E. L.

Деси и Р. М. Райан (ред.), Справочник по исследованию самоопределения (стр. 3-33). Рочестер, штат Нью-Йорк: Университет Рочестера Press.

До, С. Л., и Шаллерт, Д. Л. (2004). Эмоции и разговоры в классе: к модели роли аффекта в опыте учащихся во время обсуждения в классе. Журнал педагогической психологии, 96 (4), 619-634.

Двек, С. С. (1999). Я-теории: их роль в мотивации, личности и развитии .Филадельфия: Тейлор и Фрэнсис / Psychology Press.

Двек, С. С. (2002). Развитие представлений о способностях. В A. Wigfield & J. Eccles (Eds.), Развитие мотивации достижения (стр. 57-88). Сан-Диего, Калифорния: Academic Press.

Экклс, Дж. С., и Розер, Р. (1999). Школа и сообщество влияют на человеческое развитие. В М. Борнштейн и М. Лэмб (ред.), Психология развития: расширенный учебник (4-е изд., Стр. 503-554).Махва, Нью-Джерси: Эрлбаум.

Экклс, Дж. С., и Вигфилд, А. (1992). Развитие ценности задачи достижения: теоретический анализ. Обзор развития , 12 , 265-310.

Экклс, Дж. С., Вигфилд, А., и Шифеле, У. (1998). Мотивация к успеху. В Н. Айзенберге (ред.), , Справочник по детской психологии по социальному, эмоциональному и личностному развитию, Том 3 (стр. 1017-1096). Нью-Йорк: Вили.

Элиас, М. Дж., Брюн-Батлер, Л., Блюм, Л., и Шайлер, Т. (1997). Как запустить программу социального и эмоционального обучения. Лидерство в образовании, 54 (8), 15-19.

Феррер, К. и Скиннер, Э. (2003). Чувство родства как фактор академической активности и успеваемости детей. Журнал педагогической психологии, 95 (1), 148-162.

Гоулман Д. (1995). Эмоциональный интеллект . Нью-Йорк: Bantam Books.

Грэм, С. (1994). Мотивация у афроамериканцев. Обзор исследований в области образования, 64 , 55–117.

Грэм С., Тейлор А. З. и Хадли К. (1998). Изучение ценностей достижений среди раннего подросткового возраста из числа этнических меньшинств. Журнал педагогической психологии , 90 , 606-620.

Хартер, С. (2006). Когнитивное и социальное построение развивающейся личности . Нью-Йорк: Guilford Press.

Heine, S. Lehman, D., Markus, H., & Kitayama, S. (1999). Есть ли универсальная потребность в позитивном самоуважении? Психологический обзор, 106 , 766-794.

Холлоуэй, С. (1988). Концепции способностей и усилий в Японии и США. Обзор исследований в области образования, 58 , 327-345.

Айенгар С. и Леппер М. (1999). Переосмысление ценности выбора: культурный взгляд на внутреннюю мотивацию. Журнал личности и социальной психологии, 76 , 349-366.

Дженсен Э. (1998). Обучение с умом . Александрия, Вирджиния: Ассоциация по надзору и разработке учебных программ.

Канфер Р. и Маккомбс Б. Л. (2000). Мотивация: применение текущей теории к критическим вопросам обучения. В С. Тобиас и Д. Т. Флетчер (ред.), Обучение и переподготовка: Справочник для бизнеса, промышленности, правительства и вооруженных сил (стр. 85-108). Нью-Йорк: Макмиллан.

Кинг А., Стаффиери А. и Адельгаис А. (1998). Взаимное обучение со стороны сверстников: эффекты структурирования учебного взаимодействия для поддержки взаимного обучения. Журнал педагогической психологии, 90 (1), 134-152.

Клем, А.М., и Коннелл, Дж. П. (2006). Вовлечение молодежи в школу. В L.R. Шеррорд, К. Фланаган и Р. Кассимир (редакторы), Молодежный активизм: международная энциклопедия (стр. 551-555) . Вестпорт, Коннектикут: Greenwood Publishing Co.

Лазарус Р. С. (2000). К лучшему исследованию стресса и преодоления трудностей. Американский психолог, 55 (6), 665-673.

Леппер, М. Р., Корпус, Дж. Х., и Айенгар, С. С. (2005). Внутренняя и внешняя мотивационная ориентация в классе: возрастные различия и академические корреляты.Журнал педагогической психологии , 97 (2), 184-196.

Лодевик, К. Р. и Винн, П. Х. (2005). Отношения между структурой учебных задач, достижениями и изменениями в самоэффективности учащихся средних школ. Журнал педагогической психологии. 97 (1), 3-12.

Маршалл, Х. Х. и Вайнштейн, Р. (1986). Классный контекст воспринимаемого учеником дифференцированного отношения учителя. Журнал педагогической психологии, 78 , 441-453.

Маккомбс, Б. Л. (1986). Роль самосистемы в саморегулируемом обучении. Современная педагогическая психология , 11 , 314-332.

МакКомбс, Б. Л. (1988). Тренировка мотивационных навыков: сочетание метакогнитивных, когнитивных и эмоциональных стратегий обучения. В C. E. Weinstein, E. T. Goetz, & P. ​​A. Alexander (Eds.), Обучение и стратегии обучения: проблемы оценки, обучения и оценки (стр. 141-169). Нью-Йорк: Academic Press.

Маккомбс, Б. Л. (1991). Мотивация и непрерывное обучение. Психолог-педагог, 26 (2), 117-127.

Маккомбс, Б. Л. (1999). Какую роль сегодня играет психология восприятия в реформе образования? В Х. Дж. Фрейберге (ред.), Восприятие, поведение, становление: извлеченные уроки (стр. 148-157). Александрия, Вирджиния: Ассоциация по надзору и разработке учебных программ.

Маккомбс, Б. Л. (2001). Саморегулируемое обучение и академическая успеваемость: феноменологический взгляд.В Б. Дж. Циммермане и Д. Х. Шунке (ред.), Саморегулируемое обучение и академические достижения: теория, исследования и практика (2-е изд.) (Стр. 67-123). Махва, Нью-Джерси: Лоуренс Эрлбэм Ассошиэйтс.

МакКомбс, Б. Л. (2007). Стратегии создания положительного влияния на старшеклассников. В R. J. Seidel & A. L. Kett (Eds.), Workbook Companion for: Принципы обучения к стратегиям обучения: Акцент на учениках старшей школы, основанный на потребностях (стр.323-337). Норвелл, Массачусетс: Спрингер.

Маккомбс, Б. Л. (2006). Практики, ориентированные на учащегося: создание условий для позитивного развития, мотивации и достижений учащегося. В J. Meece & J. Eccles (Eds.), Справочник по исследованиям в школах, школьном обучении и человеческом развитии . Махва, Нью-Джерси: Эрлбаум.

МакКомбс, Б. Л. (2007). Уравновешивание требований подотчетности с подтвержденными исследованиями и ориентированными на учащихся практиками преподавания и обучения. В C.E.Sleeter (Ed.), Обучение демократии и справедливости в эпоху подотчетности (стр. 41-60). Нью-Йорк: издательство Teachers College Press.

Маккомбс Б. Л. и Марцано Р. Дж. (1990). Включение себя в саморегулируемое обучение: Я как агент в интеграции навыков и воли. Психолог-педагог, 25 (1), 51-69.

Маккомбс Б. Л. и Миллер Л. (2007). Практика и оценивание, ориентированные на учащихся: максимальное повышение мотивации, обучения и достижений учащихся .Таузенд-Оукс, Калифорния: Corwin Press.

Маккомбс Б. Л. и Поуп Дж. Э. (1994). Мотивация труднодоступных студентов. В Психология в классе Серия . Вашингтон, округ Колумбия: Американская психологическая ассоциация.

Маккомбс, Б. Л., и Уислер, Дж. С. (1989). Роль аффективных переменных в автономном обучении. Психолог-педагог, 24 (3), 277-306.

Мердок Т. Б., Миллер А. и Колхардт Дж. (2004). Влияние переменных контекста класса на суждения старшеклассников о приемлемости и вероятности обмана. Journal of Educational Psychology, 96 (4), 765-777.

Нарцисс, С. (2004). Влияние информативной обратной связи и самоэффективности на мотивацию и достижения в концептуальном обучении. Experimental Psychology, 51 (3), 214-228.

Нисбетт, Р., Пэн, К., Чой, И. , и Норензаян, А. (2001). Культура и системы мышления: холистическое и аналитическое познание. Психологический обзор, 108 , 291-310.

Пейн, Б.Д. и Мэннинг Б. Х. (1992). Базовая инструкция по чтению: влияние тренировки по мониторингу понимания прочитанного на понимание прочитанного, использование стратегии и отношение. Чтение исследований и инструкций, 32 (1), 29-38.

О’Доннелл А.М. (ред.) (1999). Когнитивные перспективы взаимного обучения . Махва, Нью-Джерси: Лоуренс Эрлбаум Ассошиэйтс.

О’Мара, А. Дж., Марш, Х. У., Крейвен, Р. Г., и Дебус, Р. Л. (2006). Имеют ли значение вмешательство в самооценку? Синергетическое сочетание проверки конструкции и метаанализа.Психолог-педагог , 41 (3), 181-206.

Отис, Н., Грузе, Ф. М. Э., и Пеллетье, Л. Г. (2005). Скрытые мотивационные изменения в академической среде: трехлетнее продольное исследование. Журнал педагогической психологии, 97 (2), 170-183.

Паларди, Дж. М. (199). Некоторые стратегии мотивации студентов. Бюллетень НАССП, 83 (604), 116-121.

Pajares, F. (1997). Актуальные направления исследований самоэффективности.В M. Maehr & P. ​​R. Pintrich (Eds.), Успехи в мотивации и достижениях (Том 10, стр. 1-49). Гринвич, Коннектикут: JAI Press.

Paris, S. G., & Winograd, P. (1990). Как метапознание может способствовать академическому обучению и обучению. В Б. Ф. Джонс и Л. Идол (ред.), Измерения мышления: рамки для учебной программы и обучения (стр. 15-51). Хиллсдейл, Нью-Джерси: Lawrence Erlbaum Associates, Inc.

Пенг, К., Нисбетт, Р., и Вонг, Н.(1997). Проблемы достоверности сравнения ценностей разных культур и возможные решения. Психологические методы, 2 , 329-344.

Перри Р. П. (2003). Воспринимаемый (академический) контроль и причинное мышление в настройках достижений. Canadian Psychology, 44 (4), 312-331.

Питч Дж., Уокер Р. и Чепмен Э. (2003). Взаимосвязь между самооценкой, самоэффективностью и успеваемостью по математике в средней школе. Журнал Психология образования. 95 (3), 589-603.

Пинтрих П. Р. (2003). Мотивационная наука о роли мотивации студентов в обучении и преподавании. Журнал педагогической психологии, 95 (4), 667-686.

Пинтрих, П. Р., ДеГрут, Э. В. (1990). Мотивационные и саморегулируемые учебные компоненты успеваемости в классе. Журнал педагогической психологии, 82 (1), 33-40.

Прессли М., Рафаэль Л., Галлахер, Дж. Д., и ДиБелла, Дж. (2004). Providence-St. Mel School: Как работает школа для афроамериканских студентов. Журнал педагогической психологии, 96 (2), 216-235.

Рив, Дж., Никс, Г., & Хамм, Д. (2003). Тестирование моделей опыта самоопределения во внутренней мотивации и головоломка выбора. Журнал педагогической психологии, 95 (2), 375-392.

Ридли, Д. С. (1991). Рефлексивное самосознание: основной мотивационный процесс.В Б. Л. МакКомбс (ред.), Unraveling мотивация: новые перспективы из исследований и практики. Специальный выпуск журнала экспериментального образования . 60 (1), 31-48.

Роджерс, К. Р. (1961). Как стать лицом . Бостон: Houghton Mifflin Co.

Саловей, П. и Майер, Дж. Д. (1990). Эмоциональный интеллект. Воображение, познание и личность, 9 , 185-211.

Шунк, Д. Х. (1989). Самоэффективность и поведение для достижения. Обзор педагогической психологии, 1 , 173-207.

Шунк, Д. Х. (1994). Саморегуляция самоэффективности и атрибуции в академической среде. В Д. Х. Шунк и Б. Дж. Циммерман (ред.), Саморегуляция обучения и производительности: проблемы и образовательные приложения (стр. 75-99). Хиллсдейл, Нью-Джерси: Эрлбаум.

Швайнхарт, Л. Дж., Барнс, Х. В., и Вейкарт, Д. П. (1993). Значительные преимущества: Исследование дошкольного учреждения High / Scope Perry до возраста 27 (Монографии Фонда исследований в области образования High / Scope, 10).Ypsilanti: High / Scope Press.

Швайнхарт, Л. Дж., Монти, Дж., Сян, З., Барнетт, У. С., Белфилд, К. Р., & Норес, М. (2005). Эффекты на всю жизнь: исследование High / Scope Perry Preschool до 40 лет . (Монографии High / Scope Educational Research Foundation, 14). Ипсиланти, Мичиган: High / Scope Press.

Зайдель, Р. Дж., Перенцевич, К. К., и Кетт, А. Л. (2005). От принципов обучения к стратегиям обучения: эмпирически обоснованные ингредиенты для руководства развитием обучения .Нью-Йорк: Спрингер.

Селигман, М. Э. П. и Чиксентмихайи. М. (2000). Позитивная психология: Введение. Американский психолог, 55 (1), 5-14.

Штернберг, Р. Дж. (2006). Признание забытых сильных сторон. Лидерство в образовании, 64 (1), 30-35.

Тишман, С., Джей, Э. и Перкинс, Д. Н. (1992). Обучающие мыслительные установки: от передачи к приобщению . Кембридж, Массачусетс: Гарвардский университет.

Урдан, Т. (2004). Предикторы академической самооценки и достижений: изучение целей достижения, структуры целей в классе и культуры. J журнал педагогической психологии, 96 (2), 251-264.

Ванстенкисте, М., Саймонс, Дж., Ленс, В., Шелдон, К. М., Деци, Э. Л. (2004). Мотивация к обучению, результативности и настойчивости: синергетический эффект внутреннего содержания цели и контекстов, поддерживающих автономию. Журнал личности и социальной психологии. 87 (2), 246-260.

Уокер, Р. А., Прессик-Килборн, К., Арнольд, Л. С., и Сейнсбери, Э. Дж. (2004). Изучение мотивации в контексте: развитие социокультурных перспектив. Европейский психолог, 9 (4), 245-256.

Уоллс, Т.А., и Литтл, Т.Д. (2005). Отношения между личной волей, мотивацией и школьной адаптацией в раннем подростковом возрасте. Журнал педагогической психологии, 97 (1), 23-31.

Вайнер, Б.(2000). Внутриличностные и межличностные теории мотивации с точки зрения атрибуции. Обзор педагогической психологии , 12 , 1-14.

Уислер, Дж. С. (1991). Влияние взаимоотношений и взаимодействия учителей на саморазвитие и мотивацию. В Б. Л. МакКомбс (ред.), Unraveling мотивация: новые перспективы из исследований и практики . Специальный выпуск журнала экспериментального образования , 60 (1), 15-30.

Вигфилд, А., & Экклс, Дж. (2002). Развитие убеждений в компетентности, ожиданий успеха и ценностей достижений с детства до подросткового возраста. В A. Wigfield & J. Eccles (Eds.), Развитие мотивации достижения (стр. 91-120). Сан-Диего, Калифорния: Academic Press.

Циммерман Б. Дж. (1994). Измерения академического саморегулирования: концептуальная основа образования. В D. H. Schunk & B.J. Zimmerman (Eds.), Саморегуляция обучения и производительности: проблемы и образовательные приложения (стр.3-21). Махва, Нью-Джерси: Эрлбаум.

Циммерман, Б. и Шунк, Д. Х. (ред.) (2001). Саморегулируемое обучение и академическая успеваемость: теория, исследования и практика (2-е изд.). Махва, Нью-Джерси: Эрлбаум.

Зинс, Дж. Э., Элиас, М. Дж., Гринберг, М.