Урок по теме «Способ подстановки». 7-й класс
Девиз урока
“Деятельность – единственный путь к знанию” (слайд№1)
Дж. Бернард Шоу
Цели урока: Научить учащихся решать системы уравнений методом подстановки; составить алгоритм решения системы уравнений; формировать личностный подход к изучаемой теме.
Формирование компетентности в сфере изучения данной темы; навыка самостоятельной обработки информации; формирования математической грамотности, интереса к предмету; воспитание ответственности за начатое дело; чувство коллективизма.
Ход урока
Орг. момент( слайд №2)
Друзья всегда тебе помогут,
Они с тобой, ты не один.
Поверь в себя –
И ты все сможешь,
Иди вперед и победишь!
Вводная беседа.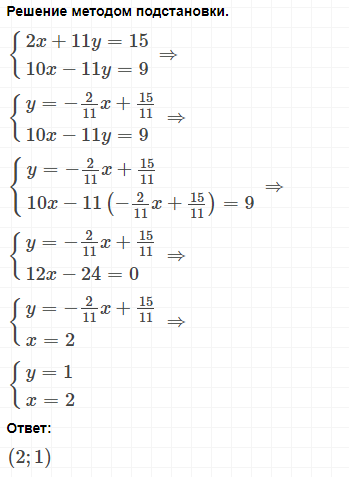
Новые знания нам будет очень трудно осваивать без умения быстро и верно решать простейшие уравнения с одной переменной и умения выражать одну переменную через другую.
Устная работа:
ТЭЙК ОФ – ТАЧ ДАУН
Презентация.
1. Является ли пара чисел ( 3; 1 ) решением уравнения: (слайд №3)
а) 3х + у = 10;
б) х2 – 2у =1;
в) х/у + 2 = — 5у.
(слайд №4)
2. Является ли решением системы пара чисел:
( — 1; 1), ( 2; — 1 ), ( 6; 2,5 )?
3. Что является графиком линейного уравнения с двумя переменными?
а) парабола
б) кубическая парабола
в) прямая
(слайд №5)
4. Приведите пример уравнения с переменными х и у, равносильного линейному уравнению:
а) х – у = 3;
б) 2х + у = о.
Мотивация: (слайд №6)
Ребята, давайте с вами решим систему:
{3х – у = 5
{2х + у = 7.
а) Что значит решить систему?
б) Каким способом можно решить систему? (графическим)
в) Графики каких уравнений необходимо построить? (3х – у = 5; 2х + у = 7)
г) Что собой представляет график уравнения :
3х – у = 5? ( прямая)
2х + у = 7? ( прямая)
д) Для построения прямой сколько необходимо взять точек?
е) Что будет являться решением системы? (координаты точки пересечения графиков). В чем заключается трудность этого метода?
ж) Как вы думаете, а можно ли решить эту систему без построения графика, используя наши умения выражать одну переменную через другую? ( да)
з) Каким образом?( выразить переменную х из первого и подставить во второе уравнение. Затем решить уравнение относительно у и найти потом х)
и) Как вы думаете- как мы будем называть этот способ? (подстановки)
к)Запишите тему урока: “Способ подстановки ” (слайд №7)
л) Что вы знаете о способе подстановки? Что вы хотите узнать? (подставить; узнать и научиться как решать систему уравнений способом подстановки )
Это и будет нашими целями на урок.
(слайд
№8)
Изучение нового материала:
Попробуем составить алгоритм решения системы способом подстановки
{х — у = 3
{4х + у =2
Алгоритм: (слайд №9)
1-й шаг:
Выразить из какого-нибудь уравнения системы одну переменную через другую. х = 3+у
2-й шаг:
Подставить в другое уравнение системы вместо этой переменной полученное выражение:
{ х = 3 + у
{ 4(3+у)+у=2
3-й шаг:
Решить полученное уравнение с одной переменной:
4(3+у)+у=2
12+4у+у=2
5у=-10
у=-2
4-й шаг:
Найти соответствующее значение второй переменной:
х=3+у
х=3+(-2)
х=1
Ответ: (1; -2).
МИКС – ФРИЗ – ГРУПП (слайд №10)
1. Сколько координат имеет точка на плоскости? (две)
2.Сколько уравнений входит в систему с двумя переменными? (два)
3. Сколько шагов входит в алгоритм решения системы способом подстановки? (четыре)
4. Какой по счету идет сейчас месяц? (четвертый)
5. Сколько решений имеет система, если к1=к2 и в1 =в2? (множество)
Закрепление изученного материала: (слайд № 11)
Решить систему уравнений способом подстановки:
у-х=1
6х-у=7
СИМАЛТИНИУС РАУНД ТЭЙБЛ (слайд№12)
(самостоятельная работа по вариантам по кругу)
Домашнее задание:(слайд №13)
П.42 №№ 1134, 1136.
Рефлексия( слайд №14)
Притча:
Шел мудрец, а навстречу ему три человека, которые везли под горячим солнцем тележки с камнями для строительства.
Мудрец остановился и задал вопрос каждому. У первого спросил: “А что ты делал целый день?”. И тот с ухмылкой ответил, что целый день возил проклятые камни. У второго мудрец спросил: “А что ты делал целый день?” и тот ответил: “А я добросовестно выполнил свою работу.” А третий улыбнулся, его лицо засветилось радостью и удовольствием: “А я принимал участие в строительстве храма!”
Мудрец остановился и
задал вопрос каждому. У первого спросил: “А что
ты делал целый день?”. И тот с ухмылкой ответил,
что целый день возил проклятые камни. У второго
мудрец спросил: “А что ты делал целый день?” и
тот ответил: “А я добросовестно выполнил свою
работу.” А третий улыбнулся, его лицо
засветилось радостью и удовольствием: “А я
принимал участие в строительстве храма!”— Ребята! Давайте мы попробуем с вами оценить каждый свою работу за урок.
— Кто работал как первый человек?
— Кто работал добросовестно?
— Кто принимал участие в строительстве храма?
Оцените себя.
(Слайд№15)
Порой задача не решается,
Но это в общем, не беда,
Ведь солнце все же улыбается,
Не унывайте никогда.
Спасибо за урок! (слайд №16).
7 класс. Алгебра. Системы двух уравнений с двумя переменными. — Способы решения систем уравнений с двумя неизвестными.
Системы двух уравнений с двумя переменными. — Способы решения систем уравнений с двумя неизвестными.Комментарии преподавателя
Метод подстановки.
Существует несколько методов решения систем. Один из них метод подстановки
Пример 1:
Суть метода подстановки заключается в том, что в одном из уравнений нужно выразить одну переменную через вторую и подставить полученное выражение во второе уравнение.
В данном случае удобно выразить х во втором уравнении:
Подставим полученное выражение в первое уравнение:
Преобразуем первое уравнение:
,
,
,
Подставим полученное значение во второе уравнение:
, ,
Получаем следующее решение системы:
Пример 2:
В данном случае некоторая сложность заключается в том, что исходную систему нужно преобразовать, чтобы была возможность удобно и без ошибок применить метод подстановки.
Выразим у из первого уравнения:
Подставим полученное выражение во второе уравнение и выполним преобразования:
, ,
,
Подставим полученное значение в первое уравнение:
Получаем единственное решение системы, пара чисел:
Вывод:
на данном уроке мы ознакомились с понятием системы двух линейных уравнений с двумя неизвестными и одним из методов ее решения – способом подстановки. Мы решили примеры для понимания и закрепления данной техники.
Источник конспекта: http://interneturok.ru/ru/school/algebra/7-klass/glava-3-sistema-dvuh-lineynyh-uravneniy-s-dvumya-peremennymi/osnovnye-ponyatiya-metod-podstanovki?konspekt&chapter_id=10
Метод сложения.
Рассмотрим еще один способ решения систем двух линейных уравнений с двумя неизвестными – способ алгебраического сложения. Мы решим несколько различных примеров для закрепления техники.
Мы решим несколько различных примеров для закрепления техники.Метод алгебраического сложения, как и метод подстановки, заключается в том, что изначально из двух уравнений с двумя переменными нужно получить одно уравнение с одной переменной. Рассмотрим метод алгебраического сложения на примере:
Пример 1:
Задана система двух линейных уравнений с двумя неизвестными, и нужно найти такую пару х и у, чтобы при подстановке ее в уравнения получились верные числовые равенства.
Несложно заметить, что в первом уравнении у стоит с минусом, а во втором – с плюсом, и если сложить эти уравнения, то у уничтожится, и мы получим одно уравнение с одной неизвестной:
+
Получаем:
Найдем значение х:
,
Подставим значение х во второе уравнение и найдем у:
Ответ: (2,4; 2,2)
Обратим внимание на то, что мы рассматриваем метод алгебраического сложения, значит, уравнения можно не только складывать, но и вычитать.
Пример
При сложении уравнений получим:
,
Попробуем вычесть уравнения, причем, вычтем первое из второго:
,
Ответ: (5,5; 0,5)
Вывод:
на данном уроке мы рассмотрели новый метод решения систем двух линейных уравнений – метод алгебраического сложения. Мы решили несколько примеров для закрепления данной техники.
- Способ заключается в построении графика каждого уравнения, входящего в данную систему, в одной координатной плоскости и нахождении точки пересечения этих графиков. Координаты этой точки (x; y) и будут являться решением данной системы уравнений.
- Если прямые, являющиеся графиками уравнений системы, пересекаются, то система уравнений имеет единственное решение.
- Если прямые, являющиеся графиками уравнений системы, параллельны, то система уравнений не имеет решений.
- Если прямые, являющиеся графиками уравнений системы, совпадают, то система уравнений имеет бесконечное множество решений.
Примеры. Решить графическим способом систему уравнений.
Графиком каждого уравнения служит прямая линия, для построения которой достаточно знать координаты двух точек. Мы составили таблицы значений х и у для каждого из уравнений системы.
Прямую y=2x-3 провели через точки (0; -3) и (2; 1).
Прямую y=x+1 провели через точки (0; 1) и (2; 3).
Графики данных уравнений системы 1) пересекаются в точке А(4; 5). Это и есть единственное решение данной системы.
Ответ: (4; 5).
Выражаем у через х из каждого уравнения системы 2), а затем составим таблицу значений переменных х и у для каждого из полученных уравнений.
Прямую y=2x+9 проводим через точки (0; 9) и (-3; 3). Прямую y=-1,5x+2 проводим через точки (0; 2) и (2; -1).
Наши прямые пересеклись в точке В(-2; 5).
Ответ: (-2; 5).
Источники конспекта: http://interneturok.ru/ru/school/algebra/7-klass/glava-3-sistema-dvuh-lineynyh-uravneniy-s-dvumya-peremennymi/metod-algebraicheskogo-slozheniya?konspekt&chapter_id=10
http://www.mathematics-repetition.com/6-klass-mathematics/6-9-1-reshenie-sistem-lineynh-uravneniy-grafitcheskim-sposobom.html
Источник видео: https://www.youtube.com/watch?v=VltC62A-Tt4
Способы решения систем уравнений с двумя неизвестными
Линейные системы уравнений
Системы линейных уравнений. Метод подстановки
Метод подстановки + показать
• Выражаем одну переменную через другую.
• Выраженную из одного уравнения переменную подставляем во второе уравнение. Получаем уравнение относительно одной переменной, которое и решаем.
• Опираясь на найденное значение одной переменной, находим значение второй, подставляя в оставшееся уравнение.
Решить систему уравнений:
Решение: + показать
Системы линейных уравнений. Метод сложения
+ показать
• Добиваемся, путем равносильных преобразований, наличия равных (или противоположных) коэффициентов при одной из неизвестных переменных в уравнениях.
• Вычитаем (или складываем) полученные уравнения с целью выхода на уравнение с одной неизвестной.
• Решаем полученное уравнение с одной неизвестной.
• Найденное значение одной переменной подставляем в любое из уравнений системы, находим значение второй.
1. Решить систему уравнений:
Решение: + показать Складываем уравнения системы, заменяя результатом одно из уравнений, оставляя другое. Ответ:
2. Решить систему уравнений:
Решение: + показать
Нелинейные системы уравнений
Системы уравнений, сводящихся к линейным
1. Решить систему уравнений:
Решение: + показать Можно сделать замену и Тогда выходим на систему линейных уравнений: Систему можно решить методом сложения, например. Но приведем решение без замены. Умножим первое уравнение системы на , второе – на и произведем сложение полученных уравнений, оставим при этом в системе, например, первое уравнение исходной системы. Ответ:
2.
Решить систему уравнений:
Решение: + показать Можно сделать замену и выйти на систему линейных уравнений: Приведем решение без замены. Выражаем из второго уравнения системы и подставляем в первое. Ответ:
Нелинейные системы уравнений. Метод подстановки
Решить систему уравнений:
Решение: + показать Выражаем из первого уравнения системы и подставляем во второе. Ответ:
Нелинейные системы уравнений. Метод сложения
Решить систему уравнений:
Решение: + показать Складываем уравнения системы, заменяя результатом одно из уравнений, оставляя другое. Ответ:
Нелинейные системы уравнений. Метод почленного умножения (деления)
1.
Решить систему уравнений:
Решение: + показать Производим деление первой строки на вторую, оставляем в системе вторую строку без изменений. Ответ:
Симметрические системы. Метод введения переменной
Симметрическая система – система, все уравнения которой симметрические. Симметрическое уравнение от двух переменных и – уравнение, которое не изменяется при замене на и на .
Для таких систем удобно использовать замену
Решить систему уравнений:
Решение: + показать При замене приходим к следующей системе которую будем решать способом подстановки: Производим обратную замену: Ответ:
Системы однородных уравнений и приводящиеся к ним системы
Однородным уравнением с двумя неизвестными будем называть уравнение вида
1.
Решить систему уравнений:
Решение: + показать
2. Решить систему уравнений:
Решение: + показать Применим прежде к системе метод сложения. После чего выйдем на однородное уравнение. Ответ:
Графический метод решения систем уравнений
1. Решите графически систему уравнений:
Решение: + показать Выразим в обеих строках системы через : Первое уравнение системы задает прямую, второе – гиперболу. Строим графики в одной системе координат, находим координаты точек пересечения графиков. Ответ:
2. Решите графически систему уравнений:
Решение: + показать
3. Решите графически систему уравнений:
Решение: + показать
Задания для самостоятельной работы
+ показать Решите системы уравнений: 1. Ответ: 2. Ответ: 3. Ответ: 4. Ответ: 5. Ответ: 6. Ответ: 7. Ответ: 8. Ответ: Решите графически системы уравнений: 9. Ответ: 10. Ответ:
Интеграция путем замены
«Интегрирование путем подстановки» (также называемое «u-подстановкой» или «Правило обратной цепочки») — это метод нахождения интеграла, но только тогда, когда он может быть установлен особым образом.
Первый и самый важный шаг — научиться записывать наш интеграл в такой форме:
Обратите внимание, что у нас есть g (x) и его производная g ‘(x)
Как в этом примере:
Здесь f = cos , и у нас есть g = x 2 и его производная 2x
Этот интеграл годится!
Когда наш интеграл настроен таким образом, мы можем выполнить эту замену :
Затем мы можем интегрировать f (u) и закончить на , вернув g (x) как u .
Как это:
Пример: ∫cos (x 2 ) 2x dx
Мы знаем (сверху), что он находится в правильной форме для замены:
Теперь интегрировать:
∫cos (u) du = sin (u) + C
И, наконец, снова положим u = x 2 :
sin (x 2 ) + C
Итак ∫ cos (x 2 ) 2x dx = sin (x 2 ) + C
Это действительно здорово сработало! (Ну, я знал, что так и будет.)
Но этот метод, конечно, работает только с и некоторыми интегралами , и может потребоваться перестановка:
Пример: ∫cos (x 2 ) 6x dx
О нет! Это 6x , а не 2x , как раньше. Нашей идеальной установки больше нет.
Не бойтесь! Просто переставьте интеграл так:
∫cos (x 2 ) 6x dx = 3∫cos (x 2 ) 2x dx
(Мы можем извлечь постоянные множители вне интеграции, см. Правила интеграции.)
Тогда продолжайте, как прежде:
3∫cos (u) du = 3 sin (u) + C
Теперь снова положим u = x 2 :
3 sin (x 2 ) + C
Готово!
Теперь давайте попробуем пример посложнее:
Пример: ∫x / (x 2 +1) dx
Позвольте мне посмотреть .
.. производная x 2 +1 равна 2x … итак, как насчет того, чтобы переставить это так:
∫x / (x 2 +1) dx = ½∫2x / (x 2 +1) dx
Тогда имеем:
Затем интегрируйте:
½∫1 / u du = ½ ln (u) + C
Теперь снова положим u = x 2 +1 :
½ дюйма (x 2 +1) + C
А как насчет этого:
Пример: ∫ (x + 1) 3 dx
Дай посмотреть… производная x + 1 … ну, это просто 1.
Итак, мы можем получить это:
∫ (x + 1) 3 dx = ∫ (x + 1) 3 · 1 dx
Тогда имеем:
Затем интегрируйте:
∫u 3 du = (u 4 ) / 4 + C
Теперь снова положим u = x + 1 :
(x + 1) 4 /4 + C
Мы можем развить эту идею так:
Пример: ∫ (5x + 2) 7 dx
Если бы это было в ЭТОЙ форме, мы могли бы это сделать:
∫ (5x + 2) 7 5 dx
Итак, давайте сделаем это так:
1 5 ∫ (5x + 2) 7 5 dx
1 5 и 5 отменяются, так что все в порядке.
И теперь мы можем иметь u = 5x + 2
А затем интегрировать:
1 5 ∫u 7 du = 1 5 u 8 8 + C
Теперь снова верните u = 5x + 2 и упростите:
(5x + 2) 8 40 + К
А теперь потренируйтесь, хорошо?Резюме
Когда мы можем представить интеграл в такой форме:Тогда мы можем сделать u = g (x) и проинтегрировать ∫f (u) du
И закончите, снова вставив g (x) , где u .
Лекция 19: Методы замещения и мастера
Лекция 19: Методы замещения и мастераМетод замещения
В предыдущей лекции мы показали, что можем вычислить асимптотические границы производительности
путем вычисления решения в замкнутой форме для рекурсии и последующего преобразования
решение асимптотической сложности.
Более короткий путь к цели —
непосредственно докажите оценку сложности, используя индукцию. Это известно как метод замены по причинам, которые станут понятны.Короче
рецепт доказательства асимптотической сложности:
- Определите параметр n управления производительностью.
- Вывести повторение из кода.
- Угадайте асимптотическую оценку , а не решение.
- Докажите, что повторяемость ограничена.
Например, версия отношения повторения для сортировки слиянием, которая не подметать какие-то детали под коврик довольно сложно, и мы не хотим чтобы создать для него решение в закрытой форме:
T (n) = T (⌊n / 2⌋) + T (⌈n / 2⌉) + c 1 n + c 2
Фактически, равенство на самом деле является неравенством с ≤, потому что мы не показали что слияние двух списков всегда занимает линейное время.К счастью, Метод подстановки отлично работает и с неравенствами.
Мы хотим показать, что T (n) ≤ kn lg n для некоторых k и n≥n 0 .
Мы знаем, что T (n) зависит от T (⌊n / 2⌋) и T (⌈n / 2⌉).
План состоит в том, чтобы использовать гипотезу индукции для замены T (⌊n / 2⌋)
и T (⌈n / 2⌉) с оценкой. Однако для этого нам понадобится
чтобы наша гипотеза индукции была верна для n / 2, которое может быть меньше, чем
№ 0 . Поэтому докажем наше свойство для всех n.
К сожалению, наше свойство не выполняется для n = 1, потому что kn lg n = 0.Итак, мы немного ослабим доказываемое свойство до T (n) ≤ k (n lg n + 1) = kn lg n + k, что верно для всех n, пока k≥1. Добавление младшего члена (1) конечно, не влияет на показываемую нами асимптотическую сложность. На практике мы не нужно беспокоиться о малых значениях n, потому что комбинация умножения и добавление k обычно можно использовать, чтобы гарантировать, что для любого конечного набора малых n, неравенство выполнено. Для значений n до некоторого n 0 выбираем k достаточно большой, чтобы убедиться, что собственность удерживается.
Теперь для n≥n 0 мы должны показать T (n) ≤ kn lg n + k, предполагая, что
такое же неравенство верно для n ‘
Докажем это случаями четности
из п.
- Случай четный.
Следовательно, T (n) ≤ kn lg n + k, пока к + (с 1 — к) п + с 2 <0.Но если мы выберем k> c 1 , это будет очевидно для больших n.T (n) = T (⌊n / 2⌋) + T (⌈n / 2⌉) + c 1 n + c 2 ≤ k ⌊N / 2⌋ lg ⌊n / 2⌋ + k + k⌈n / 2⌉ lg ⌈n / 2⌉ + k + c 1 n + c 2 (замена на IH) ≤ k (n / 2) lg (n / 2) + k (n / 2) lg (n / 2) + 2k + c 1 n + c 2 ≤ kn (lg n — 1) + 2k + c 1 n + c 2 ≤ kn lg n — kn + 2k + c 1 n + c 2 ≤ kn lg n + k + k + ( 1 — к) н + с 2 - Корпус № нечетный.
Снова T (n) ≤ kn lg n + k, пока k> c 1 .Обратите внимание, что мы использовали тот факт, что (lg (n-1) + lg (n + 1)) / 2 ≤ lg n, что верно, потому что lg n всюду имеет отрицательную вторую производную.T (n) = T (⌊n / 2⌋) + T (⌈n / 2⌉) + c 1 n + c 2 ≤ k ⌊N / 2⌋ lg ⌊n / 2⌋ + k + k⌈n / 2⌉ lg ⌈n / 2⌉ + k + c 1 n + c 2 (по IH) ≤ k ((n-1) / 2) lg ((n-1) / 2) + k ((n + 1) / 2) lg ((n + 1) / 2) + 2k + c 1 n + c 2 ≤ k (n-1) / 2 * (lg (n-1) — 1) + k (n + 1) / 2 * (lg (n + 1) — 1) + 2k + c 1 n + c 2 ≤ kn (lg (n-1) + lg (n + 1)) / 2 — k (n-1) / 2 + k (n + 1) / 2 + c 1 n + c 2 ≤ kn lg n + k + (c 1 — k) n + c 2
Таким образом, мы можем использовать эту технику для доказательства асимптотической сложности без срезание любых углов по форме повторения.
Усиление индукционной гипотезы
Иногда гипотезу индукции нужно немного подправить, чтобы усилить ее. Например, рассмотрим рекурсию T (n) = 2T (n / 2) + 1, которая равна O (n).Но когда мы пытаемся доказать T (n) ≤kn методом подстановки, получаем
T (n) = 2T (n / 2) + 1 ≤ 2k (n / 2) + 1 (замена на IH) ≤ kn + 1 (замена по IH)
Мы не доказали, что нам нужно, из-за этого члена +1. Ключ к усилить IH, доказав, что T (n) ≤ kn — b для некоторого положительного b, что будет также докажи, что T (n) ≤ kn, конечно.Тогда все наладится:
T (n) = 2T (n / 2) + 1 ≤ 2k (n / 2) — 2b + 1 (замена на IH) ≤ кн — 2b + 1 ≤ kn — b + (1 — b) ≤ кн — b (если b ≥ 1)
Мастер-метод
«Основной метод» — это метод из поваренной книги для решения повторяющихся
очень удобен для борьбы со многими рецидивами, наблюдаемыми на практике.
Предположим
у вас есть рекурсивная функция, которая делает рекурсивных вызовов и уменьшает размер проблемы как минимум в b на каждом
вызов, и предположим, что каждый вызов занимает время ч ( n ).
Мы можем визуализировать это как дерево вызовов, в котором узлы дерева имеют коэффициент разветвления a . У верхнего узла есть работа h ( n ), связанный с ним, следующий уровень имеет работу h ( n / b ), связанную с каждым узлы, следующий уровень h ( n / b 2 ), и так далее.Дерево имеет бревно b n уровней, поэтому общее количество листьев в дереве составляет a log b n = n log b a .
Затраченное время — это просто сумма условий ч ( n / b i ) на всех узлах. Как выглядит эта сумма, зависит
от того, как асимптотический рост h ( n )
сравнивается с асимптотическим ростом количества листьев.
Есть три случая:
- Случай 1: h ( n ) — O ( n log b a — ε ). Так как листья растут быстрее h, асимптотически вся работа выполняется на листах, поэтому T ( n ) составляет Θ (n log b a ).
- Случай 2: h ( n ) равен Θ ( n log b a ).В листья растут с той же скоростью, что и h, поэтому такой же порядок работы делается на каждом уровне дерево. Дерево имеет O (lg n) уровней, умноженное на работу, выполненную на одном уровне, что дает T ( n ) — это & Theta (n log b a lg n ).
- Случай 3: h ( n ) — Ω ( n log b a +
ε ). Нам также необходимо показать, что ah ( n / b ) ≤ kh ( n ) для некоторого k
и большое n, что означает, что h растет быстрее, чем количество листьев. Асимптотически вся работа выполняется в корневом узле, поэтому T ( n ) равно Θ ( h ( n )).
Асимптотически вся работа выполняется в корневом узле, поэтому T ( n ) равно Θ ( h ( n )).Пример: еще один алгоритм сортировки
Следующая функция сортирует первые две трети списка, затем вторую две трети, затем снова первые две трети:
пусть sort3 (a: int list): int list =
сопоставить с
([] | [_]) -> а
| [x, y] => [Int.min (x, y), Int.max (x, y)]
| _ -> let n = List.length (a)
и m = (2 * n + 2) / 3 дюйма
пусть res1 = sort3 (List.взять (а, м)) в
пусть res2 = sort3 (List.drop (res1, n-m) @
List.drop (a, m)) в
пусть res3 = sort3 (List.take (res1, n-m) @
List.take (res2, 2 * m-n)) в
res3 @ List.drop (res2,2 * m-n)
Может показаться удивительным, но этот алгоритм сортирует список. Мы
оставьте доказательство правильности сортировки в качестве упражнения для читателя. В
Ключевым моментом является наблюдение, что первые два прохода гарантируют, что хвост финального
list List. действительно содержит правильные элементы
в правильном порядке.
drop (res2,2 * m-n)
Время выполнения алгоритма мы можем определить по его повторяемости. Процедура делает некоторые O ( n ) work, а затем выполняет три рекурсивных вызова списков длиной 2 n /3. Следовательно, его повторяемость:
T ( n ) = cn + 3 T (2 n /3)
Если мы применим мастер-метод к алгоритму sort3 , мы увидим
легко, что мы находимся в случае 1, поэтому алгоритм O ( n log 3/2 3 ) = O (n 2.7 ),
что делает его медленнее, чем сортировка вставкой!
Нижняя граница производительности сортировки
Оказывается, ни один алгоритм сортировки не может иметь меньшее асимптотическое время работы
чем O ( n lg n ), и, следовательно,
кроме постоянных факторов во времени выполнения, сортировка слиянием является таким же хорошим алгоритмом
как и следовало ожидать при сортировке общих данных.
Его постоянные коэффициенты также довольно хороши, так что это полезный
алгоритм на практике. Мы видим, что O ( n lg n ) нужно время, чтобы подумать о сортировке списка n различные числа.Есть n !
= n × ( n −1) × ( n −2) × … × 3 × 2 × 1
возможных списков, и алгоритм сортировки должен сопоставить их все с одним и тем же
отсортированный список путем применения соответствующей обратной перестановки. Для общих данных,
алгоритм должен
сделать достаточно наблюдений о входном списке (сравнивая элементы списка
попарно) к
определите какой из n !
перестановки были заданы как входные, так что соответствующая обратная перестановка может
применить и отсортировать список.Каждое сравнение двух элементов, чтобы увидеть, какой из них
больше генерирует один бит информации о том, какая перестановка была дана; в
минимум lg ( n !) бит информации
необходимо. Поэтому алгоритм должен принимать не менее O (lg ( n !))
время.
Несложно заметить, что n ! — O ( n n );
Обратите внимание, что lg n n = n lg n .
С немного
чем сложнее, тем сильнее результат: lg ( n !)
( n lg n ).Поэтому сортировка слиянием не только намного быстрее, чем сортировка вставкой в больших списках,
это действительно оптимально с точностью до постоянного множителя! Это показывает ценность
тщательно разрабатывать алгоритмы.
Примечание: есть алгоритмы сортировки для специализированных входов, которые
иметь лучше, чем O ( n lg n )
производительность: например, поразрядная сортировка. Это возможно, потому что сортировка по основанию
не работает при попарном сравнении элементов; извлекает информацию о
перестановка с использованием самого элемента в качестве индекса в массиве.Эта индексация
операция может выполняться в постоянное время и в среднем извлекает lg n бит информации о перестановке.
Таким образом, поразрядная сортировка может
выполняется с использованием времени O ( n ),
предполагая, что список плотно заполнен целыми числами или элементами, которые могут
монотонно и плотно отображается на целые числа. Под плотностью мы подразумеваем, что
наибольшее целое число в списке длиной n равно O ( n )
по размеру. Под монотонностью мы подразумеваем, что порядок целых чисел такой же
как порядок сортировки соответствующих данных.В общем не можем найти
плотное монотонное отображение, поэтому Θ ( n lg n ) — лучшее, что мы можем сделать для сортировки произвольных данных.
Алгебраические методы
|
Есть два алгебраических метода , Подстановка
Метод и метод исключения.
