Спиши ру алгебра 7 класс макарычев: ГДЗ по Алгебре за 7 класс: Макарычев (Решебник)

kyopreponrui1970

Моя страница

• Стартовая страница
• нижней страницы
• Контакт
• решебник рабочая тетрадь обществознание
• гдз поглиблене вивчення математики 7-8 клас &
• смотреть решебник по математике 6 класс ви
• решебник пр new millennium english
• гдз по задачнику ершовой и голобородько о
• гдз для учебника по математике 5-класс виле
• решебник по алгебре 7 класса ю. н макарычев
• фізика божинова 9 решебник
• гдз английскому языку для перевода
• гдз по литература 5класс
• физика.рымкевич.решебник
• гдз по геометрии за 7 класс автроры: л.с анаст
• гдз по русском языку 10 11 класс власенков упрk
• гдз по английскому языку enjoy english-1 учебник англи
• ответы на егэ английский язык 2007 помогите вл
• решебник по физике г.я.мякишев 10 класса меха
• гдз по природоведение природа. неживая и ж
• спиши.ру гдз по русскому языку
• переводы текстов enjoy english 9 класс гдз
• егораева русский язык егэ 2012 практикум отве
• ответы на гиа по математике 2012 ященко, семенl
• гдз по алгебре7 класс макарычев ю а миндюк н
• решебник по астрономии 11 кл
• решебник по engoy english
• решебник для 9 класса дорофеев
• ответы на контрольную работу №112 9 класс по фl
• скачать ответы к рабочей тетради по биоло
• решебник по дидактическим материалам алг
• конституционное право россии ответы к экk
• гдз на учебник алгебры виленкина 9 класс
• готовое домашнее задание л. с. атанасян ска
• решебник на алгебру автор а.в.шевкин и м.к.по
• гдз геометрия 1999 г скачать
• правовая ответвенность врача pf жалобы бол

Этот сайт был создан бесплатно с помощью homepage-konstruktor.ru. Хотите тоже свой сайт?

Зарегистрироваться бесплатно

связанных понятий, примеры. Понятие монома. Стандартный вид монома

Урок на тему: «Стандартный вид монома. Определение. Примеры»

Дополнительные материалы
  Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, предложения. Все материалы проверяются антивирусным ПО.

Учебные пособия и тренажеры в интернет-магазине Интеграл для 7 класса
Электронный учебник «Понятная геометрия» для 7-9 классов
Мультимедийный учебник «Геометрия за 10 минут» для 7-9 классов

Моном.

3$.
  С уверенностью можно сказать, что это выражение является мономом.

Стандартный вид монома

  При расчетах желательно привести моном к стандартному виду. Это самая лаконичная и понятная мономиальная запись.

Порядок приведения монома к стандартному виду следующий:
  1. Умножить коэффициенты монома (или числовые множители) и поставить результат на первое место.
  2. Выберите все степени с одинаковой буквенной основой и перемножьте их. 95с $.

Понятие монома

Определение монома: моном – это алгебраическое выражение, в котором используется только умножение.

Стандартный вид монома

Какова стандартная форма монома? Одночлен записывается в стандартной форме, если у него на первом месте стоит числовой множитель и этот множитель, он называется коэффициентом одночлена, в одночлене только один, буквы одночлена расположены в алфавитном порядке и каждая буква происходит только один раз.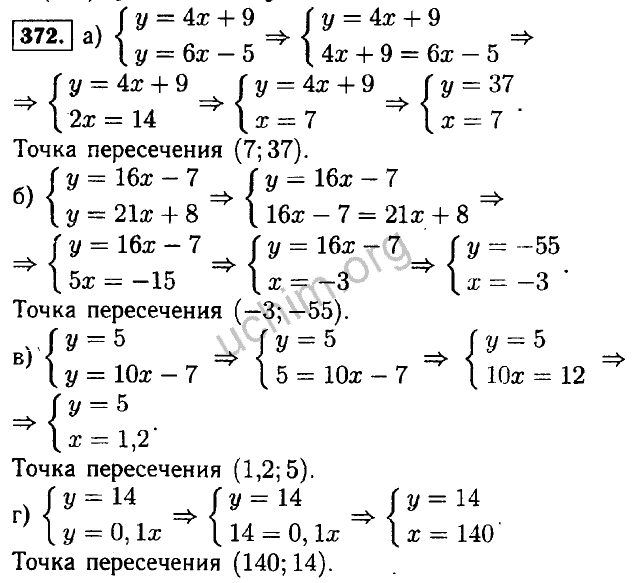

Пример монома в стандартной форме:

здесь на первом месте стоит число, коэффициент монома, а это число всего одно в нашем мономе, каждая буква встречается только один раз и буквы расположены в алфавитном порядке, в данном случае это латинский алфавит.

Другой пример монома в стандартной форме:

каждая буква встречается только один раз; они расположены в латинском алфавитном порядке, но где коэффициент при одночлене, т.е. числовой множитель, который должен стоять первым? Здесь он равен единице: 1адм.

Может ли мономиальный коэффициент быть отрицательным? Да, может пример: -5а.

Может ли мономиальный коэффициент быть дробным? Да, может пример: 5.2а.

Если моном состоит только из цифры, т.е. без букв, как привести его к стандартному виду? Любой моном, представляющий число, уже находится в стандартной форме, например: число 5 является мономом стандартной формы.

Приведение одночлена к стандартному виду

Как привести одночлен к стандартному виду? Давайте посмотрим на некоторые примеры.

Пусть задан моном 2a4b, нам нужно привести его к стандартному виду. Умножьте два его числовых множителя и получите 8ab. Теперь моном записывается в стандартной форме, т.е. в нем на первом месте пишется только один числовой множитель, каждая буква в мономе встречается только один раз и эти буквы расположены в алфавитном порядке. Значит 2а4б = 8аб.

Дано: одночлен 2a4a, приведите одночлен к стандартному виду. Перемножаем числа 2 и 4, произведение аа заменяем на вторую степень а 2. Получаем: 8а 2. Это стандартный вид этого одночлена. Значит 2а4а = 8а 2.

Подобные мономы

Что такое подобные мономы? Если одночлены различаются только коэффициентами или равны, то они называются подобными.

Пример подобных мономов: 5а и 2а. Эти мономы различаются только коэффициентами, значит, они подобны.

Похожи ли мономы 5abc и 10cba? Приведем второй одночлен к стандартному виду, получим 10abc. Теперь мы видим, что мономы 5abc и 10abc отличаются только своими коэффициентами, а значит, они подобны.

Сложение мономов

Какова сумма мономов? Мы можем только суммировать подобные мономы. Рассмотрим пример сложения мономов. Чему равна сумма одночленов 5а и 2а? Суммой этих мономов будет аналогичный им моном, коэффициент которого равен сумме коэффициентов при слагаемых. Итак, сумма одночленов равна 5а + 2а = 7а.

Еще примеры сложения мономов:

2а 2 + 3а 2 = 5а 2
   2а 2 b 3 с 4 + 3а 2 b 3 с 4 = 5а 2 b 3 с 4

Снова. Можно добавлять только подобные одночлены; сложение сводится к сложению их коэффициентов.

Вычитание одночленов

В чем отличие одночленов? Мы можем вычитать только одинаковые одночлены. Рассмотрим пример вычитания одночленов. В чем разница между мономами 5а и 2а? Разностью этих мономов будет аналогичный им моном, коэффициент которого равен разности коэффициентов этих мономов. Итак, разность одночленов 5а — 2а = 3а.

Еще примеры вычитания одночленов:

10а 2 — 3а 2 = 7а 2
   5а 2 b 3 с 4 — 3а 2 b 3 с 4 = 2а 2 b 3 с 4

Одночленное умножение

4 произведение одночленов? Рассмотрим пример:

т.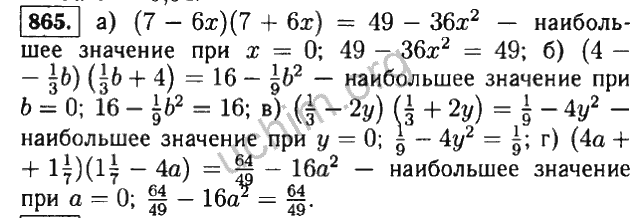 е. произведение мономов равно моному, множители которого составлены из множителей исходных мономов.

Другой пример:

2а 2 б 3 * а 5 б 9 = 2а 7 б 12.

Как вы получили этот результат? Каждый множитель имеет «а» в степени: в первом «а» в степени 2, а во втором – «а» в степени 5. Следовательно, произведение будет иметь «а» в степени 7, так как при умножении одинаковые буквы, их степени складываются:

А 2 * а 5 = а 7.

То же самое относится и к фактору «b».

Коэффициент первого множителя равен два, а второго один, поэтому в итоге получаем 2*1=2.

Вот как был рассчитан результат 2a 7 b 12.

Из этих примеров видно, что коэффициенты при мономах перемножаются, а одинаковые буквы заменяются суммами их степеней в произведении.

   Назад вперед

Внимание! Предварительный просмотр слайдов используется только в ознакомительных целях и может не давать представления обо всех возможностях презентации.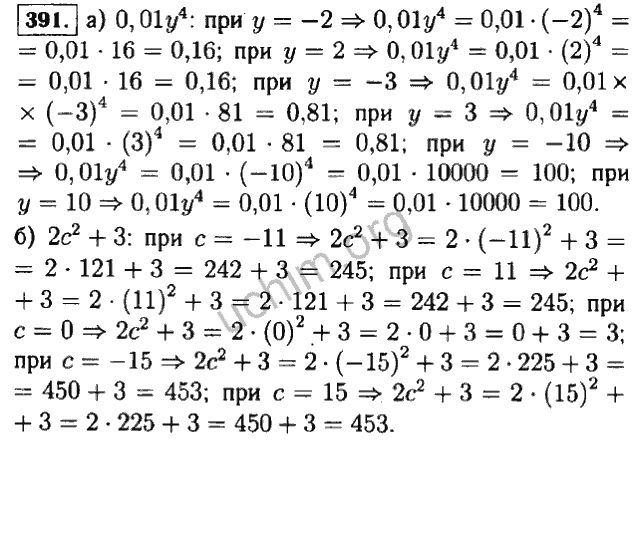 Если вас заинтересовала эта работа, пожалуйста, скачайте полную версию.

Тип урока: интегрированный (с ИКТ), урок по внедрению новых знаний.

Цели и задачи (алгебра):   ввести понятие одночлена; мономиальная степень; стандартный вид монома. Учить учащихся приводить одночлены к стандартной форме. Продолжайте развивать навыки выполнения действий со степенями. Совершенствовать вычислительные навыки учащихся. Развивать внимательность, аккуратность.

Цели и задачи (ИКТ): научить пользоваться на практике встроенным редактором формул в MS Office Word; развивать навык самостоятельной работы.

Материалы, используемые на занятии: презентация, компьютерный класс с установленным пакетом MS Office (Word), опорный конспект практической работы, карточки с заданием для самостоятельной работы, мультимедийная установка.

Во время занятий

I. Организационный момент .

Приветствие студентов.

II. Устные упражнения.

(слайд на экране 2).

• Представить в виде степени: у 3 * у 2; (у 3) 5; у 7 * у 3; (у 7) 4; а 10 / а 8.
• Какое число (положительное или отрицательное) является значением выражения: (-8) 10; (-5) 27; 7 5; -2 8; — (- 1) 7.
• Вычислить: (3 * 2) 2 -3 * 2 2; (-3) 8/3 7.

III. Изучение нового материала.

Сообщение темы урока и целей и задач урока (слайд 3.4).

6*х2*у; 2*х3; мин 7; аб; -8 (слайд 5)

• Прочитайте выражения, написанные на доске.
• Что это за выражения?

Выражения такого рода называются мономами.

ОПРЕДЕЛЕНИЕ: Одночлен есть произведение чисел и переменных, степеней переменных или число, переменная, степень переменной.

Посмотрите внимательно на экран (слайд 7). Какие из следующих выражений являются мономами? Почему?

IV. Закрепление нового материала.

№463 — самостоятельно.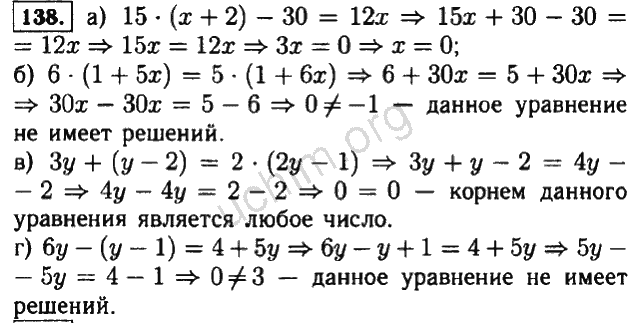 Фронтальная проверка. (Слайд 8).

V. Изучение нового материала.

Можно мономы

2х2у*9у2 и 8х*9ху (слайд 9)

Мы используем трансляционный и комбинационный законы умножения. Получаем:

2 * 9 * х 2 * у * у 2 = 18х 2 у 3 и 8 * 9 * х * х * у = 72х 2 у.

• Что мы получили?
• Каково это?

Мы представили одночлен в виде произведения числового множителя, стоящего первым, и степеней различных переменных. Такой моном называется стандартной формой.

• Какой одночлен называется одночленом стандартной формы?

ОПРЕДЕЛЕНИЕ: одночлен называется одночленом стандартного вида, если у него на первом месте (коэффициенте) стоит 1 числовой множитель, произведение тех же переменных записано в нем как степень.

Читать те мономы, которые записаны в стандартной форме. Каковы их шансы?

VI. Закрепление нового материала.

№464 — устно, №465 — под руководством преподавателя.

VII. Задание выполняется на компьютере (практическая работа).

Программа MS Word. Встроенный редактор формул. Использование встроенного редактора формул для записи мономов. Файл «Стандартный вид монома» на рабочий стол. Заполните подготовленную таблицу с помощью встроенного редактора формул.

Заполните таблицу. (Слайд 15)

Проверка — на экране (слайд 16) и сохраненных файлах учащихся.

VIII. Изучение нового материала.

• Что написано на доске?
• Чему равен показатель степени переменной X?
• Чему равен показатель степени переменной Y?
• Найдите сумму показателей. Это число называется степенью монома .

На странице 84 учебника найдите определение степени монома. Прочтите это.

IX. Штифт Новый материал .

№ 473 — устно;

№467 (а;г) — прокомментировал доску.

X. Самостоятельная работа .

На экране по вариантам (слайд 19). (У каждого учащегося на парте лист с заданием на выполнение работы — Приложение 2 )

Проверка — самопроверка с записью (на экране слайд 20).

Си. Подведение итогов.

• Что такое моном?
• Одночлен, какой тип называется стандартным одночленом?
• Что называется мономиальной степенью?

XII. Домашнее задание.

стр.19, №466, 468, 476, 470.

Спасибо за урок! (слайд 23)

Список использованной литературы:

1. Алгебра. 7 класс: учебник для общеобразовательных учреждений / [Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворов]; под редакцией С.А. Теляковского. — М.: Просвещение, 2007.

Одночлены являются одним из основных видов выражений, изучаемых в школьном курсе алгебры. В этом материале мы расскажем, что это за выражения, определим их стандартный вид и покажем примеры, а также разберемся с такими родственными понятиями, как степень одночлена и его коэффициент.

Что такое моном?

В школьных учебниках обычно дается следующее определение этого понятия:

Определение 1

Одночлены включают   числа, переменные, а также их степени с натуральным показателем и разные виды произведений, составленных из них.

Основываясь на этом определении, мы можем привести примеры таких выражений. Итак, все числа 2, 8, 3004, 0, — 4, — 6, 0, 78, 1 4, — 4 3 7 будут относиться к одночленам. Все переменные, например, x, a, b, p, q, t, y, z также будут мономами по определению. Сюда же относятся степени переменных и чисел, например, 6 3, (- 7, 41) 7, x 2 и  t 15 , а также выражения вида 65 · x, 9· (- 7) · х · у 3 · 6, х · х · у 3 · х · у 2 · z и т. д. Обратите внимание, что в состав монома может входить как одно число или переменная, так и несколько, причем , они могут упоминаться несколько раз в составе одного полинома.

К одночленам относятся также такие типы чисел, как целые, рациональные, натуральные. Вы также можете включать действительные и комплексные числа. Итак, выражения вида 2 + 3 · i · x · z 4, 2 · x, 2 · π · x 3 также будут мономами.

Что такое стандартная форма одночлена и как привести к ней выражение

Для удобства все мономы сначала приводят к специальной форме, называемой стандартной. Сформулируем конкретно, что это значит.

Определение 2

Стандартный вид монома   называют такой вид, в котором он является произведением числового множителя и натуральных степеней различных переменных. Числовой множитель, также называемый мономиальным коэффициентом, обычно пишется первым слева.

Для наглядности выделим несколько мономов стандартного вида: 6 (это моном без переменных), 4 · а, — 9· x 2 · y 3, 2 3 5 · x 7. Сюда же относится выражение   x · y   (здесь коэффициент будет равен 1),   — x 3   (здесь коэффициент равен -1).

Теперь приведем примеры мономов, которые необходимо привести к стандартному виду: 4 · а · а 2 · а 3 (здесь нужно объединить одинаковые переменные),   5 · х · (- 1) · 3 · y 2   (здесь нужно сложить числовые множители слева).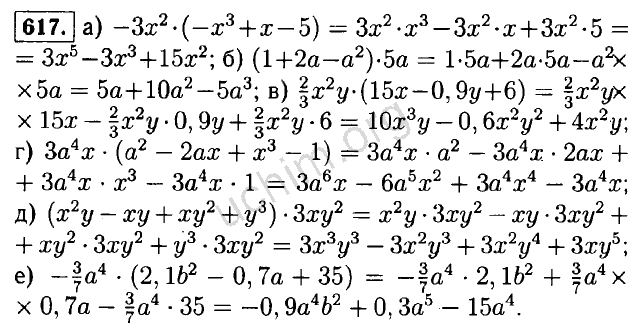

Обычно в случае, когда одночлен имеет несколько переменных, записанных буквами, буквенные множители записываются в алфавитном порядке. Например, запись предпочтительнее.   6 · а · б 4 · в · г 2 чем   б 4 · 6 · а · г 2 · в . Однако порядок может быть другим, если этого требует цель расчета.

Любой моном можно привести к стандартной форме. Для этого нужно выполнить все необходимые идентичные преобразования.

Концепция мономиальной степени

Очень важным является сопутствующее понятие мономиальной степени. Напишем определение этого понятия.

Определение 3

Мономиальная степень , записанное в стандартной форме, представляет собой сумму показателей степени всех переменных, которые входят в его запись. Если в нем нет ни одной переменной, а сам моном отличен от 0, то его степень будет равна нулю.

Приведем примеры степеней монома.

Пример 1

Итак, моном а имеет степень равную 1, так как а = а 1. Если у нас есть моном 7, то он будет иметь нулевую степень, так как у него нет переменных и он отличается с 0. А вот и запись

  7 · a 2 · x · y 3 · a 2   будет мономом 8-й степени, так как сумма показателей всех степеней входящих в него переменных будет равна 8: 2 + 1 + 3 + 2 = 8 .

Одночлен, приведенный к стандартной форме, и исходный многочлен будут иметь одинаковую степень.

Пример 2

Покажем, как вычислить степень монома 3 · x 2 · y 3 · x · (- 2) · x 5 · y . В стандартной форме это можно записать как  — 6 x 8 y 4 . Вычисляем степень: 8 + 4 = 12 . Следовательно, степень исходного полинома также равна 12.

Понятие мономального коэффициента

Если мы имеем одночлен, приведенный к стандартной форме, в который входит хотя бы одна переменная, то мы говорим о нем как о произведении с одним числовым коэффициентом. Этот коэффициент называется числовым коэффициентом, или коэффициентом одночлена. Пишем определение.

Определение 4

Коэффициент при мономе называется числовым множителем монома, приведенным к стандартной форме.

Возьмем, например, коэффициенты различных мономов.

Пример 3

Итак, в выражении 8 · a 3 коэффициентом будет число 8, а в (- 2,3) x x y z будут − 2 , 3 .

Особое внимание следует обратить на коэффициенты, равные единице и минус единице. Как правило, они не указываются явно. Считается, что в одночлене стандартного вида, в котором нет числового множителя, коэффициент равен 1, например, в выражениях а, х · z 3, а · t · х, так как их можно рассматривать как 1 · а, х · з 3 — как   1 x x z 3   и т. д.

Точно так же в мономах, в которых нет числового множителя и которые начинаются со знака минус, можно рассматривать коэффициент — 1.

Пример 4

Например, выражения — х, — х 3 · у · z 3 будут иметь такой коэффициент, так как их можно представить в виде — х = (- 1) · х, — х 3 · у · z 3 = (- 1) · х 3 · y · z 3 и т.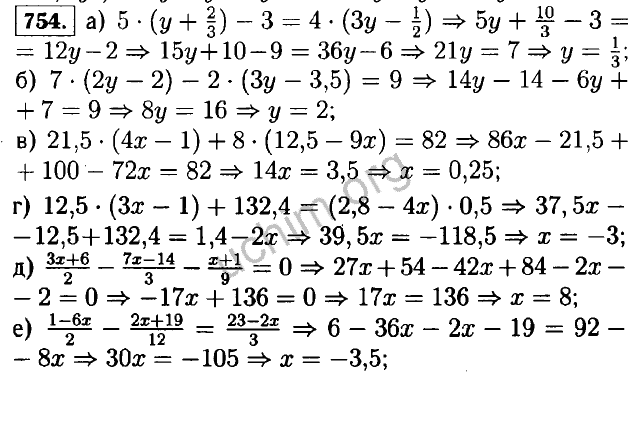 д.

Если в мономе нет однобуквенного множителя, то и в этом случае можно говорить о коэффициенте. Коэффициентами таких числовых мономов будут сами эти числа. Так, например, коэффициент при одночлене 92. Этот тип называется стандартной формой монома. То есть стандартная форма монома есть произведение коэффициента (в первую очередь) на степени переменных. Коэффициенты 1 и -1 не пишут, а от -1 держат минус. Одночлен и его стандартная форма

Выражения 5a2x, 2a3(-3)x2, b2x являются произведениями чисел, переменных и их степеней. Такие выражения называются мономами. Одночленами также считаются числа, переменные и их степени.

Например, выражения — 8, 35, y и y2 — мономы.

Стандартной формой монома является моном в виде произведения числового множителя в первую очередь и степеней различных переменных. Любой одночлен можно привести к стандартному виду, перемножив все входящие в него переменные и числа. Приведем пример приведения одночлена к стандартной форме:

4x2y4(-5)yx3=4(-5)x2x3y4y=-20x5y5

Числовой множитель одночлена, записанного в стандартной форме, называется коэффициентом монома.