Как научиться решать задачи по геометрии? | Консультация (7 класс) на тему:
Опубликовано 17.08.2013 — 14:57 — Жалыбина Елена Викторовна
Как научиться решать задачи по геометрии?
Скачать:
Предварительный просмотр:
Как научиться решать задачи по геометрии?
Дорогие ребята, Вы начали изучать геометрию. Это новая для вас дисциплина, и вы поначалу можете испытывать трудности в её освоении. Не пугайтесь: пройдет некоторое время, и вы научитесь с легкостью решать любые геометрические задачи. Для приобретения необходимого навыка нужно лишь приложить немного усилий. Итак, как решать задачи по геометрии?
Вам понадобится: учебник, тетрадь, ручка, карандаш, линейка, транспортир, циркуль, ластик.
Инструкция:
- Внимательно прочитайте условие задачи.
- Сделайте чертеж.
- Отметьте на чертеже то, что вам дано: длины сторон, величины углов. Если в условии задачи сказано, что какие-то отрезки равны, поставьте на них одинаковые штрихи.
 Равные по величине углы отмечайте одинаковыми дужками: одинарными, двойными, волнистыми. Углы разных величин выделяйте разными дужками.
Равные по величине углы отмечайте одинаковыми дужками: одинарными, двойными, волнистыми. Углы разных величин выделяйте разными дужками. - Исследуйте фигуры, представленные в задаче. Вспомните их определения и свойства.
- Определите тему, к которой относится ваша задача. Освежите в голове теоретический материал по этой теме, повторите основные теоремы.
- Рассмотрите примеры решения задач по этой теме. В задачах, приводимых в учебнике в качестве примеров, часто рассматриваются принципиальные вопросы, которые вы должны знать.
- Если вы чувствуете себя в теме достаточно уверенно, приступайте к решению задачи. Начните с того, что требуется найти или доказать. Подумайте, каким путем это можно сделать. То есть, решайте задачу «с конца».
- Если вы не видите путей решения задачи, попробуйте найти хоть что-нибудь, используя имеющиеся данные. Возможно, так к вам придет идея, как решать задачу.
Полезные советы: не увлекайтесь «устными» доказательствами. Записывайте решение задачи как можно более подробно, если не оговорено иное.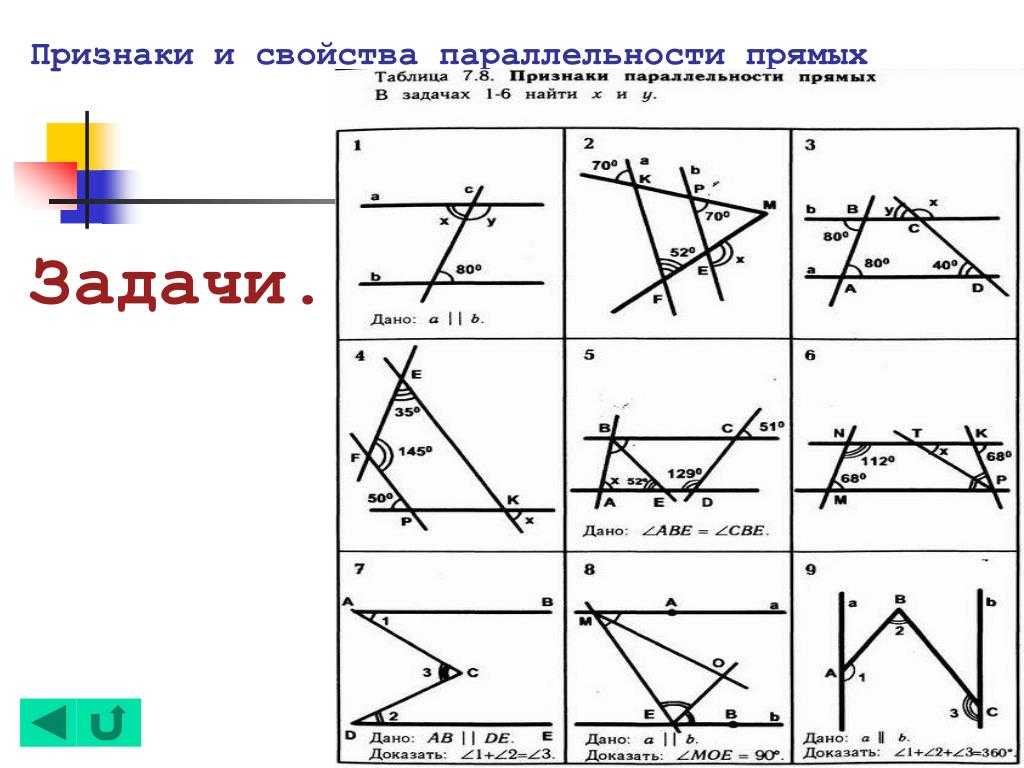 Некоторые вещи могут казаться вам очевидными, но всё равно прописывайте их. Так у вас будет отрабатываться навык, вы лучше запомните идею.
Некоторые вещи могут казаться вам очевидными, но всё равно прописывайте их. Так у вас будет отрабатываться навык, вы лучше запомните идею.
Рекомендации от учителя математики Е.В.Жалыбиной
По теме: методические разработки, презентации и конспекты
Памятка для родителей (как научить решать задачи по математике)
Мно Многие из вас хотят помочь своим детям научиться решать задачи, но не знают , как это сделать. Поэтому, как показывает опыт, родители просто реш…
Как научить решать задачи по физике
Предлагаю Вашему вниманию простые, но очень нужные правила для решения задач по физике…
Как научиться решать задачи.( из опыта работы)
Работа содержит материал по решению задач в основной школе….
Как научиться решать задачи.
Решение задач-это работа,умственная работа. А чтобы научиться какой-либо работе,нужно предварительно хорошо изучить нужный материал,над которым придется работать,те инструменты,с помощью которых выпол. ..
..
Технологическая «находка» по химии «Как научить решать задач на растворы, используя математический метод решения»
Рассмотрен алгоритм решения задач на растворы…
Как научиться решать задачи
Данные советы по геометрии актуальны для учащихся 7 класса…
Как научиться решать задачи по геометрии?
В помощь обучающимся….
Поделиться:
Как понять Геометрию? Основы с нуля
Идеальные объекты
Геометрия — раздел математики, который изучает пространственные структуры и отношения, а также их обобщения.
Математика занимается объектами и делает о них некие заключения, которые называют теоремами. Эти треугольники похожи, и о них можно сделать близкое заключение, которое будет описывать свойства обоих.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Базовые геометрические объекты
Базовые геометрические фигуры — это точки, отрезки, лучи, прямые, плоскости.
Точка — это идеальный математический объект, у которого нет длины и ширины.
Отрезок — это часть прямой, у которого есть начало и конец.
Смежные отрезки — это отрезки, которые не лежат на одной прямой и имеют один общий конец. На рисунке изобразили смежные отрезки АВ и АС, где точка А — общий конец.
Прямая — это «не кривая». Более точное определение вряд ли можно сформулировать.
Когда мы рисуем прямую на листе бумаги, мы изображаем только ее часть, потому что прямая не имеет начала и конца.
Обозначать прямые принято малыми латинскими буквами (a, b, c), но можно и большими латинскими буквами (АВ, CD, MN). Точки всегда обозначают большими латинскими буквами (А, В, С).
Два варианта расположения точек относительно прямой:
Точки лежат на данной прямой. Или еще говорят, что прямая проходит через эти точки — на рисунке выше такими точками являются А и В. При решении задач для краткости используют запись A ∈ a (читается так: точка А принадлежит прямой a или точка А лежит на прямой a), аналогично будет и для точки В (B ∈ b).
Точки не лежат на данной прямой. Говорят так: прямая не проходит через эти точки — на рисунке такими точками являются С и D. При решении задач для краткости используют запись C ∉ a (читается так: точка С не принадлежит прямой a или точка С не лежит на прямой a), аналогично будет и для точки D (D ∉ a).

Важно знать
Через любые две точки можно провести прямую и притом только одну.
Если рассмотреть две прямые, то возможны два варианта их расположения:
Прямые пересекаются, то есть имеют одну общую точку.
Для записи пересекающихся прямых используют специальный знак — ∩, то есть a∩b (читают: прямая a пересекает прямую b). Чтобы обозначить точку пересечения прямых, пишут a∩b = O (читается: прямая a
- Прямые не пересекаются, то есть не имеют общих точек.
Для записи не пересекающихся прямых используют специальный знак — , то есть m n (читают: прямая m не пересекает прямую n).
 В дальнейшем для обозначения не пересекающихся прямых мы будем использовать знак параллельности ||.
В дальнейшем для обозначения не пересекающихся прямых мы будем использовать знак параллельности ||.
Луч — это часть прямой, ограниченная с одной стороны. Луч имеет начало, но не имеет конца.
На рисунке точка О разбивает прямую АВ на две части:
Каждая из этих частей называется лучом, а точка О является началом одного и другого луча.
Назовем получившиеся лучи:
-
Луч ОА, точка О — начало луча ОА; конца у луча ОА нет.
Луч ОВ, точка О — начало луча ОВ; конца у луча ОВ нет.
Лучи ОА и ОВ принадлежат одной прямой АВ. Лучи ОА и ОВ имеют общее начало (точка О). Лучи ОА и ОВ противоположно направлены. При таких условиях лучи ОА и ОВ называются дополнительными.
Плоскость — это бесконечная поверхность, к которой принадлежат все прямые, которые проходят через какие-либо две точки плоскости
Комбинации простейших объектов
Поговорим про комбинации простейших объектов. Например, две прямые, которые мы уже разглядели — либо пересекаются на плоскости, либо нет (тогда они параллельны).
Например, две прямые, которые мы уже разглядели — либо пересекаются на плоскости, либо нет (тогда они параллельны).
Когда прямые пересекаются, можно ввести понятие отношения между двумя прямыми. Аналогично мы поступали с числами: ввели натуральные числа — количество предметов в множестве. А после этого изучали отношения между этими числами: дроби, возведение в степень.
Точно так же мы изучали множества, а после — отношения между множествами, функции.
Две прямые образуют углы. По сути, угол — это отношение между прямыми. Если один из них нулевой, то прямые параллельны. Если нет — прямые пересекаются.
Максимальный угол – это полный оборот, он составляет 360 градусов.
Угол — это часть плоскости, ограниченная двумя лучами, которые выходят из одной точки.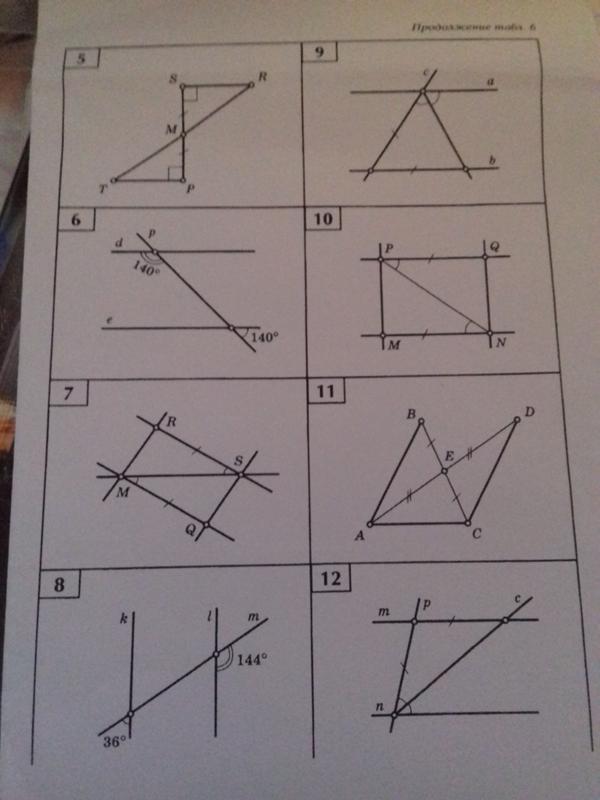 Углы измеряются в градусах. Углов бесконечно много, так как от 0° до 360° угол может принимать бесконечное множество значений.
Углы измеряются в градусах. Углов бесконечно много, так как от 0° до 360° угол может принимать бесконечное множество значений.
Есть разные виды углов, выделим самые часто встречающиеся:
Если градусная мера угла меньше 90° — угол острый.
Если градусная мера угла равна 90° — угол прямой.
Если градусная мера угла больше 90°, но меньше 180° — угол тупой.
Если градусная мера угла равна 180° — угол развернутый.
Общая точка, из которой исходят лучи, называется вершиной угла, а лучи — сторонами угла.
Два угла называются вертикальными, если их стороны являются дополнительными лучами. Свойство вертикальных углов звучит так: вертикальные углы равны.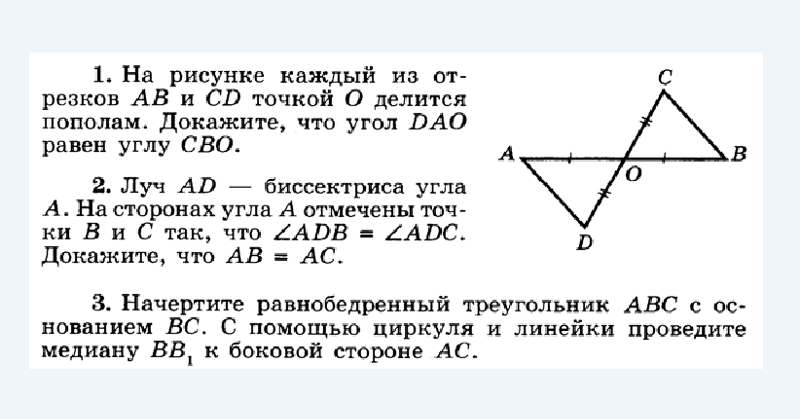
Два угла называются смежными, если одна сторона у них общая, а две другие являются дополнительными лучами. Свойство смежных углов: сумма смежных углов равна 180°.
Биссектриса угла — это луч с началом в вершине угла, который делит угол на две равные части.
А теперь посмотрим на взаимное расположение трех прямых.
Первый случай: все три прямые параллельны.
Второй случай: две прямые параллельны, а третья их пересекает.
Третий случай: если провести три прямые на плоскости случайным образом, велика вероятность образования треугольника. Поэтому этой фигуре мы уделяем так много времени в школе на уроках геометрии.
Треугольник
Треугольник образуют три прямые. Но на треугольник также можно посмотреть, как на фигуру, которая состоит из трех отрезков.
Но на треугольник также можно посмотреть, как на фигуру, которая состоит из трех отрезков.
Из треугольников можно получить остальные многоугольники и к треугольникам можно приближать другие фигуры. Например, пятиугольник состоит из трех треугольников.
Треугольник можно использовать для измерения расстояний. А еще треугольник можно рассматривать в отношениях с окружностью, которая тоже является элементарной конструкцией. Читайте про вписанные и описанные углы.
Треугольник можно легко вычислить, то есть найти его площадь по трем элементам:
Свойства треугольников
Раз треугольник можно задать тремя элементами, значит их можно классифицировать. Если два треугольника похожи, значит у них есть общие свойства.
Треугольник можно составить совсем не из любых трех отрезков: они должны удовлетворять важному свойству — неравенству треугольника.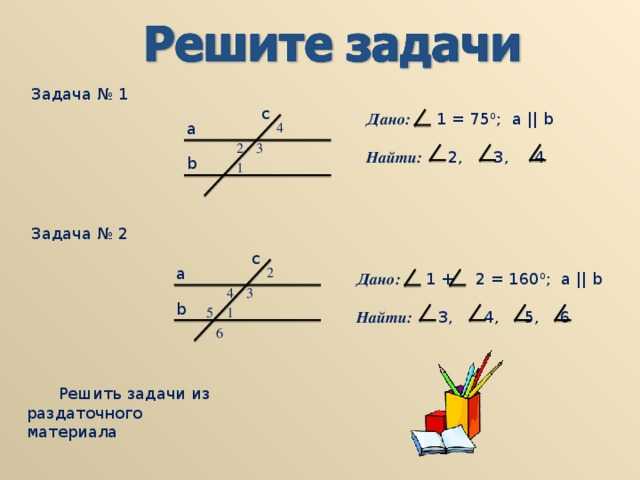
Кратчайшее расстояние между двумя точками — это длина отрезка, который их соединяет. Из этого следует, что любой другой путь между двумя точками будет длиннее, чем этот отрезок.
Неравенство треугольника Сумма любых двух сторон треугольника больше его третьей стороны. |
Один из распространенных типов — прямоугольный треугольник
. Если один из углов прямой, то это накладывает определенные свойства на треугольник. Прямоугольный треугольник — это также половина прямоугольника.Если две стороны треугольника равны, то это равнобедренный треугольник — и тогда у него есть ось симметрии. Если нарисовать такой треугольник и сложить лист пополам, то две части треугольника совпадут.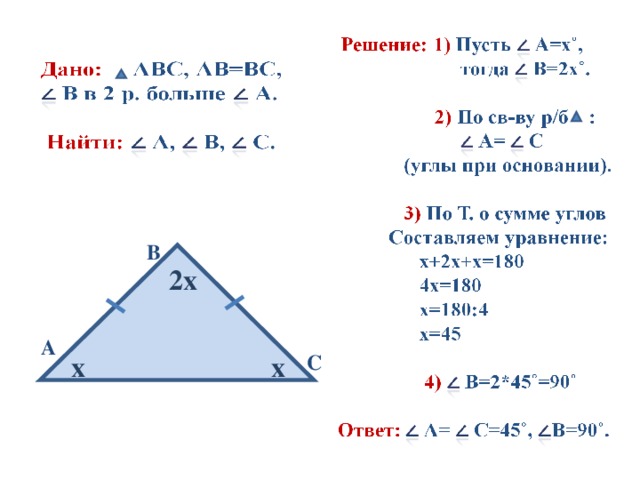 Эта особенность дает треугольнику определенные свойства.
Эта особенность дает треугольнику определенные свойства.
Симметричный треугольник, у которого все углы и стороны равны — это равносторонний треугольник. У таких треугольников три оси симметрии. Это значит, что если мы повернем треугольник на 60 градусов, то получим точно такой же треугольник.
Такой треугольник задается одним параметром — длиной стороны. Она полностью определяет все другие значения и размеры в этом треугольнике.
От правильного треугольника может плавно перейти к правильным многоугольникам. У треугольника 3 угла, у четырехугольника — 4, а у пятиугольника — 5 углов. У многоугольника много углов🙃
Четырехугольники
Про четырехугольники мы много говорим на уроках в школе: прямоугольник, квадрат, ромб.
Но говорим о них не в общем случае, как для треугольников (такие вещи, как теорема синусов, косинусов), а можем формулировать только какие-то свойства для определенных видов четырехугольников.
Четырехугольникам лучше уделить побольше времени — у каждого из них есть особые свойства, которые не пригодятся для других фигур. Поэтому каждый четырехугольник лучше внимательно изучить на уроке или почитать в наших материалах:
площадь фигуры
периметр фигуры
площадь прямоугольника
периметр прямоугольника
площадь квадрата
периметр квадрата
параллелограмм
прямоугольный параллелепипед.
Окружность
Окружность — это еще один объект, который полезно изучить. Ее легко описать, она задается одним параметром — радиусом. А еще часто встречается в физике и в обычной жизни. Например, когда капля падает в воду, от нее остаются следы — маленткие окружности.
Например, когда капля падает в воду, от нее остаются следы — маленткие окружности.
Практическая сторона геометрии
Название «геометрия» переводится с греческого, как «гео» — земля и «метрео» — мерить. Изначально геометрию использовали для разметки земли и других работ с землей. Но, оказалось, что сфера ее влияния безгранична.
Чтобы понять, зачем нам нужны знания по геометрии, просто оглянитесь вокруг: геометрия окружает нас в предметах разных форм. Взять хотя бы круг: его используют в искусстве, строительстве, технике. То же самое и с другими фигурами: чтобы сконструировать автомобиль или айфон, сшить одежду или построить дом — не обойтись без геометрии.
А еще геометрия помогает научиться рассуждать логически, искать связи и противоречия — полезный навык в диджитал-мире, когда информация окружает нас повсюду.
Вот, в каких профессиях пригодится геометрия: архитектор, айтишник, дизайнер, инженер, конструктор, строитель, smm-менеджер, декоратор, летчик, водитель, художник, проектировщик, астроном, спортсмен, музыкант и другие.
Почему изучать геометрию просто: мы видим объемный мир каждый день и регулярно прикасаемся к предметам, строим планы, размышляем и считаем в уме. В геометрии все знания подкреплены научными теориями — это помогает взаимодействовать с пространством по-другому, более осознанно.
Почему изучать геометрию сложно: некоторые правила придется учить наизусть.
Чтобы понять геометрию, двигайтесь от простого к сложному. Многие теоремы могут показаться очевидными. Но эта видимость может быть верной только для одного рисунка. Невозможно нарисовать все ситуации, ведь их их бесконечное множество. Именно поэтому важно доказать истину, чтобы никогда не сомневаться в ней.
Общие базовые стандарты для 7-го класса
Ниже приведены общие базовые стандарты для 7-го класса со ссылками на поддерживающие их ресурсы. Мы также поощряем множество упражнений и работу с книгами.
7 класс | Соотношения и пропорциональные отношения
Анализируйте пропорциональные отношения и используйте их для решения реальных и математических задач.
7.RP.A.1 Вычислить удельные нормы, связанные с отношениями дробей, включая соотношения длин, площадей и других величин, измеренных в одинаковых или разных единицах. Например, если человек проходит 1/2 мили каждые 1/4 часа, рассчитайте удельную скорость как комплексную дробь (1/2)/(1/4) мили в час, что эквивалентно 2 милям в час.
Соотношения
Эквивалентные фракции
Соотношение — Рецепт шоколадных хрустящих хлопьев
Соотношение — Приготовление шоколадных хрустящих хлопьев
7.RP.A.2 Распознавать и представлять пропорциональные отношения между величинами.
а. Определите, находятся ли две величины в пропорциональном соотношении, например, проверив эквивалентные отношения в таблице или нарисовав график на координатной плоскости и наблюдая, является ли график прямой линией, проходящей через начало координат.
б. Определите константу пропорциональности (единичную норму) в таблицах, графиках, уравнениях, схемах и словесных описаниях пропорциональных отношений.
с. Представьте пропорциональные отношения уравнениями. Например, если общая стоимость t пропорциональна количеству n товаров, купленных по постоянной цене p, соотношение между общей стоимостью и количеством товаров может быть выражено как t = pn.
д. Объясните, что означает точка (x, y) на графике пропорциональной зависимости с точки зрения ситуации, обратив особое внимание на точки (0, 0) и (1, r), где r — единичная ставка.
Коэффициенты
Цена за единицу
Игра с ценой за единицу
Головоломка «Стадо верблюдов»
Стадо верблюдов — решение
Задание: трава для сада
Ratio — Рецепт шоколадных чипсов
Ratio — Приготовьте шоколадные чипсы
7.RP.A.3Используйте пропорциональные соотношения для решения многошаговых задач на соотношение и проценты. Примеры: простые проценты, налоги, надбавки и уценки, чаевые и комиссионные, сборы, процентное увеличение и уменьшение, процентная ошибка.
Коэффициенты
процентная ошибка
процентное изменение
процентные пункты
процент калькулятора
Процент Разница
Проверьте свои проценты
Введение в проценты
процентные процентные процентные проценты Процент. Система счисления
Применение и расширение предыдущего понимания операций с дробями для сложения, вычитания, умножения и деления рациональных чисел.
7.NS.A.1 Применение и расширение предыдущего понимания сложения и вычитания для сложения и вычитания рациональных чисел; представляют сложение и вычитание на горизонтальной или вертикальной диаграмме с числовыми линиями.
а. Опишите ситуации, в которых противоположные величины объединяются, чтобы получить 0. Например, атом водорода имеет нулевой заряд, потому что две его составляющие заряжены противоположно.
б. Под p + q понимается число, расположенное на расстоянии |q| от p в положительном или отрицательном направлении в зависимости от того, является ли q положительным или отрицательным. Покажите, что число и его противоположность имеют сумму 0 (аддитивные инверсии). Интерпретируйте суммы рациональных чисел, описывая контексты реального мира.
Покажите, что число и его противоположность имеют сумму 0 (аддитивные инверсии). Интерпретируйте суммы рациональных чисел, описывая контексты реального мира.
с. Поймите вычитание рациональных чисел как добавление обратного аддитивного, p — q = p + (-q). Покажите, что расстояние между двумя рациональными числами на числовой прямой равно абсолютному значению их разности, и примените этот принцип в контексте реального мира.
д. Применяйте свойства операций как стратегии сложения и вычитания рациональных чисел.
Обратное
Кейси Раннер
Абсолютное значение
Рациональные числа
Использование числовой строки
Сложение и вычитание положительных и отрицательных чисел
7.NS.A.2 Применить и расширить прежнее понимание умножения и деления и дробей для умножения и деления рациональных чисел.
а. Поймите, что умножение распространяется с дробей на рациональные числа, требуя, чтобы операции продолжали удовлетворять свойствам операций, в частности свойству распределения, что приводит к таким продуктам, как (-1)(-1) = 1 и правилам умножения чисел со знаком. Интерпретируйте произведения рациональных чисел, описывая контексты реального мира.
Интерпретируйте произведения рациональных чисел, описывая контексты реального мира.
б. Поймите, что целые числа можно делить при условии, что делитель не равен нулю, и каждое частное целых чисел (с ненулевым делителем) является рациональным числом. Если p и q целые числа, то -(p/q) = (-p)/q = p/(-q). Интерпретируйте частные рациональных чисел, описывая контексты реального мира.
с. Применяйте свойства операций как стратегии умножения и деления рациональных чисел.
д. Преобразование рационального числа в десятичное с использованием длинного деления; известно, что десятичная форма рационального числа оканчивается на 0 или со временем повторяется.
Обратный
Взаимный
Long Division
Разделение на ноль
Разделительные фракции
Фракционные рабочие листы
Умножение фракции
. Рабочие листы деления
Обратная дробь
Умножение смешанных чисел
Полное деление — введение
Длинное деление на десятичные разряды
Умножение отрицательных значений дает положительное число
7. NS.A.3 Решите реальные и математические задачи, связанные с четырьмя операциями с рациональными числами. (Вычисления с рациональными числами расширяют правила обращения с дробями до сложных дробей.)
NS.A.3 Решите реальные и математические задачи, связанные с четырьмя операциями с рациональными числами. (Вычисления с рациональными числами расширяют правила обращения с дробями до сложных дробей.)
Обратное
Длинное деление
Сложение дробей
Деление дробей
Таблицы дробей
Умножение дробей3
04 Фракции вычитания
с использованием номеров
с использованием рациональных номеров
Анимация длинного дивизиона
Математические листы по математике
Рабочие листы длинного подразделения
Умножение смешанных номеров
Долгое подразделение — Введение
Long Division To Decimal Places
Долгое подразделение. и вычитание смешанных дробей
Умножение отрицательных чисел дает положительное число
Сложение и вычитание положительных и отрицательных чисел
7 класс | Выражения и уравнения
Используйте свойства операций для создания эквивалентных выражений.
7.EE.A.1 Применение свойств операций в качестве стратегий для сложения, вычитания, факторизации и расширения линейных выражений с рациональными коэффициентами.
Подобные термины
Факторинг в алгебре
Наибольший общий делитель
7.EE.A.2 Поймите, что переписывание выражения в разных формах в контексте задачи может пролить свет на проблему и на то, как связаны в ней величины. Например, a + 0,05a = 1,05a означает, что «увеличение на 5%» равнозначно «умножению на 1,05».
Подобные термины
Рациональные числа
Использование рациональных чисел
Десятичные дроби и проценты
Решайте реальные и математические задачи, используя числовые и алгебраические выражения и уравнения.
7.EE.B.3 Решайте многоэтапные задачи из реальной жизни и математические задачи, связанные с положительными и отрицательными рациональными числами в любой форме (целые числа, дроби и десятичные дроби), стратегически используя инструменты. Применяйте свойства операций как стратегии для расчетов с числами в любой форме; конвертировать между формами по мере необходимости; и оценить обоснованность ответов, используя умственные вычисления и стратегии оценки. Например: если женщина, зарабатывающая 25 долларов в час, получает повышение на 10%, она будет получать дополнительную 1/10 своей зарплаты в час, или 2,50 доллара, за новую зарплату в 27,50 долларов. Если вы хотите разместить полотенцесушитель 93/4 дюйма длиной в центре двери шириной 27 1/2 дюйма, вам нужно будет разместить планку примерно в 9 дюймах от каждого края; эту оценку можно использовать в качестве проверки точного вычисления.
Применяйте свойства операций как стратегии для расчетов с числами в любой форме; конвертировать между формами по мере необходимости; и оценить обоснованность ответов, используя умственные вычисления и стратегии оценки. Например: если женщина, зарабатывающая 25 долларов в час, получает повышение на 10%, она будет получать дополнительную 1/10 своей зарплаты в час, или 2,50 доллара, за новую зарплату в 27,50 долларов. Если вы хотите разместить полотенцесушитель 93/4 дюйма длиной в центре двери шириной 27 1/2 дюйма, вам нужно будет разместить планку примерно в 9 дюймах от каждого края; эту оценку можно использовать в качестве проверки точного вычисления.
Оценка
Абсолютное значение
Рациональные номера
Закругление номеров
Использование рациональных чисел
Советы по оценке и хитростям
Орден операции — BODMAS
Орден операции — PEMDAS
Фракции Depimals и проценты
.0003
7.EE.B.4Используйте переменные для представления величин в реальной или математической задаче и создавайте простые уравнения и неравенства для решения задач, рассуждая о величинах.
а. Решите текстовые задачи, ведущие к уравнениям вида px + q = r и p(x + q) = r, где p, q и r — конкретные рациональные числа. Решите уравнения этих форм бегло. Сравните алгебраическое решение с арифметическим, указав последовательность операций, используемых в каждом подходе. Например, периметр прямоугольника равен 54 см. Его длина составляет 6 см. Какова его ширина?
б. Решите текстовые задачи, ведущие к неравенствам вида px + q > r или px + q < r, где p, q и r — конкретные рациональные числа. Нарисуйте график множества решений неравенства и интерпретируйте его в контексте проблемы. Например: как продавец, вам платят 50 долларов в неделю плюс 3 доллара за продажу. На этой неделе вы хотите, чтобы ваша зарплата была не менее 100 долларов. Напишите неравенство для количества продаж, которое вам нужно сделать, и опишите решения.
Инверсия
Аналогичные термины
Решение уравнений
График неравенства
Решение неравенства
Решение вопросов Word
Введение в алгебру
Введение в неравенство
Баланс при добавлении и подключении
. | Геометрия
| Геометрия
Рисовать, строить и описывать геометрические фигуры и описывать отношения между ними.
7.G.A.1 Решение задач, связанных с чертежами геометрических фигур в масштабе, включая вычисление фактических длин и площадей по чертежу в масштабе и воспроизведение чертежа в масштабе в другом масштабе.
Соотношения
Подобные
Подобные треугольники
Активность: Насколько высоко?
7.Г.А.2 Нарисуйте (от руки, с линейкой и транспортиром и с техникой) геометрические фигуры с заданными условиями. Сосредоточьтесь на построении треугольников по трем мерам углов или сторон, отмечая, когда условия определяют уникальный треугольник, более одного треугольника или отсутствие треугольника.
Градусы
Круговая диаграмма
3 4 5 Треугольник
Использование транспортира
Упражнение: Как высоко?
Интерактивные треугольники
Треугольники, содержащие 180 градусов
Построение треугольника с 3 известными сторонами
7. G.A.3 Опишите двумерные фигуры, которые получаются в результате разрезания трехмерных фигур, таких как плоские сечения прямоугольных призм и прямоугольных пирамид.
G.A.3 Опишите двумерные фигуры, которые получаются в результате разрезания трехмерных фигур, таких как плоские сечения прямоугольных призм и прямоугольных пирамид.
Пирамиды
Поперечные сечения
Призмы с примерами
Упражнение: Исследование твердых тел
Решайте реальные и математические задачи, связанные с измерением угла, площади, площади поверхности и объема.
7.R.B.4 Знать формулы площади и длины окружности и использовать их для решения задач; дать неформальный вывод отношения между длиной окружности и площадью круга.
Пи
Периметр
Калькулятор площади
Площадь круга
Упражнение: Олимпийская легкая атлетика
Упражнение: Найдите приблизительное значение числа Пи
Площадь круга Треугольник Квадрат Прямоугольник Параллелограмм Трапеция Эллипс и сектор
7.RUS5Используйте факты о дополнительных, дополнительных, вертикальных и смежных углах в многошаговой задаче, чтобы написать и решить простые уравнения для неизвестного угла в фигуре.
Градусы
Внешний уголок
Внутренний уголок
Прямые углы
Вертикальные углы
Комплементарные углы
Дополнительные углы
Вертикально противоположные углы
Внешние углы многоугольников
Треугольники содержат 180 градусов
У углы
. Прямая линия Добавить к 180
7.RUS6Решение реальных и математических задач, связанных с площадью, объемом и площадью поверхности двух- и трехмерных объектов, состоящих из треугольников, четырехугольников, многоугольников, кубов и прямых призм.
Заливная жидкость
Площадь калькулятор
Активность: суп банка
Объем кубоидных
Призмы с примерами
Прямоугольные призмы и кубики
Площадь квадратной площади треугольника. Прямоугольная параллелограмма Trapezium ellipsse и сектор
4
карта 77 7. 700044 40004 карка 7 7. 700044 40004. Статистика и вероятность
700044 40004. Статистика и вероятность
Используйте случайную выборку, чтобы делать выводы о населении.
7.SP.A.1 Понимать, что статистику можно использовать для получения информации о населении путем изучения выборки населения; обобщения о совокупности из выборки действительны только в том случае, если выборка репрезентативна для этой совокупности. Поймите, что случайная выборка, как правило, дает репрезентативные выборки и поддерживает достоверные выводы.
Что такое данные?
Вопросы опроса
Как провести опрос
Упражнение: Оценка
Упражнение: Длина листьев
Отображение результатов опроса
7.SP.A.2Используйте данные из случайной выборки, чтобы сделать выводы о совокупности с неизвестной интересующей характеристикой. Создайте несколько выборок (или смоделированных выборок) одинакового размера, чтобы оценить различия в оценках или прогнозах. Например, оцените среднюю длину слова в книге путем случайной выборки слов из книги; предсказать победителя школьных выборов на основе случайно выбранных данных опроса. Оцените, насколько далеко может быть оценка или прогноз.
Оцените, насколько далеко может быть оценка или прогноз.
Вопросы опроса
Как провести опрос
Упражнение: Оценка
Демонстрация результатов опроса
Сделайте неформальные сравнительные выводы о двух популяциях.
7.SP.B.3 Неформально оценить степень визуального перекрытия двух распределений числовых данных с похожими вариациями, измеряя разницу между центрами, выражая ее как кратное мере вариации. Например, средний рост игроков баскетбольной команды на 10 см больше, чем средний рост игроков футбольной команды, что примерно вдвое превышает вариабельность (среднее абсолютное отклонение) в любой из команд; на точечном графике заметно разделение между двумя распределениями высот.
Гистограммы
Построение гистограммы
Среднее значение
Поиск центрального значения
Как вычислить среднее значение
Демонстрация результатов опроса
7.SP.B.4 Используйте меры центра и меры изменчивости для числовых данных из случайных выборок, чтобы сделать неформальные сравнительные выводы о двух совокупностях. Например, решите, длиннее ли слова в главе учебника по естествознанию для седьмого класса, чем слова в главе из учебника по естествознанию для четвертого класса.
Например, решите, длиннее ли слова в главе учебника по естествознанию для седьмого класса, чем слова в главе из учебника по естествознанию для четвертого класса.
Квартили
Диапазон
Среднее значение
Поиск центрального значения
Как найти медианное значение
Как вычислить среднее значение
Как вычислить модальное значение
Исследование случайных процессов и разработка, использование и оценка вероятностных моделей.
7.SP.C.5 Поймите, что вероятность случайного события — это число от 0 до 1, которое выражает вероятность наступления события. Большие числа указывают на большую вероятность. Вероятность, близкая к 0, указывает на маловероятное событие, вероятность около 1/2 указывает на событие, которое не является ни маловероятным, ни вероятным, а вероятность, близкая к 1, указывает на вероятное событие.
Вероятность
Линия вероятности
7.SP.C.6 Аппроксимация вероятности случайного события путем сбора данных о случайном процессе, который его производит, и наблюдения за его долгосрочной относительной частотой, а также предсказание приблизительной относительной частоты с учетом вероятности. Например, подбрасывая числовой куб 600 раз, предскажите, что число 3 или 6 выпадет примерно 200 раз, но, вероятно, не ровно 200 раз.
Например, подбрасывая числовой куб 600 раз, предскажите, что число 3 или 6 выпадет примерно 200 раз, но, вероятно, не ровно 200 раз.
Вероятность
Линия вероятности
Относительная частота
Действие: Оценка
Действие: Случайно или нет?
Упражнение: Игла Бюффона
Упражнение: Бросание монеты на сетку
7.SP.C.7 Разработайте вероятностную модель и используйте ее для определения вероятностей событий. Сравните вероятности из модели с наблюдаемыми частотами; если согласие неудовлетворительное, объясните возможные источники несоответствия.
а. Разработайте единую вероятностную модель, назначив всем исходам равную вероятность, и используйте эту модель для определения вероятностей событий. Например, если из класса случайным образом выбран ученик, найдите вероятность того, что будет выбрана Джейн, и вероятность того, что будет выбрана девочка.
б. Разработайте вероятностную модель (которая может быть неоднородной), наблюдая частоты в данных, полученных в результате случайного процесса. Например, найдите приблизительную вероятность того, что крутящийся пенни упадет решкой вверх или что брошенный бумажный стаканчик упадет открытым концом вниз. Судя по наблюдаемым частотам, результаты для крутящегося пенни кажутся равновероятными?
Например, найдите приблизительную вероятность того, что крутящийся пенни упадет решкой вверх или что брошенный бумажный стаканчик упадет открытым концом вниз. Судя по наблюдаемым частотам, результаты для крутящегося пенни кажутся равновероятными?
Вероятность
Линия вероятности
Пазл с мешочками шариков
Условная вероятность
Упражнение: Игла Бюффона
Диаграммы деревьев вероятностей
Спиннер — ваше лицо, принимающее решения
Упражнение: Бросание монеты на сетку
7.SP.C.8 Найдите вероятности составных событий, используя упорядоченные списки, таблицы, древовидные диаграммы и моделирование.
а. Поймите, что, как и в случае с простыми событиями, вероятность составного события представляет собой долю исходов в выборочном пространстве, для которого происходит составное событие.
б. Представляйте примеры пространств для составных событий, используя такие методы, как организованные списки, таблицы и древовидные диаграммы. Для события, описанного повседневным языком (например, «выпадение двойных шестерок»), определите исходы в выборочном пространстве, составляющие событие.
Для события, описанного повседневным языком (например, «выпадение двойных шестерок»), определите исходы в выборочном пространстве, составляющие событие.
с. Разработайте и используйте симуляцию для генерации частот для составных событий. Например, используйте случайные числа в качестве инструмента моделирования для аппроксимации ответа на вопрос: если 40% доноров имеют кровь группы А, какова вероятность того, что потребуется не менее 4 доноров, чтобы найти одного с кровью группы А?
Вероятность
Мешки с шариками
Условная вероятность
Диаграммы деревьев вероятностей
Вероятность: типы событий
Вероятность: независимые события
Стандарты Toolkit »Математика 7 Стандарты общего ядра
K123
4567
89-12
класс 7 PDF
. развитие понимания и применение пропорциональных отношений; (2) развитие понимания операций с рациональными числами и работы с выражениями и линейными уравнениями; (3) решение задач, связанных с чертежами в масштабе и неформальными геометрическими построениями, а также работа с двух- и трехмерными формами для решения задач, связанных с площадью, площадью поверхности и объемом; и (4) делать выводы о популяциях на основе выборок.
1. Учащиеся расширяют свое понимание соотношений и развивают понимание пропорциональности для решения одношаговых и многошаговых задач. Учащиеся используют свое понимание соотношений и пропорциональности для решения самых разных задач на проценты, в том числе связанных со скидками, процентами, налогами, чаевыми и процентным увеличением или уменьшением. Учащиеся решают задачи о чертежах в масштабе, связывая соответствующие длины между объектами или используя тот факт, что отношения длин внутри объекта сохраняются в подобных объектах. Учащиеся изображают пропорциональные отношения и неофициально понимают единичную норму как меру крутизны связанной линии, называемой наклоном. Они отличают пропорциональные отношения от других отношений.
2. Учащиеся развивают единое понимание числа, распознавая дроби, десятичные дроби (которые имеют конечное или повторяющееся десятичное представление) и проценты как различные представления рациональных чисел. Учащиеся распространяют сложение, вычитание, умножение и деление на все рациональные числа, сохраняя свойства операций и отношения между сложением и вычитанием, а также умножением и делением. Применяя эти свойства и рассматривая отрицательные числа с точки зрения повседневного контекста (например, суммы долга или температуры ниже нуля), учащиеся объясняют и интерпретируют правила сложения, вычитания, умножения и деления с отрицательными числами. Они используют арифметику рациональных чисел, формулируя выражения и уравнения с одной переменной и используя эти уравнения для решения задач.
Применяя эти свойства и рассматривая отрицательные числа с точки зрения повседневного контекста (например, суммы долга или температуры ниже нуля), учащиеся объясняют и интерпретируют правила сложения, вычитания, умножения и деления с отрицательными числами. Они используют арифметику рациональных чисел, формулируя выражения и уравнения с одной переменной и используя эти уравнения для решения задач.
3. Учащиеся продолжают работу с площадью с 6 класса, решая задачи на площадь и длину окружности и площадь поверхности трехмерных объектов. При подготовке к работе на конгруэнтность и подобие в 8 классе рассуждают об отношениях между двухмерными фигурами, используя чертежи в масштабе и неформальные геометрические построения, знакомятся с отношениями между углами, образованными пересекающимися линиями. Учащиеся работают с трехмерными фигурами, связывая их с двухмерными фигурами, рассматривая поперечные сечения. Они решают реальные и математические задачи, связанные с площадью, площадью поверхности и объемом двух- и трехмерных объектов, состоящих из треугольников, четырехугольников, многоугольников, кубов и прямых призм.
4. Учащиеся опираются на свою предыдущую работу с отдельными распределениями данных, чтобы сравнить два распределения данных и ответить на вопросы о различиях между группами населения. Они начинают неформальную работу со случайной выборкой для создания наборов данных и узнают о важности репрезентативных выборок для получения выводов.
| Домен | Кластер | Код | Единый основной государственный стандарт |
|---|---|---|---|
| Соотношения и отношения пропорциональности | Анализируйте пропорциональные отношения и используйте их для решения реальных и математических задач. | 7.РП.1 | Расчет удельных расходов, связанных с отношениями дробей, включая отношения длин, площадей и других величин, измеренных в одинаковых или разных единицах. Например, если человек проходит 1/2 мили каждые 1/4 часа, рассчитайте удельную скорость как комплексную дробь (1/2)/(1/4) мили в час, что эквивалентно 2 милям в час. |
| 7.РП.2 | Распознавать и изображать пропорциональные отношения между величинами. а. Определите, находятся ли две величины в пропорциональном отношении, например, проверив эквивалентные отношения в таблице или нарисовав график на координатной плоскости и наблюдая, является ли график прямой линией, проходящей через начало координат. б. Определите константу пропорциональности (единичную норму) в таблицах, графиках, уравнениях, схемах и словесных описаниях пропорциональных отношений. в. Представьте пропорциональные отношения уравнениями. Например, если общая стоимость t пропорциональна количеству n товаров, купленных по постоянной цене p, , соотношение между общей стоимостью и количеством товаров может быть выражено как t = pn. д. Объясните, что означает точка (x, y) на графике пропорциональной зависимости с точки зрения ситуации, обратив особое внимание на точки (0, 0) и (1, r) , где r — единичная ставка. | ||
7. RP.3 RP.3 | Используйте отношения пропорциональности для решения многошаговых задач на соотношение и проценты. Примеры: простые проценты, налоги, надбавки и уценки, чаевые и комиссионные, сборы, процентное увеличение и уменьшение, процентная ошибка. | ||
| Система счисления | Применение и расширение предыдущего понимания операций с дробями для сложения, вычитания, умножения и деления рациональных чисел. | 7.НС.1 | Применение и расширение предыдущего понимания сложения и вычитания для сложения и вычитания рациональных чисел; представляют сложение и вычитание на горизонтальной или вертикальной диаграмме с числовыми линиями. а. Опишите ситуации, в которых противоположные величины объединяются, чтобы получить 0. Например, атом водорода имеет нулевой заряд, потому что две его составляющие заряжены противоположно. б. Под p + q понимается число, расположенное на расстоянии |q| от p в положительном или отрицательном направлении в зависимости от того, является ли q положительным или отрицательным.  Показать, что число и его противоположность имеют сумму 0 (являются аддитивными инверсиями). Интерпретируйте суммы рациональных чисел, описывая контексты реального мира. с. Поймите вычитание рациональных чисел как добавление обратного аддитивного, p — q = p + (-q). Покажите, что расстояние между двумя рациональными числами на числовая линия представляет собой абсолютное значение их разности, и этот принцип применяется в реальных контекстах. д. Применяйте свойства операций как стратегии сложения и вычитания рациональных чисел. |
| 7.НС.2 | Применять и расширять предыдущие знания об умножении и делении, а также о дробях для умножения и деления рациональных чисел. а. Поймите, что умножение распространяется с дробей на рациональные числа, требуя, чтобы операции продолжали удовлетворять свойствам операций, особенно распределительное свойство, приводящее к таким произведениям, как (–1)(–1) = 1, и к правилам умножения чисел со знаком.  Интерпретируйте продукты Интерпретируйте продукты рациональных чисел, описывая контексты реального мира. б. Поймите, что целые числа можно делить при условии, что делитель не равен нулю, и каждое частное целых чисел (с ненулевым делителем) является рациональным числом. Если p и q целые числа, то –(p/q) = (–p)/q = p/(–q). Интерпретируйте частные рациональных чисел, описывая контексты реального мира. с. Применяйте свойства операций как стратегии умножения и деления рациональных чисел. д. Преобразование рационального числа в десятичное с использованием длинного деления; знать, что десятичная форма рационального числа оканчивается на 0 или в итоге повторяется | ||
| 7.НС.3 | Решите реальные и математические задачи, связанные с четырьмя операциями с рациональными числами. (Вычисления с рациональными числами распространяют правила обращения с дробями на сложные дроби.) | ||
| Выражения и уравнения | Используйте свойства операций для создания эквивалентных выражений. | 7.EE.1 | Применение свойств операций в качестве стратегий для сложения, вычитания, факторизации и расширения линейных выражений с рациональными коэффициентами. |
| 7.EE.2 | Поймите, что переписывание выражения в разных формах в контексте задачи может пролить свет на проблему и на то, как связаны в ней величины. Например, a + 0,05a = 1,05a означает, что «увеличение на 5%» равнозначно «умножению на 1,05». | ||
| Решайте реальные и математические задачи, используя числовые и алгебраические выражения и уравнения. | 7.EE.3 | Решайте многоэтапные задачи из реальной жизни и математические задачи, связанные с положительными и отрицательными рациональными числами в любой форме (целые числа, дроби и десятичные дроби), стратегически используя инструменты. Применяйте свойства операций как стратегии для расчетов с числами в любой форме; конвертировать между формами по мере необходимости; и оценить обоснованность ответов, используя умственные вычисления и стратегии оценки. Например: если женщина, зарабатывающая 25 долларов в час, получает повышение на 10%, она будет получать дополнительную 1/10 своей зарплаты в час, или 2,50 доллара, за новую зарплату в 27,50 долларов. Если вы хотите разместить полотенцесушитель 93/4 дюйма длиной в центре двери шириной 27 1/2 дюйма, вам нужно будет разместить планку примерно в 9 дюймах от каждого края; эту оценку можно использовать в качестве проверки точного вычисления. Например: если женщина, зарабатывающая 25 долларов в час, получает повышение на 10%, она будет получать дополнительную 1/10 своей зарплаты в час, или 2,50 доллара, за новую зарплату в 27,50 долларов. Если вы хотите разместить полотенцесушитель 93/4 дюйма длиной в центре двери шириной 27 1/2 дюйма, вам нужно будет разместить планку примерно в 9 дюймах от каждого края; эту оценку можно использовать в качестве проверки точного вычисления. | |
| 7.EE.4 | Используйте переменные для представления величин в реальной или математической задаче и создавайте простые уравнения и неравенства для решения задач, рассуждая о величинах. а. Решите текстовые задачи, ведущие к уравнениям вида px + q = r и p(x + q) = r, где p, q и r — конкретные рациональные числа. Решите уравнения этих формируется плавно. Сравните алгебраическое решение с арифметическим, указав последовательность операций, используемых в каждом подходе. Например, периметр прямоугольника равен 54 см.  Его длина составляет 6 см. Какова его ширина? Его длина составляет 6 см. Какова его ширина? б. Решайте текстовые задачи, приводящие к неравенствам вида px + q > r или px + q неравенству, и интерпретируйте его в контексте задачи. Например: как продавец, вам платят 50 долларов в неделю плюс 3 доллара за продажу. На этой неделе вы хотите, чтобы ваша зарплата составляла не менее 100 долларов. Напишите неравенство для количества продаж, которое вам нужно сделать, и опишите решения. | ||
| Геометрия | Рисовать, строить и описывать геометрические фигуры и описывать отношения между ними. | 7.G.1 | Решение задач, связанных с чертежами геометрических фигур в масштабе, включая вычисление фактических длин и площадей на основе чертежа в масштабе и воспроизведение чертежа в масштабе в другом масштабе. |
| 7.G.2 | Чертить (от руки, с линейкой и транспортиром и с техникой) геометрические фигуры с заданными условиями. Сосредоточьтесь на построении треугольников по трем мерам углов или сторон, отмечая, когда условия определяют уникальный треугольник, более одного треугольника или отсутствие треугольника.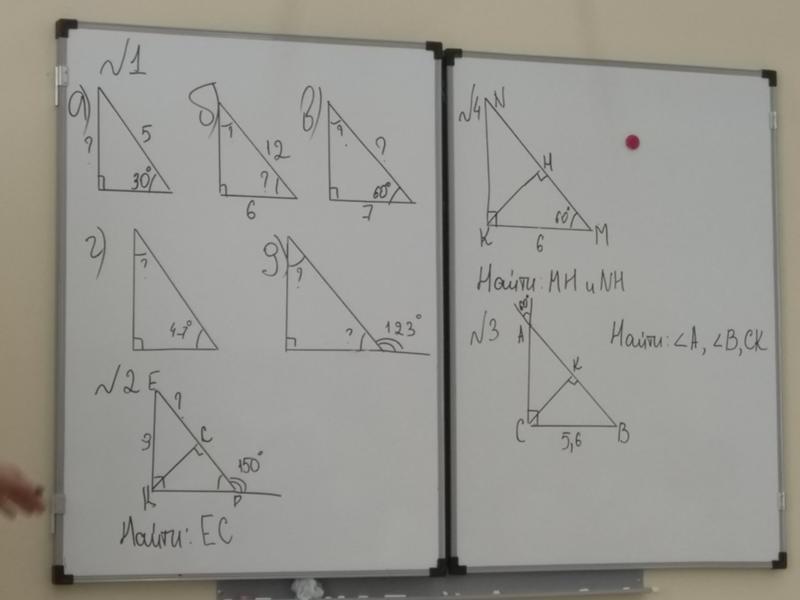 | ||
| 7.G.3 | Опишите двумерные фигуры, которые получаются в результате разрезания трехмерных фигур, таких как плоские сечения прямоугольных призм и прямоугольных пирамид. | ||
| Решайте реальные и математические задачи, связанные с измерением угла, площади, площади поверхности и объема. | 7.G.4 | Знать формулы площади и длины окружности и использовать их для решения задач; дать неформальный вывод отношения между длиной окружности и площадью круга. | |
| 7.G.5 | Используйте факты о дополнительных, дополнительных, вертикальных и смежных углах в многоэтапной задаче, чтобы написать и решить простые уравнения для неизвестного угла в фигуре. | ||
| 7.G.6 | Решайте реальные и математические задачи, связанные с площадью, объемом и площадью поверхности двух- и трехмерных объектов, состоящих из треугольников, четырехугольников, многоугольников, кубов и прямых призм.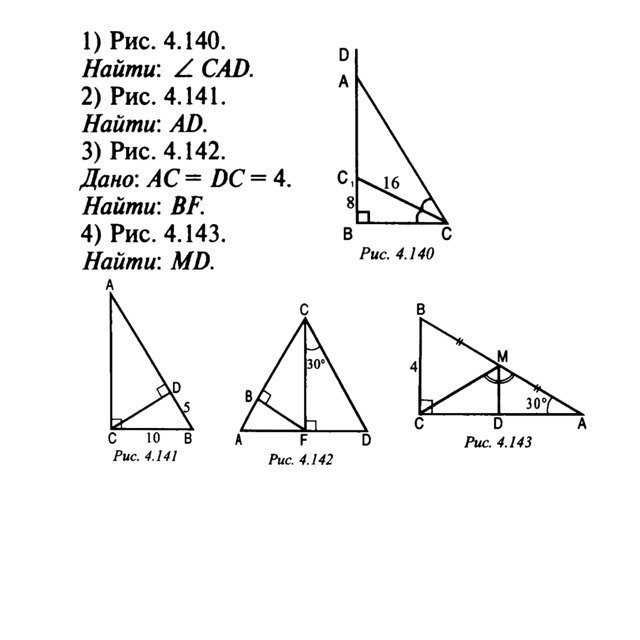 | ||
| Статистика и вероятность | Используйте случайную выборку, чтобы делать выводы о населении. | 7.СП.1 | Понимать, что статистику можно использовать для получения информации о населении путем изучения выборки населения; обобщения о совокупности из выборки действительны только в том случае, если выборка репрезентативна для этой совокупности. Поймите, что случайная выборка, как правило, дает репрезентативные выборки и поддерживает достоверные выводы. |
| 7.СП.2 | Используйте данные из случайной выборки, чтобы сделать выводы о совокупности с неизвестной интересующей характеристикой. Создайте несколько выборок (или смоделированных выборок) одинакового размера, чтобы оценить различия в оценках или прогнозах. Например, оцените среднюю длину слова в книге путем случайной выборки слов из книги; предсказать победителя школьных выборов на основе случайно выбранных данных опроса. Оцените, насколько далеко может быть оценка или прогноз. Оцените, насколько далеко может быть оценка или прогноз. | ||
| Сделайте неформальные сравнительные выводы о двух популяциях. | 7.СП.3 | Неформально оценить степень визуального перекрытия двух распределений числовых данных с похожими вариациями, измеряя разницу между центрами, выражая ее как кратное мере вариации. Например, средний рост игроков баскетбольной команды на 10 см больше, чем средний рост игроков футбольной команды, что примерно вдвое превышает вариабельность (среднее абсолютное отклонение) в любой из команд; на точечном графике заметно разделение между двумя распределениями высот. | |
| 7.СП.4 | Используйте меры центра и меры изменчивости для числовых данных из случайных выборок, чтобы сделать неформальные сравнительные выводы о двух популяциях. Например, решите, длиннее ли слова в главе учебника по естествознанию для седьмого класса, чем слова в главе из учебника по естествознанию для четвертого класса. | ||
| Исследование случайных процессов и разработка, использование и оценка вероятностных моделей. | 7.СП.5 | Поймите, что вероятность случайного события — это число от 0 до 1, которое выражает вероятность возникновения события. Большие числа указывают на большую вероятность. Вероятность, близкая к 0, указывает на маловероятное событие, вероятность около 1/2 указывает на событие, которое не является ни маловероятным, ни вероятным, а вероятность, близкая к 1, указывает на вероятное событие. | |
| 7.СП.6 | Аппроксимируйте вероятность случайного события, собирая данные о случайном процессе, который его производит, и наблюдая его долгосрочную относительную частоту, и предскажите приблизительную относительную частоту с учетом вероятности. Например, подбрасывая числовой куб 600 раз, предскажите, что число 3 или 6 выпадет примерно 200 раз, но, вероятно, не ровно 200 раз. | ||
7.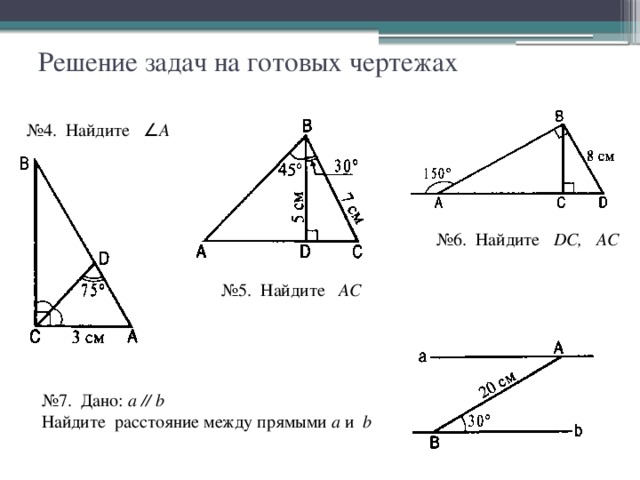 СП.7 СП.7 | Разработайте вероятностную модель и используйте ее для определения вероятностей событий. Сравните вероятности из модели с наблюдаемыми частотами; если согласие неудовлетворительное, объясните возможные источники несоответствия. а. Разработайте единую вероятностную модель, назначив всем исходам равную вероятность, и используйте эту модель для определения вероятностей событий. Например, , если учащийся выбран случайным образом из класса, найдите вероятность того, что будет выбрана Джейн, и вероятность того, что будет выбрана девочка. б. Разработайте вероятностную модель (которая может быть неоднородной), наблюдая частоты в данных, полученных в результате случайного процесса. Например, найдите приблизительную вероятность того, что крутящийся пенни упадет решкой вверх или что брошенный бумажный стаканчик упадет открытым концом вниз. Судя по наблюдаемым частотам, результаты вращения пенни кажутся равновероятными? | ||
7. |

 Равные по величине углы отмечайте одинаковыми дужками: одинарными, двойными, волнистыми. Углы разных величин выделяйте разными дужками.
Равные по величине углы отмечайте одинаковыми дужками: одинарными, двойными, волнистыми. Углы разных величин выделяйте разными дужками.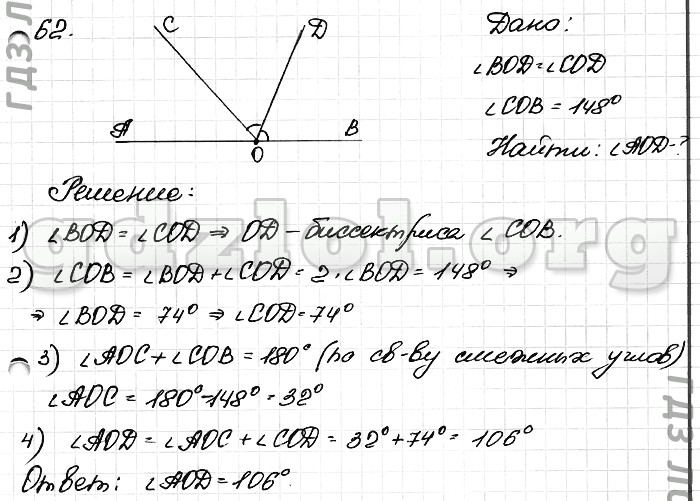
 В дальнейшем для обозначения не пересекающихся прямых мы будем использовать знак параллельности ||.
В дальнейшем для обозначения не пересекающихся прямых мы будем использовать знак параллельности ||.