Поиск материала «Алгебра, 7 класс, Решение задач, Луканов Н.Д., 2005» для чтения, скачивания и покупки
Ниже показаны результаты поиска поисковой системы Яндекс. В результатах могут быть показаны как эта книга, так и похожие на нее по названию или автору.
Search results:
- Читать ГДЗ для 7 классов по алгебре под авторством Луканова…
Размер книги (учебника): 6,60 мб. Количество страниц: 288. Автор (-ы) книги, решебника, учебника: Луканов Н.Д . Предмет : алгебра. Класс: 7. Как только обычная математика разделяется на алгебру и геометрию, школьники начинают испытывать трудности с решением задач по этим двум дисциплинам. Чтобы облегчить жизнь школярам, мы предлагаем скачать специальное издание, призванное посодействовать в решении задач по алгебре в 7 классе. Пособие было составлено Лукановым Н.Д. и вышло в 2005 году.
books.gdz-online.ws
- Луканов Н.
 Д. (авт.) Решение задач из учебника Ю.Н. Макарычева…
Д. (авт.) Решение задач из учебника Ю.Н. Макарычева…Издание карманного формата. В пособии решены, и в большинстве случаев подробно разобраны задачи и упражнения из учебника «Алгебра.
Данный учебник предназначен для углубленного изучения алгебры в 7 классе и входит в комплект из трех книг: «Алгебра-7», «Алгебра-8» и «Алгебра-9». Его содержание полностью соответствует современным образовательным стандартам, а особенностями являются расширение и углубление традиционных учебных тем за счет теоретико-множественной, вероятностно
www.studmed.ru
-
Купить эту книгу
- Канцтовары
Канцтовары: бумага, ручки, карандаши, тетради. Ранцы, рюкзаки, сумки. И многое другое.
my-shop.ru
- Учебники по алгебре 7 класс скачать в pdf бесплатно
Дидактические материалы по алгебре для 7 класса — Зив Б.
 Г., Гольдич В.А. cкачать в PDF.
Г., Гольдич В.А. cкачать в PDF.Рабочая тетрадь по алгебре: 7 класс: к учебнику Мордковича А.Г. — Ключникова Е.М., Комиссарова И.В. cкачать в PDF.
reshaemvpr.ru
- 1-11klasses | Учебники по алгебре 7 класс скачать в pdf бесплатно
На нашем сайте 1-11klasses вы имеете возможность читать либо скачать самые новые и актуальные Учебники по алгебре 7 класс скачать в pdf бесплатно а.
1-11klasses.ru
- Учебники по алгебре 7 класс скачать в pdf бесплатно
Решение заданий ЕГЭ 2021. Русский язык.
Алгебра. 7 класс. Учебник — Никольский С.М., Потапов М.К. cкачать в PDF. 10 ALGEBRA_U7.
Алгебра. 7 класс — Кузнецова Е.П., Муравьева Г.Л. и др. cкачать в PDF. 12 ALGEBRA_U7.
fizikadlyvas.net
- Учебник по алгебре
Призвана возможность скачать учебник по алгебре 7 класс и в спокойной домашней обстановке заучить сложные алгебраические законы и принципы.

11klasov.net
- Алгебра. 7 класс. Учебник. Углубленный уровень — Макарычев…
Данное учебное пособие предназначено для углублённого изучения алгебры в 7 классе. Это первое пособие завершённой линии учебных пособий по алгебре для 7—9 классов, подготовленных в соответствии со всеми требованиями Федерального государственного образовательного стандарта основного общего образования.
11klasov.net
- Алгебра 7 класс Учебник Никольский Потапов | Текст из книги
Пояснение: Для скачивания книги (с Гугл Диска), нажми сверху справа — СТРЕЛКА В ПРЯМОУГОЛЬНИКЕ . Затем в новом окне сверху справа — СТРЕЛКА ВНИЗ .
Тем самым он решал не одну задачу с конкретными данными, а целый класс однотипных задач, отличающихся только числовыми значениями величин. Решение таких и более сложных задач потребовало развития буквенного счисления — правил действий над буквенными выражениями (одночленами, многочленами, алгебраическими дробями), обозначгшшими первоначально числа.

uchebniki-shkola.com
- Сборник задач по Алгебре (Часть 1) 6-7 классы 1958
Нестандартные задачи по алгебре (Бартенев) 1976 год -… Сборник задач по геометрии Планиметрия ДЛЯ 6—7 КЛАССОВ (Никитин, Маслова) 1959 год скачать Советский учебник. Сборник задач по геометрии Планиметрия ДЛЯ 6—7 КЛАССОВ… Учебник немецкого языка 6 класс (Бим, Голотина) 1987 год — старые учебники.
sovietime.ru
- Алгебра 7 класс Углубленный уровень Ю.Н. Макарычев…
Пособие предназначено для углубленного изучения алгебры в 7 классе. Это первое пособие завершенной линии учебных пособий по алгебре для 7-9 класса, подготовленных в соответствии со всеми требованиями ФГОС основного общего образования. Особенностями данного пособия является расширение и углубление традиционных учебных тем за счет теоретико-множественных, вероятностно-статистических и историко-культурных линий.

www.math-express.ru
- Учебники по математике 7 класс — Математика — экспресс
На странице собраны учебники математики, алгебры и геометрии для 7 класса, используемые в школьном курсе в настоящее время. Вы можете посмотреть информацию по каждому из представленных учебников математики для 7 класса, читать нужную книгу прямо на сайте или скачать нужный учебник бесплатно.
www.math-express.ru
- Алгебра. 7 класс. Задачник — Мордкович А.Г.
Задачник содержит разнообразные системы упражнений, тщательно выстроенные на четырех уровнях — по степени нарастания трудности. В задачнике учтен опыт работы учителей. Рубрика: Алгебра / 7 класс. Автор: Мордкович А.Г. Год: 2009,2013.
Задачник для 10-11 классов — Шабунин М.И. и др. Алгебра. 8 класс. Задачник — Звавич Л.И., Рязановский А.Р.
11klasov.
 net
net - Учебник Алгебра 7 класс Колягин Ткачева | Текст из
Пояснение: Для скачивания книги (с Гугл Диска), нажми сверху справа — СТРЕЛКА В ПРЯМОУГОЛЬНИКЕ . Затем в новом окне сверху справа — СТРЕЛКА ВНИЗ . Для чтения — просто листай колесиком страницы вверх и вниз.
В сохранившихся книгах Диофанта содержится 189 задач с решениями. Если в первой из сохранившихся книг рассмотрены задачи, приводящиеся к линейным и квадратным уравнениям (квадратные уравнения вы будете решать в 8 классе), то в остальных пяти книгах рассматривались неопределённые уравнения.
uchebniki-shkola.com
- Алгебра 7 класс Учебник Макарычев Миндюк | Текст из книги
ISBN 978-5-346-02329-6 Данный учебник предназначен для углублённого изучения алгебры в 7-м классе и входит в комплект из трёх книг: «Алгебра-7», «Алгебра-8» и «Алгебра-9».
Его содержание полностью соответствует современным образовательным стандартам, а особенностями являются расширение и углубление традиционных учебных тем за счёт теоретико-множественной, вероятностно-статистической и историко-культурной линий.
uchebniki-shkola.com
- Алгебра 7 класс Учебник Макарычев Миндюк углубленное изучение
Вы начинаете изучать новый учебный предмет — алгебру, являющуюся одним из важнейших разделов математики. Алгебра возникла под влиянием нужд общественной практики, в результате поисков общих приёмов решения разнообразных задач. Алгебра используется в современном мире очень широко: в физике, биологии, экономике, информатике, архитектуре и др. Изучая математику в 5 и 6 классах, вы научились выполнять различные действия с целыми числами и дробями, находить корни уравнений, решать текстовые задачи.
uchebnik-skachatj-besplatno.com
- Учебники по алгебре 7 класс скачать в pdf бесплатно1-11klasses
Задание 1.
 Простейшие текстовые задачи. Задание 2. Чтение графиков и диаграмм.
Простейшие текстовые задачи. Задание 2. Чтение графиков и диаграмм.Алгебра. Дидактические материалы. 7 класс — Евстафьева Л.П., Карп А.П. cкачать в PDF.
Дидактические материалы по алгебре для 7 класса — Зив Б.Г., Гольдич В.А. cкачать в PDF.
textbooks1-11.ru
- Сборник задач 7 класс
Сборники задач по физике (9-11 кл). Презентация к исследовательской работе » Сборник задач по математике на основе материалов о национальном парке «Алханай»». Сборник задач по математике на развитие функциональной грамотности (Задачи повышенной сложности, включая задачи для 5-6 класса).
multiurok.ru - Алгебра. 7 класс | Скачать | Учебники.by
7 класс. Учебное пособие для 7 класса учреждений общего среднего образования с русским языком обучения. Пособие выпущено издательством «Народная асвета».
 Допущено Министерством образования Республики Беларусь.
Допущено Министерством образования Республики Беларусь.Воспроизведение материалов сайта, в том числе материалов для скачивания и изображений обложек пособий, с целью извлечения прибыли (в коммерческих или рекламных целях) без разрешения правообладателей ЗАПРЕЩЕНО.
uchebniki.by
- Алгебра. 7 класс. Углубленный уровень. Макарычев…
Дорогие семиклассники! Вы приступаете к изучению нового для вас школьного предмета – алгебры. Этот раздел математики появился много веков назад как наука о решении уравнений. Первым сочинением, посвящённым вопросам алгебры, считают книгу среднеазиатского учёного. В переводе с арабского название этого трактата звучит так: «Книга о восстановлении и противопоставлении». «Восстановление» по-арабски – аль-джебр. От этого слова и произошло название алгебра.
uchebniksonline.ru
- Книжки по Алгебре 7 класс
Сайт учебники и ГДЗ по алгебре для 7 класса поможет вам с выполнением упражнений, задач и даже домашнего задания!
Не всегда всем ученикам хватает учебников, эту проблему могут решить электронные ученики на нашем сайте.
 Помимо этого, электронные учебники очень удобны для того, чтобы ими пользоваться, нужен только интернет и телефон. А если вы хотите скачать книги совершенно бесплатно, то можете так же пользоваться файлом и без подключения к сети.
Помимо этого, электронные учебники очень удобны для того, чтобы ими пользоваться, нужен только интернет и телефон. А если вы хотите скачать книги совершенно бесплатно, то можете так же пользоваться файлом и без подключения к сети.books.gdz-online.ws
- Макарычев, Миндюк учебник углубленный уровень 7 класс…
Автор: Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков. Предмет (категория): Алгебра углубленный уровень. Класс: 7. Читать онлайн: Да. Скачать бесплатно: Да. Формат книги: jpg. Размер книги/ГДЗ: 23,7 Мб.
Читать онлайн или скачать учебник по алгебре углубленный уровень для 7 класса Макарычева 2018 года
books.gdz-online.ws
- Алгебра 7 Мордкович УЧЕБНИК 2019-2021 | 7 класс Онлайн
Алгебра 7 класс Мордкович Ознакомительная версия с цитатами из учебника для принятия решения о покупке книги: Алгебра.
 7 класс. Учебник для общеобразовательных учреждений.
7 класс. Учебник для общеобразовательных учреждений.xn--7-8sb3ae5aa.xn--p1ai
- ГДЗ (решебники) для учебников 7 класса по алгебре: решения…
Столкнулись с задачей, для которой никак не можете найти решение? Откройте ГДЗ, найдите похожее задание, посмотрите, по какому алгоритму его делали, какие формулы использовали. А теперь закройте наш сайт и попробуйте решить свой пример тем же способом. Вышло – сверьте ответы. При таком подходе ГДЗ к учебнику за 7 класс – это то, что поможет чувствовать себя на уроке более уверенно, а значит и проявлять более активно. Зная, что ты все сделал, как надо, можно смело поднимать руку, вызываться к доске и получать высшие отметки!
Reshalka.com
- Алгебра 7 Мерзляк Поляков (угл.) | 7 класс Онлайн
Графический метод решения системы двух линейных уравнений с двумя переменными § 31 Решение систем линейных уравнений методом подстановки § 32 Решение систем линейных уравнений методом сложения § 33 Решение задач с помощью систем линейных уравнений Итоги главы 4.

Вы смотрели «Алгебра 7 Мерзляк Поляков (угл.)» (цитаты из пособия). Учебник предназначен для углублённого изучения алгебры в 7 классе и входит в комплект учебников: «Алгебра.
xn--7-8sb3ae5aa.xn--p1ai
- Ю. Н. Макарычев H. I. Миндюк К. И. Нешков АЛГЕБРА У
К. И. Нешков. АЛГЕБРА Учебник. Ю. Н. Макарычев. Н. Г. Миндюк. К. И. Нешков. И. Е. Феоктистов. Алгебра Учебник. для учащихся общеобразовательных учреждений. 73-е издание, стереотипное.
Мнемозина, 2013. ISBN 978-5-346-02329-6. Данный учебник предназначен для углублённого изучения алгебры в 7-м классе и входит в комплект из трёх книг. Ero содержание полностью соответствует современным образовательным стандартам
ege-ok.ru
- ФГОС Задачник Часть 2 ЗАДАЧНИК учащихся вбщео
А. Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина,, E. E. Тульчинская. Алгебра. 7 класс. В 2 ч. Ч. 2. Задачник для учащихся обще- A45 образовательных учреждений / [А.
 Г. Мордкович и др.]. ред. А. Г. Мордковича.
Г. Мордкович и др.]. ред. А. Г. Мордковича.ege-ok.ru
- Алгебра. 7 класс. Дидактические материалы к учебнику…
Дидактические материалы предназначены для проверки знаний учащихся 7-го класса с углубленным изучением математики. Пособие содержит комментарии для учителя и примерное поурочное планирование.
Тексты самостоятельных, контрольных и тестовых работ даны в соответствии с учебником Ю. Н. Макарычева, Н. Г. Миндюк, К. Н. Нешкова, И. Е. Феоктистова Алгебра. 7 класс. Задания могут быть использованы педагогами для составления различных видов проверочных работ для школьников, изучающих алгебру по учебникам других авторов.
11klasov.net
- Алгебра 7 класс Учебник Макарычев Миндюк углубленное изучение
Пояснение: Для скачивания книги (с Гугл Диска), нажми сверху справа — СТРЕЛКА В ПРЯМОУГОЛЬНИКЕ .
 Затем в новом окне сверху справа — СТРЕЛКА ВНИЗ . Для чтения — просто листай колесиком страницы вверх и вниз.
Затем в новом окне сверху справа — СТРЕЛКА ВНИЗ . Для чтения — просто листай колесиком страницы вверх и вниз.Алгебра возникла под влиянием нужд общественной практики, в результате поисков общих приёмов решения разнообразных задач. Алгебра используется в современном мире очень широко: в физике, биологии, экономике, информатике, архитектуре и др.
uchebniki-shkola.com
- Скачать бесплатно Алгебра. 7 класс. Учебник. Углубленный…
Данное учебное пособие предназначено для углублённого изучения алгебры в 7 классе. Это первое пособие завершённой линии учебных пособий по алгебре для 7—9 классов, подготовленных в соответствии со всеми требованиями Федерального государственного образовательного стандарта основного общего образования.
fizikadlyvas.net
- Учебник Алгебра 7 класс Мерзляк Полонский Якир
Алгоритм успеха ФГОС Москва Издательский центр «Вентана-Граф» 2015 ББК 22.
 141я721 М52 Учебник включён в федеральный перечень Мерзляк А.Г. М52 Алгебра : 7 класс : учебник для учащихся общеобразовательных организаций / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир.
141я721 М52 Учебник включён в федеральный перечень Мерзляк А.Г. М52 Алгебра : 7 класс : учебник для учащихся общеобразовательных организаций / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир.ISBN 978-5-S60-05509-9 Учебник предназначен для изучения алгебры в 7 классе обще-обра.зовательных организаций. В нём предусмотрена уровневая дифференциация, позволяющая формировать у школьников познавательный интерес к алгебре.
uchebniki-shkola.com
- Сборник задач по алгебре. 7 класс (А. Н. Рурукин) — скачать…
Сборник задач по алгебре. 7 классА. Н. Рурукин. Скачать. Бумажный вариант.
Еще книги этого автора. Поурочные разработки по математике. 5 класс (К УМК Г.В. Дорофеева и др.
Поурочные разработки по алгебре и началам анализа. 10 класс (к УМК А. Г. Мордковича и др.
child-class.ru
- Учебник по алгебре 7 класс / Макарычев
8.
 Решение задач с помощью уравнений. § 4. Статистические характеристики. 9. Среднее арифметическое, размах и мода.
Решение задач с помощью уравнений. § 4. Статистические характеристики. 9. Среднее арифметическое, размах и мода.45. Решение задач с помощью систем уравнений. 46. Линейные неравенства с двумя переменными и их системы. Дополнительные упражнения к главе VI. Задачи повышенной трудности. Как появилась алгебра. Сведения из курса математики 5-6 классов.
tepka.ru
На данной странице Вы можете найти лучшие результаты поиска для чтения, скачивания и покупки на интернет сайтах материалов, документов, бумажных и электронных книг и файлов похожих на материал «Алгебра, 7 класс, Решение задач, Луканов Н.Д., 2005»
Для формирования результатов поиска документов использован сервис Яндекс.XML.
Нашлось 16 млн ответов. Показаны первые 32 результата(ов).
Дата генерации страницы:
ГДЗ по алгебре. 7 класс. Морозов А.В. К учебнику по алгебре за 7 класс.
 Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. 2003
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. 2003Название: ГДЗ по алгебре. 7 класс. К учебнику по алгебре за 7 класс.
Автор: Морозов А.В., Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
2003
В пособии решены и в большинстве случаев подробно разобраны задачи и упражнения из учебников «Алгебра. 7 класс: учебник для общеобразовательных учреждений».
Пособие адресовано родителям, которые смогут проконтролировать правильность решения, а в случае необходимости помочь детям в выполнении домашней работы по алгебре.
Числовые выражения
№1. а) 6,965 + 23,3 = 30,265; б) 76,73+3,27 = 80; в) 50,4 — 6,98 = 43,42; г) 88-9,804 = 78,196; д) 6,5 • 1,22 = 7,93; с) 0,48 • 2,5 = 1,2;
ж) 3,725-3,2 =11,92; з) 0,016 • 0,25 = 0,004; и) 53,4 : 15 = 3,56;
к) 16,94 : 2,8 = 6,05; л) 75 : 1,25 = 60; м) 123,12 : 30,4 = 4,05.
№2. а) 481,92:12-20,16=40,16-20,16=20;
б) 6,05 (53,8+50,2)=6,05-104=629,2; в) 1,08-30,5-9,72:2,4=32,94-4,05=28,89; г) 44,69 + 0,5 • 25,5 : 3,75 = 44,69 + 3,4 = 48,09.
№3. а) 155,5-5,5 • 20,7 = 155,5 — 113,85 =41,65;
б) 85,68 : (4,138 + 2,162) = 85,68 : 6,3 = 13,6;
в) 3,6 : 0,08 + 5,2 • 2,5 = 45 + 13 = 58;
г) (9,885 — 0,365): 1,7 + 4,4 = 9,52: 1,7+4,4 = 5,6+4,4= 10.
Оглавление
ГЛАВА I. ВЫРАЖЕНИЯ. ТОЖДЕСТВА, УРАВНЕНИЯ
§ 1. Выражения 5
1. Числовые выражения 5
2. Выражения с переменными 7
3. Сравнение значений выражений 10
§ 2. Преобразование выражений _ 13
4. Свойства действий над числами 13
5. Тождества. Тождественные преобразования выражений 14
§ 3. Уравнения с одной переменной 17
6. Уравнение и его корни 17
7. Линейное уравнение с одной переменной 19
8. Решение задач с помощью уравнений 21
§ 4. Статические характеристики
9. Среднее арифметическое, размах, мода 24
10. Медиана как статическая характеристика 27
11. Формулы 28
ГЛАВА II. ФУНКЦИИ
§ 5. Функции и их графики 36
12. Что такое функция 36
13. Вычисление значений функции по формуле 37
14.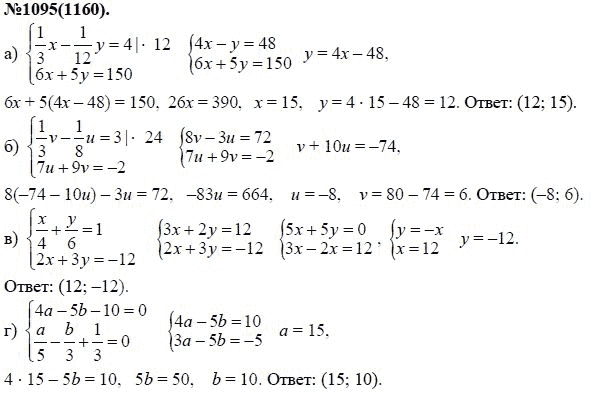 =х1 и у=х3 и их графики 67
=х1 и у=х3 и их графики 67
24. О простых и составных числах 69
Абсолютная и относительная погрешность (с) 70
22. Абсолютная погрешность (с) 70
23. Относительная погрешность (с) 71
Дополнительные упражнения к главе III 72
ГЛАВА IV. МНОГОЧЛЕНЫ
§ 9. Сумма и разность многочленов 79
25. Многочлен и его стандартный вид 79
26 Сложение и вычитание многочленов 80
§ 10. Произведение одночлена и многочлена 84
27 Умножение одночлена на многочлен 84
28 Вынесение общего множителя за скобки 92
§ 11. Произведение многочленов 95
29. Умножение многочлена на многочлен 95
30. Разложение многочлена на множители способом группировки 99
31. Деление с остатком 100
Доказательство тождеств (с) 101
Дополнительные упражнения к главе IV 103
ГЛАВА V. ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ
§ 12. Квадрат суммы и квадрат разности 113
32. Возведение в квадрат суммы и разности двух выражений 113
33. Разложение на множители с помощью формул квадрата суммы и квадрата разности 117
§ 13.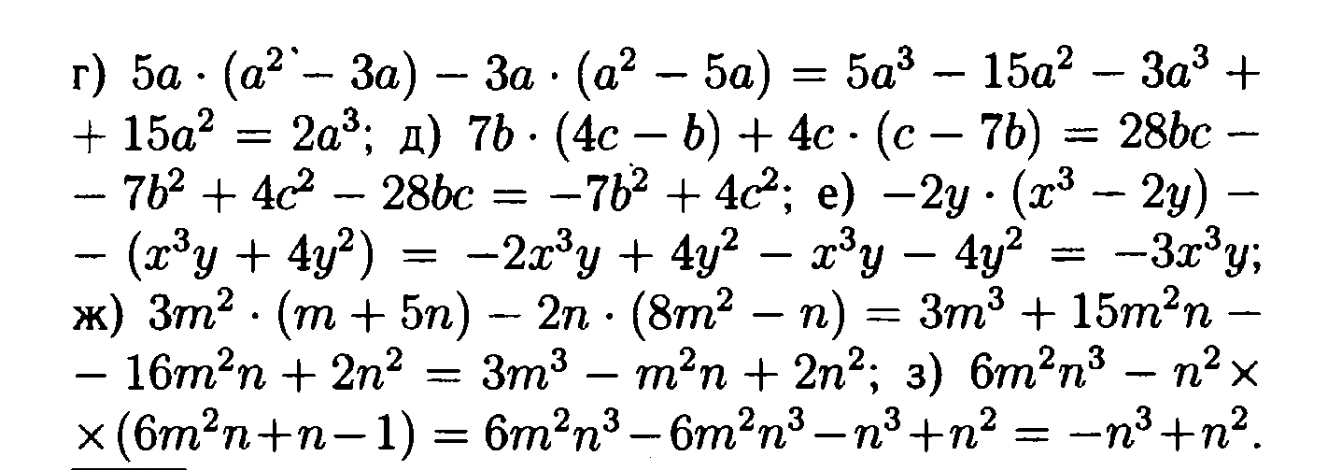 Разность квадратов. Сумма и разность кубов 120
Разность квадратов. Сумма и разность кубов 120
34. Умножение разности двух выражений на их сумму 120
35. Разложение разности квадратов на множители 120
36. Разложение на множители суммы и разности кубов 126
§ 14. Преобразование целых выражений 127
37. Преобразование целого выражения в многочлен 127
38. Применение различных способов для разложения на множители 130
39. Возведение двучлена в степень 133
Применение преобразований целых выражений (с) 134
Дополнительные упражнения к главе V 135
ГЛАВА VI. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
§ 15. Линейные уравнения с двумя переменными и их системы 145
40. Линейное уравнение с двумя переменными 145
41. График линейного уравнения с двумя переменными 146
42. Системы линейных уравнений с двумя переменными 149
§ 16. Решение систем линейных уравнений 154
43. Способ подстановки 154
44. Способ сложения 159
45. Решение задач с помощью систем уравнений 163
46. Линейные неравенства с двумя переменными и их системы 167
Дополнительные упражнения к главе VI 169
Задачи повышенной трудности 181
Купить.
По кнопкам выше и ниже «Купить бумажную книгу» и по ссылке «Купить» можно купить эту книгу с доставкой по всей России и похожие книги по самой лучшей цене в бумажном виде на сайтах официальных интернет магазинов Лабиринт, Озон, Буквоед, Читай-город, Литрес, My-shop, Book24, Books.ru.
По кнопке «Купить и скачать электронную книгу» можно купить эту книгу в электронном виде в официальном интернет магазине «ЛитРес», и потом ее скачать на сайте Литреса.
По кнопке «Найти похожие материалы на других сайтах» можно найти похожие материалы на других сайтах.
On the buttons above and below you can buy the book in official online stores Labirint, Ozon and others. Also you can search related and similar materials on other sites.
Купить бумажную книгуКупить и скачать электронную книгу
Дата публикации:
Теги: ГДЗ по алгебре 7 класс :: алгебра :: Морозов :: Макарычев :: Миндюк :: Нешков :: Суворова
Следующие учебники и книги:
- ГДЗ по алгебре.
 8 класс. К учебнику по алгебре за 8 класс. Алимов Ш.А. 2001
8 класс. К учебнику по алгебре за 8 класс. Алимов Ш.А. 2001 - ГДЗ по алгебре. 8 класс. К учебнику по алгебре за 8 класс. Макарычев Ю.Н. 2001
- ГДЗ по алгебре. 10 класс. К учебнику алгебра и начала анализа за 10-11 класс. Колмогоров А.Н. 2001
- ГДЗ по алгебре. 9 класс. К задачнику по алгебре за 9 класс. Макарычев Ю.Н. 2000
Предыдущие статьи:
- ГДЗ по алгебре для 8 классов, Кубатько О.И. К учебнику по алгебре за 8 класс, Макарычев Ю.Н. Миндюк Н.Г., Нешков К.И., Суворова С.Б., Теляковский С.А., 2010
- ГДЗ по алгебре и началам анализа. 11 класс. Сапожников А.А. К задачнику по алгебре и началам анализа за 10-11 класс. Мордкович А.Г., Денищева Л.О., Корешкова Т.А., Мишустина Т.Н., Тульчинская Е.Е., 2001
- ГДЗ по алгебре для 7 класса, Попов М.А. К задачнику по алгебре за 7 класс. Мордкович А.Г. 2010
- ГДЗ по алгебре для 9 класса. Бачурин В.Е. К учебнику по алгебре за 9 класс. Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. 2009
<< Предыдущая статьяСледующая статья >>
Моментные неравенства для сумм случайных матриц и их применение в оптимизации
Ай В.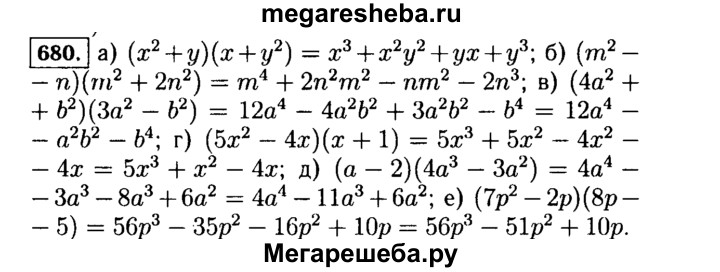 , Чжан С.: Сильная двойственность для подзадачи CDT: необходимое и достаточное условие. СИАМ Дж. Оптим. 19 (4), 1735–1756 (2009)
, Чжан С.: Сильная двойственность для подзадачи CDT: необходимое и достаточное условие. СИАМ Дж. Оптим. 19 (4), 1735–1756 (2009)
Артикул MathSciNet МАТЕМАТИКА Google Scholar
Алон Н., Макарычев К., Макарычев Ю., Наор А.: Квадратичные формы на графах. Изобретать. Мат. 163 (3), 499–522 (2006)
Статья MathSciNet МАТЕМАТИКА Google Scholar
Anstreicher K., Chen X., Wolkowicz H., Yuan Y.X.: Сильная двойственность для релаксации типа доверенной области квадратичной задачи о назначениях. Приложение линейной алгебры. 301 (1–3), 121–136 (1999)
Статья MathSciNet МАТЕМАТИКА Google Scholar
Анстрейхер К., Волкович Х.: О лагранжевой релаксации квадратичных матричных ограничений. СИАМ Дж. Матричный анал. заявл. 22 (1), 41–55 (2000)
заявл. 22 (1), 41–55 (2000)
Статья MathSciNet МАТЕМАТИКА Google Scholar
Арора С., Ли Дж. Р., Наор А.: Евклидово искажение и синтаксический анализ. Варенье. Мат. соц. 21 (1), 1–21 (2008)
Статья MathSciNet МАТЕМАТИКА Google Scholar
Арора, С., Рао, С., Вазирани, У.: Расширяющие потоки, геометрические вложения и разбиение графов. Дж. АСМ 56 (2): Статья 5 (2009)
Барвинок А.И.: Проблемы дистанционной геометрии и выпуклых свойств квадратичных отображений. Дискретный. вычисл. геом. 13 , 189–202 (1995)
Статья MathSciNet МАТЕМАТИКА Google Scholar
Бек А., Эльдар Ю.К.: Сильная двойственность в невыпуклой квадратичной оптимизации с двумя квадратичными ограничениями.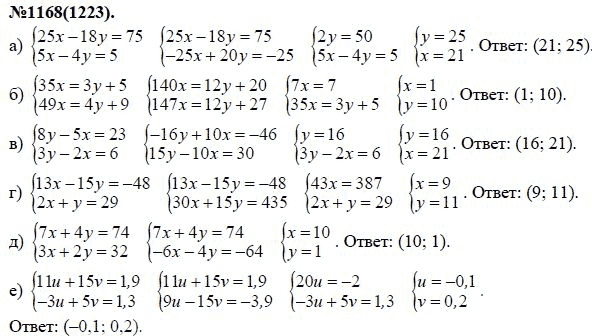 СИАМ Дж. Оптим. 17 (3), 844–860 (2006)
СИАМ Дж. Оптим. 17 (3), 844–860 (2006)
Артикул MathSciNet МАТЕМАТИКА Google Scholar
Бен-Таль А., Немировский А.: О безопасных податливых аппроксимациях линейных матричных неравенств с ограничениями на случайность. Мат. Опер. Рез. 34 (1), 1–25 (2009)
Статья MathSciNet МАТЕМАТИКА Google Scholar
Бухгольц А.: Операторное неравенство Хинчина в некоммутативной вероятности. Мат. Анна. 319 , 1–16 (2001)
Статья MathSciNet МАТЕМАТИКА Google Scholar
Делаж, Э., Йе, Ю.: Распределительно-надежная оптимизация в условиях неопределенности момента с применением к задачам, управляемым данными. Чтобы появиться в опер. Рез. (2009)
Дупачова, Дж.: Стохастическое программирование: минимаксный подход. В: Floudas, C.A., Pardalos, P.M. Энциклопедия оптимизации, 2-е изд., Springer Science+Business Media, LLC, Нью-Йорк (2009 г.).)
В: Floudas, C.A., Pardalos, P.M. Энциклопедия оптимизации, 2-е изд., Springer Science+Business Media, LLC, Нью-Йорк (2009 г.).)
Goemans MX: Полуопределенное программирование в комбинаторной оптимизации. Мат. Программа. 79 , 143–161 (1997)
MathSciNet МАТЕМАТИКА Google Scholar
Goemans MX, Williamson DP: Улучшенные алгоритмы аппроксимации для задач максимального сокращения и выполнимости с использованием полуопределенного программирования. J. ACM 42 (6), 1115–1145 (1995)
Статья MathSciNet МАТЕМАТИКА Google Scholar
Gower JC, Dijksterhuis GB: Procrustes Problems, Oxford Statistical Science Series, vol. 30. Издательство Оксфордского университета, Нью-Йорк (2004)
Google Scholar
Grötschel M. , Lovász L., Schrijver A.: Геометрические алгоритмы и комбинаторная оптимизация, Алгоритмы и комбинаторика, том. 2, 2-е исправленное изд. Спрингер, Берлин (1993)
, Lovász L., Schrijver A.: Геометрические алгоритмы и комбинаторная оптимизация, Алгоритмы и комбинаторика, том. 2, 2-е исправленное изд. Спрингер, Берлин (1993)
Google Scholar
Хорн Р.А., Джонсон К.Р.: Матричный анализ. Издательство Кембриджского университета, Кембридж (1985)
МАТЕМАТИКА Google Scholar
Каргер Д., Мотвани Р., Судан М.: Приближенная раскраска графа с помощью полуопределенного программирования. J. ACM 45 (2), 246–265 (1998)
Статья MathSciNet МАТЕМАТИКА Google Scholar
Хинчин А.: Über dyadische brüche. Мат. Цайт. 23 , 109–116 (1923)
Артикул MathSciNet Google Scholar
Купманс Т.С., Бекманн М.: Проблемы распределения и местонахождения экономической деятельности. Econometrica 25 (1), 53–76 (1957)
Econometrica 25 (1), 53–76 (1957)
Статья MathSciNet МАТЕМАТИКА Google Scholar
Леду М., Талагран М.: Вероятность в банаховых пространствах: изопериметрия и процессы, Математические расчеты и их расчеты. 3. Folge/A Series of Modern Surveys in Mathematics, vol. 23. Спрингер, Берлин (1991)
Google Scholar
Li, W.L., Zhang, Y.J., So, A.M.C., Win, M.Z.: Медленное адаптивное OFDMA через случайное программирование с ограничениями. Препринт (2009)
Луо З.К., Сидиропулос Н.Д., Ценг П., Чжан С.: Аппроксимационные оценки для квадратичной оптимизации с однородными квадратичными ограничениями. СИАМ Дж. Оптим. 18 (1), 1–28 (2007)
MathSciNet МАТЕМАТИКА Google Scholar
Lust-Piquard F. : Inégalités de Khintchine dans C р (1 < p < ∞). Comptes Rendus de l’Académie des Sciences de Paris, Série I 303 (7), 289–292 (1986)
: Inégalités de Khintchine dans C р (1 < p < ∞). Comptes Rendus de l’Académie des Sciences de Paris, Série I 303 (7), 289–292 (1986)
MathSciNet МАТЕМАТИКА Google Scholar
Немировский А.: Суммы случайных симметричных матриц и квадратичная оптимизация при ограничениях ортогональности. Мат. Программа. сер. Б 109 (2–3), 283–317 (2007)
Статья MathSciNet МАТЕМАТИКА Google Scholar
Немировский А., Роос К., Терлаки Т.: О максимизации квадратичной формы над пересечением эллипсоидов с общим центром. Мат. Программа. сер. А 86 , 463–473 (1999)
Артикул MathSciNet МАТЕМАТИКА Google Scholar
Немировский А., Шапиро А. : Выпуклые аппроксимации случайных программ с ограничениями. СИАМ Дж. Оптим. 17 (4), 969–996 (2006)
: Выпуклые аппроксимации случайных программ с ограничениями. СИАМ Дж. Оптим. 17 (4), 969–996 (2006)
Статья MathSciNet МАТЕМАТИКА Google Scholar
Немировский А., Шапиро А.: Сценарные аппроксимации случайных ограничений. В: Калафиоре, Г., Даббене, Ф. Вероятностные и рандомизированные методы проектирования в условиях неопределенности, стр. 3–47. Спрингер, Лондон (2006)
Нестеров Ю.: Качество полуопределенной релаксации для невыпуклой квадратичной оптимизации. ОСНОВНОЙ документ для обсуждения 9719, Католический университет Лувена, Бельгия (1997)
Пардалос, П.М., Волкович, Х. (ред.): Квадратичные присваивания и связанные с ними проблемы, Серия DIMACS по дискретной математике и теоретической информатике, том. 16. Американское математическое общество, Провиденс, Род-Айленд (1994)
Патаки Г. : О ранге экстремальных матриц в полуопределенных программах и кратности оптимальных собственных значений. Мат. Опер. Рез. 23 (2), 339–358 (1998)
: О ранге экстремальных матриц в полуопределенных программах и кратности оптимальных собственных значений. Мат. Опер. Рез. 23 (2), 339–358 (1998)
Артикул MathSciNet МАТЕМАТИКА Google Scholar
Пешкир Г., Ширяев А.Н.: Неравенства Хинчина и мартингал, расширяющий сферу их действия. Русь. Мат. Surv. 50 (5), 849–904 (1995)
Статья MathSciNet Google Scholar
Pisier, G.: Некоммутативный вектор со значением L стр. -пробелы и полностью р -суммирующие карты. Asterisque, 247 (1998)
Куайн М.П.: основанное на исчислении доказательство формулы Стирлинга для гамма-функции. Междунар. Дж. Матем. Образовательный науч. Технол. 28 (6), 914–917 (1997)
MathSciNet Google Scholar
Шарф, Х. : Минимум-макс решение проблемы инвентаризации. В: Эрроу, К.Дж., Карлин, С., Скарф, Х. Исследования по математической теории запасов и производства, стр. 201–209.. Издательство Стэнфордского университета, Стэнфорд (1958)
: Минимум-макс решение проблемы инвентаризации. В: Эрроу, К.Дж., Карлин, С., Скарф, Х. Исследования по математической теории запасов и производства, стр. 201–209.. Издательство Стэнфордского университета, Стэнфорд (1958)
Шапиро А.: Ранговая сводимость симметричной матрицы и теория выборки анализа минимального следового фактора. Психометрика 47 (2), 187–199 (1982)
Статья MathSciNet МАТЕМАТИКА Google Scholar
Шенуда, М.Б., Дэвидсон, Т.Н.: Проекты для многопользовательских приемопередатчиков на основе сбоев. В: Материалы Международной конференции IEEE 2009 г. по акустике, речи и обработке сигналов (ICASSP 2009).), стр. 2389–2392 (2009)
Итак, AMC: О характеристиках детекторов MIMO с полуопределенной релаксацией для созвездий QAM. В: Труды Международной конференции IEEE 2009 г. по акустике, речи и обработке сигналов (ICASSP 2009), стр. 2449–2452 (2009 г.)
2449–2452 (2009 г.)
Итак, AMC: Вероятностный анализ детектора полуопределенной релаксации в цифровой связи. Для публикации в Proceedings of the 21st Annual ACM-SIAM Symposium on Discrete Algorithms (SODA 2010)
So A.M.C., Ye Y., Zhang J.: Единая теорема о снижении ранга SDP. Мат. Опер. Рез. 33 (4), 910–920 (2008)
Статья MathSciNet МАТЕМАТИКА Google Scholar
So AMC, Zhang J., Ye Y.: Об аппроксимации сложных задач квадратичной оптимизации с помощью релаксации полуопределенного программирования. Мат. Программа. сер. В 110 (1), 93–110 (2007)
Статья MathSciNet МАТЕМАТИКА Google Scholar
Томчак-Ягерманн Н.: Модули гладкости и выпуклости и средние значения Радемахера для классов следов S р (1 ≤ p < ∞). Стад. Мат. 50 , 163–182 (1974)
Стад. Мат. 50 , 163–182 (1974)
MathSciNet МАТЕМАТИКА Google Scholar
Тропп Дж. А.: Свойство случайного мощения для равномерно ограниченных матриц. Стад. Мат. 185 (1), 67–82 (2008)
Статья MathSciNet МАТЕМАТИКА Google Scholar
Е. Ю.: Аппроксимация глобальной квадратичной оптимизации с выпуклыми квадратичными ограничениями. Дж. Глобальный оптимум. 15 (1), 1–17 (1999)
Статья MathSciNet МАТЕМАТИКА Google Scholar
Е Ю., Чжан С.: Новые результаты по квадратичной минимизации. СИАМ Дж. Оптим. 14 (1), 245–267 (2003)
Статья MathSciNet МАТЕМАТИКА Google Scholar
Чжао К., Кариш С.Э., Рендл Ф. , Волкович Х.: Релаксации полуопределенного программирования для квадратичной задачи о назначениях. Дж. Комб. Оптим. 2 (1), 71–109 (1998)
, Волкович Х.: Релаксации полуопределенного программирования для квадратичной задачи о назначениях. Дж. Комб. Оптим. 2 (1), 71–109 (1998)
Статья MathSciNet МАТЕМАТИКА Google Scholar
Лапласиан
Мы с Шан-Хуа Тенг написали большую статью по проблеме решения систем линейных уравнений в лапласовских матрицах графов. В этой статье потребовалось много алгоритмов теории графов, большинство из которых были значительно улучшены. На этой странице мы попытаемся отслеживать основные разработки и приложения этих идей. Содержание
Обзоры, классы и пояснительные статьи
Комбинаторное предварительное обусловливание Комбинаторный подход к предварительному обусловливанию, также называемый теорией поддержки, был представлен Вайдьей в неопубликованной статье. Для получения дополнительной информации об истории этого поля я рекомендую страницу Брюса Хендриксона «Теория поддержки для предварительной обработки». Ниже приведены некоторые основополагающие документы в этой области:
Документы Шпильмана-Тэна -Алгоритмы линейного времени для разбиения графов, разрежения графов и решения линейных систем» (предварительная версия в STOC ’04, расширенная версия в arxiv), в которой мы показали, как решать симметричные, диагонально преобладающие линейные системы почти за линейное время. С тех пор мы разбили эту статью на три статьи, каждую из которых можно читать отдельно и которые были представлены в журналы по отдельности.
Описание содержания этих статей можно найти в учебном пособии, которое я давал на IPCO05 (вот слайды), и в некоторых лекциях моих занятий Теория спектральных графов и ее приложения. Улучшенные решателиАсимптотически самый быстрый известный решатель появляется в следующих двух статьях
Простейший быстрый решатель появляется в статье:
Это можно рассматривать как улучшение решателя в статье:
Алгоритм из последней статьи асимптотически быстрее, но слишком сложен для реальной реализации. Другой простой подход к решению этих систем появляется в статьях: 92″ Кутиса, Миллера и Пенга. В этих статьях найдены эффективные (и невероятно простые) способы построения предобуславливателей, существование которых впервые было доказано в: , Колла, Макарычев, Сабери и Тенг (STOC 2010). Эффективные параллельные алгоритмы, зависящие только от разреженности, можно найти в следующих статьях:
Решатели для направленных (несимметричных) лапласиановНедавний прорыв в решении несимметричных систем в лапласовских матрицах ориентированных графов появляется в следующих двух статьях (еще больше будет в будущем):
КодLaplacians.jl — это пакет, который реализует многие алгоритмы, обсуждаемые в этих статьях. Яннис Кутис написал код, реализующий версию комбинаторного предобусловливания. Вы можете найти это здесь. Реализация оригинального подхода Вайдьи реализована в пакете TAUCS , написанном Дороном Ченом, Владимиром Роткиным и Сиваном Толедо. Если вам нужно решить диагонально-преобладающие линейные системы, я также предлагаю попробовать Алгебраический многосеточный алгоритм. Кластеризация локального графаПроблема кластеризации локального графа была представлена в статье № 1 выше. Для заданного массивного графа и интересующей его вершины задача состоит в том, чтобы найти в графе кластер вокруг заданной вершины. Наша статья была существенно улучшена в следующих статьях:
Алгоритмы из этих документов использовались в большом количестве приложений кластеризации. Вот некоторые примеры.
Разрежение Усовершенствования в спектральном разрежении матриц Лапласа можно найти в следующих статьях.
Подходы к спектральному разрежению произвольных матриц представлены в следующих двух статьях:
Использование решателей Лапласа в методах внутренних точек
Некоторые другие алгоритмы, основанные на теории поддержки
|

 Д. (авт.) Решение задач из учебника Ю.Н. Макарычева…
Д. (авт.) Решение задач из учебника Ю.Н. Макарычева… Г., Гольдич В.А. cкачать в PDF.
Г., Гольдич В.А. cкачать в PDF.


 net
net
 Простейшие текстовые задачи. Задание 2. Чтение графиков и диаграмм.
Простейшие текстовые задачи. Задание 2. Чтение графиков и диаграмм. Допущено Министерством образования Республики Беларусь.
Допущено Министерством образования Республики Беларусь. Помимо этого, электронные учебники очень удобны для того, чтобы ими пользоваться, нужен только интернет и телефон. А если вы хотите скачать книги совершенно бесплатно, то можете так же пользоваться файлом и без подключения к сети.
Помимо этого, электронные учебники очень удобны для того, чтобы ими пользоваться, нужен только интернет и телефон. А если вы хотите скачать книги совершенно бесплатно, то можете так же пользоваться файлом и без подключения к сети.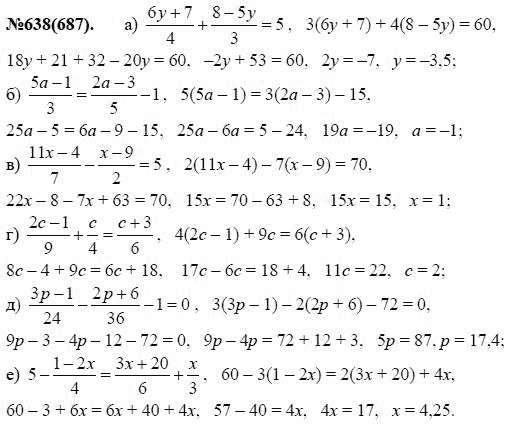 7 класс. Учебник для общеобразовательных учреждений.
7 класс. Учебник для общеобразовательных учреждений.
 Г. Мордкович и др.]. ред. А. Г. Мордковича.
Г. Мордкович и др.]. ред. А. Г. Мордковича.%D0%B0%D0%B1%D0%B2%D0%B3_efr.jpg) Затем в новом окне сверху справа — СТРЕЛКА ВНИЗ . Для чтения — просто листай колесиком страницы вверх и вниз.
Затем в новом окне сверху справа — СТРЕЛКА ВНИЗ . Для чтения — просто листай колесиком страницы вверх и вниз.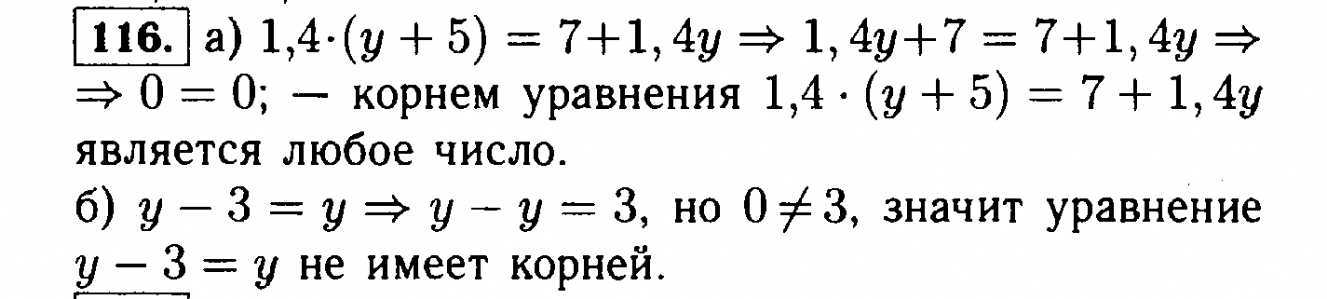 141я721 М52 Учебник включён в федеральный перечень Мерзляк А.Г. М52 Алгебра : 7 класс : учебник для учащихся общеобразовательных организаций / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир.
141я721 М52 Учебник включён в федеральный перечень Мерзляк А.Г. М52 Алгебра : 7 класс : учебник для учащихся общеобразовательных организаций / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир.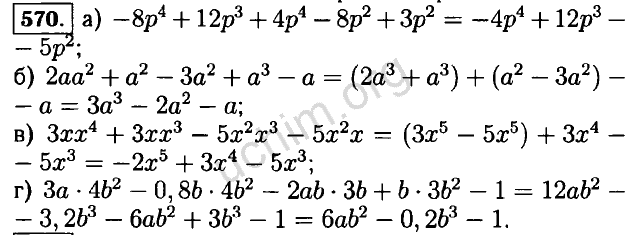 Решение задач с помощью уравнений. § 4. Статистические характеристики. 9. Среднее арифметическое, размах и мода.
Решение задач с помощью уравнений. § 4. Статистические характеристики. 9. Среднее арифметическое, размах и мода. 8 класс. К учебнику по алгебре за 8 класс. Алимов Ш.А. 2001
8 класс. К учебнику по алгебре за 8 класс. Алимов Ш.А. 2001 Новости науки Саймонса. Фонд Саймонса.
Новости науки Саймонса. Фонд Саймонса. и приложение 2003.
и приложение 2003. и Теория спектральных графов
и Теория спектральных графов
 (FOCS ’16), Коэн , Келнер, Пиблз, Пэн, Сидфорд и Владу.
(FOCS ’16), Коэн , Келнер, Пиблз, Пэн, Сидфорд и Владу. Причем мы стараемся сделать это за время, пропорциональное размеру возвращаемого кластера. Алгоритмы для этой задачи полезны по двум причинам. Во-первых, они очень эффективны, поскольку могут игнорировать большую часть графика. Во-вторых, они предоставляют один из немногих способов выявления небольших кластеров в определенных регионах.
Причем мы стараемся сделать это за время, пропорциональное размеру возвращаемого кластера. Алгоритмы для этой задачи полезны по двум причинам. Во-первых, они очень эффективны, поскольку могут игнорировать большую часть графика. Во-вторых, они предоставляют один из немногих способов выявления небольших кластеров в определенных регионах. Появился в STOC ’09.
Появился в STOC ’09.  ).)
).)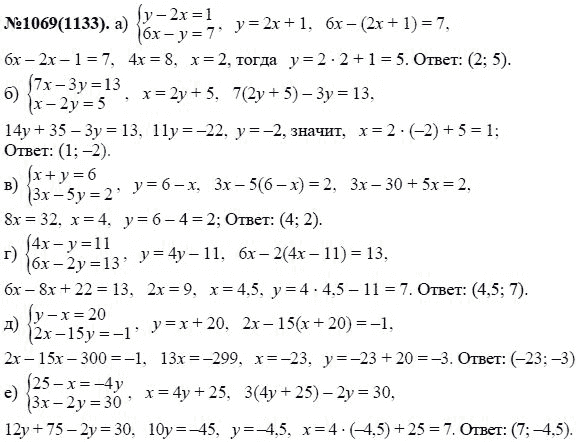
 (STOC ’17) Инь Тат Ли и Хе Сун. Это дает алгоритм почти линейного времени, который создает разрежители линейного размера.
(STOC ’17) Инь Тат Ли и Хе Сун. Это дает алгоритм почти линейного времени, который создает разрежители линейного размера. 
