Алгебра 7. Карточки-задания | Учебно-методический материал по алгебре (7 класс):
Тема. «Значение числового выражения» (1 уровень) Алгебра – 7
Найти значение числового выражения
1) , 2) ,
3) , 4) .
Тема. «Значение числового выражения» (2 уровень) Алгебра – 7
Найти значение числового выражения
1) , 2) ,
3) , 4) .
Тема. «Значение числового выражения» (2 уровень) Алгебра – 7
Вычислить:
- сумму квадратов чисел 3,1 и 2,9;
- квадрат разности чисел 5,3 и -4,7;
- куб суммы чисел 1,37 и -1,35.
Тема. «Значение числового выражения» (3 уровень) Алгебра – 7
Вычислить:
1) , 2) ,
3) , 4) .
……………………………………………………………………………………………………. .
.
Тема. «Алгебраические выражения» (1 уровень) Алгебра – 7
Найти значение выражения:
1) при ;
2) при ;
3) при ;
4) при .
Тема. «Алгебраические выражения» (2 уровень) Алгебра – 7
Найти значение выражения:
1) при и ; и ;
2) при и ; и .
Тема. «Алгебраические выражения» (2 уровень) Алгебра – 7
Найти значение выражения:
1) при и ; и ;
2) при и ; .
Тема. «Алгебраические выражения» (3 уровень) Алгебра – 7
Найти значение выражения:
1) при и ;
2) при и .
………………………………………………………………………………………………………
Тема. «Свойства арифметических действий» (1 уровень) Алгебра – 7
Вычислить наиболее рациональным способом:
1) ;
2) .
Тема. «Свойства арифметических действий» (2 уровень) Алгебра – 7
Вычислить наиболее рациональным способом:
1) 2)
3) 4) .
Тема. «Свойства арифметических действий» (2 уровень) Алгебра – 7
Найти значение выражения, используя распределительное свойство умножения:
1) , 2) , 3) , 4) .
Тема. «Свойства арифметических действий» (3 уровень) Алгебра – 7
Разберите, как выполнено умножение:
.
Используя данный прием, выполните вычисления:
1) , 2) , 3) ,
4) , 5) , 6) .
………………………………………………………………………………………………………
Тема. «Правила раскрытия скобок» (1 уровень) Алгебра – 7
Раскрыть скобки:
1) , 2) ,
3) , 4) ,
5) , 6) ,
7) , 8) .
Тема. «Правила раскрытия скобок» (1 уровень) Алгебра – 7
Раскрыть скобки и привести подобные слагаемые:
1) , 2) , 3) , 4) ,
5) , 6) ,
7) , 8) .
Тема. «Правила раскрытия скобок» (2 уровень) Алгебра – 7
Упростить выражение:
1) , 2) ,
3) , 4) ,
5) , 6) ,
7) , 8) .
Тема. «Правила раскрытия скобок» (3 уровень) Алгебра – 7
Раскрыть скобки и упростить:
1) , 2) ,
3) , 4) .
Тема. «Правила раскрытия скобок» (3 уровень) Алгебра – 7
Найти значение выражения:
1) при ;
2) при ;
3) при ;
4) при .
………………………………………………………………………………………………………
Тема. «Решение уравнений» (1 уровень) Алгебра – 7, § 2.
Решить уравнение:
1) , 2) ,
3) , 4) ,
5) , 6) .
Тема. «Решение уравнений» (1 уровень) Алгебра – 7, § 2.
Решить уравнение:
1) , 2) ,
3) , 4)
Тема. «Решение уравнений» (2 уровень) Алгебра – 7, § 2.
Решить уравнение:
1) , 2) ,
3) , 4) .
Тема. «Решение уравнений» (3 уровень) Алгебра – 7, § 2.
Решить уравнение:
1) ,
2) ,
3) ,
4).
Тема. «Решение уравнений» (3 уровень) Алгебра – 7, § 2.
При каком значении а:
1) значение выражения равно значению выражения ;
2) значение выражения в три раза больше значения выражения ;
3) значение выражения в два раза меньше значения выражения ;
4) значение выражения на 5 больше значения выражения ;
5) разность выражений и равна 36?
……………………………………………………………………………………………………. ..
..
Тема «Решение задач с помощью уравнений» (2 уровень) Алгебра – 7, § 3.
1) Двое рабочих изготовили 657 деталей, причем первый изготовил на 63 детали больше второго. Сколько деталей изготовил каждый?
2) Папе и дедушке вместе 111 лет. Сколько лет каждому, если папа в 2 раза моложе дедушки?
Тема «Решение задач с помощью уравнений» (3 уровень) Алгебра – 7, § 3.
1) За 3 ч мотоциклист проезжает то же расстояние, что велосипедист за 5 ч. Скорость мотоциклиста на 12 км/ч больше скорости велосипедиста. Определите скорость каждого.
2) На двух садовых участках 84 яблони. Если с одного из них пересадить на другой 1 яблоню, то на нем станет в 3 раза больше яблонь, чем останется на другом. Сколько яблонь на каждом участке?
…………………………………………………………………………………………………….
Тема «Свойства степени с натуральным показателем» (1 уровень) Алгебра – 7, § 6.
1) Возвести в степень произведение:
а) , б) в) , г) .
2) Вычислить значение выражения, используя свойство степени произведения:
а) б) , в) , г) .
Тема «Свойства степени с натуральным показателем» (2 уровень) Алгебра – 7, § 6
1) Выполнить возведение в степень:
а) , б) , в) , г) .
2) Упростить выражение:
а) , б) , в) , г) ,
д) , е) , ж) , з) .
Тема «Свойства степени с натуральным показателем» (3 уровень) Алгебра – 7, § 6
Найти значение выражения, используя свойства степеней:
1) , 2) . 3) , 4) ,
5) , 6) , 7) , 8) .
……………………………………………………………………………………………………..
Тема «Стандартный вид одночлена» (1 уровень) Алгебра – 7, § 7.
№1. Выполнить умножение:
1) , 2) , 3) ,
4) , 5) , 6) .
№2. Перемножить одночлены:
1) ,
2) .
Тема «Стандартный вид одночлена» (1 уровень) Алгебра – 7, § 7.
Выполнить возведение одночлена в степень:
1) , 2) , 3) , 4) ,
5) , 6) , 7) , 8) .
Тема «Стандартный вид одночлена» (2 уровень) Алгебра – 7, § 7.
Упростить выражение:
1) , 2) , 3) ,
4) , 5) , 6).
Тема «Стандартный вид одночлена» (3 уровень) Алгебра – 7, § 7.
Представить в виде одночлена стандартного вида:
1) , 2) ,
3) , 4) .
…………………………………………………………………………………………………….
Тема «Приведение подобных членов» (1 уровень) Алгебра – 7
Привести подобные члены:
1) , 2) ,
3) , 4) ,
5) , 6) .
Тема «Приведение подобных членов» (2 уровень) Алгебра – 7
Упростить выражение и найти его значение:
1) при ,
2) при ,
3) при .
……………………………………………………………………………………………………..
Тема «Сложение и вычитание многочленов» (1 уровень) Алгебра – 7, § 9
Составить сумму и разность многочленов и привести к стандартному виду:
1) и , 2) и ,
3) и , 4) и ,
5) и , 6) и .
Тема «Сложение и вычитание многочленов» (2 уровень) Алгебра – 7, § 9
Упростить выражение:
1) , 2) ,
3) , 4) .
…………………………………………………………………………………………………….
Тема «Умножение одночлена на многочлен» (1 уровень) Алгебра – 7, § 10
Выполнить умножение:
1) , 2) , 3) , 4) ,
5) , 6) , 7) ,
8) , 9) , 10) .
Тема «Умножение одночлена на многочлен» (2 уровень) Алгебра – 7, § 10
Упростить выражение:
1) , 2) , 3) ,
4) , 5) , 6) .
Тема «Умножение одночлена на многочлен» (2 уровень) Алгебра – 7, § 10
Упростить выражение:
1) , 2) ,
3) , 4) .
Тема «Умножение одночлена на многочлен» (3 уровень) Алгебра – 7, § 10
Упростить выражение и найти его значение:
1) при ,
2) при .
…………………………………………………………………………………………………….
Тема «Умножение многочленов» (1 уровень) Алгебра – 7, § 11
Выполнить умножение:
1) , 2) ,
3) , 4) ,
5) , 6) .
Тема «Умножение многочленов» (2 уровень) Алгебра – 7, § 11
Выполнить умножение:
1) , 2) ,
3) , 4) ,
5) , 6) .
Тема «Умножение многочленов» (3 уровень) Алгебра – 7, § 11
Выполнить умножение:
1) , 2) ,
3) , 4) ,
5) , 6) .
………………………………………………………………………………………………………
Тема «Вынесение общего множителя за скобки» (1 уровень) Алгебра – 7, § 12
Вынести общий множитель за скобки:
1) , 2) ,
3) , 4) ,
5) , 6) ,
7) , 8) .
Тема «Вынесение общего множителя за скобки» (1 уровень) Алгебра – 7, § 12
Вынести общий множитель за скобки:
1) , 2) ,
3) , 4) ,
5) , 6) ,
7) , 8) .
Тема «Вынесение общего множителя за скобки» (2 уровень) Алгебра – 7, § 12
Вынести общий множитель за скобки:
1) ,
2) ,
3) ,
4) ,
5) .
……………………………………………………………………………………………………. .
.
Тема «Способ группировки» (1 уровень) Алгебра – 7, § 20.
Вынести общий множитель за скобки:
1) , 2) ,
3) , 4) ,
5) , 6) .
Тема «Способ группировки» (2 уровень) Алгебра – 7, § 13
Разложите на множители:
1) , 2) ,
3) , 4) ,
5) , 6) .
Тема «Способ группировки» (3 уровень) Алгебра – 7, § 13
№1. Разложите на множители:
1) ,
2) ,
3) ,
4)
№2. Разберите, как выполнено разложение на множители многочлена ;
= .
Разложите на множители:
а) ; б) .
……………………………………………………………………………………………………..
Тема «Разность квадратов» (1 уровень) Алгебра – 7, § 15
Выполнить умножение:
1) , 2) ,
3) , 4) ,
5) , 6) ,
7) , 8) .
Тема «Разность квадратов» (2 уровень) Алгебра – 7, § 15
Выполнить умножение:
1) , 2) ,
3) , 4) ,
5) , 6) .
Тема «Разность квадратов» (3 уровень) Алгебра – 7, § 15
Выполнить умножение:
1) , 2) ,
3) , 4) ,
5) , 6) ,
7) .
……………………………………………………………………………………………………
Тема «Квадрат суммы. Квадрат разности» (1 уровень) Алгебра – 7, § 16
Выполнить преобразования по соответствующей формуле:
1) , 2) , 3) ,
4) , 5) , 6) ,
7) , 8) , 9) ,
10) , 11) , 12) .
………………………………………………………………………………………………
Алгебраические дроби
1 вариант
Выполнить действия
1) , 2) , 3) , 4),
5) :, 6) : , 7) : , 8) : ,
9) : , 10) , 11) , 12) : 6а,
13) : (), 14) ,
15) : , 16) : .
2 вариант
Выполнить действия
1) , 2) , 3) , 4),
5) :, 6) : , 7) : , 8) : ,
9) : , 10) , 11) , 12) : 6а,
13) : (), 14) ,
15) : , 16) : .
3 вариант
Выполнить действия
1) , 2) , 3) , 4),
5) :, 6) : , 7) : , 8) : ,
9) : , 10) , 11) , 12) : 6а,
13) : (), 14) ,
15) : , 16) : .
ВПР по математике 7 класс Варианты с ответами 2020 года
Осенью 2020 года прошли всероссийские проверочные работы ВПР по математике в 7 классах.
После проведения контрольной появились реальные варианты заданий с ответами.
Особенность проведения ВПР в 2020 году является то, что контрольные проходят осенью и 8 класс пишет работу за курс 7 класса.
Варианты ВПР 2020 по математике для 7 класса с ответами
| Комплект заданий 1 | |
| Вариант 1 | Ответы |
| Вариант 2 | Ответы |
| Комплект заданий 2 | |
| Вариант 1 | Ответы |
| Вариант 2 | Ответы |
| Комплект заданий 3 | |
| Вариант 1 | Ответы |
| Вариант 2 | Ответы |
| Комплект заданий 4 | |
| Вариант 1 | Ответы |
| Вариант 2 | Ответы |
| Комплект заданий 5 | |
| Вариант 1 | Ответы |
| Вариант 2 | Ответы |
| Комплект заданий 6 | |
| Вариант 1 | Ответы |
| Вариант 2 | Ответы |
| Комплект заданий 7 | |
| Вариант 1 | Ответы |
| Вариант 2 | Ответы |
| Комплект заданий 8 | |
| Вариант 1 | Ответы |
| Вариант 2 | Ответы |
| Комплект заданий 9 | |
| Вариант 1 | Ответы |
| Вариант 2 | Ответы |
| Комплект заданий 10 | |
| Вариант 1 | Ответы |
| Вариант 2 | Ответы |
Структура проверочной работы ВПР 2020 по математике 7 класс
На выполнение работы по математике даётся 90 минут.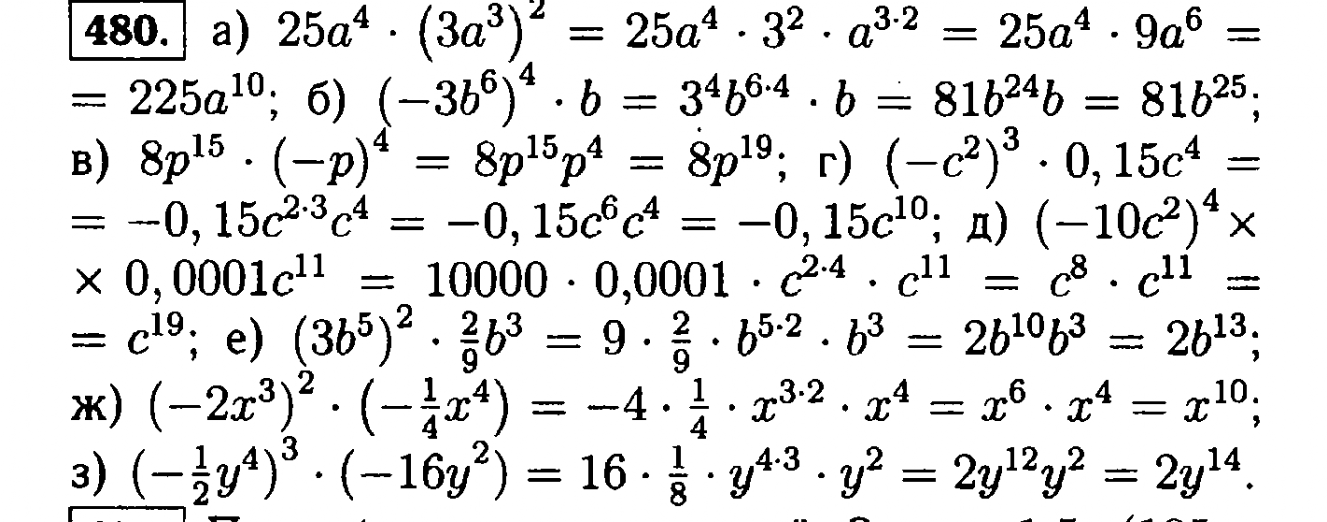 Работа содержит 16 заданий.
Работа содержит 16 заданий.
В заданиях 1–9, 11 и 13 необходимо записать только ответ.
В задании 12 нужно отметить точки на числовой прямой.
В задании 15 требуется схематично построить график функции. В заданиях 10, 14, 16 требуется записать решение и ответ.
Система оценивания выполнения отдельных заданий и проверочной работы в целом
Правильное решение каждого из заданий 1–11, 13, 15 оценивается 1 баллом.
Задание считается выполненным верно, если ученик дал верный ответ: записал правильное число, правильную величину; изобразил правильный рисунок.
Выполнение заданий 12, 14, 16 оценивается от 0 до 2 баллов.
Максимальный первичный балл — 19.
Связанные страницы:
ВПР 2019. Математика. 7 класс. Все варианты с ответами
Демоверсия ВПР 2020 по математике 7 класс
Демоверсия ВПР 2020 по математике 5 класс
ВПР по математике 5 класс Варианты с ответами 2020 год
Рабочие листы по математике для 7 класса с ответами
Рабочие листы по математике для 7 класса с ответамиРабочие листы по математике для 7 класса с ответами:
Здесь мы увидим решения 10 задач на 7-й странице математические таблицы».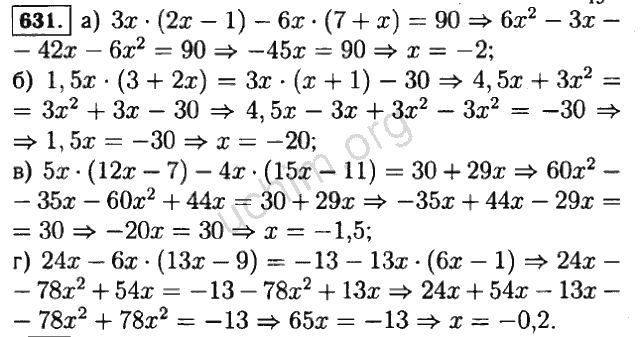
Рабочие листы по математике для 7 класса. Решение
Вопрос 1 :
В классном тесте, содержащем 15 вопросов, 4 балла даются за каждый правильный ответ и (-2) балла даются за каждый неправильный ответ. Джеймс пытается ответить на все вопросы, но только на 9.из его ответов верны. какой у него общий балл?
(a) 26 (b) 24 (c) 15
Решение:
Общее количество вопросов = 15
Количество вопросов, правильно отвечаемых Джеймсом =
Количество ответов на вопросы, неверно его
= 15 — 9 = 6
За каждый правильный ответ он получит +4 балла, а за каждый вопрос — -2 балла.
Общий балл Джеймса = 9⋅ 4 + 6 ⋅ (-2)
= 36 — 12
= 24
Следовательно, общий балл Джеймса составляет 24.
Связанная веб -страница «Упрощение целых чисел с различными знаками»
Вопрос 2:
Игрок с битой набрал следующее количество ранов за шесть иннингов:
36, 35, 50, 46, 60, 55 рассчитайте количество ранов, набранных им в иннинге.
(A) 47 (B) 50 (C) 30
Решение :
= (36 + 35 + 50 + 46 + 60 + 55)/6
= 282/6
= 47
Следовательно, он набрал 47 очков за один иннинг.
Связанная веб-страница «Задачи Word в среднем»
Вопрос 3 :
Владелец магазина продает манго в двух типах коробок, одна маленькая и одна большая. В большой коробке 8 маленьких коробочек плюс 4 манго. Задайте уравнение, которое дает количество манго в каждой маленькой коробке. Количество манго в большой коробке равно 100.
(A) 32 м = 100 (B) 8 м + 4 = 100 (C) 4 м + 100 = 4
Решение:
Количество манго в маленьких коробках = m
Количество манго в большой коробке = 4
Общее количество манго в большой коробке = 100
Следовательно, требуемое уравнение равно 8m + 4 = 100. x + 3) = 8
(A) x = -5 (B) x = -7 (C) x = -8
Решение:
-2(x + 3) = 8
Чтобы избавиться от -2, мы можем разделить на -2 с обеих сторон.
Таким образом, мы получаем
x + 3 = -4
Вычтите 3 с обеих сторон
x + 3 — 3 = -4 — 3
x = -7
Страница по теме «Решение1 линейных уравнений»
7
Вопрос 5 :
Возраст отца Кевина на 5 лет больше возраста Кевина более чем в три раза. Найдите возраст Кевина, если его отцу 44 года.
(A) 15 лет (B) 14 лет (C) 13 лет
Решение:
Let «x be x be x be a eag
Возраст отца Кевина = 3x + 5
Если возраст его отца = 44
3x + 5 = 44
Вычтите 5 с обеих сторон
3x = 44
. — 5
3x = 39
Divide на 3 с обеих сторон, мы получаем
x = 13
Следовательно, возраст Кевина составляет 13 лет.
Связанная веб -страница «Проблемы по возрасту»
Вопрос 6:
Если две прямые пересекаются в одной точке и если пара противоположных по вертикали углов является острыми углами, то другая пара противоположных по вертикали углов называется ___________
(A) Острый угол (B) Тупой угол (C) Прямой угол
Решение :
Другая пара должна быть тупым углом, потому что смежные углы являются дополнительными.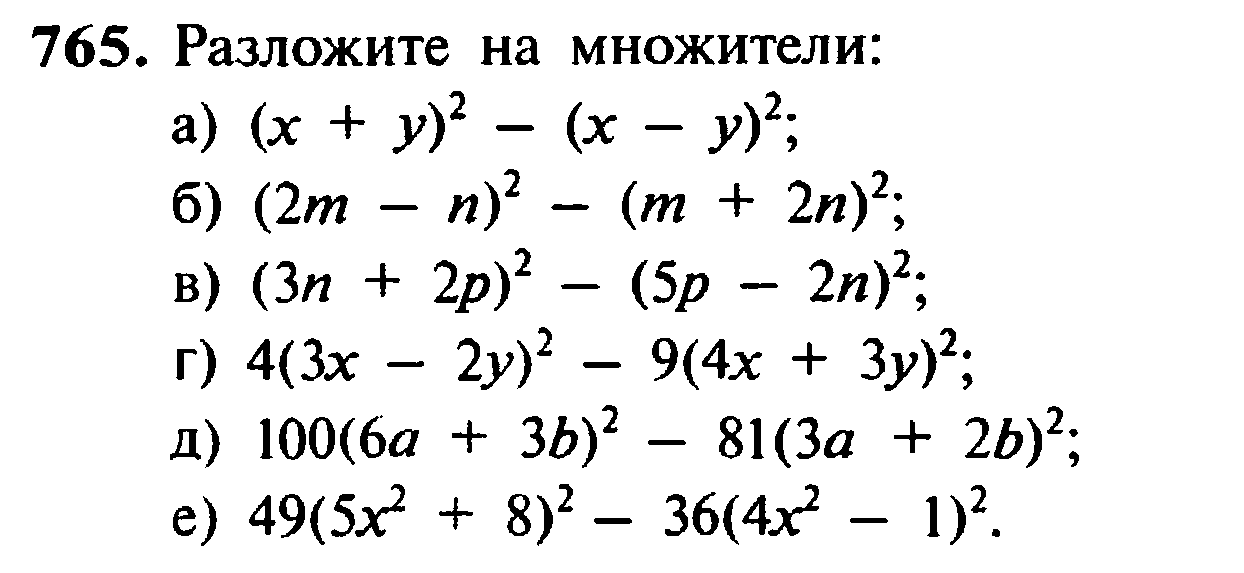
Веб-страница по теме «Прямые и углы»
Вопрос 7 :
Найдите значение x на следующем рисунке, если прямые l и m параллельны
(A) 110° (C) 50°
∠POT + ∠TOL = 180
110 + ∠TOL = 180
↑TOL = 70
↑TOL = ↑OSM (соответствующие углы)
Отсюда. угол на картинке ниже.
(A) 110° (B) 60° (C) 50 °
Решение:
Внешний угол треугольника равен сумме противолежащих внутренних углов
х 5 110 +
Вычесть 50 с обеих сторон
110 — 50 = x
x = 60
Следовательно, недостающий угол равен 60°.
Связанная веб-страница «Углы в треугольнике»
Вопрос 9 :
У нас есть два бака, в каждом из которых по 2 коврика, и на каждом из них сидело 2 кошки. Каждый кот написал 2 забавных старых шляпы. На каждой шляпке лежали тонкие крысы. На каждой крысе сидело 2 черных летучих мыши. Сколько вещей в наших чанах?
(A) 266 (B) 136 (C) 124
Решение:
Так как Количество чанов = 2
Количество матов в 1 чане = 2
Количество матов в 2 чанах = 2 × 2 = 4
Количество кошек на 1 мате = 1 2 900 Количество кошек на 4 ковриках = 4 × 2 = 8
Количество забавных старых шляп с 1 котом = 2
Количество забавных старых шляп с 8 кошками = 8 × 2 = 16
Количество тонких крыс на 1 старой шляпе = 2
Количество тонких крыс на 16 старых шляпах = 16 × 2 = 32
Количество черных летучих мышей на 1 крысе = 2
Количество черных летучих мышей на 32 крысах = 32 × 2 = 64
Прибавив 64 + 32 + 16 + 8 + 4 + 2, мы получим
= 126
Следовательно, ответ равен 126.
7
7 : Экспресс 5985,3 в стандартной форме
(A) 5,9853 x 10 3 (B) 5,9853 x 10 -3 (C) 59,853 x 10 2
. записать данное десятичное число в стандартной форме, мы должны переместить десятичную точку на 3 цифры влево.
Итак, мы должны использовать положительную силу.
Следовательно, ответ равен 5,9853 x 10 3
Связанная веб-страница «Научная нотация»
После того, как мы ознакомились с материалом, приведенным выше, мы надеемся, что учащиеся поняли «Рабочие листы по математике для 7 класса с ответами».
Помимо материала, указанного выше, если вы хотите узнать больше о «Рабочих листах по математике для 7 класса с ответами», нажмите здесь
Помимо материала «Рабочие листы по математике для 7 класса с ответами», если вам нужны какие-либо другие материалы в математика, пожалуйста, используйте наш пользовательский поиск Google здесь.
Пожалуйста, отправьте свой отзыв на v4formath@gmail. com
com
Мы всегда ценим ваши отзывы.
©Все права защищены. onlinemath5all.com
7 класс | Математика | Iowa Department of Education
В 7 классе учебное время должно быть сосредоточено на четырех важнейших областях: (1) развитие понимания и применение пропорциональных отношений; (2) развитие понимания операций с рациональными числами и работы с выражениями и линейными уравнениями; (3) решение задач, связанных с чертежами в масштабе и неформальными геометрическими конструкциями, а также работа с двух- и трехмерными формами для решения задач, связанных с площадью, площадью поверхности и объемом; и (4) делать выводы о популяциях на основе выборок.
- Учащиеся расширяют свое понимание соотношений и развивают понимание пропорциональности для решения одношаговых и многошаговых задач. Учащиеся используют свое понимание соотношений и пропорциональности для решения самых разных задач на проценты, в том числе связанных со скидками, процентами, налогами, чаевыми и процентным увеличением или уменьшением.

Учащиеся решают задачи о чертежах в масштабе, связывая соответствующие длины между объектами или используя тот факт, что отношения длин внутри объекта сохраняются в подобных объектах. Учащиеся изображают пропорциональные отношения и неофициально понимают единичную норму как меру крутизны связанной линии, называемой наклоном. Они отличают пропорциональные отношения от других отношений. - Учащиеся развивают единое понимание числа, распознавая дроби, десятичные дроби (которые имеют конечное или повторяющееся десятичное представление) и проценты как различные представления рациональных чисел. Учащиеся распространяют сложение, вычитание, умножение и деление на все рациональные числа, сохраняя свойства операций и отношения между сложением и вычитанием, а также умножением и делением. Применяя эти свойства и рассматривая отрицательные числа с точки зрения повседневного контекста (например, суммы долга или температуры ниже нуля), учащиеся объясняют и интерпретируют правила сложения, вычитания, умножения и деления с отрицательными числами.
 Они используют арифметику рациональных чисел, формулируя выражения и уравнения с одной переменной и используя эти уравнения для решения задач.
Они используют арифметику рациональных чисел, формулируя выражения и уравнения с одной переменной и используя эти уравнения для решения задач. - Учащиеся продолжают работу с площадью с 6 класса, решая задачи на площадь и длину окружности и площадь поверхности трехмерных объектов. При подготовке к работе на конгруэнтность и подобие в 8 классе рассуждают об отношениях между двухмерными фигурами, используя чертежи в масштабе и неформальные геометрические построения, знакомятся с отношениями между углами, образованными пересекающимися линиями. Учащиеся работают с трехмерными фигурами, связывая их с двухмерными фигурами, рассматривая поперечные сечения. Они решают реальные и математические задачи, связанные с площадью, площадью поверхности и объемом двух- и трехмерных объектов, состоящих из треугольников, четырехугольников, многоугольников, кубов и прямых призм.
- Учащиеся опираются на свою предыдущую работу с отдельными распределениями данных, чтобы сравнить два распределения данных и ответить на вопросы о различиях между группами населения.
 Они начинают неформальную работу со случайной выборкой для создания наборов данных и узнают о важности репрезентативных выборок для получения выводов.
Они начинают неформальную работу со случайной выборкой для создания наборов данных и узнают о важности репрезентативных выборок для получения выводов.
Соотношения и пропорциональные отношения (7.RP)
Анализируйте пропорциональные отношения и используйте их для решения реальных и математических задач. (7.РП.А)
- Расчет удельных расходов, связанных с отношениями дробей, включая отношения длин, площадей и других величин, измеренных в одинаковых или разных единицах. Например, если человек проходит 1/2 мили каждые 1/4 часа, вычислите скорость единицы как сложную дробь 1/2/1/4 мили в час, что эквивалентно 2 милям в час. (7.РП.А.1) (ДОК 1,2)
- Распознавать и представлять пропорциональные отношения между величинами.
- Определите, находятся ли две величины в пропорциональном соотношении, например, проверив эквивалентные отношения в таблице или нарисовав график на координатной плоскости и наблюдая, является ли график прямой линией, проходящей через начало координат.

- Определите константу пропорциональности (единичную норму) в таблицах, графиках, уравнениях, диаграммах и словесных описаниях пропорциональных отношений.
- Представление пропорциональных отношений уравнениями. Например, если общая стоимость t пропорциональна количеству n товаров, купленных по постоянной цене p, соотношение между общей стоимостью и количеством товаров может быть выражено как t = pn.
- Объясните, что означает точка (x, y) на графике пропорциональной зависимости с точки зрения ситуации, уделив особое внимание точкам (0, 0) и (1, r), где r — единичная ставка. (7.РП.А.2) (ДОК 1,2)
- Используйте отношения пропорциональности для решения многошаговых задач на соотношение и проценты. Примеры: простые проценты, налоги, надбавки и уценки, чаевые и комиссионные, сборы, процентное увеличение и уменьшение, процентная ошибка. (7.РП.А.3) (ДОК 1,2)
Система счисления (7.NS)
Применение и расширение предыдущего понимания операций с дробями для сложения, вычитания, умножения и деления рациональных чисел.
 (7.NS.A)
(7.NS.A)- Применение и расширение предыдущего понимания сложения и вычитания для сложения и вычитания рациональных чисел; представляют сложение и вычитание на горизонтальной или вертикальной диаграмме с числовыми линиями.
- Опишите ситуации, в которых противоположные величины объединяются, чтобы получить 0. Например, атом водорода имеет нулевой заряд, потому что две его составляющие заряжены противоположно.
- Под p + q понимают число, расположенное на расстоянии |q| от p в положительном или отрицательном направлении в зависимости от того, является ли q положительным или отрицательным. Покажите, что число и его противоположность имеют сумму 0 (аддитивные инверсии). Интерпретируйте суммы рациональных чисел, описывая контексты реального мира.
- Под вычитанием рациональных чисел следует понимать сложение обратной добавки p – q = p + (–q). Покажите, что расстояние между двумя рациональными числами на числовой прямой равно абсолютному значению их разности, и примените этот принцип в контексте реального мира.

- Применение свойств операций в качестве стратегий сложения и вычитания рациональных чисел. (7.НС.А.1) (ДОК 1,2)
- Применение и расширение предыдущего понимания умножения и деления и дробей для умножения и деления рациональных чисел.
- Понимать, что умножение распространяется с дробей на рациональные числа, требуя, чтобы операции продолжали удовлетворять свойствам операций, в частности свойству распределения, что приводит к таким произведениям, как (–1)(–1) = 1, и правилам умножения со знаком числа. Интерпретируйте произведения рациональных чисел, описывая контексты реального мира.
- Поймите, что целые числа можно делить при условии, что делитель не равен нулю, и каждое частное целых чисел (с ненулевым делителем) является рациональным числом. Если p и q целые числа, то –(p/q) = (–p)/q = p/(–q). Интерпретируйте частные рациональных чисел, описывая контексты реального мира.
- Применение свойств операций в качестве стратегий умножения и деления рациональных чисел.

- Преобразование рационального числа в десятичное с использованием длинного деления; известно, что десятичная форма рационального числа оканчивается на 0 или со временем повторяется. (7.НС.А.2) (ДОК 1,2)
- Решите реальные и математические задачи, связанные с четырьмя операциями с рациональными числами. (7.НС.А.3) (ДОК 1,2)
Выражения и уравнения (7.EE)
Используйте свойства операций для создания эквивалентных выражений. (7.EE.A)
- Применение свойств операций в качестве стратегий для сложения, вычитания, факторизации и расширения линейных выражений с рациональными коэффициентами. (7.EE.A.1) (DOK 1)
- Поймите, что переписывание выражения в разных формах в контексте задачи может пролить свет на проблему и на то, как связаны в ней величины. Например, a + 0,05a = 1,05a означает, что «увеличение на 5%» равнозначно «умножению на 1,05». (7.EE.A.2) (ДОК 1,2)
Решайте реальные и математические задачи, используя числовые и алгебраические выражения и уравнения.
 (7.EE.B)
(7.EE.B)- Решайте многоэтапные задачи из реальной жизни и математические задачи, связанные с положительными и отрицательными рациональными числами в любой форме (целые числа, дроби и десятичные дроби), стратегически используя инструменты. Применять свойства операций для вычисления с числами в любой форме; конвертировать между формами по мере необходимости; и оценить обоснованность ответов, используя умственные вычисления и стратегии оценки. Например: если женщина, зарабатывающая 25 долларов в час, получает надбавку на 10%, она будет получать дополнительную 1/10 своей зарплаты в час, или 2,50 доллара, за новую зарплату в 27,50 долларов. Если вы хотите разместить полотенцесушитель 93/4 дюйма длиной в центре двери шириной 27 1/2 дюйма, вам нужно будет разместить планку примерно в 9 дюймах от каждого края; эту оценку можно использовать в качестве проверки точного вычисления. (7.EE.B.3) (ДОК 1,2,3)
- Используйте переменные для представления величин в реальной или математической задаче и создавайте простые уравнения и неравенства для решения задач, рассуждая о величинах.

- Решите текстовые задачи, ведущие к уравнениям вида px + q = r и p(x + q) = r, где p, q и r — конкретные рациональные числа. Решите уравнения этих форм бегло. Сравните алгебраическое решение с арифметическим, указав последовательность операций, используемых в каждом подходе. Например, периметр прямоугольника равен 54 см. Его длина составляет 6 см. Какова его ширина?
- Решите текстовые задачи, ведущие к неравенствам вида px + q > r или px + q < r, где p, q и r — конкретные рациональные числа. Нарисуйте график множества решений неравенства и интерпретируйте его в контексте проблемы. Например: как продавец, вам платят 50 долларов в неделю плюс 3 доллара за продажу. На этой неделе вы хотите, чтобы ваша зарплата была не менее 100 долларов. Напишите неравенство для количества продаж, которое вам нужно сделать, и опишите решения. (7.EE.B.4) (ДОК 1,2,3)
Геометрия (7.G)
Рисовать, строить и описывать геометрические фигуры и описывать отношения между ними.
 (7.G.A)
(7.G.A)- Решение задач, связанных с чертежами геометрических фигур в масштабе, включая вычисление фактических длин и площадей по чертежу в масштабе и воспроизведение чертежа в масштабе в другом масштабе. (7.Г.А.1) (ДОК 1,2)
- Рисование (от руки, с линейкой и транспортиром и с техникой) геометрических фигур с заданными условиями. Сосредоточьтесь на построении треугольников по трем мерам углов или сторон, отмечая, когда условия определяют уникальный треугольник, более одного треугольника или отсутствие треугольника. (7.Г.А.2) (ДОК 1,2)
- Опишите двухмерные фигуры, которые получаются в результате разрезания трехмерных фигур, таких как плоские сечения прямоугольных призм и прямоугольных пирамид. (7.Г.А.3) (ДОК 1,2)
Решайте реальные и математические задачи, связанные с измерением угла, площади, площади поверхности и объема. (7.G.B)
- Знать формулы площади и длины окружности и использовать их для решения задач; дать неформальный вывод отношения между длиной окружности и площадью круга.
 (7.G.B.4) (ДОК 1,2)
(7.G.B.4) (ДОК 1,2) - Используйте факты о дополнительных, дополнительных, вертикальных и смежных углах в многоэтапной задаче, чтобы написать и решить простые уравнения для неизвестного угла в фигуре. (7.Г.Б.5) (ДОК 1,2)
- Решение реальных и математических задач, связанных с площадью, объемом и площадью поверхности двух- и трехмерных объектов, состоящих из треугольников, четырехугольников, многоугольников, кубов и прямых призм. (7.Г.Б.6) (ДОК 1,2)
Статистика и вероятность (7.SP)
Используйте случайную выборку для получения выводов о совокупности. (7.СП.А)
- Понимать, что статистику можно использовать для получения информации о населении путем изучения выборки населения; обобщения о совокупности из выборки действительны только в том случае, если выборка репрезентативна для этой совокупности. Поймите, что случайная выборка, как правило, дает репрезентативные выборки и поддерживает достоверные выводы. (7.СП.А.1) (ДОК 2)
- Используйте данные из случайной выборки, чтобы сделать выводы о совокупности с неизвестной интересующей характеристикой.
 Создайте несколько выборок (или смоделированных выборок) одинакового размера, чтобы оценить различия в оценках или прогнозах. Например, оцените среднюю длину слова в книге путем случайной выборки слов из книги; предсказать победителя школьных выборов на основе случайно выбранных данных опроса. Оцените, насколько далеко может быть оценка или прогноз. (7.СП.А.2) (ДОК 2,3)
Создайте несколько выборок (или смоделированных выборок) одинакового размера, чтобы оценить различия в оценках или прогнозах. Например, оцените среднюю длину слова в книге путем случайной выборки слов из книги; предсказать победителя школьных выборов на основе случайно выбранных данных опроса. Оцените, насколько далеко может быть оценка или прогноз. (7.СП.А.2) (ДОК 2,3)
Сделайте неформальные сравнительные выводы о двух популяциях. (7.СП.Б)
- Неформально оценить степень визуального перекрытия двух распределений числовых данных с одинаковой изменчивостью, измеряя разницу между центрами, выражая ее как кратное мере изменчивости. Например, средний рост игроков баскетбольной команды на 10 см больше, чем средний рост игроков футбольной команды, что примерно вдвое превышает вариабельность (среднее абсолютное отклонение) в любой из команд; на точечном графике заметно разделение между двумя распределениями высот. (7.СП.Б.3) (ДОК 2,3)
- Используйте меры центра и меры изменчивости для числовых данных из случайных выборок, чтобы сделать неформальные сравнительные выводы о двух совокупностях.
 Например, решите, длиннее ли слова в главе учебника по естествознанию для седьмого класса, чем слова в главе из учебника по естествознанию для четвертого класса. (7.СП.Б.4) (ДОК 2,3)
Например, решите, длиннее ли слова в главе учебника по естествознанию для седьмого класса, чем слова в главе из учебника по естествознанию для четвертого класса. (7.СП.Б.4) (ДОК 2,3)
Исследование случайных процессов и разработка, использование и оценка вероятностных моделей. (7.SP.C)
- Поймите, что вероятность случайного события представляет собой число от 0 до 1, которое выражает вероятность наступления события. Большие числа указывают на большую вероятность. Вероятность, близкая к 0, указывает на маловероятное событие, вероятность около 1/2 указывает на событие, которое не является ни маловероятным, ни вероятным, а вероятность, близкая к 1, указывает на вероятное событие. (7.SP.C.5) (ДОК 1)
- Аппроксимировать вероятность случайного события, собирая данные о случайном процессе, который его производит, и наблюдая его долгосрочную относительную частоту, и предсказывать приблизительную относительную частоту с учетом вероятности. Например, подбрасывая числовой куб 600 раз, предскажите, что число 3 или 6 выпадет примерно 200 раз, но, вероятно, не ровно 200 раз.
 (7.СП.С.6) (ДОК 2,3)
(7.СП.С.6) (ДОК 2,3) - Разработайте вероятностную модель и используйте ее для определения вероятностей событий. Сравните вероятности из модели с наблюдаемыми частотами; если согласие неудовлетворительное, объясните возможные источники несоответствия.
- Разработайте единую вероятностную модель, назначив всем исходам равную вероятность, и используйте эту модель для определения вероятностей событий. Например, если из класса случайным образом выбран ученик, найдите вероятность того, что будет выбрана Джейн, и вероятность того, что будет выбрана девочка.
- Разработайте вероятностную модель (которая может быть неоднородной), наблюдая частоты в данных, полученных в результате случайного процесса. Например, найдите приблизительную вероятность того, что крутящийся пенни упадет решкой вверх или что брошенный бумажный стаканчик упадет открытым концом вниз. Судя по наблюдаемым частотам, результаты для крутящегося пенни кажутся равновероятными? (7.СП.С.7) (ДОК 2,3)
- Найдите вероятности составных событий, используя организованные списки, таблицы, древовидные диаграммы и моделирование.

 com
com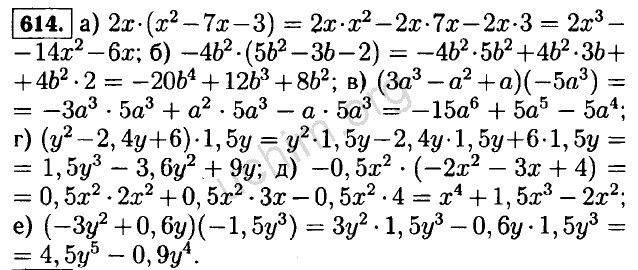
 Они используют арифметику рациональных чисел, формулируя выражения и уравнения с одной переменной и используя эти уравнения для решения задач.
Они используют арифметику рациональных чисел, формулируя выражения и уравнения с одной переменной и используя эти уравнения для решения задач. Они начинают неформальную работу со случайной выборкой для создания наборов данных и узнают о важности репрезентативных выборок для получения выводов.
Они начинают неформальную работу со случайной выборкой для создания наборов данных и узнают о важности репрезентативных выборок для получения выводов.- Определите, находятся ли две величины в пропорциональном соотношении, например, проверив эквивалентные отношения в таблице или нарисовав график на координатной плоскости и наблюдая, является ли график прямой линией, проходящей через начало координат.

- Определите константу пропорциональности (единичную норму) в таблицах, графиках, уравнениях, диаграммах и словесных описаниях пропорциональных отношений.
- Представление пропорциональных отношений уравнениями. Например, если общая стоимость t пропорциональна количеству n товаров, купленных по постоянной цене p, соотношение между общей стоимостью и количеством товаров может быть выражено как t = pn.
- Объясните, что означает точка (x, y) на графике пропорциональной зависимости с точки зрения ситуации, уделив особое внимание точкам (0, 0) и (1, r), где r — единичная ставка. (7.РП.А.2) (ДОК 1,2)
- Опишите ситуации, в которых противоположные величины объединяются, чтобы получить 0. Например, атом водорода имеет нулевой заряд, потому что две его составляющие заряжены противоположно.
- Под p + q понимают число, расположенное на расстоянии |q| от p в положительном или отрицательном направлении в зависимости от того, является ли q положительным или отрицательным. Покажите, что число и его противоположность имеют сумму 0 (аддитивные инверсии). Интерпретируйте суммы рациональных чисел, описывая контексты реального мира.
- Под вычитанием рациональных чисел следует понимать сложение обратной добавки p – q = p + (–q). Покажите, что расстояние между двумя рациональными числами на числовой прямой равно абсолютному значению их разности, и примените этот принцип в контексте реального мира.

- Применение свойств операций в качестве стратегий сложения и вычитания рациональных чисел. (7.НС.А.1) (ДОК 1,2)
- Понимать, что умножение распространяется с дробей на рациональные числа, требуя, чтобы операции продолжали удовлетворять свойствам операций, в частности свойству распределения, что приводит к таким произведениям, как (–1)(–1) = 1, и правилам умножения со знаком числа. Интерпретируйте произведения рациональных чисел, описывая контексты реального мира.
- Поймите, что целые числа можно делить при условии, что делитель не равен нулю, и каждое частное целых чисел (с ненулевым делителем) является рациональным числом. Если p и q целые числа, то –(p/q) = (–p)/q = p/(–q). Интерпретируйте частные рациональных чисел, описывая контексты реального мира.
- Применение свойств операций в качестве стратегий умножения и деления рациональных чисел.

- Преобразование рационального числа в десятичное с использованием длинного деления; известно, что десятичная форма рационального числа оканчивается на 0 или со временем повторяется. (7.НС.А.2) (ДОК 1,2)
- Решите текстовые задачи, ведущие к уравнениям вида px + q = r и p(x + q) = r, где p, q и r — конкретные рациональные числа. Решите уравнения этих форм бегло. Сравните алгебраическое решение с арифметическим, указав последовательность операций, используемых в каждом подходе. Например, периметр прямоугольника равен 54 см. Его длина составляет 6 см. Какова его ширина?
- Решите текстовые задачи, ведущие к неравенствам вида px + q > r или px + q < r, где p, q и r — конкретные рациональные числа. Нарисуйте график множества решений неравенства и интерпретируйте его в контексте проблемы. Например: как продавец, вам платят 50 долларов в неделю плюс 3 доллара за продажу. На этой неделе вы хотите, чтобы ваша зарплата была не менее 100 долларов. Напишите неравенство для количества продаж, которое вам нужно сделать, и опишите решения. (7.EE.B.4) (ДОК 1,2,3)
 (7.G.B.4) (ДОК 1,2)
(7.G.B.4) (ДОК 1,2) Создайте несколько выборок (или смоделированных выборок) одинакового размера, чтобы оценить различия в оценках или прогнозах. Например, оцените среднюю длину слова в книге путем случайной выборки слов из книги; предсказать победителя школьных выборов на основе случайно выбранных данных опроса. Оцените, насколько далеко может быть оценка или прогноз. (7.СП.А.2) (ДОК 2,3)
Создайте несколько выборок (или смоделированных выборок) одинакового размера, чтобы оценить различия в оценках или прогнозах. Например, оцените среднюю длину слова в книге путем случайной выборки слов из книги; предсказать победителя школьных выборов на основе случайно выбранных данных опроса. Оцените, насколько далеко может быть оценка или прогноз. (7.СП.А.2) (ДОК 2,3) Например, решите, длиннее ли слова в главе учебника по естествознанию для седьмого класса, чем слова в главе из учебника по естествознанию для четвертого класса. (7.СП.Б.4) (ДОК 2,3)
Например, решите, длиннее ли слова в главе учебника по естествознанию для седьмого класса, чем слова в главе из учебника по естествознанию для четвертого класса. (7.СП.Б.4) (ДОК 2,3) (7.СП.С.6) (ДОК 2,3)
(7.СП.С.6) (ДОК 2,3)- Разработайте единую вероятностную модель, назначив всем исходам равную вероятность, и используйте эту модель для определения вероятностей событий. Например, если из класса случайным образом выбран ученик, найдите вероятность того, что будет выбрана Джейн, и вероятность того, что будет выбрана девочка.
- Разработайте вероятностную модель (которая может быть неоднородной), наблюдая частоты в данных, полученных в результате случайного процесса. Например, найдите приблизительную вероятность того, что крутящийся пенни упадет решкой вверх или что брошенный бумажный стаканчик упадет открытым концом вниз. Судя по наблюдаемым частотам, результаты для крутящегося пенни кажутся равновероятными? (7.СП.С.7) (ДОК 2,3)


 (7.NS.A)
(7.NS.A)

 (7.EE.B)
(7.EE.B) (7.G.A)
(7.G.A)