Решебник 7 класса по геометрии: ГДЗ по Геометрии за 7-9 класс: Атанасян. Решебник с пояснениями

Теоремы Треугольника Калькулятор

Фигура Треугольника

Угол-Сторона-Угол (ASA)

А = угол А
B = угол B
С = угол С
а = сторона а
b = сторона b
с = сторона с

P = периметр
с = полупериметр
К = площадь
r = радиус вписанной окружности
R = радиус описанной окружности

Использование калькулятора

Каждый вариант расчета, показанный ниже, имеет подпункты, перечисляющие последовательность методов, используемых в этом калькуляторе для расчета неизвестных значений угла и стороны, включая Сумма углов треугольника, закон синусов и Закон косинусов.

Это НЕ ЕДИНСТВЕННЫЕ последовательности, которые вы можете использовать для решения подобных проблем.

• См. также тригонометрические калькуляторы:
• Калькулятор закона косинусов
• Калькулятор закона синусов

Решение теорем о треугольнике

AAA is Angle, Angle, Angle

Указание трех углов треугольника не однозначно определяет один треугольник. Таким образом, задание двух углов треугольника позволяет вычислить только третий угол.

Зная размеры двух углов треугольника, вы можете вычислить размер третьего угла. Сумма будет равна 180° или π радиан.

C = 180° — A — B (в градусах)

C = π — A — B (в радианах)

AAS — Угол, Угол, Сторона

Дан размер 2 углов и 1 стороны, противоположной по заданным углам можно вычислить размеры оставшегося 1 угла и 2 сторон.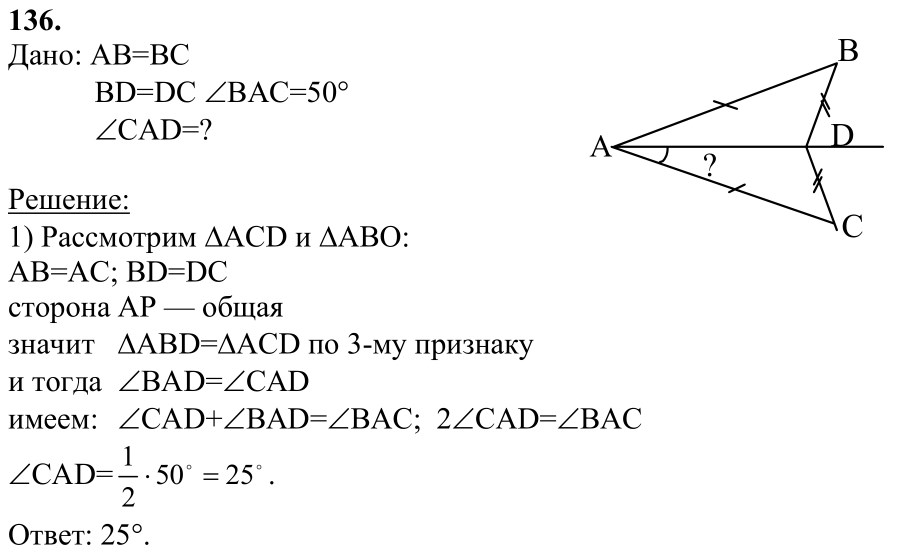

используйте Правило суммы углов, чтобы найти другой угол, затем

Используйте закон синусов, чтобы решить для каждой из двух других сторон.

ASA is Angle, Side, Angle

Зная размер 2 углов и размер стороны, которая находится между этими 2 углами, вы можете рассчитать размеры оставшегося 1 угла и 2 сторон.

используйте правило суммы углов, чтобы найти другой угол, затем

используйте закон синусов, чтобы решить для каждой из двух других сторон.

ASS (или SSA) — это угол, сторона, сторона

Учитывая размер двух сторон (a и c, где a < c) и размер угла A, который не находится между этими двумя сторонами, вы можете рассчитать размеры оставшихся 1 стороны и 2 углов в зависимости от следующих условий.

Для A ≥ 90° (A ≥ π/2)

:

Если a ≤ c нет возможных треугольников

Пример:

Если a > c существует 1 возможное решение

• используйте закон синусов для решения угла C
• используйте правило суммы углов, чтобы найти другой угол, B
• использовать закон синусов для решения последней стороны, b
• Пример:
  

Для A < 90° (A < π/2) :

Если a ≥ c существует 1 возможное решение

• используйте закон синусов для решения угла C
• используйте правило суммы углов, чтобы найти другой угол, B
• использовать закон синусов для решения последней стороны, b
• Пример:
  

Если a < c , у нас есть 3 возможных ситуации. «Если sin(A) < a/c , есть два возможных треугольника, удовлетворяющих заданным условиям. Если sin(A) = a/c , есть один возможный треугольник. Если sin(A) > a/c , возможных треугольников нет.» ^[1]

sin(A) < a/c , возможны два треугольника

найти 2 возможных значения третьей стороны b = c*cos(A) ± √[ a ² — c ² sin ² (A) ] ^[1]

для каждого набор решений, используйте закон косинусов, чтобы решить для каждого из двух других углов

представить 2 полных решения

Пример:

sin(A) = a/c

, есть один возможный треугольник

используйте Закон синусов для нахождения угла C

используйте правило суммы углов, чтобы найти другой угол, B

используйте закон синусов, чтобы найти последнюю сторону, b

Пример:

sin(A) > a/c , возможных треугольников нет

Уведомление об ошибке: sin(A) > a/c, поэтому нет ни решений, ни треугольника!

Пример:

SAS — это Side, Angle, Side

Зная размер двух сторон (c и a) и размер угла B между этими двумя сторонами, вы можете рассчитать размеры оставшихся 1 стороны и 2 углов. .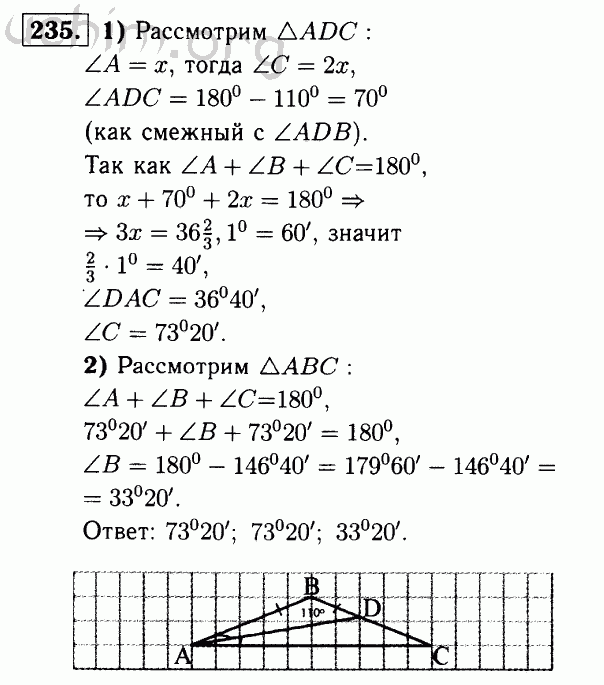

используйте закон косинусов, чтобы найти оставшуюся сторону, b

определите, какая сторона, a или c, наименьшая, и используйте закон синусов, чтобы найти размер противоположного угла, A или C соответственно.

[2]

используйте правило суммы углов, чтобы найти последний угол .

Используйте закон косинусов, чтобы найти углы. Вы также можете использовать правило суммы углов, чтобы найти окончательный угол, когда вы знаете 2 из них.

Сумма углов треугольника

В градусах A + B + C = 180°

В радианах A + B + C = π

Закон синусов

Если a, b и c — длины катетов треугольника, противоположного углам А, В и С соответственно; тогда закон синусов гласит:

a/sin A = b/sin B = c/sin C

Решение, например, для угла, A = sin ^-1 [ a*sin(B) / b ]

Закон косинусов

Если a, b и c — длины катетов треугольника, противоположных углам A, B и C соответственно; тогда закон косинусов гласит:

a ² = c ² + b ² — 2bc cos A, решение для cos A,   cos A = ( b ² + c ² — c 0 2

b ² = a ² + c ² — 2ca cos B, решение для cos B,   cos B = (c ² + a ² — b 0

c ² = b ² + a ² — 2ab cos C,   решение для cos C,   cos C = ( a ² + б ² — в ² ) / 2аб

Решение, например, для угла, A = cos ^-1 [ ( b ² + c ² — a ² ) / 2bc ]

Другие характеристики треугольника

Периметр треугольника, P = a + b + c

Полупериметр треугольника, s = 0,5 * (a + b + c)

Площадь треугольника, K = √[ s*(s-a)* (s-b)*(s-c)]

Радиус вписанной окружности в треугольник, r = √[ (s-a)*(s-b)*(s-c) / s ]

Радиус описанной окружности вокруг треугольника, R = (abc) / (4K)

Ссылки/дополнительная литература

[1] Вайсштейн, Эрик В. «Теорема ASS». От MathWorld — Веб-ресурс Wolfram. Теорема АСС.

[2] Математика — это весело — Решение треугольников SAS

Цвиллингер, Даниэль (главный редактор). Стандартные математические таблицы и формулы CRC, 31-е издание Нью-Йорк, штат Нью-Йорк: CRC Press, с. 512, 2003.

Вайсштейн, Эрик В. «Свойства треугольника». От MathWorld — Веб-ресурс Wolfram. Свойства треугольника.

Математика — это весело в Решение треугольников.

Калькулятор площади поверхности

Квадратная пирамида

ч = высота
с = наклонная высота
а = длина стороны
e = длина боковой кромки
р = а/2
В = объем
S _to = общая площадь поверхности
S _lat = площадь боковой поверхности
S _бот = площадь нижней поверхности

Рассчитайте больше с помощью
Калькулятор пирамид

Калькулятор Используйте

Онлайн-калькулятор для расчета площади поверхности геометрических тел, включая капсулу, конус, усеченный конус, куб, цилиндр, полусферу, пирамиду, прямоугольную призму, сферу, сферическую крышку и треугольную призму

Единицы: Обратите внимание, что единицы измерения показаны для удобства, но не влияют на расчеты. Единицы используются для указания порядка результатов, таких как футы, футы ² или футы ³ . Например, если вы начинаете с мм и знаете r и h в мм, ваши вычисления приведут к результату V в мм ³ и S в мм ² .

Ниже приведены стандартные формулы для площади поверхности.

Формулы площади поверхности:

Площадь поверхности капсулы

• Объем = πr ² ((4/3)r + a)
• Площадь поверхности = 2πr(2r + a)

Площадь поверхности круглого конуса

• Объем = (1/3)πr ² ч
• Площадь боковой поверхности = πrs = πr√(r ² + h ² )
• Площадь базовой поверхности = πr ²
• Общая площадь поверхности
  = L + B = πrs + πr ² = πr(s + r) = πr(r + √(r ² + h ² ))

Площадь поверхности круглого цилиндра

• Объем = πr ² ч
• Площадь верхней поверхности = πr ²
• Площадь нижней поверхности = πr ²
• Общая площадь поверхности
  = L + T + B = 2πrh + 2(πr ² ) = 2πr(h+r)

Площадь конической усеченной поверхности

• Объем = (1/3)πh (r ₁ ² + r ₂ ² + (r ₁ * r ₂ ))
• Площадь боковой поверхности
  = π(r ₁ + r ₂ )s = π(r ₁ + r ₂ )√((r ₁ — r ₂ ) ² + h ² )
• Площадь верхней поверхности = πr ₁ ²
• Площадь базовой поверхности = πr ₂ ²
• Общая площадь поверхности
  = π(r ₁ ² + r ₂ ² + (r ₁ * r ₂ ) * s)
  = π [R ₁ ² + R ₂ ² + (R ₁ * R ₂ ) * √ ((R ₁ — R ₂ ) ² + H 9 299999 2 9 + H 9 2

  + H ^{9 + H 9 + H 9 + H 9 + H 9 + H 9.}

  No related posts.