Категории: 7 класс.

Проверь себя 7 класс геометрия ответы: ГДЗ (решебник) по геометрии 7 класс Мерзляк, Полонский, Якир – РЕШАТОР!

 Комментировать

«80–90 баллов — это отличный результат». Иван Ященко — о ЕГЭ по математике и ее преподавании в школе

«ЕГЭ стабилен», — регулярно отвечает на вопросы об усложнении экзамена научный руководитель Центра педагогического мастерства и руководитель комиссии по составлению КИМ ЕГЭ Иван Ященко. Редактор «Мела» Анастасия Никушина поговорила с Иваном Валерьевичем о том, почему стобалльников становится меньше, как преподают ЕГЭ в школах и зачем поступать на физико-технические направления в 2023 году.

1. Стобалльники — яркий, публичный, но не показательный символ уровня преподавания математики или сложности экзамена. ЕГЭ стабилен: он обновляется под новый ФГОС, за последние годы из него ушли только самые простые задачи. Тут есть несколько факторов.

Во-первых, 100 баллов не то чтобы прямо необходимы для поступления в престижный университет. Человеку выгоднее вложить силы не в то, чтобы на одном экзамене поднять результат с 96 до 100, а чтобы по всем предметам у него было больше 90 баллов, без провалов.

Во-вторых, победителей ВсОШ и перечневых олимпиад по математике, физике и информатике за последние 3 года тоже стало гораздо больше: их количество увеличилось примерно на 300 человек. Все эти ребята в соответствии с законом имеют право на поступление без экзаменов. То есть, если у тебя есть диплом ВсОШ — неважно, за 9-й, 10-й или 11-й класс, — ты уже студент, осталось только аттестат получить.

Чтобы сдать ЕГЭ на 100 баллов, нужно тренироваться, чтобы не ошибиться и в простых задачах

Детям этот результат не нужен: они уже занимаются научной работой, участвуют в «Больших вызовах» в «Сириусе» и так далее. Без подготовки они набирают 80–90 баллов, и это тоже отличный результат.

Иван Ященко. Фото: Александр Натрускин / РИА Новости

2. 100 баллов — магическая цифра, за которой скрыто множество в том числе отрицательных психологических факторов. Это идеал, который не всегда достижим и не всегда нужен. Максимальный результат — не всегда показатель только хорошего знания математики, но еще и свойство характера: человек может абсолютно безошибочно, нигде не сбившись, что-то делать. Сейчас, работая преимущественно на компьютерах, мы можем перепроверять себя. Исследования показывают, что лучшие студенты даже топовых вузов — не стобалльники, а те, кто набирают 90–95 баллов, а для добротного инженерного вуза вполне достаточно и 60–75 баллов

Стобалльники и высокобалльники немного разные ребята. Любой олимпиадник получит высокий балл. Человек, который имеет 100 баллов, как правило, участвует в олимпиадах, но не всегда доходит до финала или становится призером. А чтобы выиграть олимпиаду нужны в первую очередь идея, креативность — погрешности там, зачастую, прощаются.

Подытоживая: и для 100 баллов на ЕГЭ, и для победы на олимпиаде нужно долго изучать математику. Нельзя получить максимальный результат, начав заниматься в 11-м или даже 10-м классе. Человек, который хочет получить 100 баллов или диплом ВсОШ, должен — опять же не ради самих результатов, а для успешного продолжения образования в технической области, — определяться с направлением еще в 6–7-м классе.

3. За последние 10 лет заметно вырос и интерес к предмету, и результаты. Количество ребят, которые выбирают математику и сдают ее на высокие баллы (от 60 и далее), нужные для массовых технических вузов, выросло за последние 10 лет примерно на 40%.

Почти 10 лет назад правительством была утверждена Концепция развития математического образования. Сегодня результаты применения этого документа выражаются в том числе в повышении интереса к массовым олимпиадам: количество учеников, участвующих в начальных школьных этапах ВсОШ, увеличивается. Что это показывает? То, что и ребята, и их родители видят, что многие перспективные профессии, хорошо оплачиваемые, требуют знания математики.

В новый ФГОС включили углубленку с основной школы. Долгое время она в виде профилизации предполагалась только в 10–11-м классе. При этом многие школы продолжали набирать и более младшие классы с углубленным изучением математики, а в Москве и некоторых регионах появился проект «Математическая вертикаль» в 7–9-х классах. Теперь, взяв его за основу для федерального стандарта, углубленное изучение математики вводят повсеместно.

Подчеркну: это не подготовка будущих математиков, не уровень элитных матшкол, которыми славился Советский Союз, а сейчас славится Россия. Они до сих пор существуют и не только учат своих детей, но и делятся методическими подходами с другими учреждениями: «Вторая школа», Школа № 57 в Москве, «Президентский лицей» в Санкт-Петербурге. Но я говорю про массовую углубленку. Это действительно важно для того, чтобы ребята вне зависимости от региона могли без репетиторов претендовать на место в хорошем вузе. Если они выбирают технические специальности, важно начинать углубленное изучение математики с 7-го класса.

Отдельным математическим предметом в новом ФГОС идет курс вероятности и статистики, который появился после долгих лет плавного введения. Ему отведен один час в неделю, на занятиях изучают не только собственно статистику, анализ данных, но и логику, теорию графов. Мы живем в цифровом мире, где умение работать с данными и защищать себя от обмана, адекватно оценивая информацию, представленную на красиво оформленных, но неверных диаграммах, действительно важно. Для огромного количества специальностей вероятность и статистика необходимы и во время обучения в вузе.

Возрождается геометрия. В 2010 году, когда ее включили в обязательную часть экзамена, мы увидели, насколько плохо выпускники решают простейшие задачи из серии «найдите площадь трапеции», которая просто нарисована по клеточкам и может решаться устно. Сейчас процент выполнения задач по планиметрии в первой части уже достаточно высок.

Благодаря онлайну в пандемию мы увидели, как сглаживается неравенство между детьми, которые живут в крупных университетских центрах и провинциях. «Сириус» распространил опыт Москвы по проведению школьного этапа ВсОШ на все регионы, а на математических сменах ребята, которые раньше имели «потолок» из-за отсутствия ярких преподавателей, теперь могут дотянуть свой уровень до топового. Сейчас туда ездят ребята из всех регионов страны, которые смогли пробиться на смену.

В этом году, кстати, сократилось количество неудовлетворительных оценок на ЕГЭ как по базовой, так и по профильной математике. И это здорово, что все меньше ребят оканчивают школу с ощущением, что они неуспешны в математике.

4. Волны интереса к тем или иным профессиям — не что-то новое, они были всегда. И, как ни странно, они часто запаздывают. Как я уже сказал, за 10 лет на 40% выросло количество ребят с неплохой математической подготовкой для технических специальностей. Но все реже в пару к профильной математике они выбирают физику, и все чаще — информатику. Сейчас большой спрос на айтишников, которых раньше действительно не хватало.

Из каждого утюга рассказывают про успешные IT-компании, Минцифры дает деньги на массовые курсы «Код будущего». Ребята туда идут. И они чувствуют, что в IT могут не только мечтать об успешном стартапе, который когда-нибудь в будущем заработает огромное количество денег, но и работать на престижных линейных должностях. Люди понимают, что сразу после вуза смогут получать нормальные деньги.

Интерес ребенка формируется в том числе средой, родителями, успешными примерами. В 60-е все учились на инженеров и физиков. В 90-е был пик спроса на экономистов и юристов — в СССР их не было, а после распада страны возник огромный спрос. Все по инерции пошли туда, а потом оказались не нужны.

Параллельно с расширением IT-сектора развиваются технологии, например искусственный интеллект

В будущем возможна ситуация, в которой задачи программиста-кодера, пишущего обычный код для сайта, будет выполнять искусственный интеллект. У меня в этом нет почти никаких сомнений.

Физика же, с одной стороны, нужна не просто для инженерной подготовки, например для модной сейчас робототехники. Главное, что она развивает особое мышление, причем в паре с математикой: человек, который изучал физику, придумывает множество изящных идей. Очень многие крутые айтишники, бизнесмены, экономисты получали именно физико-математическое образование, а программистами и финансистами стали потом. Поэтому пара «физика + математика», на мой взгляд, фундамент конкурентоспособности в мире искусственного интеллекта. Человек, знающий и физику, и математику, и информатику, будет более ценным кадром на рынке, чем тот, кто просто умеет писать код.

Тем более сейчас курс по физике обновляется. Принят межведомственный план Минпросвещения и Минобрнауки по развитию физического образования. В августе в образовательном центре «Сириус» состоится съезд учителей физики. Вместе с МФТИ, Минпросвещения и Минобразования работают над электронными методическими материалами для школ.

Физика очень красивая. Ее нельзя сводить чисто к математике: подставь формулу, не понимая, что там происходит. Поэтому наша задача — преобразовать курс физики так, чтобы он был связан с современными профессиями, а ребенок осознавал и видел свои перспективы. При этом курс должен быть доступным и реалистичным. Четко разделять — чему мы реально учим, решая задачи, что главное и в физике, и в математике, а о чем просто рассказываем для общего развития и мотивации.

5. В КИМах мы предлагаем экспертам только набросок решения, который экономит время и помогает быстрее войти в задачу. Но крупными буквами в критериях проверки и везде, где только можно, в ЕГЭ по математике написано: в заданиях с развернутым решением проверяется именно решение, причем не путем сличения с образцом. На полный балл оценивается любое математически корректное и обоснованное решение. Человек может использовать путь любой степени креативности и оптимальности. Бывает, что простейшие школьные задачи решают длинным экзотическим путем. Но главное, чтобы это было сделано правильно.

Фото: Валерий Шарифулин / ТАСС

Наш ЕГЭ — один из самых прозрачных экзаменов в мире. Почти нигде дети не получают скан своей работы через интернет, доступный для просмотра вместе с учителями еще перед подачей апелляции. Поэтому, если даже проверяющий — вернее, два независимых эксперта, оценивающих работу — не поймет решение, что, впрочем, бывает крайне редко, у экзаменуемого будет возможность объяснить свою правоту. Еще отмечу, что в случае расхождения у двух экспертов работу читает еще один, третий эксперт.

6. Задача ЕГЭ — проверить освоение программы, но цель обучения — развить математическое мышление и логику. Поэтому даже в базовом экзамене есть пускай несложные, но задачи на логику, или, как любят сейчас говорить, креатив.

Ошибочно было бы думать, что в цифровом мире после появления смартфонов отпала необходимость в логическом мышлении. Наоборот, как это ни смешно, человеку надо принимать больше решений, чем раньше — от выбора тарифа до вопроса доверия агрессивной рекламе.

Если же мы говорим о профильном ЕГЭ, то он ориентирован в первую очередь на массовые технические вузы. Неслучайно в научно-методическом совете комиссии разработчиков есть представители этих университетов. И если 60–70 баллов на ЕГЭ — уровень массовой инженерной или IT-специальности, то более высокие баллы получают претенденты на поступление в топовые заведения.

В ЕГЭ по математике представлены все разделы школьного курса: алгебра, геометрия, матанализ, вероятность и статистика. А есть задача 18. Кто-то называет ее «олимпиадной», но я бы не стал использовать такое слово. Самая главная ее сложность не техническая, как в задаче 17 с параметром, где нужно выполнить многоступенчатое решение. В задаче 18 человек демонстрирует, как за 11 лет обучения в школе он развил математическую креативность. Все методы решения там школьные, главное — догадаться. И мы очень рады, что ненулевой результат по этой задаче получает уже половина участников экзамена. Причем в ее решениях почти незаметна разница между ребятами из городских и сельских школ. Наверное, это и есть моя любимая задача из экзамена.

7. Самый ценный и самый ограниченный ресурс в школе — это время ребенка. Самое счастливое время жизни — детство. Да, познакомиться с тригонометрией надо каждому, и понимать, что в прямоугольном треугольнике по катету и углу ты можешь найти гипотенузу, тоже пригодится в бытовых расчетах. Но заниматься тригонометрическими преобразованиями, которые точно в быту не понадобятся, может, всем и не стоит: мне просто жалко времени ребенка. Понятно, что, когда человек не знает таблицу умножения, ее надо выучить. Но зачем человеку, который не идет на техническую специальность в вуз, сложные тригонометрические уравнения? Только потому, что «есть в программе»? Я считаю, что это нехорошо по отношению к ребятам.

«Дайте нам столько-то обязательных часов математики, как в СССР, когда все шли в инженерные вузы» — предметный снобизм, от которого сейчас отказались, введя профильное обучение и двухуровневый ЕГЭ. Ведь в советской школе те, кто «выживал», были хорошими инженерами. Остальные страдали: за них писали экзамены, была целая система показухи из-за программы, которую невозможно было освоить. Кстати, из 8-го класса в 9-й переходило меньше половины детей.

Если мы хотим, чтобы половина класса, которая сдает профиль, занималась углубленной математикой, то должны признавать право за другими детьми и родителями углубленно заниматься литературой, историей или другими предметами. Для того чтобы быть хорошим специалистом в этих областях, нужно тоже иметь много времени на соответствующие предметы и быть способным его потратить.

Математика должна быть интересной, потому что заниматься технической работой из-под палки — сидеть перемножать числа и раскрывать скобки, когда тебя заставляют — невозможно. Мы же говорим о развитии логики и креативности!

Поэтому мы и разделили ЕГЭ на базовый и профильный. Причем базовый экзамен достойный: в нем даже стереометрия есть, просто без зубодробительных выкладок. Неправильно считать, что гуманитариям достаточно троечки. Они работают с тем курсом, который достаточен для развития мышления и будущих занятий гуманитарными областями знания. Ведь и там тоже бывает нужна математика — просто без сложных технических вещей. А еще математика просто очень красивая наука! И сейчас все больше детей видят эту красоту, причем и на базовом уровне тоже.

За помощь в подготовке расшифровки благодарим стажера Илью Шувалова. Фото на обложке: Кирилл Кухмарь / ТАСС

Общий базовый тест по математике для 7 класса (примеры вопросов)

Общий базовый экзамен по математике для 7 класса с практическими вопросами

1. Изучите рисунок ниже.

Если треугольник расширить в 2 раза, каков периметр нового треугольника?
  1. 19
  2. 32
  3. 44
  4. 76
2. Изучите рисунки ниже.

Какой коэффициент масштабирования использовался для масштабирования прямоугольника?
  1. ¼
  2. 1 / 3
  3. 3
  4. 4
3 Какой из следующих наборов углов НЕ МОЖЕТ быть использован для построения треугольника?
  1. Три острых угла
  2. Два острых угла и один прямой
  3. Два острых угла и один тупой угол
  4. Два прямых угла и один острый угол
4. Если прямоугольный призма, показанная ниже, была разрезана по горизонтали , какая из следующих фигур НАИЛУЧШЕ всего описывает получившуюся двухмерную форму?

  1. Параллелограмм
  2. Прямоугольник
  3. Ромб
  4. Квадрат
5. Кевин сажает овощи в своем саду. Если сад имеет форму круга диаметром 10 футов, какова площадь сада?
  1. 15,7 футов²
  2. 31,4 футов²
  3. 78,5 футов²
  4. 314 футов²
посмотрите шоу Monster Truck на местной арене. Перед выступлением Тори удалось увидеть грузовики вблизи. Он заметил, что каждая шина грузовика-монстра имеет радиус около 3 футов. Исходя из этого радиуса, каково будет расстояние вокруг каждой шины?
  1. 9,42 фута
  2. 18,8 фута
  3. 28,3 фута
  4. 113 футов
7. Изучите рисунок ниже.

Каково значение x?
  1. 4
  2. 6
  3. 15
  4. 21
8. Что является мерой ?DBC?

  1. 10°
  2. 20°
  3. 40°
  4. 50°
9. Джейсон собирает стол для его спальня. Он хочет, чтобы письменный стол помещался в углу его комнаты, и решил использовать трапециевидную форму. Если Джейсон использует размеры, показанные на рисунке ниже, сколько квадратных футов фанеры ему понадобится для изготовления столешницы?

  1. 5 футов²
  2. 6 футов²
  3. 9 футов²
  4. 12 футов 2
9000 4 10. Недавно Натали купила шкатулку для драгоценностей, но хочет заново обтянуть шкатулку более яркой тканью. . Если шкатулка представляет собой куб со стороной 8 см, сколько ткани понадобится Натали, чтобы покрыть все стороны шкатулки?
  1. 64 см 2
  2. 192 см 2
  3. 384 см 2
  4. 512 см 2

1. D: Поскольку исходный треугольник расширен в 2 раза, длина каждой стороны будет умножена на 2, чтобы получить длины сторон нового треугольника. Следовательно, 8×2=16, 12×2=24 и 18×2=36. Тогда 16+24+36=76. Ответ A получается, если каждая из длин сторон была неправильно разделена на 2. Ответ B получается, если 2 было неправильно вычтено из каждой из длин сторон. Ответ C получается, если к длине каждой стороны было неправильно прибавлено 2.

2. A: Чтобы определить коэффициент масштабирования, возьмите длины сторон масштабированного прямоугольника и разделите их на соответствующие стороны исходного прямоугольника: 1 / 4 = 1 / 4 и 3 / 12 = 1 / 4 . Следовательно, масштабный коэффициент, используемый для масштабирования прямоугольника, равен 1/4. Ответ Б получается, если масштабный коэффициент был определен неправильно путем деления сторон внутри каждого прямоугольника в порядке  4 / 12 = 1 / 3 и 1 / 3 = 1 / 3 . Ответ C получается, если масштабный коэффициент был неправильно определен путем деления сторон внутри каждого прямоугольника в следующем порядке: 12 / 4 = 3 и 3 / 1 = 3. Ответ D получается, если масштабный коэффициент был установлен неправильно, чтобы разделить исходные длины сторон на значения масштабированных длин сторон: 12 / 3 = 4 и 4 / 1 =4.

3. D: Чтобы построить треугольник, сумма трех углов должна составлять 180°. В ответе D сумма двух прямых углов будет равна 180°, поэтому добавление к этому значению острого угла сделает сумму больше 180°. Следовательно, треугольник не может быть построен с двумя прямыми углами. Ответы A, B и C — это все возможные варианты углов для построения треугольника.

4. D: Горизонтальное разрезание правой прямоугольной призмы приведет к созданию срезов, параллельных основанию призмы. Поскольку основание призмы представляет собой квадрат со стороной 4, каждый из горизонтальных срезов также будет иметь форму квадрата. Ответы A и C — это формы, которыми выглядит основание, если не принимать во внимание рисунок трехмерного изображения и то, что призма представляет собой правильную прямоугольную призму. Ответ B — двумерная фигура, полученная в результате вертикального разреза призмы.

5. C: Формула площади круга: A=pr 2 . Поскольку диаметр сада равен 10 футам, радиус сада равен 5 футам.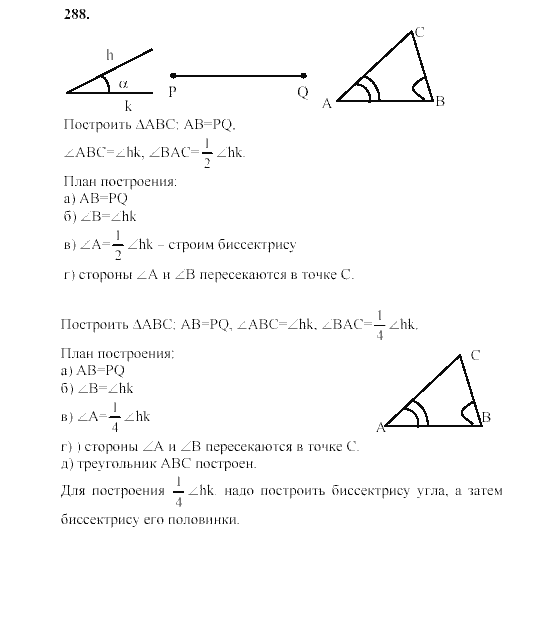 Следовательно, A=3,14(5 «футов») 2 = 78,5 дюймов   2 . Ответ А — это результат, если радиус не был возведен в квадрат, т. е. ?r. Ответ B — это результат, если была рассчитана окружность сада. Ответ D является результатом использования диаметра в формуле площади.

6. B: Расстояние вокруг каждой шины равно длине окружности: C=2pr=2(3,14)(3 фута)=18,84 фута. Ответ А — это результат, если бы радиус не удваивался. Ответ C – площадь внутри шины. Ответ D — это результат, если в формуле площади использовался диаметр.

7. C: Два угла, показанные на рисунке, являются дополнительными. Чтобы найти x, необходимо использовать следующее уравнение: 10x-5+35=180. Это уравнение упрощается: 10x+30=180. После вычитания 30 с обеих сторон уравнение становится 10x=150. Наконец, после деления обеих частей на 10, решение x=15. Ответ A получается, если считать углы равными и составить уравнение как 10x-5=35. Ответ B получается в результате рассмотрения углов как дополнительных и составления уравнения в виде 10x-5+35=9. 0. Ответ D получается, если уравнение было правильно составлено как 10x+30=180, но затем к обеим частям было неправильно добавлено 30, чтобы получить 10x=210.

8. C: Прежде чем мы сможем найти меру ?DBC, нам сначала нужно найти x. Поскольку ?ABD и ?DBC дополняют друг друга, нам нужно использовать уравнение m ?ABD + m ?DBC = 90. Подставляя значения m ?ABD и m ?DBC, уравнение принимает вид 5x+4x=90. Это уравнение упрощается: 9x=90. Наконец, после деления обеих частей уравнения на 9 результат x=10. Чтобы найти меру ?DBC, подставим x=10 в (4x)°, чтобы получить (4(10))°=40°. Ответ А — это значение х. Ответ B — это значение x, если бы углы рассматривались как дополнительные и были установлены как 5x+4x=180. Ответ D является мерой ?ABD. 92. В ответе А при расчете использовалась только база 5 футов. В ответе C для высоты использовалось значение 3 фута. В ответе D 1/2 была исключена из формулы, поэтому площадь была рассчитана неправильно: A=h(b_1+b_2).

10. C: Количество ткани, необходимое для покрытия шкатулки, равно площади поверхности шкатулки. Формула площади поверхности куба: SA=6 2 , где s — длина одной стороны. Следовательно, площадь поверхности шкатулки для драгоценностей равна SA=6(8 см) 2 = 6(64см) 2  =384 см  2 . В ответе А вычислялась площадь только одной стороны коробки. В ответе Б периметр одной стороны ящика умножался на 6. В ответе Г вычислялся объем ящика.

Соотношение углов | Геометрия прямых

В 8 классе вы определили отношения между углами на прямых линиях. В этом главе вы пересмотрите все взаимосвязи углов и напишите к ним четкие описания. 9\круг\).

  1. Ответьте на вопросы о рисунок ниже.

    1. Угол \(\hat{FOD}\) на рисунке меньше или больше прямого угла?
    2. Угол \(\hat{FOE}\) на приведенном выше рисунке меньше или больше прямого угла?

    На рисунке выше \(\text{F}\)\(\hat{\text{O}}\)\(\text{D}\) + \(\text{F}\)\( \ шляпа {\ текст {O}} \) \ (\ текст {C} \) = половина оборота = 180\(^\круг\). 9\круг\).

    1. Насколько большой \(\text{C}\)\(\шляпа{\text{M}}\)\(\text{P}\)?
    2. Объясните свои рассуждения.

  2. На рисунке ниже AMB представляет собой прямую линию и \(\text{A}\)\(\hat{\text{M}}\)\(\text{C}\) и \(\text{B}\)\(\ шляпа {\ text {M}} \) \ (\ text {C} \) равные углы.

    1. Насколько они велики углы?
    2. Откуда ты это знаешь?

    Когда одна линия образует две под равными углами там, где она встречается с другой линией, эти две линии говорят, что перпендикулярны .

    Поскольку два равных угла являются углами на прямой, их сумма равна 180°, следовательно, каждый угол составляет 90°.

  3. На рисунке ниже линии AB и CD пересекаются в точке М.

    В этой главе вы обязаны приводить веские причины для каждого заявления, которое вы делать.

    1. Похоже ли, что \(\text{C}\)\(\hat{\text{M}}\)\(\text{A}\) и \(\text{B}\)\( \шляпа{\text{M}}\)\(\text{D}\) равны?
    2. Можете ли вы объяснить, почему они равны?
    3. Что означает \(\text{C}\)\(\hat{\text{M}}\)\(\text{A}\) + \(\text{D}\)\(\hat{\text{M}}\)\(\text{A}\) равно?

      Почему ты так говоришь?

    4. Что такое \(\text{C}\)\(\hat{\text{M}}\)\(\text{A}\) + \(\text{C}\)\(\шляпа{\text{M}}\)\(\text{B}\)?

      Почему ты так говоришь?

    5. Есть верно, что \(\text{C}\)\(\hat{\text{M}}\)\(\text{A}\) + \(\текст{D}\)\(\шляпа{\текст{M}}\)\(\текст{A}\) = \(\текст{С}\)\(\шляпа{\текст{М}}\)\(\текст{А}\) + \(\текст{С}\)\(\шляпа{\текст{М}}\)\(\текст{В}\)
    6. Какой угол встречается на обоих стороны уравнения в (e)?
  4. Посмотрите внимательно на свой ответы на вопросы с 5(c) по 5(e).

    Теперь попробуй объяснить наблюдение в вопросе 5(а).

  5. На рисунке ниже AB и CD пересекаются в M. Образуются четыре угла. Угол CMB и угол AMD называются 9029\circ\), насколько велик угол AMD?
  6. Почему так говорят?

Линии и углы

Линия, пересекающая другие линий называется секущей .

В приведенном выше шаблоне AB параллельно CD и EF \(||\) GH \(||\) KB \(||\) ЛД.

  1. Уголки a , b , c , d и и равны соответствующим углам . Сделайте соответствующие углы выглядят равными?
  2. Расследовать ли соответствующие углы равны с помощью кальки. Обведите угол, который вы хотите сравнить с другими углами, и поместите его поверх другого угла, чтобы узнать, равны ли они. Что ты заметил?
  3. Уголки f , h , j , m и n также являются соответствующими углами. Определите все остальные группы соответствующих углов в шаблон.
  4. Опишите позицию соответственных углов, которые образуются при поперечном пересекает другие линии.
  5. Ниже приведены пары чередующихся уголков : g и o ; й и с ; и к и р .

    Эти углы кажутся быть равным?

  6. Расследовать ли альтернативные углы равны с помощью кальки. След угол, который вы хотите сравнить, и поместите его поверх другого угол, чтобы узнать, равны ли они.
    Что ты заметил?
  7. Определить еще две пары альтернативные углы.
  8. Четко опишите относительное положение альтернативных углов, которые образуются, когда поперечная пересекает другие прямые.
  9. Вы заметили что-то о некоторых парах соответствующих углов, когда вы провели расследование в вопросе 6? Опиши себя найти.
  10. Уголки f и o ; i и q и k и s — все пары внутренние углы . Определите еще три пары совмещенные внутренние углы в узоре.

Углы одинаковые относительное положение на каждом перекрестке, где прямая линия кресты два других называются соответствующие углы .

Углы по разные стороны поперечный и между двумя другими линиями называются

альтернативных угла . .

Углы на одной стороне поперечный и между двумя другими линиями называются co-interior углы . .

Углы, образованные параллельными прямыми

Соответствующие углы

Прямые AB и CD ниже никогда не пересекаются. Линии, которые никогда не пересекаются и находятся на фиксированном расстоянии от одной другие называются параллельными линиями. Мы пишем АВ \(||\) CD.

Параллельные линии имеют одинаковом направлении, то есть они образуют равный соответствующий углы с любой прямой, которая их пересекает.

Линия EF пересекает AB в G и CD в H.

EF — секущая, параллельные прямые AB и CD.

    1. Посмотрите внимательно на углы EGA и EHC на рисунке выше. Их называют соответствующими углами . Они кажутся равными?
    2. Измерьте два угла, чтобы проверить, они равны. Что ты заметил?
  2. Предположим, что \(\text{E}\)\(\hat{\text{G}}\)\(\text{A}\) и \(\text{E}\)\(\hat{\text {H}}\)\(\text{C}\) действительно равны. Будет ли \(\text{E}\)\(\hat{\text{G}}\)\(\text{B}\) и \(\text{E}\)\(\hat{\text{ H}}\)\(\text{D}\) тоже равны? Приведите причины поддержите свой ответ.

    Когда две параллельные линии пересеченная секущей, соответствующие углы равны.

Переменные углы

Углы \(\text{B}\)\(\hat{\text{G}}\)\(\text{F}\) и \(\text{C}\)\(\hat{ \text{H}}\)\(\text{E}\) ниже называются альтернативными углы . Они находятся на противоположных сторонах поперечной.

  1. Считаете ли вы углы AGF и DHE также следует называть альтернативными углами?
  2. Как вы думаете, альтернативный углы равны? Исследуйте, используя кальку, например вы делали ранее, или точно измерьте углы с помощью транспортир. Что вы заметили?

    При разрезании параллельных линий у секущей противоположные углы равны.

  3. Попробуйте объяснить, почему противоположные углы равны, если линии, пересекаемые поперечные параллельны, имея в виду, что соответствующие углы равны.

    Ответив на следующие вопросы, вы должны быть в состоянии увидеть, как вы можете объяснить, почему чередовать углы равны, если параллельные прямые пересечены поперечный.

  4. Уголки \(\текст{B}\)\(\шляпа{\текст{G}}\)\(\текст{H}\) и \(\text{D}\)\(\hat{\text{H}}\)\(\text{F}\) на рисунке соответствующие углы?

    Что вы знаете о соответствующие углы?

    1. Что вы можете сказать о \(\text{B}\)\(\hat{\text{G}}\)\(\text{H}\) + \(\text{A}\)\( \hat{\text{G}}\)\(\text{H}\) Укажите причину.
    2. Что вы можете сказать о \(\текст{D}\)\(\шляпа{\текст{H}}\)\(\текст{G}\) + \(\text{C}\)\(\шляпа{\text{H}}\)\(\text{G}\)? Дай причину.
    3. Правда ли, что \(\текст{B}\)\(\шляпа{\текст{G}}\)\(\текст{H}\) + \(\текст{А}\)\(\шляпа{\текст{G}}\)\(\текст{Н}\) = \(\текст{D}\)\(\шляпа{\текст{H}}\)\(\текст{G}\) + \(\text{C}\)\(\шляпа{\text{H}}\)\(\text{G}\)? Объяснять.
    4. Будет ли уравнение в (c) по-прежнему верным если вы замените угол \(\text{B}\)\(\hat{\text{G}}\)\(\text{H}\) на левая сторона с углом \(\text{C}\)\(\hat{\text{H}}\)\(\text{G}\)?
  6. Посмотрите внимательно на свой поработайте над вопросом 7 и напишите объяснение, почему чередуются углы равны, если две параллельные прямые пересечены поперечный.
    Внутренние углы

    Углы \(\text{A}\)\(\hat{\text{G}}\)\(\text{H}\) и \(\text{C}\)\(\hat{\ text{H}}\)\(\text{G}\) на рисунке ниже называются внутренние углы .

    «со-» означает вместе.

    «совместный интерьер» означает на одном и том же сторона.

    Они на той же стороне поперечной.

    1. Что вы знаете о \(\text{C}\)\(\hat{\text{H}}\)\(\text{G}\) + \(\text{D}\)\(\шляпа{\text{H}}\)\(\text{G}\)? Объяснять.
    2. Что ты знаешь о \(\текст{B}\)\(\шляпа{\текст{G}}\)\(\текст{H}\) + \(\text{A}\)\(\шляпа{\text{G}}\)\(\text{H}\)? Объяснять.
    3. Что ты знаешь о \(\текст{B}\)\(\шляпа{\текст{G}}\)\(\текст{H}\)+ \(\text{C}\)\(\шляпа{\text{H}}\)\(\text{G}\)? Объяснять. 9\круг\). Другой способ сказать это состоит в том, чтобы сказать, что два смежных внутренних угла являются 90 294 дополнительными.

      Определите и назовите углы

      1. На рисунке ниже линия RF перпендикулярна AB.

        1. Является ли RF также перпендикулярным CD? Оправдывать Ваш ответ.
        2. Назовите четыре пары дополнительных углов на рисунке. В каждом случае скажите, откуда вы знаете, что углы являются дополнительными.
        3. Назовите четыре пары внутренних углов в фигура.
        4. Назовите четыре пары соответствующих углов на рисунке.
        5. Назовите четыре пары противоположных углов в фигура.
      2. Теперь вам дан этот AB и CD на рисунке ниже параллельны.
        1. Если также указано, что РФ перпендикулярно AB, будет ли RF перпендикулярно CD? Обосновать ответ.
        2. Назовите все пары дополнительных углов на рисунке. В каждом случае скажите, откуда вы знаете, что углы являются дополнительными.
        3. Предположим, \(\text{E}\)\(\hat{\text{G}}\)\(\text{A}\) = x. Укажите размер как можно большего числа углы на рисунке как можете, через х. Каждый раз указывайте причину Ваш ответ.

      Решение проблем

      1. Отрезки AB и CD на рисунке ниже параллельны. EF и IJ также параллельно. Отметьте эти факты на рисунке, а затем ответьте на вопросы.

        Когда вы решаете проблемы в геометрии вы можете использовать сокращенный способ написать свои причины.

        No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *