Числовые выражения – как решить задачу (алгебра 7 класс) по вычислению значений числового выражения
4.7
Средняя оценка: 4.7
Всего получено оценок: 836.
4.7
Средняя оценка: 4.7
Всего получено оценок: 836.
Одним из понятий алгебры 7 класса являются числовые выражения. Они используются для решения задач. Что собой представляют числовые выражения и как их использовать?
Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.
Опыт работы учителем математики — более 33 лет.
Определение понятия
Какое же выражение является числовым в алгебре? Так обозначают запись, составленную из чисел, скобок и знаков сложения, вычитания, умножения и деления.
Понятие числового выражения допустимо только в том случае, если запись несет смысловую нагрузку. К примеру, запись 4-) не является числовым выражением, так как она бессмысленна.
Примеры числовых выражений:
- 25 х 13;
- 32 – 4 + 8;
- 12 х (25 – 5).

Характеристики понятия
Числовое выражение имеет несколько свойств, которые используются в решении примеров и задач. Рассмотрим эти свойства подробнее. Для этого возьмем такой пример – 45 + 21 – (6 х 2).
Значение
Так как числовое выражение содержит знаки различных арифметических действий, их можно выполнить и получить в результате какое-то число. Оно называется значением числового выражения. Как производится вычисление значений числового выражения? Оно соответствует правилам выполнения арифметических действий:
- в выражениях без скобок выполняют действия, начиная с высших ступеней – умножение и деление, затем сложение и вычитание;
- если имеется несколько одинаковых действий, их выполняют слева направо;
- если есть скобки, сначала выполняют действия в них;
- при вычислении дробей сначала выполняют действия в числителе и знаменателе, а затем числитель делят на знаменатель.
Применим эти правила к нашему примеру.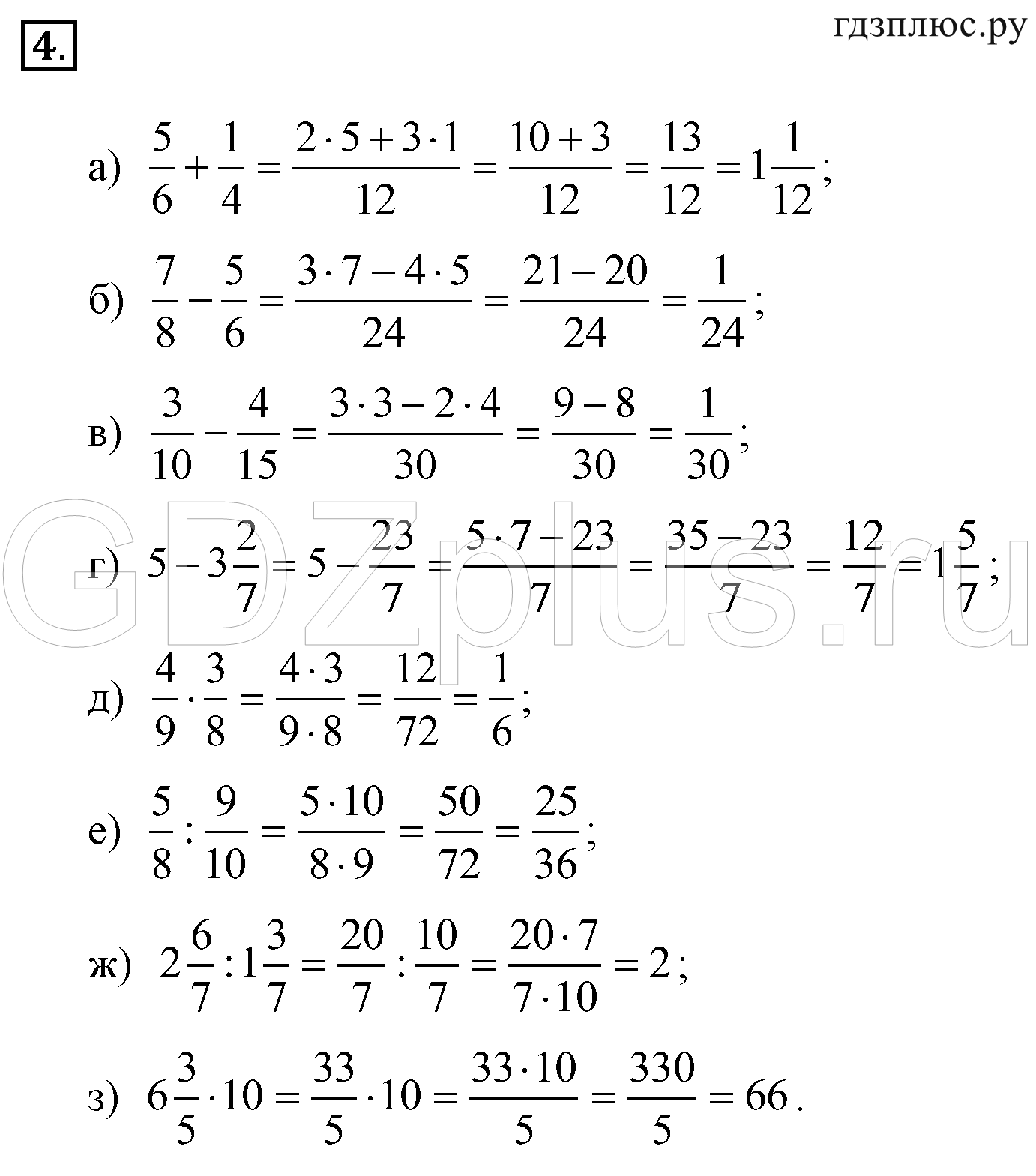
Итак, число 54 будет являться значением выражения 45 + 21 – (6 х 2).
Для того, чтобы правильно прочитать числовое выражение нужно определить, какое действие будет являться последним в подсчетах. В выражении 45 + 21 – (6 х 2) последним действием было вычитание. Соответственно, называть это выражение нужно “разность”. Если бы вместо знака “-” стоял знак “+”, выражение называли бы суммой.
Если у выражения невозможно произвести подсчет значения, его называют не имеющим смысла. Например, смысла не имеет такое выражение: 12 : (4 – 4). В скобках разность равна нулю. А по правилам математики на ноль делить нельзя. Значит, найти значение выражения невозможно.
Равенство
Так называют запись, в которой два числовых выражения разделены знаком “=”. Например, 45 + 21 – (6 х 2) = 66 – 12. Обе части записи равны числу 54, а значит, они равны друг другу. Такое равенство называют верным.
Если же написать 45 + 21 – (6 х 2) = 35 + 12, это равенство будет неверным.
Пример задачи
Для того, чтобы лучше понять тему, рассмотрим пример решения задачи. Как решить задачу числовым выражением?
Дано: две машины выезжают из одного пункта в другой. Они поедут по разным дорогам. Одной машине предстоит проехать 35 км, а другой – 42 км. Первая машина едет со скоростью 70 км/ч, а вторая – 84 км/ч Окажутся ли они в конечном пункте в одно и то же время?
Решение: нужно составить два числовых выражения, чтобы найти время в пути у каждой машины. Если они окажутся одинаковыми, значит, машины прибудут в конечный пункт одновременно. Для того, чтобы найти время, нужно расстояние разделить на скорость. 35 км : 70 км/ч = 0,5 ч. 42 км : 84 км/ч = 0,5 ч.
Итак, обе машины приехали в конечный пункт одновременно, через полчаса.
Что мы узнали?
Из темы по алгебре, изучаемой в 7 классе, мы узнали, что числовое выражение – это запись из чисел и знаков арифметических действий. С помощью числовых выражений можно решать задачи. Если последним действием в числовом выражении было вычитание (сложение), то его называют разностью (суммой). Если последним действием было бы умножение (деление), то выражение называлось бы произведением (частным).
С помощью числовых выражений можно решать задачи. Если последним действием в числовом выражении было вычитание (сложение), то его называют разностью (суммой). Если последним действием было бы умножение (деление), то выражение называлось бы произведением (частным).
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Ольга Кузина
10/10
Мария Гаврилова
10/10
Александра Веригина
9/10
Макс Чупин
6/10
Эдик Брага
10/10
Наталья Слинькова
10/10
Любовь Дружинина
8/10
Света Колодий
Джек Кортес
8/10
Александра Елисеева
9/10
Оценка статьи
4.7
Средняя оценка: 4.7
Всего получено оценок: 836.
А какая ваша оценка?
Задачи по алгебре.
 7 класс 159 ₽ + до 23 бонусов
7 класс 159 ₽ + до 23 бонусовКупить
Цена на сайте может отличаться от цены в магазинах сети. Внешний вид книги может отличаться от изображения на сайте.
Осталось мало 3Цена на сайте может отличаться от цены в магазинах сети. Внешний вид книги может отличаться от изображения на сайте.
Книга содержит задачи повышенной сложности по алгебре для учащихся 7 класса. Большинство из 11 глав начинается с перечисления основных фактов и понятий, относящихся к этой главе. Затем приводятся решения нескольких наиболее типичных задач. После этого следуют задачи для самостоятельного решения. В конце приведены ответы и почти ко всем задачам даны указания.
.Для учителей математики и для школьников, которые хотят научиться решать задачи, немного более сложные, чем задачи из учебника. По этой книге можно подготовиться к математическим олимпиадам, уровень которых ниже уровня заключительного этапа Всероссийской олимпиады.
Описание
Характеристики
Книга содержит задачи повышенной сложности по алгебре для учащихся 7 класса. Большинство из 11 глав начинается с перечисления основных фактов и понятий, относящихся к этой главе. Затем приводятся решения нескольких наиболее типичных задач. После этого следуют задачи для самостоятельного решения. В конце приведены ответы и почти ко всем задачам даны указания. .Для учителей математики и для школьников, которые хотят научиться решать задачи, немного более сложные, чем задачи из учебника. По этой книге можно подготовиться к математическим олимпиадам, уровень которых ниже уровня заключительного этапа Всероссийской олимпиады.
МЦНМО
На товар пока нет отзывов
Поделитесь своим мнением раньше всех
Как получить бонусы за отзыв о товаре
1
Сделайте заказ в интернет-магазине2
Напишите развёрнутый отзыв от 300 символов только на то, что вы купили3
Дождитесь, пока отзыв опубликуют.
Если он окажется среди первых десяти, вы получите 30 бонусов на Карту Любимого Покупателя. Можно писать неограниченное количество отзывов к разным покупкам – мы начислим бонусы за каждый, опубликованный в первой десятке.
Правила начисления бонусовЕсли он окажется среди первых десяти, вы получите 30 бонусов на Карту Любимого Покупателя. Можно писать неограниченное количество отзывов к разным покупкам – мы начислим бонусы за каждый, опубликованный в первой десятке.
Правила начисления бонусовКнига «Задачи по алгебре. 7 класс» есть в наличии в интернет-магазине «Читай-город» по привлекательной цене.
Если вы находитесь в Москве, Санкт-Петербурге, Нижнем Новгороде, Казани, Екатеринбурге, Ростове-на-Дону или любом
другом регионе России, вы можете оформить заказ на книгу
«Задачи по алгебре. 7 класс» и выбрать удобный способ его получения: самовывоз, доставка курьером или отправка
почтой. Чтобы покупать книги вам было ещё приятнее, мы регулярно проводим акции и конкурсы.
7 класс» и выбрать удобный способ его получения: самовывоз, доставка курьером или отправка
почтой. Чтобы покупать книги вам было ещё приятнее, мы регулярно проводим акции и конкурсы.
Решение словесных задач, ведущих к неравенствам: CCSS.Math.Content.7.EE.B.4b
All Common Core: Математические ресурсы для 7-го класса
7 диагностических тестов 110 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 4 5 Следующая →
Common Core: Справка по математике для 7-го класса » Выражения и уравнения » Решение задач со словами, ведущих к неравенствам: CCSS.Math.Content.7.EE.B.4b
Запишите в виде алгебраического неравенства:
Двадцать вычесть из произведения семь и число больше ста.
Возможные ответы: Правильный ответ: Объяснение: «Произведение семи и числа » равно .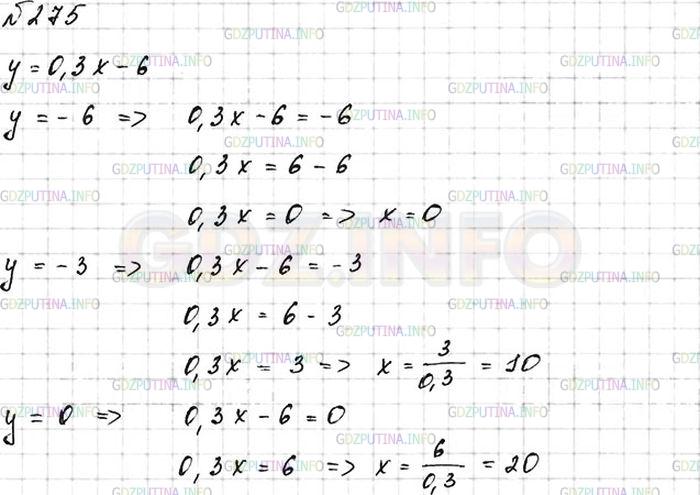 «Двадцать вычесть из произведения семи и числа» . «Превышает сто» означает, что это число больше ста, поэтому правильное неравенство
«Двадцать вычесть из произведения семи и числа» . «Превышает сто» означает, что это число больше ста, поэтому правильное неравенство
Сообщить об ошибке
Запишите в виде алгебраического неравенства:
Удвоенная сумма числа и шестнадцати не меньше шестидесяти.
Возможные ответы: Правильный ответ: Объяснение:«Сумма числа и шестнадцати» переводится как ; вдвое больше этой суммы. » Не меньше шестидесяти» означает, что оно больше или равно шестидесяти, поэтому искомое неравенство равно
.
Сообщить об ошибке
Запишите в виде алгебраического неравенства:
Удвоенная сумма числа и шестнадцати не превосходит восьмидесяти.
Возможные ответы: Правильный ответ: Объяснение:«Сумма числа и шестнадцати» переводится как ; вдвое больше этой суммы. «Не превышает восьмидесяти» означает, что оно меньше или равно восьмидесяти, поэтому искомое неравенство равно
Сообщить об ошибке
Как бы вы написали уравнения: «Сегодня я могу потратить не более долларов, когда пойду в магазин».
Формулировка предложения предполагает, что человек может потратить до долларов, но не больше. Это говорит о том, что сумма расходов может быть , но не превышать ее.
Ваш ответ:
Сообщить об ошибке
Для следующей задачи запишите неравенство.
Семь меньше, чем в два раза больше четырнадцати.
Возможные ответы: Правильный ответ: Объяснение:Семь меньше чем в два раза число больше четырнадцати.
Давайте рассмотрим проблему шаг за шагом.
Если мы не знаем значение числа, мы даем ему имя переменной. скажем х . Итак, мы видим в задаче
Семь меньше, чем в два раза число больше четырнадцати.
Итак, мы заменим на номер на x.
Семь меньше, чем в два раза x больше четырнадцати.
Теперь мы видим, что это говорит «дважды» x, поэтому мы напишем это как
На семь меньше 2 x больше четырнадцати.
Задача говорит «на семь меньше», чем в 2 раза. Это просто означает, что мы берем 2x и вычитаем семь. Таким образом, мы получаем
2x — 7 больше четырнадцати
Мы знаем символ «больше чем». Мы можем написать
2x — 7 > четырнадцать
Наконец, мы выпишем число четырнадцать.
2x — 7 > 14
Сообщить об ошибке
Выразите следующее в виде неравенства:
Количество яблок у Боба () более чем в два раза превышает количество бананов у Адама ().
Возможные ответы: Правильный ответ: Объяснение: Чтобы решить, вы должны преобразовать оператор в выражение. Ключевая работа «есть». Все, что находится слева от этого в предложении, будет в левой части выражения. То же самое касается права. Таким образом, находится слева, а находится справа.
Все, что находится слева от этого в предложении, будет в левой части выражения. То же самое касается права. Таким образом, находится слева, а находится справа.
Сообщить об ошибке
Запишите следующее в виде математического неравенства:
Число меньше или равно трехкратной сумме другого числа и пяти
Возможные ответы: Правильный ответ: 90 018 Пояснение:Запишите следующее в виде математического неравенства:
Число меньше или равно трехкратной сумме другого числа и пяти.
Начнем с
«Число», назовем его x
«…меньше или равно…»
На данный момент имеем:
Теперь
«…три раз…»
«…сумма другого числа и пяти.»
Итак, все вместе:
Сообщить об ошибке
Запишите неравенство:
Два меньше, чем удвоенное число меньше двух.
Возможные ответы: Правильный ответ: Объяснение: Разбейте оператор на части. Пусть это число будет .
Пусть это число будет .
Двойное число:
На два меньше, чем удвоенное число:
Меньше двух:
Объедините части.
Ответ:
Сообщить об ошибке
Запишите неравенство: Число в три раза меньше, чем в два раза больше, чем в три раза.
Возможные ответы: Правильный ответ: Пояснение:Разбейте предложение на части. Пусть число будет .
Удвоенное число:
На три меньше, чем удвоенное число:
На три меньше, чем удвоенное число больше, чем:
Втрое больше числа:
Объедините члены, чтобы сформировать неравенство.
Ответ:
Сообщить об ошибке
Запишите неравенство: Число меньше трех меньше трех.
Возможные ответы: Правильный ответ: Объяснение:Пусть число будет . Разделите проблему на части.
Число меньше трех:
Меньше трех:
Объедините все термины.
Ответ:
Сообщить об ошибке
← Назад 1 2 3 4 5 Далее →
Уведомление об авторских правах
All Common Core: Математические ресурсы для 7-го класса
7 Диагностические тесты 110 практических тестов Вопрос дня Карточки Обучение по концепции
Математика, 7 класс, алгебраическое мышление
CCSS.Math.Content.7.EE.A.1 7 класс, выражения и уравнения
Кластер: использование свойств операций для создания эквивалентных выражений
Стандарт: применение свойств операций в качестве стратегий для сложения, вычитания, факторизации и расширения линейных выражений с рациональными коэффициентами.
CCSS.Math.Content.7.EE.A.2 7 класс, выражения и уравнения
Кластер: использование свойств операций для создания эквивалентных выражений
Стандарт: понимание того, что переписывание выражения в разных формах в контексте задачи может пролить свет на проблему и на то, как связаны величины в ней. Например, a + 0,05a = 1,05a означает, что «увеличение на 5%» равнозначно «умножению на 1,05».
Например, a + 0,05a = 1,05a означает, что «увеличение на 5%» равнозначно «умножению на 1,05».
CCSS.Math.Content.7.EE.B.3 7 класс, выражения и уравнения
Кластер: решение реальных и математических задач с использованием числовых и алгебраических выражений и уравнений
Стандарт: решение многоэтапных реальных и математических задач, поставленных с положительными и отрицательными числа, дроби и десятичные дроби), используя инструменты стратегически. Применяйте свойства операций как стратегии для расчетов с числами в любой форме; конвертировать между формами по мере необходимости; и оценить обоснованность ответов, используя умственные вычисления и стратегии оценки. Например: если женщина, зарабатывающая 25 долларов в час, получает повышение на 10%, она будет получать дополнительную 1/10 своей зарплаты в час, или 2,50 доллара, за новую зарплату в 27,50 долларов. Если вы хотите разместить полотенцесушитель 93/4 дюйма длиной в центре двери шириной 27 1/2 дюйма, вам нужно будет разместить планку примерно в 9 дюймах от каждого края; эту оценку можно использовать в качестве проверки точного вычисления.
CCSS.Math.Content.7.EE.B.4 7 класс, выражения и уравнения
Кластер: решение реальных и математических задач с использованием числовых и алгебраических выражений и уравнений
Стандарт: использование переменных для представления величин в реальной или математической задаче и построение простых уравнений и неравенств для решения проблемы, рассуждая о количествах.
CCSS.Math.Content.7.EE.B.4a 7 класс, выражения и уравнения
Кластер: решение реальных и математических задач с использованием числовых и алгебраических выражений и уравнений
Стандарт: решение текстовых задач, приводящих к уравнениям вида px + q = r и p(x + q) = r, где p, q и r — конкретные рациональные числа. Решите уравнения этих форм бегло. Сравните алгебраическое решение с арифметическим, указав последовательность операций, используемых в каждом подходе. Например, периметр прямоугольника равен 54 см. Его длина составляет 6 см. Какова его ширина?
Какова его ширина?
CCSS.Math.Content.7.EE.B.4b 7 класс, выражения и уравнения
Кластер: решение реальных и математических задач с использованием числовых и алгебраических выражений и уравнений
Стандарт: решение текстовых задач, приводящих к неравенствам вида px + q > r или px + q < r, где p, q и r — конкретные рациональные числа. Нарисуйте график множества решений неравенства и интерпретируйте его в контексте проблемы. Например, как продавец, вам платят 50 долларов в неделю плюс 3 доллара за продажу. На этой неделе вы хотите, чтобы ваша зарплата была не менее 100 долларов. Напишите неравенство для количества продаж, которое вам нужно сделать, и опишите решения.
CCSS.Math.Practice.MP.1 Математические практики
Кластер: Математические практики
Стандарт: Разбираться в задачах и настойчиво решать их. Подкованные в математике учащиеся начинают с того, что объясняют себе смысл задачи и ищут пути ее решения. Они анализируют данные, ограничения, отношения и цели. Они строят предположения о форме и значении решения и планируют путь решения, а не просто пытаются найти решение. Они рассматривают аналогичные проблемы и пробуют частные случаи и более простые формы исходной задачи, чтобы получить представление о ее решении. Они контролируют и оценивают свой прогресс и при необходимости меняют курс. Учащиеся постарше могут, в зависимости от контекста задачи, преобразовывать алгебраические выражения или менять окно просмотра на своем графическом калькуляторе, чтобы получить необходимую им информацию. Подкованные в математике учащиеся могут объяснять соответствия между уравнениями, словесными описаниями, таблицами и графиками или рисовать диаграммы важных функций и взаимосвязей, графически отображать данные и искать закономерности или тенденции. Младшие школьники могут полагаться на использование конкретных объектов или изображений, чтобы помочь осмыслить и решить проблему. Математически подкованные учащиеся проверяют свои ответы на задачи, используя другой метод, и они постоянно спрашивают себя: «Имеет ли это смысл?» Они могут понять подходы других к решению сложных проблем и определить соответствие между различными подходами.
Они анализируют данные, ограничения, отношения и цели. Они строят предположения о форме и значении решения и планируют путь решения, а не просто пытаются найти решение. Они рассматривают аналогичные проблемы и пробуют частные случаи и более простые формы исходной задачи, чтобы получить представление о ее решении. Они контролируют и оценивают свой прогресс и при необходимости меняют курс. Учащиеся постарше могут, в зависимости от контекста задачи, преобразовывать алгебраические выражения или менять окно просмотра на своем графическом калькуляторе, чтобы получить необходимую им информацию. Подкованные в математике учащиеся могут объяснять соответствия между уравнениями, словесными описаниями, таблицами и графиками или рисовать диаграммы важных функций и взаимосвязей, графически отображать данные и искать закономерности или тенденции. Младшие школьники могут полагаться на использование конкретных объектов или изображений, чтобы помочь осмыслить и решить проблему. Математически подкованные учащиеся проверяют свои ответы на задачи, используя другой метод, и они постоянно спрашивают себя: «Имеет ли это смысл?» Они могут понять подходы других к решению сложных проблем и определить соответствие между различными подходами.
CCSS.Math.Practice.MP.2 Математические практики
Кластер: Математические практики
Стандарт: Рассуждать абстрактно и количественно. Учащиеся, обладающие математическими способностями, понимают величины и их отношения в проблемных ситуациях. Студенты привносят две взаимодополняющие способности в решение проблем, связанных с количественными отношениями: способность деконтекстуализировать — абстрагировать данную ситуацию и представлять ее символически и манипулировать репрезентирующими символами, как если бы они жили собственной жизнью, не обязательно обращая внимание на свои референты — и способность контекстуализировать, делать паузы по мере необходимости в процессе манипулирования, чтобы исследовать референты для задействованных символов. Количественное рассуждение влечет за собой привычки создавать последовательное представление проблемы; рассмотрение задействованных единиц; обращать внимание на значение величин, а не только на то, как их вычислять; знание и гибкое использование различных свойств операций и объектов.
CCSS.Math.Practice.MP.3 Математические практики
Кластер: Математические практики
Стандарт: Придумывать жизнеспособные аргументы и критиковать рассуждения других. Подкованные в математике учащиеся понимают и используют заявленные предположения, определения и ранее установленные результаты при построении аргументов. Они строят предположения и выстраивают логическую последовательность утверждений, чтобы исследовать истинность своих предположений. Они способны анализировать ситуации, разбивая их на случаи, а также могут распознавать и использовать контрпримеры. Они обосновывают свои выводы, сообщают их другим и отвечают на аргументы других. Они индуктивно рассуждают о данных, выдвигая правдоподобные аргументы, учитывающие контекст, из которого эти данные возникли. Подкованные в математике учащиеся также способны сравнивать эффективность двух правдоподобных аргументов, отличать правильную логику или рассуждения от ошибочных и, если в аргументе есть изъян, объяснять, в чем он заключается. Учащиеся начальной школы могут создавать аргументы, используя конкретные референты, такие как объекты, рисунки, диаграммы и действия. Такие аргументы могут иметь смысл и быть правильными, даже если они не обобщаются и не становятся формальными до более поздних классов. Позже учащиеся учатся определять области, к которым применяется аргумент. Учащиеся всех классов могут слушать или читать аргументы других, решать, имеют ли они смысл, и задавать полезные вопросы, чтобы прояснить или улучшить аргументы.
Учащиеся начальной школы могут создавать аргументы, используя конкретные референты, такие как объекты, рисунки, диаграммы и действия. Такие аргументы могут иметь смысл и быть правильными, даже если они не обобщаются и не становятся формальными до более поздних классов. Позже учащиеся учатся определять области, к которым применяется аргумент. Учащиеся всех классов могут слушать или читать аргументы других, решать, имеют ли они смысл, и задавать полезные вопросы, чтобы прояснить или улучшить аргументы.
CCSS.Math.Practice.MP.4 Математические практики
Кластер: Математические практики
Стандарт: Модель с математикой. Учащиеся, хорошо разбирающиеся в математике, могут применять математику, которую они знают, для решения проблем, возникающих в повседневной жизни, обществе и на рабочем месте. В младших классах это может быть так же просто, как написать уравнение сложения для описания ситуации. В средних классах учащийся может применять пропорциональные рассуждения, чтобы спланировать школьное мероприятие или проанализировать проблему в сообществе. К старшей школе учащийся может использовать геометрию для решения задачи проектирования или использовать функцию для описания того, как одна интересующая величина зависит от другой. Подкованные в математике учащиеся, которые могут применять то, что они знают, спокойно делают предположения и приближения, чтобы упростить сложную ситуацию, понимая, что позже они могут потребовать пересмотра. Они способны определять важные величины в практической ситуации и отображать их отношения, используя такие инструменты, как диаграммы, двусторонние таблицы, графики, блок-схемы и формулы. Они могут математически анализировать эти отношения, чтобы делать выводы. Они обычно интерпретируют свои математические результаты в контексте ситуации и размышляют о том, имеют ли результаты смысл, возможно, улучшая модель, если она не достигла своей цели.
К старшей школе учащийся может использовать геометрию для решения задачи проектирования или использовать функцию для описания того, как одна интересующая величина зависит от другой. Подкованные в математике учащиеся, которые могут применять то, что они знают, спокойно делают предположения и приближения, чтобы упростить сложную ситуацию, понимая, что позже они могут потребовать пересмотра. Они способны определять важные величины в практической ситуации и отображать их отношения, используя такие инструменты, как диаграммы, двусторонние таблицы, графики, блок-схемы и формулы. Они могут математически анализировать эти отношения, чтобы делать выводы. Они обычно интерпретируют свои математические результаты в контексте ситуации и размышляют о том, имеют ли результаты смысл, возможно, улучшая модель, если она не достигла своей цели.
CCSS.Math.Practice.MP.5 Математические практики
Кластер: Математические практики
Стандарт: Стратегическое использование соответствующих инструментов. Подкованные в математике учащиеся рассматривают доступные инструменты при решении математической задачи. Эти инструменты могут включать карандаш и бумагу, конкретные модели, линейку, транспортир, калькулятор, электронную таблицу, систему компьютерной алгебры, статистический пакет или программное обеспечение для динамической геометрии. Профессиональные учащиеся достаточно хорошо знакомы с инструментами, соответствующими их классу или курсу, чтобы принимать обоснованные решения о том, когда каждый из этих инструментов может быть полезен, признавая как получаемое понимание, так и их ограничения. Например, математически подкованные старшеклассники анализируют графики функций и решений, построенные с помощью графического калькулятора. Они обнаруживают возможные ошибки, стратегически используя оценку и другие математические знания. Создавая математические модели, они знают, что технологии позволяют визуализировать результаты различных предположений, исследовать последствия и сравнивать прогнозы с данными.
Подкованные в математике учащиеся рассматривают доступные инструменты при решении математической задачи. Эти инструменты могут включать карандаш и бумагу, конкретные модели, линейку, транспортир, калькулятор, электронную таблицу, систему компьютерной алгебры, статистический пакет или программное обеспечение для динамической геометрии. Профессиональные учащиеся достаточно хорошо знакомы с инструментами, соответствующими их классу или курсу, чтобы принимать обоснованные решения о том, когда каждый из этих инструментов может быть полезен, признавая как получаемое понимание, так и их ограничения. Например, математически подкованные старшеклассники анализируют графики функций и решений, построенные с помощью графического калькулятора. Они обнаруживают возможные ошибки, стратегически используя оценку и другие математические знания. Создавая математические модели, они знают, что технологии позволяют визуализировать результаты различных предположений, исследовать последствия и сравнивать прогнозы с данными. Подкованные в математике учащиеся разных классов способны идентифицировать соответствующие внешние математические ресурсы, такие как цифровой контент, размещенный на веб-сайте, и использовать их для постановки или решения задач. Они могут использовать технологические инструменты для изучения и углубления своего понимания концепций.
Подкованные в математике учащиеся разных классов способны идентифицировать соответствующие внешние математические ресурсы, такие как цифровой контент, размещенный на веб-сайте, и использовать их для постановки или решения задач. Они могут использовать технологические инструменты для изучения и углубления своего понимания концепций.
CCSS.Math.Practice.MP.6 Математические практики
Кластер: Математические практики
Стандарт: Следите за точностью. Математически подкованные ученики стараются точно общаться с другими. Они стараются использовать четкие определения в обсуждениях с другими и в собственных рассуждениях. Они заявляют о значении выбранных ими символов, включая последовательное и уместное использование знака равенства. Они внимательно относятся к указанию единиц измерения и маркировке осей, чтобы прояснить соответствие с количествами в задаче. Они рассчитывают точно и эффективно, выражают числовые ответы с точностью, соответствующей контексту задачи. 2 + x + 1) может привести их к общей формуле суммы геометрического ряда. Работая над решением задачи, математически подкованные ученики контролируют процесс, уделяя внимание деталям. Они постоянно оценивают обоснованность своих промежуточных результатов.
2 + x + 1) может привести их к общей формуле суммы геометрического ряда. Работая над решением задачи, математически подкованные ученики контролируют процесс, уделяя внимание деталям. Они постоянно оценивают обоснованность своих промежуточных результатов.
MCCRS.Math.Content.7.EE.A.1 7 класс
Область обучения: выражения и уравнения
Стандарт: использование свойств операций для создания эквивалентных выражений
Индикатор: применение свойств операций в качестве стратегий для сложения, вычитания, факторизации и расширения линейных выражений с рациональными коэффициентами.
MCCRS.Math.Content.7.EE.A.2 7 класс
Область обучения: выражения и уравнения
Стандарт: использование свойств операций для создания эквивалентных выражений
Индикатор: понимание того, что переписывание выражения в разных формах в контексте задачи может пролить свет на проблему и на то, как связаны в ней количества. Например, a + 0,05a = 1,05a означает, что «увеличение на 5%» — это то же самое, что «умножение на 1,05». —
Например, a + 0,05a = 1,05a означает, что «увеличение на 5%» — это то же самое, что «умножение на 1,05». —
MCCRS.Math.Content.7.EE.B.3 7 класс
Область обучения: выражения и уравнения
Стандарт: решение реальных и математических задач с использованием числовых и алгебраических выражений и уравнений
Индикатор: решение многоэтапных реальных и математических задач с положительными и отрицательными рациональными числами в любой форме (целые числа, дроби и десятичные дроби) , используя инструменты стратегически. Применяйте свойства операций как стратегии для расчетов с числами в любой форме; конвертировать между формами по мере необходимости; и оценить обоснованность ответов, используя умственные вычисления и стратегии оценки. Например: если женщина, зарабатывающая 25 долларов в час, получает повышение на 10%, она будет получать дополнительную 1/10 своей зарплаты в час, или 2,50 доллара, за новую зарплату в 27,50 долларов. Если вы хотите разместить полотенцесушитель 93/4 дюйма длиной в центре двери шириной 27 1/2 дюйма, вам нужно будет разместить планку примерно в 9 дюймах от каждого края; эту оценку можно использовать в качестве проверки точного вычисления.
MCCRS.Math.Content.7.EE.B.4 7 класс
Область обучения: выражения и уравнения
Стандарт: решение реальных и математических задач с использованием числовых и алгебраических выражений и уравнений
Индикатор: использование переменных для представления величин в реальной или математической задаче и построение простых уравнений и неравенства для решения проблем, рассуждая о количествах.
MCCRS.Math.Content.7.EE.B.4a 7 класс
Область обучения: выражения и уравнения
Стандарт: решение реальных и математических задач с использованием числовых и алгебраических выражений и уравнений
Индикатор: решение текстовых задач, ведущих к уравнениям вида px + q = r и p(x + q) = r, где p, q и r — конкретные рациональные числа. Решите уравнения этих форм бегло. Сравните алгебраическое решение с арифметическим, указав последовательность операций, используемых в каждом подходе. Например, периметр прямоугольника равен 54 см. Его длина составляет 6 см. Какова его ширина?
Его длина составляет 6 см. Какова его ширина?
MCCRS.Math.Content.7.EE.B.4b 7 класс
Область обучения: выражения и уравнения
Стандарт: решение реальных и математических задач с использованием числовых и алгебраических выражений и уравнений
Индикатор: решение текстовых задач, приводящих к неравенствам вида px + q > r или px + q < r, где p, q и r — конкретные рациональные числа. Нарисуйте график множества решений неравенства и интерпретируйте его в контексте проблемы. Например, как продавец, вам платят 50 долларов в неделю плюс 3 доллара за продажу. На этой неделе вы хотите, чтобы ваша зарплата была не менее 100 долларов. Напишите неравенство для количества продаж, которое вам нужно сделать, и опишите решения.
MCCRS.Math.Practice.MP.1 Классы K-12
Область обучения: Математические практики
Стандарт: Математические практики
Показатель: Разбираться в задачах и настойчиво решать их. Подкованные в математике учащиеся начинают с того, что объясняют себе смысл задачи и ищут пути ее решения. Они анализируют данные, ограничения, отношения и цели. Они строят предположения о форме и значении решения и планируют путь решения, а не просто пытаются найти решение. Они рассматривают аналогичные проблемы и пробуют частные случаи и более простые формы исходной задачи, чтобы получить представление о ее решении. Они контролируют и оценивают свой прогресс и при необходимости меняют курс. Учащиеся постарше могут, в зависимости от контекста задачи, преобразовывать алгебраические выражения или менять окно просмотра на своем графическом калькуляторе, чтобы получить необходимую им информацию. Подкованные в математике учащиеся могут объяснять соответствия между уравнениями, словесными описаниями, таблицами и графиками или рисовать диаграммы важных функций и взаимосвязей, графически отображать данные и искать закономерности или тенденции. Младшие школьники могут полагаться на использование конкретных объектов или изображений, чтобы помочь осмыслить и решить проблему.
Подкованные в математике учащиеся начинают с того, что объясняют себе смысл задачи и ищут пути ее решения. Они анализируют данные, ограничения, отношения и цели. Они строят предположения о форме и значении решения и планируют путь решения, а не просто пытаются найти решение. Они рассматривают аналогичные проблемы и пробуют частные случаи и более простые формы исходной задачи, чтобы получить представление о ее решении. Они контролируют и оценивают свой прогресс и при необходимости меняют курс. Учащиеся постарше могут, в зависимости от контекста задачи, преобразовывать алгебраические выражения или менять окно просмотра на своем графическом калькуляторе, чтобы получить необходимую им информацию. Подкованные в математике учащиеся могут объяснять соответствия между уравнениями, словесными описаниями, таблицами и графиками или рисовать диаграммы важных функций и взаимосвязей, графически отображать данные и искать закономерности или тенденции. Младшие школьники могут полагаться на использование конкретных объектов или изображений, чтобы помочь осмыслить и решить проблему. Математически подкованные учащиеся проверяют свои ответы на задачи, используя другой метод, и они постоянно спрашивают себя: «Имеет ли это смысл?». Они могут понять подходы других к решению сложных задач и определить соответствие между различными подходами.
Математически подкованные учащиеся проверяют свои ответы на задачи, используя другой метод, и они постоянно спрашивают себя: «Имеет ли это смысл?». Они могут понять подходы других к решению сложных задач и определить соответствие между различными подходами.
MCCRS.Math.Practice.MP.2 Классы K-12
Область обучения: Математические практики
Стандарт: Математические практики
Индикатор: Рассуждение абстрактно и количественно. Учащиеся, обладающие математическими способностями, понимают величины и их отношения в проблемных ситуациях. Студенты привносят две взаимодополняющие способности в решение проблем, связанных с количественными отношениями: способность деконтекстуализировать — абстрагировать данную ситуацию и представлять ее символически и манипулировать репрезентирующими символами, как если бы они жили собственной жизнью, не обязательно обращая внимание на свои референты — и способность контекстуализировать, делать паузы по мере необходимости в процессе манипуляции, чтобы исследовать референты для задействованных символов. Количественное рассуждение влечет за собой привычки создавать последовательное представление проблемы; рассмотрение задействованных единиц; обращать внимание на значение величин, а не только на то, как их вычислять; знание и гибкое использование различных свойств операций и объектов.
Количественное рассуждение влечет за собой привычки создавать последовательное представление проблемы; рассмотрение задействованных единиц; обращать внимание на значение величин, а не только на то, как их вычислять; знание и гибкое использование различных свойств операций и объектов.
MCCRS.Math.Practice.MP.3 Классы K-12
Область обучения: Математические практики
Стандарт: Математические практики
Показатель: Придумывать обоснованные аргументы и критиковать рассуждения других. Подкованные в математике учащиеся понимают и используют заявленные предположения, определения и ранее установленные результаты при построении аргументов. Они строят предположения и выстраивают логическую последовательность утверждений, чтобы исследовать истинность своих предположений. Они способны анализировать ситуации, разбивая их на случаи, а также могут распознавать и использовать контрпримеры. Они обосновывают свои выводы, сообщают их другим и отвечают на аргументы других. Они индуктивно рассуждают о данных, выдвигая правдоподобные аргументы, учитывающие контекст, из которого эти данные возникли. Подкованные в математике учащиеся также способны сравнивать эффективность двух правдоподобных аргументов, отличать правильную логику или рассуждения от ошибочных и «если в аргументе есть изъян» объяснять, в чем он заключается. Учащиеся начальной школы могут создавать аргументы, используя конкретные референты, такие как объекты, рисунки, диаграммы и действия. Такие аргументы могут иметь смысл и быть правильными, даже если они не обобщаются и не становятся формальными до более поздних классов. Позже учащиеся учатся определять области, к которым применяется аргумент. Учащиеся всех классов могут слушать или читать аргументы других, решать, имеют ли они смысл, и задавать полезные вопросы, чтобы прояснить или улучшить аргументы.
Они индуктивно рассуждают о данных, выдвигая правдоподобные аргументы, учитывающие контекст, из которого эти данные возникли. Подкованные в математике учащиеся также способны сравнивать эффективность двух правдоподобных аргументов, отличать правильную логику или рассуждения от ошибочных и «если в аргументе есть изъян» объяснять, в чем он заключается. Учащиеся начальной школы могут создавать аргументы, используя конкретные референты, такие как объекты, рисунки, диаграммы и действия. Такие аргументы могут иметь смысл и быть правильными, даже если они не обобщаются и не становятся формальными до более поздних классов. Позже учащиеся учатся определять области, к которым применяется аргумент. Учащиеся всех классов могут слушать или читать аргументы других, решать, имеют ли они смысл, и задавать полезные вопросы, чтобы прояснить или улучшить аргументы.
MCCRS.Math.Practice.MP.4 Классы K-12
Область обучения: Математические практики
Стандарт: Математические практики
Индикатор: Модель с математикой. Учащиеся, хорошо разбирающиеся в математике, могут применять математику, которую они знают, для решения проблем, возникающих в повседневной жизни, обществе и на рабочем месте. В младших классах это может быть так же просто, как написать уравнение сложения для описания ситуации. В средних классах учащийся может применять пропорциональные рассуждения, чтобы спланировать школьное мероприятие или проанализировать проблему в сообществе. К старшей школе учащийся может использовать геометрию для решения задачи проектирования или использовать функцию для описания того, как одна интересующая величина зависит от другой. Подкованные в математике учащиеся, которые могут применять то, что они знают, спокойно делают предположения и приближения, чтобы упростить сложную ситуацию, понимая, что позже они могут потребовать пересмотра. Они способны определять важные величины в практической ситуации и отображать их отношения, используя такие инструменты, как диаграммы, двусторонние таблицы, графики, блок-схемы и формулы.
Учащиеся, хорошо разбирающиеся в математике, могут применять математику, которую они знают, для решения проблем, возникающих в повседневной жизни, обществе и на рабочем месте. В младших классах это может быть так же просто, как написать уравнение сложения для описания ситуации. В средних классах учащийся может применять пропорциональные рассуждения, чтобы спланировать школьное мероприятие или проанализировать проблему в сообществе. К старшей школе учащийся может использовать геометрию для решения задачи проектирования или использовать функцию для описания того, как одна интересующая величина зависит от другой. Подкованные в математике учащиеся, которые могут применять то, что они знают, спокойно делают предположения и приближения, чтобы упростить сложную ситуацию, понимая, что позже они могут потребовать пересмотра. Они способны определять важные величины в практической ситуации и отображать их отношения, используя такие инструменты, как диаграммы, двусторонние таблицы, графики, блок-схемы и формулы. Они могут математически анализировать эти отношения, чтобы делать выводы. Они обычно интерпретируют свои математические результаты в контексте ситуации и размышляют о том, имеют ли результаты смысл, возможно, улучшая модель, если она не достигла своей цели.
Они могут математически анализировать эти отношения, чтобы делать выводы. Они обычно интерпретируют свои математические результаты в контексте ситуации и размышляют о том, имеют ли результаты смысл, возможно, улучшая модель, если она не достигла своей цели.
MCCRS.Math.Practice.MP.5 Классы K-12
Область обучения: Математические практики
Стандарт: Математические практики
Индикатор: Стратегически используйте соответствующие инструменты. Подкованные в математике учащиеся рассматривают доступные инструменты при решении математической задачи. Эти инструменты могут включать карандаш и бумагу, конкретные модели, линейку, транспортир, калькулятор, электронную таблицу, систему компьютерной алгебры, статистический пакет или программное обеспечение для динамической геометрии. Профессиональные учащиеся достаточно хорошо знакомы с инструментами, соответствующими их классу или курсу, чтобы принимать обоснованные решения о том, когда каждый из этих инструментов может быть полезен, признавая как получаемое понимание, так и их ограничения. Например, математически подкованные старшеклассники анализируют графики функций и решений, построенные с помощью графического калькулятора. Они обнаруживают возможные ошибки, стратегически используя оценку и другие математические знания. Создавая математические модели, они знают, что технологии позволяют визуализировать результаты различных предположений, исследовать последствия и сравнивать прогнозы с данными. Подкованные в математике учащиеся разных классов способны идентифицировать соответствующие внешние математические ресурсы, такие как цифровой контент, размещенный на веб-сайте, и использовать их для постановки или решения задач. Они могут использовать технологические инструменты для изучения и углубления своего понимания концепций.
Например, математически подкованные старшеклассники анализируют графики функций и решений, построенные с помощью графического калькулятора. Они обнаруживают возможные ошибки, стратегически используя оценку и другие математические знания. Создавая математические модели, они знают, что технологии позволяют визуализировать результаты различных предположений, исследовать последствия и сравнивать прогнозы с данными. Подкованные в математике учащиеся разных классов способны идентифицировать соответствующие внешние математические ресурсы, такие как цифровой контент, размещенный на веб-сайте, и использовать их для постановки или решения задач. Они могут использовать технологические инструменты для изучения и углубления своего понимания концепций.
MCCRS.Math.Practice.MP.6 Классы K-12
Область обучения: математические практики
Стандарт: математические практики
Показатель: внимание к точности. Математически подкованные ученики стараются точно общаться с другими. Они стараются использовать четкие определения в обсуждениях с другими и в собственных рассуждениях. Они заявляют о значении выбранных ими символов, включая последовательное и уместное использование знака равенства. Они внимательно относятся к указанию единиц измерения и маркировке осей, чтобы прояснить соответствие с количествами в задаче. Они рассчитывают точно и эффективно, выражают числовые ответы с точностью, соответствующей контексту задачи. В начальных классах учащиеся дают тщательно сформулированные объяснения друг другу. К тому времени, когда они переходят в старшие классы, они уже научились анализировать утверждения и явно использовать определения.
Они стараются использовать четкие определения в обсуждениях с другими и в собственных рассуждениях. Они заявляют о значении выбранных ими символов, включая последовательное и уместное использование знака равенства. Они внимательно относятся к указанию единиц измерения и маркировке осей, чтобы прояснить соответствие с количествами в задаче. Они рассчитывают точно и эффективно, выражают числовые ответы с точностью, соответствующей контексту задачи. В начальных классах учащиеся дают тщательно сформулированные объяснения друг другу. К тому времени, когда они переходят в старшие классы, они уже научились анализировать утверждения и явно использовать определения.
MCCRS.Math.Practice.MP.7 Классы K-12
Область обучения: Математические практики
Стандарт: Математические практики
Индикатор: Ищите и используйте структуру. Математически подкованные учащиеся внимательно смотрят, чтобы различить закономерность или структуру. Например, учащиеся младшего возраста могут заметить, что три и еще семь — это то же самое, что семь и еще три, или они могут отсортировать набор фигур по количеству сторон у фигур. 2 + 92 как 5 минус положительное число, умноженное на квадрат, и используйте это, чтобы понять, что его значение не может быть больше 5 для любых действительных чисел x и y.
2 + 92 как 5 минус положительное число, умноженное на квадрат, и используйте это, чтобы понять, что его значение не может быть больше 5 для любых действительных чисел x и y.
MCCRS.Math.Practice.MP.8 Классы K-12
Область обучения: Математические практики
Стандарт: Математические практики
Индикатор: Ищите и выражайте регулярность в повторяющихся рассуждениях. Подкованные в математике учащиеся замечают, повторяются ли вычисления, и ищут как общие методы, так и упрощения. Учащиеся старших классов могут заметить, что при делении 25 на 11 они повторяют одни и те же вычисления снова и снова, и прийти к выводу, что у них есть повторяющаяся десятичная дробь. Уделяя внимание вычислению наклона, постоянно проверяя, находятся ли точки на прямой, проходящей через (1, 2) с наклоном 3, учащиеся средней школы могут абстрагироваться от уравнения (y — 2)/(x -1) = 3. Заметив регулярность в том, как члены сокращаются при расширении (x — 1) (x + 1), (x — 1) (x ^ 2 + x + 1) и (x — 1) (x ^ 3 + x ^ 2 + x + 1) может привести их к общей формуле суммы геометрического ряда.

