№ | Этапы | Деятельность учителя | Деятельность учащихся | Примечание |
1. | Организационный момент | -Здравствуйте, ребята. Я рада видеть вас в хорошем настроении. Надеюсь, что оно у вас сохранится на протяжение всего урока. Проверьте свою готовность к уроку. | Приветствуют учителя, проверяют готовность к уроку. | Фронтальная беседа |
2. | Мотивация к учебной деятельности | Задание на доске. 1.Функция задана формулой у=3х-8. Найдите значение функции, если аргумент функции равен х= — 1; -3; 2 2. Скажите, какой формулой задана функция, и заполните пустые ячейки таблицы. | — Верно. Ответы детей. | Фронтальная беседа |
3. | Проверка домашнего задания | |||
4. | Актуализация знаний | Ответьте мне,пожалуйста, на следующие вопросы: -Что такое функция? -Что называют аргументом функции? -Что называют значением функции? -Что нужно указать, чтобы функция считалась заданной? -Какие способы задания функции вы знаете? | Ответы детей. | Фронтальная беседа |
5. | Закрепление изученного материала | № 801(Один ученик у доски), 803(самостоятельно), 805-1 у доски, 806-1,3,6(у доски с подробным разбором), 808(в паре) , 810 811, 813 | Фронтальная (801,805,806,810), индивидуальная(803,804-2,811,813), парная(808). | |
6. | Повторение | № 816, 817 | индивидуальная | |
7. | Рефлексия | Продолжите высказывания об уроке. 1. Знания, полученные на уроке, мне необходимы … . 2. Я получил(а) полезную информацию о том, что … . | Заканчивают работу; Участвуют в рефлексии. | отвечают на вопросы |
8. | Информация о домашнем задании. | -Запишите домашнее задание в дневники. § 21, № 802, 804, 807(1,4), 809 | Записывают домашнее задание в дневники. | Учитель контролирует процесс записи д/з. |
5. | Итог урока. | Осталось совсем немного времени. Дежурные, соберите тетради. Спасибо Вам за урок! | Заканчивают выполнение работы. Сдают тетради. | Сдают тетради |
«Способы задания функции» (7 класс)
Урок по алгебре
в 7 классе
по теме:
«Способы задания функции»
1) Ребята! Слово «Функция» происходит от латинского «function” – исполнение, осуществление. В математике впервые употреблено лишь в 17 веке Г.В. Лейбницем, но сами функции и способы их задания изучались людьми давно.
Сформулируйте определение функции.
Как называется независимая переменная, зависимая?
Все значения, которые принимает независимая переменная, образуют (область определения функции).
Значения независимой переменной называют (значениями функции).
Какие способы задания функции вы знаете?(описание, формула, таблица, график).
2) А теперь, посмотрим, как вы справились с домашним заданием. Расскажите, как может функция связать воедино окружающий мир?
(выступления с результатами своей исследовательской домашней работы)
1.На экране зависимости. Все ли они являются функциями? Какой способ мы рассмотрели? (Описание)
2. Второй способ задания функции — формула.
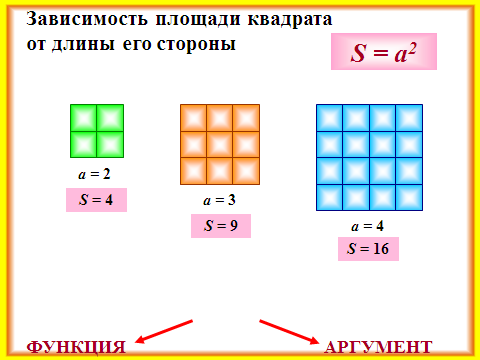
А) задание следующее — Запишите формулой зависимость площади у данной фигуры от Х.
( у = 6,4(5-4х)=32-4х) учащийся у доски выполняет задание, остальные в тетрадях)
Найдите значение у, если значение х=1,2 ( у=27,2)
Найдите значение х, если значение у=40 (х=-2)
Б)Самостоятельно по вариантам ( самооценка) двое учащихся на доске.
1 вариант
Запишите формулой зависимость периметра р данной фигуры от х.
( р=2х+9х+7х+13,6+6.2+7,4=18х+26,2)
Найдите значение периметра р, при х=2( 62,2)
2 вариант
(р=4х+4х+8х+7,8+4,4+3,4=16х+15,6)
Найдите значение периметра р, при х=2 (47,6)
В) «Самый, самый»
Работа по вариантам.
1 вариант
Найдите значение функции и определите, как называется самая высокая вершина на Земле.(Эверест 8848м)
У=8(1200-х), при х=94
2 вариант
Найдите значение функции и определите, как называется самое глубокое место на Земле.(Марианский желоб 11022м)
У=6(1927-х), при х=90
И) задание (двое учащихся)
1. Найдите значение функции и определите, как называется самое глубокое озеро. (Байкал 1620м)
У=(х-123)6, при х=393
2.Найдите значение функции и определите, как называется самый высокий действующий вулкан.( Килиманджаро 5895м)
У=(х-140)9
При х=795
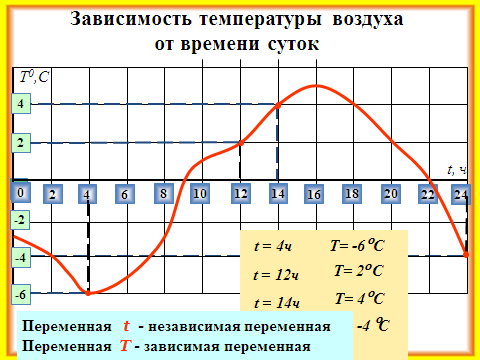
3.Следующий способ – таблица. Метеорологи составили зависимость температуры воздуха от времени суток и занесли все данные в таблицу.
Постройте график функции и ответьте на вопросы.
4.Следующее задание выполним по рядам, трое у доски.
Стр 51 №292 учебник.
1 ряд кривая ОА а)25м; б)80км/ч.
2 ряд кривая ОВ а)70м; б)45км/ч
3 ряд кривая ОС а)160м; б)27км/ч.
Сделать вывод по технике безопасности на дороге.
5. Некоторые пословицы, поговорки, загадки также можно назвать функцией.
Как аукнется, так и откликнется.
Светит, да не греет.
Ни кола, ни двора.
Чем дальше в лес, тем больше дров.
Чем скорее поедешь, тем скорее приедешь.
Назовите аргумент и функцию.
Сегодня на уроке мы закрепили……..
Повторили…..
Рассмотрели….
Домашнее задание: Стр 66 №361(а,б) №357
Урок «Способы задания функции» (алгебра, 7 класс)
Тема: Способы задания функции, Алгебра 7 класс, А.Г. Мерзляк
Урок усвоения новых знаний
Цели:
Перечислить способы задания функции, используя текст учебника
Распознать способ задания функции, работая в паре
Переводить информацию из графического или символьного представления в текстовое или наоборот с проговариванием во внешней речи
Планируемые результаты:
Перечисляет способы задания функции
Распознаёт способ задания функции
Умеет переводить информацию из графического или символьного представления в текстовое или наоборот
Дает оценку своей работе на уроке.
и дидактические материалы
1. Организационный этап
Словесный метод
Эмоциональный настрой «Подари улыбку соседу»
Приветствие. Проверка готовности
к уроку. Учитель свою улыбку дарит учащимся, а они смотрят друг на друга и дарят улыбки соседям. Настрой учащихся на работу.
2. Постановка цели и задач урока. Мотивация учебной деятельности учащихся
Диалог с классом
Прием: « Синквейн »
Создание условий для формирования внутренней потребности учеников при включении в учебную деятельность.
Предлагается написать синквейн на тему «Функции». Учащиеся пытаются сформулировать цели урока.
3. Актуализация знаний
Практический метод.
Работа в парах.Прием: «Сигналы рукой»
Предлагается ответить на вопросы. На рисунке изображен график движения туриста №150 (дидактические материалы). Ответ поясните, проверка работы в парах.
4. Первичное усвоение новых знаний
Практический метод.
Работа в группах.
Прием: «Заполнить таблицу»
Перечислить способы задания функции, используя текст учебника §21стр. 147-149,заполните таблицу с последующей проверкой.
5. Первичная проверка понимания
Практический метод.
Прием: «Рассуждение по алгоритму»
Прием: «Перевод информации»
Учитель у доски демонстрирует оформление решения заданий
Учебник№790
№795 Переводят информацию с проговариванием во внешней речи
6. Первичное закрепление
Фронтальный опрос
Прием: «Перевод информации»
Прием: «Сигналы рукой»
Прием: «Две звезды и желание»
Учебник №789
Каким способом задана функция? №797, 799(1)
№793 Самостоятельно выполните задание и проверьте правильность выполнения
№792 Работа в паре.
Учитель индивидуально работает
с учащимися, испытывающими трудности.
7. Информация о домашнем задании, инструктаж по его выполнению
«Индекс-карточки»
Учитель просит написать на одной стороне основные мысли по теме,
а на другой стороне — то, что учащиеся не поняли по теме и хотели бы спросить. Учащиеся записывают
в дневники Д. З.:
§21, вопросы1, 2 №791,794,796,798
8. Рефлексия (подведение итогов занятия)
Словесный метод.
Прием: «одноминутное эссе»
Подведение итогов урока.
Я научился—
Было трудно—
Сегодня я узнал—
У меня получилось—
Теперь я могу—
Функции. Основные виды, графики, способы задания
Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».
Понятие «функция» человеческим языком
Понятие «функция» пронизывает все сферы математики и не только.
Мы все знаем, что функция записывается как , но можешь ли ты ответить, что обозначает эта формула?
Если да, то ты большой молодец! А если нет – не страшно! Сейчас быстренько во всем разберемся!
Так вот, функция отражает зависимость величин друг от друга: то есть при изменении одного числа , по некоторому закону изменяется .
Зависимость, или взаимосвязь — вот ключевые слова при определении понятия функции.
СОДЕРЖАНИЕ СТАТЬИ
Попробуй самостоятельно придумать несколько примеров из жизни, где четко проявляется зависимость одного от другого.
И?… Не можешь придумать ни один пример? Как так! Смотри:
Допустим автомобиль движется со средней скоростью км/ч, как тогда выразить зависимость пути от времени ?
Правильно:
То есть чем больше времени автомобилист проведет за рулем, тем больше расстояние он преодолеет на своем автомобиле. Чем не зависимость?
Что в этом случае будет , что , и как будет выражено в итоге ? Проведем параллели между физической формулой и привычной нам записью функции :
- , то есть путь, который проедет автомобилист;
- , время, которое он проведет в пути;
- — зависимость пути от времени, учитывая, что скорость на всем пути постоянна.
Разобрался что к чему? Теперь перейдем на математический язык.
Итак. Еще раз смотрим на нашу формулу:
Слева стоит — это и есть функция. За этой буквой может быть все что угодно: температура, скорость, сила, путь – неважно! — зависимая величина. Она может зависеть от множества критериев. Например, как в нашем случае, зависимость пути от времени, проведенном в дороге при движении с постоянной скоростью.
Справа у нас стоит . Эта величина переменная, или, как говорят математики, «аргумент». Логично, что чем больше времени проведет автомобилист в дороге, тем большее расстояние он проедет (конечно, если скорость будет постоянна, и он не встрянет намертво в московских пробках).
Справа у нас также есть , за этим скрываются все действия, совершаемые над . В нашем случае мы говорим, что , а так как км/ч, то под скрывается умножение на , вот мы и получаем — .
Теперь думаю тебе все понятно?
Подведем краткий итог:
- — это формула, обозначающая функцию, то есть зависимость одной переменной от другой;
- — переменная величина, или, аргумент;
- — зависимая величина – изменяется при изменении аргумента, то есть согласно какой-либо определенной формуле , отражающей зависимость одной величины от другой.
Теперь, когда ты понял суть понятия «функция», знаешь что такое переменная величина, а что постоянная, посмотрим на определение функции, каким его дают математики.
Определение функции, каким его дают математики.
| Функцией называется правило , по которому каждому элементу множества ставится в соответствие единственный элемент множества . |
Вроде и есть… и есть, и даже правило есть, но что это за множества такие? «О них мы ни слова не говорили!» — воскликнешь ты.
Не паникуй!:) Множества – это очень просто, сейчас все-все проясним!
Вернемся к нашему примеру
Автомобилист едет с постоянной скоростью и проезжает расстояние, которое зависит от того, сколько времени он провел в пути.
Все верно?
Разбираемся дальше. Мы говорили, что , это как раз и есть время, проведенное в пути.
Каким оно может быть?
Ты сейчас можешь быть крайней удивлен такой постановкой вопроса, но все же, каким может быть это время?
Правильно, чисто теоретически от до .
Вот ты сам и определил для нашего конкретного случая множество , а иначе говоря, допустимые значения аргумента или область определения функции .
Запомнить очень легко: что определяет нашу функцию? От чего зависит игрек, и что мы меняем?
Функцию определяет икс! Соответственно, область определения – это возможные значения .
Теперь давай рассматривать, что такое множество .
Думаю, ты сам ответишь, что путь не может быть отрицательным, так что в нашей с тобой придуманной функции так же может принимать значения в промежутке от до .
Это называется областью значений функции , то есть множество , которые существуют для данной функции.
Итак, сделаем небольшой вывод по последнему:
|
Легко? То-то же.
Давай потренируемся находить области определения функции и ее допустимые значения.
Как найти область определения функции и ее допустимые значения
Для начала попробуй найти область определения функции:

Справился? Сравним ответы:
А)
Б)
В)
Г)
Все верно? Молодец!
Теперь попробуем найти область значений функции:

Нашел? Сравниваем:
А)
Б)
В)
Г)
Сошлось? Молодец!
Еще раз поработаем с графиками, только теперь чуть-чуть посложнее – найти и область определения функции, и область значений функции.
Как найти и область определения и область значений функции (продвинутый вариант)

Вот что получилось:
А)
Б)
С графиками, я думаю, ты разобрался. Теперь попробуем в соответствии с формулами найти область определения функции (если ты не знаешь как это сделать, прочитай раздел про ОДЗ):
Справился? Сверим ответы:
- , так как подкоренное выражение должно быть больше или равно нулю.
- , так как на ноль делить нельзя и подкоренное выражение не может быть отрицательным.
- , так как , соответственно при всех .
- , так как на ноль делить нельзя.
Однако, у нас остался еще один не разобранный момент…
Еще раз повторю определение и сделаю на нем акцент:
| Функцией называется правило , по которому каждому элементу множества ставится в соответствие единственный элемент множества . |
Заметил? Слово «единственный» — это очень-очень важный элемент нашего определения. Постараюсь объяснить тебе на пальцах.
Допустим, у нас есть функция, заданная прямой. . При , мы подставляем данное значение в наше «правило» и получаем, что . Одному значению соответствует одно значение . Мы даже можем составить таблицу различных значений и построить график данной функции, чтобы убедится в этом.
А вот и график с нашими отмеченными точками:

Как ты убедился – графиком является прямая, в которой одному значению соответствует одно значение (данный факт показан красными линиями).
Соответственно, данная зависимость подходит под определение функции.
А что ты скажешь о такой зависимости: , то есть параболы? Является ли она функцией? Давай составим также табличку значений:
«Смотри! — скажешь ты, -« » встречается два раза!» Так быть может парабола не является функцией? Нет, является!
То, что « » встречается два раза далеко не повод обвинять параболу в неоднозначности!
Дело в том, что, при расчёте для , мы получили один игрек. И при расчёте с мы получили один игрек. Так что все верно, парабола является функцией. Посмотри на график:

Разобрался? Если нет, вот тебе жизненный пример сооовсем далекий от математики!
Допустим, у нас есть группа абитуриентов, познакомившихся при подаче документов, каждый из которых в разговоре рассказал, где он живет:

Согласись, вполне реально, что несколько ребят живут в одном городе, но невозможно, чтобы один человек жил в нескольких городах одновременно. Это как бы логичное представление нашей «параболы» — нескольким разным икс соответствует один и тот же игрек.
Теперь придумаем пример, когда зависимость не будет функцией. Допустим, эти же ребята рассказывали, на какие специальности они подали документы:

Здесь у нас совершенно другая ситуация: один человек может спокойно подать документы как на одно, так и на несколько направлений. То есть одному элементу множества ставится в соответствие несколько элементов множества . Соответственно, это не функция.
Проверим твои знания на практике.
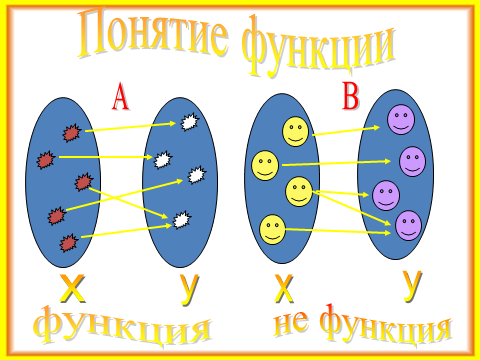
Определи по рисункам, что является функцией, а что нет:

Разобрался? А вот и ответы:
- Функцией является – В,Е.
- Функцией не является – А, Б, Г, Д.
Ты спросишь почему? Да вот почему:

На всех рисунках кроме В) и Е) на один приходится несколько !
Уверена, теперь, ты с легкостью отличишь функцию от не функции, скажешь, что такое аргумент и что такое зависимая переменная, а так же определишь область допустимых значений аргумента и область определения функции. Приступаем к следующему разделу – как задать функцию?
Способы задания функции
Как ты думаешь, что означают слова «задать функцию»? Правильно, это значит объяснить всем желающим, о какой функции в данном случае идет речь. Причем объяснить так, чтобы каждый понял тебя правильно и нарисованные людьми по твоему объяснению графики функций были одинаковы.
Как это можно сделать? Как задать функцию? Самый простой способ, который уже не раз применялся в этой статье – с помощью формулы. Мы пишем формулу, и, подставляя в нее значение , высчитываем значение . А как ты помнишь, формула – это закон, правило, по которому нам и другому человеку становится ясно, как икс превращается в игрек.
Обычно, именно так и делают – в заданиях мы видим уже готовые функции, заданные формулами, однако, существуют и другие способы задать функцию, про которые все забывают, в связи с чем вопрос «как еще можно задать функцию?» ставит в тупик. Разберемся во всем по порядку, а начнем с аналитического способа.
Аналитический способ задания функции
Аналитический способ это и есть задание функции с помощью формулы. Это самый универсальный и исчерпывающий и однозначный способ. Если у тебя есть формула, то ты знаешь о функции абсолютно все – ты можешь составить по ней табличку значений, можешь построить график, определить, где функция возрастает, а где убывает, в общем, исследовать ее по полной программе.
Рассмотрим функцию . Чему равно ?
«Что это значит?» – спросишь ты. Сейчас объясню.
Напомню, что в записи выражение в скобках
Разработка урока по алгебре «Понятие функции. Способы задания функции»(7 класс)
муниципальное автономное общеобразовательное учреждение
средняя общеобразовательная школа №45
Разработка урока по теме
«Понятие функции. Способы задания функции»,
алгебра, 7 класс.
Автор учитель математики
высшей категории
МАОУ СОШ №45 г. Калининграда
Гавинская Елена Вячеславовна.
г. Калининград
2016 – 2017 учебный год
Автор – Гавинская Елена Вячеславовна
Образовательное учреждение – муниципальное автономное общеобразовательное учреждение города Калининграда средняя общеобразовательная школа № 45
Предмет – математика (модуль «Алгебра»)
Класс – 7
Тема – «Понятие функции. Способы задания функции»
Учебно-методическое обеспечение:
Алгебра. 7 класс: учебник для общеобразовательных учреждений /Ю.М.Колягин и др., — М.: Просвещение, 2012 г.
Данные о программах, в которых выполнена мультимедийная составляющая работы — Microsoft Office Power Point 2010
Цель:
ввести понятие функции, зависимой и независимой переменных, рассмотреть способы задания функции.
Задачи обучающие:
развивающие:
формирование способности анализировать, обобщать полученные знания;
развитие навыков применения компьютерных технологий;
формирование логического мышления;
воспитательные:
активизировать интерес к получению новых знаний,
воспитывать графическую культуру, формировать точность и аккуратность при выполнении чертежей.
Обоснование выбора методов, средств и форм обучения:
оптимизировать обучение путем разумного сочетания и соотношения методов, средств и форм, направленных на получение высокого результата за время урока.
Оборудование и материалы для урока: проектор, экран (интерактивная доска, далее ИД), компьютеры или ноутбуки индивидуально для каждого учащегося, презентация для сопровождения урока, раздаточный материал.
Тип урока: комбинированный.
Структура урока:
Целесообразность использования медиа продукта на занятии продиктована следующими факторами:
интенсификацией учебно-воспитательного процесса:
автоматизацией процесса контроля,
улучшением наглядности изучаемого материала,
увеличением количества предлагаемой информации,
уменьшением времени подачи материала;
повышением эффективности усвоения учебного материала за счет групповой и самостоятельной деятельности учащихся.
Обоснование выбора форм и методов работы на обобщающем уроке по теме «Понятие функции. Способы задания функции» и методические рекомендации по применению презентации на уроке.
Тема «Понятие функции. Способы задания функции» входит в тему «Линейная функция и её график» (первый урок по теме) по авторскому планированию Ш.А.Алимова или Ю.М.Колягина. В заданиях ОГЭ прошлых лет указанная тема встречается как основной компонент при решении заданий. Поэтому предлагаемые формы и методы работы по данной теме способствуют отработке навыков применения понятия функции к решению различных заданий. Задания, предложенные на уроке, подбирались с учетом возрастных особенностей учащихся и способствуют развитию логического мышления, математической интуиции, умению анализировать, применять знания в нестандартных ситуациях с учетом меж предметных связей при решении задач практического содержания. Предложенные формы и методы применяются для групповой, самостоятельной и фронтальной работ. Однако их можно использовать и как тренажёр для отдельного учащегося, работающего за компьютером.
И последнее примечание: все учащиеся класса с начала учебного года разделены на три типологические группы: группа А – самые «слабые» учащиеся, группа В – «средние» учащиеся, группа С – учащиеся с высоким уровнем обученности по предмету.
Ход урока.
1.Организационный момент.
Объявляется цель и план урока.
Записывается домашнее задание: №538, 545, 547.
2.Актуализация опорных знаний.
С комментированием у доски (наиболее подготовленный учащийся) решается №556.
3.Изложение нового материала.
С помощью презентации и фронтальной беседы вводится понятие функции, независимой и зависимой переменной, рассматриваются способы задания функции. Слайды №3 — №16.








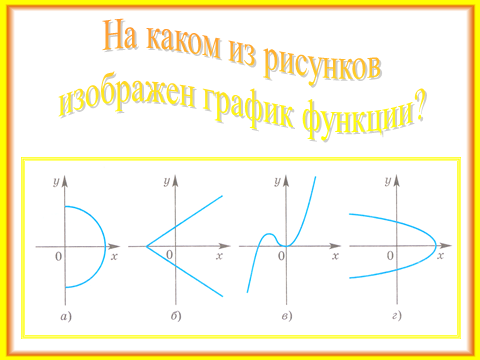

4. Гимнастика для глаз.
5. Закрепление первичных знаний.
Учащиеся работают в парах, выполняют задания, предложенные на слайдах №23 — №25.
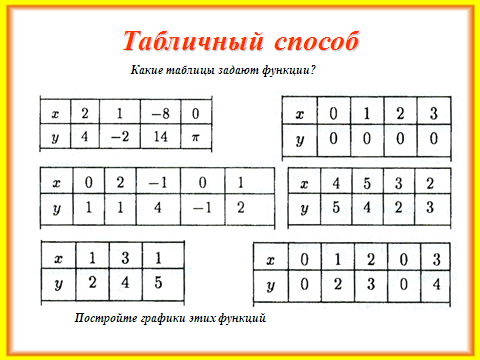
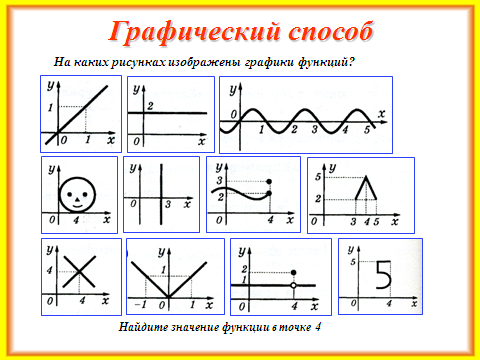
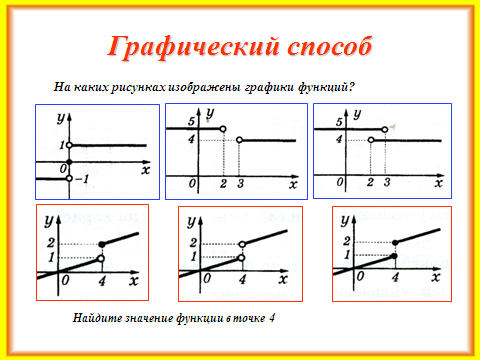
В это время учитель помогает учащимся группы А (которые сидят вместе за одним столом) выполнить те же задания. При необходимости учитель оказывает помощь и остальным ребятам. По окончании работы – фронтальная проверка с обсуждением трудностей, с которыми столкнулись ребята при выполнении указанных заданий.
7.Подведение итогов урока, выставление отметок.
Учащимся предлагается ответить на вопрос: что вызвало наибольшие затруднения на уроке? Какова ценность сегодняшнего урока? Чему же мы сегодня с вами научились?
Анкетирование можно провести с помощью системы Verdict:
Выставить отметки за работу на уроке.
Графический способ задания функции
Предмет: алгебра Класс: 10 «Б» Утверждаю:_________
Тема урока: графический способ задания функции
Тип урока: Формирование и закрепление нового материала.
ТСО, наглядные пособия: карточки с заданиями, формулы
I. Организационный этап:
II. Проверка домашнего задания:
Решение: На первых трех графиках имеются точки с одинаковыми абсциссами и разными ординатами. Это значит, что на этих линиях одному и тому же значению х соответствует более одного значения у, то есть эти линии не являются графиками функций. На четвертом графике каждому значению х соответствует не более одного значения у – это график функции.
Решение: В первой и второй таблице имеются значения х, которым соответствуют два разных значения у, то есть эти таблицы не являются таблицами функций. В третьей таблице каждому значению х соответствует не более одного значения у – это таблица функции.
Среди формул а)
 ; б)
; б)  ; в)
; в)  найти такую, которая задает функцию.
найти такую, которая задает функцию.
Решение: а, б) Для любого значения х по данной формуле значение у находится единственным образом, например, при 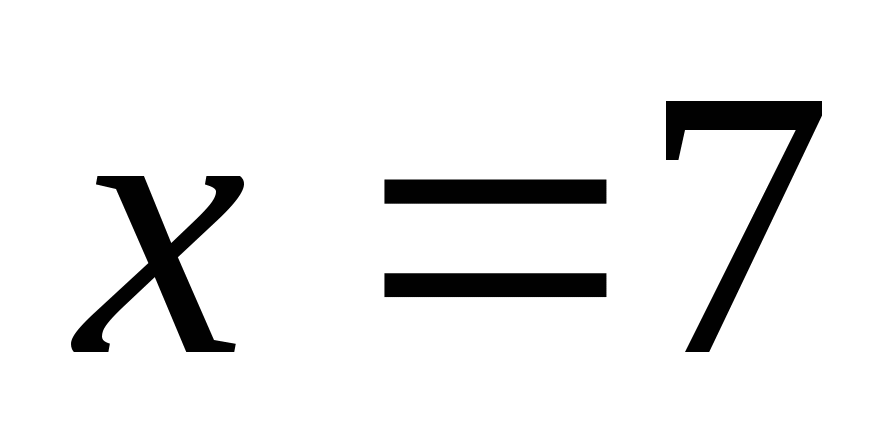 получим, что
получим, что 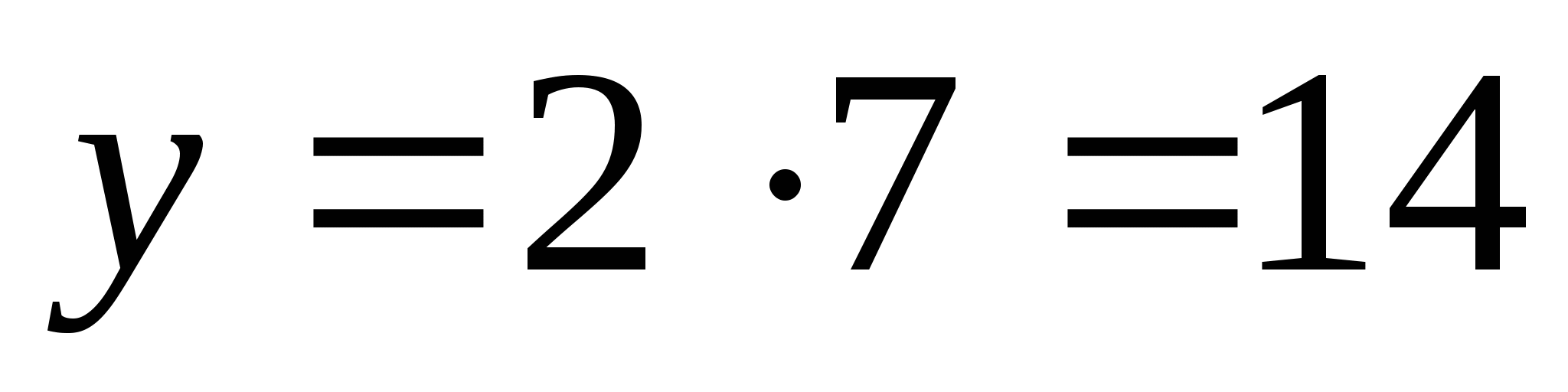 , значит
, значит 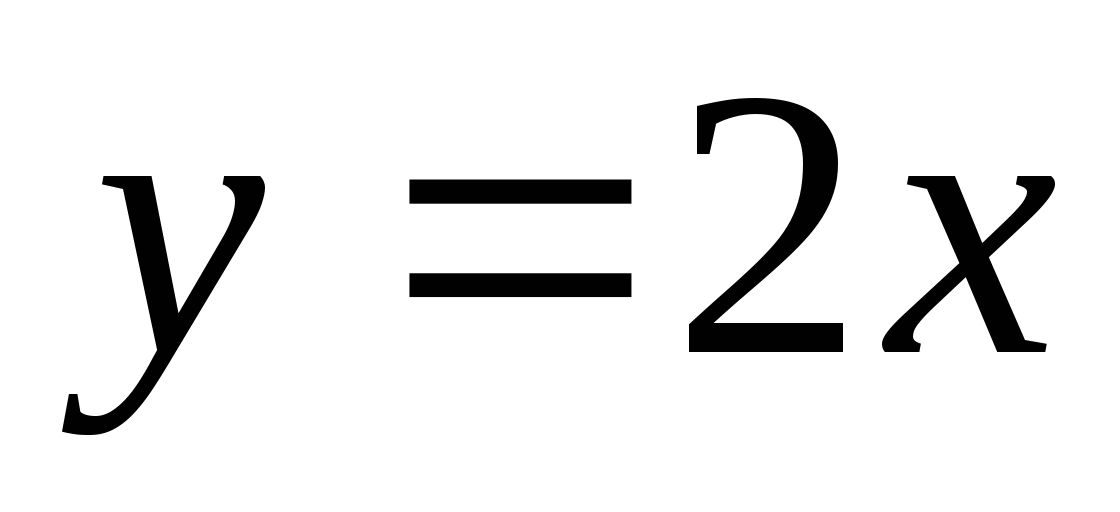 – формула, задающая функцию у от х. в) Формула
– формула, задающая функцию у от х. в) Формула 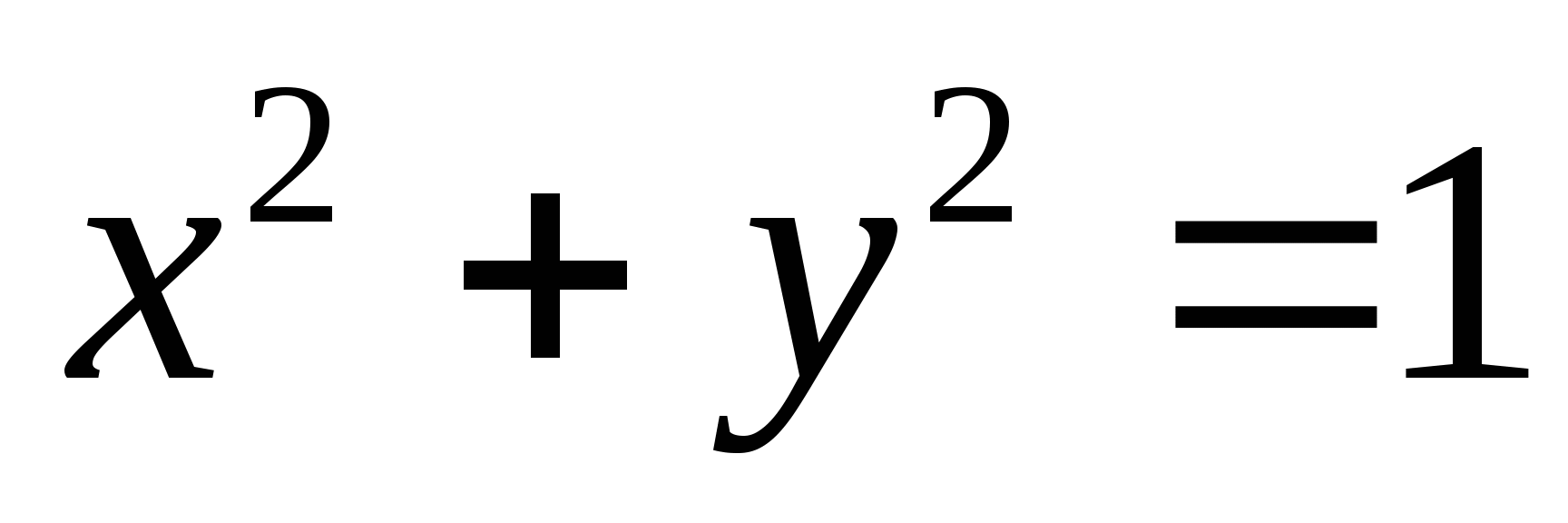 не задает функцию, так как, например, значению
не задает функцию, так как, например, значению 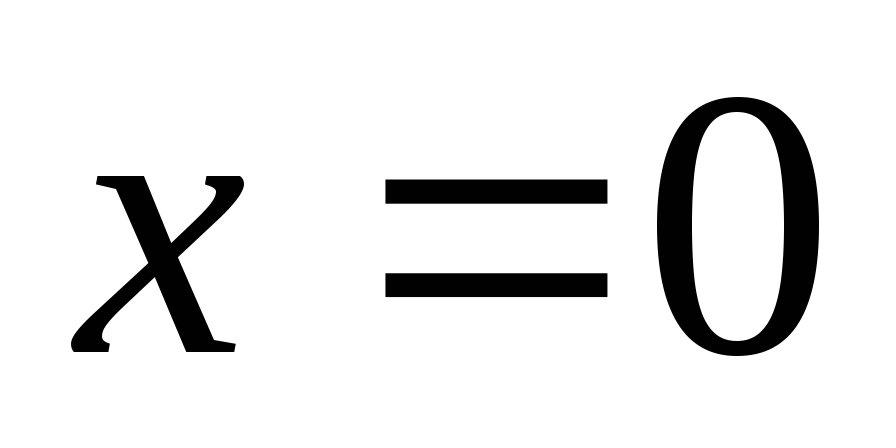 , можно найти два соответствующих значения у: 1 и -1.
, можно найти два соответствующих значения у: 1 и -1.
III. Изучение нового материала
Функция считается заданной, если указаны: область определения  ;
;
правило, или закономерность, между значениями х и у;
множество значений 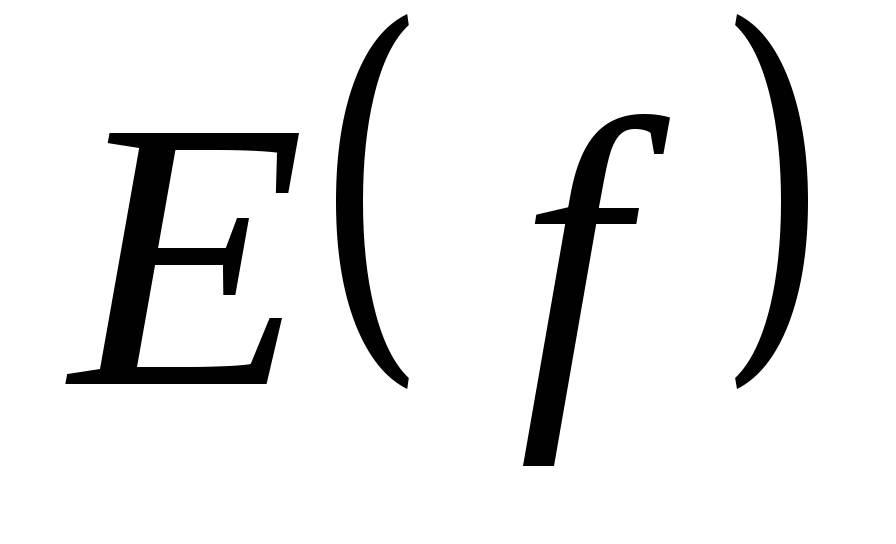 .
.
В зависимости от конкретных условий некоторые из этих величин принимают одно и то же постоянное значение, т.е. не меняются; другие наоборот, принимают различные значения.
IV. Решение задач у доски и самостоятельно в тетрадях: _____________________
V. Итоги урока:
Выставление оценок, инструктаж домашнего задания
VI. Задание на дом: _____________________
Индивидуальные задания для учащихся:______________________________
Рефлексия.
Конспект урока !Графический способ задания функции!
Тема: Графический способ задания функции
Цели:
1) Совершенствовать навыки построения графиков функций, используя таблицу
2) Уметь по графику находить соответственные значения аргумента и функции
3) Развивать внимание, мышление, память
I. Оргмомент
2. с/р
1)f(x)=x²+8xАргумент= -5. Найти значение функции
2) f(x)=2x-7
Значение функции = (-4). Найти значение аргумента
3) f(x)=
Найти D(x)
4)Продолжите предложение:
Графиком функции называется…
5) Функцией называется…
1) f(x)=3x-5
Значение функции = (-8). Найти значение аргумента
2)f(x)=4x-x²
Аргумент = (-2). Найти значение функции
3) f(x)=
Найти D(x)
4) Продолжите предложение:
Областью определения функции называется…
5) Табличный способ задания функции это…
IIВ тетрадях число, тему
Составить таблицу и построить график функции
IВIIВ
Y= x(2-x)Составить таблицу для -2 ≤x≤3 с шагом 1
У=x(x+4)
Составить таблицу для -4≤x≤1 с шагом 1
По графику движения туристов определить ( по вариантам)
Первоначальную ϑ туристов (на ОА)
Найти время, потраченное на отдых
Найти скорость на участках ВС
Найти среднюю скорость движения
Переписать ответы, самопроверку за доской
IВ4км/ч
3ч
2км/ч
2км/ч
II В
5км/ч
4ч
2,4 км/ч
Решение занимательных задач
У всех детей карточки с цифрами от 1 до 6
14 детей учились плавать, 5 из них еще не научились, а 3 уже утонули. Сколько детей научились плавать и не утонули? (6)
В доме 12 чашек и 9 блюдечек. Дети разбили половину чашек и 7 блюдечек. Сколько чашек осталось без блюдечек? (4)
Когда младенца Кузю поцарапала кошка, он орал 4 минуты, когда его укусила пчела, он орал на 3 минуты больше. А когда мама стала мыть его с мылом, он орал в 2 раза больше чем после укуса пчелы. Мама мыла Кузю 11 минут. Сколько минут орал уже вымытый Кузя? (3)
У старшего брата 12 конфет, а у младшего 2 конфеты. Сколько конфет должен забрать младший брат у старшего, чтобы справедливость восторжествовала? (5)
В тетради:
В магазине было 300кг яблок. Продавалиxдней, каждый день продавали по 20кг яблок. В магазине осталось укг яблок. Задайте формулой зависимости у от х.
Y(x)=300-20x
Найдите у(7)=300-140=160
Проверяем у доски.
Считаем количество правильных ответов по рядам.
Вопрос каждому ряду
Что называют 1%?
Какую часть часа составляют 20 мин? ()
Прибор для построения окружности?
Результат деления? (частное)
Наименьшее четное число? (2)
S квадрата = 49см². Найти Pквадрата. (28)
Что называют хордой окружности?
К однозначному числу приписали такую же цифру. Во сколько раз увеличилось число (11раз)
Найти D(х) функции f(х)=?
Как называется Iкоординаты точки?
Результат вычисления (разность)
Определение натурального числа
Прибор для измерения углов
Найти D(x) функции f(x)=
Какую часть составляют 15 минут? ()
Pпрямоугольника равен 36см. Найти сторону квадрата с таким же Р. (9см)
Как найти длину окружности?
Как называется равенство с переменой? (уравнение)
Что называют R окружности?
Определение координатной плоскости
Как называется треугольник, у которого две стороны равны?
Какую часть часа составляют 10 минут?
Результат умножения! (произведение)
Как найти Sкруга?
Аргумент это…
Р квадрата равен 20 см. Найдите его S. (25см²)
Что называют окружности?
Как называется вторая координата точки?
Что называют биссектрисой угла!
Что называют функцией?
IV Подведение итогов (выставление оценок)
V Домашнее задание:
наборов, взаимосвязей и функций — учебный материал для IIT JEE

Общие сведения о взаимосвязях и функциях
 Эта тема « Отношения и функции » является основанием или фундаментальной алгеброй в математике.Отношения и функции — это два разных слова, математически имеющих разное значение. Многих нас может смутить их различие. Мы подробно изучим обе эти концепции здесь.
Эта тема « Отношения и функции » является основанием или фундаментальной алгеброй в математике.Отношения и функции — это два разных слова, математически имеющих разное значение. Многих нас может смутить их различие. Мы подробно изучим обе эти концепции здесь.
Так же, как отношения, которые у нас есть в нашей повседневной жизни, в алгебре существует своего рода отношения. В повседневной жизни отношения подобны брату и сестре, друзьям, ученику и учителю и многим другим. В математике мы также видим некоторые отношения, например, прямая параллельна или перпендикулярна другой, любая одна переменная больше или меньше другой переменной.Любой набор A является подмножеством B, все это примеры отношений.
Одна вещь, которую мы видим общим при изучении отношений, — это то, что требовалось два разных объекта, чтобы связать два разных объекта через отношения.
Что означает отношение в математике?
Для понимания отношений требуется базовое знание множеств. A Set — это набор четко определенных объектов определенного типа . Например, — набор исходов игральных костей, набор английского алфавита.
Связь между двумя наборами всегда изучается. Если у нас есть два непустых (или нулевых / пустых) набора A и B, тогда отношение R из набора A к набору B представлено как R b, где a — это набор элементов, принадлежащих набору A, а b принадлежит к группе Б.
Отношение из набора A к набору B является подмножеством Декартово произведение A и B, то есть подмножеством A x B. Отношение другим способом также можно определить как набор упорядоченных пар (a, b ), где a принадлежит элементам из множества A и b из множества B, и отношение — от A к B, но не наоборот.
Например,
Рассмотрим набор A, содержащий элементы как {1, 2, 3}, а набор B содержит элементы как {2, 4, 6}.
Тогда отношение между набором A и B от A до B будет задано любыми комбинациями от набора A до набора B.

Из приведенной выше диаграммы мы видим, что отношение от A к B, т.е. R будет установлено равным {(1,4). (1,2), (3,4), (3,2)}. Это отношение является подмножеством декартова произведения двух множеств A X B.
Давайте возьмем другой пример, где установите A = {1, 2, 3} и установите B = {1, 2, 3, 4, 5, 6, 7, 8, 9}.
Если отношение между A и B такое: элементы B — это квадраты элементов множества A, то отношение записывается в форме множеств как:
R = {(a, b): где b — квадрат a и a ∈ A & b ∈ B}
Тогда R = {(1,1), (2,4), (3,9)}
Как и множества, отношение также может быть представлено алгебраически либо с помощью метода Roster , либо с помощью метода Set-builder .
Отношение также можно определить как линейную операцию, которая устанавливает взаимосвязь между элементами двух наборов в соответствии с некоторым определенным правилом взаимосвязи.
R: {(a, b) | (a, b) ∈ A x B и a R b}
Например: 1 A равно {2, 3, 5}
B равно {1, 4, 9, 25, 30}
Если a R b → b является квадратом
Дискретным элементом отношения являются {(2, 4), (3, 9). (5, 25)}
Например: 2 A = {Джайпур, Лакхнау, Канпур, Бхопал}
B = {Раджастан, Уттар-Прадеш, Мадхья-Прадеш}
aRb → a заглавная буква b,
A X B = {(Джайпур, Раджастан), (Лакхнау, Уттар-Прадсе), (Бхопал, Мадхья-Прадеш}
Общее количество отношений от A до B
Пусть количество отношений от A до B равно x.
Пусть A содержит «m» элементов, а B содержит «n» элементов
Количество элементов в A x B → m x n
Количество непустых подмножеств = 
Таким образом, для A = {1, 2, 3) & B = {x, y, z}
Количество непустых подмножеств или количество возможных отношений = = 2 9 — 1 = 511
Что такое функции?
Функции — это особый класс отношений, или мы можем сказать, что особых типов отношений называются функциями .Функция — одно из самых важных понятий в математике, поскольку каждая ситуация в реальной жизни решается и анализируется в первую очередь путем написания математического уравнения или функции.
Функция подобна машине, которая выдает уникальный вывод для каждого ввода, который в нее подается. Но каждая машина предназначена для определенных определенных входов, например Стиральная машина предназначена для стирки тканей, а не дерева. Аналогичным образом функции определены для определенных входов, которые называются  как его домен , а соответствующие выходы называются Range.
как его домен , а соответствующие выходы называются Range.
Пусть A и B будут двумя наборами и пусть существует правило или способ или соответствие ‘f’, которое связывает каждый элемент A с уникальным элементом в B, тогда f называется Функция или Отображение от А до Б. Обозначается символом

Читается, что «f является функцией от A до B» или «f отображает A в B.
»Если элемент a ∈ A связан с элементом b ∈ B, то b называется « f изображение a» или «изображение a под f» или «значение функции f при a. ».Также a называется прообразом b или аргументом b функции f. мы пишем это как
f: (a, b) или f: a → b или b = f (a)
Отношение f из множества A к множеству B называется функцией, если оно удовлетворяет следующим условиям:
- Все элементы A должны быть сопоставлены с элементами B. То есть не должно быть никаких элементов в A, которые не отображаются на B.
и.е. ∀a, (a, f (a)) ∈ f, где, a — элементы множества A
- Элементы набора A должны быть однозначно сопоставлены с элементами набора B.
т.е. если (a, b) ∈ f & (a, c) ∈f, ⇒ b = c
Таким образом, упорядоченные пары f должны удовлетворять тому свойству, что каждый элемент A появляется в некоторой упорядоченной паре и никакие две упорядоченные пары не имеют одинаковых первых элементов.
См. Рисунки ниже, чтобы понять вышеуказанные моменты.

Примечание : Каждая функция является отношением, но каждое отношение не обязательно является функцией.

Какова область действия функции? Также объясните его совместный домен и диапазон
Для отношения из набора A в набор B, то есть R b, все элементы набора A называются доменом отношения R, в то время как все элементы набора B называются ко-домен отношения R.
Диапазон — это набор всех вторых элементов из упорядоченных пар (a, b) в отношении a R b.
Область f = {a | a ∈ A, (a, f (a)) ∈ f}
Диапазон значений f = {f (a) | a ∈ A, f (a) ∈ B, (a, f (a)) ∈ f}
 Для отношения aRb домен рассматривается как вход в отношение R, в то время как ко-домен — это возможные выходы, а диапазон — фактический выход.
Для отношения aRb домен рассматривается как вход в отношение R, в то время как ко-домен — это возможные выходы, а диапазон — фактический выход.
Аналогично для функции f: A → B элементы множества A являются входами, а B — множеством возможных выходов.Но вторые элементы всей упорядоченной пары f (A, B) будут фактическими выходами.
Следует отметить, что диапазон — это подмножество совмещенного домена. Если задано только правило функции, то область определения функции — это набор тех действительных чисел, в которых функция определена. Для непрерывной функции интервал от минимального до максимального значения функции дает диапазон.
Что не является графиком функции?
Чтобы идентифицировать любой график, независимо от того, является он функцией или нет, мы должны еще раз понять его определение, но с точки зрения графического значения.
Первое условие функции гласит: «Все элементы A должны быть сопоставлены с элементами B». Это означает, что графически для каждого ввода в своей области функция должна выдавать или обеспечивать соответствующий вывод.
Второе условие функции гласит: «Элементы множества A должны быть однозначно сопоставлены с элементами множества B». Это означает, что для любого входа x у нас должен быть один и только один выход. Лучший способ проверить это условие для функции y = f (x) — провести линию, параллельную оси y.Если он разрезает график в двух или более различных точках, это означает, что для одного значения x мы получаем более одного вывода. Следовательно, это не будет функцией.
Пример
y = x 3
Здесь все прямые, параллельные оси y, разрезают y = x 3 только в одной точке.

Пример
x 2 + y 2 = 1
Здесь прямая, параллельная оси y, пересекает круг в двух точках, следовательно, это не функция.

Четная функция: Пусть f (x) будет действительной функцией действительной переменной. Тогда f даже если следующее уравнение выполняется для всех x и -x в области определения f:
f (x) = f (-x)
Геометрически график четной функции симметричен относительно оси y.
Нечетная функция: Опять же, пусть f (x) будет действительной функцией действительной переменной. Тогда f является нечетным, если для всех x и -x в области определения f выполняется следующее уравнение:
f (-x) = — f (x) или f (x) + f (-x) = 0.
Возрастающая функция: Считается, что функция f возрастает, если всякий раз, когда a> b, тогда
f (а) = f (б). Далее функция называется строго возрастающей, если
Если a> b, то f (a)> f (b). График возрастающей функции выглядит примерно так:

Вы также можете посмотреть видео о функции увеличения
Что такое классификация функций?
Функции классифицируются следующим образом:
- Полиномиальная функция: Если функция f определяется с помощью

, где n — неотрицательное целое число, а n , a n-1 ,…, a, a 0 — действительное число и n ≠ 0, тогда f называется полиномиальной функцией степень n.Полиномиальная функция всегда непрерывна.
- Алгебраическая функция: Функция f называется алгебраической функцией, если она может быть построена с использованием алгебраических операций, таких как сложение, вычитание, умножение, деление и извлечение корней, начиная с полиномов.
Пример

Примечание: Все полиномы алгебраические, но обратное неверно. Функции, которые не являются алгебраическими, известны как Transcidental Function .
Пример

 Экспоненциальная функция: Функция f (x) = a x = e xlna (a> 0, a ≠ 1, x ∈ R) называется экспоненциальной функцией . f (x) = a x называется экспоненциальной функцией, потому что переменная x является показателем. Не следует путать с функцией мощности. g (x) = x 2 , в котором переменная x является базой. Для f (x) = e x домен в R и диапазон R + .
Экспоненциальная функция: Функция f (x) = a x = e xlna (a> 0, a ≠ 1, x ∈ R) называется экспоненциальной функцией . f (x) = a x называется экспоненциальной функцией, потому что переменная x является показателем. Не следует путать с функцией мощности. g (x) = x 2 , в котором переменная x является базой. Для f (x) = e x домен в R и диапазон R + .- Логарифмическая функция: Функция вида y = log a x, x> 0 , a> 0, a 1, называется Логарифмической функцией .


Для f (x) = | x | домен — R, а диапазон — R + U {0}. Его рисунок см. Ниже.

-
 Signum Функция: Функция y = f (x) = sgn (x) определяется следующим образом:
Signum Функция: Функция y = f (x) = sgn (x) определяется следующим образом:

Также записывается как 
 -1 ≤ х <0; [x] = -1
-1 ≤ х <0; [x] = -1
0 ≤ х <1; [x] = 0
1 ≤ х <2; [x] = 1
2 ≤ х <3; [x] = 2 и так далее.
Для f (x) = [x], домен равен R, а диапазон равен I.

 Константа Функция: Функция f: A → B называется постоянной функцией, если каждый элемент A имеет одно и то же изображение f в B. Таким образом, f: A → B; f (x) = c, ∀ x ∈ A, c ∈ B — постоянная функция. Обратите внимание, что диапазон постоянной функции является одноэлементным, а постоянная функция может быть один — один или несколько — один, на или в.
Константа Функция: Функция f: A → B называется постоянной функцией, если каждый элемент A имеет одно и то же изображение f в B. Таким образом, f: A → B; f (x) = c, ∀ x ∈ A, c ∈ B — постоянная функция. Обратите внимание, что диапазон постоянной функции является одноэлементным, а постоянная функция может быть один — один или несколько — один, на или в.
Пример
f (x) = [{x}]; g (x) = sin 2 x + cos 2 x; h (x) = sgn (x 2 — 3x + 4) и т.д., все являются постоянными функциями.
Связанные ресурсы
Чтобы узнать больше, купите учебные материалы по Установить взаимосвязи и функции , включая учебные заметки, заметки о пересмотре, видеолекции, решенные вопросы за предыдущий год и т. Д. Также просмотрите дополнительные учебные материалы по математике здесь ,
Другие чтения
Взаимосвязи и функции

Особенности курса
- 731 Видеолекция
- Примечания к редакции
- Документы за предыдущий год
- Интеллектуальная карта
- Планировщик исследований
- Решения NCERT
- Обсуждение Форум
- Тестовая бумага с видео-решением
,
Есть ли способ использовать два оператора «…» в функции в R?
Переполнение стека- Товары
- Клиенты
- Случаи использования
- Переполнение стека Общественные вопросы и ответы
- Команды Частные вопросы и ответы для вашей команды
- предприятие Частные вопросы и ответы для вашего предприятия
- работы Программирование и связанные с ним возможности технической карьеры
- Талант Нанять технических талантов
- реклама Обратитесь к разработчикам по всему миру
Загрузка…
- Авторизоваться зарегистрироваться

 ; в)
; в)  Экспоненциальная функция: Функция f (x) = a x = e xlna (a> 0, a ≠ 1, x ∈ R) называется экспоненциальной функцией . f (x) = a x называется экспоненциальной функцией, потому что переменная x является показателем. Не следует путать с функцией мощности. g (x) = x 2 , в котором переменная x является базой. Для f (x) = e x домен в R и диапазон R + .
Экспоненциальная функция: Функция f (x) = a x = e xlna (a> 0, a ≠ 1, x ∈ R) называется экспоненциальной функцией . f (x) = a x называется экспоненциальной функцией, потому что переменная x является показателем. Не следует путать с функцией мощности. g (x) = x 2 , в котором переменная x является базой. Для f (x) = e x домен в R и диапазон R + . Signum Функция: Функция y = f (x) = sgn (x) определяется следующим образом:
Signum Функция: Функция y = f (x) = sgn (x) определяется следующим образом: Константа Функция: Функция f: A → B называется постоянной функцией, если каждый элемент A имеет одно и то же изображение f в B. Таким образом, f: A → B; f (x) = c, ∀ x ∈ A, c ∈ B — постоянная функция. Обратите внимание, что диапазон постоянной функции является одноэлементным, а постоянная функция может быть один — один или несколько — один, на или в.
Константа Функция: Функция f: A → B называется постоянной функцией, если каждый элемент A имеет одно и то же изображение f в B. Таким образом, f: A → B; f (x) = c, ∀ x ∈ A, c ∈ B — постоянная функция. Обратите внимание, что диапазон постоянной функции является одноэлементным, а постоянная функция может быть один — один или несколько — один, на или в.