Урок №5 Системы уравнений. Графический способ решения системы уравнений 7 класс
Цель уроков: Ввести понятие функции, функциональной зависимости и как частный случай, линейная функция. Подведение под понятие системы с помощью построения пересекающихся прямых.
I этап. Вопросы по домашнему заданию и Упражнения на вычисления. (10 мин)
1 ПРОВЕРЯЕМ ГРАФИКИ ИЗ Д/Р:
Эти графики пересекаются в точке (0;1)
Точка пересечения с OY: (-2;0) (-1;0)
Все эти графики проходят через начала координат и явл графиками прямой пропорциональности.
Как вы думаете, от чего зависит наклон прямой?
Конечно от k – коэффициента пропорциональности!!!
Если k>0, то прямая y=kx наклоненра вправо ↗
Если k<0, то прямая y=kx наклонена влево ↖
2. Вычисления: (вспоминаем вычисления с дробями)
———————-
( ОТВЕТЫ:
1) y=; 2) 3) 4) 5) )
——————
II этап. Исследование взаимного расположение прямых и ввод понятия «Системы уравнений»
Вернемся к прошлому уроку.
У нас есть три варианта построения пар прямых.
I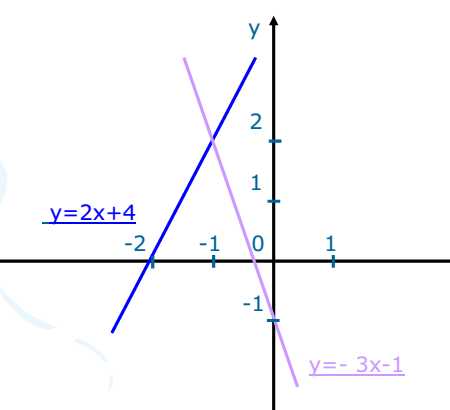 II
II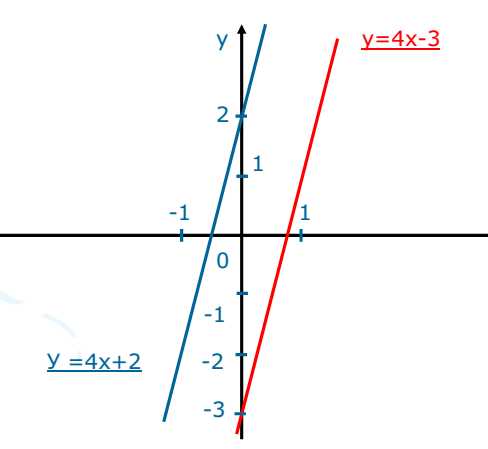
III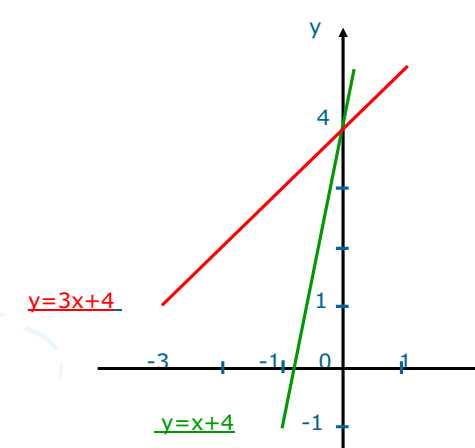
Смотрим с конца.
См. III Две прямые пересекаются в точке (0;4).
Посмотрите внимательно на уравнения прямых? Придумайте третью прямую, похожую на эти уравнения. (y=kx+4)
См. II Две прямые параллельные. Придумайте похожее уравнение и постройте эту прямую ( строим вместе). (вывод любая прямая вида y=4x+b будет параллельна остальным)
III этап. «Системы уравнений»
I) Решение графически: или точка (-1;2)
решения нет, т.к. общих точек нет и это докажем позже…
III
Системы уравнений с двумя неизвестными.
IV этап. Решение систем уравнений графически. (доделать дома)
План решения:
Для того, чтобы решить графически систему уравнений, нужно:
1) Построить графики каждого из уравнений системы;
2) найти координаты точки пересечения построенных прямых (если они пересекаются)
ЗАДАНИЕ: — (забыла задать)
Решить графически систему уравнений:
РЕШЕНИЕ:
Изучение алгебры в 7-9 классах: Кн. Для учителя / Ю.М. Колягин, Ю.В. Сидоров, М.В. Ткачева и др. – М. : Просвещение, 2002. – 287 с.: — ISBN 5-09-010414-X.
Алгебра. Дидактические материалы. 8 класс / М.В. Ткачева, Н.Е. Федорова, М.И. Шабунин. – 2-е изд., дораб. – М.: Просвещение, 2013. – 96 с. : ил. – ISBN 978-5-09-028132-4
Мерзляк А.Г. Алгебра: 9 класс: учебник для учащихся общеобразовательных организация/ А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. — М.: Вентана-Граф, 2014. – 304 c.: ил. ISBN 978-5-360-05308-8
Колягин Ю.М., Ткачева М.В., Федорова Н.Е., Шабунин М.И. АЛГЕБРА. Рабочая тетрадь. 8 класс. Пособие для учащихся общеобразовательных организаций в двух частях. Издательство «Просвещение», 2013 ISBN 978-5-09-032404-5(общ.) ISBN 978-5-09-032403-8(1)
infourok.ru
Урок изучения нового материала с использованием презентации Графический способ решения систем уравнений 7 класс
Министерство образования Республики Башкортостан
Муниципальное казенное учреждение Отдел образования
МР Альшеевский район РБ
Муниципальное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа с. Шафраново
Алгебра 7 класс
(учебник Ю.Н. Макарычев,Н.Г. Миндюк и др.)
Подготовила и провела
Митрофанова Наталья Анатольевна
2016/17 учебный год
«Математику нельзя изучать,
наблюдая как это делает сосед»
А. Нивен.
Тип урока: Урок изучения нового материала с использованием презентации
Цели урока:
Образовательные: сформировать у учащихся понятие о системе двух линейных уравнений с двумя переменными, закрепить навыки построения графиков функций; научить анализировать данные для нахождения решения системы уравнений по графику, формировать потребность приобретения новых знаний
Развивающие: Развитие творческой деятельности и познавательного интереса учащихся, развитие критического мышления; культуры графического построения
Воспитательные: воспитывать уважение друг к другу, взаимопонимание, уверенность в себе, работоспособность.
Оборудование: Компьютер, проектор, компьютерная презентация, рабочие карты урока.
План урока:
1. Организационный момент.
2.Мотивация урока.
3. Актуализация знаний.
4.Конструирование новых знаний
5. Физкультминутка.
6. Формирование навыков графического решения систем .Первичное осмысление и применение изученного способа решения систем уравнений.
7. Подведение итогов. (Рефлексия).
8. Выставление оценок. Домашнее задание.
Ход урока
1.Оргмомен. Приветствие.
1. Организационный момент.
1) Приветствие учителя. Создание доброжелательной атмосферы в классе.
2) Отметить отсутствующих.
3) Проверка подготовки учащихся к уроку.
4) Сообщение темы, целей и задач урока.
2. Мотивация урока.
Математика много дает для умственного развития человека – заставляет думать, соображать, искать простые и красивые решения, помогает развивать логическое мышление, умение правильно и последовательно рассуждать, тренирует память, внимание, закаляет характер. Надеюсь, что сегодня вы все будете работать с большим желанием узнать, что-то новое и в тоже время закрепить свои прошлые знания. Ведь как гласит народная мудрость: «Была бы охота – заладится всякая работа».
Сегодня на уроке мы рассмотрим один из способов решения систем уравнений, разработаем алгоритм решения.
При этом вы должны быть внимательными, аккуратными, логически мыслить, анализировать, делать выводы.
Слайд№1
Николай Егоровия Жуковский сказал: «В математике есть своя красота, как в живописи и поэзии».
Сегодня на уроке мы с вами в этом постараемся убедиться.
Итак, мы должны настроиться на урок…
Перед вами лежит листок бум аги. Обведите на нем свою руку. Продолжите предложения, характеризующее ваше эмоциональное состояние в данный момент:
3.Актулизация знаний.
Внимание, начинаем наше путешествие в повторение.
Запись на доске: 2х-y=1
Фронтальный опрос:
Что записано на доске?
Что является графиком уравнения?
Что является решением уравнения?
Как найти решения уравнения?
Как узнать будет ли пара (1;1), (1;5) решением?
3. Актуализация знаний
1.Что такое система уравнений?(системой уравнений называется некоторое количество уравнений, объединенных фигурной скобкой)
2.Что значит фигурная скобка? (все уравнения решаются одновременно)

3.Что называется решением системы уравнений?
( .Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство)
4.Решить систему уравнений — это значит найти все её решения или установить, что их нет.

5.Какие способы решения систем вы знаете?(подстановки)
4. Конструирование новых знаний.
Запись на доске: х+y=3, y=х-5
Ставит проблему:
Как найти решение, которое будет являться решением и одного и другого уравнения?
Рассмотрим систему:
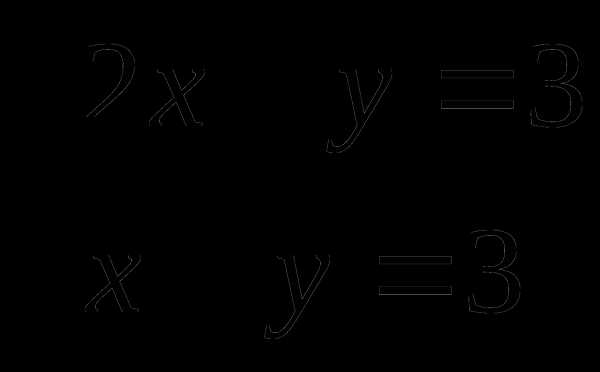
Выразим из каждого уравнения у через х:
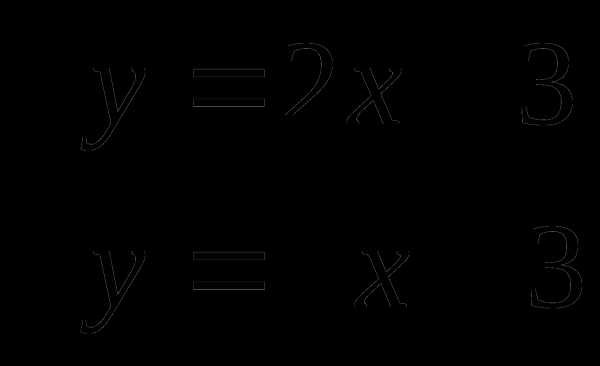
Уравнения задаются линейными функциями
Запишем тему урока .
Слайд№ 4
Дети в тетрадях пишут дату, тему урока «Графический способ решения систем уравнений»,
1.Выразить у через х в каждом уравнении.
2.Построить в одной системе координат график каждого уравнения.
3.Определить координаты точки пересечения графиков.
4.Записать ответ: х=…; у=… , или (х; у)
Но, к сожалению, графический способ не всегда обеспечивает высокую точность результата, не всегда решения являются точными. В основном этот метод применяется для:
* нахождения приближенных решений;
* с помощью этого метода легко выяснить, сколько решений может иметь система уравнений
Слайд№ 5

5. Физкультминутка.
. Частные случаи решения систем:
На доске переходим к слайду 6.
Все объекты на слайде появляются последовательно по щелчку в ходе фронтального обсуждения хода построения графиков.
Цель – подвести учащихся к самостоятельному выводу о том, что система не имеет решений.
Обращаем внимание учащихся на то, как записываются ответ.
Случай 2.
(т. е. неопределенна)
Слайд 7.

6. Формирование навыков графического решения систем
Слайд 8.
Учащиеся выполняют работу в тетрадях и после решения задания большинством учащихся на экран выводится решение для проведения самоконтроля.
7.Итог урока — рефлексия.
1) Составление кластера ( алгоритм решения системы уравнений графическим способом)
Сколько решений может иметь систем линейных уравнений с двумя переменными?
одна точка, если прямые пересекаются;
если прямые параллельны, то нет решения;
если прямые совпадают, то бесконечное множество ре
8.Задание на дом:
§ 18,№1231( а), 1235(а,б)
Комментируются и выставляются оценки за урок ученикам, работавшим у доски, а также наиболее отличившимся на уроке.
— Наш урок подошел к концу. Благодарю всех за работу и желаю успехов при выполнении домашнего задания. Урок окончен. До свидания.
infourok.ru
План-конспект урока по алгебре (7 класс) на тему: Урок – исследование по алгебре в 7 классе «Графический метод решения системы двух линейных уравнений с двумя переменными» (разработка+презентация)
Слайд 1
Цель Научить решать систему уравнений с двумя переменными графическим методом. Рассмотреть частные случаи решения системы линейных уравнений. Тип урока: урок –открытие нового знани я Форма урока: урок-исследованиеСлайд 2
Какую тему мы сейчас с вами изучаем? Каким способом вы научились решать системы линейных уравнений? Необходимо ли было строить графики этих функций, чтобы решить СЛУ? А сегодня мы будем строить графики линейных функций, каким же способом мы будем решать СЛУ?
Слайд 3
Графический метод решения системы двух линейных уравнений с двумя переменными разработала учитель математики Гладченко М.А. МОУ-СОШ с. Ямское 7 класс 2018 г.
Слайд 4
Давайте вспомним: 1. у = 3 х – 5 2. у = –0,5 х + 7 3. у = х + 4,8 Назовите угловые коэффициенты линейных функций. Что является графиком линейной функции? Какие прямые образуют с осью Х острый угол? Тупой угол? От чего это зависит? Назовите координаты точки пересечения первой прямой с осью У . Найдите значение второй функции в точке с абсциссой 6.
Слайд 5
1) y – 2 x = – 3 2) x + y = 3 Рассмотрим два линейных уравнения: Что называют системой уравнений? Системой уравнений называется некоторое количество уравнений, объединенных фигурной скобкой. Фигурная скобка означает, что все уравнения должны выполняться одновременно. y – 2 x = – 3 x + y = 3
Слайд 6
Решить систему уравнений — значит найти все её решения или установить, что их нет. Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство. Каждая пара значений переменных, которая одновременно является решением всех уравнений системы, называется решением системы.
Слайд 7
Способы решения систем уравнений
Слайд 8
Алгоритм решения системы уравнений графическим способом 1. Приводим оба уравнения к виду линейной функции y = k x + m. 2. Составляем расчётные таблицы для каждой функции. 3. Строим графики функций в одной координатной плоскости. 4. Определяем число решений: Если прямые пересекаются, то одно решение пара чисел (х ; у) – координаты точки пересечения; Если прямые параллельны, то нет решений; Если прямые совпадают, то бесконечно много решений. 5. Записываем ответ.
Слайд 9
1 0 1 2 10 x 4 6 10 -2 y y=10 — x y=x+2 у – х = 2, у + х = 10; у = х + 2, у = 10 – х ; Построим график первого уравнения х у 0 2 -2 0 у = х + 2 Построим график второго уравнения у = 10 – х х у 0 10 10 0 Ответ: (4; 6) Решение системы графическим способом Выразим у через х
Слайд 10
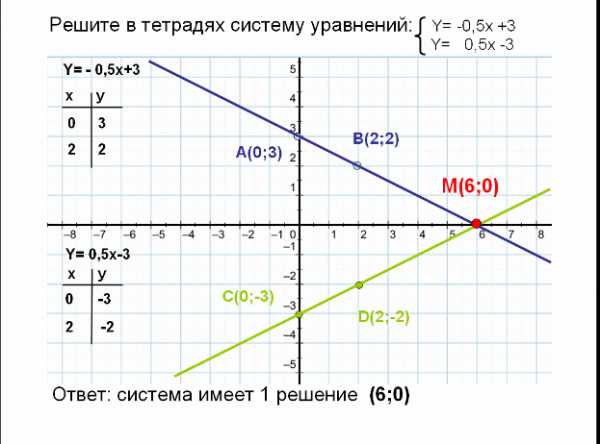
Графический метод решения системы x + y = 3 y – 2 x = – 3 у = 3 – x у = 2x – 3 x y 0 3 x y 0 3 3 0 – 3 3 A(0;3) B(3;0) C(0; – 3) D(3;3) M(2;1) X=2 у =1 Ответ: (2; 1)
Слайд 11
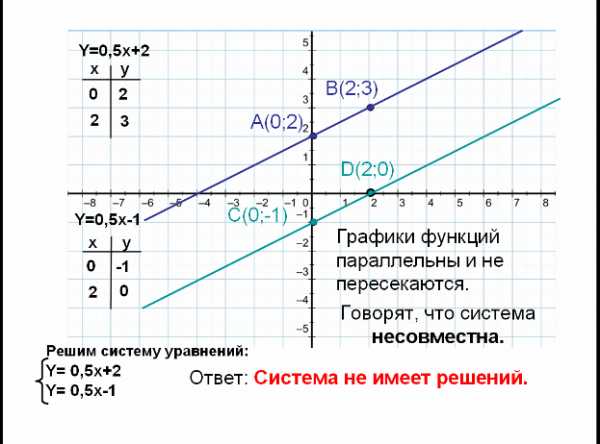
Y=0,5x-1 Y=0,5x+2 x x y y 0 2 2 3 0 -1 2 0 A(0;2) B(2;3) C(0;-1) D(2;0) Решим систему уравнений : Y= 0 ,5 x+2 Y= 0,5x-1 Графики функций параллельны и не пересекаются. Говорят, что система несовместна. Ответ: Система не имеет решений.
Слайд 12
Y=x+3 Y=x + 3 x y 0 — 3 x y 1 -1 3 0 4 2 A(0;3) B( — 3;0) C( -1 ; 2 ) D( 1 ; 4 ) Система Y=x+3 Y=x+3 Графики функций совпадают. Говорят, что система неопределенна Ответ: система имеет бесконечное множество решений
Слайд 13
Если система уравнений не имеет решений, то она называется несовместной. Если система уравнений имеет бесконечно много решений, то она называется неопределённой. Достоинство графического способа – наглядность. Недостаток графического способа– приближённые значения переменных.
Слайд 14
Проверим, что у нас получилось !
Слайд 15
Зарядка для глаз
Слайд 16
Частные случаи пересечения графиков линейных функций (памятка)
Слайд 17
Решите систему уравнений графическим способом (памятка) Х 0 2 У у = 3 х + 4 у = 3 х — 2 х 0 -2 у у = 3 х — 2 у = 3 х + 4
Слайд 18
1 группа Решите систему уравнений графическим способом у = 2 х — 3 у = — х + 3 2 группа у = 0,5 х + 1 у = 3 х — 4 Самостоятельная работа
Слайд 19
Проверим, что у нас получилось ! вывод: 1) угловые коэффициенты не равны , 2) прямые пересекаются. у х х у . . . . А(2;1) . . . . . . В(2;2) У = 2х — 3 У = — х + 3 У = 0,5 х + 1 У = 3 х — 4 Ответ: А ( 2; 1) Ответ: В ( 2; 2)
Слайд 20
Найдём координаты точек пересечения графиков 2х – 3 = — х + 3, 2х + х = 3 + 3, 3х = 6, х = 2, у = 2 • 2 — 3, у = 1. Ответ: А ( 2; 1). 3х – 4 = 0,5х + 1, 3х – 0,5х = 1 + 4, 2,5х = 5, х = 2, у = 3 • 2 – 4, у = 2. Ответ: В ( 2; 2).
Слайд 21
Решите систему уравнений графическим способом х 0 3 у У = — 3х + 6 у = 2х — 4 х 0 1 у у = 2х — 4 у = — 3х + 6
Слайд 22
Домашнее задание: § 26, № 1011, 1017, 1024 (доп.)
Слайд 23
3 4 1 2 Методика «Мухомор» Научился ли я решать систему графическим методом; понял ли я алгоритм решения систем линейных уравнений графическим методом; смогу ли я использовать при решении частные случаи; могу ли я по виду системы узнать о количестве решений системы.
Слайд 24
С п а с и б о за у р о к Б ы л о п р и я т н о с В а м и р а б о т а т ь!
Слайд 25
В презентации использованы материалы: Интернет ресурсы: festival.1september.ru festival.1september.ru›articles/597050 edu.cap.ru images.yandex.ru
nsportal.ru
Урок » Графический способ решения систем уравнений», 7 класс
Урок «Графический способ решения систем уравнений»
Для учащихся 7 класса.
Урок усвоения новых знаний.
Цели урока:
Образовательные
. Обучить соответствующим навыкам
. Вывести необходимые формулы
. Закрепить полученные знания в ходе решения задач
. Повторение и актуализация опорных знаний
Развивающие
. Развитие умения анализировать, обобщать и систематизировать знания
. Формирование у учащихся самостоятельности мышления.. Развивать творческие способности путем решения задач
. Развитие речи, умение лаконично излагать свои мысли, анализировать и делать выводы
Воспитательные
.Побуждать учащихся к самоконтролю и взаимоконтролю своей деятельности
. Воспитание взаимопомощи и взаимовыручки
Методы организации урока:
. Наглядность (использование ИКТ, построение графиков с помощью «Живой математики»)
. Фронтальный и индивидуальный опросы
. нарастающая сложность решаемой проблемы
Этапы урока
1. Организационная
2. постановка задачи в ее развитии
3. Домашняя работа
1. Вспомним понятие линейной функции и построим графики функций:
1.
2.
3.
(трое учащихся строят графики на доске)
2. 1.Решим системы уравнений и построим графики уравнений, входящих в системы:
1.
2.
( Выполняем задания самостоятельно в тетрадях)
Сравним решение систем уравнений с координатами точек пересечения графиков.
Вывод: Решение систем уравнений совпадают с координатами точек пересечения графиков.
2. Всегда ли система уравнений имеет решение? Нет.
Решим систему уравнений и построим графики уравнений:
Имеет ли эта система решение? Как расположены графики уравнений?
Вывод: Если система уравнений не имеет решения, то графики уравнений параллельны.
3. Может ли система уравнений иметь бесконечное множество решений? Да.
Решим систему уравнений и построим графики уравнений:
Сколько решений имеет эта система? Как расположены графики?
Вывод: Если система уравнений имеет бесконечное множество решений,
то графики уравнений совпадают.
4. Закрепление.
Решаем задания из учебника № 644(2), 647(2), 648(2)
3. Домашнее задание № 644(2), 647(1), 648(1), 642(4)
infourok.ru
Презентация «Графический метод решения системы уравнений с двумя переменными» 7 класс
‘Графический метод решения системы уравнений с двумя переменными’
Пластун Наталья Анатольевна
Математика уступает
Свои крепости лишь
Сильным и смелым
А.П. Конфорович
Цель урока: Научить решать систему уравнений с двумя переменными графическим методом. Рассмотреть частные случаи решения системы линейных уравнений. Что называют системой уравнений? Рассмотрим два линейных уравнения: 1) y – 2x = – 3 2) x + y = 3Системой уравнений называется некоторое количество уравнений, объединенных фигурной скобкой. Фигурная скобка означает, что все уравнения должны выполняться одновременно.
y – 2x = – 3
x + y = 3
Решить систему уравнений — значит найти все её решения или установить, что их нет. Решить систему уравнений — значит найти все её решения или установить, что их нет.Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство.
Каждая пара значений переменных, которая одновременно является решением всех уравнений системы, называется решением системы.
1
0
1
2
10
x
4
6
10
-2
y
y=10 — x
y=x+2
у – х = 2,
у + х = 10;
у = х + 2,
у = 10 – х;
Построим график первого уравнения
х
у
0
2
-2
0
у = х + 2
Построим график второго уравнения
у = 10 – х
х
у
0
10
10
0
Ответ: (4; 6)
Решение системы графическим способом
Выразим у
через х
Алгоритм решения системы уравнений графическим способом 1. Приводим оба уравнения к виду линейной функции y = k x + m. 2. Составляем расчётные таблицы для каждой функции. 3. Строим графики функций в одной координатной плоскости. 4. Определяем число решений:- Если прямые пересекаются, то одно решение пара чисел (х ; у) – координаты точки пересечения;
- Если прямые параллельны, то нет решений;
- Если прямые совпадают, то бесконечно много решений. 5. Записываем ответ.
у = 3 – x
у = 2x – 3
x
y
0
3
x
y
0
3
3
0
– 3
3
A(0;3)
B(3;0)
C(0; – 3)
D(3;3)
M(2;1)
X=2
у =1
Ответ: (2; 1)
Y=0,5x-1
Y=0,5x+2
x
x
y
y
0
2
2
3
0
-1
2
0
A(0;2)
B(2;3)
C(0;-1)
D(2;0)
Решим систему уравнений: Y= 0,5x+2 Y= 0,5x-1
Графики функций параллельны и не пересекаются.
Ответ: Система не имеет решений.
Y=x+3
Y=x+3
x
y
0
-3
x
y
1
-1
3
0
4
2
A(0;3)
B(-3;0)
C(-1;2)
D(1;4)
Система
Y=x+3
Y=x+3
Графики функций совпадают.
Ответ: система имеет бесконечное множество решений
|
Прямые |
Общие точки |
Система имеет |
О системе говорят |
|
Одна общая точка |
Одно решение |
Имеет решение |
|
|
Нет общих точек |
Не имеет решений |
несовместна |
|
|
Много общих точек |
Много решений |
неопределена |
Частные случаи пересечения графиков линейных функций (памятка)
Решите систему уравнений графическим способом 1 варианту = 2х — 3
у = — х + 3
2 варианту = 0,5х + 1
у = 3х — 4
вывод: 1) угловые коэффициенты не равны,
2) прямые пересекаются.
у
х
х
у
.
.
.
.
А(2;1)
.
.
.
.
.
.
В(2;2)
У = 2х — 3
У = — х + 3
У = 0,5 х + 1
У = 3 х — 4
Ответ: А ( 2; 1)
Ответ: В ( 2; 2)
Графический способ
решения систем уравнений
1) Решите систему уравнений:
1) 3х +2у = 7,
у = -1,5х + 3,5 х у
1 2
3 -1
х
у
1
2
1
3
3
2
4
1
2) 2х + 4у = 2,
у = 0,5 – 0,5х
х у
1 0
3 -1
Ответ: х = 3, у = -1.
Графический способ
решения систем уравнений
2) Решите систему уравнений:
1) х – у = -1,
у = х + 1
х у
0 1
2 3
х
у
1
2
1
3
3
2
4
1
2) 2х + у = 4,
у = 4 — 2х
х у
0 4
2 0
Ответ: х = 1, у = 2.
Домашнее задание: 1. Решите с помощью графиков систему уравнений: 2. Подберите если возможно, такое значение к, при котором данная система имеет единственное решение; не имеет решений; имеет бесконечное множество решений: а) б) в)3
4
1
2
- Научился ли я решать систему графическим методом;
- понял ли я алгоритм решения систем линейных уравнений графическим методом;
- смогу ли я использовать при решении частные случаи;
- могу ли я по виду системы узнать о количестве решений системы.
uchitelya.com
Открытый урок по алгебре 7 класс по теме Решение систем линейных уравнений с двумя переменными графическим способом
Школа: Беловская средняя школаДата:«____»____________20___г.
ФИО учителя: Иманова М.В.
Класс: 7класс.
Количество присутствующих:
отсутствующих:
Тема урока:
Решение системы линейных уравнений с двумя переменными графическим способом
Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу):
7.4.2.4
решать системы линейных уравнений графическим способом
Цели урока:
изучить графический метод решения систем уравнений
Критерии успеха
научиться решать системы линейных уравнений с двумя переменными графическим способом.
. Выполнять различные задания по данной теме.
Привитие
ценностей
Ценности, основанные на национальной идее «Мәңгілік ел»: казахстанский патриотизм и гражданская ответственность; уважение; сотрудничество; труд и творчество; открытость; образование в течение всей жизни.
Межпредметные
Связи
Взаимосвязь с предметами: обучение грамоте на родном языке, самопознание, познание мира, естествознание, музыка.
Навыки
использования
ИКТ
На данном уроке учащиеся используют GeoGebra, которую можно загрузить на планшет или мобильный телефон
Предварительные
знания
Умение строить график линейной функции. Умение решать линейные уравнения и находить значения выражения при заданном значении переменной.
Ход урока
Этапы урока
Запланированная деятельность на уроке
Ресурсы
Начало урока
I. Организационный момент.
Проверка готовности учащихся к уроку. Приветствие.(Круг радости,пожелания друг другу)
Деление на группы( В кругу выбирают стикеры разного цвета для образование пар с обратной стороны номера)
II. Актуализация и систематизация знаний, умений и навыков.Математический диктант 10 минут(взаимопроверка)
Дайте определение линейного уравнения с двумя переменными.
2.Что называется решением линейного уравнения с двумя переменными?
3. Что называется графиком линейного уравнения с двумя переменными?
4.Сколько точек определяет прямую?
5.Что значит решить систему уравнений?
6.Что называется решением системы линейных уравнений с двумя переменными?
7.Когда две прямые на плоскости пересекаются?
8.Когда две прямые на плоскости параллельны?
9.Когда две прямые на плоскости совпадают?
У каждого ученика лист
Самооценивания
Критерии успеха
научиться решать системы линейных уравнений с двумя переменными графическим способом.
Середина урока
Мини-исследование
Как вы понимаете выражение «графический способ решения систем уравнений?»
Вы уже умеете строить график линейного уравнения, это самое главное умение, которое нужно для решения систем уравнений графическим способом. Для того, чтобы научиться решать системы уравнений графическим способом, вам нужен алгоритм решения. Алгоритм у вас на партах. Следуя четким указаниям алгоритма, вы сами научитесь решать системы уравнений графическим способом. И ещё вы должны исследовать, сколько решений может иметь система линейных уравнений? (Система уравнений решается с помощью графиков линейных уравнений с двумя переменными) Правильность построения проверить с помощью программыGeoGebra
Учитель раздает задания на 3ряда и знакомит с дескрипторами для оценивания
приводит уравнения функций к виду y=kx+b1балл
выполняет построение графика первого уравнения
1
выполняет построение графика второго уравнения
1
определяет точку пересечения графиков на плоскости;
1
записывает ответ решения системы
1
1 рядРешить систему уравнений графическим способом, используя алгоритм.
Ответ: 1 решение, (2,4)
2 . рядРешить систему уравнений графическим способом, используя алгоритм.
Ответ: прямые совпали, множество решений.
3 ряд Решить систему уравнений графическим способом, используя алгоритм.
Ответ: прямые параллельны, нет решений.
Вывод:
1. Если угловые коэффициенты прямых различны, то система имеет единственное решение.
2. Если угловые коэффициенты прямых одинаковы, то система не имеет решений.
3. Если угловые коэффициенты прямых и коэффициент b одинаковы, то система имеет бесконечно много решений.
Решить систему уравнений:
2) Работа в парах. Один проговаривает и решает. Другой слушает и проверяет. Потом меняетесь местами. Решить с.л.у. графическим способом:
х+у=1 х+у=0
х+3у=9 ; (у=4 ,х=-3 ) -3х+4у=14; ( х=-2,у=2)
А теперь, проверим как работает наш алгоритм.
Самостоятельная работа с самопроверкой.
Задания для самостоятельной работы.
Решите сисстему линейных уравнений графическим способом.
х-2у=6
3х+2у=-6; ( х=0,у=-3)
Решите задачу, используя графический метод решения с.л.у.:
Сумма двух чисел равна 12, а их разность равна 2. Найдите эти числа. (х=5,у=7)
Учебник:
Рабочая тетрадь:
Рабочий лист
Ресурсы
Алгоритм
Алгоритм решения системы уравнений графическим способом
1. Приводим оба уравнения к виду линейной функции
y = k x + b.
2. Cоставляем расчётные таблицы для каждой функции.
3. Строим графики функций в одной координатной плоскости.
4. Записываем координаты точки пересечения графиков функций как ответ.
программаGeoGebra
Критерии успеха
Составлять план решения задачи совместно с группами. Определять степень успешности выполнения своей работы, исходя из имеющихся критериев оценки знаний.
Конец урока
Карточки с заданиями
1 гр.
Решить систему уравнений графическим способом, используя алгоритм.
Как расположены прямые на плоскости?
Сколько общих точек?
Сколько решений имеет система уравнений?
Сделайте общий вывод.
2гр
Решить систему уравнений графическим способом, используя алгоритм.
Как расположены прямые на плоскости?
Сколько общих точек?
Сколько решений имеет система уравнений?
Сделайте общий вывод.
3 гр.
Решить систему уравнений графическим способом, используя алгоритм.
Как расположены прямые на плоскости?
Сколько общих точек?
Сколько решений имеет система уравнений?
Сделайте общий вывод.
За каждое задание математического диктанта 1балл,9 баллов оценка 5,7-8баллов оценка 4,5-6баллов оценка3,4 и ниже оценка2
За каждую систему уравнений 5 баллов
Итого за урок
Домашнее задание: придумать систему линейных уравнений решить графически
Критерии успеха
Учащиеся анализируют свою работу, выражают вслух свои впечатления . сдают карточки самооценивания.
Дифференциация
Каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися?
Оценивание
Как Вы планируете проверить уровень усвоения материала учащимися?
Используйте данный раздел для записи методов, которые Вы будете использовать для оценивания того, чему учащиеся научились во время урока.
Здоровье и соблюдение техники безопасности
Здоровьесберегающие технологии.
Используемые физминутки и активные виды деятельности.
К концу урока учащиеся должны уметь:
Проведите работу по самооцениванию учащихся спомощью Лестницы успеха в рабочей тетради.
№1:
Одолела вас дремота… Шевельнуться неохота?
Ну-ка, делайте со мною упражнение такое:
Вверх, вниз потянись, окончательно проснись.
Руки вытянуть пошире – раз, два, три, четыре, пять.
Наклониться – три, четыре – и на месте поскакать.
На носок, потом на пятку, все мы делаем зарядку.
infourok.ru
Презентация урока для интерактивной доски по алгебре (7 класс) на тему: Презентация «Системы линейных уравнений с двумя переменными. Графический способ решения.» 7 класс
Слайд 1
МОБУ СОШ № 24 г. Сочи Собина Н.Н. Системы линейных уравнений с двумя переменными . Графический способ решения.Слайд 2
1. На рисунке изображен график функции y = х – 1: Проверить истинность утверждения: 2. Значение функции y = 2x – 1 в точке x = 3 равно 5. 3. Значение функции у = 0,5 x – 4 равно -5 при х = 2. 4. Уравнение вида ax + by = c называют линейным уравнением с тремя переменными.
Слайд 7
Система имеет множество решений Система решений не имеет
Слайд 8
Используя блок-схему, найдите количество решений систем уравнений: Система имеет единственное решение Система имеет множество решений Система решений не имеет
Слайд 9
Выразить переменную у через х , т.е. представить уравнения в виде линейной функции y = kx + b . 2. Составить расчётные таблицы для каждой функции. 3. Строим графики функций в одной координатной плоскости. 4. Определяем число решений: Если прямые пересекаются, то одно решение пара чисел ( х ; у) – координаты точки пересечения. Если прямые параллельны, то нет решений. Если прямые совпадают, то бесконечно много решений. 5. Записываем ответ. Алгоритм решения системы линейных уравнений с двумя переменными графическим способом.
Слайд 10
Решить систему графическим способом: Решение: Построим график первого уравнения: x 1 0 y -1 1 Построим график второго уравнения: x 1 0 y -1 -4 Ответ: (1; -1)
Слайд 11
Решить системы уравнений графическим способом: (2; 4) Множество решений Нет решений
Слайд 12
Рефлексия : ЗНАЮ УМЕЮ Определение линейного уравнения с двумя переменными Приводить примеры линейных уравнений с двумя переменными Что является решением системы линейных уравнений с двумя переменными Строить график линейного уравнения с двумя переменными Сколько решений может иметь система уравнений с двумя переменными Выяснять, сколько решений имеет система уравнений с двумя переменными Алгоритм графического способа решения систем уравнений с двумя переменными Находить решения системы уравнений
Слайд 13
СПАСИБО ЗА УРОК!
nsportal.ru
