ГДЗ Геометрия 7 класс. Ответы и решения по Геометрии для 7 го класса на VipGDZ.ru
Во время обучения школьники достаточно часто сталкивались с различными трудностями, справится с которыми, им помогали учебники. Но, с усложнениями в процессе обучения, данных книг стало не хватать для того, чтобы дети смогли качественно усваивать новый материал, а также выполнять по нему множество упражнений. Именно поэтому на помощь ученикам пришли ГДЗ, расположившие к себе еще и родителей. Кроме того, данными справочниками увлеклись и педагоги, для которых решебники стали настоящими советчиками в вопросе доступного изложения детям новых тем.
Стоит отметить, что ГДЗ оказались любимчиками семиклассников, которые начали сотрудничать с пособиями такого типа для изучения геометрии. Работая с решебниками за седьмой класс, ученики значительно повысили планку своих знаний и уровень отметок. Но, все положительные аспекты книг-выручалочек можно почувствовать только от надежных их представителей, имеющих правильную структуру.
Инновационный способ получения знаний – ответы по геометрии
Давайте рассмотрим, из чего же должны состоять ГДЗ. В первую очередь, открыв ГДЗ по геометрии за 7 класс, мы встречаемся с содержанием, благодаря которому очень легко осуществлять поиск необходимой нам информации. В данном элементе книги показаны разделы и темы, которые должны полностью соответствовать учебнику по этому предмету.
Далее решебники показывают выполнения задач, которые подаются в развернутой форме и написаны поэтапно. Процесс выполнения упражнений является чрезвычайно важным, поскольку демонстрирует алгоритм применения правила на практике. Благодаря этому компоненту ГДЗ, достаточно легко найти ошибку в собственном решении задачи.
Ни одно ГДЗ не может обойтись без такой важной части как правильные ответы, которые помогают проверять верность выполнения упражнений. Именно благодаря конечным результатам ученик будет получать только высокие баллы, и повышать свою успеваемость.
В готовых домашних заданиях за 7 класс ученики смогут ознакомиться еще с одним необходимым элементом этих учебных пособий — объяснениями. Такие небольшие, но содержательные заметки помогают лучше усвоить материал, а также использовать его во время выполнения упражнений.
Такие небольшие, но содержательные заметки помогают лучше усвоить материал, а также использовать его во время выполнения упражнений.
Ищем надежные и правильные решения на VIPGDZ.ru
Для лучшего выполнения упражнений или задач нам необходимо всегда иметь под рукой качественные решебники по геометрии. Чаще всего дети и взрослые используют для этого только проверенные временем и пользователями интернет ресурсы, к которым и относится наш сайт VIPGDZ.ru.
Наш портал VIPGDZ.ru выделяется рядом преимуществ над другими ресурсами. Одним из основных плюсов нашего сайта считается отрытый допуск к материалам, поданным абсолютно бесплатно.
Благодаря этому нашим пользователям совершенно не нужно тратить свободное время на регистрацию или же вносить какую-либо оплату. Они в любое время могут просматривать онлайн книги на нашем портале.
Мы уверены, что наших пользователей обязательно порадует и огромный ассортимент книг, которые предлагает VIPGDZ.ru. На наших страницах находится невероятное количество литературы по геометрии для учеников 7 класса. Сюда входят не только качественные решебники, но и учебники, а также тетради для работы в классе.
Сюда входят не только качественные решебники, но и учебники, а также тетради для работы в классе.
Семиклассники не только полюбят геометрию, но и раскроют все ее секреты, если возьмут в напарники лучшие ГДЗ на нашем сайте VIPGDZ.ru!
ГДЗ Геометрия 7 класс Бутузов, Кадомцев, Прасолов
Геометрия 7 класс
Учебник
Бутузов, Кадомцев, Прасолов
Просвещение
Геометрия стоит где-то на периферии между сложными и простыми дисциплинами. Если подойти к ее изучению ответственно, то у школьников не должно возникнуть никаких сложностей. А вот в противном случае остается только надеяться на то, что недостаток знаний еще не стал настолько глобальным, что дневнике будут пестреть одни двойки. Родителям вполне под силу самостоятельно проверить познания своего чада, а так же следить за выполнением д/з, чтобы предотвратить множество негативных последствий. Для этого им понадобится решебник к учебнику «Геометрия 7 класс» Бутузов, Кадомцев, Просолов, где можно найти полноценное отражение всего материала.
Что вошло в основную часть издания
Сто девяносто пять упражнений сопровождаются вопросами для повторения, которые распределены по трем главам. Так же в сборнике имеются задания с практическим содержанием, что позволит дополнительно потренироваться с их выполнением. Авторы позаботились о том, чтобы ГДЗ по геометрии 7 класс
Зачем им надо пользоваться
Данный предмет можно в некотором смысле назвать простым, особенно если школьники хорошо поняли теорию. Тогда не возникает практически никаких сложностей и любая задача поддается решению. Однако если упущена хоть одна теорема, то некоторые действия уже даются с трудом. А так как в этой науке все взаимосвязано, то недопонимание нарастает с прямо пропорциональными темпами. В итоге это может привести к тому, что успеваемость ребенка может снизится до крайней степени, так что наверстать упущенное будет очень сложно. Чтобы не допускать до подобного, необходимо выявлять проблемы на начальном этапе и сразу же их разрешать. Поможет в этом решебник к учебнику «Геометрия 7 класс» Бутузов. «Просвещение», 2015 г.
Поможет в этом решебник к учебнику «Геометрия 7 класс» Бутузов. «Просвещение», 2015 г.
Похожие ГДЗ Геометрия 7 класс
Название
Условие
Решение
Основные определения и теоремы по геометрии. 7 класс — Студопедия
Основные определения и теоремы по геометрии. 7 класс — Студопедия- Геометрия – наука, занимающаяся изучением геометрических фигур (в переводе с греческого слово «геометрия» означает «землемерие»).
- В планиметрии изучаются свойства фигур на плоскости. В стереометрии изучаются свойства фигур в пространстве.
- Отрезок — это часть прямой, ограниченная двумя точками. Эти точки называются концами отрезка.
- Угол — это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки.
 Лучи называются сторонами угла, а точка — вершиной угла.
Лучи называются сторонами угла, а точка — вершиной угла. - Угол называется
- Две геометрические фигуры называются равными, если их можно совместить наложением.
- Середина отрезка — это точка отрезка, делящая его пополам, т.е. на два равных отрезка.
- Биссектриса угла — это луч, исходящий из вершины угла и делящий его на два равных угла.
- Угол называется прямым, если он равен 90°.
- Угол называется острым, если он меньше 90° (т.е. меньше прямого угла).
- Угол называется тупым, если он больше 90°, но меньше 180°. (т.е. больше прямого, но меньше развёрнутого).
- Два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой, называются смежными. Сумма смежных углов равна 180°.

- Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого. Вертикальные углы равны.
- Две пересекающиеся прямые называются перпендикулярными, если они образуют четыре прямых угла.
- Треугольник — это геометрическая фигура, которая состоит из трех точек, не лежащих на одной прямой и трех отрезков, соединяющих эти точки. Точки называются вершинами, а отрезки — сторонами треугольника.
- Если два треугольника равны, то элементы (т.е. стороны и углы) одного треугольника соответственно равны элементам другого треугольника.
- Теорема – утверждение, справедливость которого устанавливается путём рассуждений. Сами рассуждения называются доказательством теоремы.
- (Т. Первый признак равенства треугольников) Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

- (Т. о перпендикуляре к прямой) Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.
- Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
- Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.
- Высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону.
- (Свойства медианы, биссектрисы и высоты треугольника) В любом треугольнике медианы пересекаются в одной точке; биссектрисы пересекаются в одной точке; высоты или их продолжения также пересекаются в одной точке.
- Треугольник называется равнобедренным, если две его стороны равны. Равные стороны называются боковыми сторонами, а третья сторона — основанием равнобедренного треугольника.

- Треугольник называется равносторонним, если все его стороны равны.
- (Т. о свойстве равнобедренного треугольника) В равнобедренном треугольнике углы при основании равны.
- (Т. о свойстве равнобедренного треугольника) В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
- В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
- В равнобедренном треугольнике высота, проведенная к основанию, является медианой и биссектрисой.
- (Т. Второй признак равенства треугольников) Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
- (Т. Третий признак равенства треугольников) Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.

- Окружностью называется геометрическая фигура, состоящая из всех точек, расположенных на заданном расстоянии от данной точки. Данная точка называется центром окружности.
- Радиус окружности – отрезок, соединяющий центр окружности с какой-либо её точкой.
- Отрезок, соединяющий две точки окружности, называется ее хордой.
- Хорда, проходящая через центр окружности, называется диаметром.
- Круг — это часть плоскости, ограниченная окружностью.
- Две прямые на плоскости называются параллельными, если они не пересекаются.
- При пересечении двух прямых секущей образуется восемь углов: накрест лежащие, односторонние и соответственные.
- (Т. Признак параллельности двух прямых по накрест лежащим углам) Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.

- (Т. Признак параллельности двух прямых по соответственным углам) Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
- (Т. Признак параллельности двух прямых по односторонним углам) Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.
- Аксиомы – это утверждения о свойствах геометрических фигур, которые принимаются в качестве исходных положений, на основе которых доказываются теоремы и строится вся геометрия.
- (Аксиома) Через любые две точки проходит прямая, и притом только одна.
- (Аксиома параллельных прямых) Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
- Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.
- Если две прямые параллельны третьей прямой, то они параллельны.
- Во всякой теореме две части: условие (то, что дано) и заключение (то, что требуется доказать).

- Теоремой, обратной данной,называется такая теорема, в которой условием является заключение данной теоремы, а заключением – условие данной теоремы.
- (Т. Свойство параллельных прямых) Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
- (Т. Свойство параллельных прямых) Если две параллельные прямые пересечены секущей, то соответственные углы равны.
- (Т. Свойство параллельных прямых) Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°.
- (Т. о сумме углов треугольника) Сумма углов треугольника равна 180°.
- Внешним углом треугольника называется угол, смежный с каким-нибудь углом этого треугольника.
- Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
- Если все три угла треугольника острые, то треугольник называется остроугольным.

- Если один из углов треугольника тупой, то треугольник называется тупоугольным.
- Если один из углов треугольника прямой, то треугольник называется прямоугольным.
- Сторона прямоугольного треугольника, лежащая против прямого угла, называется гипотенузой, а две стороны, образующие прямой угол — катетами.
- (Т. о соотношениях между сторонами и углами треугольника) В треугольнике против большей стороны лежит больший угол, и обратно, против большего угла лежит большая сторона.
- В прямоугольном треугольнике гипотенуза больше катета.
- (Признак равнобедр. треугольника) Если два угла треугольника равны, то треугольник равнобедренный.
- (Т. Неравенство треугольника) Каждая сторона треугольника меньше суммы двух других сторон.
- (Свойство прямоугольного треугольника) Сумма двух острых углов прямоугольного треугольника равна 90°.
- (Свойство прямоугольного треугольника) Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.

- (Свойство прямоугольного треугольника) Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°.
- (Признак равенства прямоугольных треугольников по двум катетам) Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны.
- (Признак равенства прямоугольных треугольников по катету и острому углу) Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему острому углу другого, то такие треугольники равны.
- (Т. Признак равенства прямоугольных треугольников по гипотенузе и острому углу) Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.
- (Т. Признак равенства прямоугольных треугольников по гипотенузе и катету) Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны.

- Расстоянием от точки до прямой называется длина перпендикуляра, проведённого из этой точки к прямой.
- (Т. Свойство параллельных прямых) Все точки каждой из двух параллельных прямых равноудалены от другой прямой.
- Расстоянием между параллельными прямыми называется расстояние от произвольной точки одной из параллельных прямых до другой прямой.
Как начать понимать алгебру и геометрию в 7 классе. Секреты самостоятельного изучения
Каждый учащийся постоянно слышит о том, что повторять пройденный материал необходимо систематически. Но по разным причинам это не всегда получается. И наступает момент, когда совершенно непонятно, что происходит на уроках алгебры и геометрии. Эти предметы имеют характерную черту – новые темы обязательно опираются на предыдущие. И достаточно одного пропуска, чтобы непонимание, как лавина, потянуло за собой неуспеваемость.
Чтобы подтянуть знания чаще всего рекомендуются занятия с репетитором. Но этот вариант не всем подходит. Неужели нереально выучить алгебру и геометрию самостоятельно? Нет ничего не возможного, когда под рукой решебник по алгебре для 7 класса под редакцией Макарычева. Также на помощь приходят ГДЗ, главное уметь правильно ими пользоваться.
Изучаем алгебру без слез
Это один из самых сложных предметов, изложенный сухим языком с массой формул и правил. Здесь мало просто вызубрить, материал необходимо понять. Особое внимание необходимо уделить решению практических задач, ответы на которые красноречиво указывают, есть ли пробелы в знаниях. Важно не торопиться и постепенно переходить от простого к сложному. Если какая-то тема осталась непонятой, ее необходимо разобрать самостоятельно. Поможет в этом решебник под редакцией Макарычева.
Этот учебник отличное пособие для самопроверки, так как в нем можно найти все подсказки. Материал изложен максимально доступно, что позволяет семиклассникам понять тему, даже если урок был пропущен по болезни. Также к решебнику есть ГДЗ, где все задания уже решены и имеют обязательные разъяснения по ходу выполнения работы. В процессе изучения можно обнаружить непонятные для себя выражения, их нельзя оставлять без внимания. Если вникнуть в слово или предложение самостоятельно не получилось, необходимо задать вопрос учителю на уроке и попросить их объяснить.
Также к решебнику есть ГДЗ, где все задания уже решены и имеют обязательные разъяснения по ходу выполнения работы. В процессе изучения можно обнаружить непонятные для себя выражения, их нельзя оставлять без внимания. Если вникнуть в слово или предложение самостоятельно не получилось, необходимо задать вопрос учителю на уроке и попросить их объяснить.
Готовые домашние задания по геометрии в помощь родителям
Редко кто из родителей может самостоятельно вспомнить и решить упражнения практикума по геометрии в седьмом классе. Им в помощь были создано ГДЗ по геометрии 7-9 класс Атанасяна Л.С. Пособие включает в себя четыре объемных главы, где собраны все рассматриваемые в школе темы. С помощью учебника можно изучить:
- что такое луч, прямая, отрезок и способы их измерения;
- треугольники, их свойства и все законы;
- свойства перпендикулярных и параллельных прямых;
- все виды многоугольников;
- векторы и действия с ними;
- разновидности окружностей и расчет их площадей.

Отдельный раздел в решебнике отведен разбору задач повышенной сложности и примерам на повторение пройденного материала. Детальный алгоритм решения позволит не только подготовиться к следующему уроку семиклассникам, но и восполнить пробелы в знаниях всем тем, кто готовится к ЕГЭ.
Особенно удобно то, что оба этих учебника можно найти онлайн на сыйте gdzplus. Просмотреть нужную информацию можно просто воспользовавшись смартфоном или любым другим подходящим гаджетом. Пошаговые алгоритмы, разобранные в решебниках позволят сэкономить на найме репетитора и убрать пробелы в знаниях.
Примеры по геометрии 7 класс. | Геометрия
Примеры по геометрии 7 класс. | Геометрия — просто!Добрый день!
Сегодня мы с вами разберём несколько примеров по геометрии 7 класса, которые даются в ОГЭ-2015.
Ведь действительно, Основной Государственный Экзамен — ОГЭ, рассчитан не только на знания 9 класса, но и на те знания, которые ученики получают в 7 и 8 классах по геометрии, и, начиная с 5 класса, по математике и алгебре.
Поэтому, в модуле «Геометрия» есть задачи из курса 7 класса.
Задача 1. В треугольнике АВС точка D на стороне АВ выбрана так, что АС=AD. Угол А треугольника АВС равен 16°, а угол АСВ равен 134°. Найти угол DCB.
Решение: Из треугольника ADC видно, что он равнобедренный, поскольку 2 боковые стороны его равны.
А в равнобедренном треугольнике углы при основании равны.
Значит, угол ADC равен углу АСВ.
Но сумма внутренних углов треугольника равна 180°.
Отсюда, сумма двух углов при основании равна 180-16=164°.
Углы, как мы уже сказали, равны. Поэтому, каждый из них равен 164:2 = 82°.
Угол АСВ по условию равен 134°.
А если внутри угла провести луч, то он разделит угол на 2 угла, сумма градусных мер которых будет равна градусной мере первоначального угла.
Т.е. Угол АСВ равен сумме углов АCD и DCB.
Отсюда, угол DCB равен 134 — 82 = 52°.
Ответ: угол DCB равен 52°.
Задача 2. Два отрезка АС и BD пересекают в точке О. Причём, АО=СО и ∠А=∠С. Доказать, что треугольники АОВ и OC равны.
Доказательство: В искомых треугольниках есть по одной равной стороне и одному равному углу. Значит, согласно признакам равенства треугольников, нам необходимо ещё либо по одной равной стороне, либо по одному равному углу.
Стороны как-то не проглядываются, а вот по равному углу можно ещё найти.
Углы АОВ и DOC — вертикальные.
А вертикальные углы, как мы знаем, равны.
В каждом из треугольников мы имеем по равной стороне и двум равным углам, прилежащим к ней.
Треугольники равны по 2 признаку.
Задача 3. В треугольнике АВС проведена биссектриса АК. Угол АКС равен 94°, а угол АВС равен 62°. Найти угол С треугольника АВС.
Решение: Угол АКС является внешним для треугольника АВК и равным сумме двух внутренних углов, не смежных с ним, т.
 е. сумме углов В и ВАК.
е. сумме углов В и ВАК.Отсюда мы можем найти угол ВАК.
Он равен 94 — 62 = 32°.
Поскольку АК — биссектриса угла А, то угол КАС тоже равен 32°.
А теперь, рассматривая треугольник АКС и зная в нём 2 угла, можно найти третий.
∠С = 180 — 32 — 94 = 54°.
Ответ: угол С равен 54°.
Задача 4. В треугольнике АВС боковые стороны АС и АВ равны между собой. Внешний угол при вершине В равен 110°. Найти угол С.
Решение: Внешний угол В равен 110°, значит, смежный с ним внутренний угол в треугольнике равен
180-10 = 70°.
Но внутренний угол В равен углу А, как углы при основании равнобедренного треугольника. Значит, угол А равен 70°.
А сумма внутренних углов треугольника равна 180°.
И если 2 из них равны по 70, то на долю третьего угла С приходится 180 — 70 — 70 = 40°.
Ответ: угол с равен 40°.
Задача 5. В треугольнике АВС проведены высоты, которые пересекаются в точке О. Угол СОВ равен 119°. Найти угол А.
Решение: Угол ВОМ смежный углу СОМ и равен 180-119 = 61°.

Угол СМА внешний в треугольнике СМВ и равен сумме двух внутренних, не смежных с ним.
Отсюда, угол ОВМ равен 90-61 = 29°.
А из прямоугольного треугольника ВКА можно найти угол А, т.к. сумма острых углов в прямоугольном треугольнике равна 90°.
Значит, угол А равен 90 — 29 = 61°.
Ответ: угол А равен 61°.
На сегодня всё. В следующий раз мы продолжим решение геометрических задач для подготовки к ОГЭ.
Вам так же будет интересно:
Оставить комментарий
Итоговая контрольная работа по геометрии за курс 7 класса
При проверке работы за каждое из заданий №1-№13 выставляется 1 балл, если ответ правильный и 0 баллов, если ответ неправильный. За каждое из заданий №14 или №15 выставляется 2 балла, если решение правильное и 0 баллов, если решения нет.
Максимальное количество баллов за работу – 17.
НОРМЫ ВЫСТАВЛЕНИЯ ОЦЕНОК
|
Баллы |
0 — 5 |
6 — 10 |
11 — 13 |
15 — 17 |
|
Оценка |
«2» |
«3» |
«4» |
«5» |
Итоговый тест по геометрии за курс 7 класса.
Вариант 1.
Часть 1.
- Длина отрезка АВ равна 4,3 см, длина отрезка СD в 5 раза больше. Найти сумму длин этих отрезков.
А) 17,2см Б) 21,5см В) 25,8см Г) 32,9см
- Точка С лежит на отрезке АВ. Сравните длины отрезков
А) АС >АВ Б) СВ < АВ В) АВ <СВ Г) АВ =АС
- Найдите периметр треугольника АВС, если АВ равно 8 см, АС на 1см больше АВ, а отрезок ВС в 2 раза больше АВ.
А) 25см Б) 26см В) 29см Г) 33см
- Треугольник с какими сторонами можно изобразить?
А) 2; 2; 4 Б) 8; 11; 2 В) 11; 6; 6 Г) 18; 9; 8
-
В треугольнике МКЕ угол М равен 41°, угол К на 52° больше.
 Вычислите угол Е.
Вычислите угол Е.
А) 54° Б) 46° В) 39° Г) 27°
- Углы треугольника АВС относятся как 5:3 :1. Вычислите самый большой угол этого треугольника.
А) 140 ° Б) 130 ° В) 100 ° Г) 80°
- Найдите самый маленький угол в треугольнике АВС, если АВ< АС<ВС.
А) С Б) В В) А Г) все углы равны
- Один из смежных углов на 48° больше другого. Найдите меньший угол.
А) 48 ° Б) 66° В) 78 ° Г) 84°
-
Сумма вертикальных углов равна 136°.
 Вычислите один из вертикальных углов.
Вычислите один из вертикальных углов.
А) 56° Б) 102 ° В) 284 ° Г) 68°
- Выберите верное утверждение. Если две параллельные прямые пересечены секущей, то
А) накрест лежащие углы в сумме дают 180 °
Б) смежные углы равны
В) соответственные углы равны
Г) односторонние углы равны
- В прямоугольном треугольнике АВС угол В равен 90 °, угол С равен 45 °. Сравните стороны треугольника.
А) АВ < ВС Б) АВ >АС В) АВ = ВС Г) СА< ВС
12. Для фигуры, изображенной на рисунке, известно, что KL=MN, KN=LM.
Какой признак равенства треугольников позволяет доказать равенство треугольников KLN и MNL?
А) Первый признак Б) Второй признак
В) Третий признак Г) Ни один признак неприменим
13. Продолжите предложение (свойство прямоугольного треугольника):
Если катет прямоугольного треугольника равен половине ___________
_____________________________________________________________.
Часть 2.
- Один из углов треугольника в два раза меньше другого угла, и на 8 ° меньше третьего угла этого треугольника. Вычислите углы треугольника.
-
Периметр равнобедренного треугольника равен 26см, разность двух сторон равна 5 см, а один из его внешних углов – острый.
 Найдите стороны треугольника.
Найдите стороны треугольника.
Итоговый тест по геометрии за курс 7 класса.
Вариант 2.
Часть 1.
1. Длина отрезка ВС равна 3,8 см, длина отрезка АD в 6 раз больше. Найти сумму длин этих отрезков.
А) 17,2см Б) 26,6см В) 28,4см Г) 32,4см
2. Точка В лежит на отрезке АС. Сравните длины отрезков:
А) АС > АВ Б) СВ < АВ В) АВ < СВ Г) АВ = АС
3. Найдите периметр треугольника АВС , если АС равно 7 см, АВ на 1 см больше АC, а отрезок ВС в 2 раза больше АС.
А) 24см Б) 25 см В) 29 см Г) 34 см
4. Треугольник с какими сторонами можно изобразить?
Треугольник с какими сторонами можно изобразить?
А) 6; 2; 3 Б) 18; 11; 4 В) 15; 6; 6 Г) 25; 9; 17
5. В треугольнике МКЕ угол К равен 42°, угол М на 57 ° больше. Вычислите
угол Е.
А) 101° Б) 82° В ) 39° Г) 27°
6 . Углы треугольника АВС относятся как 4:3 :2. Вычислите самый большой угол этого треугольника.
А) 140 ° Б) 130 ° В) 100 ° Г) 80°
- Найдите самый маленький угол в треугольнике АВС, если АВ< АС <ВС.
А) B Б) C В) А Г) все углы равны
-
Один из смежных углов на 54° больше другого.
 Найдите больший угол.
Найдите больший угол.
А) 117° Б) 108° В) 84° Г) 78°
- Сумма вертикальных углов равна 132°. Вычислите один из вертикальных углов.
А) 56° Б) 66° В) 102° Г) 264°
- Выберите верное утверждение. Если две параллельные прямые пересечены секущей, то
А) накрест лежащие углы равны
Б) смежные углы равны
В) соответственные углы сумме дают 180 °
Г) односторонние углы равны
- В прямоугольном треугольнике АВС угол А равен 90 °, угол В равен 42°. Сравните стороны треугольника.
А) АВ <АС Б) СВ >АВ В) АВ =АС Г) СВ <АС
12. На рисунке AD=BC, угол ACB равен углу CAD.
На рисунке AD=BC, угол ACB равен углу CAD.
Какой признак равенства треугольников позволяет доказать равенство треугольников ABC и ADC?
А) Первый признак Б) Второй признак
В) Третий признак Г) Ни один признак неприменим
13. Продолжите предложение (свойство прямоугольного треугольника):
Катет прямоугольного треугольника, лежащий против угла в _________
_____________________________________________________________.
Часть 2.
- Один из углов треугольника в два раза больше другого угла и на 30 ° больше третьего угла этого треугольника. Вычислите углы треугольника.
-
Периметр равнобедренного треугольника равен 37см, разность двух сторон равна 4 см, а один из его внешних углов – острый.
 Найдите стороны треугольника.
Найдите стороны треугольника.
Геометрия 7 Атанасян (Мельникова) | КОНТРОЛЬНЫЕ РАБОТЫ
Геометрия 7 Атанасян (Мельникова) — цитаты контрольных работ в 2-х вариантах с ответами из пособия «Геометрия 7 класс. Контрольные работы по геометрии к учебнику Л.С. Атанасяна и др» (авт. Н.Б. Мельникова). Цитаты из пособия указаны в учебных целях. При постоянном использовании контрольных работ по геометрии в 7 классе рекомендуем купить книгу: Наталия Мельникова: Геометрия. 7 класс. Контрольные работы к учебнику Л.С. Атанасяна и др. ФГОС, в которой контрольные работы представлены в 4-х вариантах.
Геометрия 7 класс (Атанасян)
Контрольные работы:
Контрольная работа № 1. Начальные геометрические сведения: измерение отрезков и углов; перпендикулярные прямые; биссектриса угла; смежные и вертикальные углы.
К-1. Вариант 0 К-1. Вариант 1 К-1. Вариант 2 К-1. Вариант 3 К-1. Вариант 4
Контрольная работа № 2. Треугольники: признаки равенства треугольников; медиана, биссектриса, высота треугольника; свойства равнобедренного треугольника; окружность.
К-2. Вариант 0 К-2. Вариант 1 К-2. Вариант 2 К-2. Вариант 3 К-2. Вариант 4
Контрольная работа № 3. Параллельные прямые: свойства углов при параллельных прямых и секущей; признаки параллельности прямых; свойства равнобедренного треугольника; окружность.
К-3. Вариант 0 К-3. Вариант 1 К-3. Вариант 2 К-3. Вариант 3 К-3. Вариант 4
Контрольная работа № 4. Соотношения между сторонами и углами треугольника: сумма углов треугольника; внешний угол треугольника; свойства прямоугольных треугольников; признаки равенства прямоугольных треугольников.
К-4. Вариант 0 К-4. Вариант 1 К-4. Вариант 2 К-4. Вариант 3 К-4. Вариант 4
Контрольная работа № 5 Итоговая за курс 7 класса: медиана, биссектриса, высота треугольника; свойства и признак равнобедренного треугольника; свойства углов при параллельных прямых и секущей; признаки параллельности прямых; окружность; сумма углов треугольника.
К-5. Вариант 0 К-5. Вариант 1 К-5. Вариант 2 К-5. Вариант 3 К-5. Вариант 4
Каждая контрольная работа направлена на проверку усвоения материала главы учебника. Указанные ниже проверяемые элементы знаний отражают только тот материал, который изучался в данной теме. При этом, естественно, задачи тематической контрольной работы могут проверять также и усвоение сведений, изучавшихся в предыдущих темах. Так, например, в контрольной работе № 3 для решения задач нужно применять сведения о вертикальных и смежных углах, о равенстве треугольников, о свойствах равнобедренного треугольника.
Геометрия 7 Атанасян (Мельникова) — цитаты контрольных работ в 2-х вариантах с ответами из пособия «Геометрия 7 класс. Контрольные работы по геометрии к учебнику Л.С. Атанасяна и др» (авт. Н.Б. Мельникова). Цитаты из пособия указаны в учебных целях.
Контрольные работы по геометрии к учебнику Л.С. Атанасяна и др» (авт. Н.Б. Мельникова). Цитаты из пособия указаны в учебных целях.
Обновление … ĉ Angle Application.doc(60k) Джошуа Кокерхэм, 3 февраля 2014 г., 8:51 ĉ B3 Quiz 2 Review G1-G4.doc(61k) Джошуа Кокерхэм, 3 февраля 2014 г., 8:51 ĉ Challenging Angle Questions.docx(87k) Джошуа Кокерхэм, 25 марта 2014 г., 4:23 ĉ Circum и Площадь кругов.docx(97k) Джошуа Кокерхэм, 3 февраля 2014 г., 8:51 ĉ Джошуа Кокерхэм, 3 февраля 2014 г., 8:35 ĉ Джошуа Джошуа , 3 февраля 2014 г., 8:36ĉ Geometric Concepts Quiz.doc(232k) Joshua Cockerham, 21 марта 2014 г., 11:46 ĉ Geometry Quiz 4 B3. doc doc( 113k) Джошуа Кокерхэм, 3 февраля 2014 г., 8:37 ĉ Тест геометрии I.doc(109k) Joshua Cockerham, 3 февраля 2014 г., 8:37 AM ĉ Geometry Test III B1 и B2.doc(156k) Джошуа Кокерхэм, 3 февраля 2014 г., 8 : 38 AM ĉ Geometry Test III Review.doc(73k) Джошуа Кокерхэм, 3 февраля 2014 г., 8:37 AM ĉ Geometry and Probability EOG.doc(121k) Джошуа Cockerham, 3 февраля 2014 г., 8:36 ĉ Введение в геометрию поперечного сечения.docx(133k) Джошуа Кокерхэм, 10 апреля 2014 г., 4:32 ĉ Примечания к масштабному коэффициенту.doc(26k) Джошуа Кокерхэм, 3 февраля 2014 г., 8:50 ĉ Джошуа Кокерхэм, 3 февраля 2014 г., 8:50 ĉ Проблемы со словом поверхности и объема.doc(420 КБ) Джошуа Кокерхэм, 3 февраля 2014 г., 8:52 AM ĉ Площадь и объем поверхности. doc doc(29k) Джошуа Кокерхэм, 3 февраля 2014 г., 8:52 AM ĉ Обзор теста Конец 9-й недели.docx(34k) Джошуа Кокерхэм, 26 марта 2014 г., 12:25 ĉ Объем и площадь поверхности.doc(66k) Джошуа Кокерхэм, 3 февраля 2014 г., 8: 56 AM ĉ Формулы объема и площади поверхности.doc(29k) Джошуа Кокерхэм, 3 февраля 2014 г., 8:56 |
| A | B | ||||||
|---|---|---|---|---|---|---|---|
| угол | два луча с общей конечной точкой | ||||||
| острый угол | угол менее 90 градусов | obtuse angle | угол измерения более 90 градусов | ||||
| прямой угол | угол измерения 90 градусов | ||||||
| прямой угол | угол, который измеряет 180 градусов | ||||||
| смежные углы | разделяют вершину и одну сторону | ||||||
| сумма размеров двух углов составляет 90 градусов | |||||||
| дополнительных углов | сумма размеров двух углов составляет 180 градусов | ||||||
| разносторонний треугольник | нет конгруэнтных сторон | ||||||
| isos треугольник | не менее двух равных сторон | ||||||
| равносторонний треугольник | три конгруэнтных стороны | ||||||
| прямоугольный треугольник | один прямой угол | ||||||
| острый треугольник | три острых угла | ||||||
| тупой треугольник | одна параллельная | одна параллельная | 9017 лежат в одной плоскости, но не пересекаются | ||||
| трапеция | ровно одна пара параллельных сторон | ||||||
| параллелограмм | обе пары противоположных сторон параллельны | ||||||
| прямоугольник | параллелограмм | с 4-мя прямыми углами||||||
| ромб | параллелограмм с 4 конгруэнтными сторонами | ||||||
| квадрат | параллелограмм с 4 прямыми углами и 4 конгруэнтными сторонами | ||||||
| правильный многоугольник | все стороны конгруэнтны 907 | окружности 901 | конгруэнтны 901 907 | окружности 901 очков в плоскости, которые находятся на одинаковом расстоянии от центра | |||
| радиус | сегмент, который имеет одну конечную точку в центре и другую конечную точку на окружности | ||||||
| диаметр | сегмент, который проходит через центр окружности с обоими конечные точки на окружности | ||||||
| центральный угол | угол с вершиной в центре окружности | ||||||
| хорда | сегмент, оба конца которого находятся на окружности | ||||||
| дуга | часть окружности | ||||||
| полукруг | полукруг | ||||||
| компас | геометрический инструмент, используемый для рисования окружностей и дуг | ||||||
| вписанный многоугольник | многоугольник, стороны которого являются хордами окружности | линий | |||||
| пересекаются, образуя прямые углы | |||||||
| биссектриса перпендикуляра | a линия, которая перпендикулярна сегменту в его средней точке | ||||||
| биссектриса сегмента | линия, проходящая через середину сегмента |
Открытые учебники | Сиявула
Математика
Наука
- Читать онлайн
Учебники
Английский
Класс 7A
Марка 7Б
Оценка 7 (вместе A и B)
Африкаанс
Граад 7А
Граад 7Б
Граад 7 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Марка 8A
Марка 8Б
Оценка 8 (вместе A и B)
Африкаанс
Граад 8А
Граад 8Б
Граад 8 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Марка 9А
Марка 9Б
9 класс (A и B вместе)
Африкаанс
Граад 9А
Граад 9Б
Граад 9 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Класс 4A
Класс 4Б
Класс 4 (вместе A и B)
Африкаанс
Граад 4А
Граад 4Б
Граад 4 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Марка 5А
Марка 5Б
Оценка 5 (вместе A и B)
Африкаанс
Граад 5А
Граад 5Б
Граад 5 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Класс 6A
класс 6Б
6 класс (A и B вместе)
Африкаанс
Граад 6А
Граад 6Б
Граад 6 (A en B saam)
Пособия для учителя
Наша книга лицензионная
Эти книги не просто бесплатные, они также имеют открытую лицензию! Один и тот же контент, но разные версии (брендированные или нет) имеют разные лицензии, как объяснено:
CC-BY-ND (фирменные версии)
Вам разрешается и поощряется свободное копирование этих версий. Вы можете делать ксерокопии, распечатывать и распространять их сколько угодно раз. Вы можете скачать их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственное ограничение заключается в том, что вы не можете адаптировать или изменять эти версии учебников, их содержание или обложки каким-либо образом, поскольку они содержат соответствующие бренды Siyavula, спонсорские логотипы и одобрены Департаментом базового образования. Для получения дополнительной информации посетите Creative Commons Attribution-NoDerivs 3.0 Непортированный.
Вы можете делать ксерокопии, распечатывать и распространять их сколько угодно раз. Вы можете скачать их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственное ограничение заключается в том, что вы не можете адаптировать или изменять эти версии учебников, их содержание или обложки каким-либо образом, поскольку они содержат соответствующие бренды Siyavula, спонсорские логотипы и одобрены Департаментом базового образования. Для получения дополнительной информации посетите Creative Commons Attribution-NoDerivs 3.0 Непортированный.
Узнайте больше о спонсорстве и партнерстве с другими организациями, которые сделали возможным выпуск каждого из открытых учебников.
CC-BY (версии без бренда)
Эти небрендированные версии одного и того же контента доступны для вас, чтобы вы могли делиться ими, адаптировать, трансформировать, модифицировать или дополнять их любым способом, с единственным требованием — дать соответствующую оценку Siyavula. Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.
Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.
Геометрия — 7 класс по математике
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или несколько ваших авторских прав, сообщите нам об этом, отправив письменное уведомление («Уведомление о нарушении»), содержащее то информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении может быть направлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в качестве
ChillingEffects. org.
org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
7-й класс, уровень 1 — желтый класс
7-й класс, уровень 1 — желтый класс — миссис МакГоверн / отдел геометрии- Дом
- Наша школа
- Родители и студенты
- Академики
- Классы MS
- Нет навигации
- »
- Человеческие ресурсы
- Комплексная борьба с вредителями
- База данных MSDS
- Бенсон, Сара
- Bourque, Dena
- Бушнелл, Эйлин
- Чаггарис, Мишель
- Дэвис, Элисон
- Хилтон, Дебра
- Лихтер, Бонни
- Маккин, Александр
- Миетт, Пейдж
- Миетт, Стив
- Осборн, Джейми
- Зессис, Адрия
- Программа Раздела I
- STEM (наука, технологии, инженерия и математика)
- Физическая культура
- Музыка
- Удаленное обучение KPMS
- Учителя
- »
- Адамс, Дженнифер
- Аллен, Дэн
- Андерсон, Дебра
- Остин, Мишель
- Барретт, Арианна
- Барри, Лия
- Bois, Lynn
- Бин, Ховард
- Болл, Дэвид
- Бонд, Сара
- Брэди, Эрин
- Брэди, Дженна
- Бреннейс, Кэтлин
- Куни, Джош
- Кроппер, Лиза
- Кертин, Кэти
- Делука, Элисон
- ДеВулф, Райан
- Даффи, Лорен
- Эллис, Кэтрин
- Фекто, Келли
- Гольдштейн, Шана
- Холл, Сьюзен
- Хартвелл, Уитни
- Хоган, Хизер
- Голландия, Патрик
- Хьюз-Роган, Пэм
- Якобсен, Конор
- Джонс, Шон
- Кин, Кара
- Котуч, Кори
- Келли, Нола
- Кригсман, Мерил
- L’Esperance, Кассандра
- Лангмид, Эшли
- ЛаВалли, Бетани
- Леоне, Эмили
- Lussiez de Narvaez, Laetitia
- Мэннинг, Кейтлин
- Марш, Эллисон
- Макговерн, Дженис
- Макинтайр, Лиза
- Макналти, Сара
- Монтгомери, Сара
- Луна, Эван
- Миетт, Пейдж
- Паркер, Дэниел
- Паркер, Мелинда
- Реддингтон, Джозеф
- Рейес, Элисон
- Руньон, МэриБет
- Рассел, Шелби
- Райан, Дениз
- Спинелли, Дженнили
- Susi, Allison
- Тиге, Кристина
- Варриккионе, Дженнифер
- Уилферт, Джейми
- Уильямс, Кейт
- Wolloff, Джош
- Справочник MS
- Команды
- Деятельность
Пойдите по математике, 7 класс.
 Ключ ответов на вопросы Глава 8 Моделирование геометрических фигур — Пойдите по математике. Ключ ответов
Ключ ответов на вопросы Глава 8 Моделирование геометрических фигур — Пойдите по математике. Ключ ответовИдите по математике для 7-го класса. Ключ ответов на вопросы Глава 8 Моделирование геометрических фигур: Присоединяйтесь к списку лучших учащихся, используя ключ-ответ для 7-го класса по математике.Получите доступ к бесплатной загрузке Go Math Grade 7 Answer Key Chapter 8 Modeling Geometric Figures. Мы должны подготовить решения таким образом, чтобы все студенты могли легко понять концепцию. Быстрое и легкое обучение возможно только с помощью нашего ключа ответов HMH Go Math.
Иди по математике, 7 класс. Ключевой ответ Глава 8 Моделирование геометрических фигур
Мы предлагаем учащимся обратиться к Главе 8 «Моделирование геометрических фигур» по математике для 7 класса, чтобы получить наивысший балл на экзаменах.Это вызывает у студентов интерес к изучению математики. Изучите понятия геометрических фигур таким образом, чтобы самостоятельно подготовить вопросы. Нажмите на прикрепленные ниже ссылки и получите пошаговое объяснение.
Нажмите на прикрепленные ниже ссылки и получите пошаговое объяснение.
Глава 8 — Моделирование геометрических фигур — Урок: 1
Глава 8 — Моделирование геометрических фигур — Урок: 2
Глава 8 — Моделирование геометрических фигур — Урок: 3
Глава 8 — Моделирование геометрических фигур — Урок: 4
Глава 8 — Моделирование геометрических фигур
Практическое руководство — стр.240
Вопрос 1.
Размер комнаты на чертеже составляет 3 дюйма: 5 футов. Стена на том же чертеже имеет размер 18 дюймов. Заполните таблицу.
а. Какова длина самой стены?
______ футов
Ответ: 30 футов
Пояснение:
Мы заполняем таблицу, используя прямую пропорциональность.
3 дюйма: 5 футов.
Стена на том же чертеже имеет размер 18 дюймов на 30 футов.
Вопрос 1.
б. Окно в комнате имеет фактическую ширину 2,5 фута.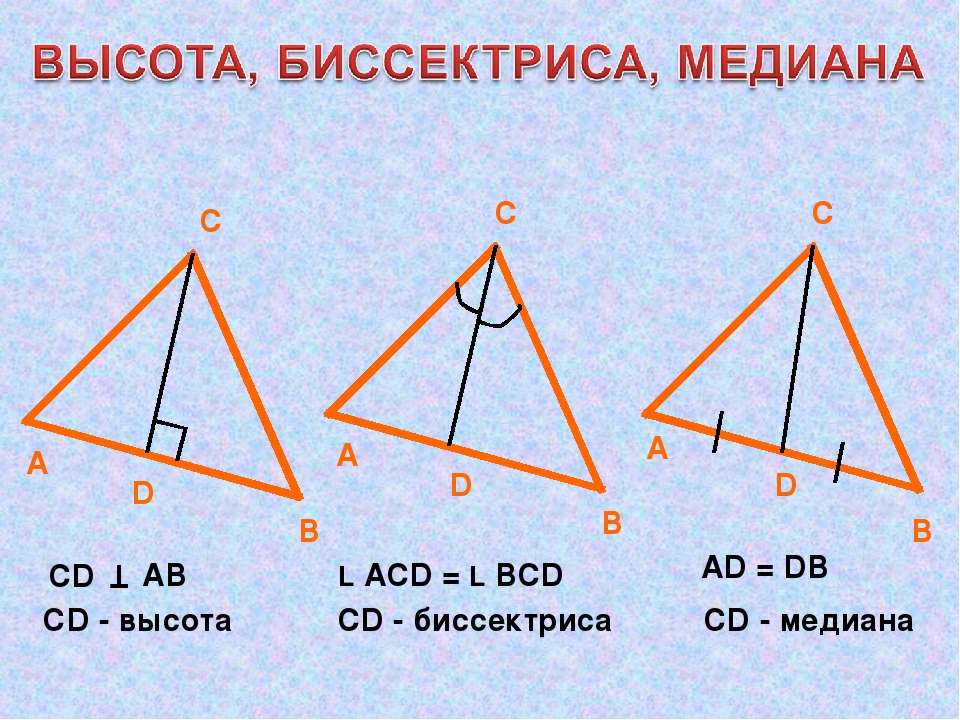 Найдите ширину окна на чертеже.
Найдите ширину окна на чертеже.
______ дюймов
Ответ: 1,5 дюйма
Пояснение:
Мы определяем количество дюймов, соответствующее 1 футам на реальном окне
3 дюйма / 5 дюймов
Умножаем и делим на 5
(3 дюйма ÷ 5) / (5 футов ÷ 5) = 0,6 / 1 фут
Таким образом, 1 фут соответствует 0,6 дюйма, поэтому ширина окна в таблице составляет
2,5 × 0,6 = 1,5 дюйма
Вопрос 2.
Масштаб чертежа составляет 2 дюйма: 4 фута. Каковы длина и ширина фактического помещения? Найдите площадь реальной комнаты.
Ширина: _________ футов
Длина: _________ футов
Площадь: _________ квадратных футов
Ответ:
Ширина: 28 футов
Длина: 14 футов
Площадь: 392 кв. Футов
Пояснение:
Мы определяем количество футов, соответствующее 1 дюйму на чертеже
2 дюйма / 4 дюйма = (2 дюйма ÷ 2) / (4 дюйма ÷ 2) = 1/2
Таким образом, 1 дюйм соответствует 2 футам от реальных габаритов помещения.
Определяем реальную длину комнаты, обозначенную на чертеже 14 дюймами.
14 × 2 = 28 футов
Определяем реальную ширину комнаты, обозначенную на чертеже как 7 дюймов.
7 × = 14 футов
Мы вычисляем площадь реальной комнаты:
28 × 14 = 392 квадратных фута.
Вопрос 3.
Масштаб чертежа 2 см: 5 м. Какова фактическая длина и ширина комнаты? Найдите площадь реальной комнаты.
Ширина: _________ м
Длина: _________ м
Площадь: _________ кв.м
Ответ:
Ширина: 25 м
Длина: 15 м
Площадь: 375 кв.м
Пояснение:
Определяем количество метров, соответствующее 1 сантиметру на чертеже:
2 см / 5 см = (2 см ÷ 2) / (5 см ÷ 2) = 1 см / 2.5 м
Определяем реальную длину помещения, обозначенную на чертеже 10 см:
10 × 2,5 = 25 м
Определяем реальную ширину помещения, обозначенную на чертеже 6 см:
6 × 2,5 = 15 м
Вычисляем площадь комнаты:
25 × 15 = 375 квадратных футов.
Вопрос 4.
Чертеж кафетерия в масштабе нарисован на бумаге с сантиметровой сеткой, как показано.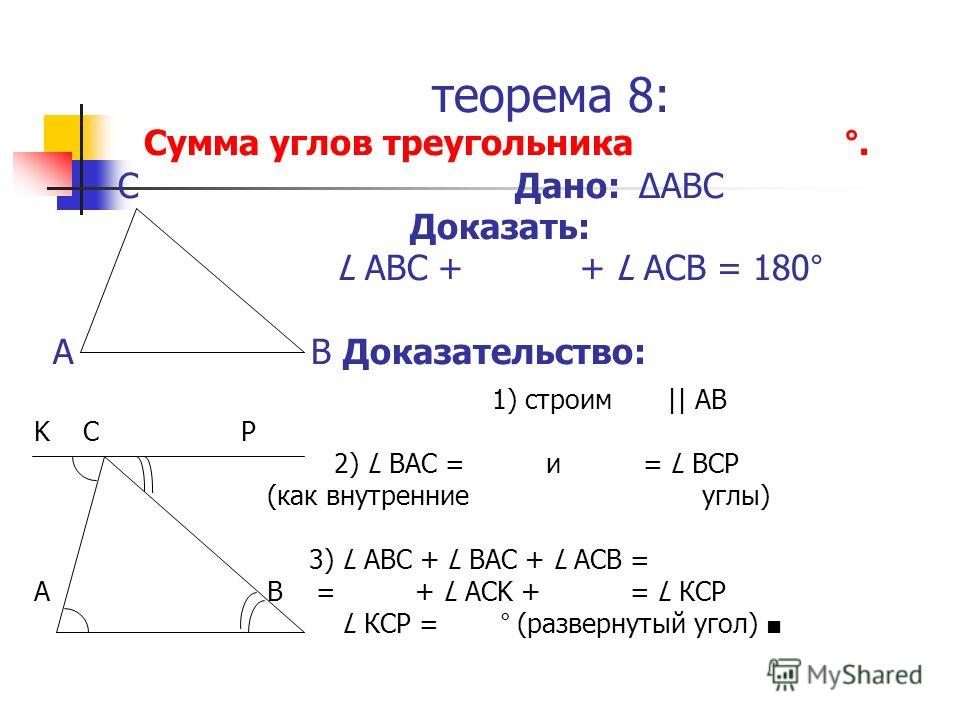 Масштаб 1 см: 4 м.
Масштаб 1 см: 4 м.
а. Нарисуйте прямоугольник на бумаге с сантиметровой сеткой в масштабе 1 см: 6 м.
Тип ниже:
_____________
Ответ:
Вопрос 4.
г. Какова фактическая длина и ширина кафетерия при исходных масштабах? Каковы реальные размеры кафетерия при использовании новых весов?
Длина: _________ м
Ширина: _________ м
Ответ:
В исходном масштабе размеры на чертеже равны
l1 = 9 см
w1 = 6 см
Реальную длину определяем по оригинальному масштабу:
9 × 4 = 36
Фактическую ширину определяем с помощью исходный масштаб:
6 × 4 = 24
Во втором масштабе размеры на чертеже равны
l2 = 6 см
w1 = 4 см
Мы определяем фактическую длину, используя исходный масштаб:
6 × 6 = 36
We Определите фактическую ширину, используя исходную шкалу:
4 × 6 = 24
Таким образом, длина равна 36 м
Ширина равна 24 м
Регистрация основных вопросов
Вопрос 5.
Если у вас есть точный, полный чертеж в масштабе и масштаб, какие размеры объекта на чертеже вы можете найти?
Тип ниже:
_____________
Ответ:
Если у нас есть точный, полный чертеж в масштабе и масштабе, мы можем определить все измерения объекта, потому что все они пропорциональны размерам на чертеже, а соотношение является масштабом.
Независимая практика — стр. № 241
Вопрос 6.
Art
У Мари есть уменьшенная копия знаменитой картины Рене Магритта «Школьный учитель».Ее копия имеет размеры 2 на 1,5 дюйма. Масштаб копии — 1 дюйм: 40 см.
а. Найдите размеры оригинальной картины.
Длина: _________ см
Ширина: _________ см
Ответ:
Длина: 80 см
Ширина: 60 см
Пояснение:
Нам даны данные
Масштаб: 1 дюйм: 40 см
Копия l1 = 2 дюйма
w1 = 1,5 дюйма
Определяем длину l оригинальной картины
l = 2 × 40 = 80см
Определяем ширина w оригинальной картины
w = 1. 5 × 40 = 60 см
5 × 40 = 60 см
Вопрос 6.
б. Найдите область оригинальной картины.
_____________ см кв.
Ответ: 4800 кв. См
Пояснение:
Определяем ширину w оригинальной картины
A = l.w
A = 80 × 60 = 4800 кв. См
Вопрос 6.
c. Так как 1 дюйм равен 2,54 см, найдите размеры оригинальной картины в дюймах.
Длина: _________ дюймов
Ширина: _________ дюймов
Ответ:
Длину l оригинальной картины определяем в дюймах:
1 дюйм.= 2,54 см
l = 80 / 2,54 см ≈ 31,5 дюйма
Определяем ширину w исходной картины в дюймах:
w = 60 / 2,54 ≈ 23,6 дюйма
Вопрос 6.
г. Найдите площадь оригинальной картины в квадратных дюймах
_____________ квадратных дюймов
Ответ: 743,4 квадратных дюйма
Пояснение:
Мы находим площадь оригинальной картины в квадратных дюймах:
l × w = 31,5 × 23,6 = 743,4 квадратных дюйма
Таким образом, площадь оригинальной картины равна 743.4 квадратных дюйма.
Вопрос 7.
Пол игровой комнаты составляет 120 на 75 футов. В масштабном чертеже пола на сетке используется масштаб 1 единица: 5 футов. Каковы размеры чертежа в масштабе?
Длина: _________ шт.
Ширина: _________ шт.
Ответ:
Длина: 24 шт.
Ширина: 15 шт.
Пояснение:
Нам даны данные:
Масштаб: 1 единица: 5 футов
Фактические размеры: l = 120 футов, w = 75 футов
Мы определяем количество единиц на чертеже, соответствующее 1 футу, исходя из фактических размеров.
1 единица / 5 футов
(1 единица ÷ 5) / (5 футов ÷ 5) = 0,2 единицы / 1 фут
Определяем длину чертежа в масштабе:
120 × 0,2 = 24 единицы
Определяем ширину чертеж в масштабе:
75 × 0,2 = 15 шт.
Вопрос 8.
Множественные представления
Длина стола 6 футов. На чертеже в масштабе длина составляет 2 дюйма. Напишите три возможных масштаба рисунка.
Тип ниже:
_____________
Ответ:
l = 6 футов
l1 = 2 дюйма
l = фактическая длина
l1 = длина на чертеже в масштабе
2 дюйма: 6 футов
1 дюйм: 3 фута
2/6 × 12 = 2/72 = 1/36
1 см: 36 см
Вопрос 9.
Анализ взаимосвязей
Масштаб чертежа составляет 10 см: 1 мм. Что больше, реальный объект или масштабный рисунок? Объяснять.
_____________
Ответ:
Нам дан масштаб
10 см: 1 мм
100 мм: 1 м
Это означает, что соответствующий фактический размер для 100 мм чертежа равен 1 мм, поэтому большему на чертеже соответствует меньший фактический размер. расстояние, поэтому масштаб чертежа больше.
Вопрос 10.
Архитектура
Масштабная модель здания 5.4 фута высотой.
а. Если первоначальное здание было 810 метров в высоту, в каком масштабе была сделана модель?
______ футов: ______ м
Ответ: 1 фут: 150 м
Пояснение:
Отметим:
h2 = высота на масштабной модели
h = фактическая высота
Нам даны данные
h2 = 5,4 фута
h = 810 метров
Определяем масштаб для модели
h2 / h = 5,4 фута / 810 м = (5,4 фута ÷ 5,4) / (810 ÷ 5,4)
1 фут / 150 м
1 фут: 150 м
Вопрос 10.
г. Если модель сделана из крошечных кирпичей, каждый размером 0,4 дюйма, сколько кирпичей в высоту эта модель?
___________ кирпич
Ответ: 14 кирпичей
Пояснение:
Определяем масштаб для модели:
х2 / 0,4 = 5,4 / 0,4 = 13,5
Количество кирпичей: 14
Стр. № 242
Вопрос 11.
Вас попросили построить масштабную модель вашей школы из зубочисток. Представьте, что ваша школа имеет высоту 30 футов. Ваш масштаб — 1 фут: 1.26 см.
а. Если высота зубочистки 6,3 см, сколько зубочисток будет у вашей модели?
______ зубочистки
Ответ: 6
Пояснение:
Учитывая, что
h = 30 футов
1 фут: 1,26 см
h2 = высота на масштабной модели
h = фактическая высота
Мы определяем высоту h2 модели:
h2 = 30 × 1,26 = 37,8 см
h2 / 6,3 = 37,8 / 6,3 = 6
Таким образом, количество зубочисток = 6
Вопрос 11.
б. У вашей матери закончились зубочистки, и она предлагает вам использовать вместо них ватные палочки. Вы измеряете их, а они высотой 7,6 см. Сколько ватных тампонов высотой будет у вашей модели?
Вы измеряете их, а они высотой 7,6 см. Сколько ватных тампонов высотой будет у вашей модели?
______ ватные палочки
Ответ: 5
Пояснение:
Находим количество хлопковых мазков
h2 / 7,6 = 37,8 / 7,6 ≈ 5
Таким образом, количество хлопковых мазков = 5
H.O.T.
Сосредоточьтесь на мышлении высшего порядка
Вопрос 12.
Выводы по розыгрышу
Площадь квадратного пола на чертеже в масштабе составляет 100 квадратных сантиметров, а масштаб чертежа составляет 1 см: 2 фута.Какова реальная площадь пола? Каково соотношение площади рисунка к фактической площади?
Площадь = ______ кв. Футов
Ответ: 400 кв. Футов
Пояснение:
A1 = площадь чертежа
A = площадь фактического пола
Нам даны данные:
A1 = 100 см²
1 см: 2 фута
1 см соответствует 2 футам
1 см × 1 см соответствует 2 фута × 2 фута
1 см² соответствует 4 футам²
A = 100.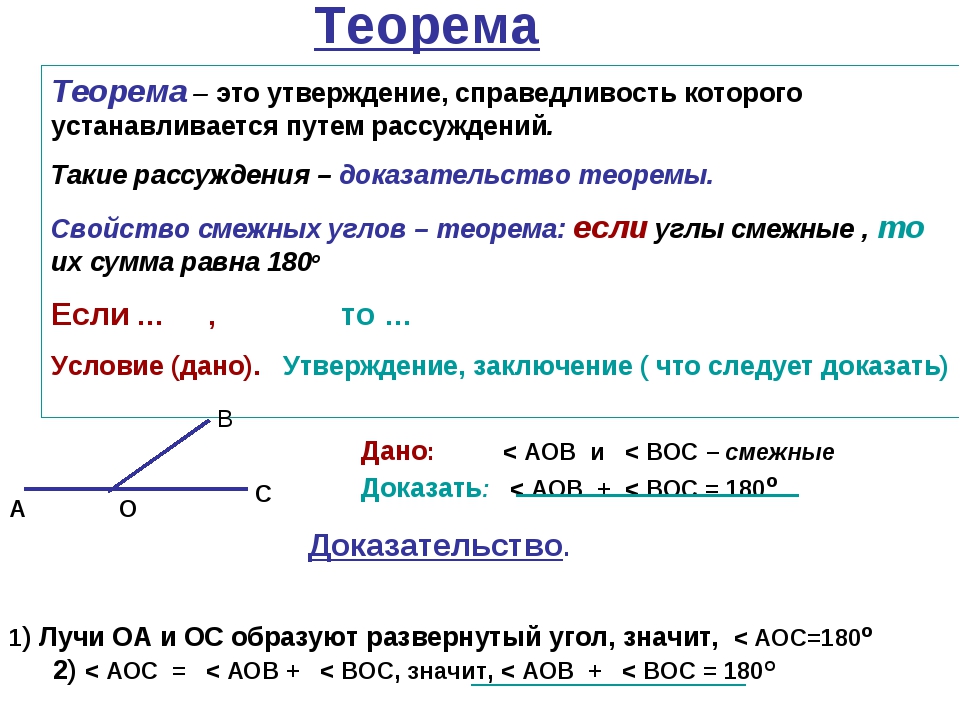 4 = 400 фут²
4 = 400 фут²
Мы определяем отношение площади на чертеже к фактической площади:
1 фут = 0.3048 м = 30,48 см
A1 / A = 100/400 × 30,48² ≈ 0,0003
Вопрос 13.
Множественные представления
Опишите, как перерисовать масштабный чертеж с новым масштабом.
Тип ниже:
_____________
Ответ:
Чтобы перерисовать масштабный чертеж с новым масштабом, мы выполняем 2 шага:
1. Мы находим, во сколько раз новый масштаб больше или меньше старого.
2. Мы умножаем этот коэффициент масштабирования на размеры старого чертежа в масштабе, чтобы получить новый чертеж.
Вопрос 14.
Представьте проблемы реального мира
Опишите, как несколько рабочих мест или профессий могут использовать масштабные чертежи на работе.
Тип ниже:
_____________
Ответ:
Масштабные чертежи чрезвычайно полезны в работах, которые должны представлять большие площади на небольших устройствах, таких как
1. Архитектура / конструкции
2. Медицина
Медицина
3. Сельское хозяйство
4. Туризм
5. Транспорт
Практическое руководство — стр. № 245
Сообщите, создает ли каждая фигура условия для образования уникального треугольника, более одного треугольника или отсутствия треугольника.
Вопрос 1.
Введите ниже:
_____________
Ответ: Уникальный треугольник
Пояснение:
Нам даны два угла и включенная сторона, таким образом, получается уникальный треугольник, поскольку стороны, выходящие из B и A, пересекаются в единственной точке.
Вопрос 2.
Тип ниже:
_____________
Ответ: Нет треугольника
Пояснение:
Нам даны три стороны треугольника. Мы проверяем, больше ли сумма любых двух сторон другой.
4 + 11 = 15> 3
11 + 3 = 14> 4
3 + 4 = 7 не больше 11.
Поскольку одно неравенство не проверено, треугольник не существует.
Вопрос 3.
Тип ниже:
_____________
Ответ: Уникальный треугольник
Пояснение:
Нам даны два угла и включенная сторона, таким образом, получается уникальный треугольник, поскольку стороны, выходящие из B и A, пересекаются в единственной точке.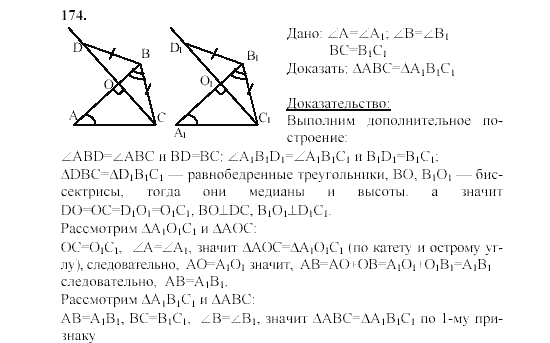
Вопрос 4.
Введите ниже:
_____________
Ответ: Уникальный треугольник
Пояснение:
Нам даны три стороны треугольника.Мы проверяем, больше ли сумма любых двух сторон другой.
6 + 12 = 18> 7
12 + 7 = 19> 6
6 + 7 = 13> 12
Поскольку все неравенства проверены, получается уникальный треугольник.
Регистрация основных вопросов
Вопрос 5.
Опишите длины трех сегментов, которые нельзя использовать для образования треугольника.
Тип ниже:
_____________
Ответ:
Найдите длины трех отрезков, которые не должны быть сторонами треугольника, по крайней мере, одна сумма двух сторон должна быть меньше другой стороны.
Пусть a, b, c — длины трех сегментов.
a + b не> a + b + k = c
Независимая практика
Вопрос 6.
На отдельном листе бумаги попробуйте нарисовать треугольник с длиной сторон 3 и 6 см и включенным углом 120 °. Определите, образуют ли данные сегменты и угол уникальный треугольник, более одного треугольника или нет треугольника.
Определите, образуют ли данные сегменты и угол уникальный треугольник, более одного треугольника или нет треугольника.
Тип ниже:
_____________
Ответ: Уникальный треугольник
Пояснение:
∠A = 120 °
AB = 6
AC = 3
Рисуем отрезок AB, угол A и отрезок AC, затем соединяем B и C.В результате получился уникальный треугольник.
Вопрос 7.
Ландшафтный архитектор представил заказчику проект цветочного сада треугольной формы с длиной сторон 21 фут, 37 футов и 15 футов. Объясните, почему не наняли архитектора для создания цветника.
Тип ниже:
_____________
Ответ:
Нам даны стороны треугольника
21 + 37 = 58> 15
37 + 15 = 52> 21
15 + 21 = 36 not> 37
Мы проверили неравенства трех треугольников
Таким образом, треугольник не существуют, поэтому архитектора не наняли для создания цветника.
Стр. № 246
Вопрос 8.
Сделайте предположение
Углы на реальном дорожном знаке в форме треугольника имеют размер 60 °. Углы на чертеже знака в масштабе имеют размер 60 °. Объясните, как вы можете использовать эту информацию, чтобы решить, можно ли использовать три заданные угловые меры для образования уникального треугольника или более чем одного треугольника.
Углы на чертеже знака в масштабе имеют размер 60 °. Объясните, как вы можете использовать эту информацию, чтобы решить, можно ли использовать три заданные угловые меры для образования уникального треугольника или более чем одного треугольника.
Тип ниже:
_____________
Ответ: Три заданные угловые меры, сумма которых равна 180 °, могут быть использованы для образования бесконечного числа треугольников, имеющих свойство пропорциональности их соответствующих сторон.
H.O.T.
Сосредоточьтесь на мышлении высшего порядка
Вопрос 9.
Сообщайте математические идеи
На рисунке слева показан отрезок линии длиной 2 дюйма, образующий угол 45 °, с пунктирной линией, длина которой не указана. На рисунке справа показан компас, установленный на ширину 1 \ (\ frac {1} {2} \) дюймов с точкой на верхнем конце 2-дюймового сегмента. Строится дуга, дважды пересекающая пунктирную линию.
Объясните, как вы можете использовать этот рисунок, чтобы решить, можно ли использовать две стороны и угол, не входящий между ними, для образования уникального треугольника, более одного треугольника или без треугольника.
Тип ниже:
_____________
Ответ:
Тринагла не существует, потому что одна сторона короче двух других. Круг пересекает пунктирную линию только один раз, так что один угол составляет 45 °, поэтому есть только одно решение. Круг с центром в точке B дважды пересекает пунктирную линию, таким образом, образуются два треугольника.
Вопрос 10.
Критическое мышление
Две стороны равнобедренного треугольника имеют длину 6 дюймов и 15 дюймов соответственно.Найдите длину третьей стороны. Объясните свои рассуждения.
_______ дюймов
Ответ: 15 дюймов
Пояснение:
Даны две стороны равнобедренного треугольника
a = 6
b = 15
Есть две возможности, третья сторона равна a или b. Давайте изучим их оба. 21> 15 = c
a + c = 6 + 15 = 21> 15 = b
b + c = 15 + 15 = 30> 6 = a
Случай 2: a = 6, b = c = 15
Таким образом, третий сторона треугольника равна 15.
Практическое руководство — Страница № 249
Опишите каждое поперечное сечение.
Вопрос 1.
Введите ниже:
_____________
Ответ: Треугольник / Четырехугольный треугольник
Данное поперечное сечение в кубе представляет собой треугольник / равносторонний треугольник.
Вопрос 2.
Тип ниже:
_____________
Ответ: Прямоугольник
Заданное поперечное сечение цилиндра — прямоугольник.
Вопрос 3.
Тип ниже:
_____________
Ответ: Треугольник
Пояснение:
Поперечное сечение в призме — треугольник.
Вопрос 4.
Введите ниже:
_____________
Ответ: Кривая в форме радуги
Данное поперечное сечение конуса представляет собой кривую в форме радуги.
Регистрация основных вопросов
Вопрос 5.
Каков первый шаг в описании того, какая фигура получается, когда данная плоскость пересекает данную трехмерную фигуру?
Тип ниже:
_____________
Ответ:
Первый шаг в описании того, какая фигура получается, когда данная плоскость пересекает данную трехмерную фигуру, — это установить количество сторон, которые имеет поперечное сечение.
Независимая практика
Вопрос 6.
Опишите различные способы, которыми плоскость может пересекать цилиндр, и полученное поперечное сечение.
Тип ниже:
_____________
Ответ:
Поперечное сечение может быть:
1. круг
2. эллипс
3. прямоугольник
Стр. № 250
Вопрос 7.
Сделайте гипотезу
Какие поперечные сечения вы можете увидеть, когда плоскость пересекает конус, чего вы не увидите, когда плоскость пересекает пирамиду или призму?
Тип ниже:
_____________
Ответ:
Сечение может быть:
1.окружность
2. эллипс
3. парабола
4. гипербола
5. треугольник
H.O.T.
Сосредоточьтесь на мышлении высшего порядка
Вопрос 8.
Критическое мышление
Две фигуры слева внизу показывают, что вы можете сформировать поперечное сечение куба, представляющего собой пятиугольник. Представьте себе плоскость, разрезающую куб под углом таким образом, чтобы разрезать пять из шести граней куба. Нарисуйте пунктирные линии на третьем кубе, чтобы показать, как образовать поперечное сечение, представляющее собой шестиугольник.
Представьте себе плоскость, разрезающую куб под углом таким образом, чтобы разрезать пять из шести граней куба. Нарисуйте пунктирные линии на третьем кубе, чтобы показать, как образовать поперечное сечение, представляющее собой шестиугольник.
Тип ниже:
_____________
Ответ:
Рисуем плоскость, разрезающую куб так, чтобы сечение было шестиугольником: для этого берем середину из 6 смежных сторон:
Вопрос 9.
Анализировать взаимосвязи
Сфера имеет радиус 12 дюймов. Горизонтальная плоскость проходит через центр сферы.
а. Опишите поперечное сечение, образованное плоскостью и сферой.
Тип ниже:
_____________
Ответ: Круг
Пояснение:
Нам дана сфера и поперечное сечение, проходящее через центр сферы:
Поперечное сечение, проходящее через центр сферы, представляет собой круг с радиусом, равным радиусу сферы.
Вопрос 9.
б. Опишите поперечные сечения, образовавшиеся, когда плоскость пересекает внутреннюю часть сферы, но удаляется от центра.
Тип ниже:
_____________
Ответ: Поперечные сечения, образованные плоскостью, пересекающей внутреннюю часть сферы за пределами центра, являются кругами.
Вопрос 10.
Сообщайте математические идеи
Правая прямоугольная призма пересекается горизонтальной плоскостью и вертикальной плоскостью. Поперечное сечение, образованное горизонтальной плоскостью и призмой, представляет собой прямоугольник размером 8 дюймов.и 12 дюймов. Поперечное сечение, образованное вертикальной плоскостью и призмой, представляет собой прямоугольник с размерами 5 дюймов и 8 дюймов. Опишите грани призмы, включая их размеры. Затем найдите его объем.
Тип ниже:
_____________
Ответ: 480 куб. Дюймов
Пояснение:
Горизонтальное сечение имеет размеры 8 × 12, а вертикальное — 5 × 8.
Призма имеет размеры:
5 дюймов, 8 дюймов, 12 дюймов
Находим объем призмы:
5 × 8 × 12 = 480 кубических дюймов
Вопрос 11.
Представление реальных проблем
Опишите реальную ситуацию, которая может быть представлена плоскостями, разрезающими трехмерную фигуру для формирования поперечных сечений.
Тип ниже:
_____________
Ответ:
Примеры реальных ситуаций, которые могут быть представлены плоскостями, разрезающими трехмерные фигуры для образования поперечных сечений:
— электрические провода
— водопроводные / газовые трубы
— проект дома
— геология
— сейсмология
Практическое руководство — стр.256
Для 1–2 используйте цифру.
Вопрос 1.
Словарь
Сумма измерений ∠UWV и ∠UWZ равна 90 °, поэтому UWV и ∠UWZ равны _____ углам.
Тип ниже:
_____________
Ответ: Дополнительные углы
Пояснение:
Сумма ∠UWV и ∠UWZ равна 90 °, поэтому UWV и ∠UWZ являются дополнительными углами.
Вопрос 2.
Словарь
∠UWV и ∠VWX имеют общую вершину и одну сторону. Они не перекрываются, поэтому ∠UWV и ∠VWX — это _____ углы.
Тип ниже:
_____________
Ответ: Смежные углы
Пояснение:
∠UWV и ∠VWX имеют общую вершину и одну сторону. Они не перекрываются, поэтому ∠UWV и ∠VWX — смежные углы.
Они не перекрываются, поэтому ∠UWV и ∠VWX — смежные углы.
Для 3–4 используйте цифру.
Вопрос 3.
∠AGB и ∠DGE — _____ углы, поэтому m∠DGE = _____.
Тип ниже:
_____________
Ответ: ∠AGB и ∠DGE — вертикальные углы, поэтому m∠DGE = m∠AGB = 30 °
Вопрос 4.
Найдите меру ∠EGF.
_______ °
Ответ: 100 °
Пояснение:
m∠CGD + m∠DGE + m∠EGF = 180 °
50 ° + m∠AGB + m∠EGF = 180 °
50 ° + 30 ° + 2x = 180 °
2x = 180 ° — 80 °
2x = 100 °
мм EGF = 2x = 100 °
Вопрос 5.
Найдите значение x и меру ∠MNQ.
x = _______ °
мMNQ = _______ °
Ответ:
∠MNQ + ∠QNP = 90 °
3x — 13 ° + 58 ° = 90 °
3x = 90 ° + 13 ° — 58 °
3x = 45 °
x = 15 °
м∠MNQ = 3x — 13 °
= 3 × 15 ° — 13 °
= 45 ° — 13 °
= 32 °
Регистрация основных вопросов
Вопрос 6.
Предположим, что вы знаете, что ∠T и ∠S являются дополнительными и что m∠T = 3 (m∠S). Как найти m∠T?
Как найти m∠T?
Тип ниже:
_____________
Ответ:
m∠T + m∠S = 180 °
m∠T = 3 (m∠S)
m∠S = m∠T / 3
Сформируем второе уравнение, запишем m∠S через m∠ T
m∠T + m∠T / 3 = 3 × 180 °
3m∠T + m∠T = 3 × 180 °
4m∠T = 540 °
m∠T = 540 ° / 4
m∠T = 135 °
Независимая практика — стр. № 257
Для 7–11 используйте цифру.
Вопрос 7.
Назовите пару смежных углов. Объясните, почему они рядом.
Тип ниже:
_____________
Ответ:
Пара смежных углов:
∠SUR и ∠RUN (общая вершина U и одна общая сторона — UR — без перекрытия)
∠NUQ и ∠QUP (общая вершина U и одна общая сторона — UQ — без перекрытия )
∠PUT и ∠TUS (общая вершина U и одна общая сторона — UT — без перекрытия)
Вопрос 8.
Назовите пару острых вертикальных углов.
Тип ниже:
_____________
Ответ:
Глядя на рисунок выше, мы можем сказать, что ∠SUR и ∠PUQ — это вертикальные углы.
Вопрос 9.
Назовите пару дополнительных углов.
Тип ниже:
_____________
Ответ:
На рисунке выше показано, что ∠SUR и ∠RUQ являются дополнительными углами.
Вопрос 10.
Обоснуйте рассуждение
Найдите m∠QUR. Обосновать ответ.
_______ °
Ответ:
Мы должны найти m∠QUR.
∠SUR и ∠QUR — дополнительные уголки.
м∠SUR + m∠QUR = 180 °
м∠QUR + 41 ° = 180 °
м∠QUR = 180 ° — 41 °
м∠QUR = 139 °
Вопрос 11.
Выводы по розыгрышу
Что больше, m∠TUR или m∠RUQ? Объяснять.
Тип ниже:
_____________
Ответ:
m∠QUR = 139 °
m∠TUR = m∠TUS + m∠SUR
90 ° + 41 ° = 131 °
Находим m∠TUR
139 °> 131 °
m∠QUR> m∠
Для 12–13 используйте цифру. Велосипедная дорожка пересекает дорогу, как показано. Решите для каждой указанной угловой меры или переменной.
Вопрос 12.
x =?
_______ °
Ответ: x = 21 °
Пояснение:
KMI и ∠HMG расположены вертикально, поэтому совпадают.
Определяем x:
84 ° = 4x
4x = 84 °
x = 84 ° / 4
x = 21 °
Вопрос 13.
м∠KMH =?
_______ °
Ответ: 96 °
Пояснение:
KMI и ∠KMH являются дополнительными.
Определяем m∠KMH:
м∠KMH + m∠KMI = 180 °
м∠KMH + 84 ° = 180 °
м∠KMH = 180 ° — 84 °
м∠KMH = 96 °
Для 14–16 используйте цифру. Решите для каждой указанной угловой меры.
Вопрос 14.
m∠CBE =?
_______ °
Ответ: 118 °
Пояснение:
Определяем m∠CBE:
м∠CBE + m∠EBF = 180 °
м∠CBE + 62 ° = 180 °
м∠CBE = 180 ° — 62 °
м∠CBE = 118 °
Вопрос 15.
m∠ABF =?
_______ °
Ответ: 28 °
Пояснение:
Определяем m∠ABF
m∠ABF + m∠EBF = 90 °
м∠ABF + 62 ° = 90 °
м∠ABF = 90 ° — 62 °
м∠ABF = 28 °
Вопрос 16.
m∠CBA =?
_______ °
Ответ: 152 °
Пояснение:
Определяем m∠CBA
m∠CBA = m∠DBF = m∠DBE + m∠EBF
90 ° + 62 ° = 152 °
m∠CBA = 152 °
Вопрос 17.
Размер ∠A на 4 ° больше меры measureB.Эти два угла дополняют друг друга. Найдите размер каждого угла.
мА = __________ °
мБ = __________ °
Ответ:
мА = 47 °
мБ = 43 °
Пояснение:
Нам даны данные:
m∠A = m∠B + 4 °
m∠A + m∠B = 90 °
m∠B + 4 ° + m∠B = 90 °
2m∠B = 90 ° — 4 °
2m∠B = 86 °
m∠B = 86 ° / 2
m∠B = 43 °
m∠A = m∠B + 4 °
m∠A = 43 ° + 4 °
м∠A = 47 °
Вопрос 18.
Измерение ∠D в 5 раз больше меры ∠E.Два угла являются дополнительными. Найдите размер каждого угла.
мД = __________ °
мД = __________ °
Ответ:
mD = 150 °
mE = 30 °
Пояснение:
Нам даны данные
m∠D = 5 (m∠E)
m∠D + m∠E = 180 °
5 (m∠E) + m∠E = 180 °
6 m∠E = 180 °
м∠E = 180 ° / 6
м∠E = 30 °
м∠D = 5 (м∠E)
м∠D = 5 × 30 °
м∠D = 150 °
Стр. № 258
Вопрос 19.
Астрономия
Иногда астрономы используют угловые меры, разделенные на градусы, минуты и секунды. Один градус равен 60 минутам, а одна минута равна 60 секундам. Предположим, что ∠J и ∠K дополняют друг друга, а величина ∠J составляет 48 градусов, 26 минут, 8 секунд. Какова мера ∠K?
Один градус равен 60 минутам, а одна минута равна 60 секундам. Предположим, что ∠J и ∠K дополняют друг друга, а величина ∠J составляет 48 градусов, 26 минут, 8 секунд. Какова мера ∠K?
_______ ° _______ ‘_______”
Ответ: 41 ° 33 ‘52 ″
Пояснение:
Нам даны данные
м∠Дж + м∠К = 90 °
м∠Дж = 48 ° 26 ‘8 ″
90 ° — 48 ° 26′ 8 ″
89 ° 60 ‘- 48 ° 26 ‘8 ″
89 ° 59’60 ”- 48 ° 26′ 8 ″ = 41 ° 33 ’52 ″
Таким образом, размер ∠K составляет 41 ° 33′ 52 ″
H.О.
Сосредоточьтесь на мышлении высшего порядка
Вопрос 20.
Представляют проблемы реального мира
Железнодорожные пути пересекаются с дорогой, как показано. Город разрешит парковку под углом K, если угол K больше 38 °. Можно ли построить автостоянку под углом К? Почему или почему нет?
_______
Ответ:
m∠K = 180 ° — 50 ° — 90 ° = 40 °
Поскольку m∠K = 40 °> 38 °, парковка может быть построена.
Вопрос 21.
Обоснование рассуждений
Кендра говорит, что она может нарисовать ∠A и ∠B так, что m∠A равно 119 °, а ∠A и ∠B — дополнительные углы.Ты согласен или несогласен? Объясните свои рассуждения.
_______
Ответ:
Нам даны данные
m∠A = 119 °
m∠A + m∠B = 90 °
m∠B = 90 ° — m∠A
= 90 ° — 119 ° = -29 °
Поскольку m∠B <0, Кендра ошибается, она не может нарисовать углы.
Вопрос 22.
Вывод заключения
Если два угла дополняют друг друга, каждый угол называется дополнением другого. Если два угла являются дополнительными, каждый угол называется добавлением другого.
а. Предположим, что m∠A = 77 °.Какова мера дополнения к A? Объяснять.
_______ °
Ответ: 77 °
Пояснение:
90 ° — (90 ° — m∠A) = 90 ° — (90 ° — 77 °)
90 ° — 77 ° = 13 °
77 °
Вопрос 22.
б. Какой вывод можно сделать о дополнении угла? Объяснять.
Тип ниже:
_____________
Ответ:
Дополнением к углу является сам угол:
90 ° — (90 ° — m∠A)
90 ° — 90 ° + m∠A
8.
 1 Подобные фигуры и чертежи в масштабе — Стр. № 259
1 Подобные фигуры и чертежи в масштабе — Стр. № 259 Вопрос 1.
План дома имеет масштаб 1 дюйм: 4 фута. Длина и ширина каждой комнаты в реальном доме показаны в таблице. Заполните таблицу, найдя длину и ширину каждой комнаты на чертеже.
Тип ниже:
_____________
Ответ:
Таким образом, на каждые 4 фута в фактическом измерении на чертеже приходится 1 дюйм.
8.2 Геометрические чертежи
Вопрос 2.
Можно ли сформировать треугольник со сторонами 8 см, 4 см и 12 см?
______
Ответ:
Нам даны длины сторон
8 + 12 = 20> 4
4 + 12 = 16> 8
8 + 4 not> 12
Поскольку одно из неравенств не проверено, три заданные длины сторон не могут образовать треугольник.
Вопрос 3.
Треугольник имеет длину стороны 11 см и 9 см. Каким может быть значение третьей стороны, 20 см или 15 см?
______
Ответ: 15 см
Пояснение:
Нам даны длины сторон
11, 9
11 + 9 = 20 not> 20
Мы проверяем неравенства треугольника, если добавляем третью сторону 20 см.
Поскольку одно из неравенств не проверено, три заданная длина сторон не может образовывать треугольник.
11, 9, 15
11 + 9 = 20> 15
11 + 15 = 26> 9
15 + 9 = 24> 11
Мы проверяем, что неравенства треугольника проверены, 15 может быть значением третьей стороны.
8.3 Поперечные сечения
Вопрос 4.
Назовите одно возможное поперечное сечение сферы.
Тип ниже:
_____________
Ответ: Круг
Одно из возможных поперечных сечений сферы — это круг.
Вопрос 5.
Назовите хотя бы две формы, которые являются поперечными сечениями цилиндра.
Тип ниже:
_____________
Ответ: Три возможных поперечных сечения цилиндра — это круг, эллипс и прямоугольник.
Регистрация основных вопросов
Вопрос 5.
Как можно моделировать геометрические фигуры для решения реальных задач?
Тип ниже:
_____________
Ответ: Вы можете моделировать геометрию для создания зданий и небоскребов, а также магазинов.
8.4 Угловые отношения
Вопрос 6.
∠BGC и ∠FGE — _____ углы, поэтому m∠FGE = _____
_____ °
Ответ: ∠BGC и ∠FGE — вертикальные углы, поэтому m∠FGE = m∠BGC = 90 ° — 40 ° = 50 °
Вопрос 7.
Предположим, вы знаете, что ∠S и ∠Y дополняют друг друга и что m∠S = 2 (m∠Y) — 30 °. Найдите MY.
м? Y = _____ °
Ответ: 40 °
Пояснение:
m∠S + m∠Y = 90 °
m∠S = 2 (m∠Y) — 30 °
Заменим выражение m∠S из второго уравнения на первое, мы можем найти m∠Y
2 (m∠Y) — 30 ° + m∠Y = 90 °
3m∠Y = 90 ° + 30 °
3m∠Y = 120 °
m∠Y = 120 ° / 3
m∠Y = 40 °
Выбранный ответ — стр.260
Вопрос 1.
Какое число можно добавить к 15, чтобы получить сумму 0?
Опции:
а. -10
б. -15
с. 0
г. 15
Ответ: -15
Пояснение:
Число, которое мы добавляем к числу, чтобы получить нулевую сумму, является его противоположностью. В любом случае мы должны добавить -15 к 15.
В любом случае мы должны добавить -15 к 15.
15 + (-15) = 0
Таким образом, правильный ответ — вариант B.
Вопрос 2.
Ученики рисуют задник для школьного спектакля. Фон имеет ширину 15 футов и высоту 10 футов.Каждые 16 дюймов на масштабном чертеже представляют 5 футов на заднем плане. Какова площадь масштабного чертежа?
Опции:
а. 150 в 2
б. 6 в 2
c. 3096
г. 1536 в 2
Ответ: 1536 из 2
Пояснение:
Нам даны размеры l и w фона и масштаб чертежа:
l = 15 футов
w = 10 футов
16 дюймов: 5 футов
16 дюймов / 5 футов = (16 дюймов ÷ 5 ) / (5 футов ÷ 5) = 3,2 дюйма / 1 фут
l1 = 15 × 3.2 = 48 дюймов
w1 = 10 × 32 = 320 дюймов
l1 × w1 = 48 × 32 = 1536 квадратных дюймов
Таким образом, правильный ответ — вариант D.
Вопрос 3.
Две стороны треугольника имеют размер 8 см и 12 см. Что из перечисленного НЕ МОЖЕТ быть мерой третьей стороны?
Опции:
а. 4
4
б. 12
с. 8
г. 16
Ответ: 4 см
Пояснение:
Даны две стороны треугольника
a. 4
4 + 8 не> 12
b. 12
12 + 8> 12
12 + 12> 8
c.8
8 + 8> 12
8 + 12> 12
д. 16
8 + 12> 16
8 + 16> 12
12 + 16> 8
Таким образом, единственное измерение, которое не может быть мерой третьей стороны треугольника, составляет 4 см.
Таким образом, правильный ответ — вариант А.
Вопрос 4.
Поперечное сечение — это пересечение трехмерной фигуры и _____.
Опции:
а. пункт
б. самолет
c. линия
д. набор
Ответ: Самолет
Пояснение:
Поперечное сечение — это взаимодействие трехмерной фигуры и плоскости.
Таким образом, правильный ответ — вариант Б.
Для 5–6 используйте диаграмму.
Вопрос 5.
Каков показатель ∠BFC?
Опции:
а. 18
г. 108
г. 72
г. 144
Ответ: 108 °
Пояснение:
∠BFC + ∠BFA = 180 °
∠BFC + 72 ° = 180 °
∠BFC = 180 ° — 72 °
∠BFC = 108 °
Углы ∠BFC и ∠BFA являются дополнительными. Определяем ∠BFC.
Определяем ∠BFC.
Таким образом, правильный ответ — вариант Б.
Вопрос 6.
Что описывает отношения между ∠BFA и ∠CFD?
Опции:
а. прилегающие углы
б. дополнительные углы
c. дополнительные уголки
d. вертикальные углы
Ответ: вертикальные углы
Пояснение:
Углы ∠BFA и ∠CFD являются вертикальными углами, поскольку они представляют собой противоположные углы, образованные на пересечении двух прямых.
Таким образом, правильный ответ — вариант D.
Вопрос 7.
На всю одежду уценены 15%. Какое выражение представляет новую розничную цену?
Опции:
а.0,85x
б. 1,15x
c. 1.85x
г. 0,15 х
Ответ: 0,85x
Пояснение:
x = начальная цена
Поскольку цена снизилась на 15%, новая цена будет уменьшена на 15/100 x
x — 0,15x = 0,85x
Таким образом, правильный ответ — вариант A.
Мини-задачи
Вопрос 8.
Ира построила модель Великой пирамиды в Египте для школьного проекта. Великая пирамида имеет квадратное основание со сторонами длиной 756 футов. Высота Великой пирамиды 481 фут.Ира построил свою модель пирамиды в масштабе 1 дюйм: 20 футов.
Великая пирамида имеет квадратное основание со сторонами длиной 756 футов. Высота Великой пирамиды 481 фут.Ира построил свою модель пирамиды в масштабе 1 дюйм: 20 футов.
а. Какова длина каждой стороны основания пирамиды Иры?
_____ из
Ответ: 37,8 дюйма
Мы вычисляем количество дюймов, соответствующее 1 футу, исходя из фактических размеров:
1 дюйм / 20 фут = (1 дюйм ÷ 20) / (20 футов ÷ 20) = 0,05 дюйма / 1 фут.
На 1 фут 0,05 дюйма.
Определяем длину основания пирамиды Иры:
756 × 0,05 = 37,8 дюйма
Вопрос 8.
б. Какова площадь основания пирамиды Иры?
_____ квадратных дюймов
Ответ: 1428.84 квадратных дюйма
Пояснение:
Определяем площадь основания пирамиды Иры:
37,8 × 37,8 = 1428,84 квадратных дюйма.
Вопрос 8.
c. Какова высота пирамиды Иры?
_____ из
Ответ:
Определяем высоту пирамиды Иры:
481 × 0,05 = 24,05 дюйма
Вопрос 8.
г. Ира построила свою модель, используя поперечные сечения, вырезанные параллельно основанию. Какой формы было каждое поперечное сечение?
Какой формы было каждое поперечное сечение?
Тип ниже:
____________
Ответ: Поперечные сечения, параллельные основанию, имеют форму квадрата.
Заключение:
Поэтому подготовьте своих детей, заставив их попрактиковаться в тесте с помощью Go Math Grade 7 Answer Key Глава 8 Моделирование геометрических фигур. Получите ответы на все вопросы с помощью простых приемов для всех глав Go Math Answer Key. Удачи!!!
Нарисуйте (от руки, с помощью линейки, транспортира и техники) геометрические фигуры в заданных условиях. Сосредоточьтесь на построении треугольников из трех углов или сторон, обращая внимание на то, когда условия определяют уникальный треугольник, более одного треугольника или отсутствие треугольника.
Стороны треугольников: Учащимся предлагается определить, определяет ли треугольник заданная длина.
Тип: Формирующее оценивание
Рисование треугольников SSS:Учащимся предлагается нарисовать треугольник с заданной длиной сторон и объяснить, определяют ли эти условия уникальный треугольник.
Тип: Формирующее оценивание
Рисование треугольников SSA:Учащимся предлагается нарисовать треугольник с учетом длины двух его сторон и размера невключенного угла и решить, определяют ли эти условия уникальный треугольник.
Тип: Формирующее оценивание
Рисование треугольников SAS: Учащимся предлагается нарисовать треугольник с учетом размеров двух сторон и их угла, а также объяснить, определяют ли эти условия уникальный треугольник.
Тип: Формирующее оценивание
Рисование треугольников ASA:Учащимся предлагается нарисовать треугольник с учетом размеров двух углов и их стороны и объяснить, определяют ли эти условия уникальный треугольник.
Тип: Формирующее оценивание
Рисование треугольников AAS:Учащимся предлагается нарисовать треугольник с двумя углами и стороной без учета и объяснить, определяют ли эти условия уникальный треугольник.
Тип: Формирующее оценивание
Рисование треугольников AAA: Учащимся предлагается нарисовать треугольник с заданными углами и объяснить, определяют ли эти условия уникальный треугольник.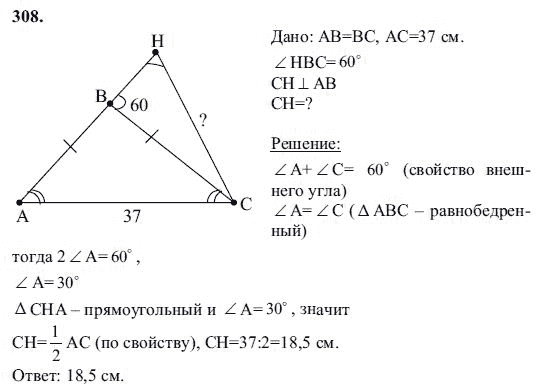
Тип: Формирующее оценивание
Задачи кодирования геометрии # 1-7, 14 и 15: Этот набор задач по геометрии фокусируется на создании множества многоугольников по мере того, как учащиеся решают задачи и думают, когда они учатся кодировать с помощью программного обеспечения для блочного кодирования.Студенту необходимо будет использовать свои знания об атрибутах многоугольников и математических принципах геометрии для выполнения заданных задач. Задачи начинаются с довольно простых и переходят к более сложным ситуациям, в которых учащиеся могут исследовать в своем собственном темпе или работать в команде. Стандарты компьютерных наук неразрывно связаны со стандартами математики, в то же время предлагая «Шаг вперед!» и «Прыгай!» возможности для повышения строгости.
Тип: План урока
Задача кодирования геометрии №16, 18 и 19: Этот набор задач по геометрии фокусируется на создании множества многоугольников с использованием координатной плоскости, когда учащиеся решают задачи и думают, когда они учатся кодировать с помощью программного обеспечения для блочного кодирования.Студенту необходимо будет использовать свои знания об атрибутах многоугольников и математических принципах геометрии для выполнения заданных задач. Задачи начинаются с довольно простых и переходят к более сложным ситуациям, в которых учащиеся могут исследовать в своем собственном темпе или работать в команде. Стандарты компьютерных наук неразрывно связаны со стандартами математики, в то же время предлагая «Шаг вперед!» и «Прыгай!» возможности для повышения строгости.
Тип: План урока
Исследование неравенства треугольников:Студенты используют практические материалы, чтобы понять, что только определенные комбинации длин могут создавать замкнутые треугольники.
Тип: План урока
Designing Geo-World: тематический парк на основе геометрии: На этом уроке учащиеся исследуют контекстную задачу, в которой им нужно будет построить двумерный многоугольник, вычислить фактическую длину и площади, а затем воспроизвести масштабный чертеж фигуры в другом масштабе.

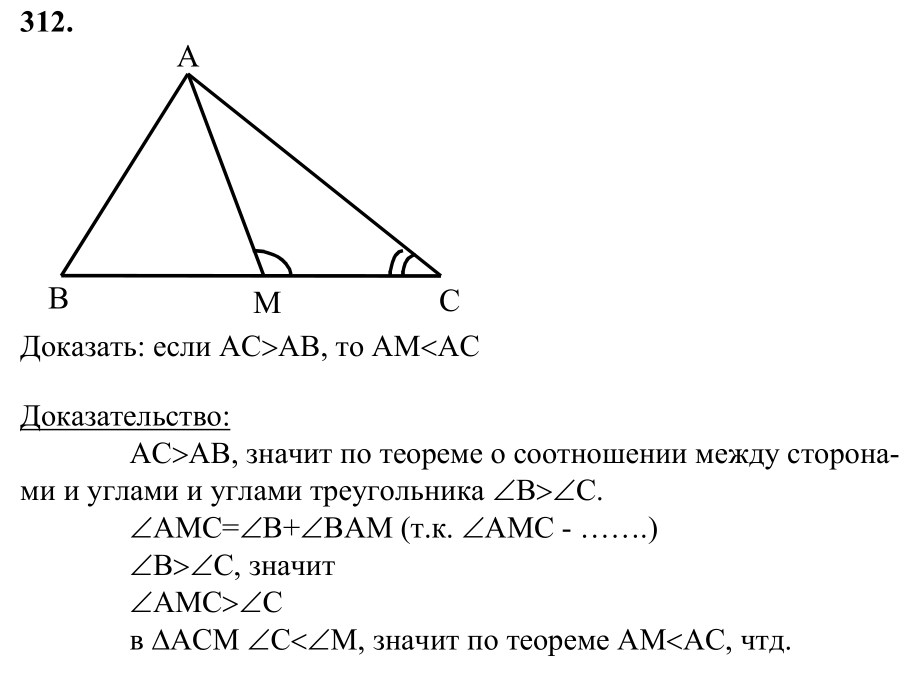 Лучи называются сторонами угла, а точка — вершиной угла.
Лучи называются сторонами угла, а точка — вершиной угла.
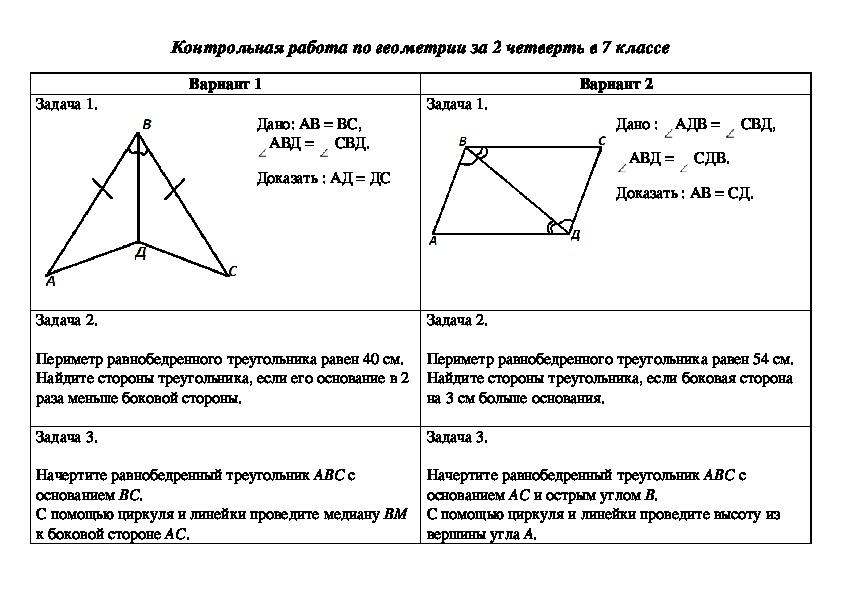
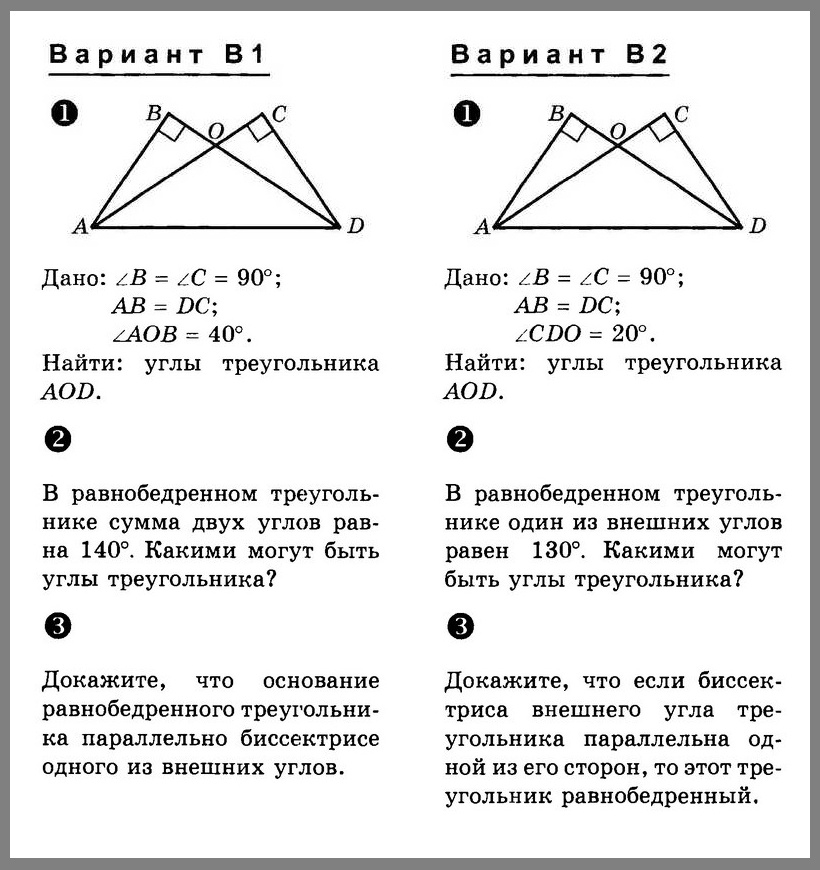
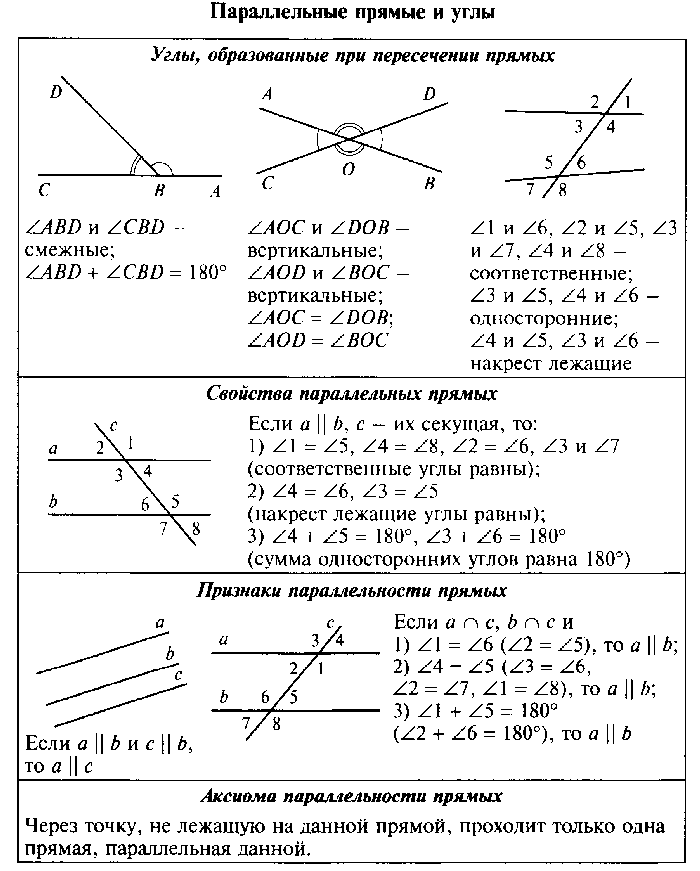





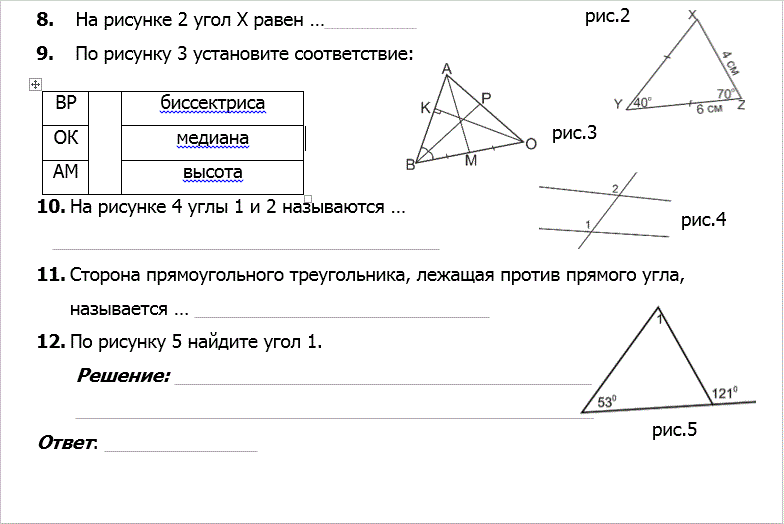
 Вычислите угол Е.
Вычислите угол Е.
 Вычислите один из вертикальных углов.
Вычислите один из вертикальных углов.
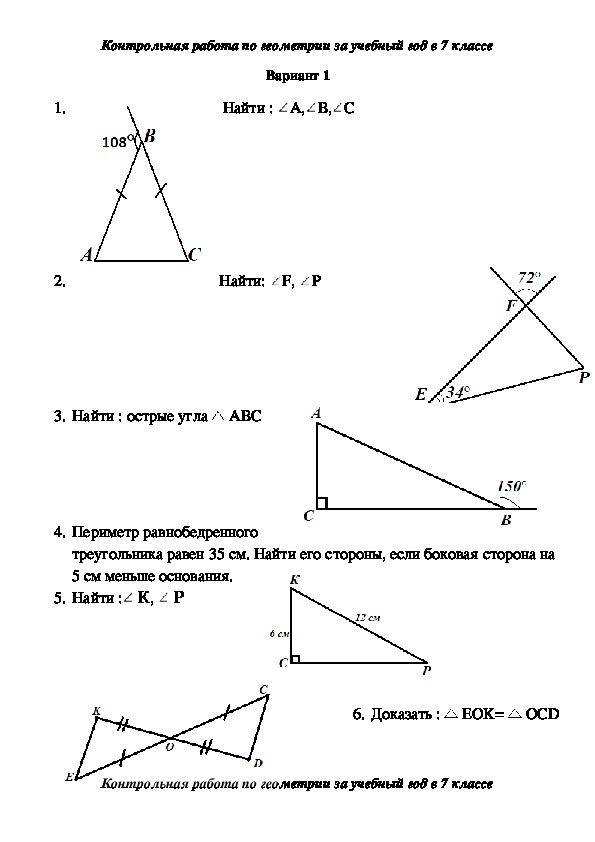 Найдите стороны треугольника.
Найдите стороны треугольника.
 Найдите больший угол.
Найдите больший угол.
 Найдите стороны треугольника.
Найдите стороны треугольника.