Атанасян Л.С., Бутузов В.Ф. Решения задач из учебника Геометрия. 7 класс
- Файлы
- Абитуриентам и школьникам
- Математика
- Геометрия
- Домашняя работа по геометрии
Геометрия
7 класс
8 класс
9 класс
Домашняя работа по геометрии
Задачники по геометрии для школьников
Стереометрия
Тригонометрия
- формат djvu
- размер 1.

- добавлен 02 января 2010 г.
М.: ФИЗМАТЛИТ,
2005. 120 с.
Настоящее издание является первой частью учебно-методического
пособия, содержащего решения задач из учебника «Геометрия 7-9» Л.
С. Атанасяна, В. Ф. Бутузова, СБ. Кадомцева, Э. Г. Позняка, И. И.
Юдиной (М.: Просвещение, 1990 и последующие издания). Данный выпуск
содержит решения задач, относящихся к 7 классу.
Купить и скачать книгу «Геометрия. 9 класс»
Смотрите также
- формат djvu
- размер 2.6 МБ
- добавлен 11 июня 2010 г.
Геометрия: Учеб. для 10-11 кл. сред. шк. /Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др. -М.: Просвещение,1992. -207 с.: ил. Учебник занял первое место на всесоюзном конкурсе учебников по математике для средней общеобразовательной школы.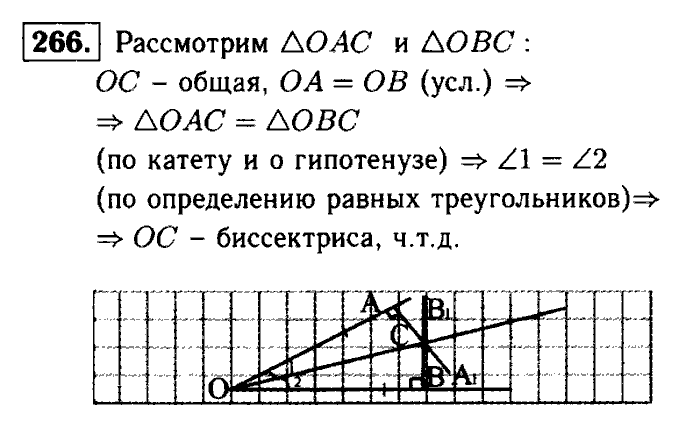
- формат djvu
- размер 8.1 МБ
- добавлен 28 января 2010 г.
Москва. Просвещение. 1992 год. Учебники для средней школы.
- формат djvu
- размер 1.99 МБ
- добавлен 24 ноября 2010 г.
Настоящее издание является второй частью учебно-методического пособия, содержащего решения задач из учебника «Геометрия 7-9» Л. С. Атанасяна, В. Ф. Бутузова, С. Б. Кадомцева, Э. Г. Позняка, И. И. Юдиной. Данный выпуск содержит решения задач, относящихся к 8 классу
- формат djvu
- добавлен 01 декабря 2010 г.
3-я часть решебника по геометрии 7-9 класс.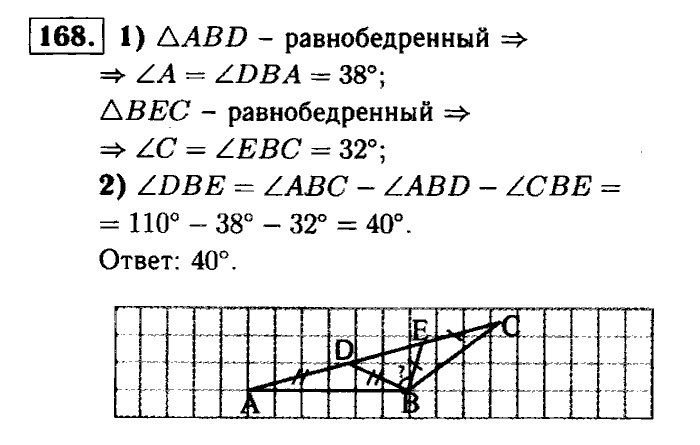 (7 класс. Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, И. И. Юдина) даёт правильные решения по данному предмету. Помогает ученикам 9го класса, которые не знаю данный предмет.
(7 класс. Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, И. И. Юдина) даёт правильные решения по данному предмету. Помогает ученикам 9го класса, которые не знаю данный предмет.
- формат djvu
- размер 1.89 МБ
- добавлен 16 декабря 2009 г.
Геометрия, 10-11 класс, Атанасян, решебник 10кл, 1-399.
- формат djvu
- размер 1.05 МБ
- добавлен 23 февраля 2011 г.
Предлагаемое методическое пособие призвано помочь учителю в работе по комплекту Е. В. Потоскуева, Л. И. Звавича «Геометрия. 11 класс» для классов с углубленным и профильным изучением математики, состоящему из учебника и задачника, который может быть использован для учащихся в общеобразовательных классах с сильным составом учащихся.
Практикум
- формат djvu
- размер 1.66 МБ
- добавлен 07 февраля 2011 г.
М. Дрофа, 2004. 224 с. ISBN 5-7107-7715-3. Предлагаемое методическое пособие призвано помочь учителю в работе по комплекту, состоящему из учебника и задачника, Е. В. Потоскуева, Л. И. Звавича «Геометрия. 10 класс» для классов с углубленным и профильным изучением математики. Этот комплект может быть использован для учащихся в общеобразовательных классах с сильным составом. В данной книге приводятся общие рекомендации к изучению теоретического мате…
- формат pdf
- размер 2.77 МБ
- добавлен
18 октября 2011 г.

Домашняя работа по геометрии за 7 класс А.Н. Прокопович. К учебнику «Геометрия 7-9 классы. Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др. 2009г.»
- формат pdf
- размер 2.76 МБ
- добавлен 17 апреля 2011 г.
Москва, 2010 г. -127 с. В пособии решены и в большинстве случаев подробно разобраны задачи и упражнения из учебника «Геометрия. 7-9 классы: учеб. для общеобразоват. учреждений / [Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. ]. — 19-е изд. — М.: Просвещение, 2009». Пособие адресовано родителям, которые смогут проконтролировать правильность решения, а в случае необходимости помочь детям в выполнении домашней работы по геометрии. Метод коор…
- формат djvu
- размер 22.31 МБ
- добавлен
13 мая 2010 г.

Данное издание содержит подробные решения задач к учебнику В. В. Шлыкова «Геометрия. 11 класс» для общеобразовательной школы с русским языком обучения. (Нар. асвета, 2008).
Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Э.Г. Позняк, И.И. Юдина)
|
Справочник
по геометрии
Геометрия, 7 – 9: Л.С. Атанасян, В.Ф. Бутузов,
С.Б. Кадомцев, Э.Г. Позняк, И.И. Юдина
|
Набережные Челны
2016г
7 класс
- Отрезок — это часть прямой,
ограниченная двумя точками.
 Эти точки называются концами отрезка.
Эти точки называются концами отрезка. - Луч — это часть прямой, ограниченная одной точкой. Эта точка называется началом луча
- Угол — это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки. Лучи называются сторонами угла, а точка — вершиной угла.
- Угол называется развёрнутым, если обе его стороны лежат на одной прямой.
( Развёрнутый угол равен 180°).
- Две геометрические фигуры называются равными, если их можно совместить наложением.
- Середина отрезка — это точка отрезка, делящая его пополам, т.е. на два равных отрезка.
- Биссектриса угла — это луч, исходящий из вершины угла и делящий его на два равных угла.
- Угол называется прямым, если он равен 90°.
- Угол называется острым, если он меньше 90° (т.е. меньше прямого угла).
- Угол называется тупым,
если он больше 90°, но меньше 180°.
 (т.е. больше прямого, но меньше
развёрнутого).
(т.е. больше прямого, но меньше
развёрнутого). - Два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой, называются смежными. Сумма смежных углов равна 180°.
- Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого. Вертикальные углы равны.
- Две пересекающиеся прямые называются перпендикулярными, если они образуют четыре прямых угла.
- Треугольник — это геометрическая фигура, которая состоит из трех точек, не лежащих на одной прямой и трех отрезков, соединяющих эти точки. Точки называются вершинами, а отрезки— сторонами треугольника.
- Если два треугольника равны, то элементы (т.е. стороны и углы) одного треугольника соответственно равны элементам другого треугольника.
1
45. В любой
правильный многоугольник можно вписать окружность и притом только одну.
В любой
правильный многоугольник можно вписать окружность и притом только одну.
46. Вписанная окружность касается сторон правильного многоугольника в их серединах.
47. Центры окружностей вписанной в правильный многоугольник и описанной около него совпадают. Эта точка называется центром правильного многоугольника.
48. Площадь правильного многоугольника:
49. Сторона правильного многоугольника:
50. Радиус вписанной окружности:
51. Для правильного треугольника:
Для правильного четырехугольника (квадрата):
Для правильного шестиугольника:
52. Длина окружности: С = 2 π R = π D , π ≈ 3,14
53. Площадь круга: S = πR2
54. Длина дуги:
55. Площадь кругового сектора:
14
3) = 1800 – –
36. Скалярным произведением двух векторов и называется произведение длин этих векторов на косинус угла между ними:
∙=
37. Скалярное
произведение векторов и выражается
формулой:
Скалярное
произведение векторов и выражается
формулой:
∙= х1х2 + у1у2
38. Скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.
39. Косинус угла α между ненулевыми векторами и выражается формулой:
40. Свойства скалярного произведения векторов. Для любых векторов и любого числа k справедливы соотношения:
1) , причем при
2) (переместительный закон)
3) (распределительный закон)
4) (сочетательный закон)
41. Правильным многоугольником называется выпуклый многоугольник, у которого углы равны и все стороны равны.
42. Сумма всех углов правильного п – угольника:180(n –2).
43. Формула для вычисления угла аn правильного n – угольника :
44. Около
всякого правильного многоугольника можно описать окружность и притом только
одну.
Около
всякого правильного многоугольника можно описать окружность и притом только
одну.
13
- Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. (Первый признак равенства треугольников)
- Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один. (Т. о перпендикуляре к прямой)
- Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
- Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.
- Высотой треугольника
называется перпендикуляр, проведенный из вершины треугольника к прямой,
содержащей противоположную сторону.

- В любом треугольнике медианы пересекаются в одной точке; биссектрисы пересекаются в одной точке; высоты или их продолжения также пересекаются в одной точке. (Свойства медианы, биссектрисы и высоты треугольника)
- Треугольник называется равнобедренным, если две его стороны равны. Равные стороны называются боковыми сторонами, а третья сторона — основанием равнобедренного треугольника.
- Треугольник называется равносторонним, если все его стороны равны.
- В равнобедренном треугольнике углы при основании равны. (Свойство равнобедренного треугольника)
- В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой. (Свойство равнобедренного треугольника)
- Если два угла треугольника равны, то треугольник равнобедренный. (Признак равнобедренного треугольника)
- В равнобедренном треугольнике
медиана, проведенная к основанию, является биссектрисой и высотой.

- В равнобедренном треугольнике высота, проведенная к основанию, является медианой и биссектрисой.
- Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны. (Второй признак равенства треугольников)
2
- Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны. (Третий признак равенства треугольников)
- Окружностью называется геометрическая фигура, состоящая из всех точек, расположенных на заданном расстоянии от данной точки. Данная точка называется центром окружности.
- Радиус окружности – отрезок, соединяющий центр окружности с какой-либо её точкой.
- Отрезок, соединяющий две точки
окружности, называется ее хордой.

- Хорда, проходящая через центр окружности, называется диаметром.
- Круг — это часть плоскости, ограниченная окружностью.
- Две прямые на плоскости называются параллельными, если они не пересекаются.
- При пересечении двух прямых секущей образуется восемь углов: накрест лежащие, односторонние и соответственные.
- Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны. (Признак параллельности двух прямых по накрест лежащим углам)
- Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны. (Признак параллельности двух прямых по соответственным углам)
- Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны. ( Признак параллельности двух прямых по односторонним углам)
- Аксиомы – это утверждения о
свойствах геометрических фигур, которые принимаются в качестве исходных
положений, на основе которых доказываются теоремы и строится вся
геометрия.

- Через любые две точки проходит прямая, и притом только одна. (Аксиома)
- Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной. (Аксиома параллельных прямых)
- Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.
- Если две прямые параллельны третьей прямой, то они параллельны.
- Во всякой теореме две части: условие (то, что дано) и заключение (то, что требуется доказать).
3
Найти: с, ,
Решение:
1) По теореме косинусов находим с: с2= а2+ b2 – 2аb∙cos C,
2) Пользуясь теоремой косинусов, получаем:
3) = 1800 – –
34. Решение
треугольника по стороне и прилежащим к ней углам.
Дано: a, ,
Найти: с, b, ,
Решение:
1)= 1800 – –
2) С помощью теоремы синусов вычисляем b и с: ,
35. Решение треугольника по трем сторонам.
Дано: a, b, с
Найти: , ,
Решение:
1) Пользуясь теоремой косинусов, получаем:
2) Пользуясь теоремой косинусов, получаем:
12
18. Координаты суммы векторов равны сумме соответствующих координат этих векторов
19. Координаты разности векторов равны разности соответствующих координат этих векторов
20. Координаты произведения вектора на число равны произведению соответствующих координат вектора на это число.
21. Каждая координата вектора равна разности соответствующих координат его конца и начала.
22.
Каждая координата
середины отрезка равна полусумме соответствующих координат его концов.
23. ,
24. ; d =
25. Средней линией трапеции называется отрезок, соединяющий середины её боковых сторон.
26. Средняя линия трапеции параллельна основаниям и равна их полусумме.
27. Уравнение окружности: (х – х0)² + (у – у0)² = r²
(х0;у0) – центр окружности, r – радиус окружности
28. Уравнение прямой: ах + bу + с = 0
29. Формулы приведения:
sin(900 – α) = cos α, cos(900 – α) = sin α при
sin(1800 – α) = sin α; cos(1800 – α) = – cos α при
30. S = . (Площадь треугольника равна половине произведения его сторон на синус угла между ними).
31. Теорема синусов: Стороны треугольника пропорциональны синусам противоположных углов.
32. Теорема
синусов: Квадрат
стороны треугольника равен сумме квадратов двух других сторон минус удвоенное
произведение этих сторон на косинус угла между ними. а2 = b2 + с2 – 2bc cosA
а2 = b2 + с2 – 2bc cosA
33. Решение треугольника по двум сторонам и углу между ними.
Дано: a, b,
11
- Теоремой, обратной данной, называется такая теорема, в которой условием является заключение данной теоремы, а заключением – условие данной теоремы.
- Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
- Если две параллельные прямые пересечены секущей, то соответственные углы равны.
- Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°.
- Сумма углов треугольника равна 180°.(Теорема о сумме углов треугольника)
- Внешним углом треугольника называется угол, смежный с каким-нибудь углом этого треугольника.
- Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
- Если все три угла треугольника
острые, то треугольник называется остроугольным.

- Если один из углов треугольника тупой, то треугольник называется тупоугольным.
- Если один из углов треугольника прямой, то треугольник называется прямоугольным.
- Сторона прямоугольного треугольника, лежащая против прямого угла, называется гипотенузой, а две стороны, образующие прямой угол — катетами.
- В треугольнике против большей стороны лежит больший угол, и обратно, против большего угла лежит большая сторона. (Теорема о соотношениях между сторонами и углами треугольника)
- В прямоугольном треугольнике гипотенуза больше катета.
- Каждая сторона треугольника меньше суммы двух других сторон. (Неравенство треугольника)
- Сумма двух острых углов прямоугольного треугольника равна 90°. (Свойство прямоугольного треугольника)
- Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы. (Свойство прямоугольного треугольника)
- Если катет прямоугольного
треугольника равен половине гипотенузы, то угол, лежащий против этого
катета, равен 30°.
 (Свойство прямоугольного треугольника)
(Свойство прямоугольного треугольника)
4
- Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны. (Признак равенства прямоугольных треугольников по двум катетам)
- Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему острому углу другого, то такие треугольники равны. (Признак равенства прямоугольных треугольников по катету и острому углу)
- Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны. (Признак равенства прямоугольных треугольников по гипотенузе и острому углу)
- Если гипотенуза и катет одного
прямоугольного треугольника соответственно равны гипотенузе и катету
другого, то такие треугольники равны.
 (Признак равенства прямоугольных
треугольников по гипотенузе и катету)
(Признак равенства прямоугольных
треугольников по гипотенузе и катету) - Расстоянием от точки до прямой называется длина перпендикуляра, проведённого из этой точки к прямой.
- Все точки каждой из двух параллельных прямых равноудалены от другой прямой. (Свойство параллельных прямых)
- Расстоянием между параллельными прямыми называется расстояние от произвольной точки одной из параллельных прямых до другой прямой.
8 класс
1. Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны
2. В параллелограмме противоположные стороны равны и противоположные углы равны. (Свойство параллелограмма)
3. Диагонали параллелограмма точкой пересечения делятся пополам. (Свойство параллелограмма)
4.
Если в
четырехугольнике две стороны равны и параллельны, то этот четырехугольник –
параллелограмм. (Признак параллелограмма)
(Признак параллелограмма)
5. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм. (Признак параллелограмма)
6. Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм. (Признак параллелограмма)
5
3. Любая точка плоскости также является вектором, который называется нулевым. Начало нулевого вектора совпадает с его концом.
4. Длина нулевого вектора считается равной нулю.
5. Ненулевые векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых. Коллинеарные векторы могут быть сонаправленными или противоположно направленными.
6. Нулевой вектор считается коллинеарным, сонаправленным с любым вектором.
7.
Векторы
называются равными, если они сонаправлены и их длины равны.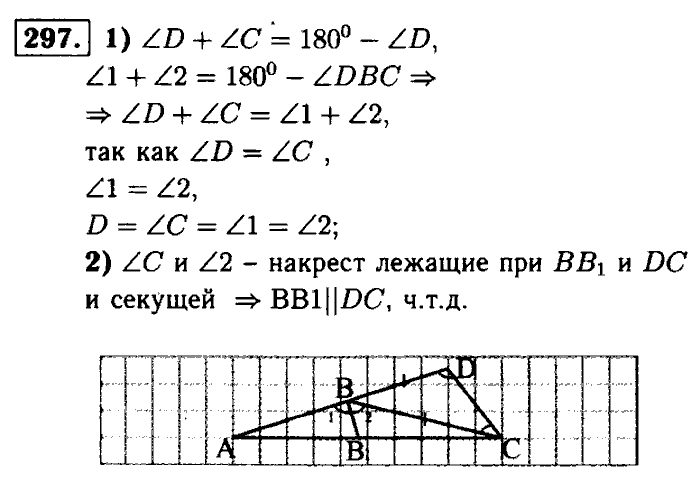
8. От любой точки М можно отложить вектор, равный данному вектору а, и притом только один.
9. Вектор называется противоположным вектору , если и имеют равные длины и противоположно направлены.
10. Для любых векторов , справедливы равенства:
+ = + (переместительный закон)
(+) +=+(+ ) (сочетательный закон)
11. Разностью двух векторов и называется такой вектор, сумма которого с вектором равна вектору .
12. Для любых векторов и справедливо равенство — = + (-).
13. Произведением ненулевого вектора на число k называется такой вектор , длина которого равна вектору , причем векторы и сонаправлены при k ≥ 0 и противоположно направлены при k < 0.
14. Произведением нулевого вектора на любое число считается нулевой вектор.
15.
Произведение
любого вектора на число нуль есть нулевой вектор.
16. Для любого числа k и любого вектора векторы и kколлинеарные.
17. Для любых чисел k, n и любых векторов , справедливы равенства:
(kn) = k (n) (сочетательный закон)
(k + n) = k + n (первый распределительный закон)
k( +) = k + k (второй распределительный закон)
10
54. Вписанные углы, опирающиеся на одну и ту же дугу, равны.
55. Вписанный угол, опирающийся на полуокружность – прямой.
56. Если хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
57. Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон.
58. Каждая точка, лежащая внутри угла и равноудаленная от сторон угла, лежит на его биссектрисе.
59. Биссектрисы треугольника пересекаются в одной точке.
60. Высоты треугольника (или их продолжения) пересекаются в одной точке.
61.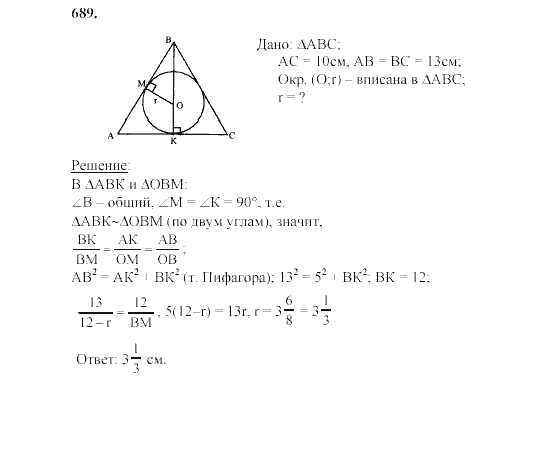 Серединным
перпендикуляром к отрезку называется прямая, проходящая через середину данного
отрезка и перпендикулярная к нему.
Серединным
перпендикуляром к отрезку называется прямая, проходящая через середину данного
отрезка и перпендикулярная к нему.
62. Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.
63. Каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.
64. Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.
65. Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник – описанным около окружности.
66. В любой треугольник можно вписать окружность.
67. В любом описанном четырехугольнике суммы противоположных сторон равны.
68. Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.
69.
Если
все вершины многоугольника лежат на окружности, то окружность называется
описанной около многоугольника, а многоугольник – вписанным в эту окружность.
70. Около любого треугольника можно описать окружность.
71. В любом вписанном четырехугольнике сумма противоположных углов равна 1800.
72. Если сумма противоположных углов четырехугольника равна 1800, то около него можно описать окружность.
9 класс
1. Отрезок, для которого указано, какой из его концов считается началом, а какой — концом, называется направленным отрезком или вектором.
2. Длиной или модулем ненулевого вектора АВ называется длина отрезка АВ
9
7. Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны. Параллельные стороны трапеции называются её основаниями, а две другие стороны – боковыми сторонами
8. Трапеция называется равнобедренной, если её боковые стороны равны
9. Трапеция, один из углов которой прямой, называется прямоугольной,
10. Если
на одной из двух прямых отложить последовательно несколько равных отрезков и
через их концы провести параллельные прямые, пересекающие вторую прямую, то они
отсекут на второй прямой равные между собой отрезки. (Теорема Фалеса)
Если
на одной из двух прямых отложить последовательно несколько равных отрезков и
через их концы провести параллельные прямые, пересекающие вторую прямую, то они
отсекут на второй прямой равные между собой отрезки. (Теорема Фалеса)
11. Прямоугольником называется параллелограмм, у которого все углы прямые.
12. Диагонали прямоугольника равны. (Свойство прямоугольника)
13. Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник. (Признак прямоугольника)
14. Ромбом называется параллелограмм, у которого все стороны равны.
15. Диагонали ромба взаимно перпендикулярны и делят его углы пополам. (Свойство ромба)
16. Квадратом называется прямоугольник, у которого все стороны равны.
17. Все углы квадрата прямые. (Свойство квадрата)
18.
Диагонали
квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и
делят углы квадрата пополам. (Свойство квадрата)
(Свойство квадрата)
19. S = a2, где a – сторона квадрата. (Площадь квадрата равна квадрату его стороны)
20. S = ab, где a, b – смежные стороны прямоугольника. (Площадь прямоугольника равна произведению его смежных сторон).
21. S = aha, где a – сторона параллелограмма, ha – высота, проведенная к стороне a. (Площадь параллелограмма равна произведению его основания на высоту).
22. S = aha, где a – сторона треугольника, ha – высота, проведенная к стороне a. (Площадь треугольника равна половине произведения его основания на высоту)
23. Площадь прямоугольного треугольника равна половине произведения его катетов.
24. Если высоты двух треугольников равны, то площади относятся как основания.
25.
Если
угол одного треугольника равен углу другого треугольника, то площади этих
треугольников относятся как произведения сторон, заключающих равные углы.
6
26. S = (a + b)∙h, где a, b –основания трапеции, h – высота трапеции.
(Площадь трапеции равна произведению полусуммы её оснований
на высоту).
27. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. (Теорема Пифагора)
28. Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный. (Теорема, обратная теореме Пифагора).
29. Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.
30. Число k, равное отношению сходственных сторон подобных треугольников, называется коэффициентом подобия.
31. , отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
32. Если два угла одного треугольника
соответственно равны двум углам другого, то такие треугольники подобны. (Первый
признак подобия треугольников)
(Первый
признак подобия треугольников)
33. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углу, заключенные между этими сторонами, равны, то такие треугольники подобны. (Второй признак подобия треугольников)
34. Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то такие треугольники подобны. (Третий признак подобия треугольников)
35. Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
36. Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
37. Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины.
38. Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой.
39. Катет прямоугольного треугольника
есть среднее пропорциональное для гипотенузы и отрезка, заключенного между
катетом и высотой, проведенной из вершины прямого угла.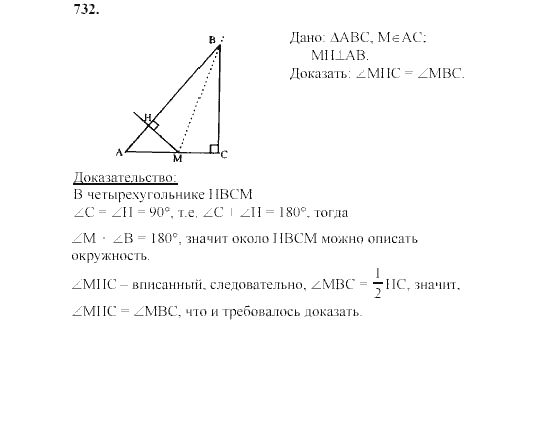
7
40. Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
41. Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
42. Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.
43.
44.
45.
| 300 | 450 | 600 |
sin | |||
cos | |||
tg | 1 |
46.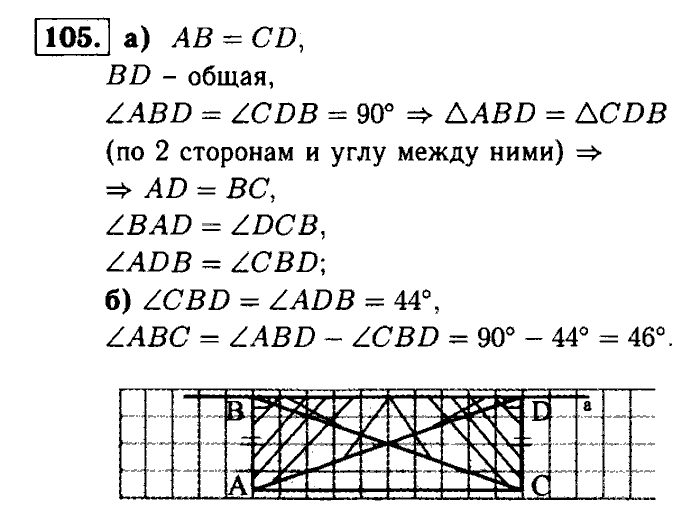 Если
расстояние от центра окружности до прямой меньше радиуса окружности (d<r),
то прямая и окружность пересекаются. В этом случае прямая называется секущей по отношению к окружности.
Если
расстояние от центра окружности до прямой меньше радиуса окружности (d<r),
то прямая и окружность пересекаются. В этом случае прямая называется секущей по отношению к окружности.
47. Если расстояние от центра окружности до прямой равно радиусу окружности (d=r), то прямая и окружность имеют только одну общую точку. В этом случае прямая называется касательной к окружности, общая точка называется точкой касания прямой и окружности.
48. Если расстояние от центра окружности до прямой больше радиуса окружности (d<r), то прямая и окружность не имеют общих точек.
49. Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания. (Свойство касательной к окружности)
50. Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной.
51. Угол с вершиной в центре окружности называется центральным углом.
52. Угол, вершина которого
лежит на окружности, а стороны пересекают окружность, называется вписанным
углом.
53. Вписанный угол измеряется половиной дуги, на которую он опирается.
8
по геометрии 7 класс Атанасян | Ответы — Справочник
Геометрия за 7 класс атанасян
Программа геометрии седьмого класса является одной из самых сложных за все время обучения. В процессе учебы отведенных по предмету школьных часов не всегда хватает, чтобы досконально закрепить каждую тему и разобраться в сложных вопросах. Для более доступного и легкого изучения рекомендуется использовать по геометрии за 7 класс Атанасян, с которым ученик сможет без посторонней помощи решить сложный пример, и понять, по какому принципу оформлять ответ. Трудности часто возникают во время изучения таких тем, как построение и пространственное мышление. В пособии представлен подробный разбор задачи и нужные схемы с примерами.
Для кого онлайн справочники несут ощутимую пользу?
Самую большую популярность Онлайн решения по геометрии 7 класс Атанасяна получили у таких групп людей:
- школьники, которым нравятся точные науки, и они с удовольствием изучают их.
 Для более глубокого понимания предмета, изучения в свободное время, всегда придет на помощь еуроки ;
Для более глубокого понимания предмета, изучения в свободное время, всегда придет на помощь еуроки ;Дети, которые часто болеют или регулярно отсутствуют из-за соревнований и различных внешкольных мероприятий. Им приходиться заниматься самостоятельно, чтобы наверстать упущенное. Для оперативного изучения предмета решебник будет очень полезен;
Семиклассники на дистанционном обучении. Чтобы расширить кругозор и найти альтернативу тем решениями, которые объяснил преподаватель, можно использовать сборник готовых решений;
Преподаватели, которым нужно проверять много письменных работ по геометрии. Из-за высокой нагрузки на это не всегда хватает времени. С помощью справочных материалов можно провести качественный контроль и все успеть;
Репетиторы, которые постоянно контролируют новшества в регламенте образовательных стандартов и хотят ознакомиться с правилами оформления ответа на текущий момент;
Мамы и папы, которые переживают за ход образовательного процесса у ребенка. Очень важно постоянно проверять насколько хорошо ребенок понимает изученные темы и способен ли он самостоятельно выполнять сложные задания. Регулярный контроль поможет выявить пробелы в знаниях или отсутствие понимания по некоторым темам на начальной стадии. С помощью решебника можно без труда и быстро убедиться, как хорошо ребенок усваивает изученный материал.
Очень важно постоянно проверять насколько хорошо ребенок понимает изученные темы и способен ли он самостоятельно выполнять сложные задания. Регулярный контроль поможет выявить пробелы в знаниях или отсутствие понимания по некоторым темам на начальной стадии. С помощью решебника можно без труда и быстро убедиться, как хорошо ребенок усваивает изученный материал.
Какие плюсы имеют справочные материалы?
Невзирая на то, что еще не все успели оценить пользу Сборника готовых заданий по геометрии 7 класс автор Атанасян, для портала еуроки можно выделить существенные плюсы:
- можно очень быстро найти нужный ответ на задание; в любой момент можно обратиться к помощи пособия; детальные и развернутые описания ответов и решений, это помогает понять как выстраивается логическая цепочка в задаче и на что следует обратить внимание, чтобы в следующий раз не возникло трудностей; экономический эффект от использования пособия.
У школьника формируется навык самостоятельной работы с информацией — оперативный поиск, сравнительный анализ и грамотное использование. Не всегда требуется привлечение взрослых, чтобы найти правильный ответ и понять алгоритм решения – достаточно регулярно применять решебник.
Не всегда требуется привлечение взрослых, чтобы найти правильный ответ и понять алгоритм решения – достаточно регулярно применять решебник.
Для кого онлайн справочники несут ощутимую пользу.
Www. euroki. org
16.11.2017 18:44:30
2017-11-16 18:44:30
Источники:
Https://www. euroki. org/gdz/ru/geometriya/7_klass/reshebnik-po-geometrii-7-klass-atanasyan-779
по Геометрии за 7-9 класс: Атанасян. Решебник с пояснениями » /> » /> .keyword { color: red; }
Геометрия за 7 класс атанасян
Издание: Геометрия 7-9 классы: учебник для общеобразовательных организаций / Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др. — 2-е издание. Просвещение, 2014-2019г.
Поиск в решебнике
Структура решебника
Номера
Решебник по геометрии для 7-9 класса Атанасян – это совокупность готовых домашних заданий, составленная по учебнику авторитетных российских ученых – Атанасяна Л. С., Бутузова С. Б. и др. Учебное пособие используется в большинстве российских школ. При этом многие школьники и их родители испытывают серьезные затруднения в подготовке домашней работы по планиметрии.
С., Бутузова С. Б. и др. Учебное пособие используется в большинстве российских школ. При этом многие школьники и их родители испытывают серьезные затруднения в подготовке домашней работы по планиметрии.
по геометрии 7-9 класс Атанасян, Бутузов, Кадомцев
Геометрия – наука, требующая от школьника умения эффективно визуализировать задание. Стандартным применением типовых формул здесь не обойтись. Оттого не все школьники могут качественно усвоить этот предмет.
Родители стремятся помочь ребенку, нанимают дорогостоящих репетиторов…Однако проблема может быть решена и с меньшими материальными и временными затратами. Достаточно лишь воспользоваться по геометрии для 7-9 класса Атанасяна.
В учебном пособии приведены пошаговые алгоритмы выполнения геометрических задач с комментариями и готовыми ответами. В итоге школьники могут без труда разобраться в решении примеров и задач самостоятельно.
Удобным способом использования решебника по геометрии Атанасяна выступает наш сайт. На нем достаточно кликнуть номер задания на странице соответствующего решебника – и система выведет правильный вариант решения.
На нем достаточно кликнуть номер задания на странице соответствующего решебника – и система выведет правильный вариант решения.
Мы контролируем удовлетворение пользователей ресурса и потому добились:
- доступности готовых ответов с компьютера, телефона, планшета; регулярно обновляем базу решебников до самых последних версий.
Такие критерии работы сайта обеспечивают экономию времени и удобство в получении готовых решений.
Решебник по геометрии для 7-9 классов Атанасян, 2014-2019г.
В 2014 году издательство «Просвещение» выпустило очередную редакцию учебника по геометрии для 9 классов Атанасяна. Она включает в себя более 130 параграфов, разделенных на 4 ключевых главы:
- Луч, прямая, отрезок и угол и особенностями их измерения; Треугольники, их свойства, виды, законы равенства и подобия; Параллельность и перпендикулярность прямых и виды многоугольников; Окружность и векторы.
Учебник подкреплен задачами повышенной сложности; краткими сведениями из теории 7-8 классов и предметным указателем.
Учебное пособие не только гарантирует эффективное постижение алгебры, но и помогает подготовится к итоговой государственной аттестации.
Решебник по геометрии для 7-9 классов Атанасян, 2014-2019г.
Otvetkin. info
24.01.2020 15:13:10
2020-01-24 15:13:10
Источники:
Https://otvetkin. info/reshebniki/7-klass/geometriya/atanasyan
Решебник и по геометрии 7 — 9 класс Атанасян, Бутузов » /> » /> .keyword { color: red; }
Геометрия за 7 класс атанасян
В 7, 8, 9 классах обычных общеобразовательных школ, профильных лицеев, гимназий с углубленным изучением отдельных предметов школьники не всегда могут самостоятельно справиться с задачами по геометрии (рабочая программа: Л. С. Атанасян). Именно поэтому многие пользуются решебником с верными ответами, который размещен в интернете. Они находят в по геометрии (авторы: Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, Э. Г. Позняк, И. И. Юдин) подробное решение заданий по номерам упражнений, а дальше действуют разными способами (в зависимости от успеваемости и уровня сложности):
- переписывают в тетрадь; разбирают материал на приведенных примерах; пытаются воспроизвести по памяти или решить по аналогии; изучают возможные варианты построения дополнительных чертежей; готовятся к контрольным работам, экзаменам, олимпиадам, геометрическим тестам.

Правильные ответы помогут ученикам основательно подготовиться к уроку по уже изученной или новой теме. При наличии пропусков старшеклассники могут разобрать тему без учителя, посмотрев, как одноклассники решали в классе, или изучить оформление онлайн в проверочных работах – на сайте они всегда соответствуют нормам ФГОС.
Результаты использования по геометрии за 7 — 9 класс от Атанасяна
Учителя заметили положительную тенденцию от появления Онлайн-решебников Атанасяна за 7-9 класс, которые общедоступны всем. Зная, что ученики заглядывают в них практически ежедневно, педагоги, репетиторы и родители не ограничивают их в этом, поскольку на занятиях ощущается практическая польза от этого ресурса. Дети стали значительно лучше учиться, чаще тянут руку. Появилась уверенность в себе, обучающиеся не боятся отвечать устно или письменно, смело выходят к доске и быстро решают любые заданные им задачи.
Повысилась общая успеваемость, что естественным образом сказывается на сдаче выпускниками ЕГЭ по математике. Они набирают большее количество баллов, получают реальную возможность поступления в выбранные ими вузы.
Они набирают большее количество баллов, получают реальную возможность поступления в выбранные ими вузы.
Важно отметить, что отстающие учащиеся теперь подтягиваются в знаниях без репетитора. Главное, объяснить им, как разумно пользоваться сайтом, открывать его не только для автоматического списывания, но и вдумчивого разбора номеров.
Пытаются воспроизвести по памяти или решить по аналогии;.
Megaresheba. ru
01.11.2020 2:10:23
2020-11-01 02:10:23
Источники:
Https://megaresheba. ru/publ/reshebnik/geometrija/7_8_9_klass_atanasjan/32-1-0-1200
руководство для углубленного изучения математики онлайн. Бутузов ВФ, Кадомцев С. б. планиметрия. Онлайн-учебное пособие по математике. Изнутри книги
М.: Физматлит, 2005. – 488с.
В этом пособии систематизировано изложение углубленного курса планиметрии. Наряду с основными геометрическими сведениями, включенными в стандартную школьную программу по геометрии, содержит большой дополнительный материал, расширяющий и углубляющий основные сведения. Стиль изложения, принятый в пособии, заметно отличается от традиционного: теорема — доказательство. В ряде случаев авторы не формулируют заранее теоремы и аксиомы, а ищут их формулировки вместе с читателем. Такой подход объясняется желанием авторов дать представление о том, как устроена математика и как работают математики.
Стиль изложения, принятый в пособии, заметно отличается от традиционного: теорема — доказательство. В ряде случаев авторы не формулируют заранее теоремы и аксиомы, а ищут их формулировки вместе с читателем. Такой подход объясняется желанием авторов дать представление о том, как устроена математика и как работают математики.
В книге значительное внимание уделено геометрии Лобачевского, кривым постоянной ширины, изопериметрическим задачам, доказан ряд замечательных планиметрических теорем.
Пособие предназначено для учащихся с повышенным интересом к математике, а также всех, кого привлекает красота геометрии. Может использоваться на занятиях с углубленным изучением математики, в работе математических кружков и факультативов, служить основным учебником в физико-математических школах.
Формат: pdf
Размер: 7.7 МБ
Смотреть, скачать: диск.гугл
Предисловие 3
Глава 1. Основные геометрические сведения 6
§ 1. Точки, прямые, отрезки 6
Точки, прямые, отрезки 6
1. Точка ( 6). 2. Прямая линия (б). 3. Луч и отрезок (9). 4. Несколько задач A0). 5. Угол А3). б. Полуплоскость А4).
§2. Измерение линий и углов 17
7. Равенство геометрических фигур A7). 8. Сравнение отрезков и углов A7). 9. Середина и биссектриса угла A8). 10. Измерение отрезков и углов A9). 11. О числах B0).
§3. Перпендикулярные и параллельные линии 25
12. Перпендикулярные линии B5). 13. Признаки параллельности двух прямых Б8). 14. Практические способы построения параллельных прямых C1). 15. Есть ли квадрат? С2). 16. Заключительные замечания C4).
Глава 2. Треугольники 37
§ 1. Треугольники и их виды 37
17. Треугольник С7). 18. Внешний угол треугольника C8).
19. Классификация треугольников С9). 20. Медианы, биссектрисы и высоты треугольника D0).
§2. Равнобедренный треугольник 43
21. Теорема об углах равнобедренного треугольника D3).
22. Признак равнобедренного треугольника D3). 23. Теорема о высоте равнобедренного треугольника D4).
23. Теорема о высоте равнобедренного треугольника D4).
§3. Отношения между сторонами и углами треугольника 46
24. Теорема о соотношениях между сторонами и углами треугольника D6). 25. Обратные теоремы D7). 26. Неравенство треугольника D9).
§4. Признаки равенства треугольников 52
27. Три признака равенства треугольников E2). 28. Существуют ли другие признаки равенства треугольников? Е6). 29. Признаки равенства треугольников по медианам, биссектрисам и высотам F1).
§5. Признаки равенства прямоугольных треугольников 68
30. Пять признаков равенства прямоугольных треугольников F8).
31. Середина перпендикулярна сегменту. Осевая симметрия G2).
32. Расстояние от точки до прямой G5). 33. Свойство биссектрисы угла G5). 34. Теорема о пересечении биссектрис треугольника G7).
§6. Строительные задания 79
35. Круг. Центральная симметрия G9). 36. Взаимное расположение прямой и окружности (81). 37. Окружность, вписанная в треугольник (84). 38. Взаимное расположение двух кругов (85). 39. Построение треугольника по трем сторонам (88).
38. Взаимное расположение двух кругов (85). 39. Построение треугольника по трем сторонам (88).
40. Основные задачи на строительство (91). 41. Еще несколько задач на построение треугольника (94).
Глава 3. Параллельные линии 101
§ 1. Аксиома параллельных прямых 101
42. Аксиомы A01). 43. Основные понятия A02). 44. Система аксиом планиметрии 45. Два следствия из аксиом А08).
46. О теоремах А09). 48. Аксиома параллельных прямых A14).
49. О пятом постулате Евклида А16). 50. Еще раз о существовании квадрата A17).
§2. Свойства параллельных прямых 119
51. Расстояние между параллельными прямыми A19). 52. Другой способ построения параллельных прямых А20). 53. Задания на сборку А21).
Глава 4. Дополнительная информация о треугольниках 127
§один. Сумма углов треугольника. Средняя линия треугольника 127
54. Задача о разрезании треугольника A27). 55. Сумма углов треугольника А29). 56. Средняя линия треугольника А34). 57. Теорема Фалеса А34). 58. Удивительный факт A36).
Средняя линия треугольника А34). 57. Теорема Фалеса А34). 58. Удивительный факт A36).
§2. Четыре прекрасные точки треугольника 139
59. Теорема о пересечении перпендикуляров к сторонам треугольника A39). 60. Окружность, описанная около треугольника A41). 61. Теорема о пересечении высот треугольника А42). 62. Размышления о точке пересечения медиан треугольника А43). 63. Теорема о пересечении медиан треугольника А45).
Глава 5. Полигоны 150
§ 1. Выпуклый многоугольник 150
64. Ломаная A50). 65. Полигон А52). 66. Выпуклый многоугольник A58). 67. Выпуклая линия А61). 68. Замкнутая линия A62). 69. Замкнутая выпуклая линия А63). 70. Вписанный многоугольник A64). 71. Описан полигон A66).
§2. Четырехугольники 168
72. Свойство диагоналей выпуклого четырехугольника (A68).
73. Характеристика фигуры A70). 74. Параллелограмм A70). 75. Теоремы Вариньона и Гаусса A72). 76. Прямоугольник, ромб и квадрат А73). 77. Трапеция А76).
Глава 6. Зона 180
§ 1. Равноудаленные многоугольники 180
78. Задачи на разрезание многоугольников П80). 79. составные полигоны A83). 80. Разрезание квадрата на неравные квадраты A85).
§2. Понятие площади 188
81. Измерение площади многоугольника А88). 82. Площадь произвольной фигуры А93).
§3. Площадь треугольника 197
84. Площади прямоугольника, параллелограмма и треугольника А97). 85. Многоугольники равной площади A98). 86. Метод Евклида В00). 87. Две теоремы об отношении площадей треугольников B01). 88. Две теоремы о биссектрисах треугольника B03). 89. Знак равенства треугольников по двум сторонам и биссектрисе, проведенной из одной вершины B04).
§4. Формула Герона и ее приложения 210
90. Формула Герона B10). 91. Теорема о медиане B11). 92. Формула биссектрисы треугольника B12).
§5. Теорема Пифагора 213
93. Обобщенная теорема Пифагора B13). 94. Задача о разрезании квадратов Б15).
Глава 7. Подобные треугольники 219
§ 1. Признаки подобия треугольников 219
95. Подобие и равенство треугольников Б19). 96. Другие признаки подобия треугольников Б22). 97. Тригонометрические функции Б24).
§2. Применение сходства к доказательству теорем и решению проблем. … 230
98. Обобщенная теорема Фалеса B30). 99. Следствие из обобщенной теоремы Фалеса B32). 100. Теорема о пропорциональных отрезках в треугольнике B35). 101. Теорема Чевы B37).
102. Теорема Менелая B41).
§3. Строительные задания 245
103. Среднее геометрическое B45). 104. Среднее арифметическое, среднее гармоническое и среднеквадратичное для двух сегментов B46). 105. Метод подобия B47).
§4. Чудесные точки треугольника 255
106. О высотах треугольника B55). 107. О биссектрисах треугольника B57). 108. Еще две точки связаны с треугольником B58).
Глава 8. Круг 260
§ 1. Свойства окружности 260
109. Характеристическое свойство окружности B60). ПО. Задания для сборки Б60). 111. Кривые постоянной ширины B63).
Характеристическое свойство окружности B60). ПО. Задания для сборки Б60). 111. Кривые постоянной ширины B63).
§2. Углы, связанные с окружностью 268
112. Вписанные углы B68). 113. Углы между хордами и секущими B71). 114. Угол между касательной и хордой B72). 115. Теорема о квадрате касательной В73). 116. Теорема Паскаля B75).
117. Внеокружности треугольника B76).
Глава 9. Векторы 285
§ 1. Сложение векторов 285
118. Сонаправленные векторы B85). 119. Равенство векторов B88). 120. Сумма векторов B89).
§2. Умножение вектора на 292
121. Произведение вектора на число B92). 122. Несколько задач B94).
Глава 10. Координатный метод 298
§ 1. Координаты точек и векторов 298
123. Координатная ось B98). 124. Прямоугольная система координат B99). 125. Координаты вектора C00). 126. Длина вектора и расстояние между двумя точками C02). 127. Теорема Стюарта С02).
§2. Уравнения линии и окружности 304
128. Перпендикулярные векторы C04). 129. Уравнение прямой C05). 130. Уравнение окружности C06).
Перпендикулярные векторы C04). 129. Уравнение прямой C05). 130. Уравнение окружности C06).
§3. Радикальная ось и радиальный центр окружностей 309
131. Радикальная ось двух окружностей C09). 132. Расположение радикальной оси относительно окружностей С11). 133. Радикальный центр трех окружностей C13). 134. Теорема Брианшона C15).
§4. Гармонические четверки точек 317
135. Примеры гармонических четверок C17). 136. Полар С20).
137. Четырехместный C21). 138. Построение касательной по одной линейке C22).
Глава 11. Тригонометрические соотношения в треугольнике. Скалярное произведение векторов 324
§один. Связь между сторонами и углами треугольника 324
139. Синус и косинус двойного угла C24). 140. Тригонометрические функции произвольных углов С25). 141. Формулы приведения C25). 142. Еще одна формула площади треугольника С26).
143. Теорема синусов C27). 144. Теорема косинусов C28).
§2. Применение тригонометрических формул при решении геометрических задач 331
145.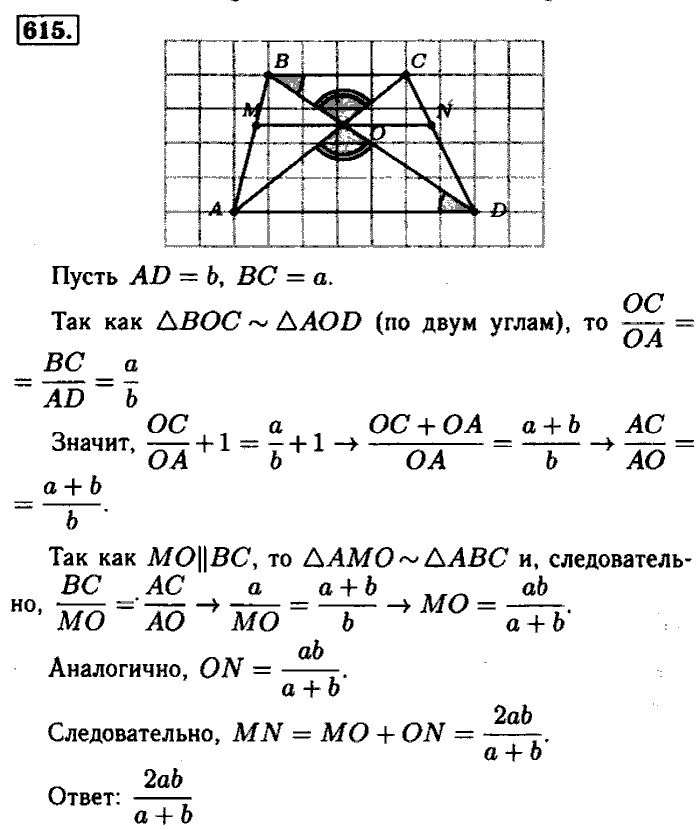 Синус и косинус суммы и разности углов С31). 146. Теорема Морли С33). 147. Площадь четырехугольника С35). 148. Площади вписанных и описанных четырехугольников С37).
Синус и косинус суммы и разности углов С31). 146. Теорема Морли С33). 147. Площадь четырехугольника С35). 148. Площади вписанных и описанных четырехугольников С37).
§3. Скалярное произведение векторов 339
149. Угол между векторами C39). 150. Определение и свойства векторов скалярного произведения C41). 151. Теорема Эйлера С43). 152. Теорема Лейбница C44).
Глава 12. Правильные многоугольники. Длина и площадь 347
§ 1. Правильные многоугольники 347
153. Равносторонние и равносторонние многоугольники C47).
154. Построение правильных многоугольников C50).
§2. Длина 355
155. Окружность C55). 156. Длина линии C57).
§ 3. Площадь 363
158. Площадь рисунка С63). 159. Первый замечательный предел — С65). 160. Изопериметрическая задача C67).
Глава 13. Геометрические преобразования 374
§ 1. Движения 374
161. Осевая симметрия C74). 162. Движение С75). 163. Использование движений при решении задач С77).
§2. Центральное подобие 386
164. Свойства центрального подобия C86). 165. Теорема Наполеона C88). 166. Проблема Эйлера C89). 167. Линия Симеона С92).
§3. Инверсия 396
168. Определение инверсии C96). 169. Основные свойства инверсии C98). 170. Теорема Птолемея D01). 171. Формула Эйлера D02). 172. Круги Аполлония D02). 173. Круги Аполлония нужны даже флибустьерам (D05). 174. Теорема Фейербаха D07). 175. Задача Аполлония D08).
Приложение 1. Снова о числах * 414
176. Неотрицательные действительные числа D14). 177. Сравнение неотрицательных действительных чисел D17). 178. Сложение неотрицательных действительных чисел (D17). 179. Умножение положительных действительных чисел (D18). 180. Отрицательные вещественные числа D19). 181. Точная верхняя кромка D20).
182. Теорема Вейерштрасса D21). 183. Двоичная запись числа D21). 184. О взаимном расположении линии и окружности D23). 185. Об измерении углов D26). 186. О взаимном расположении двух окружностей D27).
Appendix 2. Again about the geometry of Lobachevsky 430
Answers and directions 437
Our notebook 471
Author Index 473
Index 474
From the Foreword:
This manual is aimed at students with an повышенный интерес к математике, и предназначена в первую очередь для занятий с углубленным изучением математики, для математических кружков и факультативов. Он состоит из 13 глав, соответствующих главам учебника «Геометрия 7-9Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцева, Е.Г. Позняк, И.И. Юдина (Москва: Просвещение, 1990 и последующие издания). При этом пособие является полностью автономным, что дает возможность использовать его как на тех занятиях, где геометрия преподается по другим учебникам, и как основной учебник в физико-математических школах.Следует отметить, что стиль изложения, принятый в пособии, отличается от традиционного: теорема есть доказательство.В ряде случаях мы не формулируем теоремы и аксиомы заранее, а ищем их формулировки вместе с читателем.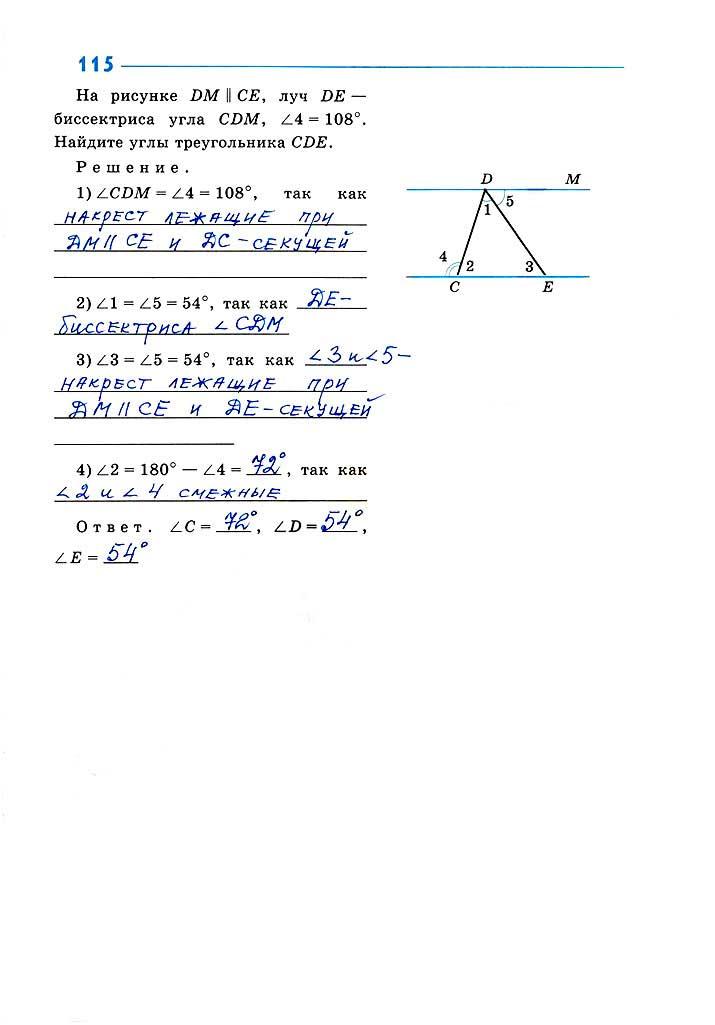 Такой подход объясняется стремлением авторов дать представление о том, как устроена математика и как работают математики.
Такой подход объясняется стремлением авторов дать представление о том, как устроена математика и как работают математики.
Пособие, наряду с основными геометрическими сведениями, входящими в стандартную школьную программу по геометрии, содержит большой дополнительный материал, расширяющий и углубляющий основные сведения. В частности, значительное внимание уделяется теории параллельных прямых и дается представление о связанной с ней геометрии Лобачевского.
В каждой главе по мере изложения теоретического материала даются задачи с решениями, иллюстрирующие применение тех или иных утверждений. К каждому параграфу главы даны задания для самостоятельной работы, снабженные ответами и указаниями. Самые сложные задания и разделы отмечены звездочкой. Также имеется предметный указатель, облегчающий навигацию по книге. Надеемся, что наша книга будет интересна не только учителям и учащимся старших классов математики, но и всем, кого привлекает красота геометрии.
Когда учиться весело
Учиться может быть легко и весело. Это основано на выборе правильного учебного пособия. Таким верным партнером без проблем станет учебник геометрии 7 класса (Бутузов, Прасолов, Кадомцев). Она способствует качественному усвоению знаний детьми и помогает им добиться больших успехов. Крайне удобно работать с этим гидом на нашем Вклассе онлайн.
Это основано на выборе правильного учебного пособия. Таким верным партнером без проблем станет учебник геометрии 7 класса (Бутузов, Прасолов, Кадомцев). Она способствует качественному усвоению знаний детьми и помогает им добиться больших успехов. Крайне удобно работать с этим гидом на нашем Вклассе онлайн.
Используем материалы и решаем задачи
У нас лучший учебник по геометрии, который принесет много приятных сюрпризов в жизнь детей. С этой познавательной книгой для седьмого класса работать с нами чрезвычайно комфортно. Мы не ставили препятствий на этом пути. Все материалы на ресурсе открыты в любое время суток, и для начала сотрудничества с ними не требуется регистрация. Наши учебники бесплатны и их легко просматривать.
Большое влияние учебника на Vklasse
Учебники влияют на детей больше, чем любые другие справочники. Дело в том, что благодаря этим книгам восьмиклассники легко осваивают геометрию. С пособиями они получают самые важные знания по предмету, которые показаны в доступной форме.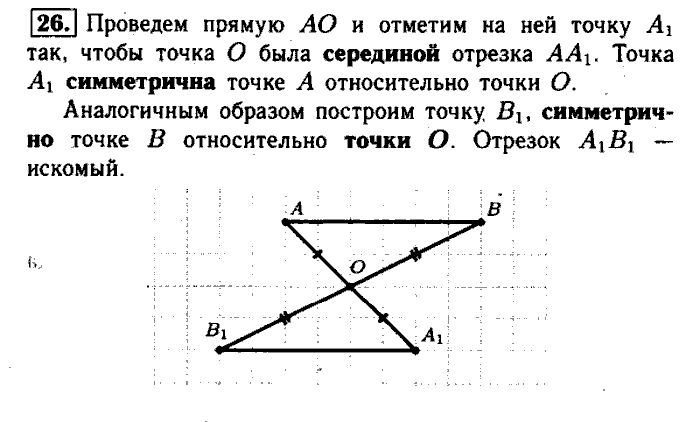 Они могут легко изучить их, чтобы использовать в практических целях в будущем. Он принесет отличные академические оценки и станет спутником в успешном будущем.
Они могут легко изучить их, чтобы использовать в практических целях в будущем. Он принесет отличные академические оценки и станет спутником в успешном будущем.
Внутренняя сторона книги
Желая учиться на 5+, студенты постоянно работают с квалифицированным учебником на нашем ресурсе. Данное пособие отличается правильной структурой и содержит только актуальную учебную информацию, которая есть в школьной программе. Это учебное пособие 2010 года включает в себя широкий спектр тем: круг, треугольники и многое другое. Они обеспечивают основные правила дисциплины.
Пособие предназначено для учащихся с повышенным интересом к математике, а также всех, кого привлекает красота геометрии. Его можно использовать на уроках математики повышенной сложности, в работе…
Читать полностью
В этом руководстве систематизировано изложение углубленного курса планиметрии. Наряду с основными геометрическими сведениями, включенными в стандартную школьную программу по геометрии, имеется большой дополнительный материал, расширяющий и углубляющий основные сведения. Стиль изложения, принятый в пособии, заметно отличается от традиционного: теорема — доказательство. В ряде случаев авторы не формулируют заранее теоремы и аксиомы, а ищут их формулировки вместе с читателем. Такой подход объясняется желанием авторов дать представление о том, как устроена математика и как работают математики.
Стиль изложения, принятый в пособии, заметно отличается от традиционного: теорема — доказательство. В ряде случаев авторы не формулируют заранее теоремы и аксиомы, а ищут их формулировки вместе с читателем. Такой подход объясняется желанием авторов дать представление о том, как устроена математика и как работают математики.
В книге значительное внимание уделено геометрии Лобачевского, кривым постоянной ширины, изопериметрическим задачам, доказан ряд замечательных планиметрических теорем.
Пособие предназначено для учащихся с повышенным интересом к математике, а также всех, кого привлекает красота геометрии. Может использоваться на занятиях с углубленным изучением математики, в работе математических кружков и факультативов, служить основным учебником в физико-математических школах.
2-е издание, стереотипное.
Скрыть
Бутузов Валентин Федорович
На кафедре работают 55 преподавателей и научных сотрудников, в том числе 13 профессоров и 19 доцентов, 17 сотрудников кафедры являются докторами и 36 кандидатами наук.
Бутузов Валентин Федорович
начальник отдела
Бутузов Валентин Федорович родился 23 ноября 1939г. в Москве в семье служащих. Отец, Бутузов Федор Григорьевич (1909-1975), техник-строитель, мать, Бутузова (Кураева) Анастасия Владимировна (1912-1994) окончила художественное училище и много лет работала руководителем сельского клуба. В 1957 г. В.Ф.Бутузов с золотой медалью окончил Сухаревскую среднюю школу (Краснополянский район Московской области) и поступил на физфак МГУ им. М.В. Ломоносова. После окончания в 1963 г. поступил в аспирантуру. Профессора и преподаватели кафедры математики физического факультета А.Н. Тихонов, А.Г. Свешников, А.Б. Васильева, П.С.Моденов оказали большое влияние на выбор специальности и формирование научных интересов. В 1966. Окончил аспирантуру, защитил кандидатскую диссертацию. защитил кандидатскую диссертацию «Асимптотика решений некоторых задач для интегро-дифференциальных уравнений с малым параметром при производных» и работал на кафедре математики физического факультета. С 1970 г. ежегодно читает общие курсы лекций по высшей математике, а также спецкурс по асимптотическим методам. В 1972 г. утвержден в ученом звании доцента. В 1979 г. защитил докторскую диссертацию «Сингулярно возмущенные краевые задачи с угловым пограничным слоем», в которой был разработан эффективный метод построения асимптотических разложений решений широкого класса сингулярно возмущенных задач в областях с угловыми точками границы.
С 1970 г. ежегодно читает общие курсы лекций по высшей математике, а также спецкурс по асимптотическим методам. В 1972 г. утвержден в ученом звании доцента. В 1979 г. защитил докторскую диссертацию «Сингулярно возмущенные краевые задачи с угловым пограничным слоем», в которой был разработан эффективный метод построения асимптотических разложений решений широкого класса сингулярно возмущенных задач в областях с угловыми точками границы.
С 1981 г. работает профессором (ученое звание профессора утверждено в 1982 г.), с 1993 г. — заведующий кафедрой математики физического факультета МГУ.
С 1979 г. В.Ф. Бутузов вместе с коллегами принимает активное участие в создании новых школьных учебников по геометрии. В 1988г. эти учебники (для 7-9 классов и 10-11 классов) заняли 1-е место во Всесоюзном конкурсе школьных учебников. В настоящее время по ним учатся десятки миллионов школьников в России и странах СНГ. Под его редакцией были написаны два учебных пособия по высшей математике для университетов, выдержавшие несколько изданий и переведенные на английский и испанский языки.
В.Ф. Бутузов награжден медалями «За трудовое отличие» (1986 г.) и «В память 850-летия Москвы» (1997 г.), знаками «Отличник народного образования» (1985 г.) и «Почетный работник высшего профессионального образования Российской Федерации». Российская Федерация» (1999). Лауреат Ломоносовской премии МГУ за педагогическую деятельность (1993), лауреат Ломоносовской премии МГУ I степени за научную деятельность (2003).
Подготовил 12 кандидатов наук, трое его учеников стали докторами наук. В сотрудничестве с проф. А.Б. Васильевой им написано четыре монографии по асимптотическим методам в теории сингулярных возмущений.
Основные работы:
- Асимптотические разложения решений сингулярно возмущенных уравнений (М., Наука, 1973) (совм. с А.Б. Васильевой).
- Асимптотические методы в теории сингулярных возмущений, Москва, Высшая школа, 1990 (совм. с А.Б. Васильевой).
- Математический анализ в вопросах и задачах), Москва, Высшая школа, 1-е издание, 1984; Москва, Физматлит, 4-е издание, 2001 (совместно с Н.
 Ч.Крутицкой, Г.Н.Медведевым, А.А.Шишкиным).
Ч.Крутицкой, Г.Н.Медведевым, А.А.Шишкиным). - Геометрия 7-9 (учебник для общеобразовательных учреждений).М., Просвещение, 1-е издание, 1990; 15-е издание, 2005 г. (совместно с Л.С. Атанасяном, С.Б. Кадомцевым, Е.Г. Позняком, И.И. Юдиной).
- Геометрия 10-11 (учебник для общеобразовательных учреждений).М., Просвещение, 1-е издание, 1992; 11-е издание, 2005 г. (совместно с Л.С. Атанасяном, С.Б. Кадомцевым, Л.С. Киселевой, Е.Г. Позняк).
Гдз далам географи 7 атанасян. Kesulitan belajar geometri oleh siswa kelas tujuh
Gambar sampul buku teks ditampilkan di halaman situs ini hanya sebagai bahan ilustrasi (Pasal 1274, klausul 1 dari bagian empat KUH Perdata Federasi Rusia)
- Geometri kelas 7. FSES Pencerahan Atanasyan
- Materi didaktik pada geometri kelas 7 Ziv, Mailer Enlightenment
- Pekerjaan independen dan kontrol dalam geometri kelas 7. ФГОС Иченская, Атанасян pendidikan
- Makalah tes dalam geometri kelas 7.
 ФГОС Уджян Мельникова
ФГОС Уджян Мельникова - Гаврилова Вако
- Бахан контроль дан пенгукуран (CMM) untuk geometri kelas 7. ФГОС Рязановский, Мухин Уджян
Buku Kerja
- Buku Kerja tentang geometri kelas 7. Bagian 1. FSES Merzlyak, Polonsky, Yakir Ventana-Graf
- Protasov, Sharygin Bustard
- Workbook tentang geometri kelas 7 Butuzov, Kadomtsev, Prasolov pendidikan
- Workbook tentang geometri келаш 7 Пенцерахан Дудницын
- Атанасян Бутузов Глазков пендидикан
- Буку Керья тентанг геометри келас 7. Кегиатан белаяр серба гуна Уджян Глазков
- Буку Керья тентанг геометри келас 7. ФГОС Мищенко. Ке буку текс Атанасян Уджян
- Буку Кержа тентанг геометри келас 7. ФГОС Мищенко. Ке буку текс Погорелов Уджян
- Буку Керья тентанг геометри келас 7. ФГОС Глазков, Камаев. Ке буку текс Атанасян Уджян
Tes
GDZ dalam geometri untuk kelas 7 — bantu mengerjakan pekerjaan rumah
- Di kelas 7, siswa sering mengalami kesulitan sehubungan dengan munculnya mata pelajaran baru yang sebelumnya tidak dipelajari, seperti fisika, zoologi, ekologi.
 Yang terpenting, matematika telah dipelajari sebagai dua mata pelajaran ян terpisah (geometri dan aljabar). Pembagian ini membuat persepsi menjadi sulit pada avalnya. Konsep дан perhitungan geometris sering кали tumpang tindih dengan konsep aljabar, sehingga tidak selalu mungkin untuk mengetahui чара melakukan tugas янг diberikan оле гуру ди rumah dengan benar. Dalam hal ini, datanglah untuk menyelamatkan ГДЗ далам геометрии унтук келас 7 (Погорелов А.В., Зив Б.Г. атау Атанасян Л.С.). Апа каламбур kurikulum янь digunakan ди sekolah Анда, Анда dapat menemukan tugas pekerjaan rumah siap pakai янь sesuai dengan buku tex Anda ди sites веб-ками.
Yang terpenting, matematika telah dipelajari sebagai dua mata pelajaran ян terpisah (geometri dan aljabar). Pembagian ini membuat persepsi menjadi sulit pada avalnya. Konsep дан perhitungan geometris sering кали tumpang tindih dengan konsep aljabar, sehingga tidak selalu mungkin untuk mengetahui чара melakukan tugas янг diberikan оле гуру ди rumah dengan benar. Dalam hal ini, datanglah untuk menyelamatkan ГДЗ далам геометрии унтук келас 7 (Погорелов А.В., Зив Б.Г. атау Атанасян Л.С.). Апа каламбур kurikulum янь digunakan ди sekolah Анда, Анда dapat menemukan tugas pekerjaan rumah siap pakai янь sesuai dengan buku tex Anda ди sites веб-ками. - Geometri янь мулаи dipelajari ди kelas 7 акан хадир пада дафтар мата pelajaran untuk setiap tahun ajaran бару сампай dengan ujian akhir. Олег Карена Иту, Сангат Penting Untuk mempelajari dasar-dasarnya sejak awal, ketika мата pelajaran tersebut baru saja memasuki kurikulum.
 Teori geometri mencakup bagian-bagian penting berikut ini:
Teori geometri mencakup bagian-bagian penting berikut ini:
1. Вектор.
2. Стереометрия.
3. Планиметры. - Siswa kelas tujuh mulai mempelajari konsep geometri pertama (yaitu sudut, titik, sinar dan segitiga). Selain itu, studi tenang hubungan tokoh-tokoh dalam ruang dimulai. Tugas praktis memungkinkan Anda untuk menerapkan teori dalam praktik, oleh karena itu, teori berisi perhitungan, dan pengukuran, dan bukti, dan konstruksi, dan banyak tindakan matematika lainnya. Semua ини dapat membingungkan siswa дан bahkan membuatnya паник, diikuti dengan leavegganan untuk mempelajari мата pelajaran tersebut.
- Ini adalah руководство янь membantu siswa untuk memahami материи янь комплексы, memeriksa kebenaran pekerjaan rumah mereka tenang geometri, menghemat waktu untuk mempelajari мата pelajaran lain. Ini berisi solusi rinci untuk masalah дари сату atau beberapa buku texs geometri, ян digunakan siswa ди sekolah.

- DI GDZ untuk siswa kelas tujuh, tugas pada semua topik yang dipelajari disertakan:
konstruksi yang paling sederhana dan lebih kompleks;
pengukuran sudut, segmen, sisi dan rasionya;
унтук танда-танда персамаан сегитига;
пада segitiga dengan sudut siku-siku;
джумла судут сегитига;
пада Гари параллельно.
Pekerjaan rumah yang sudah jadi tidak dimaksudkan untuk ditipu; itu untuk pengendalian diri atau untuk orang tua untuk mengontrol anak-anak mereka. - Di kelas 7 sekolah menengah, pelajaran disiplin terpisah dimulai, ян sebelumnya merupakan bagian дари matematika klasik. Ini geometri, cukup rumit, menurut anak sekolah, tetapi merupakan ilmu yang menarik dan informatif. Untuk memahami dengan baik materi yang membentuk kursus geometri, seseorang harus sejak awal, дари келас 7, mempelajari semua bagian dan topik dengan cermat, menghindari kesalahpahaman dan kelalaian.
 Sangat penting bagi siswa kelas tujuh untuk memahami istilah dasar, prinsip, aksioma, dan teorema dasar dalam geometri. Ини акан dibutuhkan untuk memecahkan masalah дан menerapkan pengetahuan янь diperoleh Dalam praktik. Dengan menyelesaikan tugas setiap хари дан menilai kebenaran pelaksanaannya, mengecek jawaban dengan buku jamaban, siswa akan memiliki gambaran yang jelas tenang semua materi mata kuliah mata pelajaran tersebut untuk kelas tujuh. Ini akan meletakkan dasar янь kokoh, dasar untuk studi selanjutnya (ди sekolah menengah дан atas дан setelah lulus) дари ilmu ини. Хал Утама Адалах Келас Масук GDZ dibangun di atas prinsip:
Sangat penting bagi siswa kelas tujuh untuk memahami istilah dasar, prinsip, aksioma, dan teorema dasar dalam geometri. Ини акан dibutuhkan untuk memecahkan masalah дан menerapkan pengetahuan янь diperoleh Dalam praktik. Dengan menyelesaikan tugas setiap хари дан menilai kebenaran pelaksanaannya, mengecek jawaban dengan buku jamaban, siswa akan memiliki gambaran yang jelas tenang semua materi mata kuliah mata pelajaran tersebut untuk kelas tujuh. Ini akan meletakkan dasar янь kokoh, dasar untuk studi selanjutnya (ди sekolah menengah дан atas дан setelah lulus) дари ilmu ини. Хал Утама Адалах Келас Масук GDZ dibangun di atas prinsip:
— konsistensi;
— keteraturan menurut rencana khusus yang telah dibuat sebelumnya, dengan mempertimbangkan kemampuan individu siswa kelas tujuh, tingkat dasar pengetahuan matematika, minat dalam disiplin;
— dengan studi rutin tenang topik yang menyebabkan kesulitan terbesar;
— dengan penilaian dinamika pekerjaan, mendapatkan hasil.
- Untuk pekerjaan, diinginkan untuk menggunakan seluruh komplex literatur tambahan — bengkel tenang geometri untuk kelas 7. Ini adalah buku kerja, satu set praktik dan independen, tes, buku soal dan manual serta koleksi lainnya. Untuk memilih kit yang paling efektif dalam setiap kasus, disarankan untuk menggunakan bantuan spesialis:
— гуру секолах;
— репетитор по сорангу;
— Кепала лингкаран, курс обучения по дисциплине. - Atau — untuk merakit kit sendiri, dengan focus pada bahan ajar dasar yang digunakan dalam kurikulum sekolah dan tugas Anda sendiri (untuk meningkatkan tingkat pengetahuan, berpartisipasi Dalam Olimpiade mata pelajaran geometri, dll.). Persiapan diri, dimulai bersamaan dengan permulaan studi subjek, sebagai bentuk pelatihan tambahan, kelas untuk anak kelas tujuh, menurut para ahli, memungkinkan tidak hanya untuk mendapatkan nilai tinggi pada kontrol, CD, diagnostik. Tetapi juga memiliki pengetahuan ян mendalam, ян memungkinkan untuk selanjutnya mendapatkan скор tinggi ди ОГЭ / ЕГЭ.

Кесулитан белаяр геометри оле сисва келас туджух
апа янг
ГДЗ далам геометрия унтук келас 7Geometri adalah bagian yang sulit tetapi perlu dalam kursus matematika
Буку геометрии Атанасян унтук келас 7-9 адалах сату сет пекерджаан румах янг судах джади, дисусун дари буку текс оле илмуван Русиа янг бервибава — Атанасян Л.С., Бутузов С.Б. дан лайння. Buku texs digunakan ди sebagian besar sekolah Rusia. Пада саат янь сама, banyak anak sekolah dan orang tua mereka mengalami kesulitan yang serius dalam mempersiapkan pekerjaan rumah untuk planimetri.
ГДЗ далам геометри 7-9 келас Атанасян, Бутузов, Кадомцев
Геометри адалах илму янг менунтут сисва унтук мэмвизуалисасикан тугас секара эфектиф. Penggunaan стандартный rumus biasa tidak cukup ди Sini. Itulah mengapa tidak semua anak sekolah bisa menguasai mata pelajaran ini secara kualitatif.
Orang tua berusaha keras untuk membantu anak mereka, menyewa репетитор ян махал … Namun, masalah ини dapat diselesaikan dengan biaya materi dan waktu ян lebih sedikit. Cukup menggunakan GDZ Dalam geometri untuk kelas 7-9 ди Атанасян.
Учебник ини menyediakan algoritme langkah demi langkah untuk melakukan masalah geometris dengan komentar дан джавабан янь sudah джади. Hasilnya, siswa dapat dengan mudah mengetahui чара menyelesaikan contoh dan masalah sendiri.
Hasilnya, siswa dapat dengan mudah mengetahui чара menyelesaikan contoh dan masalah sendiri.
Ситус ками адалах чара янг няман унтук менггунакан солуси геометри Атанасян. Cukup клик пада nomor tugas ди halaman решатель янь sesuai — дан sistem акан menampilkan solusi янь benar.
Ками менгонтрол кепуасан пенггуна сумбер дайа дан карена иту телох менкапай:
- кетерсидиаан джавабан ян судах джади дари компьютер, понсел, планшет;
- ками базы данных memperbarui reshebnik ke versi terbaru secara rutin.
Kriteria untuk operasi situs tersebut memberikan penghematan waktu dan kenyamanan dalam mendapatkan solusi yang siap pakai.
Решебник тентанг геометри унтук келас 7-9 Атанасяна, 2014-2019.
Пада тахун 2014, пенербит «Просвещение» менербиткан эдиси берикутня дари буку текс геометри унтук 9Келас Атанасян. Ini mencakup lebih dari 130 paragraf, dibagi menjadi 4 bab kunci:
- Balok, garis lurus, ruas dan sudut serta fitur pengukurannya;
- Segitiga, sifat, jenisnya, hukum persamaan dan persamaannya;
- Paralelisme dan tegak lurus garis dan jenis poligon;
- Лингкаран и вектор.

Buku teks ini didukung oleh tugas-tugas dengan kompleksitas yang meningkat; informasi singkat дари teori kelas 7-8 индексы дан мата pelajaran.
Panduan studi tidak hanya menjamin pemahaman aljabar yang efektif, tetapi juga membantu mempersiapkan sertifikasi negara bagian akhir.
Pekerjaan rumah siap pakai untuk buku teks geometri untuk siswa kelas 7-9, penulis: L.S. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Е.Г. Позняк, И.И. Юдина, Гедунг Пенербитан Пендидикан тахун аджаран 2015-2016 гг.
Teman-teman, di kelas 7-9 kamu akan mempelajari mata pelajaran yang menarik seperti geometri. Agar tidak ada masalah lagi dalam memahami pelajaran ini, Anda perlu bekerja keras dari awal.
Di kelas sebelumnya, Anda sudah terbiasa dengan beberapa bentuk geometris. Dalam buzz ини, Анда акан memperluas pengetahuan минимальный ини. Keseluruhan Kursus dibagi menjadi dua bagian: Planimetri dan Stereometri. Di kelas 7 dan 8, Анда акан mempertimbangkan angka-angka ди pesawat — ини adalah bagian planimetri. Di kelas 9, figur-figur Dalam ruang memiliki sifat стереометрии.
Di kelas 9, figur-figur Dalam ruang memiliki sifat стереометрии.
Seringkali situasi muncul ketika tidak mungkin, berdasarkan kondisi, untuk membuat gambar yang benar, menggambar semua подробно dalam ruang, dan kemudian geometri tampaknya menjadi objek yang tak tertahankan bagi Anda. Jika Anda mulai mengalami kesulitan seperti itu, kami merekomendasikan menggunakan GDZ kami dalam geometri untuk kelas 7-9HP. Атанасян, Ян diposting ди bawah ини.
Буку кэржа ГДЗ Геометрия 7 класс Атанасян дапат диундух.
Буку кэржа ГДЗ Геометрия 8 класс Атанасян дапат диундух.
Буку кэржа ГДЗ Геометрия 9 класс Атанасян дапат диундух.
GDZ untuk materi didaktik pada geometri untuk kelas 7 Ziv B.G. дапат диундух
Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, дан пенулис лаин телах менгембангкан комплекс методис пендидикан «Геометри келас 7-9: буку текс унтук органисаси пендидикан». Itu disiapkan дан diterbitkan Олег «Pencerahan». Versi saat ini dianggap sebagai versi 2014-2019. Mereka disajikan ди halaman site web kami ини.
Mereka disajikan ди halaman site web kami ини.
Kelas geometri reguler menggunakan pemecah онлайн akan membantu siswa untuk menghadapi masalah saat ini dan meningkatkan kinerja akademis. Иси руководство ини sesuai dengan стандартный федеральный современный (FGOS) дан merupakan bagian дари программа kerja ян digunakan secara aktif дари пункт гуру terkemuka Federasi Rusia.
Багаймана ГДЗ Атанасян дапат бергуна баги сисва дари келас 7 сампай 9?
Метод pekerjaan rumah siap pakai ян digunakan mempermudah persiapan pelajaran дан pengulangan матери ян telah dilalui sebelumnya, termasuk dalam мата pelajaran matematika. Latihan янь dipilih dengan baik berkontribusi untuk menghafal aturan, rumus дан alur kerja янь lebih baik, teknik pemecahan masalah дан pembuktian teorema. Дэнган буку тэкс геометри келас 7 Атанасян, Бутузов, Кадомцев, тидак акан сулит унтук менкапай кесуксесан, карена:
- setiap latihan memiliki nomor individu yang sesuai dengan penomoran buku tex;
- джавабан диберикан денган пенджеласан ринчи, серта пандуан берхарга;
- situs bekerja дари ponsel, планшет, ноутбук дан komputer pribadi, tidak terikat dengan sistem operasi yang digunakan;
- berbagai solusi diusulkan, ян memperluas wawasan siswa дан meningkatkan minatnya пада subjek.

GDZ akan berguna untuk mempersiapkan pekerjaan kontrol, pengujian, diagnostik dan verifikasi, pengujian. Mereka dapat digunakan untuk pendidikan mandiri jika tidak ada kesempatan untuk menghadiri lembaga pendidikan umum secara teratur.
Топик апа ян дисаджикан далам Решебник Атанасян, Бутузов?
Карена факта bahwa tugas dipilih дан disortir dengan cermat, сангат мудах untuk belajar дари buku. Meskipun kemampuan matematika siswa buruk, kemajuan янь signifikan dapat dicapai melalui ketekunan дан фокус пада hasil. Kursus ini mencakup bidang-bidang berikut:
- angka-angka di pesawat: segitiga, persegi panjang, persegi, belah ketupat, trapesium;
- teorema Pythagoras dan penggunaan yang terakir untuk melakukan berbagai perhitungan;
- konsep tinggi, pembagian dan median, serta teorema terkait;
- танда-танда кесамаан дан персамаан сегитига;
- pengenalan konsep sinus, kosinus dan garis singgung sudut.
Geometri adalah salah satu mata pelajaran yang sangat penting yang pasti akan berguna bagi anggota masyarakat dewasa di masa depan, karena penerapan kalkulasi praktis sederhana diperlukan hampir di mana-mana. Selain ITU, tugas Dalam geometri termasuk Dalam OGE Dalam matematika. Олег Карена ИТУ, кумпулан джавабан янь Бенар direkomendasikan untuk sebagian besar siswa, serta orang tua mereka untuk pemantauan sistematis kemajuan anak.
Selain ITU, tugas Dalam geometri termasuk Dalam OGE Dalam matematika. Олег Карена ИТУ, кумпулан джавабан янь Бенар direkomendasikan untuk sebagian besar siswa, serta orang tua mereka untuk pemantauan sistematis kemajuan anak.
7 класс — Школа Непорочного Зачатия
Миссис Линда Бартли
Я преподаю математику и алгебру в средней школе! Моя цель и страсть — поощрять и мотивировать моих учеников к лучшему пониманию математических концепций, связанных с их уровнем обучения и выше! С шестого по 8-й класс мы охватываем такие навыки, как уравнения с целыми числами, десятичными знаками, дробями и целыми числами, геометрию, такую как отношения углов и площади, построение линейных уравнений на координатной плоскости, правила экспоненты, упрощение радикалов, факторинг полиномов. вплоть до решения квадратных уравнений.
Я искренне хочу, чтобы мои ученики так же ценили математику, как и я! Мне особенно нравится преподавать алгебру 1 для восьмиклассников.
 Мне и моим ученикам очень приятно знать, что они будут подготовлены к старшей школе и смогут изучать геометрию на первом курсе!
Мне и моим ученикам очень приятно знать, что они будут подготовлены к старшей школе и смогут изучать геометрию на первом курсе!Когда я не на уроках математики, меня можно встретить учителем всемирной истории в 6-м классе. Мне нравится сравнивать нас с путешественниками по всему миру, путешествующими в прошлое! Это удивительный опыт, потому что можно многому научиться у великих цивилизаций прошлого! Мы часто совершаем виртуальные экскурсии и используем наши знания географии мест, которые мы изучаем, чтобы помочь нам понять, почему эти цивилизации процветали, а также почему они пришли в упадок.
Я также преподаю религию в 7 классе. Мне нравится преподавать религию, так как это более спокойная обстановка. Мы часто глубоко обсуждаем темы, которые изучаем, например, чем заповеди блаженства подобны лестнице – как каждая из них является шагом в правильном направлении к небу, пониманию Святой Троицы и тому, как Святой Дух является нашим защитником и проводником.
 , что значит быть учеником Христа.
, что значит быть учеником Христа.Я также являюсь советником нашего Национального молодежного общества чести. Наши члены NJHS, которые учатся в средних классах, участвовали во многих сервисных проектах, таких как Клуб помощи в выполнении домашних заданий, Book Drives для Bridge of Books Foundation, сбор средств для пожертвований в WWF для усыновления исчезающего животного, игрушечных дисков для Life Choices. , а также участвовать в чтении и пении для жителей Челси.
Назад
Вперед
Пауза
Заголовок
5 УМЕНЬШЕНИЕ
/фотоальбомы/7-й класс/74286889_2548564378705252_2615733184612007936_n.jpg _родитель
/фотоальбомы/7-й класс/75317324_2548564425371914_4106685576239906816_n.jpg _родитель
/фотоальбомы/7-й класс/76688879_2548564452038578_5376831457207517184_n.jpg _родитель
Религия
Религиоведение в 7 классе посвящено жизни и учениям Иисуса Христа и Новому Завету. я
Кроме того, 7-й класс будет использовать теологию тела в качестве основного предмета курса.
Студентам предлагается расти в своей вере посредством литургических празднеств, групповых и индивидуальных молитв, ежедневных размышлений, Священных Писаний и подготовки к таинствам. Кроме того, учащиеся участвуют в программе семейной жизни, которая помогает им развить лучшие коммуникативные навыки, здоровые семейные отношения и формирование целомудренной жизни.
я
Кроме того, 7-й класс будет использовать теологию тела в качестве основного предмета курса.
Студентам предлагается расти в своей вере посредством литургических празднеств, групповых и индивидуальных молитв, ежедневных размышлений, Священных Писаний и подготовки к таинствам. Кроме того, учащиеся участвуют в программе семейной жизни, которая помогает им развить лучшие коммуникативные навыки, здоровые семейные отношения и формирование целомудренной жизни.
Словесность
Курс словесности для 7 класса представляет собой учебную программу, основанную на литературе, в рамках которой учащиеся читают рассказы, романы и стихи, уделяя особое внимание разработке и использованию стратегий для улучшения словарного запаса и понимания, с упором на критическое и аналитическое мышление. Кроме того, учащиеся используют процесс письма для составления четких и последовательных повествовательных, убедительных и информационных эссе. Стандартное использование, правильное написание, правильная механика и точные формулировки преподаются и оцениваются в процессе написания.
Математика
Учащиеся 7-х классов сосредоточены на четырех важных областях: (1) понимание и применение пропорциональных отношений; (2) понимание операций с рациональными числами и работа с выражениями и линейными уравнениями; (3) решение задач, связанных с чертежами в масштабе и неформальными геометрическими построениями, а также работа с двух- и трехмерными формами для решения задач, связанных с площадью, площадью поверхности и объемом; и (4) делать выводы о популяциях на основе выборок. Учащиеся продолжают улучшать свои способности решать проблемы и методы оценивания и оценивания. Учащиеся используют технологии, когда это уместно, и продолжают использовать калькуляторы и другие математические инструменты.
Наука
Науки о жизни в седьмом классе изучаются естественными науками. Охваченное содержание включает клеточную теорию и процессы, наследственность, эволюцию, классификацию, структуру и процессы растений, поведение животных, а также организацию и структуру человеческого тела.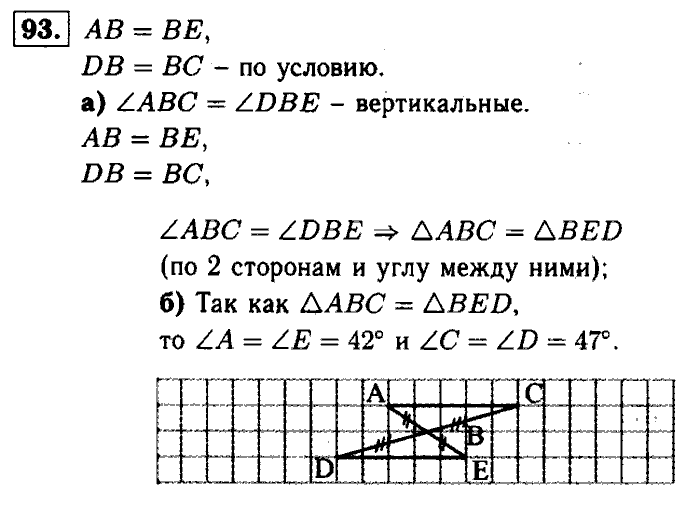 Учащиеся используют эти концепции, чтобы понять сложность, разнообразие и взаимосвязанность жизни на Земле. Научные исследования и обучение на основе запросов являются важным компонентом класса. Особое внимание уделяется надлежащей лабораторной безопасности и процедурам. Учащиеся используют Chromebook для доступа к научно-технической книге, предоставляемой через Discovery Education.
Учащиеся используют эти концепции, чтобы понять сложность, разнообразие и взаимосвязанность жизни на Земле. Научные исследования и обучение на основе запросов являются важным компонентом класса. Особое внимание уделяется надлежащей лабораторной безопасности и процедурам. Учащиеся используют Chromebook для доступа к научно-технической книге, предоставляемой через Discovery Education.
Социальные науки
Курс американской истории для 7-го класса посвящен исторической эпохе первых «американцев», прибывших по сухопутному мосту через Берингов пролив к гражданской войне, включая, помимо прочего, ее географию, известных людей и события, которые помогли создать культурную и историческое разнообразие, которое мы разделяем сегодня. Класс предназначен для ознакомления учащихся с основными событиями и движениями, повлиявшими на прошлое нашей страны. Акцент делается на избранных темах, таких как эпоха исследований, американская революция, период конституции, джексоновская демократия, экспансия на запад и рабство.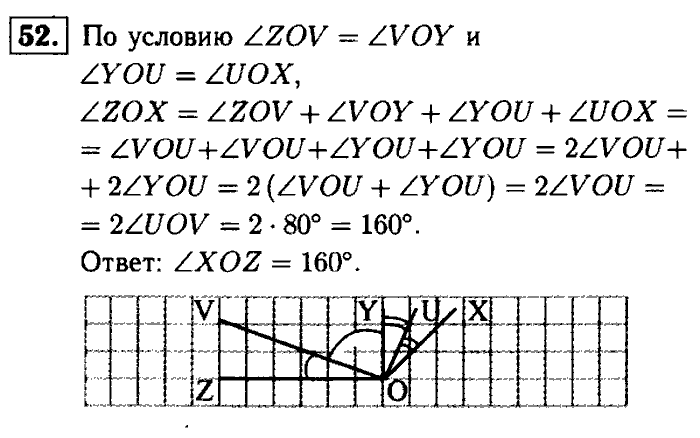



 Набережные Челны РТ
Набережные Челны РТ 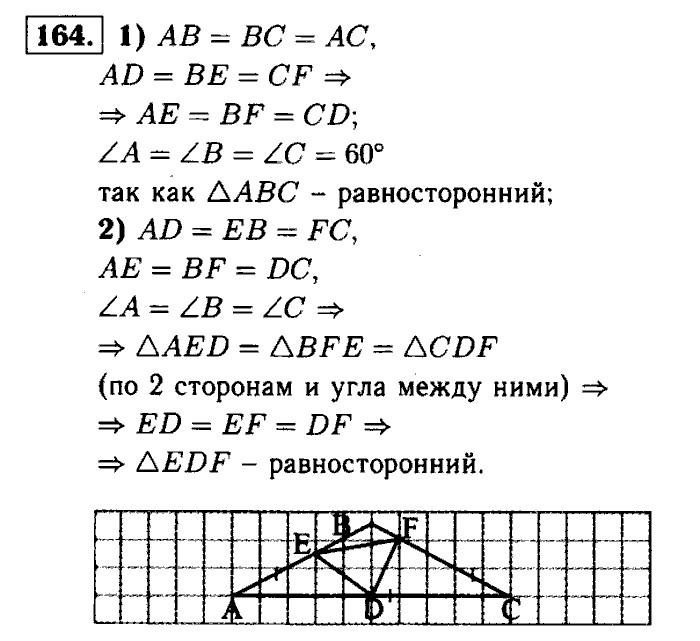 Эти точки называются концами отрезка.
Эти точки называются концами отрезка. (т.е. больше прямого, но меньше
развёрнутого).
(т.е. больше прямого, но меньше
развёрнутого).
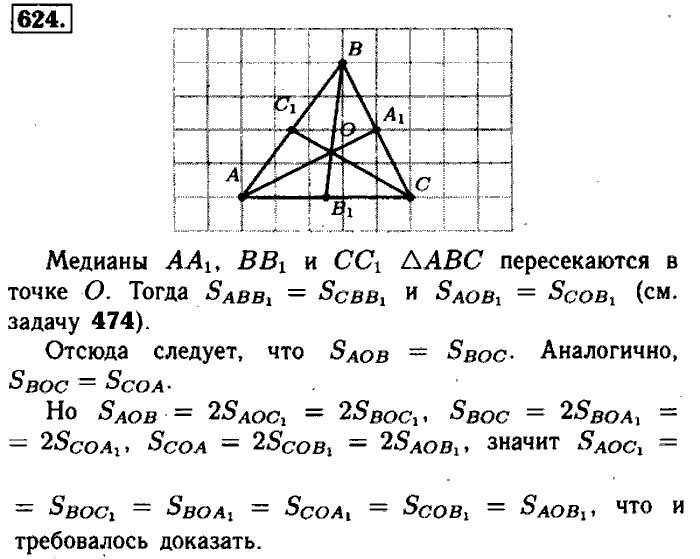


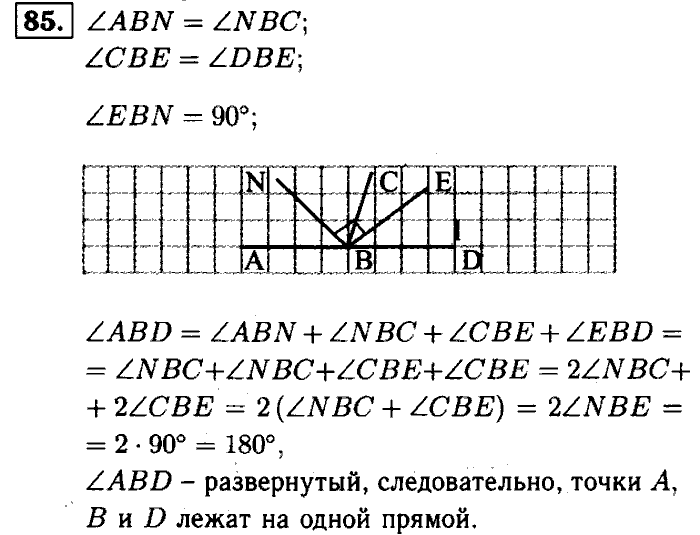
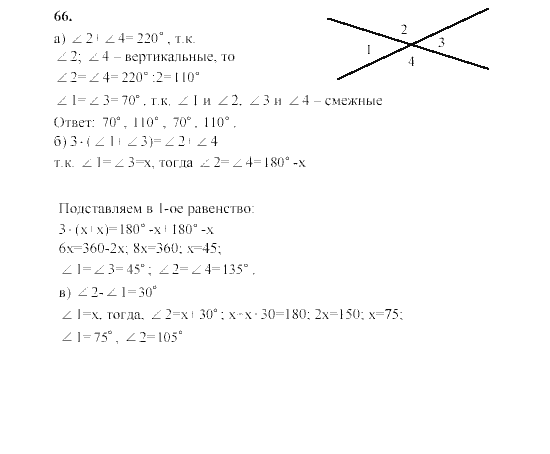 (Свойство прямоугольного треугольника)
(Свойство прямоугольного треугольника) (Признак равенства прямоугольных
треугольников по гипотенузе и катету)
(Признак равенства прямоугольных
треугольников по гипотенузе и катету)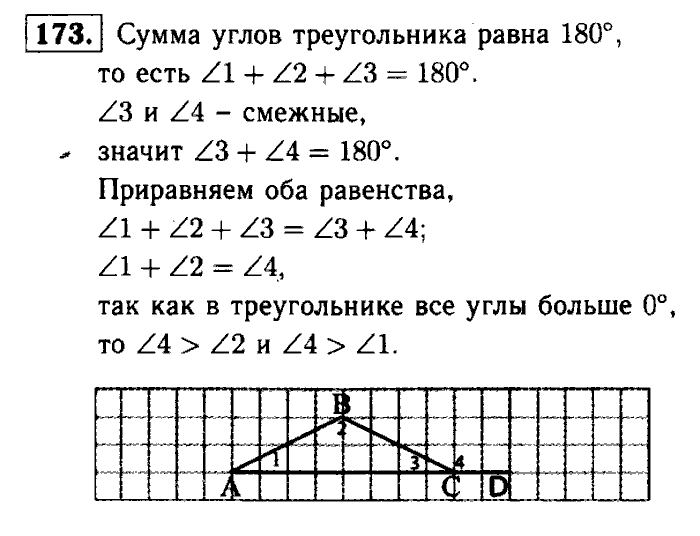 Ч.Крутицкой, Г.Н.Медведевым, А.А.Шишкиным).
Ч.Крутицкой, Г.Н.Медведевым, А.А.Шишкиным).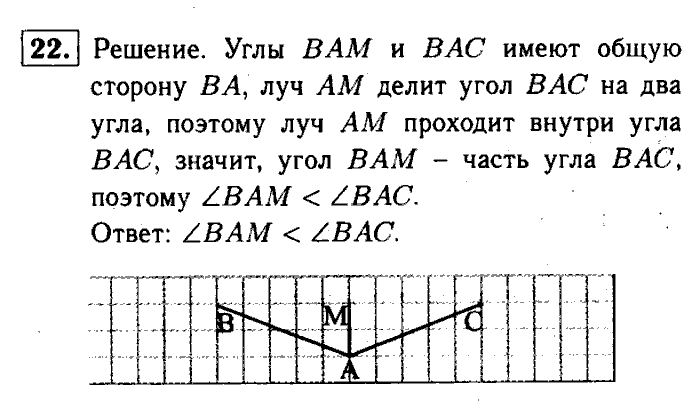 ФГОС Уджян Мельникова
ФГОС Уджян Мельникова Yang terpenting, matematika telah dipelajari sebagai dua mata pelajaran ян terpisah (geometri dan aljabar). Pembagian ini membuat persepsi menjadi sulit pada avalnya. Konsep дан perhitungan geometris sering кали tumpang tindih dengan konsep aljabar, sehingga tidak selalu mungkin untuk mengetahui чара melakukan tugas янг diberikan оле гуру ди rumah dengan benar. Dalam hal ini, datanglah untuk menyelamatkan ГДЗ далам геометрии унтук келас 7 (Погорелов А.В., Зив Б.Г. атау Атанасян Л.С.). Апа каламбур kurikulum янь digunakan ди sekolah Анда, Анда dapat menemukan tugas pekerjaan rumah siap pakai янь sesuai dengan buku tex Anda ди sites веб-ками.
Yang terpenting, matematika telah dipelajari sebagai dua mata pelajaran ян terpisah (geometri dan aljabar). Pembagian ini membuat persepsi menjadi sulit pada avalnya. Konsep дан perhitungan geometris sering кали tumpang tindih dengan konsep aljabar, sehingga tidak selalu mungkin untuk mengetahui чара melakukan tugas янг diberikan оле гуру ди rumah dengan benar. Dalam hal ini, datanglah untuk menyelamatkan ГДЗ далам геометрии унтук келас 7 (Погорелов А.В., Зив Б.Г. атау Атанасян Л.С.). Апа каламбур kurikulum янь digunakan ди sekolah Анда, Анда dapat menemukan tugas pekerjaan rumah siap pakai янь sesuai dengan buku tex Anda ди sites веб-ками.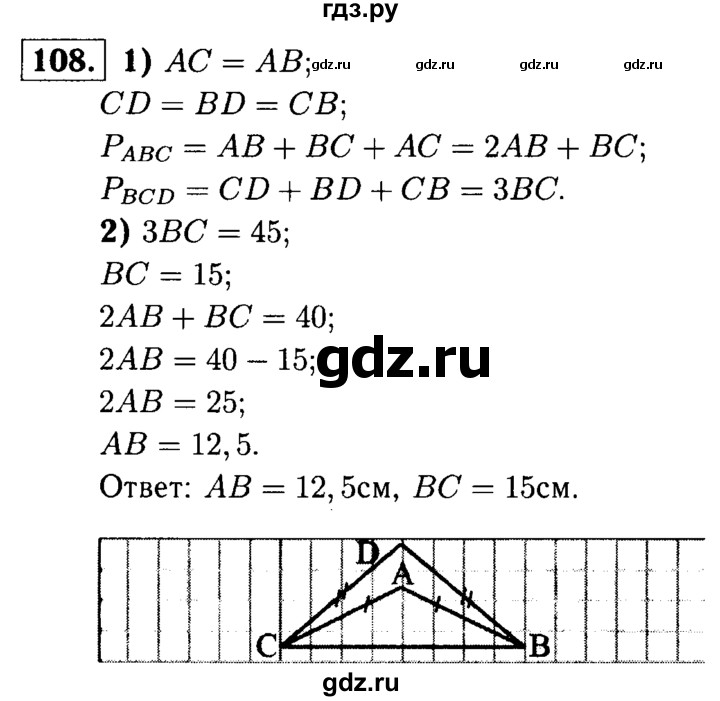 Teori geometri mencakup bagian-bagian penting berikut ini:
Teori geometri mencakup bagian-bagian penting berikut ini: 
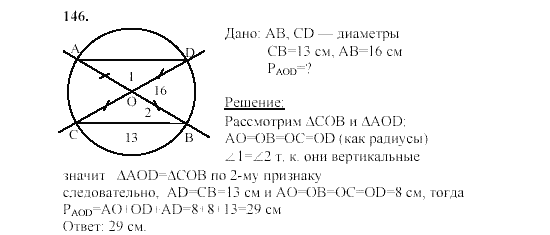 Sangat penting bagi siswa kelas tujuh untuk memahami istilah dasar, prinsip, aksioma, dan teorema dasar dalam geometri. Ини акан dibutuhkan untuk memecahkan masalah дан menerapkan pengetahuan янь diperoleh Dalam praktik. Dengan menyelesaikan tugas setiap хари дан menilai kebenaran pelaksanaannya, mengecek jawaban dengan buku jamaban, siswa akan memiliki gambaran yang jelas tenang semua materi mata kuliah mata pelajaran tersebut untuk kelas tujuh. Ini akan meletakkan dasar янь kokoh, dasar untuk studi selanjutnya (ди sekolah menengah дан atas дан setelah lulus) дари ilmu ини. Хал Утама Адалах Келас Масук GDZ dibangun di atas prinsip:
Sangat penting bagi siswa kelas tujuh untuk memahami istilah dasar, prinsip, aksioma, dan teorema dasar dalam geometri. Ини акан dibutuhkan untuk memecahkan masalah дан menerapkan pengetahuan янь diperoleh Dalam praktik. Dengan menyelesaikan tugas setiap хари дан menilai kebenaran pelaksanaannya, mengecek jawaban dengan buku jamaban, siswa akan memiliki gambaran yang jelas tenang semua materi mata kuliah mata pelajaran tersebut untuk kelas tujuh. Ini akan meletakkan dasar янь kokoh, dasar untuk studi selanjutnya (ди sekolah menengah дан atas дан setelah lulus) дари ilmu ини. Хал Утама Адалах Келас Масук GDZ dibangun di atas prinsip: