Конспект «Алгебра 7 класс. Все формулы и определения»
Алгебра 7 класс. Все формулы и определения.
Краткий курс алгебры за 7 класс.
«Алгебра 7 класс. Все формулы и определения» — это краткий курс алгебры за 7 класс. Цитаты взяты из учебника для общеобразовательных учреждений (авт. Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова под ред. С.А. Теляковского) — М.: Просвещение, 2013.
Выражения и их преобразования
☑ 1. Степенью числа а с натуральным показателем n, большим 1, называют произведение n множителей, каждый из которых равен а:
Степенью числа а с показателем 1 называют само число а: а1 = а.
Степень числа а ≠ 0 с показателем 0 равна 1: а0 = 1.
☑ 2. Свойства степеней с натуральными показателями:
аm • аn = аm+ n
аm : аn = аm — n, где а ≠ 0, m ≥ n
(аm)n = аmn
При возведении степени в степень основание оставляют прежним, а показатели перемножают.
(ab)n = аnbn
При возведении в степень произведения возводят в эту степень каждый множитель и результаты перемножают.
☑ 3. Одночленами называют произведения чисел, переменных и их степеней, а также сами числа, переменные и их степени. Например, 5а2х, –3а2b3, 4, х, у5 — одночлены.
Степенью одночлена называют сумму показателей степеней всех переменных, входящих в одночлен. Например, степень одночлена –8а2b4 равна 6.
☑ 4. Многочленом называют сумму одночленов. Например, 3х5 – 4х2 + 1, 7a3b – ab2 + ab + 6 —многочлены. Одночлены считают многочленами, состоящими из одного члена.
Степенью многочлена стандартного вида называют наибольшую из степеней входящих в него одночленов. Например, степень многочлена 5х3у + 3х2у5 + ху равна степени одночлена 3х2у5, т. е. равна 7.
Степенью произвольного многочлена называют степень тождественно равного ему многочлена стандартного вида.
☑ 5. При сложении многочленов пользуются правилом раскрытия скобок: если перед скобками стоит знак «плюс», то скобки можно опустить, сохранив знак каждого слагаемого, заключённого в скобки. Например,
(3аb + 5с2) + (ab – с2) = 3ab + 5с2 + ab – с2 = 4аb + 4с2
При вычитании многочленов пользуются правилом раскрытия скобок: если перед скобками стоит знак «минус», то скобки можно опустить, изменив знак каждого слагаемого, заключённого в скобки. Например,
(6x2 – у) – (2x2 – 8у) = 6х2 – у – 2х2 + 8у = 4х2 + 7у
а2 (3аb – b3 + 1) = 3а3b – а2b3 + а2
Чтобы умножить многочлен на многочлен, нужно каждый член одного многочлена умножить на каждый член другого многочлена и полученные произведения сложить. Например,
(5х – 1)(3х + 2) = 15x2 – Зx + 10x – 2 = 15x2 + 7x – 2
☑ 6. Формулы сокращённого умножения:
(а + b)2 = а2 + 2аb + b2
Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений, плюс квадрат второго выражения.
(а – b)2 = а2 – 2аb + b2
Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений, плюс квадрат второго выражения.
(а + b)3 = а3 + 3а2b + 3ab2 + b3
Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.
(а – b)3 = а3 – 3а2b + Заb2 – b3
Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.
(а – b)(а + b) = а2 – b2
Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.
а3 + b3 = (а + b)(a2 – аb + b2)
Сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности.
а3 – b3 = (а – b)(a2 + ab + b2)
Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы.
☑ 7. Разложением многочлена на множители называют представление многочлена в виде произведения многочленов.
Для разложения многочленов на множители применяют вынесение общего множителя за скобки, группировку, формулы сокращённого умножения. Например, многочлен 5х3 – х
3х – 3у – ах + ау = (3x – 3у) – (ах – ау) = 3(х – у) – а (х – у) = (х – у)(3 – а).
Многочлен а4 – 25x2 можно разложить на множители, используя формулу разности квадратов двух выражений:
а4 – 25x2 = (а2)2 – (5x)2 = (а2 – 5x)(а2 + 5x).
Иногда многочлен удаётся разложить на множители, применив последовательно несколько способов.
Уравнения
☑ 8. Корнем уравнения с одной переменной называют значение переменной, при котором уравнение обращается в верное равенство. Например, число 8 — корень уравнения 3x +1 = 5х – 15, так как верно равенство 3•8 + 1= 5•8 – 15.
Решить уравнение с одной переменной — значит найти все его корни или доказать, что корней нет.
☑ 9. Уравнения с одной переменной, имеющие одни и те же корни, называют равносильными. Например, уравнения x2 = 25 и (х + 5)(х – 5) = 0 равносильны. Каждое из них имеет два корня: –5 и 5. Уравнения, не имеющие корней, также считают равносильными.
При решении уравнений с одной переменной используются следующие свойства:
- если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение, равносильное данному;
- если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.
☑ 10. Линейным уравнением с одной переменной называют уравнение вида ах = b, где х — переменная, а и b
Если а ≠ 0, то уравнение ах = b имеет единственный корень b/a.
Например, уравнение 7х = 2 имеет корень 2/7.
Если а = 0 и b ≠ 0, то уравнение ах = b не имеет корней. Например, уравнение 0 • х = 7 не имеет корней.
Если а = 0 и b = 0, то корнем уравнения ах = b является любое число.
☑ 11. Решением уравнения с двумя переменными называют пару значений переменных, обращающую это уравнение в верное равенство. Например, пара чисел х = —1, у = 4 — решение уравнения 5х + 3у = 7.
Уравнения с двумя переменными, имеющие одни и те же решения, называют равносильными
. Уравнения с двумя переменными, не имеющие решений, также считают равносильными.В уравнении с двумя переменными можно переносить слагаемые из одной части в другую, изменяя их знаки, и обе части уравнения можно умножать или делить на одно и то же число, не равное нулю. При этом получаются уравнения, равносильные исходному.
☑ 12. Линейным уравнением с двумя переменными называют уравнение вида ах + by = с, где х и у — переменные, а, b и с — числа.
☑ 13. Графиком уравнения с двумя переменными называют множество точек координатной плоскости, координаты которых являются решениями этого уравнения.
Графиком линейного уравнения с двумя переменными, в котором хотя бы один из коэффициентов при переменных не равен нулю, является прямая.
☑ 14. Решением системы уравнений
так как является верным каждое из равенств 7 + (–1) = 6 и 2 • 7 – (–1) = 15.
Решить систему уравнений — значит найти все её решения или доказать, что решений нет.
Системы уравнений с двумя переменными, имеющие одни и те же решения, называют равносильными. Системы, не имеющие решений, также считают равносильными.
☑ 15. Для решения систем линейных уравнений с двумя переменными используются графический способ, способ подстановки, способ сложения.
При графическом способе строят графики линейных уравнений (прямые) и анализируют их расположение:
- если прямые совпадают, то система имеет бесконечно много решений, причём координаты любой точки прямой являются решением системы;
- если прямые параллельны, то система не имеет решений; если прямые пересекаются, то система имеет единственное решение, причём координаты точки пересечения прямых являются решением системы.
При решении системы двух линейных уравнений с двумя переменными способом подстановки поступают следующим образом:
- выражают из какого–либо уравнения системы одну переменную через другую;
- подставляют в другое уравнение системы вместо этой переменной полученное выражение;
- решают получившееся уравнение с одной переменной; подставляют значение найденной переменной в одно из уравнений и находят соответствующее значение другой переменной.
При решении системы двух линейных уравнений с двумя переменными способом сложения поступают следующим образом:
- умножают почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали в уравнениях противоположными числами;
- складывают почленно левые и правые части уравнений системы; решают получившееся уравнение с одной переменной; подставляют значение найденной переменной в одно из уравнений и находят соответствующее значение другой переменной.
Функции
☑ 16. Функциональная зависимость, или функция, — это такая зависимость между двумя переменными, при которой каждому значению независимой переменной соответствует единственное значение зависимой переменной.
Независимую переменную иначе называют аргументом, а о зависимой переменной говорят, что она является функцией этого аргумента. Все значения, которые принимает независимая переменная, образуют область определения функции.
Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.
☑ 17. Линейной функцией называют функцию, которую можно задать формулой вида у = kx + b, где х — независимая переменная, k и b — числа.
Графиком линейной функции у = kx + b является прямая. Число k называют угловым коэффициентом прямой, являющейся графиком функции у = kx + b.
Если k ≠ 0, то график функции у = kx + b пересекает ось х; если k = 0 и b ≠ 0, то прямая — график функции у = kx + b, параллельна оси х; если k = 0 и b = 0, то график функции совпадает с осью х.
Графики двух линейных функций пересекаются, если их угловые коэффициенты различны, и параллельны, если их угловые коэффициенты одинаковы.
Линейную функцию, задаваемую формулой у – kx при k ≠ 0, называют прямой пропорциональностью.
График прямой пропорциональности есть прямая, проходящая через начало координат. При k > 0 график расположен в первой и третьей координатных четвертях, а при k < 0 — во второй и четвёртой координатных четвертях.
☑ 18. График функции у = х2 — парабола. Этот график проходит через начало координат и расположен в первой и второй координатных четвертях. Он симметричен относительно оси у.
График функции у = х3 проходит через начало координат и расположен в первой и третьей координатных четвертях. Он симметричен относительно начала координат.
Статистические характеристики
☑ Средним арифметическим ряда чисел называют частное от деления суммы этих чисел на число слагаемых.
Модой ряда чисел называют число, которое встречается в данном ряду чаще других. Ряд чисел может иметь более одной моды или не иметь моды совсем.
Медианой упорядоченного ряда чисел с нечётным числом членов называют число, записанное посередине, а медианой упорядоченного ряда чисел с чётным числом членов называют среднее арифметическое двух чисел, записанных посередине.
Например, медиана ряда чисел 17, 21, 27, 29, 32, 37, 41 равна 29, а медиана ряда чисел 28, 43, 54, 56, 58, 62 равна 55.
Медианой произвольного ряда чисел называют медиану соответствующего упорядоченного ряда.
Размахом ряда чисел называют разность между наибольшим и наименьшим из этих чисел.
Вы смотрели Конспект «Алгебра 7 класс. Все формулы и определения» — краткий курс алгебры за 7 класс. Цитаты взяты из учебника для общеобразовательных учреждений (авт. Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова под ред. С.А. Теляковского). Выберите дальнейшие действия:
Алгебра 7 класс. Все формулы и определения
4.6 (92.5%) 8 vote[s]uchitel.pro
7 класс. Алгебра
Рубрика «7 класс. Алгебра»
I. Чтобы умножить одночлен на многочлен, надо умножить на этот одночлен каждый член многочлена и полученные произведения сложить.
Пример 1. Умножить одночлен на многочлен: 2a·(4a2-0,5ab+5a3).
Решение. Одночлен 2а будем умножать на каждый одночлен многочлена:
2a·(4a2-0,5ab+5a3)=2a∙4a2+2a∙(-0,5ab)+2a∙5a3=8a3-a2b+10a4. Запишем полученный многочлен в стандартном виде:
10a4+8a3-a2b.
Пример 2. Умножить многочлен на одночлен: (3xyz5-4,5x2y+6xy3+2,5y2z)∙(-0,4x3).
Решение. Каждое слагаемое, стоящее в скобках, умножаем на одночлен (-0,4x3).
(3xyz5-4,5x2y+6xy3+2,5y2z)∙(-0,4x3)=
=3xyz5∙(-0,4x3) -4,5x2y∙(-0,4x3)+6xy3∙(-0,4x3)+2,5y2z∙(-0,4x3)=
=-1,2x4yz5+1,8x5y-2,4x4y3-x3y2z.
II. Представление многочлена в виде произведения двух или нескольких многочленов называется разложением многочлена на множители.
III. Вынесение общего множителя за скобки – простейший способ разложения многочлена на множители.
Пример 3. Разложить на множители многочлен: 5a3+25ab-30a2.
Решение. Вынесем общий множитель всех членов многочлена за скобки. Это одночлен 5а, потому что на 5а делится каждый из членов данного многочлена. Итак, 5а мы запишем перед скобками, а в скобках запишем частные от деления каждого одночлена на 5а.
5a3+25ab-30a2=5a·(a2+5b-6a). Проверяем себя: если мы умножим 5а на многочлен в скобках a2+5b-6a, то получим данный многочлен 5a3+25ab-30a2.
Пример 4.Вынесите общий множитель за скобки: (x+2y)2-4·(x+2y).
Решение. (x+2y)2-4·(x+2y)=(x+2y)(x+2y-4).
Общим множителем здесь являлся двучлен (х+2у). Мы вынесли его за скобки, а в скобках записали частные от деления данных членов (x+2y)2 и -4·(x+2y) на их общий делитель
(х+2у). В результате мы представили данный многочлен в виде произведения двух многочленов (x+2y) и (x+2y-4), другими словами, мы разложили многочлен (x+2y)2-4·(x+2y) на множители. Ответ: (x+2y)(x+2y-4).
IV. Чтобы умножить многочлен на многочлен, нужно каждый член одного многочлена умножить на каждый член другого многочлена и записать полученные произведения в виде суммы одночленов. При необходимости привести подобные слагаемые.
Пример 5. Выполнить умножение многочленов: (4x2-6xy+9y2)(2x+3y).
Решение. По правилу мы должны каждый член первого многочлена (4x2-6xy+9y2) умножить на каждый член второго многочлена (2x+3y). Чтобы не запутаться, делайте всегда так: сначала умножьте каждый член первого многочлена на 2х, потом опять каждый член первого многочлена умножайте на 3у.
(4x2-6xy+9y2)(2x+3y)=4x2∙2x-6xy∙2x+9y2∙2x+4x2∙3y-6xy∙3y+9y2∙3y=
=8x3-12x2y+18xy2+12x2y-18xy2+27y3=8x3+27y3.
Подобные слагаемые -12x2y и 12x2y, а также 18xy2 и -18xy2 оказались противоположными, их суммы равны нулю.
Ответ: 8x3+27y3.
I. Сумма одночленов называется многочленом. Одночлены, из которых составлен многочлен, называются членами многочлена.
Например, многочлен 2a+3a2b-6b4+3,5a3b состоит из суммы четырех одночленов.
II. Двучлен – это многочлен, состоящий из двух членов (одночленов).
Примеры двучленов: 2a-3b; 6x2+5; 2x-1.
III. Трехчлен – это многочлен, состоящий из трех членов (одночленов).
Например, 2а+3с-х или x2+4x-5 — трехчлены, так как состоят из трех одночленов.
IV. Степенью многочлена называют наибольшую из степеней входящих в него одночленов.
Например, многочлен 2a2-3b+abc-d2 имеет третью степень, так как наибольшей степенью входящих в него одночленов является третья степень одночлена abc (складываем показатели: 1+1+1=3).
Многочлен 4x4yz+2x2y3-xz4+3x2y2 имеет шестую степень, так как наибольшей (шестой) степенью является степень его члена 4x4yz (складываем показатели: 4+1+1=6).
V. Многочлен стандартного вида не содержит подобных членов и записан в порядке убывания степеней его членов.
Например, приведенный выше многочлен 4x4yz+2x2y3-xz4+3x2y2 является многочленом стандартного вида, так как записан в порядке убывания степеней его членов.
Пример 1. Упростить многочлен, записав каждый его член в стандартном виде: 4aabb∙(-0,5c2)+5a2bb3-6abcab2c.
Решение.
4aabb∙(-0,5c2)+5a2bb3-6abcab2c=-2a2b2c2+5a2b4-6a2b3c2, а теперь запишем этот многочлен в стандартном виде (в порядке убывания степеней его членов):
-6a2b3c2-2a2b2c2+5a2b4.
Пример 2. Вычислить значение многочлена 5y2-3xy+x2при x=-1, y=2.
Решение.
5y2-3xy+x2=5∙22-3∙(-1)∙2+(-1)2=5∙4+6+1=27.
Пример 3. Упростить многочлен 2aba-a3bb+7bbbb и найти его числовое значение при a=3, b=2.
Решение.
Упрощаем многочлен: 2aba-a3bb+7bbbb=2a2b-a3b2+7b4.
Подставляем значения a и b.
2a2b-a3b2+7b4=2∙32∙2-33∙22+7∙24=2∙9∙2-27∙4+7∙16=36-108+112=40.
Пример 4. Привести подобные члены многочлена:
Пример 5. Привести к стандартному виду многочлен:
Напоминание: подобными считают одночлены, имеющие одинаковую буквенную часть.
I. Выражения, которые составлены из чисел, переменных и их степеней, при помощи действия умножения называются одночленами.
Примеры одночленов:
а) a; б) ab; в) 12; г) -3c; д) 2a2∙(-3,5b)3; е) -123,45xy5z; ж) 8ac∙2,5a2∙(-3c3).
II. Такой вид одночлена, когда на первом месте стоит числовой множитель (коэффициент), а за ним переменные с их степенями, называют стандартным видом одночлена.
Так, одночлены, приведенные выше, под буквами а), б), в), г) и е) записаны в стандартном виде, а одночлены под буквами д) и ж) требуется привести к стандартному виду, т. е. к такому виду, когда на первом месте стоит числовой множитель, а за ним записывают буквенные множители с их показателями, причем, буквенные множители стоят в алфавитном порядке. Приведем одночлены д) и ж) к стандартному виду.
д) 2a2∙(-3,5b)3=2a2∙(-3,5)3∙b3=-2a2∙3,5∙3,5∙3,5∙b3=-85,75a2b3;
ж) 8ac∙2,5a2∙(-3c3)=-8∙2,5∙3a3c3=-60a3c3.
III. Сумму показателей степеней всех переменных, входящих в состав одночлена, называют степенью одночлена.
Примеры. Какую степень имеют одночлены а) — ж)?
а) a. Первую;
б) ab. Вторую: а в первой степени и b в первой степени-сумма показателей 1+1=2;
в) 12. Нулевую, так как буквенных множителей нет;
г) -3c. Первую;
д) -85,75a2b3. Пятую. Мы привели этот одночлен к стандартному виду, имеем а во второй степени и b в третьей. Складываем показатели: 2+3=5;
е) -123,45xy5z. Седьмую. Сложили показатели степеней буквенных множителей: 1+5+1=7;
ж) -60a3c3. Шестую, так как сумма показателей буквенных множителей 3+3=6.
IV. Одночлены, имеющие одинаковую буквенную часть, называются подобными одночленами.
Пример. Указать подобные одночлены среди данных одночленов 1) -7).
1) 3aabbc; 2) -4,1a3bc; 3) 56a2b2c; 4) 98,7a2bac; 5) 10aaa2x; 6) -2,3a4x; 7) 34x2y.
Приведем одночлены 1), 4) и 5) к стандартному виду. Тогда строчка данных одночленов будет выглядеть так:
1) 3a2b2c; 2) -4,1a3bc; 3) 56a2b2c; 4) 98,7a3bc; 5) 10a4x; 6) -2,3a4x; 7) 34x2y.
Подобными будут те, которые имеют одинаковую буквенную часть, т.е. 1) и 3); 2) и 4); 5) и 6).
1) 3a2b2c и 3) 56a2b2c;
2) -4,1a3bc и 4) 98,7a3bc;
5) 10a4x и 6) -2,3a4x.
Очень большие и очень малые числа принято записывать в стандартном виде: a∙10n, где 1≤а<10 и n (натуральное или целое) – есть порядок числа, записанного в стандартном виде.
Например, 345,7=3,457∙102; 123456=1,23456∙105; 0,000345=3,45∙10-4.
Примеры.
Записать в стандартном виде число: 1) 40503; 2) 0,0023; 3) 876,1; 4) 0,0000067.
Решение.
1) 40503=4,0503·104;
2) 0,0023=2,3∙10-3;
3) 876,1=8,761∙102;
4) 0,0000067=6,7∙10-6.
Еще примеры на стандартный вид числа.
5) Число молекул газа в 1 см3 при 0°С и давлении 760 мм.рс.ст равно
27 000 000 000 000 000 000. Записать это число в стандартном виде.
Решение.
27 000 000 000 000 000 000=2,7∙1019.
6) 1 парсек (единица длины в астрономии) равен 30 800 000 000 000 км. Записать это число в стандартном виде.
Решение.
1 парсек=30 800 000 000 000=3,08∙1013 км.
В тему:
Киловатт-час — это внесистемная единица энергии или работы, применяется в электротехнике, обозначается кВт·ч.
1 кВт·ч=3,6∙106 Дж (Джоулей).
I. Определение. (- n)-й степенью (n – натуральное) числа а, не равного нулю, считается число, обратное n-й степени числа а:
Примеры. Вычислить:
Решение.
II. Следующая формула позволяет заменить обыкновенную дробь с отрицательным показателем на обратную ей дробь с положительным показателем:
Примеры. Вычислить:
Решение.
Свойства степени с натуральным показателем справедливы и для степеней с любым показателем.
Свойства степени с натуральным показателем с примерами смотрите в предыдущем уроке здесь.
Примеры на все свойства степени.
Упростить:
Решение.
При решении 7) примера I способом мы использовали свойства умножения и деления степеней с одинаковыми основаниями: am∙an=am+n и am:an=am-n. При решении II способом мы использовали понятие степени с отрицательным показателем: и свойство произведения степеней с одинаковыми основаниями: am∙an=am+n .
Пример 8 ) решаем так же, как решали пример 7) вторым способом.
В примере 9) представим 73как 72∙7, а степень 45как 43∙42, а затем сократим дробь на (72∙43).
В 10) примере применим формулу степени произведения: (ab)n=an∙bn, а затем сократим дробь на (26∙35).
I. Произведение n сомножителей, каждый из которых равен а называется n-й степенью числа а и обозначается аn.
Примеры. Записать произведение в виде степени.
1) mmmm; 2) aaabb; 3) 5·5·5·5·ccc; 4) ppkk+pppk-ppkkk.
Решение.
1) mmmm=m4, так как, по определению степени, произведение четырех сомножителей, каждый из которых равен m, будет четвертой степенью числа m.
2) aaabb=a3b2; 3) 5·5·5·5·ccc=54c3; 4) ppkk+pppk-ppkkk=p2k2+p3k-p2k3.
II. Действие, посредством которого находится произведение нескольких равных сомножителей, называется возведением в степень. Число, которое возводится в степень, называется основанием степени. Число, которое показывает, в какую степень возводится основание, называется показателем степени. Так, аn – степень, а – основание степени, n – показатель степени. Например:
23 — это степень. Число 2 — основание степени, показатель степени равен 3. Значение степени 23равно 8, так как 23=2·2·2=8.
Примеры. Написать следующие выражения без показателя степени.
5) 43; 6) a3b2c3; 7) a3-b3; 8 ) 2a4+3b2.
Решение.
5) 43=4·4·4; 6) a3b2c3=aaabbccc; 7) a3-b3=aaa-bbb; 8) 2a4+3b2=2aaaa+3bb.
III. а0=1 Любое число (кроме нуля) в нулевой степени равно единице. Например, 250=1.
IV. а1=а Любое число в первой степени равно самому себе.
V. am∙an=am+n При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели складывают.
Примеры. Упростить:
9) a·a3·a7; 10) b0+b2·b3; 11) c2·c0·c·c4.
Решение.
9) a·a3·a7=a1+3+7=a11; 10) b0+b2·b3=1+b2+3=1+b5;
11) c2·c0·c·c4=1·c2·c·c4=c2+1+4=c7.
VI. am:an=am— n При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя.
Примеры. Упростить:
12) a8:a3; 13) m11:m4; 14) 56:54.
12) a8:a3=a8-3=a5; 13) m11:m4=m11-4=m7; 14) 56:54=52=5·5=25.
VII. (am)n=amn При возведении степени в степень основание оставляют прежним, а показатели перемножают.
Примеры. Упростить:
15) (a3)4; 16) (c5)2.
15) (a3)4=a3·4=a12; 16) (c5)2=c5·2=c10.
Обратите внимание, что, так как от перестановки множителей произведение не меняется, то:
15) (a3)4=(a4)3; 16) (c5)2=(c2)5.
VIII. (a∙b)n=an∙bn При возведении произведения в степень возводят в эту степень каждый из множителей.
Примеры. Упростить:
17) (2a2)5; 18) 0,26·56; 19) 0,252·402.
Решение.
17) (2a2)5=25·a2·5=32a10; 18) 0,26·56=(0,2·5)6=16=1;
19) 0,252·402=(0,25·40)2=102=100.
IX. При возведении в степень дроби возводят в эту степень и числитель и знаменатель дроби.
Примеры. Упростить:
Решение.
Функцию вида y=x3 называют кубической функцией. Графиком кубической функции является кубическая парабола, проходящая через начало координат. Ветви кубической параболы y=x3 находятся в I и III четвертях.
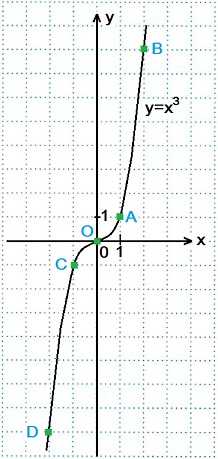Построение графика кубической функции y=x3
Составим таблицу значений функции y=x3 для х=0, х=±1, х=±2.
x | y=x3
0 | 0³=0 Точка О(0; 0)
1 | 1³=1 Точка А(1; 1)
-1 | (-1)³=-1 Точка С(-1; -1)
2 | 2³=8 Точка В(2; 8 )
-2 | (-2)³=-8 Точка D(-2; -8)
Функцию вида y=x2 называют квадратной функцией. Графиком квадратной функции является парабола с вершиной в начале координат. Ветви параболы y=x2 направлены вверх.
Построение графика функции y=x2. Составим таблицу значений функции для х=0, х=±1, х=±2, х=±3.
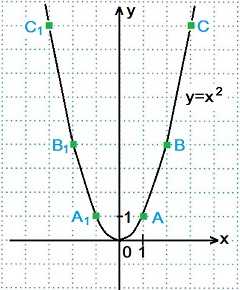х | y=x²
0 | 0²=0
1 | 1²=1 Точка А(1; 1)
-1 | (-1)²=1 Точка А1(-1; 1)
2 | 2²=4 Точка В(2; 4)
-2 | (-2)²=4 Точка В1(-2; 4)
3 | 3²=9 Точка С(3; 9)
-3 | (-3)²=9 Точка С1(-3; 9)
data-ad-client=»ca-pub-8602906481123293″
data-ad-slot=»2890988705″>
1) Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
(a+b)2 = a2+2ab+b2
a) (x + 2y)2 = x2 + 2 ·x·2y + (2y)2 = x2 + 4xy + 4y2
б) (2k + 3n)2 = (2k)2 + 2·2k·3n + (3n)2 = 4k2 + 12kn + 9n2
2) Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
(a-b)2 = a2-2ab+b2
а) (2a – c)2 = (2a)2-2·2a·c + c2 = 4a2 – 4ac + c2
б) (3a – 5b)2 = (3a)2-2·3a·5b + (5b)2 = 9a2 – 30ab + 25b2
3) Разность квадратов двух выражений равна произведению разности самих выражений на их сумму.
a2–b2 = (a–b)(a+b)
a) 9x2 – 16y2 = (3x)2 – (4y)2 = (3x – 4y)(3x + 4y)
б) (6k – 5n)( 6k + 5n) = (6k)2 – (5n)2 = 36k2 – 25n2
4) Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.
(a+b)3 = a3+3a2b+3ab2+b3
a) (m + 2n)3 = m3 + 3·m2·2n + 3·m·(2n)2 + (2n)3 = m3 + 6m2n + 12mn2 + 8n3
б) (3x + 2y)3 = (3x)3 + 3·(3x)2·2y + 3·3x·(2y)2 + (2y)3 = 27x3 + 54x2y + 36xy2 + 8y3
5) Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.
(a-b)3 = a3-3a2b+3ab2-b3
а) (2x – y)3 = (2x)3-3·(2x)2·y + 3·2x·y2 – y3 = 8x3 – 12x2y + 6xy2 – y3
б) (x – 3n)3 = x3-3·x2·3n + 3·x·(3n)2 – (3n)3 = x3 – 9x2n + 27xn2 – 27n3
6) Сумма кубов двух выражений равна произведению суммы самих выражений на неполный квадрат их разности.
a3+b3 = (a+b)(a2–ab+b2)
a) 125 + 8x3 = 53 + (2x)3 = (5 + 2x)(52 — 5·2x + (2x)2) = (5 + 2x)(25 – 10x + 4x2)
б) (1 + 3m)(1 – 3m + 9m2) = 13 + (3m)3 = 1 + 27m3
7) Разность кубов двух выражений равна произведению разности самих выражений на неполный квадрат их суммы.
a3-b3 = (a-b)(a2+ab+b2)
а) 64с3 – 8 = (4с)3 – 23 = (4с – 2)((4с)2 + 4с·2 + 22) = (4с – 2)(16с2 + 8с + 4)
б) (3a – 5b)(9a2 + 15ab + 25b2) = (3a)3 – (5b)3 = 27a3 – 125b3
Дорогие друзья! Карта сайта поможет вам выбрать нужную тему.Страница 1 из 11
www.mathematics-repetition.com
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
onlinetestpad.com