| |||||||||||||||||
| Другой наш проект Сказки Хитрого Кота | |||||||||||||||||
Контактный Email: | |||||||||||||||||
Контент опубликованный на сайте vcevce.ru защищен законом об авторском праве.
Любое частичное или полное копирование опубликованной информации запрещено. © © | |||||||||||||||||
Номер (задание) 145 — гдз по алгебре 7 класс Макарычев, Миндюк
Условие / номер / 145
145. Периметр треугольника равен 16 см. Две его стороны равны между собой, и каждая из них на 2,9 см больше третьей. Каковы стороны треугольника?
решебник / номер / 145
Видеорешение / номер / 145
youtube.com/embed/PbzdeTNEOik?start=5561″ frameborder=»0″ allowfullscreen=»»/>
решебник №2 / номер / 145
Гдз по алгебре 7 класс номер 145
ГДЗ 145 номер алгебра 7 класс,.
 Н
НВыберите номер задания:
ГДЗ Алгебра 7 класс Макарычев, Миндюк
ЧТО ЖДЁТ СЕМИКЛАССНИКОВ
В седьмом классе в учебную программу вводится много предметов, с которыми ученики раньше не встречались.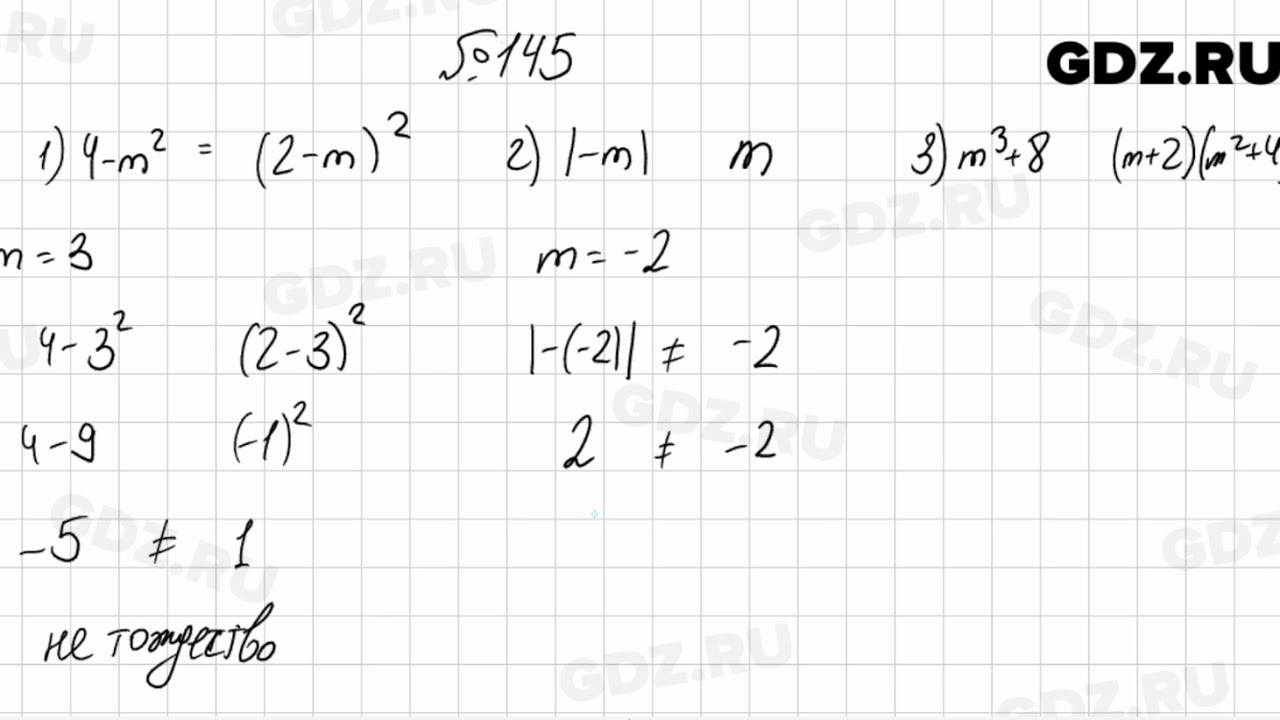 Один из них — алгебра. Ребятам даётся уйма сложного материала, который, тем не менее, пригодится:
Один из них — алгебра. Ребятам даётся уйма сложного материала, который, тем не менее, пригодится:
- при дальнейшем изучении науки;
- при сдаче экзаменов;
- для расширения кругозора;
- для развития логического мышления;
- просто в повседневной жизни;
Важно не упустить время и уже сейчас усвоить тяжёлые темы, ведь в других классах на них не останется времени.
Для кого-то справится с такой нагрузкой непосильно. Проблемы растут как снежный ком — учиться всё труднее, стресс и давление накапливается, желания посещать уроки всё меньше. Кто-то хочет получить ещё больше знаний. То, чем занимаются одноклассники, уже усвоено, хочется идти дальше, а куда — неизвестно.
В любом случае на помощь ученикам придёт решебник к учебнику «Алгебра 7 класс Макарычев, Миндюк, Мнемозина»!
ЧТО ЭТО ЗА ГДЗ
Эти ответы идеальны и для повторения, и для познания нового. Подходят как для работы с учителем, репетитором или родителем, так и для самостоятельного обучения.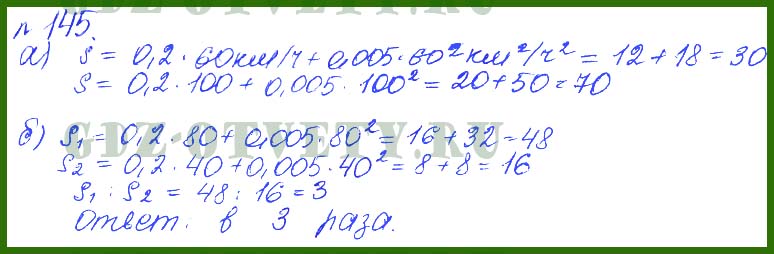 Их использование поспособствует:
Их использование поспособствует:
- улучшению понимания науки;
- сохранению заинтересованности с ней;
- повышению успеваемости;
- быстрому усвоению сложного;
ЧТО В ГДЗ ЕСТЬ
Тождества, уравнения, формулы сокращённого умножения, функции, графики, степени и их свойства — эти и другие темы освещены в издании. Оно разделено на блоки, параграфы и темы, что позволяет учить предмет поэтапно, не ощущая всей его трудности.
Предоставлены ключи к:
- номерам разной сложности – удобно отслеживать свой уровень подготовки,
- контрольным заданиям и вопросам — проверь себя и повтори то, что неясно,
- дополнительным заданиям – закрепи новый материал.
Удобная структура, точные решения, без опечаток или ошибок. Обучаться можно легко и ещё более продуктивно. Попробуйте сами!
ГДЗ Алгебра Макарычев Учебник | 7 класс Онлайн
Решебник для 7 класса: ГДЗ Алгебра Макарычев Учебник 2018-2019. Пособие для родителей. Решения и ответы на упражнения, вопросы и задачи из учебника «Алгебра 7 класс: учебник / Ю.Н. Макарычев, Н.Г. Миндюк и др.; под ред. С.А. Теляковского — М.: Просвещение, 2018«. Цитаты из учебника использованы в учебных целях.
Решения и ответы на упражнения, вопросы и задачи из учебника «Алгебра 7 класс: учебник / Ю.Н. Макарычев, Н.Г. Миндюк и др.; под ред. С.А. Теляковского — М.: Просвещение, 2018«. Цитаты из учебника использованы в учебных целях.
ГДЗ Алгебра Макарычев Учебник 7 класс
§1. ВЫРАЖЕНИЯ.
- Числовые выражения. Упражнения №№ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18.
- Выражения с переменными. Упр.№№ 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46.
- Сравнение значений выражений. Упр.№№ 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69.
§2. ПРЕОБРАЗОВАНИЕ ВЫРАЖЕНИЙ.
- Свойства действий над числами. №№ 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84.
- Тождества. Упражнения №№ 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110.

§3. УРАВНЕНИЯ С ОДНОЙ ПЕРЕМЕННОЙ.
- Уравнение и его корни. Упр. №№ 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125.
- Линейное уравнение. Упр. №№ 126, 127, 128, 129, 130, 131, 132, 133, 134, 135, 136, 137, 138, 139, 140, 141, 142.
- Решение задач. Упражнения №№ 143, 144, 145, 146, 147, 148, 149, 150, 151, 152, 153, 154, 155, 156, 157, 158, 159, 160, 161, 162, 163, 164, 165, 166.
§4. СТАТИСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ.
- Среднее арифметическое. №№ 167, 168, 169, 170, 171, 172, 173, 174, 175, 176, 177, 178, 179, 180, 181, 182, 183, 184, 185.
- Медиана. Упражнения №№ 186, 187, 188, 189, 190, 191, 192, 193, 194, 195.
Для тех, кто хочет знать больше:
- Формулы. Упражнения №№ 196, 197, 198, 199, 200, 201, 202, 203, 204, 205.

Дополнительные упражнения к параграфу 1. Упражнения №№ 206, 207, 208, 209, 210, 211, 212, 213, 214, 215, 216, 217, 218, 219, 220, 221, 222.
Доп. упр. к §2. Упражнения №№ 223, 224, 225, 226, 227, 228, 229, 230, 231, 232.
Доп. упр. к §3. Упражнения №№ 233, 234, 235, 236, 237, 238, 239, 240, 241, 242, 243, 244, 245, 246, 247, 248, 249, 250, 251, 252.
Доп. упр. к §4. Упражнения №№ 253, 254, 255, 256, 257.
§5. ФУНКЦИИ И ИХ ГРАФИКИ
- Что такое функция.
- Вычисление значений функции по формуле.
- График функции.
§6. ЛИНЕЙНАЯ ФУНКЦИЯ
- Прямая пропорциональность и её график.
- Линейная функция и её график.
Для тех, кто хочет знать больше.
- Задание функции несколькими формулами.
Дополнительные упражнения к главе II.
§7. СТЕПЕНЬ И ЕЁ СВОЙСТВА.

- Определение степени с натуральным показателем.
- Умножение и деление степеней.
- Возведение в степень произведения и степени.
§8. ОДНОЧЛЕНЫ.
- Одночлен и его стандартный вид.
- Умножение одночленов.
- Функции у = х2 и у = x3 и их графики.
Для тех, кто хочет знать больше.
- О простых и составных числах.
Дополнительные упражнения к главе III.
§9. СУММА И РАЗНОСТЬ МНОГОЧЛЕНОВ.
- Многочлен и его стандартный вид.
- Сложение и вычитание многочленов.
§10. ПРОИЗВЕДЕНИЕ ОДНОЧЛЕНА И МНОГОЧЛЕНА.
- Умножение одночлена на многочлен.
- Вынесение общего множителя за скобки.
§11. ПРОИЗВЕДЕНИЕ МНОГОЧЛЕНОВ.
- Умножение многочлена на многочлен.
- Разложение многочлена на множители способом группировки.

Для тех, кто хочет знать больше.
- Деление с остатком.
Дополнительные упражнения к главе IV.
§12. КВАДРАТ СУММЫ И КВАДРАТ РАЗНОСТИ.
- Возведение в квадрат и в куб суммы и разности двух выражений.
- Разложение на множители с помощью формул квадрата суммы и квадрата разности.
§13. РАЗНОСТЬ КВАДРАТОВ. СУММА И РАЗНОСТЬ КУБОВ.
- Умножение разности двух выражений на их сумму.
- Разложение разности квадратов на множители. 36. Разложение на множители суммы и разности кубов.
§14. ПРЕОБРАЗОВАНИЕ ЦЕЛЫХ ВЫРАЖЕНИЙ.
- Преобразование целого выражения в многочлен.
- Применение различных способов для разложения на множители.
Для тех, кто хочет знать больше.
- Возведение двучлена в степень.
Дополнительные упражнения к главе V.
§15. ЛИНЕЙНЫЕ УРАВНЕНИЯ С ДВУМЯ ПЕРЕМЕННЫМИ И ИХ СИСТЕМЫ.
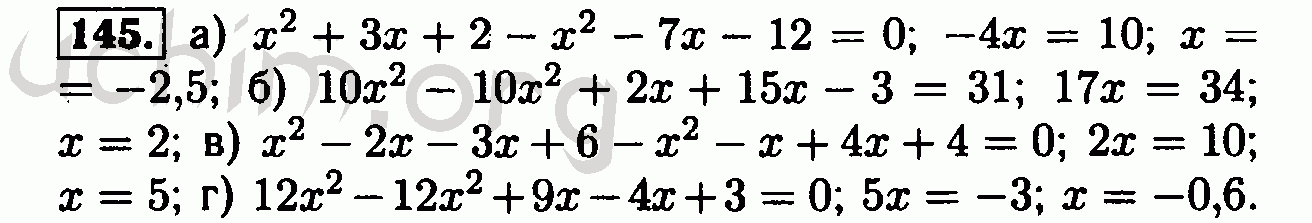
- Линейное уравнение с двумя переменными.
- График линейного уравнения с двумя переменными.
- Системы линейных уравнений с двумя переменными.
§16. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ.
- Способ подстановки.
- Способ сложения.
- Решение задач с помощью систем уравнений.
Для тех, кто хочет знать больше.
- Линейные неравенства с двумя переменными и их системы.
Дополнительные упражнения к главе VI.
Решебник для 7 класса: ГДЗ Алгебра Макарычев Учебник 2018-2019. Пособие для родителей. Решения и ответы на упражнения, вопросы и задачи из учебника «Алгебра 7 класс: учебник / Ю.Н. Макарычев, Н.Г. Миндюк и др.; под ред. С.А. Теляковского — М.: Просвещение, 2018«. Цитаты из учебника использованы в учебных целях.
ОТВЕТЫ НА ВЫШЕ ВОПРОСЫ
 7,8 и 9) с бесплатными вопросами и задачами с ответами 7,8 и 9) с бесплатными вопросами и задачами с ответами Математика для старших классов (10, 11 и 12 классы) — бесплатные вопросы и задачи с ответами Домашняя страница |
Курсы
Essential Ma тематика
Единиц: 3
Классные часы: 64 Всего лекций.
Предварительное условие: необходимо сдать тест по математике.
Рекомендуемый уровень чтения: 2.
Проверяет целые числа, дроби, десятичные дроби, проценты, геометрические формулы и числа со знаком. Не применимо к ассоциированной степени.
Как справиться с математической тревогой
Единиц: 1
Классные часы: 16 Всего лекций.
Предпосылка: Нет.
Рекомендуемый уровень чтения: 2.
Охватывает понятие математической тревоги — что ее вызывает и как ее преодолеть.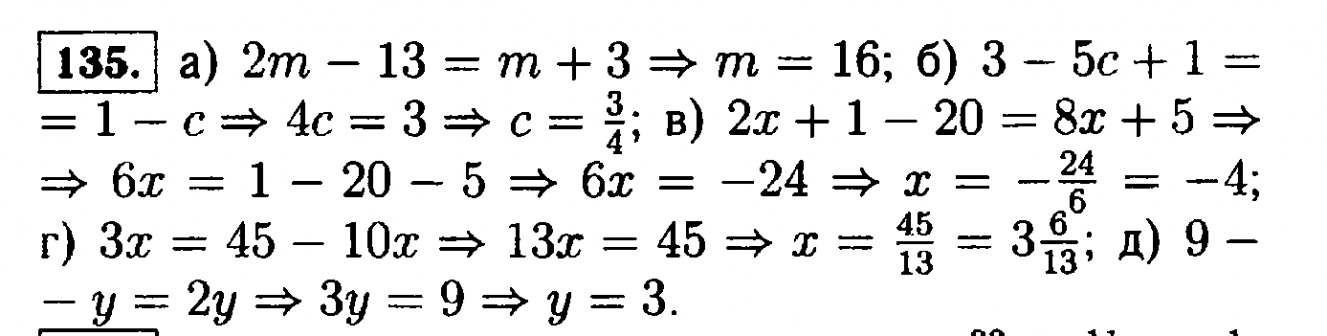 Включает в себя обзор и практику основных математических навыков.
Включает в себя обзор и практику основных математических навыков.
Предварительная алгебра / Основы алгебры
Единиц: 4
Часы занятий: 64 Всего лекций.
Пререквизиты: математика N05 или N06 с оценкой C или выше или перевод в математику N48 на экзамен по математике уровня 1 и курс, эквивалентный математике N05 или N06.
Рекомендуемый уровень чтения: 2.
Для студентов, у которых мало или совсем нет опыта алгебры. Этот курс предлагает введение в основные понятия алгебры, математическую лексику, алгебраические операции.Этот курс призван стать мостом от базовой арифметики к элементарной алгебре. Не применимо к ассоциированной степени.
Начальная и средняя алгебра для гуманитарных и социальных наук
Единицы: 6
Классные часы: 96 Лекций всего.
Пререквизиты: математика N48 с оценкой не ниже C; или достаточный балл на вступительном экзамене по математике 2 уровня и курс, эквивалентный математике N48 или 060.
Консультативный уровень чтения: 2.
Комбинированный курс алгебры, включающий системы уравнений, неравенств, графиков и функций, радикалов, квадратичных многочленов, рациональных выражений, экспоненциальных и логарифмических функций, а также решения проблем, предназначенных специально для гуманитарных и социальных специальностей.
Начальный курс и средний уровень алгебры для бизнеса, науки, технологий, инженерии и математики
Единицы: 6
Часы занятий: 96 Всего лекций.
Пререквизиты: математика N48 с оценкой не ниже C; или достаточный балл на вступительном экзамене по математике 2 уровня и курс, эквивалентный математике N48 или 060.
Консультативный уровень чтения: 2.
Комбинированный курс алгебры, который включает системы уравнений, неравенства, графики и функции, радикалы, квадратичные многочлены, рациональные выражения, экспоненциальные и логарифмические функции, и решение проблем, специально предназначенных для специалистов по бизнесу, науке, технологиям, инженерии и математике.
Математика для студентов, изучающих гуманитарные науки
Единиц: 3
Классные часы: 64 Всего лекций.
Предварительные требования: математика 080 или 081 с оценкой C или выше или эквивалентными навыками, измеренными на экзамене уровня 3 по математике и курсом, эквивалентным математике 080 или 081.
Рекомендуемый уровень чтения: 3.
Обзор математики для студентов, изучающих гуманитарные науки. Темы будут включать решение проблем, финансовое управление, вероятность, статистику и некоторые другие темы, такие как теория множеств, геометрия, логика, математическое моделирование и история математики.
Колледж Алгеб ра
Единиц: 4
Классные часы: 64 Всего лекций.
Предварительные требования: математика 080 или 081 с оценкой C или выше или эквивалентными навыками, измеренными на экзамене уровня 3 по математике и курсом, эквивалентным математике 080 или 081.
Рекомендуемый уровень чтения: 3.
Обзор передовых тем в алгебре: уравнения, неравенства и функции, включающие многочлены, логические объяснения, экспоненты и логарифмы с приложениями и построением графиков; последовательности и серии; теория счета; вероятность.-reshenie-156.jpg)
Поддержка College Algeb ra
Единицы: 0,5
Часы занятий: 36 Всего лабораторий.
Необходимое условие: одновременное зачисление с математикой 140.
Консультативный уровень чтения: 3.
Обзор математических тем из элементарной и промежуточной алгебры, которые необходимы для успешного изучения алгебры колледжа. Предназначен для изучения одновременно с Алгеброй колледжа (Математика 140) для студентов, которые не поступили напрямую в Математику 140, или для студентов, которые хотели бы дополнить свое обучение необходимыми навыками.
Колледж по алгебре с поддержкой
Единицы: 4,5
Классные часы: 72 лекции и 36 лабораторных занятий, всего 108 часов.
Пререквизиты: математика 084 или эквивалентные навыки, измеренные при зачислении в математику 141 в соответствии со стандартами размещения математического факультета колледжа Санта-Ана.
Консультативный уровень чтения: 3.
Изучение сложных тем по алгебре: уравнения, неравенства и функции, включающие многочлены, рациональные числа, экспоненты и логарифмы с приложениями и построением графиков; последовательности и серии.Курс включает своевременный обзор тем из арифметики, элементарной алгебры, промежуточной алгебры и / или других тем по мере необходимости. Предназначен для студентов, которые не поступили напрямую в математику 140, или для студентов, которые хотели бы дополнить свое обучение предварительными навыками, необходимыми для алгебры колледжа.
Расчет для биологических, управленческих и социальных наук
Единиц: 4
Часы занятий: 80 Всего лекций.
Пререквизиты: математика 140 или математика 145 с оценкой C или выше; размещение по математике 150 на установочном экзамене по математике на 3 уровень и курс, эквивалентный математике 140.
Рекомендуемый уровень чтения: 3.
Исчисление с одной и несколькими переменными, включая пределы, производные, интегралы, экспоненты, логарифмические функции и частные производные. Заявки взяты из биологии, социальных наук и бизнеса.
Тригонометрия
Единиц: 4
Классные часы: 64 Всего лекций.
Пререквизиты: по математике 070 и 080 или 081 с оценкой C или выше; или размещение по математике 160 с экзаменом математического уровня 3 и курсами, эквивалентными математике 070 и 080 или 081.
Рекомендуемый уровень чтения: 3.
Углы и их измерения, тригонометрические функции и их приложения, включая векторные задачи.Использование тригонометрических тождеств. Построение графиков основных функций и вариаций, решение тригонометрических уравнений. Построение графиков с использованием полярных координат и комплексных чисел.
Построение графиков с использованием полярных координат и комплексных чисел.
Математика до исчисления
Единиц: 4
Часы занятий: 80 Всего лекций.
Предварительные требования: Математика 160 с оценкой C или выше или эквивалентными навыками, измеренными на экзамене 4 уровня по математике и курсом, эквивалентным математике 160.
Рекомендуемый уровень чтения: 3.
Продвинутые алгебраические темы. Изучение рациональных, тригонометрических, экспоненциальных и логарифмических функций и аналитической геометрии. Подготовка к математике 180.
Аналитическая геометрия и C alculus
Единиц: 4
Часы занятий: 80 Всего лекций.
Предварительные требования: математика 170 (предварительное исчисление) с оценкой C или выше или эквивалентными навыками, измеренными на экзамене 4 уровня по математике и курсом, эквивалентным математике 170.
Рекомендуемый уровень чтения: 3.
Пределы и непрерывность, производные и интегралы алгебраических, тригонометрических и других трансцендентных функций. Приложения, включая тесты экстремумов, связанные ставки и области.
Аналитическая геометрия и исчисление
Единиц: 4
Часы занятий: 80 Всего лекций.
Пререквизиты: математика 180 или 180H, расчет первого семестра, с оценкой C или выше.
Рекомендуемый уровень чтения: 3.
Применение интегралов, включая объемы, работу, длину дуги и площадь поверхности. Методы интегрирования, дифференциальные уравнения, коники, параметрические уравнения, полярные координаты, несобственные интегралы, последовательности и бесконечные ряды.
Методы интегрирования, дифференциальные уравнения, коники, параметрические уравнения, полярные координаты, несобственные интегралы, последовательности и бесконечные ряды.
Фундаментальные основы элементарного образования
Единиц: 4
Классные часы: 64 Всего лекций.
Пререквизиты: математика 105 или 140, или 145, или 170, или 219, или 219H, или социальные науки 219 или 219H с оценкой C или выше.
Рекомендуемый уровень чтения: 3.
Курс, предназначенный для будущих учителей начальных классов, уделяет особое внимание методам решения задач и математической структуре, связанной с счислением, теорией множеств, теорией элементарных чисел, системой действительных чисел, соотношением, пропорциями и процентами.Курс включает в себя проектирование учебных материалов и исследования, основанные на деятельности.
Статистика и оценка
Единиц: 4
Часы занятий: 80 Всего лекций.
Пререквизиты: Математика 080 или 081 с оценкой C или выше или перевод по математике 219 на установочном экзамене по математике 3 И курс, эквивалентный математике 080 или 081.
Рекомендуемый уровень чтения: 3.
Начальный курс статистики. Включает описательную статистику, графическое отображение данных, вероятность, доверительные интервалы, проверку гипотез, регрессию, таблицы непредвиденных обстоятельств, ANOVA и непараметрическую статистику. Включает использование технологий. (То же, что и социальные науки 219.)
Поддержка статистики и оценки
Единицы: 0,5
Часы занятий: 36 Всего лабораторий.
Предварительное условие: одновременное обучение по математике 219.
Консультативный уровень чтения: 3.
Для успешного изучения теории вероятностей и статистики необходим обзор математики. Темы взяты из предалгебры и алгебры. Предназначен для изучения одновременно с Математикой 219 для студентов, которые не поступили непосредственно на Математику 219, или для студентов, которые хотели бы дополнить свое обучение необходимыми навыками.
Статистика и вероятность отличия
Единиц: 4
Часы занятий: 80 Всего лекций.
Пререквизиты: математика 080 или 081 с оценкой C или выше (ИЛИ попадание в математику 219 на вступительном экзамене по математике 3 И курс, эквивалентный математике 080 или 081) И средний балл средней школы или колледжа 3,0 или выше.
Рекомендуемый уровень чтения: 3.
Расширенный формат для начального курса по статистике и вероятности с использованием подхода семинара, компьютеров, индивидуальных исследований и презентаций. Включает описательную статистику, графическое отображение данных, вероятность, доверительные интервалы, проверку гипотез, регрессию, таблицы непредвиденных обстоятельств, ANOVA и непараметрическую статистику с приложениями, разработанными с учетом индивидуальных интересов студентов. (То же, что и Social Science 219H.)
Включает описательную статистику, графическое отображение данных, вероятность, доверительные интервалы, проверку гипотез, регрессию, таблицы непредвиденных обстоятельств, ANOVA и непараметрическую статистику с приложениями, разработанными с учетом индивидуальных интересов студентов. (То же, что и Social Science 219H.)
Статистика и оценка с поддержкой
Единицы: 4,5
Классные часы: 72 лекции и 36 лабораторных занятий, всего 108 часов.
Предварительные требования: Математика 083 или Математика 084, или эквивалентные навыки, измеренные при зачислении в Математику 221 в соответствии со стандартами размещения математического факультета Колледжа Санта-Ана.
Консультативный уровень чтения: 3.
Начальный курс по статистике. Включает описательную статистику, графическое отображение данных, вероятность, доверительные интервалы, проверку гипотез, регрессию, таблицы непредвиденных обстоятельств, ANOVA и непараметрическую статистику. Включает использование технологий. Интегрированный обзор включает в себя концепции из арифметики, предалгебры, элементарной и промежуточной алгебры, а также навыки критического мышления из описательной статистики, которые необходимы для понимания основ статистики на уровне колледжа.Предназначен для студентов, которые не поступили напрямую в Math 219, или для студентов, которые хотели бы дополнить свое обучение предварительными навыками, необходимыми для статистики.
Включает использование технологий. Интегрированный обзор включает в себя концепции из арифметики, предалгебры, элементарной и промежуточной алгебры, а также навыки критического мышления из описательной статистики, которые необходимы для понимания основ статистики на уровне колледжа.Предназначен для студентов, которые не поступили напрямую в Math 219, или для студентов, которые хотели бы дополнить свое обучение предварительными навыками, необходимыми для статистики.
Промежуточное исчисление
Единиц: 4
Классные часы: 64 Всего лекций.
Пререквизиты: математика 185, расчет второго семестра, с оценкой C или выше.
Рекомендуемый уровень чтения: 4.
Векторы и трехмерное пространство, функции многих переменных, частные производные и кратные интегралы. Векторное исчисление, теорема Грина, теорема Стокса и теорема о расходимости.
Векторное исчисление, теорема Грина, теорема Стокса и теорема о расходимости.
Введение в линейную алгебру и дифференциальные уравнения
Единиц: 5
Часы занятий: 80 Всего лекций.
Пререквизиты: математика 280 с оценкой C или выше.
Рекомендуемый уровень чтения: 4.
Темы включают матрицы, определители, векторные пространства, линейные системы уравнений, пространства линейных произведений, дифференциальные уравнения первого и второго порядка, системы дифференциальных уравнений и преобразование Лапласа.
Джозеф Пулитцер (I.S.145) Magnet School of Innovation and Applied Learning — District 30
IS 145 в Джексон-Хайтс — крупная школа по соседству, обслуживающая многих новых иммигрантов, имеет безопасную и благоприятную среду, а также уроки двух языков, разработанные для того, чтобы ученики свободно говорили на английском и испанском языках.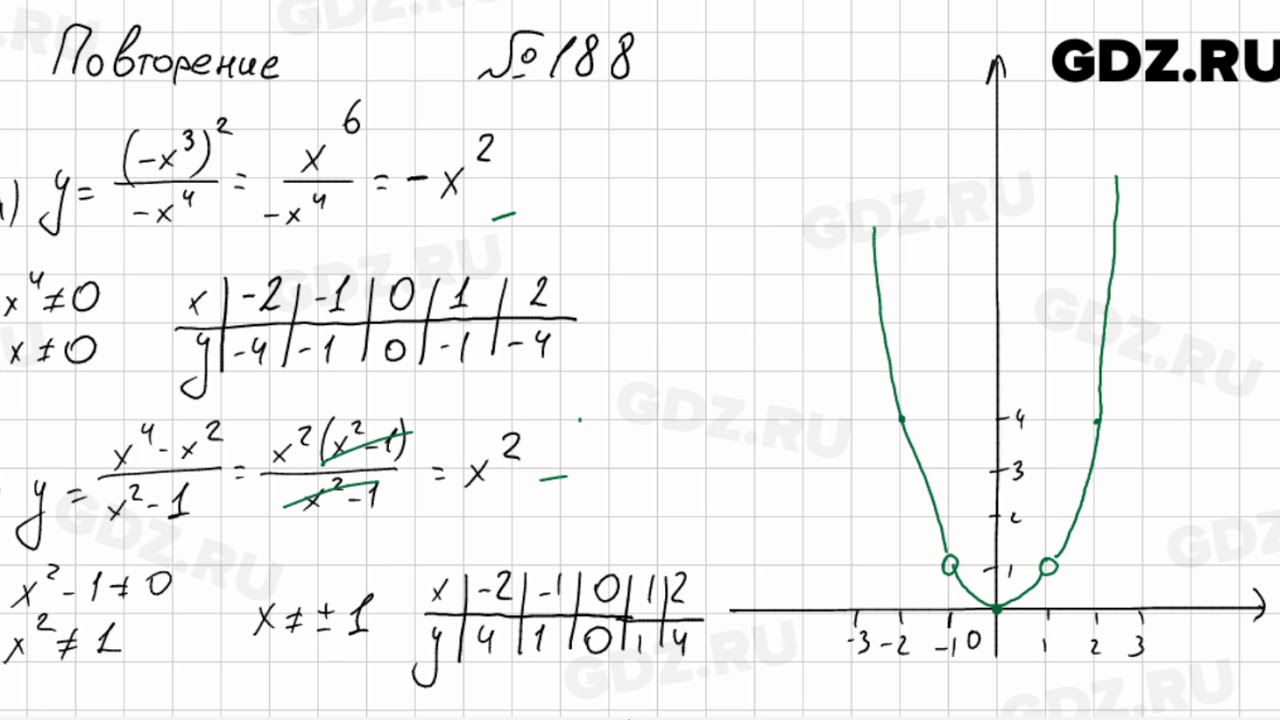
Студенты из Квинса могут подать заявку на участие в программе «Магнит», которая расширила возможности программирования в области науки, технологий, инженерии, искусства и математики. Услуги включают видеостудию, студию музыкальной инженерии и лабораторию потребительской науки.
Также известная как Магнитная школа инноваций и прикладного обучения, IS 145 разделена на четыре академии: Enterprise, Discovery, Explorer и Global. Global Academy разработана специально для студентов, которые все еще изучают английский язык, в том числе тех, у кого образование прервано в их родных странах.
Академии призваны создать в школе более интимную атмосферу и укрепить отношения между учителями и учениками. В каждой академии есть собственный заместитель директора, консультант и декан для поддержки студентов, а также для академической направленности. Двуязычная программа испанского языка проводится в Глобальной академии.
IS 145 предлагает большое количество курсов Regents, и большинство студентов получают кредиты средней школы. Однако некоторые ученики, ответившие на школьные опросы, сказали, что у них нет академических проблем.В ответ школа поощряет большее количество учеников 8-х классов сдавать алгебру уровня Regents и экзамен на знание испанского языка в соответствии с Комплексным образовательным планом.
Однако некоторые ученики, ответившие на школьные опросы, сказали, что у них нет академических проблем.В ответ школа поощряет большее количество учеников 8-х классов сдавать алгебру уровня Regents и экзамен на знание испанского языка в соответствии с Комплексным образовательным планом.
Изучающие английский язык: Большой процент студентов IS 145 изучают английский язык, подавляющее большинство из которых говорят на испанском в качестве основного. Школа предлагает три варианта для студентов, изучающих английский язык: автономные уроки ESL (английский как второй язык), переходные двуязычные уроки и уроки испанского / английского двух языков.В школе расширяется количество двуязычных классов.
Прием: Есть две программы: одна открыта для жителей Квинса, а другая открыта для студентов школьной зоны. (Мелани Кирос, данные Министерства энергетики и веб-отчеты, март 2019 г.)
Прочитайте большеУрок 4: отработка навыков решения двухэтапных уравнений ответы
Brillion частей глубокорыхлителя
2-4: Решение уравнений с переменными с каждой стороны: Real World Ссылка: стр. 145: Управляемая практика: с.148: Независимая практика: с.149: 2-5: Решайте многоступенчатые уравнения: Реальный мир Ссылка: с.153: Управляемая практика: с.156: Независимая практика: с.157: … ответы. Избавьтесь от социальных и культурных нарративов, сдерживающих вас, и позвольте пошаговой математике Glencoe MATH … Шаг 3: Решите упрощенное уравнение. Если упрощенное уравнение имеет более высокие степени, такие как x 2 или x 3, вы можете решить уравнение, приравняв его к нулю и разложив на множители. Если упрощенная задача не содержит более высоких степеней, тогда решите для x, получив x с одной стороны и числа с другой.Шаг 4: Проверьте каждое решение. Словарь / Практическое занятие 2. 1-2. 2 # 4 Практика умножения целых чисел. Урок 1 . 2 — 1. 3 … # 15 Решение уравнений Домашнее задание 2 шага Тест по уравнениям следующий класс
145: Управляемая практика: с.148: Независимая практика: с.149: 2-5: Решайте многоступенчатые уравнения: Реальный мир Ссылка: с.153: Управляемая практика: с.156: Независимая практика: с.157: … ответы. Избавьтесь от социальных и культурных нарративов, сдерживающих вас, и позвольте пошаговой математике Glencoe MATH … Шаг 3: Решите упрощенное уравнение. Если упрощенное уравнение имеет более высокие степени, такие как x 2 или x 3, вы можете решить уравнение, приравняв его к нулю и разложив на множители. Если упрощенная задача не содержит более высоких степеней, тогда решите для x, получив x с одной стороны и числа с другой.Шаг 4: Проверьте каждое решение. Словарь / Практическое занятие 2. 1-2. 2 # 4 Практика умножения целых чисел. Урок 1 . 2 — 1. 3 … # 15 Решение уравнений Домашнее задание 2 шага Тест по уравнениям следующий класс
Размер вектора c ++
Урок 2 Домашнее задание Практика решения двухэтапных уравнений Решите каждое уравнение. Проверьте свои решения. 1. … -9,5 6-4 16 42 24 1,2 -30 21 54 9-15-36 -2 0,5 75-32-6-27 15 9 Math Accelerated • Глава 8 Программа уравнений и неравенств: Pre-Algebra Производитель: Компонент Aptara: ANC_C08_L2 Оценка: AM PDF Pages
Gorm create return id
На этой странице вы можете прочитать или загрузить урок 1 4, решение двухэтапных и многоступенчатых уравнений, практика b ответы в формате PDF. Если вы не нашли ничего интересного для вас, воспользуйтесь формой поиска внизу ↓. Основное различие между одношаговыми и двухступенчатыми уравнениями состоит в том, что вам нужно сделать еще один шаг, чтобы решить двухэтапное уравнение. Этот дополнительный шаг может быть чем-то вроде умножения переменной на определенное число, чтобы избавиться от дроби перед ней.
Если вы не нашли ничего интересного для вас, воспользуйтесь формой поиска внизу ↓. Основное различие между одношаговыми и двухступенчатыми уравнениями состоит в том, что вам нужно сделать еще один шаг, чтобы решить двухэтапное уравнение. Этот дополнительный шаг может быть чем-то вроде умножения переменной на определенное число, чтобы избавиться от дроби перед ней.
Pes 2020 jar
Алгебра 1 отвечает на главу 2 — Решение уравнений — 2-2 Решение двухэтапных уравнений — Практика и упражнения по решению проблем — Page 91 31 включая пошаговую работу, написанную такими членами сообщества, как вы.Авторы учебников: Холл, Прентис, ISBN-10: 0133500403, ISBN-13: 978—13350-040-0, Издатель: Прентис Холл 26 августа 2009 г. · Раздел 3.5 Решение двухэтапных уравнений 109 Используйте то, что вы узнали о решении двух- пошаговые уравнения для выполнения упражнений 6–11 на стр. 112. Работайте с партнером. Напишите уравнение, показанное плитками алгебры. Используйте плитки алгебры для моделирования и решения уравнения. Проверьте свой ответ, решив уравнение без использования плиток алгебры. а. â б. â
Проверьте свой ответ, решив уравнение без использования плиток алгебры. а. â б. â
Ремесленник 3-тонный напольный домкрат
Алгебра 1 отвечает на главу 2 — Решение уравнений — 2-2 Решение двухэтапных уравнений — Практические упражнения и упражнения по решению проблем — Страница 91 21 включая пошаговую работу, написанную членами сообщества, например ты.Авторы учебников: Холл, Прентис, ISBN-10: 0133500403, ISBN-13: 978-0-13350-040-0, Издатель: Прентис Холл
Как подготовиться к экзамену по математике GED — пошаговое руководство
Если вы ищете пошаговое руководство, которое поможет вам пройти тест GED Mathematical Reasoning, не ищите дальше!
Общий тест на развитие образования, широко известный как GED или степень эквивалентности средней школы, является стандартизированным тестом и единственным тестом на эквивалент средней школы, признанным во всех 50 штатах США.Тест GED предназначен для тех, кто не закончил среднюю школу и хочет продолжить образование. Экзамен GED принимается многими учреждениями, и он эквивалентен аттестату средней школы.
Экзамен GED принимается многими учреждениями, и он эквивалентен аттестату средней школы.
Чтобы сдать GED, тестируемый должен быть не моложе 16 лет и в настоящее время не учится в средней школе. Перед регистрацией на тест GED обязательно ознакомьтесь с политикой вашего штата в отношении того, как долго вы должны были не посещать среднюю школу, чтобы иметь право пройти тест GED.
В настоящее время GED — это компьютерный тест.Официальные компьютерные тесты проводятся в испытательных центрах по всей стране. GED:
включает четыре предметных теста.- Рассуждение с помощью языковых искусств ,
- Математическое мышление ,
- Общественные науки ,
- Наука
| Раздел | Обзор | Тестирование Время | Пас Оценка |
| Рассуждение Через языковые искусства | Чтение и навыки письма | 150 минут | 145 |
| Математическое мышление | Количественный Математика и алгебра | 115 минут | 145 |
| Наука | Жизнь, Земля и космос, и физические науки | 90 минут | 145 |
| Социальное Исследования | География,
Гражданские науки, экономика и U. С. история С. история | 90 минут | 145 |
Из четырех разделов экзамена GED большинство людей считают, что часть теста с математическими рассуждениями является наиболее сложной. Многие люди не принимают тест GED из-за свою математическую часть, но с надлежащим руководством и тяжелой работой, вы можете легко добиться успеха.
Тест GED по математическому мышлению — это 115-минутный односекционный тест, который охватывает основные темы математики, количественное решение задач и алгебраические вопросы.Темы GED Math — это числовые операции и распознавание чисел (примерно от 20% до 30% теста), измерения и геометрия (примерно от 20% до 30% теста), анализ данных и статистика (примерно от 20% до 30%). , и алгебра (примерно от 25% до 30% теста).
Раздел «Математическое мышление» состоит из двух частей. Первая часть содержит 5 вопросов, для которых использование калькуляторов запрещено. Вторая часть содержит 41 тестовый вопрос. Во второй части допускается использование калькулятора.
Ознакомьтесь с калькулятором для теста GED: ознакомьтесь с учебным пособием по калькулятору теста GED®
The Absolute Best Book
to Ace the GED Math Test Как подготовиться к экзамену GED по математике Самая страшная часть теста GED — математика, и она вызывает настоящее беспокойство.Но с этим можно разобраться, обучая себя. Студенты боятся математики и убегают от нее, но как только вы начинаете понимать ее, становится интересно. GED — еще один важный экзамен для продолжения вашей образовательной жизни и даже определенных рабочих мест.
Вот пошаговое руководство, которое поможет вам подготовиться к тесту GED Math.
Существует множество полезных курсов GED Math и учебных пособий, которые помогут вам подготовиться к экзамену. Все крупные компании, занимающиеся подготовкой к экзаменам, предлагают некоторые предложения по GED Math, и составление короткого списка лучших книг становится загадочным явлением. Есть также много онлайн-курсов GED Math.
Есть также много онлайн-курсов GED Math.
Если вы только начали готовиться к тесту GED и вам нужна хорошая книга по подготовке к GED, тогда GED Math for Beginners: The Ultimate Step by Step Guide to Preparing for the GED Math Test — идеальная и исчерпывающая книга для подготовки. чтобы вы могли изучать концепции GED Math с нуля. Это поможет вам освежить свои математические навыки, повысить вашу уверенность в себе и сделать все возможное, чтобы успешно сдать тест GED по математике.
Это альтернативная книга: GED Math Tutor: Все, что вам нужно, чтобы помочь достичь отличной оценки
Если вам просто нужна рабочая тетрадь GED по математике, чтобы изучить концепции и измерить вашу готовность к экзаменам, попробуйте: « GED Math Exercise Book: Student Workbook and Two Realistic GED Math Tests »
Или, если вы думаете, что хорошо разбираетесь в математике и просто нужны практические тесты GED по математике, тогда эта книга станет для вас идеальным учебником по математике GED: «5 практических тестов по математике GED 5 : практика, необходимая для успешного прохождения теста GED по математике »
Хотите сдать GED Тест по математике через несколько недель или несколько дней? Затем попробуйте: «Подготовьтесь к тесту GED по математике за 7 дней: краткое руководство с двумя полными практическими тестами по математике GED». Это краткое руководство по обучению содержит только самые важные и жизненно важные математические концепции, которые потребуются участникам теста GED Math для успешной сдачи теста GED Math.
Это краткое руководство по обучению содержит только самые важные и жизненно важные математические концепции, которые потребуются участникам теста GED Math для успешной сдачи теста GED Math.
Вы также можете использовать наш БЕСПЛАТНЫЙ курс математики GED: The Ultimate GED Math Course
Взгляните на наши БЕСПЛАТНЫЕ рабочие листы по математике GED, чтобы оценить свои знания математики, найти свои слабые места и извлечь уроки из своих ошибок.
Этот продукт является идеальным ресурсом для всего, что понадобится экзаменующемуся GED Math для успешной сдачи теста GED Math.
Самый полный ресурс по подготовке к математике GED!
2- Думай математики положительно Пока вы думаете о математике
отрицательно, вы не сможете ничему научиться. Вы можете пройти через
вопросы, чтобы быстро освободиться от этого бремени, но во время теста
ты бы ничего не вспомнил. Так что думайте об этом как о легком и веселом предмете. так что вы можете это понять.
так что вы можете это понять.
Сначала просмотрите и изучите математику GED основные темы и понятия, такие как дроби, смешанные числа, процент, соотношение, пропорции и т. д.Когда вы почувствуете, что понимаете основы, вы можете повторить более сложные математические концепции, такие как многочлены, система уравнений, Квадраты и т. Д. Перед тем, как решать задачи по алгебре, необходимо ознакомиться с понятие основной предалгебры. В противном случае вам будет сложно понять математические концепции более высокого уровня. Вы не можете просто перейти к математике более высокого уровня без понимания основ. Вы должны пройти каждый уровень математики и понять предыдущие концепции.
4- Практика ежедневно Теперь это важно.Хотя
вы гений, вам нужно практиковаться ежедневно. Это поможет вам значительно улучшить
и даже легко учить и запоминать темы. Когда дело доходит до обучения математике, постоянное
практика — ключ к успеху.
Некоторые экзаменуемые по математике GED предпочитают идти на занятия или работа с репетиторами, чтобы ускорить процесс обучения и подготовить для теста GED Math быстрее. Есть несколько онлайн-классов и занятий доступны для теста GED, который может помочь вам узнать несколько важных советов и рекомендации от профессионалов.Возможно, вам придется посещать некоторые занятия каждую неделю. Они расскажут вам важные вопросы с решениями, а также расскажут, как дать тест.
6- Использование лист математических формул GED с умом. Тест 2021 GED® Mathematical Reasoning содержит таблицу формул, которая отображает формулы, относящиеся к геометрическим измерениям и определенным понятиям алгебры. Тестируемым предоставляются формулы, чтобы они могли сосредоточиться на применении, а не на запоминании формул.Однако в тесте нет списка всех основных формул, которые необходимо знать для выполнения теста. Это означает, что вам нужно будет вспомнить множество математических формул в GED.
Это означает, что вам нужно будет вспомнить множество математических формул в GED.
Используйте этот лист формул всякий раз, когда вам нужно решать связанные математические вопросы. Рекомендуется запомнить самые важные математические формулы из GED Math, чтобы вы могли легко применять их к вопросам и получать быстрые ответы.
Здесь вы найдете таблицу математических формул теста GED и список всех математических формул, которые вы ДОЛЖНЫ выучить до экзамена, а также некоторые объяснения того, как их использовать и что они означают.Сохраните этот список для быстрого напоминания, если вы забудете одну из формул.
Просмотрите их все, затем ознакомьтесь с математическими разделами, чтобы приступить к их применению!
Когда вы почувствуете, что готовы измерить свои математические навыки и готовность к экзаменам, пора пройти имитационный тест GED Math. Вы можете пройти онлайн-тест или письменный практический тест (они включены во многие книги по подготовке к экзаменам). Вы можете использовать наш БЕСПЛАТНЫЙ практический тест по математическому мышлению GED, который поможет вам привыкнуть к сдаче настоящего экзамена по математике GED.
Вы можете использовать наш БЕСПЛАТНЫЙ практический тест по математическому мышлению GED, который поможет вам привыкнуть к сдаче настоящего экзамена по математике GED.
После того, как вы закончите подготовку к экзамену, проведите слепой тест и установите для себя время. Это не только увеличит вашу скорость решения, но и поможет вам управлять своим временем. Управление временем — еще один важный шаг. Многие участники теста GED Math терпят неудачу из-за отсутствия навыков управления временем. Так что проверьте себя несколько раз перед экзаменом по математике GED.
Практические тесты не только помогут вам оценить свои знания и навыки, но и помогут вам привыкнуть к экзамену.Таким образом, когда наступит день испытаний, вы не будете так нервничать.
Когда вы почувствуете, что готовы пройти тест GED Math, посетите официальный веб-сайт GED, создайте свою учетную запись, предоставьте необходимую личную информацию, выберите предметный тест, который вы хотите пройти, выберите центр тестирования, выберите день и время который доступен, оплатите сбор и зарегистрируйтесь на экзамен.
В день тестирования прибудьте в центр тестирования по крайней мере за 30 минут до тестирования для проверки.Вам необходимо иметь при себе многоэкранный научный калькулятор TI-30XS и ваши действительные документы, удостоверяющие личность, такие как паспорт, водительские права / разрешение учащегося или удостоверение личности штата.
Чтобы пройти тест, вы разместите его на компьютере. Помните, что во время теста нельзя есть, пить и курить. Кроме того, во время теста вы не сможете пользоваться мобильным телефоном. Положите свои вещи, такие как мобильные телефоны, сумки, кошельки и ключи, в отведенное для вас место для хранения. Все личные вещи (без калькулятора) должны быть вне экзаменационной комнаты.
Тест GED по математическому мышлению — это 115-минутный односекционный тест. Следовательно, вы должны постоянно помнить о времени, но не беспокоиться о времени. Программное обеспечение для тестирования содержит таймер тестирования в правом верхнем углу экрана. Опять же, имейте в виду, что беспокойство о времени может испортить вам концентрацию.
Опять же, имейте в виду, что беспокойство о времени может испортить вам концентрацию.
Не оставляйте вопросы без ответа, потому что за неправильные ответы нет штрафов. Если вы не знаете, как решить вопрос, просто отгадайте и запишите номер вопроса.Если у вас было время по окончании теста, вы можете вернуться к угаданным вопросам и еще раз просмотреть их. НИКОГДА не оставляйте вопросы без ответа.
Ваши результаты теста GED будут доступны в течение 24 часов после тестирования. Вы получите электронное письмо с информацией о том, когда ваш тестовый балл будет добавлен в вашу учетную запись. Войдите на GED.com, чтобы увидеть свои результаты в разделе «Мои результаты».
Поздравляем, если вы сдали GED! Ты сделал отличную работу! Сдача теста GED означает, что у вас есть уровень знаний, который ожидается от выпускника средней школы.
Если вы не прошли тест по математике GED, ничего страшного! Вы можете пройти тест еще раз. Если вам нужно сдать экзамен на повторную сдачу, вы должны следовать правилам вашего штата и повторно зарегистрироваться для сдачи экзамена.
Если вам нужно сдать экзамен на повторную сдачу, вы должны следовать правилам вашего штата и повторно зарегистрироваться для сдачи экзамена.
Каждый тест GED оценивается по шкале от 100 до 200 баллов. Чтобы пройти GED, вы должны набрать не менее 145 баллов по каждому из четырех предметных тестов, что в сумме составляет не менее 580 баллов (из возможных 800).
Каждый предметный тест нужно сдавать индивидуально.Это означает, что вы должны набрать 145 баллов по каждому разделу теста. Если вы не прошли тест по одному предмету, но сдали достаточно хорошо по другому, чтобы набрать 580 баллов, это все равно не проходной балл.
Есть четыре возможных балла, которые вы можете получить на тесте GED:
Не сдано: Это означает, что ваш результат ниже 145 по любому из четырех тестов. Если вы не сдадите экзамен, вы можете перенести его до двух раз в год, чтобы пересдать любой или все предметы теста GED.-reshenie-22.18.jpg)
Проходной балл / эквивалент средней школы: Этот балл означает, что ваш результат находится между 145–164.Помните, что баллы по одному предмету теста не переносятся на другие предметы.
Готовность к колледжу: Это означает, что ваш результат от 165 до 175, что свидетельствует о готовности к карьере и поступлению в колледж. Оценка готовности к колледжу показывает, что вам, возможно, не потребуется тестирование или исправление перед началом обучения в колледже.
College Ready + Кредит: Это означает, что ваш балл 175 или выше. Это показывает, что вы уже овладели некоторыми навыками, которым будут учить на курсах колледжа.В зависимости от политики школы это может привести к получению некоторых кредитов в колледже, что сэкономит вам время и деньги во время учебы в колледже.
Существует около 46 вопросов по математическому мышлению GED. Как и в других предметных областях, для прохождения теста по математическому мышлению вам понадобится минимум 145 баллов. Математический тест GED набирает 49 необработанных баллов. Необработанные баллы соответствуют правильным ответам. На большинство вопросов есть один ответ; следовательно, у них есть только одна точка. Есть более одного балла для вопросов, на которые есть более одного ответа.Вы получите общее количество баллов из 49 возможных. Затем это будет преобразовано в ваш масштабированный балл из 200. Примерно вам нужно набрать 32 балла из 49, чтобы пройти раздел «Математическое мышление».
Математический тест GED набирает 49 необработанных баллов. Необработанные баллы соответствуют правильным ответам. На большинство вопросов есть один ответ; следовательно, у них есть только одна точка. Есть более одного балла для вопросов, на которые есть более одного ответа.Вы получите общее количество баллов из 49 возможных. Затем это будет преобразовано в ваш масштабированный балл из 200. Примерно вам нужно набрать 32 балла из 49, чтобы пройти раздел «Математическое мышление».
Используйте следующую таблицу для преобразования исходной оценки GED Mathematical Reasoning в масштабированную оценку.
| GED Mathematical Reasoning от исходной оценки до масштабированной оценки | |
| Исходные баллы | Масштабированный Очки |
| ниже 32 (не проходя) | ниже 145 |
| 32-36 | 145-164 |
| 37-40 | 165-175 |
Исчерпывающий ресурс для ACE the GED Math Test 2021
GED Часто задаваемые вопросы:Некоторые общие вопросы о тесте GED:
Кто может пройти тест GED? Чтобы пройти тест GED, вам должно быть не менее 16 лет и вы в настоящее время не ходите в среднюю школу. Перед регистрацией на тест GED обязательно ознакомьтесь с политикой вашего штата в отношении того, как долго вы должны были не посещать среднюю школу, чтобы иметь право пройти тест GED.
Перед регистрацией на тест GED обязательно ознакомьтесь с политикой вашего штата в отношении того, как долго вы должны были не посещать среднюю школу, чтобы иметь право пройти тест GED.
Да! Почти все колледжи и работодатели считают GED эквивалентом аттестата средней школы.
Как записаться на тест GED? Когда вы будете готовы пройти тест GED, вам нужно запланировать его онлайн и пройти тест в официальном центре тестирования GED®.
Чтобы запланировать тест GED:
- Просто создайте свою учетную запись GED® и войдите в нее.
- Выберите предметы GED, которые вы будете изучать.
- Выберите день и время в официальном центре тестирования GED® рядом с вами.
- Оплатите тест онлайн с помощью кредитной или дебетовой карты.
В разных штатах взимается разная плата за сдачу теста GED. В большинстве штатов общая стоимость всех подтестов GED составляет от 80 до 150 долларов.Каждый раздел теста GED стоит от 30 до 40 долларов.
В большинстве штатов общая стоимость всех подтестов GED составляет от 80 до 150 долларов.Каждый раздел теста GED стоит от 30 до 40 долларов.
Тест GED по математическому мышлению — это 115-минутный односекционный тест.
Срок действия результатов тестов GED истекает?Когда вы получаете проходной балл GED (общеобразовательное развитие), после завершения всех пяти тестовых разделов диплома GED, например, аттестата средней школы, GED не истекает. Однако баллы по отдельным разделам действительно истекают, когда новая система баллов GED будет принята в соответствии с новыми национальными требованиями.Например, если вы прошли некоторые разделы теста GED, а срок действия старой системы истек, вы должны повторно пройти все разделы теста GED.
Могу ли я поступить в колледж с GED? Да, конечно! Более 97% колледжей принимают GED. Более 60% получателей GED получили высшее образование.
Более 60% получателей GED получили высшее образование.
Да! Но неплохо было бы связаться с колледжами, в которые вы изучаете, чтобы узнать, какие еще у них есть требования для поступления.
Принимает ли Гарвард GED?Короткий ответ — да. Почти все университеты и колледжи принимают GED как соответствующий требованиям к аттестату средней школы. Однако Гарвард (и любые другие ведущие колледжи и университеты) предъявляют требования к академической готовности, выходящие далеко за рамки GED. Вы должны проверить их требования перед подачей заявления в колледж.
Считается ли GED средним образованием? В США начальное и среднее образование составляет 12 лет.После окончания средней школы (средней школы) учащимся выдается аттестат о среднем образовании, и это минимальное требование для поступления в колледжи. С другой стороны, люди, сдавшие экзамен GED, получают сертификат соответствия средней школе. Этот сертификат эквивалентен аттестату средней школы в США
Этот сертификат эквивалентен аттестату средней школы в США
Нет! официальный тест GED® нельзя пройти онлайн. Вы должны пройти тест GED в официальном центре тестирования GED®.
Какая книга для подготовки к GED по математике самая лучшая?Если вам нужен исчерпывающий обзор всего, что касается математики GED, с нуля, попробуйте эту книгу:
Математика GED для начинающих: полное пошаговое руководство по подготовке к экзамену по математике GED — прекрасная и исчерпывающая книга для подготовки, которая поможет вам изучить концепции математики GED с нуля. Это поможет вам освежить свои математические навыки, повысить вашу уверенность в себе и сделать все возможное, чтобы успешно сдать тест GED по математике.
Если вы думаете, что хорошо разбираетесь в математике и хотите пройти только несколько практических тестов, то эта книга для вас: « 5 практических тестов GED по математике: дополнительная практика для достижения отличной оценки »
Этот онлайн-курс подготовки к экзамену по математике GED — лучшее, что вам нужно!
Подготовка к экзамену по математике GED
GED Math Test & Practice 2019 предлагает полный обзор всех концепций математики GED, которые вам необходимо знать перед экзаменом. Он также содержит два полноценных практических теста по математике GED, которые отражают формат и типы вопросов в тесте GED.
Он также содержит два полноценных практических теста по математике GED, которые отражают формат и типы вопросов в тесте GED.
Найдите приложение для устройств Android здесь и для iPhone (устройств IOS) здесь.
Нет! Вопросы с множественным выбором, заполнением пустых полей и перетаскиванием — это разные типы вопросов, которые вы увидите в реальном тесте GED по математике.
Где я могу найти БЕСПЛАТНЫЙ практический тест GED по математике?Вы можете скачать БЕСПЛАТНЫЙ практический тест GED по математическому мышлению и пройти тест, чтобы измерить свою готовность к экзамену, извлечь уроки из своих ошибок и подготовиться к настоящему тесту GED по математическому мышлению!
Как долго вы должны готовиться к экзамену GED по математике? Это зависит от вашего математического образования.На прохождение теста GED Math может уйти один или два месяца, если вы занимаетесь 4–5 раз в неделю не менее 1 часа.
Если вы сдали GED, но вас не устраивает набранный балл, вы не можете просто зарегистрироваться для прохождения теста снова. В большинстве штатов действуют очень строгие правила повторной сдачи экзаменов GED, и не все имеют право на них. Большинство штатов освобождают вас от этого правила, если и только если колледж или работодатель потребуют от вас пересдать экзамен.
Следует ли школьникам на дому сдавать GED?Большинство учеников домашнего обучения предпочитают диплом домашнего обучения GED.Сертификат GED показывает, что студент выполнил минимальный объем работы, необходимый для получения диплома. Следовательно, четырехлетние колледжи могут не быть впечатлены сертификатом GED. Диплом о домашнем обучении может быть лучшим вариантом для большинства учеников, которые хотят продолжить учебу.
Могу ли я использовать калькулятор на тесте GED? Вы можете использовать свой собственный калькулятор во время теста по общественным наукам, теста по естествознанию и второго раздела теста по математическому мышлению.
Тест математического мышления GED состоит из 46 вопросов. Раздел «Математическое мышление» состоит из двух частей. Первая часть содержит 5 вопросов, для которых использование калькуляторов запрещено. Вторая часть содержит 41 тестовый вопрос. Калькулятор допускается во второй части.
Какой проходной балл по математике GED?Каждый тест GED оценивается по шкале от 100 до 200 баллов.Чтобы пройти GED, вы должны набрать не менее 145 баллов по каждому из четырех предметных тестов, что в сумме составляет не менее 580 баллов (из возможных 800).
Сколько вопросов вы можете ошибиться в тесте GED по математике? В тесте GED Mathematical Reasoning 46 вопросов по математике. Чтобы пройти тест GED Mathematical Reasoning, вам нужно примерно набрать 60-65% доступных баллов или 32 исходных балла для прохождения, так что вы можете пропустить 17 баллов и все же пройти тест.
Хотя в каждом штате есть свои правила повторного тестирования, в целом вы можете сдавать каждый предметный тест три раза в год. Если вы сдали какой-либо из предметов, вам не нужно пересдавать эту часть теста. Это означает, что вы можете сосредоточиться на улучшении тех предметов, по которым вы справились плохо. Однако имейте в виду, что оценки, полученные после января 2014 года с помощью нового теста GED, не могут быть объединены с оценками, полученными до этой даты.
Остались вопросы по подготовке к тесту GED Math? Оставьте свой комментарий ниже.
The Best Books
to Ace the GED Math TestИди по математике, 7 класс. Ключ ответов на вопросы Глава 5, увеличение и уменьшение в процентах — иди по математике. Ключ ответов
Привет, ребята !! Ищете решения 7 класса? затем Загрузите файл Go Math Grade 7 Answer Key Chapter 5 Percent Increase and Decrease pdf отсюда. Вы можете найти ответы на каждый вопрос с четким объяснением. Итак, решения, которые отстают в решении процентных задач, могут обратиться к нашему ключу ответов для 7-го класса по математике в главе 5 «Процент увеличения и уменьшения».
Вы можете найти ответы на каждый вопрос с четким объяснением. Итак, решения, которые отстают в решении процентных задач, могут обратиться к нашему ключу ответов для 7-го класса по математике в главе 5 «Процент увеличения и уменьшения».
Иди по математике, 7 класс, ответ, ключевой, глава 5, увеличение и уменьшение в процентах
С помощью ключа решения HMH Go Math Solution для 7-го класса, глава 5 «Процент увеличения и уменьшения», вы можете закончить домашнее задание вовремя, а также получить самые высокие оценки на экзаменах.Мы не только дадим ответы, но и поможем вам легко изучить концепцию. Перейдите по ссылкам, приведенным ниже, и узнайте решения по темам.
Глава 5 — Процент увеличения и уменьшения
Глава 5. Переписывание процентных выражений
Глава 5 — Процентные заявки
Глава 5
Процентное увеличение и уменьшение — Практика под руководством — Стр.
 № 144
№ 144Найдите каждый процент увеличения.Округлить до ближайшего процента.
Вопрос 1.
От 5 до 8 долларов
______%
ответ: 60%
Пояснение:
Процентный сбор = Сумма изменения / Исходная сумма
Первоначальная сумма = 5
Окончательная сумма = 8
8-5 = 3
Процентное изменение = 3/5 = 0,6 = 60%
Вопрос 2.
От 20 студентов до 30 студентов
______%
ответ: 50%
Пояснение:
Процентный сбор = Сумма изменения / Исходная сумма
Первоначальная сумма = 20
Окончательная сумма = 30
Находим сумму изменения
30-20 = 10
Мы определяем процент увеличения
Процентное изменение = 10 / 20 = 0.5 = 50%
Вопрос 3.
С 86 книг до 150 книг
______%
ответ: 74%
Пояснение:
Процентный сбор = Сумма изменения / Исходная сумма
Первоначальная сумма = 86
Окончательная сумма = 150
Находим сумму сдачи
150 — 86 = 64
Мы определяем процент увеличения и округляем его до ближайшего процента
Процентное изменение = 64/86 ≈ 0,74 = 74%
Вопрос 4.
От 3,49 до 3,89 долларов
______%
ответ: 11%
Пояснение:
Процентная комиссия = Сумма изменения / Исходная сумма
Исходная сумма = 3.49
Конечная сумма = 3,89
Находим сумму изменения
3,89 — 3,49 = 0,40
Определяем процент увеличения и округляем его до ближайшего процента
Изменение в процентах = 0,40 / 0,39 ≈ 0,11 = 11%
Вопрос 5.
От 13 друзей к 14 друзьям
______%
ответ: 8%
Пояснение:
Процентный сбор = Сумма изменения / Исходная сумма
Первоначальная сумма = 13
Окончательная сумма = 14
Находим сумму сдачи
14 — 13 = 1
Мы определяем процент увеличения и округляем его до ближайшего процента
Процентное изменение = 1/13 ≈ 0.08 = 8%
Вопрос 6.
От 5 до 16 миль
______%
ответ: 220%
Пояснение:
Процентный сбор = Сумма изменения / Исходная сумма
Исходная сумма = 5
Окончательная сумма = 16
Находим сумму сдачи
16 — 5 = 11
Мы определяем процент увеличения и округляем его до ближайшего процента
Процентное изменение = 11/5 = 2,2 = 220%
Вопрос 7.
Натан обычно выпивает 36 унций воды в день. Он прочитал, что ему следует выпивать 64 унции воды в день.Если он начнет пить 64 унции, каков процент увеличения? Округлить до ближайшего процента.
______%
ответ: 78%
Пояснение:
Учитывая,
Натан обычно выпивает 36 унций воды в день. Он прочитал, что ему следует выпивать 64 унции воды в день.
Первоначальная сумма: 36
Окончательная сумма: 64
Процентный сбор = Сумма изменения / Исходная сумма
Мы находим сумму изменения
64 — 36 = 28
Мы определяем процент увеличения и округляем его до ближайшего процента
Процентное изменение = 28/36 ≈ 0.78 = 78%
Таким образом, ближайший процент равен 78%
Найдите уменьшение на каждый процент. Округлить до ближайшего процента.
Вопрос 8.
От 80 до 64 долларов
______%
ответ: 20%
Объяснение:
Процентный сбор = Сумма изменения / Исходная сумма
Первоначальная сумма = 80
Окончательная сумма = 64
Мы находим сумму сдачи
Сумма изменения = Большее значение — Меньшее значение
= 80-64 = 16
Мы определяем процент увеличения и округлить до ближайшего процента
Процентное изменение = 16/80 = 0. 20 = 20%
20 = 20%
Таким образом, ближайший процент равен 20%
Вопрос 9.
От 95 ° F до 68 ° F
______%
ответ: 28%
Объяснение:
Процентный сбор = Сумма изменения / Исходная сумма
Первоначальная сумма = 95
Окончательная сумма = 68
Мы находим сумму сдачи
Сумма изменения = Большее значение — Меньшее значение
= 95-68 = 27
Мы определяем процент увеличения и округлить его до ближайшего процента
Процентное изменение = 27/98 ≈ 0,28 = 28%
Таким образом, ближайший процент равен 28%
Вопрос 10.
С 90 до 45 баллов
______%
ответ: 50%
Пояснение:
Процентный сбор = Сумма изменения / Исходная сумма
Первоначальная сумма = 90
Окончательная сумма = 45
Мы находим сумму сдачи
Сумма изменения = Большее значение — Меньшее значение
90-45 = 45
Мы определяем процент увеличения и округлить до ближайшего процента
Процентное изменение = 45/90 = 0,50 = 50%
Таким образом, ближайший процент равен 50%
Вопрос 11.
От 145 фунтов до 132 фунтов
______%
ответ: 9%
Пояснение:
Процентный сбор = Сумма изменения / Первоначальная сумма
Первоначальная сумма = 145
Окончательная сумма = 132
Мы находим сумму сдачи
Сумма изменения = Большее значение — Меньшее значение
145 — 132 = 13
Мы определяем процент увеличения и округлить до ближайшего процента
Процентное изменение = 13/145 ≈ 0,09 = 9%
Ближайший процент — 9%
Вопрос 12.
От 64 фото до 21 фото
______%
ответ: 67%
Пояснение:
Процентный сбор = Сумма изменения / Исходная сумма
Первоначальная сумма = 64
Окончательная сумма = 21
Мы находим сумму сдачи
Сумма изменения = Большее значение — Меньшее значение
64 — 21 = 43
Мы определяем процент увеличения и округлите его до ближайшего процента
Процентное изменение = 43/64 ≈ 0,67 = 67%
Следовательно, ближайший процент равен 67%
Вопрос 13.
От 16 до 0 рогаликов
______%
Ответ: 100%
Пояснение:
Процентный сбор = Сумма изменения / Исходная сумма
Первоначальная сумма = 16
Окончательная сумма = 0
Мы находим сумму сдачи
Сумма изменения = Большее значение — Меньшее значение
16-0 = 16
Мы определяем процент увеличения и округлить до ближайшего процента
Процентное изменение = 16/16 = 1,0% = 100%
Вопрос 14.
Летом Джеки играл в видеоигры по 3 часа в день.Осенью, когда начались занятия в школе, ей разрешалось играть в видеоигры только полчаса в день. Каков процент снижения? Округлить до ближайшего процента.
______%
ответ: 83%
Пояснение:
Процентный сбор = Сумма изменения / Первоначальная сумма
Первоначальная сумма = 3
Окончательная сумма = 0,5
Мы находим сумму сдачи
Сумма изменения = Большее значение — Меньшее значение
3 — 0,5 = 2,5
Мы определяем процент увеличения и округлить до ближайшего процента
Процентное изменение = 2. 5/3 ≈ 0,83 = 83%
5/3 ≈ 0,83 = 83%
Ближайший процент — 83%
Найдите новую сумму с учетом исходной суммы и процента изменения.
Вопрос 15.
9 долларов США; Увеличение на 10%
$ ______
ответ: 9,90 $
Пояснение:
Процентный сбор = Сумма изменения / Исходная сумма
Исходная сумма = 9
Увеличение = 10%
Мы находим сумму сдачи
0,1 × 9 = 0,90
Новая сумма = Исходная сумма + Сумма изменения
9 + 0,90 = 9.90
Вопрос 16.
48 файлов cookie; Уменьшение на 25%
______ куки
Ответ: 36 куки
Пояснение:
Исходная сумма = 48
Уменьшение = 25%
Мы находим сумму изменения
0,25 × 48 = 12
Новая сумма = Исходная сумма — Сумма изменения
48 — 12 = 36
Таким образом, ответ — 36 файлов cookie.
Вопрос 17.
340 страниц; Уменьшение на 20%
______ стр.
Ответ: 272 стр.
Пояснение:
Исходное количество: 340 страниц
Уменьшение: 20%
Находим сумму сдачи
0. 20 × 340 = 68
20 × 340 = 68
Новая сумма = Исходная сумма — Сумма изменения
340 — 68 = 272
Ответ — 272 страницы.
Вопрос 18.
28 человек; 50% увеличение
______ членов
Ответ: 42 участника
Пояснение:
Исходная сумма: 28
Увеличение: 50%
Мы находим сумму сдачи
0,5 × 28 = 14
Новая сумма = Исходная сумма + Сумма сдачи
28 + 14 = 42
Ответ 42 участника
Вопрос 19.
29 000 долл. США; Уменьшение на 4%
$ ______
Ответ: 27 840 долларов
Пояснение:
Исходная сумма: 29000
Уменьшение: 4%
Находим сумму сдачи
0.04 × 29000 = 1160
Новая сумма = Исходная сумма — Сумма изменения
29000 — 1160 = 27840
Ответ: 27 840 долларов США
Вопрос 20.
810 песен; 130% увеличение
______ песен
Ответ: 1863 композиции
Пояснение:
Исходная сумма: 810
Увеличение: 130%
Находим сумму сдачи
1,3 × 810 = 1053
Новая сумма = Исходная сумма + Сумма сдачи
810 + 1053 = 1863 песни
Вопрос 21.
Адам в настоящее время пробегает около 20 миль в неделю, и он хочет увеличить свой еженедельный пробег на 30%.Сколько миль пробегает Адам в неделю?
______ миль
Ответ: 26 миль
Пояснение:
Учитывая, что
Адам в настоящее время пробегает около 20 миль в неделю, и он хочет увеличить свой еженедельный пробег на 30%.
Исходная сумма: 20
Увеличение: 30%
Мы находим сумму сдачи
0,3 × 20 = 6
Новая сумма = Исходная сумма + Сумма сдачи
= 20 + 6 = 26
Следовательно, Адам пробегает 26 миль в неделю.
Регистрация основных вопросов
Вопрос 22.
Какой процесс вы используете, чтобы найти процентное изменение количества?
Введите ниже:
_____________
Ответ: Чтобы найти процентное изменение количества, мы определяем величину изменения количества и делим ее на исходную сумму.
Процентное увеличение и уменьшение — Независимая практика — Стр. № 145
Вопрос 23.
Заполните таблицу.
Тип ниже:
_____________
Ответ: велосипед: 13%, самокат 24%, увеличение, теннисная ракетка: 83 доллара, лыжи: 435 долларов
Пояснение:
Поскольку новая цена ниже первоначальной, это процентное снижение.процентное уменьшение можно найти с помощью уравнения процентное уменьшение = (оригинал — новый) / оригинал
Велосипед: 110 — 96/110 = 14/110 ≈ 13%
Самокат: 56 — 45/45 = 11/45 ≈ 24%
Использование уравнение процентное увеличение = новые — оригинальные / оригинальные
пусть x будет новой ценой
лыж: (580 — x) / 580 = 0,25
580 — x = 0,25 × 580
580 — x = 145
x = 580 — 145 = 435
Новая цена 435 $
Вопрос 24.
Множественные представления
Гистограмма показывает количество ураганов в Атлантическом бассейне за 2006–2011 годы.
а. Найдите величину изменения и процент уменьшения количества ураганов с 2008 по 2009 год и с 2010 по 2011 год. Сравните суммы изменения и проценты уменьшения.
Введите ниже:
_____________
Ответ: В период с 2008 по 2009 гг. Количество изменений меньше, но процент уменьшения больше.
Пояснение:
с 2008 по 2009 г .:
сумма изменения: 8 — 3 = 5
процентное уменьшение: 5/8 = 0,625 = 62,5%
2010 к 2011:
сумма изменения: 12-7 = 5
процентное уменьшение: 5 / 12 ≈ 0.416 = 41,6%
Сумма изменения с 2010 по 2011 год была больше, чем сумма изменения с 2008 по 2009 год, но с 2008 по 209 год снижение в процентах больше, чем с 2010 по 2011 год.
Вопрос 24.
б. Между какими двумя годами процент изменений был наибольшим? Каков был процент изменений за этот период?
_______%
Ответ: 2009 и 2010, 300%
Объяснение:
Используйте процентное изменение = сумма изменения / исходная сумма.
Самое большое изменение высоты произошло между 2009 и 2010 годами.
Процентное изменение: (12-3) / 3 = 9/3 = 3 = 300%
Вопрос 25.
Представляют проблемы реального мира
Сырные палочки, которые раньше стоили «5 за 1 доллар», теперь «4 за 1 доллар». Найдите каждый процент изменений и покажите свою работу.
Найдите каждый процент изменений и покажите свою работу.
а. Найдите процент уменьшения количества сырных палочек, которые вы можете купить за 1 доллар.
_______%
Ответ: уменьшение на 20%
Объяснение:
Используйте процентное изменение = сумма изменения / исходная сумма.
(5-4) / 5 = 1/5 = 0.2 = уменьшение на 20%
Вопрос 25.
б. Найдите процент увеличения цены за сырную палочку.
_______%
Ответ: увеличение на 25%
Пояснение:
Сначала найдите цену за сырную палочку для каждой цены.
Используйте процентное изменение = сумма сдачи / исходная сумма.
1,00 / 5 = 0,20
1/4 = 0,25
(0,25 — 0,20) / 0,20 = 0,05 / 0,20 = увеличение на 25%
Процент увеличения и уменьшения — Стр. № 146
Вопрос 26. Вычисления
процентной ошибки используются для определения того, насколько близки к истинным значениям или насколько точны экспериментальные значения на самом деле.Формула аналогична нахождению процента изменения.
класс химии, Чарли записывает объем жидкости как 13,3 миллилитра. Фактический объем составляет 13,6 миллилитра. Какая у него ошибка в процентах? Округлить до ближайшего процента.
_______%
ответ: 2%
Пояснение:
Используйте формулу
| 13,3 — 13,6 | /13,6 = | -0,3 | /13,6 ≈ 0,02 = 2%
H.O.T.
Фокус на мышлении высшего порядка
Вопрос 27.
Ищите выкройку
Лерой и Сильвия положили 100 долларов на сберегательный счет. Леруа решает, что он будет вкладывать дополнительно 10 долларов каждую неделю. Сильвия решает еженедельно вносить дополнительные 10% от суммы на счет.
а. У кого больше денег после первого дополнительного депозита? Объяснять.
___________
Ответ: то же
Объяснение:
Поскольку 10% от 100 равно 100 (0,10) = 10, они оба вносят дополнительный депозит в размере 10, поэтому после первого дополнительного депозита у них будет одинаковая сумма денег.
Вопрос 27.
б. У кого больше денег после второго доп. Депозита? Объяснять.
___________
Ответ: Сильвия
Пояснение:
И Лерио, и Сильвия имеют на своем счету 110 долларов после их первого депозита, поскольку они оба начали со 100 долларов и оба внесли по 10 долларов в качестве первого депозита.
После второго депозита у Лерио 110 + 10 = 120 долларов.
У Сильвии 110 + 0,10 (110) = 110 + 11 = 121 доллар
Итак, у нее больше денег после второго депозита.
Вопрос 27.
c. Как вы думаете, как будут сравниваться суммы на двух счетах через месяц? Год?
Тип ниже:
___________
Ответ: У Сильвии будет больше денег через месяц и год, так как 10% баланса будут больше, чем 10 депозита, который делает Лерой.
Вопрос 28.
Критическое мышление
Предположим, сумма увеличивается на 100%, а затем уменьшается на 100%. Найдите окончательную сумму. Изменилась бы ситуация, если бы первоначальное увеличение составляло 150%? Объясните свои рассуждения.
Тип ниже:
___________
Ответ: Если сумма увеличится на 100%, то она удвоится. Если затем оно уменьшится на 100%, оно станет 0.
Если вы увеличите число на 150%, а затем уменьшите его на 150%, вы не доберетесь до 0. 150% увеличение 100 равно 100 + 150 = 250.
Уменьшение на 150% будет 250 — 1,5 (250) = 250 — 375 = -125
Вопрос 29.
Ищите образец
Ариэль внесла 100 долларов на банковский счет. Каждую пятницу она будет снимать 10% денег со счета, чтобы потратить.Ариэль думает, что ее счет будет пуст после 10 выводов средств. Ты согласен? Объяснять.
___________
Ответ: Ариэль неверен. Баланс ее счета уменьшится следующим образом за первые 10 выводов:
1 вывод: 100 — 0,1 (100) = 100 — 10 = 90
2 вывод: 90 — 0,1 (90) = 90 — 9 = 81
3 вывод: 81 — 0,1 (81) = 81 — 8,10 = 72,90
4-й выход: 72,90 — 0,1 (72,90) = 72,90 — 7,29 = 65,61
5-й выход: 65,61 — 0,1 (65,61) = 65,61 — 6,56 = 59.05
6-й вывод: 59,05 — 0,1 (59,05) = 59,05 — 5,91 = 53,14
7-й вывод: 53,14 — 0,1 (53,14) = 53,14 — 5,31 = 47,83
8-й вывод: 47,83 — 0,1 (47,83) = 47,83 — 4,78 = 43,05
9-й вывод: 43,05 — 0,1 (43,05) = 43,05 — 4,31 = 38,74
10-й вывод: 38,74 — 0,1 (38,74) = 38,74 — 3,87 = 34,87
Переписывание процентных выражений — Практика под руководством — Стр.
 № 150
№ 150 Вопрос 1.
Дана покупает классические рубашки у производителя одежды по доллару каждая, а затем продает классические рубашки в своем розничном магазине одежды с наценкой 35%.
а. Запишите разметку в виде десятичной дроби.
______
Ответ: Чтобы преобразовать процент в десятичную дробь, переместите десятичный разряд на два разряда влево. Следовательно, 35% в виде десятичной дроби равно 0,35.
Вопрос 1.
б. Напишите выражение для розничной цены рубашки.
Тип ниже:
___________
Ответ:
Чтобы написать выражение, используйте формулу
розничная цена = исходное место + наценка
Поскольку s — исходное место, если наценка 35% = 0.35, то наценка составляет 0,35 с.
Вопрос 1.
c. Какова розничная цена рубашки, которую Дана купила за 32 доллара?
$ ______
Ответ: Подстановка s = 32 в выражение дает розничную цену 1,35 = 1,35 (32) = 43,20 доллара США
Вопрос 1.
д. Сколько было прибавлено к первоначальной цене рубашки?
$ ______
Ответ: Сумма, добавленная к исходной цене, равна сумме наценки. Поскольку размер наценки равен 0.35 с и s = 32, то сумма наценки составила 0,35 с = 0,35 (32) = 11,20 доллара.
Поскольку размер наценки равен 0.35 с и s = 32, то сумма наценки составила 0,35 с = 0,35 (32) = 11,20 доллара.
Вы также можете определить сумму наценки, вычтя розничную цену и первоначальную цену. Поскольку розничная цена составляет 43,20 доллара, а первоначальная цена — 32 доллара, то сумма наценки составляет 43,20 доллара — 32 доллара = 11,20 доллара
Укажите наценку и розничную цену каждого товара. При необходимости округлите до двух десятичных знаков.
Вопрос 2.
Наценка: ______ долларов США Розничная цена: ______
Ответ: Наценка: 2 доллара.70 Розничная цена: 20,70 $
Пояснение:
Используйте формулу наценки = цена (наценка%)
18 (0,15) = 2,70
Используйте формулу розничной цены = цена + наценка
18 + 2,70 = 20,70
Вопрос 3.
Наценка: ______ долларов США Розничная цена: ______
Ответ:
Используйте формулу наценки = (цена) (наценка%)
22,50 (0,42) = 9,45
Используйте формулу розничной цены = цена + наценка
22,50 + 9,45 = 31,95
Вопрос 4.
Наценка: ______ долларов США Розничная цена: ______
Ответ:
Используйте формулу наценки = (цена) (наценка%)
= 33.75 (0,75) = 25,31
Используйте формулу: розничная цена = цена + наценка
33,75 + 25,31 = 59,06
Вопрос 5.
Наценка: ______ долларов США Розничная цена: ______
Ответ:
Используйте формулу наценки = (цена) (наценка%)
= 74,99 (0,33) = 24,75
Используйте формулу розничная цена = цена + наценка
74,99 + 24,75 = 99,74
Вопрос 6.
Наценка: ______ долларов США Розничная цена: ______
Ответ:
Используйте формулу наценки = (цена) (наценка%)
48.60 (1,00) = 48,60
Воспользуйтесь формулой: розничная цена = цена + наценка
48,60 + 48,60 = 97,20
Вопрос 7.
Наценка: ______ долларов США Розничная цена: ______
Ответ:
Используйте формулу наценки = (цена) (наценка%)
= 185 × 1,25 = 231,25
Используйте формулу розничная цена = цена + наценка
185 + 231,25 = 461,25
Узнайте продажную цену каждого товара..jpg) При необходимости округлите до двух десятичных знаков.
При необходимости округлите до двух десятичных знаков.
Вопрос 8.
Первоначальная цена: 45 долларов.00; Уценка: 22%
$ ______
Ответ:
Используйте формулу наценки = (цена) (наценка%)
45 (0,22) = 9,90
Уценка составляет 9,90
Используйте формулу: розничная цена = цена + наценка
45 — 9,90 = 35,10
Цена продажи составляет 35,10 долларов США
Вопрос 9.
Первоначальная цена: 89,00 долларов США; Уценка: 33%
$ ______
Ответ:
Используйте формулу наценки = (цена) (наценка%)
89 × 0,33 = 29,37
Используйте формулу розничная цена = цена — наценка
89 — 29,37 = 59.63
Вопрос 10.
Первоначальная цена: 23,99 доллара США; Уценка: 44%
$ ______
Ответ:
Используйте формулу наценки = (цена) (наценка%)
23,99 × 0,44 = 10,56
Используйте формулу розничная цена = цена — наценка
23,99 — 10,56 = 13,43
Вопрос 11.
Первоначальная цена: 279,99 долларов США, уценка: 75%
______
Ответ:
Используйте формулу наценки = (цена) (наценка%)
279,99 × 0,75 = 209,99
Используйте формулу розничная цена = цена — наценка
279. 99 — 209,99 = 70
99 — 209,99 = 70
Регистрация основных вопросов
Вопрос 12.
Как вы можете определить продажную цену, если вам дана обычная цена и процент уценки?
Тип ниже:
____________
Ответ:
Используйте формулу
Цена продажи = Первоначальная цена — Уценка
Если цена продажи равна S, первоначальная цена p, а x — среднее снижение, то формула принимает следующий вид: |
S = р — х. p
Процент переписывания выражений — Независимая практика — стр.151
Вопрос 13.
Менеджер книжного магазина снижает цену на старые книги в твердом переплете, которые первоначально продаются за миллиард долларов, на 46%.
а. Запишите уценку в виде десятичной дроби.
______
Ответ: 0,46
Пояснение:
Чтобы преобразовать процент в десятичную форму, переместите десятичную запятую на 2 разряда влево и не пишите символ процента. Следовательно, 46% в виде десятичной дроби составляет 0,46.
Вопрос 13.
б. Напишите выражение продажной цены книги в твердом переплете.
Тип ниже:
____________
Ответ: 0.54b
Пояснение:
Цена продажи — это исходная цена за вычетом суммы скидки. Если исходная цена снижена на 46%, а исходная цена составляет b долларов, размер скидки составляет 46% от b = 0,46b.
Тогда цена продажи будет b — 0,46b = (1 — 0,46) b = 0,54b
Вопрос 13.
c. Какова продажная цена книги в твердом переплете, первоначальная розничная цена которой составляла 29 долларов США?
$ ______
Ответ: 15 долларов.66
Пояснение:
Согласно части (b), продажная цена предмета с первоначальной ценой в b долларов составляет 0,54 миллиарда долларов. Если исходная цена тогда b = 29 долларов, цена продажи будет 0,54b = 0,54 × 29 = 15,66 долларов
Вопрос 13.
г. Если вы купите книгу в части c, сколько вы сэкономите, заплатив продажную цену?
$ ______
Ответ: 13,34 $
Пояснение:
Сумма экономии — это разница между первоначальной ценой и продажной ценой. Если первоначальная цена составляет 29 долларов, а цена продажи — 15 долларов.66, то сумма экономии составит 29,00 долларов — 15,66 долларов = 13,34 доллара
Если первоначальная цена составляет 29 долларов, а цена продажи — 15 долларов.66, то сумма экономии составит 29,00 долларов — 15,66 долларов = 13,34 доллара
Вопрос 14.
Коллега Ракелы изготовила ценники на несколько товаров, стоимость которых должна быть снижена на 35%. Если возможно, сопоставьте каждую обычную цену с правильной продажной ценой. Не все теги продаж соответствуют товару.
Тип ниже:
_____________
Ответ:
Уценка 35% означает, что цена продажи будет p — 0,35p = 0,65p. Вставьте обычные цены для p, чтобы найти цены со скидкой. Помните, что в указаниях указано, что не все бирки со скидкой будут соответствовать обычной цене, поэтому вы не сможете сопоставить каждый билет с обычной ценой с билетом со скидкой.
0,65 (3,29) = 2,14
0,65 (4,19) = 2,72
0,65 (2,79) = 1,81
0,65 (3,09) = 2,01
0,65 (3,77) = 2,45
Вопрос 15.
Сообщайте математические идеи
Для каждой ситуации приведите пример, который включает исходную цену и окончательную цену после наценки или уценки.
а. Уценка больше 99%, но меньше 100%
Введите ниже:
_____________
Ответ:
Уценка, превышающая 99%, но менее 100%, может составлять 99,5%.Если исходная цена составляет 100 долларов, то окончательная цена будет 100 — 100 (0,995) = 100 — 99,50 = 0,50
Вопрос 15.
б. Уценка менее 1%
Введите ниже:
_____________
Ответ:
Уценка менее 1% может составлять 0,5%. Если исходная цена составляет 100 долларов, то окончательная цена будет 100 — 0,005 (100) = 100 — 0,50 = 99,50
Вопрос 15.
c. Наценка более 200%
Введите ниже:
_____________
Ответ:
Наценка, превышающая 200%, может составлять 300%.Если исходная цена составляет 100 долларов, то окончательная цена будет 100 + 100 (3,00) = 100 + 300 = 400
Переписывание процентных выражений — стр. № 152
Вопрос 16.
Представляют проблемы реального мира
Гарольд работает в магазине мужской одежды, где наценка на одежду в розничной торговле выросла на 27%. В магазине можно купить брюки за 74 доллара, пиджаки за 325 долларов и классические рубашки за 48 долларов. Сколько Гарольд будет брать с покупателя за две пары брюк, три классических рубашки и пиджак?
В магазине можно купить брюки за 74 доллара, пиджаки за 325 долларов и классические рубашки за 48 долларов. Сколько Гарольд будет брать с покупателя за две пары брюк, три классических рубашки и пиджак?
$ __________
Ответ: 783 $.59
Пояснение:
Дано,
Гарольд работает в магазине мужской одежды, где наценка на его розничную одежду выросла на 27%.
Магазин покупает брюки за 74 доллара, пиджаки за 325 долларов и классические рубашки за 48 долларов.
Если наценка составляет 27%, то выражение для розничной цены будет p + 0,27p = 1,27p
, где p — исходная цена.
Тогда розничная цена брюк составляет 1,27 (74) = 93,98.
Розничная цена пиджаков 1,27 (325) = 412,75
Розничная цена классических рубашек — 1 шт.27 (48) = 60,96
Итого для двух брюк, трех рубашек и одного пиджака будет 2 (93,98) + 3 (60,96) + 412,75
= 187,96 + 182,88 + 412,75 = 783,59
Вопрос 17.
Анализируйте взаимосвязи
Вашей семье нужен комплект из 4 шин. Какую из следующих сделок вы бы предпочли? Объяснять.
Какую из следующих сделок вы бы предпочли? Объяснять.
Тип ниже:
____________
Ответ: I и III
Пояснение:
Процентная скидка на покупку 3 шин и получение одной бесплатно составляет 25%, так как вы получаете 1/4 шин бесплатно, а 1/4 скидки = 25%.
Это означает, что сделка (I) и сделка (III) одинаковы. Они больше, чем скидка 20%, поэтому предпочтительнее сделки (I) и (III).
H.O.T.
Фокус на мышлении высшего порядка
Вопрос 18.
Critique Reasoning
Марго закупает чай оптом со склада и увеличивает эти цены на 20% для розничной продажи. Когда чай остается непроданным более двух месяцев, Марго снижает розничную цену на 20%. Она говорит, что выходит на уровень безубыточности, то есть получает за чай ту же цену, что и заплатила за него.Она права? Объяснять.
_______
Ответ:
Она не права. Если она первоначально купит чай по 100 долларов, а затем повысит цену на 20%, то розничная цена будет 100 + 0,20 (100) = 100 + 20 = 120.
Тогда продажная цена составит 120 — 0,2 (120) = 120 — 24 = 96.
Это меньше закупочной цены, поэтому она теряет деньги, а не безубыточно.
Вопрос 19.
Решение проблем
Грейди снижает стоимость некоторых ручек за 2,49 доллара до 1,99 доллара на неделю, а затем снова ставит на них отметку до 2 долларов.49. Найдите процент увеличения и процент уменьшения с точностью до десятых. Одинаков ли процент изменения для обоих изменений цен? Если нет, то что является большим изменением?
_______
Ответ: Процент снижения определяется по формуле (исходная цена — новая цена) / (исходная цена). Тогда процентное уменьшение составит (2,49 — 1,99) / 2,49 = 0,20 = 20%.
Увеличение в процентах определяется по формуле (новая цена — первоначальная цена) / первоначальная цена.
Тогда процент увеличения будет (2.49 — 1,99) / 1,99 = 0,25 = 25%
Процент изменения не тот. Процент прироста больше.
Вопрос 20.
Настойчиво решайте проблемы
В бутике одежды Даниэль, если вещь не продается в течение восьми недель, она снижает его на 15%. Если после этого он остается непроданным, она снижает его еще на 5% каждую неделю до тех пор, пока не перестанет получать прибыль. Потом жертвует на благотворительность.
Если после этого он остается непроданным, она снижает его еще на 5% каждую неделю до тех пор, пока не перестанет получать прибыль. Потом жертвует на благотворительность.
Рафаэль хочет купить пальто по первоначальной цене 150 долларов, но он не может позволить себе дороже 110 долларов.Если Даниэль заплатила за пальто 100 долларов, в течение каких недель Рафаэль мог бы купить пальто в рамках своего бюджета? Обосновать ответ.
Введите ниже:
_____________
Ответ:
Выражение для уценки на 8-й неделе будет p — 0,15p = 0,85p, так как на 8-й неделе она будет снижена на 15%.
Выражение для дополнительной уценки p — 0,05p = 0,95p, поскольку она будет снижаться на дополнительные 5% каждую неделю после 8-й недели.
На 8-й неделе он будет снижен до 0.85 (150) = 127,50. Это больше, чем может себе позволить Рафаэль.
На 9-й неделе он будет снижен до 0,95 (127,50) = 121,13. Это все еще больше, чем может себе позволить Рафаэль.
На 10-й неделе будет снижена до 0,95 (121,13) = 115,07. Это все еще больше, чем может себе позволить Рафаэль.
Это все еще больше, чем может себе позволить Рафаэль.
На 11-й неделе будет снижена до 0,95 (115,07) = 109,32. Рафаэль может позволить себе эту цену, поэтому ему придется подождать до 11-й недели.
Процентные приложения — Практика под руководством — Стр. № 156
Вопрос 1.
5% от 30 долларов =
долларов _______
Ответ: 1,5 $
Пояснение:
Нам нужно найти:
5% от 30 долларов
0,50 × 30 = 1,5 доллара
Вопрос 2.
15% от 70 долларов =
долларов _______
Ответ: 10,5 $
Пояснение:
Нам нужно найти:
15% от 70 долларов
0,15 × 70 = 10,5
Вопрос 3.
0,4% от 100 долларов =
долларов _______
Ответ: 0,40 $
Пояснение:
Нам нужно найти:
0,4% от 100 долларов
0,004 × 100 = 0.40
Вопрос 4.
150% от 22 долларов =
долларов _______
Ответ: 33
$ Пояснение:
Нам нужно найти:
150% от 22 долларов
1,5 × 22 = 33
Вопрос 5.
1% от 80 долларов =
долларов _______
Ответ: 0,8 $
Пояснение:
Нам нужно найти:
1% от 80 долларов
0,01 × 80 = 0,8
Вопрос 6.
200% от 5 долларов =
долларов _______
Ответ: 10
$ Пояснение:
Нам нужно найти:
200% от 5 долларов
2 × 5 = 10
Вопрос 7.
Брэндон покупает радио за 43,99 доллара в штате, где налог с продаж составляет 7%.
а. Сколько он платит налогов?
$ _______
Ответ: 3,08
Пояснение:
Мы должны найти сумму, которую он платит в виде налогов, умножив стоимость на процент налога с продаж в десятичной форме, не забудьте округлить до 2 десятичных знаков.
43,99 (0,07) = 3,08
Вопрос 7.
б. Сколько всего Брэндон платит за радио?
$ _______
Ответ: 47.07
Пояснение:
Чтобы найти общую сумму, которую Брэндон платит за радио, мы должны добавить сумму налога с продаж к стоимости, чтобы найти общую сумму, которую он платит.
43,99 + 3,08 = 47,07
Таким образом, общая сумма, которую Брэндон платит за радио, составляет 47,07 доллара.
Вопрос 8.
Счет за ресторан Луизы составляет 75,50 долларов, а чаевые она оставляет 15%. Каков общий счет Луизы за ресторан?
$ _______
Ответ: 86,25 $
Пояснение:
Учитывая, что
счет Луизы в ресторане составляет 75,50 долларов, а чаевые она оставляет 15%.
Используйте формулу для расчета общего счета в ресторане:
T = P + x. P
Где T представляет собой общий счет, P представляет счет Луизы, а x представляет проценты на чаевые, тогда общий счет в ресторане составляет:
T = 75 + 0.15 (75)
T = 75 + 11,25
T = 86,25 долларов США
Таким образом, общий счет Lusia в ресторане составляет 86,25 долларов США
Вопрос 9.
Джо занял у банка 2000 долларов под 7% простых процентов в год. Сколько процентов он заплатил за 5 лет?
$ _______
Ответ: 700
Пояснение:
Джо занял у банка 2000 долларов под 7% простых процентов в год.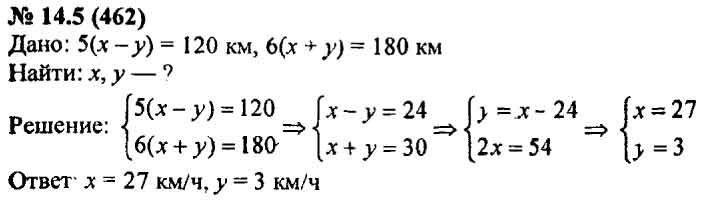
Мы должны найти сумму процентов за год
2000 (0,07) = 140
Найти сумму процентов за 5 лет
140 (5) = 700
Таким образом, Джо заплатит 700 долларов за 5 лет.
Вопрос 10.
У вас есть 550 долларов на сберегательном счете, который приносит 3% простых процентов каждый год. Сколько будет на вашем счету через 10 лет?
$ _______
Ответ: 715 $
Пояснение:
Дано,
У вас есть 550 долларов на сберегательном счете, который приносит 3% простых процентов каждый год.
Используйте формулу для простых процентов:
Bt = B0 (1 + tr)
Где t — временной интервал, Bt — деньги через t лет, B0 — депозит и r — проценты за один год, тогда формула принимает следующий вид:
B10 = В0 (1 + 10.г)
B10 = 550 (1 + 10 (0,03))
B10 = 715 $
На вашем счету через 10 лет будет 715 $.
Вопрос 11.
Мартин находит рубашку со скидкой 10% в универмаге. Первоначальная цена составляла 20 долларов. Мартин также должен заплатить 8,5% налог с продаж.
а. Сколько стоит рубашка без учета налогов?
$ _______
Ответ: 18
Пояснение:
Нам нужно найти продажную цену рубашки
20 — 0,1 (20) = 20 — 2 = 18
Цена рубашки без учета налогов составляет 18 долларов.
Вопрос 11.
б. Сколько стоит рубашка после уплаты налогов?
$ _______
Ответ: 19,53
Пояснение:
Нам нужно найти цену после уплаты налогов
18 + 0,085 (18) = 18 + 1,53 = 19,53
Цена рубашки после уплаты налогов составляет 19,53 доллара США
Вопрос 12.
Счет за ресторан Терезы составляет 29,99 доллара до налогообложения. Если налог с продаж составляет 6,25%, а она дает официанту чаевые в размере 20%, какова общая стоимость еды?
$ _______
Ответ: 37.86
Пояснение:
Учитывая,
счет за ресторан Терезы составляет 29,99 доллара до налогообложения. Если налог с продаж составляет 6,25%, и она дает официанту чаевые в размере 20%.
Найдите сумму налога с продаж
29,99 (0,0625) = 1,87
Найдите сумму чаевых
29,99 (0,20) = 6,00
Общая стоимость, добавив счет по счету, налог с продаж и сумму чаевых.
29,99 + 1,87 + 6,00 = 37,86
Таким образом, общая стоимость еды составляет 37,86 долларов США
Регистрация основных вопросов
Вопрос 13.
Как определить общую стоимость предмета, включая налог, если вы знаете цену предмета и ставку налога?
Введите ниже:
_____________
Ответ: Вы можете найти общую стоимость товара, включая налог, сначала умножив цену товара на ставку налога в десятичной форме, чтобы получить сумму налога с продаж. Затем добавьте к цене сумму налога с продаж, чтобы получить общую стоимость.
Процентные приложения — Независимая практика — Стр. № 157
Вопрос 14.
Еда Эмили стоит 32,75 доллара, а Даррена — 39,88 доллара. Эмили лечит Даррена, оплачивая оба приема пищи, и оставляет ему 14% чаевых. Найдите общую стоимость.
$ _______
Ответ: 82,80
Пояснение:
Еда Эмили стоит 32,75 доллара, а Даррена — 39,88 доллара.
Итак, общая стоимость обеда до чаевых составляет 32,75 доллара + 39,88 доллара = 72,63 доллара.
Эмили лечит Даррена, оплачивая оба приема пищи, и оставляет 14% чаевых.
72,63 доллара = 0,14 (72,63) ≈ 10,17 доллара
Округлить до двух десятичных знаков, поскольку суммы в долларах должны округляться до ближайшего цента.
Общая стоимость, которую платит Дарин, равна стоимости до чаевых + сумма чаевых = 72,63 доллара США + 10,17 доллара США = 82,80 доллара США
Вопрос 15.
Семья Джейден ест в ресторане, в котором действует акция со скидкой 15%. Их еда стоит 78,65 долларов, а чаевые они оставляют 20%. Если чаевые относятся к стоимости еды до скидки, какова общая стоимость еды?
$ _______
Ответ: 82,58
Пояснение:
Семья Джейден ест в ресторане, в котором действует акция со скидкой 15%.
Общая стоимость еды = стоимость еды + сумма чаевых — сумма скидки
Их еда стоит 78,65 долларов, и они оставляют 20% чаевых.
Нам нужно найти сумму чаевых и сумму скидки, используя данную стоимость еды, процент чаевых и процент скидки.
20% от 78,65 = 0,20 × 78,65 = 15,73 доллара
Поскольку стоимость обеда до скидки составляет 78,65 долларов, а процент скидки составляет 15%, то сумма скидки составляет
15% от 78365 = 0,15 × 78,65 долларов ≈ 11,80 долларов
Общая стоимость тогда составляет
78.65 + 15,73 — 11,80 = 82,58 $
Вопрос 16.
Ювелир покупает кольцо у производителя ювелирных изделий за 125 долларов. Он увеличивает цену на 135% для продажи в своем магазине. Какова продажная цена кольца с учетом налога с продаж 7,5%?
$ _______
Ответ: 315,78
Пояснение:
Ювелир покупает кольцо у ювелирного мастера за 125 долларов. Он увеличивает цену на 135% для продажи в своем магазине.
125 × 1,35 = 168,75
Мы можем найти розничную цену, добавив наценку к закупочной цене
125 + 168.75 = 293,75
Сумма налога с продаж составляет 293,75 × 0,075 = 22,03
Мы можем найти продажную цену, добавив сумму налога к розничной цене.
293,75 + 22,03 = 315,78
Следовательно, продажная цена кольца с учетом налога с продаж 7,5% составляет 315,78 долларов США
Вопрос 17.
Луис хочет купить скейтборд, который обычно продается за 79,99 доллара. На все товары действует скидка 12%. Какова общая стоимость скейтборда, если Луис должен заплатить государственный налог с продаж в размере 6,75%?
$ _______
Ответ: 75.14
Пояснение:
Учитывая,
Луис хочет купить скейтборд, который обычно продается за 79,99 доллара. На все товары действует скидка 12%.
79,99 × 0,12 = 9,60
79,99 — 9,60 = 70,39
Сначала нам нужно найти сумму, уплаченную в виде налогов, а затем добавить ее к цене со скидкой, чтобы получить общую стоимость.
70,39 × 0,0675 = 4,75
70,39 + 4,75 = 75,14
Общая стоимость скейтборда, если Луис должен заплатить государственный налог с продаж в размере 6,75%, составит 75,14 долларов США
Вопрос 18.
Кедар получает ежемесячную зарплату в размере 2200 долларов плюс 3 доллара.75% комиссии от суммы его продаж в магазине мужской одежды. Что бы он заработал в этом месяце, если бы продал одежду на 4500 долларов? Округлить до ближайшего цента.
$ _______
Ответ: 2368,75
Пояснение:
Учитывая,
Кедар получает ежемесячную зарплату в размере 2200 долларов плюс 3,75% комиссионных от суммы его продаж в магазине мужской одежды.
4500 × 0,0375 = 168,75
Общий заработок можно узнать, сложив его ежемесячную зарплату и его комиссионные.
2200 + 168,75 = 2368.75
Вопрос 19.
Даниэль получает комиссию в размере 7,25% от всего, что она продает в магазине электроники, где она работает. Она также получает базовую зарплату в 750 долларов в неделю. Сколько она заработала на прошлой неделе, если продала электронику на 4500 долларов? Округлить до ближайшего цента.
$ _______
Ответ: 1076,25
Пояснение:
Даниэль получает комиссию в размере 7,25% от всего, что она продает в магазине электроники, где она работает.
Она также получает базовую зарплату 750 долларов в неделю.
Сумма, которую она внесла в комиссию, составляет 4500 × 0,0725 = 326,25
Мы можем найти общий заработок, сложив ее еженедельную зарплату и комиссию.
750 + 326,25 = 1076,25
Таким образом, на прошлой неделе она заработала 1076,25 доллара, если продала электронику на 4500 долларов.
Вопрос 20.
Франсуа получает еженедельную зарплату в размере 475 долларов плюс 5,5% комиссионных от продаж в сувенирном магазине. Сколько он заработал бы за неделю, если бы продал товаров на 700 долларов? Округлить до ближайшего цента.
$ _______
Ответ: 513.50
Пояснение:
Учитывая это, Франсуа получает еженедельную зарплату в размере 475 долларов плюс 5,5% комиссионных от продаж в сувенирном магазине.
Сумма, которую он заработал в качестве комиссии
700 × 0,055 = 38,50
Мы можем найти общую сумму, которую он заработал, сложив его еженедельную зарплату и комиссию
475 + 38,50 = 513,50 долларов США
Вопрос 21.
Рост Сандры 4 фута. Пабло на 10% выше Сандры, а Микаэла на 8% выше Пабло
a. Объясните, как определить рост Микаэлы, используя предоставленную информацию.
Введите ниже:
_____________
Ответ:
Сначала мы должны найти 10% роста Сандры: 0,10 × 4 = 0,4
Это означает, что тогда рост Пабло 4 + 0,4 = 4,4 фута.
Затем найдите 8% роста Пабло: 4,4 × 0,08 = 0,352
Это означает, что рост Микаэлы 4,4 + 0,353 = 4,752 фута.
Вопрос 21.
б. Какой примерный рост Микаэлы в футах и дюймах?
_______ футов _______ дюймов
Ответ:
Преобразование футов в дюймы.
1 фут = 12 дюймов
4.752 = 4 + 0,752
0,752 = 12 × 0,752 = 9 дюймов
4 фута = 12 × 4 = 48 дюймов
Таким образом, приблизительная высота Микаэлы составляет 4 фута 9 дюймов.
Вопрос 22.
Юджин хочет купить джинсы в магазине, который дает скидку 10 долларов на все. Бирка на джинсах имеет скидку 50%. Первоначальная цена — 49,98 долларов.
а. Найдите общую стоимость, если скидка 50% применяется до скидки 10 долларов.
$ _______
ответ: 14,99 $
Пояснение:
Учитывая это,
Евгений хочет купить джинсы в магазине, который дает скидку 10 долларов на все.
Бирка на джинсах имеет скидку 50%. Первоначальная цена — 49,98 долларов.
0,5 × 49,98 = 24,99
Теперь вычтите скидку 10 долларов.
24,99 — 10 = 14,99
Общая стоимость, если скидка 50% применяется до скидки 10 долларов США, составляет 14,99 долларов США
Вопрос 22.
б. Найдите общую стоимость, если скидка 10 долларов применяется до 50% скидки.
$ _______
Ответ: 19,99 $
Пояснение:
Мы должны найти цену после скидки в 10 долларов, а затем найти 50% от этой цены, чтобы найти цену со скидкой.
49,98 — 10 = 39,98
0,5 × 39,98 = 19,99
Таким образом, общая стоимость, если скидка 10 долларов применяется до 50% скидки, составляет 19,99 долларов США
Процентные заявки — стр. № 158
Вопрос 23.
Multistep
Эрик загружает показанный купон и идет за покупками в Gadgets Galore, где он покупает цифровую камеру за 95 долларов и дополнительную батарею за 15,99 долларов.
а. Какова общая стоимость купона на цифровую камеру?
$ _______
Ответ: 101.49
Пояснение:
Используйте формулу для скидки:
DP = P — xP
Цена цифровой камеры:
DP = 95 — 0,1 (95)
DP = 95 — 9,5
DP = 85,5 $
Общая стоимость = 85,5 + 15,99 = 101,49 долл. США
США
Вопрос 23.
б. Какова общая стоимость, если купон применяется к дополнительной батарее?
$ _______
Ответ: 109,391
Пояснение:
Используйте формулу цены со скидкой:
DP = P — x.P
Цена цифровой камеры:
DP = 15.99 — 0,1 (15,99)
DP = 15,99 — 1,599
DP = 14,399 долларов США
Общая стоимость = 95 + 14,399 = 109,391 долларов США
Вопрос 23.
c. К какому товару Эрику следует применить скидку? Объяснять.
____________
Ответ: Ему следует применить скидку на цифровую камеру, потому что тогда общая стоимость будет меньше.
Вопрос 23.
д. После применения купона Эрик должен заплатить налог с продаж в размере 8%. Сколько стоит его общий счет?
$ _______
Ответ:
Используйте формулу для скидки
Если он использует купон на цифровую камеру, то его общая стоимость будет
T = DP + 0.08 × DP
T = 101,49 + 8,1192
T = 109,6029 долларов США
Если он использует купон для дополнительной батареи, его общая стоимость составит
T = DP + 0,08 × DP
T = 109,391 + 0,08 (109,391)
T = 118,14228 долларов США
Вопрос 24.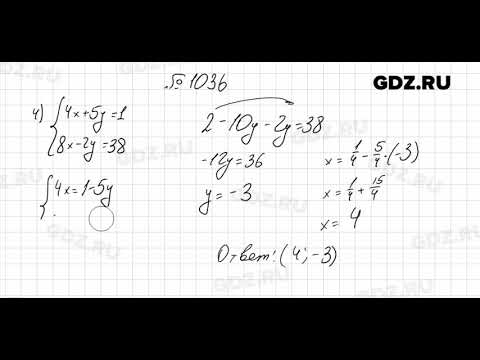
Два магазина продают одни и те же рубашки. Распродажа в Магазине 1 — «2 рубашки по 22 доллара», а в Магазине 2 — «Скидка 10% на каждую рубашку за 12,99 долларов».
а. Объясните, сколько вы сэкономите, купив в магазине 1.
$ _______
Ответ:
Для магазина 1 рубашки 2 за 22 доллара.Тогда рубашка Ecah стоит 22 доллара США ÷ 2 = 11
долларов8. В магазине 2 каждая рубашка имеет 10% скидку от 12,99 долларов США, поэтому каждая рубашка стоит:
долларов США — 0,1 (12,99) = 12,99 долларов США — 1,30 доллара США = 11,69 долларов США. за рубашку, если вы покупаете их в магазине 1.
Вопрос 24.
б. Если в Магазине 3 рубашки изначально продаются по цене 20,98 долларов со скидкой 55%, есть ли в нем более выгодные предложения, чем в других магазинах? Обосновать ответ.
_______
Ответ:
Если Store 3 продает рубашки со скидкой 55% от 20 долларов.98, то каждая рубашка стоит:
$ 20,98 — 0,55 (20,98 $) = 20,98 $ — 11,54 $ = 9,44 $
Это ниже, чем стоимость рубашки в Магазине 1 и Магазине 2, поэтому у него более выгодная сделка.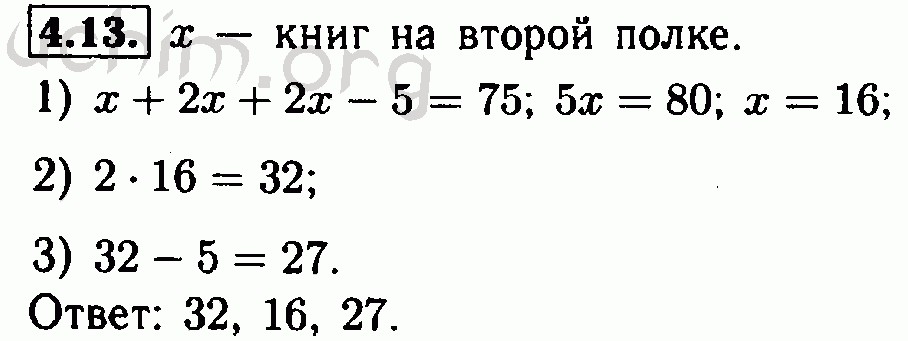
H.O.T.
Фокус на мышлении высшего порядка
Вопрос 25.
Анализ отношений
Маркус может выбирать между ежемесячной зарплатой в размере 1500 долларов плюс 5,5% от продаж или 2400 долларов плюс 3% от продаж. Он ожидает, что объем продаж составит от 5000 до 10 000 долларов в месяц. Какой вариант зарплаты выбрать? Объяснять.
_______
Ответ: Второй вариант зарплаты лучше
Пояснение:
E = 1500 + 0,055 (5000)
E = 1500 + 275
E = 1775 долларов США
Во втором случае он заработает
E = 2400 + 0,03 (5000)
E = 2400 + 150
E = 2550 долларов США
Вопрос 26.
Multistep
На уроке химии Боб записал объем жидкости как 13,2 мл. Фактический объем составлял 13,7 мл. Воспользуйтесь формулой, чтобы найти процентную ошибку измерения Боба с точностью до десятых долей процента.
_______%
ответ: 3,6%
Пояснение:
| 13,2 — 13,7 | /13,7 = | -0,5 | /13,7
0,5 / 13,7 ≈ 0,036 = 3,6%
ВИКТОРИНА ПО МОДУЛЮ — 5,1 процент увеличения и уменьшения — Стр.
 № 159
№ 159Найдите процентное изменение первого значения ко второму.
Вопрос 1.
36; 63
_______%
ответ: 75%
Пояснение:
Используйте формулу процентное изменение = сумма изменения / первое значение
сумма изменения = 27
Первое значение = 36
(63 — 36) / 36 = 27/36 = 0.75 = 75%
Вопрос 2.
50; 35
_______%
ответ: 30%
Пояснение:
Используйте формулу процентное изменение = сумма изменения / первое значение
сумма изменения = 15
Первое значение = 50
(50-35) / 35 = 15/50 = 0,3 = 30%
Вопрос 3.
40; 72
_______%
ответ: 80%
Пояснение:
Используйте формулу процентное изменение = сумма изменения / первое значение
сумма изменения = 32
Первое значение = 40
(72-40) / 40 = 32/40 = 0.8 = 80%
5.2 Наценка и уценка
Используйте исходную цену и уценку или наценку, чтобы найти розничную цену.
Вопрос 5.
Первоначальная цена: 60 долларов; Наценка: 15%
$ _______
Ответ: 69
$ Пояснение:
Используйте формулу: розничная цена = первоначальная цена + наценка
60 + 60 × 0,15 = 60 + 9 = 69
Вопрос 6.
Первоначальная цена: 32 доллара; Наценка: 12,5%
$ _______
Ответ: 36
Пояснение:
Используйте формулу: розничная цена = первоначальная цена + наценка
32 + 32 × 0.125 = 32 + 4 = 36
долларов Вопрос 7.
Первоначальная цена: 50 долларов США; Уценка: 22%
$ _______
Ответ: 39
Пояснение:
Используйте формулу: розничная цена = первоначальная цена + наценка
50-50 × 0,22 = 50-11 = 39
Вопрос 8.
Первоначальная цена: 125 долларов США; Уценка: 30%
$ _______
Ответ: 87,50
Пояснение:
Используйте формулу: розничная цена = первоначальная цена + наценка
125 — 125 × 0.3 = 125 — 37,50 = 87,50
5. 3 Процентные заявки
3 Процентные заявки
Вопрос 9.
Мэй Линг получает зарплату в размере 325 долларов в неделю плюс 6,5% комиссионных от продаж в сувенирном магазине. Сколько она заработала бы в рабочую неделю, если бы продала товаров на 4800 долларов?
$ _______
Ответ: 637
Пояснение:
Еженедельный заработок Мае Линг равен ее недельной зарплате плюс комиссионные.
Поскольку она получает комиссию от продаж в размере 6,5%, если она продала товаров на сумму 4800 долларов, ее комиссионный доход составил бы 6.5% от 4800 = 0,065 × 4800 = 312 долларов.
Поскольку ее недельная зарплата составляет 325, то ее общий недельный заработок составляет 325 долларов + 312 долларов = 637 долларов
Вопрос 10.
Рамон зарабатывает 1 735 долларов в месяц и платит 53,10 доллара за электричество. Какой процент заработка Рамона с точностью до десятых долей процента тратится на электроэнергию каждый месяц?
_______%
ответ: 3,1%
Пояснение:
Разделите оплату за электроэнергию на его ежемесячную зарплату
53,10 / 1735 = 0,031 = 3. 1%
1%
Вопрос 11.
Джеймс, Прия и Шивон работают в продуктовом магазине. Джеймс зарабатывает 7 долларов в час. Прия зарабатывает на 20% больше, чем Джеймс, а Шивон зарабатывает на 5% меньше, чем Прия. Сколько зарабатывает Шивон в час?
$ _______
Ответ: 7,98 в час
Пояснение:
Поскольку Джеймс зарабатывает 7 долларов в час, а прия зарабатывает на 20% больше, найдите 20% от 7, а затем прибавьте это к 7, чтобы найти почасовую оплату для Прии.
7 + 0,2 (7) = 7 + 1,40 = 8,40
Так как Прия зарабатывает 8 долларов.40 в час, а Шивон получает на 5% меньше, найдите 5% от 8,40 и вычтите это из 8,40, чтобы найти почасовую оплату Шивон.
8,40 — 0,05 (8,40) = 8,40 — 0,42 = 7,98
Вопрос 12.
Семья Ху идет обедать, цена обеда — 45 долларов. Налог с продаж на еду составляет 6%, и семья также оставляет чаевые в размере 20% от суммы до налогообложения. Какова общая стоимость еды?
$ _______
Ответ: 56,70
Пояснение:
Найдите сумму налога
45 × 0. 06 = 2,70
06 = 2,70
Найдите сумму чаевых
45 × 0,20 = 9
Найдите общую стоимость, сложив стоимость еды, налог и чаевые.
45 + 2,70 + 9 = 56,70 долл. США
Основной вопрос
Вопрос 13.
Приведите три примера того, как проценты используются в реальном мире. Скажите, представляет ли каждая ситуация процентное увеличение или процентное уменьшение.
Тип ниже:
____________
Ответ:
Один из примеров — давать чаевые, когда вы едите в ресторане.Поскольку стоимость увеличивается, она представляет собой увеличение в процентах.
Второй пример — налог на покупку. Поскольку цена увеличивается, это процентное увеличение.
Третий пример — использование купона при покупке товара. Поскольку цена снижается, это процентное снижение.
Выбранный ответ — стр. № 160
Вопрос 1.
Залмон проходит \ (\ frac {3} {4} \) милю за \ (\ frac {3} {10} \) час. Какая у него скорость в милях в час?
Опции:
а. 0,225 миль в час
0,225 миль в час
б.2,3 мили в час
c. 2,5 мили в час
d. 2,6 миль в час
Ответ: 2,5 мили в час
Пояснение:
Учитывая это,
Залмон проходит \ (\ frac {3} {4} \) милю за \ (\ frac {3} {10} \) часа.
Разделите количество миль на количество часов, чтобы получить его скорость в милях в час.
\ (\ frac {3} {4} \) ÷ \ (\ frac {3} {10} \)
\ (\ frac {3} {4} \) ÷ \ (\ frac {10} {3} \) = \ (\ frac {5} {2} \)
Преобразует дробь в десятичную форму.
\ (\ frac {5} {2} \) = 2.5 миль в час
Таким образом, правильный ответ — вариант C.
Вопрос 2.
Найдите процентное изменение от 70 до 56.
Варианты:
a. Снижение на 20%
б. 20% рост
c. Снижение на 25%
d. 25% рост
Ответ: увеличение на 20%
Объяснение:
Используйте процентное изменение = сумма изменения / исходная сумма.
Так как количество уменьшилось с 70 до 56, это уменьшение на процент.
= (70 — 56) / 70 = \ (\ frac {14} {70} \) = 0,2 = 20%
Таким образом, правильный ответ — вариант А.
Вопрос 3.
Общее количество осадков два года назад составляло 10,2 дюйма. Итого в прошлом году было на 20% больше. Сколько было осадков в прошлом году?
Опции:
а. 8.16 дюймов
b. 11,22 дюймов
c. 12,24 дюйма
d. 20,4 дюймов
Ответ: 12,24 дюйма
Пояснение:
Дано,
Всего два года назад выпало 10,2 дюйма. Итого в прошлом году было на 20% больше.
Найдите 20% от 10,2
10,2 × 0,20 = 2,04
Добавьте значение к исходной сумме 10.2
10,2 + 2,04 = 12,24
Следовательно, правильный ответ — вариант C.
Вопрос 4.
Пара баскетбольных кроссовок изначально была оценена в 80 долларов, но была повышена на 37,5%. Какова была розничная цена на обувь?
Опции:
а. $ 50
б. $ 83
c. $ 110
д. $ 130
Ответ: 110
$ Пояснение:
Первоначально цена пары баскетбольных кроссовок составляла 80 долларов, но была наценка на 37,5%.
Используйте формулу: розничная цена = первоначальная цена + наценка
80 + 80 × 0. 375 = 80 + 30 = 110
375 = 80 + 30 = 110
Таким образом, правильный ответ — вариант C.
Вопрос 5.
Ставка налога с продаж в городе Ян составляет 7,5%. Если она купит 3 лампы по 23,59 доллара каждая и диван за 769,99 доллара, сколько налога с продаж она должна?
Опции:
а. $ 58,85
б. $ 63.06
c. $ 67,26
д. 71,46 $
Ответ: 63,06 $
Пояснение:
Ставка налога с продаж в городе Ян составляет 7,5%.
Если она купит 3 лампы по 23,59 доллара каждая и диван за 769,99 доллара
Общая стоимость до налогообложения составляет 3 × 23.59 + 769,99
= 70,77 + 769,99 = 840,76
Найдите сумму налога, умножив налоговую ставку и общую стоимость из приведенного выше решения, а затем округлите до 2 десятичных знаков.
840,76 × 0,075 = 63,06
Таким образом, правильный ответ — вариант Б.
Вопрос 6.
На следующий день после национального праздника украшения уценены на 40%. Перед праздником патриотический баннер стоил 5,75 доллара. Сколько стоил баннер после праздника?
Сколько стоил баннер после праздника?
Опции:
а. 1,15 $
б. $ 2.30
c. 3 доллара.45
г. 8,05 долл. США
Ответ: 3,45 $
Пояснение:
На следующий день после национального праздника украшения были уценены на 40%. Перед праздником патриотический баннер стоил 5,75 доллара.
используйте формулу: розничная цена = исходная цена — уценка
5,75 — 5,75 × 0,4 = 5,75 — 2,30 = 3,45
Таким образом, правильный ответ — вариант C.
Вопрос 7.
Дастин зарабатывает 2330 долларов в месяц и платит 840 долларов за аренду. Какой процент заработка Дастина с точностью до десятых долей процента тратится на аренду?
Опции:
а.84%
б. 63,9%
г. 56,4%
г. 36,1%
ответ: 36,1%
Пояснение:
Дастин зарабатывает 2330 долларов в месяц и платит 840 долларов за аренду.
Разделите его ренту на его ежемесячный доход. округлить до трех знаков после запятой, а затем преобразовать в процентную форму.
840/2330 = 0,361 = 36,1%
Таким образом, правильный ответ — вариант D.
Вопрос 8.
Аквалангист находится на высоте -30 футов. На сколько футов ей придется подняться, чтобы сменить положение на -12 футов?
Опции:
а.-42 футов
б. -18 футов
c. 18 футов
д. 42 футов
Ответ: 18 футов
Пояснение:
Дано,
Аквалангист находится на высоте -30 футов.
-12 — (-30) = 12 + 30 = 18 футов
Таким образом, правильный ответ — вариант C.
Вопрос 9.
Банк предлагает годовую простую процентную ставку в размере 8% по ссудам на улучшение жилищных условий. Тобиас занял 17000 долларов сроком на 2 года. Сколько он всего вернул?
Опции:
а. 1360 $
б. $ 2720
c. $ 18360
д.$ 19720
Ответ: 19720 $
Пояснение:
Учитывая это,
Банк предлагает годовую простую процентную ставку в размере 8% по ссудам на улучшение жилищных условий.
Тобиас взял взаймы 17000 долларов на период в 2 года
Найдите сумму процентов, которые он уплатил, используя формулу
I = prt
, где p — сумма займа
r — процентная ставка
t — количество лет
17000 × 0,08 × 2 = 2720
Добавьте сумму займа и сумму процентов
17000 + 2720 = 19720.
Таким образом, правильный ответ — вариант D.
Мини-задание
Вопрос 10.
Мюсли, закупаемые летом, раньше стоили 6 долларов за фунт, но сейчас наценка была на 15%.
а. Сколько стоило Лето купить 2,6 фунта мюсли по старой цене?
$ ___________
Ответ: 15,60 $
Пояснение:
Умножьте 2,6 на старую цену 6 долларов
2,6 × 6 = 15,60
Купить 2,6 фунта мюсли по старой цене стоит 15,60 доллара.
Вопрос 10.
г. Во сколько ей обойдется покупка 2,6 фунта мюсли по новой цене?
$ _______
Ответ: 17,94 $
Пояснение:
Найдите новую цену по формуле: розничная цена = первоначальная цена + наценка
Затем найдите общую стоимость, купив 2,6 фунта по новой цене.
6 + 6 × 0,15 = 6 + 0,9 = 6,90
2,6 × 6,90 = 17,94
Новая цена 17,94 $
Вопрос 10.
c. Предположим, Саммер покупает 3,5 фунта мюсли. Насколько дороже он будет стоить по новой цене, чем по старой цене?
$ _______
Ответ: 3 доллара. 15
15
Пояснение:
3,5 × 6 = 21
3,5 × 6,90 = 24,15
24,15 — 21 = 3,15
Модуль 5 — Стр. № 162
УПРАЖНЕНИЯ
Вопрос 1.
В январе Мишель купила 25 аудиофайлов. В феврале она приобрела 40 аудиофайлов. Найдите процент увеличения.
_______%
ответ: 60%
Пояснение:
Дано,
Мишель купила 25 аудиофайлов в январе. В феврале она приобрела 40 аудиофайлов.
Используйте процентное изменение = сумма сдачи / исходная сумма.
(40-25) / 25 = 15/25 = 0,6 = 60%
Таким образом, процентное увеличение составляет 60%
Вопрос 2.
Собака Сэма весит 72 фунта. Ветеринар предполагает, что для здоровья собаки ее вес должен уменьшиться на 12,5 процента. По мнению ветеринара, какой здоровый вес для собаки?
_______ фунтов
Ответ: 63 фунта
Пояснение:
Дано, собака Сэма
весит 72 фунта. Ветеринар предполагает, что для здоровья собаки ее вес должен снизиться на 12,5 процента.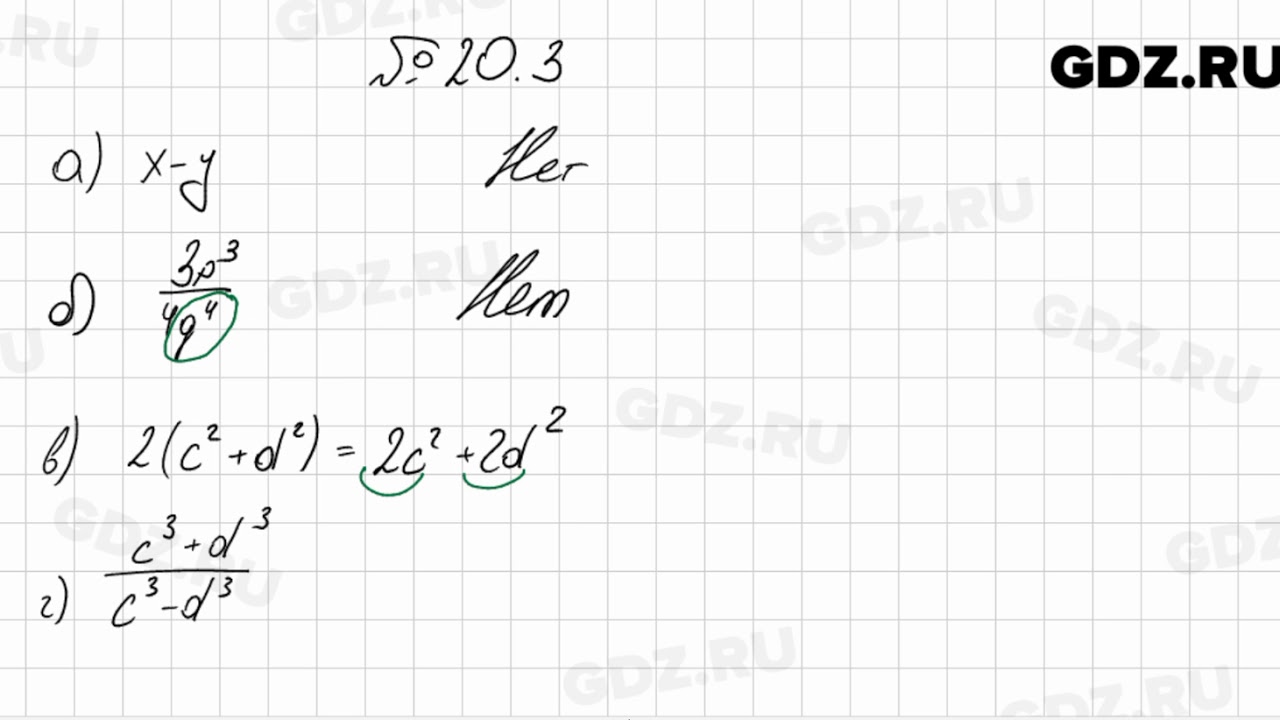
72 × 0.125 = 9
Найдите здоровый вес, вычтя изменение веса из исходного веса
72 — 9 = 63
Здоровый вес собаки составляет 63 фунта.
Вопрос 3.
Первоначальная цена гриля для барбекю составляет 79,50 долларов. Гриль уценен на 15%. Какова продажная цена гриля?
$ _______
Ответ: 67,57
Пояснение:
Дано,
Первоначальная цена гриля для барбекю составляет 79,50 долларов. Гриль уценен на 15%.
Используйте формулу продажная цена = исходная цена — уценка
= 79.50 — 79,50 × 0,15 = 79,50 — 11,93 = 67,57 долларов США
Таким образом, отпускная цена гриля составляет 67,57 долларов США
Вопрос 4.
Магазин спорттоваров увеличивает стоимость футбольных мячей на 250%. Напишите выражение, представляющее розничную стоимость футбольных мячей. Магазин покупает футбольные мячи по 5 долларов за штуку. Какова розничная цена футбольных мячей?
$ _______
Ответ: 17,5 $
Объяснение:
Используйте формулу розничная цена = исходная цена + наценка, чтобы найти выражение для исходной цены s и процента наценки 250%
s + 2. 5s = 3,5s
5s = 3,5s
подставьте в выражение s = 5, чтобы найти розничную цену
3,5 × 5 = 17,50
Таким образом, розничная цена футбольных мячей составляет 17,50 долларов США
Задачи выполнения блока 2 — Стр. № 163
Вопрос 1.
Виктор — велосипедный туроператор, и ему необходимо заменить два своих туристических велосипеда. Он заказывает два велосипеда в магазине спортивных товаров на общую сумму 2000 долларов и расплачивается кредитной картой. Когда приходит счет, он читает следующую информацию:
Остаток: 2000 долларов
Годовая процентная ставка: 14.9%
Минимальная сумма платежа: 40 долларов США
Комиссия за просрочку платежа: 10 долларов США, если платеж не получен до 1 марта 2013 г.
a. Чтобы сохранить хорошую репутацию, Виктор незамедлительно отправляет минимальный платеж в размере 40 долларов. Когда приходит следующий счет, он очень похож на предыдущий.
Остаток: 1984,34 доллара
Годовая процентная ставка: 14,9%
Минимальный причитающийся платеж: 40 долларов
Комиссия за просрочку: 10 долларов, если платеж не получен до 01.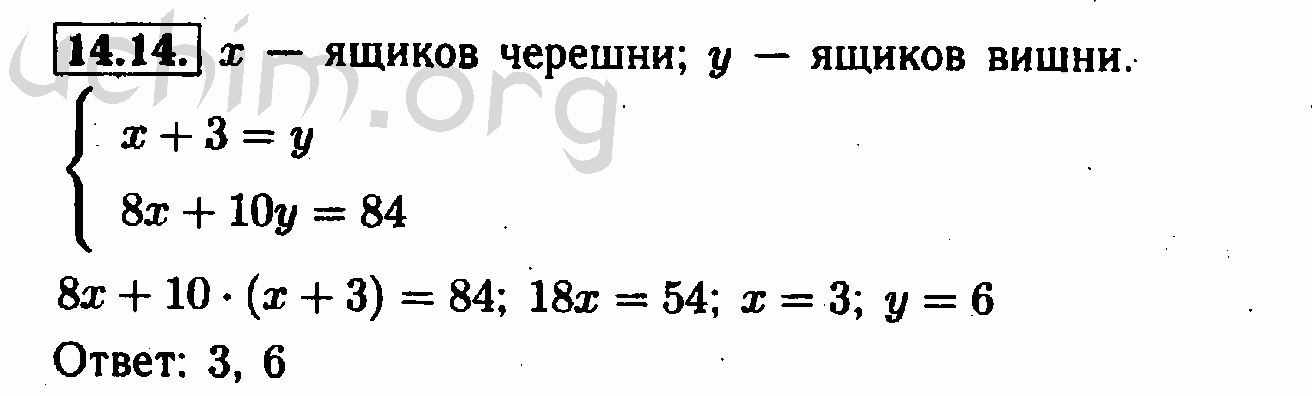 04.2013
04.2013
Объясните, как компания-эмитент кредитной карты рассчитала новый баланс. Обратите внимание, что указанная процентная ставка является годовой, но выплата ежемесячная.
Введите ниже:
_____________
Ответ:
Мы должны найти баланс после первого счета, вычтя платеж в размере 40 долларов из первоначального баланса в 2000 долларов.
Остаток после первого векселя: 2000 — 40 = 1960
Затем найдите сумму процентов, начисленных на второй вексель, умножив остаток в размере 1960 долларов на процентную ставку.
Помните, поскольку процентная ставка является годовой, вы должны разделить ее на 12, чтобы получить ежемесячную процентную ставку.
Проценты по второй купюре: 1960 × 0.149/12 = 24,34
И затем добавьте эту сумму процентов к остатку в 1960 долларов, чтобы получить остаток по второму счету.
Новый баланс: 1960 + 24,34 = 1984,34
Вопрос 1.
б. Виктор был расстроен новым счетом и решил внести 150 долларов в качестве оплаты за апрель.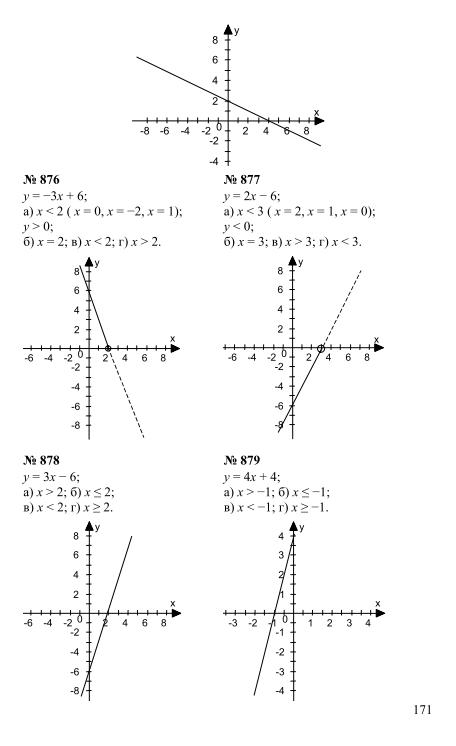 Минимальный платеж по его счету рассчитывается как 2% от баланса (с округлением до ближайшего доллара) или 20 долларов, в зависимости от того, что больше. Заполните детали нового счета Виктора.
Минимальный платеж по его счету рассчитывается как 2% от баланса (с округлением до ближайшего доллара) или 20 долларов, в зависимости от того, что больше. Заполните детали нового счета Виктора.
Введите ниже:
_____________
Ответ:
Найдите остаток после выплаты 150 долларов.Процентная ставка не изменилась, поэтому годовая процентная ставка по этому новому векселю такая же, как и по предыдущим векселям.
остаток после оплаты: 1984,34 — 150 = 1834,34
годовая процентная ставка: 14/9%
Найдите проценты по третьему векселю. Найдите остаток на третьем счете, добавив начисленные проценты к остатку в размере 1834,34 доллара.
процентов по третьему счету: 1834,34 × 0,149 / 12 = 22,78
остаток: 1834,34 + 22,78 = 1857,12
Чтобы узнать, какой будет минимальный платеж, сначала найдите 2% от баланса.
2% от баланса: 0,02 × 1857,12 = 37,14
Минимальный платеж: 37,00 долларов
Так как это больше 20 долларов, минимальный платеж составляет 2% от баланса, округленный до ближайшего доллара, что дает 37 долларов в качестве платежа.
Более поздняя дата сбора — один месяц после даты просрочки уплаты 01.04.2013 в предыдущем счете, который дает 01.05.2013.
Вопрос 1.
c. Банк Виктора предлагает кредитную карту с начальной процентной ставкой 9,9% годовых. Он может перевести свой текущий баланс за плату в размере 40 долларов.Через год ставка вернется к обычной ставке банка, которая составляет 13,9%. Банк взимает штраф за просрочку платежа в размере 15 долларов США. Назовите две причины, по которым Виктору следует перевести баланс, и две причины, почему он не должен.
Введите ниже:
_____________
Ответ: Две причины, по которым он должен перейти, заключаются в том, что более низкая начальная ставка будет означать меньшие проценты, взимаемые в первый год, а более низкая нормальная ставка будет означать меньшие проценты, взимаемые и после этого первого года. Две причины, по которым ему не следует переводить остаток, заключаются в том, что ему придется заплатить комиссию за перевод в размере 40 долларов и что плата за просрочку платежа составляет 15 долларов вместо 10 долларов, если он переводит остаток.
Задачи выполнения блока 2 (прод.) — Стр. № 164
Вопрос 2.
В таблице ниже показано, как далеко могут пройти несколько животных на своей максимальной скорости за заданное время.
а. Запишите скорость каждого животного в футах в секунду.
Лось: _________ футов в секунду
Жираф: _________ футов в секунду
Зебра: _________ футов в секунду
Ответ:
Посмотрев на приведенную выше таблицу, мы можем найти единицы измерения, разделив пройденное расстояние на время в секундах.
лось: 33 ÷ 1/2 = 33 × 2 = 66 футов в секунду
Жираф: 115 ÷ 2 1/2 = 115 ÷ 5/2 = 115 2/5 = 46 футов в секунду
Зебра: 117 ÷ 2 = 58,5 футов в секунду
Вопрос 2.
б. У какого животного самая быстрая скорость?
_____________
Ответ: У лося самая высокая удельная скорость, поэтому у него самая быстрая скорость.
Вопрос 2.
c. Сколько миль могло бы пройти самое быстрое животное за 2 часа, если бы оно сохраняло скорость, рассчитанную вами в части а? Используйте формулу d = rt и округлите ответ до ближайшей десятой мили..jpg) Показать свою работу.
Показать свою работу.
Лось: _________ миль
Жираф: _________ миль
Зебра: _________ миль
Ответ:
Лось: 90 миль
Жираф: 62 мили
Зебра: 72 мили
Пояснение:
В одной минуте 60 секунд, а в часе 60 минут, поэтому 2 × 60 × 60 = 7200 секунд в 2 часах.
Умножьте скорость лося на 7200 секунд, чтобы получить пройденное расстояние в футах.
В 1 миле 5280 футов, поэтому разделите расстояние в футах на 5280, чтобы получить расстояния в милях.
Лось:
66 × 7200 = 475200 футов
Теперь конвертируем из футов в мили
475200 футов = 90 миль
Жираф: 46 футов в секунду
62 × 7200 = 331200 футов
Теперь конвертируем из футов в мили.
331200 = 62 мили
Зебра: 58,5 футов в секунду
58,5 × 7200 = 421200 футов
Теперь конвертируем из футов в мили.
421200 футов = 72 мили
Вопрос 3.
д. Данные в таблице показывают, насколько быстро каждое животное может двигаться с максимальной скоростью. Разумно ли ожидать, что животное из части b преодолеет это расстояние за 2 часа? Объясните, почему да или почему нет.
Разумно ли ожидать, что животное из части b преодолеет это расстояние за 2 часа? Объясните, почему да или почему нет.
______
Ответ: Это неразумно. Животное может двигаться со своей максимальной скоростью только в течение короткого промежутка времени, который обычно составляет всего пару минут.
Выбранный ответ — Страница № 165
Вопрос 1.
Если соотношение между расстоянием y в футах и временем x в секундах пропорционально, какая скорость представлена выражением \ (\ frac {y} {x} \) = 0,6?
Опции:
а. 3 фута за 5 с
б. 3 фута за 9 с
c. 10 футов за 6 с
д. 18 футов за 3 с
Ответ: 3 фута за 5 с
Объяснение:
\ (\ frac {y} {x} \) = 0.6
0,6 = \ (\ frac {6} {10} \)
Поскольку \ (\ frac {6} {10} \) = \ (\ frac {3} {5} \), он представляет собой коэффициент 3 футов за 5 секунд,
Следовательно, правильный ответ — вариант A.
Вопрос 2.
Баграмы регулярно делают ежемесячные вклады на сберегательный счет. График показывает взаимосвязь между количеством месяцев x и суммой y в долларах на счете.
График показывает взаимосвязь между количеством месяцев x и суммой y в долларах на счете.
Какое уравнение для депозита?
Опции:
а. \ (\ frac {y} {x} \) = 25 долларов в месяц
б. \ (\ frac {y} {x} \) = 40 долларов в месяц
c.\ (\ frac {y} {x} \) = 50 долларов в месяц
d. \ (\ frac {y} {x} \) = 75 долларов в месяц
Ответ: \ (\ frac {y} {x} \) = 50 долларов в месяц
Пояснение:
Глядя на график выше, мы можем сказать, что это точка (2, 100). Это означает, что \ (\ frac {y} {x} \) = \ (\ frac {100} {2} \) = 50.
Таким образом, правильный ответ — вариант C.
Вопрос 3.
Какая десятичная форма у −4 \ (\ frac {7} {8} \)?
Опции:
а. -4.9375
б. -4.875
с. -4,75
г. -4,625
Ответ: -4,875
Пояснение:
Дано дробь
−4 \ (\ frac {7} {8} \)
Первое деление \ (\ frac {7} {8} \) = 0.875
4 + 0,875 = 4,875
Итак, −4 \ (\ frac {7} {8} \) = -4,875
Следовательно, ответ — вариант B.
Вопрос 4.
Найдите процентное изменение от 72 до 90.
Варианты:
a. Снижение на 20%
б. 20% рост
c. Снижение на 25%
d. 25% рост
Ответ: увеличение на 25%
Объяснение:
Используйте формулу процентного изменения = сумма изменения / исходная сумма.
значение увеличилось с 72 до 90, так что это процентное увеличение.
(90-72) / 72 = 18/72 = 0.25 = 25%
Таким образом, правильный ответ — вариант D.
Вопрос 5.
В магазине была распродажа товаров для искусства. Цена p каждого товара была снижена на 60%. Какое выражение представляет новую цену?
Опции:
а. 0,4п
б. 0,6п
г. 1.4п
г. 1.6p
Ответ: 0.4p
Пояснение:
Учитывая это,
В магазине была распродажа художественных принадлежностей.
Цена p каждого товара была снижена на 60%
Используйте формулу продажная цена = исходная цена — уценка
p — это исходная цена, а процент уценки составляет 40%, затем объедините аналогичные условия.
p — 0,6p = 0,4p
Следовательно, правильный ответ — вариант А.
Вопрос 6.
Кларк занимает 16 000 долларов на покупку автомобиля. Он платит простые проценты по ставке 6% годовых в течение 3,5 лет. Сколько он вообще платит?
Опции:
а. 18800 $
б. $ 19360
c. $ 19920
д. $ 20480
Ответ: 19360 $
Пояснение:
Учитывая, что
Кларк занимает 16 000 долларов на покупку машины.
Он платит простые проценты по ставке 6% годовых в течение 3 лет.5 лет.
Найдите общую сумму процентов по формуле
I = prt
, где p — это сумма займа
r — процентная ставка
t — количество лет
16000 × 0,06 × 3,5 = 3360
Теперь добавьте сумму процентов к сумме заимствования, чтобы найти общую сумму
16000 + 3360 = 19,360
Таким образом, правильный ответ — вариант B.
Вопрос 7.
К какому набору или наборам принадлежит число 37?
Опции:
а. только целые числа
б. только рациональные числа
c.только целые и рациональные числа
d. целые, целые и рациональные числа
Ответ: целые, целые и рациональные числа
Пояснение:
37 можно записать как 37/1, так что это рациональное число. 37 не имеет десятичной дроби или дроби, поэтому является целым числом. Поскольку это положительное целое число, это также целое число.
Таким образом, подходящий ответ — вариант D.
Стр. № 166
Вопрос 8.
В каком уравнении коэффициент пропорциональности 5?
Опции:
а.х = 5у
б. y = 5x
c. у = х + 5
г. у = 5 — х
Ответ: y = 5x
Пояснение:
Уравнения прямой пропорциональности имеют вид y = kx
, где k — коэффициент пропорциональности.
Если k = 5, то уравнение y = 5x.
Таким образом, правильный ответ — вариант Б.
Вопрос 9.
Сури подрабатывает выгуливанием собак. Она берет 6,25 доллара за выгул собаки один раз в день 5 дней в неделю и 8,75 доллара за выгул собаки один раз в день 7 дней в неделю. Какое уравнение представляет эту взаимосвязь?
Опции:
а.y = 7x
б. y = 5x
c. y = 2,50x
г. y = 1,25x
Ответ: y = 1,25x
Пояснение:
Учитывая это,
Сури подрабатывает выгуливанием собак. Она берет 6,25 доллара за выгул собаки один раз в день 5 дней в неделю и 8,75 доллара за выгул собаки один раз в день 7 дней в неделю.
Так как 6,25 / 5 = 1,25
Итак, уравнение y = 1,25x
, где x — количество дней, а y — общий заряд.
Итак, правильный ответ — вариант D.
Вопрос 10.
Рэнди проходит \ (\ frac {1} {2} \) милю за каждый \ (\ frac {1} {5} \) час.Как далеко Рэнди пройдет за час?
Опции:
а. \ (\ frac {1} {2} \) миль
б. 2 мили
c. 2 \ (\ frac {1} {2} \) миль
дн. 5 миль
Ответ: 2 \ (\ frac {1} {2} \) миль
Пояснение:
Учитывая,
Рэнди проходит \ (\ frac {1} {2} \) милю за каждый \ (\ frac {1} {5} \) час.
\ (\ frac {1} {2} \) ÷ \ (\ frac {1} {5} \)
\ (\ frac {1} {2} \) × \ (\ frac {5} {1} \) = \ (\ frac {5} {2} \)
Преобразуйте дробь в неправильные дроби.
\ (\ frac {5} {2} \) = 2 \ (\ frac {1} {2} \) миль
Следовательно, правильный ответ — вариант C.
Вопрос 11.
Во время поездки в Испанию Шейла купила ювелирное изделие стоимостью 56,75 доллара. Она заплатила за это своей кредитной картой, которая взимает комиссию за иностранную транзакцию в размере 3%. Какова комиссия за зарубежную транзакцию?
Опции:
а. $ 0,17
б. $ 1,07
c. $ 1,70
д. 17,00 $
Ответ: 1,70 $
Пояснение:
Во время поездки в Испанию Шейла купила украшение стоимостью 56,75 доллара.
Она заплатила за это своей кредитной картой, которая взимает комиссию за зарубежную транзакцию в размере 3%.
Найдите сумму комиссии за иностранную транзакцию, умножив стоимость на процент комиссии за иностранную транзакцию.
56,75 × 0,03 = 1,70
Таким образом, правильный ответ — вариант C.
Вопрос 12.
Пекарь ищет рецепт, который имеет наименьшую удельную норму муки на партию кексов. Какой рецепт ей следует использовать?
Опции:
а. \ (\ frac {1} {2} \) стакан муки для \ (\ frac {2} {3} \) партии
б. \ (\ frac {2} {3} \) стакан муки для \ (\ frac {1} {2} \) партии
c. \ (\ frac {3} {4} \) стакан муки для \ (\ frac {2} {3} \) партии
d. \ (\ frac {1} {3} \) стакан муки для \ (\ frac {1} {4} \) партии
Ответ: \ (\ frac {1} {2} \) стакан муки для \ (\ frac {2} {3} \) партии
Пояснение:
а.\ (\ frac {1} {2} \) ÷ \ (\ frac {2} {3} \) = \ (\ frac {1} {2} \) × \ (\ frac {3} {2} \ ) = \ (\ frac {3} {4} \)
б. \ (\ frac {2} {3} \) ÷ \ (\ frac {1} {2} \) = \ (\ frac {2} {3} \) × \ (\ frac {2} {1} \ ) = \ (\ frac {4} {3} \) = 1 \ (\ frac {1} {3} \)
c. \ (\ frac {3} {4} \) ÷ \ (\ frac {2} {3} \) = \ (\ frac {3} {4} \) × \ (\ frac {3} {2} \ ) = \ (\ frac {9} {8} \) = 1 \ (\ frac {1} {8} \)
г. \ (\ frac {1} {3} \) ÷ \ (\ frac {1} {4} \) = \ (\ frac {1} {3} \) ÷ \ (\ frac {4} {1} \ ) = 1 \ (\ frac {1} {3} \)
Таким образом, правильный ответ — вариант A.
Мини-задание
Вопрос 13.
Кевин умел печатать 2 страницы за 5 минут, 3 страницы за 7,5 минут и 5 страниц за 12,5 минут.
а. Составьте таблицу данных.
Тип ниже:
___________
Ответ:
| Количество страниц | 2 | 3 | 5 |
| Минуты | 5 | 7,5 | 12,5 |
Вопрос 13.
b. Изобразите зависимость между количеством набранных страниц и количеством минут.
Тип ниже:
___________
Ответ:
Вопрос 13.
c. Объясните, как использовать график для определения удельной стоимости.
Тип ниже:
___________
Ответ: Скорость печати 2,5 стр. В минуту
Пояснение:
С помощью графика нам нужно найти наклон прямой.
Мы можем сделать это, используя формулу наклона:
м = (y2-y1) / (x2-x1) = (7,5-5) / (3-2) = 2,5
Таким образом, удельная ставка составляет 2,5 страницы на минута.
Заключение:
Оставайтесь с нами, чтобы получить ключ с ответом по математике для всех классов по главам. Обратитесь к нашему Ключу ответов для 7-го класса по математике, чтобы получить решения с пояснениями. После подготовки проверяет свои знания, решая вопросы в заданиях на исполнение.
Свойства умножения
Чтения к Сессии 10 — Свойства сложения и стандартный алгоритм
Свойства для добавления целых чисел
Коммутативная собственность Умножение: Коммутативная собственность Умножение целых чисел говорит о том, что порядок факторов не меняет продукт.
Общая собственность: ab = ба
Числовой пример: 3 × 5 = 15 = 5 × 3
Алгебраический пример: (3 x ) (4 x ) = (4 x ) (3 x )
Ассоциативное свойство Умножение: Ассоциативное свойство Умножение из Целые числа говорят, что то, как сгруппированы факторы, не поменять товар.
Общая недвижимость: ( ab ) c = a ( до н.э. )
Числовой пример: (2 × 6) × 8 = 12 × 8
знак равно
96
= 2 ×
48
= 2 × (6 ×
8)
Алгебраический пример: 2 ∙ (3 x ) = (2 ∙ 3) x
знак равно 6 х
Обратите внимание, что в этом случае перегруппировка позволяет упростить выражение.
Пример: Мы покажем, как ассоциативные и коммутативные свойства для умножения целых чисел используются для упрощения алгебраическое выражение.
(3 x ) (4 x ) = 3 ( х ∙ 4) х Ассоциативное свойство умножения
знак равно 3 (4 ∙ x ) х Коммутативное свойство умножения
знак равно (3 ∙ 4) ( х ∙ x ) Ассоциативное свойство умножения
знак равно 12 x 2
Свойство идентичности для Умножение: Identity Property для Умножение из Целые числа говорят, что когда значение умножается на единицу продукт и есть эта ценность; я.е. умножение на единицу не изменить значение числа. Один называется мультипликативная идентичность.
Общая собственность: 1 ∙ = a ∙ 1 = a
Числовой пример: 1 ∙ 5 = 5 ∙ 1 = 5
Алгебраический пример: 1 (4 x ) = (4 x ) ∙ 1 = 4 x
Распределительные свойства умножения: Распределительная собственность Умножение на сложение целых чисел ( Распределительная собственность Умножение над вычитанием целых чисел ) показывает нам, как умножение значения на сумму (разницу) может быть разбивается на сумму (разность) отдельных товаров.
Общая собственность: а ( б + с ) = ab + ac или же а ( б — с ) = ab — ac
Числовой пример: 4 (145) = 4 (100 + 40 + 5)
знак равно 4 (100) + 4 (40) + 4 (5)
знак равно 400 + 160 + 20
знак равно 580
Алгебраический пример: 5 (3 x + 9) = 5 (3 x ) + 5 (9)
знак равно (5 ∙ 3) х + 5 (9)
знак равно 15 х + 45
Обратите внимание, что ассоциативное свойство умножения используется в второй шаг.


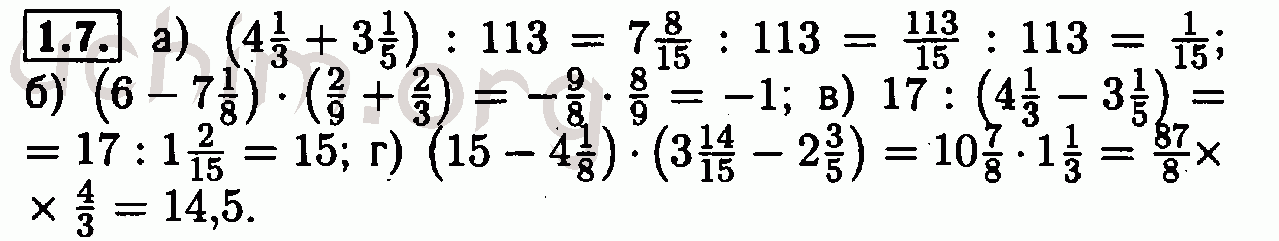

 Запишите этот номер в стандартной форме, используя цифры.
Запишите этот номер в стандартной форме, используя цифры.  92 до ближайшего целого числа.
92 до ближайшего целого числа. 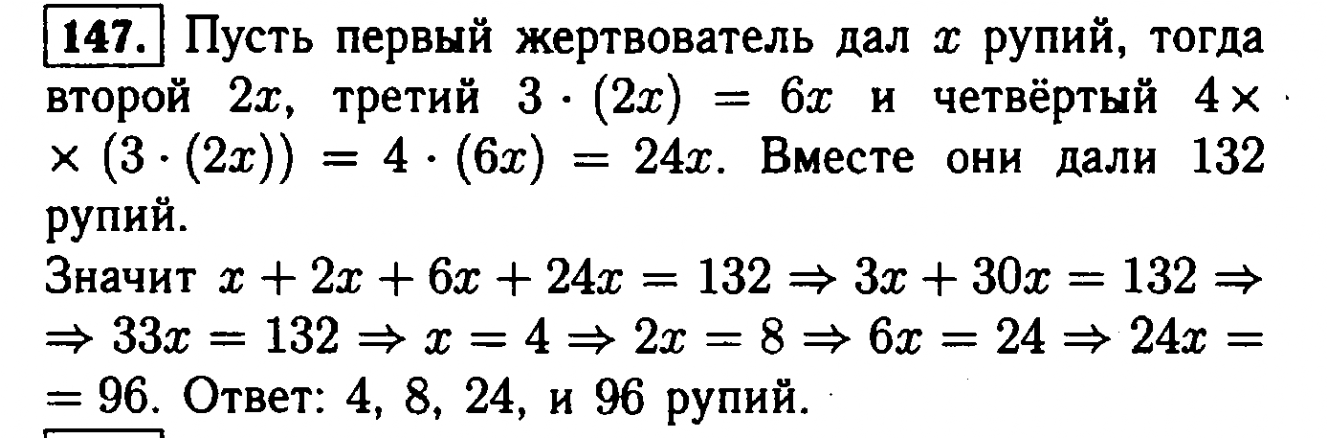 Она читала по 16 страниц каждый день в течение первых 15 дней и 18 страниц каждый день в течение последних 5 дней.Сколько страниц прочитала Юля?
Она читала по 16 страниц каждый день в течение первых 15 дней и 18 страниц каждый день в течение последних 5 дней.Сколько страниц прочитала Юля?  5
5