Законы сложения целых чисел. — tutomath.ru репетитор по математике
Home » 6 класс » Законы сложения целых чисел.
Posted on Author admin 0
Законы сложения целых чисел нужны для того, чтобы упростить сложения чисел. Ведь, прибавить все подряд числа не всегда легко, иногда лучше их сгруппировать. Для этого и нужны законы сложения целых чисел.
Переместительный закон сложения.
Правило и формула переместительного закона сложения.
Сложение двух целых чисел не зависит от их порядка.
a+b=b+a
Пример:
Если мы сложим 3+5=8 или 5+3=8 результат сложения не измениться.
Если мы сложим (-3)+7=4 или 7+(-3)=4 результат сложения не измениться.
Сочетательный закон сложения.
Правило и формула сочетательного закона сложения.
К сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего, и результат не измениться.
(a+b)+c=a+(b+c)
Рассмотрим пример:
(3+5)+9=8+9=17
3+(5+9)=3+14=17
От сочетания слагаемых сумма не поменялась.
Делаем вывод на основе переместительного и сочетательного законов:
- Можно слагаемые менять местами.
- Записывать пример со слагаемыми со скобками, для более простого вычисления суммы.
Доказательство:
a+b+c+d=(a+b+c)+d=d+(a+b+c)= d+((a+b)+c)= d+(c+(a+b))=(d+c)+(a+b)=(c+d)+(a+b)
a+b+c+d=(c+d)+(a+b)
6+8+(-6)+(-8)=(6+(-6))+(8+(-8))=0+0=0
Вопросы по теме:
Какие законы сложения вы знаете?
Ответ: переместительный и сочетательный закон.
Можно ли менять местами слагаемые?
Ответ: да по переместительному закону.
Обязательно ли при сложении числа заключать в скобки?
Ответ: нет.
Пример №1:
Вычислите, применяя законы сложения: а) 12+479+88 б) 3+154+16
Решение:
а) 12+479+88=(12+88)+479=100+479=579
б) 3+154+16=3+(154+16)=3+170=173
Пример №2:
Примените переместительный закон сложения: а) 4+5 б) 1298+34
Решение:
а) 4+5=5+4=9
б) 1298+34=34+1298=1332
Пример №3:
Примените сочетательный закон сложения: а) 2+(-4+5) б) (-1+3)+(-8)
Решение:
а) 2+(-4+5)=(2+(-4))+5=(-2)+5=3
б) (-1+3)+(-8)=-1+(3+(-8))=-1+(-5)=-6
Пример №4:
Вычислите, применяя законы сложения: а) 23+((-23)+50) б) -2+(-4)+(-8)+8+4+2
Решение:
а) 23+((-23)+50)=(23+(-23))+50=0+50=50
б) -2+(-4)+(-8)+8+4+2=(-2+2)+(-4+4)+(-8+8)=0
Ответы Задание 6 1 Часть § 2.
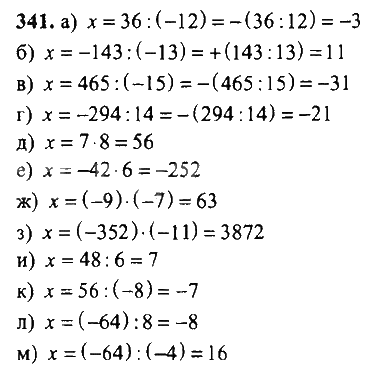5. Законы сложения целых чисел ГДЗ по математике 6 класс рабочая тетрадь Ерина к учебнику Никольского1 Часть
§ 1.1. Отношения чисел и величин
12345678910111213
§ 1.2. Масштаб
123456789101112
§ 1.3. Деление числа в данном отношении
12345678
§ 1.4. Пропорции
12345678910111213
§ 1.5. Прямая и обратная пропорциональность
123456789101112
§ 1.6. Понятие о проценте
123456789
§ 1.7. Задачи на проценты
1234567891011121314
§ 1.8.. Круговые диаграммы
1234567
§ 1.8. Дополнение к главе 1
1. Задачи на перебор всех возможных вариантов
12345678910111213141516
2. Вероятность события
12345678910
3.
Занимательные задачи
1234567891011
§ 2.1. Отрицательные целые числа
123456789101112
§ 2.2. Противоположные числа. Модуль числа
12345678910111213141516
§ 2.3. Сравнение целых чисел
1234567891011
§ 2.4. Сложение целых чисел
1234567891011121314151617181920
§ 2.5. Законы сложения целых чисел
1234567
§ 2.6. Разность целых чисел
1234567891011
§ 2.7. Произведение целых чисел
123456789101112
§ 2.8. Частное целых чисел
12345678
§ 2.9. Распределительный закон
123456789101112
§ 2.10. Раскрытие скобок и заключение в скобки
1234567891011
§ 2.
11. Действия с суммами нескольких слагаемых12345678910
§ 2.12.. Представление целых чисел на координатной оси
1234567891011
§ 2.12. Дополнения к главе 2
1. Фигуры на плоскости, симметричные относительно точки
1234567891011
2. Занимательные задачи
1234567
§ 3.1. Отрицательные дроби
12345678910111213141516
§ 3.2. Рациональные числа
1234567891011
§ 3.3. Сравнение рациональных чисел
12345678910
§ 3.4. Сложение и вычитание дробей
1234567891011121314151617181920
§ 3.5. Умножение и деление дробей
123456789101112131415161718
§ 3.6. Законы сложения и умножения
123456789
§ 3.
7. Смешанные дроби произвольного знака1234567891011121314
2 Часть
§ 3.8. Изображение рациональных чисел на координатной оси
1234567891011121314
§ 3.9. Уравнения
1234567891011
§ 3.10.. Решение задач с помощью уравнений
12345678910
§ 3.10. ДОПОЛНЕНИЯ К ГЛАВЕ 3
1. Буквенные выражения
123456789101112131415161718192021
2. Фигуры на плоскости, симметричные относительно прямой
1234
§ 4.1. Понятие положительной десятичной дроби
23456789
§ 4.2. Сравнение положительных десятичных дробей
1234567891011
§ 4.3. Сложение и вычитание положительных десятичных дробей
123456789
§ 4.4. Перенос запятой в положительной десятичной дроби
123456789101112131415
§ 4.
5. Умножение положительных десятичных дробей12345678910111213
§ 4.6. Деление положительных десятичных дробей
1234567891011121314
§ 4.7. Десятичные дроби и проценты
12345678910
§ 4.8. Сложные задачи на проценты
12345678910
§ 4.9. Десятичные дроби произвольного знака
123456789
§ 4.10. Приближение десятичных дробей
1234567891011
§ 4.11.. Приближение суммы, разности, произведения и частного двух чисел
123456
§ 4.11. ДОПОЛНЕНИЯ К ГЛАВЕ 4
1. Расчеты с помощью микрокалькулятора
1234
2. Процентные расчеты с помощью калькулятора
1234
3. Фигуры в пространстве, симметричные относительно плоскости
12345
§ 5.
1. Разложение положительной обыкновенной дроби в конечную десятичную дробь1234567891011
§ 5.2. Бесконечные периодические десятичные дроби
1234567
§ 5.3. Периодичность десятичного разложения обыкновенной дроби
12345
§ 5.4. Непериодические бесконечные десятичные дроби
123456
§ 5.5. Действительные числа
123456789
§ 5.6. Длина отрезка
12345678910
§ 5.7. Длина окружности. Площадь круга
1234567891011121314151617
§ 5.8. Координатная ось
1234567891011121314
§ 5.9. Декартова система координат на плоскости
123456789
§ 5.10. Столбчатые диаграммы и графики
1234567891011121314
Средняя оценка 0 / 5.
Количество оценок: 0
Оценок пока нет. Поставьте оценку первым.
Сложение целых чисел — правила, шаги
Сложение целых чисел — это процесс нахождения суммы двух или более целых чисел. Это может привести к увеличению или уменьшению значения, в зависимости от того, являются ли целые числа положительными или отрицательными или смесью. Сложение целых чисел — это арифметическая операция, выполняемая над целыми числами с одинаковым или разными знаками для нахождения суммы. Давайте узнаем больше о добавлении целых чисел в этой статье.
| 1. | Правила сложения целых чисел |
| 2. | Добавление целых чисел в числовую строку |
| 3. | Часто задаваемые вопросы о добавлении целых чисел |
Правила сложения целых чисел
Существуют определенные правила, которым необходимо следовать, чтобы сложить два или более целых числа.
Целые числа — это полные числа, не имеющие дробных частей. Он включает в себя положительные целые числа, ноль и отрицательные целые числа. Правила сложения целых чисел приведены ниже:
- Сумма целого числа и его обратного сложения равна 0.
- Сложение двух положительных целых чисел всегда приводит к положительному значению, которое больше обоих целых чисел.
- Сложение двух отрицательных целых чисел всегда приводит к отрицательному числу, которое меньше заданных чисел.
- Сложение положительного числа с отрицательным выполняется путем нахождения разницы между абсолютным значением обоих чисел. Затем к сумме присоединяется знак с большим числом.
- Сложение целых чисел с 0 приводит к тому же числу.
Правила сложения целых чисел можно понять с помощью приведенной ниже таблицы.
Сложение целых чисел с одинаковым знаком
Когда мы складываем два целых числа с одинаковым знаком, мы складываем их абсолютные значения и присоединяем к сумме общий знак.
Например, 2 + 3 = 5, (-2) + (-3) = — (2 + 3) = -5. Абсолютное значение числа — это положительное значение данного числа. Например, абсолютное значение 6 равно 6, абсолютное значение -6 равно 6 и так далее. Ниже приведены некоторые примеры сложения целых чисел с одинаковым знаком:
- (-1) + (-9) = — (1 + 9) = -10
- 3 + 8 = 11
- (-2) + (-17) = — (2 + 17) = -19
Воспользуйтесь онлайн-калькулятором Cuemath для сложения целых чисел, чтобы проверить эти ответы.
Сложение целых чисел с разными знаками
Сложение двух целых чисел с разными знаками выполняется путем вычитания абсолютных значений и последующего присоединения знака числа с большим абсолютным значением. Например, если мы хотим сложить -2 и 3, сначала мы найдем абсолютные значения обоих. Абсолютное значение -2 равно 2, а 3 равно 3. Теперь найдите разницу между этими абсолютными значениями, которая равна 3 — 2 = 1. Поскольку 3 > 2, а 3 имеет положительный знак, знак результирующего числа будет положительным.
Добавление целых чисел в числовую строку
Сложение целых чисел в числовой строке основано на данных принципах:
- Добавление положительного числа осуществляется перемещением к правой стороне (или положительной стороне) числовой строки.
- Добавление отрицательного целого числа выполняется перемещением к левой стороне (или отрицательной стороне) числовой строки.
- Любое из заданных целых чисел принимается за исходную точку, с которой мы начинаем движение по числовой прямой.
Теперь давайте научимся складывать целые числа в числовой строке.
- Шаг 1: Первым шагом является выбор шкалы на числовой прямой. Например, хотим ли мы отображать числа, кратные 1, 5, 10, 50 и т. д., зависит от заданных целых чисел. Например, если нам нужно сложить 10 и -30, мы можем взять шкалу 10 на числовой прямой, чтобы упростить нашу работу.
- Шаг 2: Если нам нужно добавить -2 и 7, мы можем взять шкалу счета чисел, начиная с 1.
- Шаг 3: Следующим шагом является поиск любого целого числа в числовой строке, предпочтительно числа с большим абсолютным значением. Например, если нам нужно сложить 2 и 19, будет лучше, если мы сначала найдем 19 на линии, а затем сделаем 2 прыжка вправо, а не найдем 2, а затем сделаем 19 прыжков.
- Шаг 4: Последним шагом является прибавление второго целого числа к числу, расположенному на предыдущем шаге, с помощью прыжков либо влево, либо вправо, в зависимости от того, положительное это число или отрицательное.
Давайте рассмотрим пример, чтобы лучше понять сложение целых чисел в числовой строке.
Пример: Используйте числовую строку и добавьте следующие целые числа: 5 + (-10)
Решение:
Поскольку нам нужно добавить отрицательное число (-10), мы будем двигаться влево по числу линия. Начиная с 5, мы сделаем 10 шагов влево, что приведет нас к -5.☛ Похожие темы
- Целочисленные формулы
- Сложение и вычитание целых чисел
- Умножение и деление целых чисел
Сложение целых чисел Примеры
Пример 1: Сложите следующие целые числа, используя правила сложения целых чисел.
4 + (-6) + 13
Решение: Даны три целых числа. Итак, сначала давайте сложим оба положительных целых числа 4 и 13, что даст нам 17. Теперь у нас осталось следующее выражение 17 + (-6). Здесь мы должны применить правило сложения отрицательного и положительного целых чисел. Получаем 17 + (-6) = 11. Следовательно, 11 — это результат данных целых чисел.
Решение: Пусть x нужно вычесть из 13, чтобы получить -10. Итак, мы можем составить уравнение относительно х.
13 — х = -10
— х = -10 — 23
х = -23
х = 23
Следовательно, 23 нужно вычесть из 13, чтобы получить -10.
Пример 3: Сложите следующие целые числа: -2 и -9.
Решение: При сложении целых чисел с одинаковым знаком складываем их абсолютные значения и присоединяем к ответу общий знак слагаемых.
-2 + (-9) = — (2 + 9) = -11
Следовательно, сумма -2 и -9 равна -11.
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по сложению целых чисел
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о добавлении целых чисел
Что такое сложение целых чисел?
Сложение целых чисел означает, что мы находим сумму целых чисел. Поскольку целые числа включают положительные числа, отрицательные числа и ноль, их добавление может привести к увеличению или уменьшению значения. Это зависит от того, являются ли целые числа положительными или отрицательными. Например, 5 + 6 = 11, и 5 + (-6) = -1, и -5 + 0 = -5
Каковы правила сложения целых чисел?
Ниже перечислены правила сложения целых чисел:
- Сумма целого числа и его обратной аддитивной величины равна 0. Например, 6 + (-6) = 0
- Сложение двух положительных целых чисел всегда приводит к положительному значению, которое больше обоих целых чисел. Например, 6 + 6 = 12 .
- Сложение двух отрицательных целых чисел всегда приводит к отрицательному числу, которое меньше заданных чисел. Например, -6 + (-6) = -12
- Сложение положительного числа с отрицательным выполняется путем нахождения разницы между абсолютным значением обоих чисел. Затем к сумме присоединяется знак с большим числом. Например, +6 — 2 = +4
- Сложение целых чисел с 0 приводит к тому же числу. Например, 6 + 0 = 6 или -6 + 0 = -6 .
Например, 6 + (-6) = 0Каково правило сложения целых чисел с разными знаками?
Для сложения целых чисел с разными знаками мы следуем шагам, указанным ниже. Складываем 5 и (-8)
- Шаг 1: Найдите абсолютные значения заданных целых чисел. Это означает, что это будет 5 и 8.
- Шаг 2: Найдите разницу между абсолютными значениями, найденными на шаге 1. Разница между 5 и 8 равна 3.
- Шаг 3: Прикрепите знак числа с большим абсолютным значением. Так как 8 имеет отрицательный знак, ответ также будет иметь отрицательный знак. Это означает, что 5 + (-8) = -3
Разница между 5 и 8 равна 3.Каково правило сложения целых чисел с одинаковым знаком?
Чтобы сложить целые числа с одинаковым знаком, мы складываем абсолютные значения чисел, а затем присоединяем общий знак к окончательному ответу. Например, (-9) + (-3) = -12.
Как вычитание целых чисел связано со сложением целых чисел?
Вычитание целых чисел связано со сложением целых чисел, потому что, когда мы складываем два целых числа с разными знаками, мы находим их абсолютные значения, а затем находим их разницу. Это означает, что мы используем вычитание при сложении целых чисел с разными знаками. Кроме того, сложение и вычитание являются обратными операциями. Это означает, что каждое выражение сложения может быть выражено вычитанием и наоборот. Вычитание целых чисел связано со сложением целых чисел, потому что оба они могут быть выражены в форме друг друга.
Например, мы можем написать 2 + (-9) как 2 — 9. Точно так же мы можем записать — 3 — 5 как -3 + (-5).
Каковы шаги для сложения целых чисел?
Шаги для сложения целых чисел приведены ниже:
- Найдите абсолютные значения заданных чисел.
- Если оба числа одного знака, то сложите значения. Присоедините общий знак к ответу.
- Если они имеют разные знаки, то вычтите их и найдите разницу между абсолютными значениями. Тогда к окончательному ответу будет присоединен знак целого числа с большим абсолютным значением.
Каков пример сложения целых чисел?
Ниже приведены некоторые примеры сложения целых чисел:
- 3 + 8 = 11
- (-9) + (-4) = -13
- -6 + 4 = -2
- 12 + (-8) = 4
Что такое элемент идентификации для сложения целых чисел?
Элемент идентификации для сложения целых чисел равен нулю (0). Это связано с тем, что при добавлении 0 к любому целому числу получается само число.