Сборник нестандартных задач по математике 6 класс
1.Кувшинки на пруду
На поверхности пруда плавает одна кувшинка, которая постоянно делится и разрастается. Таким образом, каждый день площадь, которую занимают кувшинки, увеличивается в два раза. Через месяц покрытой оказывается вся поверхность пруда. За сколько времени покроется кувшинками вся поверхность пруда, если изначально на поверхности будут плавать две кувшинки?
ОТВЕТ: Две кувшинки покроют озеро за месяц минус один день.
2.Сумма чисел
В XIX веке один учитель задал своим ученикам вычислить сумму всех целых чисел от единицы до ста. Компьютеров и калькуляторов тогда еще не было, и ученики принялись добросовестно складывать числа. И только один ученик нашел правильный ответ всего за несколько секунд. Им оказался Карл Фридрих Гаусс — будущий великий математик. Как он это сделал?
ОТВЕТ: Он выделил 49 пар чисел: 99 и 1, 98 и 2, 97 и 3 .
Либо 100 и 1, 99 и 2, 98 и 3… В сумме каждая пара дает 101, следовательно 101*50=5050
3.Король и премьер-министр
Один король хотел сместить своего премьер-министра, но при этом не хотел его слишком обидеть. Он позвал премьер-министра к себе, положил при нем два листка бумаги в портфель и сказал: «На одном листке я написал «Уходите», а на втором — «Останьтесь». Листок, который вы вытащите, решит вашу судьбу». Премьер-министр догадался, что на обоих листках было написано «Уходите». Как же, однако, умудрился он при этих условиях сохранить свое место?
ОТВЕТ: Премьер-министр вытащил листок бумаги и, не глядя на него, скатал из него шарик — и проглотил. Поскольку на оставшемся листке стояло «Уходите», то королю пришлось признать, что на проглоченном листке значилось «Останьтесь».
4.
Кто изображен на портрете?
Один джентльмен, показывая своему другу портрет, нарисованный по его заказу одним художником, сказал: «У меня нет ни сестер, ни братьев, но отец этого человека был сыном моего отца».
Кто был изображен на портрете?
ОТВЕТ: На портрете изображен сын этого джентльмена.
5.Пожар на острове
Человек находится на острове. Из-за долгой засухи трава и кусты на острове сильно пересохли. Внезапно на одном конце острова возник пожар, и ветер погнал огонь в сторону человека. Спастись в море человек не может, так как в море у самого берега плавает множество акул. Берегов без растительности на острове нет. Как человеку спастись?
ОТВЕТ: Человеку нужно зажечь огонь на подветренной от себя стороне и немного отойти навстречу основному пожару. Ветер погонит огонь, зажженный человеком, к подветренному концу острова. Когда этот участок выгорит, человек сможет вернуться на него и спокойно ждать, пока основной пожар дойдет до этого участка и погаснет, так как гореть уже будет нечему.
6.Переправа через реку
Отец с двумя сыновьями отправился в поход. На их пути встретилась река, у берега которой находился плот. Он выдерживает на воде или отца, или двух сыновей. Как переправиться на другой берег отцу и сыновьям?
ОТВЕТ: Вначале переправляются оба сына. Один из сыновей возвращается обратно к отцу. Отец перебирается на противоположный берег к сыну. Отец остается на берегу, а сын переправляется на исходный берег за братом, после чего они оба переправляются к отцу.
7.Незадачливый рыбак
Один рыбак купил себе новую удочку длиной 5 футов. Домой ему приходиться добираться общественным транспортом, в котором правилами запрещено перевозить предметы длиной более 4-х футов. Как необходимо упаковать удочку, чтобы проехать в общественном транспорте не нарушая правил?
ОТВЕТ: Удочку необходимо упаковать в коробку длиной 4 фута и шириной 3 фута (расположить по диагонали коробки).
8.Приготовление краски
Для того чтобы получить краску оранжевого цвета, необходимо смешать краски желтого цвета (6 частей) и красного цвета (2 части). Сколько грамм краски оранжевого цвета можно получить (максимально), имея в наличии 3 грамма желтой и 3 грамма красной краски?
ОТВЕТ: Из условия задачи видно, что желтой краски требуется в 3 раза больше, чем красной. Следовательно, имея в наличии 3 грамма желтой краски, необходимо взять 1 грамм красной краски. То есть оранжевой краски при смешивании получиться 4 грамма.
9.Сколько страниц в книге?
При издании книги потребовалось 2 775 цифр того, чтобы пронумеровать ее страницы. Сколько страниц в книге?
ОТВЕТ: На первые 9 страниц требуется 9 цифр. С 10-й по 99-ю страницу (90 страниц) требуется 90х2=180 цифр. С 100-й по 999-ю страницу (900 страниц) требуется 900х3=2700 цифр (по 300 цифр на каждую сотню страниц с трехзначной нумерацией).
Следовательно, на 999 страниц необходимо 2700+180+9=2889 цифр. Мы перебрали (2889-2775)/3=38 страниц. Итого: 999-38=961 страница была в книге.
Олимпиадные задачи по математкие 5-6 класс — Колпаков Александр Николаевич
В последнее время увеличился поток писем от посетителей сайта с просьбами о помощи в решении олимпиадных задач для самых маленьких (5 — 6 класс). Это приятно, ибо работать с талантливыми и целеустремленными детьми одно удовольствие. Кто обычно пишет репетитору по математике? Как правило, это родители учеников, решающих сложные задачи для собственного удовлетворения и развития. Чуть меньше писем от самих участников математических олимпиад и конкурсов «Кенгуру». Последние присылают задачи, оказавшиеся им не по зубам на школьном или на районном туре. Репетитор по математике он-лайн в таких случаях является хорошим источником проверки правильности решения, а иногда и единственной надеждой узнать его вообще. Не каждому родителю удается справиться с олимпиадной задачей (и тем более объяснить ее в 5 классе), а возможности придти после олимпиады домой и посмотреть решение задачи в учебнике нет.
К сожалению, не всегда удается найти время на полное оформление задач в том объеме, в котором ни приходят ко мне по e-mail. Не забывайте, что я 
Олимпиадные задачи для 5 — 6 класса. Ответы на Ваши вопросы.
Вопрос репетитору по математике от Валентины
Часы Юры отстают на 8 минут, но он считает, что часы спешат на 2 минуты. Часы Коли спешат на 2 минуты, однако он думает, что они отстают на 8 минут. Друзья договорились, что встретиться в 5 часов вечера. Кто раньше окажется у места встречи и на сколько минут?
Решение репетитора (Колпаков А.Н.)
Отметим, что мальчики приходят в точку встречи по своему «внутреннему» таймеру (который рассчитывают), а не по реальному. Поэтому надо узнать, каково реальное время в момент прихода каждого. Найдем разницу между реальным временем и тем временем, которое представляет себе Юра. Пусть точное время x минут, тогда на часах Юры x-8 минут. Так как он думает, что они спешат, значит считает, что сейчас x-8-2 минут. Поэтому значение реального времени больше того, которое представляет себе Юра на 10 минут. Это означает, что к моменту прихода Юры в точку встречи реальное время составит 17 ч 10 мин.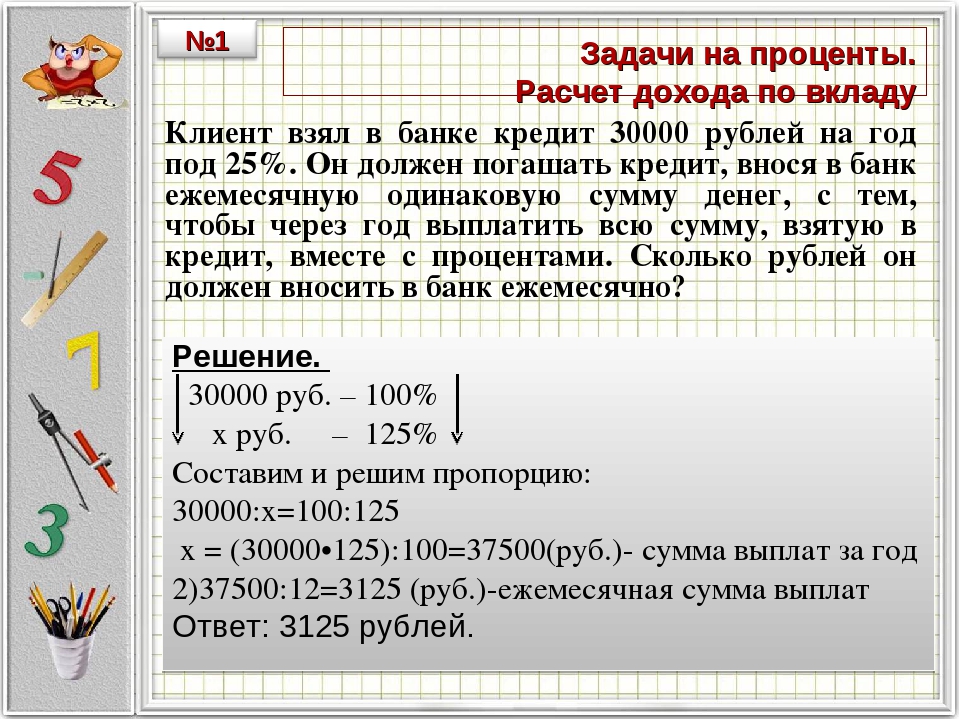
Аналогично рассуждая можно получить расклад по Коле. Пусть y (мин) — реальное время. Тогда часы Коли в этот момент показывают y+2 (мин). Так как он думает, что часы отстают на 8 минут, значит считает, что в этот момент y+2+8 минут.
Поэтому значение реального времени меньше представляемого Колей на 10 минут. Это значит, что к моменту прихода Коли реально 16 ч 50 мин. Поэтому Коля пришел раньше Юры на 20 минут.
Задача репетитору по математике от Катерины.
Доброе утро, ребёнку в школе задали решить задачу с олимпиады, ну ни как не получается! Задача: Петя в трамвае заметил Васю, который поравнялся с трамваем следуя вдоль трамвайных путей в противоположном направлении. Через минуту Петя вышел и побежал вдогонку за Васей вдвое быстрее его, но в 4 раза медленнее трамвая. Через какое время Петя догонит Васю? Помогите.
Решение (А.Н.Колпаков) Прежде всего, нужно понять, что означает «в два раза быстрее». Это значит, что скорость больше в два раза.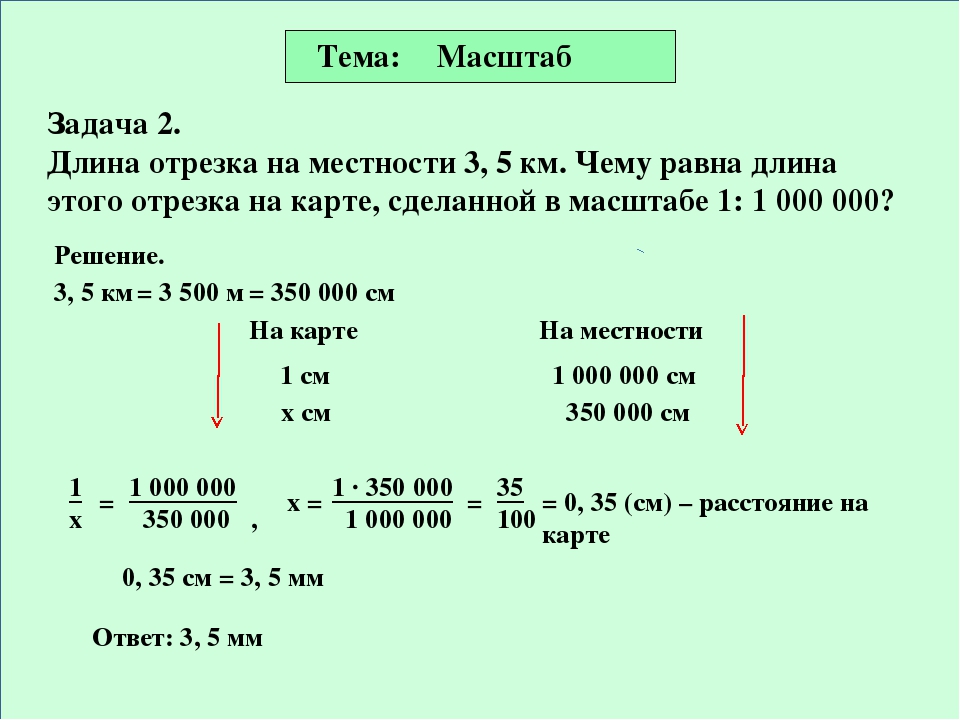
Поэтому если за одну минуту Вася проходит какой-то отрезок пути, то трамвай проезжает 8 таких отрезков. Поэтому расстояние между мальчиками в момент выхода Пети составляет 9 отрезков. За ту же минуту Петя проходит 2 отрезка (раз его скорость в 2 раза больше). Введем единицу измерения длины, равную этому же отрезку. Тогда мы имеем стандартные начальные данные для самой обычной задачи на скорость сближения. Скорости мальчиков известны – это 1 (отрезок/мин) и 2 (отрезка/мин), а расстояние для сближения составляет 9 отрезков.
За каждую минуту оно сокращается на 2-1=1 отрезок (это и есть скорость сближения). А нам надо узнать, за какое время расстояние в 9 отрезков сократится до нуля, то есть надо узнать время сближения. Его можно найти, разделив путь сближения на скорость сближения.
Вопрос репетитору по математике от Ибрагилава.
Как решить задачу? Свете втрое больше лет, чем было Максиму тогда, когда она была в его нынешнем возрасте. Когда Максим будет в возрасте Светы, то им вместе будет 28 лет. Сколько сейчас лет Максиму и сколько сейчас лет Свете?
Решение (Колпаков А.Н.)
Запутанные (олимпиадные) задачи на возраст удобно показывать на временной оси, на которой возраста представляются точками. Если у нас 2 человека и их возраста меняются, то изображающие их точки будут просто двигаться по оси. При этом расстояние между ними (разница в возрасте) будет сохраняться. Покажем нынешний возраст Светы и Максима точками С и М (верхний ряд букв на рисунке). В нижнем ряду поставим буквы С и М для того момента, когда «Света была в нынешнем возрасте Максима». Получим равные отрезки, концы которых (нижняя М и верхняя С) согласно условию «в 3 раза» можно обозначить как х и 3х.
Тогда нынешний возраст Максима (середина отрезка) будет иметь координату 2х, а значит разница в возрасте составит ровно х (лет). Теперь покажем, какими будут координаты возрастов в тот момент, когда Максим окажется в возрасте Светы. Эти буквы стоят в ряду «будущее». Длина их отрезка тоже равна х (лет) и поэтому возраст Светы в этот момент окажется равным 4х (лет). Так как в будущем им вместе будет 28 лет, то 3х+4х=28, откуда получаем, что х=4. Поэтому Максиму сейчас лет, а Свете сейчас лет.
Вопрос репетитору по математике от Миши
Здравствуйте! Помогите решить олимпиадную задачку за 5 — 6 класс. Вася написал в тетради 4 числа. Сложил их по два всеми возможными способами получил шесть таких сумм: 2, 4, 9, 9, 14, 16. Какие числа записал Вася?
Решение (Колпаков А.Н.)
Пусть a, b, с, d – искомые числа, расположенные в порядке возрастания. Составим последовательность их суммы также в порядке возрастания используя неравенство a < b < c < d.
Получим такой ряд:
1) a+b=2
2) a+c=4
3,4) b+c и a+d
5) b+d=14
6) c+d=16
Первые две суммы явно наименьшие и поэтому равны 2 и 4. Две последние явно наибольшие и равны соответственно 14 и 16. Осталось выяснить судьбу двух оставшихся: b+с и a+d. Но так на них приходятся две девятки, то каждая из них равна 9. По первым двум суммам делаем вывод, что с на 2 больше чем b. Поэтому c=b+2. Подставляя выражение для числа с в равенство b+c=9 получим, что b+b+2=9. Поэтому b=3,5 и значит c=3,5+2=5,5. Из первого равенства вытекает, что a=2-3,5=-1,5, а из последнего, что d=16-5,5=10,5
В итоге ответ оказывается таким: -1,5; 3,5; 5,5 и 10,5
Задача репетитору от Эльдара. Помогите решить: Всего 5555 человек, на 10 солдат приходится 1 капрал, на 5 капралов 1 офицер, на 9 офицеров 1 генерал. Решение: сколько всего было солдат?
Репетитор по математике Ермакова Диана
Для начала определим, сколько человек в одном таком «наборе», состоящем из генерала, капралов, офицеров и солдат.
Один генерал и девять офицеров у нас уже есть. Так как на каждого офицера приходится 5 капралов, то на 9 офицеров приходится капралов.
Так как на каждого капрала приходится 10 солдат, то на 45 капралов приходится солдат.
Всего человек в «наборе»
Так как всего в армии 5555 человек, то количество «наборов» равно
. В одном «наборе» солдат, поэтому в 11 «наборах» будет солдат.
Ответ: солдат.
Иногда мне помогают оформлять решения другие репетиторы по математике. Я рассылаю условия тем, кто дал свое согласие на участие в виртуальной работе. Для репетитора по математике такая активность — хороший шанс обратить на себя внимание будущих учеников. Поэтому, если Вы регистрируетесь у меня на сайте как репетитор по математике — укажите при заполнении анкеты (в поле дополнительной информации) готовы ли Вы к такому сотрудничеству. Тот репетитор по математике, кто будет присылать решения для публикации регулярно, скорее всего, может рассчитывать на размещение еще и в рекомендованном списке репетиторов.
Pages: 1 2
Сборник задач для учащихся 6 классов по теме «Отношение, пропорции, проценты»
Муниципальное бюджетное общеобразовательное учреждение «Гимназия №5» г.Брянска
Сборник задач для учащихся 6 классов по теме «Отношение, пропорции, проценты»
Автор
Лущик Никита Павлович,
учащийся МБОУ «Гимназия №5» г.Брянска
Руководители
Васина Ольга Григорьевна,
учитель математики
МБОУ «Гимназия №5» г.Брянска,
Легоцкая Вера Сергеевна,
учитель русского языка и литературы
МБОУ «Гимназия №5» г.Брянска
Брянск-2017
Оглавление
Сборник задач для учащихся 6 классов по теме «Отношение, пропорции, проценты»……………………………………………………………………….
3
Отношение……………………………………………………………………….4
Прямая и обратная пропорциональность………………………………………4
Масштаб…………………………………………………………………………..6
Задачи на проценты………………………………………………………………8
Круговые диаграммы……………………………………………………………19
Актуальность проблемы, цели, задачи…………………………………………35
Этапы и методы работы над проектом…………………………………………37
Описание процесса исполнения………………………………………………..38
Заключение ………………………………………………………………………43
Использованная литература…………………………………………………….44
1.1 Сборник задач для учащихся 6 классов по теме «Отношение, пропорции, проценты»
Отношение
Задача 1.
Сокол сапсан считается самым быстрым и самым глазастым живым существом на Земле. (Занесен в Красную книгу РФ и Брянской области). Его средняя скорость 322 км/ч. Найдите путь, который может преодолеть сапсан, если будет лететь 2 часа.
Решение:
S=v×t V= 322 км/ч найти S-? t=2ч
S=322 км/ч ×2ч = 644 км
Ответ: 644 км
Задача 2.
Известно, что 1 га леса вырабатывает за 1 час 3580 г кислорода. Сколько кислорода вырабатывает 1 га леса за сутки?
Решение:
1 час 3580г
24 часа х
х== 24358 г
Ответ: 24538 г
Задача 3
По стволу дерева к кронам поднимается вода, которую испаряют лучи Солнца. Если вырубить деревья, эта вода будет скапливаться, и образуется болото. Взрослая берёза за сутки испаряет в среднем 80 литров воды, а липа – 200 литров. Сколько вёдер воды ежедневно испаряет каждое из этих деревьев, если одно ведро вмещает 10 литров?
Решение:
Береза 80 л/сут х
Липа 200 л/сут х
1 ведро= 10л
х= 80л=8 ведер
х= 200л=20ведер
Ответ: 8,20 ведер.
Задача 4.
Двигаясь с постоянной скоростью, поезд прошел 60 м за 2 с. Какой путь пройдет поезд за 15 с?
Решение:
60 м -2 с
х м- 15 с
х= = 450 м
Ответ: 450 м
ПРЯМАЯ И ОБРАТНАЯ ПРОПОРЦИОНАЛЬНОСТЬ
Задача 1.
Европейская болотная черепаха — редкий вид, занесенный в Красную книгу Брянской области. Все привыкли думать, что черепахи очень медлительны. Однако это не совсем так. В воде черепаха может развивать немалую скорость. Так, расстояние 7 км черепаха проплыла под водой за 15 мин. Найдите скорость Европейской болотной черепахи и запишите ответ в км/ч.
Решение:
S = 7 км,
t = 15 мин. t =15мин= ч=ч
Найти: V -?
V=St
V = 7: =28 км/ч
Ответ: 28 км/ч
Задача 2.
Известно, что 70-80% всей потребляемой людьми пресной воды расходуется в сельском хозяйстве.-reshenie-356.jpg)
Так, чтобы получить 2 кг говядины, требуется 30 000 литров воды. А сколько говядины получено, если известно, что потрачено 270 000 литров воды?
Решение:
2 кг -30 000 литров
х кг -270 000 литров
х= 2∙ 270000÷30000=18 кг
Ответ: 18 кг
Задача 3.
Самая длинная река в Австралии Муррей-Дарлинг – 3750 км. За какое время группа исследователей преодолеет путь от истока до устья реки, если будет двигаться на байдарках со средней скоростью 25км\ч.
S=3750 км
V=25км/ч
t-? t= х
х=3750 км : 25км/ч ==150ч
Ответ: 150 ч
Задача 4.
Высочайшая гора мира Джомолунгма (Эверест) находится в Китае (Непале), ее высота 8848 м. За какое время альпинисты покорят эту вершину, если будут совершать восхождение со средней скоростью 1000 м / сут.
S-8848 км
v-1000м/сут
t-? t= х
х=8848 км ==8,848 сут
Ответ: 8,848 сут
Задача 5.
Озера Земли содержат природную воду в объеме 176, 4 тыс.км3 . Например, озеро Байкал содержит примерно 23 тыс. км3 и считается самым чистым в мире по химическому составу воды. Какой процент составляют воды Байкала от общей озерной воды планеты?
Решение:
Пусть х- процент воды от общего объема воды в озерах
176,4 тыс. км³ 100 %
23 тыс. км³ х%
х===13
Ответ: 13%
МАСШТАБ
Задача 1.
В Суражском районе Брянской области разрабатывается проект освоения месторождения, здесь предполагается строительство цементного завода. Современное производство цемента не более вредно, чем большинство других производств, тем более местонахождение будет на расстоянии 15 километров от Суража. Определите расстояние между изображениями Суража и предполагаемого цементного завода на карте, если численный масштаб карты равен 1:1 000 000?
Решение:
S = 15 км = 1.
500.000 см
1500000 см : 1000000= 1,5 см
Ответ: 1,5 см
Задача 2.
От регионального ботанического памятника природы «Брасовские дубравы» до регионального ландшафтного памятника природы «Холмечский родник», которые находятся в Брасовском районе Брянской области, 11 км. Определите расстояние между изображениями памятника природы «Брасовские дубравы» и регионального ландшафтного памятника природы «Холмечский родник» на карте, если численный масштаб карты равен
1:500 000?
Решение:
S = 11 км = 1.100.000 см
1.100.000 см ÷500.000=2,2 см
Ответ: 2,2 см
Задача 3.
В пгт. Комаричи Брянской области яблоневый сад имеет вид прямоугольника, длина которого 560 м, а ширина 420 м. Какие размеры будет иметь изображение этого сада на плане, выполненном в масштабе 1:1000?
Решение:
Масштаб 1: 1000
Длина 560м=56000 см
Ширина 420м=42000 см
1)56000÷1000=56 см
2)42000÷1000=42 см
Ответ: 42 см, 56 см
Задача 4.
Первый в мире национальный парк основан вокруг озера Йеллоустон (на западе США) в 1872 году по решению президента США Гранта. Определите расстояние между изображениями этого парка и ближайшего к нему национального парка Гранд-Титон 45 км, если численный масштаб карты равен 1: 4 500 000?
Решение:
45 км = 4.500.000 см
4.500.000÷4.500.000=1 см
Ответ: 1 см
Задача 5.
От самого населенного города мира Токио (26,4 млн. чел.) до печально известного вулкана Фудзияма (3776 м.) 102 км. Определите расстояние от Токио до вулкана, если численный масштаб карты 1: 16 000 000?
S=102 км=10.200.000 см
1)10.200.000÷16.000.000= см
Ответ: см
ЗАДАЧИ НА ПРОЦЕНТЫ
Задача 1.
В начале 1980-х годов общая площадь коралловых рифов составляла около 600 тыс. км². С 2000 года кислотность вод Мирового океана увеличилась в 10 раз и поэтому 19% всех коралловых рифов навсегда исчезло с лица Земли.
Сколько тыс. км² коралловых рифов исчезло?
Решение:
Пусть х тыс. км² коралловых рифов исчезло
600 тыс. км² 100%
х 19%
х==114 тыс.км²
Ответ: 114 тыс. км²
Задача 2.
На Земле при общем размере поверхности 510 млн. км2 .360 млн. км2 занимает воды. Среди этого количества 3% пригодно для питья. Сколько млн. км2 питьевой воды на Земле? Сколько процентов занимает площадь воды по отношению ко всей площади Земли?
Решение:
Пусть х % занимает вода на Земле
510 млн. км² — 100%
360 млн. км² — х%
х==70,588%
2)Пусть х млн. км²- питьевая вода
360 млн. км² 100%
х млн км² 3%
х==10,8 млн. км² Ответ: 70,588% занимает вода, 10,8 млн. км²- питьевая вода на Земле
Задача 3.
Известно, что на а Земле 130.000 рек. Каждый год человек загрязняет 2%.
Сколько всего рек загрязняет человек в год? (Для сведения Цитарум-самая грязная река в мире- находится в Индонезии, протекает рядом со столицей страны Джакартой и собирает отходы девятимиллионного города, а самая грязная река России-Волга, в нее сбрасывается 38% всех сточных вод).
Решение:
Пусть х рек загрязняют каждый день
130.000 рек — 100% х рек — 2%
х==2600 рек
Ответ: 2600 рек
Задача 4.
Вода составляет 92% арбуза. (Арбуз очень полезен для здоровья: обладает мочегонными свойствами, способностью выводить токсические вещества из печени, а также избыток холестерина). Сколько кг воды в 42 кг арбуза?
Решение:
Пусть х кг воды в 42 кг арбуза
42 кг — 100%
х кг -92%
х==38,64 кг
Ответ 38,64 кг воды в 42 кг арбуза
Задача 5.
В связи со значительным ростом производства напитков и продуктов питания, разливаемых в стеклянную тару, в Российских регионах в последние годы резко увеличились объемы отходов стеклобоя.
По оценке экологов, только в Москве ежегодно образуется более 150.000 т отходов стекла. Реальный объем сбора стеклобоя ориентировочно составляет 57 000 т в год. Сколько процентов стеклобоя собирается ежегодно?
Решение:
Пусть х % — процент сбора
150.000 т — 100%
57.000 т — х%
х==38%
Ответ: 38%
Задача 6.
В п. Ржаница Жуковского района Брянской области расположены две войсковые части, на нужды которых в 2015 г. забрано из подземных источников 502570 м³/год. Использованная вода поступала на очистные сооружения, сброс сточных вод осуществлялся в реку Рача в объёме 462520 м³/год и в ручей Броничка – 14010 м³/год. Сколько процентов использованной войсковыми частями воды не прошло очистку?
Решение:
1) 502.570-(462.520+14.014)= 26.040(м³)- воды не прошло очистку
2) Пусть х %- процент неочищенной воды
502.570 м³ — 100%
26.040 м³ — х%
х==5,18%
Ответ: 5,18%
Задача 7.
МУП «Клетня – Сервис» осуществляет забор воды из подземных источников для нужд населения п. Клетня и сельских населённых пунктов Клетнянского района Брянской области. В 2015 г. его объём составил 304 720 м³. Промышленные и хозяйственно-бытовые стоки п. Клетня поступают на очистные сооружения биологической очистки, проектная мощность которых составляет всего 7 тыс. м³/сутки. Сброс сточных вод после очистных сооружений в объёме 53 960 м³ по каналу осуществляется в реку Надву. Сколько процентов сточных вод не подвергается биологической очистке?
Решение:
1) 304720-53960=250760(м³)- вода, которая не подвергается биологической очистки 2) Пусть х% — процент сточных вод не подвергшие очистки
304720 м³ — 100%
250760 м³ — х%
х==82%
Ответ: 82 %
Задача 9.
По состоянию на 2015 год в государственном природном биосферном заповеднике «Брянский лес» отмечено 5 видов растений, внесённых в Красную книгу России, что составляет 0,382% от общего числа растений, произрастающих в заповеднике.
Сколько всего видов растений отмечено в заповеднике?
Решение:
Пусть х видов – всего растений в заповеднике
х видов — 100%
5 видов – 0,382%
х==1309 видов
Ответ: 1309 видов
Задача 10.
По состоянию на 2015 год в государственном природном биосферном заповеднике «Брянский лес» отмечено 56 видов растений, внесённых в Красную книгу Брянской области, что составляет 4,2755 % от общего числа растений, произрастающих в заповеднике. Сколько всего видов растений отмечено в заповеднике?
Решение:
Пусть х- всего растений в заповеднике Брянской области
х — 100%
56 видов – 4,275%
х==1309 видов
Ответ: 1309 видов растений
Задача 11.
В государственном природном биосферном заповеднике «Брянский лес» обитает 878 видов животных. В заповеднике отмечено 25 видов животных, внесённых в Красную книгу России и 42 вида животных, внесённых в Красную книгу Брянской области.
Сколько процентов составляют виды животных, внесённых в Красную книгу России и в Красную книгу Брянской области соответственно?
Решение:
1)25+42=67- всего видов в красной книге
2) Пусть х % — процент животных в красной книге
878 видов — 100%
87 видов – х %
х==7
Ответ: 7 %
Задача 12.
Вода составляет 76% картофеля (но следует помнить о несомненной пользе картофеля: в нем есть и витамины С, В6, В2 и В3, а еще соли калия, магния, железа). Сколько кг воды в 35 кг картофеля?
Решение:
Пусть х кг- воды в картофеле
35 кг — 100%
х — 76%
х== 26,6 кг
Ответ: 26,6 кг
Задача 13.
На Земле 7,825 млрд. человек. (Самая населенная страна в мире — Китай, численность ее населения составит 1,367 млрд. человек. На втором месте — Индия — 1,252 млрд. человек. Третье место — у США).
Каждый год рождается 350.000 человек. Сколько процентов рождается каждый год?
Решение:
Пусть х % — процент рождения детей в год
7825млн — 100%
350.000 — х%
х %== %
Ответ: %
Задача 14.
В реку Чусовую, которая находится в Пермском крае, поступают промышленные и бытовые сточные воды из пяти крупных населённых пунктов. В 1993 г. из этих пунктов было сброшено свыше 90 млн. м³. сточных вод. Из них загрязнённых – 47 млн. м³. Какой процент сточных вод составляли загрязнённые?
Решение:
Пусть х – млн. м³ загрязненные сточные воды
90 млн. м³ — 100%
47 млн. м³ — х%
х%==52 %
Ответ: 52 %
Задача 15.
В Африке раньше леса занимали 60% территории, в настоящее время — только 17%. На сколько млн. км сократились площадь лесов Африки, если ее территория 30,3 млн. км?
Решение:
1 способ
Пусть х млн.
км – раньше занимали леса
Пусть y млн. км – сейчас занимают леса
30,3 млн. км — 100%
х — 60%
y — 17%
1) х==18,18 млн км
2) y==5,151 %
3)18,18-5,151 =13,029 млн. км
Ответ13,03 млн. км
2 способ
1) Пусть х млн. км составляют леса, занимающие 60%
1. Вася прочитал две пятых книги, что составило 80 страниц. На другой день он прочитал четверть оставшихся страниц. Вопросы: 1) Сколько страниц в книге? 2) Сколько страниц осталось не прочитано?
Решение.
1) 80:(2/5)=200 – Страниц в книге
2) 1-2/5=3/5 книги осталось прочитать после 1-го дня
3) 200*3/5=120 остаток после 1-го дня
4) 120*1/4=30 страниц книги прочитано во второй день.
5) 200-80-30=90 страниц в книге не прочитано
Ответ: 1) 200; 2) 90 страниц в книге не прочитано
2. Мастер и ученик, работая вместе, покрасили забор за 12ч.
Если бы мастер красил забор один, он выполнил бы эту работу за 21ч. За сколько часов покрасил бы этот забор ученик?
Решение.
1) 1/12 совместная скорость работы мастера и ученика.
2) 1/21 скорость мастера
3) 1/12-1/21=1/28 скорость ученика.
4) 1:(1/28)=28 часов понадобится ученику.
Ответ: 28 часов.
4. Расстояние между селами Мордино и Солнечное 720км. Из Мордино в Солнечное вышел скоростной поезд со скоростью 80км /ч. Через 2 часа навстречу ему из Солнечного в Мордино вышел обычный поезд со скоростью 60км/ч. Через сколько часов после выхода пассажирского поезда эти поезда встретятся?
Решение.
1) 80×2=160 (км) – прошёл скорый поезд за 2 часа.
2) 720-160=560 (км) – осталось проехать поездам.
3) 80+60=140 (км/ч) – скорость сближения скоростного и обычного поезда.
4) 560:140=4(ч) – ехал обычный поезд.
Ответ:4часа ехал обычный поезд.
5.
Из двух пунктов навстречу друг другу одновременно выехали два автобуса. Скорость одного автобуса 45 км /ч, а скорость другого автобуса 72км /ч. Первый автобус до встречи проехал 135км. Найти расстояние между пунктами.
1) 135 : 45 = 3 (часа) – ехали автобусы до встречи.
2) 72 * 3 = 216 (км) – проехал второй автобус до встречи.
3) 135 + 216 = 351 (км) – расстояние между пунктами.
Ответ: 351км.
Самостоятельная работа
Байкер в первый час проехал 3/8 всего пути, во второй час 3/5 остатка, а в третий час остальные 40 км. Найдите весь путь.
P.S. Эти задачи могут быть полезными не только для школьников 6-го класса, но и для 11-классников, готовящихся к ЕГЭ. Мой опыт показывает, что к сожалению не все выпускники могут решить данные задачи.
P.P.S. Неплохую подборку законодательных актов содержит сайт управления образования. Кроме этого имеется информация по контрольным работам по математике.
Связанные статьи
Олимпиада по математике 6 класс
Вар-т 1 Вар-т 2 Вар-т 3Задание 1.
Все натуральные числа раскрасили в три цвета.
Число 1 стало красным, 2 — синим,
3 — зеленым, 4 — красным, 5 — синим, 6 — зеленым, и так далее.
Какого цвета может быть сумма красного и синего чисел?
А — только зеленого Б — только красного В — только синего
Г — красного или синего Д — может быть любого цвета
Задание 2.
Два велосипедиста одновременно выехали навстречу друг другу по одной и той же дороге,
соединяющей два села.
Одному на весь путь требуется 1 час, а другому полтора часа.
Через сколько минут они встретятся?
А — 20 Б — 24 В — 30 Г — 36 Д — 40
Задание 3.
Петя хочет разрезать прямоугольник 6 х 7 на квадраты с целыми сторонами.
Какое наименьшее число квадратов может при этом получиться?
А — 4 Б — 5 В — 7 Г — 9 Д — 42
Задание 4.
На доске написано несколько натуральных чисел.
Сумма этих чисел равна их произведению и равна 2012.
Какое самое маленькое количество чисел может быть на доске?
А — 1006 Б — 1507 В — 1508 Г — 1556 Д — 2012
Задание 5.
В войске 5555 человек.
На 10 солдат приходится 1 капрал, на 5 капралов — 1 офицер, на 9 офицеров — 1 генерал.
Сколько в войске солдат?
А — 505 Б — 4950 В — 5000 Г — 5050 Д — 5500
Ответы к заданиям:
1 — А 2 — Г 3 — Б 4 — А 5 — Б
Олимпиада по математике 6 класс с решением
Задание 1.
На некотором острове необычайно регулярный климат :
по понедельникам и средам всегда идут дожди,по субботам — туман, зато в остальные дни — солнечно.
Утром какого дня недели нужно начать свой отдых группе туристов, если они хотят пробыть там 44 дня и захватить при этом как можно больше солнечных дней?
A — в понедельник; B — в среду; C — в четверг; D — в пятницу; E — во вторник
Решение :
Выясним, сколько полных недель в 44 днях.
Получим 6 недель.
В течении этих недель число солнечных дней не зависит от того, когда начнется отдых.
В качестве оставшихся двух дней выбираем четверг и пятницу — солнечные дни.
Следовательно, отправляем туристов утром в четверг.
То есть верный ответ — (С).
Задание 2.
У двузначного числа «n» цифра десятков в два раза больше, чем цифра единиц.
Тогда число «n» обязательно: A — четное; B — нечетное; C — меньше 20; D — делится на 3; E — делится на 6.
Решение :
Ищем число «n» среди ряда чисел: 10 — 99.
По условию, у всех подозреваемых чисел — десятки четны (2,4,6,8), а единицы — в два раза меньше (1,2,3,4,).
Перечислим все эти числа: 21, 42, 63, 84. Все они делятся на 3.
Следовательно верен ответ (D).
Задание 3.
Остаток от деления 100 на некоторое число равен 4. При делении 90 на это же число в остатке получается 18. На какое число делили? A — 18; B — 32; C — 24; D — 36; A — 48;
Решение :
Из условия следует, что 100-4=96 делится на искомое число.
Также 90-18=72 делится на искомое число.
Их разность также делится на искомое число: 96-72=24.
Следовательно, искомое число — 24, так как на него делится и 96, и 72.
Верен ответ (С).
Задание 4.
Раньше называли число, равное миллиону миллионов , словом «легион».
Если разделить миллион легионов на легион миллионов,
то получится : A — легион; B — миллион; C — миллион миллионов; D — легион легионов; E — 1
Решение :
Перепишем заново:
делимое: миллион легионов — это миллион миллионов миллионов,
делитель: легион миллионов — это миллион миллионов миллионов,
следоватально частное равно 1.
Верен ответ (Е).
Задание 5.
Есть 10 монет, среди них ровно две фальшивые.
Детектор R7 за одну операцию исследует три монеты и указывает на одну из них.
Известно, что детектор не может указать на настоящую монету,
если среди тестируемых монет есть хотя бы одна фальшивая.
Как за шесть тестов выявить обе фальшивые монеты?
Решение:
Выберем три кучки по три монеты, протестируем каждую из них,
и возьмём те три монет, на которые указал детектор.
Среди них, очевидно есть хоть одна фальшивая.
Протестируем эти монеты и таким образом определим одну из фальшивых.
Вторая фальшивая монета может быть только среди тех четырёх монет,
с которыми тестировалась найденная фальшивая или быть той монетой, которая ещё не была задействована.
Среди этих пяти монет за два теста определить одну фальшивую уже совсем легко
(каждый тест выявляет две настоящие монеты).
Задание 6.
На доске написано пять двузначных натуральных чисел.
Чебурашка каждую минуту прибавляет ко всем числам единицу или (тоже ко всем числам) двойку.
После того, как Чебурашка увеличивает числа, К. Гена может стереть какое-нибудь число,
делящееся на 13, или число, сумма цифр которого делится на 7 (если, конечно, такое число на доске есть).
Докажите, что при любых действиях Чебурашки,
Гена через некоторое время сумеет стереть с доски все числа.
Решение:
Гена может найти пять пар не более чем пятизначных соседних чисел,
так, чтобы в каждой паре он мог стереть любое число.
Чебурашка сможет «провести» через одну такую пару не более одного числа,
а значит все пять чисел Гена сможет стереть.Подобных пар очень много,
например годятся пары 142 и 143, 312 и 313, 3120 и 3121, 1312 и 1313, 69999 и 70000…
Вар-т 1 Вар-т 2 Вар-т 3
Задачи по математике для 6-го класса с ответами
Задачи по математике для 6-го класса с ответами:
В этом разделе мы увидим несколько практических вопросов для учеников 6-го класса.
Вопрос 1:
Значение (1/2!) — (3/3!)
(A) 1 (B) 5 (C) 0
Решение:
= (1 / 2!) — (3/3!)
= (1/2 x 1) — (3/3 x 2 x 1)
= (1/2) — (1/2)
= 0
Итак, ответ — 0.
Вопрос 2:
Угол между осями x и y на любом графическом листе равен
(A) 10 (B) 50 (C) 90
Решение:
Угол между x и y оси на любом графическом листе — 90 °.
Таким образом, правильный ответ на этот вопрос — 90 °.
Вопрос 3:
Джон на два года младше Джека. Джек на 3 года старше Кевина. Если Кевину 35 лет, сколько лет Джону?
(A) 50 (B) 36 (C) 17
Решение:
Возраст Джона сравнивается с возрастом Джека,
Возраст Джека сравнивается с возрастом Кевина.
Возраст Кевина = 35
Возраст Джека = 35 + 3
= 38 лет
Возраст Джона = 38-2
= 36 лет
Итак, ответ — 36 лет.
Вопрос 4:
Какова вероятность выпадения трех орлов, когда четыре справедливых монеты подбрасываются один раз?
(A) 2/5 (B) 1/4 (C) 1/8
Решение:
Пробел
S = {HHHH, HHHT, HHTH, HTHH, THHH, HHTT, HTHT, HTTH, THTH, TTHH, THHT, HTTT, THTT, TTHT, TTTH, TTTT}
n (S) = 16
Пусть A будет событием получения трех орлов.
A = {HHHT, HHTH, HTHH, THHH}
n (A) = 4
P (A) = n (A) / n (S)
= 4/16
= 1/4
Вероятность выпадения трех орлов при подбрасывании четырех монет = 1/4
Итак, ответ — 1/4.
Вопрос 5:
Найдите площадь сектора с периметром 110 см и радиусом 20 см.
(A) 600 кв. См (B) 500 кв. См (C) 700 кв. См
Решение:
Периметр сектора = 110 см
радиус сектора = 20 см
Отсюда нужно найти площадь сектора
л + 2р = 110
л + 2 (20) = 110
л + 40 = 110
л = 110-40
l = 70 см
Площадь сектора = lr / 2
= 70 (20) / 2
= 70 (10)
= 700 см 2
Итак, ответ 700 см 2 .
Вопрос 6:
Мистер Рой продает рубашку за 24 доллара и получает прибыль в размере 4 долларов. Какой процент прибыли?
(A) 10% (B) 20% (C) 15%
Решение:
Цена продажи рубашки = 24 доллара США
прибыль = 4 доллара США
Себестоимость = продажная цена — прибыль
Себестоимость = 24 — 4
Процент прибыли = (прибыль / себестоимость) ⋅ 100%
= (4/20) ⋅ 100%
= 20%
Следовательно, требуемый процент прибыли составляет 20%.
Вопрос 7:
Если 2, a, 3, 6 пропорциональны, то значение a равно
(A) 7 (B) 4 (C) 2
Решение:
Так как 2, a, 3, 6 пропорциональны
Произведение крайностей = произведение средних
2 ⋅ 6 = a ⋅ 3
12 = 3a
a = 12/3
a = 4
Итак, ответ 4.
Вопрос 8:
Какое значение равно -5 + 3?
(A) -1 (B) -2 (C) -7
Решение:
Символ двух чисел не совпадает.
Поскольку данные числа имеют разные знаки, мы должны вычесть их и принять положительный знак за ответ.
-5 + 3 = -2
Итак, правильный ответ на этот вопрос — -2.
Вопрос 9:
У вас есть две земли для покупки по одинаковой цене. Один квадратной формы с длиной стороны 40 футов. Другой прямоугольной формы с длиной 30 футов и шириной 50 футов. Что лучше?
(A) Прямоугольник (B) Квадрат (C) Ни один из этих
Решение:
Чтобы найти, какая сделка лучше, мы должны найти площадь двух разных земель отдельно.
Площадь квадратной земли = 2
= (40) 2
= 1600 квадратных футов
Площадь прямоугольной земли = длина x ширина
= 30 ⋅ 50
= 1500 квадратных футов
Отсюда мы узнаем, что площадь квадратного земельного участка больше, чем площадь прямоугольного участка
Квадратная сделка лучше. Итак, правильный ответ квадратный.
Вопрос 10:
(A) 1 (B) 3 (C) 6
Решение:
Расстояние между двумя точками = √ (x 2 — x 1 ) 2 + (y 2 — y 1 ) 2
Поскольку две точки находятся на оси x, значение координаты y будет равно 0.
A (-3, 0) B (3, 0)
Расстояние между AB = √ (3 + 3) 2 + (0-0) 2
= √36
= 6 единиц
Итак, правильный ответ на этот вопрос — 6 единиц.
Кроме того, что описано в этом разделе, если вам нужны другие математические данные, воспользуйтесь нашим пользовательским поиском Google здесь.
Если у вас есть отзывы о наших математических материалах, напишите нам:
v4formath @ gmail.com
Мы всегда ценим ваши отзывы.
Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики.
ЗАДАЧИ СО СЛОВАМИ
Задачи со словами HCF и LCM
Задачи со словами на простых уравнениях
Задачи со словами на линейных уравнениях
Задачи со словами на квадратных уравнениях
Проблемы со словами в поездах
Проблемы со словами по площади и периметру
Проблемы со словами по прямой и обратной вариациям
Проблемы со словами по цене за единицу
Проблемы со словами по скорости работы
задачи по сравнению ставок
Преобразование обычных единиц в текстовые задачи
Преобразование метрических единиц в текстовые задачи
Word задачи по простому проценту
Word по сложным процентам
ngles
Проблемы с дополнительными и дополнительными углами
Проблемы со словами с двойными фактами
Проблемы со словами тригонометрии
Проблемы со словами в процентах
Проблемы со словами
Задачи со словами
Задачи с десятичными словами
Задачи со словами на дроби
Задачи со словами на смешанные фракции
Одношаговые задачи с уравнениями со словами
Проблемы со словами с линейным неравенством
ЗадачиПроблемы со временем и рабочими словами
Задачи со словами на множествах и диаграммах Венна
Проблемы со словами для возрастов
Проблемы со словами из теоремы Пифагора
Процент числового слова проблемы
Проблемы со словами при постоянной скорости
Проблемы со словами при средней скорости
Проблемы со словами при сумме углов треугольника 180 градусов
ДРУГИЕ ТЕМЫ
Сокращения прибыли и убытков
Сокращение в процентах
Сокращение в таблице времен
Сокращение времени, скорости и расстояния
Сокращение соотношения и пропорции
Область и диапазон рациональных функций
Область и диапазон рациональных функций
функции с отверстиями
Графики рациональных функций
Графики рациональных функций с отверстиями
Преобразование повторяющихся десятичных знаков в дроби
Десятичное представление рациональных чисел
с использованием длинного корня видение
Л.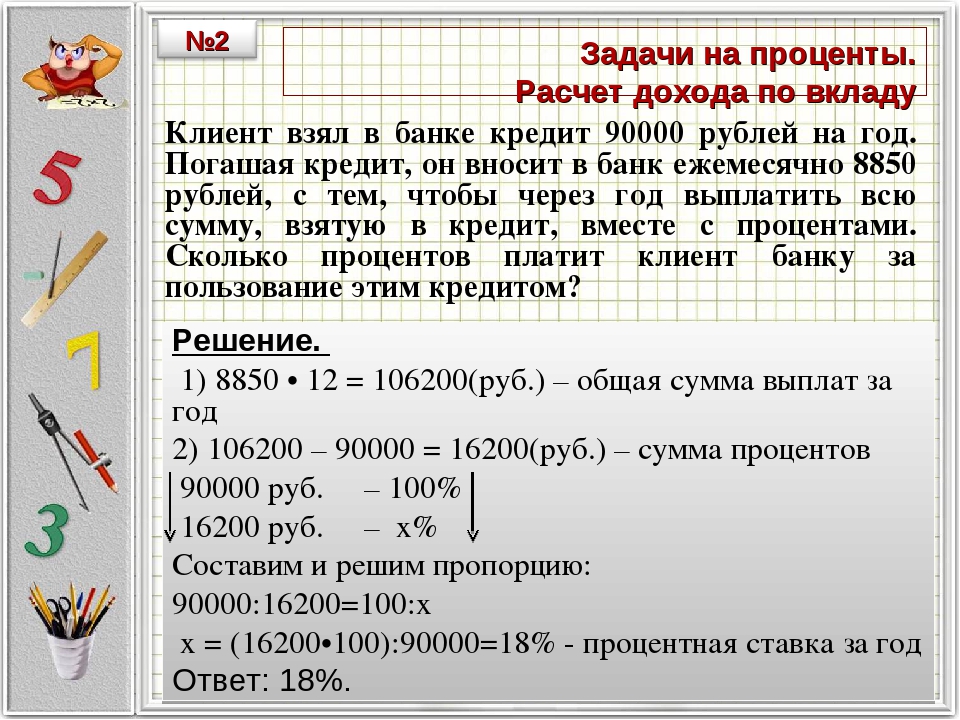
Метод CM для решения временных и рабочих задач
Преобразование задач со словами в алгебраические выражения
Остаток при делении 2 в степени 256 на 17
Остаток при делении в степени 17 на 16
Сумма всех трехзначных чисел, делимых на 6
Сумма всех трехзначных чисел, делимых на 7
Сумма всех трехзначных чисел, делимых на 8
Сумма всех трехзначных чисел, образованных с использованием 1, 3 , 4
Сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами
Сумма всех трех четырехзначных чисел, образованных с использованием 0, 1, 2, 3
Сумма всех трех четырехзначных чисел числа, образованные с использованием 1, 2, 5, 6
Репетитор по математике 6, помощь и практика онлайн
Не видите, что вам нужно?
Не волнуйтесь, попробуйте поискать по всем нашим темам
Искать по всему StudyPugЧто вы изучаете по математике в 6-м классе?
Изучая математику в шестом классе, вы будете изучать математические области, связанные со ставками единиц, десятичными знаками, отношениями, факторами, процентами, дробями и т.
Д.Вы также разовьете свою способность решать алгебраические задачи и научитесь использовать PEMDAS, чтобы помочь вам.
В 6 классе вы начнете изучать следующие области геометрии, такие как площадь поверхности и объем трехмерных фигур, мозаика и системы измерения. Вы также изучите фундаментальные принципы алгебры и тригонометрии, которые в совокупности предоставят вам знания, необходимые для прохождения курсов базовой алгебры, тригонометрии и, в конечном итоге, предварительного вычисления.
Это программа обучения, разработанная на основе того, что вы узнали в 5-м классе, и подготовит вас к более продвинутым этапам математики в 7–12 классах. На каждом уроке математики, который вы посещаете в 6-м классе, StudyPug будет присутствовать. . Мы отличный помощник для помощи с повторными и домашними заданиями. Мы доступны круглосуточно и без выходных, и предлагаем высококачественные видеоуроки, которые разбивают материалы, которые вы изучали на занятиях, в более доступной форме. Кроме того, каждое видео, которое мы предлагаем, содержит пошаговые примеры, которые могут прояснить ситуацию.
Их также можно приостанавливать, перематывать и перематывать вперед, чтобы вы никогда не отставали и могли учиться в своем собственном темпе.
Как подписчик на наш сервис, вы получите доступ к тысячам онлайн-видео, которые охватывают все темы, которые вы ожидаете найти в 6 классе по математике и выше, что делает StudyPug репетитором на всю жизнь.
Как получить хорошие отметки на экзамене по математике в 6-м классе
Чтобы получить хорошие оценки на экзамене по математике, вам необходимо уметь эффективно продемонстрировать, что вы умеете разбираться в различных математических задачах и можете найти эффективный способ их решения.Экзаменаторам необходимо будет убедиться, что вы умеете писать, интерпретировать и использовать выражения и уравнения, а также правильно использовать эти математические инструменты, чтобы прийти к правильным выводам.
По сути, они хотят увидеть, как работает ваш мозг. Недостаточно просто ответить на вопрос путем запоминания. Покажите свою тренировку и то, как вы пришли к ответам, чтобы иметь больше шансов получить высшие оценки.
Если вы хотите получить дополнительную помощь по математике в шестом классе вне класса и хотите повысить свои шансы на получение более высоких оценок на предстоящих экзаменах по математике, вам следует пересматривать и делать это регулярно.Нельзя не подчеркнуть, что лучший способ выучить математику — это повторять. Чем больше вы практикуетесь в решении математических задач, тем больше вероятность, что вы запомните эту информацию.
Вам следует пересмотреть то, чему вас учили в классе, и использовать это для создания эффективных учебных занятий, направленных на ваши слабые стороны. Если вы не уверены, в чем заключаются ваши сильные и слабые стороны, воспользуйтесь нашими простыми практическими материалами, которые помогут вам определить темы и вопросы, с которыми у вас могут возникнуть трудности. Просмотр заметок на уроке каждый вечер поможет вам улучшить свое понимание математика.
Мы понимаем, что сделать это и выработать у себя хорошую учебную привычку легче сказать, чем сделать, поэтому мы предлагаем наш контент в виде коротких и информативных видеоуроков, которые можно смотреть дома или в дороге.
Наш контент работает с вашим расписанием, поэтому, когда у вас есть свободный час или два, StudyPug доступен, чтобы помочь вам просмотреть любые темы в рамках программы математики 6-го класса.
Кроме того, мы настоятельно рекомендуем вам использовать нашу платформу, чтобы помочь вам сдавать практические работы и пробные экзамены.Это поможет вам обрести уверенность перед фактическими испытаниями и еще больше поможет вам сузить свои сильные и слабые стороны. При сдаче пробных экзаменов вы должны работать в рамках ограничений по времени, установленных для каждой работы, и попросить кого-нибудь еще пометить ваши тесты за вас. Если вы посмотрите на свою производительность и увидите улучшения, это покажет вам, что версия действительно работает, и побудит вас придерживаться ее!
Проще говоря, хорошо спланированная стратегия проверки, направленная на устранение вашей слабости, и удобный помощник для проверки, такой как StudyPug, могут значительно повысить ваши шансы на получение более высоких оценок на экзаменах.
Помимо подготовки к экзаменам, мы также можем помочь вам лучше учиться в классе. Если в вашем уроке есть что-то, что вы не можете понять, перейдите в Интернет и просмотрите наш контент. У нас есть видеоуроки по этой теме, которые помогут устранить любую вашу путаницу. Наши видеоролики по математике для 6-х классов содержат то же содержание, которое вы ожидаете найти в современных учебниках, и будут отвечать на вопросы, которые, скорее всего, появятся на ваших тестах по математике для 6-го класса.
Думайте об StudyPug как о вашем собственном виртуальном репетиторе математики в 6-м классе, доступном в любое время, когда мы вам понадобимся, и за небольшую часть стоимости личного репетитора.
Сложна ли математика в 6-м классе?
Если вас беспокоит изучение математики в шестом классе, вы не одиноки. Тысячи таких же учеников, как и вы, нуждаются в помощи в понимании более сложной терминологии и предметов, которые будут вводиться в течение учебного года. Хотя это действительно кажется сложной задачей, предметы математики для 6-го класса не так уж и сложны для понимания, если вы твердо понимаете основы.
Помните, что в первый день от вас не ждут, что вы все узнаете.Изучение математики требует времени, и хорошая основа математических знаний значительно повысит ваши шансы поступить в колледж / университет и найти работу в дальнейшей жизни.
Если вам нужна помощь в понимании математики в 6-м классе или вы хотите получить дополнительные уроки по математике перед предстоящими викторинами и экзаменами, наш онлайн-контент поможет вам решить даже самые сложные математические задачи для 6-го класса. В настоящее время мы предлагаем пошаговые уроки по следующим популярным темам:
∙ \ bullet ∙ Понимание чисел и теории чисел∙ \ bullet ∙ Сложение, вычитание, умножение и деление целых чисел
∙ \ bullet ∙ Соотношения, коэффициенты и проценты
∙ \ bullet ∙ Тесселяция
∙ \ bullet ∙ И многое другое!
Контент, который мы предлагаем по каждой теме математики в шестом классе, был разработан опытными учителями, которые имеют глубокое понимание предмета.Мы также работали над тем, чтобы каждый урок отражал то, чему вас учат в школе, чтобы они затрагивали проблемы и содержание, которые наиболее важны для вас.
В StudyPug мы понимаем и ценим, что каждый ученик учится по-своему. С этой целью мы решили применить подход «Математика для 6-го класса для чайников», который начинается с основ, не предполагает никаких предварительных знаний и охватывает все области математики для 6-го класса. Каждая область нашего контента была разработана так, чтобы плавно переходить от одной темы к другой, что позволяет вам развивать то, что вы только что узнали, и вводить более сложные элементы, когда вы будете готовы.
Как подписчик на нашу услугу онлайн-обучения, вы получите прямой доступ ко всем нашим видео для всех доступных классов, что позволит вам пользоваться нашими услугами в течение многих лет. Благодаря тысячам уроков и круглосуточной поддержке, мы всегда готовы удовлетворить все ваши потребности в математике.
Если вы хотите испытать наши услуги перед покупкой, просмотрите нашу коллекцию бесплатных уроков математики для 6-го класса, которые охватывают множество тем. Попробуйте их сегодня и прочтите отзывы наших клиентов, чтобы узнать, как мы помогаем учащимся, так же как и вы, улучшать их успеваемость по математике в шестом классе.
2b
20 задач по математике для четвертого класса Учащиеся должны знать, как решать
На этой странице показаны двадцать задач по математике для 4-го класса, которые могут быть заданы ученикам 4-го класса. Эти математические задачи для 4-го класса были хорошо подобраны, чтобы охватить широкий спектр тем, изучаемых в 4-м классе.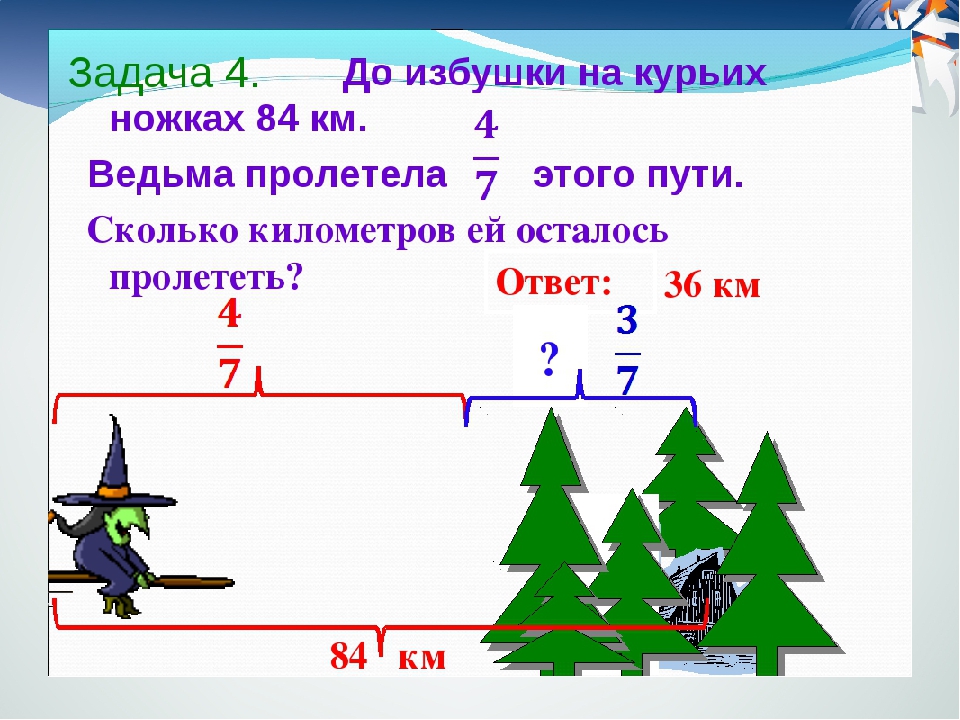
1
Репетитор математики берет 20 долларов за первый час и 10 долларов за каждый дополнительный час. Учащийся брал уроки репетиторства с 14:00 до 19:00. Сколько денег зарабатывал репетитор по математике?
2
Дневной абонемент в парк развлечений стоит 10 долларов для взрослых и 4 доллара для детей. Парк посещает семья из двух взрослых и четверых детей. Сколько денег заплатила семья?
3
Дом Джонатана находится в упорядоченной паре (3, 4).Чтобы пойти в школу, он проходит 5 кварталов на север и 2 квартала на восток. Какую упорядоченную пару можно использовать, чтобы найти школу Джонатана?
4
Алисия плачет, потому что не смогла прокатиться. Когда ее мама спросила ее, почему она плачет, она ответила: «Мне должно быть не менее 5 футов, чтобы кататься». Если Алисия 54 дюйма, то на сколько дюймов она от 5 футов?
5
Семья проедет 240 миль, чтобы поехать к родственникам. Отец ездит со скоростью 60 миль в час.
Как долго будет поездка?
6
Начиная с 23:00, собака лает дважды в 11:09, 11:15 и 11:21.Во сколько это будет, когда собака снова лает?
7
В коробке 4 фунта муки. Моя мама использовала три четверти (3/4) муки, чтобы сделать торт. Сколько муки осталось в ящике?
8
Директор заказал батончики мюсли для 3000 учеников, чтобы отметить окончание учебного года. Батончики мюсли поставлялись в ящиках, в каждом ящике по 15 коробок, а в каждой — по 20 батончиков. Сколько случаев пришло?
9
Один фунт равен 16 унциям.Сколько фунтов будет весить мешок риса весом 112 унций?
10
Если мешок яблок весит около 2 1/2 фунтов, сколько будут весить 10 пакетов?
11
Мешок винограда стоил 4,57 доллара. Если вы заплатите 5 долларов, какие сдачи вам вернут?
12
Твоя мама использовала 5/4 фунта муки, чтобы приготовить тесто для пиццы. А вы, тетя, потребляете 3/4 фунта муки.
Насколько больше муки потребляет ваша мама?
13
Если четыре числа меньше 100, нечетные, кратные 5 и больше 60, то какие числа?
14
В магазине продается 546 конфет в понедельник, 567 во вторник и 588 в среду.Сколько конфет продаст магазин в четверг?
15
Библиотека возле дома Стефани находится по заказанной паре (5, 6). Чтобы вернуться домой, она проходит 4 квартала на юг и 3 квартала на запад. Какую упорядоченную пару можно использовать, чтобы определить местонахождение дома Стефани?
16
Какое я число, если сумма моих двух цифр равна 10, а цифра в разряде единиц в четыре раза больше, чем цифра в разряде десятков?
17
Четыре автобуса везут студентов в музей науки.Сколько детей в каждом автобусе, если в каждом автобусе 100 учеников и в каждом автобусе одинаковое количество учеников?
18
Если у вас в кармане 2 четвертака, 4 десятицентовика, 6 пятаков и 10 пенни, сколько у вас денег?
19
У Марии 3/5 фунта риса.
У Джона 2/3 фунта воды. У кого больше муки?
20
После продажи конфет по 25 центов за каждую вы заработали 5,50 доллара. Сколько конфет вы продали?
Если ученик может решить хотя бы 18 из этих 20 математических задач 4-го класса, можно сделать вывод, что он хорошо решает математические задачи 4-го класса.
Введение в физику
18 ноя, 20 13:20
Первоклассное введение в физику. Универсальный ресурс для глубокого понимания важных концепций физики
Подробнее
Новые уроки математики
Ваша электронная почта в безопасности. Мы будем использовать его только для информирования вас о новых уроках математики.
Трудные задачи по математике для 7-го класса: 10 самых сложных вопросов
EdSearch
Войти здесь- 888-309-8227
- 732-384-0146
- Дом
- Школы
- Рабочие тетради SkillBuilder Оценка
- PARCC
- PARCC — Бесплатные образцы eSamples от tedBook
- PARCC — Бесплатная учетная запись учителя
- Запросить ценовое предложение
- Руководство PARCC
- Колорадо
- Округ Колумбия
- Иллинойс
- Мэриленд
- Массачусетс
- Нью-Джерси
- Нью-Мексико
- Род-Айленд
- Интеллектуальная сбалансированная оценка
- SBAC- tedBook Free eSamples
- SBAC — Бесплатная учетная запись учителя
- Запросить ценовое предложение
- Оценка ACT Aspire
- Арканзас
- Флорида — FSA
- Грузия — GMAS
- Индиана — ISTEP
- Миссисипи — КАРТА
- Миссури — КАРТА
- Огайо — ОСТ
- Теннесси — TNReady
- Учебные ресурсы CCSS
- Общие печатные ресурсы для практических занятий
- Нью-Йорк
- Подписка на портал для учителей
- Летняя программа обучения 2016
- Акции
- Родители
- Lumos StepUp ™
- Lumos tedBook ™ — издание PARCC
- 3 класс
- 4 класс
- 5 класс
- 6 класс
- 7 класс
- 8 класс
- Lumos tedBook ™ — выпуск SBAC
- Lumos tedBook ™ — Common Core Edition
- Общие основные ресурсы для 3-го класса
- Общие основные ресурсы для 4-го класса
- Общие основные ресурсы для 5-го класса
- Общие основные ресурсы для 6-го класса
- Общие основные ресурсы для 7-го класса
- Общие основные ресурсы для 8-го класса
- Пишите лучше
- Акции
- Библиотеки
- Дом библиотеки
- Доступ к библиотечной программе Lumos StepUp ™
- Помогите покровителям писать лучше
- Master Study Skills: интерактивный семинар для молодых покровителей
- Акции
- Демо
- ресурсов
- Доступ к онлайн-книгам
- Практические тесты и примеры вопросов
- Бесплатные отрывки для чтения
- Бесплатные рабочие листы
- Библиотека ресурсов RTI
- Домашнее задание
- Общие основные государственные стандарты, классы 3-8
- Другие ресурсы
- Ресурсы Академии Хана
- Приложения для студентов, родителей и учителей — Lumos Apps
- Lumos SchoolUp — приложение от сообщества для родителей
- Lumos StepUp — приложение Common Core
- Блог: Учителя говорят
- Новости
- События
- Конференции
- EdSearch
- Приложения
- Книги
- Обучающие видео
- EdFinder
- О нас
- Наши учителя — Lumos Learning
- Наши консультанты
- Стать научным консультантом
PPT — Текстовые математические задачи Для 1-го класса Математические задачи и решения Презентация в PowerPoint
Текстовые математические задачи Для 1-го класса Математические задачи и решения
Что такое текстовая математическая задача? • Текстовая математическая задача • Осенью с дерева упали 2 красных и 3 желтых листа.
• Сколько листьев упало с дерева?
В корзине 2 груши и 3 яблока. Это СОСТОЯНИЕ текстовой математической задачи. Сколько фруктов в корзине? Это ВОПРОС математической задачи.
На лугу 2 цветка и 3 дерева. • Сколько цветов и деревьев на лугу? • 2 + 3 = 5 • Наконец, у нас есть два ответа на текстовую математическую задачу. ОТВЕТ: 5 flowersandtrees
ТЕКСТОВАЯ МАТЕМАТИКА ПРОБЛЕМА ОТВЕТ НА ВОПРОС УСЛОВИЕ ВЫ ЗНАЕТЕ!
Я ЗНАЮ! 1.Это называется проблемой слова, потому что написано текстом. 2. У текстовой математической задачи есть условие и вопрос. 3. То, что я знаю, находится в состоянии. То, что я должен найти, находится в вопросе. 4. Отвечаю на вопрос о слове проблема с решением. 5. Я должен написать ответ на математическую задачу.
Давайте проверим, что вы запомнили! Отметьте красным цветом условие, а зеленым цветом — вопрос математической задачи.
4 птицы садятся на дерево, одна птица — на другое дерево.Сколько птиц садится на два дерева? 1 + 4 = 5 • Решение: …………… • Ответ: 5 птиц
Текстовая математическая задача с числовыми данными • В каждой текстовой математической задаче есть числовые данные. В корзине 10 яблок и 5 игл. Сколько там фруктов? • Решение: 10 + 5 = 15 • Ответ: 15 фруктов • Числовые данные помогают нам написать решение. • Числовые данные находятся в состоянии задачи со словом. Они написаны цифрами.
Ой, где они? • Кто правильно распознал • числовые данные в словесной проблеме? • Найди решение.• Белка собрала 10 желудей и четыре грецких ореха. Сколько фруктов собрала белка? 10 • Ани: 10 и 4 • Боби: • Решение: 10 + 4 = 14 • Ответ: 14 фруктов • Числовые данные в словарной математической задаче можно записать словами и числами.
Проверьте, что вы помните! Цвет условия математической задачи — синий, вопрос — красный, а числовые данные — желтый.
• Некоторые дети посадили 12 деревьев и кусты. Сколько деревьев и кустов • они посадили? • Решение: 12 + 8 = 20 • Ответ: 20 деревьев и кустов Превосходно
Что означают слова «больше» и «меньше» в текстовой математической задаче ? • Катядрю 4 гриба и 6 деревьев.• Сколько грибов меньше деревьев? • Сколько деревьев больше, чем грибов? • Решение: 6 — 4 = 2 (деревья> грибы) • (грибы <деревья)
Сравните задачи со словами. • Ребенок собрал 12 каштанов и 8 грецких орехов. На сколько орехов меньше каштанов? • Ребенок собрал 12 каштанов и 8 грецких орехов. • Сколько каштанов • больше, чем грецких орехов? • Решение: 12 — 8 = 4 • Ответ: 4 каштана> • Решение: 12 — 8 = 4 • Ответ: 4 грецких ореха <Проблемы со словами имеют одинаковые условия да нет Проблемы со словами имеют разные вопросы нет да Решения разные да нет
Сравните словесные задачи и решите их. Мими елафуршери.
Herbrotherate2 вишни меньше, чем у Мими. Сколько вишен съел брат Мими? • Mimiatefourcherries. Ее брат съел еще 2 вишни. Сколько вишни он съел? • Решение: 4 + 2 = 6 • Ответ: 6 вишен • Решение: 4 — 2 = 2 • Ответ: 2 вишенки
Я знаю! ДОПОЛНИТЕЛЬНАЯ ВЫПИСКА Я участвую в олимпиаде по математике и получаю награды!
Раскрасьте истинное решение. Anacollectedcones. Она находит 9 шишек ели и еще 2 шишки сосны.Сколько сосновых шишек собрала Ана? сосна 9 + 2 = 11 9 — 2 = 7 Я знаю, какое решение! Я победитель! Ель
Проблемы со словами на картинке 13 16 14
Используйте картинку и решения рядом с ней. • Сделайте слово проблемой. На дереве было 8 птиц, три — спустились под дерево. Сколько птиц осталось на дереве? 5 птиц сели на дерево, а 3- на землю под деревом. Сколько всего птиц? 5 + 3 = 8 • На дереве было 8 птиц.