Номер 365 — ГДЗ по Математике 6 класс Учебник Виленкин, Жохов, Чесноков, Шварцбурд 2020. Часть 2 (решебник)
Номер 365 — ГДЗ по Математике 6 класс Учебник Виленкин, Жохов, Чесноков, Шварцбурд 2020. Часть 2 (решебник) — GDZwowПерейти к содержанию
Search for:
Авторы: Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И.
Издательство: Мнемозина
Тип: Учебник
Новая версия
ЧАСТЬ 1
Выберите номер упражнения
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244245246247248249250251252253254255256257258259260261262263264265266267268269270271272273274275276277278279280281282283284285286287288289290291292293294295296297298299300301302303304305306307308309310311312313314315316317318319320321322323324325326327328329330331332333334335336337338339340341342343344345346347348349350351352353354355356357358359360361362363364365366367368369370371372373374375376377378379380381382383384385386387388389390391392393394395396397398399400401402403404405406407408409410411412413414415416417418419420421422423424425426427428429430431432433434435436437438439440441442443444445446447448449450451452453454455456457458459460461462463464465467468469470471472473474475476477478479480481482483484485486487488489490491492493494495496497498499500501502503504505506507508509510511512513514515516517518519520521522523524525526527528529530531532533534535536537538539540541542543544545546547548549550551552553554555556557558559560561562563564565566567568569570571572573574575576577578579580581582583584585586587588589590591592593594595596597598599600601602603604605606607608609610611612613614615616617618619620621622623624625626627628629630631632633634635636637638639640641642643644645646647648649650651652653654655656657658659660661662663664665666667668669670671672673674675676677678679680681682683684685686687688689690691692693694695696697698699700701702703704705706707708709710711712713714715716717718719720721722723724725726727728729730731732733734735736737738739740741742743744745746747748749750751753754755756757758759760761762763764765766767768769770771772773774775776777778779780781782783784785786787788789790791792793794795796797798799800801802803804805806807809810811812813814815816817818819820821822823824825826827828829830831832833834835836837838839840841842843844845846847848849850851852853854855856857858859860861862863864865866867868869870871872873874875876877878879880881882883884885886887888889890891892893894895896897
ЧАСТЬ 2
Выберите номер упражнения
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192939495969798991001011021031041051061071081091101111121131141151161171181191201211221231241251261271281291301311321331341351361371381391401411421431441451461471481491501511521531541551561571581591601611621631641651661671681691701711721731741751761771781791801811821831841851861871881891901911921931941951961971981992002012022032042052062072082092102112122132142152162172182192202212222232242252262272282292302312322332342352362372382392402412422432442452462472482492502512522532542552562572582592602612622632642652662672682692702712722732742752762772782792802812822832842852862872882892902912922932942952962972982993003013023033043053063073083093103113123133143153163173183193203213223233243253263273283293303313323333343353363373383393403413423433443453463473483493503513523533543553563573583593603613623633643653663673683693703713723733743753763773783793803813823833843853863873883893903913923933943953963973983994004014024034044054064074084094104114124134144154164174184194204214224234244254264274284294304314324334344354364374384394404414424434444454464474484494504514524534544554564574584594604614624634644654664674684694704714724734744754764774784794804814824834844854864874884894904914924934944954964974984995005015025035045055065075085095105115125135145155165175185195205215225235245255265275285295305315325335345355365375385395405415425435445455465475485495505515525535545555565575585595605615625635645655665675685695705715725735745755765775785795805815825835845855865875885895905915925935945955965975985996006016026036046056066076086096106116126136146156166176186196206216226236246256266276286296306316326336346356366376386396406416426436446456466476486496506516526536546556566576586596606616626636646656666676686696706716726736746756766776786796806816826836846856866876886896906916926936946956966976986997007017027037047057068928938948958968978988999009019029039049059069079089099109119129139149159169179189199209219229239249259269279289299309319329339349359369379389399409419429439449459469479489499509519529539549559569579589599609619629639649659669679689699709719729739749759769779789799809819829839849859869879889899909919929939949959969979989991000100110021003100410051006100710081009101010111012101310141015101610171018101910201021102210231024102510261027102810291030103110321033103410351036103710381039104010411042104310441045104610471048104910501051105210531054105510561057105810591060106110621063106410651066106710681069107010711072107310741075107610771078107910801081108210831084108510861087108810891090109110921093109410951096109710981099110011011102110311041105110611071108110911101111111211131114111511161117111811191120112111221123112411251126112711281129113011311132113311341135113611371138113911401141114211431144114511461147114811491150115111521153115411551156115711581159116011611162116311641165116611671168116911701171117211731174117511761177117811791180118111821183118411851186118711881189119011911192119311941195119611971198119912011202120312041205120612071208120912101211121212131214121512161217121812191220122112221223122412251226122712281229123012311232123312341235123612371238123912401241124212431244124512461247124812491250125112521253125412551256125712581259126012611262126312641265126612671268126912701271127212731274127512761277127812791280128112821283128412851286128712881289129012911292129312941295129612971298129913001301130213031304130513061307130813091310131113121313131413151316131713181319132013211322132313241325132613271328132913301331133213331334133513361337133813391340134113421343134413451346134713481349135013511352135313541355135613571358135913601361136213631364136513661367136813691370137113721373137413751376137713781379138013811382138313841385138613871388138913901391139213931394139513961397139813991400140114021403140414051406140714081409141014111412141314141415141614171418141914201421142214231424142514261427142814291430143114321433143414351436143714381439144014411442144314441445144614481449145014511452145314541455145614571458145914601461146214631464146514681469147014711472147314741475147614771478147914801481148214831484148514861487148814891490149114921493149414951496149714981499150015011502150315041505150615071508150915101511151215131514151515161517151815191520152115221523152415251526152715281529153015311532153315341535153615371538153915401541154215431544154515461547154815491550155115521553155415551556155715581559156015611562156315641565156615671568156915701571157215731574157515761577157815791580158115821583158415851586158715881589159015911592159315941595
Adblockdetector
Номер 365 — ГДЗ по Математике для 6 класса Учебник Виленкин, Жохов, Чесноков, Шварцбурд Часть 1.

Номер 365 — ГДЗ по Математике для 6 класса Учебник Виленкин, Жохов, Чесноков, Шварцбурд Часть 1. — ГДЗ РЕДПерейти к содержанию
Search for:
Авторы: Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И.
Издательство: Мнемозина
Тип: Учебник
Новая версия
Старая версия
ЧАСТЬ 1
Выберите номер упражнения
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244245246247248249250251252253254255256257258259260261262263264265266267268269270271272273274275276277278279280281282283284285286287288289290291292293294295296297298299300301302303304305306307308309310311312313314315316317318319320321322323324325326327328329330331332333334335336337338339340341342343344345346347348349350351352353354355356357358359360361362363364365366367368369370371372373374375376377378379380381382383384385386387388389390391392393394395396397398399400401402403404405406407408409410411412413414415416417418419420421422423424425426427428429430431432433434435436437438439440441442443444445446447448449450451452453454455456457458459460461462463464465467468469470471472473474475476477478479480481482483484485486487488489490491492493494495496497498499500501502503504505506507508509510511512513514515516517518519520521522523524525526527528529530531532533534535536537538539540541542543544545546547548549550551552553554555556557558559560561562563564565566567568569570571572573574575576577578579580581582583584585586587588589590591592593594595596597598599600601602603604605606607608609610611612613614615616617618619620621622623624625626627628629630631632633634635636637638639640641642643644645646647648649650651652653654655656657658659660661662663664665666667668669670671672673674675676677678679680681682683684685686687688689690691692693694695696697698699700701702703704705706707708709710711712713714715716717718719720721722723724725726727728729730731732733734735736737738739740741742743744745746747748749750751753754755756757758759760761762763764765766767768769770771772773774775776777778779780781782783784785786787788789790791792793794795796797798799800801802803804805806807809810811812813814815816817818819820821822823824825826827828829830831832833834835836837838839840841842843844845846847848849850851852853854855856857858859860861862863864865866867868869870871872873874875876877878879880881882883884885886887888889890891892893894895896897
ЧАСТЬ 2
Выберите номер упражнения
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192939495969798991001011021031041051061071081091101111121131141151161171181191201211221231241251261271281291301311321331341351361371381391401411421431441451461471481491501511521531541551561571581591601611621631641651661671681691701711721731741751761771781791801811821831841851861871881891901911921931941951961971981992002012022032042052062072082092102112122132142152162172182192202212222232242252262272282292302312322332342352362372382392402412422432442452462472482492502512522532542552562572582592602612622632642652662672682692702712722732742752762772782792802812822832842852862872882892902912922932942952962972982993003013023033043053063073083093103113123133143153163173183193203213223233243253263273283293303313323333343353363373383393403413423433443453463473483493503513523533543553563573583593603613623633643653663673683693703713723733743753763773783793803813823833843853863873883893903913923933943953963973983994004014024034044054064074084094104114124134144154164174184194204214224234244254264274284294304314324334344354364374384394404414424434444454464474484494504514524534544554564574584594604614624634644654664674684694704714724734744754764774784794804814824834844854864874884894904914924934944954964974984995005015025035045055065075085095105115125135145155165175185195205215225235245255265275285295305315325335345355365375385395405415425435445455465475485495505515525535545555565575585595605615625635645655665675685695705715725735745755765775785795805815825835845855865875885895905915925935945955965975985996006016026036046056066076086096106116126136146156166176186196206216226236246256266276286296306316326336346356366376386396406416426436446456466476486496506516526536546556566576586596606616626636646656666676686696706716726736746756766776786796806816826836846856866876886896906916926936946956966976986997007017027037047057068928938948958968978988999009019029039049059069079089099109119129139149159169179189199209219229239249259269279289299309319329339349359369379389399409419429439449459469479489499509519529539549559569579589599609619629639649659669679689699709719729739749759769779789799809819829839849859869879889899909919929939949959969979989991000100110021003100410051006100710081009101010111012101310141015101610171018101910201021102210231024102510261027102810291030103110321033103410351036103710381039104010411042104310441045104610471048104910501051105210531054105510561057105810591060106110621063106410651066106710681069107010711072107310741075107610771078107910801081108210831084108510861087108810891090109110921093109410951096109710981099110011011102110311041105110611071108110911101111111211131114111511161117111811191120112111221123112411251126112711281129113011311132113311341135113611371138113911401141114211431144114511461147114811491150115111521153115411551156115711581159116011611162116311641165116611671168116911701171117211731174117511761177117811791180118111821183118411851186118711881189119011911192119311941195119611971198119912011202120312041205120612071208120912101211121212131214121512161217121812191220122112221223122412251226122712281229123012311232123312341235123612371238123912401241124212431244124512461247124812491250125112521253125412551256125712581259126012611262126312641265126612671268126912701271127212731274127512761277127812791280128112821283128412851286128712881289129012911292129312941295129612971298129913001301130213031304130513061307130813091310131113121313131413151316131713181319132013211322132313241325132613271328132913301331133213331334133513361337133813391340134113421343134413451346134713481349135013511352135313541355135613571358135913601361136213631364136513661367136813691370137113721373137413751376137713781379138013811382138313841385138613871388138913901391139213931394139513961397139813991400140114021403140414051406140714081409141014111412141314141415141614171418141914201421142214231424142514261427142814291430143114321433143414351436143714381439144014411442144314441445144614481449145014511452145314541455145614571458145914601461146214631464146514681469147014711472147314741475147614771478147914801481148214831484148514861487148814891490149114921493149414951496149714981499150015011502150315041505150615071508150915101511151215131514151515161517151815191520152115221523152415251526152715281529153015311532153315341535153615371538153915401541154215431544154515461547154815491550155115521553155415551556155715581559156015611562156315641565156615671568156915701571157215731574157515761577157815791580158115821583158415851586158715881589159015911592159315941595
Adblockdetector
5 класс.
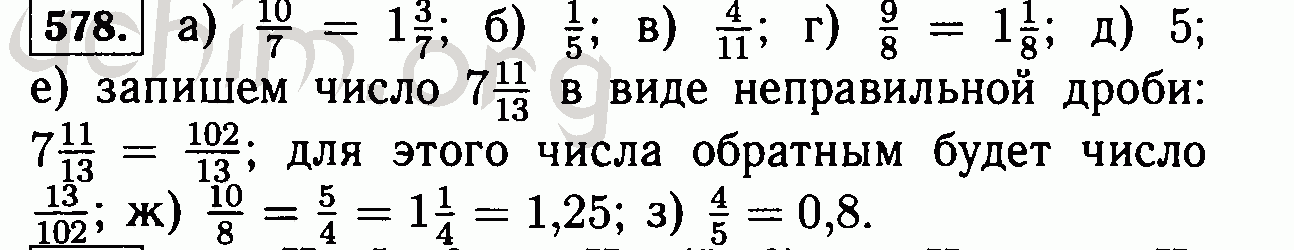 Математика. Виленкин. Учебник. Ответы к стр. 7
Математика. Виленкин. Учебник. Ответы к стр. 7Натуральные числа
Натуральные числа и шкалы
Обозначение натуральных чиселОтветы к стр. 7
3. Запишите цифрами числа:
а) восемьсот девять;
б) пять тысяч двести одиннадцать;
в) двадцать два миллиона три тысячи восемь;
г) двадцать восемь миллионов пятнадцать тысяч триста два;
д) пятьсот семь миллионов восемьдесят тысяч;
е) один миллиард десять миллионов девять тысяч;
ж) четыреста двадцать три миллиарда триста сорок миллионов шестьсот тысяч девятьсот восемьдесят;
з) пятьдесят два миллиарда восемь тысяч двенадцать;
и) семьсот семьдесят семь миллиардов шестьдесят восемь тысяч;
к) девять миллиардов пятьдесят пять тысяч.
а) 809;
б) 5211;
в) 22 003 008;
г) 28 015 302;
д) 507 080 000;
е) 1 010 009 000;
ж) 423 340 600 980;
з) 52 000 008 012;
и) 777 000 068 000;
к) 9 000 055 000.
4. Число 580043000707 разбивают на классы так: 580 043 000 707 — и читают: пятьсот восемьдесят миллиардов сорок три миллиона семьсот семь.
Разбейте на классы и прочитайте числа: 2407; 35810; 500215; 6570000; 3048504325; 24000670001; 300100234129.
2407 — две тысячи четыреста семь;
35 810 — тридцать пять тысяч восемьсот десять;
500 215 — пятьсот тысяч двести пятнадцать;
6 570 000 — шесть миллионов пятьсот семьдесят тысяч;
3 048 504 325 — три миллиарда сорок восемь миллионов пятьсот четыре тысячи триста двадцать пять;
24 000 670 001 — двадцать четыре миллирда шестьсот семьдесят тысяч один;
300 100 234 129 — триста миллиардов сто миллионов двести тридцать четыре тысячи сто двадцать девять.
5. Прочитайте числа: 509; 6001; 90 050; 7 000 850 127; 56 000 709 000; 21 085 000 000; 340 004 090 300; 86 820 000 800; 1 000 000 031; 63 009 000 050; 1 000 100 999; 383 365 409 707.
509 — пятьсот девять;
6001 — шесть тысяч один;
90 050 — девяносто тысяч пятьдесят;
7 000 850 127 — семь миллиардов восемьсот пятьдесят тысяч сто двадцать семь;
56 000 709 000 — пятьдесят шесть миллиардов семьсот девять тысяч;
21 085 000 000 — двадцать один миллиард восемьдесят пять миллионов;
340 004 090 300 — триста сорок миллиардов четыре миллиона девяносто тысяч триста;
86 820 000 800 — восемьдесят шесть миллиардов восемьсот двадцать миллионов восемьсот;
1 000 000 031 — один миллиард тридцать один;
63 009 000 050 — шестьдесят три миллиарда девять миллионов пятьдесят;
1 000 100 999 — один миллиард сто тысяч девятьсот девяносто девять;
383 365 409 707 — триста восемьдесят три миллиарда триста шестьдесят пять миллионов четыреста девять тысяч семьсот семь.
6. Запишите цифрами числа: 5 тыс.; 702 тыс.; 5081 тыс.; 68 303 тыс.; 12 млн; 306 млн; 487 млрд; 15 млн 205 тыс.; 65 млрд 913 млн.
5 тыс. — 5000;
702 тыс. — 702 000;
5081 тыс. — 5 081 000;
68 303 тыс. — 68 303 000;
12 млн — 12 000 000;
306 млн — 306 000 000;
487 млрд — 487 000 000 000;
15 млн 205 тыс. — 15 205 000;
65 млрд 913 млн — 65 913 000 000.
7. Запишите цифрами числа, встречающиеся в тексте: «Миллиард — очень большое число. За тридцать лет с первого января тысяча девятьсот семидесятого года по тридцать первое декабря тысяча девятьсот девяносто девятого года прошло десять тысяч девятьсот пятьдесят семь суток, что составляет двести шестьдесят две тысячи девятьсот шестьдесят восемь часов, или девятьсот сорок шесть миллионов шестьсот восемьдесят четыре тысячи восемьсот секунд. Значит, за тридцать лет не проходит и миллиарда секунд».
1 000 000 000, 30, 1, 1970 31, 1999, 10957, 262 968, 946 684 800, 30, 1 000 000 000.
8. Запишите пять раз подряд цифру 6. Прочитайте получившееся число.
66 666 — шестьдесят шесть тысяч шестьсот шестьдесят шесть
9. Запишите пять раз подряд число 80. Прочитайте получившееся число.
8 080 808 080 — восемь миллиардов восемьдесят миллионов восемьсот восемь тысяч восемьдесят
10. Прочитайте число, которое получится, если число 674 записать подряд:
а) два раза; б) три раза; в) четыре раза.
а) 674 674 — шестьсот семьдесят четыре тысячи шестьсот семьдесят четыре;
б) 674 674 674 — шестьсот семьдесят четыре миллиона шестьсот семьдесят четыре тысячи шестьсот семьдесят четыре;
в) 674 674 674 674 — шестьсот семьдесят четыре миллиарда шестьсот семьдесят четыре миллиона шестьсот семьдесят четыре тысячи шестьсот семьдесят четыре.
11. Запишите все трёхзначные числа, для записи которых употребляются только цифры 1 и 2.
Р е ш е н и е. В записи числа на первом слева месте (в разряде сотен) может стоять цифра 1 или цифра 2: [1][ ][ ] или [2][ ][ ].
В записи числа на первом слева месте (в разряде сотен) может стоять цифра 1 или цифра 2: [1][ ][ ] или [2][ ][ ].
На втором месте (в разряде десятков) в каждом случае также одна из двух цифр — 1 или 2:
[1] [1]
[1] 〈 [2] 〈
[2] [2]
На третьем месте (в разряде единиц) в каждом из полученных четырёх случаев также можно записать либо 1, либо 2:
[1] [1]
[1]< [2] [1]< [2]
[1] 〈 [2] 〈
[2]< [1] [2]< [1]
[2] [2]
Получили восемь чисел: 111, 112, 121, 122, 211, 212, 221, 222.
Ответы по математике. 5 класс. Учебник. Виленкин Н. Я., Жохов В. И., Чесноков А. С., Шварцбурд С. И
Математика. 5 класс
100 лет математической космологии: Модели, теории и проблемы, часть Б
1. Старобинский А.А. 1980.
Новый тип изотропных космологических моделей без сингулярности. физ. лат. Б 91 , 99-102. ( 10.1016/0370-2693(80)-X) [CrossRef] [Google Scholar]
физ. лат. Б 91 , 99-102. ( 10.1016/0370-2693(80)-X) [CrossRef] [Google Scholar]
2. Казанас Д. 1980. Динамика Вселенной и спонтанное нарушение симметрии. Ап. Дж. Летт. 241 , Л59. ( 10.1086/183361) [CrossRef] [Google Scholar]
3. Guth AH. 1981. Инфляционная вселенная: возможное решение проблем горизонта и плоскостности. физ. Преподобный Д 23 , 347-356. ( 10.1103/PhysRevD.23.347) [CrossRef] [Google Scholar]
4. Steinhardt PJ. 1982. Естественная инфляция. В The Very Early Universe (под редакцией GW Gibbons, SW Hawking, STC Siklos), Proc. Семинар Наффилда, 21 июня — 9 июля г., стр. 251–266. Кембридж, Великобритания: Издательство Кембриджского университета.
5. Вайнберг С.В. 1972. Гравитация и космология. Нью-Йорк, штат Нью-Йорк: Аддисон-Уэсли. [Google Scholar]
6. Brandenberger RH. 1985.
Методы квантовой теории поля и инфляционные модели Вселенной. Преподобный Мод. физ. 57 , 1-60. ( 10.1103/RevModPhys.57.1) [CrossRef] [Google Scholar]
физ. 57 , 1-60. ( 10.1103/RevModPhys.57.1) [CrossRef] [Google Scholar]
7. Колб Э.В., Тернер М.С. 1990. Ранняя Вселенная. Нью-Йорк, штат Нью-Йорк: Аддисон-Уэсли. [Google Scholar]
8. Вайнберг С.В. 2007. Космология. Оксфорд, Великобритания: Издательство Оксфордского университета. [Google Scholar]
9. Аде ПАР и др. Сотрудничество BICEP/Keck, 2021 г. Улучшены ограничения на первичные гравитационные волны с использованием наблюдений Planck , WMAP и BICEP/ Keck в течение сезона наблюдений 2018 года. физ. Преподобный Летт. 127 , 151301. ( 10.1103/PhysRevLett.127.151301) [PubMed] [CrossRef] [Google Scholar]
10. Виленкин А. 1983. Рождение инфляционных вселенных. физ. Преподобный Д 27 , 2848-2855. ( 10.1103/PhysRevD.27.2848) [CrossRef] [Google Scholar]
11. Linde AD. 1986 год.
Вечно существующая самовоспроизводящаяся хаотическая инфляционная вселенная. физ. лат. Б 175 , 395-400. ( 10.1016/0370-2693(86)
( 10.1016/0370-2693(86)
12. Linde AD. 1995. Квантовая космология и структура инфляционной Вселенной. В PASCOS / HOPKINS 1995 (Совместное собрание Международного симпозиума по частицам, струнам и космологии и 19-го семинара Джона Хопкинса по текущим проблемам теории частиц ), стр. 349–394.
13. Виленкин А. 2004. Вечная инфляция и хаотичная терминология. (http://arxiv.org/abs/gr-qc/0409055 [gr-qc])
15. Холландс С., Уолд Р.М. 2002. Эссе: альтернатива инфляции. Генерал Отн. Грав. 34 , 2043-2055. ( 10.1023/A:1021175216055) [CrossRef] [Google Scholar]
16. Linde AD. 1990. Физика элементарных частиц и инфляционная космология. Швейцария: Harwood Academic Publishers. [Google Scholar]
17. Борде А., Гут А.Х., Виленкин А. 2003.
Инфляционное пространство-время неполно в прошлых направлениях. физ. Преподобный Летт. 90 , 151301. ( 10.1103/PhysRevLett.90.151301) [PubMed] [CrossRef] [Google Scholar]
Борде А., Гут А.Х., Виленкин А. 2003.
Инфляционное пространство-время неполно в прошлых направлениях. физ. Преподобный Летт. 90 , 151301. ( 10.1103/PhysRevLett.90.151301) [PubMed] [CrossRef] [Google Scholar]
18. Агирре А., Граттон С. 2003. Инфляция без начала: предложение нулевой границы. физ. Преподобный Д 67 , 083515. ( 10.1103/PhysRevD.67.083515) [CrossRef] [Google Scholar]
19. DeWitt BS. 1967. Квантовая теория гравитации. I. Каноническая теория. физ. преп. 160 , 1113-1148. ( 10.1103/PhysRev.160.1113) [CrossRef] [Google Scholar]
20. Wheeler JA. 1968 год. Суперпространство и природа квантовой геометродинамики. В Battelle Rencontres (редакторы CM DeWitt, JA Wheeler), Лекции по математике и физике. Нью-Йорк, штат Нью-Йорк: В. А. Бенджамин.
21. Хартл Дж.Б., Хокинг С.В. 1983. Волновая функция Вселенной. физ. Преподобный Д 28 , 2960-2975. ( 10.1103/PhysRevD.28.2960) [CrossRef] [Google Scholar]
22. Виленкин А. 1985.
Граничные условия в квантовой космологии. физ. Преподобный Д 33 , 3560-3569. ( 10.1103/PhysRevD.33.3560) [PubMed] [CrossRef] [Google Scholar]
Виленкин А. 1985.
Граничные условия в квантовой космологии. физ. Преподобный Д 33 , 3560-3569. ( 10.1103/PhysRevD.33.3560) [PubMed] [CrossRef] [Google Scholar]
23. Виленкин А. 1987.
Квантовая космология и начальное состояние Вселенной. физ. Преподобный Д
24. Гиббонс Г.В., Грищук Л.П. 1989. Какова типичная волновая функция Вселенной? Нукл. физ. Б 313 , 736-748. ( 10.1016/0550-3213(89)-7) [CrossRef] [Google Scholar]
25. Halliwell JJ. 1991 Вводные лекции по квантовой космологии. В Квантовая космология и детские вселенные (редакторы С. Коулман, Дж. Б. Хартл, Т. Пиран, С. Вайнберг). Сингапур: Мировой научный.
26. Аштекар А. 2021. Краткий обзор петлевой квантовой гравитации. Представитель прог. физ. 84 , 042001. (10.1088/1361-6633/abed91) [PubMed] [CrossRef] [Google Scholar]
27. Bojowald M. 2008.
Петлевая квантовая космология. Живой преподобный отн. 11
Bojowald M. 2008.
Петлевая квантовая космология. Живой преподобный отн. 11
28. Белинский В.А., Грищук Л.П., Зельдович Ю.Б., Халатников И.М. 1985. Инфляционные стадии в космологических моделях со скалярным полем. сов. физ. Дж. Эксп. Теор. физ. 62 , 195. [Google Scholar]
29. Halliwell JJ. 1987. Скалярные поля в космологии с экспоненциальным потенциалом. физ. лат. Б 185 , 341-344. ( 10.1016/0370-2693(87)
30. Henneaux M. 1983. Производство энтропии Гиббса в общей теории относительности. Нуово Сим. лат. 38 , 609-614. ( 10.1007/BF02782751) [CrossRef] [Google Scholar]
31. Гиббонс Г.В., Хокинг С.В., Стюарт Дж.М. 1987. Естественная мера на множестве всех вселенных. Нукл. физ. Б 281 , 736-751. ( 10.1016/0550-3213(87)-1) [CrossRef] [Google Scholar]
32.
33. DN страницы. 1987. Вероятность инфляции R2. физ. Преподобный Д 36 , 1607-1624. ( 10.1103/PhysRevD.36.1607) [PubMed] [CrossRef] [Google Scholar]
34. Chmielowski P, Page DN. 1988 год. Вероятность инфляции типа Бьянки I. физ. Преподобный Д 38 , 2392. (10.1103/PhysRevD.38.2392) [PubMed] [CrossRef] [Google Scholar]
35. Gibbons GW, Turok N. 2008. Проблема меры в космологии. физ. Преподобный Д 77 , 063516. (10.1103/PhysRevD.77.063516) [CrossRef] [Google Scholar]
36. Страница DN. 2011. Конечная каноническая мера для неособых космологий. Дж. Космол. Астропарт. физ. 1106 , 038. (10.1088/1475-7516/2011/06/038) [CrossRef] [Google Scholar]
37. Schiffrin JS, Wald RM. 2012.
Мера и вероятность в космологии. физ.
38. Линде А., Нурбала М. 2010. Проблема меры для вечной и невечной инфляции. Дж. Космол. Астропарт. физ. 09 , 008. (10.1088/1475-7516/2010/09/008) [CrossRef] [Google Scholar]
39. Ellis GFR, Maartens R, MacCallum MAH. 2012. Релятивистская космология. Кембридж, Великобритания: Издательство Кембриджского университета. [Google Scholar]
40. Хокинг С.В. 1988 год. Червоточины в пространстве-времени. физ. Преподобный Д 37 , 904-910. ( 10.1103/PhysRevD.37.904) [PubMed] [CrossRef] [Google Scholar]
41. Coleman S. 1988. Почему нет ничего, а не что-то: теория космологической постоянной. Нукл. физ. Б 310 , 643-668. ( 10.1016/0550-3213(88)-1) [CrossRef] [Google Scholar]
42. Fischler W, Susskind L. 1989. Катастрофа червоточины. физ. лат. Б 217 , 48-54. ( 10.1016/0370-2693(89)-1) [CrossRef] [Google Scholar]
43. Коулман С., Хартл Дж. Б., Пиран Т., Вайнберг С. (ред.). 1991.
Квантовая космология и детские вселенные. Сингапур: Мировой научный. [Google Scholar]
Коулман С., Хартл Дж. Б., Пиран Т., Вайнберг С. (ред.). 1991.
Квантовая космология и детские вселенные. Сингапур: Мировой научный. [Google Scholar]
44. Моррис М.С., Торн К.С. 1988 год. Червоточины в пространстве-времени и их использование для межзвездных путешествий: инструмент для обучения общей теории относительности. Являюсь. Дж. Физ. 56 , 395-412. ( 10.1119/1.15620) [CrossRef] [Google Scholar]
45. Моррис М.С., Торн К.С., Юрцевер Ю. 1988. Червоточины, машины времени и слабое энергетическое состояние. физ. Преподобный Летт. 61 , 1446-1449. ( 10.1103/PhysRevLett.61.1446) [PubMed] [CrossRef] [Google Scholar]
46. Бронников К.А., Мельников В.Н., Денен Х. 2003. Общий класс черных дыр мира браны. физ. Преподобный Д 68 , 024025. ( 10.1103/PhysRevD.68.024025) [CrossRef] [Google Scholar]
47. Бронников К.А., Скворцова М.В., Старобинский А.А. 2010.
Заметки о существовании червоточин в скалярно-тензорной и F(R) гравитации. Грав. Космол. 16 , 216-222. ( 10.1134/S020228
Грав. Космол. 16 , 216-222. ( 10.1134/S020228
48. Бронников К.А., Lemos JPS. 2009. Цилиндрические червоточины. физ. Преподобный Д 79 , 104019. (10.1103/PhysRevD.79.104019) [CrossRef] [Google Scholar]
49. Visser M. 1995. Лоренцевы червоточины — от Эйнштейна до Хокинга. Нью-Йорк, штат Нью-Йорк: AIP Press. [Google Scholar]
50. Molina-Paris C, Visser M. 1999.
Минимальные условия для создания вселенной Фридмана-Робертсона-Уокера из «отскока». физ. лат. Б
51. Freund PGO. 1982. Космологии Калуцы-Клейна. Нукл. физ. Б 209 , 146-156. ( 10.1016/0550-3213(82)-7) [CrossRef] [Google Scholar]
52. Abbott RB, Barr SM, Ellis SD. 1984. Космологии Калуцы-Клейна и инфляция. физ. Преподобный Д 30 , 720-727. ( 10.1103/PhysRevD.30.720) [PubMed] [CrossRef] [Google Scholar]
53. Okada Y. 1982.
Эволюция вселенной Калуцы-Клейна. Нукл. физ. Б 264 , 197-220. ( 10.1016/0550-3213(86)-7) [CrossRef] [Google Scholar]
Okada Y. 1982.
Эволюция вселенной Калуцы-Клейна. Нукл. физ. Б 264 , 197-220. ( 10.1016/0550-3213(86)-7) [CrossRef] [Google Scholar]
54. Overduin JM, Wesson PS. 1997. Калуца-Кляйн Гравитация. физ. Представитель 283 , 303-378. ( 10.1016/S0370-1573(96)00046-4) [CrossRef] [Google Scholar]
55. Furusawa T, Hosoya A. 1985. Хаотична ли анизотропная модель Калуцы-Клейна Вселенной? прог. Теор. физ. 73 , 467-475. ( 10.1143/PTP.73.467) [CrossRef] [Google Scholar]
56. Барроу Дж.Д., Стейн Шабес Дж.А. 1985. Миксмастерские вселенные Калуцы-Кляйна. физ. Преподобный Д 32 , 1595-1596. ( 10.1103/PhysRevD.32.1595) [PubMed] [CrossRef] [Google Scholar]
57. Демаре Дж., Хенно М., Шпиндель П. 1985. Неколебательное поведение в космологии Калуцы-Клейна в вакууме. физ. лат. Б 164 , 27-30. ( 10.1016/0370-2693(85)-3) [CrossRef] [Google Scholar]
58. Demaret J, Hanquin JL, Henneaux M, Spindel P, Taormina A. 1986.
Судьба миксмастерского поведения в неоднородных космологических моделях Калуцы-Клейна в вакууме. физ. лат. Б 175 , 129-132. ( 10.1016/0370-2693(86)
1986.
Судьба миксмастерского поведения в неоднородных космологических моделях Калуцы-Клейна в вакууме. физ. лат. Б 175 , 129-132. ( 10.1016/0370-2693(86)
59. Демаре Дж., де Роп Ю., Хенно М. 1988. Хаос в недиагональных пространственно-однородных космологических моделях в пространственно-временных размерностях ≤10. физ. лат. Б 211 , 37-41. ( 10.1016/0370-2693(88)
60. Хосоя А., Дженсен Л.Г., Стейн Шабес Дж.А. 1987. Критическое измерение для хаотической космологии. Нукл. физ. Б 283 , 657-668. ( 10.1016/0550-3213(87)-4) [CrossRef] [Google Scholar]
61. Гасперини М. 2007. Элементы струнной космологии. Нью-Йорк, штат Нью-Йорк: Издательство Кембриджского университета. [Академия Google]
62. Питер П., Узан Дж.-П. 2009. Первичная космология. Оксфорд, Великобритания: Издательство Оксфордского университета. [Google Scholar]
63. Гасперини М., Венециано Г. 1993.
До большого взрыва в струнной космологии. Астропарт. физ. 1 , 317-339. ( 10.1016/0927-6505(93)-8) [CrossRef] [Google Scholar]
Гасперини М., Венециано Г. 1993.
До большого взрыва в струнной космологии. Астропарт. физ. 1 , 317-339. ( 10.1016/0927-6505(93)-8) [CrossRef] [Google Scholar]
64. Billyard AP, Coley AA, Lidsey JE. 2000. Циклическое поведение в космологиях ранней Вселенной. Дж. Матем. физ. 41 , 6277-6283. ( 10.1063/1.1286878) [CrossRef] [Google Scholar]
65. Барроу Д.Д., Кунце К.Е. 1997. Пространственно однородные струнные космологии. физ. Преподобный Д 55 , 623-629. ( 10.1103/PhysRevD.55.623) [CrossRef] [Google Scholar]
66. Барроу Д.Д., Кунце К.Е. 1997. Неоднородные струнные космологии. физ. Преподобный Д 56 , 741-752. ( 10.1103/PhysRevD.56.741) [CrossRef] [Google Scholar]
67. Lidsey JE, Wands D, Copeland EJ. 2000. Суперструнная космология. физ. Представитель 337 , 343-492. ( 10.1016/S0370-1573(00)00064-8) [CrossRef] [Google Scholar]
68. Ланцош К. 1957.
Электричество и общая теория относительности. Преподобный Мод. физ. 19 , 337-350. ( 10.1103/RevModPhys.29.337) [CrossRef] [Google Scholar]
Преподобный Мод. физ. 19 , 337-350. ( 10.1103/RevModPhys.29.337) [CrossRef] [Google Scholar]
69. Lanczos C. 1957. Расщепление тензора Римана. Преподобный Мод. физ. 34 , 379-389. ( 10.1103/RevModPhys.34.379) [CrossRef] [Google Scholar]
70. Buchdahl HA. 1970. Нелинейные лагранжианы и космологическая теория. Пн. Нет. Р. Астрон. соц. 150 , 1-8. ( 10.1093/mnras/150.1.1) [CrossRef] [Google Scholar]
71. Гурович В.Т. 1971. Нелинейная поправка к лагранжевой плотности гравитационного поля и космологические решения без сингулярности. сов. физ. Доклады 15 , 1105. [Google Scholar]
72. Нариай Х. 1973. Гравитационная неустойчивость регулярных моделей вселенных в модифицированной общей теории относительности. прог. Теор. физ. 49 , 165-180. ( 10.1143/PTP.49.165) [CrossRef] [Google Scholar]
73. Кернер Р. 1982.
Космология без сингулярности и нелинейные гравитационные лагранжианы. Генерал Отн. Грав. 14 , 453-469. ( 10.1007/BF00756329) [CrossRef] [Google Scholar]
Генерал Отн. Грав. 14 , 453-469. ( 10.1007/BF00756329) [CrossRef] [Google Scholar]
74. Барроу Д.Д., Оттевилл А.С. 1983. Устойчивость общей релятивистской космологической теории. Дж. Физ. А 16 , 2757-2776. (10.1088/0305-4470/16/12/022) [CrossRef] [Google Scholar]
75. Барроу Дж. Д., Коцакис С. 1988. Инфляция и конформная структура теорий гравитации высшего порядка. физ. лат. Б 214 , 515-518. ( 10.1016/0370-2693(88)-4) [CrossRef] [Google Scholar]
76. Мангейм П.Д., Казанас Д. 1989. Точное вакуумное решение конформной гравитации Вейля и кривых вращения галактики. Астрофиз. Дж. 342 , 635-638. ( 10.1086/167623) [CrossRef] [Google Scholar]
77. Cotsakis S, Miritzis J, Querella L. 1999. Вариационная и конформная структура нелинейных метрически-связных гравитационных лагранжианов. Дж. Матем. физ. 40 , 3063-3071. ( 10.1063/1.532744) [CrossRef] [Google Scholar]
78. Барроу Дж. Д., Коцакис С. 2020.
Инфляция без следа лямбды. Евро. физ. Дж. С. 80 , 839. ( 10.1140/epjc/s10052-020-8428-2) [CrossRef] [Google Scholar]
Барроу Дж. Д., Коцакис С. 2020.
Инфляция без следа лямбды. Евро. физ. Дж. С. 80 , 839. ( 10.1140/epjc/s10052-020-8428-2) [CrossRef] [Google Scholar]
79. Harrison ER. 1967. Нормальные моды колебаний Вселенной. Преподобный Мод. физ. 39 , 862-882. ( 10.1103/RevModPhys.39.862) [CrossRef] [Google Scholar]
80. Гиббонс Г.В. 1988 год. Энтропия и стабильность Вселенной. Нукл. физ. Б 292 , 784-792. ( 10.1016/0550-3213(87)-5) [CrossRef] [Google Scholar]
81. Гиббонс Г.В. 1988 год. Неравенство Соболева, теорема Йенсена и масса и энтропия Вселенной. Нукл. физ. Б 310 , 636-642. ( 10.1016/0550-3213(88)
-X) [CrossRef] [Google Scholar]
82. Ellis GFR, Maartens R. 2004. Эмерджентная Вселенная: инфляционная космология без сингулярности. Учебный класс. Квант. Грав. 21 , 223-232. ( 10.1088/0264-9381/21/1/015) [CrossRef] [Google Scholar]
83. Барроу Д.Д., Эллис Г. Ф.Р., Мартенс Р., Цагас К.Г. 2003.
Об устойчивости статической Вселенной Эйнштейна. Учебный класс. Квант. Грав. 20 , L155-L164. (10.1088/0264-9381/20/11/102) [CrossRef] [Google Scholar]
Ф.Р., Мартенс Р., Цагас К.Г. 2003.
Об устойчивости статической Вселенной Эйнштейна. Учебный класс. Квант. Грав. 20 , L155-L164. (10.1088/0264-9381/20/11/102) [CrossRef] [Google Scholar]
84. Барроу Дж. Д., Ямамото К. 2012. Неустойчивости статических вселенных Эйнштейна типа IX Бьянки. физ. Преподобный Д 85 , 083505. ( 10.1103/PhysRevD.85.083505) [CrossRef] [Google Scholar]
85. Барроу Д.Д. 2020. Пересмотрен принцип конечного действия. физ. Преподобный Д 101 , 023527. (10.1103/PhysRevD.101.023527) [CrossRef] [Google Scholar]
86. Wainwright J, Ellis GFR. 1993. Динамические системы в космологии. Нью-Йорк, штат Нью-Йорк: Издательство Кембриджского университета. [Академия Google]
87. Барроу Д.Д., Сонода Д.Х. 1985. Асимптотическая устойчивость вселенных типа Бьянки. физ. Респ. 139 , 1-49. ( 10.1016/0370-1573(86)
-6) [CrossRef] [Google Scholar] 88. Вальд Р.М. 1983.
Асимптотика однородных космологических моделей при наличии положительной космологической постоянной. физ. Преподобный Д 28 , 2118-2120. ( 10.1103/PhysRevD.28.2118) [CrossRef] [Google Scholar]
физ. Преподобный Д 28 , 2118-2120. ( 10.1103/PhysRevD.28.2118) [CrossRef] [Google Scholar]
89. Cotsakis S, Flessas G. 1993. Обобщенные космические теоремы об отсутствии волос. физ. лат. Б 319 , 69-73. ( 10.1016/0370-2693(93)
90. Cotsakis S, Miritzis J. 1998. Доказательство космической гипотезы об отсутствии волос для некоторых квадратичных однородных космологий. Учебный класс. Квант. Грав. 15 , 2795-2801. ( 10.1088/0264-9381/15/9/024) [CrossRef] [Google Scholar]
91. Yokoyama J, Maeda K. 1990. Квантовый космологический подход к космической гипотезе об отсутствии волос в пространстве-времени Бьянки типа IX. физ. Преподобный Д 41 , 1047-1053. ( 10.1103/PhysRevD.41.1047) [PubMed] [CrossRef] [Google Scholar]
92. Уэйнрайт Дж., Эллис ГФР. 1989.
Динамический системный подход к космологии Бьянки: ортогональные модели класса А. Класс. Квант. Грав. 6 , 1409-1431. ( 10.1088/0264-9381/6/10/011) [CrossRef] [Google Scholar]
Грав. 6 , 1409-1431. ( 10.1088/0264-9381/6/10/011) [CrossRef] [Google Scholar]
93. Богоявленский О.И. 1985. Методы качественной теории динамических систем в астрофизике и газовой динамике. Нью-Йорк, штат Нью-Йорк: Спрингер. [Google Scholar]
94. Александр С., Бранденбергер Р.Х., Иссон Д.А. 2000. Бранные газы в ранней Вселенной. физ. Преподобный Д 62 , 103509. (10.1103/PhysRevD.62.103509) [CrossRef] [Google Scholar]
95. Barrow JD, Dabrowski MP. 1998. Струнная космология и хаос. физ. Преподобный Д 57 , 7204. [Google Scholar]
96. Damour T, Henneaux M. 2000. Хаос в суперструнной космологии. физ. Преподобный Летт. 85 , 920-923. ( 10.1103/PhysRevLett.85.920) [PubMed] [CrossRef] [Google Scholar]
97. Damour T, de Buyl S. 2008. Описание общих космологических особенностей переменных Ивасавы. физ. Преподобный Д 77 , 043520. (10.1103/PhysRevD.77.043520) [CrossRef] [Google Scholar]
98. Damour T, Николай. 2008.
Симметрии, сингулярности и исчезновение пространства. Междунар. Дж. Мод. физ. Д 17 , 525-531. ( 10.1142/S0218271808012206) [CrossRef] [Google Scholar]
Damour T, Николай. 2008.
Симметрии, сингулярности и исчезновение пространства. Междунар. Дж. Мод. физ. Д 17 , 525-531. ( 10.1142/S0218271808012206) [CrossRef] [Google Scholar]
99. Лукас А., Оврут Б.А., Уолдрам Д. 1997. Струнная и М-теория космологических решений с формами Рамона. Нукл. физ. Б 495 , 365-399. ( 10.1016/S0550-3213(97)00194-6) [CrossRef] [Google Scholar]
100. Лукас А., Оврут Б.А., Уолдрам Д. 1998 Космология и М-теория суперструн типа II. (http://arxiv.org/abs/hep-th/9802041)
101. Billyard AP, Coley AA, Lidsey JE, Nilsson US. 2000. Динамика космологии М-теории. физ. Преподобный Д 61 , 043504. (10.1103/PhysRevD.61.043504) [CrossRef] [Google Scholar]
102. Таунсенд П. 2003 Космическое ускорение и М-теория. (http://arxiv.org/abs/hep-th/0308149 [hep-th])
103. Андерссон Л., Марк Хайнцле Дж. 2007.
Вечное ускорение из М-теории. Доп. Теор. Мат. физ. 11 , 371-398. ( 10.4310/ATMP.2007.v11.n3.a2) [CrossRef] [Google Scholar]
( 10.4310/ATMP.2007.v11.n3.a2) [CrossRef] [Google Scholar]
104. Townsend P, Wohlfarth MNR. 2004. Космология как геодезическое движение. Учебный класс. Квант. Грав. 21 , 5375-5396. ( 10.1088/0264-9381/21/23/006) [CrossRef] [Google Scholar]
105. Марольф Д. Струны/М-браны для релятивистов, 1999. (http://arxiv.org/abs/gr-qc/9
| |||||
| 3 | (10) | |||
| 3 | (1) | |||
| 4 | (3) | |||
| 7 | (6) | |||
| 13 | (18) | |||
| 13 | (3) | |||
| 16 | (3) | |||
| 19 | (1) | |||
| 20 | (2) | |||
| 22 | (4) | |||
| 26 | (1) | |||
| 27 | (4) | |||
| 31 | (28) | |||
| 31 | (4) | |||
| 35 | (4) | |||
| 39 | (2) | |||
| 41 | (1) | |||
| 42 | (2) | |||
| 44 | (2) | |||
| 45 | (1) | |||
| 46 | (1) | |||
| 47 | (4) | |||
| 51 | (8) | |||
| 59 | (24) | |||
| 60 | (3) | |||
| 63 | (4) | |||
| 63 | (3) | |||
| 66 | (1) | |||
| 67 | (5) | |||
| 67 | (3) | |||
| 70 | (2) | |||
| 72 | (3) | |||
| 75 | (8) | |||
| 75 | (2) | |||
| 77 | (1) | |||
| 77 | (1) | |||
| 78 | (5) | |||
| 83 | (14) | |||
| 83 | (3) | |||
| 86 | (3) | |||
| 89 | (8) | |||
| 97 | (12) | |||
| 98 | (1) | |||
| 99 | (2) | |||
| 101 | (4) | |||
| 105 | (4) | |||
| 109 | (16) | |||
| 110 | (3) | |||
| 113 | (1) | |||
| 114 | (1) | |||
| 115 | (1) | |||
| 116 | (1) | |||
| 117 | (1) | |||
| 118 | (2) | |||
| 120 | (5) | |||
| 125 | (6) | |||
| 125 | (3) | |||
| 128 | (3) | |||
| 131 | (12) | |||
| 131 | (5) | |||
| 136 | (4) | |||
| 140 | (3) | |||
| 143 | (12) | |||
| 143 | (2) | |||
| 145 | (3) | |||
| 148 | (3) | |||
| 151 | (4) | |||
| 155 | (20) | |||
| 155 | (3) | |||
| 158 | (3) | |||
| 161 | (1) | |||
| 162 | (3) | |||
| 165 | (3) | |||
| 168 | (2) | |||
| 170 | (5) | |||
| 175 | (12) | |||
| 175 | (4) | |||
| 179 | (1) | |||
| 180 | (2) | |||
| 182 | (1) | |||
| 183 | (4) | |||
| 187 | (14) | |||
| 187 | (2) | |||
| 189 | (4) | |||
| 193 | (1) | |||
| 194 | (2) | |||
| 196 | (5) | |||
| 201 | (26) | |||
| 201 | (4) | |||
| 205 | (3) | |||
| 206 | (1) | |||
| 206 | (2) | |||
| 208 | (3) | |||
| 211 | (2) | |||
| 213 | (2) | |||
| 213 | (2) | |||
| 215 | (5) | |||
| 216 | (1) | |||
| 217 | (3) | |||
| 220 | (1) | |||
| 220 | (7) | |||
| |||||
| 227 | (8) | |||
| 227 | (2) | |||
| 229 | (3) | |||
| 232 | (1) | |||
| 232 | (3) | |||
| 235 | (20) | |||
| 235 | (1) | |||
| 236 | (4) | |||
| 236 | (2) | |||
| 238 | (2) | |||
| 240 | (3) | |||
| 240 | (1) | |||
| 241 | (1) | |||
| 242 | (1) | |||
| 242 | (1) | |||
| 242 | (1) | |||
| 243 | (4) | |||
| 243 | (1) | |||
| 244 | (1) | |||
| 245 | (2) | |||
| 247 | (2) | |||
| 249 | (6) | |||
| 249 | (1) | |||
| 250 | (5) | |||
| 255 | (14) | |||
| 255 | (1) | |||
| 256 | (4) | |||
| 260 | (4) | |||
| 264 | (5) | |||
| 269 | (22) | |||
| 269 | (2) | |||
| 271 | (3) | |||
| 274 | (1) | |||
| 275 | (4) | |||
| 279 | (2) | |||
| 281 | (3) | |||
| 284 | (7) | |||
| 284 | (1) | |||
| 285 | (6) | |||
| 291 | (10) | |||
| 292 | (2) | |||
| 294 | (1) | |||
| 295 | (1) | |||
| 296 | (1) | |||
| 297 | (4) | |||
| 301 | (12) | |||
| 302 | (2) | |||
| 302 | (1) | |||
| 303 | (1) | |||
| 303 | (1) | |||
| 303 | (1) | |||
| 304 | (3) | |||
| 304 | (1) | |||
| 305 | (2) | |||
| 307 | (2) | |||
| 309 | (4) | |||
| 313 | (14) | |||
| 313 | (1) | |||
| 314 | (1) | |||
| 315 | (1) | |||
| 316 | (3) | |||
| 317 | (1) | |||
| 317 | (2) | |||
| 319 | (2) | |||
| 321 | (6) | |||
| 322 | (1) | |||
| 323 | (4) | |||
| 327 | (6) | |||
| 327 | (2) | |||
| 329 | (4) | |||
| 330 | (1) | |||
| 331 | (2) | |||
| 333 | (10) | |||
| 333 | (3) | |||
| 336 | (2) | |||
| 337 | (1) | |||
| 338 | (1) | |||
| 339 | (4) | |||
| 343 | (10) | |||
| 343 | (2) | |||
| 343 | (1) | |||
| 344 | (1) | |||
| 345 | (5) | |||
| 345 | (1) | |||
| 346 | (1) | |||
| 346 | (1) | |||
| 347 | (3) | |||
| 350 | (1) | |||
| 351 | (2) | |||
| Приложение А | 353 | (8) | |||
| Дополнительная литература | 361 | (4) | |||
| Индекс | 365 |
Научные интересы ДЕЛИИ ПЕРЛОВ сосредоточены на вечно раздувающейся мультивселенной и касаются различных аспектов космологии, теории струн, квантовой теории поля и общей теории относительности. Она получила докторскую степень. из Университета Тафтса, а затем провела несколько лет, работая научным сотрудником в докторантуре, также в Тафтсе, где она теперь читает лекции на неполный рабочий день. АЛЕКС ВИЛЕНКИН был одним из ключевых исследователей в авангарде теоретической космологии и внес значительный вклад в эту область. Он наиболее известен своими теориями вечной космической инфляции, создания Вселенной из ничего и своей новаторской работой о космических струнах. Он является директором Института космологии Тафтса.
АЛЕКС ВИЛЕНКИН был одним из ключевых исследователей в авангарде теоретической космологии и внес значительный вклад в эту область. Он наиболее известен своими теориями вечной космической инфляции, создания Вселенной из ничего и своей новаторской работой о космических струнах. Он является директором Института космологии Тафтса.
Пятимерная космологическая модель анизотропной облачной струны Бьянки типа I с электромагнитным полем в теории Саеса-Баллестера
1 Введение
Многих авторов привлекала возможность пространства-времени иметь более четырех измерений. Это пробудило любопытство космологов и физиков-теоретиков до такой степени, что в последние десятилетия среди авторов появилась тенденция исследовать космологию в многомерном пространстве-времени. В попытке объединить гравитацию и электромагнетизм в (Kaluza, 19) была представлена многомерная модель.21; Кляйн, 1926). Позднюю парадигму ускоренного расширения можно проиллюстрировать с помощью модели более высокого измерения (Banik and Bhuyan, 2017). Исследование пространства-времени в более высоких измерениях является критически важной задачей, поскольку космос мог пройти через эпоху более высоких измерений в течение своей ранней истории (Singh et al., 2004). Согласно (Guth, 1981; Alvax and Gavela, 1983), дополнительные измерения генерируют большое количество энтропии, что может обеспечить решение проблем плоскостности и горизонта. Согласно (Марчиано, 1984). (Шинкай и Тории, 2015 г.; Сингх и Сингх, 2019 г.; Монтефальконе и др., 2020 г.; Даймари и Баруа, 2021 г.; Сингх и Баро, 2021 г.) — это лишь некоторые из заслуживающих внимания исследований многомерного пространства-времени, опубликованных в предыдущих нескольких годы.
Исследование пространства-времени в более высоких измерениях является критически важной задачей, поскольку космос мог пройти через эпоху более высоких измерений в течение своей ранней истории (Singh et al., 2004). Согласно (Guth, 1981; Alvax and Gavela, 1983), дополнительные измерения генерируют большое количество энтропии, что может обеспечить решение проблем плоскостности и горизонта. Согласно (Марчиано, 1984). (Шинкай и Тории, 2015 г.; Сингх и Сингх, 2019 г.; Монтефальконе и др., 2020 г.; Даймари и Баруа, 2021 г.; Сингх и Баро, 2021 г.) — это лишь некоторые из заслуживающих внимания исследований многомерного пространства-времени, опубликованных в предыдущих нескольких годы.
Согласно разным литературным источникам наша Вселенная растет ускоренными темпами. Теория гравитации Саеса-Баллестера считается идеальным объяснением для описания нашей расширяющейся Вселенной в пространстве-времени FRW. Булл и др. (Bull et al., 2016) исследовали альтернативную космологию и резюмировали текущее положение ΛCDM как физической теории в дополнение к стандартной модели ΛCDM в расширенной космологии. Только изотропная и однородная Вселенная описывается пространством-временем FRW в огромном масштабе. Однако недавние открытия и рассуждения показывают, что на всем протяжении космического расширения Вселенной существует анизотропная фаза, прежде чем она перейдет в изотропную. Однородные и анизотропные вселенные представлены космологическими моделями типа Бьянки, и их изотропную природу можно исследовать во времени. Кроме того, с теоретической точки зрения анизотропные миры имеют большую общность, чем изотропные модельные вселенные. Несколько публикаций (Singh et al., 2021; Amirhashchi et al., 2009).; Акарсу и Килинц, 2010b, а; Sahoo and Mishra, 2015) рассмотрели анизотропную космологическую модель типа Бьянки с разных сторон. Киббл (Kibble, 1976) в своем исследовании «Топология космических доменов и струн» определил стабильные топологические дефекты, возникающие на протяжении фазового сдвига, как струны. Он также показал, что группа однородности многообразия вырожденных вакуумов влияет на топологические дефекты доменной структуры.
Только изотропная и однородная Вселенная описывается пространством-временем FRW в огромном масштабе. Однако недавние открытия и рассуждения показывают, что на всем протяжении космического расширения Вселенной существует анизотропная фаза, прежде чем она перейдет в изотропную. Однородные и анизотропные вселенные представлены космологическими моделями типа Бьянки, и их изотропную природу можно исследовать во времени. Кроме того, с теоретической точки зрения анизотропные миры имеют большую общность, чем изотропные модельные вселенные. Несколько публикаций (Singh et al., 2021; Amirhashchi et al., 2009).; Акарсу и Килинц, 2010b, а; Sahoo and Mishra, 2015) рассмотрели анизотропную космологическую модель типа Бьянки с разных сторон. Киббл (Kibble, 1976) в своем исследовании «Топология космических доменов и струн» определил стабильные топологические дефекты, возникающие на протяжении фазового сдвига, как струны. Он также показал, что группа однородности многообразия вырожденных вакуумов влияет на топологические дефекты доменной структуры. Летелье (Letelier, 1983) использовал космологические модели пространства-времени Бьянки типа I и Кантовского-Сакса для исследования струнной космологии. Модели Bianchi типа VII, согласно Коллинзу и Хокингу (Collins and Hawking, 1972), являются наиболее общими однородными космологическими моделями, бесконечными во всех трех пространственных направлениях. Эти модели включают в себя широкий класс начальных условий, что позволяет использовать максимально возможное количество произвольных констант. Он также продемонстрировал, что, хотя все исходные анизотропные вселенные не достигают изотропии, ее достигает подкласс вселенных со скоростью убегания.
Летелье (Letelier, 1983) использовал космологические модели пространства-времени Бьянки типа I и Кантовского-Сакса для исследования струнной космологии. Модели Bianchi типа VII, согласно Коллинзу и Хокингу (Collins and Hawking, 1972), являются наиболее общими однородными космологическими моделями, бесконечными во всех трех пространственных направлениях. Эти модели включают в себя широкий класс начальных условий, что позволяет использовать максимально возможное количество произвольных констант. Он также продемонстрировал, что, хотя все исходные анизотропные вселенные не достигают изотропии, ее достигает подкласс вселенных со скоростью убегания.
Из-за важности струн для описания ранних стадий эволюции нашей Вселенной некоторые авторы в последнее время сосредоточились на струнных космологических моделях. Струна может одновременно описывать природу и фундаментальную конфигурацию раннего космоса. Наиболее активно изучаемый подход к квантовой гравитации — это теория струн, и ее можно использовать для обсуждения механики раннего космоса. Теория струн объединяет всю материю и силы в единую теоретическую структуру и описывает ранние стадии нашего космоса в терминах вибрирующих струн, а не частиц. По словам Киббла (Киббл, 1976), космические струны — это стабильные линейчатые топологические объекты/дефекты, возникающие в какой-то момент во время фазового перехода в ранней истории нашей Вселенной. Согласно ТВО (теории великого объединения) [Зельдович и др. (Зельдович и др., 1974), Киббл (Kibble, 1976; Киббл, 1980), Эверетт (Everett, 1981), Виленкин (Виленкин, 1981а; Виленкин, 1981б)], симметрия нарушается при фазовом переходе в ранние стадии Вселенной после Большого взрыва, и эти струны появляются, когда космическая температура падает ниже критической температуры. Таким образом, струны могут играть важную роль в изучении ранних стадий Вселенной. Массивные замкнутые петли струн также создают огромные структуры, такие как галактики и скопления галактик. Гравитационное поле взаимодействует с космическими струнами, которые могут включать в себя энергию-импульс.
Теория струн объединяет всю материю и силы в единую теоретическую структуру и описывает ранние стадии нашего космоса в терминах вибрирующих струн, а не частиц. По словам Киббла (Киббл, 1976), космические струны — это стабильные линейчатые топологические объекты/дефекты, возникающие в какой-то момент во время фазового перехода в ранней истории нашей Вселенной. Согласно ТВО (теории великого объединения) [Зельдович и др. (Зельдович и др., 1974), Киббл (Kibble, 1976; Киббл, 1980), Эверетт (Everett, 1981), Виленкин (Виленкин, 1981а; Виленкин, 1981б)], симметрия нарушается при фазовом переходе в ранние стадии Вселенной после Большого взрыва, и эти струны появляются, когда космическая температура падает ниже критической температуры. Таким образом, струны могут играть важную роль в изучении ранних стадий Вселенной. Массивные замкнутые петли струн также создают огромные структуры, такие как галактики и скопления галактик. Гравитационное поле взаимодействует с космическими струнами, которые могут включать в себя энергию-импульс. В результате одним из самых интересных проектов является исследование гравитационных эффектов, исходящих от космических струн.
В результате одним из самых интересных проектов является исследование гравитационных эффектов, исходящих от космических струн.
Летелье (Letelier, 1983) удалось получить огромные струнные космологические модели в пространстве-времени типа I Бьянки и Кантовского-Сакса в 1983 году. Вслед за Летелье множество авторов исследовали струнные космологические модели в различных условиях.
Крори (Krori et al., 1990) и Ван (Wang, 2003) исследовали космологическую модель струны Летелье и получили их точные решения, используя пространства-времени типа II, -VI0, -VIII и -IX Бьянки. Взяв коэффициент объемной вязкости как степенную функцию плотности энергии, Син (Xing-Xiang, 2004) разработал космологическую модель строки точного решения с объемной вязкостью с использованием метрики LRS Bianchi type-I. Явуз (Явуз и др., 2005) исследовал заряженную странную кварковую материю, связанную со струнным облаком в сферически-симметричном пространстве-времени, и продемонстрировал существование однопараметрической группы конформных движений. В рамках общей теории относительности Йилмаз (Yilmaz, 2006) установил космологические решения Калуцы-Клейна для кварковой материи, связанной со струнным облаком. Рао (Rao et al., 2008) установил точную космологическую модель идеальной жидкости на основе многообразия Лиры, где вектор смещения является константой, при исследовании пространства-времени типа V Бианки в скалярно-тензорной теории. Однако если β является функцией космического времени t, то эта модель имеет место исключительно в случае излучения. В рамках скалярно-тензорной теории Саеса-Баллестера Трипати (Tripathy et al., 2009) исследовал анизотропное и пространственно однородное пространство-время типа VI0 по Бьянки и разработал космологические модели струнных облаков. В теории гравитации Бранса-Дикке Адхав и др. (Адхав и др., 2007) построили струнные космологические модели, решив уравнения поля с условием, что сумма плотности натяжения и плотности энергии равна нулю. Павар (Pawar et al., 2018) исследовал струнную космологическую модель Калуцы-Клейна в контексте f (R, T)-теории гравитации и решил уравнения поля, используя степенную зависимость между масштабным фактором и изменяющимся во времени замедлением.
В рамках общей теории относительности Йилмаз (Yilmaz, 2006) установил космологические решения Калуцы-Клейна для кварковой материи, связанной со струнным облаком. Рао (Rao et al., 2008) установил точную космологическую модель идеальной жидкости на основе многообразия Лиры, где вектор смещения является константой, при исследовании пространства-времени типа V Бианки в скалярно-тензорной теории. Однако если β является функцией космического времени t, то эта модель имеет место исключительно в случае излучения. В рамках скалярно-тензорной теории Саеса-Баллестера Трипати (Tripathy et al., 2009) исследовал анизотропное и пространственно однородное пространство-время типа VI0 по Бьянки и разработал космологические модели струнных облаков. В теории гравитации Бранса-Дикке Адхав и др. (Адхав и др., 2007) построили струнные космологические модели, решив уравнения поля с условием, что сумма плотности натяжения и плотности энергии равна нулю. Павар (Pawar et al., 2018) исследовал струнную космологическую модель Калуцы-Клейна в контексте f (R, T)-теории гравитации и решил уравнения поля, используя степенную зависимость между масштабным фактором и изменяющимся во времени замедлением. параметр.
параметр.
При наличии электромагнитного поля космологическая модель играет решающую роль в эволюции космоса и построении крупномасштабных структур, таких как галактики и другие небесные тела. Наличие космического электромагнитного поля, образующегося при инфляции, обусловливает текущую фазу ускоренного расширения космоса. В космологических масштабах Хименес и Марото (Jimenez and Maroto, 2009) показали, что наличие электромагнитного поля обеспечивает эффективную космологическую постоянную, которая объясняет ускоренное расширение Вселенной. В общей теории относительности Tripathy et al. (Tripathi et al., 2017) исследовали неоднородную струнную космологическую модель с электромагнитным полем. Парих (Парих и др., 2018) недавно исследовал космологическую модель струнной пыли Бьянки типа II в геометрии Лиры с электромагнитным полем. Прадхан (Pradhan and Jaiswal, 2018) исследовал класс анизотропных и однородных космологических моделей типа V Бьянки с тяжелыми струнами в присутствии магнитного поля в f (R, T)-теории гравитации. Грассо (Grasso and Rubinstein, 2000) изучил широкий спектр характеристик магнитных полей в ранней Вселенной, а также современные временные поля и их эволюцию в галактиках и скоплениях. Магнитное поле также способствует нарушению статистической однородности и изотропии. Магнитные поля можно найти в крупномасштабных галактиках и скоплениях галактик. В своем исследовании Субраманиан (Subramanian, 2016) продемонстрировал, что первичные магнитные поля оказывают значительное влияние на создание звездных структур, особенно в масштабах карликовых галактик.
Грассо (Grasso and Rubinstein, 2000) изучил широкий спектр характеристик магнитных полей в ранней Вселенной, а также современные временные поля и их эволюцию в галактиках и скоплениях. Магнитное поле также способствует нарушению статистической однородности и изотропии. Магнитные поля можно найти в крупномасштабных галактиках и скоплениях галактик. В своем исследовании Субраманиан (Subramanian, 2016) продемонстрировал, что первичные магнитные поля оказывают значительное влияние на создание звездных структур, особенно в масштабах карликовых галактик.
Альтернативные теории гравитации, такие как теория гравитации Бранса-Дикке (Brans and Dicke, 1961), теория гравитации Саеса-Баллестера (Saez and Ballester, 1986), f (R) гравитация (Capozziello et al., 2003 ; Nojiri and Odintsov, 2003), f (R, T) сила тяжести (Harko et al., 2011). Каждая из этих теорий гравитации имеет свое значение. Мы построили космологическую модель в рамках теории гравитации Саеса-Баллестера, чтобы изучить некоторые особенности космоса в этом исследовании. Как известно, метрика легко соединяется с безразмерным скалярным полем в теории Саеса и Баллестера. Несмотря на безразмерное поведение скалярного поля, эта связь дает удовлетворительное описание слабых полей, в которых возникает режим ускоренного роста. Многие авторы, в том числе наши коллеги, построили космологические модели, основанные на теории гравитации Саеса-Баллестера, для исследования различных особенностей Вселенной (Сингх и Агравал, 1991; Адитья и Редди, 2018 г.; Мишра и Дуа, 2019 г.; Мишра и Чанд, 2020 г.; Расули и др., 2020 г.). Санти и Собханбабу (Santhi and Sobhanbabu, 2020) изучили динамику голографической модели темной энергии Тсаллиса типа III Бьянки в рамках теории гравитации Саеса-Баллестера и пришли к некоторым интересным выводам. В теории гравитации Саеса-Баллестера Найду и др. (Naidu et al., 2021) исследовали поведение моделей темной энергии Калуцы-Кляйна FRW, найдя решение уравнений поля с использованием I гибридного закона расширения и (ii) переменного параметра замедления.
Как известно, метрика легко соединяется с безразмерным скалярным полем в теории Саеса и Баллестера. Несмотря на безразмерное поведение скалярного поля, эта связь дает удовлетворительное описание слабых полей, в которых возникает режим ускоренного роста. Многие авторы, в том числе наши коллеги, построили космологические модели, основанные на теории гравитации Саеса-Баллестера, для исследования различных особенностей Вселенной (Сингх и Агравал, 1991; Адитья и Редди, 2018 г.; Мишра и Дуа, 2019 г.; Мишра и Чанд, 2020 г.; Расули и др., 2020 г.). Санти и Собханбабу (Santhi and Sobhanbabu, 2020) изучили динамику голографической модели темной энергии Тсаллиса типа III Бьянки в рамках теории гравитации Саеса-Баллестера и пришли к некоторым интересным выводам. В теории гравитации Саеса-Баллестера Найду и др. (Naidu et al., 2021) исследовали поведение моделей темной энергии Калуцы-Кляйна FRW, найдя решение уравнений поля с использованием I гибридного закона расширения и (ii) переменного параметра замедления.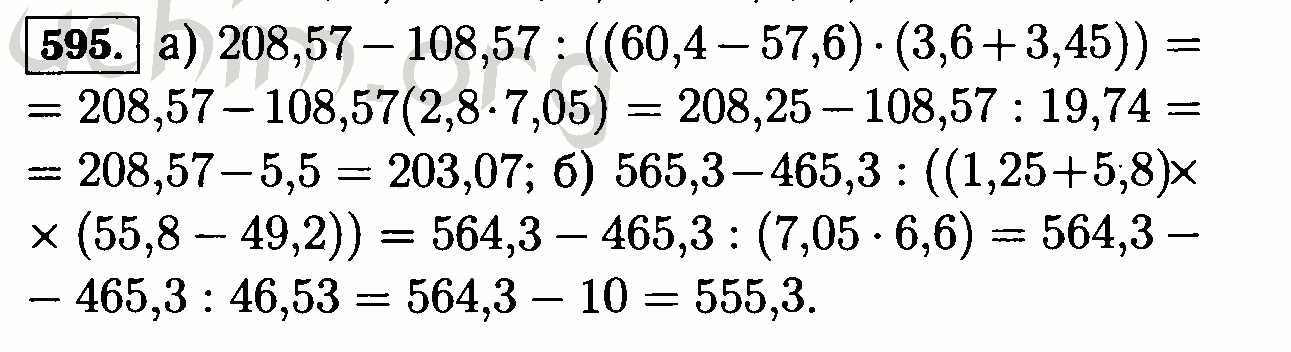 Саес-Баллестер дает уравнения поля Эйнштейна для объединенных скалярного и тензорного полей
Саес-Баллестер дает уравнения поля Эйнштейна для объединенных скалярного и тензорного полей
Rij−12Rgij−ωϕmϕ,iϕ,j−12gijϕ,kϕ,k=−Tij(1)
и скалярное поле также удовлетворяет уравнению
2ϕmϕ;i,i+mϕm−1ϕ,kϕ,k=0 (2)
Мы решили уравнения Саеса-Баллестера для тензора энергии-импульса облачной струны, взаимодействующей с электромагнитным полем, и подробно рассмотрели все элементы физических и кинематических свойств в этой статье, что было мотивировано изучением вышеуказанной литературы. Структура статьи следующая: метрика и уравнения поля представлены в разделе 2; решение уравнений поля предлагается в разделе 3; физические характеристики нашей модели Вселенной представлены в разделе 4; а иллюстрации и рисунки представлены в Разделе 5. Наконец, в Разделе 6 мы рассматриваем результаты и приводим некоторые последние наблюдения.
2 Уравнения метрики и поля
Мы рассматриваем метрику Бьянки типа I, пространственно однородную и анизотропную
ds2=−dt2+A2dx2+dy2+B2dz2+C2dψ2(3)
все функции космического времени t.
For the metric (3) we assume
x 1 = x , x 2 = y , x 3 = z , x 4 = ψ , и x 5 = t
Тензор энергии-импульса облачной струны (Reddy, 2003) имеет вид
Tij=ρuiuj−λxixj+Eij(4)
, λ — плотность натяжения струны, ρ — плотность энергии покоя облака струн с прикрепленными к ним частицами ρ = ρ p + λ . x i — это единичный пространственный вектор, представляющий направление струн, с x 2 = 0 = x 3 = x 4 = x 5 and x 1 ≠ 0, and u i is the пять векторов скорости, которые удовлетворяют следующим условиям направление x я , задаются как
ui=0,0,0,0,1(7)
и
xi=1A,0,0,0,0(8)
, где направление струн параллельно ось х.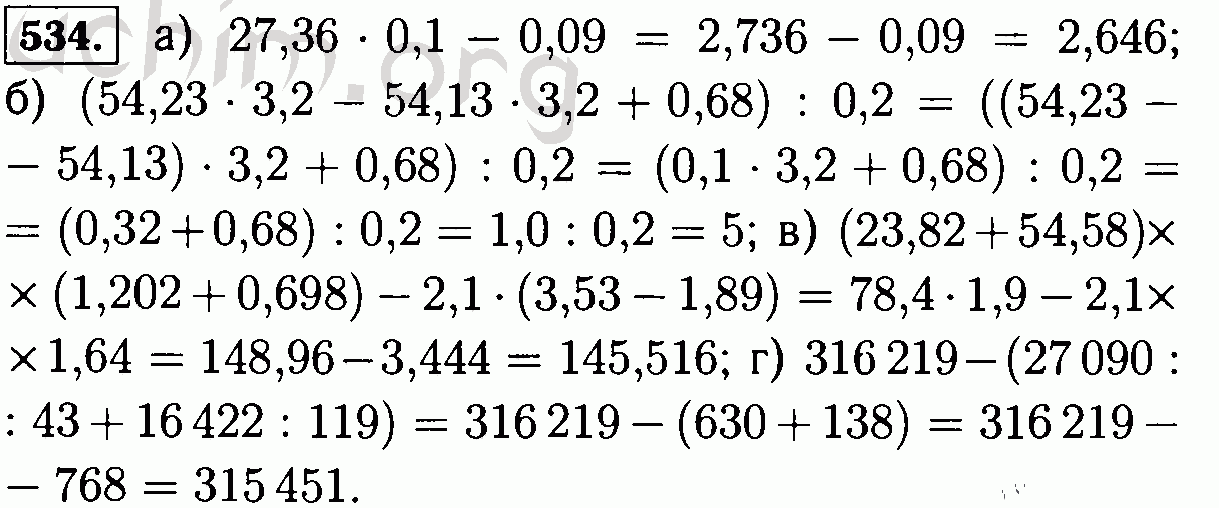
The electromagnetic field E ij , which is a component of the energy momentum tensor, is referred to as
Eij=14πgαβFiαFiβ−14gijFαβFαβ(9)
Here F αβ is обозначен тензор электромагнитного поля.
Ф 15 — единственная ненулевая компонента тензора электромагнитного поля F ij , если мы квантуем магнитное поле по оси x. Assuming infinite electromagnetic conductivity, it can be obtain that F 12 = F 13 = F 14 = F 23 = F 24 = F 25 = F 34 = F 35 = 0 (Singh et al., 2020).
В результате нетривиальные компоненты электромагнитного поля E ij могут быть рассчитаны по уравнению. 9, как указано ниже
9, как указано ниже
E11=-E22=-E33=-E4=E11=-12g11g55F152=12A2F152(10)
Или, если мы возьмем магнитное поле вдоль оси x в сопутствующих координатах, F 34 — единственная ненулевая компонента тензора электромагнитного поля F иж . Предполагая, что бесконечная электромагнитная проводимость, можно определить, что F 15 = F 25 = F 35 = F
12 = = F 12 = = F 12 = = F 12 = = F 12 = . = 0 (Сингх и др., 2020 г.).В результате нетривиальные компоненты электромагнитного поля E ij могут быть рассчитаны по уравнению. 9
E11=-E22=-E33=-E4=E11=-12A2F342(11)
Важные физические величины для метрики (3) включают пространственный объем V, средний масштабный коэффициент R, скаляр расширения θ , параметр Хаббла H, параметр замедления q, скаляр сдвига σ 2 и средний параметр анизотропии △:
V=R4=A2BC(12)
θ=u;ii=2ȦA+ḂB+ĊC(13)
H=ṘR=142ȦA+ḂB+ĊC(14)
q= −RR̈Ṙ2=ddt1H−1(15)
σ2=12σijσij=122Ȧ2A2+Ḃ2B2+Ċ2C2−θ28(16)
△=14∑i=14Hi−Hh3(17)
Относительно космического времени t точка над головой представляет первую производную, а двойная точка над головой представляет вторую.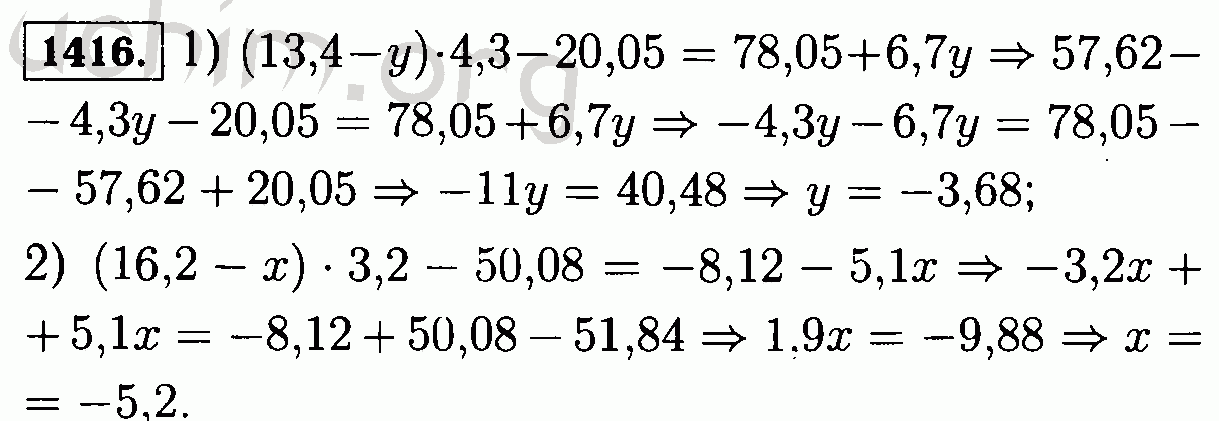 Также H i ( i = 1, 2, 3, 4) обозначают направленные параметры Хаббла в направлении осей x, y, z и ψ и получены для метрики (1) так как h2=h3=ȦA, h4=ḂB и h5=ĊC.
Также H i ( i = 1, 2, 3, 4) обозначают направленные параметры Хаббла в направлении осей x, y, z и ψ и получены для метрики (1) так как h2=h3=ȦA, h4=ḂB и h5=ĊC.
Уравнения поля Саеса-Баллестера 1, 2 сводятся к следующей системе уравнений в сочетании с уравнением 4 для линейного элемента Ур. 3:
äa+b̈b+c̈c+ȧaḃb+ȧaċc+ḃbċc = λ -12a2f152+ω мало чистого 2ȧAċC = 12A2F152+ωϕmϕ̇22 (20)
2äa+ȧ2A2+B̈B+2ȧAḃB = 12A2F152+ωϕMϕ̇22 (21)
ȧ2A2+2ȧAḃB+2ȧAċC+ρC = ρ12a2a2A2+2ȧAḃB+2ȧAċC+ρC = ρ12a2a2+2ȧaḃB+2ȧaċC+ρC = ρ12a2+2a2+2a2+2ȧaḃb+2ȧaċC+rρC = ρ12a2+2a2+2ȧaḃb+2ȧaċC+rTism 2A2+2. ĊC+m2ϕ̇2ϕ=0(23)
3 Решение уравнений поля
Уравнения поля 18–22 представляют собой набор из пяти уравнений с семью неизвестными параметрами (A, B, C, ρ , λ , ϕ и F 15 ). В результате два дополнительных ограничения, связывающие эти параметры, необходимы для достижения явных системных решений.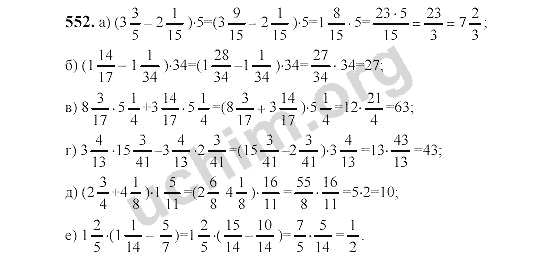 Эти два соотношения считаются
Эти два соотношения считаются
1) Мы можем воспользоваться тем фактом, что скаляр сдвига σ пропорционален скалярному расширению θ (Коллинз и др., 1983; Рао и др., 2015).
B=Cn(24)
здесь n — константа.2) Берман (Берман, 1983) и Ram et al. (Ram et al., 2010) вывели связь между параметром Хаббла H и средним коэффициентом масштабирования R. Берман и Гомид (Berman and Gomide, 1988) и Ram et al. (Ram et al., 2010) решали модели FRW, используя этот тип отношения, тогда как Ram et al. (Ram et al., 2010) решили космологические модели Бьянки типа V в Lyra’s Geometry.
H=aR−k1(25)
a ≥ 0, k 1 ≥ 0 являются константами.
Уравнение 25 дает нам
R=ak1t+k21k1ifk1≠0(26)
и
R=k3eatifk1=0(27)
k 2 и k В результате уравнения 15 определяется параметр замедления q k 1 ≠ 0, имеемУравнения 19, 20, 24, 26 дадут нам следующий результат C=k5ek4ak1t+k2k1−4k1ak1−4(30) k 4 , k 5 являются константами в этом уравнении. Мы можем принять k 4 = k 5 = 1, не теряя общности, что дает нам C=eak1t+k2k1−4k1ak1−4(31) . 26 даст нам A=ak1t+k22k1e−ak1t+k2k1−4k1n+12ak1−4(32) и B=enak1t+k2k1−4k1ak1−4(33) В результате строка элемент Уравнение 3 превращается в ds2=-dt2+ak1t+k24k1e-ak1t+k2k1-4k1n+1ak1-4dx2+dy2+e2nak1t+k2k1-4k1ak1-4dz2+e2ak1t+k2k1-4k1ak1-4dψ2(34) космологическая модель Вселенная с электромагнитным полем и особым законом параметра Хаббла, который становится сингулярным при k 1 = 4. Теперь, используя уравнения 18–22, мы можем вычислить значения плотность энергии ρ , плотность натяжения струны λ , и тензор электромагнитного поля F 15 для нашей модели Вселенной, представленной уравнением 34. ρ=−4a2k1−4ak1t+k2−2(35) 2a23k1−8ak1t+k2−2−4an+1ak1t+k2−k1+4k1−ωk62ak1t+k2−8k1(36) F15=2143n2+2n+3ak1t+k2−4k1−4a2k1−3ak1t+k2−2k1−2k1− 2an+1ak1t+k2−1−ωk622ak1t+k2−8k112×eak1t+k2k1−4k1n+1ak1−4(37) Используя соотношение ρ = ρ p 0, получаем теперь ρp=2a2k1ak1t+k2−2−123n2+2n+3ak1t+k2−8k1+4an+1ak1t+k2−k1+4k1+ωk62ak1t+k2−8k1(38) Собственный объем физических величин V, параметр Хаббла H , скаляр расширения θ , скаляр поля ϕ скаляр сдвига σ 2 и средний параметр анизотропии △ вычисляются следующим образом: (40) θ=4aak1t+k2(41) ϕ=k6m+22ak1−42m+2ak1t+k2k1−4k12m+2(42) σ2=3n2+2n+34ak1t+k2−8k1−2an+1ak1t +k2−k1+4k1+2a2ak1t+k2−2(43) △=1−n+1aak1t+k2k1−4k1+3n2+2n+32a2ak1t+k22k1−4k1(44) Из уравнений 41, 43 получаем limt→∞σ2θ2≠0(45) Параметр замедления q является постоянным и отрицательным, как показано в выражении Eq. 28. Это указывает на то, что начиная с космического времени t = 0 предлагаемая нами модель Вселенной раздувается и расширяется с постоянной скоростью. В ходе эволюции скорость расширения Вселенной постоянна. q = константа (отрицательное значение) для k 1 < 1. Также при t = 0 во время Большого взрыва плотность частиц имеет огромное положительное значение. С течением времени он приближается к положительному значению, в конечном итоге достигая конечного постоянного значения при t → ∞ (как показано на рисунке 1). Это демонстрирует, что частица продолжает доминировать в космосе с течением времени и что общее количество частиц во Вселенной остается постоянным. Скаляр расширения, параметр Хаббла, демонстрирует аналогичные колебания во времени. После перехода от бесконечности при t = 0 к конечному значению при t → ∞ , как параметр Хаббла H, так и скаляр расширения уменьшаются с космическим временем t (показано на рисунках 2, 3). РИСУНОК 1 . Плотность частиц ρ p в зависимости от времени. РИСУНОК 2 . Скалярное расширение θ в зависимости от времени. РИСУНОК 3 . Параметр Хаббла H в зависимости от времени. РИСУНОК 4 . Плотность энергии ρ в зависимости от времени. РИСУНОК 5 . Плотность натяжения λ в зависимости от времени. РИСУНОК 6 . Объем V против времени. РИСУНОК 7 . Тензор электромагнитного поля F 15 в зависимости от времени. В первой сингулярности скаляр сдвига параметров σ 2 и средний параметр анизотропии △ расходятся (как показано на рисунках 8, 9). Модель изображает сдвигающий, невращающийся космос с возможностью сильного сжатия примерно на 9°.0015 t = 0 начальная эпоха. Кроме того, мы можем наблюдать из математической формулировки уравнения. 45 изотропное условие limt→∞σ2θ2≠0(константа) остается постоянным на протяжении всей эволюции Вселенной (от раннего до позднего времени), что указывает на то, что модель не достигает изотропии (Sahoo et al., 2017). РИСУНОК 8 . Напряжение сдвига σ 2 в зависимости от времени. РИСУНОК 9 . Параметр анизотропии △ в зависимости от времени. В общей теории относительности исследуется взаимодействие анизотропной струнной космологической модели Вселенной Бьянки I типа с электромагнитным полем. Оригинальные материалы, представленные в исследовании, включены в статью, дальнейшие запросы можно направлять соответствующему автору. Все перечисленные авторы внесли значительный, непосредственный и интеллектуальный вклад в работу и дали свое разрешение на ее публикацию. Авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могли бы быть истолкованы как потенциальный конфликт интересов. Все утверждения, изложенные в этой статье, принадлежат исключительно авторам и не обязательно представляют претензии их дочерних организаций или издателя, редакторов и рецензентов. Любой продукт, который может быть оценен в этой статье, или претензии, которые могут быть сделаны его производителем, не гарантируются и не поддерживаются издателем. Адхав, К.С., Нимкар, А.С., и Даванде, М.В. (2007). N-мерная струнная космологическая модель в теории гравитации Бранса-Дикке. Астрофиз. Космические науки. 310, 231–235. doi:10.1007/s10509-007-9506-8 Полный текст CrossRef | Google Scholar Адитья Ю. и Редди Д. Р. К. (2018). Анизотропная новая голографическая модель темной энергии в теории гравитации Саеса-Баллестера. Полный текст CrossRef | Google Scholar Акарсу О. и Килинч С. Б. (2010a). Модели Бьянки типа III с анизотропной темной энергией. Общ. отн. Гравит. 42 (4), 763–775. doi:10.1007/s10714-009-0878-7 Полный текст CrossRef | Google Scholar Акарсу О. и Килинч С. Б. (2010b). Модели LRS Bianchi Type I с анизотропной темной энергией и постоянным параметром замедления. Генерал Отн. Гравит. 42 (1), 119–140. doi:10.1007/s10714-009-0821-y Полный текст CrossRef | Google Scholar Альварес Э. и Гавела М. Б. (1983). Энтропия из дополнительных измерений. Физ. Преподобный Летт. 51, 931–934. doi:10.1103/PhysRevLett.51.931 Полный текст CrossRef | Google Scholar Амирхащи, Х., Зайнуддин, Х., и Дезфули, Х. Н. С. (2009). Геометрическое поведение космологической модели Lrs Bianchi Type-I. Э. Дж. Теор. физ. 6 (22), 79–84. Google Scholar Баник С.К. и Бхуян К. (2017). Динамика многомерной космологии FRW в R p exp (λR) Гравитация. Pramana — J. Phys. 88, 1–17. doi:10.1007/s12043-016-1335-2 Полный текст CrossRef | Google Scholar Беннетт К.Л., Халперн М., Хиншоу Г., Яросик Н., Когут А., Лимон М. и др. (2003). Наблюдения с помощью микроволнового зонда анизотропии Уилкинсона (WMAP) первого года обучения: предварительные карты и основные результаты. Astrophys J. Suppl. С 148, 1–27. doi:10.1086/377253 CrossRef Полный текст | Google Scholar Берман, М. С. (1983). Специальный закон изменения параметра Хаббла. Нуов. Сим. Б 74 (2), 182–186. doi:10.1007/BF02721676 Полный текст CrossRef | Google Scholar Берман М.С. и де Мелло Гомиде Ф. (1988). Космологические модели с постоянным параметром торможения. Генерал Рел. Полный текст перекрестной ссылки | Google Scholar Бранс, К., и Дике, Р. Х. (1961). Принцип Маха и релятивистская теория гравитации. Физ. Ред. 124 (3), 925–935. doi:10.1103/PhysRev.124.925 Полный текст CrossRef | Google Scholar Булл П., Акрами Ю., Адамек Дж., Бейкер Т., Беллини Э., Хименес Дж. Б. и др. (2016). Beyond λ cdm Проблемы, решения и путь вперед, Физика темной Вселенной. Физ. Темная Вселенная 12, 56–99. doi:10.1016/j.dark.2016.02.001 Полный текст CrossRef | Google Scholar Капоцциелло С., Карлони С. и Троизи А. (2003). Квинтэссенция без скалярных полей. Недавние рез. Дев. Астрон. Астрофиз. 1, 1–46. arXiv:astro-ph/0303041. Google Scholar Коллинз С. Б., Гласс Э. Н. и Уилкинсон Д. А. (1983). Точные пространственно однородные космологии. Генерал Отн. Гравит. 12, 805–823. Google Scholar Коллинз, С. CrossRef Полный текст | Google Scholar Даймари, Дж., и Баруа, Р.Р. (2021). Пятимерная космологическая модель струн Бьянки типа I с электромагнитным полем. Дж. Матем. вычисл. науч. 11, 6599–6613. doi:10.28919/jmcs/6267 Полный текст CrossRef | Google Scholar de Bernardis, P., Ade, P.A.R., Bock, J.J., Bond, J.R., Borrill, J., Boscaleri, A., et al. (2000). Плоская Вселенная по картам высокого разрешения космического микроволнового фонового излучения. Природа 404, 955–959. doi:10.1038/35010035 PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar Эверетт, А. Э. (1981). Космические струны в единых калибровочных теориях. Физ. Ред. D 24, 858–868. doi:10.1103/PhysRevD.24.858 Полный текст CrossRef | Google Scholar Грассо, Д., и Рубинштейн, Х. Р. (2000). Магнитные поля в ранней Вселенной. Полный текст CrossRef | Google Scholar Гут, А. Х. (1981). Инфляционная Вселенная: возможное решение проблем горизонта и плоскостности. Физ. Ред. D 23, 347–356. doi:10.1103/physrevd.23.347 Полный текст перекрестной ссылки | Google Scholar Ханани С., Аде П., Балби А., Бок Дж., Боррилл Дж., Боскалери А. и др. (2000). MAXIMA-1: Измерение анизотропии космического микроволнового фона по угловым шкалам 10[угл.мин]-5°. Астрофиз. Дж. Летт. 545, Л5–Л9. doi:10.1086/317322 CrossRef Полный текст | Google Scholar Харко Т., Лобо Ф. С. Н., Нодзири С. И. и Одинцов С. Д. (2011). f(R,T) Гравитация. Физ. Ред. D 84 (2), 1–11. doi:10.1103/PhysRevD.84.024020 Полный текст перекрестной ссылки | Google Scholar Хименес, Дж. Б., и Марото, А. Л. (2009). Космологические электромагнитные поля и темная энергия. arXiv:0811.0566v2 [astro-ph] 2009, 1–13. Полный текст CrossRef | Google Scholar Калуца, Т. (2018). К проблеме объединения в физике. Междунар. Дж. Мод. физ. Д 27, 1870001–1870972. doi:10.1142/S0218271818700017 Полный текст CrossRef | Академия Google Киббл, TWB (1980). Некоторые следствия космологического фазового перехода. Физ. Респ. 67, 183–199. doi:10.1016/0370-1573(80) Полный текст CrossRef | Google Scholar Kibble, TWB (1976). Топология космических доменов и струн. J. Phys. А: Математика. Быт. 9 (8), 1387–1398. doi:10.1088/0305-4470/9/8/029 Полный текст CrossRef | Google Scholar Киран М., Редди Д. Р. К. и Рао В. У. М. (2015). Минимально взаимодействующая голографическая модель темной энергии в теории Бранса-Дикке. Космические науки астрофизики. 356 (2), 407–411. doi:10.1007/s10509-014-2213-3 Полный текст CrossRef | Google Scholar Кляйн, О. (1926). Квантовая теория и теория относительности измерений. Полный текст CrossRef | Google Scholar Крори К.Д., Чаудхури Т., Маханта Ч.Р. и Мазумдар А. (1990). Некоторые точные решения в струнной космологии. Генерал Рел. Гравит. 22, 123–130. дои: 10.1007/BF00756203 Полный текст перекрестной ссылки | Google Scholar Летелье, PS (1983). Струнные космологии. Физ. Ред. D 28, 2414–2419. doi:10.1103/PhysRevD.28.2414 Полный текст CrossRef | Google Scholar MacCallum, MAH (1971). Класс однородных космологических моделей III: асимптотическое поведение. Комм.мат. физ. 20, 57–84. doi:10.1007/bf01646733 Полный текст перекрестной ссылки | Google Scholar Марчиано, В. Дж. (1984). Изменение во времени фундаментальных «констант» и теории Калуцы-Клейна. Физ. Преподобный Летт. 52, 489–491. doi:10.1103/PhysRevLett.52.489 Полный текст CrossRef | Google Scholar Мишра Р.К. и Чанд А. (2020). Полный текст CrossRef | Google Scholar Мишра Р.К. и Дуа Х. (2019). Космологические модели объемной вязкой струны в теории гравитации Саеса-Баллестера. Астрофиз. Космические науки. 364 (11), 1951. doi:10.1007/s10509-019-3689-7 CrossRef Полный текст | Google Scholar Монтефальконе Г., Стейнхардт П.Дж. и Уэсли Д.Х. (2020). Темная энергия, дополнительные измерения и болота. Дж. Высокая энергия. физ. 91, 1–12. doi:10.1007/JHEP06(2020)091 Полный текст CrossRef | Google Scholar Найду, Р. Л., Адитья, Ю., Дэниел Раджу, К., Винута, Т., и Редди, Д. Р. К. (2021). Калуца-Кляйн FRW Модели темной энергии в теории гравитации Саеса-Баллестера. Новый Астрон. 85, 101564–101567. doi:10.1016/j.newast.2020.101564 Полный текст CrossRef | Google Scholar Нодзири С. Полный текст CrossRef | Google Scholar Парих С., Тьяги А. и Трипати Б. Р. (2018). Геометрия Лиры в космологической модели струнной пыли Бьянки типа II. Prespacetime J. 9 (4), 288–296. Доступно по адресу: https://prespacetime.com/index.php/pst/article/viewFile/1423/1365. Google Scholar Павар Д. Д., Бхуттампалле Г. Г. и Агравал П. К. (2018). Калуца-Кляйн f(R, T) Теория гравитации. Новый Астрон. 65, 1–6. doi:10.1016/j.newast.2018.05.002 Полный текст CrossRef | Google Scholar Прийокумар С.К., Баро Дж. и Джитен Б. (2021). Космологическая модель струны I типа Lrs Bianchi высшего измерения с объемной вязкостью в общей теории относительности. Индийский журнал J. Sci. Технол. 14, 1239–1249. Полный текст CrossRef | Google Scholar Рам С., Зейауддин М. и Сингх С.П. (2010). Анизотропные космологические модели идеальной жидкости типа V Бьянки в геометрии Лиры. J. Geometry Phys. 60 (11), 1671–1680. doi:10.1016/j.geomphys.2010.06.010 CrossRef Full Text | Google Scholar Рао В.У.М., Винута Т. и Виджая Шанти М. (2008). Космологическая модель Бьянки типа V с идеальной жидкостью с использованием отрицательного постоянного параметра замедления в скалярной тензорной теории, основанной на многообразии Лиры. Астрофиз. Космические науки. 314, 213–216. doi:10.1007/s10509-008-9757-z Полный текст CrossRef | Google Scholar Расули С.М.М., Пачеко Р., Сакеллариаду М. и Мониз П.В. (2020). Космическое ускорение позднего времени в модифицированной теории Саеса-Баллестера. Физ. Темная Вселенная 27, 1–20. doi:10.1016/j.dark.2019.100446 Полный текст CrossRef | Google Scholar Редди, ДРК (2003). Полный текст CrossRef | Google Scholar Саес Д. и Баллестер В. Дж. (1986). Простое соединение с космологическими следствиями. Физ. лат. А 113 (9), 467–470. doi:10.1016/0375-9601(86)-0 Полный текст CrossRef | Google Scholar Саху, П.К., и Мишра, Б. (2015). Многомерная Вселенная Бьянки типа III со странной кварковой материей, прикрепленной к струнному облаку в общей теории относительности. Терк Дж. Физ. 39, 43–53. doi:10.3906/fiz-1403-5 Полный текст CrossRef | Google Scholar Саху П.К., Саху П. и Биши Б.К. (2017). Анизотропные космологические модели в гравитации f(R,T) с переменным параметром замедления. Междунар. Дж. Геом. Методы Мод. физ. 14, 1750097. doi:10.1142/S0219887817500979 CrossRef Полный текст | Google Scholar Санти, М. CrossRef Full Text | Google Scholar Синкай Х.-А. и Тории Т. (2015). Червоточина в многомерном пространстве-времени. J. Phys. конф. сер. 600, 012038. doi:10.1088/1742-6596/600/1/012038 CrossRef Полный текст | Google Scholar Сингх Г. П., Дешпанде Р. В. и Сингх Т. (2004). Многомерная космологическая модель с переменной гравитационной постоянной и объемной вязкостью в геометрии лиры. Прамана — J. Phys. 63, 937–945. doi:10.1007/BF02704332 Полный текст CrossRef | Google Scholar Сингх К.П., Баро Дж. и Мейтей А.Дж. (2021). Многомерные космологические модели Бьянки типа I с массивной струной в общей теории относительности. Фронт. Астрон. Космические науки. 8, 1–6. doi:10.3389/fspas.2021.777554 Полный текст CrossRef | Google Scholar Сингх К. CrossRef Полный текст | Google Scholar Сингх, К.П., и Сингх, П.С. (2019). Темная энергия в многомерной сферически-симметричной Вселенной Бранса-Дикке. Подбородок. Дж. Физ. 60, 239–247. doi:10.1016/j.cjph.2019.05.003 Полный текст CrossRef | Google Scholar Сингх Т. и Агравал А. К. (1991). Некоторые космологические модели типа Бьянки в новой скалярно-тензорной теории. Астрофиз. Космические науки. 182 (2), 289–312. doi:10.1007/bf00645008 Полный текст CrossRef | Google Scholar Субраманиан, К. (2016). Происхождение, эволюция и признаки первичных магнитных полей. Респ. прог. физ. 79 (7), 076901–076957. doi:10.1088/0034-4885/79/7/076901 PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar Трипати Б. Google Scholar Tripathy, S.K., Nayak, S.K., Sahu, S.K., and Routray, T.R. (2009). Космологии массивных струнных облаков в теории гравитации Саеса-Баллестера. Междунар. Дж. Теор. физ. 48, 213–225. doi:10.1007/s10773-008-9796-9 Полный текст CrossRef | Google Scholar Виленкин А. (1981а). Космические струны. Физ. Версия D 24, 2082–2089 гг. doi:10.1103/PhysRevD.24.2082 CrossRef Полный текст | Google Scholar Виленкин А. (1981б). Гравитационное поле вакуумных доменных стенок и струн. Физ. Ред. D 23 (24), 852–857. doi:10.1103/PhysRevD.23.852 Полный текст CrossRef | Google Scholar Син-Сян, В. (2003). Точные решения для струнной космологии. Полный текст CrossRef | Академия Google Син-Сян, В. (2004). Локально вращательно-симметричная космологическая модель струны Бьянки типа I с объемной вязкостью. Подбородок. физ. лат. 21 (7), 1205–1207. doi:10.1088/0256-307X/21/7/006 Полный текст CrossRef | Google Scholar Явуз И., Йилмаз И. и Байсал Х. (2005). Странная кварковая материя, прикрепленная к струнному облаку в сферическом симметричном пространстве-времени, допускающем конформное движение. Междунар. Дж. Мод. физ. Д 14 (1), 1365–1372. doi:10.1142/S0218271805007061 Полный текст перекрестной ссылки | Google Scholar Йылмаз, И. (2006). Струнное облако и доменные стены с кварковой материей в 5-D космологической модели Калуцы-Клейна. Генерал Отн. Гравит. 38 (9), 1397–1406. doi:10.1007/s10714-006-0322-1 Полный текст CrossRef | Google Scholar Зельдович Ю.0 9 константы. 
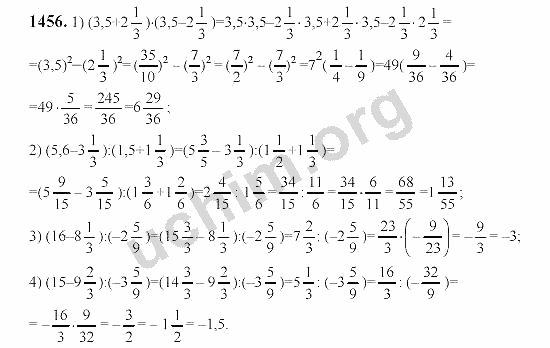
4 Некоторые физические свойства модели
25 fluctuation of some of the parameters is depicted using the values
a = k 1 = k 6 = n = 1 and k 2 = 0.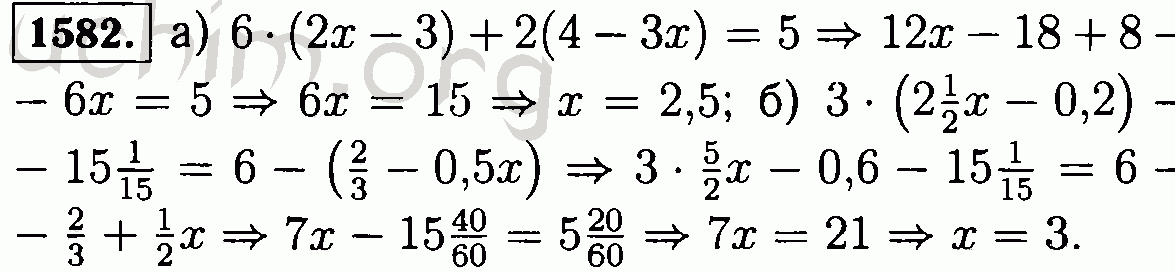
5 Physical Interpratation
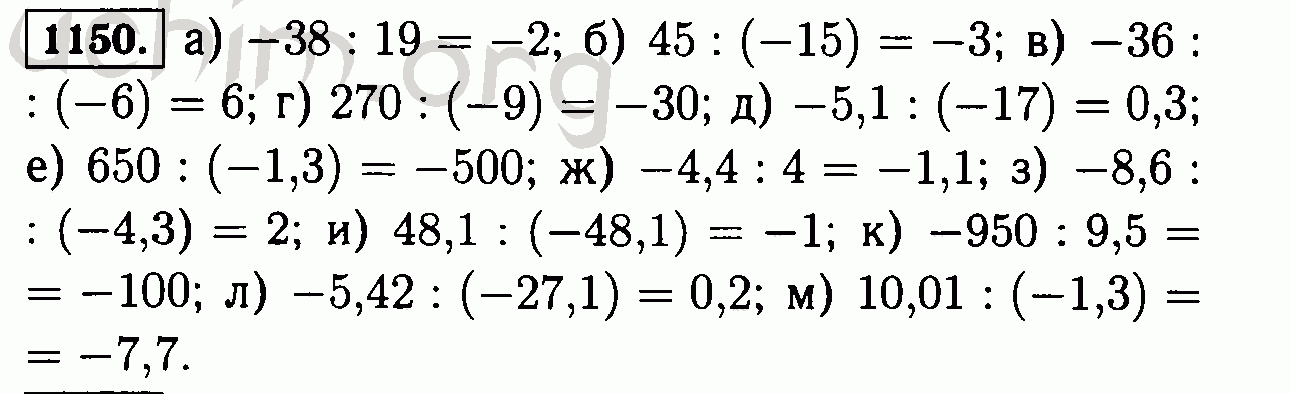 Расширение космоса, по-видимому, ускоряется, и параметр замедления в этом сценарии отрицательный, R̈>0. Наша модель удовлетворяет энергетическим условиям ρ ≥ 0 и ρ p ≥ 0. Электромагнитное поле изменяет поведение модели, а также выражения физических параметров. В присутствии электромагнитного поля плотность энергии покоя и натяжение струны уменьшаются (как показано на рисунках 4, 5). Плотность частиц и плотность натяжения струны также сравнимы, хотя плотность натяжения струны исчезает быстрее, чем плотность частиц. Это показывает, что наша модель отображает Вселенную с преобладанием материи в позднем временном масштабе, что согласуется с текущими данными наблюдений. Мы можем видеть из выражения уравнения 39, что собственный объем V=k24k1 при t = 0 увеличивается с космическим временем t (показано на рисунке 6). Это означает, что Вселенная начинается с конечного объема при t = 0, а затем растет по мере прохождения космического времени.
Расширение космоса, по-видимому, ускоряется, и параметр замедления в этом сценарии отрицательный, R̈>0. Наша модель удовлетворяет энергетическим условиям ρ ≥ 0 и ρ p ≥ 0. Электромагнитное поле изменяет поведение модели, а также выражения физических параметров. В присутствии электромагнитного поля плотность энергии покоя и натяжение струны уменьшаются (как показано на рисунках 4, 5). Плотность частиц и плотность натяжения струны также сравнимы, хотя плотность натяжения струны исчезает быстрее, чем плотность частиц. Это показывает, что наша модель отображает Вселенную с преобладанием материи в позднем временном масштабе, что согласуется с текущими данными наблюдений. Мы можем видеть из выражения уравнения 39, что собственный объем V=k24k1 при t = 0 увеличивается с космическим временем t (показано на рисунке 6). Это означает, что Вселенная начинается с конечного объема при t = 0, а затем растет по мере прохождения космического времени. Соответствующий объем V становится бесконечным в момент времени t. Уравнение 37 показывает, что неисчезающий тензор электромагнитного поля F 15 экспоненциально растет как функция космического времени t (показано на рисунке 7). Если a ≠ 0, мы можем видеть, что тензор электромагнитного поля F 15 не исчезает. Он оказывает существенное влияние на формирование струн на ранних стадиях эволюции Вселенной. В этом сценарии струна и электромагнитное поле сосуществуют.
Соответствующий объем V становится бесконечным в момент времени t. Уравнение 37 показывает, что неисчезающий тензор электромагнитного поля F 15 экспоненциально растет как функция космического времени t (показано на рисунке 7). Если a ≠ 0, мы можем видеть, что тензор электромагнитного поля F 15 не исчезает. Он оказывает существенное влияние на формирование струн на ранних стадиях эволюции Вселенной. В этом сценарии струна и электромагнитное поле сосуществуют.
6 Заключение
 В приведенной выше космологической модели H > 0 и q < 0, что демонстрирует, что Вселенная расширяется по степенному закону после Большого взрыва, начиная с конечного объема в космическое время t = 0 и расширяясь с ускорением. Для приведенной выше космологической модели Вселенной предполагаемая связь между параметром Хаббла и средним масштабным коэффициентом приводит к постоянному отрицательному значению параметра замедления. Сингулярность точечного типа (MacCallum, 1971) существует в производной модели в момент времени 9.0015 t = 0. Плотность частиц и плотность натяжения струны сравнимы, но плотность натяжения падает быстрее, чем плотность частиц, показывая, что с течением времени частицы доминируют в космосе. В нашей гипотезе Вселенная имеет шанс быть анизотропной в любой момент своего существования, от начала до конца. Согласно недавним исследованиям, существует несоответствие в оценке интенсивности микроволн, излучаемых с разных направлений неба.
В приведенной выше космологической модели H > 0 и q < 0, что демонстрирует, что Вселенная расширяется по степенному закону после Большого взрыва, начиная с конечного объема в космическое время t = 0 и расширяясь с ускорением. Для приведенной выше космологической модели Вселенной предполагаемая связь между параметром Хаббла и средним масштабным коэффициентом приводит к постоянному отрицательному значению параметра замедления. Сингулярность точечного типа (MacCallum, 1971) существует в производной модели в момент времени 9.0015 t = 0. Плотность частиц и плотность натяжения струны сравнимы, но плотность натяжения падает быстрее, чем плотность частиц, показывая, что с течением времени частицы доминируют в космосе. В нашей гипотезе Вселенная имеет шанс быть анизотропной в любой момент своего существования, от начала до конца. Согласно недавним исследованиям, существует несоответствие в оценке интенсивности микроволн, излучаемых с разных направлений неба.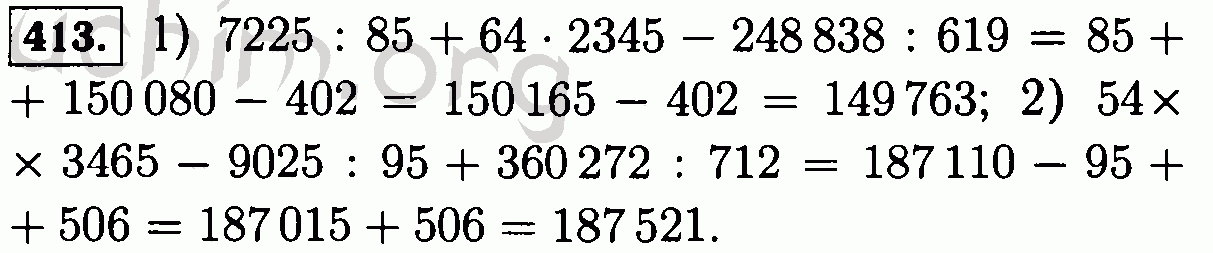 Это побудило нас исследовать мир с помощью анизотропной метрики типа I Бьянки, чтобы лучше описать нашу Вселенную. Несколько аномалий CMB (de Bernardis et al., 2000; Hanany et al., 2000), таких как температурная анизотропия в CMB, которые не согласуются с точной однородной и изотропной моделью FRW, зарегистрированной COBE/WMAP (Bennet et al., 2003 ) спутники, передний план/систематика и новые топологии также являются свидетельством того, что мы живем в глобально анизотропной Вселенной. Сдвиг уменьшается во время надувания, что в конечном итоге приводит к изотропной фазе без сдвига. Чтобы в последние годы произвести какой-либо значительный сдвиг, нужно сначала вызвать анизотропию в пространстве-времени.
Это побудило нас исследовать мир с помощью анизотропной метрики типа I Бьянки, чтобы лучше описать нашу Вселенную. Несколько аномалий CMB (de Bernardis et al., 2000; Hanany et al., 2000), таких как температурная анизотропия в CMB, которые не согласуются с точной однородной и изотропной моделью FRW, зарегистрированной COBE/WMAP (Bennet et al., 2003 ) спутники, передний план/систематика и новые топологии также являются свидетельством того, что мы живем в глобально анизотропной Вселенной. Сдвиг уменьшается во время надувания, что в конечном итоге приводит к изотропной фазе без сдвига. Чтобы в последние годы произвести какой-либо значительный сдвиг, нужно сначала вызвать анизотропию в пространстве-времени. Заявление о доступности данных
Вклад авторов
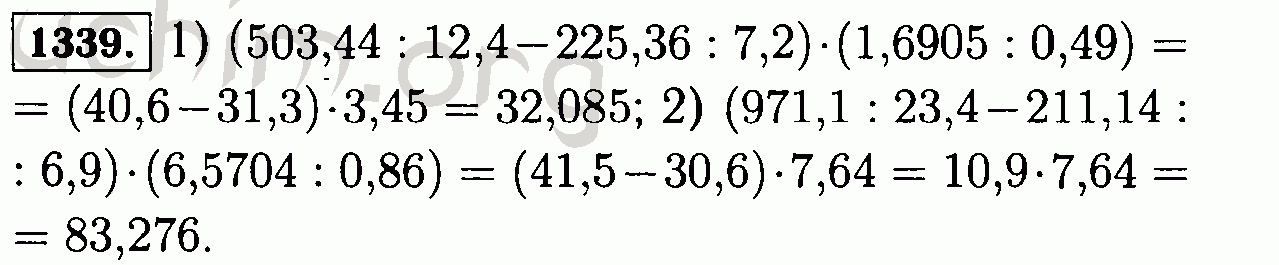
Конфликт интересов
Примечание издателя
Ссылки
 Астрофиз. Космические науки. 363 (10), 1–11. doi:10.1007/s10509-018-3429-4
Астрофиз. Космические науки. 363 (10), 1–11. doi:10.1007/s10509-018-3429-4 Доступно по адресу: http://www.ejtp.com/articles/ejtpv6i22p79.pdf.
Доступно по адресу: http://www.ejtp.com/articles/ejtpv6i22p79.pdf. Гравит. 20 (2), 191–198. doi:10.1007/BF00759327
Гравит. 20 (2), 191–198. doi:10.1007/BF00759327 Б., и Хокинг, С. В. (1973). Почему Вселенная изотропна? ApJ 180, 317–334. doi:10.1086/151965
Б., и Хокинг, С. В. (1973). Почему Вселенная изотропна? ApJ 180, 317–334. doi:10.1086/151965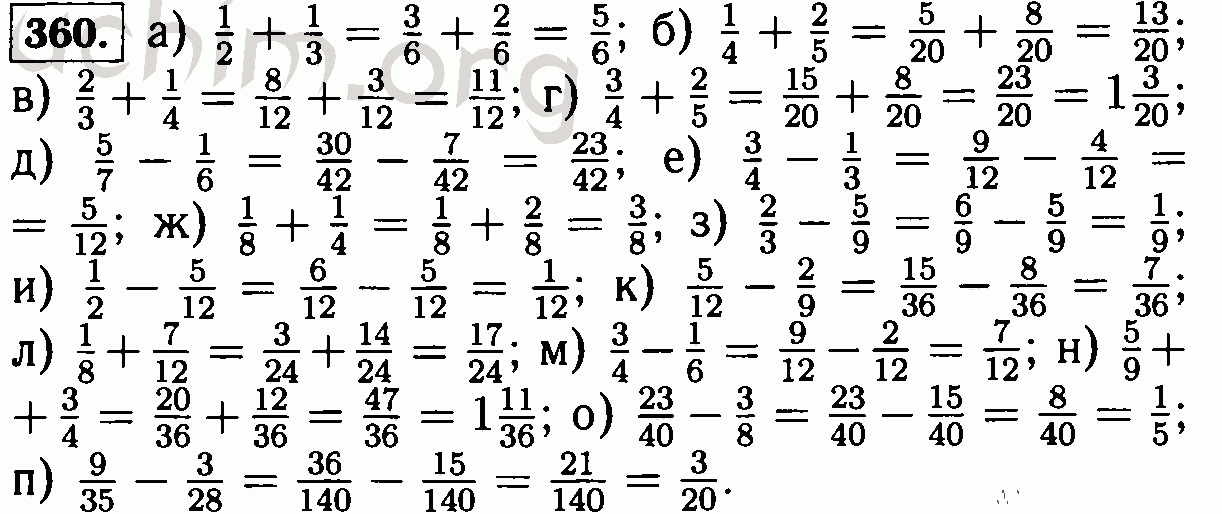 Физ. Респ. 348 (3), 163–266. doi:10.1016/S0370-1573(00)00110-1
Физ. Респ. 348 (3), 163–266. doi:10.1016/S0370-1573(00)00110-1 doi:10.1088/1475-7516/2009/03/016
doi:10.1088/1475-7516/2009/03/016 З. Физик 37, 895–906. doi:10.1007/BF01397481
З. Физик 37, 895–906. doi:10.1007/BF01397481 Космологические модели в теории Саэса-Баллестера с билинейно изменяющимся параметром замедления. Астрофиз. Космические науки. 365, 1–9. doi:10.1007/s10509-020-03790-w
Космологические модели в теории Саэса-Баллестера с билинейно изменяющимся параметром замедления. Астрофиз. Космические науки. 365, 1–9. doi:10.1007/s10509-020-03790-w И. и Одинцов С.Д. (2003). Модифицированная гравитация с отрицательной и положительной кривизной: объединение инфляции и космического ускорения. Физ. Ред. D 68 (12), 1–10. doi:10.1103/PhysRevD.68.123512
И. и Одинцов С.Д. (2003). Модифицированная гравитация с отрицательной и положительной кривизной: объединение инфляции и космического ускорения. Физ. Ред. D 68 (12), 1–10. doi:10.1103/PhysRevD.68.123512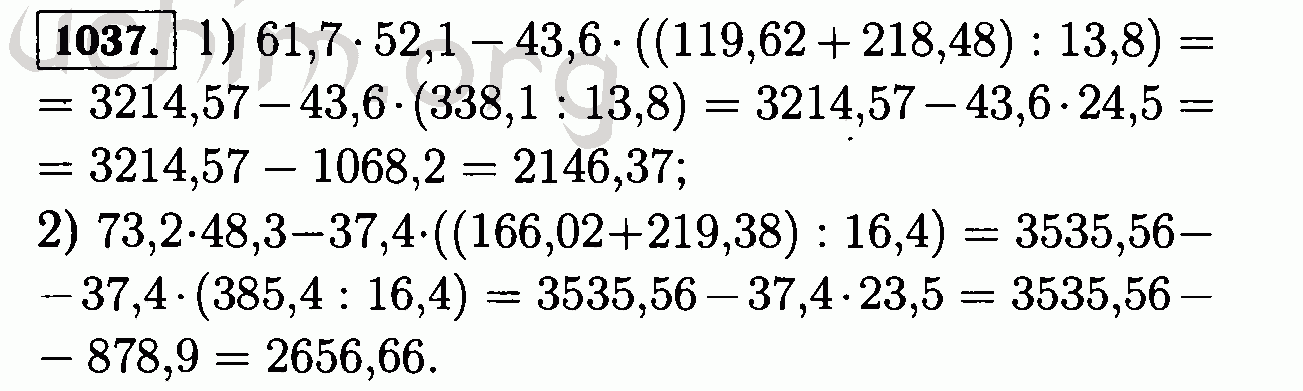 doi:10.17485/IJST/v14i16.240
doi:10.17485/IJST/v14i16.240 Струнная космологическая модель в скалярно-тензорной теории гравитации. Астрофиз. Космические науки. 286, 359–363. doi:10.1023/A:1026370732619
Струнная космологическая модель в скалярно-тензорной теории гравитации. Астрофиз. Космические науки. 286, 359–363. doi:10.1023/A:1026370732619 В., и Собханбабу, Ю. (2020). Голографическая модель темной энергии Тсаллиса типа III Бьянки в теории гравитации Саеса-Баллестера. Евро. физ. JC 80 (12), 1–15. doi:10.1140/epjc/s10052-020-08743-9
В., и Собханбабу, Ю. (2020). Голографическая модель темной энергии Тсаллиса типа III Бьянки в теории гравитации Саеса-Баллестера. Евро. физ. JC 80 (12), 1–15. doi:10.1140/epjc/s10052-020-08743-9 П., Молла М.Р., Баруа Р.Р. и Даймари М. (2020). Взаимодействие анизотропной облачной струны Бьянки I типа космологической модели Вселенной с электромагнитным полем. Междунар. Дж. Геом. Методы Мод. физ. 17 (8), 2050133. doi:10.1142/S0219887820501339
П., Молла М.Р., Баруа Р.Р. и Даймари М. (2020). Взаимодействие анизотропной облачной струны Бьянки I типа космологической модели Вселенной с электромагнитным полем. Междунар. Дж. Геом. Методы Мод. физ. 17 (8), 2050133. doi:10.1142/S0219887820501339 Р., Парих С. и Тьяги А. (2017). Космологическая модель неоднородной струны типа I Бьянки с электромагнитным полем в общей теории относительности. Prespacetime J. 8 (4), 474–483. Доступно по адресу: https://www.prespacetime.com/index.php/pst/article/viewFile/1220/1201.
Р., Парих С. и Тьяги А. (2017). Космологическая модель неоднородной струны типа I Бьянки с электромагнитным полем в общей теории относительности. Prespacetime J. 8 (4), 474–483. Доступно по адресу: https://www.prespacetime.com/index.php/pst/article/viewFile/1220/1201. Подбородок. физ. лат. 20 (5), 615–617. doi:10.1088/0256-307X/20/5/307
Подбородок. физ. лат. 20 (5), 615–617. doi:10.1088/0256-307X/20/5/307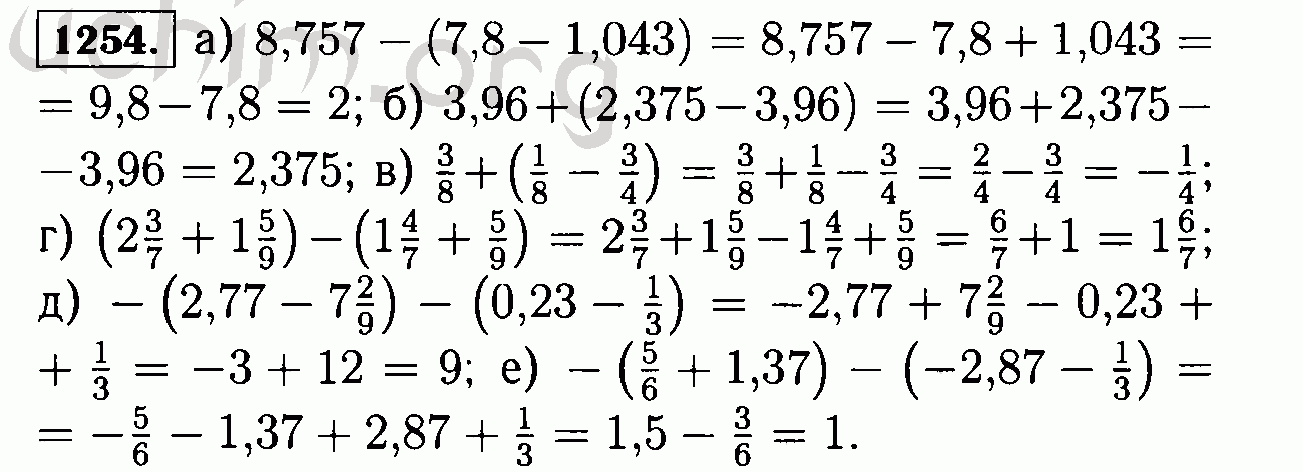

 Живой преподобный отн. 7 , 7. (10.12942/lrr-2004-7) [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
Живой преподобный отн. 7 , 7. (10.12942/lrr-2004-7) [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]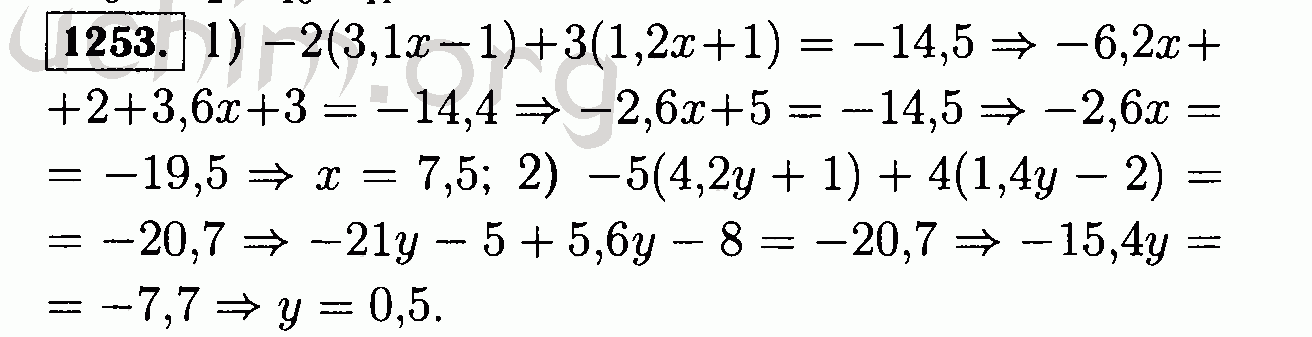 2021.
Регулярные бранные миры с нелинейными объемными жидкостями. Евро. физ. Дж. С. 81 , 771. (10.1140/epjc/s10052-021-09558-y) [CrossRef] [Google Scholar]
2021.
Регулярные бранные миры с нелинейными объемными жидкостями. Евро. физ. Дж. С. 81 , 771. (10.1140/epjc/s10052-021-09558-y) [CrossRef] [Google Scholar]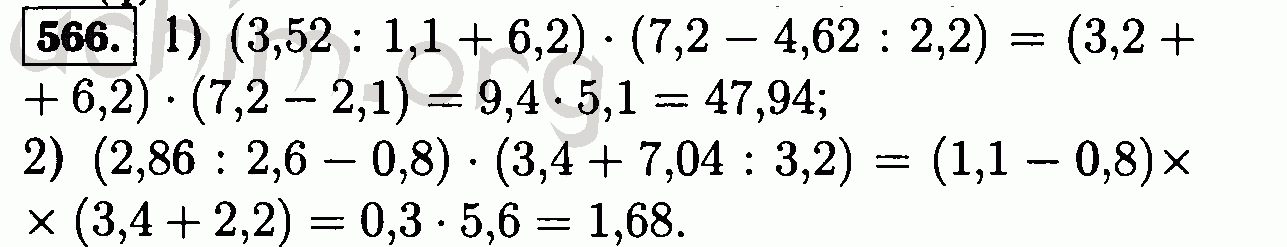 (10.1103/PhysRevD.73.123527) [CrossRef] [Google Scholar]
(10.1103/PhysRevD.73.123527) [CrossRef] [Google Scholar]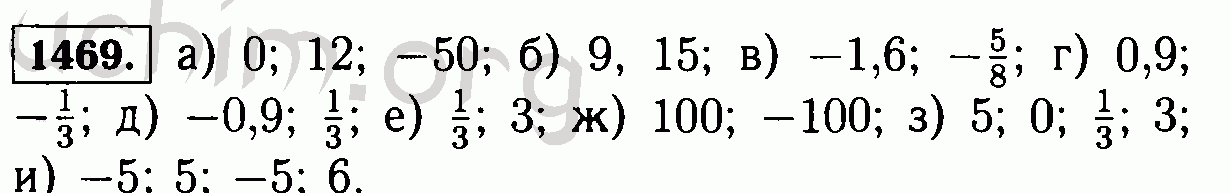 Сов Астрон. лат. 10 , 135-137. [Google Scholar]
Сов Астрон. лат. 10 , 135-137. [Google Scholar]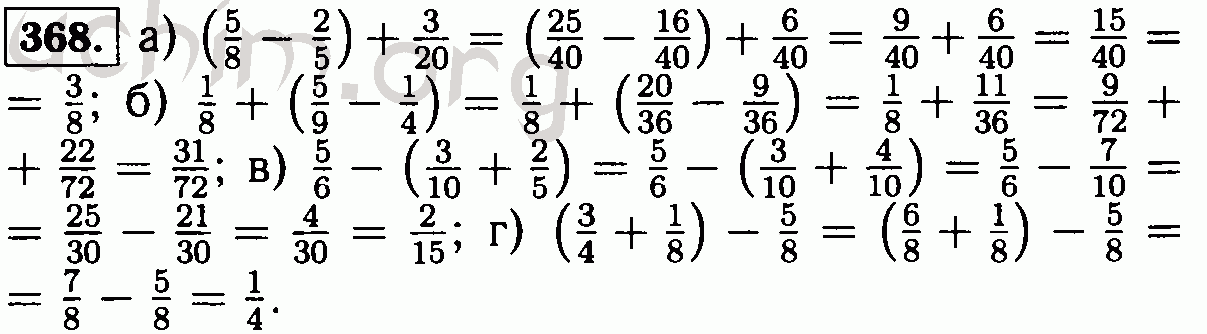 Танимото М., Койке Т., Хосоя А. 1997.
Динамика компактных однородных вселенных. Дж. Матем. физ. 38 , 350-368. ( 10.1063/1.531853) [CrossRef] [Google Scholar]
Танимото М., Койке Т., Хосоя А. 1997.
Динамика компактных однородных вселенных. Дж. Матем. физ. 38 , 350-368. ( 10.1063/1.531853) [CrossRef] [Google Scholar] В. Гиббонс), том. 460, стр. 111–173. Конспекты лекций по физике. Берлин, Германия: Springer.
В. Гиббонс), том. 460, стр. 111–173. Конспекты лекций по физике. Берлин, Германия: Springer.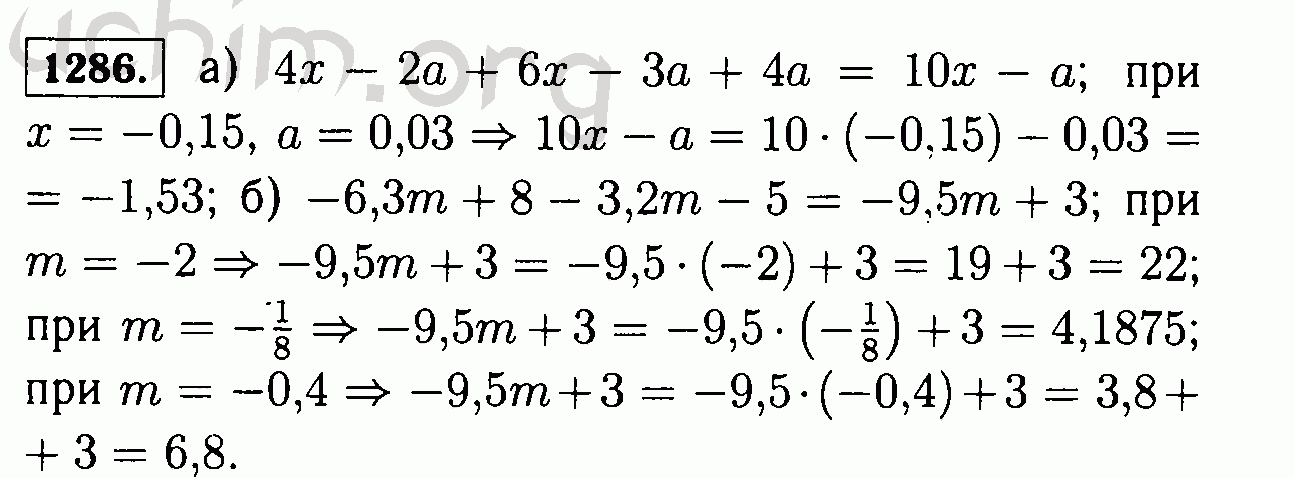 ( 10.1016/0370-1573(79)-6) [CrossRef] [Google Scholar]
( 10.1016/0370-1573(79)-6) [CrossRef] [Google Scholar] ( 10.1016/j.geomphys.2006.10.007) [CrossRef] [Google Scholar]
( 10.1016/j.geomphys.2006.10.007) [CrossRef] [Google Scholar]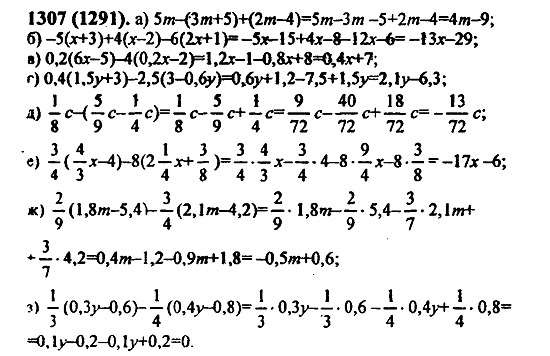 2007.
Доминирующий баланс в космологических сингулярностях. Дж. Физ. конф. сер. 68 , 012004. ( 10.1088/1742-65968.06.01.012004) [CrossRef] [Google Scholar]
2007.
Доминирующий баланс в космологических сингулярностях. Дж. Физ. конф. сер. 68 , 012004. ( 10.1088/1742-65968.06.01.012004) [CrossRef] [Google Scholar] Марк Хайнцле Дж., Сандин П. 2012.
Исходная сингулярность ультражестких идеально-жидких пространств-времен без симметрий. Комм. Мат. физ. 313 , 385-403. ( 10.1007/s00220-012-1496-x) [CrossRef] [Google Scholar]
Марк Хайнцле Дж., Сандин П. 2012.
Исходная сингулярность ультражестких идеально-жидких пространств-времен без симметрий. Комм. Мат. физ. 313 , 385-403. ( 10.1007/s00220-012-1496-x) [CrossRef] [Google Scholar] ( 10.1088/1475-7516/2003/03/001) [CrossRef] [Google Scholar]
( 10.1088/1475-7516/2003/03/001) [CrossRef] [Google Scholar]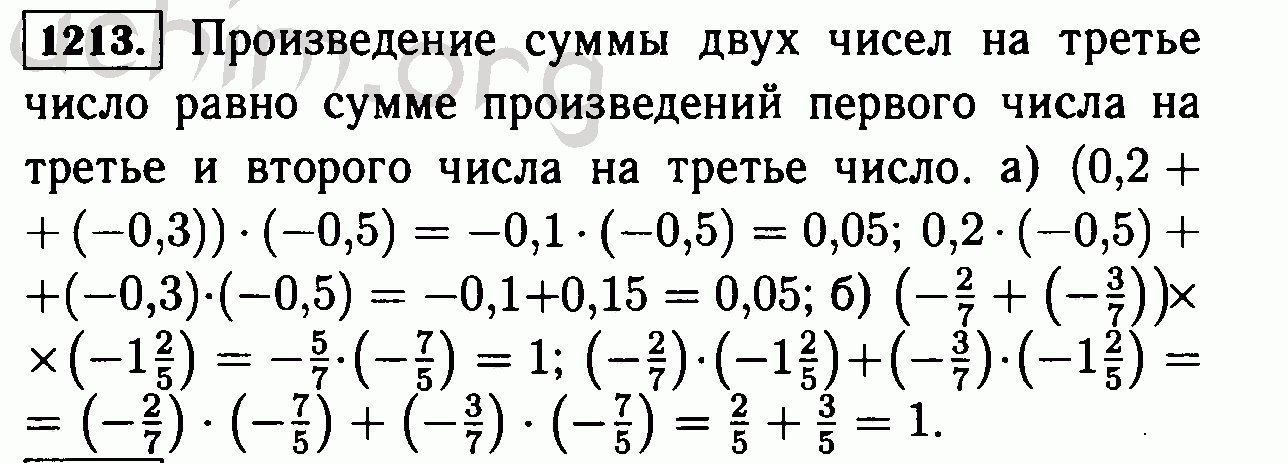 Perlmutter S, et al.
1999.
Измерения Ω и Λ 42 сверхновых с большим красным смещением. Астрофиз. Дж. 517 , 565-586. ( 10.1086/307221) [CrossRef] [Google Scholar]
Perlmutter S, et al.
1999.
Измерения Ω и Λ 42 сверхновых с большим красным смещением. Астрофиз. Дж. 517 , 565-586. ( 10.1086/307221) [CrossRef] [Google Scholar] Представитель физ. 568 , 1-98. ( 10.1016/j.physrep.2014.12.002) [CrossRef] [Google Scholar]
Представитель физ. 568 , 1-98. ( 10.1016/j.physrep.2014.12.002) [CrossRef] [Google Scholar] Фил. Транс. Р. Соц. А 380 , 20210178. ( 10.1098/rsta.2021.0178) [CrossRef] [Google Scholar]
Фил. Транс. Р. Соц. А 380 , 20210178. ( 10.1098/rsta.2021.0178) [CrossRef] [Google Scholar]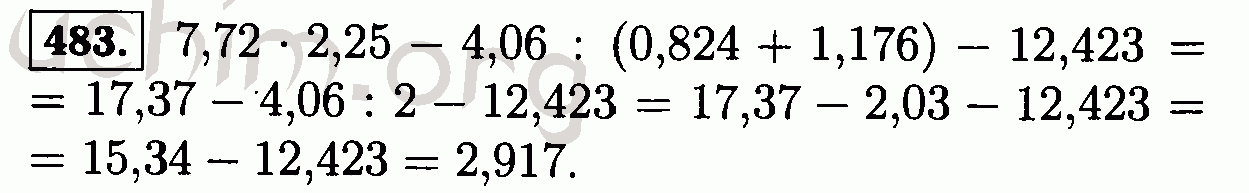 Эриксон К.В., Леунг Р., Стелле К.С. 2022.
Эффект Хиггса без обеда. Фил. Транс. Р. Соц. А 380 , 20210184. (10.1098/rsta.2021.0184) [CrossRef] [Google Scholar]
Эриксон К.В., Леунг Р., Стелле К.С. 2022.
Эффект Хиггса без обеда. Фил. Транс. Р. Соц. А 380 , 20210184. (10.1098/rsta.2021.0184) [CrossRef] [Google Scholar] ( 10.1098/rsta.2021.0405) [CrossRef] [Google Scholar]
( 10.1098/rsta.2021.0405) [CrossRef] [Google Scholar]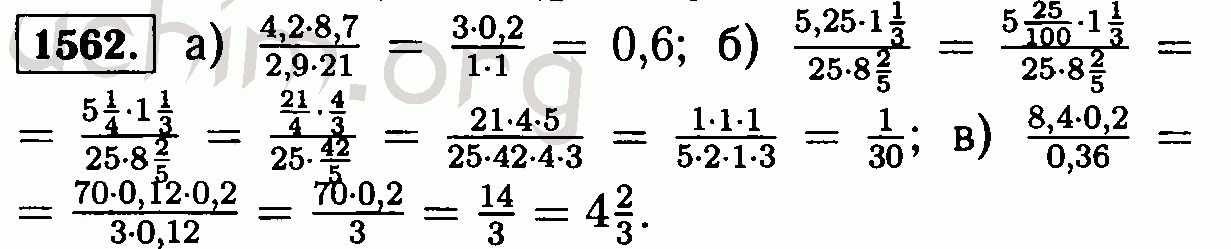 Он не предполагает никаких предварительных знаний по физике или математике, кроме элементарной математики средней школы. Необходимый физический фон вводится по мере необходимости. Каждая глава включает список вопросов и упражнений разной степени сложности.
Он не предполагает никаких предварительных знаний по физике или математике, кроме элементарной математики средней школы. Необходимый физический фон вводится по мере необходимости. Каждая глава включает список вопросов и упражнений разной степени сложности. Математическое приложение и указатель безупречны ». (Иоахим Дж. Кер, Journal of Space Operations & Communicator, Vol. 15 (1), 2018 г.) «Космология для любопытных предлагает отличный обзор ключевых идей космологии. Она также четко отделяет наше эмпирически определенное понимание от более спекулятивных областей. текущих исследований. В настоящее время я использую его на вводном уроке космологии». (Приямвада Натараджан, Physics Today, апрель 2018 г.) «Это вводный учебник, предназначенный для студентов-первокурсников-физиков, со знакомыми элементами учебника, такими как вопросы, на которые нужно ответить в конце каждой главы… Идеальным рынком для этой книги является … студент, собирающийся начать изучение физики в университете и желающий облегчить изучение курса. Делию Перлов и Алекса Виленкина следует поздравить с тем, что они сделали большой шаг к доступности такой книги». (Популярная наука, popsciencebooks.blogspot.de, октябрь 2017 г.)
Математическое приложение и указатель безупречны ». (Иоахим Дж. Кер, Journal of Space Operations & Communicator, Vol. 15 (1), 2018 г.) «Космология для любопытных предлагает отличный обзор ключевых идей космологии. Она также четко отделяет наше эмпирически определенное понимание от более спекулятивных областей. текущих исследований. В настоящее время я использую его на вводном уроке космологии». (Приямвада Натараджан, Physics Today, апрель 2018 г.) «Это вводный учебник, предназначенный для студентов-первокурсников-физиков, со знакомыми элементами учебника, такими как вопросы, на которые нужно ответить в конце каждой главы… Идеальным рынком для этой книги является … студент, собирающийся начать изучение физики в университете и желающий облегчить изучение курса. Делию Перлов и Алекса Виленкина следует поздравить с тем, что они сделали большой шаг к доступности такой книги». (Популярная наука, popsciencebooks.blogspot.de, октябрь 2017 г.)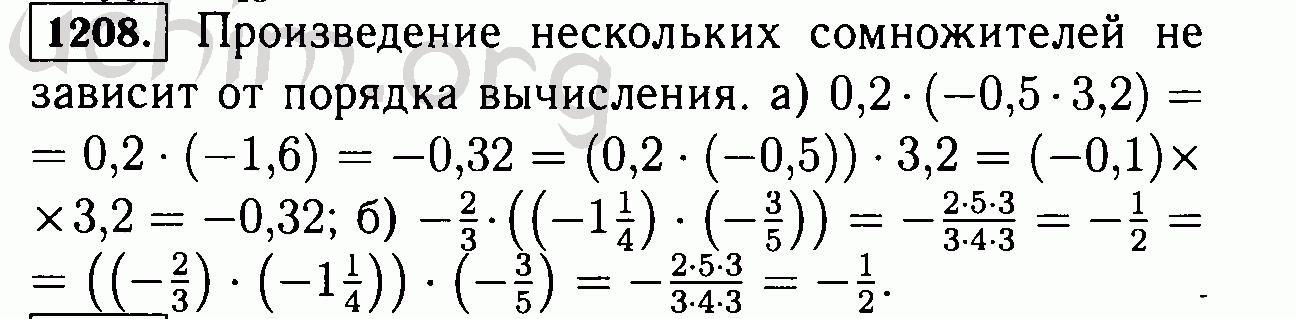 1 Большие космические вопросы
1 Большие космические вопросы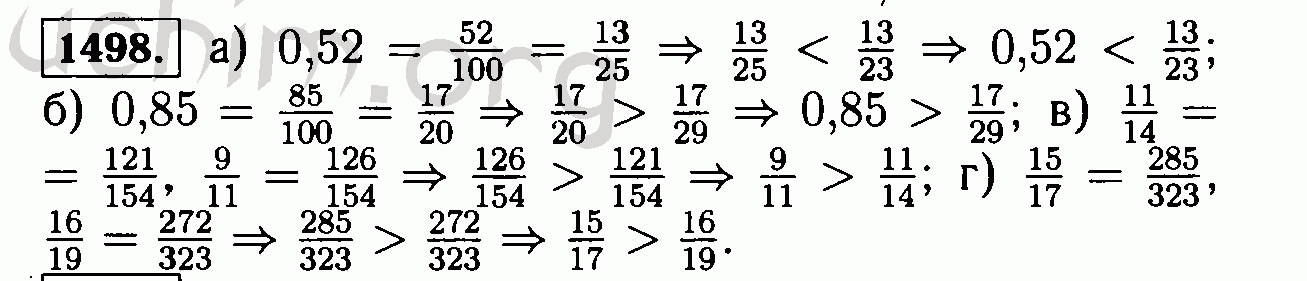 3 Ускорение свободного падения
3 Ускорение свободного падения 1 Принцип относительности
1 Принцип относительности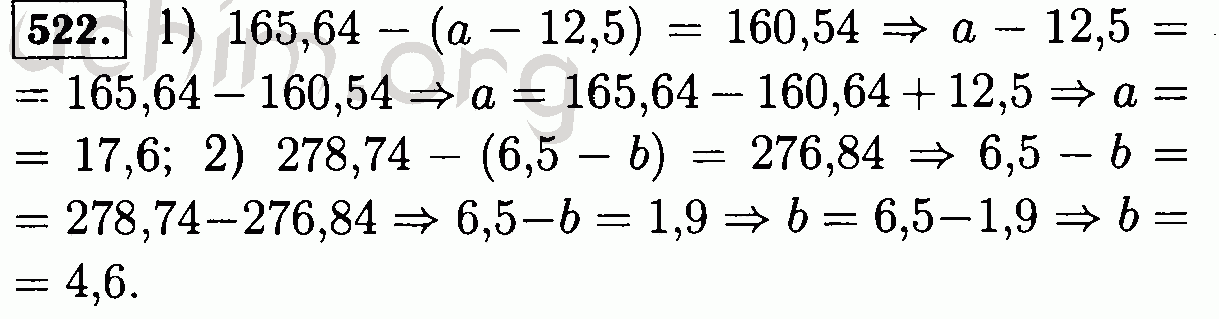 6.1 Ускорение мюонов
6.1 Ускорение мюонов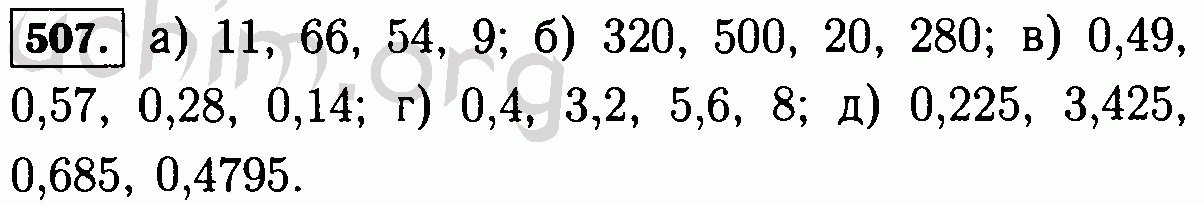 2 Геометрия пространства
2 Геометрия пространства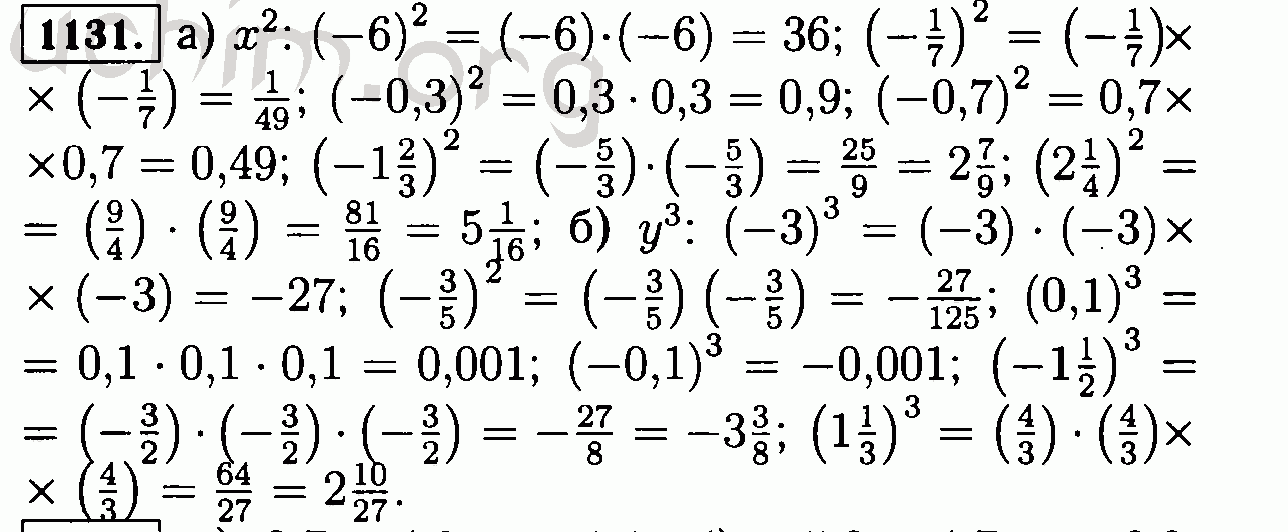 4 Общая теория относительности
4 Общая теория относительности 5.4 Гравитационные волны
5.4 Гравитационные волны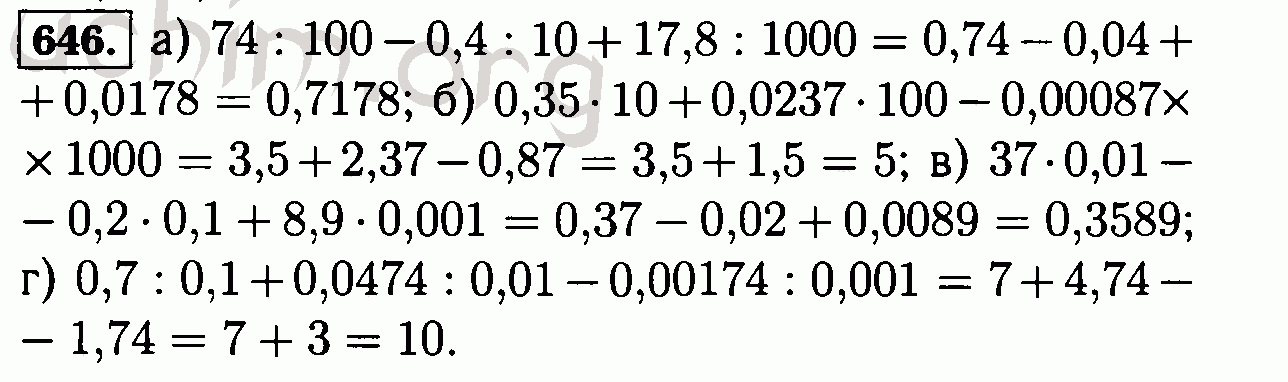 1 Отпечатки пальцев элементов
1 Отпечатки пальцев элементов 2 Начало Вселенной?
2 Начало Вселенной? 8 Не все расширяется
8 Не все расширяется 2 Темная энергия
2 Темная энергия 4 Многомировая интерпретация
4 Многомировая интерпретация 5 Образы Детской Вселенной
5 Образы Детской Вселенной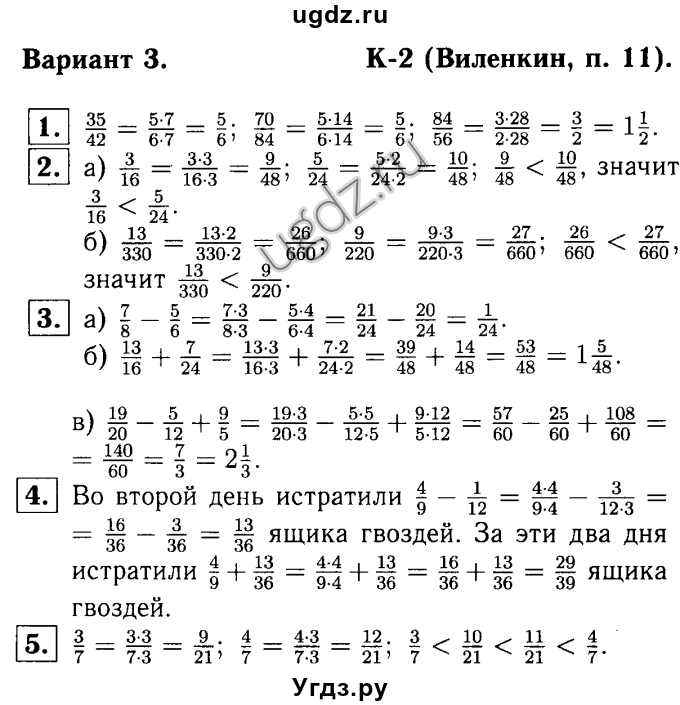 3 Наблюдение за эволюцией космических структур
3 Наблюдение за эволюцией космических структур 2 Нуклеосинтез Большого Взрыва
2 Нуклеосинтез Большого Взрыва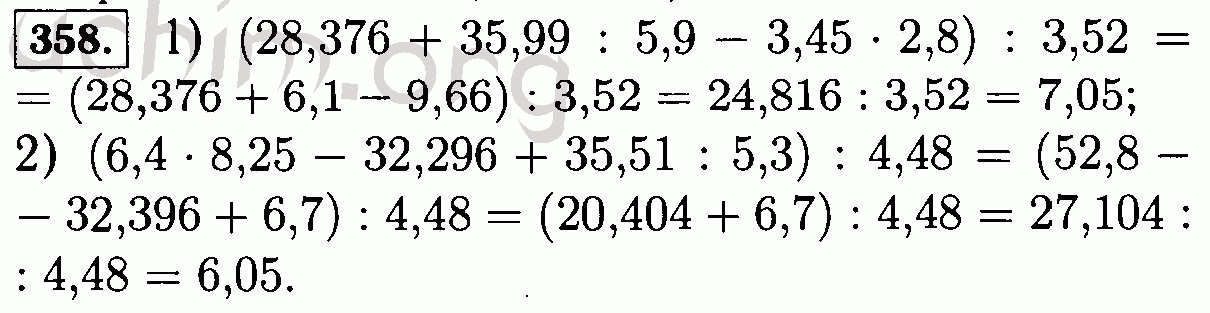 2 Стандартная модель физики элементарных частиц
2 Стандартная модель физики элементарных частиц 5.1 Объединение основных сил
5.1 Объединение основных сил 1 Проблема плоскостности: почему геометрия Вселенной плоская?
1 Проблема плоскостности: почему геометрия Вселенной плоская?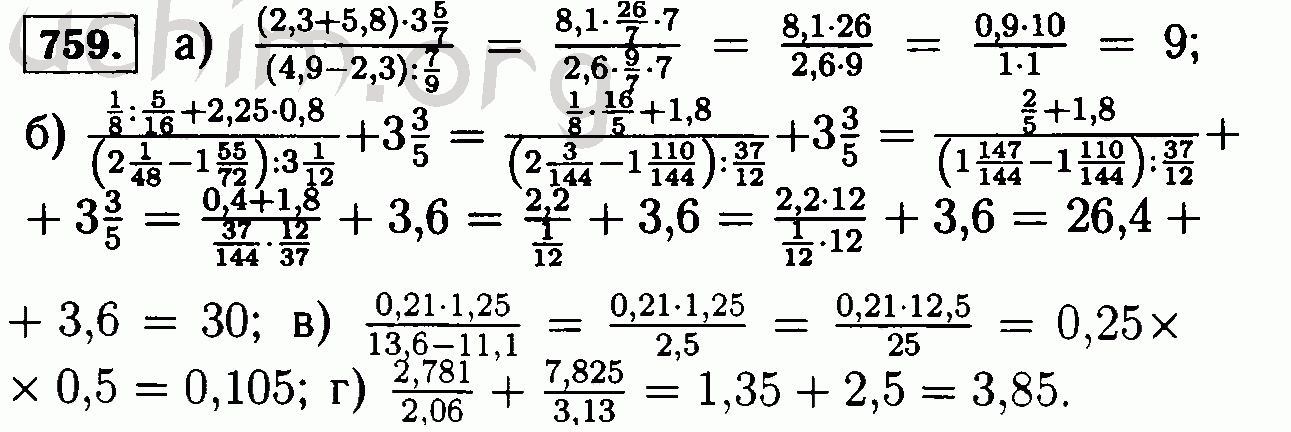 1 Решение задач плоскостности и горизонта
1 Решение задач плоскостности и горизонта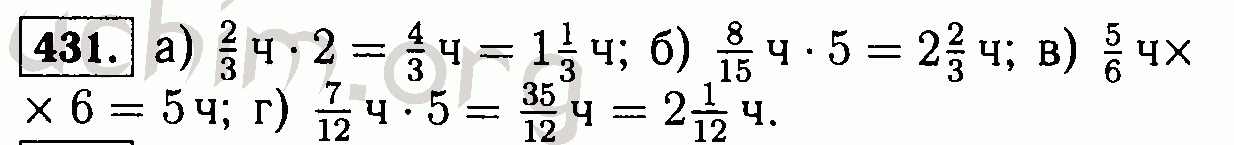 3.2 Проблема горизонта
3.2 Проблема горизонта 4.2 Проблема изящного выхода
4.2 Проблема изящного выхода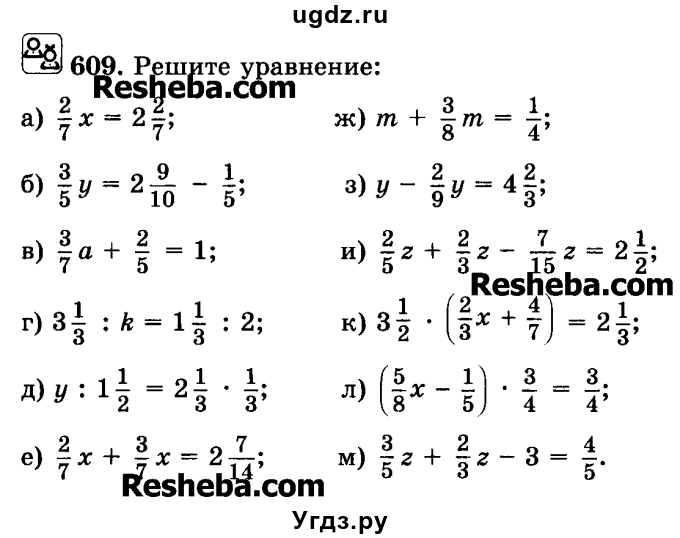 6.2 Энергосбережение
6.2 Энергосбережение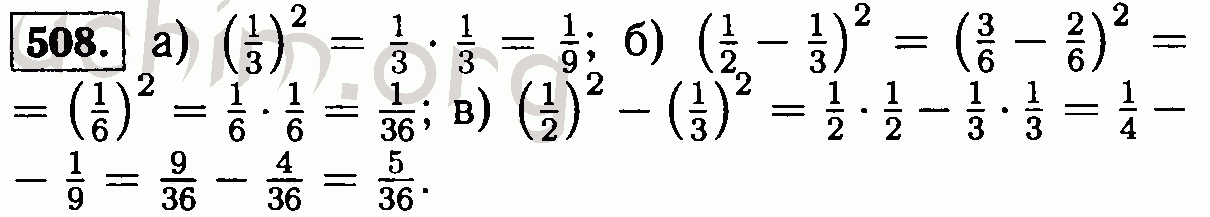 1 Увеличение объема и распад
1 Увеличение объема и распад 6 Мультивселенная
6 Мультивселенная 2 Дополнительные размеры
2 Дополнительные размеры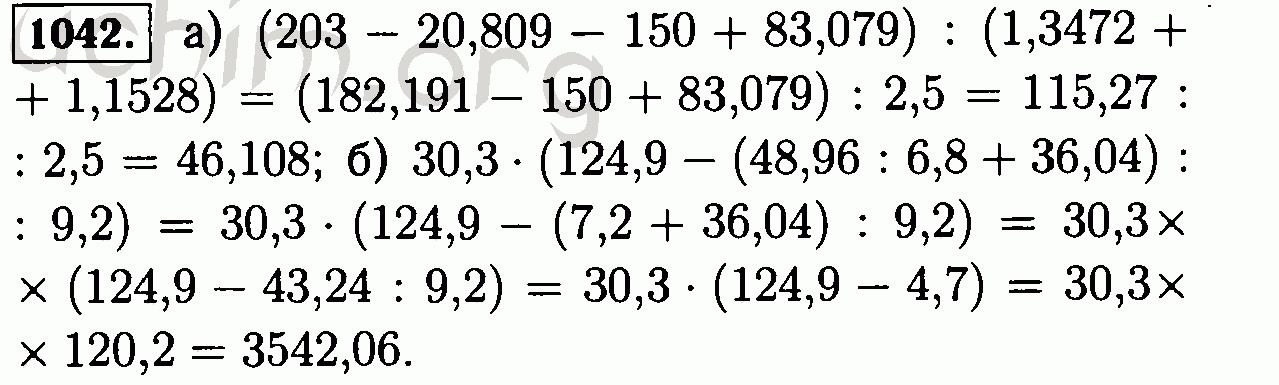 1.1 Нейтронная масса
1.1 Нейтронная масса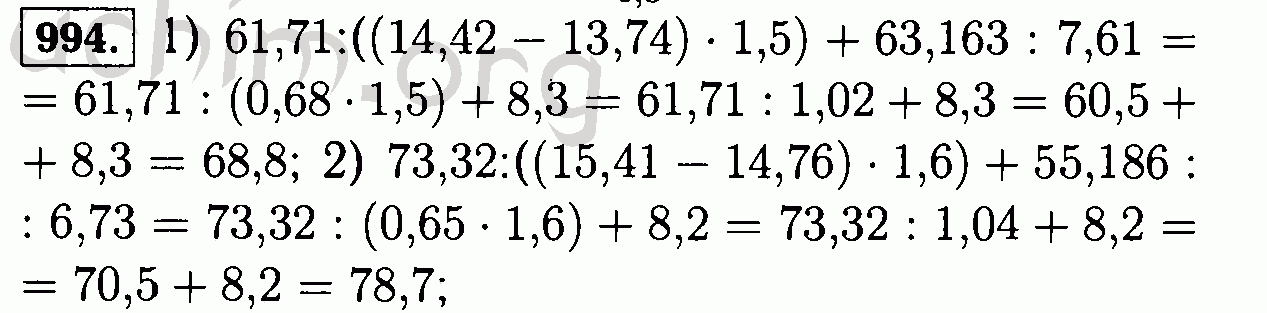 2.2 Настроен на жизнь?
2.2 Настроен на жизнь?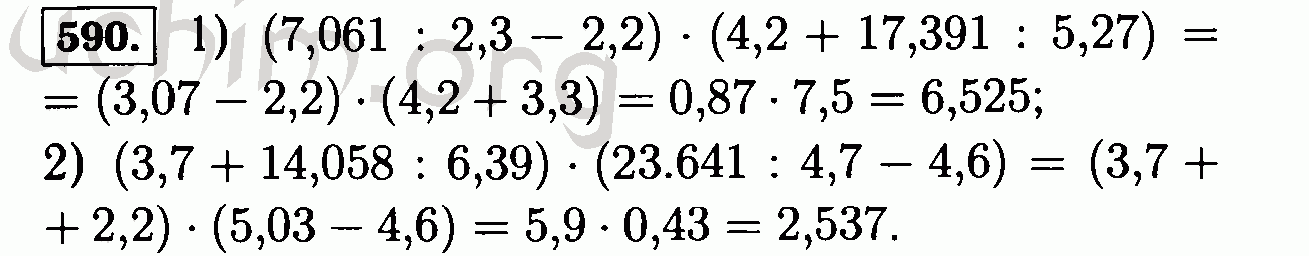 3 Получение распределения наблюдателями за подсчетом голосов
3 Получение распределения наблюдателями за подсчетом голосов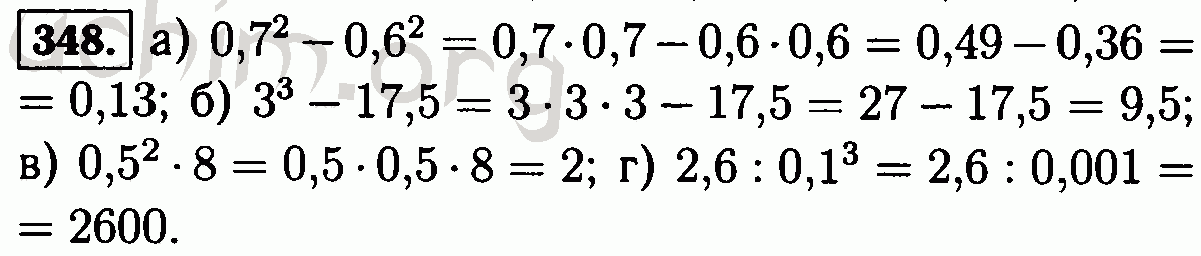 6 Аргумент Судного дня и будущее нашей цивилизации
6 Аргумент Судного дня и будущее нашей цивилизации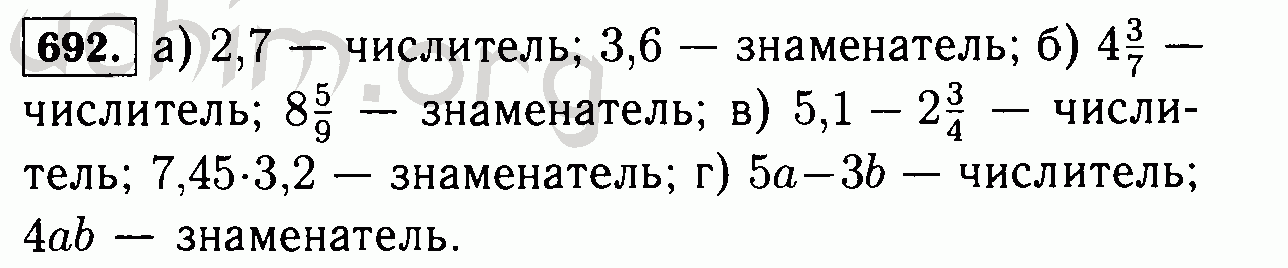 2 Теорема BGV
2 Теорема BGV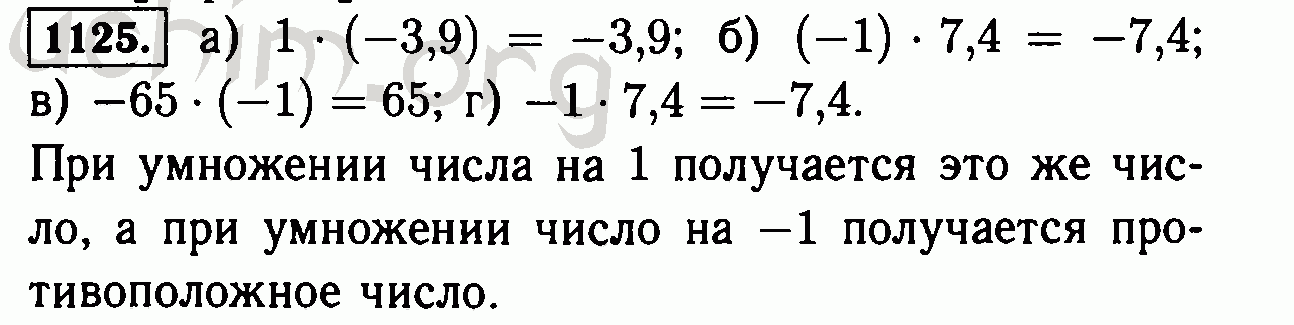 2.1 Евклидово время
2.1 Евклидово время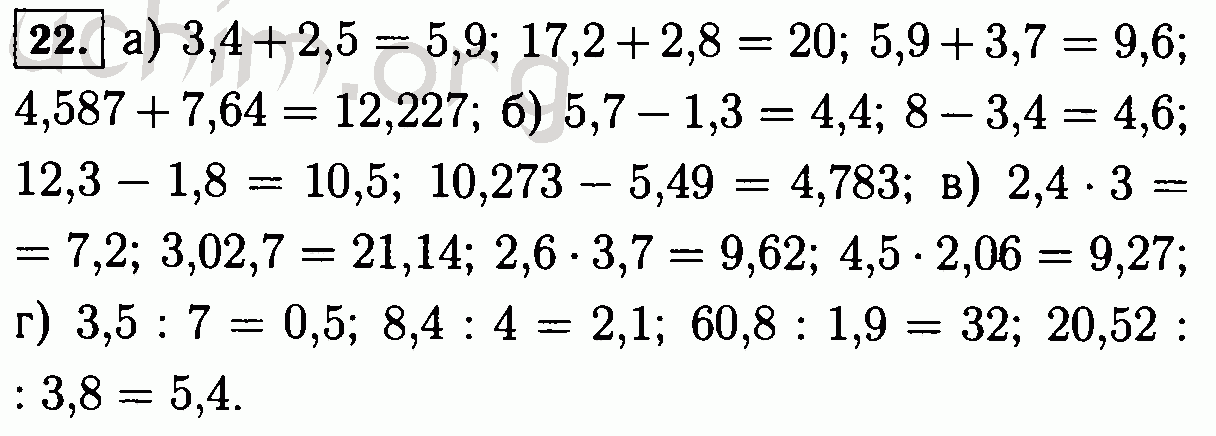 1.2 Космическая инфляция
1.2 Космическая инфляция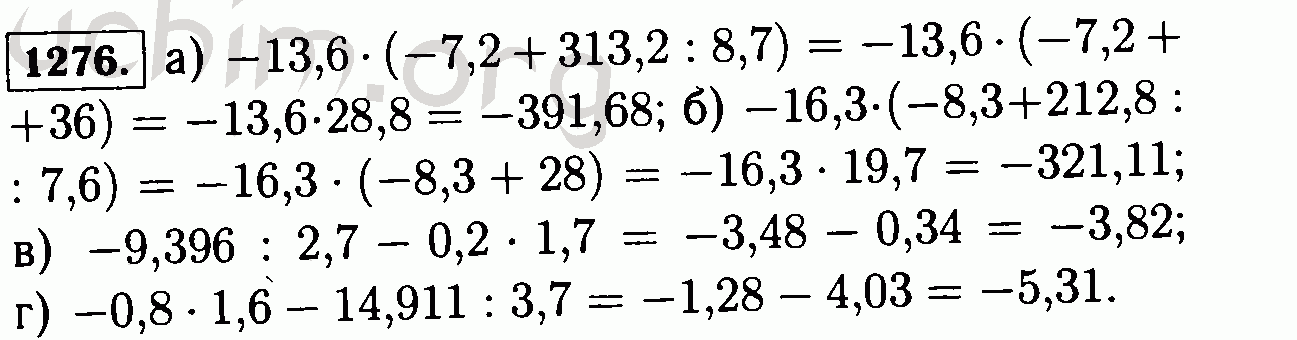 3 Ответы на «Большие вопросы»
3 Ответы на «Большие вопросы»