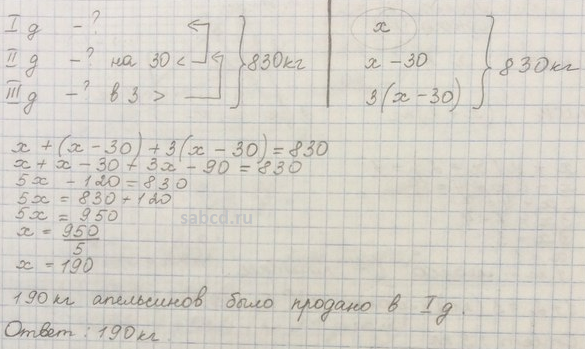Номер 301 — ГДЗ по Математике 6 класс Учебник Виленкин, Жохов, Чесноков, Шварцбурд 2020. Часть 2 (решебник)
Номер 301 — ГДЗ по Математике 6 класс Учебник Виленкин, Жохов, Чесноков, Шварцбурд 2020. Часть 2 (решебник) — GDZwowПерейти к содержанию
Search for:
Авторы: Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И.
Издательство: Мнемозина
Тип: Учебник
Новая версия
ЧАСТЬ 1
Выберите номер упражнения
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244245246247248249250251252253254255256257258259260261262263264265266267268269270271272273274275276277278279280281282283284285286287288289290291292293294295296297298299300301302303304305306307308309310311312313314315316317318319320321322323324325326327328329330331332333334335336337338339340341342343344345346347348349350351352353354355356357358359360361362363364365366367368369370371372373374375376377378379380381382383384385386387388389390391392393394395396397398399400401402403404405406407408409410411412413414415416417418419420421422423424425426427428429430431432433434435436437438439440441442443444445446447448449450451452453454455456457458459460461462463464465467468469470471472473474475476477478479480481482483484485486487488489490491492493494495496497498499500501502503504505506507508509510511512513514515516517518519520521522523524525526527528529530531532533534535536537538539540541542543544545546547548549550551552553554555556557558559560561562563564565566567568569570571572573574575576577578579580581582583584585586587588589590591592593594595596597598599600601602603604605606607608609610611612613614615616617618619620621622623624625626627628629630631632633634635636637638639640641642643644645646647648649650651652653654655656657658659660661662663664665666667668669670671672673674675676677678679680681682683684685686687688689690691692693694695696697698699700701702703704705706707708709710711712713714715716717718719720721722723724725726727728729730731732733734735736737738739740741742743744745746747748749750751753754755756757758759760761762763764765766767768769770771772773774775776777778779780781782783784785786787788789790791792793794795796797798799800801802803804805806807809810811812813814815816817818819820821822823824825826827828829830831832833834835836837838839840841842843844845846847848849850851852853854855856857858859860861862863864865866867868869870871872873874875876877878879880881882883884885886887888889890891892893894895896897
ЧАСТЬ 2
Выберите номер упражнения
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192939495969798991001011021031041051061071081091101111121131141151161171181191201211221231241251261271281291301311321331341351361371381391401411421431441451461471481491501511521531541551561571581591601611621631641651661671681691701711721731741751761771781791801811821831841851861871881891901911921931941951961971981992002012022032042052062072082092102112122132142152162172182192202212222232242252262272282292302312322332342352362372382392402412422432442452462472482492502512522532542552562572582592602612622632642652662672682692702712722732742752762772782792802812822832842852862872882892902912922932942952962972982993003013023033043053063073083093103113123133143153163173183193203213223233243253263273283293303313323333343353363373383393403413423433443453463473483493503513523533543553563573583593603613623633643653663673683693703713723733743753763773783793803813823833843853863873883893903913923933943953963973983994004014024034044054064074084094104114124134144154164174184194204214224234244254264274284294304314324334344354364374384394404414424434444454464474484494504514524534544554564574584594604614624634644654664674684694704714724734744754764774784794804814824834844854864874884894904914924934944954964974984995005015025035045055065075085095105115125135145155165175185195205215225235245255265275285295305315325335345355365375385395405415425435445455465475485495505515525535545555565575585595605615625635645655665675685695705715725735745755765775785795805815825835845855865875885895905915925935945955965975985996006016026036046056066076086096106116126136146156166176186196206216226236246256266276286296306316326336346356366376386396406416426436446456466476486496506516526536546556566576586596606616626636646656666676686696706716726736746756766776786796806816826836846856866876886896906916926936946956966976986997007017027037047057068928938948958968978988999009019029039049059069079089099109119129139149159169179189199209219229239249259269279289299309319329339349359369379389399409419429439449459469479489499509519529539549559569579589599609619629639649659669679689699709719729739749759769779789799809819829839849859869879889899909919929939949959969979989991000100110021003100410051006100710081009101010111012101310141015101610171018101910201021102210231024102510261027102810291030103110321033103410351036103710381039104010411042104310441045104610471048104910501051105210531054105510561057105810591060106110621063106410651066106710681069107010711072107310741075107610771078107910801081108210831084108510861087108810891090109110921093109410951096109710981099110011011102110311041105110611071108110911101111111211131114111511161117111811191120112111221123112411251126112711281129113011311132113311341135113611371138113911401141114211431144114511461147114811491150115111521153115411551156115711581159116011611162116311641165116611671168116911701171117211731174117511761177117811791180118111821183118411851186118711881189119011911192119311941195119611971198119912011202120312041205120612071208120912101211121212131214121512161217121812191220122112221223122412251226122712281229123012311232123312341235123612371238123912401241124212431244124512461247124812491250125112521253125412551256125712581259126012611262126312641265126612671268126912701271127212731274127512761277127812791280128112821283128412851286128712881289129012911292129312941295129612971298129913001301130213031304130513061307130813091310131113121313131413151316131713181319132013211322132313241325132613271328132913301331133213331334133513361337133813391340134113421343134413451346134713481349135013511352135313541355135613571358135913601361136213631364136513661367136813691370137113721373137413751376137713781379138013811382138313841385138613871388138913901391139213931394139513961397139813991400140114021403140414051406140714081409141014111412141314141415141614171418141914201421142214231424142514261427142814291430143114321433143414351436143714381439144014411442144314441445144614481449145014511452145314541455145614571458145914601461146214631464146514681469147014711472147314741475147614771478147914801481148214831484148514861487148814891490149114921493149414951496149714981499150015011502150315041505150615071508150915101511151215131514151515161517151815191520152115221523152415251526152715281529153015311532153315341535153615371538153915401541154215431544154515461547154815491550155115521553155415551556155715581559156015611562156315641565156615671568156915701571157215731574157515761577157815791580158115821583158415851586158715881589159015911592159315941595
Adblockdetector
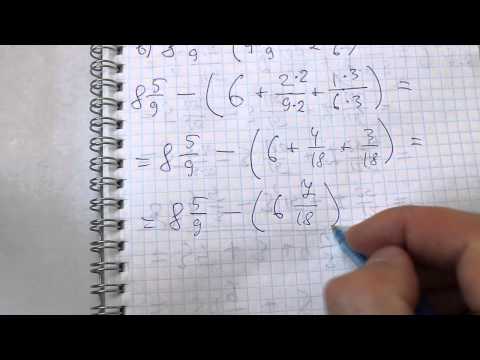
Ответы Задание 301 .
ГДЗ по математике 6 класс Виленкин Жохов Чесноков Шварцбурд учебник 12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091929394959697989910010110210310410510610710810911011111211311411511611711811912012112212312412512612712812913013113213313413513613713813914014114214314414514614714814915015115215315415515615715815916016116216316416516616716816917017117217317417517617717817918018118218318418518618718818919019119219319419519619719819920020120220320420520620720820921021121221321421521621721821922022122222322422522622722822923023123223323423523623723823924024124224324424524624724824925025125225325425525625725825926026126226326426526626726826927027127227327427527627727827928028128228328428528628728828929029129229329429529629729829930030130230330430530630730830931031131231331431531631731831932032132232332432532632732832933033133233333433533633733833934034134234334434534634734834935035135235335435535635735835936036136236336436536636736836937037137237337437537637737837938038138238338438538638738838939039139239339439539639739839940040140240340440540640740840941041141241341441541641741841942042142242342442542642742842943043143243343443543643743843944044144244344444544644744844945045145245345445545645745845946046146246346446546646746846947047147247347447547647747847948048148248348448548648748848949049149249349449549649749849950050150250350450550650750850951051151251351451551651751851952052152252352452552652752852953053153253353453553653753853954054154254354454554654754854955055155255355455555655755855956056156256356456556656756856957057157257357457557657757857958058158258358458558658758858959059159259359459559659759859960060160260360460560660760860961061161261361461561661761861962062162262362462562662762862963063163263363463563663763863964064164264364464564664764864965065165265365465565665765865966066166266366466566666766866967067167267367467567667767867968068168268368468568668768868969069169269369469569669769869970070170270370470570670770870971071171271371471571671771871972072172272372472572672772872973073173273373473573673773873974074174274374474574674774874975075175275375475575675775875976076176276376476576676776876977077177277377477577677777877978078178278378478578678778878979079179279379479579679779879980080180280380480580680780880981081181281381481581681781881982082182282382482582682782882983083183283383483583683783883984084184284384484584684784884985085185285385485585685785885986086186286386486586686786886987087187287387487587687787887988088188288388488588688788888989089189289389489589689789889990090190290390490590690790890991091191291391491591691791891992092192292392492592692792892993093193293393493593693793893994094194294394494594694794894995095195295395495595695795895996096196296396496596696796896997097197297397497597697797897998098198298398498598698798898999099199299399499599699799899910001001100210031004100510061007100810091010101110121013101410151016101710181019102010211022102310241025102610271028102910301031103210331034103510361037103810391040104110421043104410451046104710481049105010511052105310541055105610571058105910601061106210631064106510661067106810691070107110721073107410751076107710781079108010811082108310841085108610871088108910901091109210931094109510961097109810991100110111021103110411051106110711081109111011111112111311141115111611171118111911201121112211231124112511261127112811291130113111321133113411351136113711381139114011411142114311441145114611471148114911501151115211531154115511561157115811591160116111621163116411651166116711681169117011711172117311741175117611771178117911801181118211831184118511861187118811891190119111921193119411951196119711981199120012011202120312041205120612071208120912101211121212131214121512161217121812191220122112221223122412251226122712281229123012311232123312341235123612371238123912401241124212431244124512461247124812491250125112521253125412551256125712581259126012611262126312641265126612671268126912701271127212731274127512761277127812791280128112821283128412851286128712881289129012911292129312941295129612971298129913001301130213031304130513061307130813091310131113121313131413151316131713181319132013211322132313241325132613271328132913301331133213331334133513361337133813391340134113421343134413451346134713481349135013511352135313541355135613571358135913601361136213631364136513661367136813691370137113721373137413751376137713781379138013811382138313841385138613871388138913901391139213931394139513961397139813991400140114021403140414051406140714081409141014111412141314141415141614171418141914201421142214231424142514261427142814291430143114321433143414351436143714381439144014411442144314441445144614471448144914501451145214531454145514561457145814591460146114621463146414651466146714681469147014711472147314741475147614771478147914801481148214831484148514861487148814891490149114921493149414951496149714981499150015011502150315041505150615071508150915101511151215131514151515161517151815191520152115221523152415251526152715281529153015311532153315341535153615371538153915401541154215431544154515461547154815491550155115521553155415551556155715581559156015611562156315641565156615671568156915701571157215731574157515761577157815791580158115821583158415851586158715881589159015911592159315941595
[PDF] Теорема о сильной сходимости для средних значений Виленкина-Фейера
- title={Сильная теорема сходимости для средних Виленкина-Фейера},
автор={Иств{\’а}н Благота и Георгий Тефнадзе},
journal={arXiv: классический анализ и ОДУ},
год = {2014}
}
- И.
Благота, Г. Тефнадзе - Опубликовано 1 июля 2014 г.
- Математика
- arXiv: Классический анализ и ОДУ
В качестве основного результата мы доказываем теоремы о сильной сходимости средних Виленкина-Фейера при $0
Посмотреть PDF на arXiv Системы Виленкина
- Л. Перссон, Г. Тефнадзе, Г. Тутберидзе, П. Уолл
Математика
- 2020
по системе Виленкина.
Теорема о сильной сходимости средних Чезаро по системе Уолша }ro средние одномерных рядов Уолша-Фурье являются равномерно ограниченными операторами в мартингальном пространстве Харди $H_{p}$ при $% 0
Некоторые неравенства, связанные с сильной сходимостью логарифмических средних Рисса
- Д. Луккассен, Л. Перссон, Г. Тефнадзе, Г. Тутберидзе
Математика
- 2020
ряд (Уолша – Фурье). Указывается соответствующее неравенство и…
Результат о точной ограниченности некоторых максимальных операторов средних Виленкина–Фейера
- Л. Перссон, Г. Тефнадзе
Математика
- 2014
В этой статье мы выводим максимальное подпространство положительных чисел, для которого ограниченный максимальный оператор средних Фейера в этом подпространстве ограничен из пространства Харди Hp в пространство Lp для всех…
Ограничено последующих виленкин-Фейрских средств на Мартингейл Харди Пространства
- L. Persson, G. Tephnadze, G. Tutberidze
Математика
- 2020
. относительно систем Виленкина, ограниченных из пространства Харди $H_{p}$ в пространство Лебега $L_{p},$ для всех $0
О сходимости средних Фейера рядов Уолша-Фурье в пространстве Hp
Основная цель настоящей работы — найти необходимые и достаточные условия для модуля непрерывности мартингала F ∈ Hp, для которого средние Фейера Серия Walsh-Fourier Coverge в HP-Norm,…
на Nörlund Mades of Vilenkin-Fourier Series
- I. Blahota, L. Persson, G. Tephnadze
Mathematics
- 2015
We Arwe обсудим некоторые новые неравенства (Hp,Lp)-типа взвешенных максимальных операторов средних Виленкина-Нёрлунда с невозрастающими коэффициентами {qk: k ⩾ 0}. Эти результаты являются лучшими из возможных в…
О максимальных операторах Т-средних по системе Уолша–Качмарца
В этой статье мы доказываем и обсуждаем некоторые неравенства нового типа (Hp, Lp,∞) максимальных операторов Т-средних с монотонными коэффициентами по Уолшу – Качмарская система. Также доказано, что…
Точные неравенства типа Hp$H_{p}$-Lp$L_{p}$ взвешенных максимальных операторов средних Виленкина-Нёрлунда и их приложения
- Л. Барамидзе, Л. Перссон, Г. Тефнадзе, П. Стена
Математика
- 2016
Доказаны и обсуждены некоторые новые неравенства типа Hp$H_{p}$-Lp$L_{p}$ взвешенных максимальных операторов средних Виленкина-Нёрлунда с монотонными коэффициентами.
It is also proved that these inequalities are…SHOWING 1-10 OF 26 REFERENCES
SORT BYRelevanceMost Influenced PapersRecency
Strong convergence theorems for Walsh–Fejér means
- G. Tephnadze
Mathematics
- 2014
В качестве основного результата мы доказываем, что средние Фейера рядов Уолша–Фурье являются равномерно ограниченными операторами из Hp в Hp (0
Теорема сильной сходимости для рядов Виленкина–Фурье☆
- P. Simon Математика
- И.
- 2000
Благота, Г. Тефнадзе
Перссон, Г. Тефнадзе
Persson, G. Tephnadze
It is also proved that these inequalities are…Аннотация Будут рассмотрены так называемые системы Виленкина и пространства Харди H p (0 p ≤ 1) по отношению к группам Виленкина.Исследуются некоторые средние частичных сумм Виленкина–Фурье…
Средние Фейера ряда Виленкина-Фурье
- Г. Тефнадзе
Математика
- 2012
Ряд Виленкина-Фурье мартингала f не ограничен равномерно в пространстве L1/2.
МАКСИМАЛЬНЫЕ ОПЕРАТОРЫ СРЕДНИХ ФЕЙЕРА РЯДОВ ВИЛЕНКИНА-ФУРЬЕ
- И. Благота, Г. Гат, У. Гогинава
Математика
- 2006
Основная цель данной работы — доказать, что максимальный оператор σ∗ := sup n |σn| средних Фейера ряда Виленкина-Фурье не ограничена из пространства Харди h2/2 в пространство L1/2.
Теоремы сильной сходимости для двухпараметрических рядов Виленкина-Фурье -ряды Фурье — это равномерно ограниченные операторы из HP в Lp (0
< p ⩽ 1). Пространство Харди Hp (0 < p ⩽ 1) будет…О частных суммах рядов Виленкина-Фурье
- Г. Тефнадзе
Математика
- 2014
Также полученные результаты мы используем для доказательства теорем приближения и сильной сходимости…
ЗАМЕЧАНИЕ О КОЭФФИЦИЕНТАХ ФУРЬЕ И ЧАСТИЧНЫХ СУММАХ РЯДОВ ВИЛЕНКИНА-ФУРЬЕ
- Г. Тефнадзе
Математика
- 2014
Основной целью данной работы является исследование неравенств типа Пэли и Харди-Литтлвуда и сильной теоремы сходимости частных сумм рядов Виленкина-Фурье.
на максимальном операторе Walsh-Kaczmarz-Fejér означает
- U. Goginava, K. Nagy
Математика
- 2011
. среднего ряда Уолша-Качмарца-Фурье, ограничена из пространства Харди h2/2(G) в пространство L1/2(G). 9{\ast}f:=\underset{n\in\mathbb{N}}{% \sup}\frac{\left\vert \sigma_{n}f\right\vert…
Начало Вселенной нужна причина? – Необычный спуск
Большой взрыв Космология Умный дизайн Математика Философия Физика
Опубликовано Автор НовостиКомментарии(45)
Распространяйте любовь
Александр ВиленкинФилософский вопрос, который вас разбудит. Читатель обращает наше внимание на статью космолога Александра Виленкина 2015 года в Inference Review (2015):
ОТВЕТ на вопрос «Было ли у Вселенной начало?» то есть: «Вероятно, так и было». У нас нет жизнеспособных моделей вечной вселенной.
Теорема БГВ дает нам основания полагать, что такие модели просто невозможно построить. Более.Он предлагает теорему Борде-Гута-Виленкина (БГВ) в качестве доказательства:
Грубо говоря, наша теорема утверждает, что если Вселенная в среднем расширяется, то ее история не может бесконечно продолжаться в прошлом . Точнее, если средняя скорость расширения положительна вдоль данной мировой линии или геодезической, то эта геодезическая должна закончиться через конечное время. Разные геодезические, разные времена. Важным моментом является то, что прошлая история Вселенной не может быть полной.
К статье прилагается схема математического доказательства БГВ.
Виленкин продолжает утверждать, что
Современная физика может описать возникновение Вселенной как физический процесс, не требующий причины.
Он объясняет,
Если все сохраняющиеся числа замкнутой вселенной равны нулю, то ничто не мешает такой вселенной спонтанно возникнуть из ничего.
А согласно квантовой механике с некоторой вероятностью произойдет любой процесс, не запрещенный строго законами сохранения.
Новорожденная вселенная может иметь множество различных форм и размеров и может быть заполнена различными видами материи. Как обычно в квантовой теории, мы не можем сказать, какая из этих возможностей реализуется на самом деле, но можем рассчитать их вероятности. Это говорит о том, что может существовать множество других вселенных.
Он уступает,
Уильям Лейн КрейгТеория квантового творения — не более чем спекулятивная гипотеза. Неясно, как и можно ли это проверить наблюдательно. Тем не менее это первая попытка сформулировать проблему космического происхождения и решить ее количественным путем.
Апологет Уильям Лейн Крейг не согласен с аргументом (2017):
Допустим, что положительная энергия, связанная с материей, точно уравновешена отрицательной энергией, связанной с гравитацией, так что в итоге энергия равна нулю.
Ключевым ходом Виленкина является заявление о том, что в таком случае «ничто не мешает такой вселенной быть спонтанно созданной из ничего». Теперь это утверждение тривиально. Обязательно, если нет ничего, то нет ничего, что могло бы помешать возникновению Вселенной. Точно так же, если нет ничего, то нет ничего, что позволило бы Вселенной возникнуть. Если бы было что-то, что предотвратило бы или допустило бы возникновение вселенной, то было бы что-то, а не ничто. Если ничего нет, то нет ничего, и точка.
…
Виленкин, однако, делает вывод, что «никакая причина не нужна» для возникновения Вселенной, потому что законы сохранения не помешают этому и «согласно квантовой механике любой процесс, который строго не запрещен сработают законы сохранения». (Виленкин полагает, что если бы ничего не было, то и законы сохранения, и законы квантовой физики по-прежнему выполнялись бы. Однако это далеко не очевидно, так как при отсутствии вообще чего-либо неясно, чтобы законы, управляющие нашей Вселенной, были бы верны.
.) Но даже при условии, что законы все равно будут выполняться, почему мы должны думать, что с учетом законов квантовой механики произойдет что-то, что строго не запрещено законами сохранения? … законы сохранения строго не запрещают возникновение чего-либо, но они также не запрещают ничего не возникать, но и то, и другое не может произойти. Логически абсурдно думать, что если что-то не запрещено законами сохранения, то оно и произойдет.
Наконец, вывод Виленкина о том, что, поскольку положительная и отрицательная энергии во Вселенной в сумме равны нулю, следовательно, причина возникновения Вселенной не нужна, трудно принимать всерьез. Это все равно, что сказать, что если ваши долги уравновешивают ваши активы, то ваш собственный капитал равен нулю, и поэтому нет никакой причины вашего финансового положения! Более.
Вероятно, мы еще не слышали последний вопрос, но приятно видеть, что он обсуждается за пределами цирка с тремя аренами безумной космологии.