Сокращение дробей 6 класс самостоятельная работа: Самостоятельная работа по математике: «Сокращение дробей» 6 класс

Самостоятельная работа по математике: «Сокращение дробей» 6 класс

I Вариант	II Вариант
1. Сократите дроби: 2. Выполните действия, ответ представьте в виде несократимой дроби: 3. Приведите дробь: а) к знаменателю 8; б) к знаменателю 14; в) к знаменателю 84.	1. Сократите дроби: 2. Выполните действия, ответ представьте в виде несократимой дроби: 3. Приведите дробь: а) к знаменателю 12; б) к знаменателю 30; в) к знаменателю 93.

I Вариант

II Вариант

1.

Сократите дроби:

2. Выполните действия, ответ представьте в виде несократимой дроби:

3. Приведите дробь:

а) к знаменателю 8;

б) к знаменателю 14;

в) к знаменателю 84.

1. Сократите дроби:

2. Выполните действия, ответ представьте в виде несократимой дроби:

3. Приведите дробь:

а) к знаменателю 12;

б) к знаменателю 30;

в) к знаменателю 93.

I Вариант

II Вариант

1. Сократите дроби:

2. Выполните действия, ответ представьте в виде несократимой дроби:

3. Приведите дробь:

а) к знаменателю 8;

б) к знаменателю 14;

в) к знаменателю 84.

1. Сократите дроби:

2. Выполните действия, ответ представьте в виде несократимой дроби:

3. Приведите дробь:

а) к знаменателю 12;

б) к знаменателю 30;

в) к знаменателю 93.

Самостоятельная работа по математике Сокращение дробей 6 класс

Самостоятельная работа по математике Сокращение дробей 6 класс с ответами. Самостоятельная работа включает 2 варианта, в каждом по 6 заданий.

Вариант 1

1. Сократите дроби:

³/₆; ⁸/₁₆; ⁸/₁₂; ⁴²ⁿ/_49n.

2. Представьте числа в виде обыкновенной несократимой дроби:

а) 0,36
б) 0,7
в) 0,625

3. Андрей красит за 2 часа 7 м² забора, а Иван 15 м² забо­ра за 6 ч. Кто из них красит 1 м² забора быстрее и на сколь­ко?

4. Выполните действия:

3²/₈ − ¹⁴/₈ + ¹⁶/₈.

5. Сократите дробь

¹⁵⁵⁴/₃₄₆₅

6. Сколько трехзначных чисел можно составить из чет­ных цифр, если цифры в записи числа не повторяются?

Вариант 2

1. Сократите дроби:

⁴/₈; ⁶/₈; ⁷/₁₄; ²²ⁿ/_33n.

2. Представьте числа в виде обыкновенной несократимой дроби:

а) 0,24
б) 0,3
в) 0,875

3. Маша выпекает 6 пирожных за час, а Аня — 12 пирожных за 3 часа. Кто из них выпекает 1 пирожное быстрее и насколько?

4. Выполните действия:

4²/₆ − ¹³/₆ − ⁴/₆

5. Сократите дробь

¹⁸⁸⁷/₂₆₆₄

6. Сколько трехзначных чисел можно составить из не­четных цифр, если цифры в записи числа не повторяются?

Ответы на самостоятельную работу по математике Сокращение дробей 6 класс
Вариант 1
1. ¹/₂; ¹/₂; ²/₃; ⁶/₇
2.
а) ⁹/₂₅
б) ⁷/₁₀
в) ⁵/₈
3. Андрей, на ⁴/₃₅ часа
4. 3¹/₂
5. ⁷⁴/₁₆₅
6. 48
Вариант 2

1. ¹/₂; ³/₄; ¹/₂; ²/₃
2.
а) ⁶/₂₅
б) ³/₁₀
в) ⁷/₈
3. Маша, на ¹/₁₂ часа
4. ³/₂
5. ¹⁷/₂₄
6. 60

6 класс. Самостоятельная работа «Сокращение дробей» | Учебно-методический материал по математике (6 класс) по теме:

6 класс         Самостоятельная работа  «Сокращение дробей» Вариант – 1 № 1 Закончите предложение и запишите его: «Чтобы сократить дробь, нужно разделить ___________». № 2 Сократите дроби:     № 3 Напишите 2 несократимые дроби. № 4 Представьте в виде обыкновенной несократимой дроби: 0,25; 0,324 № 5 Какую часть минуты составляют 20 секунд, 33 секунды. Ответ запишите в виде несократимой обыкновенной дроби.

6 класс         Самостоятельная работа  «Сокращение дробей» Вариант – 1 № 1 Закончите предложение и запишите его: «Чтобы сократить дробь, нужно разделить ___________». № 2 Сократите дроби:     № 3 Напишите 2 несократимые дроби. № 4 Представьте в виде обыкновенной несократимой дроби: 0,25; 0,324 № 5 Какую часть минуты составляют 20 секунд, 33 секунды. Ответ запишите в виде несократимой обыкновенной дроби.

6 класс         Самостоятельная работа  «Сокращение дробей» Вариант – 2 № 1 Закончите предложение и запишите его: «Чтобы сократить дробь, нужно разделить ___________». № 2 Сократите дроби:     № 3 Напишите 2 несократимые дроби. № 4 Представьте в виде обыкновенной несократимой дроби: 0,34; 0,268. № 5 Какую часть часа составляют 45 минут, 55 минут. Ответ запишите в виде несократимой обыкновенной дроби.

6 класс         Самостоятельная работа  «Сокращение дробей» Вариант – 2 № 1 Закончите предложение и запишите его: «Чтобы сократить дробь, нужно разделить ___________». № 2 Сократите дроби:     № 3 Напишите 2 несократимые дроби. № 4 Представьте в виде обыкновенной несократимой дроби: 0,34; 0,268. № 5 Какую часть часа составляют 45 минут, 55 минут. Ответ запишите в виде несократимой обыкновенной дроби.

Математика 6 Виленкин Контрольная 2 + ОТВЕТЫ

Контрольная работа по математике 6 класс Виленкин с ответами «Основное свойство дроби. Сокращение дробей» (4 варианта). Цитаты из пособия «Дидактические материалы по математике 6 класс к учебнику Н. Я. Виленкина и др. «Математика 6 класс» ФГОС (к новому учебнику) / М.А. Попов — М.: Издательство «Экзамен», 2017» использованы в учебных целях. Математика 6 Виленкин Контрольная 2. Проверочные работы ориентированы на школьный учебник Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд «Математика 6 класс». Ответы на контрольные работы адресованы родителям, которые смогут проконтролировать правильность выполнения задания.

Математика 6 класс (Виленкин)

Контрольная работа № 2

Основное свойство дроби. Сокращение дробей. Приведение дробей к общему знаменателю. Сравнение, сложение и вычитание дробей с разными знаменателями. Сложение и вычитание смешанных чисел

КР-01. Вариант 1 (транскрипт)

1. Сократите дроби: 2/4; 5/15; 6/10 8n/14n.
2. Приведите к наименьшему общему знаменателю дроби: 2/7 и 5/8.
3. Сравните дроби: а) 5/7 и 2/3; б) 3/11 и 2/9.
4. Найдите значение выражения:
5. Решите уравнение:
6. Сколькими способами могут разместиться 3 пассажира в 6-местной лодке?

КР-01.

Вариант 2 (транскрипт)

1. Сократите дроби: 3/6; 4/12; 5/20; 6n/18n.
2. Приведите к наименьшему общему знаменателю дроби: 4/9 и 5/12.
3. Сравните дроби: а) 2/11 и 3/14; б) 1/15 и 2/29.
4. Найдите значение выражения:
5. Решите уравнение:
6. Сколькими способами могут разместиться 4 пассажира в 6-местной лодке?

 

ОТВЕТЫ на контрольную работу

 

---

Вы смотрели: Контрольная работа по математике 6 класс Виленкин (2 варианта) «Основное свойство дроби. Сокращение дробей» с ответами (4 варианта). Цитаты из пособия «Дидактические материалы по математике 6 класс к учебнику Н.Я. Виленкина и др. «Математика 6 класс» (к новому учебнику) / М.А. Попов — М.: Издательство «Экзамен», 2017» использованы в учебных целях. Математика 6 Виленкин Контрольная 2. Проверочные работы ориентированы на школьный учебник Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд «Математика 6 класс».

Вернуться к Списку контрольных работ по математике в 6 классе по УМК Виленкин и др.

 

Самостоятельная работа №1 по теме «Сокращение дробей», ФГОС, УМК А. Г. Мерзляка

Самостоятельная работа№1 по теме: Сокращение дробей 8 класс
Вариант 1 1) 2) 5)	Вариант 2 1) 2) 3) 4) 5)
Самостоятельная работа№1 по теме: Сокращение дробей 8 класс
Вариант 1 1) 2) 5)	Вариант 2 1) 2) 3) 4) 5)
Самостоятельная работа№1 по теме: Сокращение дробей 8 класс
Вариант 1 1) 2) 5)	Вариант 2 1) 2) 3) 4) 5)
Самостоятельная работа№1 по теме: Сокращение дробей 8 класс
Вариант 1 1) 2) 5)	Вариант 2 1) 2) 3) 4) 5)
Самостоятельная работа№1 по теме: Сокращение дробей 8 класс
Вариант 1 1) 2) 5)	Вариант 2 1) 2) 3) 4) 5)
Самостоятельная работа№1 по теме: Сокращение дробей 8 класс
Вариант 1 1) 2) 5)	Вариант 2 1) 2) 3) 4) 5)
Самостоятельная работа№1 по теме: Сокращение дробей 8 класс
Вариант 1 1) 2) 5)	Вариант 2 1) 2) 3) 4) 5)
Самостоятельная работа№1 по теме: Сокращение дробей 8 класс
Вариант 1 1) 2) 5)	Вариант 2 1) 2) 3) 4) 5)
Самостоятельная работа№1 по теме: Сокращение дробей 8 класс
Вариант 1 1) 2) 5)	Вариант 2 1) 2) 3) 4) 5)
Самостоятельная работа№1 по теме: Сокращение дробей 8 класс
Вариант 1 1) 2) 5)	Вариант 2 1) 2) 3) 4) 5)
Самостоятельная работа№1 по теме: Сокращение дробей 8 класс
Вариант 1 1) 2) 5)	Вариант 2 1) 2) 3) 4) 5)
Самостоятельная работа№1 по теме: Сокращение дробей 8 класс
Вариант 1 1) 2) 5)	Вариант 2 1) 2) 3) 4) 5)

«Основное свойство дроби.

Сокращение дробей»

16.09.2020г.

Классная работа

Основное свойство дроби.

Сокращение дробей

1. Что значит сократить дробь?

– Сократим дробь

– Сократите дроби:

2. Как привести дробь к новому знаменателю?

– Приведём дробь к знаменателю 28.

– Приведите дроби к знаменателю 60.

3. Каким свойством мы воспользовались при сокращении дробей и приведении дробей к новому знаменателю? Сформулируйте основное свойство дроби.

ОСНОВНОЕ СВОЙСТВО ДРОБИ

Если числитель и знаменатель рациональной дроби умножить на один и тот же ненулевой многочлен, то получится равная ей дробь.

д в а т и п а з а д а н и й, при выполнении которых применяется основное свойство дроби :

– приведение дробей к новому знаменателю;

– сокращение дробей.

Упражнения

1. Умножьте числитель и знаменатель дроби на указанное число.

а) на 5; б) на 2; в) на 6.

Упражнения

2. Разделите числитель и знаменатель дроби на указанное число:

а) на 2; б) на 3; в) на 5.

Упражнения

3. Заполните пустые места так, чтобы равенство было верным:

4) ; 5) ; 6) .

Устно

– Сократите дробь:

а) ; б) ; в) ; г) ;

д) ; е) ; ж) ; з) .

Способы разложения многочлена на множители:

• Вынесение общего множителя за скобки:

 

2) Способ группировки:

=

3) Применение формул сокращенного умножения:

=(=

=

Разложите на множители многочлен:

а) х 2 у – 2 х ; д) х 2 + 6 х + 9;

б) 3 a 2 b

– 9 ab 2 ; е) а 2 – 10 а + 25;

в) т 2 – 4 п ; ж) ax + bx + ay + by .

г) а 3 – а ; з) ab – b + 3 a – 3.

Тождеством называется равенство, верное при всех допустимых значениях входящих в него переменных.

Если изменить знак числителя (или знак знаменателя) дроби и знак перед дробью, то получим выражение, тождественно равное данному.

Работа в классе:

№ 23,

№ 25 (а, в, д),

№ 26,

№ 28 (а, б).

№ 47.

Домашнее задание:

п.2! + РЭШ

№ 24,

№ 25 (б, г, е),

№ 28

Упражнения

1. № 29, № 30 (а, в, д), № 32 (а, в).

2. № 31(а, б), № 34.

3. № 35 (а, в).

4. № 36 (а)*.

Р е ш е н и е

№ 23

Р е ш е н и е

№ 25(а, в, д)

№ 26

а)

в)

б)

г)

Р е ш е н и е

№ 28 (а, б).

№ 47.

Сокращение дробей

Устно

– Сократите дробь:

а) ; б) ; в) ; г) ;

д) ; е) ; ж) ; з) .

Способы разложения многочлена на множители:

• Вынесение общего множителя за скобки:

 

2) Способ группировки:

=

3) Применение формул сокращенного умножения:

=(=

=

З а д а н и я и в о п р о с ы :

Разложите на множители многочлен:

а) х 2 у – 2 х ; д) х 2 + 6 х + 9;

б) 3 a 2 b – 9 ab 2 ; е) а 2 – 10 а + 25;

в) т 2 – 4 п ; ж) ax + bx + ay + by .

г) а 3 – а ; з) ab – b + 3 a – 3.

в ы в о д: чтобы сократить рациональную дробь, нужно сначала разложить на множители её числитель и знаменатель.

Упражнения

1. № 29, № 30 (а, в, д), № 32 (а, в).

2. № 31(а, б), № 34.

3. № 35 (а, в).

4. № 36 (а)*.

Решение

№ 29

Решение

№ 30 (а, в, д)

Решение

№ 32 (а, в)

Решение

№ 31 (а, б)

Решение

№ 34

Решение

№ 35 (а, в)

а)

в)

Решение

№ 36 (а)*.

Областью определения этой функции является множество всех чисел, кроме х = –5. Сократим дробь, задающую функцию:

Графиком функции является прямая, а графиком функции –та же прямая, но с «выколотой» точкой (–5;–5).

Тождеством называется равенство, верное при всех допустимых значениях входящих в него переменных.

Если изменить знак числителя (или знак знаменателя) дроби и знак перед дробью, то получим выражение, тождественно равное данному.

Самостоятельная работа

Вариант 1

1. В чём состоит основное свойство дроби?

2. Что нужно сделать, чтобы сократить рациональную дробь?

3. Формулы: квадрат разности двух выражений;

сумма кубов двух выражений.

Сократить дробь:

4. 5.

Вариант 2

1. Когда применяется основное свойство дроби?

2. Что нужно сделать, чтобы сократить рациональную дробь?

3. Формулы: разность квадратов двух выражений;

куб суммы двух выражений.

Сократить дробь:

4. 5.

В о п р о с ы:

– В чём состоит основное свойство рациональной дроби?

– Что такое тождество?

– Когда применяется основное свойство дроби?

Задание на самоподготовку:

№ 24, № 25 (б, г, е)

№ 30 (б, г, е), № 32 (б, г), № 33.

Литература и Интернет–ресурсы :

• Алгебpа. 8 класс. Учебник. ФГОС. Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова. Под ред. С.А.Теляковского. 2013г.
• Алгебра, 8 класс, Поурочные планы, Дюмина Т. Ю., Махонина А.А., 2012: CD;
• http://www.arms-expo.ru/049049052052124049051054055.html
• http://s4.goodfon.ru/wallpaper/previews-middle/219776.jp

Математика 6 класс Виленкин К-02

Контрольная работа по математике в 6 классе с ответами «Основное свойство дроби. Сокращение дробей» по УМК Виленкин и др. (4 варианта). Цитаты из пособия «Дидактические материалы по математике 6 класс к учебнику Н.Я. Виленкина и др. «Математика 6 класс» ФГОС / М.А. Попов — М.: Издательство Экзамен» использованы в учебных целях. Проверочные работы ориентированы на школьный учебник Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. Математика 6 класс Виленкин К-02. Ответы на контрольные работы адресованы родителям, которые смогут проконтролировать правильность выполнения задания.

 

Математика 6 класс (УМК Виленкин)

Контрольная работа № 2 (4 варианта)

Тема контрольной: Основное свойство дроби. Сокращение дробей. Приведение дробей к общему знаменателю. Сравнение, сложение и вычитание дробей с разными знаменателями. Сложение и вычитание смешанных чисел.

К-02. Вариант 1

1. Сократите дроби: 2/4; 5/15; 6/10; 8n/14n.
2. Приведите к наименьшему общему знаменателю дроби: 2/7 и 5/8.
3. Сравните дроби: а) 5/7 и 2/3; б) 3/11 и 2/9.
4. Найдите значение выражения: (2 ³/₅ – 1 ⁷/₁₀) + (1 ¹/₂ — 7/20)..
5. Решите уравнение: х + 2 ¹/₃ +3 ¹/₉ — 1 ¹/₁₂ = 5 ⁷/₁₂.
6. Сколькими способами могут разместиться 3 пассажира в 6-местной лодке?

К-02. Вариант 2

1. Сократите дроби: 3/6; 4/12; 5/20; 6n/18n.
2. Приведите к наименьшему общему знаменателю дроби: 4/9 и 5/12.
3. Сравните дроби: а) 2/11 и 3/14; б) 1/15 и 2/29.
4. Найдите значение выражения (3 ¹/₇ – 2 ³/₁₄) + (2 ³/₄₂ – 1 ¹/₇).
5. Решите уравнение: 3 ¹/₅ + 2 ²/₅ —х = 3 ¹/₁₀ — 1 ¹/₅.
6. Сколькими способами могут разместиться 4 пассажира в 6-местной лодке?

К-02. Вариант 3

1. Сократите дроби: 14/21; 13/39; 24/36; 27n/51n.
2. Приведите к наименьшему общему знаменателю дроби 3/14 и 5/21.
3. Сравните дроби: а) 3/8 и 2/5; б) 4/13 и 2/7.
4. Найдите значение выражения: (4 ²/₇ – 3 ¹/₁₄) + (1 ¹/₂₈ – ³/₁₄).
5. Решите уравнение: 3 ²/₅ – х – 1 ¹/₄ = 1 ¹/₁₂.
6. Сколькими способами могут разместиться 3 пассажира в 5-местной лодке?

К-02. Вариант 4

1. Сократите дроби: 3/18; 4/16; 18/54; 13n/52n.
2. Приведите к наименьшему общему знаменателю дроби 5/11 и 1/6.
3. Сравните дроби: а) 3/7 и 1/3; б) 4/19 и 2/11.
4. Найдите значение выражения: (5 ¹/₈ – 2 ¹/₄) + (3 ⁷/₁₆ – ⁹/₈).
5. Решите уравнение: х + 2 ⁶/₁₃ – 1 ¹/₃₉ = 2 ³/₁₃ + 3 ²/₁₃.
6. Сколькими способами могут разместиться 4 пассажира в 5-местной лодке?

 

ОТВЕТЫ на контрольную работу № 2.

 

---

Вы смотрели: Контрольная работа по математике в 6 классе с ответами «Основное свойство дроби. Сокращение дробей. Приведение дробей к общему знаменателю. Сравнение, сложение и вычитание дробей с разными знаменателями. Сложение и вычитание смешанных чисел» (4 варианта). Проверочные работы ориентированы на школьный учебник Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. Математика 6 класс Виленкин К-02. Ответы на контрольные работы адресованы родителям, которые смогут проконтролировать правильность выполнения задания.

Вернуться к Списку контрольных работ по математике в 6 классе (УМК Виленкин и др.)

 

Поиск эквивалентных дробей и простейшая форма

Демонстрация

Просмотрите словарный запас и то, что учащиеся знают об эквивалентных дробях. Покажите модели эквивалентных дробей и объясните, что, хотя числители и знаменатели в дробях различаются, дроби представляют собой одно и то же количество, что означает, что они эквивалентны.

Используйте модели, чтобы показать дроби 1/2 и 2/4, или нарисуйте их для учащихся. Попросите учащихся указать, что они знают о дробях.Приведите их к выводу, что на чертеже 2/4 фигур вдвое больше, чем на чертеже 1/2, но они представляют такое же количество.

Проверьте, что числа, умноженные на единицу, равны одному и тому же числу. Попросите студентов привести несколько примеров единицы в виде дроби, например: 3/3, 4/4, 2/2. Напишите 1/2 x 2/2 = 2/4 и покажите, что числитель и знаменатель удвоены, чтобы показать новую дробь.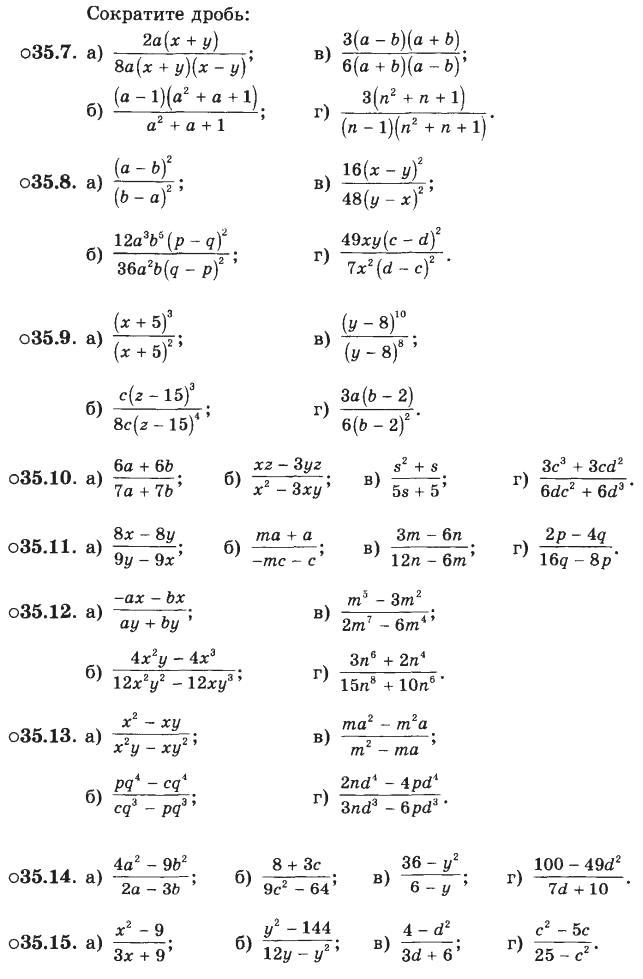 Объясните, что это еще один способ найти эквивалентные дроби.

Умножьте числитель и знаменатель на то же число, чтобы найти эквивалентную дробь.Или разделите числитель и знаменатель на одно и то же число. Важно записывать дроби как «сложенные», а не рядом. Это поможет ученикам при умножении и делении.

Покажите несколько примеров:

3/12 x 4/4 = 12/48
3/12 (знак деления) 3/3 = 1/4
Все эти дроби эквивалентны, потому что они называют одно и то же количество: 1 / 4

После нескольких примеров предложите учащимся придумать правило для этого принципа. Они должны быть в состоянии сказать вам, что если вы умножите или разделите числитель и знаменатель на одно и то же число, новая дробь будет эквивалентна исходной дроби.Единственный раз, когда это не сработает, — это если ученики умножат на ноль.

Объясните, что иногда дроби нужно переименовывать, чтобы с ними было легче работать. Подчеркните, что дроби будут по-прежнему равны или эквивалентны, но числитель и знаменатель будут отличаться от исходной дроби.

Чтобы упростить дроби, найдите общий множитель, который равномерно разделит числитель и знаменатель. Например, покажите студентам эту дробь: 12/18

Найдите множители числителя и знаменателя.Множители 12 равны 2, 3, 4 и 6. Множители 18 равны 2, 3, 6 и 9. Общие делители — 2, 3 и 6.

Чтобы упростить дробь, разделите на 6, поскольку 6 — наибольший общий множитель. Покажите учащимся, как делить дробь: 12/18 (знак деления) 6/6 = 2/3

Объясните, что дробь имеет простейшую форму, если 1 является единственным общим делителем числителя и знаменателя. Попросите учащихся определить, является ли эта дробь самой простой формой.
2/3 — это простейшая форма 12/18.

Чтобы уменьшить дробь до наименьшего значения, объясните, что учащиеся могут делить на любой общий множитель, и продолжать до тех пор, пока он не станет наименьшим числом, или они могут разделить на наибольший общий множитель. Например, ученики могут разделить дробь 12/18 на 2/2, а затем разделить на 3/3, чтобы показать дробь в простейшей форме. Или студенты могут разделить 12/18 на 6/6 и показать дробь 2/3 за один шаг.

Обсудите значение слова эквивалент и что делает дроби эквивалентными.Попросите студентов написать в своих дневниках, как они могут найти эквивалентные дроби. Попросите их ответить на вопрос: как узнать, что у вас есть дробь в простейшей форме?

Что ДЕЙСТВИТЕЛЬНО означает упрощение дроби?

Обучение дробей учащимся иногда может быть затруднено, особенно когда учитель полагается на то, как его или ее учили дробям. Я помню, когда я был в школе, мой учитель называл упрощение дробью сокращением. Когда я понял, что так сильно люблю математику, я решил перестать преподавать математику и естественные науки в 5-м классе и войти в мир математики в средней школе.К тому времени, когда я начал преподавать в средней школе, слова, сокращающие дроби, были исключены из списка слов математической лексики и заменены на упрощающие дроби. Сначала я был сбит с толку, почему уменьшающие дроби были заменены упрощающими дробями. Итак, я решил копнуть немного глубже и найти слово «упрощать». Определение «упрощать» означает «сделать менее сложным или сложным»; сделать проще или проще. Я начал задаваться вопросом, как это определение применимо к обучению дробям.

3/9 не в простейшей форме

Я понял, что при работе с дробями знаменатель всегда находится в центре внимания.То же самое верно и при применении слова «упростить» к дроби. На рисунке дробь 3/9 состоит из 9 частей и представлена ​​не в простейшей форме, потому что есть 9 отдельных частей, составляющих часть дроби. В мире дробей дробь, состоящая из нескольких частей, более сложна или сложна.

3/9 эквивалентно 1/3

Чтобы сделать дробь менее сложной или сложной, ученик должен уметь разделить девять частей на равные группы, сохраняя числитель вместе в группе или нескольких группах.Также каждая группа должна иметь наибольшее количество цветных плиток, которые подходят для каждой группы, чтобы фракция не могла быть снова разделена поровну. Когда фракция 3/9 сгруппирована, создается эквивалентная дробь. Дробь 1/3 имеет простейшую форму, потому что дробь начиналась с 9 отдельных частей и теперь состоит из 3 групп.

Разложение на дроби и эквивалентные дроби

Общие основные стандарты сделали упрощение дробей математическим стандартом 4-го класса. Изучая этот стандарт, я понял, что мои ученики должны понимать, что дробь можно разложить на единицы, составляющие целую дробь.Постигнув понимание разложения, они узнали, что единицу дроби можно разделить, чтобы получить эквивалентную дробь, однако было понятно, что если они собирались разделить одну единицу, все единицы должны быть разделены, потому что все единицы были связаны. . Пока я вел этот урок, один из моих учеников понял, что когда вы делите единицы, это похоже на умножение. Я был так взволнован, что она смогла установить связь между умножением и делением каждой единицы, потому что это облегчило мне обучение студентов, как создать эквивалентную дробь посредством умножения.

Когда в 2007 году я учил своих шестиклассников тому, как упрощать дроби с помощью цветных плиток, я понятия не имел, что 5 лет спустя я буду обучать своих учеников четвертого класса той же концепции. Этот опыт заставил меня поверить в то, что если студенты понимают значение слова «упрощение» применительно к дробям, то любой студент, имеющий надлежащие основы работы с дробями, может с легкостью упростить дроби. Если вы хотите попробовать упростить дроби с помощью цветных плиток, вы можете получить план урока уже сегодня!

Задания по математике

Дополнение

На этой странице указателя вы найдете ссылки на все типы рабочих листов для сложения, включая основные факты, двухзначные дополнения, трехзначные дополнения, четырехзначные дополнения, сложение дробей, десятичное сложение, семейства фактов и денежное добавление. .

Дополнение: основные факты

Рабочие листы с основными однозначными фактами сложения (суммы до 18).

Дополнение: 3-значные добавления

Попрактикуйтесь в сложении 3-значных чисел вместе с этими печатными листами, карточками задач и играми.

Сложение: 4- и 5-значные слагаемые

Предложите своим ученикам решить задачи на сложение с 4- и 5-значными числами.

Сложение: 3 или более слагаемых

Проблемы с добавлением столбца с 3 или более слагаемыми 1, 2, 3 и 4-значными числами.

Комбинация сложения и вычитания: базовая

Рабочие листы, карточки и числовые строки на этой странице содержат сочетание основных задач сложения и вычитания однозначных чисел.

Сложение: Дроби

Сложите дроби и смешанные числа с одинаковыми знаменателями, а также с разными знаменателями.

Свойства сложения

Эти рабочие листы были созданы для обучения студентов коммутативным и ассоциативным свойствам сложения.

Квадраты сложения

Развивайте навыки логического мышления с помощью этих листов для головоломок сложения квадратов.

Семейства фактов сложения-вычитания

Треугольники семейства основных фактов, числовые связи и таблицы фактов для сложения и вычитания.

Дополнение: игра на сумму (базовое дополнение)

На этих печатных игровых досках учащиеся раскрашивают пары чисел, которые равны заданной сумме.

Алгебра и предварительная алгебра

Напишите алгебраические выражения, научитесь определять независимые / зависимые переменные, находить переменные в уравнениях, работать с неравенствами и т. Д.

Углы: типы и измерение

Использование транспортира для измерения прямых, острых и тупых углов.

Углы: дополнительные, дополнительные, вертикальные

Загрузите рабочие листы, чтобы попрактиковаться в геометрических концепциях, связанных с вертикальными, дополнительными и дополнительными углами.

Площадь треугольников

Используйте формулу A = 1/2 x (b x h) для вычисления площади треугольников

Рабочие листы с площадью

Вычислите площадь (в квадратных единицах) фигур на этих листах.

Ящичковые диаграммы (диаграммы «ящик и усы»)

Используйте эти рабочие листы, чтобы помочь студентам узнать о статистике и построении диаграмм с ячейками и усами. Существуют также рабочие листы по вычислению Q1, Q3, медианы, минимального и максимального значений.

Календари (математика)

Календари, чтобы помочь студентам с годами, месяцами, неделями и днями в календаре.

Рабочие листы вместимости

Рабочие листы объема или вместимости (галлоны, кварты, пинты и чашки).

Круги: радиус, диаметр, окружность

Вычислить диаметр и радиус окружности; также включает рабочие листы окружности и площади.

Рабочие листы для раскраски по номерам

Раскрасьте загадочные картинки в соответствии с цифровой клавишей внизу.

Подсчет денег (австралийский)

Используйте эти рабочие листы, чтобы попрактиковаться в подсчете австралийских денег.

Подсчет денег (канадский)

Подсчитайте мультяшек, психов, четвертаков, пятак и десятицентовиков с помощью этих рабочих листов канадской валюты.

Подсчет денег (британские фунты)

Научитесь считать фунты и пенсы, монеты, используемые в Соединенном Королевстве.

Подсчет денег (США)

Потренируйтесь считать американские деньги (пенни, пятак, десять центов и четвертаки).

Рабочие листы подсчета 0–30 (очень простой)

Научитесь считать и записывать числа до 30.

Рабочие листы счета (более продвинутый уровень)

Научитесь точно считать двух, трех и четырехзначные числа. Заполните числовые строки, скажите, какое число идет раньше, и пропустите счет.

Daily Math Review

На этой странице вы найдете более 100 рабочих листов для ежедневного повторения («Math Buzz»), рассчитанных для классов с 1 по 5.

Ежедневные словесные задачи

В этой области есть ежедневные словесные задачи по математике для учащихся с 1 по 5. Есть сотни графических текстовых задач, которые нужно решить учащимся, и достаточно места для демонстрации своей работы.

Сложение и вычитание десятичных чисел

Сложение и вычитание десятичных чисел с разрядами десятых, сотых и тысячных долей.

Десятичное деление

Практикуйте деление в столбик с десятичными числами.

Десятичное умножение

Попрактикуйтесь в задачах умножения с десятичными множителями и произведениями.

Десятичные рабочие листы

Именование и работа с десятичными числами.

Рабочие листы деления: базовые

Рабочие листы основных разделов, игры и мероприятия.

Рабочие листы для деления: длинные деления

Рабочие листы для длинных делений с 2-, 3- и 4-значными дивидендами.

Уравнения (базовая алгебра)

Научитесь балансировать простые алгебраические уравнения и находить значения переменных.

Четные и нечетные рабочие листы

Определение нечетных и четных чисел

Рабочие листы с показателями

Найдите показатели однозначных чисел на этих печатных листах и ​​карточках с заданиями.

Рабочие листы факторинга

Заполните факторные деревья, найдите наибольшие общие множители и наименьшие общие множители.

Таблицы дробей (продвинутый уровень)

Сокращение дробей, упорядочивание дробей, эквивалентные дроби и сравнение дробей.

Рабочие листы фракций (базовые)

Определение основных фракций, полос фракций, манипуляторов дробей.

Дроби: сложение

Найдите суммы дробей и смешанных чисел. Включает в себя рабочие листы с дробями с одинаковым знаменателем и дробями с разным знаменателем.

Дроби: Дивизион

Делите дроби и смешанные числа. Многие из этих рабочих листов включают в себя иллюстрированные задачи, задачи с графической моделью, а также текстовые задачи.

Fractions: Mixed Numbers

Практикуйте базовые навыки смешанных чисел.

Дроби: Умножение

Умножение дробей и смешанных чисел. Многие рабочие листы включают модели и диаграммы, а также текстовые задания.

Дроби: обратные дроби

Распечатайте эти рабочие листы, чтобы помочь студентам узнать о взаимных дробях.

Дроби: вычитание

Практикуйтесь в вычитании дробей и смешанных чисел. Включает подобные и непохожие знаменатели.

Практика со стрелками и рамками

Используйте упражнения с рамками и стрелками для развития навыков логического мышления.

Графики: гистограммы

Прочтите гистограммы на рабочих листах и ​​ответьте на вопросы.

Графики: линейные графики

Расскажите о линейных графиках на рабочих листах и ​​ответьте на вопросы.

Графики: линейные графики

Линейные графики — это особый тип числовой линии, который представляет частоту данных.

Графики: пиктограммы

Изучите пиктограммы на рабочих листах и ​​ответьте на вопросы.

Графики: круговые диаграммы

Анализируйте круговые диаграммы на рабочих листах и ​​отвечайте на вопросы.

Больше, меньше рабочих листов

Сравните числа больше, меньше и равные.

Таблицы сотен

Воспользуйтесь этими полезными таблицами размеченных значений, графиками сотен и графиками девяноста девяти.

Ящики ввода и вывода

Заполните эти поля ввода и вывода для печати или поля правил.

Неравенства

Решите и изобразите неравенства.Включает неравенства с одной переменной, одноэтапным и двухэтапным неравенством.

Целые числа (базовые)

Сравнить, упорядочить, сложить и вычесть положительные и отрицательные числа.

Наименьшее общее кратное (НОК)

Определите наименьшее общее кратное для каждого набора чисел

Линии, сегменты, лучи

Узнайте о прямых, отрезках, лучах, параллельных и перпендикулярных линиях.

Математические кроссворды

Решайте математические задачи и используйте ответы, чтобы разгадывать кроссворды.

Загадки по математике

Решайте математические задачи, чтобы расшифровать ответ на забавные загадки.Включает в себя широкий спектр математических навыков, включая сложение, вычитание, умножение, деление, разметку, округление и многое другое.

Отрывки для математических рассказов

На этой странице есть отрывки для чтения на всю страницу. Учащиеся используют информацию из отрывков для решения математических задач. Они намного длиннее, чем «обычные» задачи со словами.

Рабочие листы для средних (средних) значений

Вычислите среднее или среднее значение чисел.

Среднее значение, Медиана, Режим и Диапазон

Вычислить режим, медиану, среднее значение и диапазон заданных чисел.

Индекс измерений

Выберите типы таблиц измерений, которые вам нужны, включая линейные измерения, емкость и температуру.

Измерение: CM, MM и M

Практикуйте метрические линейные измерения: сантиметры, миллиметры и метры.

Измерение: футы, ярды, дюймы

Изучение американских линейных измерений; дюймы, футы и ярды.

Измерение: граммы и килограммы

Измерение веса и преобразование в граммы и килограммы и обратно.

Измерение: литры и миллилитры

Оцените и преобразуйте измерения емкости в литры и миллилитры.

Измерение: фунты и унции

Измерьте вес и преобразуйте его в унции и фунты и обратно.

Математика в средней школе

На этой странице указателя вы найдете ссылки на десятки тем по математике в средней школе на этом сайте. Темы включают неравенство, абсолютное значение, алгебру и многое другое.

Minute Math Drills

Листы упражнений и практики для базового сложения, вычитания, умножения и деления.

Кратные

Эти рабочие листы помогут студентам научиться находить и определять кратные числа.

Умножение (Свойства)

Узнайте об ассоциативных, распределительных, коммутативных и тождественных свойствах умножения.

Таблицы умножения

Распечатайте эти таблицы и таблицы умножения, чтобы студенты могли использовать их в качестве справки.

Рабочие листы умножения: Расширенный

Решайте задачи двузначного и трехзначного умножения.

Рабочие листы умножения: базовые

Изучите основные факты умножения с помощью этих рабочих листов, загадочных картинок и игр.

Семейства фактов с делением-умножением

Связи основных чисел, рабочие листы семейства фактов и треугольники для деления и умножения.

Умножение: сеточное умножение

Умножение на 2-, 3- или 4-значные числа с решеткой.

Mystery Graph Art

Постройте упорядоченные пары, чтобы раскрыть загадочные картинки.

Mystery Math Pictures

Решите факты сложения, вычитания, умножения и деления, чтобы раскрыть загадочную картинку.

Детектив по числам (секретные числа)

Ученики будут использовать подсказки, размещаемые каждый день, чтобы вычислить еженедельное секретное число.

Числовые строки

Печатные рабочие листы числовых строк для обучения счету, сложению, вычитанию, числовым образцам, дробям и десятичным знакам.

Порядок операций

Практический порядок операций: скобки и показатели, затем умножение и деление, затем сложение и вычитание.

Заказанные пары; Координатные плоскости

Координатные плоскости и рабочие листы упорядоченных пар.

Порядковые номера

Порядковые номера определяют позицию в серии. (примеры: первый, второй, третий, четвертый и т. д.)

Шаблоны: Число

Учащиеся должны указать числа, которые идут следующими в этих шаблонах.

Выкройки: Рисунок

Учащиеся определяют, какие изображения будут следующими в выкройках.

Рабочие листы с процентами

Преобразование десятичных чисел и дробей в проценты.

Рабочие листы периметра

Добавьте, чтобы найти периметры многоугольников на этих листах.

Рабочие листы для разметки

Определение значения подчеркнутой цифры; стандартная и развернутая форма; округление.

Простые и составные числа

Узнайте о различиях между простыми и составными числами. Кроме того, научитесь определять и находить простые числа путем факторизации или с помощью решета Эратосфена.

Рабочие листы по полигонам

Определение многоугольников и работа с ними.

Рабочие листы вероятности

Определите вероятность определенных результатов.

Puzzle Match Math Games

Пазлы для печати, которые вы можете вырезать, чтобы ученики соответствовали друг другу. Отлично подходит для учебных центров, занятий в небольших группах и самостоятельной практики.

Теорема Пифагора

Найдите длины сторон прямоугольного треугольника по формуле теоремы Пифагора.

Рабочие листы с QR-кодами

Учащиеся используют iPad или смартфон для сканирования QR-кодов, чтобы заполнить или проверить задачи на каждом из этих математических листов.

Коэффициенты

Попрактикуйтесь в сравнении пар величин с помощью соотношений.

Отражение, вращение и перенос

Определите отраженные, повернутые и перемещенные формы.

Римские цифры

Научитесь читать и писать римские цифры с помощью этих распечатываемых листов и заданий.

Рабочие листы округления чисел

Округление чисел до ближайших десятков и сотен.

Научное представление

Научитесь записывать числа в экспоненциальном представлении.

Математика секретного кода

На этих рабочих листах учащиеся будут использовать ключ для декодирования секретных чисел в каждой задаче сложения, вычитания, умножения или деления.

Подобные и совпадающие рабочие листы

Определите похожие и совпадающие формы.

Счет на 100 секунд с пропуском

Используйте эти рабочие листы, чтобы научить студентов считать, пропускать сотни.

Пропустить счет по 10 с

Просмотрите счет по десяткам с помощью этих печатных форм.

Пропустить счет на 11 секунд

Подсчитать одиннадцать, умножить на одиннадцать и заполнить пропущенные числа.

Пропуск подсчета по 12 с.

Заполните пустые поля и задачи со словами, считая по двенадцати.

Пропуск счета на 25 секунд

Пропуск счета на двадцать пять секунд важен, если вы учите своих учеников считать деньги.

Пропуск счета на 2 секунды

Используйте эти распечатки, чтобы научить студентов пропускать счет с интервалом в два.

Пропустить счет на 3 секунды

Набор рабочих листов на этой странице поможет учащимся научиться считать по тройкам.

Пропустить счет по четверкам

Если вы учите учеников счету по четыре, попробуйте эти рабочие листы.

Пропустить счет по 5 шек.

Эти рабочие листы могут быть вам полезны, когда вы учите студентов считать по пятакам или по пятеркам.

Рабочие листы «Слайды, переворачивания и повороты»

Сообщите, были ли формы перевёрнуты, сдвинуты или повернуты.

Наклон

На этих рабочих листах учащиеся будут использовать графики, упорядоченные пары и таблицы для вычисления наклона прямых линий.

Рабочие листы твердых форм

Назовите твердые геометрические формы: прямоугольные призмы, кубы, сферы и цилиндры.

Специальные числа

Эти рабочие листы охватывают множество концепций разряда, включая четное / нечетное, определение значения цифр и запись чисел в развернутой форме.

Вычитание

Вычитание однозначных и многозначных чисел. Включает 1, 2, 3 и 4-значные числа.Также есть ссылки на десятичную дробь и вычитание денег.

Вычитание: базовое

Практика базового вычитания однозначных чисел; концепции и рабочие листы.

Вычитание дробей

Практикуйтесь в вычитании дробей и смешанных чисел с помощью этих распечатываемых листов и карточек задач.

Площадь поверхности

Рассчитайте площадь поверхности прямоугольных призм и других трехмерных форм.

Рабочие листы симметрии

Найдите линии симметрии, определите симметричные фигуры и завершите симметричные формы.

Tally Marks

Научитесь считать объекты по счетным меткам.

Таблицы температуры

Считайте показания термометров Цельсия и Фаренгейта и укажите температуру.

Математика с десятью кадрами

Упражнения с десятью кадрами для печати для обучения счету, базовому сложению и простому вычитанию.

Рабочие листы тесселяции

Научите учащихся распознавать геометрическую мозаику двумерных фигур.

Рабочие листы времени

Узнайте, как определять время с точностью до минуты, часа и четверти часа.

Время: прошедшее время

Определите количество прошедшего времени.

Диаграммы Венна (математика)

На этой странице есть рабочие листы математических диаграмм Венна.

Объем — Градуированные цилиндры

Эти рабочие листы содержат изображения градуированных цилиндров. Студенты должны указать правильный объем в миллилитрах.

Рабочие листы по объему

Расчет объема твердых форм. Включает объемные «счетные кубики», прямоугольные призмы, конусы, цилиндры и сферы.

Рабочие листы задач со словами (по типам)

Практические задачи со словами на сложение, вычитание, умножение и деление.

Рабочие листы для задач со словами (смешанные)

Проанализируйте навыки работы со смешанными словами на разных уровнях обучения.

Задачи со словами (несколько шагов)

Эти задачи со словами состоят из нескольких этапов и требуют от учащихся навыков критического мышления.

Рабочие листы сложения

Здесь вы можете ссылаться на все типы рабочих листов сложения, включая основные факты, сложение дробей, 2-значное, 3-значное и 4-значное сложение.

Рабочие листы дробей

Указатель наших рабочих листов базового и продвинутого уровней.

Рабочие листы по геометрии

Изучите площадь, периметр, симметрию, многоугольники, твердые формы и многое другое.

Рабочие листы для построения графиков

Выбирайте из круговых диаграмм, гистограмм и линейных диаграмм.

Пропуск рабочих листов

Счет по 2, 3, 4, 5, 10, 25 или 100 секунд.

Рабочие листы вычитания

Вот индексная страница, которая содержит ссылки на все разделы вычитания нашего веб-сайта.

Рабочие листы по математическим навыкам

Эта страница содержит только частичный указатель рабочих листов по математическим навыкам на S.T.W.

Полный указатель веб-сайта

Просмотрите полный указатель всех рабочих листов по математике, английскому языку, правописанию, фонетике, грамматике, естествознанию и общественным наукам, которые можно найти на этом веб-сайте.

План урока с эквивалентными дробями

| Study.com

Длина:

Материалы

• Цветные плитки размером 1 дюйм разных цветов в мешочках; 1 на каждого ученика
• тетрадь по математике
• мелки или цветные карандаши

Ключевые слова

• числитель
Знаменатель
• эквивалентная дробь
• крест умножить

Стандарты учебных программ

• CCSS.Math.Content.4.NF.A.1

Объясните, почему дробь a / b эквивалентна дроби (n * a) / (n * b), используя визуальные модели дробей, обращая внимание на то, как количество и размер частей различаются, даже если сами две дроби такого же размера. Используйте этот принцип, чтобы распознавать и генерировать эквивалентные дроби.

• CCSS.Math.Content.4.NF.A.2

Сравните две дроби с разными числителями и разными знаменателями, например, создав общие знаменатели или числители, или сравнив с эталонной дробью, такой как 1/2.Признайте, что сравнения действительны только тогда, когда две дроби относятся к одному и тому же целому. Запишите результаты сравнений с помощью символов>, = или <и обоснуйте выводы, например, используя модель визуальной фракции.

Инструкции

• Начните с того, что попросите учащихся пометить свои математические тетради «Эквивалентные дроби». Спросите, предпочитают ли они 1/3 пакета M&M или 3/9 пакета? Предложите им подумать и записать свои ответы в свои тетради по математике.
• Делитесь и обсуждайте ответы и рассуждения.Нарисуйте картинки, чтобы продемонстрировать рассуждения.
• Скажите студентам, что они будут работать над эквивалентными дробями. Определите термин и попросите учащихся записать в тетрадях по математике.
• Покажите видеоурок на Study.com Что такое эквивалентные дроби? — Определение и примеры.
• Поставьте видео на паузу в следующих местах, чтобы поработать с учащимися и проверить понимание.
  • 32 секунды — Определите и пересмотрите концепции числителя и знаменателя, если необходимо.
  • 2:05 — Умножение для определения эквивалентных дробей.
  • 2:29 — Деление для определения эквивалентных дробей.
  • 3:34 — Сложение и вычитание дробей с разными знаменателями.
  • 4:24 — Перекрестное умножение для проверки эквивалентных дробей.
• Воспроизведите краткое содержание урока и просмотрите все концепции, которые нужно пояснить учащимся. Проверьте понимание, демонстрируя проблемы и руководя работой ученика.

Мероприятие

• Раздайте каждому студенту пакетик цветных плиток.Скажите студентам, что они будут использовать плитки для создания серии мозаик.
• Попросите учащихся создать мозаику из 10 плиток, половина из которых должна быть зеленой.
• Обходите комнату, пока студенты создают мозаику. Поддерживайте и поддерживайте их обучение.
• Попросите учащихся набросать мозаику в своих тетрадях и записать дроби, обозначающие каждое число. Например, Дебби может создать мозаику из 5 зеленых, 3 красных, 1 синего и 1 желтого. Ее фракции — зеленые, 5/10 или 1/2; красный, 3/10; синий и желтый, 1/10.
• Разрешите ученикам внимательно обойти комнату и рассмотреть мозаики других учеников. Спросить:
  • Все ли мозаики одинаковы? Почему или почему нет?
  • У всех нас одинаковая доля зеленых плиток? Объяснять.
• Повторите то же самое с другими цветовыми комбинациями и фракциями.

Расширения

• Используйте мозаику в учебных центрах или для домашних заданий. Добавьте больше цветных плиток и попросите учащихся построить мозаику большего размера.
• Расширьте мозаику, создав карточки с заданиями, предлагая учащимся показать различные способы создания фракции.Например, «Покажи 3 способа сделать 1/5».
• Для учащихся, испытывающих трудности, создайте цветные полосы, чтобы показать эквивалентные дроби. Используя цветной картон, вырежьте красную полосу размером 1 на 12 дюймов с цифрой «1». Используйте две желтые полоски 1×6 дюймов, чтобы показать «1/2», три оранжевых 3×6, чтобы показать «1/3», и так далее. Позвольте ученикам манипулировать и сравнивать.

Сокращение дробей (элементарное, специальное издание)

).

План урока

Тема: Математика Дата: 5 февраля 2007 г.

Поведенческая цель:
Получив устную подсказку, каждый ученик выполнит практический набор (подлежит уточнению после управляемой практики) задач на рабочем листе, требуя от учеников сокращать правильные дроби и писать их в простейшей форме с точностью 75%, задачи решаются самостоятельно.

Стандарт обучения штата Иллинойс:
6. B.2 Решение одно- и двухэтапных задач, включающих дроби

Шаги обучения:

Повестка дня

Уменьшение дробей
1. Ознакомьтесь с условиями
2. Я покажу вам (2/4, 3/6)
3. Словарь
Простейшая форма
Уменьшить
4. Мы делаем что-то вместе (4/8, 6/8, 3/12)
5. Зарегистрируем
6. Вы сделаете что-то самостоятельно (Практический рабочий лист )
7. Проверьте ответы
8. Домашнее задание

1. Предвосхищающий набор (фокус, крючок для привлечения внимания студентов):
На прошлой неделе, когда мы проводили числовые линии, мы выяснили, что дроби могут быть записаны более чем в одну сторону.Верхняя и нижняя части числовых линий выглядели по-разному, но все равно представляли одно и то же. Сегодня мы познакомимся с другими способами записи дробей.

2. Цель (цель):
В математике нам нужно, чтобы наша работа была ясной и максимально возможной, а это означает, что нам, возможно, придется изменить способ представления наших дробей. (Приведите письменный пример) Для наших товарищей-математиков проявление любезности состоит в том, что наши дроби выглядят как можно лучше.

3.Сырьевой материал:
Раздайте каждому учащемуся раздаточный материал с математическими терминами. Давайте рассмотрим эти термины и решим, какие из них мы уже выучили во время этого урока, а какие, возможно, еще не видели в этом году.

4. Моделирование (показать):
Итак, если я хочу показать дробь как можно лучше, мне нужно сначала взглянуть на нее и решить, есть ли способ сделать ее более понятной. Я покажу вам, как это сделать.
Я хочу, чтобы вы сначала присмотрели за мной, а потом мы сможем поработать вместе.
Я смотрю на 2/4. Я действительно ничего не замечаю сразу. Я собираюсь взглянуть на свои математические слова и посмотреть, смогу ли я взглянуть на них по-другому. Чтобы помочь мне, я использую свой математический мозг и смотрю на 2 числа. Я знаю, что 2 — это коэффициент 4. Я также знаю, что 4 кратно 2. Если моя цель состоит в том, чтобы облегчить чтение, я постараюсь уменьшить его. Думаю, я начну с перечисления множителей двух и четырех.
2—1,2
4—1,2,4
GCF — 2
2 разделить на 2 — это что?
4 разделить на 2 это что?
Напишите ответ
Отметьте ответ в моем калькуляторе

Попробуйте другой.. . 3/6 (повторить процесс)

VOCAB и КОНТРОЛЬНЫЙ СПИСОК

5. Практика с инструкциями (следуйте за мной):
Пройдите процесс со студентами для дроби 4/8:
Используйте числа в наших предложениях
Напишите множители
Выберите наибольшее Общий множитель
Уменьшить дробь
Проверьте ответ в калькуляторе.
При необходимости окажите помощь.

6. Проверьте понимание:
Вы заметили закономерность?
Каков был ответ на все наши вопросы?
Уменьшатся ли ВСЕ дроби до?

7.Дополнительная практика:
Давайте проверим. Почему бы нам не попробовать 6/8
Можем ли мы использовать числитель и знаменатель в нашем предложении? №
Что ж, давайте перейдем к следующему шагу и найдем GCF для двух чисел.
Закончите шаги.

Сделайте еще одну задачу с дробью 3/12.

7. Независимая практика:
Думаю, вы готовы показать мне, что можете делать это самостоятельно. Сделайте как можно больше, используя оставшееся время, и мы вместе их проверим. (Более или менее, в зависимости от времени)

8.Закрытие:
Большинство / все вы показали мне много тяжелой работы и усилий. Давайте в последний раз рассмотрим шаги. Кто мне скажет, каковы 5 шагов для приведения правильных дробей к их простейшей форме?
В качестве домашнего задания я хочу, чтобы вы ответили на все вопросы на этой странице. Убедитесь, что вы показываете всю свою работу, и используйте бумагу для заметок, если вы не можете разместить ее на этом листе. Давайте вместе прочитаем инструкции и убедимся, что знаем, как решить все задачи.

9. Материалы:
Словарные термины
Контрольный список
Карандаш
Калькулятор
Доска / ручка
Таблица умножения
Рабочие листы
Домашние задания

Преобразование дробей в простейшую форму

Математическое мышление

предложений

_________________ является множителем ____________________

_________________ кратно ___________________

Контрольный список

Шаг 1: Запишите множители для числителя и знаменателя

Шаг 2: Выберите наибольший общий множитель

Шаг 3: Уменьшите дробь путем деления

Шаг 4 : Запишите уменьшенную дробь

Шаг 5: Отметьте ответ в калькуляторе

Что делает обучение дробям таким сложным?

Если вы следили за мной или смотрели какой-либо из моих вебинаров, вы знаете, что я искренне верю, что все ученики могут изучать математику на высоком уровне — и мы, как учителя, должны постоянно стремиться совершенствовать наши стратегии и методы обучения, чтобы мы достигаем ВСЕХ студентов… независимо от их отправной точки. Это особенно верно для дробей, которые могут быть одной из самых сложных вещей, которым мы учим. Этот пост начинает серию об инструкциях по дробям, которые, я надеюсь, вы найдете полезными и значимыми.

Для начала, я не думаю, что было бы удивительно, если бы я сказал вам, что большинство учителей промежуточных классов заявляют, что дроби являются одним из (или САМЫХ) самых сложных понятий для них и для обучения их учеников. Так почему это? И что еще важнее — что с этим делать ?! Эти вопросы станут основой этой серии сообщений в блоге.Мы МОЖЕМ изменить то, как мы достигаем наших учеников и углубляем их знания.

Что делает обучение дробям таким сложным?

Я провел некоторое исследование (формальное и неформальное), изучив то, что сказали эксперты, и опросив бесчисленное количество учителей в окопах, и я думаю, что у меня есть некоторые ответы на то, что делает эту тему такой подавляющей для многих. Почему это важно? Если мы сможем идентифицировать камни преткновения, то мы сможем начать устранять их и начать больше узнавать о том, что БУДЕТ работать и как мы можем преодолеть эти препятствия. Я постоянно нахожусь в поисках способов «понять» дроби для моих учеников (что привело к тому, что я создал единицу полной дроби для использования с моими учениками!)

Фракции не всегда «конкретны».

Хотя мы можем начать нашу инструкцию по дробям с объектов — например, складок из бумаги или пластмассовых деталей — мы слишком часто очень быстро переходим от этих реальных моделей к вычислениям с использованием бумаги и карандаша. Я собираюсь возразить, что даже рисунков дробей не могут быть достаточно конкретными для некоторых студентов с ограниченным чувством дроби.Для многих это просто круг с линиями. Физический процесс разрезания, складывания и манипулирования очень важен для многих.

Чтобы усложнить ситуацию — это только начало! Умножая целые числа, мы можем образовывать «группы» объектов, верно? 3 раза по 6 можно представить 3 стопками по 6 предметов. Находят ли мы время, чтобы действительно реализовать наши более продвинутые концепции дробей, такие как умножение и деление бетона? Действительно ли ученики «видят», что происходит, когда мы умножаем дроби (ПОДСКАЗКА: мы все еще можем смоделировать 3 группы по 1/4 или 6 групп по 2/3… и это может иметь огромное значение!). Когда мы слишком быстро переходим к «голым числам», мы делаем много предположений о том, что наши ученики действительно понимают.

Дроби — это числа — правда!

Вот еще одно утверждение, которое кажется немного очевидным, не так ли? Конечно, дроби — это числа! Но подождите … попытайтесь войти в образ мыслей учащегося, который испытывает трудности. Мы показываем им картинки нарезанных на маленькие кусочки пиццы и шоколадных батончиков. Мы говорим о картинках по-разному… и мы помогаем студентам научиться «маркировать» их как представляющие 1/5 или 3/8 или что-то еще, что изображено на картинке.Действительно ли мы помогаем им понять, что дроби позволяют нам представлять действительные числа и даже части чисел? Что когда у нас рисунок 3/8, это означает, что у нас МЕНЬШЕ всего объекта или количества? Что дроби позволяют отображать суммы МЕЖДУ целыми числами? Это важная часть дробного понимания; рисунки, которые мы используем, чтобы показать дроби, являются просто представлениями чисел из числовой линии. Подробнее в следующих публикациях.

(Эти числовые строки являются частью моего ресурса строки дробных чисел — также являются частью моего набора инструментов для десяти дробных дробей)

Отсутствует понимание «единичной дроби»

Это подводит меня непосредственно к этой концепции.Термин «единичная дробь» относится к дроби с

«1» в числителе… например, 1/4, 1/7 или даже 1/500. Понимание того, что это «единица» измерения или суммы, очень важно. Мне нравится обмениваться терминами «единичная дробь» и «подсчет дроби» с моими учениками, потому что я действительно хочу, чтобы они понимали, что, как и целые числа, единичные дроби можно подсчитывать, складывать, вычитать, составлять и разлагать — и многое другое.

В начальные годы много времени уходит на подсчет целых чисел разными способами — по единицам.К 5-м. К 10 годам. Мы даже практикуем обратный счет, который помогает развить понимание вычитания. То же самое и с дробями — и мы действительно не можем предположить, что все наши ученики могут делать это автоматически.

Когда мы считаем дробные части («единичные дроби») с помощью манипуляторов, на числовых линиях и даже устно, это помогает понять, что дроби — это числа. Это помогает учащимся развить чувство относительного размера дробей. Это помогает лучше понять, что происходит, когда мы считаем и получаем один и тот же числитель и знаменатель (новое «целое»), а затем считаем после этого, чтобы получить неправильные дроби и смешанные числа.Когда мы можем считать дроби, мы начинаем видеть их аддитивный характер … У меня 2/5, и я считаю еще одну пятую и получаю 3/5 — и это то, что часто может отсутствовать в понимании учащимися, если времени не хватает. потратил на работу над этим. Это действительно основа для сложения и вычитания дробей, и это действительно важный навык.

Фракционные вмешательства

На самом деле, это одно из первых вмешательств, которые я провожу с учащимися, которые испытывают трудности. Я достаю какой-то манипулятор (я связался с некоторыми из моих любимых… заметьте, это партнерские ссылки), и мы тренируемся в подсчете.Мы замечаем, что происходит, когда мы достигаем «целого», а затем и за его пределами. По сути, мы «играем» с этими счетными дробями, а затем начинаем записывать наши выводы на бумаге и карандашом. Я часто вытаскиваю их, когда нужно переучивать. Кроме того, при поиске манипуляторов обратите внимание на то, что на некоторых из них написана дробная часть, а на других — пусто — оба хороши, но принимайте решения, основываясь на том, чего вы хотите достичь. Точно так же, если вы используете ТОЛЬКО круги или ТОЛЬКО дробные линейки, учащимся может быть сложно обобщить полученные знания.Даже использование таких инструментов, как блоки шаблонов, может быть действительно полезным при изучении основных концепций дроби.

Обозначение дробей и терминология могут быть сложными

Итак, говоря об игре с единичными дробями и подсчете дробей, я упомянул, что я работаю над соединением физических дробей (дробные круги, сложенная бумага и т. Д.) С письменными символами — и это подводит меня к еще одной проблеме, связанной с дробями — обозначения и терминология. Мы используем такие слова, как «числитель» и «знаменатель», и иногда забываем, что студенты, возможно, не усвоили эти термины и, скорее всего, никогда их не слышали.Такие слова, как «эквивалентность», «несоответствие» и «уменьшение» также могут усугубить путаницу. Если вы видите другие мои сообщения из прошлого (или другие уроки из моей единицы дроби), чтобы было хуже? Мы можем писать дроби по-разному!

Посмотрите изображение ниже, а затем подумайте через призму борющегося математика. Обе зеленые дроби обозначают одно и то же, но записываются по-разному. Один, если он написан небрежно, может в конечном итоге выглядеть как 2110 — другой легко читать, но сложно сделать с помощью технологий.Как насчет фиолетовых? Студенты должны понимать, что оба они представляют собой одно и то же значение, написанное двумя разными способами. Даже понимание того, что «1» — это «целое», а 7/8 представляет собой часть другого целого, может сбить с толку многих. Нам необходимо постоянно оценивать этот тип недоразумений. Наконец, с привязкой к единичным дробям учащиеся должны понимать, что одно «целое» равнозначно тому, когда оно записано одним и тем же числителем и знаменателем. Мы не можем делать предположений, что такое понимание существует.Копайтесь и выясняйте — и исправляйте любые заблуждения по ходу дела.

Дроби появляются в нескольких контекстах

Я почти закончил — обещаю! Я знаю, что многие из этих вещей кажутся тривиальными — но если мы не улавливаем их в наших борцах, мы просто продолжаем продвигать их вперед, имея нестабильную основу — и мы ЗНАЕМ, что действительно понимание дробей является ключом к успеху в алгебре и других высших знаниях. математические классы. Мы не можем подвести наших учеников! Еще одно разочарование для студентов — это то, что дроби появляются во многих контекстах.Мы можем разделить пиццу на четверти. И мы можем разделить НАБОРЫ вещей (например, пакеты с мармеладом или бейсбольными мячами) на группы.

Кроме того, нам нужно использовать дроби более абстрактных вещей, таких как единицы измерения, например, доли дюйма или фунта. Неудивительно, что студенты запутались — 1/2 может означать так много разных вещей! Даже если подумать о половине пиццы … это пицца 7 дюймов? Пицца 16 дюймов? Эти половинки одинаковые? А как насчет половины пиццы в ресторане? Или половину ломтика?

Поскольку 1/2 может ВАРИАТЬСЯ, это очень сбивает с толку многих студентов.Фактически, эта задача составляет основу большей части работы с дробями, которую я выполняю в своем классе, чтобы действительно помочь студентам понять, насколько жидкими являются фракции. Вы можете увидеть множество примеров этого в моем модуле полной дроби, который изменил правила игры для меня и буквально тысяч учителей, которые его использовали.

Отсутствует установка на рост!

Это, пожалуй, труднее всего преодолеть. Студенты не рождаются с мыслью, что фракции трудны — где-то по пути они поняли это послание.Будь то от их семей («Я тоже был ужасен в дробях!») Или от того, как мы, как учителя, представляем информацию — каким-то образом мы посылаем сообщения о том, что дроби — наш враг, что-то только для того, чтобы их понимали счастливчики. . Мы должны подумать о наших собственных предубеждениях и убедиться, что мы НЕ отправляем эти сообщения с установкой на данность нашим ученикам. Фракции доступны каждому … но нам нужно убедиться, что мы создаем и взращиваем прочную основу понимания и мышления, направленного на рост и настойчивость.

Надеюсь, я дал вам кое-что для размышления сегодня — и следите за новостями, скоро появятся новые сообщения о дробях!

Хотите проверить устройство, о котором я говорил?

Или, может быть, проверить набор из 10 фракционных ресурсов, которые я использую, чтобы помочь понять это?

Хотите закрепить на потом?

Fractions

Уровни классов: PreK, детский сад, 1-й класс, 2-й класс, 3-й класс, 4-й класс, 5-й класс, 6-й класс, 7-й класс, 8-й класс, 9-й класс, 10-й класс, 11-й класс, 12-й класс

IEP Goals: Учитывая наглядное руководство и полосы бумаги, которые нужно вырезать, СТУДЕНТ будет разрезать изображение на части 1/4, 1/3, 1/2 или целое, произнося или записывая правильную представленную дробь, с точностью 80%, в 4 из 5 возможностей, по МЕСЯЦУ, ГОДУ.

Имея визуальное руководство и объекты для размещения в графическом органайзере, СТУДЕНТ будет формировать дроби 1/4, 1/3, 1/2 или 1 целое, выполняя набор задач независимо, с точностью 80%, за 4 секунды. из 5 возможностей по МЕСЯЦУ, ГОДУ.

Получив наглядные пособия для помощи в измерении дробей, СТУДЕНТ сопоставит каждое изображение, чтобы определить 1/2, 1/4, 1/3, 1 целое с точностью 80%, в 4 из 5 возможных вариантов, по МЕСЯЦУ, ГОДУ. (Дата окончания IEP)

Для объекта, разделенного на простые дроби (целое-1 / 3–1 / 4), СТУДЕНТ определит дробь с точностью 80%, в 4 из 5 возможностей, по МЕСЯЦУ, ГОДУ.

Учитывая визуальные эффекты, изображающие 1/2, 1/3, 1/4 и 1 целое, СТУДЕНТ будет соответствовать соответствующему изображению с точностью 80% в 4 из 5 возможных вариантов по МЕСЯЦУ, ГОДУ.

Пазлы с картинками, разделенные на 1/2, 1/4, 1/3, СТУДЕНТ сопоставит правильные картинки, чтобы сформировать одно целое, с точностью 80%, в 4 из 5 возможных вариантов, по МЕСЯЦУ, ГОДУ.