Как сокращать обычные дроби. Математика 6 класс
Что такое «сокращение дробей»
Математика любит точность и краткость: лохматыми громоздкими числами ее расположение не заслужить. Поэтому, следуя негласному правилу, сокращайте все, что можно сократить.
Сократить дробь — значит разделить ее числитель и знаменатель на их общий делитель. Общий делитель должен быть положительным и не равен нулю и единице.
В результате сокращения вы получаете новую дробь, равную исходной дроби. Такие дроби равны по основному свойству:
Основное свойство дробиЕсли числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число — получится дробь, равная данной. |
С основным свойством дроби знакомятся в 5 классе, но встречаться оно будет до самого окончания школы. Поэтому запоминаем, как выглядит основное свойство дроби в виде буквенных выражений:
=
=
где a, b, m — натуральные числа.
Графически сокращение дробей обычно записывается вот так:
Числитель и знаменатель зачеркиваются черточками. В этом примере числитель — 8, знаменатель — 36. Справа над ними записывают результаты деления числителя и знаменателя на их общий делитель. Общий делить 8 и 36 — 4. Это число не нужно записывать.
Больше наглядных примеров и понятных объяснений — на курсах обучения математике в онлайн-школе Skysmart.
Пример 1. Сократим обыкновенную дробь
Разделим числитель и знаменатель на общий делитель 3.
3 : 3 =1
15 : 3 = 5
= =
Сокращение выполнено: =
Пример 2. Сократим обыкновенную дробь
Разделим числитель и знаменатель на общий делитель 2.
4 : 2 = 2
16 : 2 = 8
= =
Сокращение выполнено: =
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Приведение дробей к несократимому виду
Смысл сокращения дробей в том, чтобы в результате сокращения в числителе и знаменателе оказались наименьшие из возможных чисел.
Так, в результате сокращения в примере 2, мы из дроби получили дробь
Выходит, что дробь выдержит еще одно сокращение и придет к виду
Сокращая дробь, стремитесь в итоге получить несократимую дробь.
Разделите числитель и знаменатель дроби на их НОД (наибольший общий делитель). Так вы приведете дробь к несократимому виду.
— несократимая дробь, так как по свойствам НОД мы знаем, что:
a : НОД(a, b) и b : НОД(a, b) — взаимно простые числа.
Два целых числа a и b называются взаимно простыми, если их наибольший общий делитель равен единице, НОД(a, b) = 1.
- Несократимые дроби: ; ; ;
Пример 3. Приведите обыкновенную дробь к несократимому виду
Найдем НОД числителя и знаменателя. НОД = 12
Найдем частное: 12 : 12 = 1
36 : 12 = 3
= =
Сокращение выполнено: =
Пример 4. Приведите обыкновенную дробь к несократимому виду
Найдем НОД числителя и знаменателя. НОД = 5
НОД = 5
Найдем частное: 15 : 5 = 3
25 : 5 = 5
= =
Сокращение выполнено: =
Правило сокращения дробей
Чтобы без труда сокращать любую обыкновенную дробь, запомните правило.
Выполняйте сокращение дробей по следующему алгоритму:
- Найдите НОД числителя и знаменателя дроби.
- Разделите числитель и знаменатель дроби на НОД.
В 6 классе каждая вторая задачка — с дробями. Чтобы легко управляться с ними и уметь сокращать любые числа, нужно хорошо потренироваться. Давайте разберем еще несколько примеров сокращения обыкновенных дробей.
Чтобы легко сокращать дроби, нужно уметь быстро находить НОД числителя и знаменателя. Для этого неплохо бы знать таблицу умножения и уметь раскладывать числа на простые множители.
- Например, дана дробь
Чтобы найти НОД числителя и знаменателя, разложим числа на простые множители.
36 = 2 * 2 * 3 * 3
84 = 2 * 2 * 3 * 7
Перемножаем все общие множители между собой 2 * 2 * 3 = 12.
НОД 36 и 84 = 12.
Пример 5. Сократите дробь
Разложим числа в числителе и знаменателе на множители.
135 = 9 * 3 * 5
180 = 9 * 2 * 2 * 5
Мысленно убираем все общие множители и перемножаем оставшиеся.
= =
Сокращение выполнено: =
Пример 6. Сократите обыкновенную дробь
Найдем НОД числителя и знаменателя. НОД = 9
18 : 9 = 2
81 : 9 = 9
= =
Сокращение выполнено: =
Дробь можно сократить, последовательно сокращая числитель и знаменатель на общий делитель. Такой способ подходит, если в числителе и знаменателе стоят крупные числа, и вы не уверены в подобранном НОД.
Пример 6. Сократите дробь:
= = =
Сокращение выполнено: =
Пример 7. Сократите дробь
Найдем НОД, разложив числитель и знаменатель на простые множители.
168 = 2 * 2 * 2 * 3 * 7
240 = 2 * 2 * 2 * 2 * 3 * 5
Перемножаем все общие множители между собой 2 * 2 * 2 * 3 = 24
НОД 168 и 240 равен 24
Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 168 : 24 = 7
240 : 24 = 10
= =
Сокращение выполнено: =
Пример 8. Сократите дробь
Сократите дробь
Найдем НОД, разложив числитель и знаменатель на простые множители.
360 = 2 * 2 * 2 * 3 * 3 * 5
540 = 2 * 2 * 3 * 3 * 3 * 5
Перемножаем все общие множители между собой 2 * 2 * 3 * 3 * 5 = 180
НОД 360 и 540 равен 180
Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 360 : 180 = 2
540 : 180 = 3
= =
Сокращение выполнено: =
Пример 8. Сократите дробь
Найдем НОД, разложив числитель и знаменатель на простые множители.
420 = 2 * 2 * 3 * 5 * 7
2520 = 2 * 2 * 2 * 3 * 3 * 5 * 7
Перемножаем все общие множители между собой 2 * 2 * 3 * 5 * 7 = 420
НОД 420 и 2520 равен 420
Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 420 : 420 = 1
2520 : 420 = 6
= =
Сокращение выполнено. Дробь приведена к несократимому виду: =
Пример 9. Сократите дробь
Найдем НОД, разложив числитель и знаменатель на простые множители.
1575 = 3 * 3 * 5 * 5 * 7
3450 = 2 * 3 * 5 * 5 * 23
Перемножаем все общие множители между собой 3 * 5 * 5 = 75
НОД 1575 и 3450 равен 72
Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 1575 : 75 = 21
3450 : 75 = 46
= =
Сокращение выполнено. Дробь приведена к несократимому виду: =
Иногда разложение на простые множители занимает немало времени, особенно если раскладываемые числа большие, как в двух предыдущих примерах. Чтобы быстро разложить любое число на простые множители, можно обратиться к онлайн-калькулятору — в интернете их много. Воспользуйтесь одним из них.
Если времени совсем не хватает — можно использовать онлайн-калькулятор и для нахождения НОД. Однако не стоит постоянно прибегать к калькулятору для решения задач, пока вы не научитесь уверенно и быстро вычислять сами.
Организационно – технологический блок | Деятельность учителя | Деятельность учащихся | ||||
1. Организационно – психологический настрой детей на урок | Задача: организационная деятельность учащихся. Форма: фронтальная Результат: учащиеся настроены на восприятие информации. Подготовленность к уроку. Прием контроля: наблюдение и самоконтроль. | — Сегодня очень хороший солнечный день. — Давайте мы улыбнёмся друг другу. — Откроем тетради, запишем число, классная работа. — Пусть наш урок будет интересным и даст нам возможность открыть новые знания. — Желаю всем нам успеха! В путь! -Один мудрец однажды сказал: “Не для школы, а для жизни мы учимся!” — В чём заключается смысл данной пословицы? (Слайд 1) — А для чего же мы изучаем такую сложную науку, как математика? | Приветствуют учителя. Настраиваются на работу на уроке. Активизация познавательного внимания, его концентрация на словах учителя. Записывают дату. Высказывают своё мнение. | |||
2. Актуализация знаний с последующей мотивацией. | Задача: мотивировать учащихся к учебной деятельности. Форма: работа в парах. Результат: учащиеся настроены на восприятие информации. Подготовленность к уроку. Прием контроля: наблюдение и самоконтроль. |
Молодцы, все справились с заданием!
у каждого на парте лежат цветные фигуры (кружки и квадраты) и на карточках записано задание: разрезать фигуру на указанные части. Пары с кругами делят: 1 ученик: 1/3 2 ученик: 2/6 Пары с квадратами делят: 1 ученик: 3/4 2 ученик: 12/16
— Молодцы! Все хорошо потрудились! (Слайд 2, 3) Мы убедились, что разные дроби могут обозначать одну и ту же часть фигуры. Как из дроби 1/3 получить дробь 2/6? А как из дроби 12/16 получить дробь 3/4? А давайте найдем НОД(6,8) Т.е. мы разделили числитель и знаменатель дроби 6/8 на НОД числителя и знаменателя, тем самым мы её сократили. | Учащиеся в группах выполняют задание, один ученик от группы озвучивает примеры и ответы. работа в парах Наблюдают и делают выводы Умножить числитель и знаменатель дроби на 2 Разделить числитель и знаменатель дроби на 4 Число 2 | |||
3. Формулировка темы и цели урока. | Задача. Мотивировать учащихся на формулировку темы и цели урока. Форма: беседа. Результат: сформирована тема и цель урока | Так сегодня на уроке чем мы будем заниматься? (Слайд5) — Попробуйте сформулировать наше новое правило сокращения дробей. Где мы можем проверить нашу гипотезу? Откройте учебник на стр. 39 — Прочитаем утверждение, которое здесь записано. — Сравните данное утверждение с тем, которое мы сделали сами. (Слайд 6) — Что нового вы узнали из этого правила о дробях? Рассмотрим пример: сократить дробь: 18/24 Найдем НОД(18,24) = 6 Значить на какое число мы можем сократить дробь? Разделим числитель и знаменатель на 6. А какой НОД у чисел 3 и 4? Дроби, у которых НОД числителя и знаменателя равен 1, называются несократимыми дробями. (слайд 7) Приведите свои примеры несократимых дробей | Учащиеся в тетради записывают тему урока Пробуют формулировать правило. Предлагают в учебнике. Сравнивают результаты. Убеждаются в совпадении. Что дроби можно сокращать на НОД Учащиеся работают в тетрадях, раскладывают числа 18 и 24 на простые множители, находят НОД. Один ученик работает на доске На 6 3/4 1 | |||
4. Физминутка. | Но не всегда удобно сокращать дроби, находя НОД, есть и другой способ: сокращать поэтапно. Но прежде, чем мы рассмотрим этот способ, давайте отдохнем. (Слайд 8,9) | Выполняют гимнастику для глаз. | ||||
5. | Задача. Формирование умения по применению на практике правила сокращения дробей. Форма: работа у доски и самостоятельно. Результат: применяют правило сокращения дробей | — Давайте дальше рассмотрим, как еще можно сокращать дроби. А для этого повторим признаки делимости. (Слайд 10) Сократим дробь 1170/4410: Вначале на 2, потом на 5, на 3, еще раз на 3 и получи несократимую дробь 13/49 2∙5∙3∙3 = 90 Т.е. можно было сразу сократить на 90, это НОД. Бывает сложно сказать на какое число делится числитель и знаменатель дроби: 161/42 – это неправильная дробь. Но пусть вас это не пугает. Начнем с числа 42: 42 : 2, но 161 не дел. на 2 42 : 3, но 161 не дел. на 3 42 не дел. на 4 42 не дел. на 5 42 : 6, но 161 не дел. на 6 42 : 7, 161 дел. на 7, проверим в столбик, делится, получим 23 А теперь попробуйте сами сократить дробь:
| Работа в тетрадях Работа у доски по очереди. | |||
6.Самостоятельная работа. | Задача. Организовать самоконтроль учащихся по умению применять правило сокращения дробей. Форма: идвидуальная Результат: выполнение с.р. Прием контроля: самооценивание. |
| 2 ВАРИАНТ | |||
1. Правило с пропущенными словами | 1.Правило с пропущенными словами | |||||
2. Заполни пропуски. 105/165=105:5/165: ? =? : ?/? : 3 | 2. Заполни пропуски. 60/130 = 60: ?/130: 5 = ? : 2/ ? : ? = | |||||
3.Сократи дробь 98/126 | 3. 105/147 | |||||
7. Итог урока. Д/з Рефлексия | Ребята, дома вы продолжите закреплять навык применения правила сокращения дробей — Мне сегодня было очень комфортно с вами на уроке. Спасибо вам. Продолжи фразу: (Слайд 13) — Так какое правили мы сегодня изучали? — Как формулируется правило сокращения дробей? — Где мы можем его использовать? | Записывают домашнее задание. П.9 № 268(б) № 269 № 272 Высказывают своё мнение. | ||||
Как вы сами оцениваете свою работу на уроке. -А теперь крепко потрите свои ладошки, так, чтобы стало жарко. — На этом мы и заканчиваем наш урок. Пусть тепло души ваших друзей согревает вас. | Концентрация внимания на словах учителя. | |||||
Сведения об общеобразовательной организации
Сведения об общеобразовательной организации Цвет:C C CИзображения Вкл. Выкл.
Обычная версия сайта
- Телефон доверия: 8 800 200-01-22
Ошибка 404
К сожалению запрашиваемая страница не найдена.
Но вы можете воспользоваться поиском или картой сайта ниже
|
|
Контрольные и самостоятельные работы по математике.
 6 класс К учебник
6 класс К учебникДанное пособие полностью соответствует новому образовательному стандарту (второго поколения).
Пособие является необходимым дополнением к школьному учебнику Н.Я. Виленкина и др. «Математика. 6 класс», рекомендованному Министерством образования и науки Российской Федерации и включенному в Федеральный перечень учебников.
Пособие содержит различные материалы для контроля и оценки качества подготовки учащихся 6-х классов, предусмотренной программой 6 класса по курсу «Математика».
Представлены 36 самостоятельных работ, каждая в двух вариантах, так что при необходимости можно проверить полноту знаний учащихся после каждой пройденной темы; 10 контрольных работ, представленных в четырех вариантах, дают возможность максимально точно оценить знания каждого ученика.
Пособие адресовано учителям, будет полезно учащимся при подготовке к урокам, контрольным и самостоятельным работам.
СОДЕРЖАНИЕ
САМОСТОЯТЕЛЬНЫЕ РАБОТЫ 8
К § 1. Делимость чисел 8
Самостоятельная работа № 1. Делители и кратные 8
Делители и кратные 8
Самостоятельная работа № 2. Признаки делимости на 10, на 5 и на 2. Признаки делимости на 9 и на 3 9
Самостоятельная работа № 3. Простые и составные числа. Разложение на простые множители 10
Самостоятельная работа № 4. Наибольший общий делитель. Взаимно простые числа 11
Самостоятельная работа № 5. Наименьшее общее кратное 12
К § 2. Сложение и вычитание дробей с разными знаменателями 13
Самостоятельная работа № 6, Основное свойство дроби. Сокращение дробей 13
Самостоятельная работа № 7, Приведение дробей к общему знаменателю 14
Самостоятельная работа № 8. Сравнение, сложение и вычитание дробей с разными знаменателями 16
Самостоятельная работа № 9. Сравнение, сложение и вычитание дробей с разными знаменателями 17
Самостоятельная работа №10. Сложение и вычитание смешанных чисел 18
Самостоятельная работа №11. Сложение и вычитание смешанных чисел 19
К § 3. Умножение и деление обыкновенных дробей 20
Самостоятельная работа №12. Умножение дробей 20
Умножение дробей 20
Самостоятельная работа №13. Умножение дробей 21
Самостоятельная работа №14. Нахождение дроби от числа 22
Самостоятельная работа №15. Применение распределительного свойства умножения.
Взаимообратные числа 23
Самостоятельная работа № 16. Деление 25
Самостоятельная работа №17. Нахождение числа по его дроби 26
Самостоятельная работа № 18. Дробные выражения 27
К § 4. Отношения и пропорции 28
Самостоятельная работа №19.
Отношения 28
Самостоятельная работа Л£ 20. Пропорции, Прямая и обратная пропорциональные
зависимости 29
Самостоятельная работа № 21. Масштаб 30
Самостоятельная работа № 22. Длина окружности и площадь круга. Шар 31
К § 5. Положительные и отрицательные числа 32
Самостоятельная работа Л£ 23. Координаты на прямой. Противоположные
числа 32
Самостоятельная работа № 24. Модуль
числа 33
Самостоятельная работа № 25. Сравнение
чисел. Изменение величин 34
К § 6. Сложение и вычитание положительных
и отрицательных чисел 35
Самостоятельная работа № 26. Сложение чисел с помощью координатной прямой.
Сложение чисел с помощью координатной прямой.
Сложение отрицательных чисел 35
Самостоятельная работа № 27, Сложение
чисел с разными знаками 36
Самостоятельная работа № 28. Вычитание 37
К § 7. Умножение и деление положительных
и отрицательных чисел 38
Самостоятельная работа № 29.
Умножение 38
Самостоятельная работа № 30. Деление 39
Самостоятельная работа № 31.
Рациональные числа. Свойства действий
с рациональными числами 40
К § 8. Решение уравнений 41
Самостоятельная работа № 32. Раскрытие
скобок 41
Самостоятельная работа № 33.
Коэффициент. Подобные слагаемые 42
Самостоятельная работа № 34. Решение
уравнений . 43
К § 9. Координаты на плоскости 44
Самостоятельная работа № 35. Перпендикулярные прямые. Параллельные
прямые. Координатная плоскость 44
Самостоятельная работа № 36. Столбчатые
диаграммы. Графики 45
КОНТРОЛЬНЫЕ РАБОТЫ 46
К § 1 46
Контрольная работа № 1. Делители
и кратные. Признаки делимости на 10, на 5
Признаки делимости на 10, на 5
и на 2. Признаки делимости на 9 и на 3.
Простые и составные числа. Разложение
на простые множители. Наибольший общий
делитель. Взаимно простые числа.
Наименьшее общее кратное 46
К § 2 50
Контрольная работа № 2. Основное
свойство дроби. Сокращение дробей.
Приведение дробей к общему знаменателю.
Сравнение, сложение и вычитание дробей
с разными знаменателями. Сложение
и вычитание смешанных чисел 50
К § 3 54
Контрольная работа № 3. Умножение
дробей. Нахождение дроби от числа.
Применение распределительного свойства
умножения. Взаимно обратные числа 54
Контрольная работа № 4. Деление.
Нахождение числа по его дроби. Дробные
выражения 58
К § 4 62
Контрольная работа № 5. Отношения.
Пропорции. Прямая и обратная
пропорциональные зависимости. Масштаб.
Длина окружности и площадь круга 62
К § 5 64
Контрольная работа № 6. Координаты на прямой. Противоположные числа.
Модуль числа. Сравнение чисел. Изменение
величин 64
К § 6 68
Контрольная работа № 7. Сложение чисел
с помощью координатной прямой. Сложение
отрицательных чисел. Сложение чисел
с разными знаками. Вычитание 68
К § 7 70
Контрольная работа № 8, Умножение.
Деление. Рациональные числа. Свойства
действий с рациональными числами 70
К § 8 74
Контрольная работа № 9. Раскрытие скобок.
Коэффициент. Подобные слагаемые. Решение
уравнений 74
К § 9 78
Контрольная работа №10. Перпендикулярные прямые. Параллельные прямые. Координатная плоскость. Столбчатые
диаграммы. Графики 78
ОТВЕТЫ 80
7-е изд., перераб. и доп. — М.: 2011. — 96 с.
Скачать 2011 г.
Урок 23. Сокращение дробей | Поурочные планы по математике 6 класс
Цели: ввести понятие сокращения дробей и дать определение несократимой дроби; учить сокращать дроби, используя признаки делимости чисел и основное свойство дроби; отрабатывать умение решать задачи на движение по воде; развивать умение самостоятельно мыслить.
Ход урока
I. Организационный момент
II. Устный счет
1. Найдите наибольший общий делитель и наименьшее общее кратное чисел: а) 12 и 8; б) 9 и 15; в) 11 и 44; г) 8 и 20; д) 12 и 20; е) 10 и 15.
2. Замените каждую из следующих дробей дробью, знаменатель которой равен 36.
3. Найдите длину отрезка, если
а) половина его равна 8 см;
б) треть длины отрезка равна 5 см;
в) четверть равна 6 см;
г) шестая часть длины отрезка равна 2 см.
4. Маша ходит на каток раз в 2 дня, Оля — в 3 дня и Катя — в 4 дня. Они все вместе встретились на катке в субботу. Через сколько дней они встретятся опять? (12 дней.)
5. Имеются две банки: 3 л и 5 л. Как с помощью таких сосудов набрать из водопроводного крана 4 л воды?
5 л | 5 л | 2 л | 2 л | — | 5 л | 4 л |
3 л | — | 3 л | — | 2 л | 2 л | 3 л |
III. Индивидуальная работа
Индивидуальная работа
1 карточка
1. Найдите наибольший общий делитель чисел: а) 12 и 48; б) 14 и 35; в) 5 и 17; г) 40 и 60.
2. Найдите наименьшее общее кратное чисел: а) 54 и 27; б) 19 и 3; в) 45 и 54.
2 карточка
1. Найдите наибольший общий делитель чисел: а) 27 и 36; б) 15 и 45; в) 3 и 19; г) 90 и 60.
2. Найдите наименьшее общее кратное чисел: а) 64 и 72; б) 17 и 5; в) 14 и 52.
IV. Сообщение темы урока
— Прочитайте тему урока. Мы сегодня будем сокращать дроби, а в этом нам помогут: основное свойство дроби и признаки делимости чисел.
— А знаете, как в первых учебниках математики XVII века назывались дроби? (Ломаные числа).
V. Изучение нового материала
1. Подготовительная работа.
— Какие числа называются взаимно простыми.
— Приведите примеры взаимно простых чисел. (2 и 5, 4 и 9, 15 и 28 и т.д.)
2. № 261 стр. 42 (устно).
— На основании чего мы можем умножать числитель и знаменатель дроби? (На основании основного свойства дроби. )
)
Решение:
3. Работа над новой темой.
— Дана дробь 24/36. На какие числа можно разделить числитель и знаменатель дроби? (На 2, 3, 4, 6, 12.)
— Разделите числитель и знаменатель дроби 24/36 на наибольший общий делитель числителя и знаменателя, на 12.
— Какая получилась дробь? (2/3.)
— Сравните дроби 24/36 и 2/3. (Они равные, т. е. 24/36 = 2/3.)
— Такое преобразование называется сокращением дроби.
Определение. Деление числителя и знаменателя на их общий делитель, отличный от единицы, называют сокращением дроби.
— При сокращении дроби ее числовое значение не меняется, изменилась только ее запись.
— Можно ли еще сократить дробь 2/3? (Нет.)
— Что можете сказать о числах 2 и 3? (Они взаимно простые.)
— Если дробь больше сократить нельзя, то ее называют несократимой.
— Дайте самостоятельно определение несократимой дроби.
Определение. Дробь, числитель и знаменатель которой взаимно простые числа, называется несократимой.
— Рассмотрим способы сокращения дробей.
135
— Дана дробь 135/180.
I способ
— Сокращать дроби можно постепенно, используя признаки делимости.
— Назовите общие делители чисел. (3 и 5.)
— Можно сначала числитель и знаменатель дроби разделить на 3, потом на 5 и т.д., а можно, наоборот, разделить сначала на 5, потом на 3.
— Как называется дробь 3/4? (Несократимой.)
— Почему? (Числа 3 и 4 взаимно простые.)
II способ
— Найдите наименьший общий делитель числителя и знаменателя дроби. (НОД (135; 180) = 45.)
— Разделите числитель и знаменатель дроби на 45. (135/180 = 3/4.)
III способ
— Разложим числитель и знаменатель на несколько множителей.
— Сократим дробь на произведение общих множителей. (На 3 · 3 · 5.)
— Получим несократимую дробь 3/4.
VI. Физкультминутка
VII. Закрепление изученного материала
1. Назовите несократимые дроби:
— Почему эти дроби являются несократимыми?
2. № 242 стр. 39 (под руководством учителя с подробным комментированием).
№ 242 стр. 39 (под руководством учителя с подробным комментированием).
— Назовите наибольший делитель числителя и знаменателя.
— Разделите числитель и знаменатель данной дроби на их общий делитель.
— Как называется получившаяся дробь? (Несократимая.)
Решение:
3. № 246 стр. 40 (после краткого разбора самостоятельно, с последующей проверкой).
— Сколько минут в 1 ч? (60 мин.)
— Какую часть часа составляет 1 мин? (1 мин = 1/60 ч.)
VIII. Самостоятельная работа
Вариант I
1. Запишите дроби в виде несократимой обыкновенной дроби: 0,4; 0,88; 0,025; 0,004; 0,0125.
2. Какую часть:
а) метра составляют 8 дм;
б) килограмма составляют 45 г;
в) километра составляют 64 м;
г) тонны составляют 75 ц.
Вариант II
1. Запишите дроби в виде несократимой обыкновенной дроби: 0,6; 0,36; 0,075; 0,008; 0,0025.
2. Какую часть:
а) сантиметра составляют 4 мм;
б) центнера составляют 16 кг;
в) дециметра составляют 6 см;
г) тонны составляют 25 ц.
(Учитель выборочно проверяет тетради.)
IX. Работа над задачей
1. а) Один рабочий изготовил за 4 ч 12 деталей.
— Какие вопросы можно задать, чтобы данное высказывание стало задачей? Ответьте на них.
— Сколько деталей изготавливал рабочий за 1 ч? (12 : 4 = 3 (д.) — за 1 ч.)
— Сколько времени тратил рабочий на изготовление 1 детали?
б) № 250 стр. 40 (у доски и в тетрадях).
— Прочитайте задачу.
— Что известно?
— Что неизвестно?
— Можно сразу ответить на вопрос задачи?
Решение:
1) Сколько времени тратил первый рабочий на изготовление одной детали?
(Ответ: )
2) Сколько времени тратил первый рабочий на изготовление одной детали?
(Ответ: )
3) Какой из рабочих тратил на изготовление детали больше времени?
(Ответ: (второй рабочий).)
4) На сколько больше времени тратил второй рабочий на изготовление одной детали, чем первый?
(Ответ: на 1/4.)
2. Собственная скорость катера 12 км/ч. Скорость течения реки 3 км/ч. Найдите скорость катера по течению и против течения реки.
Скорость течения реки 3 км/ч. Найдите скорость катера по течению и против течения реки.
(Можно записать на доске текст задачи, а можно предложить самостоятельно составить задачу по краткой записи).
— Составьте задачу о движении по воде по краткой записи.
— Как найти скорость по течению и против течения реки, зная собственную скорость и скорость течения?
X. Подведение итогов урока
— Какую дробь называют несократимой?
— Приведите примеры несократимых дробей.
— На каком свойстве основано сокращение дробей
Домашнее задание: № 268 (а) стр. 42; № 270, 274 (а) стр. 43; № 263 стр. 42.
Дополнительный материал
Старинная задача
На дворе бегают куры и поросята. У всех вместе 20 голов и 52 ноги. Сколько всего кур и сколько поросят?
I способ
Решение методом перебора:
Поросята | Куры |
|
1 | 19 | 4 + 38 = 42 (ноги) |
2 | 18 | 8 + 36 = 44 (н. |
4 | 16 | 16 + 32 = 48 (н.) |
6 | 14 | 24 + 28 = 52 (н.) |
II способ
Решение:
Пусть ног у поросят и кур будет поровну, по 2.
2 · 20 = 40 (ног) — без двух ног у каждого поросенка.
52 — 40 = 12 (ног) — лишних на всех поросят.
12 : 2 = 6 (поросят).
20 — 6 = 14 (кур).
(Ответ: 14 кур, 6 поросят.)
Организационно – технологический блок | Деятельность учителя | Деятельность учащихся | ||||||||||||||
1. Организационно – психологический настрой детей на урок | Задача: организационная деятельность учащихся. Форма: фронтальная Результат: учащиеся настроены на восприятие информации. Подготовленность к уроку. Прием контроля: наблюдение и самоконтроль. | — Сегодня очень хороший солнечный день. — Давайте мы улыбнёмся друг другу. — Откроем тетради, запишем число, классная работа. — Пусть наш урок будет интересным и даст нам возможность открыть новые знания. — Желаю всем нам успеха! В путь! -Один мудрец однажды сказал: “Не для школы, а для жизни мы учимся!” — В чём заключается смысл данной пословицы? (Слайд 1) — А для чего же мы изучаем такую сложную науку, как математика? | Приветствуют учителя. Настраиваются на работу на уроке. Активизация познавательного внимания, его концентрация на словах учителя. Записывают дату. Высказывают своё мнение. | |||||||||||||
2. Актуализация знаний с последующей мотивацией. | Задача: мотивировать учащихся к учебной деятельности. Форма: работа в парах. Результат: учащиеся настроены на восприятие информации. Подготовленность к уроку. Прием контроля: наблюдение и самоконтроль. |
Молодцы, все справились с заданием!
у каждого на парте лежат цветные фигуры (кружки и квадраты) и на карточках записано задание: разрезать фигуру на указанные части. Пары с кругами делят: 1 ученик: 1/3 2 ученик: 2/6 Пары с квадратами делят: 1 ученик: 3/4 2 ученик: 12/16
— Молодцы! Все хорошо потрудились! (Слайд 2, 3) Мы убедились, что разные дроби могут обозначать одну и ту же часть фигуры. Как из дроби 1/3 получить дробь 2/6? А как из дроби 12/16 получить дробь 3/4? А давайте найдем НОД(6,8) Т.е. мы разделили числитель и знаменатель дроби 6/8 на НОД числителя и знаменателя, тем самым мы её сократили. | Учащиеся в группах выполняют задание, один ученик от группы озвучивает примеры и ответы. работа в парах Наблюдают и делают выводы Умножить числитель и знаменатель дроби на 2 Разделить числитель и знаменатель дроби на 4 Число 2 | |||||||||||||
3. Формулировка темы и цели урока. | Задача. Мотивировать учащихся на формулировку темы и цели урока. Форма: беседа. Результат: сформирована тема и цель урока | Так сегодня на уроке чем мы будем заниматься? (Слайд5) — Попробуйте сформулировать наше новое правило сокращения дробей. Где мы можем проверить нашу гипотезу? Откройте учебник на стр. 39 — Прочитаем утверждение, которое здесь записано. — Сравните данное утверждение с тем, которое мы сделали сами. (Слайд 6) — Что нового вы узнали из этого правила о дробях? Рассмотрим пример: сократить дробь: 18/24 Найдем НОД(18,24) = 6 Значить на какое число мы можем сократить дробь? Разделим числитель и знаменатель на 6. А какой НОД у чисел 3 и 4? Дроби, у которых НОД числителя и знаменателя равен 1, называются несократимыми дробями. (слайд 7) Приведите свои примеры несократимых дробей | Учащиеся в тетради записывают тему урока Пробуют формулировать правило. Предлагают в учебнике. Сравнивают результаты. Убеждаются в совпадении. Что дроби можно сокращать на НОД Учащиеся работают в тетрадях, раскладывают числа 18 и 24 на простые множители, находят НОД. Один ученик работает на доске На 6 3/4 1 | |||||||||||||
4. Физминутка. | Но не всегда удобно сокращать дроби, находя НОД, есть и другой способ: сокращать поэтапно. Но прежде, чем мы рассмотрим этот способ, давайте отдохнем. (Слайд 8,9) | Выполняют гимнастику для глаз. | ||||||||||||||
5. | Задача. Формирование умения по применению на практике правила сокращения дробей. Форма: работа у доски и самостоятельно. Результат: применяют правило сокращения дробей | — Давайте дальше рассмотрим, как еще можно сокращать дроби. А для этого повторим признаки делимости. (Слайд 10) Сократим дробь 1170/4410: Вначале на 2, потом на 5, на 3, еще раз на 3 и получи несократимую дробь 13/49 2∙5∙3∙3 = 90 Т.е. можно было сразу сократить на 90, это НОД. Бывает сложно сказать на какое число делится числитель и знаменатель дроби: 161/42 – это неправильная дробь. Но пусть вас это не пугает. Начнем с числа 42: 42 : 2, но 161 не дел. на 2 42 : 3, но 161 не дел. на 3 42 не дел. на 4 42 не дел. на 5 42 : 6, но 161 не дел. на 6 42 : 7, 161 дел. на 7, проверим в столбик, делится, получим 23 А теперь попробуйте сами сократить дробь:
| Работа в тетрадях Работа у доски по очереди. | |||||||||||||
6.Самостоятельная работа. | Задача. Организовать самоконтроль учащихся по умению применять правило сокращения дробей. Форма: идвидуальная Результат: выполнение с.р. Прием контроля: самооценивание. |
После выполнения работы раздается эталон выполнения. Критерии оценивания. (Слайд 12) Оцени. — если есть исправь свои ошибки. | ||||||||||||||
7. Итог урока. Д/з Рефлексия | Ребята, дома вы продолжите закреплять навык применения правила сокращения дробей — Мне сегодня было очень комфортно с вами на уроке. Спасибо вам. Продолжи фразу: (Слайд 13) — Так какое правили мы сегодня изучали? — Как формулируется правило сокращения дробей? — Где мы можем его использовать? | Записывают домашнее задание. П.9 № 268(б) № 269 № 272 Высказывают своё мнение. | ||||||||||||||
Как вы сами оцениваете свою работу на уроке. -А теперь крепко потрите свои ладошки, так, чтобы стало жарко. — На этом мы и заканчиваем наш урок. Пусть тепло души ваших друзей согревает вас. | Концентрация внимания на словах учителя. | |||||||||||||||
Обзор эквивалентных образовательных ресурсов
Целые обычные библиотеки рабочих листов.
Результаты фильтрации
By Grade
- Preschool
- Kindergarten
- 1st grade
- 2nd grade
- 3rd grade
- 4th grade
- 5th grade
- 6th grade
- 7th grade
- 8th grade
By Субъект
- Кодирование
- Изобразительное искусство
- иностранный язык
Математика
- Число.0018
- Addition
- Subtraction
- Multiplication
- Division
- Mixed Operations
Fractions
- Fraction Models
Эквивалентные дроби
- Целые числа в виде дробей
- Сравнение дробей
- Смешанные числа и неправильные дроби
- Добавление и вычитание фракций
- Умножение и разделение фракций
- Decimals
- Percents, Ratios, и скорость
- Percent
- Измерение
- Время
- ДЕНЬГА МАТЕРИЯ
- Данные и графики
- Проблемы по математике .
 0018
0018 - Math Puzzles
- Reading & Writing
- Science
- Social emotional
- Social studies
- Typing
By Topic
- Праздники
- Офлайн-игры
- Сезонные
- Ресурсы для учителей
- Common Core
Фракции 4
Уровень управления
Фракции 4
Студенты собираются глубже погрузиться в фракции в этом устройстве! Учащиеся будут применять предыдущие знания о нахождении эквивалентных дробей и преобразовании между дробями и смешанными числами, чтобы работать с дробями более сложными способами. Студенты будут продолжать использовать визуальные модели для обучения и практики сложения, вычитания, умножения и деления дробей.
5 -й класс
MATH
Урок с гидом
Фракции 2
Урок
Фракции 2
Учащиеся будут иметь базовое понимание фракций. В этом модуле студенты смогут изучить новые способы представления дробей, в том числе в наборе данных, на числовых линиях и с использованием моделей площадей. Учащиеся будут использовать свои знания о дробях для сравнения дробей с одинаковыми и разными знаменателями.
4 -й класс
Math
Урок с гидом
Фракции 1
Урок управления
Фракции 1
Фракции могут быть трюком для третьих класс. урок может помочь детям добраться туда. Он предоставляет целенаправленные инструкции, разработанные учителями и экспертами по учебным программам, которые относятся к учебной программе третьего класса. Упражнения и практические примеры помогают детям соотносить дроби с реальными математическими задачами. Когда закончите урок, ознакомьтесь с нашими рабочими листами дробей для большей практики.
Когда закончите урок, ознакомьтесь с нашими рабочими листами дробей для большей практики.3 -й класс
MATH
Урок с гидом
Фракции 3
Урок
Фракции 3
Фракции могут быть оспаривающими, когда они будут вызорами. Вот почему этот модуль предлагает учащимся работать с дробями и смешанными числами очень наглядными и конкретными способами, используя числовые линии, ленточные диаграммы и модели областей. Студенты изучат различные стратегии, чтобы практиковать определение и создание эквивалентных дробей.
5 -й класс
Math
Урок с гидом
Измерение и данные 4
Руководство. и дизайн. Построение данных с использованием дробных единиц делает их обучение еще на один шаг вперед. Также в этом блоке учащиеся учатся измерять, используя как традиционные единицы (такие как дюймы, футы и ярды), так и метрические единицы, а также как преобразовывать измерения в каждой системе. Концепция измерения становится двухмерной, когда учащиеся изучают измерение углов и работу с ними.
Концепция измерения становится двухмерной, когда учащиеся изучают измерение углов и работу с ними.
4-й класс
Математика
Урок с пошаговыми инструкциями
Поиск эквивалентной дроби Образовательные ресурсы
Ваш ребенок учит числители и доминирует над знаменателями. Теперь, когда ваш ученик понимает, что такое дробь, пришло время помочь ему узнать об эквивалентных дробях. Равные дроби — это дроби, которые выглядят по-разному, но на самом деле одинаковы. Если вашему ученику нужно освежить знания, вы можете вернуться к нашим ресурсам по фракциям. Если ваш ребенок чувствует, что готов взяться за эквивалентные дроби, погрузитесь в наши ресурсы ниже.
Узнайте больше об эквивалентных дробях
Эквивалентные дроби — это дроби, которые выглядят по-разному, но на самом деле имеют одинаковое значение, если их упростить. Вы можете сделать эквивалентные дроби, умножив или разделив числитель и знаменатель на одно и то же целое число.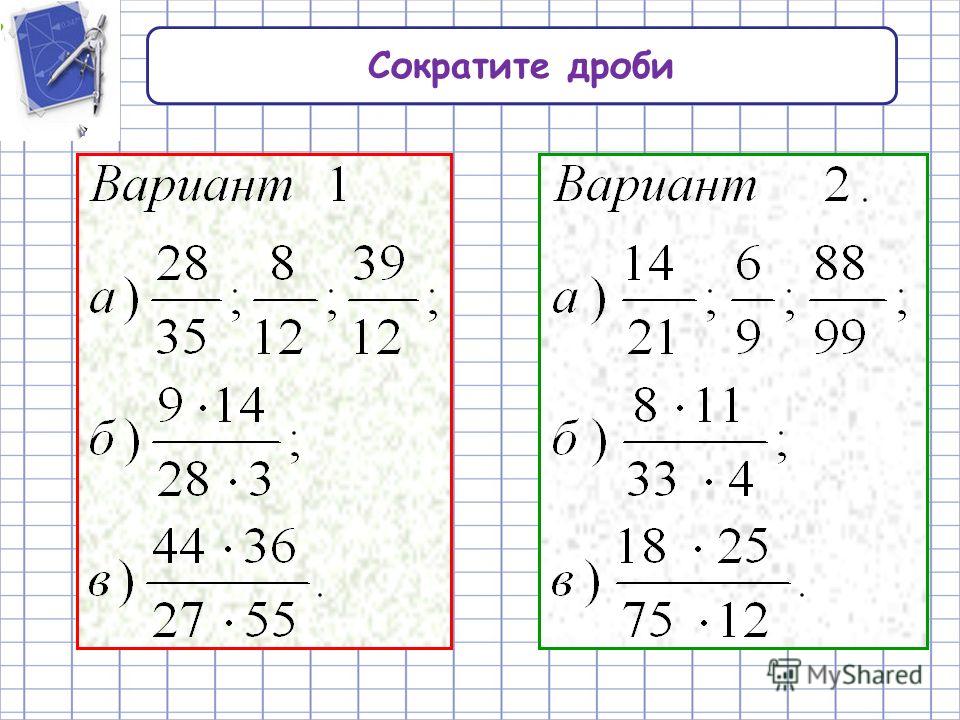 Нужно больше объяснений? Смотрите наши примеры ниже!
Нужно больше объяснений? Смотрите наши примеры ниже!
Умножение
Вы можете умножить числитель и знаменатель на одно и то же число, чтобы получить эквивалентную дробь. Давайте посмотрим, как составить три эквивалентные дроби от 9.0348 2 ⁄ 3 through multiplication:
- 2 ⁄ 3 × 2 ⁄ 2 = 4 ⁄ 6
- 2 ⁄ 3 × 3 ⁄ 3 = 6 ⁄ 9
- 2 ⁄ 3 × 4 ⁄ 4 = 8 ⁄ 12
Глядя на эти дроби, мы видим, что 2 ⁄ 3 = 4 ⁄ 6 = 6 ⁄ 9 = 8 ⁄ 12 . Это все равные дроби!
Деление
Теперь, когда вы узнали, как находить эквивалентные дроби путем умножения, теперь вы можете получить эквивалентные дроби путем деления.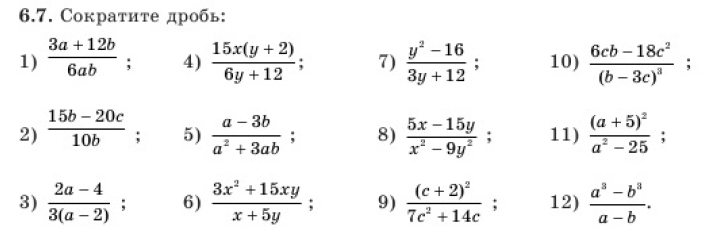 Давайте разделим 18 ⁄ 36 , чтобы получить эквивалентные фракции:
Давайте разделим 18 ⁄ 36 , чтобы получить эквивалентные фракции:
- 6 ⁄ 12 ÷ 2 ⁄ 2 = 3 ⁄ 2 = 3 ⁄ 2 = 3 ⁄ 2 = 3 ⁄ 2 = 3 ~ 2 = 3 ⁄ 2 = ÷ ⁄ 2 .0015 6 ⁄ 12 ÷ 3 ⁄ 3 = 2 ⁄ 4
- 6 ⁄ 12 ÷ 6 ⁄ 6 = 1 ⁄ 2
Подобно тому, что мы делали ранее, теперь мы сделали четыре эквивалентные фракции: 6 ⁄ 12 = 3 ⁄ 6 = 2 ⁄ 4 = 1 . 2 .
Если вы помните, что для работы с эквивалентными дробями вы должны умножать или делить числитель и знаменатель на одно и то же целое число, вы быстро пролистаете наши таблицы эквивалентных дробей!
Пятый класс упрощающий фракции
Unit 2lesson 4Цель
разминка/запуск
Практика управления
Независимая практика
Group Share
17 учителей, такие как этот урок
Урок печати
Объект
. SWBAT упрощает дроби до простейшей формы.
SWBAT упрощает дроби до простейшей формы.
Большая идея
Этот урок поможет учащимся определить простейшую форму дробей.
Автор урока
Джули Келли
Tyngsborough, MA
Уровень
Пятый класс
Субъекты
Math
Фракции
Стандарты
5.NF.A.1
Добавление и подборе. чисел) путем замены данных дробей эквивалентными дробями таким образом, чтобы получить эквивалентную сумму или разность дробей с одинаковыми знаменателями. Например, 2/3 + 5/4 = 8/12 + 15/12 = 23/12. (В общем, a/b + c/d = (ad + bc)/bd.)
Разминка/Запуск
15 минут
Сегодняшний урок по-прежнему посвящен эквивалентным дробям. Акцент этого урока сделан на упрощении дробей, а также на определении того, когда дробь имеет простейшую форму.
Чтобы разогреть студентов, я начну со вчерашнего обзора. Для этого я вывешиваю на доске 3 дроби и прошу учащихся найти для каждой по 3 равнозначные дроби.
Пример трех дробей, которые я мог бы использовать:
1/8
6/24
3/9
После того, как учащимся будет предоставлено время для самостоятельной работы, я призываю их повернуться и рассказать об использованных стратегиях, а не о найденных решениях. Пока учащиеся работают над этим разминочным заданием. Я вытаскиваю небольшую группу студентов, у которых вчера были проблемы. Я хочу помочь им успешно начать сегодня.
Я призываю учащихся выйти к доске и поделиться своими решениями и стратегиями. Важно напомнить учащимся, что существует неограниченное количество эквивалентных дробей. Эти ответы не являются единственными правильными примерами.
Я уверен, что по крайней мере один ученик поделится примером упрощения дробей, потому что это также стратегия поиска эквивалентности.
Чтобы помочь учащимся понять, куда мы движемся в этом уроке, я обращаю особое внимание на упрощенную дробь. Затем я пишу основные вопросы на доске.
• Можно ли упростить эту дробь?
• В простейшей форме?
• Откуда вы знаете?
Я говорю учащимся, что сегодня эти вопросы будут в центре внимания.
Практика под руководством
15 минут
Пополнение словарного запаса по математике
Как узнать, что дробь имеет простейшую форму?
Студенты пытаются объяснить этот вопрос. Они используют терминологию, которая недостаточно конкретна, чтобы сказать, что они на самом деле имеют в виду. Важно помочь учащимся стать более точными в своем языке, чтобы они могли более эффективно выражать свое понимание (MP6 — Внимание к точности).
Я пишу 1/5 на доске и прошу учащихся подумать над ключевыми вопросами.
• Можно ли упростить?
• Это самая простая форма?
• Откуда вы знаете?
(первые 2 вопроса я использую взаимозаменяемо, потому что мне нравится задавать важные вопросы по-разному, чтобы попытаться наладить связь со студентами, которые по-разному обрабатывают информацию)
Эта дробь является простой отправной точкой, потому что 1 имеет только 1 фактор — 1 Учащиеся понимают, что это нельзя упростить, потому что «кроме 1 числитель нельзя делить ни на что» . Я записываю это объяснение на доске как хорошую отправную точку. Я никогда не стираю его по мере продвижения, потому что мне нравится, когда учащиеся видят, насколько их мысли могут развиваться в ходе обсуждения в классе.
Я записываю это объяснение на доске как хорошую отправную точку. Я никогда не стираю его по мере продвижения, потому что мне нравится, когда учащиеся видят, насколько их мысли могут развиваться в ходе обсуждения в классе.
Далее я записываю дробь 3/5 и оспариваю их объяснение. Три имеет больше делителей, чем просто 1. Но эта дробь все еще имеет простейшую форму. Откуда вы знаете? «Эта дробь является простейшей из, потому что я знаю, что 3 и 5 являются простыми числами» Необходимы подсказки, чтобы помочь учащимся объяснить, что простые числа — это числа, имеющие только 1 пару множителей. Они чувствуют себя комфортно, объясняя, что, поскольку они 90 575 оба простые, вы не можете их больше разделить.
Чтобы развить это, я пишу 3/15 на доске. И скажите, что 3 — простое число. Означает ли это, что эта дробь имеет простейшую форму? Я позволяю студентам повернуться и обсудить этот вопрос.
Согласитесь, что это не так, потому что 3, хотя и простое, является делителем 15.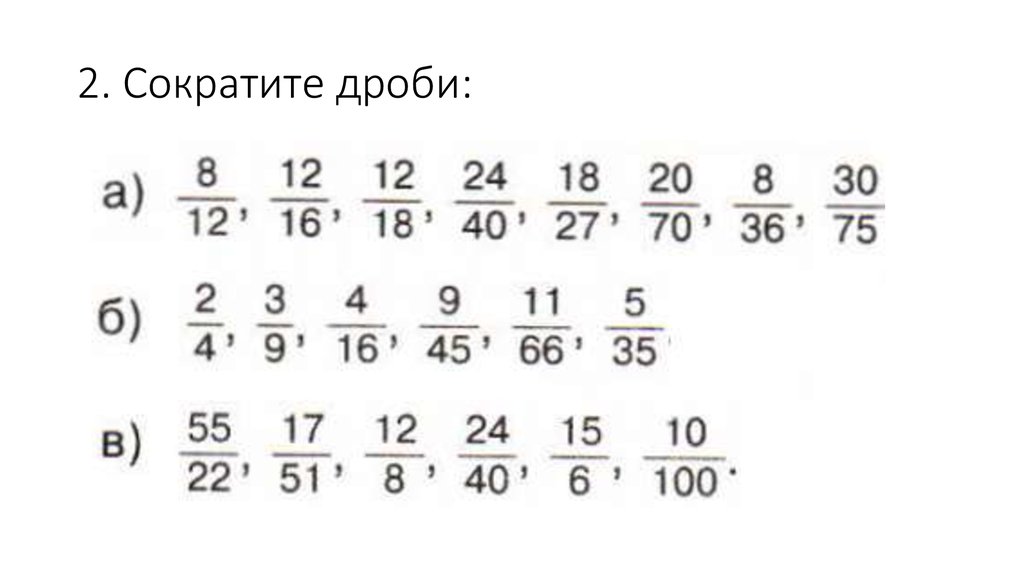 Значит, и 3, и 15 можно разделить на 3.
Значит, и 3, и 15 можно разделить на 3.
Это обсуждение позволяет мне ввести сокращающие коэффициенты как метод сокращения дробей. (См. скринкаст Использование факторизации для упрощения дробей.)
Я покажу еще несколько примеров этого метода сокращения дробей. Всегда представляю метод сокращающих коэффициентов и деление на дробное представление 1. Делая это, я неоднократно использую фразу общие знаменатели. Я не ввел этот термин официально, но постоянно использую его, чтобы познакомить с ним студентов.
Самостоятельная практика
20 минут
Учащиеся практикуются в упрощении дробей и поиске простейшей формы заданных дробей (на основе различных предоставленных указаний).
Пока они работают в парах, я хожу по разным группам и задаю им 3 основных вопроса.
• Можно ли упростить?
• Это самая простая форма?
• Откуда вы знаете?
Я хочу, чтобы учащиеся думали не только о процессе.
Я поощряю учащихся, которые предпринимают много шагов, чтобы добраться до простейшей формы, а также тех, кто сразу определяет наибольший общий множитель. Пока учащиеся могут определить общий множитель, а затем оценить новую дробь на предмет общего множителя между числителем и знаменателем.
Пока учащиеся могут определить общий множитель, а затем оценить новую дробь на предмет общего множителя между числителем и знаменателем.
Я прикрепил несколько видео дискуссий, которые у меня были со студенческими парами во время распространения.
Групповой обмен
5 минут
Это моя любимая часть урока. Учащимся предлагается выбрать проблему дня, которую они хотят обсудить. У нас есть время для 3 разных задач. Меня всегда впечатляют вопросы, которые задают студенты.
Раздел «Выбор проблемы» позволяет учащимся накапливать общий опыт, устанавливать связи, делиться стратегиями и задавать вопросы.
Я приложил a Откуда вы знаете, что это в простейшей форме? скринкаст, чтобы объяснить обсуждение, которое возникло из-за вопроса одного студента. Это показывает, как посредством диалога учащиеся могут обогатить свое языковое развитие в математике.
Похожие уроки
5 способов сделать сравнение дробей более увлекательным!
Сравнение дробей — это БОЛЬШОЙ шаг вперед по сравнению с простым определением дробей и форм разбиения. Теперь мы просим студентов посмотреть на две разные письменные дроби и использовать язык сравнения, например больше, меньше или равно. Это не шутка!
Теперь мы просим студентов посмотреть на две разные письменные дроби и использовать язык сравнения, например больше, меньше или равно. Это не шутка!
Если вы когда-либо преподавали сравнение дробей, вы знаете, что сложный характер содержания иногда может мешать учащимся полностью погрузиться в процесс обучения. В этом посте я описал пять моих любимых способов сделать сравнение дробей более увлекательным для ваших учеников!
Сравнение дробей в искусстве и фотографии
Если вы не знали, «Разговоры о числах» — одно из моих самых любимых занятий! Они создают такое сильное сообщество математиков и создают удивительные возможности для студентов, чтобы развивать навыки общения вокруг их математического мышления!
Дроби могут стать интересной темой для разговоров о числах. В то время как мы можем абсолютно точно написать несколько дробей на доске и попросить учащихся сравнить их (это СОВЕРШЕННО действительные и полезные разговоры о числах), также может быть интересно поменять местами! Один из моих любимых способов — спроецировать фотографию и предложить учащимся найти в ней дроби.
Некоторые примеры могут включать работы таких художников, как Пит Мондриан (см. изображение его работы ниже). Они отлично подходят для начала разговора и предлагают так много возможностей для обсуждения цветов и представления различных фракций. Мне также нравится, что в подобных беседах с цифрами есть несколько точек доступа, поэтому учащиеся могут изменять или расширять беседу, чтобы легче бросить вызов себе на своем «нужном уровне».
Изображение предоставлено Creative Commons, художник RоbsоnДругие забавные изображения включают здания, окна, фотографии организационных решений (вы знаете… с десятками ящиков!) С ними есть неограниченные возможности!
Создайте прогулку по галерее фракций
После демонстрации того, как обсуждать дроби на фотографиях/картинах во время «Разговоров о числах», вы можете превратить это в независимый центр в своих классах! Разместите фотографии/картины в своей комнате или сделайте их ксерокопии, чтобы ученики могли поместить их в свои математические журналы и позволить им начать писать о том, что они видят. Позвольте им рисовать, писать и/или использовать числа, чтобы поделиться своими мыслями о различных дробях, которые они видят.
Позвольте им рисовать, писать и/или использовать числа, чтобы поделиться своими мыслями о различных дробях, которые они видят.
Вы можете добавить к этому упражнению «банк слов», если хотите, чтобы они начали сравнивать дроби определенным образом (например, больше, меньше, целое, равно и т. д.).
Scaffolding Student Work
Прежде чем предложить учащимся начать самостоятельно сравнивать дроби, я обязательно включу несколько бесед о числах и мини-уроков по следующим темам:
- Сравнение дробей с одинаковым числителем
- Сравнение дробей с одинаковым знаменателем
- Использование эталонных дробей для сравнений
Однако, как только мы выработали базовое понимание и разработали несколько полезных стратегий, пришло время дать им возможность попробовать их самостоятельно… конечно, с некоторой подготовкой!
У меня есть несколько любимых занятий, когда нужно помочь учащимся сравнивать дроби. Они начинаются ОЧЕНЬ просто, и их можно использовать снова и снова, чтобы получить повторяющуюся, но содержательную практику (лично я держусь как можно дальше от одноразовых рабочих листов).
В этих упражнениях с дробями домино (также доступны с кубиками, если у вас нет домино) учащиеся сравнивают дроби с помощью встроенных визуальных средств.
Во-первых, мне нравится, когда они разделяют и затеняют свои формы (мы уже вместе поработали над этим). Имея на месте эти конкретные изображения, учащиеся могут легче расшифровать, какая дробь больше другой, а затем написать предложение для сравнения. По мере того, как они знакомятся, я предлагаю им сначала попытаться обосновать сравнение, а затем использовать визуальные эффекты, чтобы подтвердить (или нет) свои первоначальные мысли.
Вторая версия меняет изображение на числовую строку. Мои ученики часто сталкиваются с трудностями при работе с дробями на числовой прямой, поэтому предоставление им возможности поработать с ними было очень полезно! Я всегда стараюсь делать это в одну секунду, потому что тогда они уже знакомы с идеей и самим действием, так что теперь все, что им нужно сделать, это сосредоточиться на числовой прямой.
Предложение выбора вместо сравнения дробей
Всякий раз, когда я предлагаю своим ученикам ВЫБОР, вовлеченность возрастает! Это означает, что я ввожу несколько разных занятий (их не должно быть много, но 2-3) и позволяю им выбирать, как они хотят учиться.
Два из моих любимых заданий, которые я могу предложить учащимся на выбор, — это «Переверни дроби и сравни » (вы, возможно, знаете его как старую карточную игру «Война») и одно, которое я создал вместе со своими учениками под названием « Order’s Up! ”
Fraction Flip & Compare очень легко реализовать, потому что учащиеся часто имеют предыдущий опыт игры. Мне лично нравится иметь доску или какое-нибудь наглядное пособие, которое помогает учащимся отделить числитель от знаменателя.
Ученики ведут записи во время игры по трем причинам:
- Это позволяет мне видеть их понимание, даже если меня нет, потому что я работаю с небольшой группой.

- Студенты несут ответственность за свою работу. Внедрение листов для записей стало отличным лайфхаком для управления классом!
- Дает мне чистое и аккуратное место для включения модели линейки дробей, чтобы помочь учащимся стать более независимыми.
Заказ готов! Это еще один фаворит класса (я имею в виду, это пицца!). Это задание сложнее, чем «Перевернуть и сравнить дроби», потому что оно переходит от сравнения двух дробей к упорядочению четырех разных дробей от наименьшей к наибольшей. Опять же, я обязательно включаю модель дроби для поддержки и часто прошу студентов вести страницу с записью по всем тем же причинам, упомянутым выше.
Моим ученикам НРАВИТСЯ возможность выбирать, как они будут сравнивать дроби. Когда они мотивированы выбором, их уровень вовлеченности повышается. Когда их уровень вовлеченности повышается, их внимание увеличивается, и они с большей вероятностью улучшат свое понимание. ПОБЕДИТЬ!!!
Бесплатное упражнение «Сравнение дробей»
У ваших учеников возникают трудности при сравнении дробей с помощью эталонных дробей? Загрузите эту бесплатную загрузку со встроенной визуальной поддержкой, чтобы помочь им практиковаться!
Дай это мне!
Групповые игры, которыми они не могут насытиться!
Если вы раньше посещали мой блог, то знаете, что моя любимая игра для небольших групп — Kaboom! Я клянусь, вы можете использовать эту игру практически для каждого навыка в каждом предмете, который вы преподаете…. так что, конечно, я использую его, когда учу сравнивать дроби!
так что, конечно, я использую его, когда учу сравнивать дроби!
Если вы не знакомы с Kaboom, вам определенно захочется просмотреть этот пост в блоге, где я разбиваю его и даю несколько полезных советов о том, как его настроить и организовать в вашем классе.
Несколько лет назад я проходил собеседование на новую преподавательскую должность, и пришло время администрации прийти и посмотреть демонстрационный урок. На самом деле я поставил эту ТОЧНУЮ игру в один из моих математических центров, когда я преподавал в небольшой группе по математике. (Да, я достаточно доверяю этой игре, чтобы сделать это во время формального наблюдения во время интервью.)
Я получил много положительных отзывов, касающихся как уровня вовлеченности, так и ответственности учащихся на странице записи. И… если вам интересно, я получил работу!
Надеюсь, эти советы были вам полезны. ВСЕ студенческие игры и задания можно найти в моем Fraction Mega Pack , и он не зря называется мегапаком! Это почти 400 страниц ВСЕХ моих любимых игр для обучения дробям в третьем классе. Нажмите ЗДЕСЬ, чтобы проверить!
Нажмите ЗДЕСЬ, чтобы проверить!
Сокращение дробей (начальный, специальный курс)
Планы уроков
Уроки на уровне класса
Дошкольное учреждение, детский сад, классы 1–2, классы 3–5, средняя школа, старшая школа, продвинутый уровень, другое, все
Уроки предметной области
Искусство и ремесла, Компьютеры, Игры, География, Здоровье, История, Язык, Литература, Математика, Музыка, Физическое образование, Чтение/Письмо, Наука, Социальные науки, Специальное обучение, Другое
Специальное издание, уровень: Элементарный
Опубликовано в пятницу, 27 июля, 08:30:39 PDT 2007 Сарой Донцов ([email protected]).
Начальная школа Уайтли, Хоффман Эстейтс, США
Необходимые материалы: см. шаг 9 урока.
Время занятий: 1-2 урока
Преподаваемые понятия: дроби
План урокаПредмет: Математика Дата: 5 февраля 2007 г.
Поведенческая цель:
Получив словесную подсказку, каждый учащийся должен выполнить практический набор (подлежит уточнению после управляемой практики) задач на рабочем листе, требуя от учащихся сокращения правильных дробей и запишите их в простейшей форме с точностью 75% задач, решенных самостоятельно.Иллинойс Стандарт обучения:
6.B.2 Решение одно- и двухэтапных задач на дробиЭтапы обучения:
Повестка дня
Сокращение дробей
1. Повторение терминов
2. Я покажу вам (2/4, 3/6)
3 Словарный запас
Простейшая форма
Сокращение
4. Мы делаем что-то вместе (4/8, 6/8, 3/12)
5. Отмечаем
6. Вы делаете что-то самостоятельно (практический лист)
7. Проверяем ответы
8. Домашнее задание
1. Упреждающий набор (фокус, крючок для привлечения внимания учащихся): 907:56 На прошлой неделе, когда мы занимались числовыми рядами, мы выяснили, что дроби можно записывать более чем одним способом.Верхняя часть нашей числовой линии и нижняя часть нашей числовой линии выглядели по-разному, но по-прежнему представляли одно и то же. Сегодня мы познакомимся с другими способами записи дробей.
2. Цель (задача):
В математике нам нужно, чтобы наша работа была ясной и максимально возможной, а это значит, что нам, возможно, придется изменить вид наших дробей. (Приведите пример написания) Наши коллеги-математики проявляют любезность к тому, чтобы наши дроби выглядели как можно лучше.
3. Введите:
Раздайте каждому учащемуся раздаточный материал с математическими терминами. Давайте пройдемся по этим терминам и решим, какие из них мы уже изучили в этом блоке, а какие, возможно, еще не видели в этом году.4. Моделирование (показать):
Итак, если я хочу показать дробь наилучшим образом, мне нужно сначала посмотреть на нее и решить, есть ли способ сделать ее более понятной. Я собираюсь показать вам, как это сделать.
Я хочу, чтобы вы сначала посмотрели на меня, а потом мы могли бы сделать кое-что вместе.907:56 Я смотрю на 2/4. Я ничего сразу не замечаю. Я собираюсь посмотреть на свои математические слова и посмотреть, смогу ли я взглянуть на них по-другому. Чтобы помочь мне, я собираюсь использовать свой математический мозг и посмотреть на 2 числа. Я знаю, что 2 — это множитель 4. Я также знаю, что 4 кратно 2. Если моя цель — упростить чтение, я попытаюсь сделать его меньше. Думаю, я начну с перечисления множителей двойки и множителя четвёрки.
2—1,2
4—1,2,4
GCF—2
2 разделить на 2 это что?
4 разделить на 2 это сколько?
Напишите ответ
Проверьте ответ в моем калькулятореПопробуйте другой . . . 3/6 (повторите процесс)
СЛОВАРЬ и КОНТРОЛЬНЫЙ СПИСОК
5. Управляемая практика (следуйте за мной):
Проведите процесс со студентами для дроби 4/8:
Используйте числа в наших предложениях
Запишите множители
Выбрать наибольшее Общий множитель
Уменьшение дроби
Проверьте ответ в калькуляторе.
При необходимости окажите помощь.6. Проверка на понимание:
Вы заметили закономерность?
Каков был ответ на все наши вопросы?
Будут ли ВСЕ дроби уменьшаться до ?7. Дополнительная практика:
Давайте проверим. Почему бы нам не попробовать 6/8
Можем ли мы использовать числитель и знаменатель в нашем предложении? №
Что ж, давайте перейдем к следующему шагу и найдем GCF для двух чисел.
Завершите шаги.Решите еще одну задачу с дробью 3/12.
7. Независимая практика:
Я думаю, вы готовы показать мне, что можете сделать это самостоятельно. Сделайте столько, сколько сможете, за оставшееся время, и мы проверим их вместе. (Больше или меньше, в зависимости от времени)
8. Завершение:
Большинство/все вы приложили ко мне много тяжелой работы и усилий. Давайте рассмотрим шаги в последний раз. Кто может сказать мне, каковы 5 шагов для приведения правильных дробей к их простейшей форме?
В качестве домашнего задания я хочу, чтобы вы ответили на все вопросы на этой странице.Обязательно покажите всю свою работу и используйте черновую бумагу, если вы не можете уместить все на этом листе. Давайте вместе прочитаем инструкции и убедимся, что знаем, как решить все задачи.
9. Материалы:
Условия слока
Контрольный список
Кальцинирование
Калькулятор
Белая доска/ручка
Диаграмма умножения
Рабочие листы
Дома множитель _____________________________________ кратен ___________________
Контрольный список
Шаг 1: Напишите множители для числителя и знаменателя
Шаг 2: Выберите наибольший общий множитель
Шаг 3: Уменьшите дробь путем деления
Шаг 4: Запишите уменьшенную дробь
Шаг 5: Проверьте ответ в калькуляторе ! Не знаю, как вы, а мы по колено в изучении дробей. Так много нужно узнать и так мало времени, чтобы изучить все это! Я несколько раз писал о различных мероприятиях, которые мы проделали, особенно об операциях с фракциями, но на этот раз ВСЕ внимание сосредоточено на концепциях фракций! Мы должны охватить так много основных понятий: упрощение дробей, нахождение эквивалентных дробей, работа с дробями на числовой прямой, сравнение дробей, неправильные дроби и смешанные числа и т.
д. ТАК МНОГО! Ниже вы найдете некоторые из лучших уроков фракций, мероприятий, бесплатных материалов и ресурсов из моего класса и от учителей по всей стране. Пост длинный, но он того стоит! 🙂 Удачного планирования!
Привязка к дробям и примечания
Как всегда, у нас есть привязка к единице дроби. Прежде чем вы посмотрите на это и паникуете из-за количества информации на нем, эта якорная таблица предназначена для заполнения в течение нескольких недель, когда вы обучаете каждой из концепций. Я начал только с шаблона, а затем заполнял каждое поле по мере того, как они узнавали об этом. НЕ делайте всю эту якорную диаграмму за один день! 🙂 Это отличная справочная таблица, которую можно оставить висеть в комнате до конца года, не занимая слишком много места на стене.
Я также создал эту папку для интерактивной тетради моих учеников. Опять же, мы помещаем сюда заметки по мере прохождения блока. Мне очень нравятся эти блокноты, потому что они могут легко получить доступ к своим заметкам и концепциям, когда им нужны небольшие напоминания.
Не знаю, что бы я делала без интерактивных блокнотов!
В этом году наш блок математики разделен: час до обеда и двадцать минут после обеда. В течение этих последних двадцати минут мы обычно заканчиваем нашу последнюю математическую ротацию и оформляем выходной билет. Я создал билеты на выход для всех вышеперечисленных концепций. Вы также можете использовать их в качестве доказательств или самостоятельной работы в своих блокнотах!
Здесь вы можете БЕСПЛАТНО скачать раскладушку и ШЕСТЬ выходных билетов!
Карточки с заданиями на дроби
Вот моя любимая часть моего раздела по дробям просто потому, что он такой красивый и организованный, и как только он будет выполнен, один раздел моего математического семинара ЗАВЕРШЕН для всего раздела! Мои Карточки с заданиями на дроби , на мой взгляд, идеально подходят для студенческой практики. У меня все организовано и готово к работе, чтобы учащиеся могли легко получить доступ к карточкам, листам для записей и ключам для ответов.
Я могу легко взять их для работы с небольшими группами или со всем классом, если это необходимо.
Вы можете просмотреть мои карточки заданий ЗДЕСЬ.
Уроки эквивалентных дробей
Вот запись в блокноте, которую мы сделали для эквивалентных дробей. Это такой огромный навык для детей, и кажется, что как только они его освоят, они действительно его ПОЛУЧАЮТ! Для этой записи в журнале мы использовали манипуляции с блоками шаблонов. Это изображение страницы моего блокнота, где я проследил блоки, но я использовал машину для высечки Эллисона, чтобы вырезать бумажные версии блоков шаблонов, чтобы они могли манипулировать ими и фактически вклеивали в свои блокноты. Это была настоящая тренировка рук, позволяющая избавиться от всех этих манипуляций! 🙂
Мы начали с определения эквивалентных дробей. Я объяснил им, что значение желтого шестиугольника равно единице. Затем я попросил их сделать шестиугольники из всех других форм и вычислил значение каждой формы.
Мы пришли к выводу, что каждый раз, когда ваши числитель и знаменатель совпадают, значение дроби составляет одно целое. Для них это был ОТЛИЧНЫЙ визуальный способ увидеть это. Они также увидели, что все они были эквивалентными или равными дробями. Затем мы перешли к трапеции, и я попросил их использовать треугольники, чтобы составить эквивалентную дробь. Затем вы можете увидеть, где я записал две дроби и спросил их, что мы сделали с первой дробью, чтобы получить вторую дробь. Они сделали БОЛЬШУЮ работу, делая выводы! Все это было под руководством учителей, но когда мы закончили, они проделали ФЕНОМЕНАЛЬНУЮ работу, применив свои навыки, используя мои Карточки с заданиями на эквивалентные дроби. Мы играли в БИНГО с карточками. Так весело!
Вот изображение наших игровых досок для игры в бинго. Вы можете использовать их с ЛЮБЫМ набором карточек задач!
Вы можете скачать БЕСПЛАТНЫЕ доски для карточек с заданиями Бинго ЗДЕСЬ.

Еще один способ, которым я всегда предлагаю своим ученикам визуализировать эквивалентные дроби, — это Fraction Fringe! Это высечки от Элисон, и это такой УДИВИТЕЛЬНЫЙ ресурс! Я использовал их в течение многих лет, и они очень ценны для детей.
Когда ваши ученики будут готовы продемонстрировать свои эквивалентные навыки дроби, Рецепт катастрофы — идеальный вариант!
Уроки упрощения дробей
Упрощение дробей, хотя это и не является стандартом в моем классе, по моему мнению, является важным навыком, который изучают учащиеся, поэтому мы всегда освещаем его. Одно из их любимых занятий в подразделении фракций — это занятие «Восхитительно упрощенные дроби»! Мы используем M&Ms (вы также можете использовать Skittles) и идем в город с упрощением!
Вы можете БЕСПЛАТНО скачать мою работу по упрощению дробей ЗДЕСЬ!
Мне нравится, как Стефани из Преподавание в комнате 6 объясняет упрощение самым простым способом.
Обучение учащихся нахождению наибольших общих факторов при упрощении дробей является КЛЮЧЕВЫМ в устранении разочарования, с которым сталкиваются многие учащиеся, связанные с этой концепцией. Она проведет вас через это шаг за шагом…
Еще уроки дробей
Мне очень нравится эта якорная диаграмма от Тессы в 9 лет.0679 Истории вне класса. Все дело в выводах, и мне нравится, что вы можете сказать, что она сделала это со своими учениками и действительно обсудила ПОЧЕМУ каждое из этих утверждений.
Еще один предмет, который я всегда готовлю заранее, — это мой математический проект Fractions Math Project . Я делаю несколько разных пакетов, которые включают разные страницы в зависимости от способностей моих учеников. Я использую эти пакеты в своей модели мастерской, для тех, кто рано заканчивает, и в качестве домашней работы. Проект охватывает ТАКОЕ множество концепций, что здорово иметь пакет увлекательных заданий для моих учеников.
Вы можете увидеть мой математический проект дробей ЗДЕСЬ.
Эта идея от Curious Firsties НАСТОЛЬКО умна! У нее есть ученики, создающие часть музея фракций, а затем все они проходят через музей и выполняют задание. Так весело!
Теперь, если вы, студенты, наконец-то избавились от сахарного опьянения после задания «Упрощение дробей M&M», пришло время добавить в смесь немного Skittles. 🙂 Эта страница взята из моего пакета Skittles Math, и внизу на самом деле много эквивалентной работы с дробями, поэтому она всегда появляется во время работы всей группы!
Вы можете увидеть мой математический пакет Skittles ЗДЕСЬ.
Для учащихся очень важно уметь обосновывать свои мысли, и у Мэг из The Teacher Studio есть так много замечательных уроков дробей, которые действительно заставят детей критически относиться к дробям.
Мне нравится эта идея и то, как она заставляет их пытаться убедить других учеников, почему они должны быть в команде «Да или Нет»!
В конце нашего модуля я всегда ставлю мини-оценку своим ученикам. Вот моя оценка дроби, которую я буду использовать. Вы можете использовать его для оценки, обзора или распечатки для вашего подразделения.
Мне нравится, как Грег из Мистер Элементарная Математика отлично помогает учащимся визуализировать понятия дробей. У него есть солидные идеи для обучения дробям на числовых рядах, а печатные формы, которые вы видите здесь, БЕСПЛАТНЫ!
Как только я увидел этот удивительный проект фракции, Я ЗНАЛ, что должен добавить его в свой список планов в этом году! У Тары из Fourth Grade Frolics ТАКАЯ хорошая идея с этим.
Я видел много разных версий этой визуальной дроби числовых линий, и я думаю, что они имеют решающее значение для учащихся! Это так кинестетично и так наглядно.
Для этого изображения нет ссылки на оригинальный источник, поэтому, если вы знаете источник, сообщите мне об этом.
Вот еще одна замечательная модель для сравнения и упорядочивания дробей. Визуальные модели очень важны, и я чувствую, что для студентов невероятно важно иметь возможность создавать свои собственные визуальные модели. Источник ЗДЕСЬ.
Я действительно чувствую, что могу опубликовать еще двадцать идей в этом блоге, и это ВСЕ ЕЩЕ не будет отдавать должное всем замечательным идеям! Если вы ищете еще больше, зайдите на мою доску Fractions в Pinterest, чтобы найти множество идей. Надеюсь, вы нашли здесь полезные идеи!
Оценки фракций
Вы можете БЕСПЛАТНО скачать обзор фракций или оценку ЗДЕСЬ.
Другие уроки дробей на Pinterest
Если вы ищете идеи по урокам дробей для ОПЕРАЦИЙ, ознакомьтесь с некоторыми из моих старых постов в блоге!
<
Просмотры сообщений: 26,577
Калькулятор дробей
Использование калькулятора
Используйте этот калькулятор дробей для сложения, вычитания, умножения и деления дробей.
Ответы представляют собой дроби в наименьшем выражении или смешанные числа в сокращенной форме.
Введите правильные или неправильные дроби, выберите математический знак и нажмите «Рассчитать». Это калькулятор дробей с шагами, показанными в решении.
Если у вас есть отрицательные дроби, поставьте знак минус перед числителем. Итак, если одна из ваших дробей равна -6/7, вставьте -6 в числитель и 7 в знаменатель.
Иногда в математических задачах используется слово «из», например, Что такое 1/3 от 3/8? Из средств нужно умножить, поэтому нужно решить 1/3 × 3/8.
Для выполнения математических операций со смешанными числами (целыми числами и дробями) используйте Калькулятор смешанных чисел.
Математика дробей с разными знаменателями
Есть 2 случая, когда вам нужно знать, имеют ли ваши дроби разные знаменатели:
- если вы складываете дроби
- если вы вычитаете дроби
Как складывать и вычитать дроби
- Найти наименьший общий знаменатель
- Вы можете использовать ЖК-калькулятор для нахождения наименьшего общего знаменателя набора дробей
- Для первой дроби найдите, на какое число нужно умножить знаменатель, чтобы получить наименьший общий знаменатель
- Умножьте числитель и знаменатель первой дроби на это число
- Повторите шаги 3 и 4 для каждой фракции
- Для уравнений сложения добавьте числители дробей
- Для уравнений вычитания вычтите числители дробей
- Преобразование неправильных дробей в смешанные числа
- Сократить дробь до наименьшего члена
Как умножать дроби
- Умножить все числители вместе
- Умножить все знаменатели вместе
- Уменьшить результат до минимального значения
Как делить дроби
- Перепишите уравнение, как в «Сохранить, изменить, перевернуть»
- Сохранить первую дробь
- Заменить знак деления на умножение
- Переверните вторую дробь, поменяв местами верхние и нижние числа
- Умножить все числители вместе
- Умножить все знаменатели вместе
- Уменьшить результат до минимального значения
Формулы дробей
Существует способ складывать или вычитать дроби, не находя наименьший общий знаменатель (LCD).
Этот метод предполагает перекрестное умножение дробей. См. формулы ниже.
Возможно, вы обнаружите, что использовать эти формулы проще, чем вычислять наименьший общий знаменатель.
Формулы для умножения и деления дробей следуют тому же процессу, что описан выше.
Сложение дробей
Формула сложения дробей:
\( \dfrac{a}{b} + \dfrac{c}{d} = \dfrac{ad + bc}{bd} \)
Пример шаги:
\( \dfrac{2}{6} + \dfrac{1}{4} = \dfrac{(2\times4) + (6\times1)}{6\times4} \)
\( = \dfrac{14}{24} = \dfrac {7}{12} \)
Вычитание дробей
Формула для вычитания дробей:
\( \dfrac{a}{b} — \dfrac{c}{d} = \dfrac{ad — bc}{bd} \)
Пример шагов:
\( \dfrac{2}{6 } — \dfrac{1}{4} = \dfrac{(2\times4) — (6\times1)}{6\times4} \)
\( = \dfrac{2}{24} = \dfrac { 1}{12} \)
Умножение дробей
Формула умножения дробей:
\( \dfrac{a}{b} \times \dfrac{c}{d} = \dfrac{ac}{bd } \)
Пример шагов:
\( \dfrac{2}{6} \times \dfrac{1}{4} = \dfrac{2\times1}{6\times4} \)
\( = \dfrac{2}{24} = \dfrac {1}{12} \)
Деление дробей
Формула деления дробей:
\( \dfrac{a}{b} \ div \dfrac{c}{d} = \dfrac{ad}{bc} \)
Пример шагов:
\( \dfrac{2}{6} \div \dfrac{1}{4} = \dfrac {2\times4}{6\times1} \)
\( = \dfrac{8}{6} = \dfrac {4}{3} = 1 \dfrac{1}{3} \)
Связанные калькуляторы
Для выполнения математических операций над дробями смешанных чисел используйте наш Калькулятор смешанных чисел.

 год
год



 Какая дробь получилась?
Какая дробь получилась? Первичное закрепление.
Первичное закрепление.
 Сократи дробь
Сократи дробь Быстро передайте тепло другу, соединив свои ладошки с ладошками соседа.
Быстро передайте тепло другу, соединив свои ладошки с ладошками соседа. Педагогический (научно-педагогический) состав
Педагогический (научно-педагогический) состав Курсы/ Кружки/ Факультативы
Курсы/ Кружки/ Факультативы )
)



 Какая дробь получилась?
Какая дробь получилась? Первичное закрепление.
Первичное закрепление.
 Сократи дробь
Сократи дробь Быстро передайте тепло другу, соединив свои ладошки с ладошками соседа.
Быстро передайте тепло другу, соединив свои ладошки с ладошками соседа. 0018
0018

 Верхняя часть нашей числовой линии и нижняя часть нашей числовой линии выглядели по-разному, но по-прежнему представляли одно и то же. Сегодня мы познакомимся с другими способами записи дробей.
Верхняя часть нашей числовой линии и нижняя часть нашей числовой линии выглядели по-разному, но по-прежнему представляли одно и то же. Сегодня мы познакомимся с другими способами записи дробей. 907:56 Я смотрю на 2/4. Я ничего сразу не замечаю. Я собираюсь посмотреть на свои математические слова и посмотреть, смогу ли я взглянуть на них по-другому. Чтобы помочь мне, я собираюсь использовать свой математический мозг и посмотреть на 2 числа. Я знаю, что 2 — это множитель 4. Я также знаю, что 4 кратно 2. Если моя цель — упростить чтение, я попытаюсь сделать его меньше. Думаю, я начну с перечисления множителей двойки и множителя четвёрки.
907:56 Я смотрю на 2/4. Я ничего сразу не замечаю. Я собираюсь посмотреть на свои математические слова и посмотреть, смогу ли я взглянуть на них по-другому. Чтобы помочь мне, я собираюсь использовать свой математический мозг и посмотреть на 2 числа. Я знаю, что 2 — это множитель 4. Я также знаю, что 4 кратно 2. Если моя цель — упростить чтение, я попытаюсь сделать его меньше. Думаю, я начну с перечисления множителей двойки и множителя четвёрки. 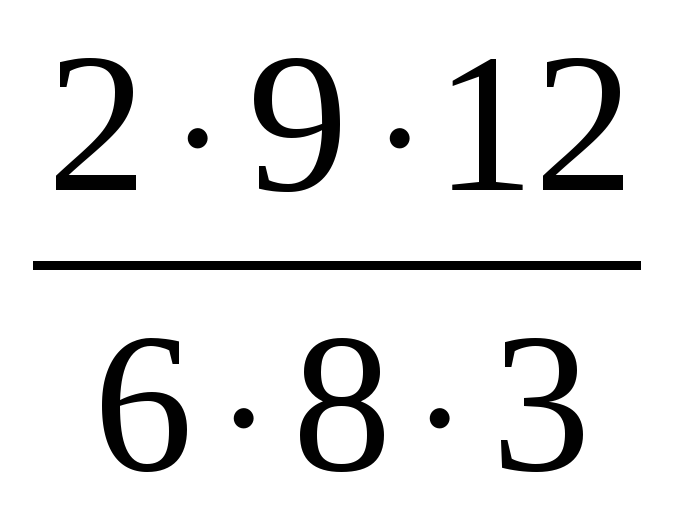
 Обязательно покажите всю свою работу и используйте черновую бумагу, если вы не можете уместить все на этом листе. Давайте вместе прочитаем инструкции и убедимся, что знаем, как решить все задачи.
Обязательно покажите всю свою работу и используйте черновую бумагу, если вы не можете уместить все на этом листе. Давайте вместе прочитаем инструкции и убедимся, что знаем, как решить все задачи. д. ТАК МНОГО! Ниже вы найдете некоторые из лучших уроков фракций, мероприятий, бесплатных материалов и ресурсов из моего класса и от учителей по всей стране. Пост длинный, но он того стоит! 🙂 Удачного планирования!
д. ТАК МНОГО! Ниже вы найдете некоторые из лучших уроков фракций, мероприятий, бесплатных материалов и ресурсов из моего класса и от учителей по всей стране. Пост длинный, но он того стоит! 🙂 Удачного планирования! Не знаю, что бы я делала без интерактивных блокнотов!
Не знаю, что бы я делала без интерактивных блокнотов! Я могу легко взять их для работы с небольшими группами или со всем классом, если это необходимо.
Я могу легко взять их для работы с небольшими группами или со всем классом, если это необходимо. Мы пришли к выводу, что каждый раз, когда ваши числитель и знаменатель совпадают, значение дроби составляет одно целое. Для них это был ОТЛИЧНЫЙ визуальный способ увидеть это. Они также увидели, что все они были эквивалентными или равными дробями. Затем мы перешли к трапеции, и я попросил их использовать треугольники, чтобы составить эквивалентную дробь. Затем вы можете увидеть, где я записал две дроби и спросил их, что мы сделали с первой дробью, чтобы получить вторую дробь. Они сделали БОЛЬШУЮ работу, делая выводы! Все это было под руководством учителей, но когда мы закончили, они проделали ФЕНОМЕНАЛЬНУЮ работу, применив свои навыки, используя мои Карточки с заданиями на эквивалентные дроби. Мы играли в БИНГО с карточками. Так весело!
Мы пришли к выводу, что каждый раз, когда ваши числитель и знаменатель совпадают, значение дроби составляет одно целое. Для них это был ОТЛИЧНЫЙ визуальный способ увидеть это. Они также увидели, что все они были эквивалентными или равными дробями. Затем мы перешли к трапеции, и я попросил их использовать треугольники, чтобы составить эквивалентную дробь. Затем вы можете увидеть, где я записал две дроби и спросил их, что мы сделали с первой дробью, чтобы получить вторую дробь. Они сделали БОЛЬШУЮ работу, делая выводы! Все это было под руководством учителей, но когда мы закончили, они проделали ФЕНОМЕНАЛЬНУЮ работу, применив свои навыки, используя мои Карточки с заданиями на эквивалентные дроби. Мы играли в БИНГО с карточками. Так весело!
 Обучение учащихся нахождению наибольших общих факторов при упрощении дробей является КЛЮЧЕВЫМ в устранении разочарования, с которым сталкиваются многие учащиеся, связанные с этой концепцией. Она проведет вас через это шаг за шагом…
Обучение учащихся нахождению наибольших общих факторов при упрощении дробей является КЛЮЧЕВЫМ в устранении разочарования, с которым сталкиваются многие учащиеся, связанные с этой концепцией. Она проведет вас через это шаг за шагом…
 Мне нравится эта идея и то, как она заставляет их пытаться убедить других учеников, почему они должны быть в команде «Да или Нет»!
Мне нравится эта идея и то, как она заставляет их пытаться убедить других учеников, почему они должны быть в команде «Да или Нет»! Для этого изображения нет ссылки на оригинальный источник, поэтому, если вы знаете источник, сообщите мне об этом.
Для этого изображения нет ссылки на оригинальный источник, поэтому, если вы знаете источник, сообщите мне об этом. Ответы представляют собой дроби в наименьшем выражении или смешанные числа в сокращенной форме.
Ответы представляют собой дроби в наименьшем выражении или смешанные числа в сокращенной форме. Этот метод предполагает перекрестное умножение дробей. См. формулы ниже.
Этот метод предполагает перекрестное умножение дробей. См. формулы ниже.