Дробные выражения 6 класс онлайн-подготовка на Ростелеком Лицей
Дробное выражение
Что же такое дробь? Например, дробь – это деление числа 7 на число 12, записанное с помощью дробной черты.
Частное двух чисел или выражений, в котором знак деления обозначен чертой, называют дробным выражением.
Примеры дробных выражений:
Дробь также является дробным выражением.
Упрощение дробных выражений
У дробного выражения существуют эквивалентные, равные ему, выражения. Выбрать из всех эквивалентных выражений самое простое – значит упростить дробное выражение.
Пример
Упростить дробное выражение:
Решение
Выполним вычитание в числители и сложение в знаменателе:
Разделим числитель и знаменатель на 17:
Ответ: .
Задача 1
Упростите дробное выражение:
Решение
В числителе и знаменателе – смешанные дроби. Чтобы разделить одну смешанную дробь на другую, нужно обе записать как неправильные.
Получившееся дробное выражение эквивалентно произведению дробных выражений:
Сократим знаменатель первой дроби и числитель второй дроби на 3:
Ответ: .
Задача 2
Сложите дробные выражения:
Решение
1 способ
Приведем эти дробные выражения к одному знаменателю, для этого умножим числитель и знаменатель первой дроби на 2:
Чтобы избавиться от десятичной дроби в знаменателе, умножим числитель и знаменатель на 10:
Сократим числитель и знаменатель на 7:
2 способ
Можно сразу избавиться от десятичных дробей в знаменателях, для этого умножим числитель и знаменатель каждой дроби на 10:
Далее приводим два дробных выражения к общему знаменателю:
Сократим числитель и знаменатель на 7:
Ответ: .
Задача 3
Упростите дробное выражение:
Решение
Преобразуем числитель и знаменатель в обыкновенные дроби:
Запишем получившееся выражение с помощью знака деления:
Чтобы разделить на дробь, нужно умножить на перевернутую дробь:
Числитель первой дроби и знаменатель второй можно сократить на 5 и на 4:
Ответ: .
Задача 4
Упростите дробное выражение:
1.
Решение
Преобразуем числитель и знаменатель в обыкновенные дроби:
Запишем это дробное выражение с помощью знака деления, а далее заменим знак деления на знак умножения и перевернем вторую дробь:
Сократим числитель первой дроби и знаменатель второй на 3 и 7, а числитель второй дроби и знаменатель первой – на 5:
Сократим числитель и знаменатель на 2:
2)
Решение
Преобразуем числитель первого дробного выражения и знаменатель второго:
Распишем данные дробные выражения с помощью знака деления:
Заменим знаки деления на знаки умножения и перевернем соответствующие дроби:
Первое дробное выражение сократим на 9:
Приведем дробные выражения к общему знаменателю, для этого числитель и знаменатель первого выражения умножим на 3, а числитель и знаменатель второго выражения умножим на 7:
Вычислим числители обеих дробей и сложим эти дроби:
Сократим полученную дробь на 2:
Ответ: 1.
; 2. .
Преобразование «многоэтажных» дробей
Существует очень простой алгоритм, который позволяет за одно действие разобрать «многоэтажную» дробь и получить обычную «двухэтажную».
Необходимо после знака равно начертить дробную черту и для каждого элемента из «многоэтажной» дроби найти его место в новой дроби. Для этого нужно рассмотреть каждое число в исходной дроби.
Если число находилось в исходной дроби нечетное число раз в знаменателе, то в новой дроби оно окажется в знаменателе; если число находилось в исходной дроби четное число раз в знаменателе или не находилось в знаменателе вообще, то в новой дроби оно окажется в числителе.
Рассмотрим примеры.
Упростите дробные выражения.
1.
Рассмотрим каждое число данного дробного выражения:
Число 5 (в данном выражении две пятерки, их рассматриваем отдельно) находится в числителе дроби и в числителе всего исходного дробного выражения.
То есть не находится в знаменателе, следовательно, в новой дроби это число окажется в числителе;
число 7 находится в знаменателе дроби и в числителе всего исходного дробного выражения. То есть находится в знаменателе нечетное число раз, следовательно, в новой дроби это число окажется в знаменателе;
число 16 находится в числителе всего исходного дробного выражения. То есть не находится в знаменателе, следовательно, в новой дроби это число окажется в числителе;
число 4 находится в числителе дроби и в знаменателе всего исходного дробного выражения. То есть находится в знаменателе нечетное число раз, следовательно, в новой дроби это число окажется в знаменателе;
число 3 находится в знаменателе дроби и в знаменателе всего исходного дробного выражения. То есть находится в знаменателе четное число раз, следовательно, в новой дроби это число окажется в числителе;
число 5 находится в знаменателе всего дробного выражения.
То есть находится в знаменателе нечетное число раз, следовательно, в новой дроби это число окажется в знаменателе.
Запишем полученное дробное выражение:
Сократим числитель и знаменатель на 5 и на 4:
2.
Рассмотрим каждое число данного дробного выражения:
Число 3 не находится в знаменателе, следовательно, в новой дроби это число окажется в числителе;
число 5 находится в знаменателе дроби , то есть нечетное количество раз, следовательно, в новой дроби это число окажется в знаменателе;
число 7 не находится в знаменателе, следовательно, в новой дроби это число окажется в числителе;
число 6 находится в знаменателе всего дробного выражения, то есть нечетное количество раз, следовательно, в новой дроби это число окажется в знаменателе;
число 8 находится в знаменателе дроби и в знаменателе всего дробного выражения, то есть четное количество раз, следовательно, в новой дроби это число окажется в числителе;
число 7 находится в знаменателе всего дробного выражения, то есть нечетное количество раз, следовательно, в новой дроби это число окажется в знаменателе;
число 5 находится в знаменателе всего дробного выражения и в знаменателе выражения , то есть четное количество раз, следовательно, в новой дроби это число окажется в числителе;
число 9 находится в знаменателе всего дробного выражения, то есть нечетное количество раз, следовательно, в новой дроби это число окажется в знаменателе.
Запишем полученное дробное выражение:
Сократим числитель и знаменатель на 5, 7, 2 и 3:
3.
Рассмотрим числа в каждом дробном выражении:
а) выражение
Число 5 не находится в знаменателе, следовательно, в новой дроби это число окажется в числителе;
число 7 находится в знаменателе дроби , то есть нечетное количество раз, следовательно, в новой дроби это число окажется в знаменателе;
число 9 не находится в знаменателе, следовательно, в новой дроби это число окажется в числителе;
число 18 находится в знаменателе всего дробного выражения, то есть нечетное количество раз, следовательно, в новой дроби это число окажется в знаменателе.
б) выражение
Число 5 не находится в знаменателе, следовательно, в новой дроби это число окажется в числителе;
число 2 находится в знаменателе всего дробного выражения, то есть нечетное количество раз, следовательно, в новой дроби это число окажется в знаменателе;
число 7 находится в знаменателе дроби и в знаменателе всего дробного выражения, то есть четное количество раз, следовательно, в новой дроби это число окажется в числителе;
число 3 находится в знаменателе всего дробного выражения, то есть нечетное количество раз, следовательно, в новой дроби это число окажется в знаменателе.
Запишем полученные дробные выражения:
Сократим числитель и знаменатель первого выражения на 9:
Приведем дробные выражения к общему знаменателю, для этого числитель и знаменатель первого выражения умножим на 3, а числитель и знаменатель второго выражения умножим на 7:
Вычислим числители обеих дробей и сложим эти дроби:
Сократим полученную дробь на 2:
Ответ: 1.
; 2. ; 3. .
Задача 5 (дробные выражения с переменными)
Чтобы найти значение выражения с переменными, необходимо подставить в это выражение значения этих переменных. Но предварительно имеет смысл упростить выражение, если это возможно.
Найти значение выражения.
1. , при ;
Решение
Упростим данное выражение. Приведем слагаемые к общему знаменателю, для этого умножим числитель и знаменатель второй дроби на 2:
Подставим в полученное выражение значение переменных:
2. , при ;
Решение
Упростим данное выражение. Приведем слагаемые к общему знаменателю, для этого умножим числитель и знаменатель второй дроби на 2:
Так как , то:
Мы получили ответ, даже не подставив значения переменных.
Ответ: . 1; 2. 0.
Список литературы
1. Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. – М.: Мнемозина, 2012.
2. Мерзляк А.Г., Полонский В.В., Якир М.С. Математика 6 класс. – Гимназия. 2006.
3. Депман И.Я., Виленкин Н.Я. За страницами учебника математики. – М.: Просвещение, 1989.
4. Шеврин Л.Н., Гейн А.Г., Коряков И.О., Волков М.В. Математика: Учебник-собеседник для 5–6 классов средней школы. – М.: Просвещение, Библиотека учителя математики, 1989.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. Интернет портал «School-assistant.ru» (Источник)
2. Интернет портал «School.xvatit.com» (Источник)
3. Видеохостинг «YouTube» (Источник)
Домашнее задание
1.
Задания 695 (ж, и), 698, 703 (в) (стр. 111–113) – Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6
2. Найдите значение выражения:
3. Найдите значение выражения
, при
Найдите значение выражения (действия с дробями) – как решать
Формулировка задачи: Найдите значение выражения (действия с дробями).
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 1 (Действия с дробями).
Рассмотрим, как решаются подобные задачи на примерах.
Пример задачи 1:
Найдите значение выражения 5/4 + 7/6 : 2/3.
Решение:
Вычислим значение выражения. Для этого определим порядок действий: сначала умножение и деление, затем сложение и вычитание. И выполним необходимые действия в нужном порядке:
Ответ: 3
Пример задачи 2:
Найдите значение выражения (3,9 – 2,4) ∙ 8,2
Решение:
Вычислим значение выражения.
Для этого определим порядок действий: сначала умножение и деление, затем сложение и вычитание. При этом действия в скобках выполняются раньше, чем действия за скобками. И выполним необходимые действия в нужном порядке:
Ответ: 12,3
Пример задачи 3:
Найдите значение выражения 27 ∙ (1/3 – 4/9 – 5/27).
Решение:
Вычислим значение выражения. Для этого определим порядок действий: сначала умножение и деление, затем сложение и вычитание. При этом действия в скобках выполняются раньше, чем действия за скобками. И выполним необходимые действия в нужном порядке:
Ответ: –8
Пример задачи 4:
Найдите значение выражения 2,7 / (1,4 + 0,1)
Решение:
Вычислим значение выражения. Для этого определим порядок действий: сначала умножение и деление, затем сложение и вычитание. При этом действия в скобках выполняются раньше, чем действия за скобками. И выполним необходимые действия в нужном порядке:
Ответ: 1,8
Пример задачи 5:
Найдите значение выражения 1 / (1/9 – 1/12).
Решение:
Вычислим значение выражения. Для этого определим порядок действий: сначала умножение и деление, затем сложение и вычитание. При этом действия в скобках выполняются раньше, чем действия за скобками. И выполним необходимые действия в нужном порядке. Также в данном случае нужно применить формулу разности квадратов:
Ответ: 702
Решение для X — Методы нахождения значения x, Решенные примеры
Решение для x связано с нахождением значения x в уравнении с одной переменной, равной x, или с другими переменными, например, с нахождением x через y. Когда мы найдем значение x и подставим его в уравнение, мы должны получить L.H.S = R.H.S.
| 1. | Что означает Решить для х? |
| 2. | Как найти x? |
| 3. | Найдите x в треугольнике |
| 4. | Найдите x в дробях |
5. | Решить x уравнений |
| 6. | Часто задаваемые вопросы о решении для x |
Что означает Решить для х?
Решить для x означает найти значение x, для которого уравнение верно. т.е. когда мы найдем значение x и подставим в уравнение, мы должны получить Л.С.С = ПРАВ.С.С.
Если я попрошу вас решить уравнение «x + 1 = 2», это будет означать нахождение некоторого значения x, которое удовлетворяет уравнению.
Как вы думаете, является ли x = 1 решением этого уравнения? Подставьте его в уравнение и посмотрите.
1 + 1 = 2
2 = 2
LHS = RHS
Вот что значит найти x.
Как найти x?
Чтобы найти x, перенесите переменную в одну сторону, а все остальные значения перенесите в другую, применяя арифметические операции к обеим частям уравнения. Упростите значения, чтобы найти результат.
.
Как получить x сам по себе? Вычесть 2 с обеих сторон
⇒ х + 2 — 2 = 7 — 2
⇒ х = 5
Теперь проверьте ответ x = 5, подставив его обратно в уравнение. Получаем 5+2=7.
Левая сторона = правая сторона
Найдите x в треугольнике
Решите для x» неизвестную сторону или угол в треугольнике, мы можем использовать свойства треугольника или теорему Пифагора.
Давайте разберемся с решением для x в треугольнике с помощью примера.
△ ABC образует прямой угол в точке B, две стороны которого имеют длину 7 единиц и 24 единицы. Найдите гипотенузу х.
In △ABC by using the Pythagorean theorem,
we get AC 2 = AB 2 + BC 2
⇒ x 2 = 7 2 + 24 2
⇒ х 2 = 49 + 576
⇒ х 2 = 625
⇒ x = √625
⇒ x = 25 единиц
Найдите x, чтобы найти недостающий угол треугольника.
треугольник. азбука. Используя свойство суммы углов, мы можем найти значение x.угол А + угол В + угол С = 180 градусов.
50° + 60° + x° = 180° ⇒ x = 70°
Найдите x в дробях
Найдите х в дробях, мы просто делаем перекрестное умножение и упрощаем уравнение, чтобы найти х.
Например: Найдите x для уравнения ⇒ 2/5 = x/10.
Крест умножить дроби
⇒ 2 × 10 = 5 × х
Решите уравнение относительно x
⇒ х = 20/5
Упростить для x
⇒ х = 4
Чтобы проверить значение x, поместите результат 4 обратно в данное уравнение
.
⇒ 2/5 = 4/10
Крест умножить дроби
⇒ 2 × 10 = 4 × 5
⇒ 20 = 20
Левая сторона = правая сторона
Решите для x уравнения
Мы можем использовать решатель системы уравнений, чтобы найти значение x, когда у нас есть уравнения с разными переменными. Мы решаем одно из уравнений для переменной x (решаем для x через y), затем подставляем его во второе уравнение, а затем решаем для переменной y.
Наконец, мы подставляем найденное значение переменной x в одно из уравнений и находим другую переменную.
Давайте поймем решение для x и y с помощью примера.
Например, Решите для x: 2x — y = 5, 3x + 2y = 11
⇒ 2x — y = 5
Прибавив y с обеих сторон, мы получим,
⇒ 2x — y + y = 5 + y
⇒ 2x = 5 + y
⇒ x = (5 + y) / 2
Приведенное выше уравнение известно как x через y.
Подставим x = (5 + y) / 2 во второе уравнение 3(5 + y) / 2 + 2y = 11
⇒ (15 + 3y) / 2 + 2y = 11
⇒ (15 + 3y + 4y ) / 2 = 11
⇒ (15 + 7 лет) / 2 = 11
⇒ 15 + 7 лет = 22
⇒ 7y = 22 — 15
⇒ 7y = 7
⇒ y=1
Теперь подставим y = 1 в x = (5+y) / 2
⇒ x = (5 + 1) / 2
⇒ 6 / 2 = 3
Таким образом, решением данной системы уравнений является x = 3 и y = 1.
Важные замечания по решению x в уравнении), применить арифметические операции, чтобы изолировать переменную. ☛ Статьи по теме Вот калькулятор решения для x, чтобы вы могли быстро получить ответы. Попробуй сейчас. Кроме того, ознакомьтесь с этими интересными статьями, чтобы узнать больше о решении для x.
Часто задаваемые вопросы о решении для x
Как найти x в скобках?
Чтобы найти x в скобках, мы используем распределительный закон и удаляем скобки, перемещаем все члены x в одну сторону и постоянные в другую сторону и находим неизвестное x.
Например, 2(x−3) = 4
.
Используя закон распределения, 2x — 6 = 4 ⇒ 2x = 4 + 6 ⇒ 2x = 10 ⇒ x = 10/2 ⇒ x = 5
Как найти x в дроби?
Чтобы найти х в дробях, мы должны исключить знаменатель путем перекрестного умножения, а затем найти х.
Например, х/4 + 1/2 = 5/2 ⇒ (2х+4)/8 = 5/2
.
Выполняя перекрестное умножение, мы получаем 2 (2x + 4) = 8 (5)
.
⇒ 4x + 8 = 40
⇒ 4x = 40 — 8
⇒ 4x = 32
⇒ х = 32 / 4
⇒ x = 8
Как найти x для уравнения 4x + 2 = -8?
Чтобы найти x, следуйте по пунктам.
- Начните с 4x + 2 = -8
- Вычесть 2 с обеих сторон: 4x = -8 — 2 = -10
- Разделить на 4: x = -10 ÷ 4 = -5/2
- х = -5/2
Как найти x для уравнения 3x — 7 = 26?
Чтобы найти x, следуйте по пунктам.
- Начните с 3x — 7 = 26
- Прибавьте 7 к обеим сторонам: 3x — 7 + 7 = 26 + 7
- Вычислить: 3x = 33
- Разделить на 3: х = 33 ÷ 3
- х = 11
Как найти x в вертикальных углах?
Вертикальные углы конгруэнтны, или можно сказать, что они имеют одинаковую меру. Например, если вертикальный угол равен 2x, а другой равен 90-x, мы просто составим уравнение 2x = 90-x.
2х = 90 — х
Добавьте x к обеим сторонам, 2x + x = 90 -x + x
3x = 90
x = 30
Как умножить дроби? Определение, примеры, факты
Перекрестное умножение: введение
Обычно мы используем метод перекрестного умножения для нахождения неизвестных значений в любом алгебраическом уравнении. Давайте посмотрим на эти повседневные математические вопросы. Если один батончик стоит $\$$2, сколько будут стоить 10 таких батончиков?
Перекрестное умножение, как следует из названия, относится к умножению чисел, стоящих на перекрестных позициях.
Скрещиваем дроби $\frac{1}{10}$ и $\frac{2}{?}$.
$? \times 1= $\$$10$ $\times 2$
$? =$ $\$$20
Итак, 10 батончиков будут стоить $\$$20.
Давайте узнаем больше об этом методе и его применении.
Родственные игры
Что такое перекрестное умножение?
Для любого алгебраического уравнения типа $\frac{a}{b}=\frac{c}{d}$ , метод перекрестного умножения использует следующую формулу:
$a\times d = b\times c$
Чтобы скрестить дроби, мы умножаем числитель первой дроби на знаменатель второй дроби и числитель второй дроби со знаменателем первой дроби.
Перекрестное умножение можно использовать для сравнения дробей, сложения или вычитания разных дробей, поиска неизвестного значения в выражении и сравнения отношений.
Связанные рабочие листы
Как перекрестно умножать дроби?
Давайте разберемся, как скрестить дроби на примере.
Мы знаем, что $\frac{3}{4} = \frac{6}{8}$
Перемножить дроби $\frac{3}{4}$ и $\frac{6}{8}$ .
Умножьте числитель первой дроби на знаменатель второй дроби.
Умножьте числитель второй дроби на знаменатель первой дроби.
Получаем
$3\times8=24$
$6\times4=24$
Итак, перемножая дроби $\frac{a}{b} = \frac{c}{d}$ , мы получаем $a\ times d = b\times c$
Перекрестить умножение дробей для сравнения отличий от дробей
Мы только что научились скрещивать умножение дробей. Когда вы скрещиваете умножение дробей? В отличие от дробей можно сравнивать путем перекрестного умножения. Отличие от дробей — это дроби с разными знаменателями.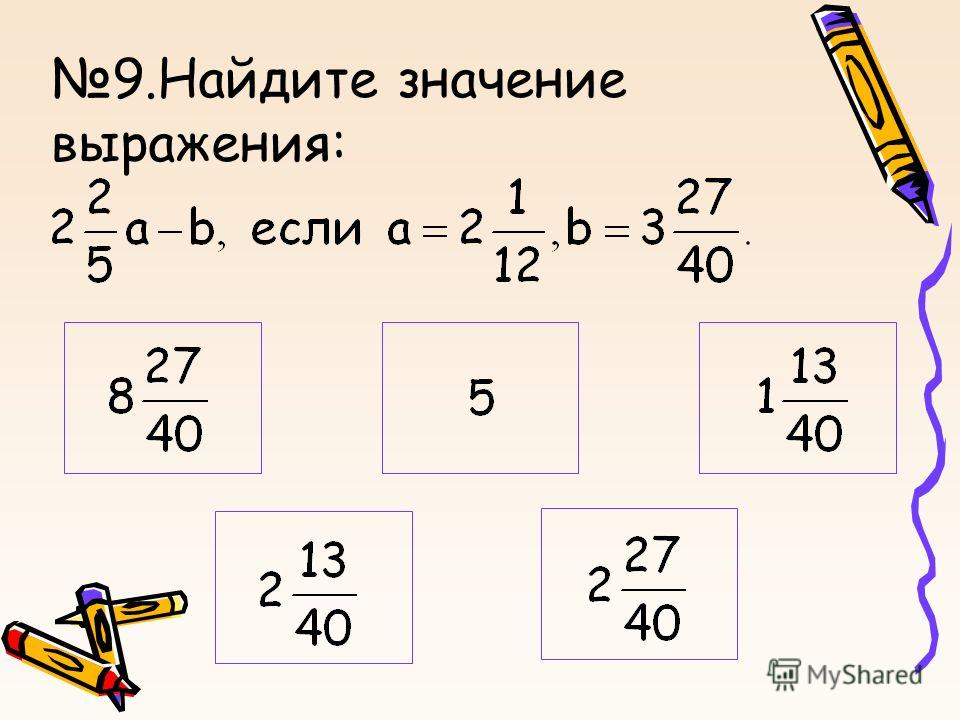
Пример :
Сравните $\frac{3}{7}$ и $\frac{5}{8}$ , используя перекрестное умножение.
Чтобы сравнить две дроби с разными знаменателями, мы делаем их знаменатели одинаковыми.
Мы делаем это, заменяя знаменатели произведением обоих знаменателей.
Итак, знаменатель обеих дробей становится $7 \times 8 = 56$
Теперь мы скрестим и умножим дроби , чтобы найти числители.
- Сначала умножим числитель первой дроби на знаменатель второй дроби.
$3 \times 8 = 24$
Таким образом, первая дробь принимает вид: $\frac{24}{56}$
- Далее умножаем числитель второй дроби на знаменатель первой дроби.
$5 \times 7 = 35$
Таким образом, вторая дробь принимает вид: $\frac{35}{56}$
Перекрестное умножение для сравнения отношений
Если два отношения равны, т. е. $\frac{a}{b} = \frac{c}{d}$, (где b и d не равны нулю), то произведение после перекрестного умножения также равно.
- $\frac{a}{b} \lt \frac{c}{d}$, если $a\times d \lt b\times c$.
Пример: $\frac{1}{2} \lt \frac{3}{4}$, начиная с $4 \lt 6$.
- $\frac{a}{b} \gt \frac{c}{d}$, если $a \times d \gt b \times c$.
Пример: $\frac{1}{10}\gt \frac{1}{100}$ начиная с $100\gt 10$.
Мы можем использовать перекрестное умножение , чтобы найти значение переменной в уравнении, содержащем отношения. Давайте лучше поймем это на примере.
Пример : Если 8 подсвечников стоят $\$$40. Сколько будут стоить 12 таких подсвечников?
Стоимость 8 подсвечников = $\$$40
Стоимость 1 подсвечника $= \frac{40}{8}$ …………(i)
Пусть стоимость 12 подсвечников равна Икс.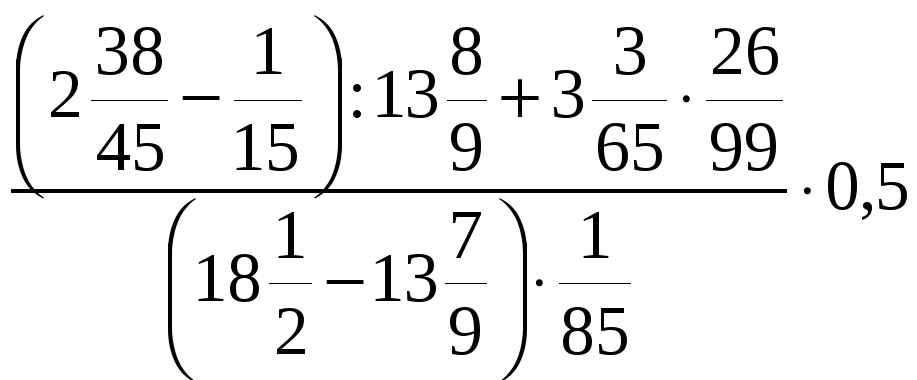
Следовательно, стоимость 1 подсвечника составит $\frac{x}{12}$. …………..(ii)
Приравнивая (i) и (ii), получаем
$\frac{40}{8} = \frac{x}{12}$
Перемножить, чтобы получить
$40 \times 12 = 8 \times x$
$\frac{480}{8}=$ x
x $=60$
Следовательно, стоимость 12 подсвечников составляет $\$$60.
Перекрестное умножение с одной переменной
Метод перекрестного умножения в основном используется для нахождения неизвестной переменной в уравнении. Давайте посмотрим на пример.
$\frac{4}{9} = \frac{x}{45}$
Когда мы пересекаем умножение:
$4 \times 45 = 180$ и $9 \times x = 9x$
Теперь, $9 х = 180$
x$ = \frac{180}{9} = 20$
Отсюда получаем $x = 20$
Решенные примеры
1. Сравните дроби 57 и 49 путем скрещивания.
Решение: Перемножая крест-накрест, мы находим
$5 \times 9 = 45$ и $4 \times 7 = 28$
Так как $45\gt 28, 57$ больше 49.
2. Джимми хочет найти значение x в данном уравнении. Вы можете помочь ему?
$\frac{12}{15} = \frac{x}{10}$
Решение:
$\frac{12}{15} = \frac{x}{10} $ (дано)
При перекрестном умножении:
$12 \times 10 = 15 \times x$
$\frac{120}{15} =$ x
$8 =$ x
Итак, значение x равно 8.
3. Что больше, $\frac{7}{12}$ или $\frac{6}{11}$ ?
Решение :
Когда мы перекрестно умножим, мы обнаружим
$ 7 \ Times 11 = 77 $ и 6 $ 12 = 72 $
$ 77 \ GT 72 $
, Следовательно,. $\frac{7}{12} \gt \frac{6}{11}$.
Практические задачи
1
Если дроби $\frac{4}{8}$ и $\frac{5}{x}$ равны, каково значение $x$?
40
5
15
10
Правильный ответ: 10
Поскольку данные дроби равны, мы можем перекрестно умножить и сказать, что $4x= 8 \times 5 = 40$
Таким образом, x $=$ 10
2
Если 4 кекса стоят $\$$12.
Сколько будут стоить 10 таких кексов?$\$30
$\$48
$\$40
$\$36
Правильный ответ: $\$30
Стоимость 4 кексов $\$$12.
Пусть стоимость 10 кексов равна x. Если мы представим это как уравнение, мы получим:
$\frac{12}{4} = \frac{x}{10}$
Когда мы умножим крест, мы получим
$12 \times 10 = 4 \times x$
$\frac{120}{4} = x$
$30 = x$
Следовательно, стоимость 10 кексов составляет $\$$30.
3
Каково значение x, если $\frac{9}{11} = \frac{x}{33}$.
10
27
18
55
Правильный ответ: 27
$\frac{9}{11}= \frac{x}{33}$
При перекрестном умножении:
3 $3 =9 \times 11\times x$
$\frac{297}{11} = x$
$x = 27$
Итак, значение $x$ равно 27.
Часто задаваемые вопросы
Когда мы используем перекрестное умножение ?
Мы используем метод перекрестного умножения для следующего:
- Процесс перекрестного умножения используется для сравнения дробей и отношений.
