Математика арифметика геометрия 6 класс задачник: ГДЗ Задачник по математике 6 класс Бунимович на Решалка

Содержание

Математика. Арифметика. Геометрия. 6 класс. Задачник. Бунимович Е. А., Кузнецова Л. В.

Главная
О магазине
Доставка
Условия возврата
Контакты

Бижутерия
Канцтовары
Посуда
Спорт и туризм
Хозтовары
Швейная галантерея
Мебель
Игрушки
Творчество
Книги
Сувениры
Зимние товары
Праздники
Текстиль
Одежда и обувь
Авто и мото
Сад и огород
Баня и сауна
Детские товары
Зоотовары
Строительство и ремонт
Интерьер
Аксессуары
Красота и здоровье
Бытовая техника и электроника
Продукты питания
Собственное производство
Оборудование для бизнеса и производства
Товары для взрослых
Освещение
Упаковка
Товары с любимыми героями
Наша разработка

Связаться с нами

Нур-Султан

О товаре

Страна производитель: Россия
Торговая марка: Просвещение
Артикул: 4553567
Мин. кол-во для заказа: 1
Школьный предмет: математика
Школьный класс: 6
Количество страниц: 111
Год издания: 2019
Автор: кузнецова л. в., бунимович е. а.
Тип обложки: мягкий переплёт
Наличие: нет в наличии

Все характеристики

2728 KZT тг

1659 тг* *при покупке от 43 шт.

нет в наличии

Описание и характеристики

Доставка и оплата

Страна производитель Россия
Торговая марка Просвещение
Артикул 4553567
Мин. кол-во для заказа 1
Школьный предмет математика
Школьный класс 6
Количество страниц 111
Год издания 2019
Автор кузнецова л. в., бунимович е. а.
Тип обложки мягкий переплёт
Длина упаковки 20
Высота упаковки 1.5
Ширина упаковки 26
Объем упаковки, куб. дм 0.780
Объем продукта, л 0.78
Ширина 26
Высота 1. 5
Габариты товара (длина × ширина × высота) 20 см × 26 см × 1,5 см
Вес, г 222
Количество в упаковке 1
Кол-во страниц 111

Передача в доставку до 01.03.2023

(Ваш заказ будет отправлен в течение 6 рабочих дней после оплаты).

Стоимость доставки оплачивается при получении заказа.

Мы принимаем к оплате

Доставка в Нур-Султан

6.

2: Арифметические и геометрические последовательности

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 40929

Ричард В. Беверидж
Общественный колледж Клэтсопа

Двумя распространенными типами математических последовательностей являются арифметические последовательности и геометрические последовательности. Арифметическая последовательность имеет постоянную разницу между каждой последовательной парой членов. Это похоже на линейные функции, которые имеют вид $y=m x+b .$ Геометрическая последовательность имеет постоянное отношение между каждой парой последовательных членов. Это создаст эффект постоянного множителя.

Примеры

Арифметическая последовательность:
$\{5,11,17,23,29,35, \dots\}$
Обратите внимание, здесь постоянная разность равна 6. Если мы хотим написать общий термин для этой последовательности, есть несколько подходов. Один из подходов состоит в том, чтобы взять постоянную разность в качестве коэффициента для члена $n$: $a_{n}=6 n+?$. Тогда нам просто нужно заполнить вопросительный знак значением, которое соответствует последовательности. Мы могли бы сказать для последовательности:
$\{5,11,17,23,29,35, \dots\}$
$a_{n}=6 n-1$
Существует также формула который вы можете запомнить, в котором говорится, что любая арифметическая последовательность с постоянной разностью $d$ выражается как:
$a_{n}=a_{1}+(n-1) d$
Обратите внимание, что если мы подставим значения из нашего примера, мы получим тот же ответ, что и раньше:

$a_{n}= a_{1}+(n-1) d$
$a_{1}=5, d=6$
Итак, $a_{1}+(n-1) d=5+(n- 1) * 6=5+6 n-6=6 n-1$
или $a_{n}=6 n-1$
Если члены арифметической прогрессии становятся меньше, то постоянная разность равна отрицательное число.

$\{24,19,14,9,4,-1,-6, \dots\}$
$a_{n}=-5 n+29$

Геометрическая последовательность
In геометрическая последовательность всегда имеет постоянный множитель. Если множитель больше, чем $1,$, то условия будут увеличиваться. Если множитель меньше $1,$, то члены будут становиться меньше. 9{n-1}\) и т. д.

Упражнения 6.2
Определите, является ли каждая последовательность арифметической, геометрической или ни той, ни другой.
Если это арифметика, определить постоянную разницу.
Если оно геометрическое, определите постоянный коэффициент.

1) $\quad\{18,22,26,30,34, \dots\}$
2) $\quad\{9,19,199,1999, \dots\}$
3) \ (\quad\{8,12,18,27, \dots\}\)
4) $\quad\{15,7,-1,-9,-17, \dots\}$
5) $\ четырехъядерный \ левый \ {\ гидроразрыва {1} {2}, \ гидроразрыва {2} {3}, \ гидроразрыва {3} {4}, \ гидроразрыва {4} {5}, \ гидроразрыва {5} 6}, \точки\справа\}$
6) \(\quad\{100,-50,25,-12.

5,\dots\}\)
7) $\quad\{-8,12,32,52,\dots\}$
8) $\quad\{1,4,9,16,25,\dots\}$
9) $\quad\{11,101,1001,10001,\ldots\}$
10) $ \quad\{12,15,18,21,24, \dots\}$
11) $\quad\{80,20,5,1.25, \dots\}$
12) $\quad \{5,15,45,135,405, \dots\}$
13) $\quad\{1,3,6,10,15, \dots\}$
$\begin{array}{ll} \text { 14) } & \{2,4,6,8,10, \dots\}\end{массив}$
15) $\quad\{-1,-2,-4,-8 ,-16, \dots\}$
16) $\quad\{1,1,2,3,5,8,13,21, \dots\}$

Эта страница под названием 6.2: Арифметические и геометрические последовательности распространяется под лицензией CC BY-NC-SA и была создана, изменена и/или курирована Ричардом В. Бевериджем.

Наверх

Была ли эта статья полезной?

Тип изделия
Раздел или страница
Автор
Ричард В. Беверидж
Лицензия
CC BY-NC-SA

Показать страницу TOC
нет
Теги
1. источник[1]-math-37270

справочный запрос — Дорожная карта для изучения арифметической геометрии

спросил 12 лет, 10 месяцев назад

Изменено 5 лет, 6 месяцев назад

Просмотрено 22к раз

$\begingroup$

Я прочитал книгу Хартсхорна «Алгебраическая геометрия » с главы 1 по главу 4, поэтому я хотел бы найти несколько предложений относительно следующего шага в изучении арифметической геометрии.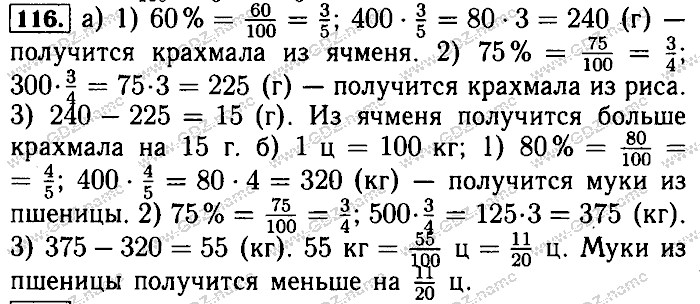

Не могли бы вы порекомендовать какие-нибудь книги или газеты? Большое спасибо!

аг.алгебра-геометрия
справочник-запрос
арифметико-геометрия
учебник-рекомендация

$\endgroup$

$\begingroup$

Мое предложение, если вы действительно проработали большую часть Хартсхорна, начать читать статьи, обращаясь к другим книгам по мере необходимости.

Начать можно с статьи Мазура «Идеал Эйзенштейна». Предложение Корнелла-Сильвермана тоже хорошо. (Это дает, по существу, полное доказательство гипотезы Тейта об абелевых многообразиях над числовыми полями и гипотезы Морделла, принадлежащее Фальтингсу.) Вы также можете просмотреть оригинальную статью Тейта о гипотезе Тейта об абелевых многообразиях над конечными полями. , что является шедевром.

Другой возможностью является изучение этальных когомологий (которую вам придется изучить в той или иной форме, если вы хотите заниматься исследованиями в области арифметической геометрии).

Для этого я предлагаю попробовать проработать первую статью Делиня о гипотезах Вейля (в которой он доказывает гипотезу Римана), обращаясь к учебникам по этальным когомологиям по мере необходимости.

$\endgroup$

$\begingroup$

Если вы можете найти (скажем, в библиотеке) копию книги Корнелла и Сильвермана Арифметическая геометрия , я очень рекомендую ее. Это всестороннее рассмотрение арифметической теории абелевых многообразий с использованием современного языка теории схем. К сожалению, в наши дни практически невозможно купить копию (обычно ее можно купить в Интернете у какого-нибудь малоизвестного продавца примерно за 9 долларов).50). Я также согласен с приведенными выше рекомендациями книги Лю

«Алгебраическая геометрия и арифметические кривые ». Он строит теорию схем с нуля (даже развивает необходимую коммутативную алгебру в первой главе) и повсюду уделяет внимание арифметическим приложениям.

В частности, в конце книги есть большая глава о приведении кривых. Если вы хотите трактовать эллиптические кривые в предельной общности (с использованием языка схем), то вам может быть интересна книга Каца и Мазура « арифметических модуля эллиптических кривых». Подчеркну, однако, что эта конкретная книга очень трудная (по крайней мере, для меня).

$\endgroup$

$\begingroup$

Сначала извинения: это скорее дополнение к ответу Чарльза, чем сам ответ. Изначально это был набор комментариев, но я не смог отформатировать комментарии так, чтобы их можно было прочитать.

«Арифметика эллиптических кривых» особенно рекомендуется тем, кто хочет впервые познакомиться с арифметическими приложениями когомологий. В главе 8 доказывается теорема Морделла-Вейля с использованием когомологий Галуа. Практически все в этой книге хорошо, и единственное совпадение с Хартсхорном — в первых двух главах. Это каноническая книга по эллиптическим кривым не просто так!

«Рациональные точки на эллиптических кривых», вероятно, не будут столь захватывающими для тех, кто уже прошел Хартсхорн.

«Расширенные темы» именно такие, но, возможно, немного более дружественные, чем большинство книг по темам. Главы в основном автономны. Особый интерес может представлять глава об эллиптических поверхностях, в которой показаны схемы ℤ во (почти) всей их красоте.

Я только просмотрел Hindry-Silverman, так что в любом случае мало что могу сказать.

«Приглашение к арифметической геометрии» для этого читателя, я думаю, в первую очередь послужит тому, чтобы показать, как алгебраическая теория чисел пересекается с арифметической геометрией.

«Алгебраическая геометрия и арифметические кривые» — фантастический справочник по арифметической геометрии, и он во многом совпадает с Хартсхорном.

редактировать: Для модулей эллиптических кривых глава 1 (Модульные формы) «Дополнительных тем» является хорошим местом для начала, и Кац-Мазур является хорошей конечной целью. Между этими двумя есть много книг по модульным формам и пространствам модулей, чтобы заполнить пробел. Я неравнодушен к Даймонду и Шурману, но оригинальные работы Шимуры заслуживают здесь признания. Ваш пробег может отличаться.

$\endgroup$

$\begingroup$

«Алгебраическая геометрия и арифметические кривые» Лю может быть хорошим, он охватывает много того же материала, но делает это более арифметически.

Есть также «Приглашение к арифметической геометрии» Лоренцини

Также не сбрасывайте со счетов «серию» Сильвермана: «Рациональные точки на эллиптических кривых» (совместно с Тейт), «Арифметика эллиптических кривых», «Дополнительные темы». по арифметике эллиптических кривых» и «Диофантова геометрия» с Хиндри.

$\endgroup$

$\begingroup$

В дополнение к упомянутой книге Корнелла—Сильвермана существует еще один сборник Корнелла—Сильвермана (+Стивенса) под названием «Модульные формы и последняя теорема Ферма» (http://www. springer.com/mathematics/numbers/book/ 978-0-387-98998-3), который я очень рекомендую. Он доступен в мягкой обложке.

Цель этого тома — охватить материал, использованный при доказательстве последней теоремы Ферма. Таким образом, большая часть арифметической геометрии рассматривается на приемлемом уровне для выпускников (хотя, возможно, несколько более требовательных опросов). Брайан Конрад (Brian Conrad) из предыдущих комментариев написал одну хорошую статью в томе.

Мне особенно нравятся статьи Тейта о схемах конечных групп и статья Мазура о теории деформации представлений Галуа.

$\endgroup$

$\begingroup$

Учитывая, что прошло уже два полных года с тех пор, как ОП задал этот вопрос, этот ответ (вероятно) предназначен исключительно для архивных целей, если кто-то (например, я) случайно наткнется на этот вопрос и найдет его полезным.

Математика арифметика геометрия 6 класс задачник: ГДЗ Задачник по математике 6 класс Бунимович на Решалка

Математика. Арифметика. Геометрия. 6 класс. Задачник. Бунимович Е. А., Кузнецова Л. В.

Популярное

6.

справочный запрос — Дорожная карта для изучения арифметической геометрии

Добавить комментарий Отменить ответ

Рубрики