Виленкин математика 5 класс – Рамблер/класс
Помогите решить! № 321 Верно ли утверждение: Виленкин математика 5 класс – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?Помогите решить!
№ 321
Верно ли утверждение:
а) если уменьшаемое увеличить на 10, то и разность увеличится
на 10;
б) если вычитаемое увеличить на 10, то и разность увеличится на 10;
в) если уменьшаемое и вычитаемое увеличить на 10, то разность не
изменится?
ответы
Помогу,чем смогу,смотри как думаю:
321
Утверждения а), в) – верны, утверждение б) – неверно.
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
3 классРепетиторХимияАлгебрапохожие вопросы 5
Координатная прямая. Математика 5 класс.Зубарева И.И.Параграф 10, задание 191Укажите начало отсчёта и координаты точек А, В, С, (Подробнее…)
ГДЗЗубарева И.И.Математика5 класс
Приветик! Кто решил? № 411 Математика 6 класс Виленкин.Выполните вычисления с помощью микрокалькулятора и резуль-
тат округлите до тысячных:
3,281 ∙ 0,57 + 4,356 ∙ 0,278 — 13,758 (Подробнее…)
ГДЗМатематика6 классВиленкин Н.Я.
Помогите установить соответствие между неравенствами. Математика базовый уровень ЕГЭ — 2017. Вар.№1. Зад.№17. Под руководством Ященко И.В.Здравствуйте! Помогите установить соответствие между неравенствами и их решениями: (Подробнее…)
ЕГЭЭкзаменыМатематикаЯщенко И.В.
Помогите выбрать утверждения. Математика базовый уровень ЕГЭ — 2017. Вар.№1. Зад.№18. Под руководством Ященко И.В.
Математика базовый уровень ЕГЭ — 2017. Вар.№1. Зад.№18. Под руководством Ященко И.В.Здравствуйте! Перед волейбольным турниром измерили рост игроков волейбольной команды города N. Оказалось, что рост каждого из (Подробнее…)
ЕГЭЭкзаменыМатематикаЯщенко И.В.
11. Выпишите слово, в котором на месте пропуска пишется буква Е. Русский язык ЕГЭ-2017 Цыбулько И. П. ГДЗ. Вариант 12.11.
Выпишите слово, в котором на месте пропуска пишется буква Е.
произнос., шь (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
Урок 10. Осевая симметрия — гдз по математике для 6 класса Зубарева И.И., Мордкович А.Г.
Класс
1 класс
2 класс
- Английский язык
- Математика
3 класс
- Русский язык
- Английский язык
- Математика
4 класс
- Русский язык
- Английский язык
- Математика
5 класс
- Русский язык
- Английский язык
- Математика
- Биология
6 класс
- Русский язык
- Английский язык
- Математика
- Биология
7 класс
- Русский язык
- Английский язык
- Математика
- Биология
- Физика
- Химия
8 класс
- Русский язык
- Английский язык
- Математика
- Биология
- Физика
- Химия
9 класс
- Русский язык
- Английский язык
- Математика
- Биология
- Физика
- Химия
10 класс
- Английский язык
- Биология
- Физика
- Химия
11 класс
- Английский язык
- Биология
- Химия
6 КЛАСС
Урок 10.
 Осевая симметрия
Осевая симметрияПервая группа: мозаика; Вторая группа: улитка; Третья группа: ящерица и бабочка.
Увеличить число на несколько единиц - использовать действие сложение, знак"+" Уменьшить на несколько единиц- использовать действие вычитание, знак "-".
Сумма, разность, произведение рациональных чисел является рациональным числом (без деления на нуль).
Сложение — это математическое действие. Числа, которые складываются, называются слагаемыми.
Квадрат разности двух чисел равен квадрату первого числа минус удвоенное произведение первого и второго чисел плюс квадрат второго числа.
Непростые натуральные числа, больше 1, называют составными числами.
Больше одной оси симметрии имеют: звезда конфета.
Приведите примеры других пространственных фигур, имеющих ось симметрии.
Вычитание — обратное сложению арифметическое действие, посредством которого от одной величины отнимается другая величина.
Куб суммы двух чисел равен кубу первого числа плюс утроенное произведение квадрата первого числа и второго плюс утроенное произведение первого числа и квадрата второго плюс куб второго числа.
Чтобы определить, делиться ли одно натуральное число на другое, можно это делимое число разложить на множители.
Запомните: натуральные числа - те, которые используем при счете (когда нам необходимо посчитать людей или предметы).
Задача на нахождение суммы всегда решается действием сложения. Задача на нахождение остатка решается действием вычитания. знак "-"
Разность квадратов двух чисел равно произведению суммы этих чисел и их разности.
Разность кубов двух чисел равна произведению разности этих чисел на неполный квадрат их суммы.
Натуральные числа не могут быть отрицательными. Поэтому натуральное число получаем, если мы из большего отнимаем меньшее, но не наоборот.
Сантиметр (см) – единица измерения длины. Дециметр (дм) – более крупная единица измерения длины.1 дм = 10 см.
10 единиц какого−либо разряда, дает 1 единицу более высокого разряда.
Два действительных числа равны между собой, если они имеют одинаковые знаки и их абсолютные величины имеют одинаковые целые части и одинаковые цифры соответствующих разрядов.
Умножение обратно делению и наоборот деление обратное умножению. Так как в примерах первое число сначала делится(умножается) на одно число и умножается(делится) на это же число, то решением уравнения будет первое число из выражения.
Сумма кубов двух чисел равна произведению суммы этих чисел на неполный квадрат их разности.
Правила: от перемены местами множителей произведение не меняется; чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель; чтобы найти неизвестное делимое, нужно частное умножить на делитель; чтобы найти неизвестный делитель, нужно делимое разделить на частное
Рациональные числа − это числа, которые можно записать в виде десятичной периодической дроби.
Иррациональные числа − это числа, которые можно записать в виде бесконечной десятичной непериодической дроби.
Действительные числа − это все рациональные и иррациональные числа.
Ответ: 19750,5.
Вопросники:
Среднее образование / GEM
Учащиеся шестого класса, имеющие право на участие в программе GEM, должны иметь уровень владения математикой 4,75 (SS347) или более высокий балл успеваемости по ELA 4 (SS 336) с одобрения родителей и рекомендации учителя.
 Программа Great Explorations in Mathematics (GEM) предназначена для ускорения двухлетнего обучения учащихся математике.
Программа Great Explorations in Mathematics (GEM) предназначена для ускорения двухлетнего обучения учащихся математике.В 6-м классе учащиеся проходят ускоренный курс математики, охватывающий 6-8 классы. Обычно учащиеся начинают алгебру I в 9й класс, геометрия в 10-м и алгебра II в 11-м. В GEM учащиеся начинают изучать алгебру I в 7
Учащиеся 6-го класса, имеющие право на участие в программе GEM, могут выбрать ускоренную математику для 6-го класса или GEM 6 Math. Оба курса ускоряют учащегося в математике, позволяя ему в конечном итоге достичь самого высокого уровня математики в средней школе, AP Calculus и AP Statistics.
Развернуть все
Ускоренная программа по математике предназначена для ускоренного изучения математики учащимися в течение одного года.
 По ускоренной математической программе учащиеся будут обучаться стандартам 6-го, 7-го и 8-го классов за два года. Успешное завершение этих двух курсов предназначено для подготовки учащихся к учебе с отличием по алгебре I в 8-м классе. Оценка, полученная учащимся на итоговом экзамене по алгебре 1, будет считаться 30% от оценки курса с отличием по алгебре 1.
По ускоренной математической программе учащиеся будут обучаться стандартам 6-го, 7-го и 8-го классов за два года. Успешное завершение этих двух курсов предназначено для подготовки учащихся к учебе с отличием по алгебре I в 8-м классе. Оценка, полученная учащимся на итоговом экзамене по алгебре 1, будет считаться 30% от оценки курса с отличием по алгебре 1.Курс ускоренной математической программы
- 6-й класс — курс 1 ускоренный
- 7 класс – курс 2 ускоренный
- 8 класс – Алгебра I с отличием
Программа Великие исследования в области математики (GEM) предназначена для ускорения двухлетнего обучения учащихся математике. Поскольку некоторые учащиеся уже являются хорошими техниками, они могут следовать правилам и применять эти правила в рутинных упражнениях. Студенты GEM должны сделать еще один шаг вперед, анализируя нестандартные задачи и копая глубже, чтобы увидеть красоту, элегантность и применение изучаемой математики.

Прохождение курса программы GEM
- 6 класс – GEM-6 (предварительная алгебра)
- На этом курсе стандарты для 6-го, 7-го и 8-го классов преподаются в течение одного года.
- Успешное завершение этого курса предназначено для подготовки учащихся к экзамену по алгебре I с отличием в 7-м классе.
- 7 класс – GEM-7 (Алгебра I с отличием)
- Балл, полученный учащимся на итоговом экзамене по алгебре 1, будет учитываться как 30 % от оценки по курсу с отличием по алгебре 1.
- 8 класс – ГЭУ-8 (с отличием по геометрии)
- Оценка, полученная учащимся на итоговом экзамене по геометрии, составляет 30 % от оценки за курс геометрии с отличием.
Шестой класс GEM требует, чтобы учащиеся сдали промежуточный и выпускной экзамен округа, что составляет 25% их оценки.
Учащиеся седьмого и восьмого классов GEM должны сдать промежуточный экзамен округа и итоговый экзамен штата (EOC).

Любые курсы средней школы, пройденные в средней школе, будут включены во взвешенный и невзвешенный средний балл учащегося в средней школе.
PRE-ALGEBRA GEM 6
6 расширенные стандарты класса
7 расширенные стандарты класса
оба курса, перечисленные выше)
Целью этого курса является чтобы включить навыки критического мышления, расширяя при этом математическое содержание, лежащее в основе курсовой работы средней школы, в частности, алгебры I с отличием. В частности, акцент будет сделан на обучении работе с переменными в алгебраических выражениях и многошаговых уравнениях. Содержание может включать, помимо прочего, алгебру, оценку, геометрию, построение графиков, теорию чисел, проценты, вероятность, статистику, решение задач, отношения, пропорции, научную запись и рациональные числа.
Сосредоточив внимание на использовании алгебраических навыков для решения задач, этот курс имеет быстрый темп, требуя 30-45 минут домашней работы ежедневно, включает в себя самостоятельную работу, следует рекомендуемой последовательности округа Броуард, которая обеспечивает углубленное освещение понятий, и использует вопросы с несколькими понятиями в тестах, которые требуют от учащихся применения полученных навыков.

Учащимся, выбравшим этот курс, настоятельно рекомендуется понимать, что учебная программа на два уровня выше курса 6-го класса.
ALGEBRA I HONORS GEM 7
Algebra 1 Honors Standards
Это курс средней школы для получения кредита средней школы. Алгебра I с отличием в 7-м классе является континуумом GEM 6. Цель этого курса — обеспечить тщательное и углубленное изучение алгебры I с отличием с упором на навыки дедуктивного мышления в качестве основы для более продвинутых курсов математики. Содержание может включать, но не ограничиваться, операции и свойства, используемые в системе действительных чисел, алгебраические и графические решения уравнений и неравенств первой степени с одной и двумя переменными, операции с полиномами, рациональные и иррациональные алгебраические выражения, квадратные уравнения. , квадратичные неравенства и квадратичные функции. Ожидается, что на протяжении всего курса студенты разовьют навыки, необходимые для решения математических задач.
 Особое внимание уделяется решению алгебраических задач.
Особое внимание уделяется решению алгебраических задач.Этот курс проходит в быстром темпе, требует 45-60 минут ежедневной домашней работы и предполагает самостоятельную работу. Студенты должны быть высоко мотивированными, ответственными, самостоятельными и готовыми тратить время, необходимое для овладения навыками содержания. Кроме того, будет промежуточный экзамен, выпускной экзамен, государственный экзамен в конце курса, а буквенная оценка будет учитываться при подсчете среднего балла средней школы.
Предполагается, что учащиеся обладают сильной трудовой этикой, могут самостоятельно выполнять домашние задания и готовиться к контрольным работам, мотивированы, прилагают 100% усилий, участвуют в обсуждениях в классе и получают удовольствие от чрезвычайно строгой учебной программы.
ПОЧЕТНАЯ ГЕОМЕТРИЯ GEM 8
Стандарты курса по геометрии с отличием
Это курс средней школы за кредит. Учащиеся, которые зачисляются на этот курс, должны быть сильными студентами по алгебре I с отличием, которые продемонстрировали мастерство навыков алгебры, о чем свидетельствуют их оценки и результаты экзаменов.
 Этот курс представляет собой строгий и углубленный курс для старших классов, который помогает заложить основу для математических работ более высокого уровня, таких как AICE, курсовая работа AP и вступительные экзамены в колледж. Акцент делается на методах доказательства, формальном языке математики, фундаментальных свойствах геометрии, понимании дедуктивных и индуктивных рассуждений, решении реальных задач с применением геометрических свойств и алгебраических навыков, а также с использованием трансформационной и координатной геометрии.
Этот курс представляет собой строгий и углубленный курс для старших классов, который помогает заложить основу для математических работ более высокого уровня, таких как AICE, курсовая работа AP и вступительные экзамены в колледж. Акцент делается на методах доказательства, формальном языке математики, фундаментальных свойствах геометрии, понимании дедуктивных и индуктивных рассуждений, решении реальных задач с применением геометрических свойств и алгебраических навыков, а также с использованием трансформационной и координатной геометрии.Этот курс проходит в быстром темпе, требуя от 45 до 60 минут домашних заданий в день, и требует большого количества самостоятельной работы, так как подход курса основан на методе исследования. Студенты должны быть высоко мотивированными, ответственными, самостоятельными и готовыми тратить время, необходимое для овладения навыками содержания. Настоятельно рекомендуется (и необходимо для успеха), чтобы учащиеся хорошо знали алгебру для этого класса.




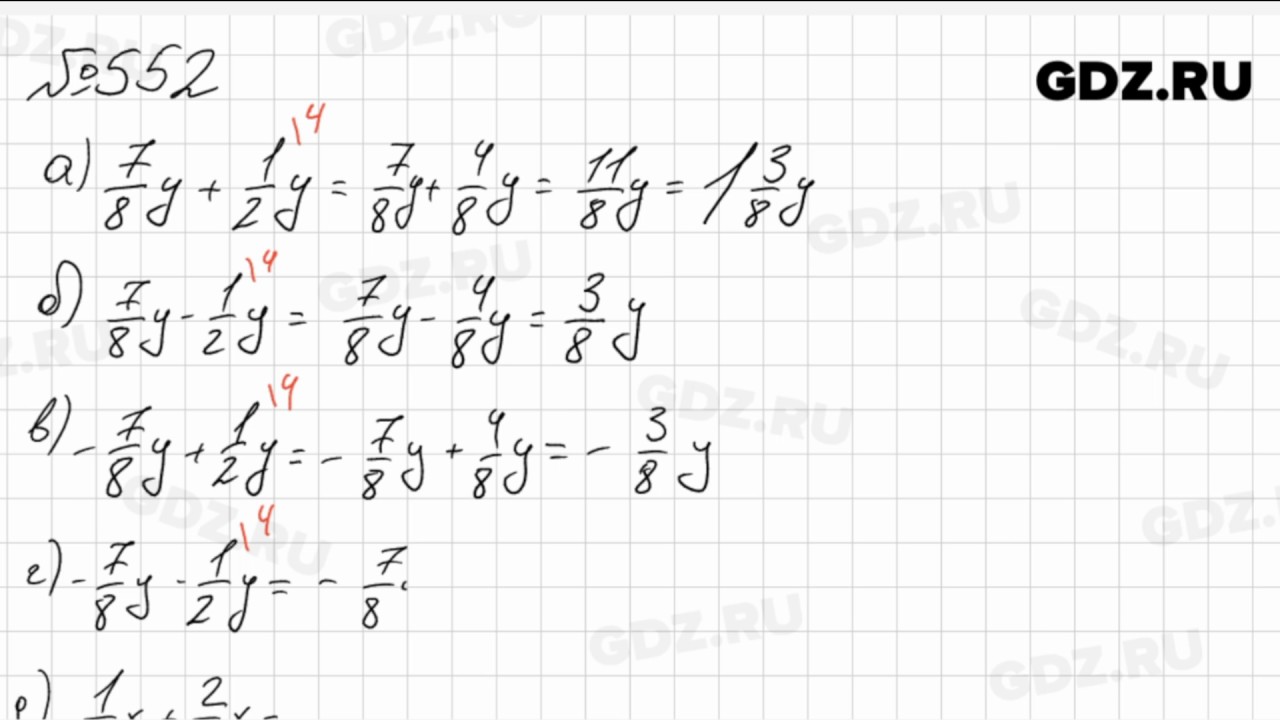 Программа Great Explorations in Mathematics (GEM) предназначена для ускорения двухлетнего обучения учащихся математике.
Программа Great Explorations in Mathematics (GEM) предназначена для ускорения двухлетнего обучения учащихся математике. По ускоренной математической программе учащиеся будут обучаться стандартам 6-го, 7-го и 8-го классов за два года. Успешное завершение этих двух курсов предназначено для подготовки учащихся к учебе с отличием по алгебре I в 8-м классе. Оценка, полученная учащимся на итоговом экзамене по алгебре 1, будет считаться 30% от оценки курса с отличием по алгебре 1.
По ускоренной математической программе учащиеся будут обучаться стандартам 6-го, 7-го и 8-го классов за два года. Успешное завершение этих двух курсов предназначено для подготовки учащихся к учебе с отличием по алгебре I в 8-м классе. Оценка, полученная учащимся на итоговом экзамене по алгебре 1, будет считаться 30% от оценки курса с отличием по алгебре 1.
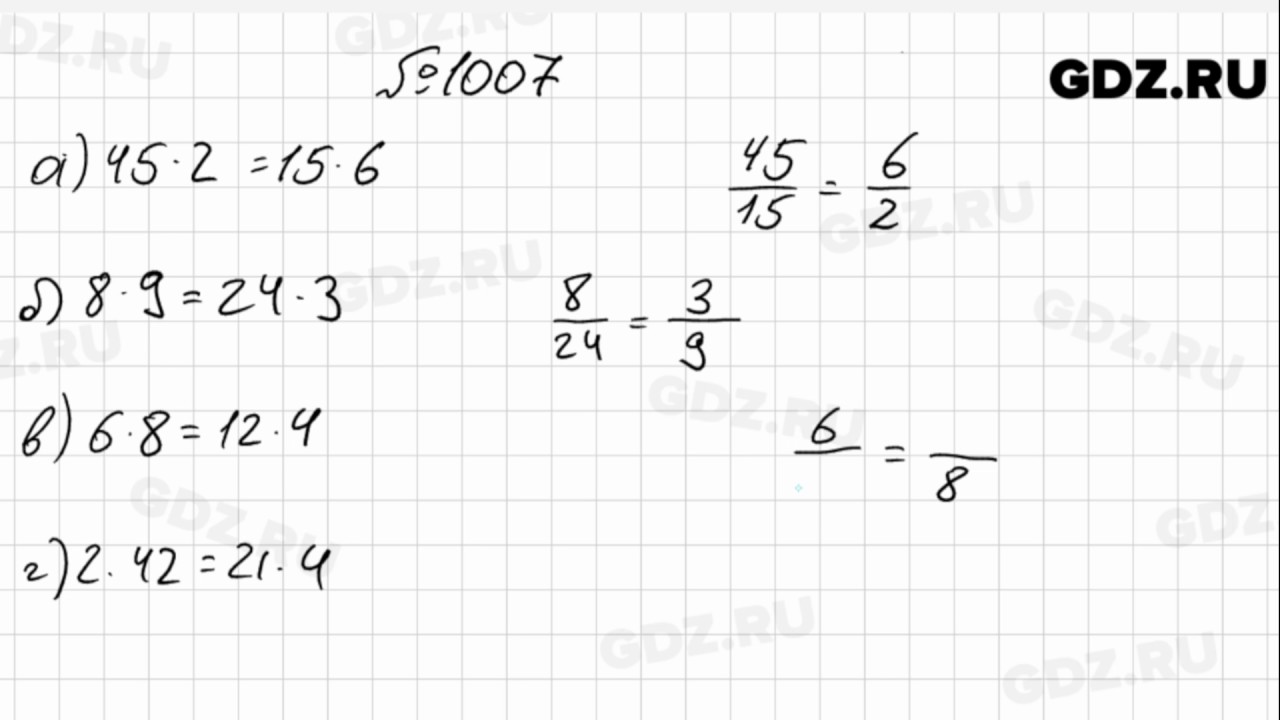

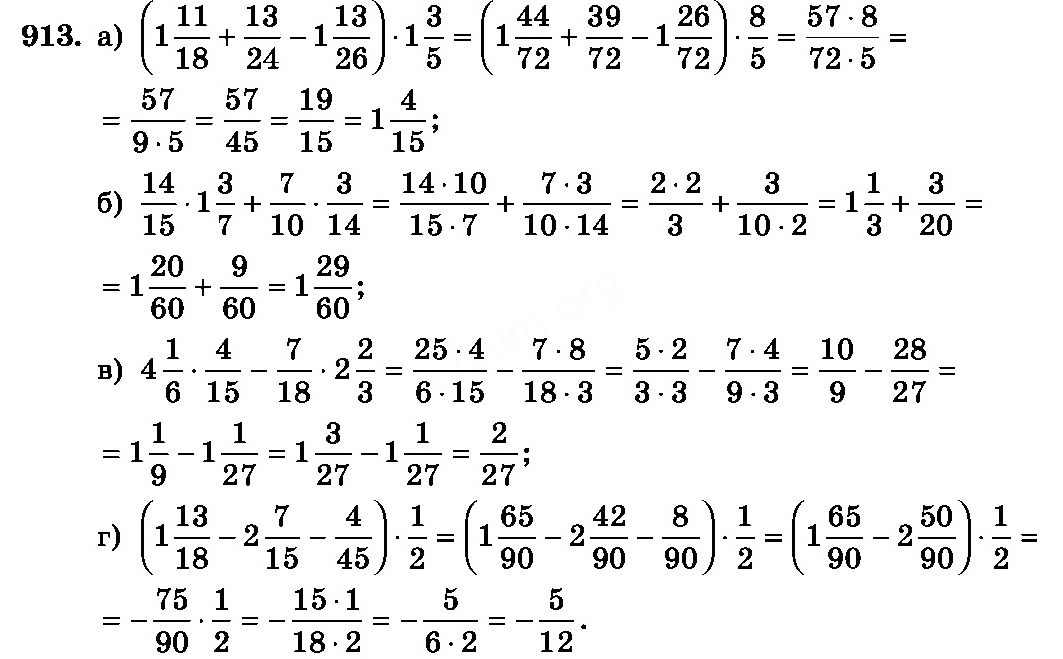 Особое внимание уделяется решению алгебраических задач.
Особое внимание уделяется решению алгебраических задач. Этот курс представляет собой строгий и углубленный курс для старших классов, который помогает заложить основу для математических работ более высокого уровня, таких как AICE, курсовая работа AP и вступительные экзамены в колледж. Акцент делается на методах доказательства, формальном языке математики, фундаментальных свойствах геометрии, понимании дедуктивных и индуктивных рассуждений, решении реальных задач с применением геометрических свойств и алгебраических навыков, а также с использованием трансформационной и координатной геометрии.
Этот курс представляет собой строгий и углубленный курс для старших классов, который помогает заложить основу для математических работ более высокого уровня, таких как AICE, курсовая работа AP и вступительные экзамены в колледж. Акцент делается на методах доказательства, формальном языке математики, фундаментальных свойствах геометрии, понимании дедуктивных и индуктивных рассуждений, решении реальных задач с применением геометрических свойств и алгебраических навыков, а также с использованием трансформационной и координатной геометрии.