Математика 6 класс виленкин номер 528: Номер №528 — ГДЗ по Математике 6 класс: Виленкин Н.Я.

Содержание

Номер №528 — ГДЗ по Математике 6 класс: Виленкин Н.Я.

войтирегистрация

Ответкин
Решебники
6 класс
Математика
Виленкин
Номер №528

НАЗАД К СОДЕРЖАНИЮ

2013г.ВыбранВыбрать ГДЗ (готовое домашние задание из решебника) на Номер №528 по учебнику Математика. 6 класс. Учебник для общеобразовательных учреждений / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. — 30-е издание. Мнемозина, 2013г.

2019г.ВыбранВыбрать ГДЗ (готовое домашние задание из решебника) на Номер №528 по учебнику Математика. 6 класс. Учебник для общеобразовательных организаций / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. — 37-е издание в двух частях. Мнемозина, 2019г.

Условие 20132019г.

Cменить на 2013 г.

Cменить на 2019 г.

С бахчи собрали 27 т арбузов. В столовую направили 2/9 этих арбузов, а 6/7 остатка отвезли на рынок, рынок? Сколько тонн арбузов отвезли на рынок?

Штангист тяжёлой весовой категории поднял штангу массой в 156 кг, а штангист лёгкой весовой категории поднял штангу, масса которой составляет 9/13 массы первой. На сколько килограммов масса первой штанги больше массы второй штанги?

Решение 1

Решение 2

Решение 3

ГДЗ по Математике 6 класс: Виленкин Н.Я.

Издатель: Виленкин Н. Я. Жохов В.И. Чесноков А.С. Шварцбурд С.И. 2013/2019г.

ГДЗ по Математике 6 класс: Мерзляк А.Г.

Издатель: А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. 2014г. / 2019г.

ГДЗ по Математике 6 класс: Никольский С.М.

Издатель: С.М. Никольский, М.К, Потапов, Н.Н. Решетников, А.В. Шевкин. 2015-2018

ГДЗ по Математике 6 класс: Зубарева, Мордкович

Издатель: И.И. Зубарева, А.Г. Мордкович. 2014-2019г.

ГДЗ по Математике 6 класс: Дорофеев Г.В.

Издатель: Г.В. Дорофеев, И.Ф. Шарыгин, С.Б. Суворова. 2016-2019г.

Сообщить об ошибке

Выберите тип ошибки:

Решено неверно

Опечатка

Плохое качество картинки

Опишите подробнее
в каком месте ошибка

Ваше сообщение отправлено
и скоро будет рассмотрено

ОК, СПАСИБО

[email protected]

Классы

Предметы

Номер 528 — ГДЗ по Математике 6 класс Учебник Виленкин, Жохов, Чесноков, Шварцбурд 2020. Часть 1 (решебник)

Номер 528 — ГДЗ по Математике 6 класс Учебник Виленкин, Жохов, Чесноков, Шварцбурд 2020. Часть 1 (решебник) — GDZwow

Перейти к содержанию

Search for:

Авторы: Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И.

Издательство: Мнемозина

Тип: Учебник

Новая версия

Старая версия

ЧАСТЬ 1
Выберите номер упражнения

ЧАСТЬ 2
Выберите номер упражнения

1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192939495969798991001011021031041051061071081091101111121131141151161171181191201211221231241251261271281291301311321331341351361371381391401411421431441451461471481491501511521531541551561571581591601611621631641651661671681691701711721731741751761771781791801811821831841851861871881891901911921931941951961971981992002012022032042052062072082092102112122132142152162172182192202212222232242252262272282292302312322332342352362372382392402412422432442452462472482492502512522532542552562572582592602612622632642652662672682692702712722732742752762772782792802812822832842852862872882892902912922932942952962972982993003013023033043053063073083093103113123133143153163173183193203213223233243253263273283293303313323333343353363373383393403413423433443453463473483493503513523533543553563573583593603613623633643653663673683693703713723733743753763773783793803813823833843853863873883893903913923933943953963973983994004014024034044054064074084094104114124134144154164174184194204214224234244254264274284294304314324334344354364374384394404414424434444454464474484494504514524534544554564574584594604614624634644654664674684694704714724734744754764774784794804814824834844854864874884894904914924934944954964974984995005015025035045055065075085095105115125135145155165175185195205215225235245255265275285295305315325335345355365375385395405415425435445455465475485495505515525535545555565575585595605615625635645655665675685695705715725735745755765775785795805815825835845855865875885895905915925935945955965975985996006016026036046056066076086096106116126136146156166176186196206216226236246256266276286296306316326336346356366376386396406416426436446456466476486496506516526536546556566576586596606616626636646656666676686696706716726736746756766776786796806816826836846856866876886896906916926936946956966976986997007017027037047057068928938948958968978988999009019029039049059069079089099109119129139149159169179189199209219229239249259269279289299309319329339349359369379389399409419429439449459469479489499509519529539549559569579589599609619629639649659669679689699709719729739749759769779789799809819829839849859869879889899909919929939949959969979989991000100110021003100410051006100710081009101010111012101310141015101610171018101910201021102210231024102510261027102810291030103110321033103410351036103710381039104010411042104310441045104610471048104910501051105210531054105510561057105810591060106110621063106410651066106710681069107010711072107310741075107610771078107910801081108210831084108510861087108810891090109110921093109410951096109710981099110011011102110311041105110611071108110911101111111211131114111511161117111811191120112111221123112411251126112711281129113011311132113311341135113611371138113911401141114211431144114511461147114811491150115111521153115411551156115711581159116011611162116311641165116611671168116911701171117211731174117511761177117811791180118111821183118411851186118711881189119011911192119311941195119611971198119912011202120312041205120612071208120912101211121212131214121512161217121812191220122112221223122412251226122712281229123012311232123312341235123612371238123912401241124212431244124512461247124812491250125112521253125412551256125712581259126012611262126312641265126612671268126912701271127212731274127512761277127812791280128112821283128412851286128712881289129012911292129312941295129612971298129913001301130213031304130513061307130813091310131113121313131413151316131713181319132013211322132313241325132613271328132913301331133213331334133513361337133813391340134113421343134413451346134713481349135013511352135313541355135613571358135913601361136213631364136513661367136813691370137113721373137413751376137713781379138013811382138313841385138613871388138913901391139213931394139513961397139813991400140114021403140414051406140714081409141014111412141314141415141614171418141914201421142214231424142514261427142814291430143114321433143414351436143714381439144014411442144314441445144614481449145014511452145314541455145614571458145914601461146214631464146514681469147014711472147314741475147614771478147914801481148214831484148514861487148814891490149114921493149414951496149714981499150015011502150315041505150615071508150915101511151215131514151515161517151815191520152115221523152415251526152715281529153015311532153315341535153615371538153915401541154215431544154515461547154815491550155115521553155415551556155715581559156015611562156315641565156615671568156915701571157215731574157515761577157815791580158115821583158415851586158715881589159015911592159315941595

Adblock
detector

Недостающее звено в гравитационно-волновой астрономии

1. Лонгэйр М. Космический век. Кембридж: Издательство Кембриджского университета; 2006. [Google Scholar]

2. Сатьяпракаш Б.С., Шутц Б.Ф. Физика, астрофизика и космология с гравитационными волнами. Живой преподобный отн. 2009;12:2. doi: 10.12942/lrr-2009-2. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

3. Abbott BP, et al. Наблюдение гравитационных волн от слияния двойных черных дыр. физ. Преподобный Летт. 2016;116(6):061102. doi: 10.1103/PhysRevLett.116.061102. [PubMed] [CrossRef] [Академия Google]

4. Aasi J, et al. Расширенный ЛИГО. Сорт. Квант. Грав. 2015;32:074001. doi: 10.1088/0264-9381/32/11/115012. [CrossRef] [Google Scholar]

5. Acernese F, et al. Advanced Virgo: интерферометрический детектор гравитационных волн второго поколения. Сорт. Квант. Грав. 2015;32(2):024001. doi: 10.1088/0264-9381/32/2/024001. [CrossRef] [Google Scholar]

6. Akutsu T, et al. KAGRA: интерферометрический детектор гравитационных волн 2,5 поколения. Природа Астрон. 2019;3(1):35. doi: 10.1038/s41550-018-0658-y. [Перекрестная ссылка] [Академия Google]

7. Abbott BP, et al. GWTC-1: гравитационно-волновой переходный каталог слияний компактных двойных систем, наблюдаемых LIGO и Virgo во время первого и второго сеансов наблюдений. физ. Ред. 2019;x9(3):031040. doi: 10.1103/PhysRevX.9.031040. [CrossRef] [Google Scholar]

8. Abbott BP, et al. Изучение чувствительности детекторов гравитационных волн следующего поколения. Сорт. Квант. Грав. 2017;34(4):044001. doi: 10.1088/1361-6382/aa51f4. [CrossRef] [Google Scholar]

9. Sathyaprakash B, et al. Научные задачи телескопа Эйнштейна. Сорт. Квант. Грав. 2012;29:124013. doi: 10.1088/0264-9381/29/12/124013. [CrossRef] [Google Scholar]

10. Hild S, et al. Исследования чувствительности гравитационно-волновых обсерваторий третьего поколения. Сорт. Квант. Грав. 2011;28:094013. doi: 10.1088/0264-9381/28/9/094013. [CrossRef] [Google Scholar]

11. Амаро-Сеоан П. и др.: Космическая антенна лазерного интерферометра. arXiv:1702.00786 (2017)

12. Klein A, et al. Наука с помощью космического интерферометра eLISA: двойные сверхмассивные черные дыры. физ. Ред. 2016;d93(2):024003. [Google Scholar]

13. Бабак С., Гейр Дж., Сесана А., Бараус Э., Сопуэрта К.Ф., Берри К.П.Л., Берти Э., Амаро-Сеоан П., Петито А., Кляйн А. Наука с помощью космического интерферометра LISA. V: Вдохновения с экстремальным соотношением масс. физ. 2017;d95(10):103012. [Google Scholar]

14. Берри К.П.Л., Хьюз С.А., Сопуэрта С.Ф., Чуа А.Дж.К., Хеффернан А., Холли-Боккельманн К., Михайлов Д.П., Миллер М.С., Сесана А. Уникальный потенциал спиралей с экстремальным отношением масс для гравитационно-волновых астрономия. Бык. Являюсь. Астрон. соц. 2019;51(3):42. [Google Scholar]

15. Сесана А. Перспективы многополосной гравитационно-волновой астрономии после GW150914. физ. Преподобный Летт. 2016;116(23):231102. doi: 10.1103/PhysRevLett.116.231102. [PubMed] [CrossRef] [Google Scholar]

16. Витале С. Многополосная гравитационно-волновая астрономия: оценка параметров и проверка общей теории относительности с космическими и наземными детекторами. физ. Преподобный Летт. 2016;117(5):051102. doi: 10.1103/PhysRevLett.117.051102. [PubMed] [CrossRef] [Академия Google]

17. Яни К., Шумейкер Д., Катлер С. Обнаруживаемость черных дыр промежуточной массы в многополосной гравитационно-волновой астрономии. Природа Астрон. 2019;4(3):260. doi: 10.1038/s41550-019-0932-7. [CrossRef] [Google Scholar]

18. Liu C, Shao L, Zhao J, Gao Y. Многополосное наблюдение слияний двойных черных дыр LIGO/Virgo в каталоге гравитационно-волновых транзиентов GWTC-1. Пн. Нет. Рой. Астрон. соц. 2020;496:182. doi: 10.1093/mnras/staa1512. [CrossRef] [Академия Google]

19. Брейвик К., Родригес С.Л., Ларсон С.Л., Калогера В., Расио Ф.А. Различение каналов образования двойных черных дыр с помощью LISA. Астрофиз. Дж. 2016;830(1):L18. doi: 10.3847/2041-8205/830/1/L18. [CrossRef] [Google Scholar]

20. Нисидзава А., Берти Э., Клейн А., Сесана А. Измерения эксцентриситета с помощью eLISA как трассеры образования двойной черной дыры. физ. 2016;d94(6):064020. [Google Scholar]

21. Тубиана А., Марсат С., Бабак С., Бараус Э., Бейкер Дж. Тесты общей теории относительности с двойными черными дырами звездной массы, наблюдаемыми LISA. физ. Ред. 2020;d101(10):104038. [Академия Google]

22. Манчестер RN. Международный массив пульсаров. Квант, Класс. Грав. 2013;30:224010. doi: 10.1088/0264-9381/30/22/224010. [CrossRef] [Google Scholar]

23. Mingarelli CMF, Lazio TJW, Sesana A, Greene JE, Ellis JA, Ma CP, Croft S, Burke-Spolaor S, Taylor SR. Местный наногерцовый гравитационно-волновой ландшафт от сверхмассивных двойных черных дыр. Природа Астрон. 2017;1(12):886. doi: 10.1038/s41550-017-0299-6. [CrossRef] [Google Scholar]

24. Питкин М., Кларк Дж., Хендри М.А., Хенг И.С., Мессенджер С., Тохер Дж., Воан Г., Физ Дж. Существует ли потенциальная взаимодополняемость между LISA и синхронизацией пульсаров? конф. сер. 2008;122:012004. дои: 10.1088/1742-6596/122/1/012004. [CrossRef] [Google Scholar]

25. Colpi M, et al. Гравитационно-волновой вид массивных черных дыр. Бык. Являюсь. Астрон. соц. 2019;51(3):432. [Google Scholar]

26. Sedda MA, et al. Недостающее звено в гравитационно-волновой астрономии: открытия, ожидающие в децигерцовом диапазоне. Сорт. Квант. Грав. 2020;37(21):215011. doi: 10.1088/1361-6382/abb5c1. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

27. Литтенберг Т.Б., Брейвик К., Браун В.Р., Эраклеус М., Гермес Дж.Дж., Холли-Боккельманн К., Кремер К., Купфер Т., Ларсон С.Л. Гравитационно-волновой обзор галактических сверхкомпактных двойных систем. Бык. Являюсь. Астрон. соц. 2019;51(3):34. [Google Scholar]

28. Kalogera V, et al. Глубже, шире, острее: наземные гравитационно-волновые наблюдения нового поколения за двойными черными дырами. Бык. Являюсь. Астрон. соц. 2019;51(3):242. [Google Scholar]

29. Abbott BP, et al. GW170817: Измерения радиусов нейтронных звезд и уравнения состояния. физ. Преподобный Летт. 2018;121(16):161101. doi: 10.1103/PhysRevLett.121.161101. [PubMed] [CrossRef] [Google Scholar]

30. Монтана Г., Толос Л., Ханауске М., Реззолла Л. Ограничение звезд-близнецов с помощью GW170817. физ. Версия 2019 г.;d99(10):103009. [Google Scholar]

31. Мост Э.Р., Вейх Л.Р., Резолла Л., Шаффнер-Билич Дж. Новые ограничения на радиусы и приливные деформации нейтронных звезд из GW170817. физ. Преподобный Летт. 2018;120(26):261103. doi: 10.1103/PhysRevLett.120.261103. [PubMed] [CrossRef] [Google Scholar]

32. Кафлин М.В., Дитрих Т., Маргалит Б., Мецгер Б.Д. Вывод байесовских параметров мультимессенджера о слиянии двойных нейтронных звезд. Пн. Нет. Рой. Астрон. соц. 2019;489(1):L91. doi: 10.1093/mnrasl/slz133. [Перекрестная ссылка] [Академия Google]

33. Маргалит Б., Мецгер Б.Д. Матрица с несколькими вестниками: будущее слияния нейтронных звезд, ограничения на уравнение состояния ядра. Астрофиз. Дж. 2019;880(1):L15. doi: 10.3847/2041-8213/ab2ae2. [CrossRef] [Google Scholar]

34. Abbott BP, et al. Оценка вклада динамических выбросов в Килонову, связанную с GW170817. Астрофиз. Дж. 2017;850(2):L39. doi: 10.3847/2041-8213/aa9478. [CrossRef] [Google Scholar]

35. Chornock R, et al. Электромагнитный аналог слияния двойной нейтронной звезды LIGO/Virgo GW170817. IV. Обнаружение признаков нуклеосинтеза r-процесса в ближнем инфракрасном диапазоне с помощью Gemini-South. Астрофиз. Дж. 2017;848(2):L19. doi: 10.3847/2041-8213/aa905c. [CrossRef] [Google Scholar]

36. Tanvir NR, et al. Появление богатой лантанидами Килоновой после слияния двух нейтронных звезд. Астрофиз. Дж. 2017;848(2):L27. doi: 10.3847/2041-8213/aa90b6. [CrossRef] [Google Scholar]

37. Wanajo S. Физические условия для r-процесса I. Радиоактивные источники энергии килоновых. Астрофиз. Дж. 2018;868(1):65. doi: 10.3847/1538-4357/aae0f2. [CrossRef] [Google Scholar]

38. Siegel DM, Barnes J, Metzger BD. Слияние нейтронных звезд GW170817 указывает на коллапсары как на основной источник r-процесса. Природа. 2019;569(7755):241. doi: 10.1038/s41586-019-1136-0. [PubMed] [CrossRef] [Google Scholar]

39. Abbott BP, et al. Гравитационные волны и гамма-лучи от слияния двойных нейтронных звезд: GW170817 и GRB 170817A. Астрофиз. Дж. 2017;848(2):L13. doi: 10.3847/2041-8213/aa920c. [CrossRef] [Google Scholar]

40. Abbott BP, et al. Тесты общей теории относительности с GW170817. физ. Преподобный Летт. 2019;123(1):011102. doi: 10.1103/PhysRevLett.123.011102. [PubMed] [CrossRef] [Академия Google]

41. Belgacem E, Dirian Y, Foffa S, Maggiore M. Модифицированное распространение гравитационных волн и стандартные сирены. физ. 2018;d98(2):023510. [Google Scholar]

42. Belgacem E, et al. Тестирование модифицированной гравитации на космологических расстояниях с помощью стандартных сирен LISA. JCAP. 2019;1907(07):024. doi: 10.1088/1475-7516/2019/07/024. [CrossRef] [Google Scholar]

43. Hillebrandt W, Kromer M, Röpke FK, Ruiter AJ. К пониманию сверхновых типа Ia на основе синтеза теории и наблюдений. Передний. физ. (Пекин) 2013; 8:116. doi: 10.1007/s11467-013-0303-2. [Перекрестная ссылка] [Академия Google]

44. Маоз Д., Маннуччи Ф., Нелеманс Г. Наблюдения указывают на прародителей сверхновых типа Ia. Анна. Преподобный Астрон. Астрофиз. 2014;52:107. doi: 10.1146/annurev-astro-082812-141031. [CrossRef] [Google Scholar]

45. Мандель И., Сесана А., Веккио А. Астрофизический пример децигерцового детектора гравитационных волн. Сорт. Квант. Грав. 2018;35(5):054004. doi: 10.1088/1361-6382/aaa7e0. [CrossRef] [Google Scholar]

46. Schutz BF. Определение постоянной Хаббла по наблюдениям гравитационных волн. Природа. 1986;323:310. дои: 10.1038/323310a0. [CrossRef] [Google Scholar]

47. MacLeod CL, Hogan CJ. Точность постоянной Хаббла, полученная с использованием абсолютных расстояний бинарных черных дыр и статистической информации о красном смещении. физ. Ред. 2008; D77:043512. [Google Scholar]

48. Chen HY, Fishbach M, Holz DE. Двухпроцентное постоянное измерение Хаббла от стандартных сирен за пять лет. Природа. 2018;562(7728):545. doi: 10.1038/s41586-018-0606-0. [PubMed] [CrossRef] [Академия Google]

49. Эббот БП и др. Гравитационно-волновое измерение постоянной Хаббла после второго запуска Advanced LIGO и Virgo. Астрофиз. Дж. 2021;909(2):218. doi: 10.3847/1538-4357/abdcb7. [CrossRef] [Google Scholar]

50. Kyutoku K, Seto N. Гравитационно-волновая космография с LISA и хаббловское напряжение. физ. 2017;d95(8):083525. [Google Scholar]

51. Del Pozzo W, Sesana A, Klein A. Звездные двойные черные дыры в диапазоне LISA: новый класс стандартных сирен. Пн. Нет. Рой. Астрон. соц. 2018;475(3):3485. дои: 10.1093/мнрас/sty057. [CrossRef] [Google Scholar]

52. Cutler C, Holz DE. Сверхточная космология из гравитационных волн. физ. Ред. 2009; D80:104009. [Google Scholar]

53. Нисидзава А., Таруя А., Сайто С. Отслеживание эволюции красного смещения параметра Хаббла с помощью стандартных сирен гравитационных волн. физ. Ред. 2011; D83:084045. [Google Scholar]

54. Abbott, R., et al.: GWTC-2: Компактные бинарные слияния, наблюдаемые LIGO и Virgo в первой половине третьего цикла наблюдений. arXiv: 2010.14527 (2020)

55. Мандель И., О’Шонесси Р. Компактные двойные слияния в полосе наземных детекторов гравитационных волн. Сорт. Квант. Грав. 2010;27:114007. doi: 10.1088/0264-9381/27/11/114007. [CrossRef] [Google Scholar]

56. Stevenson S, Berry CPL, Mandel I. Иерархический анализ гравитационно-волновых измерений рассогласований спиновых орбит бинарных черных дыр. Пн. Нет. Рой. Астрон. соц. 2017;471(3):2801. doi: 10.1093/mnras/stx1764. [CrossRef] [Google Scholar]

57. Talbot C, Thrane E. Определение свойств популяции вращающихся черных дыр. физ. Ред. 2017;d96(2):023012. [Google Scholar]

58. Zevin M, Pankow C, Rodriguez CL, Sampson L, Chase E, Kalogera V, Rasio FA. Ограничение моделей формирования двойных черных дыр гравитационно-волновыми наблюдениями. Астрофиз. Дж. 2017;846(1):82. doi: 10.3847/1538-4357/aa8408. [CrossRef] [Google Scholar]

59. Barrett JW, Gaebel SM, Neijssel CJ, Vigna-Gómez A, Stevenson S, Berry CPL, Farr WM, Mandel I. Точность вывода о физике двойной эволюции из гравитационно-волнового наблюдения. Пн. Нет. Рой. Астрон. соц. 2018;477(4):4685. дои: 10.1093/мнрас/сти908. [CrossRef] [Google Scholar]

60. Арка Седда М., Бенакиста М. Использование окончательных вращений и масс черных дыр для вывода истории формирования наблюдаемой популяции источников гравитационных волн. Пн. Нет. Рой. Астрон. соц. 2019;482(3):2991. [Google Scholar]

61. Арка Седда М., Мапелли М., Спера М., Бенакиста М., Джакоббо Н. Отпечатки каналов формирования бинарных черных дыр, закодированные в массе и вращении остатков слияния. Астрофиз. Дж. 2020;894(2):133. doi: 10.3847/1538-4357/ab88b2. [Перекрестная ссылка] [Академия Google] 9{16}\!\mathrm {O}$12C α,γ16O скорость. Астрофиз. Дж. Летт. 2020;902(2):L36. doi: 10.3847/2041-8213/abbadd. [CrossRef] [Google Scholar]

63. Нисидзава А., Сесана А., Берти Э., Кляйн А. Ограничение сценариев формирования звездных двойных черных дыр с помощью измерений эксцентриситета eLISA. Пн. Нет. Рой. Астрон. соц. 2017;465(4):4375. doi: 10.1093/mnras/stw2993. [CrossRef] [Google Scholar]

64. Canuel B, et al. Изучение гравитации с помощью крупномасштабного атомного интерферометра MIGA. науч. Отчет 2018;8(1):14064. дои: 10.1038/s41598-018-32165-з. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

65. Кремер К., Чаттерджи С., Брейвик К., Родригес С.Л., Ларсон С.Л., Расио Ф.А. Источники LISA в шаровых скоплениях Млечного Пути. физ. Преподобный Летт. 2018;120(19):191103. doi: 10.1103/PhysRevLett.120.191103. [PubMed] [CrossRef] [Google Scholar]

66. Рэндалл, Л., Сяньюй, З.З.: Эксцентриситет без измерения эксцентриситета: Различение каналов формирования двойных черных дыр звездной массы. архив: 1907.02283 (2019)

67. Петерс ПК. Гравитационное излучение и движение двух точечных масс. физ. 1964; 136:B1224. doi: 10.1103/PhysRev.136.B1224. [CrossRef] [Google Scholar]

68. Abbott BP, et al. Астрофизические последствия слияния двойных черных дыр GW150914. Астрофиз. Дж. 2016;818(2):L22. doi: 10.3847/2041-8205/818/2/L22. [CrossRef] [Google Scholar]

69. Samsing J, Ramirez-Ruiz E. О скорости сборки слияний черных дыр с большим эксцентриситетом. Астрофиз. Дж. 2017;840(2):L14. doi: 10.3847/2041-8213/aa6f0b. [Перекрестная ссылка] [Академия Google]

70. Родригес К.Л., Амаро-Сеоан П., Чаттерджи С., Кремер К., Расио Ф.А., Самсинг Дж., Йе К.С., Зевин М. Постньютоновская динамика в плотных звездных скоплениях: формирование, массы и скорость слияния высокоэксцентричных двойные черные дыры. физ. 2018;d98(12):123005. [PubMed] [Google Scholar]

71. Рэндалл Л., Сяньюй З.З. Прямой зонд плотности массы вблизи вдохновляющих двойных черных дыр. Астрофиз. Дж. 2019;878(2):75. doi: 10.3847/1538-4357/ab20c6. [CrossRef] [Google Scholar]

72. D’Orazio DJ, Samsing J. Слияния черных дыр из шаровых скоплений, наблюдаемые с помощью LISA II: разрешены эксцентрические источники и фон гравитационных волн. Пн. Нет. Рой. Астрон. соц. 2018;481(4):4775. дои: 10.1093/мнрас/сти2568. [CrossRef] [Google Scholar]

73. Арка-Седда, М., Ли, Г., Кочиш, Б.: Упорядочивание хаоса: слияния звездных черных дыр из неиерархических троек. arXiv:1805.06458 (2018)

74. Kremer K, et al. Постньютоновская динамика в плотных звездных скоплениях: двойные черные дыры в полосе LISA. физ. 2019;d99(6):063003. [Google Scholar]

75. Zevin M, Samsing J, Rodriguez C, Haster CJ, Ramirez-Ruiz E. Эксцентрические слияния черных дыр в плотных звездных скоплениях: роль двойных встреч. Астрофиз. Дж. 2019;871(1):91. doi: 10.3847/1538-4357/aaf6ec. [CrossRef] [Google Scholar]

76. Chen X, Amaro-Seoane P. Выявление образования двойных звездных черных дыр: необходимость децигерцовых обсерваторий гравитационных волн. Астрофиз. Дж. 2017;842(1):L2. doi: 10.3847/2041-8213/aa74ce. [CrossRef] [Google Scholar]

77. Portegies Zwart SF, McMillan S. Слияния черных дыр во вселенной. Астрофиз. Дж. 2000; 528:L17. дои: 10.1086/312422. [PubMed] [CrossRef] [Google Scholar]

78. Giersz M, Leigh N, Hypki A, Lützgendorf N, Askar A. Код MOCCA для моделирования звездных скоплений — IV. Новый сценарий образования черных дыр промежуточной массы в шаровых скоплениях. Пн. Нет. Рой. Астрон. соц. 2015;454(3):3150. дои: 10.1093/мнрас/stv2162. [CrossRef] [Google Scholar]

79. Арка Седда, М., Аскар, А., Герш, М.: База данных MOCCA-SURVEY I. Черные дыры промежуточной массы в шаровых скоплениях Млечного Пути и их связь со сверхмассивными черными дырами. arXiv:1905.00902 (2019)

80. Abbott R, et al. Свойства и астрофизические последствия слияния двойных черных дыр размером 150 M⊙ GW1

. Астрофиз. Дж. Летт. 2020;900(1):L13. doi: 10.3847/2041-8213/aba493. [CrossRef] [Google Scholar]

81. Amaro-Seoane P, Gair JR, Freitag M, Coleman Miller M, Mandel I, Cutler CJ, Babak S. Астрофизика, обнаружение и научные приложения спиралей со средним и экстремальным отношением масс . Сорт. Квант. Грав. 2007;24:R113. дои: 10.1088/0264-9381/24/17/R01. [CrossRef] [Google Scholar]

82. Браун Д.А., Фанг Х., Гейр Дж.Р., Ли С., Лавлейс Г., Мандель И., Торн К.С. Перспективы обнаружения гравитационных волн от спиралей промежуточного соотношения масс. физ. Преподобный Летт. 2007;99:201102. doi: 10.1103/PhysRevLett.99.201102. [PubMed] [CrossRef] [Google Scholar]

83. Rodriguez CL, Mandel I, Gair JR. Проверка свойства отсутствия волос массивных компактных объектов со спиралью промежуточного отношения масс в усовершенствованных детекторах гравитационных волн. физ. Ред. 2012; D85:062002. [Академия Google]

84. Haster CJ, Wang Z, Berry CPL, Stevenson S, Veitch J, Mandel I. Вывод о гравитационных волнах на основе слияния компактных объектов звездной массы и черных дыр промежуточной массы. Пн. Нет. Рой. Астрон. соц. 2016;457(4):4499. doi: 10.1093/mnras/stw233. [CrossRef] [Google Scholar]

85. Chen JH, Shen RF. Приливное разрушение звезды главной последовательности черной дырой промежуточной массы: яркое десятилетие. Астрофиз. Дж. 2018;867(1):20. doi: 10.3847/1538-4357/aadfda. [Перекрестная ссылка] [Академия Google]

86. Эраклеус М., Гезари С., Сесана А., Богданович Т., Маклауд М., Рот Н., Дай Л. Арена для астрофизики с несколькими посланниками: Вдохновенное и приливное разрушение белых карликов массивными черными дырами. Бык. Являюсь. Астрон. соц. 2019;51(3):10. [Google Scholar]

87. Ezquiaga JM, Holz DE. Преодоление разрыва: поиск самых больших черных дыр LIGO. arXiv: http://arxiv.org/abs/2006.02211. Астрофиз. Дж. Летт. 2020;909(2):L23. doi: 10.3847/2041-8213/abe638. [CrossRef] [Google Scholar]

88. Волонтери М., Натараджан П. Путешествие к соотношению MBH − σ: судьба черных дыр малой массы во Вселенной. Пн. Нет. Рой. Астрон. соц. 2009 г.;400:1911. doi: 10.1111/j.1365-2966.2009.15577.x. [CrossRef] [Google Scholar]

89. McKernan B, Ford KES, Kocsis B, Lyra W, Winter LM. Черные дыры промежуточной массы в дисках АЯГ II. Предсказания модели и наблюдательные ограничения. Пн. Нет. Рой. Астрон. соц. 2014;441(1):900. doi: 10.1093/mnras/stu553. [CrossRef] [Google Scholar]

90. Бартос И., Кочиш Б., Хайман З., Марка С. Быстрое и яркое слияние двойных черных дыр звездной массы в активных ядрах галактик. Астрофиз. Дж. 2017;835(2):165. doi: 10.3847/1538-4357/835/2/165. [Перекрестная ссылка] [Академия Google]

91. Стоун Н.К., Мецгер Б.Д., Хайман З. Вдохновение с помощью черных дыр звездной массы, встроенных в диски АЯГ: решение последней проблемы а.е. Пн. Нет. Рой. Астрон. соц. 2017;464(1):946. doi: 10.1093/mnras/stw2260. [CrossRef] [Google Scholar]

92. McKernan B, et al. Ограничение слияний черных дыр звездной массы в дисках AGN, обнаруживаемых с помощью LIGO. Астрофиз. Дж. 2018;866(1):66. doi: 10.3847/1538-4357/aadae5. [CrossRef] [Google Scholar]

93. Chen X, Li S, Cao Z. Вырождение массред-сдвига для источников гравитационных волн вблизи сверхмассивных черных дыр. Пн. Нет. Рой. Астрон. соц. 2019;485(1):L141. doi: 10.1093/mnrasl/slz046. [CrossRef] [Google Scholar]

94. Гондан Л., Кочиш Б., Раффаи П. , Фрей З. Источники захвата гравитационных волн эксцентрическими черными дырами в ядрах галактик: распределение двойных параметров. Астрофиз. Дж. 2018;860(1):5. doi: 10.3847/1538-4357/aabfee. [CrossRef] [Google Scholar]

95. Secunda A, Bellovary J, Mac Low MM, Saavik Ford KE, McKernan B, Leigh N, Lyra W, Sándor Z. Орбитальная миграция взаимодействующих черных дыр звездной массы в дисках вокруг сверхмассивной черной отверстия. Астрофиз. Дж. 2019;878(2):85. doi: 10.3847/1538-4357/ab20ca. [CrossRef] [Google Scholar]

96. Рассказов А., Кочиш Б. Скорость рассеяния черных дыр звездной массы в ядрах галактик. Астрофиз. Дж. 2019; 881:20. doi: 10.3847/1538-4357/ab2c74. [CrossRef] [Google Scholar]

97. Yang Y, Bartos I, Haiman Z, Kocsis B, Marka Z, Stone NC, Marka S. Диски AGN усиливают массовое распределение слияний двойных черных дыр звездной массы. Астрофиз. Дж. 2019;876(2):122. doi: 10.3847/1538-4357/ab16e3. [Перекрестная ссылка] [Академия Google]

98. Косовский А. , Тернер М.С. Гравитационное излучение от сталкивающихся вакуумных пузырей: аппроксимация оболочки для многих столкновений пузырей. физ. Ред. 1993; D47:4372. [PubMed] [Google Scholar]

99. Камионковский М., Косовский А., Тернер М.С. Гравитационное излучение от фазовых переходов первого рода. физ. Ред. 1994; D49:2837. [PubMed] [Google Scholar]

100. Гогоберидзе Г., Кахниашвили Т., Косовский А. Спектр гравитационного излучения первичной турбулентности. физ. Ред. 2007; 083002:D76. [Академия Google]

101. Caprini C, Durrer R, Servant G. Фон стохастических гравитационных волн от турбулентности и магнитных полей, генерируемых фазовым переходом первого рода. JCAP. 2009;0912:024. doi: 10.1088/1475-7516/2009/12/024. [CrossRef] [Google Scholar]

102. Hindmarsh M, Huber SJ, Rummukainen K, Weir DJ. Гравитационные волны от звука фазового перехода первого рода. физ. Преподобный Летт. 2014;112:041301. doi: 10.1103/PhysRevLett.112.041301. [PubMed] [CrossRef] [Академия Google]

103. Хиндмарш М., Хубер С.Дж., Руммукайнен К., Вейр Д.Дж. Численное моделирование акустически генерируемых гравитационных волн при фазовом переходе первого рода. физ. 2015;d92(12):123009. [Google Scholar]

104. Рэндалл Л., Слуга Г. Гравитационные волны из искривленного пространства-времени. JHEP. 2007;05:054. doi: 10.1088/1126-6708/2007/05/054. [CrossRef] [Google Scholar]

105. Нардини Г., Кирос М., Вульцер А. Ограничивающий сильный электрослабый фазовый переход первого рода. JHEP. 2007;09:077. doi: 10.1088/1126-6708/2007/09/077. [CrossRef] [Google Scholar]

106. Константин Т., Нардини Г., Кирос М. Влияние гравитационной обратной реакции на голографический фазовый переход. физ. Ред. 2010; D82:083513. [Google Scholar]

107. Константин Т., Сервант Г. Космологические следствия почти конформной динамики в масштабе ТэВ. JCAP. 2011;1112:009. doi: 10.1088/1475-7516/2011/12/009. [CrossRef] [Google Scholar]

108. Бруггиссер С., Фон Харлинг Б., Мацедонский О., Сервант Г. Барионная асимметрия из составного бозона Хиггса. физ. Преподобный Летт. 2018;121(13):131801. doi: 10.1103/PhysRevLett.121.131801. [PubMed] [CrossRef] [Академия Google]

109. Мегиас Э., Нардини Г., Кирос М. Космологические фазовые переходы в искривленном пространстве: гравитационные волны и сигнатуры коллайдеров. JHEP. 2018;09:095. doi: 10.1007/JHEP09(2018)095. [CrossRef] [Google Scholar]

110. Аркани-Хамед Н., Хан Т., Мангано М., Ван Л.Т. Физические возможности протонно-протонного коллайдера на 100 ТэВ. физ. Представитель 2016;652:1. doi: 10.1016/j.physrep.2016.07.004. [CrossRef] [Google Scholar]

111. Graham PW, Kaplan DE, Mardon J, Rajendran S, Terrano WA. Прямое обнаружение темной материи с помощью акселерометров. физ. Ред. 2016;d93(7):075029. [Google Scholar]

112. Вачаспати Т., Виленкин А. Гравитационное излучение космических струн. физ. Ред. 1985; D31:3052. [PubMed] [Google Scholar]

113. Бланко-Пилладо Дж. Дж., Олум К. Д., Шлаер Б. Количество петель космических струн. физ. 2014;d89(2):023512. [Google Scholar]

114. Auclair P, et al. Исследование фона гравитационных волн от космических струн с помощью LISA. JCAP. 2020;2004:034. doi: 10.1088/1475-7516/2020/04/034. [Перекрестная ссылка] [Академия Google]

115. Sanidas SA, Battye RA, Stappers BW. Ограничения на натяжение космической струны, налагаемые ограничением на фон стохастических гравитационных волн от European Pulsar Timing Array. физ. Ред. 2012; D85:122003. [Google Scholar]

116. Бланко-Пилладо Дж. Дж., Олум К. Д., Сименс X. Новые ограничения на космические струны из наблюдения гравитационных волн. физ. лат. 2018;B778:392. doi: 10.1016/j.physletb.2018.01.050. [CrossRef] [Google Scholar]

117. Бендер П.Л., Бегельман М.С., Гейр Дж.Р. Возможные научные цели последующей миссии LISA. Сорт. Квант. Грав. 2013;30:165017. дои: 10.1088/0264-9381/30/16/165017. [CrossRef] [Google Scholar]

118. Mueller G, Baker J, et al. Космическая гравитационно-волновая астрономия за пределами LISA. Бык. Являюсь. Астрон. соц. 2019;51(7):243. [Google Scholar]

119. Hu WR, Wu YL. Космическая программа Тайцзи по физике гравитационных волн и природе гравитации. Натл. науч. 2017;4(5):685. doi: 10.1093/nsr/nwx116. [CrossRef] [Google Scholar]

120. Ruan WH, Guo ZK, Cai RG, Zhang YZ. Программа Тайцзи: Источники гравитационных волн. Междунар. Дж. Мод. физ. 2020;а35(17):2050075. doi: 10.1142/S0217751X2050075X. [Перекрестная ссылка] [Академия Google]

121. Kuns KA, Yu H, Chen Y, Adhikari RX. Астрофизика и космология с децигерцовым детектором гравитационных волн: TianGO. физ. Ред. 2020;d102(4):043001. [Google Scholar]

122. Luo J, et al. TianQin: космический детектор гравитационных волн. Сорт. Квант. Грав. 2016;33(3):035010. doi: 10.1088/0264-9381/33/3/035010. [CrossRef] [Google Scholar]

123. Sato S, et al. Статус DECIGO. Дж. Физ. конф. сер. 2017;840(1):012010. doi: 10.1088/1742-6596/840/1/012010. [Перекрестная ссылка] [Академия Google]

124. Кавамура С. и др. Текущее состояние космических антенн гравитационных волн DECIGO и B-DECIGO. arXiv:2006.13545 (2020)

125. Crowder J, Cornish NJ. Помимо LISA: изучение будущих миссий гравитационных волн. физ. Ред. 2005; D72:083005. [Google Scholar]

126. Маквильямс С.Т. Геостационарная антенна для лазерной интерферометрии без помех (GADFLI). arXiv:1111.3708 (2011)

127. Тинто, М., де Араужо, Дж.С.Н., Агуяр, О.Д., да Силва Алвес, М.Э.: Геостационарный интерферометр гравитационных волн (GEOGRAWI). архив: 1111.2576 (2011)

128. Тинто М., ДеБра Д., Бухман С., Тилли С. gLISA: концепции космической антенны геосинхронного лазерного интерферометра с готовыми спутниками. преподобный наук. Инструм. 2015;86:014501. doi: 10.1063/1.4

2. [PubMed] [CrossRef] [Google Scholar]

129. Lacour S, et al. SAGE: найти IMBH в пустыне черной дыры. Сорт. Квант. Грав. 2019;36(19):195005. doi: 10.1088/1361-6382/ab3583. [CrossRef] [Google Scholar]

130. Tino GM, et al. SAGE: Предложение для исследователя космической атомной гравитации. Евро. физ. Дж. 2019;D73(11):228. [Google Scholar]

131. Колковиц С., Пиковский И., Ланжелье Н., Лукин М.Д., Уолсворт Р.Л., Йе Дж. Обнаружение гравитационных волн с помощью атомных часов на оптической решетке. физ. 2016;d94(12):124043. [Google Scholar]

132. Su J, Wang Q, Wang Q, Jetzer P. Обнаружение низкочастотных гравитационных волн с помощью двойных оптических часов в космосе. Сорт. Квант. Грав. 2018;35(8):085010. doi: 10.1088/1361-6382/aab2eb. [CrossRef] [Google Scholar]

133. Грэм П.В., Хоган Дж.М., Касевич М.А., Раджендран С., Романи Р.В.: Обнаружение гравитационных волн в среднем диапазоне с помощью прецизионных атомных датчиков. arXiv: 1711.02225 (2017) [PubMed]

134. El-Neaj YA, et al. AEDGE: атомный эксперимент по исследованию темной материи и гравитации в космосе. EPJ Квант. Технол. 2020;7:6. doi: 10.1140/epjqt/s40507-020-0080-0. [CrossRef] [Google Scholar]

135. Арка Седда, М., и др.: Недостающее звено в гравитационно-волновой астрономии: открытия, ожидающие в диапазоне децигерц. arXiv:1908.11375v1(2019) [бесплатная статья PMC] [PubMed]

136. Sesana, A, et al.: Открытие гравитационной вселенной на частотах μ Гц. arXiv:1908.11391 (2019)

137. Байбхав В. и др.: Исследование природы черных дыр: Глубоко в гравитационно-волновом небе МГц. arXiv:1908.11390 (2019) [бесплатная статья PMC] [PubMed]

138. Бейкер Дж. и др.: Астрономия гравитационных волн с высоким угловым разрешением. arXiv:1908.11410 (2019)

Удивительные свойства квадратов и их вычисления Киран Парулекар — Электронная книга

Электронная книга528 страниц4 часа

Рейтинг: 0 из 5 звезд0289

Ниже приведены характерные особенности книги «Удивительные свойства квадратов и их расчеты». Эта книга оригинальна. Это означает, что в большинстве глав обсуждаются вещи, которых мы не найдем ни в одной другой книге по скоростной арифметике. Даже если конкретное понятие встречается в какой-то книге или на сайте, автор представил его немного по-другому. — Автор привел достаточное количество примеров по каждому виду вычисления квадрата числа (минимум 3 примера), чтобы у читателя не возникло сомнений. .-Почти все главы имеют стиль, отличный от традиционного изучения математики, преподаваемого в школе или колледже, или в книгах.-Каждая глава обсуждалась отдельно без каких-либо предварительных знаний о предыдущих главах, так что читатель может читать любую главу независимо и может двигаться в любой порядок в чтении этой книги. — После прочтения этой книги у людей, испытывающих ненависть к математике, может развиться симпатия к математике не только в вычислении квадратов, но и в других областях, таких как умножение и деление. — Методы, используемые для вычисления общих и частных квадратов и свойства квадратов, подобные тем, что обсуждались в главе 21 (она занимает всего две страницы), могут быть полезны и для конкурсных экзаменов.s и отбрасывание 11 использовались для проверки расчетов, но в этой книге, в главах 17 и 18, эти два метода используются для вычисления квадрата двузначных и трехзначных чисел соответственно, что является совершенно новой вещью. Книга предполагает, что читатель знает таблицы от 1 до 10 чисел и квадраты от 1 до 25 чисел, что является очень минимальным ожиданием, поэтому для чтения этой книги не требуется большого математического образования. — Примеры объясняются шаг за шагом, и их много, и любой ученик выше 7 ‘ й стандарт может понять это. Также темы варьируются от элементарного до сложного уровня. — Здесь обсуждаются все методы вычисления квадрата числа, которые присутствуют в других книгах, в дополнение к некоторым новым методам. Ниже приведены методы, обсуждаемые в этой книге для вычисления квадрата общего числа. 1) В главе 6 квадрат находится с использованием алгебраического тождества (a+b)22) В главе 7 квадрат находится с помощью б)*(а-б)3)В главе 8 рассматривается метод ведической математики для вычисления квадрата двузначного числа.4)В главе 9и 10, метод, данный для двузначных чисел, обобщается на трех- и четырехзначные числа. 5) В главе 13 квадрат числа. близка к степени 10 или кратна степени 10 или кратна степени 10, что дано в ведической математике. Ведическая математика. 7) В главе 15 дается метод соотношения, основанный на соотношении двух последовательных цифр. 8) В главе 16 расчет с использованием винкулума, который не является другим методом, но часто используется, когда цифры большие. 9) В главе 17 квадрат двузначного числа находится с помощью метода отбрасывания девяток, который до сих пор использовался только для проверки вычислений. 10) В главе 18 квадрат трехзначного числа находится с использованием метода отбрасывания девяток и одиннадцати, который до сих пор использовалась только для проверки расчетов. Следовательно, эту книгу можно считать библией по расчету квадратов, а также по свойствам квадратов.

Пропустить карусель

ЯзыкАнглийский

Издатель Киран Парулекар

Дата выпуска: 29 декабря 2013 г.

ISBN9781311492999

Автор

Киран Парулекар

Киран Анил Парулекар, автор книги «Удивительные свойства квадратов и их вычисления», принимал участие в обширных исследованиях по теории чисел и практическим числам.

Киран — волшебник чисел, и ему нравится работать с вычислениями, содержащими большие числа. Он обладает более чем 25-летним огромным опытом в области элементарной теории чисел и расчета чисел. Киран 3 раза становился призером I.I.T. олимпиада по математике в 1991, 1992 и 1995. Олимпиада IIT по математике направлена на проверку чисто математических навыков. Киран также занимала первое место в I.I.T. Магистр наук вступительный тест по математике и M.C.A. оба вступительных испытания проводились в июле 1992 года.

Предпросмотр книги

Amazing Properties of Squares & Their Calculations — Kiran Parulekar

Amazing Properties of Squares & Their Calculations

Published by Kiran Parulekar at Smashwords

Table of Contents

Preface

Символы, используемые в книге

Глава 2. Квадрат трех чисел особого типа

Гл. 3. Квадрат Любого № 9За ним следует одна цифра

Ch4. Квадрат любого числа из 3, за которым следует одна цифра

Ch5. Квадрат любого числа из 6, за которым следует одна цифра

Ch5. Квадраты чисел, оканчивающихся на 5

Ch6. Квадраты чисел с использованием формулы (A+B)²

Ch7. Квадраты чисел по формуле A² = B² + (A+B)*(A-B)

Ch8. Квадрат любого двузначного числа с использованием метода ведической математики

Гл.9. Преобразование квадрата любого двузначного числа в квадрат трехзначного числа

Ch20. Преобразование квадрата любого трехзначного числа в квадрат четырехзначного числа

Ch21.Квадрат любого однозначного числа, повторяющегося любое число раз

Ch22.Квадрат из более чем однозначного числа. повторяется любое количество раз

Ch23.Квадрат числа, которое близко к степени 10 или близко к кратной степени 10 или близко к дольной степени 10

CH24. Square number с использованием метода Vedic ‘urdhva tiryak’

CH25.Square с использованием коэффициента

CH26.square с использованием Vinculam

CH26.square. Out 9’s Method

Ch28.Квадрат трехзначного числа. с использованием отливки 9 и отливки 11

Ch29. Квадрат особого вида трехзначных чисел

Ч30. Квадрат особого вида четырехзначных чисел

CH31. Пропорции идеальных квадратов

CH32.Square n цифровых чисел с одинаковыми последними N -цифрами для любых N.

CH33. Squares, имеющие специфические свойства, касающиеся их Digits 3903 3 334.44. Число как разность двух положительных квадратов

Ch35.Выражение числа в виде суммы двух положительных квадратов

Ch36.Нахождение квадратного корня из полного квадрата.

Предисловие
Добро пожаловать всем читателям! Спасибо за интерес к чтению Удивительные свойства квадратов и их вычисления . Эта книга содержит интересные, но малоизвестные факты о квадратах натуральных чисел. Здесь, в этой книге, вы найдете некоторые специальные типы чисел и интересные факты о квадрате таких специальных чисел. Кроме того, автор коснулся общей концепции вычисления квадратов.
Автора книги, Киран Анил Парулекар занимается изучением теории чисел и практических чисел. Он волшебник чисел и имеет большой опыт в элементарной теории чисел и вычислении чисел. Удивительные свойства квадратов и их вычисление является результатом личного опыта Киран в работе с большими натуральными числами в течение 25 лет. Он 3-кратный призер I.I.T. Математическая олимпиада в 1991, 1992 и 1995 годах. Математическая олимпиада ИИТ известна проверкой чисто математических навыков участников. Киран также занимала первое место в I.I.T. Магистр наук вступительный тест по математике и M.C.A. вступительные испытания, оба состоялись 19 июля.92. Благодаря своей самоотверженности и постоянным исследованиям натуральных чисел, Киран широко известен как «Мастер чисел ». Мы глубоко убеждены, что читатели захотят и оценят эту работу Волшебника чисел. Мы хотели бы получить откровенные отзывы наших читателей об этой работе и помочь нам исправить наши непреднамеренные ошибки.
Ниже приведены основные особенности книги «Удивительные свойства квадратов и их расчеты », и мы призываем читателей внимательно прочитать каждую главу этой книги и поделиться своими ценными комментариями о работе…
Эта книга оригинальна. Это означает, что в большинстве глав обсуждаются вещи, которых мы не найдем ни в одной другой книге по скоростной арифметике. Даже если конкретная концепция встречается в какой-то книге или на сайте, автор представил ее немного по-другому.
Автор привел достаточное количество примеров по каждому виду вычисления квадрата числа (минимум 3 примера), чтобы у читателя не осталось сомнений.
Стиль почти всех глав отличается от традиционного изучения математики, преподаваемого в школе, колледже или в книгах.
Каждая глава обсуждалась отдельно без каких-либо предварительных знаний о предыдущих главах, так что читатель может читать любую главу независимо и может двигаться в любом порядке при чтении этой книги.
Прочитав эту книгу, люди, испытывающие ненависть к математике, могут полюбить математику не только в вычислении квадратов, но и в других областях, таких как умножение и деление.
Методы, используемые для расчета общих и частных квадратов и свойств квадратов, подобные тем, что обсуждались в главе 21 (которая занимает всего две страницы), также могут быть полезны для конкурсных экзаменов.
До сих пор такие методы, как отбрасывание девяток и отбрасывание 11, использовались для проверки вычислений, но в этой книге, в главах 17 и 18, эти два метода используются для вычисления квадрата двухзначных и трехзначных чисел соответственно, что является совершенно новой вещью.
Книга предполагает, что читатель знает таблицы чисел от 1 до 10 и квадраты чисел от 1 до 25, что является очень минимальным ожиданием, поэтому для чтения этой книги не требуется особых математических знаний.
Примеры объясняются пошагово, и их очень много, и любой ученик выше 7-го уровня может их понять. Также темы варьируются от элементарного до сложного уровня.
Здесь обсуждаются все методы вычисления квадрата числа, присутствующие в других книгах, а также некоторые новые методы. Ниже приведены методы, обсуждаемые в этой книге, для вычисления квадрата общего числа.
В главе 6 квадрат находится с помощью алгебраического тождества (a+b)²
В главе 7 квадрат находится с помощью a² = b² + (a+b)*(a-b)
В главе 8 метод ведической математики считается, чтобы вычислить квадрат двузначного числа.
В главе 9и 10, метод, данный для двузначных чисел, обобщается на трех- и четырехзначные числа.
В главе 13, квадрат №. считается близкой к степени 10 или кратной степени 10 или кратной степени 10, что дано в ведической математике.
В главе 14 обсуждается самый общий метод, метод «Урдхва Тирьяк», который дан в ведической математике.
В главе 15 дается метод соотношения, основанный на соотношении двух последовательных цифр.
В главе 16 расчет с использованием винкулума, который не является другим методом, но часто используется, когда цифры большие.
В главе 17 квадрат двузначного числа находится методом отбрасывания девяток, который до сих пор использовался только для проверочного вычисления.
В главе 18 квадрат трехзначного числа находится методом отбрасывания девяток и одиннадцати, который до сих пор использовался только для проверочного вычисления.
Следовательно, эту книгу можно считать библией по вычислению квадратов, а также по свойствам квадратов.
à Подход, используемый в этой книге, основан на вычислении двух последних цифр квадрата, что отличается от других подходов, в которых рассматривается только последняя цифра квадрата.
à Объясняется теория, стоящая за каждой концепцией, что поможет увлеченным математиком гордиться собой. Поверхностные читатели могут использовать только последний результат, данный в теории.
à Вычисление, подобное 97², может быть выполнено различными методами, такими как
Используя формулу (a+b)²
Используя метод ведической математики (100-x)² = 100-2*x | х²
Использование метода для вычисления квадрата числа, близкого к степени 10
Использование ведического метода «Урдхва Тирьяк».
Метод отношения.
Метод винкулума.
Использование отливки девяток.
Следовательно, для любого квадрата существуют разные методы для выполнения одних и тех же вычислений.
à Вычисления квадратов, которые обсуждаются в других книгах, были обобщены для создания общей формулы, аналогичной всем квадратам, обсуждаемым в главах 2, 3 и 4.
à Главы 11 и 12 интересно читать как определенную цифру или конкретное число, повторяющееся любое нет. раз можно возвести в квадрат с помощью метода арифметической прогрессии.
à Акцент был сделан, чтобы объединить концепцию чистой математики и практических чисел.
Эту книгу можно разделить на пять основных категорий, а именно:
Свойства квадратов
Вычисление квадрата общего числа
Вычисление квадрата определенного типа числа
Представление числа в виде разности/суммы положительных целых квадратов разными способами
Обратный процесс возведения в квадрат (т. е. нахождение квадратного корня) 21, 22 и 23 относятся к этому типу. Здесь либо свойства отдельных цифр квадрата рассматриваются как 7225 = 85², где все цифры в квадрате являются простыми числами, ИЛИ свойство квадрата в целом рассматривается как 9 = 3² имеет точно нечетное (3) нет. положительных делителей, а именно 1,3 и 9в то время как неквадрат всегда имеет даже нет. положительных делителей. Подробнее об этом в главах с 21 по 23. В главе 23 генерация квадратов с определенными свойствами с помощью программ представляет собой интересное явление.
Второй, вычисление квадрата общего числа:- № главы. 6, 7, 8, 9, 10, 13, 14, 15, 16, 17 и 18 основаны на этом. Здесь нет ограничений на конкретную цифру числа. Например, в главе 6 рассматривается квадрат общего числа, такого как 34, что равно 34² = 1156. Также в главе 7 квадрат большого числа, такого как 197² = 38809 дано.
Третий , вычисление квадрата определенного типа числа: — Главы 1, 2, 3, 4, 5, 11, 12, 19 и 20 относятся к этой категории. Здесь рассматривается вычисление квадрата числа, имеющего определенные цифры. Например, в главе 2 квадрат числа, содержащего любое число. из девяток, за которыми следует одна цифра, считается, а в главе 11 квадрат из одной цифры повторяется любой нет. раз учитывается.
Четвертый , представляющий число как разность/сумму квадратов положительных целых чисел разными способами: Глава 24, содержащая разность двух положительных квадратов, и глава 25, содержащая сумму двух положительных квадратов. Это скорее понятие из чистой математики и для представления конкретного нет. как сумма двух положительных квадратов считается во многих книгах очень сложной, но здесь это объясняется очень легко.
Пятый , Обратный процесс возведения в квадрат (т.е. нахождение квадратного корня): — Глава 26 основана на этом. Нахождение квадратного корня методом, отличным от описанного в других книгах. Здесь мы рассматриваем последние две цифры квадрата и предсказываем последние две цифры его квадратного корня, а затем фактически находим квадратный корень.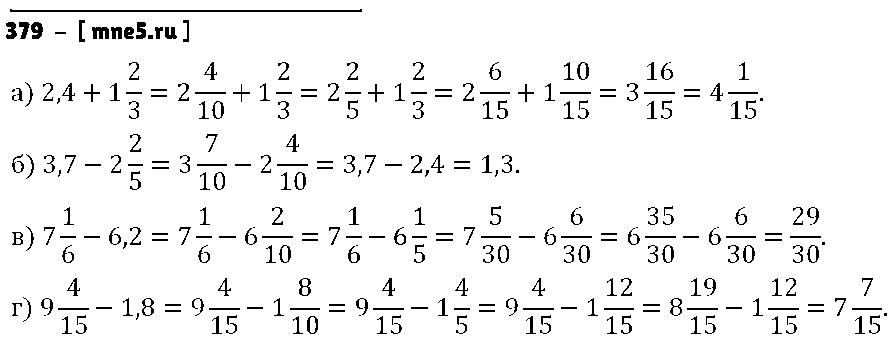 Например, рассмотрим квадратный корень из 1444. Обратите внимание, что от 1 до 100 чисел есть только четыре числа, а именно 12, 38, 62 и 88, квадрат которых заканчивается двумя последними цифрами как 44. Мы использовали этот факт, чтобы найти ответ как 38.
Так что читайте эту книгу как хобби, а не как учебник. Если у читателя возникнут вопросы, он может связаться с автором по следующему адресу электронной почты: — [email protected]
Символы, используемые в книге
В книге используются следующие символы.
Для квадрата 34 используется символ 342.
Для 2*a*b используется символ 2ab или 2*ab или 2*a*b.
В главах 22, 23, 24 и 25 символ SQR(x) используется для квадрата x.
Chapter 1
Square of Three Special Type of Numbers
Special type 1
Consider the following square pattern
1) 34² = 1156
2) 334² = 111556
3) 3334² = 11115556
4) 33334² = 1111155556
Теперь предположим, что мы хотим возвести в квадрат ((цифра 3 повторяется 20 раз), за которой следует цифра 4).
т. е. 3333333333333333333334² = 11111111111111111111155555555555555555556
Метод следующий:-
Мы должны подсчитать, сколько раз цифра 3 повторяется в исходном числе. В приведенном выше примере цифра 3 повторяется ровно 20 раз.
В квадрате цифра 1 будет повторяться 21 раз (просто на единицу больше, чем цифра 3 повторяется в исходном числе), за которой следует цифра 5, повторяющаяся 20 раз (просто равно количеству повторений цифры 3 в исходном числе) номер), за которым следует цифра 6.
Вопрос:-
Можем ли мы вычислить квадрат числа, состоящего из (цифра 3 повторяется 1000 раз, за которой следует цифра 4). Ответ положительный.
И ответ: ((Цифра 1 повторяется 1001 раз), за которой следует (цифра 5 повторяется
1000 раз) и цифра 6)
В общем,
============= ==============================================
( (цифра 3 повторяется n раз), за которой следует цифра 4)²
= (цифра 1 повторяется (n+1) раз), за которой следует (цифра 5 повторяется n раз), за которой следует цифра
цифра 6.
========================================= =================
Специальный тип 2
Перейдем к другому шаблону того же типа.
1) 67² = 4489
2) 667² = 444889
3) 6667² = 444488889
4) 66667² = 4444488889
Теперь предположим, что мы хотим до квадрата (цифр 6 Times 20).
т.е. 66666666666666666667² = 4444444444444444444488888888888888888889
Метод следующий:-
Мы должны подсчитать, сколько раз цифра 6 повторяется в исходном числе. В приведенном выше примере цифра 6 повторяется ровно 20 раз.
В квадрате цифра 4 будет повторяться 21 раз (просто на один раз больше, чем цифра 6 повторяется в исходном числе), за которой следует цифра 8, повторяющаяся 20 раз (просто равно количеству повторений цифры 6 в исходном числе). исходный номер), за которым следует цифра 9.
Вопрос:-
Можем ли мы вычислить квадрат числа, состоящего из ((цифра 6 повторяется 1000 раз), за которой следует цифра 7). Ответ положительный.
И ответ: (Цифра 4 повторяется 1001 раз), за которой следует (цифра 8 повторяется
1000 раз) и цифра 9.
В общем,
=============================================
(( цифра 6, повторенная n раз), за которой следует цифра 7)²
= (цифра 4, повторенная (n+1) раз), за которой следует (цифра 8, повторенная n раз), за которой следует цифра
цифра 9.
========================================= ================
Особый тип 3
Переходим к третьему квадратному шаблону такого же типа
1) 68² = 4624
2) 668² = 446224
3) 6668² = 44462224
4) 66668² = 4444622224
Now suppose we want to square ((digit 6 repeated 20 times) followed by digit 8)
i.e. 666666666666666666668² = 444444444444444444446222222222222222222224
Метод следующий:-
Мы должны подсчитать, сколько раз цифра 6 повторяется в исходном числе. В приведенном выше примере цифра 6 повторяется ровно 20 раз.
В квадрате цифра 4 будет повторяться 20 раз (просто равно количеству повторений цифры 6 в исходном числе), за которой ровно один раз следует цифра 6, за которой следует цифра 2, повторенная 20 раз (просто равно количеству повторений цифры 6 повторяется в исходном номере), за которым следует цифра 4.
Вопрос:-
Можем ли мы вычислить квадрат числа, состоящего из ((цифра 6 повторяется 1000 раз), за которой следует цифра 8). Ответ положительный.
И ответ: ((Цифра 4 повторяется 1000 раз), за которой следует цифра 6, затем (цифра 2 повторяется 1000 раз) и цифра 4.
В общем,
=========== ================================================
((цифра 6 повторяется n раз), за которой следует цифра 8)²
= (цифра 4 повторяется n раз), за которой следует цифра 6, за которой следует (цифра 2 повторяется n раз), за которой следует цифра 4.
=============================================== ============
Глава 2
Квадрат любого количества девяток, за которыми следует одна цифра
Теперь я собираюсь дать метод возведения в квадрат числа, содержащего повторяющуюся цифру 9 любой нет. раз, за которым следует любая одиночная цифра от 1 до 9, и самое удивительное, что мы должны знать квадраты чисел от 91 до 99 и ничего больше, чтобы вычислить это.
Нет необходимости помнить об этом, так как в ведической математике есть много методов, чтобы найти это.
Рассмотрим квадраты чисел от 91 до 99. (Читатель должен обратить внимание, что этот метод дан в книге по ведической математике.)
Рассмотрим (100-x)² = (100-x)*(100-x) = 100* (100-2*х) + х*х. Обозначьте число от 91 до 99 буквой n. Также пусть 100 – n = x. Следовательно, 100-x = n и n*n = 100*(n-x) + x*x.
Тогда квадрат n равен = (n – x) | x*x, где x*x должно быть двузначным числом. Если это не двузначное число, то мы должны поставить один ноль слева от x*x и сделать его двузначным.
Рассмотрим число 91. Здесь n = 91 и 100 – 91 = x = 9.
Отсюда 91² = (91 – 9) | 9*9 = 8281.
Возьмем другой пример, n = 97. Отсюда 100 – 97 = x = 3.
Отсюда 97² = (97 – 3) | 3*3 = 9409. (Обратите внимание, что x*x = 3*3 = 9 — однозначное число, поэтому мы добавили ноль слева.)
Таким образом, мы получим квадраты от 91 до 99, и они следующее.
1) 91² = (91 – 9) | 9*9 = 8281
2) 92² = (92 – 8) | 8*8 = 8464
3) 93² = (93 – 7) | 7*7 = 8649
4) 94² = (94 – 6) | 6*6 = 8836
5) 95² = (95 – 5) | 5*5 = 9025
6) 96² = (96 – 4) | 4*4 = 9216
7) 97² = (97 – 3) | 3*3 = 9409
8) 98² = (98 – 2) | 2*2 = 9604
9) 99² = (99 – 1) | 1*1 = 9801
Предположим, мы хотим вычислить 9999994².
Наше базовое число равно 94. (Это получается путем хранения цифры 9 ровно один раз, за которой следует последняя цифра (т.е. самая правая цифра). Мы знаем, что 94² равно 8836. Теперь, чтобы найти квадрат 9999994, мы должны выполнить 2 операции над этим квадратом, то есть 8836, просто операцию а) и б).
Вставьте цифру 9 ровно 5 раз (т. е. на единицу меньше, чем цифра 9, повторяющаяся в исходном номере) в крайнем левом углу.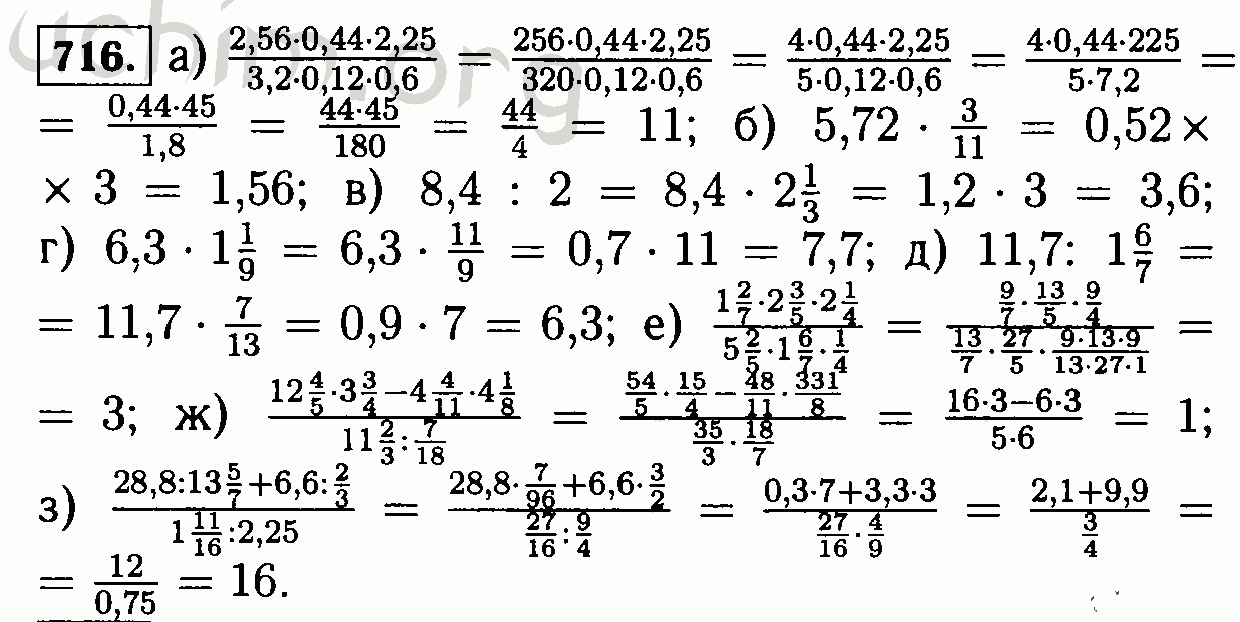
Вставить цифру 0 ровно 5 раз (т.е. на единицу меньше, чем цифра 9, повторенная в исходном числе) между 88 и 36.9999997. Его площадь нужно узнать. Наше базовое число равно 97, и мы знаем, что 97² = 9409. Следовательно, чтобы найти квадрат 9999999997, нам нужно выполнить следующие две операции.
Вставьте цифру 9 ровно 8 раз (т. е. на единицу меньше, чем цифра 9, повторяющаяся в исходном номере) в крайнем левом углу.
Вставьте цифру 0 ровно 8 раз между 94 и 09.
После выполнения 2 операций мы получим,
9999999997² = 99999999940000000009
В общем, чтобы найти квадрат числа, состоящего из (цифры 9повторил какой-то нет. количество раз, за которым следует любая ненулевая цифра) вычисляется следующим образом.
См. базовое число, которое представляет собой двузначное число, крайняя левая цифра которого равна 9, а цифра единиц является цифрой единиц исходного числа. Это должно быть ровно одно среди 9 чисел от 91 до 99. Из приведенного выше квадрата чисел от 91 до 99 мы можем вычислить квадрат этого базового числа. Просто отделите группу из двух крайних левых цифр, которую мы назовем X, от группы из двух крайних правых цифр, которую мы назовем Y.
Просто вставьте цифру 9 ровно столько раз, сколько на единицу меньше, чем нет. из девяток в исходном числе, которое нужно возвести в квадрат слева от X и
Вставить цифру 0 ровно столько раз, сколько раз на единицу меньше, чем нет. девяток в числе, которое нужно возвести в квадрат между X и Y.
Таким образом, мы получим квадрат исходного числа.
Например, мы хотим вычислить квадрат числа, состоящего из (цифра 9 повторяется 15 раз, за которой следует цифра 3). Шаги следующие: —
Базовый номер 93, а его квадрат сверху равен 8649. Отделим две крайние левые цифры 86 от двух крайних правых цифр 49.
Далее проделаем шаг (а) в нашем алгоритме, т.е. цифру 9 будем вставлять ровно 14 раз (ровно на единицу меньше, чем количество девяток в исходном числе) слева от 86.
Аналогично шагу (b) нашего алгоритма, т. е. мы вставим цифру 0 ровно 14 раз (ровно на одну меньше, чем количество девяток в исходном числе) между группами 86 и 49, чтобы получить число
(цифра 9 повторяется 14 раз), за которой следует двузначное число 86, затем (цифра 0 повторяется 14 раз) и двузначное число 49. Следовательно,
99999999999999993² = 999999999999998600000000000000049
3 абсолютно ясно в нашем уме.
Вычислить 99999999996²
Квадрат двухзначного основного числа, образованного из исходного числа, т. е. 96 равно 9216.
Просто разделите числа 92 (две крайние левые цифры) и 16 (две крайние правые цифры).
Теперь мы должны вставить цифру 9 ровно девять раз (это потому, что в исходном числе цифра 9 повторяется десять раз) слева от 92.
Также мы должны вставить цифру 0 ровно девять раз (это потому, что в исходная цифра 9 повторяется десять раз) между 92 и 16. Следовательно, мы получаем, 99999999996² = 99999999999200000000016
Глава 3
Квадрат любой цифры 2 далее к квадратам (цифра 3 повторяется любое количество раз, за которой следует одна ненулевая цифра)
В прошлый раз мы писали квадраты двухзначных чисел с основанием от 91 до 99. На этот раз очередь от 31 до 38.
Рассмотрим (30+x) ² = (30+x)*(30+x) = 30* (30+2*х) + х*х. Если мы обозначим 30+x = n, то n*n = 30*(n+x) + x*x. Используя эту формулу, мы можем вычислить квадраты от 31 до 38.

31² = (30*(31+1) + 1*1) = 0961
32² = (30*(32+2) + 2*2) = 1024
33² = (30*(33+3) + 3*3) = 1089
34² = (30*(34+4) + 4*4) = 1156
35² = (30*(35+5) ) + 5*5) = 1225
36² = (30*(36+6) + 6*6) = 1296
37² = (30*(37+7) + 7*7) = 1369
38² = (30*(38+8) + 8*8) = 1444
Мы сгруппируем 8 чисел от 31 до 38 в 3 категории так, что любые два числа в одной категории отличаются кратно 3.
Категория № 1) Здесь 31, 34 и 37 там. (Обратите внимание, что разница между 2 числами в этой категории кратна 3.)
Категория № 2) Здесь 32, 35 и 38. (Обратите внимание, что разница между двумя числами в этой категории кратна 3.)
Категория №3) Здесь 33 и там 36. (Обратите внимание, что разница между двумя числами в этой категории кратна 3. )
——————————— ————————————————— ————————-

Количество квадратов, которые лежат в категории № 1)
Допустим, мы хотим вычислить, 333331².
Двухзначное базовое число получается путем сохранения цифры 3 ровно один раз, за которой следует цифра единиц исходного числа, равная 1.
31² = 0961. Составьте две группы, полученные по номерам 09 и 61 отдельно.
Поскольку цифра 3 повторяется ровно пять раз в исходном числе, при вычислении квадрата цифра 1 будет повторяться ровно 4 раза слева от группы 09. Также цифра 5 будет повторяться ровно 4 раза, вставленная между 09 и 61 для получения квадрат как
333331² = 111109555561
Аналогично, 33333333331² = 11111111110955555555561
331² = 109561 и так далее.
В общем,
=========================================== ===================
((Цифра 3 повторяется n раз) за которой следует цифра 1)²
= (Цифра 1 повторяется (n-1) раз) за ней двумя цифрами 0 и 9, за которыми следует (цифра 5, повторяющаяся (n-1) раз), за которой следует двузначное число 61

======================== ========================================
Предположим, мы хотим рассчитать, 333334²
Двухзначное базовое число получается путем сохранения цифры 3 только один раз, за которой следует цифра единиц исходного числа, равная 4.
No related posts.