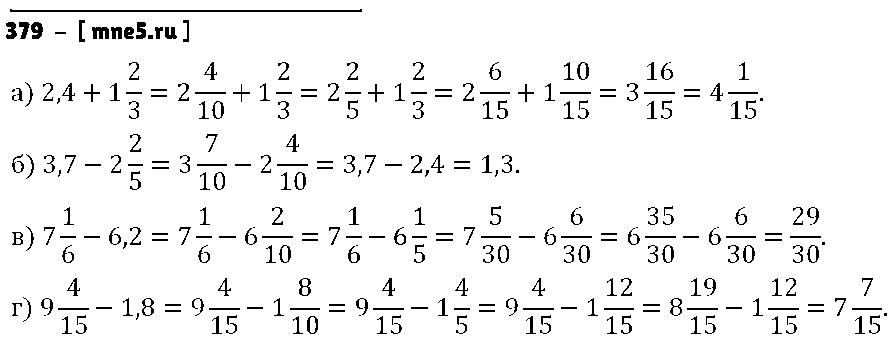Номер №321 — ГДЗ по Математике 6 класс: Виленкин Н.Я.
войтирегистрация
- Ответкин
- Решебники
- 6 класс
- Математика
- Виленкин
- Номер №321
НАЗАД К СОДЕРЖАНИЮ
2013г.ВыбранВыбрать ГДЗ (готовое домашние задание из решебника) на Номер №321 по учебнику Математика. 6 класс. Учебник для общеобразовательных учреждений / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. — 30-е издание. Мнемозина, 2013г.
2019г.ВыбранВыбрать
ГДЗ (готовое домашние задание из решебника) на Номер №321 по учебнику Математика. 6 класс. Учебник для общеобразовательных организаций / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. — 37-е издание в двух частях. Мнемозина, 2019г.
И. Шварцбурд. — 37-е издание в двух частях. Мнемозина, 2019г.
Условие 20132019г.
Cменить на 2013 г.
Cменить на 2019 г.
Найдите значение выражения:
а) 1/2 + 5/8; г) 5/7 — 3/14; ж) 5/6 + 3/8; к) 5/42 + 10/63;
б) 3/4 — 1/2; д) 5/9 — 5/12; з) 19/21 — 11/15; л) 11/21 — 2/35;
в) 7/10 — 3/5; е) 7/12 — 7/20; и) 21/22 — 3/55; м) 5/24 + 7/60.
Трёхметровое бревно распилили на 7 равных частей, а четырёхметровое — на 10. Части какого бревна длиннее?
Решение 1
Решение 1
Решение 2
Решение 2
Решение 3
Решение 3
ГДЗ по Математике 6 класс: Виленкин Н.Я.
Издатель: Виленкин Н.Я. Жохов В.И. Чесноков А.С. Шварцбурд С. И. 2013/2019г.
И. 2013/2019г.
ГДЗ по Математике 6 класс: Мерзляк А.Г.
Издатель: А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. 2014г. / 2019г.
ГДЗ по Математике 6 класс: Никольский С.М.
Издатель: С.М. Никольский, М.К, Потапов, Н.Н. Решетников, А.В. Шевкин. 2015-2018
ГДЗ по Математике 6 класс: Зубарева, Мордкович
Издатель: И.И. Зубарева, А.Г. Мордкович. 2014-2019г.
ГДЗ по Математике 6 класс: Дорофеев Г.В.
Издатель: Г.В. Дорофеев, И.Ф. Шарыгин, С.Б. Суворова. 2016-2019г.
Сообщить об ошибке
Выберите тип ошибки:
Решено неверно
Опечатка
Плохое качество картинки
Опишите подробнее
в каком месте ошибка
Ваше сообщение отправлено
и скоро будет рассмотрено
ОК, СПАСИБО
[email protected]
© OTVETKIN.INFO
Классы
Предметы
Номер 321 — ГДЗ по Математике 6 класс Учебник Виленкин, Жохов, Чесноков, Шварцбурд 2020.
 Часть 1 (решебник)Номер 321 — ГДЗ по Математике 6 класс Учебник Виленкин, Жохов, Чесноков, Шварцбурд 2020. Часть 1 (решебник) — GDZwow
Часть 1 (решебник)Номер 321 — ГДЗ по Математике 6 класс Учебник Виленкин, Жохов, Чесноков, Шварцбурд 2020. Часть 1 (решебник) — GDZwowПерейти к содержанию
Search for:
Авторы: Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И.
Издательство: Мнемозина
Тип: Учебник
Новая версия
Старая версия
ЧАСТЬ 1
Выберите номер упражнения
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244245246247248249250251252253254255256257258259260261262263264265266267268269270271272273274275276277278279280281282283284285286287288289290291292293294295296297298299300301302303304305306307308309310311312313314315316317318319320321322323324325326327328329330331332333334335336337338339340341342343344345346347348349350351352353354355356357358359360361362363364365366367368369370371372373374375376377378379380381382383384385386387388389390391392393394395396397398399400401402403404405406407408409410411412413414415416417418419420421422423424425426427428429430431432433434435436437438439440441442443444445446447448449450451452453454455456457458459460461462463464465467468469470471472473474475476477478479480481482483484485486487488489490491492493494495496497498499500501502503504505506507508509510511512513514515516517518519520521522523524525526527528529530531532533534535536537538539540541542543544545546547548549550551552553554555556557558559560561562563564565566567568569570571572573574575576577578579580581582583584585586587588589590591592593594595596597598599600601602603604605606607608609610611612613614615616617618619620621622623624625626627628629630631632633634635636637638639640641642643644645646647648649650651652653654655656657658659660661662663664665666667668669670671672673674675676677678679680681682683684685686687688689690691692693694695696697698699700701702703704705706707708709710711712713714715716717718719720721722723724725726727728729730731732733734735736737738739740741742743744745746747748749750751753754755756757758759760761762763764765766767768769770771772773774775776777778779780781782783784785786787788789790791792793794795796797798799800801802803804805806807809810811812813814815816817818819820821822823824825826827828829830831832833834835836837838839840841842843844845846847848849850851852853854855856857858859860861862863864865866867868869870871872873874875876877878879880881882883884885886887888889890891892893894895896897
ЧАСТЬ 2
Выберите номер упражнения
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192939495969798991001011021031041051061071081091101111121131141151161171181191201211221231241251261271281291301311321331341351361371381391401411421431441451461471481491501511521531541551561571581591601611621631641651661671681691701711721731741751761771781791801811821831841851861871881891901911921931941951961971981992002012022032042052062072082092102112122132142152162172182192202212222232242252262272282292302312322332342352362372382392402412422432442452462472482492502512522532542552562572582592602612622632642652662672682692702712722732742752762772782792802812822832842852862872882892902912922932942952962972982993003013023033043053063073083093103113123133143153163173183193203213223233243253263273283293303313323333343353363373383393403413423433443453463473483493503513523533543553563573583593603613623633643653663673683693703713723733743753763773783793803813823833843853863873883893903913923933943953963973983994004014024034044054064074084094104114124134144154164174184194204214224234244254264274284294304314324334344354364374384394404414424434444454464474484494504514524534544554564574584594604614624634644654664674684694704714724734744754764774784794804814824834844854864874884894904914924934944954964974984995005015025035045055065075085095105115125135145155165175185195205215225235245255265275285295305315325335345355365375385395405415425435445455465475485495505515525535545555565575585595605615625635645655665675685695705715725735745755765775785795805815825835845855865875885895905915925935945955965975985996006016026036046056066076086096106116126136146156166176186196206216226236246256266276286296306316326336346356366376386396406416426436446456466476486496506516526536546556566576586596606616626636646656666676686696706716726736746756766776786796806816826836846856866876886896906916926936946956966976986997007017027037047057068928938948958968978988999009019029039049059069079089099109119129139149159169179189199209219229239249259269279289299309319329339349359369379389399409419429439449459469479489499509519529539549559569579589599609619629639649659669679689699709719729739749759769779789799809819829839849859869879889899909919929939949959969979989991000100110021003100410051006100710081009101010111012101310141015101610171018101910201021102210231024102510261027102810291030103110321033103410351036103710381039104010411042104310441045104610471048104910501051105210531054105510561057105810591060106110621063106410651066106710681069107010711072107310741075107610771078107910801081108210831084108510861087108810891090109110921093109410951096109710981099110011011102110311041105110611071108110911101111111211131114111511161117111811191120112111221123112411251126112711281129113011311132113311341135113611371138113911401141114211431144114511461147114811491150115111521153115411551156115711581159116011611162116311641165116611671168116911701171117211731174117511761177117811791180118111821183118411851186118711881189119011911192119311941195119611971198119912011202120312041205120612071208120912101211121212131214121512161217121812191220122112221223122412251226122712281229123012311232123312341235123612371238123912401241124212431244124512461247124812491250125112521253125412551256125712581259126012611262126312641265126612671268126912701271127212731274127512761277127812791280128112821283128412851286128712881289129012911292129312941295129612971298129913001301130213031304130513061307130813091310131113121313131413151316131713181319132013211322132313241325132613271328132913301331133213331334133513361337133813391340134113421343134413451346134713481349135013511352135313541355135613571358135913601361136213631364136513661367136813691370137113721373137413751376137713781379138013811382138313841385138613871388138913901391139213931394139513961397139813991400140114021403140414051406140714081409141014111412141314141415141614171418141914201421142214231424142514261427142814291430143114321433143414351436143714381439144014411442144314441445144614481449145014511452145314541455145614571458145914601461146214631464146514681469147014711472147314741475147614771478147914801481148214831484148514861487148814891490149114921493149414951496149714981499150015011502150315041505150615071508150915101511151215131514151515161517151815191520152115221523152415251526152715281529153015311532153315341535153615371538153915401541154215431544154515461547154815491550155115521553155415551556155715581559156015611562156315641565156615671568156915701571157215731574157515761577157815791580158115821583158415851586158715881589159015911592159315941595
Adblockdetector
ПО МАКСИМАЛЬНОЙ ФУНКЦИИ И V-СОПРЯЖЕНИЮ | Садикович
Главная > Vol 31, No 5 (2016) > Sadikovic
ON MAXIMAL FUNCTION AND V-CONJUGATION
Samra Sadikovic
DOI Number
10. 22190/FUMI1605999S
22190/FUMI1605999S
First page
999
Последняя страница
1009
Аннотация
В этой статье мы доказываем, что на 3-й серии поле h2 не может быть определено с помощью V-сопряжения. Другими словами, нормы kfkh2 и k ˜ fkL1 не эквивалентны в случае поля 3-й серии. Это дает новое доказательство результата Мемича [7], отвечающего на вопрос, поставленный П. Саймоном [13]. Кроме того, мы доказываем, что среднее значение функции f ∈ L1(G) на смежном классе IN−1(x) мажорируется либо MN−1, либо MN на каком-либо сдвинутом элементе.
Ключевые слова
Максимальная функция; V-сопряжение; Группы Виленкина
Ключевые слова
V-сопряжение, максимальная функция, группы Виленкина
Полный текст:
PDFЛитература
М. Авдиспахич, Н. Мемич и Ф. Вайс: Максимальные функции, пространства Харди и теоремы Фурье о множителях для неограниченных групп Виленкина.
И. Благота, Г. Гат и Ю. Гогинава: Максимальные операторы на средних Фейера рядов Виленкина-Фурье. Дж. Неэкв. Чистый и Appl. Мат. 7(4), статья 149, (2006).
Н. Фуджи: Максимальное неравенство для функций h2 на обобщенной группе Уолша-Пэли. проц. амер. Мат. соц. 77 (1979), 111–116.
Г. Гат: Средние Чезаро интегрируемых функций по неограниченным системам Виленкина. Дж. Прибл. Теория 124 (2003), вып. 1, 25–43.
Г. Гат: На п.в. сходимость рядов Фурье по неограниченным группам Виленкина. Акта Математика. акад. Паед. Nyıregyhásiensis 15 (1999), 27–34.
У. Гогинава: Максимальный оператор средних Марцинкевича-Фейера d-мерного ряда Уолша-Фурье. Ист Дж. Около 12 (3) (2006), 295–302.
Н. Мемич: Об ограниченности оператора V-сопряжения в пространствах Харди. NZJMath. Том 42 (2012), 121–129.
Й. Пал — П. Саймон: Об обобщении понятия производной. Акта Математика. акад. науч. Висела. 29(1-2) (1977), 155–164.
Дж. Дж. Прайс: Некоторые группы ортонормированных ступенчатых функций. Канада. Дж. Матем. 9 (1957), 413–425.
Ф. Шипп: Некоторые перестановки рядов в ряду Уолша. Мат. заметки 18 (1975), 193–201.
Ф. Шипп, В. Р. Уэйд, П. Саймон и Дж. Пал: Серия Уолша: Введение в диадический гармонический анализ. Адам Хилгер, Бристоль и Нью-Йорк, 19 лет90.
П. Саймон: Суммируемость по Чезаро относительно двухпараметрических систем Уолша. Монац. Мат. 131 (2000), 321–334.
П. Саймон: Исследования по системе Виленкина. Анна. ун-т науч. Будапешт. Разд. Мат. 27 (1982), 87–101.
П. Саймон: Veraligemeinerte Walsh-Fourierreihen II. Акта Математика. акад. науч. Висела. 27 (1975), 329–341.
Н. Я. Виленкин: Об одном классе полных ортонормированных систем. Изв. акад. АН СССР, сер. Матем., 11 (1947), 363–400. (рус.), англ. пер.: амер. Мат. соц. пер., 28 (1963), 1–35.
Ф.Вайс: Ограниченные операторы в пространствах слабой выносливости и приложения. Акта Математика. Венгрия 80 (1998), 249–264.
Венгрия 80 (1998), 249–264.
Ф. Вайс: Суммируемость по Чезаро одномерных и двумерных рядов Уолша-Фурье. Анализ математики. 22 (1996), 229–242.
Ф. Вайс: Суммируемость по Чезаро двумерных рядов Уолша-Фурье. ТАМS 348(6) (1996), 2196–2181.
Ф. Вайс: Мартингальные пространства Харди и их приложения в анализе Фурье. Лект. Примечания по математике. 1568 г., Спрингер (Берлин-Гейдельберг-Нью-Йорк, 1994).
Ф. Вайс: -суммируемость рядов Фурье. Акта Математика. Венгрия. 103 (1–2) (2004), 139–176.
DOI: https://doi.org/10.22190/FUMI1605999S
Рефбеки
- На данный момент рефбеков нет.
© Нишский университет | Создано в ноябре 2013 г.
ISSN 0352-9665 (печать)
ISSN 2406-047X (онлайн)
DLMF: Bibliography V ‣ Bibliography
- Г. Валент (1986)
Интегральное преобразование, включающее функции Гойна и связанную с ним проблему собственных значений.
СИАМ Дж. Матем. Анальный. 17 (3), стр. 688–703.

- О. Валле и М. Соареш (2010) Функции Эйри и приложения к физике. Второе издание, Imperial College Press, Лондон.
- А. Л. Ван Бюрен, Р. В. Байер, С. Ханиш и Б. Дж. Кинг (1972) Расчет сфероидальных волновых функций. Дж. Акус. соц. амер. 51, стр. 414–416.
- А. Л. Ван Бурен, Р. В. Байер и С. Ханиш (1970) Компьютерная программа на Фортране для вычисления сплюснутых сфероидальных радиальных функций первого и второго рода и их первых производных. Отчет НРЛ № 6959 Военно-морской рез. лаборатория Вашингтон, округ Колумбия.
- А. Л. Ван Бюрен, Б. Дж. Кинг, Р. В. Байер и С. Ханиш (1975) Таблицы угловых сфероидальных волновых функций, Vol. 1, вытянутый, m=0; Том. 2, сплющенный, m=0. Военно-морской рез. лаборатория Отчеты, Вашингтон, округ Колумбия.
- А. Л. Ван Бюрен и Дж. Э. Бойсверт (2002)
Точное вычисление вытянутых сфероидальных радиальных функций первого рода и их первых производных.
кв. заявл. Мат. 60 (3), стр.
 589–599.
589–599. - А. Л. Ван Бюрен и Дж. Э. Бойсверт (2004) Улучшен расчет вытянутых сфероидальных радиальных функций второго рода и их первых производных. кв. заявл. Мат. 62 (3), стр. 493–507.
- А. Л. Ван Бюрен и Дж. Э. Бойсверт (2007) Точное вычисление модифицированных функций Матье целого порядка. кв. заявл. Мат. 65 (1), стр. 1–23.
- Ван Бюрен (веб-сайт) Матье и сфероидальные волновые функции: программы на Фортране для их точного расчета
- ХК ван де Хюльст (1957) Рассеяние света мелкими частицами. Джон Уайли и сыновья. Inc., Нью-Йорк.
- ХК ван де Хюльст (1980) Многократное рассеяние света. Том. 1, Академик Пресс, Нью-Йорк.
- Дж. ван де Лун, Х. Дж. Дж. Те Риле и Д. Т. Винтер (1986) О нулях дзета-функции Римана в критической полосе. IV. Мат. Комп. 46 (174), стр. 667–681.
- Х. Ван де Вель (1969)
О методе разложения в ряд для вычисления неполных эллиптических интегралов первого и второго рода.
 Мат. Комп. 23 (105), стр. 61–69.
Мат. Комп. 23 (105), стр. 61–69. - К. Г. ван дер Лаан и Н. М. Темме (1984) Вычисление специальных функций: гамма-функция, экспоненциальные интегралы и функции, подобные ошибкам. Трактат CWI, Vol. 10, Математический центр Stichting, Centrum voor Wiskunde en Информатика, Амстердам.
- Эй Джей ван дер Поортен (1980) Некоторые замечательные формулы… Введение в полилогарифмы. В материалах конференции по теории чисел королевы, 1979 г. (Кингстон, Онтарио, 1979), Р. Рибенбойм (ред.), Бумаги королевы в Pure и Appl. Матем., Том. 54, Кингстон, Онтарио, стр. 269–286.
- Б. Л. ван дер Варден (1951) О методе седловых точек. заявл. науч. Исследование Б. 2, стр. 33–45.
- Дж. Ван Деун и Р. Кулс (2008) Интегрирование произведений функций Бесселя с дополнительным экспоненциальным или рациональным множителем. вычисл. физ. Комм. 178 (8), стр. 578–59.0.
- Дж. Ф. Ван Диен и В. П. Спиридонов (2001)
Модульные гипергеометрические суммы вычетов эллиптических интегралов Сельберга.
 лат. Мат. физ. 58 (3), стр. 223–238.
лат. Мат. физ. 58 (3), стр. 223–238. - К. Ван Лоан (1992) Вычислительные основы для быстрого преобразования Фурье. Границы прикладной математики, Vol. 10, Общество промышленной и прикладной математики (SIAM), Филадельфия, Пенсильвания.
- Б. Ф. ван Миллиген и А. Лопес Фрагуас (1994) Разложение вакуумных магнитных полей по тороидальным гармоникам. вычисл. физ. Комм. 81 (1–2), стр. 74–9.0.
- А. ван Вейнгаарден (1953) О коэффициентах модулярного инварианта J(τ). Недерл. акад. Ветенш. проц. сер. A. 56 = Indagationes Мат. 15 56, стр. 389–400.
- А. Н. Варченко (1976) Многогранники Ньютона и оценки осциллирующих интегралов. Функциональный. Анальный. я приложен. 10 (3), стр. 13–38 (рус.).
- Р. С. Варма (1941) Бесконечный ряд функций параболического цилиндра Вебера. проц. Бенарес Математика. соц. (NS) 3, стр. 37.
- Д. А. Варшалович, А. Н. Москалев, В. К. Херсонский (1988)
Квантовая теория углового момента.
World Scientific Publishing Co.
 Inc., Сингапур.
Inc., Сингапур. - А. Н. Ваврек и В. Томпсон (1984) Некоторые новые бесконечные серии сферических функций Бесселя. кв. заявл. Мат. 42 (3), стр. 321–324.
- Г. Веделер (1950) Уравнение Матье для кораблей, катящихся среди волн. я, II. Norske Vid. Сельск. Forh., Trondheim 22 (25–26), стр. 113–123.
- Р. Вейн и П. Дейл (1999) Детерминанты и их приложения в математической физике. Прикладные математические науки, Vol. 134, Спрингер-Верлаг, Нью-Йорк.
- Дж. Венециано (1968) Построение кросс-симметричной редже-амплитуды для линейно возрастающих траекторий. Il Nuovo Cimento A 57 (1), стр. 190–197.
- П. Вербек (1970) Рациональные аппроксимации экспоненциальных интегралов En(x). акад. Рой. бельг. Бык. Кл. науч. (5) 56, стр. 1064–1072.
- А. Верма и В. К. Джайн (1983) Некоторые формулы суммирования q-рядов. Дж. Индийская математика. соц. (NS) 47 (1–4), стр. 71–85 (1986).
- Р. Видунас и Н. М. Темме (2002)
Символическое вычисление коэффициентов в асимптотических разложениях типа Эйри.
 Дж. Матем. Анальный. заявл. 269(1), стр. 317–331.
Дж. Матем. Анальный. заявл. 269(1), стр. 317–331. - Р. Видунас (2005) Преобразования некоторых гипергеометрических функций Гаусса. Дж. Вычисл. заявл. Мат. 178 (1-2), стр. 473–487.
- Л. Виеторис (1983) Dritter Beweis der die unvollständige Gammafunktion betreffenden Lochsschen Ungleichungen. Австрия. акад. Висс. Матем.-натур. Кл. Ситцунгсбер. II 192 (1–3), стр. 83–91 (немецкий).
- Н. Я. Виленкин и А.Ю. Климык (1991) Представление групп Ли и специальные функции. Том 1: Простейшие группы Ли, специальные функции и интегральные преобразования. Математика и ее приложения (советская серия), Vol. 72, Kluwer Academic Publishers Group, Дордрехт.
- Н. Я. Виленкин и А.Ю. Климык (1992) Представление групп Ли и специальные функции. Том 3: Классические и квантовые группы и специальные функции. Математика и ее приложения (советская серия), Vol. 75, Kluwer Academic Publishers Group, Дордрехт.
- Н. Я. Виленкин и А.Ю. Климык (1993)
Представление групп Ли и специальные функции.
 Том 2: Представления класса I, специальные функции и интегральные преобразования.
Математика и ее приложения (советская серия), Vol. 74, Kluwer Academic Publishers Group, Дордрехт.
Том 2: Представления класса I, специальные функции и интегральные преобразования.
Математика и ее приложения (советская серия), Vol. 74, Kluwer Academic Publishers Group, Дордрехт. - Н. Я. Виленкин (1968) Специальные функции и теория представлений групп. Американское математическое общество, Провиденс, Род-Айленд.
- И. М. Виноградов (1937) Представление нечетного числа в виде суммы трех простых (рус.). Докл. акад. Наук СССР 15, стр. 169–172 (рус.).
- И. М. Виноградов (1958) Новая оценка функции ζ(1+it). Изв. акад. наук СССР. сер. Мат. 22, стр. 161–164 (рус.).
- Н. Вирченко и И. Федотова (2001 г.) Обобщенные ассоциированные функции Лежандра и их приложения. World Scientific Publishing Co. Inc., Сингапур.
- Х. Фолькмер (1999) Разложения по произведениям полиномов Гейне-Стилтьеса. Констр. прибл. 15 (4), стр. 467–480.
- Х. Фолькмер и Джей Джей Вуд (2014)
Замечание об асимптотическом разложении обобщенных гипергеометрических функций.
 Анальный. заявл. (Сингап.) 12 (1), стр. 107–115.
Анальный. заявл. (Сингап.) 12 (1), стр. 107–115. - Х. Фолькмер (1982) Интегральные соотношения для функций Ламе. СИАМ Дж. Матем. Анальный. 13 (6), стр. 978–987.
- Х. Фолькмер (1983) Integralgleichungen für Periodische Lösungen Hill’scher Differentialgleichungen. Анализ 3 (1–4), стр. 189.–203 (немецкий).
- Х. Фолькмер (1984) Интегральные представления произведений функций Ламе с помощью фундаментальных решений. СИАМ Дж. Матем. Анальный. 15 (3), стр. 559–569.
- Х. Фолькмер (1998) О росте радиусов сходимости собственных значений уравнения Матье. Мат. Нахр. 192, стр. 239–253.
- Х. Фолькмер (2004a) Оценки погрешности аппроксимаций Рэлея-Ритца собственных значений и собственных функций уравнения Матье и сфероидального волнового уравнения. Констр. прибл. 20 (1), стр. 39–54.
- Х. Фолькмер (2004b) Четыре замечания о собственных значениях уравнения Ламе. Анальный. заявл. (Сингап.) 2 (2), стр. 161–175.
- Х. Фолькмер (2008)
Приближение собственных значений некоторых дифференциальных уравнений нулями ортогональных многочленов.



 589–599.
589–599. Мат. Комп. 23 (105), стр. 61–69.
Мат. Комп. 23 (105), стр. 61–69.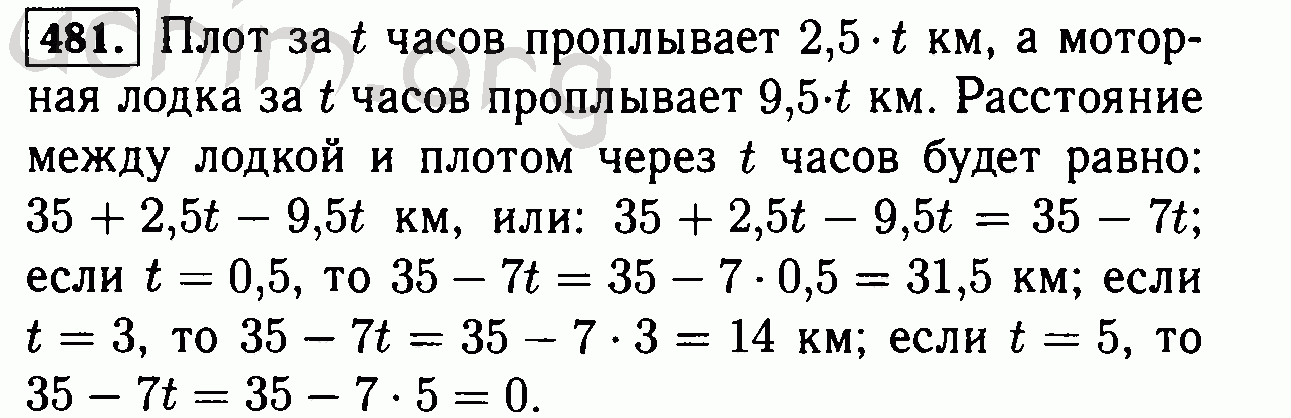 лат. Мат. физ. 58 (3), стр. 223–238.
лат. Мат. физ. 58 (3), стр. 223–238. Inc., Сингапур.
Inc., Сингапур. Дж. Матем. Анальный. заявл. 269(1), стр. 317–331.
Дж. Матем. Анальный. заявл. 269(1), стр. 317–331. Том 2: Представления класса I, специальные функции и интегральные преобразования.
Математика и ее приложения (советская серия), Vol. 74, Kluwer Academic Publishers Group, Дордрехт.
Том 2: Представления класса I, специальные функции и интегральные преобразования.
Математика и ее приложения (советская серия), Vol. 74, Kluwer Academic Publishers Group, Дордрехт.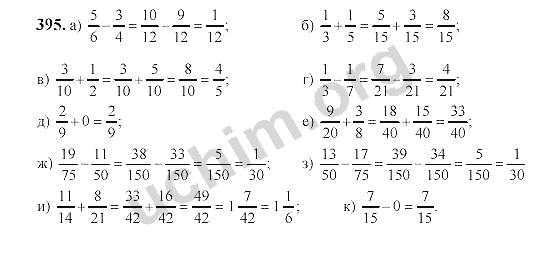 Анальный. заявл. (Сингап.) 12 (1), стр. 107–115.
Анальный. заявл. (Сингап.) 12 (1), стр. 107–115.