Математика 6 класс виленкин номер 269: Номер №269 — ГДЗ по Математике 6 класс: Виленкин Н.Я.

Содержание

Номер 269 — ГДЗ по Математике 6 класс Учебник Виленкин, Жохов, Чесноков, Шварцбурд 2020. Часть 2 (решебник)

Номер 269 — ГДЗ по Математике 6 класс Учебник Виленкин, Жохов, Чесноков, Шварцбурд 2020. Часть 2 (решебник) — GDZwow

Перейти к содержанию

Search for:

Авторы: Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И.

Издательство: Мнемозина

Тип: Учебник

Новая версия

ЧАСТЬ 1
Выберите номер упражнения

ЧАСТЬ 2
Выберите номер упражнения

1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192939495969798991001011021031041051061071081091101111121131141151161171181191201211221231241251261271281291301311321331341351361371381391401411421431441451461471481491501511521531541551561571581591601611621631641651661671681691701711721731741751761771781791801811821831841851861871881891901911921931941951961971981992002012022032042052062072082092102112122132142152162172182192202212222232242252262272282292302312322332342352362372382392402412422432442452462472482492502512522532542552562572582592602612622632642652662672682692702712722732742752762772782792802812822832842852862872882892902912922932942952962972982993003013023033043053063073083093103113123133143153163173183193203213223233243253263273283293303313323333343353363373383393403413423433443453463473483493503513523533543553563573583593603613623633643653663673683693703713723733743753763773783793803813823833843853863873883893903913923933943953963973983994004014024034044054064074084094104114124134144154164174184194204214224234244254264274284294304314324334344354364374384394404414424434444454464474484494504514524534544554564574584594604614624634644654664674684694704714724734744754764774784794804814824834844854864874884894904914924934944954964974984995005015025035045055065075085095105115125135145155165175185195205215225235245255265275285295305315325335345355365375385395405415425435445455465475485495505515525535545555565575585595605615625635645655665675685695705715725735745755765775785795805815825835845855865875885895905915925935945955965975985996006016026036046056066076086096106116126136146156166176186196206216226236246256266276286296306316326336346356366376386396406416426436446456466476486496506516526536546556566576586596606616626636646656666676686696706716726736746756766776786796806816826836846856866876886896906916926936946956966976986997007017027037047057068928938948958968978988999009019029039049059069079089099109119129139149159169179189199209219229239249259269279289299309319329339349359369379389399409419429439449459469479489499509519529539549559569579589599609619629639649659669679689699709719729739749759769779789799809819829839849859869879889899909919929939949959969979989991000100110021003100410051006100710081009101010111012101310141015101610171018101910201021102210231024102510261027102810291030103110321033103410351036103710381039104010411042104310441045104610471048104910501051105210531054105510561057105810591060106110621063106410651066106710681069107010711072107310741075107610771078107910801081108210831084108510861087108810891090109110921093109410951096109710981099110011011102110311041105110611071108110911101111111211131114111511161117111811191120112111221123112411251126112711281129113011311132113311341135113611371138113911401141114211431144114511461147114811491150115111521153115411551156115711581159116011611162116311641165116611671168116911701171117211731174117511761177117811791180118111821183118411851186118711881189119011911192119311941195119611971198119912011202120312041205120612071208120912101211121212131214121512161217121812191220122112221223122412251226122712281229123012311232123312341235123612371238123912401241124212431244124512461247124812491250125112521253125412551256125712581259126012611262126312641265126612671268126912701271127212731274127512761277127812791280128112821283128412851286128712881289129012911292129312941295129612971298129913001301130213031304130513061307130813091310131113121313131413151316131713181319132013211322132313241325132613271328132913301331133213331334133513361337133813391340134113421343134413451346134713481349135013511352135313541355135613571358135913601361136213631364136513661367136813691370137113721373137413751376137713781379138013811382138313841385138613871388138913901391139213931394139513961397139813991400140114021403140414051406140714081409141014111412141314141415141614171418141914201421142214231424142514261427142814291430143114321433143414351436143714381439144014411442144314441445144614481449145014511452145314541455145614571458145914601461146214631464146514681469147014711472147314741475147614771478147914801481148214831484148514861487148814891490149114921493149414951496149714981499150015011502150315041505150615071508150915101511151215131514151515161517151815191520152115221523152415251526152715281529153015311532153315341535153615371538153915401541154215431544154515461547154815491550155115521553155415551556155715581559156015611562156315641565156615671568156915701571157215731574157515761577157815791580158115821583158415851586158715881589159015911592159315941595

Adblock
detector

№ 269 ГДЗ Математика 6 класс Дорофеев, Петерсон Часть 1.

Помогите мне решить задачи с числами – Рамблер/класс № 269 ГДЗ Математика 6 класс Дорофеев, Петерсон Часть 1. Помогите мне решить задачи с числами – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

1) Среднее арифметическое двух чисел равно 8,2, а одно из них равно 4,5.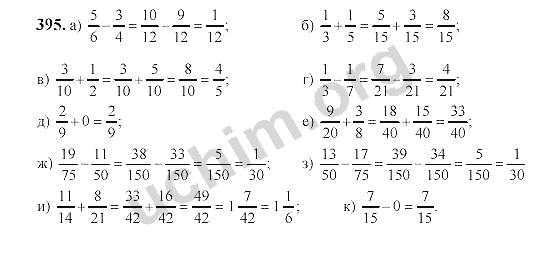

Найди второе число.

2)     Среднее арифметическое двух чисел равно 21,8, причем одно из них на 6,8 больше другого. Найди эти числа.

3)     Первое число в 5 раз меньше второго, а их среднее арифметическое равно 12,6. На сколько второе число больше первого?

4)     Среднее арифметическое трех чисел равно 10,4. Первое число равно 9,6, а второе в 2 раза больше третьего. Найди эти числа. Какую часть меньшее число составляет от 9,6? Вырази эту часть в процентах.

ответы

1) Пусть х — искомое число, тогда

Ответ: 11,9.

х = 18,4 — первое число; 25,2 -второе число.
Ответ: 18,4 и 25,2.

х = 4,2 — первое число; 5х = 21 — второе число.
Ответ: 4,2 и 21; в 5 раз.

3х + 9,6 = 31,2 ⇒ х = 7,2 — третье число;
14,4 — второе число.
7,2 – x%
9,6 — 100% х = 75%
7,2 составляет ¾ части 9,6.

Ответ: 9,6; 14,4; 7,2; ¾ или 75%.

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения

похожие темы

Психология

3 класс

5 класс

Репетитор

похожие вопросы 5

Приветик! Кто решил? № 411 Математика 6 класс Виленкин.

Выполните вычисления с помощью микрокалькулятора и резуль-
тат округлите до тысячных:
3,281 ∙ 0,57 + 4,356 ∙ 0,278 — 13,758 (Подробнее…)

ГДЗМатематика6 классВиленкин Н.Я.

Помогите установить соответствие между неравенствами. Математика базовый уровень ЕГЭ — 2017. Вар.№1. Зад.№17. Под руководством Ященко И.В.

Здравствуйте! Помогите установить соответствие между неравенствами и их решениями: (Подробнее…)

ЕГЭЭкзаменыМатематикаЯщенко И.В.

Помогите выбрать утверждения. Математика базовый уровень ЕГЭ — 2017. Вар.№1. Зад.№18. Под руководством Ященко И.В.

Здравствуйте! Перед волейбольным турниром измерили рост игроков волейбольной команды города N. Оказалось, что рост каждого из (Подробнее…)

ЕГЭЭкзаменыМатематикаЯщенко И.В.

Вырежи из бумаги № 694 ГДЗ Математика 6 класс Дорофеев Г.В. Часть3.

Вырежи из бумаги 20 одинаковых произвольных треугольников и составь
из них паркет. Всегда ли это можно сделать? Почему?

ГДЗМатематика6 классДорофеев Г. В.

11. Выпишите слово, в котором на месте пропуска пишется буква Е. Русский язык ЕГЭ-2017 Цыбулько И. П. ГДЗ. Вариант 12.

11.
Выпишите слово, в котором на месте пропуска пишется буква Е.
произнос., шь (Подробнее…)

ГДЗЕГЭРусский языкЦыбулько И.П.

Джошуа Ноуб, Кен Д. Олум и Александр Виленкин, Философские последствия инфляционной космологии

Дополнительные параметры загрузки

Джошуа Ноуб, Кен Д. Олум и Александр Виленкин

Недавние достижения в космологии показывают, что каждая история, имеющая ненулевую вероятность, реализуется в бесконечном числе различных областей пространства-времени. Таким образом, оказывается, что Вселенная содержит бесконечно много цивилизаций, точно таких же, как наша, а также бесконечно много цивилизаций, отличающихся от нашей каким-либо образом, допускаемым физическими законами. Мы исследуем значение этого вывода для этической теории и для аргумента судного дня. В бесконечной вселенной мы обнаруживаем, что аргумент судного дня применим только к эффектам, которые изменяют среднюю продолжительность жизни всех цивилизаций, а не к тем, которые влияют только на нашу цивилизацию.

Цитировать Простой текст БибТекс Форматированный текст Зотеро EndNote Менеджер ссылок РефВоркс

Параметры Отметить как дубликат Найдите его в Scholar Запросить удаление из индекса Лист регистраций изменений

Править

PhilArchive

Загрузить копию этой работы Бумаги в настоящее время заархивированы: 77 331

Внешние ссылки

Настройте учетную запись с вашей принадлежностью для доступа к ресурсам через прокси-сервер вашего университета

Через вашу библиотеку

Войдите в систему / зарегистрируйтесь и настройте свой преобразователь OpenURL
Настройте собственный преобразователь

Философские последствия инфляционной космологии. Джошуа Ноуб, Кен Д. Олум и Александр Виленкин — 2006 — Философия науки 57 (1): 47-67.

Критический взгляд на инфляционную космологию. Джон Эрман и Хесус Мостерин — 1999 —

Философия науки 66 (1):1-49.

Приближение к абсолютному нулю времени: развитие теории в космологии ранней Вселенной. Кристофер Джоэл Сминк — 2003 — Диссертация, Университет Питтсбурга

Есть ли у нас теория космологии ранней вселенной? Роберт Бранденбергер — 2014 — Исследования по истории и философии of Science Part B: Исследования по истории и философии современной физики 46 (1): 109-121.

О методологических проблемах космологии и квантовой гравитации. Панов Александр Дмитриевич — 2010 — Российские исследования в философии 49 (3):72-92.

Научный реализм и первичная космология. Фераз Ажар и Джереми Баттерфилд — неизвестно

Проблема измерения пространства-времени как камень преткновения инфляционной космологии. Ринат М. Нугаев — 2013 — В Вадим В. Казутинский, Елена А. Мамчур, Александр Д , Панов и В. Д. Ерекаев (ред.),

Метавселенная, Пространство, Время . Институт философии РАН. стр. 52-73.

Структура и интерпретация космологии. Гордон МакКейб — неизвестно

Кризис предсказуемости в космологии ранней вселенной. Крис Сминк — 2014 — Исследования по истории и философии науки Часть B: Исследования по истории и философии современной физики 46 (1): 122-133.

Концепция бесконечности в современной космологии. Массимилиано Бадино — неизвестно

Меньше интерпретации и больше декогеренции в квантовой гравитации и инфляционной космологии. Элиз М. Крулл — 2015 — Основы физики 45 (9):1019-1045.

Космический агностицизм. Тимоти Э. Истман — 2007 — Исследования процессов 36 (2): 181-197.

Меньше декогерентности и больше когерентности в квантовой гравитации, инфляционной космологии и в других местах.

Элиас Окон и Дэниел Сударски — 2016 — Основы физики 46 (7): 852-879.

Актуальность Тиллиха для диалога теологии и науки. Роберт Джон Рассел — 2001 — Zygon 36 (2): 269-308.

Добавлено в ПП
22.02.2017

Загрузки
11 (#851,517)

6 месяцев
1 (#472,860)

Исторический график загрузок

Как увеличить количество загрузок?

Хулио Дельгадо — ПУБЛИКАЦИИ

КНИГИ ПОД РЕДАКЦИЕЙ

Дельгадо Дж., Ружански М. (ред.) Анализ и уравнения в частных производных: перспективы развивающихся стран, Springer Proceedings in Mathematics & Statistics, Vol. 275, Спрингер, 2019 г.. xii+269pp ссылка, Doi.
————————————————— ————————————————— ————————-

Об этой книге:

В этом томе представлены современные тенденции в области анализа и уравнений в частных производных от исследователей из развивающихся стран. . Плод проекта «Анализ в развивающихся странах», целью которого было объединить исследователей со всего мира, том также включает некоторые работы исследователей из развитых стран.

Сосредоточив внимание на темах анализа, связанных с уравнениями в частных производных, этот том содержит избранные материалы о деятельности проекта в Имперском колледже Лондона, а именно конференции по анализу и уравнениям в частных производных, состоявшейся в сентябре 2016 года, и последующей Недели официальной помощи в целях развития, проведенной в ноябре 2016 года. Представленные темы включают анализ Фурье, псевдодифференциальные операторы, интегральные уравнения, а также смежные темы из численного анализа и теории бифуркаций, а представленные страны варьируются от Буркина-Фасо и Ганы до Армении, Кыргызстана и Таджикистана, включая вклады Бразилия, Колумбия и Куба, а также Индия и Китай.

Ж. Дельгадо и М. Ружански. Введение в исчисление Вейля-Хёрмандера. Подготовка к серии Springer Universitext.

ПУБЛИКАЦИИ

Д. Кардона, М. Чацаку, Дж. Дельгадо, В. Кумар и М. Ружанский. Ангармоническая полугруппа и приложения к корректности нелинейных УЧП. В процессе подготовки
Д. Кардона, М. Чацаку, Х. Дельгадо и М. Ружански. Вырождающиеся уравнения Шрёдингера с нерегулярными потенциалами. Поданный.
Д. Кардона, Х. Дельгадо и М. Ружански. О корректности одного класса псевдодифференциальных гиперболических уравнений на торе. В подготовке.
Д. Кардона, Х. Дельгадо и М. Ружанский. Эволюционные уравнения в общих исчислениях. В подготовке.
Х. Дельгадо и Л. Посада. Критерии ядерности ядер степенных рядов в высших измерениях. Поданный.
Дж. Дельгадо, Л. Посада и М. Ружански. Частичные следы и классы Шаттена-фон Неймана на тензорах Гильберта. В подготовке.
Д. Кардона, Х. Дельгадо и М. Ружански. Ограниченность диадической максимальной функции на градуированных группах Ли. Поданный.
Д. Кардона, Х. Дельгадо и М. Ружанский. Оценки сумм собственных функций эллиптических псевдодифференциальных операторов на компактных группах Ли. Представлено. arxiv
Д. Кардона, Х. Дельгадо и М. Ружанский. Замечание о локальной формуле Вейля на компактных группах Ли. поданный. Архив
Д. Кардона, Х. Дельгадо и М. Ружанский. Следы Диксмье, остатки Воджицкого и определители на компактных группах Ли. Поданный.
Дж. Дельгадо, Л. Посада и М. Ружанский. Классы Шаттена-фон Неймана и частичные следы на тензорах Гильберта. В подготовке.
Х. Дельгадо и А. Муньос Тельо. О множестве дифференцируемости Гато нормы L1. Междунар. Журнал нелинейного анализа и приложений. об. 14, вып. 1, с. 95-100, 2023
Д. Кардона, Х. Дельгадо и М. Ружански. Дробная диффузия и диффузия со сносом на компактных группах Ли. Журнал эволюционных уравнений. 22, ст. № 88, 2022.
Д. Кардона, Х. Дельгадо и М. Ружанский. Функциональное исчисление на градуированных группах Ли с приложениями к уравнениям диффузии. Поданный.
— -Д. Кардона, Х. Дельгадо и М. Ружанский. Формулы Племеля-Смитиса на компактных группах Ли. Monatshefte für Mathematik —, 199, вып. 3. с. 459-482 2022. Открытый доступ
М. Чацаку, Х. Дельгадо и М. Ружанский. Об одном классе ангармонических осцилляторов II: общий случай. Бюллетень математических наук. 180, арт. 103196. Ноябрь 2022 г. Открытый доступ
Дж. Дельгадо. О корректности одного класса уравнений псевдодифференциальной диффузии на торе. Результаты по математике. Том 77, выпуск 5, октябрь 2022 г.
Дж. Дельгадо. Определитель Пуанкаре на торе. Журнал псевдодифференциальных операторов и приложений. 13, № 3. Статья № 29.. 2022
Д. Кардона, Х. Дельгадо и М. Ружански. Ограниченность Lp для псевдодифференциальных операторов на градуированных группах Ли, Журнал геометрического анализа. 31, №12, с. 11603–11647, 2021 Архив
Ж. Дельгадо и М. Ружанский. Классы Шаттена-фон Неймана интегральных операторов. Journal des Mathématiques Pures et Appliquées. 154, с. 1–29, 2021. (Открытый доступ) Архив
М. Чацаку, Дж. Дельгадо и М. Ружанский. Об одном классе ангармонических осцилляторов. Journal des Mathématiques Pures et Appliquées. 153, с. 1–29, 2021. (Открытый доступ) Arxiv
Дж. Бенавидес, Дж. Дельгадо и А. Муньос Тельо. О множестве дифференцируемости по Гато соболевских норм. В подготовке.
Х. Дельгадо и Х. П. Веласкес-Родригес. Фундаментальные решения оператора Владимирова-Тейблсона на нелокально группах Виленкина. Сдано
Д. Кардона, Х. Дельгадо и М. Ружанский. Определители Пуанкаре на компактных группах Ли. В подготовке.
Д. Кардона, Х. Дельгадо и М. Ружанский. Следы Диксмье, вычеты Воджицкого и определители на компактных группах Ли. II. В подготовке.
Дж. Дельгадо. О положительности преобразования Фурье. Поданный.
Р. Даэр, Дж. Дельгадо и М. Ружанский Теоремы Титчмарша для преобразований Фурье функций Гёльдера-Липшица на компактных однородных многообразиях, Монач. Мат. 89, нет. 1, 23–49 , 2019.
Дж. Дельгадо. О корректности задачи Коши для одного класса вырождающихся параболических уравнений, Теория операторов интегральных уравнений, 90, вып. 1, ст. 3, 19 стр., 2018. Открытый доступ
Ж. Дельгадо и М. Ружански. Классы Шаттена и формула следов на компактных группах, Письма о математических исследованиях, 24, вып. 4, 979-1003, 2017. ссылка
Дж. Дельгадо и М. Ружанский. Множители Фурье, символы и ядерность на компактных многообразиях, Journal d’Analyse Mathématique. 135, нет. 2, 757-800, 2018. Открытый доступ
Дж. Дельгадо и М. Ружанский. Свойство аппроксимации и ядерность на пространствах Лебега с переменным показателем, Матем. Сканд., 122, вып. 2, 299-319, 2018.
Дж. Дельгадо, М. Ружанский и Н. Токмагамбетов. Классы Шаттена и ядерность краевых задач, J. Math. Чистый Appl. (9) 107, вып. 6, 758783, 2017. Открытый доступ
Дж. Дельгадо и М. Ружанский Оценки Lp для псевдодифференциальных операторов на компактных группах Ли, J. Inst. Мат. Жюссье, 18 лет, вып. 3, 531-559, 2019. Открытый доступ
Дельгадо Дж., Ружански М. Множители Фурье в гильбертовых пространствах, в интегральных операторах Фурье: материалы летней школы, Уагадугу, 14–25 сентября 2015 г. / Сильви Пайча; Пьер Клавье (ред.). – Потсдам: Universitätsverlag Potsdam, 2018, ссылка 9.0003
Дж. Дельгадо. О задаче Коши для одного класса вырождающихся гиперболических уравнений в исчислении Вейля-Хёрмандера. Дж. Матем. Analysis and Applications, 436, No. 1, Pages 339-354, 2016.
Дж. Дельгадо, М. Ружански и Б. Ванг. Лондонское математическое общество. 94 (2): Pages 391408, 2016. Открытый доступ
Дж. Дельгадо, М. Ружанский и Б.Ванг Гротендик-Лидский формула следа для пространств Лебега со смешанной нормой и переменной, J. Spectral. Теория. 6(4):781-791, 2016
Дж. Дельгадо. Класс обратимых субэллиптических операторов в S(m;g)-исчислении // Результаты по математике. 67, № 33, страницы 431-444, 2015.
Дж. Дельгадо, М. Ружанский Ядро и критерии символов для классов Шаттена и r-ядерность на компактных многообразиях, Comptes Rendus Mathematiques. сер. I, 352, 779-784, 2014. Открытый доступ
Дж. Дельгадо Границы Lp в S(m, g)-исчислении, Complex Var. Эллиптическое уравнение 61, нет. 3, страницы 315-337, 2016.
. Дж. Дельгадо и М. Ружанский. Классы Шаттена на компактных многообразиях: условия ядра, Журнал функционального анализа. 267, нет. 3, страницы 772-798, 2014. Открытый доступ
Дж. Дельгадо О r-ядерности некоторых интегральных операторов в пространствах Лебега, Математический журнал Тохоку. 67, нет. 1, стр. 125-135, 2015.
. Дж. Дельгадо и М. Ружанский Lp-ядерность, следы и формула Гротендика-Лидского на компактных группах Ли, Journal des Mathématiques Pures et Appliquées. (9) 102, вып. 1, 153–172, 2014. Открытый доступ
Дж. Дельгадо и М. В. Вонг Lp-ядерные псевдодифференциальные операторы на Z и S1, Proc. амер. Мат. соц. Том 141, номер 11, страницы 3935-3942, 2013.
Дж. Дельгадо Оценки Lp для псевдодифференциальных операторов на торе, Теория операторов, достижения и приложения, том. 231, с. 103-116, 2013.
Дж. Дельгадо Формулы следов для ядерных операторов в пространствах интегрируемых по Бохнеру функций, Monatshefte für Mathematik. Том 172, Выпуск 3, Страницы 259275, 2013
Дж. Дельгадо Вложения Соболева для одного класса псевдодифференциальных операторов. Журнал псевдодифференциальных операторов и приложений. Том 2, номер 3, с. 399-417 2011.
Дж. Дельгадо Lp оценки для класса дробных степеней субэллиптических операторов, Псевдодифференциальные операторы: комплексный анализ и уравнения в частных производных. Теория операторов, достижения и приложения. Родино, Л., Вонг М.В. (ред.). об. 213, с.137-154, 2011.
Дж. Дельгадо След ядерных операторов на Lp для сигма-конечной борелевской меры на пространствах со вторым счетом, Интегральные уравнения и теория операторов, 68, с.
No related posts.