Математика 6 класс подведем итоги: ГДЗ Математика 6 класс Бунимович, Кузнецова, Минаева на Решалка

ГДЗ по математике 6 класс Бунимович, Кузнецова — учебник

1. Что мы знаем о дробях

• Вопросы и задания

Упражнения

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15

2. Вычисления с дробями

• Вопросы и задания

Упражнения

• 16
• 17
• 18
• 19
• 20
• 21
• 22
• 23
• 24
• 25
• 26
• 27
• 28
• 29
• 30
• 31
• 32
• 33

3. Основные задачи на дроби

• Вопросы и задания

Упражнения

• 34
• 35
• 36
• 37
• 38
• 39
• 40
• 41
• 42
• 43
• 44
• 45
• 46
• 47
• 48

4.

Что такое процент

• Вопросы и задания

Упражнения

• 49
• 50
• 51
• 52
• 53
• 54
• 55
• 56
• 57
• 58
• 59
• 60
• 61
• 62
• 63
• 64
• 65
• 66
• 67
• 68

5. Столбчатые и круговые диаграммы

• Вопросы и задания

Упражнения

• 69
• 70
• 71
• 72
• 73
• 74
• 75

Подведём итоги

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10

6. Пересекающиеся прямые

• Вопросы и задания

• 76
• 77
• 78
• 79
• 80
• 81
• 82
• 83
• 84
• 85

7.

Параллельные прямые

• Вопросы и задания

• 86
• 87
• 88
• 89
• 90
• 91
• 92
• 93
• 94
• 95
• 96
• 97
• 98

8. Расстояние

• Вопросы и задания
• Неверно стр.41

• 99
• 100
• 101
• 102
• 103
• 104
• 105
• 106
• 107
• 108
• 109
• 110
• 111

Подведём итоги

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8

9. Какие дроби называют десятичными

• Вопросы и задания
• Неверно стр.49

• 112
• 113
• 114
• 115
• 116
• 117
• 118
• 119
• 120
• 121
• 122
• 123
• 124
• 125
• 126
• 127

10.

Перевод обыкновенной дроби на десятичную

• Вопросы и задания

• 128
• 129
• 130
• 131
• 132
• 133
• 134
• 135
• 136
• 137
• 138
• 139
• 140
• 141

11. Сравнение десятичных дробей

• Вопросы и задания

• 142
• 143
• 144
• 145
• 146
• 147
• 148
• 149
• 150
• 151
• 152
• 153
• 154
• 155
• 156
• 157
• 158
• 159
• 160

Подведём итоги

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11

12. Сложение и вычитание десятичных дробей

• Вопросы и задания

• 161
• 162
• 163
• 164
• 165
• 166
• 167
• 168
• 169
• 170
• 171
• 172
• 173
• 174
• 175
• 176
• 177
• 178
• 179

13.

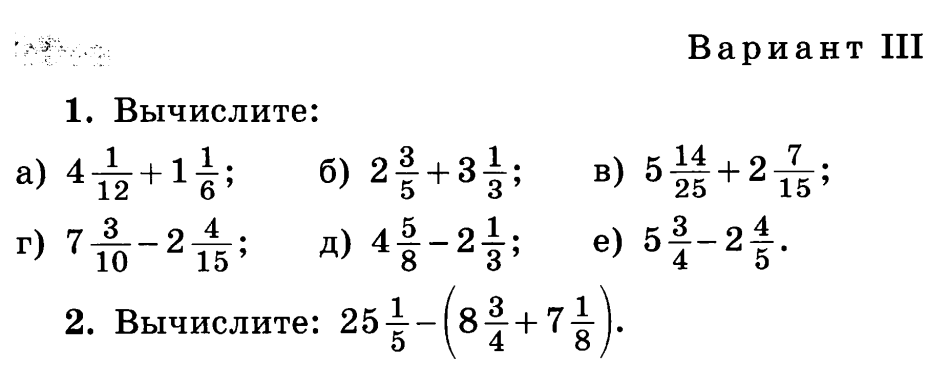Умножение и деление десятичной дроби на 10, 100, 1000

• Вопросы и задания

• 180
• 181
• 182
• 183
• 184
• 185
• 186
• 187
• 188
• 189
• 190
• 191
• 192
• 193
• 194
• 195
• 196
• 197

14. Умножение десятичных дробей

• Вопросы и задания
• Неверно стр.71

• 198
• 199
• 200
• 201
• 202
• 203
• 204
• 205
• 206
• 207
• 208
• 209
• 210
• 211
• 212
• 213
• 214
• 215
• 216
• 217

15. Деление десятичных дробей

• Вопросы и задания

• 218
• 219
• 220
• 221
• 222
• 223
• 224
• 225
• 226
• 227
• 228
• 229
• 230
• 231
• 232
• 233
• 234
• 235
• 236
• 237
• 238
• 239
• 240
• 241
• 242
• 243
• 244
• 245
• 246
• 247
• 248
• 249
• 250
• 251
• 252
• 253
• 254
• 255
• 256
• 257

16.

Округление десятичных дробей

• Вопросы и задания
• Неверно стр.83

• 258
• 259
• 260
• 261
• 262
• 263
• 264
• 265
• 266
• 267
• 268
• 269
• 270
• 271
• 272

Подведём итоги

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10

17. Прямая и окружность

• Вопросы и задания

• 273
• 274
• 275
• 276
• 277
• 278
• 279
• 280
• 281
• 282
• 283
• 284
• 285

18. Две окружности на плоскости

• Вопросы и задания

• 286
• 287
• 288
• 289
• 290
• 291
• 292
• 293
• 294
• 295
• 296
• 297

19.

Построение треугольника

• Вопросы и задания

• 298
• 299
• 300
• 301
• 302
• 303
• 304
• 305
• 306
• 307
• 308
• 309

20. Круглые тела

• Вопросы и задания

• 310
• 311
• 312
• 313
• 314
• 315
• 316
• 317
• 318
• 319
• 320
• 321

Подведём итоги

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8

21. Прямая и окружность

• Вопросы и задания

• 322
• 323
• 324
• 325
• 326
• 327
• 328
• 329
• 330
• 331
• 332
• 333
• 334
• 335
• 336
• 337
• 338
• 339

22.

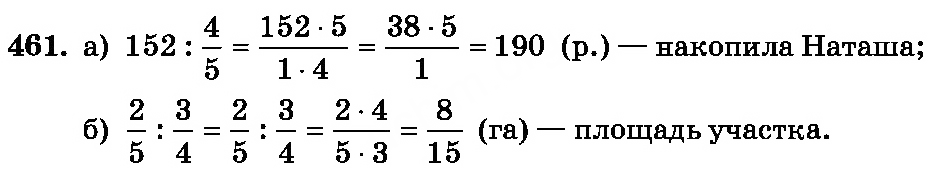Отношение величин. Масштаб

• Вопросы и задания
• Неверно стр.110
• Вопросы и задания §21 (2019)

• 340
• 341
• 342
• 343
• 344
• 345
• 346
• 347
• 348
• 349
• 350
• 351
• 352
• 353
• 354

23. Проценты и десятичные дроби

• Вопросы и задания

• 355
• 356
• 357
• 358
• 359
• 360
• 361
• 362
• 363
• 364
• 365
• 366
• 367
• 368
• 369

24. «Главная» задача на проценты

• Вопросы и задания

• 370
• 371
• 372
• 373
• 374
• 375
• 376
• 377
• 378
• 379
• 380
• 381
• 382
• 383
• 384

25.

Выражение отношения в процентах

• Вопросы и задания

• 385
• 386
• 387
• 388
• 389
• 390
• 391
• 392
• 393
• 394
• 395
• 396
• 397
• 398
• 399

Подведём итоги

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11

26. О математическом языке

• Вопросы и задания

• 400
• 401
• 402
• 403
• 404
• 405
• 406
• 407
• 408
• 409
• 410
• 411
• 412
• 413
• 414

27. Буквенные выражения и числовые подстановки

• Вопросы и задания

• 415
• 416
• 417
• 418
• 419
• 420
• 421
• 422
• 423
• 424
• 425
• 426
• 427
• 428
• 429
• 430

28.

Составление формул и вычисление по формулам

• Вопросы и задания

• 431
• 432
• 433
• 434
• 435
• 436
• 437
• 438
• 439
• 440
• 441
• 442
• 443

29. Формулы длины окружности, площади круга и объёма шара

• Вопросы и задания

• 444
• 445
• 446
• 447
• 448
• 449
• 450
• 451
• 452
• 453
• 454
• 455
• 456

30. Что такое уравнение

• Вопросы и задания

• 457
• 458
• 459
• 460
• 461
• 462
• 463
• 464
• 465
• 466
• 467
• 468
• 469
• 470
• 471
• 472

Подведём итоги

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10

31.

Осевая симметрия

• Вопросы и задания

• 473
• 474
• 475
• 476
• 477
• 478
• 479
• 480
• 481
• 482
• 483
• 484

32. Ось симметрии фигуры

• Вопросы и задания

• 485
• 486
• 487
• 488
• 489
• 490
• 491
• 492
• 493
• 494
• 495
• 496
• 497
• 498

33. Центральная симметрия

• Вопросы и задания

• 499
• 500
• 501
• 502
• 503
• 504
• 505
• 506
• 507
• 508
• 509
• 510
• 511
• 512

Подведём итоги

• 1
• 2
• 3
• 4
• 5
• 6
• 7

34.

Какие числа называют целыми

• Вопросы и задания

• 513
• 514
• 515
• 516
• 517
• 518
• 519
• 520
• 521
• 522
• 523
• 524
• 525
• 526
• 527

35. Сравнение целых чисел

• Вопросы и задания

• 528
• 529
• 530
• 531
• 532
• 533
• 534
• 535
• 536
• 537
• 538
• 539
• 540
• 541
• 542
• 543
• 544
• 545

36. Сложение целых чисел

• Вопросы и задания

• 546
• 547
• 548
• 549
• 550
• 551
• 552
• 553
• 554
• 555
• 556
• 557
• 558
• 559
• 560
• 561
• 562
• 563

37.

Вычитание целых чисел

• Вопросы и задания

• 564
• 565
• 566
• 567
• 568
• 569
• 570
• 571
• 572
• 573
• 574
• 575
• 576
• 577
• 578
• 579
• 580
• 581

38. Умножение и деление целых чисел

• Вопросы и задания
• Неверно стр.183

• 582
• 583
• 584
• 585
• 586
• 587
• 588
• 589
• 590
• 591
• 592
• 593
• 594
• 595
• 596
• 597
• 598

Подведём итоги

• 1
• 2
• 3
• 4
• 5
• 6

39. Какие числа называют рациональными

• Вопросы и задания

• 599
• 600
• 601
• 602
• 603
• 604
• 605
• 606
• 607
• 608
• 609
• 610
• 611
• 612
• 613
• 614

40.

Сравнение рациональных чисел. Модуль числа

• Вопросы и задания

• 615
• 616
• 617
• 618
• 619
• 620
• 621
• 622
• 623
• 624
• 625
• 626
• 627
• 628
• 629

41. Сложение и вычитание рациональных чисел

• Вопросы и задания

• 630
• 631
• 632
• 633
• 634
• 635
• 636
• 637
• 638
• 639
• 640
• 641
• 642
• 643
• 644
• 645
• 646

42. Умножение и деление рациональных чисел

• Вопросы и задания

• 647
• 648
• 649
• 650
• 651
• 652
• 653
• 654
• 655
• 656
• 657
• 658
• 659
• 660
• 661
• 662
• 663
• 664
• 665
• 666
• 667
• 668
• 669

43.

Координаты

• Вопросы и задания

• 670
• 671
• 672
• 673
• 674
• 675
• 676
• 677
• 678
• 679
• 680
• 681
• 682
• 683
• 684

Подведём итоги

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15

44. Параллелограмм

• Вопросы и задания

• 685
• 686
• 687
• 688
• 689
• 690
• 691
• 692
• 693
• 694
• 695
• 696
• 697
• 698
• 699
• 700

45. Правильные многоугольники

• Вопросы и задания

• 701
• 702
• 703
• 704
• 705
• 706
• 707
• 708
• 709
• 710

46.

Площади

• Вопросы и задания

• 711
• 712
• 713
• 714
• 715
• 716
• 717
• 718
• 719
• 720
• 721
• 722
• 723

47. Призма

• Вопросы и задания

• 724
• 725
• 726
• 727
• 728
• 729
• 730
• 731
• 732
• 733
• 734
• 735
• 736

Подведём итоги

• 1
• 2
• 3
• 4
• 5
• 6

48. Понятие множества

• Вопросы и задания

• 737
• 738
• 739
• 740
• 741
• 742
• 743
• 744
• 745
• 746
• 747
• 748
• 749
• 750

49.

Операции над множествами

• Вопросы и задания

• 751
• 752
• 753
• 754
• 755
• 756
• 757
• 758
• 759
• 760
• 761
• 762
• 763

50. Решение комбинаторных задач

• Вопросы и задания

• 764
• 765
• 766
• 767
• 768
• 769
• 770
• 771
• 772
• 773
• 774
• 775
• 776
• 777

Подведём итоги

• 1
• 2
• 3
• 4
• 5
• 7

Описание

ГДЗ к учебнику Е. А. Бунимович, Л. В. Кузнецовой, С. С. Минаевой «Математика 6 класс» предлагают ответы к заданиям по основным изучаемым разделам.

Материал удобно структурирован. Решения разбиты на 12 глав, внутри которых перечислены темы. После каждого урока (темы) находится от 1 до 30 упражнений. Они делятся на два вида контроля: «Вопросы и задания», «Подведём итоги». Поиск по документу занимает несколько секунд.

Пособие оказывает помощь в изучении разделов «Отношения и проценты», «Десятичные дроби», «Окружность», «Симметрия», «Множества. Комбинаторика» и др.

Ответы представляют собой отсканированный лист клетчатой тетради. Записи сделаны чёрной гелиевой ручкой. Почерк аккуратный, разборчивый. Необходимые пояснения к задачам имеются.

Комментарии

ГДЗ по Математике 6 класс Бунимович

Авторы:Бунимович

Изд-во:Просвещение

Вид УМК:учебник

Серия:Сферы

Шестиклассники, отмечая трудности в усвоении программы, выделяют, прежде всего, большое количество новых терминов и определений, с которыми они не встречались в предыдущие года учебы. Преодолеть сложности можно, дополнив подготовку самостоятельной работой. Освоить полезный навык самообучения поможет гдз по математике за 6 класс Бунимович — сборник, составленный для учеников общеобразовательных учебных заведений. Специалисты подчеркивают тот факт, что все темы изучаемого курса рассматриваются в подробном, понятном и доступном виде. Кроме того, комплект материалов позволяет развивать навыки, опираясь на полученные в младших классах знания, изучая такую науку, как математика.

Для кого предназначены онлайн решебники?

Среди тех, кто намеренно и часто использует правильные ответы по математике для 6 класса Бунимовича встречаются:

• шестиклассники, серьезно заинтересованные в приобретении основательных знаний по дисциплине, участвующие в научных и конкурсных мероприятиях по ней и желающие получить конкурентные преимущества перед другими участниками. Особенно, если тема изучалась в школе по другим учебникам;
• школьники, выбравшие этот предмет, чтобы написать выпускной экзамен в девятом классе или использовать его в одиннадцатом классе. Ресурс позволит повторить материал курса для 5 класса, а решебник станет площадкой для систематизации знаний и развития вашей подготовительной программы.
• дети, пропускающие школу по тем или иным причинам. Для них платформа является альтернативой или дополнением к объяснению учителя, которое помогает понять сложные моменты материала, хорошо подготовиться к следующему ответу на уроке или написать важную проверочную работу;
• родители учеников шестых классов, которым нужно систематически проверять домашние задания детей, следить за успеваемостью и уровнем знания.

Доводы в защиту учебно-практических пособий

На сегодняшний день не все родители и учителя понимают полезность и необходимость занятий со справочными материалами по математике 6 класс автор Бунимович для школьников. Некоторые до сих пор считают, что это просто площадка для списания готовых решений, что противоречит самостоятельному усвоению знаний. Те, кто оценил пользу и эффективность решебников, отмечают следующие достоинства:

• минимальное количество времени, которое необходимо потратить, чтобы найти и применить желаемый ответ;
• постоянная доступность ресурса для всех заинтересованных пользователей в любое время;
• возможность существенно сэкономить семейный бюджет, отказавшись от дорогостоящих репетиторов, платных курсов или клубов, либо значительно снизив стоимость этих предметов;
• все материалы составлены в соответствии с положением об образовательных стандартах, что важно при написании ВПР, прохождении олимпиад и конкурсов, сдаче экзаменов.

Грамотные и подробные математические решения на еуроки ГДЗ являются важным ресурсом для развития способностей учащихся, если они применяются правильно и систематически. Например, чтобы сверить свои ответы со справочными ответами, сначала проверьте решения задачи, прежде чем передать работу учителю, что снижает риск получения плохих оценок.

Найди ответ по номеру задания

Итоговые задания

Неверно

1617181920212223242526272829303132333435

3637383940414243444546474849505152535455

5657585960616263646566676869707172737475

7677787980818283848586878889909192939495

96979899100101102103104105106107108109110111112113114115

116117118119120121122123124125126127128129130131132133134135

136137138139140141142143144145146147148149150151152153154155

156157158159160161162163164165166167168169170171172173174175

176177178179180181182183184185186187188189190191192193194195

196197198199200201202203204205206207208209210211212213214215

216217218219220221222223224225226227228229230231232233234235

236237238239240241242243244245246247248249250251252253254255

256257258259260261262263264265266267268269270271272273274275

276277278279280281282283284285286287288289290291292293294295

296297298299300301302303304305306307308309310311312313314315

316317318319320321322323324325326327328329330331332333334335

336337338339340341342343344345346347348349350351352353354355

356357358359360361362363364365366367368369370371372373374375

376377378379380381382383384385386387388389390391392393394395

396397398399400401402403404405406407408409410411412413414415

416417418419420421422423424425426427428429430431432433434435

436437438439440441442443444445446447448449450451452453454455

456457458459460461462463464465466467468469470471472473474475

476477478479480481482483484485486487488489490491492493494495

496497498499500501502503504505506507508509510511512513514515

516517518519520521522523524525526527528529530531532533534535

536537538539540541542543544545546547548549550551552553554555

556557558559560561562563564565566567568569570571572573574575

576577578579580581582583584585586587588589590591592593594595

596597598599600601602603604605606607608609610611612613614615

616617618619620621622623624625626627628629630631632633634635

636637638639640641642643644645646647648649650651652653654655

656657658659660661662663664665666667668669670671672673674675

676677678679680681682683684685686687688689690691692693694695

696697698699700701702703704705706707708709710711712713714715

716717718719720721722723724725726727728729730731732733734735

736737738739740741742743744745746747748749750751752753754755

756757758759760761762763764765766767768769770771772773774775

776777

Математика 6 класс.

Ответы на задачи учебника Бунимовича

 

Бунимович Е.А. Кузнецова Л.В. Минаева С.С.

гдз решебник математика 6 класс

ответы готовые домашние задания

УЧЕБНИК

  

БЫСТРЫЙ ПЕРЕХОД К ЗАДАЧАМ 

ГЛАВА 1	1-75		ГЛАВА 7	400-472
ГЛАВА 2	76-111		ГЛАВА 8	473-512
ГЛАВА 3	112-160		ГЛАВА 9	513-598
ГЛАВА 4	161-272		ГЛАВА 10	599-684
ГЛАВА 5	273-321		ГЛАВА 11	685-736
ГЛАВА 6	322-399		ГЛАВА 12	737-777

 

  

ГЛАВА 1

  

ВОПРОСЫ И ЗАДАНИЯ К ГЛАВЕ 1 

1. ЧТО МЫ ЗНАЕМ О ДРОБЯХ	ОТВЕТ
2. ВЫЧИСЛЕНИЯ С ДРОБЯМИ	ОТВЕТ
3. ОСНОВНЫЕ ЗАДАЧИ НА ДРОБИ	ОТВЕТ
4. ЧТО ТАКОЕ ПРОЦЕНТ	ОТВЕТ
5. СТОЛБЧАТЫЕ И КРУГОВЫЕ ДИАГРАММЫ	ОТВЕТ

 

ЗАДАЧИ 1-75 

1	2	3	4	5	6	7	8	9	10
11	12	13	14	15	16	17	18	19	20
21	22	23	24	25	26	27	28	29	30
31	32	33	34	35	36	37	38	39	40
41	42	43	44	45	46	47	48	49	50
51	52	53	54	55	56	57	58	59	60
61	62	63	64	65	66	67	68	69	70
71	72	73	74	75

 

ИТОГИ ГЛАВЫ 1

1

2

3

4

5

6

7

8

9

10

 

 

ГЛАВА 2 

 

ВОПРОСЫ И ЗАДАНИЯ К ГЛАВЕ 2 

6. ПЕРЕСЕКАЮЩИЕСЯ ПРЯМЫЕ	ОТВЕТ
7. ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ	ОТВЕТ
8. РАССТОЯНИЕ	ОТВЕТ

 

ЗАДАЧИ 76-111

					76	77	78	79	80
81	82	83	84	85	86	87	88	89	90
91	92	93	94	95	96	97	98	99	100
101	102	103	104	105	106	107	108	109	110
111

  

ИТОГИ ГЛАВЫ 2

1

2

3

4

5

6

7

8

 

 

ГЛАВА 3

 

ВОПРОСЫ И ЗАДАНИЯ К ГЛАВЕ 3

9. КАКИЕ ДРОБИ НАЗЫВАЮТ ДЕСЯТИЧНЫМИ	ОТВЕТ
10. ПЕРЕВОД ОБЫКНОВ. ДРОБИ В ДЕСЯТИЧНУЮ	ОТВЕТ
11. СРАВНЕНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ	ОТВЕТ

 

ЗАДАЧИ 112-160  

	112	113	114	115	116	117	118	119	120
121	122	123	124	125	126	127	128	129	130
131	132	133	134	135	136	137	138	139	140
141	142	143	144	145	146	147	148	149	150
151	152	153	154	155	156	157	158	159	160

 

ИТОГИ ГЛАВЫ 3

1

2

3

4

5

6

7

8

9

10

11

 

 

ГЛАВА 4

 

ВОПРОСЫ И ЗАДАНИЯ К ГЛАВЕ 4

12. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДЕСЯТ. ДРОБЕЙ	ОТВЕТ
13. УМНОЖ. И ДЕЛЕНИЕ ДЕСЯТ. ДРОБИ НА 10, 100…	ОТВЕТ
14. УМНОЖЕНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ	ОТВЕТ
15. ДЕЛЕНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ	ОТВЕТ
16. ОКРУГЛЕНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ	ОТВЕТ

 

ЗАДАЧИ 161-272  

161	162	163	164	165	166	167	168	169	170
171	172	173	174	175	176	177	178	179	180
181	182	183	184	185	186	187	188	189	190
191	192	193	194	195	196	197	198	199	200
201	202	203	204	205	206	207	208	209	210
211	212	213	214	215	216	217	218	219	220
221	222	223	224	225	226	227	228	229	230
231	232	233	234	235	236	237	238	239	240
241	242	243	244	245	246	247	248	249	250
251	252	253	254	255	256	257	258	259	260
261	262	263	264	265	266	267	268	269	270
271	272

 

ИТОГИ ГЛАВЫ 4

1

2

3

4

5

6

7

8

9

10

 

 

ГЛАВА 5

 

ВОПРОСЫ И ЗАДАНИЯ К ГЛАВЕ 5

17. ПРЯМАЯ И ОКРУЖНОСТЬ	ОТВЕТ
18. ДВЕ ОКРУЖНОСТИ НА ПЛОСКОСТИ	ОТВЕТ
19. ПОСТРОЕНИЕ ТРЕУГОЛЬНИКА	ОТВЕТ
20. КРУГЛЫЕ ТЕЛА	ОТВЕТ

 

ЗАДАЧИ 273-321  

		273	274	275	276	277	278	279	280
281	282	283	284	285	286	287	288	289	290
291	292	293	294	295	296	297	298	299	300
301	302	303	304	305	306	307	308	309	310
311	312	313	314	315	316	317	318	319	320
321

 

ИТОГИ ГЛАВЫ 5

1

2

3

4

5

6

7

8

  

 

ГЛАВА 6

 

ВОПРОСЫ И ЗАДАНИЯ К ГЛАВЕ 6

21. ЧТО ТАКОЕ ОТНОШЕНИЕ	ОТВЕТ
22. ОТНОШЕНИЕ ВЕЛИЧИН. МАСШТАБ	ОТВЕТ
23. ПРОЦЕНТЫ И ДЕСЯТИЧНЫЕ ДРОБИ	ОТВЕТ
24. «ГЛАВНАЯ» ЗАДАЧА НА ПРОЦЕНТЫ	ОТВЕТ
25. ВЫРАЖЕНИЕ ОТНОШЕНИЯ В ПРОЦЕНТАХ	ОТВЕТ

 

ЗАДАЧИ 322-399  

	322	323	324	325	326	327	328	329	330
331	332	333	334	335	336	337	338	339	340
341	342	343	344	345	346	347	348	349	350
351	352	353	354	355	356	357	358	359	360
361	362	363	364	365	366	367	368	369	370
371	372	373	374	375	376	377	378	379	380
381	382	383	384	385	386	387	388	389	390
391	392	393	394	395	396	397	398	399

 

ИТОГИ ГЛАВЫ 6

1

2

3

4

5

6

7

8

9

10

11

 

 

ГЛАВА 7

 

ВОПРОСЫ И ЗАДАНИЯ К ГЛАВЕ 7

26. О МАТЕМАТИЧЕСКОМ ЯЗЫКЕ	ОТВЕТ
27. БУКВЕННЫЕ ВЫРАЖЕНИЯ И ЧИСЛОВЫЕ …	ОТВЕТ
28. СОСТАВЛЕНИЕ ФОРМУЛ И ВЫЧИСЛЕНИЯ …	ОТВЕТ
29. ФОРМУЛЫ ДЛИНЫ ОКРУЖНОСТИ …	ОТВЕТ
30. ЧТО ТАКОЕ УРАВНЕНИЕ	ОТВЕТ

 

ЗАДАЧИ 400-472  

									400
401	402	403	404	405	406	407	408	409	410
411	412	413	414	415	416	417	418	419	420
421	422	423	424	425	426	427	428	429	430
431	432	433	434	435	436	437	438	439	440
441	442	443	444	445	446	447	448	449	450
451	452	453	454	455	456	457	458	459	460
461	462	463	464	465	466	467	468	469	470
471	472

 

ИТОГИ ГЛАВЫ 7

1

2

3

4

5

6

7

8

9

10

 

 

ГЛАВА 8

 

ВОПРОСЫ И ЗАДАНИЯ К ГЛАВЕ 8

31. ОСЕВАЯ СИММЕТРИЯ	ОТВЕТ
32. ОСЬ СИММЕТРИИ ФИГУРЫ	ОТВЕТ
33. ЦЕНТРАЛЬНАЯ СИММЕТРИЯ	ОТВЕТ

 

ЗАДАЧИ 473-512  

		473	474	475	476	477	478	479	480
481	482	483	484	485	486	487	488	489	490
491	492	493	494	495	496	497	498	499	500
501	502	503	504	505	506	507	508	509	510
511	512

 

ИТОГИ ГЛАВЫ 8

1

2

3

4

5

6

7

 

 

ГЛАВА 9

 

ВОПРОСЫ И ЗАДАНИЯ К ГЛАВЕ 9

34. КАКИЕ ЧИСЛА НАЗЫВАЮТ ЦЕЛЫМИ	ОТВЕТ
35. СРАВНЕНИЕ ЦЕЛЫХ ЧИСЕЛ	ОТВЕТ
36. СЛОЖЕНИЕ ЦЕЛЫХ ЧИСЕЛ	ОТВЕТ
37. ВЫЧИТАНИЕ ЦЕЛЫХ ЧИСЕЛ	ОТВЕТ
38. УМНОЖЕНИЕ И ДЕЛЕНИЕ ЦЕЛЫХ ЧИСЕЛ	ОТВЕТ

 

ЗАДАЧИ 513-598  

		513	514	515	516	517	518	519	520
521	522	523	524	525	526	527	528	529	530
531	532	533	534	535	536	537	538	539	540
541	542	543	544	545	546	547	548	549	550
551	552	553	554	555	556	557	558	559	560
561	562	563	564	565	566	567	568	569	570
571	572	573	574	575	576	577	578	579	580
581	582	583	584	585	586	587	588	589	590
591	592	593	594	595	596	597	598

 

ИТОГИ ГЛАВЫ 9

1

2

3

4

5

6

 

 

ГЛАВА 10

 

ВОПРОСЫ И ЗАДАНИЯ К ГЛАВЕ 10

39. КАКИЕ ЧИСЛА НАЗЫВАЮТ РАЦИОНАЛЬНЫМИ	ОТВЕТ
40. СРАВНЕНИЕ РАЦИОНАЛ. ЧИСЕЛ. МОДУЛЬ ЧИСЛА	ОТВЕТ
41. СЛОЖЕНИЕ И ВЫЧИТАНИЕ РАЦИОНАЛ. ЧИСЕЛ	ОТВЕТ
42. УМНОЖЕНИЕ И ДЕЛЕНИЕ РАЦИОНАЛ. ЧИСЕЛ	ОТВЕТ
43. КООРДИНАТЫ	ОТВЕТ

 

ЗАДАЧИ 599-684  

								599	600
601	602	603	604	605	606	607	608	609	610
611	612	613	614	615	616	617	618	619	620
621	622	623	624	625	626	627	628	629	630
631	632	633	634	635	636	637	638	639	640
641	642	643	644	645	646	647	648	649	650
651	652	653	654	655	656	657	658	659	660
661	662	663	664	665	666	667	668	669	670
671	672	673	674	675	676	677	678	679	680
681	682	683	684

 

ИТОГИ ГЛАВЫ 10

1	2	3	4	5	6	7	8	9	10
11	12	13	14	15

   

 

ГЛАВА 11

 

ВОПРОСЫ И ЗАДАНИЯ К ГЛАВЕ 11

44. ПАРАЛЛЕЛОГРАММ	ОТВЕТ
45. ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ	ОТВЕТ
46. ПЛОЩАДИ	ОТВЕТ
47. ПРИЗМА	ОТВЕТ

 

ЗАДАЧИ 685-736  

				685	686	687	688	689	690
691	692	693	694	695	696	697	698	699	700
701	702	703	704	705	706	707	708	709	710
711	712	713	714	715	716	717	718	719	720
721	722	723	724	725	726	727	728	729	730
731	732	733	734	735	736

 

ИТОГИ ГЛАВЫ 11

1

2

3

4

5

6

 

 

ГЛАВА 12

 

ВОПРОСЫ И ЗАДАНИЯ К ГЛАВЕ 12

48. ПОНЯТИЕ МНОЖЕСТВА	ОТВЕТ
49. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ	ОТВЕТ
50. РЕШЕНИЕ КОМБИНАТОРНЫХ ЗАДАЧ	ОТВЕТ

 

ЗАДАЧИ 737-777  

						737	738	739	740
741	742	743	744	745	746	747	748	749	750
751	752	753	754	755	756	757	758	759	760
761	762	763	764	765	766	767	768	769	770
771	772	773	774	775	776	777

 

ИТОГИ ГЛАВЫ 12

1

2

3

4

5

6

7

 

 

На этой странице нашего сайта Вы найдете ответы (гдз – готовые домашние задания) к учебнику, составленному прекрасным авторским коллективом в составе Бунимовича Евгения Абрамовича, Минаевой Светланы Станиславовны, Кузнецовой Людмилы Викторовны.

Данный учебник, в известной мере, отличается от остальных своим скрупулёзным методическим подходом к изучению математики 6-го класса. Посудите сами: учебник состоит из 12 глав, каждая из которых состоит из теоретической части, далее идут вопросы по теории данного раздела, далее – вопросы и задания, проверяющие усвоение теоретической части главы, потом – практические задания и, в конце каждой главы – мини-контрольная работа для закрепления полученных знаний.

Согласитесь, такой многоуровневый подход к изучению математики свойственен далеко не каждому учебнику.

Особо хочется отметить интересные факты из истории математики, которые авторы учебника включили в теоретическую часть практически каждой главы. Это делает науку математика не скоплением сухих цифр и формул, а очень интересной, занимательной, иногда веселой наукой.

FASHION NEWS

ГДЗ Учебник по Математике 6 класс Бунимович Сферы

Глава 1 (Упражнения)

1 2 3 4 5 6 7 8 9 10

Глава 2 (Упражнения)

1 2 3 4 5 6 7 8

Глава 3 (Упражнения)

1 2 3 4 5 6 7 8 9 10 11

Глава 4 (Упражнения)

1 2 3 4 5 6 7 8 9 10

Глава 5 (Упражнения)

1 2 3 4 5 6 7 8

Глава 6 (Упражнения)

1 2 3 4 5 6 7 8 9 10 11

Глава 7 (Упражнения)

1 2 3 4 5 6 7 8 9 10

Глава 8 (Упражнения)

1 2 3 4 5 6 7

Глава 9 (Упражнения)

1 2 3 4 5 6

Глава 10 (Упражнения)

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

Глава 11 (Упражнения)

1 2 3 4 5 6

Глава 12 (Упражнения)

1 2 3 4 5 6 7

Математика Бунимович 6 класс Подведем итоги: — ГДЗ Решебники

Авторы: Бунимович, Кузнецова, (учебник) Год: 2014 год Издательство: Просвещение

На данной странице предствлены решения к учебнику по Математике для учеников 6 класса, Учебник издательства «Просвещение» 2014 года.

Популярные учебники

Дроби и проценты. (Задачи с 1 по 75)

§1. Что мы знаем о дробях

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

§2. Вычисления с дробями

16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33

§3. Основные задачи на дроби

34 35 36 37 38 39 40 41 42 43 44 45 46 47 48

§4. Что такое процент

49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68

§5. Столбчатые и круговые диаграммы

69 70 71 72 73 74 75

Подведем итоги:

1 2 3 4 5 6 7 8 9 10

Прямые на плоскости в пространстве. (Задачи с 76 по 111)

§6. Пересекающиеся прямые

76 77 78 79 80 81 82 83 84 85

§7. Параллельные прямые

86 87 88 89 90 91 92 93 94 95 96 97 98

§8. Расстояние

99 100 101 102 103 104 105 106 107 108 109 110 111

Подведем итоги:

1 2 3 4 5 6 7 8

(Задачи с 112 по 160) Десятичные дроби.

§9. Какие дроби называют десятичными

112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127

§10.

Перевод обыкновенной дроби в десятичную 128 129 130 131 132 133 134 135 136 137 138 139 140 141

§11. Сравнение десятичных дробей

142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160

Подведем итоги:

1 2 3 4 5 6 7 8 9 10 11

(Задачи с 161 по 272) Действия с десятичными дробями.

§12. Сложение и вычитание десятичных дробей

161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179

§13. Умножение и деление десятичной дроби на 10, 100, 1000

180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197

§14. Умножение десятичных дробей

198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217

§15. Деление десятичных дробей

218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257

§16. Округление десятичных дробей

258 259 260 261 262 263 264 265 266 267 268 269 270 271 272

Подведем итоги:

1 2 3 4 5 6 7 8 9 10

Окружность.

(Задачи с 273 по 321)

§17. Прямая и окружность

273 274 275 276 277 278 279 280 281 282 283 284 285

§18. Две окружности на плоскости

286 287 288 289 290 291 292 293 294 295 296 297

§19. Построение треугольника

298 299 300 301 302 303 304 305 306 307 308 309 310

§20. Круглые тела

311 312 313 314 315 316 317 318 319 320 321

Подведем итоги:

1 2 3 4 5 6 7 8

(Задачи с 322 по 399) Отношения и проценты.

§21. Что такое отношение

322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339

§22. Отношение величин. Масштаб

340 341 342 343 344 345 346 347 348 349 350 351 352 353 354

§23. Проценты и десятичные дроби

355 356 357 358 359 360 361 362 363 364 365 366 367 368 369

§24. «Главная» задача на проценты

370 371 372 373 374 375 376 377 378 379 380 381 382 383 384

§25. Выражение отношения в процентах

385 386 387 388 389 390 391 392 393 394 395 396 397 398 399

Подведем итоги:

1 2 3 4 5 6 7 8 9 10 11

(Задачи с 400 по 472) Выражения, формулы, уравнения.

§26. О математическом языке

400 401 402 403 404 405 406 407 408 409 410 411 412 413 414

§27. Буквенные выражения и числовые подстановки

415 416 417 418 419 420 421 422 423 424 425 426 427 428 429 430

§28. Составление формул и вычисление по формулам

431 432 433 434 435 436 437 438 439 440 441 442 443

§29. Формулы длины окружности, площади круга и объёма шара

444 445 446 447 448 449 450 451 452 453 454 455 456

§30. Что такое уравнение

457 458 459 460 461 462 463 464 465 466 467 468 469 470 471 472

Подведем итоги:

1 2 3 4 5 6 7 8 9 10

(Задачи с 473 по 512) Симметрия.

§31. Осевая симметрия

473 474 475 476 477 478 479 480 481 482 483 484

§32. Ось симметрии фигуры

485 486 487 488 489 490 491 492 493 494 495 496 497 498

§33. Центральная симметрия

499 500 501 502 503 504 505 506 507 508 509 510 511 512

Подведем итоги:

1 2 3 4 5 6 7

(Задачи с 513 по 598) Целые числа.

§34.

Какие числа называют целыми 513 514 515 516 517 518 519 520 521 522 523 524 525 526 527

§35. Сравнение целых чисел

528 529 530 531 532 533 534 535 536 537 538 539 540 541 542 543 544

§36. Сложение целых чисел

545 546 547 548 549 550 551 552 553 554 555 556 557 558 559 560 561 562 563

§37. Вычитание целых чисел

564 565 566 567 568 569 570 571 572 573 574 575 576 577 578 579 580 581

§38. Умножение и деление целых чисел

582 583 584 585 586 587 588 589 590 591 592 593 594 595 596 597 598

Подведем итоги:

1 2 3 4 5 6

Рациональные числа. (Задачи с 559 по 684)

§39. Какие числа называют рациональными

599 600 601 602 603 604 605 606 607 608 609 610 611 612 613 614

§40. Сравнение рациональных чисел. Модуль числа

615 616 617 618 619 620 621 622 623 624 625 626 627 628 629

§41. Сложение и вычитание рациональных чисел

630 631 632 633 634 635 636 637 638 639 640 641 642 643 644 645 646

§42. Умножение и деление рациональных чисел

647 648 649 650 651 652 653 654 655 656 657 658 659 660 661 662 663 664 665 666 667 668 669

§43.

Координаты 670 671 672 673 674 675 676 677 678 679 680 681 682 683 684

Подведем итоги:

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

Многоугольники и многогранники. (Задачи с 685 по 736)

§44. Параллелограмм

685 686 687 688 689 690 691 692 693 694 695 696 697 698 699 700

§45. Правильные многоугольники

701 702 703 704 705 706 707 708 709 710

§46. Площади

711 712 713 714 715 716 717 718 719 720 721 722 723

§47. Призма

724 725 726 727 728 729 730 731 732 733 734 735 736

Подведем итоги:

1 2 3 4 5 6

§48. Понятие множества

737 738 739 740 741 742 743 744 745 746 747 748 749 750

§49. Операции над множествами

751 752 753 754 755 756 757 758 759 760 761 762 763

§50. Решение комбинаторных задач

764 765 766 767 768 769 770 771 772 773 774 775 776 777

Подведем итоги:

1 2 3 4 5 6 7

БЕСПЛАТНОЕ ГДЗ ЗА 1-11 КЛАСС

Чтобы у учеников не было стресса от больших нагрузок, страха получить плохую оценку, но при этом оставалось время на полноценный сон, дополнительные занятия, спорт, общение со сверстниками, стоит делать уроки вместе с ГДЗ. Готовые домашние задания – это возможность качественно подготовиться по разным предметам, не платя деньги репетиторам.

Если не хочется скачивать материалы, написанные «на коленке» студентами, а нужно работать с ГДЗ, над которыми трудились опытные преподаватели, умеющие понятно рассказывать теорию и грамотно оформлять практические задания, то надо заходить на Помогалку. Здесь можно без регистрации смотреть корректные решения номеров из учебников разных авторов по всем предметам и классам. Пусть школьная жизнь проходит без проблем!

Вводные слова в русском языке — таблица, виды и примеры

Что такое вводные слова

Начнем, как всегда, с определения — разберемся, какие слова называются вводными и зачем они нужны. Школьники сталкиваются с ними, начиная с 5 класса, хотя подробно изучают только в 8 классе. Это не сложная тема, если у вас хорошая зрительная память — правил относительно вводных слов в русском языке очень мало, и какие-то вещи придется просто запомнить.

Вводные слова — это единицы предложения, которые не несут отдельной смысловой нагрузки, но усиливают эмоциональную оценку, уверенность или сомнения говорящего. Также они могут указывать на последовательность событий, привлекать внимание и т. д.

Существует несколько типов вводных слов, но все они обладают следующими особенностями:

• выделяются в тексте запятыми, скобками или с помощью тире;
• не имеют грамматических связей с другими членами предложения;
• могут быть вычеркнуты из текста без потери смысла.

Важно!

Вводные слова не являются членами предложения. Их следует отличать от совершенно таких же слов, которые выступают в роли обстоятельства, определения или дополнения. Разница заключается в том, что к вводной конструкции нельзя поставить вопрос.

Рассмотрим на примере:

• Саша все-таки пришел, правда, опоздал на полчаса.
• Саша подтвердил, что все написанное — чистая правда.

Итак, у нас есть слово «правда», которое в первом предложении выступает вводным, поскольку к нему нельзя поставить вопрос. Во втором предложении оно же является сказуемым. Мы можем поставить вопрос: «все написанное — это что?».

• Я, верно, теперь не скоро доберусь домой.
• Весь класс верно решил эту задачу.

Как видите, во втором предложении к «верно» можно поставить вопрос «как?». Следовательно, это слово не является вводным.

Такие же правила распространяются и на составные вводные слова. Они тоже могут замаскироваться под различные члены предложения, и важно научиться их распознавать.

Сравните:

• Он каждое утро просыпался с радостным предвкушением, одним словом, был счастлив. — Одним словом вы не сможете никого убедить, нужны поступки.
• Морской воздух и обилие солнца, без всякого сомнения, помогают быстро восстановиться после болезни. — Миша с детства мечтал о небе, и поэтому без всякого сомнения выбрал летное училище.

Еще один способ отличить вводные слова — убрать их вовсе и посмотреть, не потеряет ли предложение свой смысл. Попробуем это сделать на одном из наших примеров:

• Саша все-таки пришел, правда, опоздал на полчаса.
• Саша подтвердил, что все написанное — чистая правда.

Понятно, что в первом случае смысл остался тем же, а вот во втором — он был утерян. Это подтверждает, что в первом предложении мы имеем дело именно со вводным словом.

Практикующий детский психолог Екатерина Мурашова

Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков

Признаки вводных слов: таблица для 5 класса

Грамматически вводные слова могут представлять собой любую часть речи и даже короткое предложение:

• существительное — без сомнений, правда;
• прилагательное — самое меньшее, виноват;
• глагол — надеюсь, полагаю;
• наречие — несомненно, безусловно;
• деепричастие — откровенно говоря;
• словосочетание — если хотите знать, по словам экспертов;
• безличное предложение — мнилось мне, как видится.

Примеры употребления вводных слов:

• Тихий океан, без сомнений, самый большой на планете.
• Откровенно говоря, я не смог убедить его в своей правоте, да и не пытался.
• Эту роль, как мне видится, лучше всех сыграет Маша.
• — Вас ожидать к восьми утра?
  — Разумеется!

​

Курсы подготовки к ЕГЭ по русскому языку в онлайн-школе Skysmart — без стресса и на реальных экзаменационных заданиях. Попробуйте бесплатно на вводном уроке!

Разряды вводных слов по значению

Как мы уже сказали, вводные слова могут выполнять самые разные функции в устной и письменной речи. Одни из них подчеркивают позицию говорящего — его уверенность, удивление, сожаление и т. д. Другие же указывают на очередной действий или событий, на логику повествования или источник информации. Третьи и вовсе нужны лишь для того, чтобы привлечь внимание. Разберемся, что обозначают вводные слова разных видов, а в конце подведем итог с помощью таблицы с примерами.

Различная степень уверенности, предположение и допущение

Это самая распространенная категория вводных слов, к которой мы обращаемся ежедневно. Основная функция данного разряда — подчеркнуть уверенность или неуверенность в какой-либо информации, поэтому он очень важен.

Примеры: несомненно, безусловно, конечно же, разумеется, допустим, вероятно, возможно, быть может.

Если убрать такое вводное слово, предложение не потеряет смысл, но его значение все же станет немного иным.

Сравните:

• Быть может, я зайду к тебе сегодня вечером.
• Я зайду к тебе сегодня вечером.

В первом случае остается неопределенность, во втором же предложение звучит утвердительно.

Если говорить о вводных словах, которые выражают уверенность, такая разница менее заметна. С ними утверждение становится более категоричным, но не приобретает других оттенков смысла.

• Задача будет трудной, но вы, конечно, справитесь!
• Безусловно, это самая короткая дорога к центру города.
• Эта сделка, без сомнений, положила начало его успешной карьере.

Не путайте с членами предложения:

Я поверил его словам (как?) безусловно и без малейших сомнений.

Дальше мы еще рассмотрим, как обозначаются вводные слова, а пока напоминаем: если можно поставить к слову вопрос, оно является членом предложения и не выделяется запятыми.

Эмоции, чувства и оценка происходящего

С помощью данной категории вводных слов говорящий выражает свое отношение к событиям, дает оценку. Такими словами можно обозначить радость, восторг, огорчение, ужас, чувство стыда, опасения и т. д.

Примеры: к всеобщей радости, к ужасу, к моему восторгу, к несчастью, к сожалению, неровен час, того и гляди.

Они характерны для прямой речи, поскольку отражают эмоции и чувства говорящего.

• К сожалению, я не смогу лично встретить вас на вокзале.
• Время, к удивлению, пролетело очень быстро — я не успел заскучать.

В художественной литературе эти же вводные слова могут использоваться и для того, чтобы рассказать о чувствах героя или его отношении к событиям.

• Катя, к своему стыду, не знала значения этого слова и не поняла, о чем идет речь.
• Артист выходил на бис и, к восторгу зрителей, исполнил все хиты.

Не путайте с членами предложения:

(К чему?) К восторгу зрителей примешивалась доля разочарования от того, что любимый хит так и не прозвучал.

Обыденность, обычность происходящего

Довольно малочисленная категория вводных слов, в которой большую часть составляют разговорные выражения. Они не только позволяют указать на обыденный характер событий, но и оживляют текст, придают ему колорит.

Примеры: бывало, как обычно, случалось, как правило, по обычаю, по обыкновению, как всегда.

• Дед Семен отворил калитку и, по старому обычаю, наклонился к лохматой Жучке.
• После прогулки в парке мы, как обычно, зашли на чашку чая в кафе.

Не путайте с членами предложения:

Не принимая церковной реформы, община продолжала жить (как?) по старому обычаю.

Вводные слова, указывающие на источник сообщения

Основная задача вводных слов этого типа — указать на авторство, отослать к источнику информации или придать высказыванию некую авторитетность. Они типичны для новостных сообщений, обзоров, статей в СМИ и являются частью публицистического стиля, хотя используются не только в его рамках.

Примеры: по мнению экспертов, по оценке ученых, по словам премьер-министра, по сообщению корреспондента, на мой взгляд.

• Около 97% всей воды на нашей планете, по оценкам ученых, содержится в Мировом океане.
• По словам вице-премьера, рост экономики продолжится и в следующем году.

Кроме того, такие вводные слова помогают передать прямую речь, не прибегая к точному цитированию.

• Иван Иванович сказал: «Наш завод в прошлом квартале перевыполнил план на 5%».
• По словам Ивана Ивановича, завод перевыполнил план в прошлом квартале на 5%.

Не путайте с членами предложения:

Не стоит делать далеко идущих выводов (по чему?) по оценкам экспертов, ситуация еще может измениться.

Связь мыслей и последовательность изложения

Этот вид вводных слов указывает на внутреннюю логику предложения, очередность или любую другую связь между событиями. Особенно часто он используется в учебниках и научных материалах, поскольку дает возможность упорядочить текст, выстроить причинно-следственную цепочку.

Примеры: следовательно, во-первых, во-вторых, соответственно, значит, с одной стороны, прежде всего, сверх того, наконец.

• У этих треугольников есть общая гипотенуза, следовательно, они равны.
• С одной стороны, Даше нравилось жить во Франции, но с другой — она все еще скучала по дому.

Не путайте с членами предложения:

Лист бумаги был разрисован только (где?) с одной стороны, а другая оставалась чистой.

Замечания о стиле речи, способе изложения мысли

Вводные слова из этой категории обычно используются для того, чтобы указать на особенности изложения или переформулировать мысль. Как и предыдущий вид, иногда они могут предварять собой некий вывод, но не указывают прямо на связь событий, а скорее помогают выразить ту же мысль через другие факты или в другом стиле.

Примеры: иными словами, мягко говоря, точнее выражаясь, с позволения сказать, собственно говоря, короче, словом.

• Дети начали скучать и поглядывать в телефоны, иными словами, фильм был не слишком интересным.
• Это, с позволения сказать, вовсе не яшма — камень слишком быстро нагревается в руках.

Не путайте с членами предложения:

(Чем?) Иными словами можно ранить не хуже, чем кинжалом.

Вводные слова, привлекающие внимание собеседника

Слова-маркеры, с помощью которых можно обратить внимание слушателя на ту или иную часть высказывания, подчеркнуть главную мысль. Очень часто они стоят в начале предложения, но могут встречаться и в середине, а вот в конце бывают крайне редко.

Примеры: послушайте, вообразите, подчеркиваю, поверишь ли, видите ли, заметьте, что существенно, что еще важнее.

• Заметьте, никто не ушел из аудитории, хотя преподаватель опаздывал уже на полчаса.
• На этом совещании мы смогли подвести итоги и, что существенно, наметить план на следующий год.

Не путайте с членами предложения:

Марина всегда собирала портфель с вечера, что (как?) существенно экономило ей время утром.

Конечно, все вводные слова, какие есть, перечислить почти невозможно, но мы составили краткую шпаргалку — таблицу с примерами предложений.

Значение	Вводные слова	Примеры
Степень уверенности, допущения, предположения	Несомненно, однозначно, может статься, конечно, разумеется, быть может, допустим, возможно и т. д.	Возможно, наш отдел подключится к этому проекту в следующем месяце. Катя, конечно, самая лучшая ученица в классе.
Эмоции, чувства и оценка происходящего	К счастью, к удивлению, к моему стыду, на беду, неровен час, на радость, к сожалению, не дай бог, слава богам и т. д.	Погода испортилась и, неровен час, в наш город тоже придут дожди. Маша быстро нашла ошибку в задаче и, к счастью, успела ее исправить.
Обозначение источника информации	По мнению ученых, по сообщению прессы, говорят, по словам экспертов, по-моему, по-вашему и т. д.	Этим летом, говорят, в лесу будет много ягод. По мнению ученых, зеленый чай положительно влияет на нервную систему.
Указание на очередность событий или мыслей	Во-первых, следовательно, стало быть, напротив, наконец, в частности, в первую очередь, таким образом и т. д.	Катя мечтала о поездке, а Даша, напротив, хотела бы остаться дома. Зима будет суровой, стало быть, нужно задуматься об утеплении дома.
Привлечение внимания ко всему предложению или к его части	Понимаешь, знаете ли, гляди, послушайте, признайтесь, если хочешь знать, сделайте милость и т. д.	Послушайте, если он это сделал, значит у него были веские причины. Мы прождали его весь вечер, а он, видите ли, попросту забыл о встрече.
Указание на обыденность события или предмета разговора	Бывало, обыкновенно, случалось, как всегда, как правило, по обыкновению и т. д.	Я пришел на работу, как обычно, к восьми утра. Бывало, Иван опаздывал на последний автобус и шел пешком.
Замечания о стиле и характере речи, способе изложения мыслей	Мягко говоря, прямо говоря, одним словом, грубо выражаясь, иными словами, вернее сказать, что называется и т. д.	Ваш поступок, мягко говоря, выглядит бестактным и задевает окружающих. Мы живем в поселке вблизи Тулы, вернее сказать, в пригороде.

Учёба без слёз (бесплатный гайд для родителей)

Пошаговый гайд от Екатерины Мурашовой о том, как перестать делать уроки за ребёнка и выстроить здоровые отношения с учёбой.

Знаки препинания при вводных словах

Все вводные слова в русском языке выделяются знаками препинания, что хорошо видно в примерах из нашей таблицы. Этим они отличаются от таких же слов, которые выступают в качестве членов предложения и отвечают на некий вопрос. Помимо вопроса есть и другой способ понять, нужно ли ставить запятые или другие знаки препинания — попробуйте сдвинуть слово (словосочетание) в другую часть предложения.

• Как правило, Иван ест на завтрак овсяную кашу.
• Иван, как правило, ест на завтрак овсяную кашу.
• Иван ест на завтрак, как правило, овсяную кашу.

Смысл высказывания не изменился, конструкция хорошо смотрится в любой части предложения. Значит, это вводные слова и они выделяются запятыми.

Удивительно, как правило может оказаться таким запутанным и сложным для понимания.

В данном случае словосочетание «как правило» имеет жесткую синтаксическую связь с другими словами в предложении, его невозможно передвинуть без потери смысла. Значит, оно не является вводным. Можно проверить это предположение, разобрав его по составу, и мы выясним, что «правило» здесь выступает подлежащим.

Важно!

Если в сложносочиненном предложении с союзом «и» обе его части предваряет одно вставное слово, ставить запятую между этими частями не требуется.

• Видимо, урок еще не начался и дети по-прежнем шумели за дверью.
• К счастью, дождь уже прекратился и я совсем не промок по дороге домой.
• Вчера я видел этот документ, следовательно, он лежал на столе и Николай не мог забрать его.

Как еще выделяется вводное слово в предложении, кроме запятых? Иногда перед ним можно поставить тире, но это относится скорее к авторской пунктуации, которая нужна, чтобы создать особую ритмику текста или передать интонацию.

• Я понял, что забыл паспорт и очень испугался — неровен час, придется поворачивать обратно.
• Сергей был раздосадован — видите ли, он рассчитывал получить повышение уже в этом месяце.

Вводные слова и вставные конструкции

Вставные конструкции и вставные предложения отличаются от вводных слов тем, что являются автономной частью предложения и содержат завершенную мысль. Они могут выступать в качестве попутных замечаний, указаний, авторских разъяснений по отношению к главному предложению, а иногда и вовсе имеют с ним слабую синтаксическую связь.

Чтобы было понятнее, чем различаются вводные слова и вставные конструкции, мы составили небольшую таблицу.

Вводные слова	Вставные конструкции
Июль, говорят, будет теплым и солнечным.	Июль, я так думаю, будет теплым и солнечным.
Алексей, конечно, уже знал, как правильно оседлать лошадь.	Алексей, мы были уверены в этом, уже знал, как правильно оседлать лошадь.
Перстень лежал на видном месте и, безусловно, привлекал внимание.	Перстень лежал на видном месте, и — как читатель уже догадался — привлекал внимание.

Несложно заметить, что вставные конструкции, в отличие от вводных слов, имеют свое подлежащее и сказуемое. Очень часто их можно оформить в качестве отдельного предложения.

Короткие вставные конструкции могут выделяться запятыми, а более длинные часто обособляются скобками или тире. Впрочем, это зависит не столько от длины конструкции, сколько от авторского замысла. Поставить вместо запятой тире или скобки в большинстве случаев не будет ошибкой.

• Несколько ребят — их было около десятка — свернули с тропинки, чтобы полакомиться малиной.
• По улице прогрохотал старый трамвай (такие давно уже были сняты с производства) и не спеша скрылся за поворотом.
• Как-то раз — Коля и Витя надолго запомнили этот день — папа отвез всю семью на рыбалку в соседнюю область.

Обычно при выборе между запятыми, скобками и тире руководствуются следующим: если вставная конструкция имеет слабые синтаксические связи с предложением или не имеет их вовсе, лучше заключить ее в скобки.

Иногда вставное предложение ради усиления экспрессии заканчивается восклицательным или вопросительным знаком. В этом случае его можно выделить исключительно скобками или тире.

Прошлой весной — это было настоящее чудо! — старая яблоня вдруг снова покрылась цветами.

Важно!

Если вставная конструкция заканчивается восклицательным или вопросительным знаком, после этого предложение нужно продолжить со строчной буквы.

Интересно, что и вводные слова иногда могут выделяться таким же образом. Как правило, это встречается в художественной литературе и является одним из способов подчеркнуть эмоции, выразить чувства автора или героя.

• Катя осторожно зашла в темную комнату и — о ужас! — заметила, как штора слегка качнулась сама собой.
• И вскоре (чудное дело!) Петя настолько полюбил математику, что прорешал все задачи за следующую четверть.

Здесь мы имеем дело со вводными словами, которые могли бы выделяться запятыми, но ради усиления эмоциональной окраски текста представлены в виде вставных предложений с восклицательным знаком. Их с равным успехом можно обособить скобками или тире.

Вот мы и разобрались с такой обширной темой, как вводные слова в русском языке, а чтобы закрепить знания, рекомендуем напоследок пробежаться глазами по таблицам и спискам.

A+Click Вопросы для 6 класса

Какова сумма 200, 300, 150 и 250?

Что можно добавить к 7.44, чтобы получилось 8?

Какой остаток получится при делении 90 на 7?

Сколько будет 38 разделить на 20?

Какой набор десятичных знаков идет по порядку, от меньшего к большему?

Какая дробь равна десяти двенадцатым?

Какой набор дробей в порядке от наименьшей к наибольшей?

Представьте себе стену из 24 кирпичей. Три кирпича окрашены в белый цвет. Который . . .

Какое из этих выражений дает наименьшее значение?

Is -99 + 88 – 77 + 66 – 55 + 44 – 33 + 22 – 11 + 0 + 11 x 5 отрицательный или . . .

Что дает наибольший ответ?

Каково отношение количества зеленых дисков к общему количеству . . .

Если для посадки 1 квадратного метра требуется 1 грамм семян травы, сколько семян травы . . .

Что дает наибольший ответ?

Что дает наибольший ответ?

Не пользуйтесь калькулятором. Что из следующего дает наибольший результат?

Найдите сумму целых чисел от -2009 до +2011 включительно.

Разделите 132 доллара в соотношении 1:2:3. Какая самая большая часть?

Что из следующего дает наибольшее значение?

В чем разница между самым большим и самым маленьким из возможных . . .

Найдите сумму всех этих чисел.

Какая часть клавиш пианино белая?

Майк купил 57 драже. Какое утверждение является правильным?

Сердце Джона бьется с частотой 80 ударов в минуту в состоянии покоя. Ставка удваивается. . .

Произведение 12,34 x 43,21 приблизительно равно

Каждый из четырех детей выбрал одно из следующих чисел: 1, 2, 3, 4. Они . . .

4 сентября 1781 года полное название Лос-Анджелеса было Эль-Пуэбло-де-Нуэстра. . .

Какое число находится посередине между 1/4 и 1/8?

У Джона есть iPad с разрешением 1024 x 768 пикселей. Он считает, что его. . .

Джон занял пятое место сверху и шестнадцатое снизу после теста. . . .

Что верно?

Какое наименьшее целое пятизначное число состоит из пяти разных цифр?

Округлите сумму 375 и 785 до ближайших 100.

Какое число составляет половину одной четверти одной восьмой от 192?

Какое число, разделенное на 11, равно этому числу минус 11?

Каждую минуту девочка может сыграть 77 нот. Сколько нот она может сыграть за 7. . .

Какое самое большое десятизначное число, две цифры которого совпадают?

Какой остаток получится, если 111 разделить на 7?

Сколько 138 разделить на 20?

Какой набор десятичных знаков идет по порядку, от меньшего к большему?

Какое из этих выражений дает наименьшее значение?

Is -99 + 88 – 77 + 66 – 55 + 44 – 33 + 22 – 11 + 0 x 11111 отрицательный или . . .

Каково отношение количества дисков к общему количеству штук?

Каково отношение количества квадратов к общему количеству штук?

Что дает больший ответ?

Чему равно 0,06, умноженное на 2000?

Джесс умножила число само на себя и получила 441. Какое это было число?

Сколько составляет три четверти от 220 долларов?

Какое из этих выражений дает наименьшее значение?

Выберите наиболее подходящий ответ для роста Джона:

Какое наименьшее целое число в 3 раза больше суммы своих цифр?

Анна купила 28 драже. Какое утверждение является правильным?

У Энн 777 долларов, а у Билла 1111 долларов. Сколько денег Билл должен дать . . .

Какой буквы нет в этом вопросе?

Анна принесла 30 конфет, а Билл 12 конфет. Там . . .

Сколько шестизначных чисел вы можете составить?

На числовой прямой какое из этих чисел будет самым дальним справа?

Сколько стоит 33,3–3,33 доллара?

Какое число не может быть результатом умножения целого числа на 3?

Сумма всех нечетных чисел от 0 до 22 равна

Двенадцать обезьян съедали по 10 бананов каждый день в течение трех недель. Как много . . .

Сколько существует чисел, которые без остатка делятся на 8 без остатка?

Найдите минимальное значение 1 ? 2 ? 3 ? 4 ? 5 ? 6 ? 7 ? 8 ? 9, где каждый. . .

Если произведение 9 целых чисел положительное, то самое большое количество целых чисел может . . .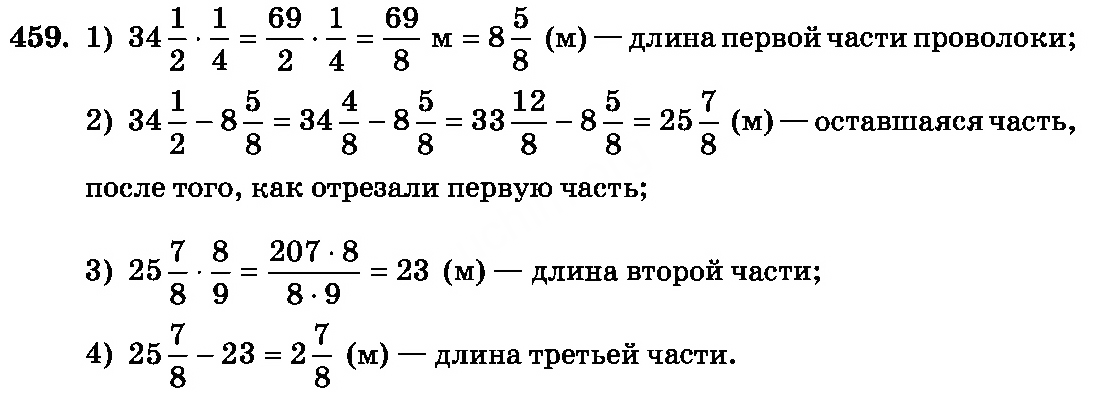

(66 х 6 + 6 х 66 + 6 – 6 х 66) / 6 – 6 = ?

А 9Парковка на 99 мест разделена на 3-х цветные секции. Есть 321 место. . .

Выразите 0,56 в виде уменьшенной дроби. (Сокращенная дробь — это дробь, в которой…

Чему равно произведение всех целых чисел от -99 до 99?

Какой математический символ нужно поставить в пропуске, чтобы сделать утверждение…

следующее, которое больше 2/3 ?

Какое целое число нельзя записать как сумму последовательных целых…0003

Сколько кубиков?

Один килограмм равен примерно 2,2 фунта. Какой вес в фунтах у собаки 55 кг?

Это красивое мозаичное изображение испанского города Ронда. Это 21. . .

999 разделить на 3 равно 9 умножить на X. Найти X.

Какая фигура ближе к (0, 0)?

Упростите выражение.

Капитан видит айсберг высотой 80 метров над уровнем воды. Только . . .

Оценка 3 ¹ 2 ² 1 ³ = ?

Общая стоимость поездки на Веселой Машинке для 4 взрослых и 5 детей составляет 39 долларов США. . . .

Какое наименьшее целое число в 4 раза больше суммы своих цифр?

Какое наименьшее натуральное число n такое, что 1 x 2 x . . . x n > 999

Что равно 999?

Произведение трех различных натуральных чисел равно 10. Какова их сумма?

Какая упорядоченная пара находится внутри треугольника?

Высота кубического аквариума Анны 52 см. Анна в два с половиной раза больше. . .

Какая точка на числовой прямой ближе всего к нулю?

Оценка 1 ³ 2 ³ 3 ³ = ?

У Анны в среднем 80 баллов по 4 различным тестам. Если самый низкий балл. . .

Красная и зеленая фигуры — две части, образующие синюю фигуру. Громкость . . .

Если к секретному числу добавить 22, результат будет в три раза больше, чем . . .

Жили-были три поросенка. Свинья построила дом из кирпичей. . . .

Число 12345 делится без остатка на указанные ниже числа, кроме . .

У шимпанзе 32 зуба, которые очень похожи на зубы человека, которых никогда не бывает. . .

Какое число, умноженное на 5, составляет четыре пятых от 250?

Восемнадцать студентов собираются на пикник. В каждой машине могут кататься четверо детей. . . .

Двадцать больше, чем число равно 11. Что это за число?

Какой самый большой делитель числа 12345 ? Факторы положительного целого числа . . .

У Джерри 24 метра забора. Длина сада в два раза больше его ширины. . . .

Есть 12 участников. Если бы одна четверть бегунов была быстрее . . .

В подвале 29 бочек. Сколько из них больших? Фотограф . . .

Половина — это четверть. Сколько это стоит?

Найдите A.

Джерри обменял 20-долларовую купюру на равное количество пятицентовиков, десятицентовиков и четвертаков. . . .

Резервуар имеет ширину 70 см, длину 70 см и высоту 50 см. Толщина стенки составляет . . .

Укажите наибольшую площадь.

Укажите наибольшую площадь.

Симметричную фигуру можно сложить пополам, и обе стороны точно совпадут. . . .

Деревянный куб со стороной 10 см. Какое наибольшее количество . . .

Какова площадь закрашенной фигуры?

На рисунке каждое число представляет длину ближайшего сегмента. Все . . .

На рисунке изображен пятиугольник и его внешние углы. Найдите сумму . . .

Какая из этих фигур имеет наименьшую площадь?

Какое общее количество линий симметрии можно провести на фигуре?

На сетке есть две точки A и B. Мы хотим нанести еще две точки. . .

Какова площадь многоугольника в квадратных единицах?

Какая фигура имеет только одну пару параллельных сторон?

Подземная труба отводит воду из дома. Труба должна упасть 11 . . .

Является ли пунктирная линия линией симметрии?

Найдите две одинаковые фигуры.

Какая фигура имеет 3 оси симметрии?

Анна и Боб играют в крестики-нолики на своем игровом поле. На картинке показано. . .

Какая фигура имеет наибольший периметр?

Если вы посмотрите на этот объект спереди, что вы увидите?

Периметр звезды равен периметру правильного шестиугольника. . . .

Прямоугольная поздравительная открытка площадью 330 см ² . Одна сторона . . .

Члены Зеленого теннисного клуба делают логотип. Логотип клуба синего цвета. . .

Как добраться из пункта А в пункт Б? Помните, что может быть более одного правильного . . .

Какой угол больше прямого?

Два треугольника образуют параллелограмм площадью 100 квадратных метров. Что такое . . .

Какова приблизительная мера этого угла в градусах?

Увеличим высоту фотографии до 22,5 см при сохранении размера . . .

Анна обматывает подарок лентой. Ей также нужно еще 34 сантиметра (см) . . .

Каков периметр заштрихованной фигуры?

Кварталы на Стейт-стрит имеют одинаковую длину. Какое расстояние. . .

Какую новую фигуру можно составить из этих треугольников?

Какие две дороги на этой карте кажутся параллельными?

Куб 7x7x7 раскрашивается, а затем разрезается на кубики 1x1x1. Сколько таких. . .

Какие отрезки равны?

Какое максимальное количество ящиков размером 0,3 м х 0,2 м х 1 м может быть . . .

Для какой буквы я использовал наименьшее количество зеленой краски?

Какая дуга выходит из большего круга?

Выберите фигуру с наибольшим периметром.

Показанная башня состоит из кубов, поставленных друг на друга. Некоторые из . . .

В сетке 3 x 3 есть 8 линий, содержащих не менее 3 точек. Как много . . .

Сколько треугольников?

Сколько различных прямых можно провести через точки C, D, E и F, равные . . .

Какая площадь самая маленькая?

Сколько на рисунке квадратов любого размера?

Какая из этих частей имеет наименьшую площадь?

Сколько различных линий можно провести через эти пять точек?

На рисунке показан правильный многоугольник. Какая прямая параллельна прямой АВ?

Удаление какого квадрата приводит к увеличению периметра этой фигуры?

Линия имеет толщину 0,25 миллиметра и длину 8 километров. В какой области находится . . .

Что из следующего может быть графиком, показывающим периметр Y квадрата? . .

Джон съел часть пиццы, а другую часть отдал своим друзьям Джиму и . . .

Оцените, во сколько раз красная область больше синей.

Я вырезал треугольник из квадратного куска картона, как показано на рисунке. . . .

У какой фигуры все стороны одинаковой длины?

Какие две фигуры имеют наибольшую общую площадь?

Сколько осей симметрии у фигуры?

Найдите вид сверху на фигуру.

Какой прямоугольник имеет наименьшую площадь?

Игра Морской бой (Морской бой или Морской бой) — это игра-угадайка, в которую играют . . .

Найдите пару бусин, расстояние между которыми точно равно длине . . .

Какая точка ближе всего к линии AB?

Какая фигура имеет наименьший периметр?

Во сколько раз больше площади буквы Т площадь квадрата?

Какая точка ближе всего к точке А?

Для какого рисунка я использовал больше всего чернил?

Какая фигура имеет наименьшую площадь?

Какие две детали идеально сочетаются друг с другом, образуя ту же форму, что и . . .

Я использую красную и желтую плитки, чтобы сделать узор, показанный справа. Если я . . .

Я начертил мелом прямую линию на шахматной доске 8×8. Какой самый большой. . .

Я провожу линию через каждую пару вершин квадрата. Во сколько. . .

Сколько линий можно провести через эти шесть точек? Каждая линия должна пройти. . .

Размеры чертежей ISO (мировой стандарт) составляют 841 x 1189 миллиметров для бумаги формата A0. . .

Если я сложу квадратный лист бумаги по вертикали, новый прямоугольник будет иметь площадь 32 кв. . .

Сколько заглавных букв выглядят одинаково при повороте на 180 градусов? Запомнить, . . .

Россия имеет площадь 17 075 200 квадратных километров. Канада имеет площадь . . .

Буква «А» симметрична. Симметричную фигуру можно сложить пополам и . . .

Какой отрезок имеет длину 9 единиц?

Какая фигура имеет наименьший угол?

Какая из этих фигур имеет наибольшую площадь?

Какая фигура имеет 4 оси симметрии?

Анна и Боб играют в крестики-нолики на своем игровом поле. На картинке показано. . .

Периметр звезды равен периметру правильного шестиугольника. . . .

Какой отрезок линии самый маленький?

Тим расширяет свой гараж прямоугольной формы. Гараж 5 метров в ширину и 7 . . .

Сколько маленьких треугольников потребуется, чтобы покрыть трапецию?

Какой угол наименьший?

На рисунке фигуры ABCDEF и UVWXYZ имеют одинаковую форму и размер. Который . . .

Какая фигура внизу имеет тот же периметр, что и фигура справа?

Сколько кубиков не видно?

Дети запустили 20 воздушных шаров. Они нашли 20 воздушных шаров. На схеме показано. . .

Дети запустили 20 воздушных шаров. На схеме показано, где были воздушные шары. . .

Пятиугольник (от пенте, что в переводе с греческого означает число 5) — это любой пятиугольник . . .

Шестиугольник (от греческого hex, означающего число 6) — это любой шестиугольник. . . .

Сколько букв в слове МАТЕМАТИКА имеют только одну линию симметрии?

Сколько кубиков со стороной 0,3 может поместиться в коробке?

Все углы прямые, а длины сторон указаны в милях в формате . . .

Найдите недостающую деталь.

Квадраты 1, 2 и 3 имеют длину сторон 1, 2 и 3 единицы соответственно. . . .

Сколько маленьких кубиков было использовано для построения этой объемной фигуры?

Каково минимальное количество прямых линий, чтобы нарисовать два квадрата?

Что верно?

Сколько раз могут пересекаться два равных шестиугольника?

Какова площадь квадратов (каждое деление на графике соответствует 1 миле)?

Оцените соотношение площадей двух частей.

Сколько здесь квадратов?

Найдите сумму углов.

Сколько маленьких квадратиков нужно, чтобы полностью покрыть поверхность грина. . .

Можем ли мы использовать каждую из четырех маленьких фигур слева ровно один раз, чтобы сделать . . .

На каком расстоянии отмеченная точка от конца шкалы?

Владелец магазина устанавливает камеру наблюдения на потолке своего магазина. Камера . . .

16 составляет 40% от какого числа?

Найдите среднее значение для следующего набора данных 70 88 97 99 100 101 103 110 112 . . .

Что дает наибольший ответ?

123 сколько процентов от 12345?

Найдите наилучшее приближение для: 717 x 114

Найдите наилучшее приближение

Оцените

В банке 24 конфеты. Прикинь, сколько будет конфет. . .

Какая часть квадрата закрашена?

Алекс подбросит монетку 33 раза. Сколько раз Алекс должен получить . . .

В местной школе ученики продавали открытки для сбора средств. Гистограмма. . .

Чтобы получить пятерку, учащиеся должны набрать не менее 90% итогового теста. . . .

В какой набор следует поместить 144?

Эта диаграмма Венна состоит из двух равных окружностей. Они пересекаются, образуя 3 части. . . .

Какой процент ниже показывает наиболее вероятный процент выпадения решки в . . .

Саша не глядя достает из коробки два мяча. Из какой коробки. . .

Чем отличаются суммы чисел в шестом и третьем рядах?

Сколько кирпичей в этих стенах?

Алекс начинает с числа 99 и считает до 66. В результате получается последовательность 99, . . .

Какая самая крупная почтовая оплата в Швейцарии не может быть оплачена точно любым числом? . .

График показывает общую сумму денег, которую Джон сэкономил за пять недель. . . .

Мы разрезаем 2000-граммовую пачку сливочного масла пополам. Затем разрезаем одну из половинок на . . .

400 это 40% от какого числа?

Что дает наименьший ответ?

В седьмом классе 48 учеников. На каждого приходится семь мальчиков. . .

Какой из них дает самый большой ответ?

Насколько быстрее движется секундная стрелка по сравнению с часовой?

Что получится, если четыре раза прибавить 4 к 44?

Заказывайте формы по весу от самой легкой до самой тяжелой.

Сколько таблеток мне нужно, если мой врач сказал мне принимать по одной каждые полчаса с . . .

Сколько таблеток мне нужно, если мой врач сказал мне принимать по одной каждые 9 минут с . . .

На карте показана сеть платных дорог с ценами на каждую часть дороги. . . .

Класс миссис Смит досчитал до 6. Каждый ученик назвал одно число. Как много . . .

Если Анна продолжит нанизывать бусины так, как показано на рисунке . . .

Сколько шагов в кратчайшем пути из A в N?

Если диаметр пера 8 мм, оцените высоту башни.

Счет — это общее количество точек , которые я вижу на двух не соприкасающихся кубиках . . .

Из 150 учащихся 87 девочек. Какую часть учащихся составляют мальчики?

Круговая диаграмма показывает количество мужчин, женщин и детей в округе. Какая часть . . .

Найдите сумму чисел.

Какая следующая строка в этом шаблоне? Это Треугольник Паскаля.

Лесли Грин спрашивает: quot;Генриетта нанизывает последнюю бусину на ожерелье. . .

Сколько рейсов по расписанию отправляется с 10:00 до 10:30 (включительно)?

Джон ведет автобус с 64 пассажирами. На каждой остановке половина пассажиров. . .

Сколько точек на трех стандартных кубиках?

Какая буква является частью другой?

Джейн считает вслух в обратном порядке от 99 до шести, говоря 99, 93, … и так далее. . . .

У Дэна есть 75 яиц, которые нужно упаковать в коробки. В каждую коробку помещается 6 яиц. Сколько ящиков. . .

У ученика есть 2 рубашки (черно-белая), 2 штана (черно-белая) и 2 . . .

С какого числа мы начали?

В классе 20 учеников. 12 студентов имеют красную звезду и 8 студентов. . .

Том пишет сорок слов на пяти пустых карточках. Он пишет девять слов. . .

Джон прочитал 308-страничную книгу за 2 недели. Он читал каждый день, включая выходные. . . .

У Стива есть три куртки, три пары носков и три рубашки, которые можно надеть . . .

Джим готовится к гонке. Он использует эту карту, чтобы найти возможные маршруты. Маршрут . . .

На диаграмме показаны некоторые результаты конкурса из шести человек. Стрелка . . .

Какое правило используется для машины In-Out? Помните, что их может быть больше, чем . . .

Дэвид построил стеллаж из 8 банок. Сколько банок он сделал. . .

Високосный год (или добавочный год) — это год, содержащий один дополнительный день. . . .

У Брэда столько же братьев, сколько и сестер. На сколько больше братьев, чем сестер. . .

Китайский календарь основан на двенадцатилетнем цикле. Каждый год в цикле. . .

Какое число, разделенное на 2001, равно числу, умноженному на 2001?

Какое наименьшее целое число можно записать полностью нулями и единицами? . .

Какова максимально возможная сумма цифр на цифровых часах между . . .

Если я расставлю числа от 1 до 6 на гранях каждой из 4 игральных костей так, что сумма . . .

Я умножаю три положительных целых числа, которые больше 1, и получаю 333. Найти . . .

X — целое число. X + 6 больше 33 X – 6 меньше 22 Найдите . . .

С наличными в кармане миссис Смит может позволить себе мороженое. . .

Возраст Юджинии сегодня в 6 раз больше, чем 10 лет назад. Сколько ей лет сегодня?

Если трое из каждых 150 космонавтов НЕ женаты, то какой процент от всех . . .

Умножьте наибольшее трехзначное число на наименьшее трехзначное число и . . .

Я хочу разделить все золотые кольца. Какое самое маленькое число. . .

Каждая коробка помечена неправильно. Я хочу, чтобы коробки были помечены правильно. . . .

В первой стопке 5 монет, во второй — 8, в третьей — 11 и 16 . . .

Сколько различных наборов из двух целых положительных чисел составляет в сумме число 33?

Сколько шагов требуется, чтобы разбить плитку швейцарского шоколада на кусочки 1 x 1? . . .

Головоломка с хитрым уравнением: приведенное ниже уравнение неверно: 102 — 99 = 1 Какой . . .

Куб состоит из маленьких черных и белых кубиков. Черное лицо всегда трогает. . .

Римские цифры — это система счисления Древнего Рима, основанная на буквах . . .

Сколькими способами можно выбрать 4 последовательных числа из первых 8 положительных . . .

Максимальный вес лифта 800 кг. Какое утверждение абсолютно. . .

Какую фигуру нужно поставить на пустое место?

Найдите среднее шести самых больших чисел в таблице.

На семейном фото я вижу 1 бабушку, 1 дедушку, 2 пап, 2 мам, 2 . . .

Треугольник Паскаля. Какого числа не хватает?

Стакан вмещает 180 мл сока, когда он пуст на четверть. Сколько это . . .

В поездке 12 детей и 2 взрослых на лодке. Если всего 98 . . .

В поездке 9 детей и 2 взрослых на лодке. Если всего 99 . . .

Джим Смит выпивает волшебное зелье, которое уменьшает его вес вдвое. Он был . . .

Джон работает с девяти утра до половины седьмого вечера. . . .

Для какой буквы я использовал наименьшее количество краски?

Римские цифры — система счисления Древнего Рима, основанная на буквах . . .

Римские цифры — система счисления Древнего Рима, основанная на буквах . . .

Сколько двузначных чисел не содержат нуля?

Анна читает в среднем три книги в месяц. Она делает перерыв и делает. . .

Пятиклассник продал 111 билетов на концерт своего класса. Стоимость каждого билета. . .

Бобу ровно 499 месяцев. Сколько ему лет?

У Джона готовы три штаны, три пары носков, три шапки и три рубашки . . .

Джим готовится к гонке. Он использует эту карту, чтобы найти возможные маршруты. Он выбирает. . .

Для школьного представления 880 стульев расставлены поровну в 44 ряда. Как много . . .

В коробке 22 яблока. Сколько яблок в 21 коробке?

Площадь первой страницы книги составляет 600 квадратных сантиметров. Что это . . .

Анна хочет заработать ровно 44 очка. Утки дают разные очки. Как . . .

Евгении 9 лет. Какое наибольшее количество дней рождения она может . . .

Страницы книги последовательно пронумерованы от 1 до 999. Сколько . . .

У каждого ребенка в семье не менее 2 братьев и 3 сестер. Что это . . .

Какая буква стоит перед О?

Если я удалю букву в слове, то останется только одна. Найдите слово.

Пять показанных звеньев цепи должны быть соединены в длинную цепь. Как много . . .

Отец сына сестры моего отца —

Банни Бенни начинает прыгать из дыры. На каждые 10 требуется шесть секунд. . .

Каждый из 20 рыцарей Круглого стола чокнулся с рыцарями на . . .

Какой из четырех рисунков меньше всего похож на остальные три?

Круглый сад Джерри имеет диаметр 1200 м и не имеет забора. Как далеко может . . .

После двухмесячного курса тенниса трое друзей зафиксировали потерю веса. . . .

Джерри и Джейн провели неделю на острове и питались только кокосами. Джерри. . .

В каком месяце этого года приходится 111 ^-й -й день?

Десять яблок распределены между Анной, Биллом, Синди и Дэном так, что все . . .

В чем разница между долларом и двадцатью пятью центами? 1 доллар = . . .

Пятнадцать школьников приняли участие в олимпиаде по математике. Количество детей, которые. . .

Щенок спит в общей сложности 100 часов в неделю из 7 дней. Обычно он спит 1 . . .

Анна, Билл и Купер — друзья. Если следующие утверждения все . . .

Если у Джейн восемь десятицентовиков, а у Джерри такая же сумма в пятицентовых монетах, сколько . . .

Джерри купил кролика Бенни за 9 долларов, продал его за 10 долларов, выкупил обратно за 11 долларов, затем . . .

Джо, Джим и Джон купили большую плитку шоколада. Джо разрезал его на 6 равных частей. . .

Каждый мальчик получает по 2 подарка, а каждая девочка получает вдвое больше подарков, чем мальчик. . . .

Каждый четный день Джон съедает 2 груши. Он съедает по 3 яблока на каждом . . .

На острове дети всегда говорят правду, а взрослые всегда лгут. Какой из . . .

В магазине стоимость двух батончиков с хлопьями и трех маленьких бутылочек молока составляет 5,50 . . .

Количество часов, оставшихся сегодня, составляет половину количества уже пройденных часов. . . .

На рисунке показана схема пола гостиной. Стены затемнены. . . .

Мы хотим купить 120 кг картофеля. Какая покупка лучше?

Британский фунт равен 1,52 доллара США. Сколько долларов вы бы. . .

Первоначальная цена зонта составляла 16 долларов. Какова была цена зонта. . .

Энн пошла в кино. Фильм начался в 11:55 утра. и длился 117 минут. . . .

В 11:30 Алекс начал красить забор. К полудню он нарисовал это. . .

Бабушка Бена попросила его пойти в магазин и купить не менее 1000 граммов . . .

Большой счетчик (круг) показывает секунды. Меньший счетчик (круг) показывает . . .

Десять процентов от счета за электроэнергию в размере 32 долларов США составляют налог. Сколько стоит налог?

Дюжина воздушных шаров стоит 48 центов. Сколько воздушных шаров стоит 1 доллар?

Фермер обычно продает овец по 200 долларов за штуку. Этой зимой фермер. . .

Три мальчика положили 4, 5 и 6 долларов в копилку. Как они могут разделить деньги. . .

Расстояние между двумя буями может составлять от 8 до 10 метров, даже . . .

Два велосипедиста мчатся по кольцевой трассе. Первый может ездить по трассе в . . .

Боксерский ринг имеет длину 6 метров с каждой стороны между канатами. Как . . .

Окружная больница с гордостью сообщает: «Каждые 20 минут рождается новый ребенок, 24…

Амеба — бесформенный одноклеточный организм. Амеба размножается простым… 0,45 кг Сколько весит…

Джим счастлив этим вечером Сколько минут до полуночи, как ты считаешь?

Берлин +6 ^o C. Лондон +3 ^o C. Москва . . .

Какой набор корзин самый дешевый?

У мистера Джонсона большой участок земли, как показано здесь. Он разделил землю. . .

В копилке Джона было 89 долларов. Он добавил 32 доллара. Как он мог разделить деньги. . .

У команды есть 105 долларов на покупку мячей. Один мяч стоит 8 долларов. Команда получает каждый шестой. . .

В 11:00 Алекс начал красить забор. К полудню он нарисовал это. . .

Сколько четвертаков в 7 с половиной долларах?

Том проехал на своей машине 150 километров за 4 часа. Он продолжал ездить на двойке. . .

Какое наибольшее количество кусков пиццы я могу получить, сделав три . . .

Что из следующего равно 3 четвертям миллиона долларов?

На сколько больше домов прямо, чем слева?

Найти W.

Страус бежит со средней скоростью 40 миль в час в течение 12 минут. Насколько это далеко? ПС: миль/ч. . .

Сколько минут осталось до полуночи?

Если Джейн выпивает стакан молока во время каждого школьного обеда, сколько молока выпивает . . .

Алекс и Билл лучшие друзья уже три года. Они планируют сохранить. . .

Если сумма возрастов Евгении и Ольги сейчас 44 года, какова будет сумма их . . .

Если ручка стоит 1,69 доллара, а карандаш — 0,79 доллара, что из следующего является . . .

Если у Джерри есть 5 долларов в десятицентовых монетах, а у Джейн такая же сумма в четвертаках, сколько . . .

Если в полночь в Лондоне идет дождь, каковы шансы, что через 72 года будет солнечно . . .

У Мартина 2000 купюр по 2000 чешских крон каждая. Насколько он богат, если 1 доллар равен . . .

У Джерри есть 1 пенни, 2 пятака и 3 десятицентовика. Сколько разных сумм денег. . .

Если я переведу все буквы в этом предложении в ВЕРХНИЙ РЕГИСТР, на каком языке . . .

Крупнейший номинал валюты, когда-либо напечатанный Бюро Гравюры. . .

Согласно . . .

Время — деньги Если одна минута стоит 0,5 доллара (50 центов), сколько стоит одна минута . . .

Бензин стоит 1,99 доллара за галлон. Сколько будет стоить Джерри заполнить его . . .

quot;бабушкина дюжинаquot; на один больше, чем на дюжину. Бабушка Джерри приготовила. . .

Рабочие листы по математике для 6-го класса

Рассчитывайте на наши распечатанные рабочие листы по математике для 6-го класса с ответами для тщательной практики. С нитями, взятыми из жизненно важных математических тем, таких как соотношение, умножение, деление, дроби, общие множители и кратные, рациональные числа, алгебраические выражения, целые числа, одношаговые уравнения, упорядоченные пары в четырех квадрантах и ​​навыки геометрии, такие как определение площади, площади поверхности , и объем, организация числовых данных в виде точечных диаграмм, гистограмм и коробчатых диаграмм, нахождение среднего значения, медианы и квартилей наборов данных, эти PDF-файлы станут вашим часто посещаемым местом. Получите билет к отличному началу с нашими бесплатными математическими таблицами для учащихся 6 класса!

All

Division

Ratio & Proportions

Fractions

Decimals

Factors & Multiples

Integers

Expressions & Equations

Coordinate Planes

Area & Perimeter

Nets of Solid Shapes

Volume & Surface Район

Статистика и вероятность

Исследуйте более 4600 рабочих листов по математике для шестого класса

Отдел | 4-значный на 2-значный и 3-значный

Разделите 4-значное число на 2-значное или 3-значное число, начиная с наибольшего разряда и деля до последней цифры, чтобы найти частное и остаток (если есть).

Рисование фигур для представления пропорций

Улучшите свои навыки пропорций с помощью наших рабочих листов по математике для 6-го класса в формате PDF. Предложите учащимся визуально представить термины каждого соотношения, нарисовав указанное количество фигур.

Умножение двух дробей путем перекрестного сокращения

Разложение числителя и знаменателя на простые множители, взаимное сокращение общих множителей и умножение несократимых частей дроби — все это должны делать учащиеся 6 класса!

Выражение десятичных знаков в словах | До миллионов

Позвольте своему пониманию десятичных разрядов достичь новых высот, когда вы погружаетесь в эти распечатанные математические листы для 6-го класса и выражаете десятичные дроби до миллионных в словах и наоборот.

Нахождение НОД двух чисел

Выполните пошаговый процесс нахождения НОД, перечислив все множители каждой пары двузначных чисел, затем сравните множители, определите общие и наибольшие среди них. это ваш ответ.

Представление целых чисел

Заложить прочную основу для работы с целыми числами становится легко, если в этих рабочих листах по математике для 6-го класса в формате pdf предлагается немного реального мира, где каждый сценарий должен быть представлен положительным или отрицательным целым числом.

Одношаговое уравнение: сложение и вычитание | Целые числа

Перестройте уравнение, сделав переменную подлежащей, и переведите целочисленную константу в другую сторону и измените ее знак, прибавьте или вычтите, чтобы найти значение неизвестной переменной.

Идентификация упорядоченных пар во всех квадрантах

Ознакомьтесь с координатной плоскостью, четырьмя квадрантами и упорядоченными парами. Определите точку, представляющую каждую упорядоченную пару в части A; и найдите и запишите координаты x-y каждой точки в части B.

Определение площади квадрата

Раздайте детям 6-го класса эти распечатанные листы по математике, если вы хотите попрактиковаться в определении площади квадрата. Попросите учащихся возвести в квадрат дробные длины сторон и вычислить площадь.

Традиционные единицы США

Метрические единицы

Идентификация сетей трехмерных фигур

Предложите учащимся 6-го класса представить, как складываются двухмерные сети, представленные в этом математическом листе для печати, вдоль краев, и визуализируйте трехмерные фигуры, которые можно построить из них.

Площадь поверхности с использованием сетей | Подсчет квадратов

Будь то уточнение или проверка навыков подсчета единичных квадратов для определения площади поверхности прямоугольных призм, кубов или треугольных призм по их сеткам, эти PDF-файлы служат цели.

Традиционные единицы США

Метрические единицы

Сводка по пяти числам

Описательно проанализируйте каждый набор данных, переставив значения в порядке возрастания и выяснив максимальное и минимальное значения, а также нижний или 1-й, медианный или 2-й и верхний или 3-й квартили.

Деление пятизначных чисел на однозначные и двузначные делители

Раздвиньте границы и отточите свои навыки деления, попрактиковавшись в этих упражнениях на деление пятизначных чисел на однозначные и двузначные делители.

Задачи на соотношение слов | Part-to-Part

Проверьте свои аналитические способности с помощью наших рабочих листов по математике для 6-го класса в формате PDF. Изучите данные, представленные на пиктограмме, и ответьте на ряд вопросов, определяющих соотношение частей к частям в каждом сценарии.

Традиционные единицы США

Метрические единицы

Умножение смешанных чисел и дробей

Легко умножайте смешанные числа и дроби путем преобразования смешанных чисел в неправильные дроби, взаимного сокращения общих множителей и последующего умножения того, что осталось.

Далее »

CMP3 6 класс — Подключенный математический проект

6-1 Prime Time

Понятия и пояснения | Примеры домашних заданий | Math Background

В Prime Time учащиеся изучат важные свойства целых чисел. Многие из этих свойств связаны с умножением и делением. Исследования помогут учащимся понять отношения между множителями, кратными, делителями и произведениями. Учащиеся также узнают, как распределительное свойство связывает умножение и сложение. Исследования в этом разделе помогут учащимся понять следующие идеи.

• Классифицировать числа как простые или составные
• Распознавать, в каких ситуациях требуются общие делители, общие кратные, наименьшее общее кратное или наибольший общий делитель
• Разработать стратегии поиска множителей и кратных, наименьших общих кратных и наибольших общих множителей
• Признать и использовать тот факт, что каждое целое число можно записать ровно одним способом в виде произведения простых чисел
• Использовать экспоненциальное представление для записи повторяющихся множителей
• Свяжите разложение двух чисел на простые множители с наименьшим общим кратным и наибольшим общим делителем двух чисел
• Признать, что распределительное свойство связывает мультипликативную и аддитивную структуры целых чисел
• Используйте свойства операций над числами, включая Распределительное свойство и соглашение о порядке операций, для записи эквивалентных числовых выражений
• Использование множителей и множителей для решения задач, объяснение некоторых числовых фактов из повседневной жизни

Когда ваш ребенок сталкивается с новой проблемой, полезно задать эти вопросы. В этом модуле вы можете задать такие вопросы, как:

• Поможет ли разбиение числа на множители решить задачу?
• Какие общие делители и общие кратные имеют числа?
• Что множители и кратные числа говорят мне о ситуации?
• Когда может быть полезно записать число в виде факторизованной формы или в виде суммы?

6-2 Сравнение деталей

Понятия и пояснения | Примеры выполненных домашних заданий | Справочная информация по математике

В задании «Сравнение кусочков и кусочков» ваш ребенок разовьет навыки использования дробей, десятичных знаков, отношений и процентов для измерения и сравнения величин.

Исследования в этом разделе помогут вам понять, как:

• Использовать язык соотношений и обозначения для сравнения величин
• Различать дроби как числа и отношения как сравнения
• Используйте различные стратегии масштабирования и разделения, чтобы рассуждать пропорционально
• Думайте о дробях и десятичных дробях как о положениях и расстояниях на числовой прямой
• Гибкое перемещение между дробными, десятичными и процентными представлениями
• Найдите абсолютные значения и противоположности и используйте их для описания величин реального мира
• Используйте дроби, десятичные числа и проценты для оценки чисел
• Используйте контекст, модели, рисунки или оценки, чтобы рассуждать о ситуациях
• Использовать эквивалентность дробей и отношений для решения задач
• Используйте таблицы тарифов и тарифы для решения задач

Пока ваш ребенок работает над задачами в этом разделе, задавайте себе вопросы о ситуациях, связанных с дробями, десятичными числами, отношениями и процентами.

• Какие модели или диаграммы могут быть полезны для понимания ситуации и отношений между величинами?
• Это сравнительная ситуация? Если да, то использую ли я отношения или вычитание?
• Какие стратегии можно использовать для поиска эквивалентных форм этих дробей, десятичных знаков, отношений или процентов?
• Какие стратегии можно использовать для сравнения или упорядочения набора дробей, десятичных знаков и процентов?
• Какие стратегии я могу использовать, чтобы рассуждать о числах больше или меньше 0?
• Как я могу использовать расценки за единицу или таблицу расценок для сравнения?

6-3 Давайте будем рациональными

Понятия и пояснения | Примеры домашних заданий | Математический фон

В задании Let’s Be Rational ваш ученик разовьет понимание четырех основных арифметических операций с дробями, включая смешанные числа. Они также описывают стратегии использования этих операций при решении задач с дробями.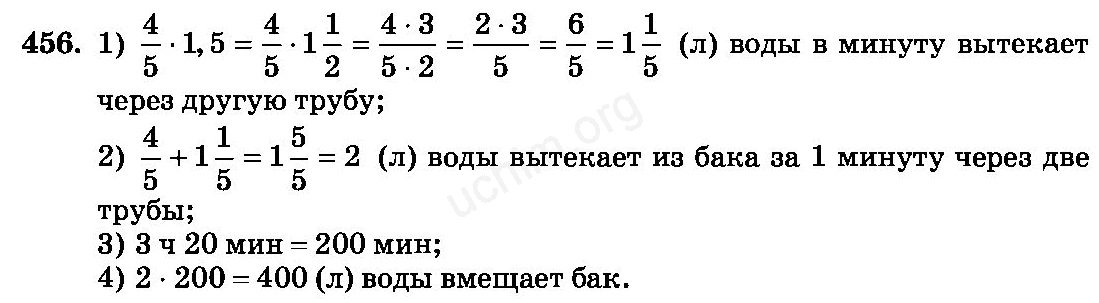

Ваш ребенок научится:

• Использовать ориентиры и другие стратегии для обоснованной оценки результатов операций с дробями, включая смешанные числа
• Разработка способов моделирования сумм, разностей, произведений и частных, включая использование площадей, полос дробей и числовых рядов
• Поиск правил для обобщения шаблонов в операциях с дробями
• Используйте свои знания о дробях, эквивалентности дробей и свойствах чисел для разработки алгоритмов сложения, вычитания, умножения и деления дробей
• Распознать, когда сложение, вычитание, умножение или деление являются подходящими операциями для решения задачи
• Напишите семейства фактов, чтобы показать обратную связь между сложением и вычитанием, а также между умножением и делением
• Решайте задачи, используя действия над дробями, включая смешанные числа
• Поиск значений переменных с помощью операций над дробями, включая смешанные числа

Когда ваш ребенок сталкивается с новой проблемой, рекомендуется задавать ему такие вопросы, как:

• Какие модели или диаграммы могут быть полезны для понимания проблемной ситуации и отношений между величинами?
• Какие модели или диаграммы могут помочь вам решить, какая операция полезна при решении проблемы?
• Какова разумная оценка ответа?

6-4 Покрытие и окружение

Понятия и пояснения | Примеры домашних заданий | Предпосылки к математике

В задании Покрытие и окружение ваш ученик будет исследовать площади и периметры фигур. Особое внимание уделяется четырехугольникам и треугольникам. Ваш ребенок также изучит площадь поверхности и объем прямоугольных призм. Расследования в этом подразделении помогут им

• Проанализируйте, что означает измерение площади и периметра
• Связать периметр с окружением фигуры и площадь с покрытием фигуры
• Разработка стратегий, процедур и формул, выраженных словами или символами, для нахождения площадей и периметров прямоугольников, параллелограммов и треугольников
• Исследовать отношения между периметром и площадью, включая то, что одно может меняться, а другое остается неизменным
• Проанализируйте, как площадь треугольника и площадь параллелограмма связаны с площадью прямоугольника
• Используйте сети, сделанные из прямоугольников и треугольников, для определения площади поверхности призм
• Найти объем прямоугольных призм с дробными длинами сторон
• Используйте периметр, площадь, площадь поверхности и объем для решения задач.

Когда ваш ребенок сталкивается с новой проблемой, рекомендуется задавать такие вопросы, как:

• Какие атрибуты формы важно измерять?
• Требуется точный ответ?
• Как узнать, задействована ли площадь или периметр фигуры?
• Что я ищу, когда нахожу площадь? Когда я найду периметр?
• Какие соотношения площади, периметра или того и другого помогут решить проблему?
• Как определить площадь поверхности призмы по сетке или трехмерному изображению призмы?
• Чем отличается площадь двумерной фигуры от площади поверхности призмы?

6-5 Decimal Ops

Понятия и пояснения | Примеры домашних заданий | Математический фон

В Decimal Ops ваш ученик научится понимать и использовать четыре операции (+, -, x, ÷,) над десятичными числами. Ваш ребенок также улучшит ваше понимание и навыки работы с процентами.

Ваш ученик научится:

• Складывать, вычитать, умножать и делить десятичные дроби
• Оценка результатов десятичных операций
• Знайте, когда использовать каждую операцию в ситуации с десятичными дробями
• Свяжите операции с десятичными дробями с задачами, связанными со скоростью единицы
• Используйте проценты для решения задач

Когда ваш ребенок сталкивается с новой задачей, полезно задать такие вопросы, как:

• Какие операции над десятичными числами или процентами помогут в решении этой задачи?
• Какие алгоритмы помогут с расчетами?
• Примерно сколько будет сумма, разность, произведение или частное?
• Что десятичные дроби и/или проценты в задаче говорят мне о ситуации?

6-6 Переменные и шаблоны

Понятия и пояснения | Примеры домашних заданий | Math Background

В разделе Variables and Patterns ваш ребенок изучит некоторые основные идеи алгебры и научится использовать эти идеи для решения задач и принятия решений.

Исследования в этом разделе помогут вашему учащемуся научиться:

• Распознавать ситуации, в которых переменные связаны предсказуемым образом
• Описать закономерности изменения слов, таблиц данных, графиков и уравнений
• Используйте таблицы данных, графики, уравнения и неравенства для решения задач

Пока ваш ребенок работает над задачами в этом разделе, задавайте ему вопросы о проблемных ситуациях, которые включают связанные количественные переменные:

• Какие переменные в задаче?
• Какие переменные зависят или изменяются по отношению к другим?
• Как можно использовать таблицу, график, уравнение или неравенство для представления и анализа связи между переменными?

6-7 Данные о нас

Понятия и пояснения | Примеры домашних заданий | Math Background

В Data About Us вы узнаете о различных способах сбора, организации, отображения и анализа данных. В этом модуле ваш учащийся научится:

• Использовать процесс исследования данных, задавая вопросы, собирая и анализируя данные и интерпретируя данные, чтобы отвечать на вопросы
• Организовывать и представлять данные с помощью таблиц, точечных диаграмм, линейных диаграмм, гистограмм, гистограмм и диаграмм типа «ящик с усами»
• Опишите общую форму распределения и определите, симметрично ли оно относительно центрального значения
• Вычислите среднее значение, медиану и режим распределения данных и используйте эти меры, чтобы указать, что является типичным для распределения
• Описать изменчивость распределения, определяя кластеры и пробелы, а также вычисляя размах, межквартильный размах (IQR) и среднее абсолютное отклонение (MAD)
• Определите, какие статистические меры центра и разброса следует использовать для описания конкретного распределения данных
• Различать категориальные данные и числовые данные и определять, какие графики и статистические данные можно использовать для представления каждого типа данных
• Сравнение двух или более распределений данных, в том числе с использованием показателей центра и разброса для сравнения

Когда вы сталкиваетесь с новой проблемой, рекомендуется задать себе вопросы.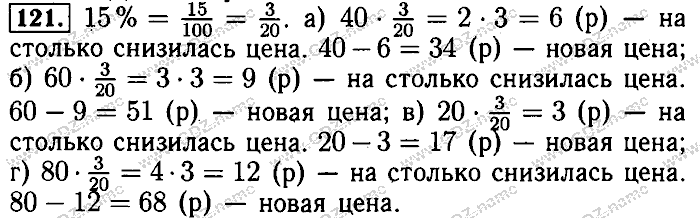 В этом разделе вы можете задать такие вопросы, как:

• Какой вопрос исследуется для сбора этих данных?
• Как можно упорядочить данные?
• Какие статистические показатели помогут описать распределение данных?
• Что эти статистические показатели расскажут мне о распределении данных?
• Как я могу использовать графики и статистику, чтобы сообщить ответ на мой первоначальный вопрос?

Рабочие листы по математике для 6 класса PDF

Рабочие листы по математике для печати для 6 класса

Рабочие листы по математике для 6 класса в формате PDF — Рабочие листы по математике для 6 класса с ответами — это идеальный инструмент, полезный для проверки навыков вашего ребенка по различным математическим темам для 6 класса. Эти наши математических печатных листов для 6 класса охватывают все основные области математики 6 класса, некоторые из которых включают; Целые числа, умножение, деление, показатели степени и квадратные корни, теория чисел, десятичные дроби, сложение и вычитание десятичных дробей, умножение и деление десятичных дробей, дроби и смешанные числа, сложение и вычитание дробей, умножение дробей.

• Разрядное значение в миллионах —
  Найти разрядное значение цифры в целом числе
  Распечатать …
• Чтение целых чисел —
  Как писать числа словами на английском языке
  Распечатать …
• Написание имен чисел —
  Написание чисел словами до 1 000 000
  Распечатать …
• Практика римских цифр —
  Преобразование числовых цифр в стандартные числа
  Распечатать …
• • Практика умножения целых чисел —
    Найдите пропущенную цифру
    Распечатать …
  • Словесные задачи на умножение целых чисел
    Распечатать …
  • Стратегии умножения — Как умножить три или более чисел
    Распечатать …
  • Разделить целые числа на двузначное число
    Распечатать . ..
  • Напишите выражение умножения, используя показатели степени
    Распечатать …
  • Оценка квадратных корней —
    Решите следующие задачи
    Распечатать …
• Узнайте, как преобразовать стандартную форму в экспоненциальную запись
  Распечатать …
• Узнайте, как написать простую факторизацию с показателями
  Распечатать …
• Найдите большой общий делитель (НОД) числа
  Распечатать …
• Найдите наименьшее общее кратное (НОК) числа
  Распечатать …
• Какое десятичное число проиллюстрировано —
  Понимание десятичных выражений
  Распечатать …
• Как нанести десятичные дроби на числовую прямую?
  Распечатать …
• Сложение и вычитание десятичных чисел —
  Карты с десятичными расстояниями
  Распечатать . ..
• Умножение десятичных чисел —
  Решите следующие задачи
  Распечатать …
• Деление с десятичными частными —
  Деление десятичных дробей на целые числа
  Распечатать …
• Представление дроби на числовой прямой
  Распечатать …
• Сравнение дробей с одинаковыми и разными знаменателями
  Распечатать …
• Интерпретация дробей как задач на деление слов
  Распечатать …
• • Сложение и вычитание дробей с разными знаменателями.
    Распечатать …
  • Дроби целого числа — Как умножить целое число на дробь?
    Распечатать …
  • Словесные задачи на умножение дробей с ответами
    Распечатать …
  • Деление дробей на целые числа с помощью моделей
    Распечатать . ..
  • Как вы оцениваете смешанные числа при делении?
    Распечатать …
  • Понимание практики работы с целыми числами — представление ситуаций с целыми числами
    Распечатать …
• Сравнение и упорядочивание целых чисел
  Распечатать …
• Практика добавления целых чисел
  Распечатать …
• Практика вычитания целых чисел
  Распечатать …
• Добавить Вычесть Умножить Разделить целые числа
  Распечатать …
• Вычислять числовые выражения, включающие десятичные дроби
  Распечатать …
• Абсолютное значение практики рациональных чисел
  Распечатать …
• Практика многошаговых задач —
  Добавить Вычесть Умножить Разделить
  Распечатать . ..
• Проблемы со словами с лишней или отсутствующей информацией
  Распечатать …
• Практика эквивалентных отношений —
  Решите следующее
  Распечатать …
• Практика решения пропорций —
  Решите следующие задачи
  Распечатать …
• Какой процент изображен? —
  Выводить проценты из моделей
  Распечатать …
• Как найти число, если известен процент?
  Распечатать …
• • Оценка и измерение с использованием обычных единиц длины
    Распечатать …
  • Оценка метрических измерений (метры дюймы фунты граммы литры)
    Распечатать …
  • Сравнение температур — Положительные и отрицательные числа
    Распечатать …
  • Добавление и вычитание денег
    Распечатать . ..
  • Умножение денег
    Распечатать …
  • Словесные задачи на деление денег
    Распечатать …
• Какая купонная практика лучше — лист сравнения цен
  Распечатать …
• Цены за единицу с дробями и десятичными знаками
  Распечатать …
• Нахождение первоначальной цены товара со скидкой
  Распечатать …
• Как рассчитать прошедшее время — Прошедшее время на числовой строке
  Распечатать …
• Простой способ выучить квадранты
  Распечатать …
• Практика карты плоскости координат
  Распечатать …
• Практика написания переменных выражений
  Распечатать …
• Свойства операций умножения
  Распечатать . ..
• Определение эквивалентных выражений —
  Найдите соответствующее выражение
  Распечатать …
• Какой x удовлетворяет уравнению
  практике
  Распечатать …
• Использование алгебраических плиток для решения одношаговых уравнений
  Распечатать …
• Решение уравнений с одинаковыми терминами — узнайте, как объединять похожие термины
  Распечатать …
• • Научитесь изображать неравенства на числовой прямой.
    Распечатать …
  • Написание и решение одношаговых неравенств
    Распечатать …
  • Математика независимых и зависимых переменных
    Распечатать …
  • Решите уравнения с двумя переменными с одним фиксированным значением
    Распечатать …
• Решение текстовых задач с двумя переменными
  Распечатать . ..
• Как найти уравнение из таблицы значений
  Распечатать …
• Как называются полигоны? — Именование и классификация полигонов
  Распечатать …
• Какие бывают виды четырехугольников
  Распечатать …
• Как найти сумму углов многоугольника
  Распечатать …
• Каковы 5 типов углов — Идентификация углов
  Распечатать …
• Практика вращения, переводов и отражений
  Распечатать …
• График отражений изображения —
  График отражений по осям
  Распечатать …
• Трехмерные фигуры и их свойства.
  Распечатать …
• Текстовые задачи на объем куба и прямоугольного параллелепипеда
  Распечатать …
• Площадь поверхности пирамиды с квадратным основанием и треугольной пирамиды
  Распечатать . ..
• Область составных фигур с треугольной практикой
  Распечатать …
• • Узнайте, как сделать пиктограмму
    Распечатать …
  • Создание частотных таблиц
    Распечатать …
  • Интерпретация двухлинейных графиков
    Распечатать …
  • Как сделать заговор из стебля и листьев
    Распечатать …
  • Определение статического вопроса
    Распечатать …
  • Среднее, медиана, практика диапазона режимов
    Распечатать …
• Как изменение значения влияет на среднее значение и медиану
  Распечатать …
• Вероятность взаимоисключающих событий и перекрывающихся событий
  Распечатать …
• Как определить, являются ли события независимыми или зависимыми
  Распечатать . ..
• Понимание вероятности с подсчетом результатов
  Распечатать …

Все рабочие листы по математике для 6 класса по категориям

• ЦЕЛЫЕ ЧИСЛА

• УМНОЖЕНИЕ

• ОТДЕЛ

• ПОКАЗАТЕЛИ & КВАДРАТНЫЕ КОРНИ

• ТЕОРИЯ ЧИСЕЛ

• ДЕСЯТИЧНЫЕ ЗНАКИ

• ДОБАВИТЬ & ВЫЧИТАНИЕ ДЕСЯТИЧНЫХ ЗНАЧЕНИЙ

  г.

• УМНОЖИТЬ & РАЗДЕЛИТЬ ДЕСЯТИЧНЫЕ ДОСТИЖЕНИЯ

• ДРОБЕЙ И AMP; СМЕШАННЫЕ НОМЕРА

• ДОБАВИТЬ & ВЫЧИТАНИЕ ДРОБЕЙ

  г.

• УМНОЖЕНИЕ ДРОБЕЙ

• ДЕЛИТЬ ДРОИ

• ЦЕЛЫЕ ЧИСЛА

• ОПЕРАЦИИ С ЦЕЛЫМИ ЧАСТЯМИ

• СМЕШАННЫЕ ОПЕРАЦИИ

• РАЦИОНАЛЬНЫЕ ЧИСЛА

• РЕШЕНИЕ ПРОБЛЕМ И ОЦЕНКА

• КОЭФФИЦИЕНТ И КОЭФФИЦИЕНТ

• ПРОЦЕНТ

• ИЗМЕРИТЕЛЬНЫЕ БЛОКИ

• ДЕНЕЖНАЯ МАТЕМАТИКА

• • ПОТРЕБИТЕЛЬСКАЯ МАТЕМАТИКА

    г.

  • ГОВОРИМ ВРЕМЯ

  • ГРАФИК КООРДИНАТ

  • АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ

  • ОДНОШАГОВЫЕ УРАВНЕНИЯ

    г.

  • РЕШИТЬ И AMP; ГРАФИЧЕСКИЕ НЕРАВЕНСТВА

• ДВУХЭТАПНЫЕ УРАВНЕНИЯ

• 2D ГЕОМЕТРИЯ

• СИММЕТРИЯ И AMP; ТРАНСФОРМАЦИЯ

• 3D ФОРМЫ

• ИЗМЕРЕНИЕ ГЕОМЕТРИИ

• ДАННЫЕ & ДИАГРАММА

• СТАТИСТИКА

• ВЕРОЯТНОСТЬ

Что вам нужно знать о наших рабочих листах по математике для 6 класса PDF

Что касается этих листов для печати по математике для 6 класса , мы можем похвастаться забавным дизайном, хорошо структурированными упражнениями и интересными задачами из реальной жизни. Эти стратегии сильно вдохновят ваших шестиклассников на непреодолимое желание решить больше математических задач.

От основ сложения, вычитания, умножения и деления до продвинутой алгебры и геометрических понятий, наши рабочие листы по математике для 6 класса в формате PDF помогут детям уверенно решать математические задачи и решать простые математические задачи.

Лучший способ добиться захватывающего прогресса в математике в 6 классе

Привет, детишки, наши стратегии настолько замечательны, что предлагают вам лучших способов добиться захватывающего прогресса в математике . Начнем с того, что каждая концепция уникальна и разработана таким образом, чтобы обеспечить четкое понимание, повысить эффективность и точность.

Также интересно отметить, что Рабочие листы по математике для 6 класса PDF с ответами сгруппированы по темам. Для этого детям будет очень легко найти конкретную тему, с которой они хотят работать в данный момент.

Будь то тест на время в школе или дома, эти замечательные рабочие листы снимут все математические стрессы и, скорее, создадут у детей навыки уверенного и логического решения задач.

Общая базовая учебная программа по математике для 6 класса

Государственные школы Audubon Привлечение учащихся ~ Создание достижения ~ Культивирование глобальных навыков 21 -го века Написано: Beth Canzanese Курс. Уровень 6   Заявления о содержании Определить значения рациональных чисел; сравнивать и упорядочивать числа, наносить точки на координатную плоскость; определять множители и кратные целых чисел; складывать, вычитать, делить и умножать десятичные дроби; делить и умножать дроби Общие базовые стандарты:   6.НС.2-7 ​​ Общие основные вопросы Какая система счисления?     Всеобъемлющее прочное понимание В повседневной жизни мне нужно знать, что числа часто представляются в виде дробей и десятичных знаков и могут быть положительными или отрицательными. Основные вопросы модуля Что такое целые числа? Что такое отрицательные числа? Как я могу использовать числовую прямую, чтобы определить противоположное число? В реальной жизненной ситуации, как я могу определить, используются ли положительные или отрицательные числа, когда я решаю задачу? Что такое рациональное число? Что такое координатная плоскость? Как найти, идентифицировать или разместить точку на координатной плоскости? Что такое квадрант на координатной плоскости? Как проверить задачу на деление? Что такое фактор? Что такое общий делитель и наибольший общий делитель (НОД)? Почему размещение десятичных точек важно при вычислениях с десятичными дробями? Как сохранить правильный разряд при умножении десятичных дробей? Как делить десятичные дроби? Как делить дроби?                     Единица прочного понимания Целые числа — это целые числа, их противоположности и ноль. Отрицательные числа — это числа меньше нуля. Я могу найти противоположное число, используя числовую прямую, чтобы определить расстояние от нуля до исходного числа, а затем от нуля на противоположной стороне до того же числа. Противоположное положительному числу — его отрицательное, а противоположное отрицательному числу — положительное. Некоторые ключевые слова для распознавания положительных целых чисел: усиление, увеличение, рост, выше, больше и выше. Некоторые ключевые слова для отрицательных целых чисел: потеря, уменьшение, падение, ниже, меньше и вниз. Рациональное число может быть представлено в виде дроби и имеет точное положение на числовой прямой. Система из двух числовых линий называется координатной плоскостью: горизонтальная линия называется осью X, а вертикальная линия называется осью Y. Две оси пересекаются в начале координат, обозначенном точкой (0, 0). Точка на координатной плоскости может быть описана ее расстоянием по обеим числовым линиям. Упорядоченная пара (x, y) используется для определения местоположения этой точки. Когда оси вытянуты в обоих направлениях, они делят координатную плоскость на 4 части, называемые квадрантами. Чтобы проверить решение задачи на деление, умножьте целую числовую часть частного на делитель, а затем прибавьте остаток, если он есть, что должно дать мне делимое, если мой ответ правильный. Делитель целого числа — это любое целое число, на которое первое число делится без остатка. Делители числа меньше или равны этому числу. Число, являющееся делителем двух или более чисел, называется общим делителем этих чисел. Наибольший общий делитель (GCF) — это наибольшее число, являющееся общим делителем. Когда я вычисляю с десятичными дробями, выстраивание десятичных точек гарантирует, что я сохраняю надлежащее разрядное значение чисел. После умножения десятичных дробей, как если бы они были целыми числами, я подсчитываю количество цифр справа от запятой в каждом множителе; затем я перемещаю десятичные точки на столько же мест слева от произведения. Если делитель является десятичной дробью, я должен переместить десятичную точку вправо, чтобы она стала целым числом; далее я передвигаю запятую в делимом вправо на такое же количество разрядов; затем я делю десятичные дроби, как если бы они были целыми числами; наконец, я должен переместить десятичную точку из ее нового положения в делимом в частное. Модель площади может помочь мне делить дроби. Я могу делить дроби, умножая делимое на обратную величину делителя. Я могу найти обратную величину, поменяв местами числитель и знаменатель. Обоснование блока Числа в повседневной жизни не всегда представляются целыми числами. Они также отображаются в виде дробей и десятичных знаков; и некоторые числа отрицательные. Чтобы точно выполнять вычисления во многих ситуациях, учащиеся должны уметь понимать и применять стратегии работы с системой счисления. Обзор устройства Учащиеся определят значения рациональных чисел; сравнивать и упорядочивать числа, наносить точки на координатную плоскость; определять множители и кратные целых чисел; складывать, вычитать, делить и умножать десятичные дроби и делить и умножать дроби. Oudubon Public Schools Вовлечение студентов ~ Фостера0144 Beth Canzanese Название курса: Математика для шестого класса   Название раздела: Соотношения и пропорциональные отношения             Класс: 6 2 2166 9214 Заявления о содержании Представление числовых отношений в виде отношений; найти процент числа и, если дан процент или часть, найти число; использовать координатную плоскость для представления скорости или отношения; использовать отношения для преобразования измерений в длину, вес и мощность.	Общие базовые стандарты: 6.РП.1-3 6.EE.9
Общие основные вопросы Что такое отношение?	Всеобъемлющее прочное понимание Соотношение сравнивает два числа и описывает взаимосвязь между двумя количествами или элементами в целом.
Основные вопросы по устройству Как выразить соотношение? Что такое процент? Чем процент похож на соотношение? Какая связь между процентом и дробью? Что такое ставка и единичная ставка? Как использовать графики при работе с коэффициентами? Как я могу использовать графики для преобразования одних единиц измерения в другие в американской или метрической системе?	Блок прочного понимания Соотношения могут быть записаны тремя способами: 2 к 3, 2:3, 2/3. Процент означает из каждой сотни и представляет части целого, разделенные на 100 равных частей. Процент — это отношение к 100. Если я знаю процент и целое, я могу найти часть целого, которую представляет процент. Коэффициент — это отношение, которое сравнивает две разные единицы измерения. Единица измерения — это отношение, сравнивающее две разные единицы измерения, в которых одно из измерений равно единице. Я могу использовать графики скорости или отношения, чтобы показать закономерности. Я могу использовать графики для преобразования одних единиц измерения в другие как в американской, так и в метрической системе.
Обоснование блока Учащиеся должны знать, как вычислять коэффициенты и коэффициенты, потому что они часто появляются в случаях, связанных со статистической информацией.	Обзор устройства Студенты будут представлять отношения; найти процент числа и, если дан процент или часть, найти число; использовать координатную плоскость для представления скорости или отношения; и используйте коэффициенты для преобразования измерений длины, веса и емкости.

 

 

 

 

Audubon Public Schools

Engaging Students ~ Fostering Achievement ~ Cultivating 21st Century Global Skills

Written By: Beth Canzanese

Название курса Пятый класс Математика   Название раздела: Выражения и уравнения       Уровень класса: 6

 

Заявления о содержании Решение переменных в математических задачах; писать и оценивать переменные выражения, неравенства и писать и решать уравнения с переменными; определять и создавать эквивалентные выражения, используя свойства чисел; создавать таблицы, чтобы показать отношения между зависимыми и независимыми переменными.	Общие базовые стандарты:   6.EE: 1-9
Общие основные вопросы Что такое выражение? Что такое уравнение?	Всеобъемлющее прочное понимание Выражение — это фраза, состоящая из чисел, символов операций и иногда переменных. Есть два вида выражений — числовые и алгебраические. Уравнение — это математическое выражение, содержащее знак равенства, разделяющий уравнение на 2 эквивалентных выражения.
Основные вопросы модуля Что такое переменная? Что такое коэффициент? Что такое термин? Как преобразовать словосочетание в математическое выражение? Как я могу вычислить выражение? Что такое эквивалентные выражения? Как узнать, эквивалентны ли два выражения? Как решить уравнение? Что такое неравенство?	Подразделение прочного понимания Переменная — это буква, представляющая неизвестное число:  когда значение одной переменной зависит от значения другой, она называется зависимой переменной; когда значение одной переменной не зависит от значения другой, она называется независимой переменной. Таблица может отображать взаимосвязь между зависимой и независимой переменной. Число, умноженное на переменную, называется коэффициентом. Терм — это число или переменная; одинаковые термины имеют одну и ту же переменную, возведенную в один и тот же показатель степени. Мне нужно идентифицировать операции по их ключевым словам, чтобы преобразовать словесное выражение в математическое выражение. Я могу вычислить выражение с переменной или символами, подставив заданное число вместо переменной или символа; далее по порядку действий. Два выражения эквивалентны, если они выглядят по-разному, но представляют одну и ту же информацию. Я могу использовать дистрибутивное, коммутативное и ассоциативное свойства, чтобы выяснить, эквивалентны ли два выражения.   Я могу решить уравнение, изолируя переменную по одну сторону от знака равенства, применяя обратные операции. Решение можно проверить, подставив его в исходное уравнение, чтобы убедиться, что оно дает верное утверждение. Не каждое уравнение имеет решение. Неравенство — это математическое предложение, сравнивающее два выражения; используются символы <, < , > и > . Чтобы решить неравенство, я могу следовать тем же правилам решения уравнений.
Обоснование блока Учащиеся сталкиваются со многими ситуациями в реальной жизни, когда им нужно определить неизвестное число, чтобы вычислить сумму, которую им нужно знать.	Обзор устройства Учащиеся найдут значения переменных в математических задачах; писать и находить решения выражений, неравенств и уравнений с переменными; определять и создавать эквивалентные выражения, используя свойства чисел; и создайте таблицы, чтобы показать отношения между зависимыми и независимыми переменными.

 

 

 

Государственные школы Audubon

Привлечение студентов ~ Создание достижения ~ Культивирование глобальных навыков 21 -го века

Написано: Бет Канзанезе

Название курса:

Название курса: Sixth

Название курса: Sixth

.

 

Заявления о содержании Повторение нахождения площади и периметра двумерных фигур; найти площадь поверхности и объем трехмерных фигур; представлять объемные фигуры в двух измерениях с помощью сетки; чертить многоугольники на координатной плоскости и определять расстояние между их вершинами	Общие базовые стандарты: 6.Г.1- 4 6.NS.8
Общие основные вопросы Что такое измерение? Как можно измерить внутреннюю часть двумерной фигуры? Как можно измерить площадь поверхности и объем трехмерной фигуры?	Всеобъемлющее прочное понимание Размер — это мера ширины, высоты или длины фигуры. Внутреннюю часть двумерной фигуры можно измерить, определив квадратные единицы, покрывающие фигуру. Я могу измерить площадь поверхности трехмерной фигуры, найдя количество квадратных единиц всех ее сторон; объем трехмерной фигуры путем нахождения количества кубических единиц, заполняющих пространство.
Основные вопросы модуля Что такое площадь? Как найти площадь двухмерной фигуры? Как найти площадь прямоугольника? Как найти площадь треугольника? Как найти площадь параллелограмма? Как найти площадь неправильного многоугольника? Что такое объем (V)? Как измерить объем? Что такое прямоугольная призма? Как измерить объем прямоугольной призмы? Что такое сеть? Что такое лицо? Что такое вершина? Что такое площадь поверхности? Как найти площадь поверхности твердого тела? Что такое координатная геометрия? Что такое абсолютное значение? Как нарисовать многоугольник?	Блок прочного понимания Площадь — это мера области внутри двухмерной фигуры. Я могу найти площадь двухмерной фигуры, посчитав квадраты внутри фигуры. Я могу найти площадь прямоугольника, умножив его длину на ширину. Площадь треугольника равна половине площади прямоугольника той же высоты и длины. Площадь параллелограмма можно найти, умножив его основание на высоту. Основание и высота пересекаются под прямым углом. Я могу найти площадь неправильного многоугольника, разбив его на треугольники и прямоугольники и найдя площади этих частей, а затем сложив площади вместе. Объем — это мера пространства внутри твердого тела, трехмерной фигуры. Прямоугольная призма — объемная фигура, имеющая шесть граней, являющихся прямоугольниками; она называется призмой, потому что имеет одинаковое поперечное сечение по длине. Я могу измерить объем прямоугольной призмы в кубических единицах, используя формулу V=lwh или V=Bh. Сеть — это двумерное связное представление твердого тела, которое показывает все грани, ребра и вершины твердого тела. Грани — это плоские фигуры, образующие стороны и основание(я) твердого тела. Грани пересекаются, образуя ребра фигуры. Вершина — угол фигуры; это точка пересечения трех или более ребер. Площадь поверхности — это площадь всех граней трехмерной фигуры. Я могу найти площадь поверхности твердого тела, найдя сумму площадей всех граней в сети твердого тела. Координатная геометрия дает мне возможность точно описать, где находится точка на координатной плоскости. Я могу использовать координатную геометрию для определения расстояния между двумя точками. Абсолютное значение — это расстояние числа от нуля. Я могу использовать абсолютное значение для определения расстояния между двумя точками. Я могу нарисовать многоугольник, используя координатную плоскость.
Обоснование блока Формы встречаются повсюду в мире природы. Учащиеся должны понимать, что рукотворный мир построен по геометрическим принципам.	Обзор устройства Учащиеся повторят нахождение площади и периметра двумерных фигур. Они также найдут объем трехмерных фигур. Они будут представлять трехмерные фигуры в двух измерениях с помощью сетей и находить их площади поверхности; и создавать многоугольники и определять расстояние между их вершинами, используя координатные плоскости.

 

 

Audubon Public Schools

Engaging Students ~ Fostering Achievement ~ Cultivating 21st Century Global Skills

Written By: Beth Canzanese

Course Title : Математика шестого класса   Название раздела: Статистика и вероятность   Уровень класса: 6

 

Заявления о содержании Определить, можно ли ответить на вопрос с помощью статистики; использовать различные меры для описания центра набора данных; наборы графических данных; и описывать наборы данных по-разному. Найти вероятность того, что данное событие произойдет.	Общие базовые стандарты: 6.СП.1-5
Общие основные вопросы Что такое статистика? Что такое вероятность?	Всеобъемлющее прочное понимание Статистика — это сбор и анализ данных. Вероятность — это вероятность того, что данное событие произойдет.
Основные вопросы модуля Что такое статистическая изменчивость? Как я могу решить вопрос, который включает тему, имеющую вариативность? Что такое среднее значение, медиана и мода для данного набора данных? Как измерить набор данных? Что такое диапазон? Что такое межквартильный размах? Что такое среднее абсолютное отклонение? Как отображать данные? Что такое точечный график? Что такое коробочная диаграмма? Что такое гистограмма? Каковы шесть шагов решения статистического вопроса? Какова вероятность того, что данное событие произойдет?	Подразделение прочного понимания Статистическая изменчивость — это когда значение чего-то может измениться. Если я решаю вопрос, который включает тему, имеющую вариативность, я могу использовать статистику. Среднее значение, медиана и мода являются индикаторами центра набора данных. Медиана — это среднее число в наборе данных, упорядоченном от наименьшего к наибольшему или от наибольшего к наименьшему. Мода — это число, которое чаще всего встречается в наборе данных. Я могу измерить набор данных, используя диапазон, межквартильный диапазон и среднее абсолютное отклонение. Диапазон — это разница между наименьшим и наибольшим числом в наборе данных. Межквартильный диапазон — это разница между первым и третьим квартилями набора данных. Среднее абсолютное отклонение — это средняя величина, на которую измерения в наборе данных отличаются от среднего значения. Я могу отображать данные в виде числовой линии, точечных диаграмм, коробчатых диаграмм и гистограмм. Точечный график показывает, сколько раз встречается каждое значение в наборе данных. Коробчатая диаграмма показывает диапазон значений и то, как они распределяются в наборе данных, включая минимальное и максимальное значение. Гистограмма показывает непрерывные данные в наборе. Чтобы решить статистический вопрос, я могу выполнить шесть шагов:  Укажите, требуется ли для вопроса статистика. Определите переменную Соберите данные для набора данных Вычисление показателей набора данных Показать данные Анализ данных Вероятность – это отношение благоприятных исходов ко всем возможным исходам, представленное в виде дроби в виде числа от 0 до 1 или от 0% до 100%.
Обоснование блока Анализ данных используется во многих повседневных ситуациях, от сельского хозяйства и дорожного движения до спорта и транспорта. Поскольку наш мир все больше зависит от производства, основанного на данных, скорее всего, студенты будут сталкиваться с данными и последующим анализом в своих классах колледжа и карьере. Вероятность используется для прогнозирования и получения статистики в таких областях, как прогнозирование погоды, контроль качества бизнеса и спортивная статистика.	Обзор устройства Учащиеся определят, можно ли ответить на вопрос с помощью статистики; использовать различные меры для описания центра набора данных; наборы графических данных; и описывать наборы данных по-разному, используя проблемы и ситуации реального мира.

 

 

шестой класс

шестой класс

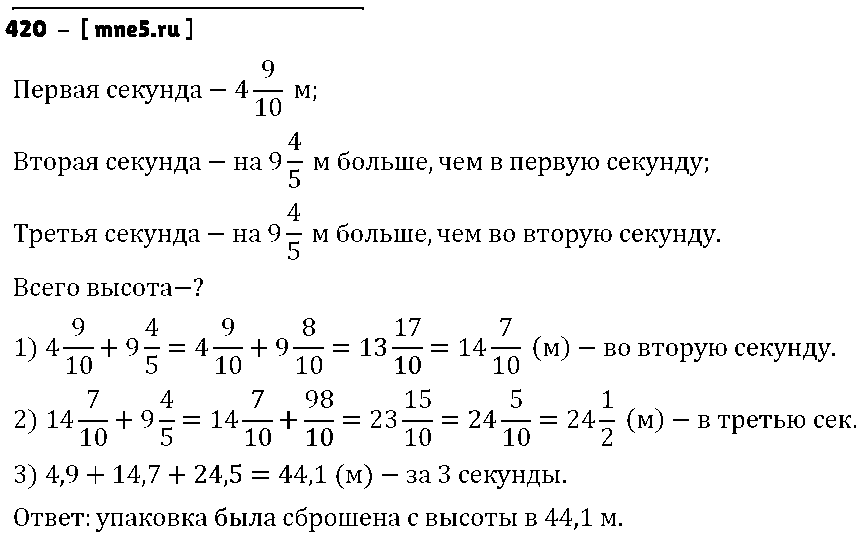
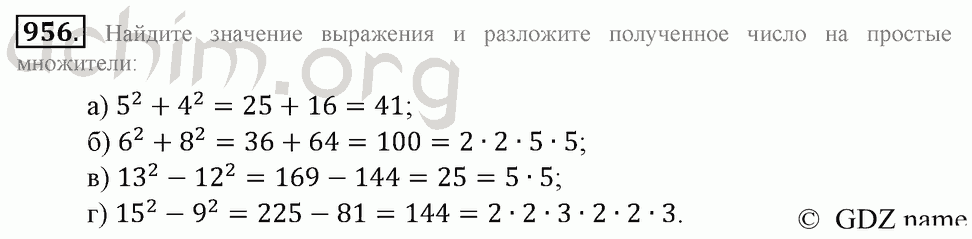
Шестой класс. Содержание Шестой класс. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт Copyright © 2004-2019 Карта сайта