Номер 415 — ГДЗ по Математике 6 класс Учебник Мерзляк, Полонский (решебник)
Номер 415 — ГДЗ по Математике 6 класс Учебник Мерзляк, Полонский (решебник) — GDZwowПерейти к содержанию
Search for:
Авторы: Мерзляк А. Г., Якир М. С., Полонский В. Б.
Издательство: Вентана-Граф
Тип: Учебник
Выберите номер
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091929394959697989910010110210310410510610710810911011111211311411511611711811912012112212312412512612712812913013113213313413513613713813914014114214314414514614714814915015115215315415515615715815916016116216316416516616716816917017117217317417517617717817918018118218318418518618718818919019119219319419519619719819920020120220320420520620720820921021121221321421521621721821922022122222322422522622722822923023123223323423523623723823924024124224324424524624724824925025125225325425525625725825926026126226326426526626726826927027127227327427527627727827928028128228328428528628728828929029129229329429529629729829930030130230330430530630730830931031131231331431531631731831932032132232332432532632732832933033133233333433533633733833934034134234334434534634734834935035135235335435535635735835936036136236336436536636736836937037137237337437537637737837938038138238338438538638738838939039139239339439539639739839940040140240340440540640740840941041141241341441541641741841942042142242342442542642742842943043143243343443543643743843944044144244344444544644744844945045145245345445545645745845946046146246346446546646746846947047147247347447547647747847948048148248348448548648748848949049149249349449549649749849950050150250350450550650750850951051151251351451551651751851952052152252352452552652752852953053153253353453553653753853954054154254354454554654754854955055155255355455555655755855956056156256356456556656756856957057157257357457557657757857958058158258358458558658758858959059159259359459559659759859960060160260360460560660760860961061161261361461561661761861962062162262362462562662762862963063163263363463563663763863964064164264364464564664764864965065165265365465565665765865966066166266366466566666766866967067167267367467567667767867968068168268368468568668768868969069169269369469569669769869970070170270370470570670770870971071171271371471571671771871972072172272372472572672772872973073173273373473573673773873974074174274374474574674774874975075175275375475575675775875976076176276376476576676776876977077177277377477577677777877978078178278378478578678778878979079179279379479579679779879980080180280380480580680780880981081181281381481581681781881982082182282382482582682782882983083183283383483583683783883984084184284384484584684784884985085185285385485585685785885986086186286386486586686786886987087187287387487587687787887988088188288388488588688788888989089189289389489589689789889990090190290390490590690790890991091191291391491591691791891992092192292392492592692792892993093193293393493593693793893994094194294394494594694794894995095195295395495595695795895996096196296396496596696796896997097197297397497597697797897998098198298398498598698798898999099199299399499599699799899910001001100210031004100510061007100810091010101110121013101410151016101710181019102010211022102310241025102610271028102910301031103210331034103510361037103810391040104110421043104410451046104710481049105010511052105310541055105610571058105910601061106210631064106510661067106810691070107110721073107410751076107710781079108010811082108310841085108610871088108910901091109210931094109510961097109810991100110111021103110411051106110711081109111011111112111311141115111611171118111911201121112211231124112511261127112811291130113111321133113411351136113711381139114011411142114311441145114611471148114911501151115211531154115511561157115811591160116111621163116411651166116711681169117011711172117311741175117611771178117911801181118211831184118511861187118811891190119111921193119411951196119711981199120012011202120312041205120612071208120912101211121212131214121512161217121812191220122112221223122412251226122712281229123012311232123312341235123612371238123912401241124212431244124512461247124812491250125112521253125412551256125712581259126012611262126312641265126612671268126912701271127212731274127512761277127812791280128112821283128412851286128712881289129012911292129312941295129612971298129913001301130213031304130513061307130813091310131113121313131413151316131713181319132013211322132313241325132613271328132913301331133213331334133513361337133813391340134113421343134413451346
Выберите параграф
1234567891011121314151718192021222425262728293031323334363739404143444546
Решаем устно
стр.
5стр.11стр.15стр.22стр.29-30стр.34стр.42стр.46стр.51стр.56-57стр.66-67стр.75стр.81стр.85стр.92стр.99стр.102стр.104-105стр.113стр.119стр.125стр.134стр.138стр.143-144стр.149стр.158стр.162стр.172стр.179стр.183стр.188стр.194стр.198стр.205стр.209стр.212стр.218стр.225стр.229стр.235стр.241стр.245стр.253стр.259стр.268стр.274стр.282
Выберите страницу учебника
5678910111213141516171822232425293031333435364243444647484951525354565758596061626364666768697071727375767778798182838586878889909192939495969799100102103104105106113114115116118119120121122123124125126127128133134135136137138139140143144145146147149150151152153154157158159162163164165166167168169172173174175179180181182183184185186188189190194195196197198199200201202204205206207208209210211212213214215216218219220221222225226227229230231232233234235236237238239241242243244245246247248249250252253254255259260261262263264265267268269270273274275276277278282283284285286287
Adblockdetector
Ответы Задание 415 . ГДЗ по математике 6 класс Мерзляк Полонский Якир учебник
11.
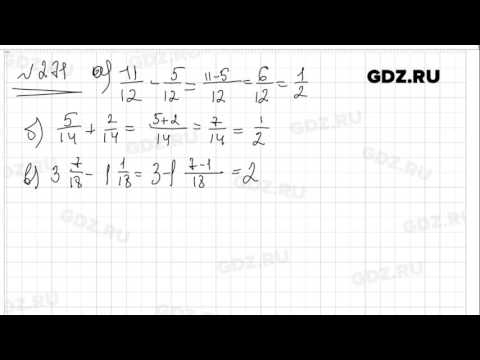Решаем устно2345678910111213141516171819202122232425262728293031323334353637383939. Решаем устно40414243444546474849505152535455565758596061626364656667686970717272. Решаем устно737475767778798081828384858687888990919293949596979899100101102103103. Решаем устно104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137137. Решаем устно138139140141142143144145146147148149150151152153154155156157158159160161162162. Решаем устно163164165166167168169170171172173174175176177178179180181182183184185186186. Решаем устно187188189190191192193194195196197198199200201202203204205206207208209209. Решаем устно210211212213214215216217218219220221222223224225226227228229230231232233234235235. Решаем устно236237238239240241242243244245246247248249250251252253254255256257258259260261262263264265266267267. Решаем устно268269270271272273274275276277278279280281282283284285286287288289290291292293294295296297298299300301302303304305306307308309310311312313314315316317318319320321322323324325326327328329330331332333333.
Решаем устно633634635636637638639640641642643644645646647648649650651652653654655656657658659660660. Решаем устно661662663664665666667668669670671672673674675676677678679679. Решаем устно680681682683684685686687688689690691692693694695696697698698. Решаем устно699700701702703704705706707708709710711712713714715716717718719720721722723724725726727728729730730. Решаем устно731732733734735736737738739740741742743744745746747748749750751752753754755756757758759760761762763764765766766. Решаем устно767768769770771772773774775776777778779780781782783783. Решаем устно784785786787788789790791792793794795796797798799800801801. Решаем устно802803804805806807808809810811812813814815816817818819820821822823824825826827828829829. Решаем устно830831832833834835836837838839840841842843844845845. Решаем устно846847848849850851852853854855856857858859860861862863864865866867868869870870. Решаем устно871872873874875876877878879880881882883884885886887888889890891892893893. Решаем устно894895896897898899900901902903904905906907908909910911912913914915916917918918.
Решаем устно11731174117511761177117811791180118111821183118411851186118711881189119011911192119311941195119611971198119912001201120212031204120512061207120812091210121112121213121412151216121712181218. Решаем устно12191220122112221223122412251226122712281229123012311232123312341235123612371238123912401241124212431243. Решаем устно1244124512461247124812491250125112521253125412551256125712581259126012611262126312641265126612671268126912701271127212731274127512761277127812791279. Решаем устно12801281128212831284128512861287128812891290129112921293129412951295. Решаем устно1296129712981299130013011302130313041305130613071308130913101311131213131314131513161317131813191320132113221323132413251326132713281329133013311332133313341334. Решаем устно133513361337133813391340134113421343134413451346MAT 415: Абстрактная алгебра
Абстрактная алгебра Вопросы и ответы
Просмотреть все решения для учебников
textbook.title ]}»> {[ textbookSolutions.textbook.title ]} {[item.headingText]}
{[ textbookSolutions.textbook.title ]}Самые важные документы недели
Документы по абстрактной алгебре
Показаны с 1 по 76 из 76
Сортировать по:
{[$select.
selected.label]}
Упражнения из учебника
Современная абстрактная алгебра Для n=5,8,12,20 и 25 найдите все положительные целые числа, меньшие n и взаимно простые с n.
Современная абстрактная алгебра
Глава 1, Раздел EoC Конец главы, Упражнение 1
С помощью рисунков и слов опишите каждую симметрию в D3 (набор симметрий равностороннего…
Современная абстрактная алгебра
Глава 2, Раздел EoC Конец главы, Упражнение 1
Какие из следующих бинарных операций закрыты? а. вычитание целых положительных чисел b.
Современная абстрактная алгебра
Глава 3, Раздел EoC Конец главы, Упражнение 1
Для каждой группы в следующем списке найдите порядок группы и порядок каждого элемента в.
..
Современная абстрактная алгебра
Глава 4, Раздел EoC Конец главы, Упражнение 1
Найти все генераторы Z6, Z8 и Z20.
Современная абстрактная алгебра
Глава 5, Раздел EoC Конец главы, Упражнение 1
Пусть α=[1 2 3 4 5 6 2 1 3 5 4 6] и β=[1 2 3 4 5 6 6 1 2 4 3 5]. Вычислите каждое из следующих.
Современная абстрактная алгебра
Глава 6, Раздел EoC Конец главы, Упражнение 1
Найдите изоморфизм из группы целых чисел по сложению в группу четных целых чисел по…
Современная абстрактная алгебра
Глава 7, Раздел EoC Конец главы, Упражнение 1
Пусть H={0,± 3,± 6,± 9, …} .
Найдите все левые смежные классы H в Z .
Современная абстрактная алгебра
Глава 8, Раздел EoC Конец главы, Упражнение 1
Докажите, что внешнее прямое произведение любого конечного числа групп является группой. (Это упражнение…
Современная абстрактная алгебра
Абстрактная алгебра Тесты Вопросы и ответы
Отображается с 1 по 8 из 128
Посмотреть все- ПРИМЕЧАНИЕ: абстрактный курс алгебры Кроме того, я бы предпочел, чтобы вы записали его, так как мне будет легче следовать и понимать, спасибо!
- ПРИМЕЧАНИЕ: абстрактный курс алгебры Кроме того, я бы предпочел, чтобы вы записали его, так как мне будет легче следовать и понимать, спасибо!
- ПРИМЕЧАНИЕ: абстрактный курс алгебры Кроме того, я бы предпочел, чтобы вы записали его, так как мне будет легче следовать и понимать, спасибо!
- ПРИМЕЧАНИЕ: абстрактный курс алгебры Кроме того, я бы предпочел, чтобы вы записали его, так как мне будет легче следовать и понимать, спасибо!
- ПРИМЕЧАНИЕ: абстрактный курс алгебры Кроме того, я бы предпочел, чтобы вы записали его, так как мне будет легче следовать и понимать, спасибо!
- ПРИМЕЧАНИЕ: абстрактный курс алгебры Кроме того, я бы предпочел, чтобы вы записали его, так как мне будет легче следовать и понимать, спасибо!
- ПРИМЕЧАНИЕ: абстрактный курс алгебры Кроме того, я бы предпочел, чтобы вы записали его, так как мне будет легче следовать и понимать, спасибо!
- ПРИМЕЧАНИЕ: абстрактный курс алгебры Кроме того, я бы предпочел, чтобы вы записали его, так как мне будет легче следовать и понимать, спасибо! Пусть G — группа (не
Недавно загруженные документы
Подробнее
Назад в отдел
Добро пожаловать в STAT 415! | СТАТ 415
Добро пожаловать в конспект курса STAT 415: Введение в математическую статистику .
Эти заметки разработаны и разработаны Департаментом статистики штата Пенсильвания и предлагаются в качестве открытых образовательных ресурсов. Эти заметки можно использовать бесплатно по лицензии Creative Commons CC BY-NC 4.0.
Этот курс является частью онлайн-программы магистра прикладной статистики, предлагаемой Всемирным кампусом штата Пенсильвания.
В настоящее время зачислен?
Если вы в настоящее время учитесь на этом курсе, см. Canvas, чтобы узнать о программе, заданиях, видеороликах уроков и сообщениях от преподавателя.
Как записаться?
Если вы хотите записаться и пройти весь курс за кредит, см. «Как записаться на курс» на веб-сайте World Campus.
Мы потратили все свое время на статистику 414, заполняя набор инструментов вероятностей только для того, чтобы в Stat 415 можно было заполнить набор инструментов статистики , которые мы могли бы использовать для ответов на исследовательские вопросы.
Например, предположим, что кто-то (исследователь? социолог? студент?) хочет что-то узнать (среднее кровяное давление? покупательские привычки? средний возраст?) о популяции из человек (пожилые люди? студенты? деревья?). Кому-то даже может быть интересно сравнить две или более популяции (мужчины и женщины, спортсмены и не спортсмены, дубы и вязы?). К сожалению, популяции часто слишком велики, чтобы измерить всех кого-то. Итак, берем случайная выборка некоторых тел из населения. Затем мы используем измерения ( данных ), сделанные для выборки, чтобы сделать выводы о большей совокупности. Мы используем расчеты вероятностей, подобные тем, которые изучены в Stat 414, чтобы помочь сделать выводы.
Пример #1
Исследователь хочет ответить на следующий исследовательский вопрос : Какая доля американских пользователей Интернета зависима от Интернета? Исследователь считает, что человек зависим от Интернета, если он демонстрирует по крайней мере пять из десяти возможных характеристик, таких как использование Интернета, чтобы сбежать от своих проблем, безуспешные попытки сократить его / ее использование и найти себя.
сама озабочена интернетом, когда больше не сидит за компьютером.
Какая часть из 230 630 000 американских интернет-пользователей ( Источник : Всемирный банк, 2008 г.) зависима от Интернета?
Ответить
Мы не собираемся отвечать на вопрос исследователя, а скорее притворяемся, что будем (как моя пятилетняя дочь любит притворяться)! Исследователь не может оценить поведение всех 230 с лишним миллионов американских интернет-пользователей. Вместо этого предположим, что исследователь берет случайную выборку из 17 251 американского интернет-пользователя и оценивает их интернет-зависимость. Результирующие данные будут представлять собой кучу … 17 251 точка данных, если быть точным … да и нет: 9) над ним, кстати, и, возможно, неудивительно, называется « п-шляпа «. В общем случае он обозначает долю в выборке с определенной характеристикой.
Теперь эта доля выборки 0,057 — это хорошо. Но нас не интересует доля в выборке зависимых от интернета.
Нас интересует «параметр населения », то есть \(p\), истинная, неизвестная доля населения , зависимых от Интернета.
Вскоре мы узнаем, особенно в разделе 6, что можно использовать доверительный интервал для количественной оценки значения параметра совокупности. « доверительный интервал » — это диапазон или интервал значений, которые, как мы можем быть уверены, содержат интересующий параметр совокупности, в данном случае \(p\), истинную неизвестную долю населения. Когда все сказано и сделано, вычислив доверительный интервал для \(p\), исследователь должен быть в состоянии сделать такое заявление:
«Мы можем быть 95% уверены, что истинная доля американцев, зависимых от интернета, находится между 0,0534 и 0,0606 (0,057±0,0036)». обычно в диапазоне от 1000 до 1600 респондентов. (и один из уроков в Разделе 10) сосредоточьтесь на получении хороших результатов» точечные оценки » и « доверительные интервалы » для:
Параметр населения. 2\) 92\) | |
|---|---|
| Доля населения, \(р\) | пропорция выборки, \(\шляпа{р}\) |
| разница в двух пропорциях населения, \(p_1-p_2\) | разница в пропорциях выборки, \(\шляпа{р}_1-\шляпа{р}_2\) |
На этих уроках мы будем работать не только над получением формул для оценок и интервалов, но и над утверждением, что они в каком-то смысле «хороши»… например, беспристрастны. Мы также рассмотрим практические вопросы, например, как размер выборки влияет на длину полученных нами доверительных интервалов. И мы также будем работать над получением хороших точечных оценок и доверительных интервалов для линии регрессии наименьших квадратов через набор точек данных \((x,y)\).
Пример #2
Исследователи хотят ответить на следующий исследовательский вопрос : снижает ли регулярное употребление орехов риск сердечных приступов у женщин? Исследователи считают, что женщина регулярно ест орехи, если она съедает более пяти унций орехов в неделю.
Снижает ли регулярное употребление орехов риск сердечного приступа у женщин?
Ответ
Мы попытаемся ответить на вопрос исследователей, используя данные, собранные на выборке из 86 000 американских женщин-медсестер в рамках национального исследования здоровья медсестер. В этом случае интересующей нас совокупностью являются все американские женщины, но, исходя из использованной выборки, технически правильнее сказать, что совокупность состоит из всех американских женщин-медсестер. Мы можем разделить выборку из 86 000 женщин на три группы: те, кто ест больше пяти унций орехов в неделю, те, кто ест немного, но меньше пяти унций орехов в неделю, и те, кто не ест орехов в неделю. При этом получаем деление выборки:
То есть 4000 женщин в выборке съедают более пяти унций орехов в неделю, 52000 женщин, которые едят немного, но менее пяти унций орехов в неделю, и 30000 женщин, которые не едят орехи еженедельно. Из 4000 женщин, которые еженедельно съедают более пяти унций орехов, 44 перенесли сердечный приступ.
Из 52 000 женщин, которые еженедельно ели немного, но менее пяти унций орехов, 669 пострадали от сердечных приступов. А из 30 000 женщин, которые вообще не едят орехи, 554 перенесли сердечный приступ. Используя эти данные, мы можем рассчитать долю выборки в каждой группе, перенесшей сердечный приступ. При этом получаем:
Вскоре в разделе 7 мы узнаем, что, используя эту выборочную статистику, мы можем провести так называемую «проверку гипотезы », чтобы помочь ответить на вопрос исследования. Если орехи не влияют на популяцию, разница в пропорциях популяции равна 0, то есть \(p_3-p_1=0\). Но обратите внимание, что разница в пропорциях выборки не равна 0:
\(\шляпа{р}_3-\шляпа{р}_1=0,018-0,011=0,007\)
Вопрос, на который мы должны ответить:
«Как вероятно (то есть какова вероятность ) того, что разница в пропорциях выборки будет равна 0,007, если разница в пропорциях населения равна 0?»
Если ответ на вопрос «маловероятно», (то есть вероятность близка к 0), то мы пришли бы к выводу, что пропорции населения различаются, то есть мы пришли бы к выводу, что имеются убедительные доказательства того, что регулярное употребление орехов снижает риск сердечных приступов у женщин
Раздел 2
Предыдущий пример иллюстрирует вопрос, на который мы ответим на уроках в Разделе 7 (и трех уроках в Разделе 10).
В частности, уроки в Разделе 7 (и три урока в Разделе 10) сосредоточены на получении хороших « тестов гипотез » для тех же параметров совокупности, которые рассматриваются в Разделе 6:
| Параметр населения… на основе… | Выборка статистики |
|---|---|
| Среднее значение населения, \(\mu\) 92\) | |
| Доля населения, \(р\) | пропорция выборки, \(\шляпа{р}\) |
| разница в двух пропорциях населения, \(p_1-p_2\) | разница в пропорциях выборки, \(\шляпа{р}_1-\шляпа{р}_2\) |
На этих уроках мы будем работать не только над получением формул для проверки гипотез, но и над утверждением, что они в каком-то смысле «хороши»… например, мощные. Мы также узнаем, как использовать метод дисперсионного анализа для сравнения более чем двух средних значений, а также как использовать набор точек данных \(x,y\) для проверки линейной зависимости между \(x\).
)-переменная и \(y\)-переменная.
Пример №3
Биолог, изучающий пауков, выбрал случайную выборку из 20 пауков и измерил длину (в миллиметрах) одной из передних ног 20 пауков. Какова средняя длина передних ног всех таких пауков в популяции?
Ответ
Опять же, мы не можем измерить длину передних ног всех пауков в популяции. Мы можем взять случайную выборку пауков из популяции и измерить их передние ноги. Биолог сделал это за нас, получив:
15,10 13,55 15,75 20,00 15,45 13,60 16,45 14,05 16,95 19,05
16,40 17,05 15,25 16,65 16,25 17,75 15,40 16,80 17,55 19,05
15.40 16,80 17,55 19,05
. миллиметры. Опять же, медиана образца 16,425 — это хорошо. Но нас не интересует медиана выборки . Нас интересует медиана населения .
Разумно предположить, что здесь можно применить методы раздела 6. То есть мы могли бы найти доверительный интервал для медианы генеральной совокупности. Единственная проблема заключается в том, что в разделе 6 не рассматриваются доверительные интервалы для медианы.
Почему это? Ну, это потому, что доверительные интервалы в разделе 6 получены путем предположений о распределении данных, предполагая, например, что длина передних ног пауков нормально распределена.
Вскоре мы узнаем, что методы из раздела 8, называемые непараметрические методы получены без допущений о распределении базовых данных. После того, как мы проработаем раздел 8, мы сможем сделать такое утверждение для биолога этого примера:
«Мы можем быть на 95% уверены, что медиана длины передних ног всех пауков находится в пределах 15,40». и 17,05 мм
И мы сможем сделать это утверждение, не делая никаких предположений о распределении длины передних ног пауков.
Раздел 3
Предыдущий пример иллюстрирует вопрос, на который мы ответим на уроках в Разделе 8. В частности, мы узнаем:
- как использовать критерий согласия хи-квадрат для оценки соответствует ли набор данных определенному распределению вероятностей
- как использовать критерий хи-квадрат для проверки независимости между двумя категориальными переменными (например, полом и мнением)
- как использовать порядковую статистику для определения выборочных процентилей и доверительных интервалов для соответствующих процентилей генеральной совокупности
- как использовать критерий Уилкоксона для сравнения медиан двух популяций
- как использовать прогон теста для проверки случайности измерений
- как использовать критерий согласия Колмогорова-Смирнова для оценки того, соответствует ли набор данных определенному распределению вероятностей
- как провести повторную выборку данных как способ изучения распределения статистической выборки
Опять же, все методы, которые мы изучим в разделе 8, разработаны с небольшими предположениями или вообще без допущений о распределении лежащих в их основе данных.
Пример #4
Ставки на победу лошадей A, B и C следующие суммы:
- Лошадь A: \$400,000
- Лошадь B: $250 000
- Лошадь C: $350,000
Предположим, что трекер хочет снять 10 % или 100 000 долл. США. Сколько ипподром должен заплатить игроку за выигрыш по ставке $2 на лошадь А?
Ответ
Вскоре в разделе 9 мы узнаем, как байесовские статистики используют субъективную вероятность для ответа на такого рода вопросы. Короче говоря, мы можем использовать сумму, поставленную на лошадь А, как показатель того, что игроки думают о том, какая лошадь выиграет. То есть вероятность того, что лошадь А выиграет, равна:
\(\dfrac{400000}{1000000}=0,40\)
Следовательно, шансы на выигрыш лошади А:
\(\dfrac{1-0,40}{0,40}=1,5\)
Итак, при ставке в 1 доллар на лошадь А дорожка может принести игроку 1,50 доллара; а при ставке в 2 доллара за трек можно было заплатить 3 доллара. Тем не менее, мы не можем останавливаться на этом, так как трек хочет снять немного денег.