навыков, необходимых детям для поступления в шестой класс
навыков, необходимых детям для поступления в шестой класс | ПонятноПерейти к содержимомуЭта страница на английском языке
Потому что различия — наша самая большая сила
ПожертвоватьОткрывается в новом окнеЗачем поддерживать Понимание?
Автор Amanda Morin
Краткий обзор
Организованность и независимость — важные навыки шестиклассников.
Шестиклассники должны понимать разрядное значение и уметь работать с десятичными знаками до сотых.
Шестиклассники должны писать, чтобы предоставить информацию, поддержать свое мнение и рассказать историю.
Шестой класс — большой переходный год. Во многих школьных округах именно в это время учащиеся переходят в среднюю школу, что предполагает перемещение из класса в класс в течение дня, а также повышенную нагрузку. Академические ожидания также делают скачок вперед.
Академические ожидания также делают скачок вперед.
Академические стандарты вашего штата определяют навыки, необходимые учащимся для каждого уровня обучения. Вот некоторые из ключевых навыков, которые дети должны освоить к концу пятого класса, чтобы быть готовыми к шестому классу.
Навыки для подготовки к 6 классу: английский язык и грамотность
Чтобы подготовиться к шестому классу, пятиклассники помимо коротких рассказов начинают читать пьесы, стихи и новостные статьи. Они расширяют словарный запас, изучая греческие и латинские корни слов. Они также работают над навыками, которые помогают им обобщать то, что они изучают — как в письменной, так и в устной форме.
Дети ежедневно пишут и улучшают свои исследовательские навыки сбора информации, а также ее интерпретации, организации и представления. Они учатся выполнять следующие виды деятельности, которые помогают развивать языковые навыки и навыки грамотности:
- Определите темы рассказов, стихов и пьес, глядя на то, как персонажи реагируют на вызовы.

- Сравните рассказы и стихи на одну и ту же тему.
- Подкрепляйте идеи фактами и деталями из текста.
- Используйте информацию из разных источников (книги, статьи, веб-сайты), чтобы найти ответ на вопрос или проблему.
- Изучите условные обозначения стандартного английского языка и изучите лексику по теме (например, научные слова), чтобы использовать ее в письменной и устной речи.
- Понимать сравнения, метафоры и другие образные выражения.
- Участвуйте в разговорах и дискуссиях, не только слушая, но и задавая вопросы и добавляя свои идеи.
- Проводите презентации, рассказывайте истории и пишите отчеты, исследовательские работы и эссе в логическом порядке и с дополнительными деталями.
Загрузите графические органайзеры, чтобы помочь ребенку писать, и узнайте, как помочь ребенку разбивать письменные задания на части. Ваш ребенок испытывает трудности с чтением? Откройте для себя способы развития фонологической осведомленности в средней школе. И посмотрите, какие навыки чтения и письма обычно развиваются у детей в разном возрасте.
И посмотрите, какие навыки чтения и письма обычно развиваются у детей в разном возрасте.
Навыки для подготовки к 6 классу: Математика
К концу пятого класса учащиеся должны понимать разрядное значение и уметь работать с десятичными знаками до сотых. Также ожидается, что они будут знать, как складывать, вычитать и умножать дроби. Пятый класс также год для построения геометрии и навыков измерения.
Вот некоторые математические упражнения, которые дети выполняют, чтобы подготовиться к шестому классу:
- Сравните два десятичных знака и узнайте, какой из них больше или меньше другого.
- Решите текстовые задачи, используя умножение, дроби или смешанные числа.
- Представление математических задач на графике.
- Измерьте объем и свяжите объем с умножением и сложением.
Загрузите графические органайзеры, чтобы помочь вашему ребенку с математикой. Получите советы, как помочь ребенку с выполнением сложных домашних заданий по математике. И узнайте больше о математических навыках, которые обычно развиваются у детей в разном возрасте.
И узнайте больше о математических навыках, которые обычно развиваются у детей в разном возрасте.
Как помочь подрастающему шестикласснику
Дети развиваются с разной скоростью. Но если ваш ребенок не овладел большинством этих навыков к концу пятого класса, было бы неплохо поговорить с учителем вашего ребенка о том, что вас беспокоит. Вместе вы и учитель можете разработать план устранения проблемных мест вашего ребенка.
Вы также можете тренировать навыки вместе с ребенком дома. Вот что вы можете сделать:
- Попросите ребенка прочитать и обсудить детали как художественных, так и информационных текстов различной длины.
- Практика умножения и деления без бумаги («в уме»).
- Потренируйтесь округлять десятичные дроби с долларами и монетами или с ценами на предметы, указанные в рекламных объявлениях.
- Обсудите положительные и отрицательные числа с точки зрения кредита и дебета, используя банковский счет или счет.
- Обсудите объем предметов вокруг вашего дома, таких как бутылка с водой, коробка или контейнер.

Имейте в виду, что деятельность детей в шестом классе требует хорошего качества. Узнайте, как помочь ребенку развить эти навыки. И следуйте инструкциям, чтобы подготовить вашего ребенка к изменениям в распорядке дня в средней школе.
Основные выводы
Чтобы быть готовыми к шестому классу, дети должны знать множество способов находить ответы на вопросы и подкреплять свои ответы фактами и подробностями.
Если вы заметили, что ваш ребенок не успевает, поговорите с учителем вашего ребенка о своих проблемах.
Практика математики и чтения дома может помочь вашему ребенку подготовиться к шестому классу.
Расскажите нам, что вас интересует
Об авторе
Об авторе
Аманда Морин — автор книги «Руководство для родителей по специальному обучению для всех» и бывший руководитель отдела идейного лидерства в Understood. Как эксперт и писатель, она помогала создавать Understanded с первых дней его существования.
Отзыв от
Отзыв от
Кристен Л. Ходнетт, MSEd, клинический профессор кафедры специального образования в Хантер-колледже в Нью-Йорке.
Узнайте, что возможно, когда вас понимают.
Мы будем присылать вам самые полезные истории и ресурсы по электронной почте.
Подробнее
Copyright © 2014-2023 Understood For All Inc.
Математика, 6 класс, Начало работы, Свойства операций
Обзор
Класс рассматривает свойства операций. Смоделировано использование вопросов типа «задай себе вопрос», чтобы разобраться в проблемах и проявить настойчивость. Учащиеся анализируют, что нужно делать, когда они чувствуют, что застряли на проблеме. Наконец, учащиеся используют свойства операций для оценки выражений.
Учащиеся используют свойства операций для подтверждения эквивалентности двух выражений.
- Чтобы начать работу над проблемой, разберитесь в ней, используя вопросы типа «задай себе вопрос».

- Будьте настойчивы в решении проблемы, даже если чувствуете, что застряли.
- Используйте свойства операций для вычисления выражений.
Просмотрите названия свойств операций и кратко обсудите их с учащимися. Сами свойства должны быть знакомы учащимся, но учащиеся могут не идентифицировать их по имени. Пока не просматривайте каждое свойство, потому что учащиеся будут иметь доступ к свойствам операций через Глоссарий во время работы.
Открытие
Что вы помните об этих свойствах операций?
Попросите учащихся молча прочитать инструкции и пример задачи. Попросите одного ученика объяснить своими словами, в чем заключается задача.
Скажите учащимся, что сегодня и в большинстве дней они будут работать над задачами самостоятельно, а затем обсудят свои идеи с партнером.
Продемонстрировать, как использовать вопросы типа «задай себе вопрос», чтобы понять проблему:
- Что мне нужно сделать, чтобы решить проблему? Проблема заключается в том, эквивалентны ли эти два выражения.

- Какие два выражения? Вот выражения: 2(8 + 7) + 5 и 5(4 + 3).
- Что означает эквивалентность двух выражений? Я знаю, что если два выражения эквивалентны, значения выражений равны.
- Как найти значение каждого выражения? Я могу использовать свойства операций для вычисления выражения.
- Каковы свойства операций? Хм… я знаю большинство из них. Я могу заглянуть в Глоссарий, чтобы прочитать о них, если мне нужно.
- Позвольте мне еще раз прочитать задачу. Что значит «использовать свойства операций для отображения каждого шага»? Я предполагаю, что это означает, что мне нужно выполнить ряд шагов, чтобы увидеть, могу ли я изменить одно выражение на другое. Может быть, для каждого шага я пишу свойство, которое это позволяет.
- Показано ли в примере использование свойств операций для каждого шага? Я могу использовать пример, чтобы помочь мне понять.
- Почему в первой строке написано «Распределительная собственность»? Левая часть уравнения умножает количество 8, добавленное к 7, на 2, а затем добавляет 5.
 Правая часть уравнения показывает количество 8, умноженное на 2, добавленное к количеству 7, умноженному на 2, а затем добавляет 5. О, я видеть. Множитель 2 был распределен как на 7, так и на 8, которые были в скобках.
Правая часть уравнения показывает количество 8, умноженное на 2, добавленное к количеству 7, умноженному на 2, а затем добавляет 5. О, я видеть. Множитель 2 был распределен как на 7, так и на 8, которые были в скобках. - Следующая строка не имеет даже свойства операции. Там написано «Умножение». Почему это? Ага, понятно. 2 раза по 8 и 2 раза по 7 умножаются, чтобы изменить выражение на 16 + 14 + 5. А в следующей строке написано «Сложение», потому что числа складываются вместе, чтобы получить 35.
- Подождите, почему следующая строка показать новую задачу на умножение? Там написано, что причина в умножении, хммм.
- Мы только что нашли результат выражения, так почему же пример затем меняет его обратно на выражение умножения? Может быть, мне следует вернуться к проблеме, чтобы выяснить, почему. У нас есть два выражения. Ага, понятно. Второе выражение использует умножение. Он умножает количество 4, добавленное к 3, на 5. Это простое выражение, потому что оно просто 5 умножает на 7.
 О, это то, что делал пример, но он показал 7 умножить на 5. Что ж, мы знаем, что эти выражения имеют такой же результат.
О, это то, что делал пример, но он показал 7 умножить на 5. Что ж, мы знаем, что эти выражения имеют такой же результат. - Какое свойство говорит, что 7 умножить на 5 даст тот же результат, что и 5 умножить на 7? Если я не знаю свойство, я могу найти его в глоссарии. Это свойство умножения, поэтому я могу искать по ключевым словам «свойство» и «умножение». (Покажите учащимся, как получить доступ к Глоссарию и выполнить поиск, используя ключевые слова «свойство» и «умножение».)
- Кажется, что этот поиск покажет множество свойств. Который из них? Я могу искать, пока не найду свойство, которое позволяет мне менять порядок множителей в выражении умножения.
- Является ли это ассоциативным свойством? Это свойство связано со скобками, но в этой строке выражения скобок нет.
- Это следующая недвижимость? Ах, да. Здесь следующее свойство, показанное в примере, — это «переместительное свойство». Это свойство позволяет переключать порядок множителей в выражении умножения.

- Почему в последней строке примера говорится «Распределительная собственность»? Хм… Похоже, 7 превратили в 4 + 3. Умножение распределяется по сложению.
- Значит ли это, что два выражения эквивалентны? Да, они. В примере первое выражение заменено вторым выражением.
После демонстрации спросите учащихся:
- Какие вопросы вы можете задать себе, чтобы разобраться в проблеме?
- Что делать, если вы застряли на проблеме?
Во-первых, пусть учащиеся несколько минут поразмышляют над этими двумя вопросами самостоятельно. Затем попросите учащихся обсудить свои идеи со своими партнерами.
Теперь пусть учащиеся поделятся своими идеями с классом. Как и в случае с предыдущими уроками, предоставление учащимся возможности генерировать собственные идеи позволяет им взять на себя ответственность за собственное обучение. Если у студентов возникают проблемы с обдумыванием вопросов, дайте им список вопросов, которые можно задать самому себе, чтобы они могли обратиться к ним.
Эти подсказки представляют собой идеи, которые учащиеся могут использовать, чтобы задать себе вопросы:
- Что означает _ _ _ ?
- О чем говорит эта проблема?
- Какие цифры в задаче и что они означают?
- Что за проблема?
Эти советы представляют собой идеи того, что учащиеся могут сделать, если они застряли на задаче:
- Посмотрите на похожие задачи, которые вы уже решали ранее.
- Смоделируйте задачу, используя фишки или другие материалы.
- Набросайте схему или другое изображение.
- Напишите, что вы знаете.
- Пишите вопросы, чтобы задать их позже.
- Проверьте другие ресурсы.
Запишите идеи учащихся в виде двух отдельных списков. После того, как все идеи перечислены, просмотрите каждую для ясности. Согласие не обязательно, потому что полезно иметь разнообразие идей. Эти списки могут продолжать расти в течение года.
Эти списки могут продолжать расти в течение года.
Математическая практика 1: Разбираться в задачах и настойчиво решать их.
Объясните, что учащимся важно осмыслить проблему в качестве первого шага в работе над ее решением, и важно, чтобы учащиеся упорно решали проблему, даже если они чувствуют, что застряли.
Вскрытие
При самостоятельной работе необходимо:
- Разобраться в проблеме.
- Используйте вопросы типа «задай себе вопрос», чтобы узнать, что вам нужно понять, прежде чем начать.
- Преодолейте трудности, используя то, что вы знаете.
Прочитать отработанную задачу. Затем посмотрите, как ваш учитель дает пример того, как использовать вопросы типа «задай себе», чтобы понять проблему.
- Эти выражения эквивалентны?
2(8 + 7) + 5
5(4 + 3)
- Используйте свойства операций, чтобы показать каждый из шагов, предпринятых для определения эквивалентности выражений.

Вот идеи для вопросов, которые можно задать самому себе:
- Что означает _ _ __ ?
- О чем говорит эта проблема?
- Какие виды сравнений рассматриваются в задаче?
- Какие цифры в задаче и что они означают?
- Что за проблема?
Вот идеи, что делать, если вы застряли:
- Посмотрите на похожие проблемы, которые вы уже решали ранее.
- Смоделируйте задачу, используя фишки или другие материалы.
- Набросайте схему или другое изображение.
- Напишите, что вы знаете.
- Запишите вопросы, чтобы задать их позже.
- Проверьте другие ресурсы.
Обсудить математическую миссию. Учащиеся обосновывают эквивалентные выражения, используя свойства операций.
Открытие
Обоснуйте эквивалентные выражения, используя свойства операций.
Предложите учащимся самостоятельно поработать над обеими задачами на рабочее время в течение 5 минут, прежде чем работать со своим партнером.
Студент не начинает с вопросов типа «задай себе».
- Какие вопросы вы задавали себе перед тем, как приступить к решению этой задачи?
Учащийся прекращает работу, когда застревает.
- Что делать, если вы застряли на проблеме?
Учащийся меняет порядок вычитания или деления.
- Почему можно изменить порядок чисел при сложении и умножении, но нельзя при вычитании и делении?
Учащийся не понимает, как убрать скобки.
- Как узнать, когда использовать круглые скобки и когда их можно удалить?
Математическая практика 1: Разбираться в задачах и настойчиво решать их.
Учащиеся начинают свою работу с того, что сначала разбираются в проблеме, используя вопросы типа «задай себе вопрос». Затем они упорствуют, используя сгенерированные ими идеи о том, что делать, когда вы застряли.
(22)(4⋅14)+2 эквивалентно 3 ⋅ 2
= 4(4 • 14) + 2 Квадрат
= 4 + 2 Тождественное свойство умножения
9 0004 = 6 Дополнение= 3 × 2 Умножение
=(22)(1)+2 Обратное свойство
Рабочее время
- Эти выражения эквивалентны?
(22)(4⋅14)+2
3 ⋅ 2
- Используйте свойства операций, чтобы показать каждый из шагов, предпринятых для определения эквивалентности выражений.

Подсказка:
- Какие вопросы вы задавали себе, прежде чем работать над этой задачей?
- Почему можно изменить порядок чисел при сложении и умножении, но нельзя при вычитании и делении?
- Откуда вы узнали, когда использовать круглые скобки, а когда их можно удалить?
Предложите учащимся самостоятельно поработать над обеими задачами на рабочее время в течение 5 минут, прежде чем работать со своим партнером.
Студент не начинает с вопросов типа «задай себе».
- Какие вопросы вы задавали себе перед тем, как приступить к решению этой задачи?
Учащийся прекращает работу, когда застревает.
- Что делать, если вы застряли на проблеме?
Учащийся меняет порядок вычитания или деления.
- Почему можно изменить порядок чисел при сложении и умножении, но нельзя при вычитании и делении?
Учащийся не понимает, как убрать скобки.
- Как узнать, когда использовать круглые скобки и когда их можно удалить?
Математическая практика 1: Разбираться в задачах и настойчиво решать их.
Учащиеся начинают свою работу с того, что сначала разбираются в проблеме, используя вопросы типа «задай себе вопрос». Затем они упорствуют, используя сгенерированные ими идеи о том, что делать, когда вы застряли.
- 58 × 31 не эквивалентно 1500+240+12(58)
58 × 31 = 58(30 + 1) Распределительное свойство
= (58 × 30) + (58 × 1) Распределительная собственность
= (58 × 30) + 58 Тождественное свойство умножения
= (30 × 58) + 58 Коммутативное свойство умножения
= 30(50 + 8) + 58 Распределительное свойство
= 1 500 + 240 + 58 Распределительное свойство и умножение
Рабочее время
- Эти выражения эквивалентны?
58 ⋅ 31
1 500+240+12(58)
- Используйте свойства операций, чтобы показать каждый из шагов, предпринятых для определения эквивалентности выражений.

Подсказка:
- Какие вопросы вы задавали себе, прежде чем работать над этой задачей?
- Почему можно изменить порядок чисел при сложении и умножении, но нельзя при вычитании и делении?
- Откуда вы узнали, когда использовать круглые скобки, а когда их можно удалить?
Пока ученики работают, пройдитесь по комнате и внимательно выслушайте их рассуждения. Следите за следующими вещами:
- Задает ли слушатель вопросы, когда говорящий не может понять?
- Объясняют ли оба партнера свои процессы, даже если они делали одно и то же?
- Понимают ли учащиеся, как возводить число в квадрат?
- Соблюдают ли учащиеся порядок операций при вычислении выражений?
- Возможные ответы:
(3 + 9) − (2 × 3)
3(4 + 2) ÷ (3 + 0)
Рабочее время
- Опишите свои стратегии определения соответствующих свойств операций.
- Укажите, какие свойства было труднее понять.

- Определите, какие ошибки вы допустили, и чему вы научились на них.
- Включите любые вопросы, которые ваш партнер задал по поводу вашего объяснения.
- Напишите два других выражения, которые эквивалентны:
(22)(4⋅14)+2
Для каждой задачи выберите двух студентов-докладчиков, которые пришли к одному и тому же выводу об эквивалентности выражений, но не разбили этапы решения одинаковым образом. Попросите класс сравнить шаги двух решений.
Потратьте несколько минут на обсуждение того, как свойства операций используются в обоснованиях учащихся.
Попросите нескольких учащихся, решивших задачу, представить созданные ими эквивалентные выражения. Попросите учащихся объяснить, откуда они узнали, что выражения эквивалентны.
Математическая практика 1: Разбираться в задачах и настойчиво решать их.
Предложите учащимся рассказать о том, как они разобрались в проблемах, и о стратегиях, которые они использовали, чтобы проявить упорство, когда застряли на проблеме.
Задача производительности
Делайте заметки о том, как ваши одноклассники использовали свойства операций в своих обоснованиях.
В присутствии одноклассников задайте такие вопросы, как:
- В чем сходство и различие этапов этих двух разных решений?
- Почему эти выражения эквивалентны, хотя выглядят по-разному?
Начните это задание с краткого обсуждения качеств хорошего резюме:
- Оно посвящено важной математике сегодняшнего урока.
- Несколько предложений объясняют математику.
- Это выходит за рамки ответов на более важные идеи урока.
Попросите каждого учащегося написать резюме по математике на уроке.
Затем вместе напишите конспект урока. Когда вы закончите, если резюме класса полезно, разместите его для справки студентов.
SWD: Направьте учащихся к подсказкам в качестве контрольного списка информации, которую им необходимо включить в свои резюме. Рассмотрите возможность создания бумажного ресурса с подсказками, чтобы учащиеся могли держать их перед собой, когда пишут свои резюме.
Рассмотрите возможность создания бумажного ресурса с подсказками, чтобы учащиеся могли держать их перед собой, когда пишут свои резюме.
Свойства операций описывают допустимые изменения выражений, которые поддерживают эквивалентность. Эквивалентность означает, что значение выражения остается неизменным. Каждое изменение должно быть показано, а операция или свойство операций должны использоваться для обоснования шага. Некоторые свойства верны только для некоторых операций. Например, свойства коммутативности и ассоциативности работают для сложения и умножения, но не для вычитания и деления.
Дополнительные вопросы, которые вы можете обсудить:
- Обратное свойство связывает сложение с вычитанием и умножение с делением.
- Свойство распределения объясняет, как распределить фактор между обоими слагаемыми.
Формирующее оценивание
Хорошее резюме ясно объясняет важную математику сегодняшнего урока.
- Напишите вкратце о том, как обосновать эквивалентность двух выражений.



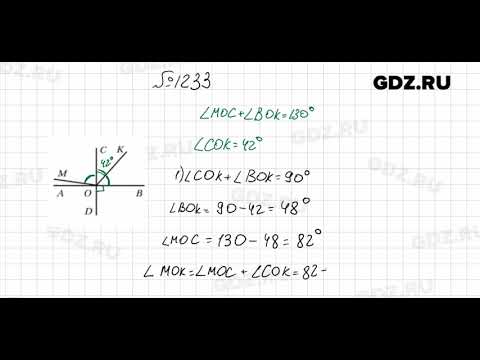
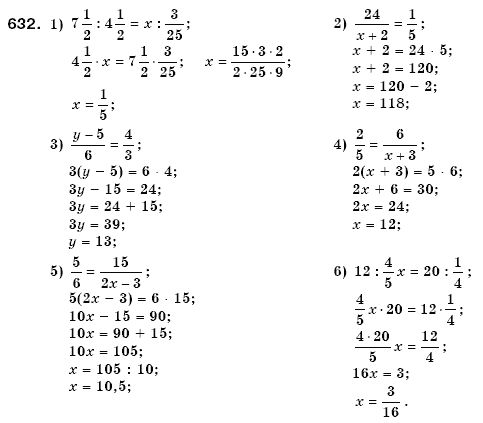
 Правая часть уравнения показывает количество 8, умноженное на 2, добавленное к количеству 7, умноженному на 2, а затем добавляет 5. О, я видеть. Множитель 2 был распределен как на 7, так и на 8, которые были в скобках.
Правая часть уравнения показывает количество 8, умноженное на 2, добавленное к количеству 7, умноженному на 2, а затем добавляет 5. О, я видеть. Множитель 2 был распределен как на 7, так и на 8, которые были в скобках. О, это то, что делал пример, но он показал 7 умножить на 5. Что ж, мы знаем, что эти выражения имеют такой же результат.
О, это то, что делал пример, но он показал 7 умножить на 5. Что ж, мы знаем, что эти выражения имеют такой же результат.