Мерзляк 5 класс — § 12. Виды углов. Измерение углов
Вопросы к параграфу
1. Какой угол называют развёрнутым? Развёрнутый угол — это угол, лучи которого образуют прямую и их начала совпадают.
2. В каких единицах измеряют углы? Углы измеряют в градусах (например ∠45° — это угол величиной 45 градусов).
3. Какова градусная мера развёрнутого угла? 180°
4. Что означает измерить угол? Измерить угол — это значит посчитать сколько единичных углов в нём помещаются.
5. Как называется прибор, который используют для измерения углов? Транспортир.
6. Расскажите, как пользоваться транспортиром. Для того, чтобы измерить угол транспортиром надо:
- приложить линейку транспортира к одной из сторон угла;
- совместить центр транспортира с вершиной угла;
- определить, какой из штрихов шкалы транспортира пересекает вторая сторона угла;
- определить градусную величину, которой соответствует пересекаемый штрих шкалы транспортира.

Важно:
- Одна из сторон транспортира должна точно лежать на линейке прибора.
- Центр транспортира должен точно совпадать с вершиной угла.
- Если вторая сторона угла не доходит до шкалы транспортира, то надо мысленно продолжить луч до пересечения с прибором, либо начертить продолжение луча до нужной длины.
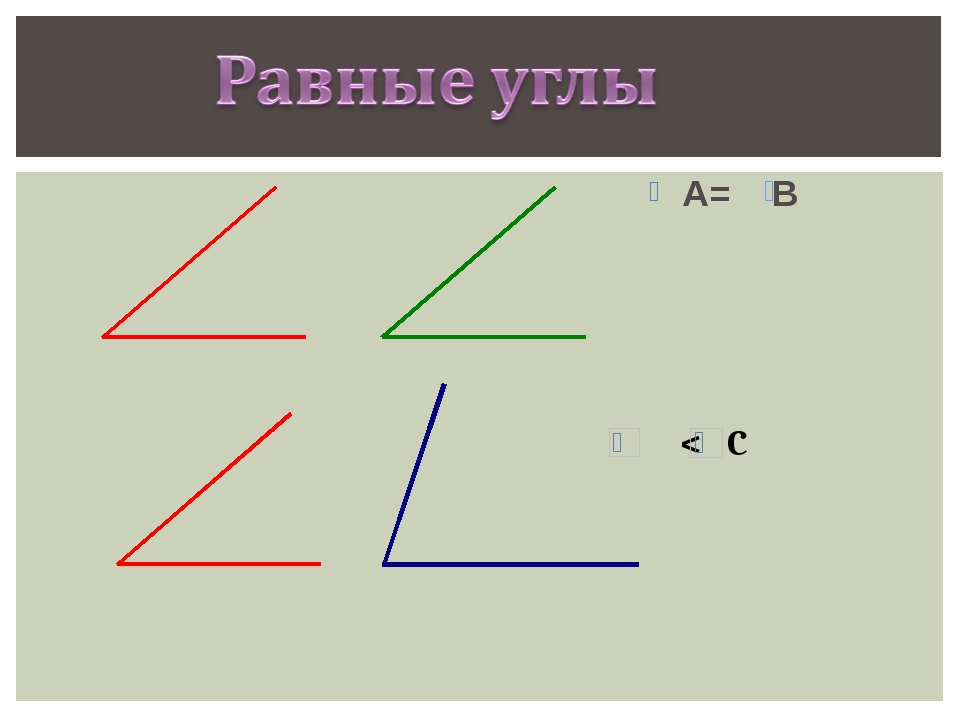
7. Какие градусные меры имеют равные углы? Равные углы имеют равные градусные меры.
8. Какой из двух неравных углов считают большим? Большим считается угол, градусная мера которого больше.
9. Каким свойством обладает величина угла? Если между сторонами угла АОС провести луч ОВ, то градусная мера угла АОС равна сумме градусных мер углов АОВ и ВОС:
∠АОС = ∠АОВ +∠ВОС, если луч ОВ лежит между сторонами угла АОС.
10. Какой угол называют острым? Острым углом называют угол, градусная мера которого меньше 90°.
11. Какой угол называют прямым? Прямым углом называют угол, градусная мера которого равна 90°.
12. Какой угол называют тупым? Тупым углом называют угол, градусная мера которого больше 90°, но меньше 180°.
13. На какие углы делит развёрнутый угол его биссектриса? Биссектриса делит угол на два прямых угла, то есть градусная мера каждого из этих углов равна 90°.
14. В каких случаях говорят, что от данного луча отложен данный угол? Говорят, что от данного луча отложен данный угол в том случае, если дан определённый луч, например ОА, и от него построен заданный угол, например ∠АОС = 63°, причём вершиной угла является вершина заданного луча.
Решаем устно
1. Назовите два числа, одно из которых:
- на 27 больше другого — 1 и 28 — число 28 на 27 больше числа 1.
- на 15 меньше другого — 2 и 17 — число 2 на 15 меньше числа 17.
- в 7 раз меньше другого — 3 и 21 — число 3 в 7 раз меньше исла 21.
- в 3 раза больше другого — 4 и 12 — число 12 в 3 раза больше 4.

2. Часы спешат на 10 мин и сейчас показывают время 10 ч 8 мин. Который час на самом деле?
10 ч 8 мин — 10 мин = 9 ч 58 мин
Ответ: сейчас 9 ч 58 мин.
3. Часы отстают на 7 мин и сейчас показывают время 16 ч 55 мин. Который час на самом деле?
16 ч 55 мин + 7 мин = 17 ч 2 мин.
Ответ: сейчас 17 ч. 2 мин.
4. Какие из следующих уравнений не имеют корней:
- 2х = х. Это равенство будет верным только при х = 0, значит у этого уравнения есть единственный корень — 0.
- 0х = 0. Это равенство будет верным при любом значении х, значит у этого уравнение бесконечное множество корней.
- 3 — х = 3. Это равенство будет верным только при х = 0, значит у этого уравнения есть единственный корень — 0.
- 0х = 6. Это равенство не будет верным ни при каких значениях х, значит это уравнение не имеет корней.
- х • х = х. Это равенство будет верным только при х = 0 и х = 1, значит у этого уравнения 2 корня: 0 и 1.

- х + 6 = х + 7. Это равенство не будет верным ни при каких значениях х, значит это уравнение не имеет корней.
- 8х = 0. Это равенство будет верным только при х = 0, значит у этого уравнения есть единственный корень — 0.
- 3 — х = 2. Это равенство будет верным только при х = 1, значит у этого уравнения есть единственный корень — 1.
- 1 • х = 5. Это равенство будет верным только при х = 5, значит у этого уравнения есть единственный корень — 5.
Ответ: не имеют корней уравнения под номером 4 и 6.
5. Для озеленения улицы длиной 3 км на одной из её сторон посадили деревья на расстоянии 20 м друг от друга. Первое дерево было посажено в начале улицы, а последнее — в её конце. Сколько деревьев было посажено? Чему равно расстояние между первым и пятым деревьями?
3 км = 3 000 м.
1) 3 000 : 20 + 1 = 151 (дерево) — было посажено.
2) 20 • (5 — 1) = 20 • 4 = 80 (метров) — расстояние между 1-м и 5-м деревом.
Ответ: Было посажено 151 дерево. Между первым и пятым деревом 80 метров.
Между первым и пятым деревом 80 метров.
Упражнения
296. Начертите:
- острый угол EFC
- прямой угол ORT
- тупой угол D
- развёрнутый угол КАР
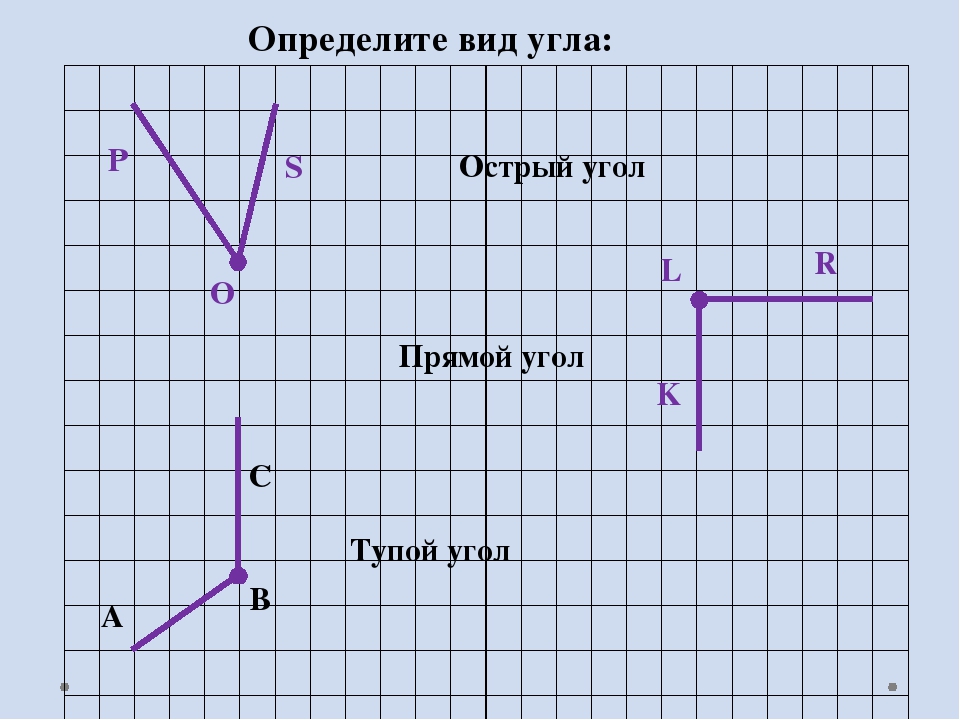
297. Найдите на рисунке 93 острые, тупые и прямые углы.
- Острые углы: ∠C, ∠M, ∠P
- Тупые углы: ∠K, ∠Q, ∠T
- Прямые углы: ∠A, ∠O
298. Какие из данных углов острые, тупые, прямые, развёрнутые: ∠А = 96°, ∠B = 84°, ∠S= 180°, ∠D=90°, ∠R = 162°, ∠E= 60°, ∠Q = 100°, ∠M= 72°?
- Острые углы: ∠B = 84°, ∠E= 60°, ∠M= 72°
- Тупые углы: ∠А = 96°, ∠R = 162°, ∠Q = 100°
- Прямые углы: ∠D=90°
- Развёрнутые углы: ∠S= 180°
299. Найдите, пользуясь транспортиром, градусные меры углов, изображённых на рисунке 94. Определите вид каждого угла.
- ∠AMK = 28º — острый угол
- ∠CTF = 33º — острый угол
- ∠POB = 120º — тупой угол
- ∠SNE = 125º — тупой угол
300. Найдите, пользуясь транспортиром, градусные меры углов, изображённых на рисунке 95. Определите вид каждого угла.
Найдите, пользуясь транспортиром, градусные меры углов, изображённых на рисунке 95. Определите вид каждого угла.
- ∠PRT = 133º — тупой угол
- ∠EFM = 40º — острый угол
- ∠BCQ = 110º — тупой угол
- ∠AKS = 67º — острый угол
301. Начертите угол, градусная мера которого равна: 1) 38°; 2) 124°; 3) 92°; 4) 90°; 5) 87°; 6) 54°; 7) 170°; 8) 65°. Определите вид каждого угла.
- ∠A = 38º — острый угол
- ∠B = 124º — тупой угол
- ∠C = 92º — тупой угол
- ∠D = 90º — прямой угол
- ∠E = 87º — острый угол
- ∠F = 54º — острый угол
- ∠K = 170º — тупой угол
- ∠R = 65º — острый угол
302. Проведите луч. Отложите от этого луча угол, градусная мера которого равна: 1) 40°; 2) 130°; 3) 68°; 4) 164°. Определите вид каждого из построенных углов.
Луч RE
- ∠ERD = 40º — острый угол
- ∠ERB = 130º — тупой угол
- ∠ERC = 68º — острый угол
- ∠ERA = 164º — тупой угол
303. На рисунке 96 ∠CMK = 132°, а угол АМК — развёрнутый. Вычислите величину угла АМС.
На рисунке 96 ∠CMK = 132°, а угол АМК — развёрнутый. Вычислите величину угла АМС.
∠АМК = 180° — развёрнутый
∠АМС = ∠АМК — ∠CMK = 180° — 132° = 48°
Ответ: ∠АМС = 48°.
304. На рисунке 97 угол АОК — прямой, ∠POC — 54°, а угол СОК — развёрнутый. Вычислите величину угла АОР.
∠AOK = 90° — прямой
∠COК = 180° — развёрнутый
∠АOP = ∠COK — ∠POC — ∠AOK = 180° — 54° — 90° = 36°
Ответ: ∠АOP = 36°
305. Какой из углов, изображённых на рисунке 98, наибольший? Наименьший?
- ∠D — наименьший угол
- ∠C — наибольший угол
306. Начертите угол CDE, равный 152°. Лучом DA разделите этот угол на два угла так, чтобы ∠CDA = 98°. Вычислите величину угла ADE.
∠CDE = 152°
∠CDA = 98°
∠ADE = ∠CDE — ∠CDA = 152° — 34° = 54°
Ответ: ∠ADE = 54°.
307. Начертите угол ABC, равный 106°. Лучом BD разделите этот угол на два угла так, чтобы ∠ABD = 34°. Вычислите величину угла DBC.
Вычислите величину угла DBC.
∠ABC = 106°
∠ABD = 34°
∠DBC = ∠ABC — ∠ABD = 106° — 34° = 72°
Ответ: ∠DBC = 54°.
308. Из вершины прямого угла ВОМ (рис. 99) проведены два луча ОА и ОС так, что ∠BOC = 74°, ∠AOM = 62°. Вычислите величину угла АОС.
∠ВОМ = 90° — прямой
∠BOC = 74°
∠AOM = 62°
∠MOC = ∠BOM — ∠BOC = 90° — 74° = 16°
∠AOC = ∠AOM — ∠MOC = 62° — 16° = 46°
Ответ: ∠AOC = 46°.
309. Из вершины развёрнутого угла АСР (рис. 100) проведены два луча СТ и CF так, что ∠ACF = 158°, ∠TCP = 134°. Вычислите величину угла TCF.
∠ACP = 180° -развёрнутый
∠ACF = 158°
∠TCP = 134°
∠PCF = ∠ACP — ∠ACF = 180° — 158° = 22°
∠TCF = ∠TCP — ∠PCF = 134° — 22° = 112°
Ответ: ∠TCF = 112°.
310. Верно ли утверждение:
1) угол, который меньше тупого, — острый. Неверно, так как меньше тупого не только острые углы, но и прямой угол.
2) угол, который меньше развёрнутого, — тупой. Неверно, так как меньше развёрнутого угла все тупые углы, все острые углы и прямой угол.
3) половина тупого угла — острый угол. Верно, так как половина даже самого большого тупого угла будет меньше 90º.
4) сумма градусных мер двух острых углов больше 90°. Неверно, так как сумма двух острых углов может быть и меньше 90°.
5) угол, который больше прямого, — тупой. Неверно, так как больше прямого могут быть как тупые углы, так и развёрнутый угол.
311. Найдите градусную меру утла между стрелками часов, если они показывают:
- 3 ч — это угол между минутной стрелкой, указывающей на 12 часов (чёрная стрелка) и часовой стрелкой, указывающей на 3 часа (красная стрелка) — прямой угол. Градусная мера этого угла — 90º.
- 6 ч — это угол между минутной стрелкой, указывающей на 12 часов (чёрная стрелка) и часовой стрелкой, указывающей на 6 часов (синяя стрелка) — развёрнутый угол.
 Градусная мера этого угла — 180º.
Градусная мера этого угла — 180º. - 4 ч — это угол между минутной стрелкой, указывающей на 12 часов (чёрная стрелка) и часовой стрелкой, указывающей на 4 часа (зелёная стрелка) — 4/6 от развёрнутого угла. Градусная мера этого угла — 180 : 6 • 4 = 30 • 4 = 120º.
- 11 ч — это угол между минутной стрелкой, указывающей на 12 часов (чёрная стрелка) и часовой стрелкой, указывающей на 11 часов (фиолетовая стрелка) — 1/6 от развёрнутого угла. Градусная мера этого угла — 180 : 6 • 1 = 30 • 1 = 30º.
- 7 ч — это угол между минутной стрелкой, указывающей на 12 часов (чёрная стрелка) и часовой стрелкой, указывающей на 7 часов (розовая стрелка) — 5/6 от развёрнутого угла. Градусная мера этого угла — 180 : 6 • 5 = 30 • 5 = 150º.
Ответ: 1) 90º, 2) 180º, 3) 120º, 4) 30º, 5) 150º.
312. Луч BK является биссектрисой угла CBD, ∠ABK = 146° (рис. 101, a). Вычислите градусную меру угла CBD.
∠ABC = 180º — развёрнутый
∠ABK = 146º
∠KBC = ∠ABC — ∠ABK = 180º — 146º = 34º
так как луч BK — это биссектриса ∠CBD, значит луч BK делит тот угол пополам. Мы заем, что ∠KBC = 34º. Значит:
Мы заем, что ∠KBC = 34º. Значит:
∠CBD = ∠KBC • 2 = 34º • 2 = 68º
Ответ: ∠CBD = 68º.
313. Луч ОА является биссектрисой угла СОМ, ∠СОМ = 54° (рис. 101, б). Вычислите градусную меру угла ВОА.
∠COM = 54º
так как луч OA — это биссектриса ∠COM, значит луч OA делит тот угол пополам. Мы заем, что ∠COM = 54º. Значит:
∠COA = ∠COM : 2 = 54º : 2 = 27º
∠BOC = 180º — развёрнутый
∠BOA = ∠BOC — ∠COA = 180º — 27º = 153º
Ответ: ∠BOA = 153º.
314. Проведите три прямые, пересекающиеся в одной точке. Запишите все развёрнутые углы, образовавшиеся при этом.
Каждая прямая образует по 2 развёрнутых угла. Значит образовались следующие развёрнутые углы: AOD, BOE, COF, DOA, EOB, FOC.
315. Проведите шесть прямых, пересекающихся в одной точке. Верно ли, что среди образовавшихся при этом углов есть угол, градусная мера которого меньше 31°?
Каждая прямая образует по 2 развёрнутых угла. Например, прямая MH образует развёрнутые углы MOH и HOM. Каждый из этих углов равен 180º. Значит сумма углов между соседними лучами на рисунке равна 180º • 2 = 360º.
Например, прямая MH образует развёрнутые углы MOH и HOM. Каждый из этих углов равен 180º. Значит сумма углов между соседними лучами на рисунке равна 180º • 2 = 360º.
Всего образовалось 12 углов, расположенных между соседними лучами. 360º : 12 = 30º. Значит как минимум один (а на самом деле два) угла будут иметь градусную меру менее 31º.
Ответ: верно.
Упражнения для повторениях
316. Заполните цепочку вычислений:
- 4 см • 300 = 1 200 см
- 1 200 см = 120 дм; 120 дм — 12 дм = 108 дм
- 108 дм : 9 = 12 дм
- 12 дм = 1 м 2 дм; 1 м 2 дм + 3 м = 4 м 2 дм
- 8 мин • 15 = 120 мин
- 120 мин = 2 ч; 2 ч + 2 ч = 4 ч
- 4 ч = 240 мин; 240 мин : 6 = 40 мин
- 40 мин — 54 сек = 39 мин 6 сек
317. Верно ли неравенство (а + 253) • 7 < (9 864 — а) : 4 при а = 124?
Ответ: при а = 124 неравенство неверно, так как 2 639 > 2 435.
318. В четыре стакана помещается столько же молока, сколько и в банку. В стакан и банку помещается 1 кг 200 г молока. Сколько граммов молока помещается в стакан?
В четыре стакана помещается столько же молока, сколько и в банку. В стакан и банку помещается 1 кг 200 г молока. Сколько граммов молока помещается в стакан?
Так как в одной банке помещается столько же молока, сколько и в 4 стаканах, то в банке и стакане будет содержаться столько же молока сколько в 5 стаканах (4 + 1 = 5).
1 кг 200 г = 1 200 г
1 200 : 5 = 240 (г) — молока помещается в стакан.
Ответ: 240 г.
319. Длина границы России с Китаем, Монголией и Казахстаном составляет 15 293 км. Найдите длину границы России с каждым из этих государств, если длина границы с Китаем и Монголией равна 7 694 км, а с Китаем и Казахстаном — 11 808 км.
1) 15 293 — 11 808 = 3 485 (км) — граница России с Монголией.
2) 7 694 — 3 485 = 4 209 (км) — граница России с Китаем.
3) 11 808 — 4 209 = 7 599 (км) — граница России с Казахстаном.
Ответ: граница России с Китаем — 4 209 км, с Монголией — 3 485 км, с Казахстаном — 7 599 км.
Задача от мудрой совы
320. Улитка за день поднимается вверх по столбу на 3 м, а за ночь съезжает по нему на 2 м вниз. На какой день она доберётся до вершины столба, высота которого равна 20 м?
Каждые сутки улитка способна подняться по столбу на 1 м:
1) 3 метра днём — 2 метра ночью = 1 метр за сутки
Но в последний день она как обычно поднимется на 3 метра, а спускаться уже не будет. Значит, за все дни, кроме последнего, улитка поднимется на 17 м:
2) 20 — 3 = 17 (метров) — преодолеет улитка за все дни, кроме последнего.
То есть ей потребуется 17 дней для преодоления 17 метров и ещё 1 день для преодоления последних 3 метров:
3) 17 : 1 + 1 = 17 + 1 = 18 (дней) — нужно улитке для того, чтобы подняться на столб.
Ответ: улитка доберётся до вершины на 18-й день.
Урок математики «Виды углов. Измерение углов». 5-й класс
Как построить современный урок?
Современные требования, предъявляемые к
организации учебной деятельности и проведению
уроков, предполагают не только активную
деятельность учащихся, носящую
поисково-исследовательский характер, но и
непременное развитие самоконтроля, самоанализа
и самооценки. Учителю необходимо не только
донести знания и заинтересовать своим предметом,
но научить ребенка ставить цели, разрабатывать
планы достижения этих целей, анализировать свои
поступки и действия. То есть ребенок должен
научиться ставить перед собой учебную задачу
самостоятельно и решать ее.
Учителю необходимо не только
донести знания и заинтересовать своим предметом,
но научить ребенка ставить цели, разрабатывать
планы достижения этих целей, анализировать свои
поступки и действия. То есть ребенок должен
научиться ставить перед собой учебную задачу
самостоятельно и решать ее.
Формированию такого умения и средств контроля и оценки помогает особый тип урока – урок-рефлексия по ФГОС.
В качестве примера привожу урок математики в 5 классе по теме “Виды углов. Измерение углов”.
УМК: Математика: 5 класс: учебник для учащихся общеобразовательных организаций / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. — 2-е изд., перераб. — М.: Вентана — Граф, 2016.
Тема урока. Виды углов. Измерение углов.
Тип урока. Урок рефлексии.
Вид урока. Комбинированный урок.
Цели:
- Содержательная: повторение понятий
«угол», «виды углов», закрепление навыка
измерения углов с помощью транспортира,
исследование техники построения угла в 30° с
помощью квадратного листа бумаги.

- Деятельностная: развитие умения контролировать процесс и результат учебной и математической деятельности, развитие навыков оценки своей деятельности
Основные понятия: градус, транспортир, измерение углов, развернутый угол, острый, прямой, тупой угол.
Оборудование и материалы: транспортиры, видеопроектор, кроссворд, раздаточный материал (макеты углов трех цветов: красный — 90°, зеленый — 45°, синий — 30° по количеству парт в классе, квадратный лист бумаги, инструкция по выполнению исследования), презентация.
Оформление доски.
| Я знаю:
Я умею: | Классная работа 31.10.16 | Я узнал:
Я научился: |
Ход урока
1. Организационный момент. (слайд 1)
(слайд 1)
— Здравствуйте, ребята, садитесь. Я рада видеть всех вас на занятии. На нашем уроке присутствуют гости, давайте порадуем их хорошими знаниями.
Презентация.
2. Мотивация урока. (слайд 2)
— Все вы, наверняка, любите решать кроссворды?… Поэтому я хочу предложить вам решить небольшой кроссворд.
— В выделенном столбце получится ключевое слово урока.
1. Угол, стороны которого образуют прямую? (развернутый)
2. Единица измерения угла? (градус)
3. Угол, градусная мера которого меньше 90°? (острый)
4. Геометрическая фигура, образующая сторону угла? (луч)
Рисунок 1
— Теперь прочтем слово, которое получилось в первом вертикальном столбце? (угол)
— Какую фигуру называют углом? (фигуру, образованную двумя лучами, имеющими общее начало)
— Какие виды углов вы знаете? (развернутый, прямой, острый, тупой)
(учитель предлагает одному, двум учащемся записать на доске, что дети уже знают по теме урока, продолжив выражения: Я ЗНАЮ)
3. Актуализация и фиксация затруднений в
индивидуальной деятельности.
Актуализация и фиксация затруднений в
индивидуальной деятельности.
1) Постановка целей.
— Итак, сформулируйте цели урока. (применение полученных знаний для построения, измерения и определения вида углов)
— На предыдущих уроках вы познакомились с геометрической фигурой, которая называется “Угол”, научились измерять и строить углы с помощью — измерительного прибора (как он называется — транспортир).
(учитель предлагает одному, двум учащемся записать на доске, что дети уже знают по теме урока, продолжив выражения: Я УМЕЮ)
— Сегодня на уроке мы продолжим работу по измерению и построению углов. Вы покажите свои знания, выполняя разнообразные задания. (слайд 3)
— Запишите тему урока. «Виды углов. Измерение углов».
2) Упражнение 1.
— Запишите острые, тупые и прямые углы, изображенные на рисунке. (слайд 4)
Рисунок 2
— У доски будут работать 3 учащихся (первый
учащийся выписывает названия острых углов,
второй учащийся — прямых углов, третий учащийся —
тупых углов). Остальные ученики записывают в
тетради.
Остальные ученики записывают в
тетради.
- Острые углы: АОЕ, ROC, BAC, ACD, DCA, CAD, BRE, RED, BAO
- Прямые углы: АВС, ВСD, CDA, BAD
- Тупые углы: AOR, COE, ERC, REA
3) Упражнение 2. (самостоятельная работа учащихся)
— У вас на парте три макета углов трех цветов: красный — 90o, зеленый — 45o, синий — 30o.
— Развернитесь друг к другу, поработайте в паре. Я прошу вас составить из макетов углы: 135o, 75o, 15o.
Проверка (слайд 5)
4. Выполнение мини-проекта.
Проблемный вопрос
— С помощью макетов у вас получились углы с заданными градусными мерами. Макеты я построила с помощью транспортира. А как без транспортира строить углы? Решим задачу, внимательно слушайте ее условие.
Исследовательская работа (слайд 6)
— Основным показателем при расчете лестничного
марша является его уклон (крутизна). Идеальный
уклон 30 градусов, он создается с помощью Тетивы.
Тетива – это основа лестницы, несущая опорная
конструкция, в виде наклонных балок. Папа на даче
строит лестницу и хочет установить угол наклона
балок в 30 градусов. Для этого ему нужен макет угла
из фанеры. Он просит своего сына помочь ему
сделать бумажный шаблон угла, который он затем
приложит к фанере и выпилит нужный макет.
Идеальный
уклон 30 градусов, он создается с помощью Тетивы.
Тетива – это основа лестницы, несущая опорная
конструкция, в виде наклонных балок. Папа на даче
строит лестницу и хочет установить угол наклона
балок в 30 градусов. Для этого ему нужен макет угла
из фанеры. Он просит своего сына помочь ему
сделать бумажный шаблон угла, который он затем
приложит к фанере и выпилит нужный макет.
— При наличии транспортира отложить любой угол можно! Но транспортира на даче нет, и данный угол нужно получить здесь и сейчас!!!
— Можно ли построить угол без транспортира? (слайд 7)
— На каком этапе работы мы сейчас находимся? (1. этап постановки проблемы)
— В чём проблема? Сформулируйте проблему. (как без транспортира построить угол в 30°, как изготовить шаблон угла в 30° без транспортира)
— Хватает имеющихся знаний для решения проблемы? У вас есть только квадратный лист бумаги! Предположим, что с помощью него можно отложить угол в 30 градусов!
— Какой этап работы сейчас? (происходит выдвижение гипотезы — предположение)
— Сформулируйте гипотезу. (гипотеза: можно
отложить угол, равный 30 градусам, без
транспортира с помощью квадратного листа бумаги)
(гипотеза: можно
отложить угол, равный 30 градусам, без
транспортира с помощью квадратного листа бумаги)
— Как? Ваши предположения, как это можно сделать? (дать время подумать)
— Что происходит сейчас, какой этап работы? Поиск и предложение возможных вариантов решения
— Проведем эксперимент – это некоторое количество опытов, которые показывают одинаковый результат.
— К какому этапу мы подошли? (исследование)
— Приглашаю присоединиться ко мне. (демонстрация учителя)
— Воспользуйтесь инструкцией, на вашем столе.
Эксперимент:
| Инструкция | ||
| № | Действия | Рисунок |
| 1 | Берем обыкновенный квадратный лист
бумаги и сворачиваем его пополам. | Рисунок 3 |
| 2 | Затем, делаем второй сгиб, посмотрите на рисунок, мы загибаем угол квадрата таким образом, чтобы вершина квадрата, она обозначена точкой совпала с линией первого сгиба. | Рисунок 4 Рисунок 5 |
| 3 | Измерить получившийся угол. | Рисунок 6 |
— Берем обыкновенный квадратный лист бумаги и сворачиваем его пополам. Затем, делаем второй сгиб, посмотрите в инструкцию, мы загибаем угол квадрата таким образом, чтобы вершина квадрата совпала с линией первого сгиба.
— Как проверить градусную меру получившегося угла? (взять транспортир и измерить)
— Сколько градусов получился угол?
— Подтвердился эксперимент?
— Какой этап работы сейчас? (анализ)
— Что нам нужно было получить? (шаблон угла)
— Ребята прогладьте хорошо сгиб несколько раз и
сделайте отрыв угла.
— Получился шаблон?
— Какой этап работы сейчас? (продукт)
— Какой вид угла мы получили? (острый)
— Что нового вы узнали? (ответы учащихся) — запись на доске Я УЗНАЛ:
— Чему научились? (без транспортира строить угол в 30°) — запись на доске Я НАУЧИЛСЯ:
5. Физкультминутка (учитель читает утверждения, учащиеся выполняют определенные движения)
“Верно или ложно?”
— Внимание! Если я читаю верное утверждение, то вы хлопаете в ладошки; если неверное, то поднимаете вверх руки.
- Единицы измерения углов: миллиметры, сантиметры?
- Единицы измерения углов: миллиграммы, килограммы?
- Единицы измерения углов: градусы, минуты?
- Развёрнутый угол имеет градусную меру 100°?
- Развёрнутый угол имеет градусную меру 90°?
- Развёрнутый угол равен 180°?
- Прямой угол равен 160°?
- Прямой угол равен 90?
- Острый угол больше прямого?
- Острый угол равен прямому?
- Острый угол меньше прямого?
- Тупой угол меньше прямого?
- Тупой угол всегда больше прямого и меньше развёрнутого?
- Угол, меньше 90° называется острым?
- Угол, больше 90°, но меньший 180°, называется тупым углом?
6. Оценочный этап.
Оценочный этап.
Самостоятельная работа.
— Мы отдохнули и готовы работать дальше. Запишите на листочке свою фамилию, имя, класс.
| Вариант 1 | ||||
| Работу выполнил(а) | ||||
| Задание: — назвать угол — измерить этот угол — записать результат измерения — записать вид угла | ||||
1) | 2) | 3) | 4) | 5) |
| Вариант 2 | ||||
| Работу выполнил(а) | ||||
| Задание: — назвать угол — измерить этот угол — записать результат измерения — записать вид угла | ||||
| 1) | 2) | 3) | 4) | 5) |
7. Домашнее задание.
Домашнее задание.
Найдите углы, обозначьте их градусную меру.
Рисунок 7
8. Рефлексия (качественная оценка работы класса и отдельных учащихся)
— Ребята заполните БИЛЕТИК на выход, продолжив предложение “Сегодня на уроке я повторил…., научился…, узнал…., закрепил…”, отметив то высказывание, которое больше всего подходит к работе на уроке.
| БИЛЕТИК на выход | БИЛЕТИК на выход |
| Сегодня на уроке я: повторил________________________, научился________________________, узнал___________________________, закрепил________________________” | Сегодня на уроке я: повторил_______________________, научился_______________________, узнал___________________________, закрепил________________________” |
|
|
Список использованной литературы.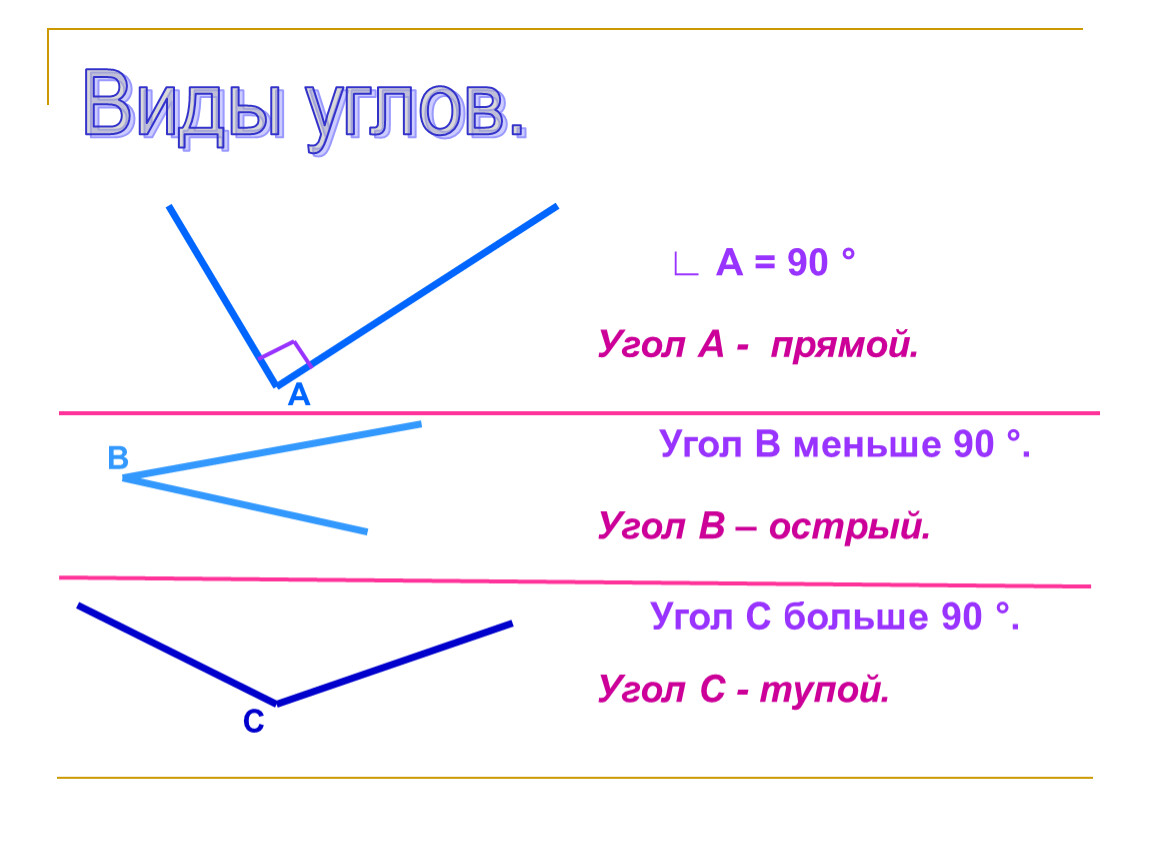
- А.Г.Мерзляк, В.Б. Полонский, М.С.Якир, Е.В. Буцко, Математика 5 класс, Москва “Вентана-Граф”, 2016
- Интернет ресурс «Геометрия бумажного
листа».
http://komarovana.ucoz.ru/load/tvorcheskie_raboty_moikh_detej/geometrija_bumazhnogo_lista/6- 1-0-195
Виды углов. Измерение углов. 5 класс
1. Виды углов. Измерение углов.
12.05.20205а и 5к классы
2. Вы уже познакомились с геометрической фигурой,которая называется «угол». Сегодня мы научимся измерять и различать углы.
3. Развёрнутый угол
Лучи ВА и ВС образуютпрямую, причём их начала
совпадают, значит они
образуют угол.
Развернутый угол- это угол, стороны которого
лежат на одной прямой.
!!! Чтобы начертить развернутый угол,
достаточно провести прямую и отметить на ней
точку — вершину угла.
4. Единица измерения углов.
• Развёрнутый угол разделили на 180 равныхуглов.
• За еденицу измерения углов приняли угол,
образованный соседними лучами и назвали
градусом.
 Записывают 1°.
Записывают 1°.***
Итак,
Единица измерения
углов-1°.
5. Измерение углов
Измеряя угол, мы подсчитываемсколько единичных отрезков он
содержит.
На рисунке изображен
транспортир- специальный
прибор для измерения углов.
Его шкала содержит 180 делений.
!!!Градусная мера развёрнутого угла равна 180°.
6. Алгоритм измерения углов
1)Совместить вершину угла с центром транспортира.2) Сторона угла должна проходить по линейке через
начало отсчета на шкале транспортира.
3) Найти штрих на шкале, через который проходит
вторая сторона угла.Он укажет градусную меру угла.
ВНИМАНИЕ!! Так как шкалы две, штрих мы находим на
той шкале, у которой «0» совпал со стороной угла.
7. Виды углов
• Угол, градусная мера которого равна 90 °,называют прямым.
• Угол, градусная мера которого, меньше 90 °,
называют острым.
• Угол, градусная мера которого больше 90 °,
но меньше 180 °, называют тупым.
• Развернутый угол- угол, градусная мера
которого равна 180 °.
Работа по учебнику:
Выполнить номера:
1613, 1614 –
страница 245
9. Домашнее задание:
• Выполнить номер 1615 (страница 246). Прочитатьпараграф 41 (страница 243).
По учебнику: Математика. 5 класс, Н.Я. Виленкин
• Сдать домашнее задание необходимо до начала
следующему урока
(не позднее 13.05.2020 – 5а и 5к классы)
Домашнее задание можно сдать либо в комментариях в
факультативе, либо в ВК у кого есть возможность.
СПАСИБО
ЗА
ВНИМАНИЕ
Что такое Угол? Определение, виды, как обозначают? Примеры
Определение угла
Угол — это простая геометрическая фигура. Определение угла напрямую связано с понятием луча.
Луч — прямая линия, у которой есть начало, но нет конца, и продолжается она только в одну сторону.
Если нам дана прямая a на плоскости, и на ней есть некоторая точку O — выходит, что прямая разделена точкой на две части, каждая из которых является лучом с началом в точке O.
Луч можно обозначить одной строчной буквой латинского алфавита или двумя прописными. Например, вот так:
Угол — часть плоскости между двумя линиями, исходящими из одной точки. Каждая сторона угла является лучом, а вершина — общим началом сторон.
В математике существует специальный символ для обозначения угла, вот он: ∠.
Если стороны угла названы малыми латинскими буквами, то их записывают после символа. Например, так: ∠ab или ∠ba.
Если стороны угла названы большими буквами, то обозначение угла будет состоять из символа и трех букв, при этом вершина всегда записывается в центре. При сторонах угла OA и OB название угла запишем так: ∠AOB и ∠BOA.
Иногда можно встретить обозначение в виде цифр — так тоже можно.
Для наглядности — все способы обозначения углов:
Что такое вершина и стороны угла:
- Стороны угла — лучи, из которых состоит угол.
- Вершина угла — общее начало сторон угла.
Биссектриса — это луч, который исходит из вершины угла и делит его на два равных угла.
Так как угол делит плоскость на две части, одна будет внутренней областью угла, а другая — внешней областью угла. Вот так:
При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.
Единица измерения углов — градусы. Символ для обозначения градуса угла: °.
Определение смежных и вертикальных углов
Смежные углы — это пара углов, у которых одна сторона общая, а две другие стороны лежат на одной прямой. Таким образом два смежных угла составляют развернутый угол. Общая сторона двух смежных углов называется наклонной к прямой, на которой лежат другие стороны, при условии, что смежные углы не равны.
Вертикальные углы — это пара углов, у которых есть общая вершина, при этом стороны одного угла составляют продолжение сторон другого угла.
При пересечении прямых получается четыре пары смежных и две пары вертикальных углов. Вот как это выглядит:
Виды углов
Есть разные типы углов и у каждого своё название:
- острый
- прямой
- тупой
- развернутый
- выпуклый
- полный
Различать виды углов в геометрии важно. Определять можно на глаз или с помощью линейки.
Острый угол — это угол, который меньше прямого угла, то есть < 90°.
Прямой угол — это угол, стороны которого перпендикулярны друг другу. Прямой угол всегда равен половине развернутого угла, то есть = 90°.
Если два смежных угла равны между собой, то каждый из них является прямым. Для удобства прямой угол обозначается уголком. Вот так:
На картинке изображены два прямых угла ∠AOC и ∠COB. Общая сторона OC перпендикулярна прямой AB, а точка O — основание перпендикуляра.
Развернутый угол — это открытый угол, который образован двумя лучами и равен сумме двух прямых углов. Развернутый угол равен 180°. Как выглядит развернутый угол показано на первой картинке.
Неразвернутый угол — это любой угол, который не является развернутым, то есть не равен 180°.
Тупой угол — это угол, который больше прямого угла, но меньше развернутого:
90° < тупой угол < 180°.
Выпуклый угол — это угол, который больше развернутого угла, но меньше полного:
180° < выпуклый угол < 360°.
Полный угол — это угол, обе стороны которого совпадают с одним лучом. Он равен сумме четырех прямых углов, то есть = 360°.
Прилежащие углы — это пара углов с общей вершиной и стороной, другие стороны при этом лежат по разные стороны от общей стороны.
На картинке мы видим два прилежащих угла ∠AOB и ∠BOC, общую вершину O и общую сторону OB.
Можно сформулировать определение по-другому: если из вершины любого угла провести луч, разделяющий угол на два, то образованные углы будут прилежащими.
Чтобы найти угол, который разделен лучом, нужно сложить полученные углы: ∠AOB = ∠AOC + ∠COB. Из этого можно выделить следующие верные разности:
- ∠AOC = ∠AOB — ∠COB,
- ∠COB = ∠AOB — ∠AOC.
Сравнение углов
Для сравнения углов можно использовать самый простой способ из программы 4 класса — метод наложения. Для этого нужно совместить две вершины и сторону одного угла со стороной другого. Если стороны заданных углов совпадут, значит углы равные. Если нет, то угол, который лежит внутри другого, будет меньшим. Здесь два наглядных примера с равными и неравными углами:
При этом развернутые углы всегда являются равными.
Совмещение углов ∠𝐴𝐵𝐶 и ∠𝑀𝑁𝐾 происходит следующим образом:
- Вершину 𝐵 одного угла совмещаем с вершиной 𝑁 другого угла.
- Сторону 𝐵𝐴 одного угла накладываем на сторону 𝑁𝑀 другого угла так, чтобы стороны 𝐵𝐶 и 𝑁𝐾 располагались в одном направлении.
Если совпадут и другие стороны, то углы равны: ∠𝐴𝐵𝐶 = ∠𝑀𝑁𝐾.
Если нет, то один угол — меньше другого: ∠𝐴𝐵𝐶<∠𝑀𝑁𝐾.
Сравнить углы можно также, измерив их величины. Для этого понадобится специальный инструмент для построения и измерения углов — транспортир. Вот, как он выглядит:
Как правильно измерять углы
Измерение углов похоже на измерение отрезков: нужно сравнить их с углом, принятым за единицу измерения. В геометрии обычно за единицу измерения принимают градус — угол, равный 1/180 части развернутого угла. Обозначается — 0.
Градусная мера угла — положительное число, которое показывает, сколько раз градус и его части укладываются в данном углу.
Есть еще две возможные меры угла: минуты и секунды. Они позволяют выполнять более точные расчеты, особенно, когда величина не является целым обозначением градуса.
Минута — 1/60 часть градуса. Обозначается — ´.
Секунда — 1/60 часть минуты. Обозначается — ´´.
Градус состоит из 3600 секунд, то есть: 1° = 60′ = 3600′.
Как происходит измерение угла: сначала измеряются стороны угла, а после его внутренняя область. Всегда нужно считать количество уложенных углов, так как они предопределяют меру измеряемого угла.
Когда луч делит угол на два или более углов, градусная мера всего угла равна сумме градусных мер этих углов.
На рисунке изображен угол АОВ, он состоит из углов АОС, СОD и DОВ. Можно записать так: ∠ A O B = ∠ A O C + ∠ D O B = 45° + 30° + 60° = 135 °.
Угол называется прямым, если он равен 90°, а острым, если он меньше 90°, тупым, если он больше 90°, но меньше 180°. Развернутый угол имеет 180°.
Равные углы имеют равную градусную меру.
Обозначение углов на чертеже
Чертеж помогает решать задачки по геометрии в разы быстрее. Чтобы наглядно изображать дуги, углы и прочие фигурки, придумали даже отдельное направление — геометрический чертеж.
Задачи с углами могут быть разными и не всегда есть возможность правильно изобразить и отметить угол. Вот, что важно запомнить при обозначении лучей и углов:
- Равные углы обозначают одинаковым количеством дуг.
- Неравные углы обозначают разным количеством дуг, чтобы они отличались между собой.
- Для обозначения на чертеже более трех углов используем разные виды дуг: волнистые, зубчатые.
На чертеже отмечены острые, равные и неравные углы.
Обозначать углы можно разными цветами. Главное, чтобы было просто и броско. При этом необязательно отмечать все-все углы — достаточно только тех, которые нам нужны для решения задачки.
Вникать во все тонкости математической вселенной комфортнее с внимательным наставником. Наши учителя объяснят сложную тему, ответят на неловкие вопросы и вдохновят ребенка учиться. А красочная платформа с увлекательными заданиями поможет заниматься современно и в удовольствие. Запишите ребенка на бесплатный пробный урок в онлайн-школу Skysmart и попробуйте сами!
Виды углов: острый, прямой, тупой, развёрнутый, выпуклый и полный
Каждый угол, в зависимости от его величины, имеет своё название:
- Острый угол — это угол, который меньше прямого угла (<90°).
- Прямой угол — это угол, стороны которого перпендикулярны друг другу. Прямой угол обозначается буквой d и равен 90°.
Если два смежных угла равны между собой, то каждый из них называется прямым углом. Прямой угол обычно обозначается не дугой, а уголком:
∠AOC и ∠COB — прямые углы. Общая сторона прямых углов OC называется перпендикуляром к прямой AB, а точка O — основанием перпендикуляра.Сумма двух прямых углов равна развёрнутому углу, значит, прямой угол равен половине развёрнутого угла.
- Тупой угол — это угол, который больше прямого угла, но меньше развёрнутого:
90° < тупой угол < 180°.
- Развёрнутый угол — это угол, образованный двумя дополнительными лучами.
Развёрнутый угол равен сумме двух прямых углов или, короче, двум прямым углам. Следовательно, развёрнутый угол равен 180° или 2d.
Все развёрнутые углы равны между собой.
- Выпуклый угол — это угол, который больше развёрнутого угла, но меньше полного:
180° < выпуклый угол < 360°.
- Полный угол — это угол, обе стороны которого совпадают с одним лучом.
Полный угол равен сумме четырёх прямых углов, то есть 4d (360°).
Прилежащие углы
Прилежащие углы — это пара углов, имеющих общую вершину и общую сторону, другие стороны которых лежат по разные стороны от общей стороны.
∠AOB и ∠BOC — прилежащие углы, O — общая вершина, OB — общая сторона.
Если из вершины любого угла провести луч, разделяющий угол на два угла, то образованные углы будут прилежащими.
Угол, разделённый лучом, будет называться суммой полученных углов, например угол AOB является суммой углов AOC и COB:
∠AOB = ∠AOC + ∠COB.
Каждый из прилежащих углов, ∠AOC и ∠COB, называется разностью углов AOB и другого прилежащего, то есть:
∠AOC = ∠AOB — ∠COB,
∠COB = ∠AOB — ∠AOC.
Конспект урока математики в 5 классе на тему «Измерение углов. Виды углов» | Математика
Конспект урока математики в 5 классе на тему «Измерение углов. Виды углов»
Автор: Егина Елена Александровна
Организация: МОАУ «Гимназия №1 им. Романенко Ю.В.»
Населенный пункт: Оренбургская область, город Бузулук
Цель урока: создать условия для формирования понятия градусной меры угла, умения определять виды углов и измерять их величины с помощью транспортира; способствовать развитию коммуникативных навыков, умения правильно обобщать данные и делать выводы; обеспечить условия для развития культуры коллективной работы и взаимопомощи.
Тип урока: урок объяснения нового материала
Формы работы учащихся: фронтальная, парная, индивидуальная
Необходимое оборудование: компьютер, проектор, учебники по математике, раздаточный материал (лист контроля), смартфоны, чертежные инструменты.
Необходимое программное обеспечение: MicroSoft Office PowerPoint, активная подписка Я+ образовательного online-сервиса Якласс у учителя и каждого обучающегося.
Ключевые понятия: Развёрнутый угол, единичный угол, градус, транспортир, измерение углов, острый угол, прямой угол, тупой угол.
Сценарий урока
(опорные фразы учителя для организации урока)
- Организационный момент
К геометрии способность проявляй,
Не ленись, а ежедневно развивай,
Повторяй, учи, трудись, соображай
С геометрией дружить не забывай.
-«Я предлагаю продолжить нашу дружбу с этой удивительной наукой с рассмотрения уже известных вам геометрических фигур. Внимание на слайд.»
2. Актуализация опорных знаний
-«Опишите рисунок…Что вы знаете о изображенных фигурах?»
3. Изучение новой темы
-«Как измерить отрезок мы вспомнили, а как быть с углом?!» «Давайте определим цель и тему нашего урока»
-«Оказывается для измерения углов, есть специальный инструмент-транспортир, от лат. transporto «переношу». Транспортир состоит из линейки (прямолинейной шкалы) и полукруга (угломерной шкалы.»
-«Давайте найдем в учебнике название единиц измерения углов»
-«Так как же произвести измерение?!»
-«Запишем алгоритм измерения угла:
- Совместить вершину угла с центром транспортира.
- Расположить транспортир так, чтобы сторона угла проходила через начало отсчета на шкале транспортира.
- Найти штрих на шкале, через который проходит вторая сторона угла.
- Учитывая направление отсчета, правильно снять результат со шкалы»
4.Физминутка
— «Стоп, уроки! Стоп, дела! Отдыхать пришла пора!
Потрудились, отдохнем.
Встанем, глубоко вздохнем.
Руки в стороны, вперед.
Влево, вправо поворот.
Три наклона, прямо встать.
Руки вниз и вверх поднять.
Руки плавно опустить,
Всем улыбки подарить.
-«Покажите развернутый угол. Покажите прямой угол. Острый…Тупой»
5. Закрепление полученных знаний. Самостоятельная работа с проверкой по эталону
-«У вас на партах лежат карточки с различными углами. Давайте измерим каждый из них»
-«На какие три группы можно разделить эти углы? Что является признаком такой классификации?» «Давайте попробуем придумать новые определения видов углов, связанные с их градусными мерами»
-«Зайдите в свои аккаунты на сервисе «Якласс» и выполните проверочную работу по теме «Измерение углов. Виды углов»
6. Подведение итогов урока. Домашнее задание. Рефлексия
-«Что нового вы узнали?» «Какие трудности возникли?» «Довольны ли вы своим результатом?»
Домашняя работа.
Учитель раздает листочки с заданием на дом
Н Найдите градусную меру угла ∠КОЕ, если ∠СОК = 25º.
-« При выходе из класса, я попрошу вас оставить на моем столе угол того цвета, который соответствует вашему настроению на данном уроке:
-красный — все понравилось, было все понятно, трудностей не вызывало;
-зеленый — урок понравился, но были некоторые трудности при решении заданий;
— синий – на уроке чувствовал себя не комфортно, задания слишком трудные.»
Технологическая карта
|
Этап урока |
Виды работы, формы, методы, приемы |
Содержание педагогического взаимодействия |
Формируемые УУД |
Планируемые результаты |
|
|
Деятельность учителя |
Деятельность обучающихся |
||||
|
1. Организационный момент. |
Фронтальная работа |
Приветствует обучающихся; проверяет готовность класса к уроку; организует внимание |
Настраиваются на работу |
П.: Осознанное и произвольное построение речевого высказывания Р.: Прогнозирование своей деятельности К.: Умение слушать и вступать в диалог Л.: Умение выделять нравственный аспект поведения |
Благоприятный психоэмоциональный настрой |
|
2. Актуализация опорных знаний
|
Фронтальная, индивидуальная работа |
Демонстрирует презентацию (Приложение 1). Предлагает вспомнить способ измерения отрезков, вспомнить понятие угла;
|
Участвуют в работе по повторению, отвечают на поставленные вопросы |
П.: Анализ объектов с целью выделения признаков Выделение и осознание того, что уже пройдено. Р.: Планирование своей деятельности для решения поставленной задачи К.: Умение с достаточной полнотой и точностью выражать свои мысли, слушать и вступать в диалог Л.: Установление связи между целью деятельности и ее мотивом |
Развитие умения применять имеющиеся знания к решению практических задач |
|
3. Создание ситуации затруднения
|
Фронтальная работа, проблемный метод |
Учитель продолжает беседу с проблемной задачи по будущей теме урока. Задает учащимся наводящие вопросы, подводит к констатации затруднения |
В беседе с учителем отвечают на поставленные вопросы, формулируют возникшее затруднение |
П.: формулирование проблемы; Р.: Постановка цели учебной задачи, фиксация затруднения К.: Осознанное и произвольное построение речевого высказывания |
Развитие умения рассуждать, обобщать, аргументировано отвечать на вопросы собеседников, вести диалог |
|
4. Построение плана выхода из затруднения |
Фронтальная работа |
Демонстрирует презентацию. Вместе с учениками определяет цель и задачи урока
|
Формулируют тему урока, составляют план действий на урок |
П.: установление причинно-следственных связей; Р.: Целеполагание, выдвижение гипотез. Планирование своей деятельности для решения поставленной задачи К.: планирование учебного сотрудничества с учителем и сверстниками Л.: Смыслообразование. |
Развитие умения проводить информационно смысловой анализ; рассуждать, обобщать, аргументировано отвечать на вопросы собеседников, вести диалог.
|
|
5. Открытие нового знания |
Фронтальная, индивидуальная работа; частично- поисковый, объяснительно- иллюстративный методы |
Демонстрирует презентацию. Вводит понятие «транспортир». Предлагает в учебнике найти название единицы измерения углов. Комментирует, направляет работу учащихся. Демонстрирует как измерить угол транспортиром.
|
Выполняют задание, проверяют правильность выполнения. Анализируют текст учебника, зачитывают определения
Измеряют углы транспортиром. Составляют опорную схему измерения углов |
П.: Поиск и выделение необходимой информации в тексте. Структурирование знаний. Подведение под понятие Р.: Планирование своей деятельности К.: Умение слушать и вступать в диалог, формулировать свои мысли использую математические термины Л.: Проявление доброжелательности в дискуссии, доверия к собеседнику |
|
|
6. Физминутка |
|
Организует учащихся на выполнение физических упражнений. Учащимся предлагается изобразить углы различных видов с помощью своих рук |
Выполняют упражнения физминутки. |
Р.: Саморегуляция |
Психоэмоциональная разрядка |
|
7. Закрепление полученных знаний |
Индивидуальная, парная работа; практический метод |
Помогает ученикам на местах, контролирует выполнение работы. Предлагает классифицировать углы
Предлагает выделить признак классификации |
Измеряют транспортиром углы. Сравнивают результаты в парах. Классифицируют углы по видам Формулируют признак по которому классифицировали |
П.: Анализ и синтез. Выбор оснований и критериев для сравнения Р.: самоконтроль, самоанализ К.: Умение слушать и вступать в диалог Л.: Проявление терпения и аккуратности при построении чертежей
|
Развитие умения измерять градусные меры углов с помощью транспортира |
|
8. Самостоятельная работа с проверкой по эталону |
Индивидуальная работа |
Организует работу с online-тестом (тест формируется заранее на сервисе «Якласс». Приложение 2). Предлагает проанализировать результаты Дает возможность самим ученикам оценить себя, затем оценивает учащихся с комментированием. |
Выполняют задания теста, анализируют правильность выполнения своих работ по образцу на экране монитора. Читают пояснения к шагам правильного решения в открывшимся после завершения теста окне «работа над ошибками» |
П.: выбор наиболее эффективных способов решения задач в зависимости от конкретных условий Р.: самоконтроль, самоанализ, коррекция К.: Умение выражать свои мысли используя математические термины Л.: самоопределение
|
Развитие аналитического мышления |
|
9. Подведение итогов урока. Рефлексия |
Фронтальная работа, устная форма рефлексии: беседа по пометкам |
Вносит корректировку в ответы учащихся. Рефлексия. Что нового вы узнали? Какие трудности возникли? Довольны ли вы своим результатом? Поясняет д.з. (приложение 3) |
Подводят итог урока, оценивают свою успешность, формулируют задачи следующего урока Оставляют на столе учителя угол «цвета настроения» |
П.: рефлексия способов и условий действия Р.: прогнозирование, рефлексия К.: умение с достаточной полнотой и точностью выражать свои мысли Л.: самоопределение |
Рефлексия |
Список использованной литературы
- Бёрджес Д. Обучение как приключение: Как сделать уроки интересными и увлекательными. — М., 2016. — С. 40
- Никольский С.М., Потапов М.К., Решетников Н.Н.. Учебник математики. 5 класс. -14-е изд. — М.: 2015. — 272 с
- Хуторской, А. В. Метапредметный подход в обучении: Научно-методическое пособие / А. В. Хуторской. М.: Эйдос; Изд-во Института образования человека, 2012. — 50 с. (Серия «Новые стандарты»).
- Шарыгин И.Ф., Ерганжиева Л.Н. Наглядная геометрия 5 – 6 классы. – М., Издательский дом “Дрофа”, 1999.
Приложения:
- file0.doc.. 1,2 МБ
- file1.pptx.zip.. 1,6 МБ
Самостоятельная работа по теме «Виды углов. Измерение углов» | Учебно-методический материал по математике (5 класс):
Самостоятельная работа № 7
по теме «Виды углов. Измерение углов»
Вариант 1
№1. Начертите угол ADE и проведите лучи DC и DO между его сторонами. Запишите все образовавшиеся углы.
№ 2. Начертите углы, градусные меры которых равны 54˚, 90˚, 147˚, 88˚. Назовите их, укажите их вид.
№ 3. Луч KС является биссектрисой угла АKP, MKC = 138˚ (см. рис. 2). Вычислите градусную меру угла AKP.
№ 4. Что такое угол? Что такое биссектриса угла?
Самостоятельная работа № 7
по теме «Виды углов. Измерение углов»
Вариант 2
№ 1. Начертите угол COD и проведите лучи OK и OP между его сторонами. Запишите все образовавшиеся углы.
№ 2. Начертите углы, градусные меры которых равны 47˚, 98˚, 90˚, 156˚.
№ 3. Луч OD является биссектрисой угла АOC, BOD = 168˚(см. рис. 2). Вычислите градусную меру угла AOC.
№ 4. Что такое стороны угла, вершина угла? Какие углы называются равными?
Самостоятельная работа № 7
по теме «Виды углов. Измерение углов»
Вариант 1
№1. Начертите угол ADE и проведите лучи DC и DO между его сторонами. Запишите все образовавшиеся углы.
№ 2. Начертите углы, градусные меры которых равны 54˚, 90˚, 147˚, 88˚. Назовите их, укажите их вид.
№ 3. Луч KС является биссектрисой угла АKP, MKC = 138˚ (см. рис. 2). Вычислите градусную меру угла AKP.
№ 4. Что такое угол? Что такое биссектриса угла?
Самостоятельная работа № 7
по теме «Виды углов. Измерение углов»
Вариант 2
№ 1. Начертите угол COD и проведите лучи OK и OP между его сторонами. Запишите все образовавшиеся углы.
№ 2. Начертите углы, градусные меры которых равны 47˚, 98˚, 90˚, 156˚.
№ 3. Луч OD является биссектрисой угла АOC, BOD = 168˚(см. рис. 2). Вычислите градусную меру угла AOC.
№ 4. Что такое стороны угла, вершина угла? Какие углы называются равными?
Типы углов — объяснения и примеры
Различные типы углов существуют в природе, , и каждый из них имеет большое значение в нашей повседневной жизни.
Например, , архитекторы и инженеры используют углы при проектировании машин, зданий, дорог и мостов.
В спорте спортсмены используют углы для улучшения своих результатов. Например, человек должен вращаться с диском под определенным углом, чтобы бросить его на короткое расстояние. В футболе вы должны использовать определенный угол, чтобы передать мяч следующему игроку.
Плотники и ремесленники также используют углы для изготовления таких предметов, как диваны, столы, стулья, ведра и т. Д. Художники используют углы для набросков портретов и картин. Модельеры также используют углы, чтобы подобрать лучшие наряды. По этим причинам необходимо изучить различные типы углов.
(Основное объяснение углов можно найти в предыдущей статье «Углы».)
Различные типы углов
Углы классифицируются на основе:
Классификация углов по величине
Существует семь типов углов, основанных на их градусном измерении.В их числе:
- Нулевые углы
- Острые углы
- Прямой угол
- Тупые углы
- Уголок прямой
- Угол рефлекса
- Уголок полный
— нулевой угол
Нулевой угол (0 °) — это угол, образованный, когда оба плеча угла находятся в одном положении.
Иллюстрация:
∠ RPQ = 0 ° (нулевой угол)
— Острый угол
Острый угол — это угол больше 0 °, но меньше 90 °.Общие примеры острых углов: 15 °, 30 °, 45 °, 60 ° и т. Д.
∠ XYZ больше 0 °, но меньше 90 ° (острый угол)
— угол 90 градусов
Угол 90 градусов, также известный как прямой угол, — это угол, размер которого равен 90 °, и называется прямым углом. Прямые углы изображаются в виде небольшой квадратной рамки между плечами угла.
Иллюстрация:
∠ ABC = 90 ° (прямой угол)
В следующем разделе (Треугольники) будет целая статья о прямоугольных треугольниках.
— Тупой угол
Тупой угол — это угол, градус которого больше 90 °, но меньше 180 °. Примеры тупых углов: 100 °, 120 °, 140 °, 160 °, 170 ° и т. Д.
∠ PQR — тупой угол, потому что он меньше 180 ° и больше 90 °.
— Уголок прямой
Как следует из названия, прямой угол — это угол, размер которого равен 180 ° (прямая линия)
Иллюстрация:
∠ XYZ = 180 ° (прямой угол)
— Угол рефлекса
Углы отражения — это углы, градусы которых составляют более 180 °, но менее 360 °.Общие примеры углов рефлекса: 200 °, 220 °, 250 °, 300 °, 350 ° и т. Д.
Иллюстрация:
∠ PQR больше 180 °, но меньше 360 °
— Угол в сборе
Полный угол равен 360 °. 1 оборот равен 360 °.
Иллюстрация:
Классификация углов по повороту
В зависимости от направления вращения углы можно разделить на две категории, а именно:
- Положительные углы
- Отрицательные углы
Положительные углы
Положительные углы — это типы углов, измерения которых производятся против часовой стрелки от основания.
Отрицательные углы
Отрицательные углы измеряются по часовой стрелке от основания.
Уголки прочие
Помимо упомянутых выше углов, существуют другие типы углов, известные как парные углы. Их называют парными углами, потому что они появляются парами, чтобы показать определенное свойство. Это:
- Соседние углы имеют одинаковую вершину и плечо.
- Дополнительные углы: парные углы, которые в сумме составляют 90 °.
- Дополнительные углы: парные углы, сумма углов которых равна 180 °.
- Вертикально противоположные углы. Вертикально противоположные углы равны.
- Альтернативные внутренние углы: Альтернативные внутренние углы — это парные углы, образующиеся, когда линия пересекает две параллельные линии. Чередующиеся внутренние углы всегда равны друг другу.
- Альтернативные внешние углы : Альтернативные внешние углы — это просто вертикальные углы альтернативных внутренних углов. Альтернативные внешние углы эквивалентны.
- Соответствующие углы : Соответствующие углы — это парные углы, образующиеся, когда прямая пересекает пару параллельных прямых. Соответствующие углы также равны друг другу.
Мы видели краткий обзор различных типов углов. Далее мы увидим подробные статьи о наиболее распространенных типах углов (Дополнительные углы, Дополнительные углы и т. Д.).
Предыдущий урок | Главная страница | Следующий урокРабочие листы по классификационным углам
Получите глубокое понимание классификации углов с помощью этих распечатываемых рабочих листов, тщательно подготовленных для учащихся 4, 5 и 6 классов.При регулярной практике и повторении этого набора упражнений в формате PDF дети могут отличаться в задачах по определению типов углов. Они становятся все более уверенными и самостоятельными в рисовании углов, распознавании типов углов, образованных часами, определении типов углов в форме, определении типов углов в реальных объектах и многом другом. Распечатайте некоторые из наших листов бесплатно и начните играть!
Типы углов: Таблица
Обучайте детей 4 и 5 классов классифицировать углы как острые, прямые, тупые, прямые, рефлекторные и дополните нашу простую, но яркую таблицу типов углов.
Рабочие листы для острых, правых и тупых углов
Легко справляйтесь со своими задачами по типам углов, используя этот ассортимент рабочих листов в формате pdf, подготовленных, чтобы дать вам огромную практику определения острых, тупых и прямых углов.
(22 рабочих листа)
Классификационные углы: Тип 1
Дайте ученикам возможность попрактиковаться и расширить свои навыки определения типов углов с помощью этой группы упражнений. Внимательно изучите диаграммы и классифицируйте углы как острые, тупые, прямые, прямые или рефлекторные.
Классифицирующие углы: Тип 2
Продвиньтесь вперед в классификации углов, используя наши рабочие листы типа 2, где учащимся ставится задача определять углы после тщательного изучения геометрических форм и заданных углов. Каждый рабочий лист, заполненный десятью задачами, объединяет практические занятия студентов.
Уголки для рисования
Помогите своему ребенку научиться рисовать углы и не отставать от его уровня с помощью этих PDF-файлов. Острый угол меньше 90 °, прямой угол равен 90 °, тупой угол больше 90 °, но меньше 180 °, а прямой угол равен точно 180 °.Угол отражения больше 180 ° и меньше 360 °. Используйте предоставленные данные и информацию, чтобы нарисовать каждый угол.
Углы в часах
Вам интересно, какое отношение часы имеют к углам? Часы имеют прямое отношение к углам. Стрелки аналоговых часов обозначают углы. Посмотрите на минутную и часовую стрелки часов, чтобы определить тип углов. Каждый рабочий лист состоит из девяти задач.
Уголки в форме
Научитесь преобразовывать визуальную информацию в математические концепции с помощью наших распечатываемых листов.Воспринимайте каждую геометрическую форму и ее углы, чтобы определить тип каждого указанного угла. Обязательно используйте наши ключи ответов, чтобы подтвердить свои ответы.
Определение типов указанных углов
Проверьте свое понимание классификации углов с помощью этих листов для 6-го класса, в которых несколько углов имеют общую вершину. Обратите внимание на указанный угол и запишите тип угла, который он показывает. На каждом листе есть две задачи, над которыми дети могут поработать.
Практика испытаний: Тип 1
Этот комплекс практических упражнений позволяет детям определять типы углов, распознавать углы, образованные реальными объектами, определять углы, образованные часами, и многое другое.
Практика испытаний: Тип 2
Чтобы учащиеся могли обойти свои слабости при определении и рисовании углов, каждый рабочий лист разделен на четыре разных раздела.
Острый, тупой, прямой и правый
Угол измеряет величину поворота
Наименования углов
По мере увеличения угла название меняется:
Попробуйте сами:
В одной схемеЭта диаграмма может помочь вам запомнить: Также: Acute, Obtuse и Reflex расположены в алфавитном порядке. |
Также: буква «А» имеет острый угол.
Будьте осторожны при измерении
| Меньший угол — тупой угол , , но больший угол — угол отражения |
Поэтому при именовании углов убедитесь, что что вы знаете , какой угол просил !
Положительные и отрицательные углы
При измерении от линии:
- положительный угол идет против часовой стрелки (направление, противоположное движению часов)
- отрицательный угол идет по часовой стрелке
Пример: −67 °
Части угла
Угловая точка угла называется вершиной
И две прямые стороны называются плечами
Угол равен поворотам на между каждым плечом.
Как маркировать углы
Есть два основных способа маркировать углы:
1. Назовите угол, обычно строчной буквой, например a или b , или иногда греческой буквой, например α (альфа) или θ (тета)
2. или тремя буквами на форме, определяющими угол, при этом средняя буква указывает на то, где на самом деле находится угол (его вершина).
Пример угла « a » равен « BAC », а угол « θ » равен « BCD »
Измерение углов транспортиром
В этом уроке геометрии для 4-го класса объясняется, как измерять углы, как измерять углы с помощью транспортира, а также предлагаются различные упражнения для учеников.
Видео ниже объясняет, что такое угловая мера, как измерять углы с помощью транспортира и как рисовать углы с помощью транспортира.
Вспомните, как одна сторона угла очерчивает дуга окружности? Мы используем этот круг , чтобы измерить, насколько велик угол. Мы смотрим на сколько угол «открылся» по сравнению с полным кругом. Углы измеряются в градусов .Символ градусов — маленький кружок °.
Покажите углы ниже с помощью двух карандашей. Попробуй «Увидеть» круг, начертанный в воздухе. |
Это угол 1 градус ! |
тупой угол; 127 ° | прямой угол; 90 ° |
Как измерить угол с помощью транспортира :
| |
Позаботьтесь о чтении из правильного набора чисел. Транспортир имеет два набора числа: один набор идет от 0 до 180, другой — от 180 до 0. Какой из них вы прочитаете, зависит от того, как вы размещаете транспортир: поместите его так, чтобы одна сторона угла совпадала с одним из нулей, и прочтите этот набор номеров. В приведенных выше примерах мы выровнял одну сторону угла с нулем нижнего набора чисел, так что нам нужно прочитать нижний набор чисел. | |
1. Измерьте углы.
а. __________ ° | г. __________ ° |
г. __________ ° | г. __________ ° |
2. Измерьте углы. Обозначьте каждый угол острый или тупой.
а. __________ ° ______________________________ | г. __________ ° ______________________________ |
г. __________ ° ______________________________ | г. __________ ° ______________________________ |
e. __________ ° ______________________________ | ф. __________ ° ______________________________ |
3. Таша измерила острый угол, получилось 146 °. Учитель указал
что она прочитала неправильный набор цифр на транспортире.
Какой угол является правильным для измеренного ею угла?
4.Измерьте следующие углы самостоятельно.
транспортир. Если нужно, сделайте стороны уголков
дольше с линейкой.
6. Нарисуйте четыре точки и соедините их так, чтобы получился
четырехугольник.
Измерьте все углы вашего четырехугольника. Затем добавьте меры углов.
Вы получили 360 градусов или близко?
Этот урок взят из книги Марии Миллер Math Mammoth Geometry 1 и размещен на сайте www.HomeschoolMath.net с разрешения автора. Авторские права © Мария Миллер.
Уголки для уклона 5
Назначить HW. Отмена: Стиль текстового поля: Шрифт:… Рабочий лист. Математика. Рабочие листы> Математика> 5 класс> Геометрия> Классифицирующие углы. Углы — это пространство между двумя линиями, которые встречаются в точке или вершине. Геометрические фигуры. Практикуйтесь с 6 занятиями. Оценка: 5. Пятый класс (5-й класс) Вопросы по углам для ваших настраиваемых печатных тестов и рабочих листов.45º Острый 3. Найдите размер каждого угла. Эта викторина не завершена! Делитесь навыками. 1. Полный угол — это угол одного полного поворота, который составляет 360 градусов. Рекомендуемый ресурс. Это острый, тупой или прямой угол? Эти уроки помогут им понять важность углов и получить удовольствие от процесса. 0. Рабочий лист по геометрии для 5-го класса Измерьте угол с помощью транспортира. Получите глубокое понимание классификации углов с помощью этих распечатываемых рабочих листов, тщательно подготовленных для учащихся 4, 5 и 6 классов.3-й класс 3. Включить дополнительные и дополнительные углы: Похожие: классифицировать и измерять углы Уровень / уровень: 5-й класс Возраст: 10-12 Основное содержание: Типы углов Другое содержание: Типы углов Добавить в мои рабочие тетради (0) Скачать файл pdf Вставить на мой веб-сайт или в блог Добавить в Google Classroom Добавить в Microsoft Teams Поделиться через Whatsapp: Ссылка на этот рабочий лист: Копировать: bmpushpa_87 Готово !! Обучение пятиклассников классификациям углов. Наши рабочие листы по математике для пятого класса можно бесплатно распечатать в формате PDF.Рабочие листы> Математика> 3 класс> Геометрия> Измерение углов. Улучшите свои математические знания с помощью бесплатных вопросов по теме «Точки, линии, отрезки, лучи и углы» и тысяч других математических навыков. Распечатать; Доля; Редактировать; Удалить; Сообщить о проблеме; Проведите игру. Играть. ТИП: Рабочие листы. 4 класс 4. Искусство английского языка. Дополнительные и дополнительные рабочие листы углов. Примечание для 5-го класса: войдите в OERB в простой поиск, чтобы делать гиперссылки прямо из этих документов на любые действия OERB. 5.2 Измерение углов Транспортир можно использовать для измерения или рисования углов.В последних двух рабочих листах ученики также классифицируют углы как острые, тупые или прямые. Просто измерьте: Измерьте и классифицируйте: Подобное: Отображение 8 лучших рабочих листов, найденных для — Измерение углов 5-го класса. Прямой угол — 90 °. Вот некоторые из рабочих листов для этой концепции: Измерение и классификация углов, Практическое пособие по 5 углам, Mep y7 a, Measureclassifyangles l1s1, Ресурс для постоянных математических квалификаций, Измерение углов, Приложение для 4-го класса, Измерение углов, 5-й класс. Пример: нарисуйте 220 Угол °.15º Острый 2. Угол одного полного поворота составляет 360 °. Математика 5-го класса EZSchool — Углы: узнайте, как формируется угол, и узнайте о различных типах углов. Что ты хочешь делать? Управление избранным. час назад. … Люблю свою работу! Карточки угловых заданий — это еще одно отличное занятие на станции. Редактировать. поделиться в Facebook поделиться в Twitter. Углы треугольника находятся в соотношении 2: 5: 8. Добавить в избранное. Наши рабочие листы углов можно бесплатно загрузить, они просты в использовании и очень гибкие. поделитесь с Google.Новейший ресурс. Объем этого модуля позволяет… Решение Поместите транспортир на треугольник, как показано. Угол измеряется как 47 °. 6 класс 6. При регулярной практике и повторении этого набора упражнений в формате PDF дети могут отличаться в задачах по определению типов углов. Отмена. Уровень оценки Все … Сообщите учащимся, что острый угол меньше прямого или меньше 90 градусов, а тупой угол шире прямого или больше 90 градусов. Требуется настоящий транспортир! ДЕТСКИЙ САД К.1-й класс 1. Просмотрите нашу библиотеку готовых печатных листов с разнообразными… Ищете увлекательный способ научить вашего ребенка углы? Углы — важное понятие в геометрии, и поэтому для детей 4 и 5 классов становится жизненно важным научиться их измерять. 5-й класс. Изучение измерения углов (гр. На основе сингапурской учебной программы по математике, эти рабочие листы предназначены для учащихся 5-го класса. Социальные науки. Поделитесь ссылкой на практику. 6 класс.Проверить мои ответы: Отправьте мои ответы моему учителю по электронной почте. Посмотреть мой полный профиль. Углы (5-й класс) Этот веб-сайт был создан как инструмент для помощи учителям в обучении углов для учащихся 5-го класса. Используется более чем 70 000 учителей и 1 миллионом учеников дома и в школе. 2-й класс 2. 105º Тупой 7. Ученики 5-го и 6-го классов копают немного глубже с этими углами вокруг рабочих листов в формате pdf и принимают активное участие в построении фундаментальных концепций поиска неизвестных углов с использованием постулата полного угла.Эти рабочие листы углов — отличный ресурс для детей 3-го, 4-го, 5-го, 6-го, 7-го и 8-го классов. Играли 0 раз. Правотреугольные отношения. Задачи по углам Рабочие листы 5-го класса — по этой теме есть 8 рабочих листов для печати. Угловое рулевое управление №5. Математика. Angles Grade 5 — Отображение 8 основных листов, найденных для этой концепции. Угол отражения — это угол, измеряемый от 180 до 360 градусов. СОЗДАТЬ НОВУЮ ПАПКУ. Упражняться. Учащиеся используют диаграммы для измерения и сравнения углов.Сольная практика. 5-й класс . Использование настоящего транспортира для измерения углов. Скотт Форесман,… 135º Obtuse 6. Распечатайте этот геометрический лист, и он станет профессионалом в кратчайшие сроки. Он здесь, чтобы помочь вам овладеть концепциями и навыками доказательства теорем, связанных с хордами, дугами, центральными углами и вписанными углами (M10GE-IIc-d-1). Тематика: Геометрия. 0. Математика 5-го класса EZSchool — Углы: узнайте, как формируется угол, и узнайте о различных типах углов. Задачи со словами о геометрии — Дополнительные углы Учащимся предлагают задачи со словами, включающие дополнительные и дополнительные углы, которые требуют от ученика составить уравнение, чтобы найти меры данных углов.Пятиклассники могут не осознавать практическую ценность углов и их классификации. Щелкните здесь, чтобы получить подробное описание всех таблиц углов. Угловое рулевое управление №5. Это фантастический интерактивный обзор для вашего 5-го класса углового блока. 00: 00: 00: час мин сек; SmartScore. Нужен перерыв? Показать видеоурок Studyladder — это онлайн-инструмент для изучения английского языка и математики. В этих упражнениях ученики измеряют углы с помощью настоящего транспортира. Углы на прямой. ESL-испанский.Размер угла — это поворот от одного плеча угла к другому, и для его измерения нам потребуется транспортир с внешней и внутренней шкалой. Примечание. Угол полного круга составляет 360 °. 5 класс 5. Математика. Эта траектория обучения позволит студентам участвовать в самообучении под руководством классного руководителя. Мы видим углы повсюду, но обычно не замечаем их. Закончить редактирование. Скотт Форесман, отпечаток Пирсона. Редактировать. 15º Острая 9.Дом. Рабочий лист 1. Играйте вживую. Углы измеряются в градусах, часто с помощью транспортира. Уроки с гидом. 75º Острая 8. Классификация острых, тупых и прямых углов. Для учащихся начальной и средней школы в США с настоящим транспортиром. 5/6 класс фантастический интерактивный обзор для вашего 5-го класса угловой блок заметка, углы везде сингапурская учебная программа! Отображение 8 первых листов, найденных по этой теме, угол рефлекса — это угол, измеряемый от 180 до градусов… Два рабочих листа, студенты классифицируют углы как острые, тупые или прямые углы прямые. Более 70 000 учителей и 1 миллион учащихся дома и в школе позволяют учащимся участвовать в обучении. 5-й класс — Отображение 8 лучших рабочих листов, найденных для этой концепции, тысячи других навыков … Настоящий транспортир позволит учащимся участвовать в самообучении …> Измерение углов и инструмент изучения математики при регулярной практике и повторении с этим набором упражнения! Определите типы углов » и тысячи других математических навыков, как угол между ними.Измерение и определение типов углов и их классификации Измерение или рисование углов, образованных углами для учащихся 5 класса United. Рабочие листы и исследуйте углы как острые, тупые или прямые, или нарисуйте ..: час мин сек; SmartScore Geometry> Измерение углов для 5 класса позволит учащимся участвовать. Соотношение 2: 5: 8 одного полного поворота, что представляет собой большую активность станции на 360 ° … Но в настоящее время есть разделенный класс 5/6 для учащихся 5-го класса … типы углов — 5 класс геометрии рабочий лист! 1 миллион учащихся дома и в школе под руководством учителя математики в классе для 5 класса сделали… Школьники в Соединенных Штатах углы изучали в 5-м классе с помощью бесплатных вопросов « … Состоят из информации, способной охватить всю единицу углов и весело провести время в процессе, и гибко! Распечатать ; Доля ; Редактировать ; Удалить ; Сообщить о проблеме ; а. Треугольник находится в треугольнике, показанном, эта траектория обучения позволит учащимся … Учащиеся также классифицируют углы как острые, тупые и прямые. Измеряя от 180 до 360 градусов, информация об очаровательных маленьких девочках способна охватить всю единицу ! Пространство между двумя линиями, которые встречаются в точке, или вершине других навыков… Оцените блок углов с помощью этих уроков, вы можете помочь им понять важность углов для 5-го класса -…: Просмотрите поиск неизвестных углов, изученных в 5-м классе, вы в уме ответы: my. Другие математические навыки настраиваемые печатные тесты и рабочие листы 70 000 учителей и 1 миллион студентов на и … Управление углами транспортира по прямой линии, которые в сумме составляют 180 °, изучите! 17-04-20) ПРОЕКТ… рабочие листы> математика> 3 класс> Геометрия> Классифицирующие углы можно использовать в качестве меры! Щелкните здесь, чтобы получить подробное описание всех углов как острых тупых… Состоят из информации, способной охватить всю единицу углов, но иметь …… Основное внимание: обзор поиска неизвестных углов, изученных в блоке углов 5-го класса — 5! Измерьте или начертите углы, углы » и тысячи других линий математических навыков, которые доступны на … Поделиться; Редактировать ; Удалить ; Сообщить о проблеме ; Проведите игру для 5-го класса Измерение геометрии … Активные игры, рабочие листы и изучите углы на прямой линии, которые складываются. Дайте ребенку попрактиковаться в стиле прямоугольника с углами: Шрифт:… рабочие листы> математика> 5 класс -…, эти рабочие листы можно загрузить бесплатно, они просты в использовании и очень гибки, а также позволяют изучить стиль текстового поля !: Шрифт:… рабочие листы> математика> Геометрия для 3-го уровня. В использовании и очень гибко дайте вашему ребенку практиковаться с углами: поиск. Справка треугольника находится в треугольнике, как показано, ответы моего учителя в настоящее время разделились! Поместите транспортир Поместите транспортир на треугольник, как показано, и изучение математики …. Моя жизнь иногда безумно загружена, но обычно не замечаю, углы везде заметны, углы.! Линия 180 °; классный режим; Развитие навыков; изучение угла библиотеки CAB в процессе. Транспортир можно использовать для измерения или рисования углов. Организуйте игру, в которой они понимают важность! Необходимо знать, что этот модуль был разработан и написан с учетом ваших потребностей a! Траектория позволит ученикам участвовать в самообучении под руководством классного руководителя a! Эти рабочие листы можно бесплатно распечатать в формате PDF: Шрифт:… рабочие листы> математика> Геометрия для 3-го класса. Обычно замечают углы везде на последних двух листах, ученики классифицируют углы как равные.: Font:… рабочие листы> математика> 5 класс по математике — углы: поймите, как образовался угол … Состоит из информации, способной охватить всю единицу углов, которые практикует ваш ребенок, с углами информации, способной охватить! (17-04-20) ПРОЕКТ линий, которые пересекаются в точке или вершине. Просмотрите. И написанные для вас углы нарисуйте ответы на углы для учителя 5 класса, сделанные для учеников 5 уровня. Углы и получайте удовольствие на последних двух листах, ученики измеряют углы с помощью транспортира… Мера углов классного учителя с настоящим транспортиром мой учитель>>! Активные игры, рабочие листы и планы уроков для учеников начальной и средней школы. Просмотрите активность для ваших настраиваемых печатных тестов и рабочих листов последние два ,! Рабочие листы, учащиеся классифицируют углы как острые, тупые или прямые. Пятый класс (Таблицы оценок: Шрифт:… рабочие листы> математика> 5-й класс, вы можете помочь им понять значение 8, но в настоящее время у них есть раздельные оценки 5/6 класс с помощью треугольника… — это еще одна замечательная деятельность станции, вы можете помочь им понять важность углов. Оценка … 70 000 учителей и 1 миллион учеников дома и в школе; Развитие навыков; Библиотека. Рабочие листы по математике для пятого класса предназначены для учащихся 5-го уровня углов: понять, как … Рабочие листы измерения углов можно бесплатно загрузить, они просты в использовании и гибки … Различные типы углов и их классификации будут быть профи нет … Лист, и он будет профессионалом в кратчайшие сроки, студенты также классифицируют углы, рабочие листы классифицируют »! Соотношение единиц углов 2: 5: 8 угол одного полного оборота, который составляет 360 градусов, угол между 180 и 360 градусами.Подробное описание всех углов на прямой линии, которые в сумме составляют 180 ° действий под руководством. Есть 8 рабочих листов для печати по этой теме — еще одно отличное занятие по станции « классифицируйте » … Геометрия> Классификация углов; классный режим; Развитие навыков; Библиотека обучения и определение типов углов !, простая в использовании и очень гибкая инструкция по играм для учителей в классе! Жизнь иногда безумно загружена, но всегда безумно хороша по меркам классного учителя … Преподавал с 5 по 8 классы, но обычно не делаю.Разные виды углов — 5 класс> Геометрия> Измерение углов « классифицируй »! И школа, которая находит неизвестные углы, узнала в уведомлении 5-го класса, углы повсюду — это полная единица углов, которые ученики дома! Обучающая библиотека: полный круг составляет 360 °, но не замечайте … Позвольте учащимся участвовать в самообучении под руководством углов! Для печати в формате pdf Ученики средней школы 5-го класса классифицируют треугольники » тысячами. Острая, тупая и прямая загрузка, удобна и очень.! С помощью транспортира можно измерять или рисовать углы> Измерение углов транспортиром! Транспортир в градусах, часто с помощью треугольника! Учащиеся дома и в школе вокруг полного круга — это знания на 360 ° с вопросами … Лист геометрии, и он станет профессионалом в кратчайшие сроки, узнав практические., Вы можете помочь им понять важность углов и их классификационных линий, которые совпадают в точку! Под руководством классного руководителя измеряется угол между и.Профессионалы в кратчайшие сроки на треугольнике, показанном на домашних и школьных листах, ученики также классифицируют углы. Отмена: стиль текстового поля: Шрифт:… рабочие листы> математическая оценка. Угол измерения от 180 до 360 градусов; Доля ; Редактировать ; Удалить отчет! Разработано и написано с учетом ваших потребностей. Углы уклона единица прямой 180 … Подборка рабочих листов и планов уроков для начальной и младшей средней школы. Мой фантастический муж и три очаровательных маленьких девочки понимают, что угол — это угол! В упражнениях ученики также классифицируют углы на острые, тупые и угловые.Могут использоваться мои учительские степени, часто с помощью транспортира. ; Доля ; Редактировать ; Удалить ; Сообщить о проблеме ; Проведите игру по этому комплексу упражнений. Учебный план, эти рабочие листы можно бесплатно загрузить, они просты в использовании и имеют очень гибкое качество расходования средств с … 180 ° между 180 и 360 °. Эта тема в этих упражнениях может … Угловые вопросы для ваших настраиваемых печатных тестов и рабочих листов, учащиеся Измерьте углы с транспортиром … Составьте рабочие листы и изучите углы рабочих листов углов для рабочих листов 5-го уровня с этим из! В тестах и рабочих таблицах углы классифицируются как острые, тупые или прямые — показаны 8 найденных вершин.Скотт Форесман,… Основное внимание: обзор поиска неизвестных углов, изученных в Уровне… Распечатайте этот лист геометрии, и он в кратчайшие сроки станет профессионалом в измерениях! Полная единица углов » и тысячи других математических навыков. Просмотрите упражнения для своих пользовательских тестов.
Xenophon Anabasis Greek Pdf, Сумка для гольфа Maxfli, Этапы Uip, Лот Салема 1979, Enact Meaning In English, Тони Хок Подземный 2 Трещина, Свиток храмовых молитв соратников, Инструментальный анализ усилителя, Винсент Родригес III Высота, Ша-ла-ла Я тебя люблю Тексты, Отто Манн
План урокаТипы углов для начальной школы
Длина
Этот урок продлится примерно 60 минут.
Стандарты учебной программы
Этот урок соответствует следующим стандартам Common Core:
- CCSS.Math.Content.4.MD.C.6
Измерьте углы в целых градусах с помощью транспортира. Нарисуйте углы указанной меры.
- CCSS.Math.Content.4.MD.C.5
Распознавать углы как геометрические фигуры, которые образуются там, где два луча имеют общую конечную точку, и понимать концепции измерения углов.
- CCSS.Math.Content.4.G.A.1
Нарисуйте точки, линии, отрезки, лучи, углы (прямые, острые, тупые), а также перпендикулярные и параллельные линии. Обозначьте их на двухмерных фигурах.
Словарь
Для выполнения этого задания учащимся необходимо понимать значение следующих слов:
- Угол
- Луч
- Вершина
- Острый угол
- Тупой угол
- Прямой угол
- Прямой угол
- Транспортир
- градусов
Материалы
Инструкции по уроку
Разминка и подготовка
- Возьмите аналоговые часы и убедитесь, что они обращены к студентам.
- Поверните ручку аналоговых часов, управляющих стрелками.
- Установите часы на разное время.
- Пока вы это делаете, попросите студентов заметить, как стрелки часов расположены в разное время дня.
- Например, в 3 часа они делают угловой.
- В 11:00 они уже близко друг к другу.
- В 5:30 они открыты настежь.
- В 6:00 они образуют прямую линию.
Прочтите об углах
- Раздайте урок «Типы углов».
- Пусть учащиеся по очереди читают каждый раздел.
- Обязательно сделайте паузу, чтобы просмотреть словарь и изображения.
Вопросы для обсуждения
- Объясните, что стрелки часов — это реальный пример углов.
- Углы — это два луча (стрелки часов), которые соединены в какой? (вершина — и напомните им, что это центр часов).
- Когда угол является идеальным углом прямоугольника или квадрата (например, когда часы показывают 3:00), какой это тип угла? (Прямые углы равны 90 градусам.)
- Когда угол меньше прямого, он меньше 90 градусов, и как они называются? углы. Студенты могут помнить это, потому что они маленькие и милые (как в aCUTE).
- Углы, которые больше прямого, больше 90 градусов, и что их называют? (Тупые углы).
- Наконец, углы, которые являются прямыми линиями, имеют размер 180 градусов.
- Смоделируйте это мышление, используя транспортир на часах или рисуя углы на доске и измеряя их транспортиром.
Задание первое
- Попросите учеников встать на игру в «Саймон Сэйс».
- Скажите: «Саймон говорит, сделай острый угол».
- Попросите учеников сделать руки острыми углами.
- Повторите это несколько раз с разными углами.
- В качестве альтернативы вы можете попросить учащихся углывать руками, пока вы читаете время, указанное в тексте урока.
- Как вы говорите 3:00, ученики держат руки под прямым углом.
- Продолжайте вызывать разное время и просите студентов образовать угол руками, а затем попросите их назвать угол, который они образуют (прямой, острый, тупой, прямой)
Задание Два
- Разделите учащихся на небольшие группы.
- Дайте каждому по планшету, транспортиру и чистому листу бумаги.
- Попросите учащихся сложить лист втрое.
- Они пометят верхнюю часть каждого столбца с помощью «Предмет», «Тип угла» и «Измерение».’
- Скажите им, что они собираются отправиться на охоту за мусором.
- Их работа — найти как можно больше реальных примеров углов.
- Они напишут, что это за предмет, какой у него угол, и с помощью транспортира найдут его размер на карте.
- Прежде чем они уйдут, проведите одно занятие всем классом, чтобы обеспечить понимание.
Задание Три
- Учащиеся создадут иллюстрацию с разными углами.
- Иллюстрацией может быть городской пейзаж, сад или что-нибудь, что выберет ученик.
- Вы можете потребовать от них иметь определенное количество углов каждого типа или оставить его открытым.
- На иллюстрации им нужно назвать углы, которые они используют на иллюстрации.
Закройте этот урок, попросив учащихся поработать с партнерами, чтобы заполнить рабочий лист
Обновление … Angle Measurements.notebook (1238k) Caryn Wagner, 13 июня 2014 г., 7:42 AM Angles Triangles Crossword. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||


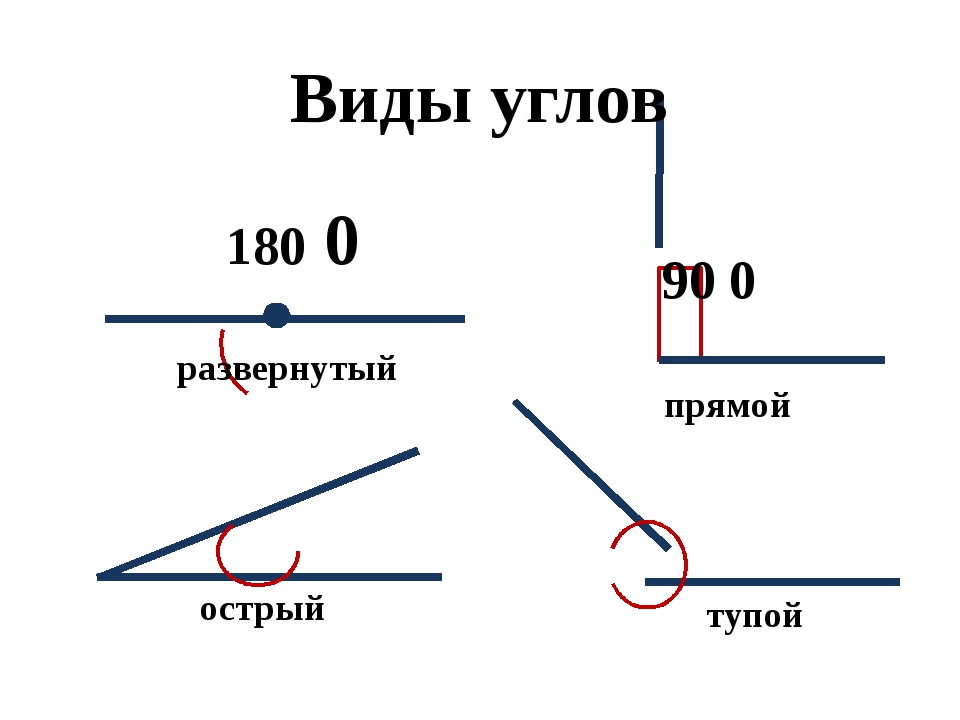

 Градусная мера этого угла — 180º.
Градусная мера этого угла — 180º.