Используемая литература Для ученика:
Для учителя
Цифровые образовательные ресурсы
Список литературы для подготовки к олимпиадам
Электронные источники для подготовки учащихся к олимпиадам. Без решений. Раздел занимательных и веселых задач.
https://homepages.compuserve.de/chasluebeck/matemat/task_1.htm — Задачи некоторых математических олимпиад и турниров. Задания региональных (Москва, Урал, Луганск, Волгоград и др.) и других (МФТИ, Соросовская и т.д.) олимпиад по математике, а также математических турниров (Ломоносовские игры). Для 6-11 классов. Указания и решения доступны зарегистрированным пользователям. https://obrnadzor.gov.ru/attestat/ — Федеральная служба по надзору в сфере образования (государственная итоговая аттестация школьников) http://www.ipkps.bsu.edu.ru – Белгородский региональный институт повышения квалификации и профессиональной переподготовки специалистов (см. раздел «Виртуальный методический кабинет»- Математика) http:/www.drofa.ru — сайт издательства Дрофа (рубрика «Математика») http://www. http://www.edu.ru — Центральный образовательный портал, содержит нормативные документы Министерства, стандарты, информацию о проведение эксперимента. http://www.ed.gov.ru — На сайте представлена нормативная база: в хронологическом порядке расположены законы, указы, которые касаются как общих вопросов образования так и разных направлений модернизации. http://www.ege.edu.ru сервер информационной поддержки Единого государственного экзамена. http://www.internet—scool. http://www.shevkin.ru — Проект Shevkin.ru. Задачи школьных математических олимпиад. Дидактический материал к УМК Никольского. |
Домашняя работа к уч. Виленкина Н.Я. (к двум изд.) ФГОС, Попов М.А. . Решебник , СПИШИ.РУ , 9785906767141 2017г. 87,40р.
Попов М.А.
Серия: Решебник
87,40р.
Только в магазинах
В наличии в 11 магазинах
Ангарск, ПродаЛитЪ Вертикаль
Иркутск, ПродаЛитЪ Ангара
Иркутск, ПродаЛитЪ Детский кварталЪ
Иркутск, ПродаЛитЪ Зачетка
Посмотреть все магазины
Цена в магазине может отличаться
от цены, указанной на сайте.
Поделиться ссылкой в:
Издательство:СПИШИ.РУ
ISBN:978-5-906767-14-1
Штрих-код:9785906767141
Страниц:190
Тип обложки:Мягкая
Год:2017
НДС:10%
Код:587393
Описание
.В пособии решены и в большинстве случаев подробно разобраны задачи и упражнения из учебников «Математика. 5 класс: учеб. для учащихся общеобразоват. организаций / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. — 33-е изд., стер. — М. : Мнемозина, 2014» и «Математика: учеб. для 5 кл. общеобразоват. учреждений / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. — 14-е изд., стереотип. — М. : Мнемозина, 2004». Пособие адресовано родителям, которые смогут проконтролировать правильность решения, а в случае необходимости помочь детям в выполнении домашней работы по математике
Смотреть все
185,00р.
-20% после регистрации
Математика.
 5 класс: Дидактические материалы к учебнику Виленкина ФГОС
(2023 г.)
5 класс: Дидактические материалы к учебнику Виленкина ФГОС
(2023 г.) Попов М.А.
324,00р.
-20% после регистрации
ЕГЭ 2023. Математика. Профильный уровень: 40 тренировочных вариантов ЕГЭ и теоретический справочник (2023 г.)
Лаппо Л.Д., Попов М.А.
157,50р.
-20% после регистрации
Математика. 6 кл.: Дидактические материалы к учеб. Виленкина Н.Я. (к новому ФПУ) (2021 г.)
Попов М.А.
177,00р.
Математика. 5 класс: Контрольные и самостоятельные работы к учебнику Виленкина (к новому ФПУ) (2023 г.
 )
)Попов М.А.
Магазины
284,00р.
ОГЭ 2023. Математика. Сборник заданий (2023 г.)
Лаппо Л.Д., Попов М.А.
Магазины
321,00р.
ОГЭ 2023. Математика. 40 тренировочных вариантов ЕГЭ и теоретический справочник (2023 г.)
Лаппо Л.Д., Попов М.А.
Магазины
320,00р.
ОГЭ 2023. Математика: Репетитор. Эффективная методика. 38 типовых вариантов экзаменационных заданий (2023 г.)
Лаппо Л.Д., Попов М. А.
А.
Магазины
321,00р.
ЕГЭ 2023. Математика. Профильный уровень: Репетитор (2023 г.)
Лаппо Л.Д., Попов М.А.
Магазины
271,00р.
ЕГЭ 2023. Математика: Базовый и профильный уровни: Экзаменационный тренажер. 20 экзаменационных вариантов (2023 г.)
Лаппо Л.Д., Попов М.А.
Магазины
123,00р.
Математика. 5 кл.: Дидактические материалы к учеб. Виленкина ФГОС (2021 г.)
Попов М.А.
Магазины
160,00р.
Математика. 5 кл.: Контрольные и самостоятельные работы к учебн. Виленкина (2021 г.)
Попов М.А.
Магазины
191,50р.
ОГЭ 2021. Математика: Экзаменационный тренажер. 20 экаменационных вариантов (2021 г.)
Лаппо Л.Д., Попов М.А.
Магазины
125,50р.
Математика. 6 кл.: Контрольные и самостоятельные работы к уч. Виленкина Н. (2019 г.)
Попов М.А.
Магазины
90,10р.
Математика. 5 кл.: Домашняя работа к учеб.
 Никольского С.М. и др.
(2018 г.)
Никольского С.М. и др.
(2018 г.)Попов М.А.
Магазины
152,00р.
Математика. 6 кл.: Дидактические материалы к учеб. Виленкина Н.Я. ФГОС (2018 г.)
Попов М.А.
Магазины
137,20р.
ОГЭ 2018. Математика: Сборник заданий (2018 г.)
Лаппо Л.Д., Попов М.А.
Магазины
144,00р.
Алгебра. 8 кл.: Дидактические материалы к учеб. Мордковича А.Г. ФГОС (2017 г.)
Попов М. А.
А.
Магазины
77,00р.
Алгебра. 7 кл.: Контрольные и самостоят. работы к уч. Мордковича А.Г. ФГОС (2017 г.)
Попов М.А.
Магазины
98,40р.
Математика. 6 кл.: Контрольные и самостоятельные работы к уч. Виленкина Н. (2017 г.)
Попов М.А.
Магазины
151,10р.
ЕГЭ. Математика: Профильный уровень. Самостоятельная подготовка к ЕГЭ (2017 г.)
Лаппо Л.Д., Попов М.А.
Магазины
Смотреть все
82,00р.
-20% после регистрации
Геометрия. 9 кл.: Домашняя работа к раб. тетр. и учеб. Атанасяна Л.С. (2018 г.)
Сапожников А.А.
129,50р.
-20% после регистрации
Математика. 3 кл.: Домашняя работа к раб. тетр. и учеб. Петерсон Л. «Учусь (2018 г.)
Петрова М.И.
75,50р.
-20% после регистрации
Английский язык. 2 кл.: Домашняя работа к учеб. Быковой Н.И. (2018 г.)
Рябинина А.А.
98,00р.
-20% после регистрации
Математика.
 4 кл.: Домашняя работа к учеб. Рудницкой + к рабочим тетр ФГОС
(2017 г.)
4 кл.: Домашняя работа к учеб. Рудницкой + к рабочим тетр ФГОС
(2017 г.) Асриева М.В.
82,00р.
-20% после регистрации
Математика. 2 кл.: Домашняя работа к учебнику В.Н.Рудницкой (2017 г.)
Бахтина С.В.
98,00р.
-20% после регистрации
Математика. 5 кл.: Решение контрольных и самост. работ к пособ. Чеснокова (2017 г.)
Лаппо Л.Д.
98,00р.
-20% после регистрации
Русский язык. 9 кл.: Домаш. работа к учеб. Разумовской М. Вертикаль ФГОС (2017 г.

Ерманок А.А.
64,68р.
-20% после регистрации
Русский язык. 6 кл.: Домашняя работа к учеб. Баранова М.Т. (2017 г.)
Кудинова А.В.
41,60р.
-20% после регистрации
Информатика. 6 кл.: к учеб. Л.Л. Босовой + к рабочим тетрадям ФГОС (2016 г.)
Шульцева О.В.
80,40р.
-20% после регистрации
Английский язык. 2 кл.: Домашняя работа к учебнику И.Н. Верещагиной ФГОС (2016 г.)
Бычкова Т.А.
41,60р.
-20% после регистрации
Немецкий язык. 4 кл.: Домашняя работа к учеб. и рабочей тетради Бим И.Л. (2016 г.)
Герасимова Е.Ю.
66,60р.
-20% после регистрации
Литература. 8 кл.: Домашняя работа к учеб. Коровиной В.Я. ФГОС (2016 г.)
Тищенко О.А.
110,00р.
Английский язык. 7 кл.: Домашняя работа к учеб. и раб. тетради Ваулиной Ю. (2018 г.)
Гарист Н.А.
Магазины
90,10р.
Геометрия. 8 кл.: Домашняя работа к уч. Атанасяна + к рабочей тетради ФГОС (2018 г.
 )
)Прокопович А.Н.
Магазины
75,50р.
Русский язык. 5 кл.: Домашняя работа к учеб. Ладыженской Т.А. ФГОС (2018 г.)
Кудинова А.В.
Магазины
79,00р.
Литература. 7 кл.: Домашняя работа к учеб. Коровиной В. ФГОС к новому учеб. (2018 г.)
Тищенко О.А.
Магазины
87,40р.
Математика. 6 кл.: Домашняя работа к уч. Виленкина Н.Я. ФГОС к новому учеб. (2018 г.)
Панов Н.А.
Магазины
82,00р.
Алгебра. 7 кл.: Домашняя работа к учеб. Макарычева Ю.Н. ФГОС (2018 г.)
Морозов А.В.
Магазины
87,40р.
Математика. 3 кл.: Домашняя работа к учеб. и раб. тетрдям Моро М.И. (2017 г.)
Бахтина С.В.
Магазины
41,60р.
Русский языкк. 2 кл.: Домашняя работа к учеб. В.П. Канакиной ФГОС (2017 г.)
Дьячкова Л.В.
Магазины
Смотреть все
242,50р.
Алгебра. 8 кл.: Дидактические материалы (2020 г.
 )
)Жохов В.И., Макарычев Ю.Н.
Магазины
766,00р.
Репетитор по биологии для старшеклассников и поступающих в вузы (2022 г.)
Шустанова Татьяна Анатольевна
Магазины
203,00р.
Математика. 7-11 классы: Карманный справочник (2022 г.)
Лысенко Ф.Ф.
Магазины
131,00р.
Математика. 3 класс: Комплексный тренажер (2022 г.)
Барковская Наталья Францевна
Магазины
172,00р.
-20% после регистрации
Математика. 5 класс: Зачетные работы к учебнику Никольского С.М. ФГОС (к новому ФПУ) (2022 г.)
Ахременкова Вера Игоревна
334,00р.
Биология в инфографике (2022 г.)
Мазур О.Ч.
Магазины
122,00р.
Физика. 7-9 кл.: Справочник ФГОС (2018 г.)
Гормцева О.И.
Магазины
419,00р.
-20% после регистрации
Математическая грамотность. Сборник эталонных заданий: Выпуск 1 Часть 1 (2022 г.
 )
)Ковалева Г.С., Рослова Л.О., Краснянская К.А.
100,00р.
3000 примеров по математике. 1 кл.: Считаем и объясняем. Сложение и вычитание (2021 г.)
Узорова Ольга Васильевна
Магазины
555,00р.
Физика. 10 класс: Базовый уровень. Сборник задач (2022 г.)
Заболотский А.А. Комиссаров В.Ф. Петрова М.А.
Магазины
94,50р.
Тренировочные примеры по математике. 3 кл.: Счет в пределах 1000 ФГОС (2021 г.)
Кузнецова Марта Ивановна
Магазины
179,50р.
Тренажер по математике. 2 класс ФГОС (2021 г.)
Яценко. И.Ф.
Магазины
153,00р.
География. 5-6 класс: Проверочные работы (2020 г.)
Бондарева М.В. Шидловский И.М.
Магазины
94,50р.
Тренировочные примеры по математике. 1 кл.: Счет от 6 до 10 (ФГОС) (2021 г.)
Кузнецова Марта Ивановна
Магазины
216,00р.
-20% после регистрации
Математика. 1-4 классы (2023 г.
 )
)Узорова Ольга Васильевна, Нефедова Елена Алексеевна
296,50р.
Геометрия. 7-11 кл.: Алгоритмы решения задач (2020 г.)
Виноградова Т.М.
Магазины
322,00р.
Решение задач по химии. 8-11 классы: Решения, методики, советы (2021 г.)
Хомченко И.Г.
Магазины
150,00р.
Математика. 4-й класс (2020 г.)
Сазонова В.А.
Магазины
81,50р.
Запоминаем таблицу умножения (2019 г.
 )
).
Магазины
118,00р.
Таблица умножения за 3 дня (2021 г.)
Узорова Ольга Васильевна
Магазины
|
Эта статья цитируется в 34 научных статьях (всего в 34 статьях) По классу полной ортонормированные системы Н. Виленкин Полный текст PDF (2338 кБ) Поступила в редакцию: 25.07.1946 Библиографические базы данных: Язык: Русский Ссылка: Н. Виленкин, “Об одном классе полных ортонормированные системы”, Изв. акад. АН СССР сер. Мат., 11:4 (1947), 363–400 Цитирование в формате AMSBIB Варианты соединения: Эта публикация цитируется в следующих статьях:
Ссылки на статьи в Google Scholar: русские цитаты,
английские цитаты | QR-? | ||||||||||||||||||||||||||||||||||||||||||||||||||||
Некоторые неравенства для средних Чезаро двойных рядов Виленкина–Фурье
- Список журналов
- Открытый выбор Спрингера
- PMC6300583
Журнал неравенств и приложений
J Неравное применение 2018; 2018(1): 352.
Опубликовано в Интернете 19 декабря 2018 г. doi: 10.1186/s13660-018-1929-y
и
мы формулируем и доказываем некоторые новые неравенства, связанные со скоростью аппроксимации Lp средними Чезаро квадратичных частных сумм двойных рядов Виленкина–Фурье функций из Lp.
Ключевые слова: Неравенства, Аппроксимация, Система Виленкина, Ряды Виленкина–Фурье, Средние Чезаро, Сходимость по норме
Пусть N+ обозначает множество натуральных чисел, и пусть N:=N+∪{0}. Пусть m:=(m0,m1,…) — последовательность натуральных чисел не менее 2. Обозначим через Zmk:={0,1,…,mk−1} аддитивную группу целых чисел по модулю mk. Определим группу Gm как полное прямое произведение групп Zmj на произведение дискретных топологий Zmj.
Прямой продукт мер
µk({j}):=1mk(j∈Zmk)
— мера Хаара на Gm с µ(Gm)=1. Если последовательность m ограничена, то Gm называется ограниченной группой Виленкина. В данной работе мы рассматриваем только ограниченные группы Виленкина. Элементы Gm могут быть представлены последовательностями x:=(x0,x1,…,xj,…) (xj∈Zmj). Групповая операция + в Gm задается выражением
В данной работе мы рассматриваем только ограниченные группы Виленкина. Элементы Gm могут быть представлены последовательностями x:=(x0,x1,…,xj,…) (xj∈Zmj). Групповая операция + в Gm задается выражением
x+y=((x0+y0)modm0,…,(xk+yk)modmk,…)
для x:=(x0,…,xk,…) и y:=(y0,…,yk ,…)∈Gm. Обратное + будет обозначаться -.
Легко дать базу для окрестностей Gm:
I0(x):=Gm,In(x):={y∈Gm|y0=x0,…,yn−1=xn−1}
для x∈Gm и n∈N. Определить In:=In(0) для n∈N+. Положим en:=(0,…,0,1,0,…)∈Gm, где n -я координата которого равна 1, а остальные нули (n∈N).
Определим так называемую обобщенную систему счисления, основанную на m , следующим образом: M0:=1, Mk+1:=mkMk (k∈N). Тогда каждое n∈N однозначно выражается как n=∑j=0∞njMj, где nj∈Zmj (j∈N+), и только конечное число nj отличны от нуля. Мы также используем следующие обозначения: |n|:=max{k∈N:nk≠0} (т. е. M|n|≤n Далее введем на Gm ортонормированную систему, называемую системой Виленкина. rk(x):=exp2πixkmk(i2=−1,x∈Gm,k∈N). Теперь определим систему Виленкина ψ:=(ψn:n∈N) на Gm как ψn(x):=∏k=0∞rknk(x)(n∈N). В частности, если m=2, то мы называем эту систему системой Уолша–Пэли. Каждый ψn является характером Gm, и все характеры Gm имеют эту норму. Более того, ψn(−x)=ψ¯n(x). Ядра Дирихле определяются формулой Dn:=∑k=0n−1ψk(n∈N+). Напомним, что (см. [20] или [23]) DMn(x)={Mnif x∈In,0if x∉In. 1 Система Виленкина ортонормирована и полна в L1(Gm) (см. [1]). Далее введем некоторые обозначения из теории двумерной системы Виленкина. Пусть m̃ будет последовательностью, подобной m . Связь между последовательностями (m˜n) и (M˜n) такая же, как между последовательностями (mn) и (Mn). Группа Gm×Gm˜ называется двумерной группой Виленкина. Нормализованная мера Хаара обозначается μ , как и в одномерном случае. Норма пространства Lp(Gm2) определяется формулой ∥f∥p:=(∫Gm2|f(x,y)|pdµ(x,y))1/p(1≤p<∞). Обозначим через C(Gm2) класс непрерывных функций на группе Gm2, снабженных супремум-нормой. Для краткости обозначений мы пишем L∞(Gm2) вместо C(Gm2). Двумерные коэффициенты Фурье, прямоугольные частичные суммы рядов Фурье и ядра Дирихле по двумерной системе Виленкина определяются следующим образом: fˆ(n1,n2):=∫Gm2f(x,y)ψ¯n1(x)ψ¯n2(y)dµ(x,y),Sn1,n2(x,y,f):=∑k1 =0n1−1∑k2=0n2−1fˆ(k1,k2)ψk1(x)ψk2(y),Dn1,n2(x,y):=Dn1(x)Dn2(y), Обозначим Sn(1)(x,y,f):=∑l=0n−1fˆ(l,y)ψ¯l(x),Sm(2)(x,y,f):=∑r=0m −1fˆ(x,r)ψ¯r(y), , где fˆ(l,y)=∫Gmf(x,y)ψl(x)dµ(x) и fˆ(x,r)=∫Gmf(x,y)ψr(y)dµ(y). Средние (C,−α) двойного ряда Виленкина–Фурье определяются следующим образом: σn−α(f,x,y)=1An−1−α∑j=1nAn−j−α−1Sj,j(f,x,y), где A0α=1,Anα=(α+1)⋯(α+n)n!. Хорошо известно, что (см. [28]) Anα=∑k=0nAkα−1, 2 Anα−An−1α=Anα−1, 3 и c1(α)nα≤Anα≤c2(α)nα, 4 где положительные константы c1 и c2 зависят от α . Диадические частичные модули непрерывности функции f∈Lp(Gm2) в Lp-норме определяются соотношениями ω1(f,1Mn)p=supu∈In∥f(⋅+u,⋅)−f(⋅,⋅)∥p и ω2(f,1Mn)p=supv∈In∥f(⋅,⋅+v)−f(⋅,⋅)∥p, , тогда как диадический смешанный модуль непрерывности определяется следующим образом: ω1,2(f,1Mn,1Mm)p=sup(u,v)∈In×Im∥f(⋅+u,⋅+v)−f(⋅+u,⋅)−f(⋅,⋅ +v)+f(⋅,⋅)∥p. Понятно, что ω1,2(f,1Mn,1Mm)p≤ω1(f,1Mn)p+ω2(f,1Mm)p. Диадический полный модуль непрерывности определяется выражением ω(f,1Mn)p=sup(u,v)∈In×In∥f(⋅+u,⋅+v)−f(⋅,⋅)∥p. Проблемы суммирования частных сумм и чезаровских средних для рядов Уолша–Фурье изучались в [2, 13–19, 21, 22, 25, 26]. Вопрос сходимости средних Фейера (и Чезаро) на группах Уолша и Виленкина для неограниченного случая изучался в [3–11]. В своей монографии [27] Жижинашвили подробно исследовал поведение чезаровских (C,α)-средних для двойных тригонометрических рядов Фурье. Гогинава [18] изучала аналогичный вопрос в случае системы Уолша. В частности, были доказаны следующие теоремы. Пусть ф принадлежат Lp(G2) для некоторых p∈[1,∞] и α∈(0,1). Затем , для любого 2k≤n<2k+1 (k,n∈N), имеем неравенство ∥σ2k−α(f)−f∥p≤c(α){2kαω1(f,1/2k−1)p+2kαω2(f,1/2k−1)p+∑r=0k−22r−kω1 (f,1/2r)p+∑s=0k−22s−kω2(f,1/2s)p}. Пусть ф принадлежат Lp(G2) для некоторых p∈[1,∞] и α∈(0,1). Затем , для любых 2k≤n<2k+1 (k,n∈N), имеем неравенство ∥σn−α(f)−f∥p≤c(α){2kαkω1(f,1/2k−1)p+2kαkω2(f,1/2k−1)p+∑r=0k−22r−kω1 (f,1/2r)p+∑s=0k−22s−kω2(f,1/2s)p}. В данной работе мы формулируем и доказываем аналогичные результаты для случая двойных рядов Виленкина–Фурье. Пусть ф принадлежат Lp(Gm2) для некоторых p∈[1,∞] и α∈(0,1). Затем , для любого Mk≤n ∥σMk−α(f)−f∥p≤c(α)(ω1(f,1/Mk−1)pMkα+ω2(f,1/Ml−1)pMkα+∑r=0k−2MrMkω1( f,1/Mr)p+∑s=0k−2MsMkω2(f,1/Ms)p). Пусть ф принадлежат Lp(Gm2) для некоторых p∈[1,∞] и α∈(0,1). Затем , для любого Mk≤n ∥σn−α(f)−f∥p≤c(α)(ω1(f,1/Mk−1)pMkαlogn+ω2(f,1/Ml−1)pMkαlogn+∑r=0k−2MrMkω1(f ,1/Mr)p+∑s=0k−2MsMkω2(f,1/Ms)p). Чтобы сделать доказательства этих теорем более ясными, мы сформулируем некоторые вспомогательные леммы в разд. 2. Некоторые из этих лемм являются новыми и представляют самостоятельный интерес. Подробные доказательства можно найти в разд. Для доказательства теорем 1 и 2 нам понадобятся следующие три леммы (см. [1, 12] и [8] соответственно) Пусть α1,α2,…,αn — действительные числа . Затем 1n∫G|∑k=1nαkDk(x)|dµ(x)≤cn(∑k=1nαk2)1/2. Лет α1,α2,…,αn — действительные числа . Затем 1n∫Gm2|∑k=1nαkDk(x)Dk(y)|dµ(x,y)≤cn(∑k=1nαk2)1/2. Пусть 0≤j DnsMs-j=DnsMs-ψnsMs-1D¯j. Нам также понадобятся следующие новые неммы, представляющие самостоятельный интерес. Пусть ф принадлежат Lp(Gm2) для некоторых p∈[1,∞]. Затем , на каждые α∈(0,1), имеем неравенство I:=1An−α∥∫Gm2∑i=1Mk−1An−i−α−1Di(u)Di(v)[f(⋅−u,⋅−)−f(⋅,⋅)]dµ( u,v)∥p≤∑r=0k−2MrMkω1(f,1/Mr)p+∑s=0k−2MsMkω2(f,1/Ms)p, где Мк≤n<Мк+1. Пусть α∈(0,1) и р=Мк,Мк+1,… . Затем II:=∫Gm2|∑i=1MkAp−i−α−1Di(u)Di(v)|dµ(u,v)≤c(α)<∞,k=1,2,…. Имеем неравенство III:=∫Gm2|∑i=1nAn−i−α−1Di(u)Di(v)|dµ(u,v)≤c(α)logn Применяя преобразование Абеля, из (2) получаем I≤1An−α∥∫Gm2∑i=1Mk−1−1An−i−α−2∑l=1iDi(u)Di(v)[f(⋅−u,⋅−v)−f(⋅ ,⋅)]dµ(u,v)∥p+1An−α∥∫Gm2An−Mk−1−α−1∑i=1Mk−1Di(u)Di(v)[f(⋅−u,⋅−v )−f(⋅,⋅)]dµ(u,v)∥p:=I1+I2, 5 где первое и второе слагаемые в правой части неравенства (5) обозначены I1 и I2, соответственно. Для I2 имеем оценку I2≤1An−α∥∫Gm2An−Mk−1−α−1∑r=1k−2∑i=MrMr+1−1Di(u)Di(v)×[f(⋅−u,⋅−v )−f(⋅,⋅)]∥pdµ(u,v)≤1An−α∥∫Gm2An−Mk−1−α−1∑r=1k−2∑i=MrMr+1−1Di(u)Di( v)×[f(⋅−u,⋅−v)−SMr,Mr(⋅−u,⋅−v,f)]dµ(u,v)∥p+1An−α∥∫Gm2An−Mk−1− α−1∑r=1k−2∑i=MrMr+1−1Di(u)Di(v)×[SMr,Mr(⋅−u,⋅−v,f)−SMr,Mr(⋅,⋅,f )]dµ(u,v)∥p+1An−α∥∫Gm2An−Mk−1−α−1∑r=1k−2∑i=MrMr+1−1Di(u)Di(v)×[SMr, Mr(⋅,⋅,f)−f(⋅,⋅)]dµ(u,v)∥p:=I21+I22+I23, 6 где первый, второй и третий члены в правой части неравенства (6) обозначаются I21, I22 и I23 соответственно. Очевидно, что ∫Gm2∑i=MrMr+1−1Di(u)Di(v)[SMr,Mr(⋅−u,⋅−v,f)−SMr,Mr(⋅,⋅,f)]dµ(u, v)=∑i=MrMr+1−1(∫Gm2Di(u)Di(v)SMr,Mr(⋅−u,⋅−v,f)dµ(u,v)−SMr,Mr(⋅,⋅, f))=∑i=MrMr+1−1(Si(⋅,⋅,SMr,Mr(f))−SMr,Mr(⋅,⋅,f))=∑i=MrMr+1−1(SMr, Mr(⋅,⋅,f)−SMr,Mr(⋅,⋅,f))=0. Отсюда I22=0. 7 Кроме того, в силу обобщенного неравенства Минковского, леммы 2 и в силу (1) и (4) получаем I21≤1An−α|An−Mk−1−α−1|∑r=1k−2∫Gm2|∑i=MrMr+1−1Di(u)Di(v)|×∥f(⋅−u ,⋅−v)−SMr,Mr(⋅−u,⋅−v,f)∥pdµ(u,v)≤c(α)Mk∑r=1k−2(ω1(f,1/Mr)p+ ω2(f,1/Mr)p)×∫Gm2|∑i=MrMr+1−1Di(x)Di(y)|dµ(u,v)≤c(α)∑r=1k−2MrMk(ω1( f,1/Mr)p+ω2(f,1/Mr)p). 8 Оценка I23 аналогична оценке I21: I23≤c(α)∑r=1k−2MrMk(ω1(f,1/Mr)p+ω2(f,1/Mr)p). 9 Аналогично можно оценить I1 следующим образом: I1≤1An−α∑r=1k−2∥∫Gm2∑i=MrMr+1−1An−i−α−2∑l=1iDl(u)Dl(v)×[f(⋅−u,⋅ −v)−SMr,Mr(⋅−u,⋅−v,f)]dµ(u,v)∥p+1An−α∑r=1k−2∥∫Gm2∑i=MrMr+1−1An−i −α−2∑l=1iDl(u)Dl(v)×[SMr,Mr(⋅−u,⋅−v,f)−SMr,Mr(⋅,⋅,f)]∥pdµ(u,v) +1An−α∑r=1k−2∥∫Gm2∑i=MrMr+1−1An−i−α−2∑l=1iDl(u)Dl(v)×[SMr,Mr(⋅,⋅,f) −f(⋅,⋅)]dµ(u,v)∥p≤1An−α∑r=1k−2∫Gm2|∑i=MrMr+1−1An−i−α−2∑l=1iDl(u) Dl(v)|×∥f(⋅−u,⋅−v)−SMr,Mr(⋅−u,⋅−v,f)∥pdµ(u,v)+1An−α∑r=1k−2∫ Gm2|∑i=MrMr+1−1An−i−α−2∑l=1iDl(u)Dl(v)|×∥SMr,Mr(⋅,⋅,f)−f(⋅,⋅)∥pdµ( u,v)≤c(α)Mkα∑r=1k−2∑i=MrMr+1−1(n−i)−α−2i(ω1(f,1/Mr)p+ω2(f,1/ Mr)p)≤c(α)Mkα∑r=1k−2∑i=MrMr+1−1(n−Mr+1−1)−α−2i(ω1(f,1/Mr)p+ω2( f,1/Mr)p)≤c(α)∑r=0k−2MrMk(ω1(f,1/Mr)p+ω2(f,1/Mr)p). 10 Комбинируя (7)–(9) с (10) для I , мы находим, что I≤c(α)∑r=0k−2MrMk(ω1(f,1/Mr)p+ω2(f,1/Mr)p). 11 Лемма 3 доказана. □ Очевидно, что II≤∫Gm2|∑i=1Mk−1Ap−Mk+i−α−1DMk−i(u)DMk−i(v)|dµ(u,v)+|Ap−Mk−α−1|∫ Gm2DMk(u)DMk(v)dµ(u,v):=II1+II2, 12 где первое и второе слагаемые в правой части неравенства (12) обозначены через II1 и II2 соответственно. Из (1) через |Ap−Mk−α−1|≤1 получаем, что II2≤1. 13 Более того, по лемме 3 имеем II1≤∫Gm2|∑i=1Mk−1Ap−Mk+i−α−1D¯i(u)D¯i(v)|dµ(u,v)+∫Gm2DMk(u)|∑i=1Mk −1Ap−Mk+i−α−1D¯i(v)|dµ(u,v)+∫Gm2DMk(v)|∑i=1Mk−1Ap−Mk+i−α−1D¯i(u)|dµ (u,v)+|∑i=1Mk−1Ap−Mk+i−α−1|∫Gm2DMk(u)DMk(v)dµ(u,v):=II11+II12+II13+II14, 14 где первое, второе, третье и четвертое слагаемые в правой части неравенства (14) обозначены символами II11, II12, II13 и II14 соответственно. Из (1) и (4) следует, что II14≤c(α)∑v=1∞v−α−1<∞. 15 Применяя преобразование Абеля, с учетом леммы 2 имеем, что II11≤∫Gm2|∑i=1Mk−2Ap−Mk+i−α−2∑l=1iD¯l(u)D¯l(v)|dµ(u,v)+∫Gm2|Ap−1 −α−1∑i=1Mk−1D¯i(u)D¯i(v)|dµ(u,v)≤c(α){∑v=1Mk−2(p−Mk+i)−α− 2i+(p−1)−α−1Mk}≤c(α){∑i=1∞i−α−1+Mk−α}<∞. 16 Оценка II12 и II13 аналогична оценке II11. Применяя преобразование Абеля, с учетом леммы 1 находим, что II12≤∫Gm2DMk(u)|∑i=1Mk−2Ap−Mk+i−α−2∑l=1iD¯l(v)|dµ(u,v)+∫Gm2DMk(u)|Ap−1 −α−1∑i=1Mk−1D¯i(v)|dµ(u,v)≤c(α){∑v=1Mk−2(p−Mk+i)−α−2i+(p−1) −α−1Mk}≤c(α){∑i=1∞i−α−1+Mk−α}<∞ 17 и III12≤∫Gm2DMk(v)|∑i=1Mk−2Ap−Mk+i−α−2∑l=1iD¯l(u)|dµ(u,v)+∫Gm2DMk(v)|Ap−1 −α−1∑i=1Mk−1D¯i(u)|dµ(u,v)≤c(α){∑v=1Mk−2(p−Mk+i)−α−2i+(p−1) −α−1Mk}≤c(α){∑i=1∞i−α−1+Mk−α}<∞. 18 Доказательство завершается комбинацией (12)–(18). □ Пусть n=nk1Mk1+⋯+nksMks,k1>⋯>ks≥0. Обозначение n(i)=nkiMki+⋯+nksMks,i=1,2,…,s. Так как (см. [20]) Dj+nAMA=DnAMA+ψnAMADj, 19 находим, что III≤∫Gm2|∑i=1nk1Mk1An−i−α−1Di(u)Di(v)|dµ(u,v)+∫Gm2|∑i=1n(2)An(2)−i−α −1Di(u)Di(v)|dµ(u,v)+∫Gm2Dnk1Mk1(u)Dnk1Mk1(v)|∑i=1n(2)An(2)−i−α−1|dµ(u,v )+∫Gm2Dnk1Mk1(u)|∑i=1n(2)An(2)−i−α−1Di(v)|dµ(u,v)+∫Gm2Dnk1Mk1(v)|∑i=1n(2)An (2)−i−α−1Di(u)|dµ(u,v):=III1+III2+III3+III4+III5, 20 где первое, второе, третье, четвертое и пятое слагаемые в правой части неравенства (20) обозначены символами III1, III2, III3, III4 и III5 соответственно. По (1) имеем, что III3≤c(α). 21 Кроме того, поскольку (см. [24]) |∑i=1nAn−i−α−1Di(u)|=O(|u|α−1), 22 для III4, получаем, что III4≤∫Gm2Dnk1Mk1(u)|v|α−1dµ(u,v)≤∫Gm|v|α−1dµ(v)=1α<∞. 23 Аналогично находим, что III5≤∫Gm2Dnk1Mk1(v)|u|α−1dµ(u,v)≤∫Gm|u|α−1dµ(v)=1α<∞. 24 Для r∈{0,…mA−1} и 0≤j Dj+rMA=(∑q=0r−1ψMAq)DMA+ψMArDj. Таким образом, мы имеем ∫Gm2∑i=1nk1Mk1−1An−i−α−1Di(u)Di(v)dµ(u,v)≤∫Gm2∑r=0nk1−1∑i=0Mk1−1An−i−rMk1−α −1Di+rMk1(u)Di+rMk1(v)dµ(u,v)≤∫Gm2∑r=0nk1−1∑i=0Mk1−1An−i−rMk1−α−1(∑q=0r−1ψMk1q) DMk1(u)×(∑q=0r−1ψMk1q)DMk1(v)dµ(u,v)+∫Gm2∑r=0nk1−1∑i=0Mk1−1An−i−rMk1−α−1(∑q= 0r−1ψMk1q)DMk1(u)ψMArDi(v)dµ(u,v)+∫Gm2∑r=0nk1−1∑i=0Mk1−1An−i−rMk1−α−1ψMArDi(u)(∑q=0r− 1ψMk1q)DMk1(v)dµ(u,v)+∫Gm2∑r=0nk1−1∑i=0Mk1−1An−i−rMk1−α−1ψMArDi(u)ψMArDi(v)dµ(u,v). С другой стороны, в силу (1) и (4) получаем, что ∫Gm2An−nk1Mk1−α−1Dnk1Mk1(u)Dnk1Mk1(v)dµ(u,v)≤c(α). Следовательно, для III1 имеем оценку III1≤∫Gm2DMk1(u)DMk1(v)|∑r=0nk1−1∑i=1Mk1An−i−rMk1−α−1|dµ(u,v)+∫Gm2DMk1(u)|∑r=0nk1 −1∑i=1Mk1An−i−rMk1−α−1Di(v)|dµ(u,v)+∫Gm2DMk1(v)|∑r=0nk1−1∑i=1Mk1An−i−rMk1−α−1Di( u)|dµ(u,v)+∫Gm2|∑r=0nk1−1∑i=1Mk1An−i−rMk1−α−1Di(u)Di(v)|dµ(u,v)+c(α) :=III11+III12+III13+III14+c(α), 25 где первое, второе, третье и четвертое слагаемые в правой части неравенства (25) обозначены через III11, III12, III13 и III14 соответственно. Из леммы 4 получаем, что III14≤c(α). 26 Оценка III11 аналогична оценке III3, и мы находим, что III11≤c(α). 27 Оценка III12 и III13 аналогична оценке III4, и мы получаем, что III12<∞ 28 и III13<∞. 29 После подстановки (21) и (23)–(29) в (20) заключаем, что ∫Gm2|∑i=1nAn−i−α−1Di(u)Di(v)|dµ(u,v)≤∫Gm2|∑i=1n(2)An(2)−i−α−1Di (u)Di(v)|dµ(u,v)+c(α)≤⋯≤∫Gm2|∑i=1n(s)An(s)−i−α−1Di(u)Di(v)| dµ(u,v)+c(α)s≤c(α)+c(α)s≤c(α)logn. Доказательство завершено. □ Теперь мы готовы доказать основные результаты. Очевидно, что ∥σMk−α(f)−f∥p≤1AMk−1−α∥∫Gm2∑i=1Mk−1AMk−i−α−1Di(u)Di(v)[f(⋅−u,⋅− v)−f(⋅,⋅)]dµ(u,v)∥p+1AMk−1−α∥∫Gm2∑i=Mk−1+1MkAMk−i−α−1Di(u)Di(v)[f (⋅−u,⋅−v)−f(⋅,⋅)]dµ(u,v)∥p:=I+II. 30 Из леммы 5 следует, что I≤c(α)∑r=0k−2MrMk(ω1(f,1/Mr)p+ω2(f,1/Mr)p). 31 Кроме того, для II , у нас есть оценка II≤1AMk−1−α∥∫Gm2∑i=Mk−1+1MkAMk−i−α−1Di(u)Di(v)×[f(⋅−u,⋅−v)−SMk−1( 1)(⋅−u,⋅−v,f)]dµ(u,v)∥p+1AMk−1−α∥∫Gm2∑i=Mk−1+1MkAMk−i−α−1Di(u)Di( v)×[SMk−1(1)(⋅−u,⋅−v,f)−f(⋅,⋅)]dµ(u,v)∥p:=II1+II2, 32 , где первое и второе слагаемые в правой части неравенства (32) обозначены соответственно II1 и II2. С учетом обобщенного неравенства Минковского в силу (4) и леммы 5 получаем, что II1≤1AMk−1−α∫Gm2|∑i=Mk−1+1MkAMk−i−α−1Di(u)Di(v)|×∥f(⋅−u,⋅−v)−SMk−1 (1)(⋅−u,⋅−v,f)∥pdµ(u,v)≤c(α)Mkαω1(f,1/Mk−1)p. 33 Оценка II2 аналогична оценке II1, и мы находим, что II2≤c(α)Mkαω2(f,1/Mk−1)p. 34 Объединяя (30)–(34), получаем доказательство теоремы 1. □ Очевидно, что ∥σn−α(f)−f∥p≤1An−1−α∥∫Gm2∑i=1Mk−1An−i−α−1Di(u)Di(v)[f(⋅−u,⋅− v)−f(⋅,⋅)]dµ(u,v)∥p+1An−1−α∥∫Gm2∑i=Mk−1+1MkAn−i−α−1Di(u)Di(v)[f (⋅−u,⋅−v)−f(⋅,⋅)]dµ(u,v)∥p+1An−1−α∥∫Gm2∑i=Mk+1nAn−i−α−1Di(u)Di (v)[f(⋅−u,⋅−v)−f(⋅,⋅)]dµ(u,v)∥p:=I+II+III, 35 где первый, второй и третий члены в правой части неравенства (35) обозначены I , II и III соответственно. Из леммы 4 следует, что I≤c(α)∑r=0k−2MrMk(ω1(f,1/Mr)p+ω2(f,1/Mr)p). 36 Далее, повторяя рассуждения точно так же, как при доказательстве теоремы 1, получаем, что II≤c(α)Mkα(ω1(f,1/Mk−1)p+ω2(f,1/Mk−1)p). 37 С другой стороны, для III имеем III≤1An−1−α∥∫Gm2∑i=Mk+1nAn−i−α−1Di(u)Di(v)×[f(⋅−u,⋅−v)−f(⋅,⋅) ]∥pdµ(u,v)≤1An−α∥∫Gm2∑i=Mk+1nAn−i−α−1Di(u)Di(v)×[f(⋅−u,⋅−v)−SMk,Mk (⋅−u,⋅−v,f)]dµ(u,v)∥p≤1An−α∥∫Gm2∑i=Mk+1nAn−i−α−1Di(u)Di(v)×[SMk, Mk(⋅−u,⋅−v,f)−SMk,Mk(⋅,⋅,f)]dµ(u,v)∥p≤1An−α∥∫Gm2∑i=Mk+1nAn−i−α− где первое, второе и третье слагаемые в правой части неравенства (38) обозначаются через III1, III2 и III3 соответственно. Легко показать, что III2=0. 39 В силу обобщенного неравенства Минковского и леммы 5 для III1 получаем, что III1≤1An−α∫Gm2|∑i=Mk+1nAn−i−α−1Di(u)Di(v)|×∥f(⋅−u,⋅−v)−SMr,Mr(⋅−u ,⋅−v,f)∥pdµ(u,v)≤c(α)Mkα(ω1(f,1/Mk−1)p+ω2(f,1/Mk−1)p)×∫Gm2|∑ v=Mk+1nAn−v−α−1Dv(u)Dv(v)|dµ(u,v)≤c(α)Mkαlogn(ω1(f,1/Mk−1)p+ω2(f,1/ Мк-1)р). 40 Оценка III3 аналогична оценке III2, и мы находим, что III3≤c(α)Mkαlogn(ω1(f,1/Mk−1)p+ω2(f,1/Mk−1)p). 41 После подстановки (36)–(37) и (41) в (35) получаем доказательство теоремы 2. □ Авторы благодарят рецензентов за полезные советы. Авторы внесли одинаковый вклад в написание этой статьи. Оба автора одобрили окончательный вариант рукописи. Неприменимо. Авторы заявляют, что у них нет конкурирующих интересов. Примечание издателя Springer Nature сохраняет нейтралитет в отношении юрисдикционных претензий в опубликованных картах и институциональной принадлежности. Т. Тепнадзе, Email: moc.liamg@ezdanfetonist. Л. Э. Перссон, электронная почта: moc.liamg@srep6kiresral. 1. Агаев Г.Н., Виленкин Н.Я., Джафарли Г.М., Рубинштейн А.И. Мультипликативные системы функций и гармонический анализ на нульмерных группах. Баку: Эльм; 1981. [Google Scholar] 2. Файн Н. Дж. Чезаро суммируемость рядов Уолша–Фурье. проц. Натл. акад. науч. США. 1995;41:558–591. [PMC free article] [PubMed] [Google Scholar] 3. Гат Г. О поточечной сходимости чезаро-средних функций двух переменных по неограниченным системам Виленкина. Дж. Прибл. Теория. 2004;128(1):69–99. doi: 10.1016/j.jat.2004.04.003. [CrossRef] [Google Scholar] 4. Гат Г. Сходимость почти всюду средних Фейера функций L1 на редко неограниченных группах Виленкина. Акта Математика. Грех. англ. сер. 2007;23(12):2269–2294. doi: 10.1007/s10114-007-0961-5. [Перекрестная ссылка] [Академия Google] 5. Гат Г. О сходимости почти всюду рядов Фурье на неограниченных группах Виленкина. 6. Гат Г. Некоторые результаты сходимости и расходимости в отношении суммирования рядов Фурье на одномерных и двумерных неограниченных группах Виленкина. Анна. ун-т науч. бп. Роландо Этвёш Nomin., Sect. вычисл. 2010; 33: 157–173. [Google Scholar] 7. Гат Г., Блахота И. Нормовая суммируемость логарифмических средних Нёрлунда на неограниченных группах Виленкина. Анальный. Теория прил. 2008;24(1):1–17. дои: 10.1007/s10496-008-0001-з. [CrossRef] [Google Scholar] 8. Гат Г., Гогинава Ю. Сходимость почти всюду (C,α)-средних квадратичных частичных сумм двойных рядов Виленкина–Фурье. Грузинская математика. Дж. 2006;13(3):447–462. [Google Scholar] 9. Гат Г., Гогинава Ю. Неравенство слабого типа для максимального оператора (C,α)-средних рядов Фурье по системе Уолша–Качмарца. Акта Математика. Висела. 2009; 125(1–2):65–83. doi: 10.1007/s10474-009-8217-8. [CrossRef] [Академия Google] 10. Гат Г., Гогинава Ю. 11. Гат Г., Гогинава Ю. Нормовая сходимость логарифмических средних на неограниченных группах Виленкина. Банах Дж. Матем. Анальный. 2018;12(2):422–438. doi: 10.1215/17358787-2017-0031. [CrossRef] [Google Scholar] 12. Глухов В.А. О суммировании кратных рядов Фурье по мультипликативным системам. Мат. Заметки. 1986;39:665–673. [Google Scholar] 13. Гогинава Ю. О равномерной сходимости рядов Уолша–Фурье. Акта Математика. Висела. 2001;93(1–2):59–70. doi: 10.1023/A:1013865315680. [CrossRef] [Google Scholar] 14. Гогинава Ю. Об аппроксимационных свойствах чезаро-средних отрицательного порядка рядов Уолша–Фурье. Дж. Прибл. Теория. 2002;115(1):9–20. doi: 10.1006/jath.2001.3632. [CrossRef] [Google Scholar] 15. Гогинава Ю. Равномерная сходимость чезаровских средних отрицательного порядка двойных рядов Уолша–Фурье. 16. Гогинава Ю. О средних Чезаро двойных тригонометрических рядов Фурье. Мат. Заметки. 2003;74(4):502–507. doi: 10.4213/mzm285. [CrossRef] [Google Scholar] 17. Гогинава У. Средние Чезаро двойных рядов Уолша–Фурье. Анальный. Мат. 2004;30(4):289–304. doi: 10.1007/s10476-005-0516-x. [CrossRef] [Google Scholar] 18. Гогинава Ю. Аппроксимационные свойства (C,α) средних двойных рядов Уолша–Фурье. Анальный. Теория прил. 2004; 20(1):77–9.8. doi: 10.1007/BF02835261. [CrossRef] [Google Scholar] 19. Гогинава Ю., Надь К. О максимальном операторе средних Уолша–Качмарца–Фейера. Чехослов. Мат. Дж. 2011;61(3):673–686. doi: 10.1007/s10587-011-0038-6. [CrossRef] [Google Scholar] 20. Голубов Б.И., Ефимов А.В., Скворцов В.А. Ряды Уолша и преобразования. Москва: Наука; 1987. [Google Scholar] 21. Надь К. Аппроксимация средними Чезаро отрицательного порядка рядов Уолша–Качмарца–Фурье. 22. Schipp F. Über gewisse Maximaloperatoren. Анна. ун-т науч. бп. Роландо Этвёш Nomin., Sect. Мат. 1975; 18: 189–195. [Google Scholar] 23. Шипп Ф., Уэйд В.Р., Саймон П. Уолш. Серия «Введение в диадический гармонический анализ». Бристоль: Хильгер; 1990. [Google Scholar] 24.
Шаварденидзе Г.: О сходимости чезаро-средних отрицательного порядка рядов Виленкина–Фурье. arXiv:1811.08367 25. Саймон П., Вайс Ф. Слабые неравенства для суммирования по Чезаро и Риссу рядов Уолша–Фурье. Дж. Прибл. Теория. 2008; 151(1):1–19. doi: 10.1016/j.jat.2007.05.004. [CrossRef] [Google Scholar] 26. Тевзадзе В.И. Равномерная (C,α)(−1≤α≤0) суммируемость рядов Фурье по системе Уолша–Пэли. Акта Математика. акад. Педагог. Нихази. 2006;22(1):41–61. [Google Scholar] 27. Жижиашвили Л.В. Тригонометрические ряды Фурье и их сопряженные. Дордрехт: Kluwer Academic; 1996. [Google Scholar] 28. Зигмунд А. Тригонометрические ряды. Сначала определим комплекснозначные функции rk(x):Gm→C, обобщенные функции Радемахера, следующим образом:
Сначала определим комплекснозначные функции rk(x):Gm→C, обобщенные функции Радемахера, следующим образом: Мы также предполагаем, что m=m˜ и Gm×Gm˜=Gm2.
Мы также предполагаем, что m=m˜ и Gm×Gm˜=Gm2.

Теорема А
Теорема B
 Нашими основными результатами являются следующие теоремы.
Нашими основными результатами являются следующие теоремы. Теорема 1
Теорема 2
 3.
3. Лемма 1
Лемма 2
Лемма 3
Лемма 4

Лемма 5
Лемма 6
Доказательство леммы 3


Доказательство леммы 4

Доказательство леммы 5



Доказательство теоремы 1

Доказательство теоремы 2
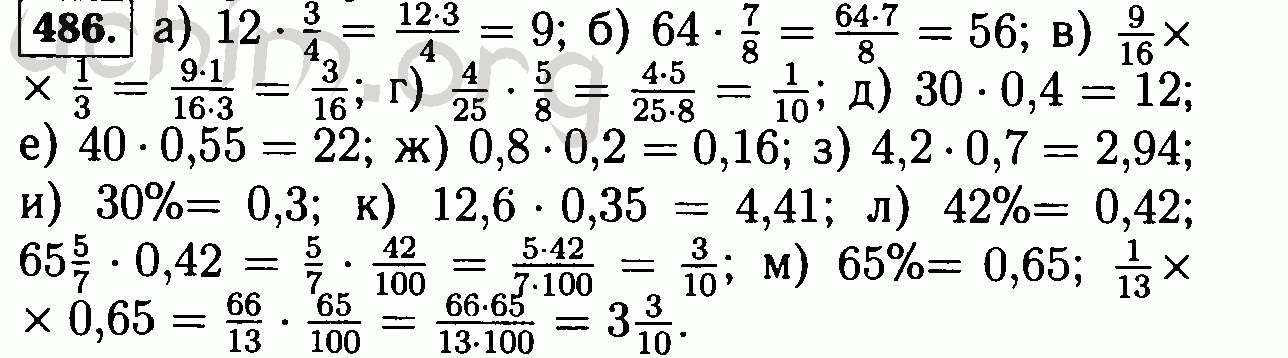
Конкурирующие интересы

 Опубл. Мат. (Дебр.) 2009;75(1–2):85–94. [Google Scholar]
Опубл. Мат. (Дебр.) 2009;75(1–2):85–94. [Google Scholar] Сходимость по норме двойных рядов Фурье на неограниченных группах Виленкина. Акта Математика. Висела. 2017;152(1):201–216. doi: 10.1007/s10474-017-0703-9. [CrossRef] [Google Scholar]
Сходимость по норме двойных рядов Фурье на неограниченных группах Виленкина. Акта Математика. Висела. 2017;152(1):201–216. doi: 10.1007/s10474-017-0703-9. [CrossRef] [Google Scholar] Дж. Прибл. Теория. 2003;124(1):96–108. doi: 10.1016/S0021-9045(03)00134-5. [CrossRef] [Google Scholar]
Дж. Прибл. Теория. 2003;124(1):96–108. doi: 10.1016/S0021-9045(03)00134-5. [CrossRef] [Google Scholar] Восток Дж. Прибл. 2010;16(3):297–311. [Google Scholar]
Восток Дж. Прибл. 2010;16(3):297–311. [Google Scholar]

 5 класс: поурочные планы по учебнику Н.Я.Виленкина и др. Первое полугодие. — / авт.-сост. З.С.Стромова, О.В.Пожарская.- Волгоград: учитель, 2008.
5 класс: поурочные планы по учебнику Н.Я.Виленкина и др. Первое полугодие. — / авт.-сост. З.С.Стромова, О.В.Пожарская.- Волгоград: учитель, 2008. Я. Виленкина и др. «математика. 5 класс» / М.А. Попов – м.: Издательство «Экзамен», 2005.
Я. Виленкина и др. «математика. 5 класс» / М.А. Попов – м.: Издательство «Экзамен», 2005.  – М.: Издательство «Первое сентября», 2000.
– М.: Издательство «Первое сентября», 2000. «Дрофа», 2007.
«Дрофа», 2007. 
 – М.: Просвещение, 1965.
– М.: Просвещение, 1965. Задачи городских туров олимпиады для школьников 8-11 классов начиная с 1999 года. Все задачи с подробными решениями и ответами. Новости олимпиады. Победители и призеры олимпиад. Статистика.
Задачи городских туров олимпиады для школьников 8-11 классов начиная с 1999 года. Все задачи с подробными решениями и ответами. Новости олимпиады. Победители и призеры олимпиад. Статистика.

 profile—edu.ru — Рекомендации и анализ результатов эксперимента по профильной школе. Разработки элективных курсов для профильной подготовки учащихся. Примеры учебно-методических комплектов для организации профильной подготовки учащихся в рамках вариативного компонента.
profile—edu.ru — Рекомендации и анализ результатов эксперимента по профильной школе. Разработки элективных курсов для профильной подготовки учащихся. Примеры учебно-методических комплектов для организации профильной подготовки учащихся в рамках вариативного компонента. ru — сайт Интернет – школы издательства Просвещение. Учебный план разработан на основе федерального базисного учебного плана для общеобразовательных учреждений РФ и представляет область знаний «Математика». На сайте представлены Интернет-уроки по алгебре и началам анализа и геометрии, с включают подготовку сдачи ЕГЭ.
ru — сайт Интернет – школы издательства Просвещение. Учебный план разработан на основе федерального базисного учебного плана для общеобразовательных учреждений РФ и представляет область знаний «Математика». На сайте представлены Интернет-уроки по алгебре и началам анализа и геометрии, с включают подготовку сдачи ЕГЭ.  Серия Математическая, 1947, Том 11, Выпуск 4, Страницы 363–400 (ми им3004)
Серия Математическая, 1947, Том 11, Выпуск 4, Страницы 363–400 (ми им3004) акад. АН СССР сер. Мат.
акад. АН СССР сер. Мат.  И. Рубинштейн, “О наилучшей сходимости”, Матем. Math., 192:2 (2001), 277–297
И. Рубинштейн, “О наилучшей сходимости”, Матем. Math., 192:2 (2001), 277–297  Notes, 81:2 (2007), 234–246
Notes, 81:2 (2007), 234–246  (Из. ВУЗ), 60:1 (2016), 42–59
(Из. ВУЗ), 60:1 (2016), 42–59  контемп. Мат. Анал.-Арм. акад., 53:6 (2018), 331–345
контемп. Мат. Анал.-Арм. акад., 53:6 (2018), 331–345  С. Целищев, “Неравенство Литтлвуда–Пэли–Рубио де Франсиа для ограниченных систем Виленкина”, Матем. Math., 212:10 (2021), 1491–1502
С. Целищев, “Неравенство Литтлвуда–Пэли–Рубио де Франсиа для ограниченных систем Виленкина”, Матем. Math., 212:10 (2021), 1491–1502