Задачи «на части» в 5-м классе, на ВПР и итоговых экзаменах
Если вы решили заниматься летом с ребёнком математикой, но с трудом вспоминаете школьную программу, наш блогер Александр Шевкин поможет вам всё наверстать. Сегодня он приводит примеры задач «на части» и объясняет, как их решать.
Рассылка «Мела»
Мы отправляем нашу интересную и очень полезную рассылку два раза в неделю: во вторник и пятницу
Задачи «на части» являются классическим типом задач, решаемых как арифметически, так и при помощи уравнения. Такие задачи встречаются в учебниках для пятого класса, в ВПР и на выпускном экзамене.
Для развития мышления и речи детей начинать лучше с арифметического способа решения. Рассмотрим решения двух задач из учебника «Математика, 5» (Просвещение, С. М. Никольский и др.) В первых задачах части упоминаются явно.
Задача 1. Для варенья из малины на 2 части ягод берут 3 части сахара. Сколько сахара следует взять на 6 кг ягод?
Решение: По условию задачи ягод 6 кг, и это количество составляет 2 части, поэтому на каждую часть приходится:
6: 2 = 3 кг.
Сахара надо взять 3 такие же части, то есть:
3 ∙ 3 = 9 кг.
Ответ: 9 кг.
В следующей задаче некоторую величину надо принять за одну или несколько равных частей. При решении таких задач полезно рисовать схематические рисунки, облегчающие решение.
Задача 2. На двух полках стоит 120 книг — на первой полке в 3 раза больше, чем на второй. Сколько книг стоит на каждой полке?
Решение: Если книги, стоящие на второй полке, составляют 1 часть, то на первой полке — 3 такие части. Выполним схематический рисунок.
1) Сколько частей составляют 120 книг?
1 + 3 = 4 (части).
2) Сколько книг приходится на 1 часть?
120: 4 = 30 (книг).
3) Сколько книг приходится на первую полку?
30 ∙ 3 = 90 (книг).
Ответ:
90 и 30 книг.Следующая задача была предложена на экзамене «Математическая грамотность» (Казахстан). Это аналог нашего ЕГЭ базового уровня для выпускников средней школы.
Задача 3. Когда отцу был 31 год, сыну было 8 лет. Сейчас отец в 2 раза старше сына. Сколько лет сыну сейчас?
Решение: Отец старше сына на 31 — 8 = 23 года. Пусть сейчас возраст сына составляет 1 часть, тогда возраст отца — 2 такие же части. Выполним схематический рисунок.
Замечание. Эту задачу преподаватель из ютьюба, обучавший выпускников казахстанских школ, решал при помощи уравнения, приняв за x число лет, прошедших между описанными в задаче событиями.
В заключение задача посложнее.
Задача 4. Для компота купили 1800 г сухофруктов. Яблоки составляют 4 части, груши 3 части, а сливы 2 части общего веса сухофруктов. Сейчас граммов яблок, груш и слив было в отдельности?
Решение:
1) 4 + 3 + 2 = 9 (частей) — приходится на 1800 г,
2) 1800: 9 = 200 (г) — приходится на 1 часть,
3) 200 ∙ 4 = 800 (г) — было яблок,
4) 200 ∙ 3 = 600 (г) — было груш,
5) 200 ∙ 2 = 400 (г) — было слив.
Ответ: 800, 600 и 400 г.
Отметим, что приём решения задач «на части» может использоваться при решении более сложных составных задач.
Задача 5. На двух полках стояли 36 книг. Когда с первой полки на вторую переставили 3 книги, то книг на второй полке стало в 2 раза больше, чем на первой. Сколько книг было на каждой полке первоначально?
Решение: Пусть количество книг на первой полке после перестановки трёх книг составляет 1 часть, тогда на второй полке — 2 части.
1) 1 + 2 = 3 (части) — приходится на 36 книг,
2) 36: 3 = 12 (книг) — приходится на 1 часть (стало на 1-й полке),
3) 36 — 12 = 24 (книг) — стало на 2-й полке.
Вернём три книги на первую полку.
4) 12 + 3 = 15 (книг) — было на первой полке первоначально,
5) 24 — 3 = 21 (книга) — была на второй полке первоначально.
Ответ: 15 и 21 книга.
Вы находитесь в разделе «Блоги». Мнение автора может не совпадать с позицией редакции.
Формулы для решения задач на дроби для 5 класса
В 5 классе на уроках математики ученики знакомятся с дробями и процентами. В 6 классе эта тема повторяется, но изучается более глубоко. А встречаться дроби и проценты продолжат вплоть до задач внешнего тестирования (ЗНО) для 11 класса.Обыкновенная дробь — это пара чисел, записанных через черту.
Число под чертой (знаменатель), показывает, на сколько частей разделили целое.
Число над чертой (числитель) показывает, сколько этих частей выбрано.
То есть дробь $\frac{3}{8}$ (три восьмых) означает, что целое было разделено на 8 частей, а взято из них три.
Существуют три класса задач на дроби: нахождение дроби от числа, нахождение числа по его дроби и выражение отношения чисел в виде дроби.
Как найти дробь от числа
В задачах на дробь от числа известно само число и дробь, которая от него взята. А найти требуется, какую величину составит эта дробь. Рассмотрим такую задачуПример 1.1.
В самолёте 120 пассажиров. $\frac{2}{5}$ (две пятых) из них летят в самолёте в первый раз. Сколько пассажиров летит в первый раз?
$\frac{2}{5}$ (две пятых) из них летят в самолёте в первый раз. Сколько пассажиров летит в первый раз?
Это задача на нахождение дроби от числа.
Есть число: 120.
Есть дробь: $\frac{2}{5}$
Нужно найти, чему равны две пятых от 120.
Решаются задачи на нахождение дроби от числа так.
Решение
Задаём себе два вопроса:
1. Чему равна $\frac{1}{5}$ (одна пятая) от 120?
2. Чему равны $\frac{2}{5}$ (две пятых) от 120?
Результат 24, корый мы получили, нужно умножить на 2.
Получаем 48.
Значит, $\frac{2}{5}$ от 120 составляет 48.
Ответ: 48 пассажиров летят впервые.
Попробуем решить ещё одну задачу на нахождение дроби от числа.
Пример 1.2.
В городе живут 1 500 000 человек. Из них $\frac{3}{25}$ — школьники. Сколько в городе школьников?
Решение
1. Чему равна $\frac{1}{25}$ от 1 500 000?
1 500 000:25 = 60 000
2. Чему равны $\frac{2}{25}$ от 1 500 000?
60 000*3 = 180 000
Ответ: 180 000 школьников.
Когда вы набрались опыта решать такие задачи по вопросам, эти два вопроса можно свести в одно действие и использовать правило:
Чтобы найти дробь от числа, нужно это число умножить на дробь
Или, что то же самое:
Пример 1.3.
В автосалон завезли 14 автомобилей. За месяц продали 2/7 этого количества. Сколько автомобилей продали?
Решение
Умножим 14 на $\frac{2}{7}$:
$14\cdot \frac{2}{7} = \frac{14\cdot 2}{7} = 2\cdot 2 = 4$
Ответ: 4 автомобиля.
Теперь рассмотрим задачи второго типа:
Как найти число по дроби
В задачах этого типа исходное число неизвестно. Зато известна величина некоторой части от этого числа и какую дробь составляет эта часть от исходного числа. Для удобства рассмотрим, как бы выглядели эти же три задачи, если бы в них требовалось найти число по дроби.Пример 2.1.
В самолёте сидят пассажиры (сколько их неизвестно!). Известно, что 48 пассажиров или $\frac{2}{5}$ (две пятых) от их количества летят впервые. Нужно найти: сколько всего пассажирова в самолёте?
Известно, что 48 пассажиров или $\frac{2}{5}$ (две пятых) от их количества летят впервые. Нужно найти: сколько всего пассажирова в самолёте?
Решение
Эти 48 пассажиров, которые летят впервые, составляют две пятых ($\frac{2}{5}$) от общего количества пассажиров в салоне. Мы можем найти одну пятую?
Да, нужно 48 разделить на 2.
48:2 = 24.
Мы узнали, что одна пятая часть от всех пассажиров — это 24 человека. Сколько всего пассажиров? В пять раз больше, то есть 24х5 = 120.
Ответ: 120 пассажиров всегов самолёте
Понятно? Давайте разберём ещё одну задачу.
Пример 2.2.
Три двадцать пятых ($\frac{3}{25}$) населения города составляют школьники. Школьников в городе 180 000. Каково общее население города?
Решение
Опять само число (то есть население города) на неизвестно, зато известно, чему равны $\frac{3}{25}$ от него.Значит, можно сначала найти, чему равна $\frac{1}{25}$ от населения города. Разделим 180 000 на 3:
180 000:3 = 60 000
Зная одну двадцать пятую, можно найти и целое, умножив 60 000 на 25.
60 000х25 = 1 500 000
Ответ: в городе 1 500 000 жителей
Когда будете уверенно решать задачи на нахождение числа по его дроби по вопросам, можно будет заменить эти вопросы одним действием и использовать правило:
Чтобы найти число по его дроби, известную величину нужно разделить на эту дробь
Или, что то же самое:
Чтобы найти число по его дроби, известную величину нужно разделить на числитель дроби и умножить на её знаменатель
Пример 2.3.
Из завезённых в автосалон автомобилей за месяц продали удалось продать всего 4, что составляет 2/7 всех автомобилей. Сколько автомобилей завезли в салон?
Решение
Разделим 4 на $\frac{2}{7}$:
$4: \frac{2}{7} = \frac{4\cdot 7}{2} = 2\cdot 7 = 14$
Ответ: 14 автомобилей завезли в салон.
И перейдём теперь к третьему типу задач на дроби, которые изучаются в математике 5 класса:
Как найти отношение двух чисел и выразить его в виде дроби
В задачах на нахождение отношения оба числа известны, а нужно найти, какую дробь второе число составляет от первого. Решаются они проще всего
Решаются они проще всегоПример 3.1.
В самолёте 120 пассажиров. Из них 48 человек летят в первый раз. Какая часть пассажиров летит в первый раз?
Решение
Чтобы найти, какую дробь 48 составляет от общего количества пассажиров (120), нужно 48 разлелить на 120 и затем скоратить, что возможно.
Доля летящих впервые пассажиров составляет $\frac{48}{120}$.
И числитель, и знаменатель делятся на 2, значит, можно сократить на 2.
$\frac{48}{120}=\frac{24}{60}$
Сократим ещё раз на 2:
$\frac{24}{60} = \frac{12}{30}$
И ещё раз:
$\frac{12}{30} = \frac{6}{15}$
Теперь можно сократить на 3:
$\frac{6}{15} = \frac{2}{5}$
Больше сокращать не на что — это и можно записать как окончательный ответ задачи.
Ответ: $\frac{2}{5}$ пассажиров летят впервые.
Так что правило для решения задач на нахождение отношения чисел самое простое:
Чтобы найти, в виде какой дроби выражается отноешние двух чисел, нужно сначала записать дробь, в которой числитель и знаменатель — эти числа, а затем сократить её.
Обратите внимание, что дробь $\frac{A}{B}$ обозначает, какую долю величина А составляет от величины В и правильно записывайте величины в числитель и знаменатель.
Разберём ещё два примера.
Пример 3.2.
В городе с населением 1 500 000 жителей живут 180 000 школьников. Какую часть населения города составляют школьники?
Решение
Нужно найти, какую часть 180 000 составляет от 1 500 000?
Записываем дробь и сокращаем:
$\frac{180000}{1500000}=\frac{18}{150}=\frac{9}{75}=\frac{3}{25}$
Ответ: школьники составляют $\frac{3}{25}$ от общего населения города
Пример 3.3.
Из завезённых в автосалон автомобилей за месяц продали удалось продать всего 4. Какую часть от всех автомобилей это составляет, если всегов автомалон завезли 14 машин?
Решение
Точно так же, берём дробь $\frac{4}{14}$ и сокращаем:
$\frac{4}{14}=\frac{2}{7}$
Ответ: продали $\frac{2}{7}$ от общего количества автомобилей.
Вот как решаются задачи на дроби. Вы найдёте справочники по формулам математики 5, 6 и других классов в разделе «Математика в школе».
Решения задач рубрики «Задача от мудрой совы» (5 класс, Мерзляк А.Г. и др.)
Решение задач рубрики «Задача от мудрой совы»
1 6. В квадрате (рис. 1) суммы чисел в каждом столбце, в каждой строке и диагоналях должны быть одинаковыми. Найдите число, которое должно быть записано вместо звёздочки.
Ответ: Сумма чисел первого столбца равна 33. Тогда в центральной клеточке квадрата должно стоять число 11, а в правом верхнем углу — 8. Следовательно, вместо знака * должно быть записано число 15.
43. В этом году день рождения отца был в воскресенье. В какой день недели праздновала свой день рождения мать, если она на 62 дня моложе отца?
Ответ: Поскольку мать младше отца, то 62 дня надо прибавить к дате дня рождения отца. Дни, номера которых делятся нацело на 7, будут приходиться на воскресенья. Поэтому шестьдесят третий день — это воскресенье. Следовательно, шестьдесят второй день — суббота.
Дни, номера которых делятся нацело на 7, будут приходиться на воскресенья. Поэтому шестьдесят третий день — это воскресенье. Следовательно, шестьдесят второй день — суббота.
8 4. Укажите наименьшее натуральное число, сумма цифр которого равна 101.
Ответ: Надо стремиться к тому, чтобы искомое число имело меньше разрядов. Поэтому основной «строительный материал» — это цифра 9. В то же время старший разряд должен содержать наименьшую из возможных цифр. Искомое число равно 299 999 999 999.
111. Как расставить 16 учеников в три ряда, чтобы в каждом ряду их было поровну?
Ответ: Один из способов расстановки показан на рисунке 25.
141. Вдоль забора растут восемь кустов малины. Количество ягод на соседних кустах отличается на одну. Может ли на всех кустах вместе расти 225 ягод?
Ответ: Общее количество ягод не может быть равным 225. Чётность количества ягод на первом, третьем, пятом и седьмом кустах одинакова. Тем же самым свойством обладают второй, четвёртый, шестой и восьмой кусты. Отсюда следует, что общее количество ягод — чётное число.
Тем же самым свойством обладают второй, четвёртый, шестой и восьмой кусты. Отсюда следует, что общее количество ягод — чётное число.
166. Семь гномов собрали вместе 28 грибов. Все они собрали разное количество грибов, и ни у кого не оказалось пустой корзинки. Сколько грибов собрал каждый гном?
Ответ: Количества грибов в корзинках гномов равны 1, 2, 3, 4, 5, 6, 7. Если предположить, что есть гном, в корзине которого 8 или более грибов, то общее количество собранных грибов было бы не менее чем 1 + 2 + 3 + 4 + 5 + 6 + 8 = 29, что противоречит условию.
196. Можно ли таблицу из пяти строк и шести столбцов заполнить натуральными числами так, чтобы сумма чисел каждой строки была равна 30, а сумма чисел каждого столбца – 20?
Ответ: Таким образом заполнить таблицу невозможно. В этой таблице сумма всех чисел, с одной стороны, была бы равной 5 ⋅ 30 = 150, а с другой — 6 ⋅ 20 = 120.
240. Во сколько раз путь по лестнице с первого этажа на десятый длиннее, чем путь с первого этажа на второй?
Во сколько раз путь по лестнице с первого этажа на десятый длиннее, чем путь с первого этажа на второй?
Ответ: Путь на десятый этаж в 9 раз длиннее, чем на второй. Действительно, обратим внимание на то, что ступеньки начинаются только с первого этажа. Поэтому если путь с первого этажа на второй равен x, то путь с первого на десятый равен 9x.
2 66. Кабинки развлекательного аттракциона «Колесо обозрения» последовательно пронумерованы числами 1, 2, 3 и т.д. Сколько всего кабинок, если известно, что когда кабинка с номеров 24 занимает самую высокую позицию, то кабинка с номером 10 – самую низкую?
Ответ: 28 кабинок. Если, например, нумерация производилась по часовой стрелке, то между кабинками с номерами 10 и 24 расположены ещё 13 кабинок с номерами 11, 12, … , 23. Столько же кабинок можно насчитать, если двигаться в противоположном направлении.
280. В трёх ящичках лежат шары: в первом ящичке – два белых, во втором – два чёрных, в третьем – белый и чёрный. На ящички наклеены этикетки ББ, ЧЧ и БЧ так, содержимое каждого из них не соответствует этикетке. Как, вынув один шар, узнать, что в каком ящичке лежит?
На ящички наклеены этикетки ББ, ЧЧ и БЧ так, содержимое каждого из них не соответствует этикетке. Как, вынув один шар, узнать, что в каком ящичке лежит?
Ответ: Достаточно взять шарик из ящичка БЧ. Понятно, что другой шарик в этом ящичке того же цвета, что и первый. Если, например, этот цвет белый, то в ящичках с надписями ББ и ЧЧ находятся два чёрных и белый с чёрным шарики соответственно.
295. На озере начали распускаться кувшинки. Каждый день количество кувшинок возрастало вдвое. На двадцатый день кувшинками заросла вся поверхность озера. На какой день половина озера была покрыта кувшинками?
Ответ: На девятнадцатый день. Поскольку на двадцатый день заросло всё озеро, то в предыдущий день кувшинками была покрыта половина озера.
320. Улитка за день поднимается вверх по столбу на 3 м, а за ночь съезжает по нему на 2 м вниз. На какой день она доберётся до вершины столба, высота которого равна 20 м?
Ответ: За 18 дней. В восемнадцатый день улитка начнёт подниматься с высоты 17 м и в конце дня достигнет вершины столба.
В восемнадцатый день улитка начнёт подниматься с высоты 17 м и в конце дня достигнет вершины столба.
337. Лимоны одинаковой массы продают поштучно. Масса каждого лимона составляет целое количество граммов. Купили больше двух, но меньше семи лимонов. Масса всей покупки составляет 850 г. Какова масса одного лимона?
Ответ: Масса одного лимона 170 г. Количество лимонов — делитель числа 850, а среди чисел, которые больше 2 и меньше 7, такое свойство имеет только число 5.
358. Каждый учащийся гимназии изучает по крайней мере один из двух иностранных языков. Английский язык изучают 328 учеников, французский язык – 246 учеников, а английский и французский одновременно – 109 учеников. Сколько всего учеников учится в гимназии?
Ответ: В гимназии 328 + 246 − 109 = 465 (учеников). Решая задачу, удобно воспользоваться рисунком 26.
383. Как с помощью пятилитрового бидона и трёхлитровой банки набрать на берегу реки 4 л воды?
О твет: Это можно сделать, например, по такому алгоритму: 1) наполнить 5-литровый бидон; 2) из бидона перелить 3 л воды в банку; 3) вылить воду из 3-литровой банки; 4) воду, оставшуюся в бидоне (2 л), перелить в банку; 5) снова наполнить бидон; 6) воду из бидона долить в банку. После этого в бидоне останется ровно 4 л воды.
После этого в бидоне останется ровно 4 л воды.
419. 1) Сложите из десяти спичек три квадрата.
2) Сложите из 19 спичек шесть квадратов.
3) Какие четыре спички надо убрать (см. рисунок), чтобы остались пять маленьких квадратов?
Ответ: Решение показано на рисунке 27.
446. В 5 классе учатся трое друзей: Миша, Дима и Саша. Один из них занимается футболом, второй – плаванием, а третий – боксом. У футболиста нет ни брата, ни сестры, он самый младший из друзей. Миша старше боксёра и дружит с сестрой Димы. Каким видом спорта занимается каждый из друзей?
Ответ: Миша занимается плаванием. Это следует из двух условий: 1) футболист — самый младший; 2) Миша старше боксёра. Миша дружит с сестрой Димы. Это означает, что Дима — боксёр. Действительно, ведь у футболиста сестры нет. Для Саши осталась единственная возможность — футбольная секция.
520. На столе расположено семь зубчатых колёс так, что первое сцеплено со вторым, второе – с третьим и т.д., а седьмое сцеплено с первым. Могут ли все колёса вращаться одновременно?
Ответ: Не могут. Два сцепленных зубчатых колеса всегда вращаются в противоположных направлениях (одно по часовой стрелке, а другое — против). Из этого следует, что все зубчатые колёса с нечётными номерами вращаются в одном направлении, а поэтому первое и седьмое колёса не могут быть сцепленными.
547. Известно, что верёвка сгорает за 4 мин и горит при этом неравномерно. Как с помощью: 1) одной верёвки отмерить 2 мин; 2) двух таких верёвок отмерить 3 мин?
Ответ: 1) Надо поджечь верёвку с обоих концов одновременно. 2) Сначала поджечь первую верёвку с одного конца, а вторую с обоих концов и, отмерив с помощью второй верёвки две минуты (см. пункт 1), поджечь второй конец первой верёвки.
563. В очереди за билетами в цирк стояли Миша, Наташа, Петя, Дима и Маша. Маша купила билет раньше, чем Миша, но позже, чем Наташа. Петя и Наташа не стояли рядом, а Дима не был рядом ни с Наташей, ни с Машей, ни с Петей. Кто за кем стоял в очереди?
В очереди за билетами в цирк стояли Миша, Наташа, Петя, Дима и Маша. Маша купила билет раньше, чем Миша, но позже, чем Наташа. Петя и Наташа не стояли рядом, а Дима не был рядом ни с Наташей, ни с Машей, ни с Петей. Кто за кем стоял в очереди?
Ответ: В очереди стояли друг за другом: Наташа, Маша, Петя, Миша, Дима.
597. Расстояние между городами А и В равно 30 км. Из города А в город В выехал велосипедист и двигался со скоростью 15 км/ч. Одновременно из города В в направлении города А вылетела птица со скоростью 30 км/ч. Встретившись с велосипедистом, птица развернулась и полетела назад. Прилетев в город В, она снова развернулась и полетела навстречу велосипедисту. Встретившись с ним, птица развернулась и полетела назад в город В и т.д. Сколько километров пролетела птица за то время, пока велосипедист ехал из города А в город В?
О твет: Птица пролетела 60 км. Велосипедист двигался 2 ч, столько же времени пребывала в полёте и птица.
Велосипедист двигался 2 ч, столько же времени пребывала в полёте и птица.
616. Как с помощью линейки измерить диагональ кирпича, имея ещё несколько таких кирпичей? (Диагональ параллелепипеда – это отрезок, соединяющий две его вершины, не принадлежащие одной грани.)
Ответ: Решение понятно из рисунка 28.
644. В записи первого трёхзначного числа используются только цифры 2 и 3, а в записи второго – только цифры 3 и 4 . Может ли произведение этих чисел записываться только цифрами 2 и 4?
Ответ: нет. Например, 233 . 344 = 80152.
673. В классе 30 учащихся. Они сидят по двое за 15 партами так, что половина всех девочек сидит с мальчиками. Можно ли учеников класса пересадить так, чтобы половина всех мальчиков сидела с девочками?
Ответ: Нет. Если половина всех девочек сидит с мальчиками, то вторая половина всех девочек сидит друг с другом. Следовательно, половина количества девочек — число чётное, а количество всех девочек делится нацело на 4. Аналогично: если таким же образом можно рассадить мальчиков, то их количество должно делиться нацело на 4. Тогда количество учащихся класса должно делиться на 4, что противоречит условию.
Следовательно, половина количества девочек — число чётное, а количество всех девочек делится нацело на 4. Аналогично: если таким же образом можно рассадить мальчиков, то их количество должно делиться нацело на 4. Тогда количество учащихся класса должно делиться на 4, что противоречит условию.
718. К пяти разным замкам есть пять ключей, причём неизвестно, какой ключ к какому замку подходит. Барон Мюнхгаузен утверждает, что можно не более чем за десять попыток подобрать ключ к каждому замку. Прав ли барон Мюнхгаузен?
Ответ: Барон прав. В наихудшем случае придётся сделать 10 попыток. Для того чтобы подобрать первый ключ, надо сделать не более 4 попыток. Действительно, если даже этот ключ не откроет первые четыре замка, то можно и без попытки быть уверенным, что к пятому замку он подойдёт. Рассуждая аналогично, второй ключ можно подобрать не более чем за 3 попытки, третий — за 2 попытки, четвёртый — за 1 попытку. После этого останется один замок и один ключ, который наверняка подойдёт к нему.
742. Мартышка, Удав, Слонёнок и Попугай съели вместе 70 бананов, причём каждый из них съел хотя бы один банан. Мартышка съела больше, чем кто-либо из них, Попугай и Слонёнок съели вместе 45 бананов. Сколько бананов съел Удав?
Ответ: Удав съел один банан. Поскольку Попугай и Слонёнок вместе съели 45 бананов, то кто-то из них съел не менее 23 бананов, а тогда Мартышка съела не менее 24 бананов. Из этого следует, что Мартышка, Попугай и Слонёнок вместе съели не менее 69 бананов.
757. В коробке лежат 4 белых, 5 чёрных и 6 красных шаров. Какое наименьшее количество шаров надо вынуть из коробки, чтобы среди них обязательно оказались: 1) 3 шара одного цвета; 2) шары всех трёх цветов?
Ответ: 1) Семь шариков. Шести шариков недостаточно. В этом случае может оказаться, что вынули по два шарика каждого из трёх цветов. 2) Двенадцать шариков. Если вынуть только 11 шариков, то возможен будет такой вариант: 5 чёрных и 6 красных.
768. В 5 классе учатся 35 учеников. Сможет ли каждый ученик этого класса обменяться открытками с пятью своими одноклассниками?
Ответ: Такое невозможно. Если это допустить, то количество всех совершённых обменов было бы равным , а это число дробное.
796. Ученики Фёдоров, Сидоров и Петров входили в сборную школы по шахматам. Имена этих учеников были Фёдор, Сидор и Пётр. Известно, что фамилия Фёдора не Петров, волосы у Сидора рыжего цвета и учится он в 6 классе; Петров учится в 7 классе, а волосы у Фёдорова чёрного цвета. Укажите фамилию и имя каждого мальчика.
Ответ: Фёдор Фёдоров, Сидор Сидоров и Пётр Петров. Сидор не может иметь фамилию Петров. Это следует из того, что Сидор — шестиклассник, а Петров — семиклассник. Если теперь учесть, что фамилия Фёдора так же не Петров, то остаётся рассмотреть две возможности:
1) Фёдор Сидоров, 2) Фёдор Фёдоров,
Сидор Фёдоров, Сидор Сидоров,
Пётр Петров; Пётр Петров.
Но первый случай невозможен, поскольку у Сидора и Фёдорова волосы разного цвета.
819. Как поделить поровну 7 яблок между 12 друзьями, если каждое яблоко можно разрезать не более чем на 4 части?
Ответ: Четыре из семи яблок надо разделить на 3 равные части каждое, а три оставшихся яблока — на 4 равные части каждое.
843. В пачке было 1000 конвертов. За какое наименьшее время почтальон сможет отложить 850 конвертов, если за 1 мин он отсчитывает 100 конвертов?
Ответ: Полторы минуты. Если отсчитать 150 конвертов, то в пачке останется как раз 850 конвертов.
862. Вася рассказал друзьям, что позавчера ему ещё было 10 лет, а в следующем году ему исполнится 13 лет. Как такое может быть?
Ответ: Это может быть только в случае, если день рождения Васи 31 декабря, а разговор с друзьями у него состоялся 1 января.
9 08. Чертёнок предложил Петру Скупердяйкину: «Каждый раз, когда ты перейдёшь мост, который я заколдую, твои деньги удвоятся. За это будешь мне каждый раз отдавать 24 монеты». Сделал Скупердяйкин так три раза и остался совсем без денег. Сколько денег было у Петра до встречи с чертёнком?
Чертёнок предложил Петру Скупердяйкину: «Каждый раз, когда ты перейдёшь мост, который я заколдую, твои деньги удвоятся. За это будешь мне каждый раз отдавать 24 монеты». Сделал Скупердяйкин так три раза и остался совсем без денег. Сколько денег было у Петра до встречи с чертёнком?
Ответ: 21 монета. Эту задачу целесообразнее решать «с конца». До того, как Скупердяйкин в третий раз перешёл мост, у него было 12 монет. Следовательно, после второго перехода (до того, как он отдал чертёнку 24 монеты) его капитал составлял 12 + 24 = 36 (монет). То есть до второго перехода у него было 36 : 2 = 18 (монет). Далее, рассуждая аналогично, приходим к выводу, что после первого перехода у него было 18 + 24 = 42 (монеты), а до встречи с чертёнком 42 : 2= 21 (монета).
962. В пятых классах учатся 100 учеников. Из них 75 учеников изучают немецкий язык, 85 учеников – французский, а 10 учеников не изучают ни один из этих языков. Сколько учеников изучают только французский язык, а сколько – только немецкий?
Ответ: Только французский язык изучают 15 учеников, а только немецкий — 5 учеников. Если обозначить количества учеников, изучающих только французский, только немецкий и оба этих языка, буквами a, b, c соответственно, то можем записать a + b + c = 90. Теперь, учитывая, что a + c = 85, а b + c = 75, получим ответ.
Если обозначить количества учеников, изучающих только французский, только немецкий и оба этих языка, буквами a, b, c соответственно, то можем записать a + b + c = 90. Теперь, учитывая, что a + c = 85, а b + c = 75, получим ответ.
1032. Семь карандашей стоят дороже восьми тетрадей. Что дороже: восемь карандашей или девять тетрадей?
Ответ: Из условия следует, что один карандаш стоит больше одной тетради. Тогда понятно, что 8 =7+1 карандашей дороже, чем 9 =8+1 тетрадей.
1055. Одновременно на сковороду можно положить два карася. Чтобы поджарить одного карася с одной стороны, нужна 1 мин. Можно ли за 3 мин поджарить с двух сторон трёх карасей?
Ответ: Поджарить трёх карасей за 3 мин можно, действуя таким образом:
1) положить на сковороду двух карасей;
2) через минуту одного из карасей перевернуть, а другого снять со сковороды, положив туда третьего карася. В конце второй минуты мы получим одного карася, поджаренного с обеих сторон, и двух карасей, поджаренных с одной стороны. Осталось за одну минуту поджарить этих двух карасей со второй стороны. А это можно сделать.
В конце второй минуты мы получим одного карася, поджаренного с обеих сторон, и двух карасей, поджаренных с одной стороны. Осталось за одну минуту поджарить этих двух карасей со второй стороны. А это можно сделать.
1091. В 5 классе диктант по русскому языку писали 30 учеников. Петя Ленивцев сделал больше всех ошибок – 14. Покажите, что по крайней мере три ученика сделали одинаковое количество ошибок (в этом классе могли быть ученики, которые не сделали ни одной ошибки).
Ответ: Из предположения, что не более двух учеников сделали 13 ошибок, не более двух — 12 ошибок и т. д. (до 0), следует, что в этом классе учится не более 2 ⋅ 14 + 1 = 29 (учеников), что противоречит условию.
1122. Для просмотра кинофильма в зрительном зале собрались ученики нескольких школ. Оказалось, что ученики одной из школ составляют 47 % количества зрителей. Сколько всего зрителей было в зале, если в нём 280 мест и более половины мест было занято?
Ответ: В зале было 200 зрителей. Если количество зрителей обозначить n, то число должно быть целым. Следовательно, n делится нацело на 100. А поскольку было занято более половины мест, то искомое число равно 200.
Если количество зрителей обозначить n, то число должно быть целым. Следовательно, n делится нацело на 100. А поскольку было занято более половины мест, то искомое число равно 200.
Урок математики 5 класс. Решение задач с мерами длины и массы.
5 класс урок 55 Решение задач с мерами длины и массы
задачи:
· образовательные: повторить известные единицы измерения длины; создать условия для закрепления наглядных представлений о них, знания отношений между ними;
· коррекционно-развивающая: способствовать развитию вычислительных навыков, мышления, речи, чертежных навыков, навыков самостоятельной работы, устного счета;
· воспитательная: содействовать воспитанию культуры письма.
Ожидаемые (планируемые) результаты:
Предметные: научатся использовать приобретенные математические знания для описания и объяснения окружающих предметов, процессов, явлений, а также для оценки их количественных и пространственных отношений.
Познавательные: получат возможность научиться осуществлять сравнение, сериацию и классификацию, самостоятельно выбирая основания и критерии для указанных логических операций.
Регулятивные: научатся различать способ и результат действия.
Коммуникативные: получат возможность с учетом целей коммуникации достаточно точно, последовательно и полно передавать партнеру необходимую информацию как ориентир для построения действия.
Личностные: получат возможность для формирования заинтересованности в приобретении и расширении знаний и способов действий.
Оборудование: наглядный материал для устного счета; опоры; шагомер; таблица соотношений мер длины.
Ход урока
I. Устный счет.
1. Математический диктант. – Запишите ответы в строчку в тетрадь.
1) 30 увеличить на 60. (90 – в.)2) 90 уменьшить на 20. (70 – е.)3) Найти сумму чисел 500 и 30. (530 – л.)
(90 – в.)2) 90 уменьшить на 20. (70 – е.)3) Найти сумму чисел 500 и 30. (530 – л.)
4) Уменьшаемое 700, вычитаемое 50. Найти разность. (650 – и.)5) Целое 60, часть 20. Найти другую часть. (40 – ч.)6) Большее число 800, разность 600. Найти меньшее число. (200 – и.)
7) Длина класса 900 см, ширина 400 см. На сколько длина больше ширины? (На 500 см – н.)8) Мама купила 300 г шоколадных конфет, а карамели 600 г. Сколько всего конфет купила мама? (900 г – а.)
Учащиеся выходят к доске и выкладывают буквы, которые соотносятся с числами, в том порядке, как зачитывались задания.
е | ч | а | в | л | и | н | и |
70 | 40 | 900 | 90 | 530 | 650 | 500 | 200 |
В итоге должно получиться слово «величина».
II. Актуализация опыта учащихся.
– С какими величинами мы знакомы? (Длина, масса, стоимость.)– Чем отличаются друг от друга длина и масса? (Длина обозначает расстояние, а масса – вес.)– Какие единицы измерения длины знаете? (Миллиметр, сантиметр, дециметр, метр.)– Длина – это величина. А миллиметр, сантиметр, дециметр, метр – это единицы измерения длины.
Величина | Единицы измерения |
Длина | Миллиметр – мм; сантиметр – см; дециметр – дм; метр – м |
– Назовите самую маленькую единицу измерения длины. (Миллиметр.)– Покажите ее на линейке. Запишите ее в тетрадь. (Записывают в тетрадях: 1 мм. )– Где встречаемся с данной единицей? (Высказывания учащихся.)– Найдите и запишите длину клеточки тетради. (Записывают в тетрадь: 5 мм.)– Какой мерой будем измерять мелкие предметы? (Миллиметрами.)– Какой мерой мы пользуемся чаще всего на уроках математики? (Высказывания учащихся.)– Покажите 1 см. Запишите в тетрадь. (Записывают в тетрадь: 1 см.)
)– Где встречаемся с данной единицей? (Высказывания учащихся.)– Найдите и запишите длину клеточки тетради. (Записывают в тетрадь: 5 мм.)– Какой мерой будем измерять мелкие предметы? (Миллиметрами.)– Какой мерой мы пользуемся чаще всего на уроках математики? (Высказывания учащихся.)– Покажите 1 см. Запишите в тетрадь. (Записывают в тетрадь: 1 см.)
– Постройте отрезок, равный 1 см.
– Найдите и запишите длину тетради. (Записывают в тетрадь: 20 см 5 мм.)– Какими мерами пользовались? (Сантиметрами и миллиметрами.)– Сравните, чем отличаются друг от друга две последние записи? (1 см выражен одной единицей измерения, а 20 см 5 мм – двумя.)– Какую единицу измерения длины будем использовать при измерении длины класса? Купленной материи на шторы? (Метры.)– Измерьте длину класса шагомером, запишите полученный результат.
III. Изучение нового материала.
– Сегодня закрепим знания о единицах измерения длины и их соотношениях, а также обобщим знания, полученные на предыдущем уроке. – Какими мерами пользуются для нахождения больших расстояний, например, расстояний между городами? (Высказывания учащихся.)– Какое расстояние мы прошли вчера? (Один километр.)– Чем измеряли данное расстояние? (Шагомером.)– Сколько метров в одном километре? (В одном километре одна тысяча метров.)– Километр – наибольшая единица измерения длины, ее составляют 1 000 метров. – Посмотрите, как записано слово «километр». Спишите данное слово, выделите орфограммы, поставьте ударение.– Произнесите его.– Слово «километр» записывают при числах: 1 км, то есть буквами «км» без точки. Например: 1 км, 8 км, 400 км.– Назовите здания, улицы, которые находятся от школы на расстоянии в 1 км. (Высказывания учащихся.)– Для определения расстояния между городами вдоль шоссе стоят столбы. Расстояние от одного столба до другого равняется 1 км.
– Какими мерами пользуются для нахождения больших расстояний, например, расстояний между городами? (Высказывания учащихся.)– Какое расстояние мы прошли вчера? (Один километр.)– Чем измеряли данное расстояние? (Шагомером.)– Сколько метров в одном километре? (В одном километре одна тысяча метров.)– Километр – наибольшая единица измерения длины, ее составляют 1 000 метров. – Посмотрите, как записано слово «километр». Спишите данное слово, выделите орфограммы, поставьте ударение.– Произнесите его.– Слово «километр» записывают при числах: 1 км, то есть буквами «км» без точки. Например: 1 км, 8 км, 400 км.– Назовите здания, улицы, которые находятся от школы на расстоянии в 1 км. (Высказывания учащихся.)– Для определения расстояния между городами вдоль шоссе стоят столбы. Расстояние от одного столба до другого равняется 1 км.
– За какое время мы прошли 1 км? (Ответ на данный вопрос соответственно занятому времени во время экскурсии.)– Ребята, человек может пройти 1 км примерно за 15–20 мин;
. физминутка
физминутка
IV. Коррекция и первичное закрепление знаний.
1. Работа по учебнику: выполнение заданий 81 и 82 на с. 47.– Начертите одну полоску длиной 12 см, а другую – на 4 см короче.– Что обозначает термин «короче»? (Меньше.)– Чему будет равна вторая полоска? (8 см.)– Как вычислили? (Так как вторая полоска короче, то надо от 12 см отнять 4 см.)– Начертите одну полоску длиной 75 мм, а другую – на 5 см короче.– В каких мерах выражены длины полосок? (Первая – в миллиметрах, вторая – в сантиметрах.)– Сможем ли сразу ответить на вопрос задачи? (Нет, потому что при выполнении арифметических действий над числами, полученными от измерения, их надо выразить одной мерой.)
– Первые единицы длины, как в России, так и в других странах, были связаны с размерами частей тела человека. Таковы сажень, локоть, пядь. В Англии и США до сих пор используется ступня – фут (31 см).
В Древней Руси в качестве единиц измерения длины применялись: косая сажень (248 см) – расстояние от пальцев левой ноги до конца пальцев поднятой правой руки; маховая сажень (176 см) – расстояние между кончиками пальцев, расставленных в стороны рук; локоть (45 см) – расстояние от концов пальцев до локтя согнутой руки. От восточных купцов пошла единица аршин (то же означает локоть) – существовали турецкий аршин, персидский аршин и др. Поэтому и возникла поговорка «Мерить на свой аршин».
От восточных купцов пошла единица аршин (то же означает локоть) – существовали турецкий аршин, персидский аршин и др. Поэтому и возникла поговорка «Мерить на свой аршин».
– Объясните смысл данной поговорки. (Высказывания учащихся.)
– Почему сегодня неудобны данные единицы для измерения? (Высказывания учащихся.)
V. Закрепление знаний.
1. Работа по учебнику: выполнение заданий 84 и 85 на с. 48.
– Прочитайте, спишите и запомните таблицу.Таблица мер длины
Работа по таблице мер длины (обратить внимание на сокращенную запись единиц измерения длины).
– Сравните, поставьте знаки «», «
1 км … 890 м 60 м … 370 м 530 см … 5 м
1 000 м … 1 км 2 км … 200 км 740 см … 7 м
Итоги урока
Оценки за урок
Дом задание
Страница 59 №216-219 ГДЗ к учебнику «Математика» 5 класс Дорофеев, Шарыгин, Суворова
Задача № 216. Автомобиль проехал расстояние между двумя городами со скоростью 80 км/ч за 3 ч. Сколько суток потребуется, чтобы пройти это расстояние пешком со скоростью 5 км/ч?
Автомобиль проехал расстояние между двумя городами со скоростью 80 км/ч за 3 ч. Сколько суток потребуется, чтобы пройти это расстояние пешком со скоростью 5 км/ч?
Решение задачи от 7 гуру
Чтобы найти расстояние умножим скорость на время:
1) 3 * 80 = 240 (км) − проехал автомобиль за 3 часа;
Чтобы найти время, которое потребуется чтобы пройти расстояние пешком, разделим расстояние на скорость ходьбы:
2) 240 : 5 = 48 ч = 2 суток потребуется, чтобы пройти это расстояние пешком со скоростью 5 км/ч.
Ответ: 2 суток.Запись задачи в тетради:
1) 3 * 80 = 240 (км) − проехал автомобиль за 3 часа;
2) 240 : 5 = 48 ч = 2 суток потребуется, чтобы пройти это расстояние пешком со скоростью 5 км/ч.
Ответ: 2 суток.
Задача № 217. Поезд проехал 80 км за 1 ч 20 мин. Сколько километров проедет поезд за 35 мин при той же скорости?
Решение задачи
1 ч 20 мин = 80 мин
1) 80 : 80 = 1 (км/мин) − скорость поезда.
2) 35 * 1 = 35 (км) − проедет поезд за 35 мин при той же скорости.
Ответ: 35 км.
Задание № 218. Прочитайте задачу и решите ее, используя предложенный план.
Велосипедист выехал с туристической базы на станцию, расстояние до которой 6 км. Какое расстояние останется ему проехать через 24 мин, если он будет ехать со скоростью 12 км/ч?
1) Рассмотрите рисунок 3. 3, на котором схематически изображено условие задачи.
Какой отрезок изображает все расстояние? расстояние, которое проехал велосипедист за 24 мин? расстояние, которое осталось проехать?
2) Узнайте, сколько метров проезжает турист за одну минуту.
3) Определите, сколько метров проехал велосипедист за 24 мин.
4) Определите расстояние (в метрах), которое ему осталось проехать, и выразите его в километрах и метрах.
Решение
1) AB = 6 км − все расстояние.
AC − расстояние, которое проехал велосипедист за 24 мин.
CB − расстояние, которое осталось проехать.
2) 12 км/ч = (12 * 1000) : 60 = 12000 : 60 = 200 м/мин, значит велосипедист проезжает 200 метров за 1 минуту;
3) 200 * 24 = 4800 (м) − проехал велосипедист за 24 мин;
4) 6 км = 6000 м;
6000 − 4800 = 1200 м = 1 км 200 м осталось проехать велосипедисту.
Ответ: 1 км 200 м.
Задание № 219. Изобразите схематически с помощью рисунка условие задачи, спланируйте ход решения и решите ее:
а) Петр идет от дома до станции метро, расстояние до которой равно 1 км 700 м. Через 16 мин после выхода ему остается пройти 340 м. Сколько минут занимает у Петра весь путь от дома до метро?
б) Андрей идет от дома до станции метро. Через 8 мин после выхода ему остается пройти 560 м, через 12 мин − 240 м. Сколько минут занимает у Андрея вся дорога и чему равно расстояние от дома до станции?
Решение
а)
1 км 700 м = 1700 м
1) 1700 − 340 = 1360 (м) − прошел Петр за 16 мин.
2) 1360 : 16 = 85 (м/мин) − скорость Петра.
3) 1700 : 85 = 20 (мин) − занимает у Петра весь путь от дома до метро.
Ответ: 20 минут.б)
1) 12 − 8 = 4 (мин).
1) 560 − 240 = 320 (м) − проходит Андрей за 4 минуты.
3) 320 : 4 = 80 (м/мин) − скорость Андрея.
4) 240 : 80 = 3 (мин) − будет идти Андрей 240 м.
5) 12 + 3 = 15 (мин) − занимает у Андрея вся дорога.
6) 15 * 80 = 1200 (м) = 1 км 200 м − расстояние от дома до станции.
Ответ: 15 мин; 1 км 200 м.
бесплатных заданий по математике для пятиклассников
Ученики пятого класса, возможно, уже запомнили факты умножения в более ранних классах, но к этому моменту они должны понимать, как интерпретировать и решать словесные задачи. Задачи со словами важны в математике, потому что они помогают учащимся развивать мышление в реальном мире, одновременно применять несколько математических концепций и мыслить творчески, отмечает ThinksterMath. Задачи со словами также помогают учителям оценить истинное понимание математики учащимися.
Задачи для пятого класса со словами включают умножение, деление, дроби, средние значения и множество других математических понятий. В разделах №№ 1 и 3 представлены бесплатные рабочие листы, которые студенты могут использовать, чтобы практиковаться и оттачивать свои навыки решения текстовых задач. В разделах № 2 и 4 приведены соответствующие ключи ответов к этим рабочим листам для упрощения выставления оценок.
Math Word Задачи Mix
Распечатать PDF-файл: Math Word Problems Mix
Этот рабочий лист представляет собой хорошее сочетание задач, включая вопросы, требующие от студентов демонстрации своих навыков умножения, деления, работы с долларовыми суммами, творческого мышления и нахождения среднего.Помогите своим пятиклассникам понять, что задачи со словами не должны быть пугающими, разрешив им хотя бы одну задачу.
Например, в задаче №1 спрашивается:
«Во время летних каникул ваш брат подрабатывает стрижкой газонов.Он косит шесть газонов в час, и ему нужно косить 21 газон. Сколько времени у него на это потребуется?»
Брат должен быть Суперменом, чтобы косить шесть газонов в час. Тем не менее, поскольку это именно то, что указывает проблема, объясните учащимся, что они должны сначала определить, что они знают и что они хотят определить:
- Твой брат может косить шесть газонов в час.
- Ему нужно покосить 21 газон.
Чтобы решить задачу, объясните учащимся, что они должны записать ее в виде двух дробей:
6 газонов / час = 21 газон / x час
Затем они должны умножиться. Для этого возьмите числитель первой дроби (верхнее число) и умножьте его на знаменатель второй дроби (нижнее число). Затем возьмите числитель второй дроби и умножьте его на знаменатель первой дроби следующим образом:
6x = 21 час
Затем разделите каждую сторону на 6 , чтобы решить для x:
6x / 6 = 21 час / 6
x = 3.5 часов
Итак, вашему трудолюбивому брату потребуется всего 3,5 часа, чтобы косить 21 газон. Он быстрый садовник.
Микс задач со словами по математике: решения
Распечатайте PDF: Смешивание задач по математическим словам: решения
В этом рабочем листе представлены решения задач, над которыми учащиеся работали, в печатной форме со слайда № 1. Если вы видите, что учащиеся испытывают трудности после сдачи своей работы, покажите им, как решить одну или две задачи.
Например, проблема No.6 на самом деле представляет собой простую задачу деления:
«Твоя мама купила тебе годичный плавательный пропуск за 390 долларов. Она делает 12 платежей, сколько денег нужно заплатить за пропуск?»
Объясните, что для решения этой проблемы вы просто разделите стоимость годового плавательного пропуска 390 долларов на количество выплат 12 следующим образом:
390 долл.США / 12 = 32,50 долл. США
Таким образом, стоимость каждого ежемесячного платежа вашей мамы составляет 32,50 доллара.Обязательно поблагодарите маму.
Еще задачи по математике
Распечатайте PDF-файл: другие задачи по математике
Этот рабочий лист содержит задачи, которые немного сложнее, чем те, что были в предыдущей печатной форме. Например, проблема №1 гласит:
«Четверо друзей едят личную пиццу. У Джейн осталось 3/4, у Джилл осталось 3/5, у Синди осталось 2/3, а у Джеффа осталось 2/5. У кого осталось больше всего пиццы?»
Объясните, что сначала вам нужно найти наименьший общий знаменатель (ЖКД), нижнее число в каждой дроби, чтобы решить эту проблему.Чтобы найти ЖК-дисплей, сначала умножьте разные знаменатели:
4 х 5 х 3 = 60
Затем умножьте числитель и знаменатель на число, необходимое для каждого, чтобы получить общий знаменатель. (Помните, что любое число, разделенное само по себе, равно единице.) Итак, у вас будет:
(Помните, что любое число, разделенное само по себе, равно единице.) Итак, у вас будет:
- Джейн: 3/4 x 15/15 = 45/60
- Джилл: 3/5 x 12/12 = 36/60
- Синди: 2/3 x 20/20 = 40/60
- Джефф: 2 / 5 х 12/12 = 24/60
У Джейн осталось больше всего пиццы: 45/60, или три четверти.У нее будет много еды сегодня вечером.
Дополнительные математические задачи со словами: решения
Распечатайте PDF-файл: Дополнительные задачи с математическими словами: решения
Если учащиеся все еще не могут найти правильные ответы, пора применить несколько разных стратегий. Вы можете просмотреть все задачи на доске и показать учащимся, как их решать. Или же разбейте студентов на группы — на три или шесть групп, в зависимости от того, сколько у вас студентов.Затем попросите каждую группу решить одну или две задачи, пока вы ходите по комнате, чтобы помочь. Совместная работа может помочь студентам мыслить творчески, когда они обдумывают одну или две проблемы; часто, как группа, они могут прийти к решению, даже если они изо всех сил пытались решить проблемы самостоятельно.
Задачи по математике для 5 класса с помощью Smartick
Задачи по математике со словами — действительно важная часть Smartick. В этой статье мы специально рассмотрим некоторые из задач для пятого класса, которые вы можете найти в Smartick.
Математические задачи со словами с одной операцией
Дополнение
Вчера многие из нас ходили завтракать в школьную столовую и выпили весь сок. Если бы они подавали на 470 литров меньше сока, они бы подавали то же количество литров, что и сегодня. Сегодня они подали 910 литров сока. Сколько литров сока подали вчера?
Вчера подали неизвестное количество литров. Если мы отнимем 470 литров от этого количества, мы получим количество литров, которое они обслужили сегодня.Чтобы вычислить, сколько литров они подали вчера, мы должны добавить:
910 + 470 = 1380
Вчера подали 1380 литров.
Вычитание
Чарли пригласил нас к себе домой попробовать клубнично-малиновый торт. Когда он начал делать это, он понял, что ему нужно на 400 больше клубники, чтобы получить столько же клубники, сколько 680 ягод малины, которые у него были. Посчитайте, сколько у него было клубники.
Когда он начал делать это, он понял, что ему нужно на 400 больше клубники, чтобы получить столько же клубники, сколько 680 ягод малины, которые у него были. Посчитайте, сколько у него было клубники.
У Чарли было на 400 ягод меньше клубники, чем малины.Так как малины у него было 680, нам нужно вычесть:
680–400 = 280
У Чарли было 280 ягод клубники.
Умножение
Сейчас сезон распродаж, и в магазине Сесилии 15 пакетов картофельных чипсов. Альфред сказал мне, что в магазине Сесилии в 5 раз меньше пакетов картофельных чипсов, чем в его. Посчитайте, сколько пакетов картофельных чипсов есть в магазине Альфреда.
В магазине Сесилии в 5 раз меньше пакетов картофельных чипсов, чем в магазине Альфреда.Это означает, что у Альфреда в 5 раз больше сумок, чем у Сесилии. Чтобы вычислить, сколько сумок в магазине Альфреда, нам нужно умножить:
15 х 5 = 75
В магазине Альфреда 75 пакетов картофельных чипсов.
Дивизион
Всего в понедельник в супермаркете было продано 1000 кг продуктов, включая овощи, фрукты, мясо, рыбу и хлеб. Во вторник они продали намного меньше, ровно в 5 раз меньше, чем продали в понедельник.Сколько килограммов еды они продали во вторник?
Они продали еды во вторник в 5 раз меньше, чем в понедельник. Поскольку мы знаем, что они продали 1000 килограммов в понедельник, нам нужно разделить, чтобы вычислить, сколько килограммов они продали во вторник:
1000 ÷ 5 = 200
Во вторник продали 200 кг еды.
Математические задачи с двумя операциями
Сложение и вычитание
Так как я люблю рыбу, я поставил в своей комнате аквариум, в котором есть 8 оранжевых и 5 зеленых рыбок.Я также добавил кое-что, чтобы украсить аквариум, например, песок, ракушки и улиток. Энтони тоже любит рыбу, но в аквариуме у него всего шесть штук. Сколько рыбы нужно было бы купить Энтони, чтобы у меня было столько же рыбы?
Прежде чем мы сможем вычесть рыбу, которая у меня есть, из рыбы Энтони, мы должны знать, сколько рыбы у меня есть. Для этого нам нужно добавить:
Для этого нам нужно добавить:
8 + 5 = 13
13 — количество рыб, которые у меня есть. Теперь нам нужно найти разницу между количеством рыб, которые у меня есть, и количеством рыбок, которые есть у Энтони.Для этого нам нужно вычесть.
13–6 = 7
Энтони пришлось бы купить 7 рыбок, чтобы у меня было столько же рыбок.
Фракции
Валентина — фотограф природы, и все фотографии в ее альбомах — это сельская местность и животные. 1/9 альбома, который она только что начала, состоит из фотографий сельской местности, а 1/6 — из фотографий животных. Какую часть альбома она заполнила?
Она заполнила одну часть альбома фотографиями сельской местности, а другую — фотографиями животных.Итак, чтобы вычислить общий объем альбома, который она заполнила, нам нужно добавить:
1/9 + 1/6 = 15/54
Она заполнила 15/54 альбома.
Таблицы
Завтра состоится премьера фильма «Алан против пришельцев», который будет показан на всех экранах Space Cinema. Осталось 14 билетов на 17:00. просмотр, что составляет половину количества билетов, оставшихся до 15:00. скрининг. Заполните таблицу имеющихся билетов.
Осталось 14 билетов на 17:00. просмотр, что составляет половину количества билетов, оставшихся до 15:00. скрининг. Заполните таблицу имеющихся билетов.
Мы должны посмотреть данные в таблице и заполнить пробелы.
Осталось 14 билетов на 17:00. скрининг. Если осталось 5 билетов для экрана 1 и 4 осталось для экрана 3, сколько осталось билетов для экрана 2?
14–5–4 = 5
Осталось 5 билетов на 17:00. отображение на Экране 2.
Осталось 28 билетов на 15:00. просмотр (удвоить количество билетов, оставшихся на просмотр в 17:00). Если осталось 11 билетов на Экран 2 и 4 осталось на Экран 3, сколько билетов осталось на Экран 1?
28–11–4 = 13
Осталось 13 билетов на 3 р.м. отображение на Экране 1.
Заполненная таблица будет выглядеть так:
Это несколько примеров математических задач со словами, которые вы можете найти в Smartick. Если вы хотите увидеть больше задач по математике, зарегистрируйтесь в Smartick и попробуйте бесплатно.
Подробнее:
Команда по созданию контента.
Многопрофильная и многонациональная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать максимально возможное математическое содержание.
Mathwire.com | Решение проблем: Gr. 5-8
Решение задач: 5–8 классы
Эти задачи предназначены для учащихся 5-8 классов:
- Лист записи «Тринадцать способов» был разработан для учащихся, чтобы записать тринадцать способов закрасить диаграмму, чтобы представить 1/2, как указано на веб-сайте PBS Cyberchase, указанном в листе для записи.
- Bulldog Travel Agency просит студентов оценить планы аренды автомобилей от трех разных компаний и порекомендовать лучший вариант, учитывая разные планы семейных путешествий.
- Jen and Berry’s Ice Creamery требует, чтобы студенты написали правило прибыли для магазина, а затем использовали это правило (функцию) для оценки прибыли с учетом количества покупателей каждый день.
- Миссия на миллион долларов просит студентов решить, какая зарплата будет лучшим предложением за один месяц работы: один миллион долларов или один цент в первый день, два цента во второй день, четыре цента в третий день и т. Д.
- TV Survey — это пример проблемы анализа данных с вопросами, разработанными для каждого уровня Таксономии Блума.
- Исследование игрушек с хлопьями имитирует получение учащимися одного из шести призов в коробке с хлопьями и просит учащихся оценить, сколько коробок с хлопьями им нужно будет купить, прежде чем они получат все 6 различных игрушек. Учащиеся делают прогноз, проводят моделирование, систематизируют данные и анализируют данные, чтобы написать письмо миссис Оутс с подробным описанием ожидаемых результатов этой рекламной акции. Инструкции и все раздаточные материалы включены для этого упражнения.
- Онлайн-симулятор исследования игрушек с хлопьями был разработан, чтобы учащиеся могли проводить множество виртуальных испытаний для сбора данных на более крупной выборке после проведения эксперимента с подбрасыванием кости.Обязательно прочтите инструкции перед загрузкой этого Java-апплета.
- Дополнительные игры и эксперименты см. В разделе Анализ данных: бросание двух игральных костей. Любая из этих игр становится упражнением по решению проблем, когда учащихся просят написать и отстоять выигрышную стратегию, которую они разработали после игры и анализа лежащей в основе вероятности.
- Сколько разных способов сделать слово СНЕГ? легко решается со ссылкой на Треугольник Паскаля, но затем попробуйте показать каждый из различных путей.Для этого нужен организованный подсчет. Используйте рабочий лист записи, чтобы оценить использование учащимися техник систематического счета, чтобы найти все способы и соотнести их с соответствующей строкой треугольника Паскаля.
- Winter Paths требует от учащихся использовать методы систематического подсчета, чтобы найти все пути, обозначающие WINTER, и соотнести решение с соответствующей строкой треугольника Паскаля.
% PDF-1.4 % 448 0 объект > эндобдж xref 448 82 0000000016 00000 н. 0000002775 00000 н. 0000002922 00000 н. 0000003419 00000 п. 0000003751 00000 п. 0000004062 00000 н. 0000004260 00000 н. 0000004374 00000 п. 0000004486 00000 н. 0000004599 00000 н. 0000004708 00000 н. 0000005172 00000 п. 0000005199 00000 п. 0000005635 00000 п. 0000005662 00000 н. 0000006228 00000 п. 0000006624 00000 н. 0000006651 00000 п. 0000006678 00000 н. 0000007142 00000 н. 0000007282 00000 н. 0000007415 00000 н. 0000007550 00000 н. 0000007687 00000 н. 0000008233 00000 н. 0000008771 00000 н. 0000009330 00000 н. 0000009891 00000 н. 0000010435 00000 п. 0000010462 00000 п. 0000010856 00000 п. 0000010994 00000 п. 0000011520 00000 п. 0000011783 00000 п. 0000012286 00000 п. 0000012575 00000 п. 0000012846 00000 п. 0000014112 00000 п. 0000025731 00000 п. 0000025844 00000 п. 0000027008 00000 н. 0000027316 00000 н. 0000027431 00000 н. 0000030282 00000 п. 0000030600 00000 п. 0000030719 00000 п. 0000031960 00000 п. 0000032273 00000 п. 0000032400 00000 п. 0000034380 00000 п. 0000034704 00000 п. 0000034774 00000 п. 0000034854 00000 п. 0000038726 00000 п. 0000039000 00000 н. 0000039288 00000 п. 0000039358 00000 п. 0000039438 00000 п. 0000044340 00000 п. 0000044609 00000 п. 0000044923 00000 п. 0000044993 00000 п. 0000045073 00000 п. 0000069237 00000 п. 0000069502 00000 п. 0000069902 00000 н. 0000069972 00000 н. 0000070052 00000 п. 00000
00000 п. 0000091070 00000 п. 0000091413 00000 п. 0000091483 00000 п. 0000091563 00000 п. 0000091772 00000 п. 0000091987 00000 п. 0000092208 00000 п. 0000092447 00000 п. 0000112047 00000 н. 0000153155 00000 н. 0000214671 00000 н. 0000002590 00000 н. 0000001936 00000 н. трейлер ] / Назад 1142289 / XRefStm 2590 >> startxref 0 %% EOF 529 0 объект > поток hb«b`TA , ` $ 009 | _9 GSXDqqE’KfZjM] Mg 斬` ᑮ M | JIS, * ygt2t, ptYoyD, & pIp8 ɯpDZ) DVmzFbSidv} | ¡v! -FgF6K9p13i5 ݘ b> Lsw϶D # W7 * N4 sirY9yEʨoH: 9mE / o _? @ 3NJЗадачи с денежным словом
Эти рабочие листы с задачами с денежным словом привлекают учащихся к реальным задачам и применению математических навыков.Задачи сгруппированы по сложению и вычитанию (подходит для учеников второго или третьего класса), или умножению и делению (подходит для учеников четвертого или пятого класса, которые освоили десятичное деление), или комбинации всех четырех операций. Нажмите одну из кнопок ниже, чтобы просмотреть отдельные рабочие листы в каждом наборе.
Умножение и деление
Проблемы с денежным словом смешанной операции
Сложение и вычитание с дополнительными фактами
Умножение и деление с дополнительными фактами
Смешанная операция Money Word Задачи с дополнительными фактами
Задачи Word для ознакомления с денежными навыками
Деньги — это мощное и знакомое приложение для выполнения основных математических операций, а рабочие листы задач с денежными историями на этой странице идеально подходят для детей младшего школьного возраста, чтобы они начали применять свои базовые арифметические навыки в работе.
Рабочие листы начинаются с наборов, которые содержат именно ту информацию, которая необходима для решения конкретных задач с денежным словом, но важным навыком является научиться определять лишние или неиспользуемые факты в описании проблемы. Поскольку денежные проблемы в реальном мире возникают в контексте большого количества информации, которая может не понадобиться для решения проблемы, понимание того, какая информация важна, часто является столь же важным навыком, как и способность выполнять базовые арифметические операции. Рабочие листы задач с денежным словом, отмеченные на этой странице как «лишние факты», подходят для учащихся 3–4 классов, которые могут уверенно решать другие задачи.
Проблемы со словами сгруппированы в наборы, посвященные сложению и вычитанию, или умножению и делению, или комбинации всех четырех операций. Если вы изучаете основные математические факты, рабочие листы, соответствующие операциям, над которыми вы работаете, могут помочь укрепить концепции и могут использоваться вместе с практикой математических фактов для дополнительной поддержки. Поскольку все это задачи с денежными историями, они обычно включают в себя и доллары, и центы, поэтому для их решения студентам потребуется некоторое знакомство с десятичной арифметикой.
Для наглядного ознакомления с деньгами посетите страницу «Денежные рабочие листы», которая включает в себя «Внесение сдачи» и действительно хороший набор печатных игровых денег, которые могут быть отличным помощником при решении задач с денежными словами и многого другого!
Математика / Решение задач в общем ядре
ОбзорИспользование моделей — важный шаг, помогающий учащимся перейти от конкретной манипулятивной работы со словесными задачами к абстрактному этапу создания уравнения для решения контекстных задач.Научившись использовать простые модели для представления ключевых математических соотношений в словесной задаче, учащиеся могут легче разбираться в словесных задачах, распознавать как числовые отношения в данной задаче, так и связи между типами задач, и успешно решать задачи с уверенностью в том, что их решения разумны.
Важность Почему моделирование текстовых задач важно?
У студентов часто возникают проблемы со словами.Многие студенты просто ищут какие-то числа и что-то с ними делают, надеясь, что они решат проблему.
Учащиеся должны выработать привычку сначала разбираться в проблеме. Диаграмма или модель часто фокусируются на понимании проблемы, а не просто на получении ответа. Затем модель можно использовать для создания продуманного уравнения. Модель и уравнение можно использовать в качестве проверки рассуждений после того, как учащийся получит решение.
Решение проблем не заканчивается на ответе.Процесс должен продолжаться после «получения ответа» на рассуждение о том, имеет ли ответ смысл.
Что такое моделирование текстовых задач?
Модели на любом уровне могут варьироваться от простых до сложных, от реалистичных до представительных. Молодые студенты часто решают начальные словесные задачи, разыгрывая их и моделируя их с реальными объектами проблемной ситуации, например плюшевых мишек или игрушечных машинок. Со временем они расширяются до использования репрезентативных рисунков, сначала рисуя картинки, которые реалистично изображают элементы проблемы, а затем переходят к многоцелевым представлениям, таким как круги или счетные метки.После множества конкретных опытов с реальными задачами со словами, включающими соединение и разделение или умножение и разделение объектов, учителя могут переводить учащихся на рисунки с перевернутой буквой V и штриховые модели, которые являются многоцелевыми графическими организаторами, привязанными к определенным типам задач со словами.
Моделирование базовых числовых соотношенийПростые диаграммы, иногда известные как числовые связи, треугольники фактов, ситуационные диаграммы или графические изображения, все чаще появляются в учебных материалах.Но способности учащихся решать проблемы и относительное мышление выиграют, если будут более рутинно использовать эти диаграммы и модели.
Маленькие дети могут начать видеть числовые отношения, существующие в семье фактов, благодаря использованию модели, из которой они выводят уравнения. Связь чисел и перевернутая буква V — это одна простая модель, которая помогает учащимся увидеть отношения сложения / вычитания в семействе фактов и может использоваться с задачами со словами, требующими простого соединения и разделения.Связь чисел, а затем модель перевернутой буквы V могут быть адаптированы для семейств фактов умножения и деления. Кроме того, учащиеся могут подумать о соотношениях между числами в перевернутой букве V в формальных терминах, , сложение, и , сумма , или, проще, , часть, , и , общая , как показано на схемах ниже.
Конкретный пример для данной суммы 10 будет следующим, в зависимости от того, какой элемент проблемы неизвестен.
6 + 4 =? 6+? = 10? + 4 = 1
4 + 6 =? 10-6 =? 10 — 4 =?
Несмотря на то, что они часто используются с семействами фактов и изучением основных фактов, диаграммы с числовыми связями и перевернутые буквы V также могут хорошо работать при решении текстовых задач. Студентам необходимо подумать о том, что они знают и чего не знают в задаче со словом — известны ли обе части или только одна из них? Правильно разместив известные величины на перевернутой V-диаграмме, учащиеся с большей вероятностью определят полезное уравнение для решения проблемы и увидят результат как разумный для ситуации.Например, рассмотрим следующую задачу:
У Захария было 10 вагонов. Захари подарил своему брату 3 вагона. Сколько вагонов сейчас у Закари?
Студенты должны определить, со сколькими суммами Захари начал (всего или всего ), и сколько он отдал ( часть от общего числа ). Итак, им нужно узнать, сколько осталось (другая часть из общего числа ). Следующая перевернутая V-диаграмма представляет отношения между номерами этой проблемы:
3 +? = 10 или 10 — 3 =?, Значит, у Закари осталось 7 вагонов.
По мере того, как учащиеся переходят к умножению и делению, модель перевернутой буквы V все еще может использоваться либо в режиме повторного сложения, либо в режиме умножения. Ситуации разделения не требуют новой модели; деление рассматривается как обратное умножению или ситуация, когда один из факторов неизвестен.
Опять же, перевернутая V-диаграмма может быть полезна при решении задач умножения и деления слов. Например, рассмотрим следующую задачу:
Фонг посадил 18 растений томатов в 3 ряда.Если в каждом ряду было одинаковое количество растений, сколько растений было в каждом ряду?
Студенты могут видеть, что они знают продукт и количество строк. Число В строке неизвестно. Любая из приведенных ниже диаграмм может помочь решить эту проблему, убедив учащихся, что шесть раз подряд — разумный ответ.
Хотя перевернутая V-диаграмма может быть расширена до многозначных чисел, она обычно используется с проблемами, связанными с базовыми семействами фактов. Расширение использования модельной диаграммы с перевернутой буквой V должно усилить взаимосвязь между числами в семействе фактов, что сделает его полезным и быстрым визуальным средством для решения простых задач со словами с дополнительным преимуществом использования и увеличения удержания основных фактов.
Модели и типы задач для вычисленийПо мере того, как дети переходят к работе с многозначными числами, учителя могут переводить учащихся на чертежи ленточных диаграмм / гистограмм, быстрые наброски, которые помогают учащимся увидеть взаимосвязь между важными числами в словесной задаче и определить, что известно и неизвестно в ситуации.
Знакомя учащихся с грифельными моделями, учитель получает важные наглядные пособия, помогающие учащимся думать о математических отношениях между числами в данной задаче со словом.
С ленточной диаграммой / гистограммой взаимосвязь между числами во всех этих типах задач становится более прозрачной и помогает студенту переходить от работы с манипуляторами и рисования изображений к символической стадии написания уравнения для ситуации. При рутинном использовании диаграмм и хорошо организованных обсуждениях учителями ученик начнет понимать части словесной задачи и то, как эти части соотносятся друг с другом.
Проблемы частично-частично-целиком.Задачи Part-Part-Whole полезны со словесными задачами, которые относятся к совокупности вещей, например коллекции. Обычно это более статичные ситуации, включающие два или более подмножества целого набора. Рассмотрим проблему,
Коул имеет 11 красных блоков и 16 синих блоков. Сколько всего блоков у Коула?
Учащиеся могут построить простой прямоугольник из двух частей, чтобы обозначить два известных набора блоков (части / дополнения). Неважно, чтобы части прямоугольника были точно пропорциональны числам в задаче, но некоторое внимание к их относительному размеру может помочь в решении проблемы.Неизвестным в этой задаче является то, сколько их всего (всего / всего / суммы), что обозначено скобкой (или перевернутой буквой V) над полосой, обозначающей общее количество двух наборов блоков. Первая барная модель ниже отражает информацию в задаче о блоках Коула.
11 + 16 =? Таким образом, у Коула всего 27 блоков.
Аналогичная модель будет работать для проблемы, когда известна вся сумма, но одна из частей (недостающее слагаемое) неизвестна. Например:
У Коула было 238 блоков.100 из них были желтыми. Если все блоки Коула синие или желтые, сколько их было синими?
Следующая модель стержня может быть полезна в решении этой проблемы.
100 +? = 238 или 238 — 100 =? Итак, у Коула 138 синих блоков.
Ответ должен быть немного больше 100, потому что 100 + 100 равно 200, но здесь всего 238, поэтому синих блоков должно быть чуть больше 100.
Модель стержня «часть-часть-весь» легко расширяется до больших чисел и других числовых типов, таких как дроби и десятичные дроби.Рассмотрим задачу:
Летисия прочитала 7 ½ книг для читателей. Всего она хочет прочитать 12 книг. Сколько еще книг ей нужно прочитать?
Первая диаграмма ниже отражает эту проблему. Любая проблема со словом, которую можно рассматривать как части и целое, реагирует на диаграммы моделирования стержней. Если у задачи есть несколько слагаемых, учащиеся просто рисуют на полосе достаточно частей, чтобы отразить количество слагаемых или частей, и указывают, является ли одна из частей или целое / сумма неизвестными, как показано на втором рисунке ниже.
12 — 7 ½ =? или 7 ½ +? = 12, поэтому Летиции нужно прочитать еще 4 ½ книг.
Задачи соединения (сложения) и разделения (вычитания).
Студенты, которые не могут решить, нужно ли им прибавлять или вычитать, а затем умножать или делить, находят организационный потенциал гистограммы невероятно полезным.
У Марии было 20 долларов. Она получила еще 11 долларов за присмотр за детьми. Сколько у нее сейчас денег? Рассмотрим эту задачу объединения:
Учащиеся могут определить, что начальная сумма в 20 долларов является одной из частей, 11 долларов — другой частью (добавочная сумма), а неизвестным является сумма / вся сумма или сколько денег она есть сейчас.Первая диаграмма ниже помогает представить эту проблему.
Рассмотрим соответствующую ситуацию с вычитанием:
У Марии был 31 доллар. Часть денег она потратила на новый компакт-диск. У Марии осталось 16 долларов.
Вторая диаграмма выше представляет эту ситуацию. Студенты могут использовать модель, чтобы помочь им определить, что общая сумма сейчас составляет 31 доллар, одна из частей (вычитающее изменение) неизвестна, поэтому другая часть — это те 16 долларов, которые у нее остались.
Проблемы сравнения. Проблемы со сравнением обычно считались трудными для детей. Частично это может быть связано с акцентом на вычитание, который используется в задачах со словами, которые включают ситуации «убрать», а не нахождение «разницы» между двумя числами. Интересно, что исследования, проведенные в странах, которые часто используют гистограммы, показали, что учащиеся не находят задачи сравнения намного более сложными, чем задачи «часть-часть-целое» (Yeap, 2010, стр. 88-89).
Модель с двойным стержнем может помочь сделать задачи сравнения менее загадочными.В основном, задачи сравнения включают две величины (либо одна величина больше другой, либо они равны) и разницу между величинами. Можно нарисовать две полосы, по одной представляющей каждое количество, с разницей, представленной пунктирной областью, добавленной к меньшему количеству. Например, с учетом задачи:
Тамека участвовал в 26 окружных ярмарочных аттракционах. Ее друг, Джексон, проехал 19 поездок. На сколько аттракционов ездил Тамека больше, чем Джексон?
Учащиеся могут создать гистограмму сравнения, показанную ниже, где большее количество, 26, является более длинным столбцом.Пунктирная часть показывает разницу между количеством поездок Джексона и Тамеки, или насколько больше у Тамека, чем у Джексона, или на сколько дополнительных поездок Джексон должен был бы проехать, чтобы иметь такое же количество поездок, как Тамека.
26-19 =? или 19+? = 26; разница в 7, так что Тамека проехал еще 7 аттракционов.
Задачи сравнения выражают несколько различных формулировок отношений. Если Тамека ездил на 7 аттракционов больше, чем Джексон, то Джексон проехал на 7 аттракционов меньше, чем Тамека.Варианты схемы модели с двойной полосой могут сделать для учащихся более наглядными отношения, сформулированные по-разному. Студентам часто бывает полезно осознать, что в какой-то момент обе величины имеют одинаковое количество, как показано на модели ниже пунктирной линией, проведенной от конца прямоугольника, представляющего меньшее количество. Но у одной из величин больше, на что указывает область справа от пунктирной линии на более длинной полосе. Разницу между количествами можно определить путем вычитания 19 из 26 или сложения от 19 до 26 и получения 7, что означает, что 26 на 7 больше, чем 19, или 19 означает, что на 7 меньше 26.
Проблемы со словами сравнения особенно проблематичны для изучающих английский язык, поскольку вопрос можно задать несколькими способами. Изменение полос сравнения может сделать вопросы более прозрачными. Вот несколько вариантов вопросов о двух количествах поездок, на которых проехали Тамека и Джексон:
- На сколько аттракционов проехал Тамека больше, чем Джексон?
- На сколько поездок Джексон совершил меньше поездок, чем Тамека?
- Сколько еще поездок пришлось бы проехать Джексону, чтобы проехать столько же поездок, что и Тамека?
- На сколько меньше поездок пришлось бы проехать Тамеке, чтобы проехать столько же поездок, что и Джексон?
Сравнения также могут быть мультипликативными.Рассмотрим проблему:
В коллекции Хуана 36 компакт-дисков. Это в 3 раза больше дисков, чем у его брата Маркоса. Сколько компакт-дисков у Маркоса?
В этой ситуации учащиеся должны построить модель стержня, показанную ниже слева, из 3 частей. Студенты могут разделить 36 на 3 равные группы, чтобы показать количество, которое нужно взять 3 раза, чтобы создать в 3 раза больше компакт-дисков для Хуана.
36 ¸ 3 =? или 3 раза? = 36 12 + 12 + 12 =? (или 3 x 12 =?)
, так что у Маркоса 12 компакт-дисков.Итак, у Хуана 36 компакт-дисков.
Аналогичную модель можно использовать, если большее количество неизвестно, но меньшее количество и мультипликативное отношение известны. Если проблема была:
У Хуана есть компакт-диски. У него в 3 раза больше компакт-дисков, чем у Маркоса, у которого 12 компакт-дисков. Сколько компакт-дисков у Хуана?
Как видно на диаграмме вверху справа, студенты могут положить 12 в коробку, чтобы показать количество компакт-дисков, которые есть у Маркоса; затем продублируйте это 3 раза, чтобы увидеть, что у Хуана в 3 раза больше компакт-дисков.Тогда общее количество, которое есть у Хуана, будет суммой этих трех частей.
Задачи умножения и деления. Та же модель, что и для мультипликативных сравнений, также будет работать для основных задач умножения слов, начиная с однозначных множителей. Рассмотрим проблему:
У Аланы было 6 пакетов жевательной резинки. В каждой упаковке 12 штук жевательной резинки. Сколько всего жевательных резинок у Аланы?
В следующей линейчатой модели для визуализации проблемы используется повторное сложение умножения.
12 + 12 + 12 + 12 + 12 + 12 = 72 (или 6 x 12 = 72)
, так что у Аланы 72 куска жевательной резинки.
По мере того, как учащиеся переходят к многозначным множителям, они могут использовать модель с многоточием, чтобы упростить гистограмму. Например:
Сэм пробегает 32 км в день в течение апреля, чтобы подготовиться к гонке. Если Сэм бегает каждый день месяца, сколько всего километров он пробежал в апреле?
30 x 32 км = 30 x 30 км + 30 x 2 км = 960 км
Сэм пробежал 960 км за 30 дней апреля.
Поскольку деление — это обратное умножение, в задачах деления слов будет использоваться модель мультипликативного столбца, в которой произведение (делимое) известно, но один из факторов (делитель или частное) неизвестен.
Задачи, связанные со ставками, дробями, процентами и несколькими шагами. По мере того, как учащиеся переходят в старшие классы, они могут применять новые концепции и многоступенчатые задачи со словами к чертежам моделей стержней. Скемп (1993) определил, что реляционное мышление имеет решающее значение для развития математики.Учащийся должен уметь расширять свое мышление на основе моделей, которые они использовали ранее, связывая и адаптируя то, что он знает, к новым ситуациям.
Рассмотрим задачу о скорости и расстоянии:
Фонг проехала 261 милю, чтобы увидеться с бабушкой. В среднем она разгонялась до 58 миль в час. Сколько времени ей понадобилось, чтобы добраться до дома бабушки?
Следующая модель основана на модели «часть-часть-целое» с использованием формата повторяющегося сложения для умножения и деления. Предполагается, что учащиеся имеют опыт использования модели для задач деления, частные которых являются не просто целыми числами.По мере того, как они наращивают (или делят) 261 милю, они вычисляют, что пять 58 будут представлять 5 часов путешествия, а оставшиеся 29 миль будут представлены половинным квадратом, поэтому решение состоит в том, что Фонг займет 5½ часов. времени в пути, чтобы добраться до дома бабушки.
Даже более сложную проблему скорости можно решить с помощью комбинации подобных моделей. Рассмотрим эту задачу:
Сью и ее подруга Энн вместе отправились в путешествие. Сью проехала первые 2/5 поездки, а Энн проехала 210 миль за последние 3/5 поездки.Средняя скорость Сью составляла 60 миль в час, а Энн — 70 миль в час. Как долго у них была поездка?
Есть несколько способов, которыми учащиеся могут комбинировать или изменять базовую модель стержня. Одно из решений может заключаться в следующем, где первое неизвестное — сколько миль проехала Сью. Полоса, разделенная на пятые, показывает, как рассчитать мили, которые проехала Сью. Поскольку мы знаем, что 210 миль, которые проехала Энн, составляют 3/5 всего пути, каждая из ящиков Анны, каждая из которых представляет 1/5 пути, составляет 70 миль. Таким образом, Сью проехала две части по 70 миль, или 140 миль, что составляет 2/5 от общей поездки.
Теперь диаграмму необходимо расширить, чтобы показать, как рассчитать количество часов. Участок 210 миль Анны, разделенный на ее скорость 70 миль в час, займет 3 часа, как указано в следующем расширении диаграммы. Расстояние Сью в 140 миль теперь необходимо разделить на сегменты со скоростью 60 миль в час, чтобы определить время ее вождения, равное 2 1/3 часа. Таким образом, общая поездка в 350 миль займет 5 1/3 часа времени вождения, учитывая две нормы вождения.
Рассмотрим более простую многоступенчатую задачу:
Роберто купил 5 спортивных напитков по 1 доллару.25 каждый. Роберто дал кассиру 20 долларов. Сколько сдачи он получил обратно?
Опять же, у учащихся могут быть вариации, когда они начнут расширять использование диаграмм в многоэтапных или более сложных задачах. Некоторые ученики могут использовать сразу две диаграммы, как показано ниже слева. Другие могут указывать вычисления на одной диаграмме, как показано на диаграмме справа.
Имея рутинный опыт моделирования стержней, учащиеся могут расширить использование моделей для решения задач, связанных с отношениями, которые могут быть выражены с помощью переменных.Рассмотрим эту простую задачу, которую можно представить алгебраически:
Каллан и Авриэль собрали в общей сложности 190 ошибок для научного проекта. Каллан собрал на 10 ошибок больше, чем Авриель. Сколько жуков собрал Каллан?
Пусть n равно количеству ошибок, собранных Авриель, а n + 10 равно количеству ошибок, собранных Калланом. Студенты могут создать следующую модель:
Поскольку n + n = 180 (или 2 n = 180), n = 90.Таким образом, Каллан собрал 90 + 10 или 100 ошибок, а Авриэль собрала 90 ошибок, всего 190 ошибок, собранных вместе.
При использовании модельного метода учащиеся должны переводить информацию и отношения в словах в визуальные представления, которые являются моделями. Они также должны манипулировать и преобразовывать визуальные представления, чтобы генерировать информацию, полезную при решении заданных проблем.
Понимание структуры словесной задачи включает в себя знание того, как связана математическая информация в данной текстовой задаче и как выделить компоненты, необходимые для решения проблемы.Чертежи ленточной диаграммы / гистограммы могут помочь учащимся лучше определять переменные, участвующие в проблеме, а также отношения между ними. Эта способность сосредотачиваться на отношениях между числами в данной задаче и распознавать математическую структуру как особый тип проблемы является частью реляционного мышления — критически важным навыком для успеха в алгебре. Использование перевернутой буквы V и гистограммы в предалгебраическую работу в классах K-7 может сделать учащихся более подготовленными к формальному изучению алгебры.
Это отличный сайт для практики решения проблем — моделирования задач с помощью ленточной диаграммы / гистограммы
Пять математических стратегий для учащихся, испытывающих трудности
Поскольку я никогда не был изучающим математику с трудностями, сначала мне было трудно понять почему студенты так боролись. На моем пути в качестве репетитора по математике, преподавателя математики с пятого класса до колледжа и специалиста по математике, специализирующегося на средних классах школы, мне пришлось научиться общаться с моими отстающими учениками.Когда эта связь устанавливается, они открываются для меня и могут принять помощь, используя стратегии, основанные на исследованиях, которые, как я знаю, работают.
Недавно я действительно познакомился с одним из моих бедных студентов. Я назову его Джоуи, хотя это не настоящее его имя.
Джои сменил школу в середине седьмого класса. Сначала он показался несоответствующим и исключен из класса. Наша оценка его математических навыков показала, что он учился на математическом уровне в третьем классе.Джои явно не хватало навыков расчетов и основных фактов.
Хотя я хочу подчеркнуть, что математические стратегии для учащихся с трудностями, представленные ниже (и в загружаемом файле), были эффективными в решении проблем этого ученика с математикой, именно мое знакомство с ним и его историей открыло ему путь к риску в процессе обучения. класс.
Студенты, которые переезжают в середине года, часто имеют проблемы с адаптацией, и, конечно же, Джои. Но более глубокая история с ним — это , почему он переехал .В предыдущих школах над ним издевались в течение нескольких лет, и он не участвовал в учебе. Услышав его историю, я смягчил мое сердце по поводу его ситуации.
Как команда учителей, мы смогли убедить Джоуи в том, что это безопасная школа, и ему не нужно возводить защитные стены. Я считаю, что именно это сообщение открыло его нам, чтобы мы могли использовать приведенные ниже стратегии для развития его концептуального понимания, математических навыков и способностей к решению проблем.
Перед внедрением математических стратегий для учащихся с трудностямиПознакомьтесь со своими учащимися, испытывающими трудности, и расскажите им их истории. Как они попали туда, где находятся? Как они относятся к отставанию в математике? Знают ли они, насколько они отстают? Готовы ли они снова пойти на риск, учитывая, что принятие риска могло не сработать для них в прошлом? В случае с Джои решение основных проблем, безусловно, помогло ему пойти на этот риск.
Итак, что мы на самом деле можем сделать, чтобы помочь студентам вроде Джоуи, которые готовы снова участвовать в учебе после многих лет неудач? В исследовательской литературе предлагается несколько математических стратегий для учащихся, испытывающих трудности, которые согласуются с моим опытом в отношении того, что последовательно работает для моих учащихся, испытывающих трудности.
5 стратегий, которые помогут вашим изучающим математику с трудностями СТРАТЕГИЯ 1: ПРЕДОСТАВЛЯЙТЕ ЯВНЫЕ ИНСТРУКЦИИ БОРЬБАМ УЧАЩИХСЯ
Я большой сторонник основанного на открытиях обучения математике.Я хочу, чтобы ученики могли исследовать богатые контекстом ситуации в классе математики, и я считаю, что каждый ученик должен быть знаком с такого рода классом. Если этот тип инструкций не работает для учащихся, страдающих хронической болезнью, им потребуется подробное указание, как решать целевые задачи шаг за шагом. Я считаю, что учащиеся, испытывающие трудности, должны быть подвергнуты экспериментальному обучению, но они могут заблудиться без последующего наблюдения.
Явное обучение может быть предоставлено на занятиях по вмешательству или с использованием различных стратегий дифференциации в основном классе.(Об этом будет рассказано в следующей публикации, так что следите за обновлениями!)
СТРАТЕГИЯ 2: ПРЕДОСТАВЛЯЙТЕ БОЛЬШИЕ КОНТЕКСТЫ В МАТЕМАТИЧЕСКОЙ КЛАССЕ
Только что отстаивая необходимость подробного обучения, которое должно следовать за исследовательской или исследовательской деятельностью в математическом классе, теперь я хочу подчеркнуть важность контекстно-зависимой деятельности.
Учащиеся, испытывающие трудности, должны участвовать в подобных мероприятиях, чтобы они могли видеть и слышать умелые математические рассуждения своих сверстников.Опыт богатого математического контекста вместе со своими более опытными сверстниками знакомит учащихся с трудностями с умелыми стратегиями решения проблем их одноклассниками и вербализацией умелых мыслительных процессов сверстников.
Наблюдая за тем, как их более опытные коллеги используют предварительные знания для решения текущих задач и настойчивость в решении проблем поможет бороться студентов улучшить свой подход к привлечению с богатыми контекстных проблем.
СТРАТЕГИЯ 3: ИСПОЛЬЗУЙТЕ ПРЕДСТАВЛЕНИЯ МОДЕЛИРОВАНИЯ ПОЛОСЫ ДЛЯ РАСШИФРОВКИ ПРОБЛЕМ СО СЛОВАМИ
Нередко учащиеся-математики, испытывающие трудности, также становятся плохо читающими.Эти студенты обычно нуждаются в подробных инструкциях по чтению словесных задач, пониманию их основной структуры, выбору операций для решения проблемы и стратегиям для представления словесной проблемы.
Моя стратегия представления арифметических задач со словами — это моделирование столбиком, которое используется в сингапурской математике. Я считаю, что когда студенты понимают эту стратегию моделирования, это помогает им интерпретировать текстовые задачи и выбирать операцию. Когда учащиеся переходят от задачи со словами к модели столбцов, а затем выбирают операцию для написания выражения или уравнения, они оттачивают свои навыки чтения.Использование моделей для задач сложения и вычитания по сравнению с. Задачи умножения и деления могут помочь им осмыслить проблему.
СТРАТЕГИЯ 4: ОСНОВНЫЕ ФАКТЫ НА ПРАКТИКЕ
Учащиеся, испытывающие трудности, должны тратить несколько минут каждый день, работая над своими основными арифметическими фактами. Десять минут в день в классе, в конце урока или в качестве остановки в серии математических заданий помогут им развить скорость и уверенность в себе. Доступно множество отличных приложений и веб-инструментов.Если у вас есть для этого доступ к технологии, воспользуйтесь ею!
Если ваш округ предоставляет услугу на основе подписки, воспользуйтесь ею; однако, если это не так, есть бесплатные онлайн-приложения для ознакомления с основными фактами. Если у вас нет доступных технологий, флеш-карты и партнеры тоже подойдут!
СТРАТЕГИЯ 5: ИСПОЛЬЗУЙТЕ МНЕМОНИКУ
В этом году в моем здании мы провели опрос студентов специального образования, которые добились больших успехов в государственных оценках. Мы спросили их, что, по их мнению, помогло им добиться успеха.Один ясный ответ заключался в том, что их учителя предоставили им стратегии. Очень часто студенты называли стратегию аббревиатурой.
Вот несколько стратегий решения проблем, которые вы, возможно, захотите использовать со своими учениками: RIDE, TINS, STAR и FAST DRAW. Эти стратегии решения проблем, наряду с «печально известной» PEMDAS, могут быть для учащихся простым способом зафиксировать проблему и найти решение.
Загрузить этот пост представляет собой памятку для учителей, которая включает в себя эти мнемонические приемы решения проблем и объясняет, что означают их аббревиатуры.
БОНУС: ДРУГИЕ СПОСОБЫ ПОМОЧИ БОРЬБАМ УЧАЩИХСЯ
Вот несколько заключительных быстрых идей, которые помогут учащимся, испытывающим трудности в математике
пусть они вербализируют процесс решения проблем, чтобы помочь противостоять импульсивному поведению при решении проблем
предоставляет внеклассные возможности помощи
организация перекрестного обучения сверстников
Работать с отстающими учениками сложно.Тем не менее, один из признаков хорошего учителя математики — это способность доходить до учеников, независимо от их уровня: трудного, среднего или суперзвездного. Все вышеперечисленные стратегии полезны при удовлетворении потребностей учащихся, испытывающих трудности с математикой.
Загрузите эти математические стратегии для учащихся, испытывающих трудности, в качестве полезных подсказок и поделитесь ими с учителями своей школы! Вы также можете найти приведенные ниже ресурсы, которые помогут учащимся, испытывающим трудности с математикой. Хватай их сейчас же.
5 способов улучшить математические инструкции | Использование соответствующих инструментов по классу | Набор для проведения тестов по математике |
В заключение я хочу вернуть нас к истории Джоуи из начала этого поста.Джои плохо разбирался в математике, отставая от своих сверстников на три или четыре года. Он чувствовал себя ужасно из-за этого, и в основе его проблемы было то, что он подавил свою готовность рисковать, потому что над ним издевались в предыдущей школе. Как только эти эмоциональные / ситуативные потребности были удовлетворены, Джои снова смог рискнуть, открыв дверь для использования этих стратегий. Он должен закончить учебный год на уровне своего класса.
Загружаемые листы с советами для этого поста охватывают три области, в которых вы можете работать, чтобы помочь учащимся, испытывающим трудности.Помещение копий в свою тетрадь или развешивание ее возле стола или на рабочем месте предоставит вам полезные возможности, когда вы будете думать о том, как помочь «приятелям» в вашем классе.
Знакомство и общение с вашими учениками, использование основанных на исследованиях стратегий и запоминание нескольких мнемоник будут иметь большое значение для помощи вашим учащимся, испытывающим трудности.




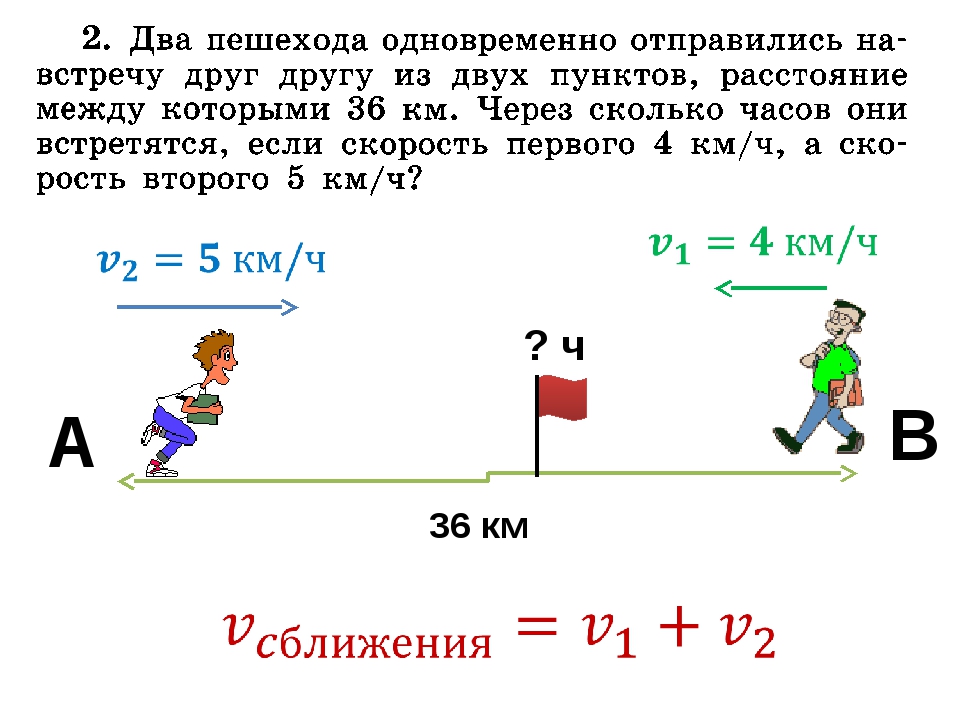 Он косит шесть газонов в час, и ему нужно косить 21 газон. Сколько времени у него на это потребуется?»
Он косит шесть газонов в час, и ему нужно косить 21 газон. Сколько времени у него на это потребуется?» 5 часов
5 часов США / 12 = 32,50 долл. США
США / 12 = 32,50 долл. США