Решение задачи 5 класса по математике: Задачи по математике 5 класс

Задачи «на части» в 5-м классе, на ВПР и итоговых экзаменах

Если вы решили заниматься летом с ребёнком математикой, но с трудом вспоминаете школьную программу, наш блогер Александр Шевкин поможет вам всё наверстать. Сегодня он приводит примеры задач «на части» и объясняет, как их решать.

Задачи «на части» являются классическим типом задач, решаемых как арифметически, так и при помощи уравнения. Такие задачи встречаются в учебниках для пятого класса, в ВПР и на выпускном экзамене.

Для развития мышления и речи детей начинать лучше с арифметического способа решения. Рассмотрим решения двух задач из учебника «Математика, 5» (Просвещение, С. М. Никольский и др.) В первых задачах части упоминаются явно.

Задача 1. Для варенья из малины на 2 части ягод берут 3 части сахара. Сколько сахара следует взять на 6 кг ягод?

Решение: По условию задачи ягод 6 кг, и это количество составляет 2 части, поэтому на каждую часть приходится:

6: 2 = 3 кг.

Сахара надо взять 3 такие же части, то есть:

3 ∙ 3 = 9 кг.

Ответ: 9 кг.

В следующей задаче некоторую величину надо принять за одну или несколько равных частей. При решении таких задач полезно рисовать схематические рисунки, облегчающие решение.

Задача 2. На двух полках стоит 120 книг — на первой полке в 3 раза больше, чем на второй. Сколько книг стоит на каждой полке?

Решение: Если книги, стоящие на второй полке, составляют 1 часть, то на первой полке — 3 такие части. Выполним схематический рисунок.

1) Сколько частей составляют 120 книг?

1 + 3 = 4 (части).

2) Сколько книг приходится на 1 часть?

120: 4 = 30 (книг).

3) Сколько книг приходится на первую полку?

30 ∙ 3 = 90 (книг).

Ответ: 90 и 30 книг.

Следующая задача была предложена на экзамене «Математическая грамотность» (Казахстан). Это аналог нашего ЕГЭ базового уровня для выпускников средней школы.

Задача 3. Когда отцу был 31 год, сыну было 8 лет. Сейчас отец в 2 раза старше сына.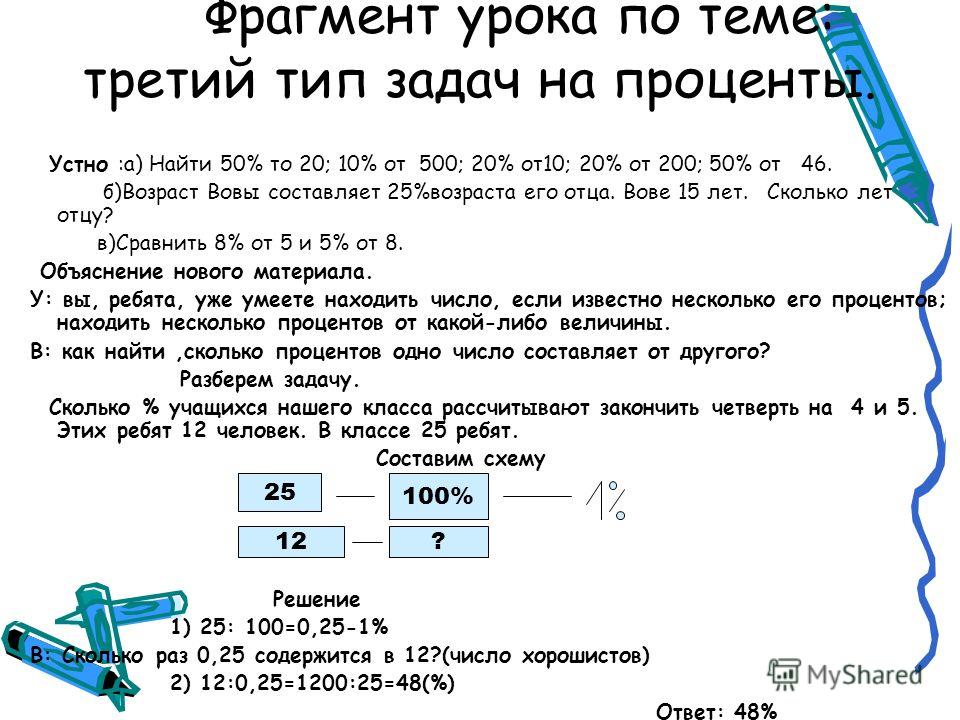 Сколько лет сыну сейчас?

Решение: Отец старше сына на 31 — 8 = 23 года. Пусть сейчас возраст сына составляет 1 часть, тогда возраст отца — 2 такие же части. Выполним схематический рисунок.

Замечание. Эту задачу преподаватель из ютьюба, обучавший выпускников казахстанских школ, решал при помощи уравнения, приняв за x число лет, прошедших между описанными в задаче событиями.

В заключение задача посложнее.

Задача 4. Для компота купили 1800 г сухофруктов. Яблоки составляют 4 части, груши 3 части, а сливы 2 части общего веса сухофруктов. Сейчас граммов яблок, груш и слив было в отдельности?

Решение:

1) 4 + 3 + 2 = 9 (частей) — приходится на 1800 г,

2) 1800: 9 = 200 (г) — приходится на 1 часть,

3) 200 ∙ 4 = 800 (г) — было яблок,

4) 200 ∙ 3 = 600 (г) — было груш,

5) 200 ∙ 2 = 400 (г) — было слив.

Ответ: 800, 600 и 400 г.

Отметим, что приём решения задач «на части» может использоваться при решении более сложных составных задач.

Задача 5. На двух полках стояли 36 книг. Когда с первой полки на вторую переставили 3 книги, то книг на второй полке стало в 2 раза больше, чем на первой. Сколько книг было на каждой полке первоначально?

Решение: Пусть количество книг на первой полке после перестановки трёх книг составляет 1 часть, тогда на второй полке — 2 части.

1) 1 + 2 = 3 (части) — приходится на 36 книг,

2) 36: 3 = 12 (книг) — приходится на 1 часть (стало на 1-й полке),

3) 36 — 12 = 24 (книг) — стало на 2-й полке.

Вернём три книги на первую полку.

4) 12 + 3 = 15 (книг) — было на первой полке первоначально,

5) 24 — 3 = 21 (книга) — была на второй полке первоначально.

Ответ: 15 и 21 книга.

Вы находитесь в разделе «Блоги». Мнение автора может не совпадать с позицией редакции.

73, 74, 75. Задачи на движение по воде

73, 74, 75. Задачи на движение по воде

Это надо знать

В задачах на движение по воде скорость реки считается постоянной и неизменной.

При движении по течению скорость реки прибавляется к собственной скорости плывущего тела, так как скорость реки помогает двигаться телу. 

При движении против течения от собственной скорости вычитается скорость реки, так как в этом случае скорость реки мешает движущемуся телу.

Скорость плота считается равной скорости реки.

Пример:

Пусть скорость движения лодки 5 км/ч, а скорость течения — 2 км/ч.
1) 5 + 2= 7 (км/ч) — скорость лодки по течению
2) 5 — 2 = 3 (км/ч) — скорость лодки против течения

Пусть наша лодка проплыла 2 часа по течению реки и 3 часа против течения реки. Найдем расстояние, которое проплывет лодка.

3) 7 ∙ 2 = 14 (км) — плыла лодка по течению
4) 3 ∙ 3 = 9 (км) — плыла лодка против течения
5) 14 + 9 = 23 (км) — все расстояние
Ответ: 23 км.

---

Видеоурок

---

Домашнее задание

К уроку 73 (на 16.12)
П. 4.11

№ 1

Скорость катера в стоячей воде (собственная скорость) 12 км/ч, а скорость течения реки 3 км/ч. Определите:
1) скорость катера по течению и против течения реки;
2) путь катера по течению реки за 3 ч;
3) путь катера против течения реки за 5 ч.

№ 2

 Скорость катера против течения равна 23 км/ч, а скорость течения 4 км/ч. Найдите скорость катера по течению.

№ 3

 Скорость моторной лодки по течению реки равна 14 км/ч/ а скорость течения 3 км/ч. Найдите скорость лодки против течения

---

К уроку 74 (на 17.12)
П. 4.11

№ 5.302
Расстояние между пристанями прогулочный теплоход проплывает  по течению за 3 ч со скоростью 24 км/ч, а за 4 ч возвращается обратно. Какова скорость катера в стоячей воде и скорость течения реки?

№ 5.303
Путешественник спустился вниз по течению реки за 2 сут. на плоту, а обратно вернулся теплоходом за 2 ч. Найдите собственную скорость теплохода, если скорость течения реки равна 2 км/ч.

№ 5.304
Наша Таня громко плачет, уронила в речку мячик. Но проплакав 2 мин, Таня поплыла за мячиком и через 2 мин догнала его. С какой скоростью плыла Таня, если скорость течения реки равна 35 м/мин?

---

К уроку 75 (на 18.12)
П. 4.11

№  5.306
Вниз по течению реки плывет моторная лодка, а навстречу ей катер. Через какое время после начала движения лодка и катер встретятся, если их собственные скорости равны 12 км/ч и 15 км/ч соответственно, скорость течения реки равна 2 км/ч; лодка и катер начали движение одновременно, находясь на расстоянии 54 км друг от друга?

№ 5.297
Из поселка Веселково одновременно в противоположных направлениях отправились два рейсовых автобуса.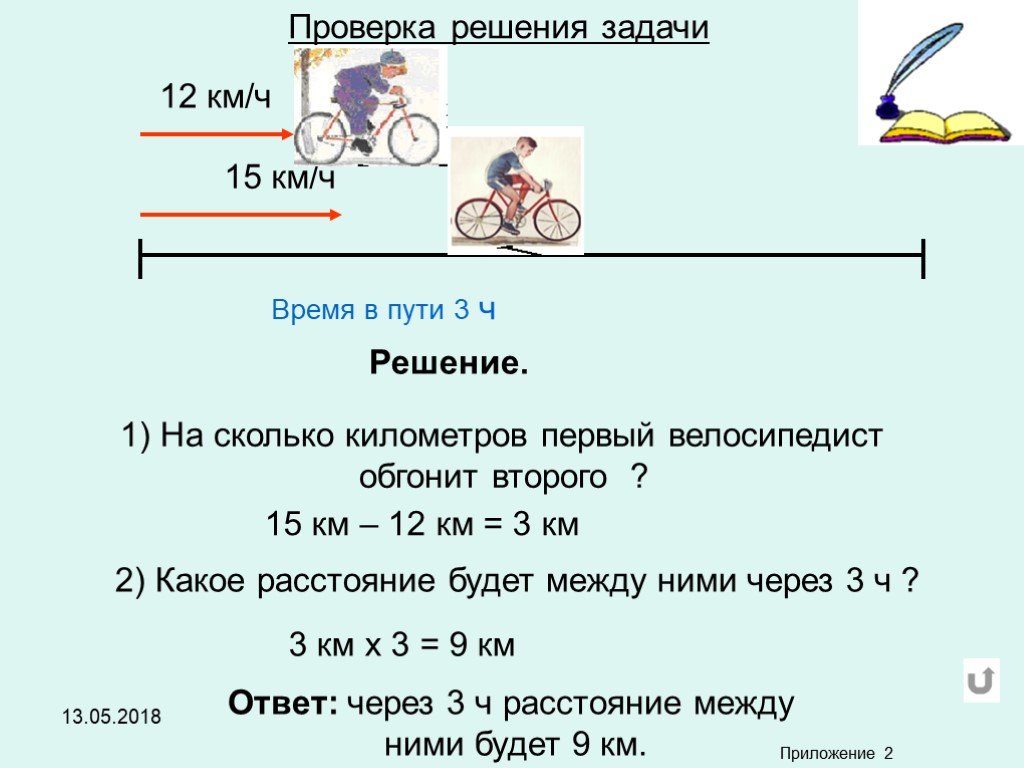 Скорость одного автобуса равна 56 км/ч, другого — на 8 км/ч больше. Через сколько часов расстояние между автобусами будет равно 480 км?

---

Главная страница

Подписаться на: Сообщения (Atom)

Решение задач Математические процессы Пятый 5-й класс Математические стандарты

Подпишитесь на нашу рассылку

Электронное письмо:

@internet4classr

I4C

5-й класс — Решение задач

Главная  > Справка по уровню оценки > Математические навыки 5-го класса > Математические процессы 5-го класса > 5-й класс Решить задачи

реклама

Решайте проблемы несколькими способами и объясняйте, почему один процесс может быть более эффективным, чем другой. 0506.1.5

Ссылки проверены 18.01.2019

1. Решение математических задач для старшеклассников с ограниченными возможностями.
Щелкните изображение, чтобы увеличить его		Ресурс, который учитель может использовать при планировании уроков. Включает процессы и стратегии решения математических задач [Эта ссылка с истекшим сроком действия доступна в интернет-архиве Wayback Machine.] Можно загрузить в виде документа Word или PDF.0014
2. Научитесь решать текстовые задачи.
Щелкните изображение, чтобы увеличить его		Коллекция словесных решателей задач, которые решают ваши проблемы и помогают понять решения. Все задачи можно настроить.&nbspПОДРОБНЕЕ
3. Учебное пособие по длинным дивизиям: двойные дивизии.
Щелкните изображение, чтобы увеличить его		Преподавание двойного деления может помочь в обучении длинному делению, укрепляя принципы деления и давая учащимся возможность добиться успеха с помощью менее разочаровывающей альтернативы. &nbspПОДРОБНЕЕ
4. Математические файлы.
Щелкните изображение, чтобы увеличить его		Просмотрите коллекцию полностью решенных математических задач по категориям. Скорее всего, вы найдете такой же, над которым работаете.&nbspПОДРОБНЕЕ
5. Математические обручи.
Щелкните изображение, чтобы увеличить его		Практика решения текстовых задач для учащихся 3–5 классов. Во всех текстовых задачах используются целые числа, но задачи варьируются от одноэтапного сложения до многошаговых уравнений. Есть также задачи, которые требуют, чтобы учащиеся интерпретировали остатки.&nbspПОДРОБНЕЕ
6. Загадки знатоков математики.
Щелкните изображение, чтобы увеличить его		Вызов всех математических детективов! Тайны раскрываются по всему городу, и нашему главному сыщику нужна ваша помощь, чтобы раскрыть каждое из них. ЕЩЕ
7. Математические истории.
Щелкните изображение, чтобы увеличить его		Цель этого веб-сайта по математике – помочь учащимся начальной школы (с 1 по 6 классы) развить навыки решения математических задач и критического мышления.&nbspПОДРОБНЕЕ
8. Обучающие видеоматериалы по математике.
Щелкните изображение, чтобы увеличить его		[Предназначен для 5–8 классов] Проект, цель которого — помочь учащимся средних классов научиться решать сложные текстовые задачи. Видео доступно по этой ссылке.&nbspПОДРОБНЕЕ
9. Математические задачи.
Щелкните изображение, чтобы увеличить его		Сотни математических задач с самопроверкой для учащихся 1–6 классов. &nbspПОДРОБНЕЕ
10. Математика через решение задач.
Щелкните изображение, чтобы увеличить его		Эта научная статья из Math Goodies — отличный ресурс, который учителя могут использовать при планировании своих уроков. &nbspПОДРОБНЕЕ
11. N-обогащен.
Щелкните изображение, чтобы увеличить его		Проблемы, которые можно решить более чем одним методом. Рассмотрите различные способы подхода к задачам и подумайте о достоинствах различных путей к решениям.&nbspПОДРОБНЕЕ
12. Открытые математические задачи.
Щелкните изображение, чтобы увеличить его		Этот сайт создан специально для подготовки учащихся средней школы к решению открытых задач на стандартизированных тестах. Задачи каждого месяца разделены на пять направлений математических стандартов. [Эта ссылка с истекшим сроком действия доступна в интернет-архиве Wayback Machine.]&nbspПОДРОБНЕЕ
13. Колоды для решения проблем — (K-8).
Щелкните изображение, чтобы увеличить его		Это сборник любимых задач, изначально созданных участниками проекта TEAM. Все эти задачи позволяют учащимся рассказывать и писать о своем мышлении. Каждый набор задач доступен для скачивания в виде файла PDF.&nbspСМОТРЕТЬ БОЛЬШЕ
14. Стратегии решения проблем (Сингапурский учитель математики).
Щелкните изображение, чтобы увеличить его		Существует множество подходов к решению математических задач. Помимо подхода с рисованием модели, есть несколько других стратегий, которые необходимо освоить учащимся, чтобы достичь мастерства в решении математических задач.
Щелкните изображение, чтобы увеличить его		Многие задачи состоят из нескольких шагов и требуют систематического подхода. Эти идеи, предлагающие общие шаги или стратегии решения математических задач, аналогичны идеям, изложенным в книге Полиа «Как это решить: новый аспект математического метода», и должны помочь вам решить даже самую сложную математическую задачу.&nbspПОСМОТРЕТЬ ЕЩЕ
16. SAT Навыки решения математических задач.
Щелкните изображение, чтобы увеличить его		Попрактикуйтесь в решении математических задач с помощью этих тестов. Используйте калькулятор только в случае необходимости. Вам не нужно более трех строк работы для любой проблемы. &nbspПОДРОБНЕЕ
17. Решите!
Щелкните изображение, чтобы увеличить его	9Видеоматериалы по математике 0044 обеспечивают практическое решение задач для учащихся 3–6 классов. Каждый комплект содержит пять многошаговых текстовых задач с пошаговыми видео решениями. Видео доступно по этой ссылке.&nbspПОДРОБНЕЕ
18. Блоки мышления.
Щелкните изображение, чтобы увеличить его		Моделируйте свои математические задачи с помощью Thinking Blocks, наполненного новыми функциями! Включает задачи на чтение вслух – визуальные подсказки – улучшенные модели – привлекательные темы – оптимизированы для мобильных устройств&nbspПОДРОБНЕЕ
19. Webmath!
Щелкните изображение, чтобы увеличить его		Вы застряли на математической задаче? Они хотели бы помочь вам решить эту проблему. Вы найдете сотни мгновенных ответов, самопомощи, математических решателей, готовых предоставить вам мгновенную помощь в вашей математической задаче. &nbspПОСМОТРЕТЬ ЕЩЕ
20. Кто может делать математику?
Щелкните изображение, чтобы увеличить его		Это упражнение предназначено для того, чтобы помочь учащимся лучше размышлять над решением проблем. Студенты начинают с того, что читают математическую задачу и думают о том, как они могли бы попытаться ее решить. Затем они слушают объяснения Джейка, Келли или Астро. На экране также появляются письменные пояснения.&nbspПОДРОБНЕЕ
21. Стратегии решения задач Word.
Щелкните изображение, чтобы увеличить его		Стратегии решения семи типов проблем [может появиться еще один]&nbspПОДРОБНЕЕ
22. Листы задач Word.
Щелкните изображение, чтобы увеличить его		Эта страница содержит ссылки на бесплатные математические листы для задач Word. Нажмите одну из кнопок ниже, чтобы просмотреть рабочий лист и его ключ ответа. Вы также можете использовать меню «Рабочие листы» сбоку на этой странице, чтобы найти рабочие листы по другим темам математики. Сьюзан Брукс и Билл Байлз.   реклама Рабочие листы с задачами по математике для 5-го класса с ответами Многоступенчатые текстовые задачи, рабочие листы для 5-го класса и многое другое 5 th Рабочие листы с ответами на математические задачи созданы для того, чтобы стимулировать у детей желание решать задачи, требующие навыков критического мышления и рассуждения. Мы также прошли милю, чтобы похвастаться захватывающими многоступенчатые текстовые задачи 5 рабочие листы класса . Эти математические задачи для 5-классников с решениями снабжены простыми стратегиями, которые помогут вашим юным ученикам выработать систематические шаги для решения сложных задач. 5 й МАТЕМАТИЧЕСКИЕ ПЕЧАТИ Лучшее из БЕСПЛАТНЫХ 5 th Класс Рабочие листы по математике Категории Смысл числа Сложение и вычитание Умножение Отдел Экспоненты Теория чисел Десятичные числа Сложение и вычитание десятичных знаков Умножение десятичных знаков Разделить десятичные дроби Дроби и смешанные числа Сложение и вычитание дробей Умножение дробей Разделить дроби Смешанные операции Решение проблем Соотношения и нормы Проценты Денежная математика Числовые серии График координат Переменные выражения Данные и графики Вероятность и статистика Определение времени Единица измерения 2D-фигуры Треугольники и четырехугольники Симметрия и преобразования 3D-фигуры Геометрические измерения 5 th Рабочая тетрадь по интегральной математике для класса Важные факты о задачах по математике для 5 класса Помимо развития у детей логического и абстрактного мышления, наша цель создания этих замечательных многошаговых задачников состоит в том, чтобы подготовить их к реальному жизненному опыту, особенно когда речь идет о покупках, счете, логических рассуждениях, точных угадываниях и т. д. Как лучше всего развивать навыки решения математических задач у детей? Как мы знаем, большинству детей всегда трудно решать текстовые задачи. С нашими таблицами математических задач 5 th с ответами вы должны меньше беспокоиться об этой проблеме. На самом деле наши многошаговые задачи со словами 5 й рабочие листы состоят из лучших способов развить навыки решения математических задач у детей. Начнем с того, что наши увлекательные словесные задачи были тщательно составлены простым языком, что влияет на способность ребенка уверенно решать их с легкостью. Кроме того, чтобы сделать их более увлекательными, наши задачи со словами демонстрируют, как повседневная деятельность включает в себя базовые математические навыки. Эти задачи со словами включают многошаговые задачи со словами, многошаговые задачи со словами с остатками, задачи со словами с дополнительной или отсутствующей информацией, задачи на угадывание и проверку, использование логических рассуждений для нахождения порядка, использование диаграмм Венна для решения задач . No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт Copyright © 2004-2019 Карта сайта