Теоретические основы законов и свойств арифметических действий. Презентация по математике на тему «Законы арифметических действий» (5 класс)
Тема: Использование законов и свойств арифметических действий
для рациональных расчетов
Назначение: Рассмотрим возможность применения законов и свойств арифметических действий для рациональных вычислений.
Планируемые результаты:
Знай : законы и свойства арифметического действия (словесная формулировка и символьная запись)
Убедитесь : Грамотно, правильно излагайте свои мысли, используйте математические символы, применяйте законы и свойства арифметических действий для упрощения вычислений.
Развивающие задачи:
Развивать логическое мышление, умственные способности, волевые навыки, математическую речь, память, внимание, интерес к математике, практичность;
Перила задач:
Воспитывать уважительное отношение друг к другу, чувство партнерства, доверия.
Наименование общей компетенции
ОК 1.
Понять сущность I. Общественное значение своей будущей профессии , сделать его устойчивым .
OK 2.
Организация собственной деятельности , определять методы решения профессиональных задач , оценить их эффективность и качество.
ОК 4.
Поиск, анализ и оценка информации, необходимой для постановки и решения профессиональных задач, профессионального и личностного развития.
ОК 6.
Работа в коллективе и коллективе , взаимодействовать с руководством , коллег и социальных партнеров.
Постановка целей и задач урока
Добрый день! Сегодняшний урок хочу начать с нескольких утверждений….
Счет и расчет — основа порядка в голове. (Иоганн Пестоцци — швейцарский учитель)
В математике нет символов для неясных мыслей. (Анри Пуанкаре — французский математик)
Именно Математика дает самые надежные правила: кому быть — обман чувств не опасен.
Прочтите еще раз эти высказывания о себе и скажите — кто угадал, о чем мы сегодня будем говорить? Что мы повторяем сегодня на уроке? Что мы будем делать?
Вы правы, тема нашего урока… Использование законов и свойств арифметических действий для рациональных вычислений
Начнем урок с математической разминки
Актуализация знаний
1. Закончи предложение. Каково правило?
Из перестановки слагаемых…
Составить сумму из суммы можно…
Произведение двух множителей умножить на третий множитель можно…
Умножить сумму по номеру можно…
Чтобы разделить число на произведение, можно…
2. Это была словесная формулировка правил, а теперь давайте вспомним, как эти правила можно записать с помощью символов математического языка. У вас на партах белые листы, на которых записаны правила. тождественные преобразования в символической, буквенной форме. Вам нужно сложить эти равенства, определить, что такое правила и вспомнить формулировку этих правил.
3. На слайде записываются примеры одинаковых преобразований числовых выражений, исходя из каких правил их можно выполнять?
Изменить местами множители
Восстановить и опустить кронштейны
Сделать общий делитель для кронштейнов
Крепление ранее изученного
Как вы думаете — зачем нужны эти правила? Их много и все они изучаются в начальных классах. (Значение слова рациональный разумный, логичный, целесообразный)
1. Найти рациональный способ Значение выражений (письменных):
а) 156 + 79 + 21 + 44 (у)
б) 2 · 5 · 126 · 4 · 25 (у)
в) (120 + 36 + 186): 6 (у)
г) 56 387 — (6 307 + 82) (у)
г) 62 · 16 + 38 · 16 (у)
г) 240 · 710 + 7100 · 76
д) 45 · 40 — 40 · 25
д) 4 · 63 + 4 · 79 + 142 · 6
г) 107 * 93 -109 * 91
2. Без выполнения вычисления, сравнить значения выражений (устно):
а) 258 · (764 + 548) и 258 · 764 + 258 · 545
в) 496 · (862 — 715) и 496 · 860+ 496 · 715
г) 6720:(7*4) и 6720:7:4
д) 732*(12*2) и 732*20+732*6
3.
В начальных классах методики устных вычислений основаны на рассмотренных законах и правилах. У вас на столах розовые листы, на которых записаны примеры. Вам нужно предложить свой вариант вычислений и объяснить, как учащиеся могут использовать начальную школу. (Работа в парах)
Пример: 60-7=(50+10)-7=50+(10-7)=53 Правило — вычитание числа из суммы.
Проверить, права ли Оля? … (видео)
36-20
26+7
124*3
6 · 28.
840:7
25*12
560:28
4. Задания по логике:
Найти ошибку в рассуждениях:
35+10-45=42+12-54
5*(7+2-9)= 6*(7+2-9)
5=6
Чем болен?
А) произведение всех натуральных чисел от 7 до 81 включительно
Б) Сумма 26*27*28+51*52*53
В) разница 43*45*47-39*41*42
Г) сумма всех трех цифр?
Д/с: придумайте сами числовые выражения Для использования правил .
Всего урока: Продолжить фразы
На уроке вспомнила….
повторила…
поняла… .. ..
Мне было тяжело…
Мне нравится….
Тема. Арифметические законы: Движение, комбинирование, распределение
Тип урока.
Урок первичного изложения новых знаний.Подраздел Древесина. Научиться записывать законы математических действий с помощью формул и давать словесную формулировку закона
МетаПеред Вуд. Коммуникативный: развивать умение делиться знаниями между одноклассниками для принятия эффективных совместных решений.
Нормативные документы: планировать свои действия в соответствии с поставленной задачей. Познавательный: уметь выделять существенную информацию из текстов разных видов
Личная древесина. Формирование познавательного интереса
План урока:
План:
1.
Организационный момент.
2. Проверить ранее изученный материал.
3. Изучение нового материала.
4. Первичная проверка усвоения знаний (работа с учебником).
6. Домашнее задание
7. Рефлексия.
Сценарий урока
Сценическое занятие
Деятельность учителя
Деятельность ученика
1. Аргмомент
Привет ребята!
Пора начинать урок.
Пора считать.
И сложные вопросы
Вы отвечаете Скажите дать!
Математика, друзья,
Нужен абсолютно всем.
На уроках работай прилежно,
И успех тебя ждёт.
Подготовиться к уроку
Ответ: Математика
2.
Проверка ранее изученного материала.
S = Vt.
Периметр прямоугольника
P = 2 (A + B)
Квадрат прямоугольника
S = AB.
Пройденное расстояние
— Открой блокнот, подпиши номер, классная работа.
1) а = 8см
б = 13см
2) v = 70км/ч
t = 5ч
3) а = 5ч
3) а = 90 0 40002
4) S = 300 км
t = 6 ч
5) S = 420 км
V = 70км/ч
S = ?
С = ?
Р = ?
В = ?
т = ?
— Работаем устно по следующему слайду. (5 слайдов).
12 + 5 + 8
25 10
250 – 50
200 – 170
30 + 15
45:3
15 + 30
45 – 17
28 25 4
Задача: найти значение выражений. (Один ученик работает у экрана.)
– Что интересного подмечено при решении примеров? На какие примеры следует обратить особое внимание? (Ответы детей.)
Проблемная ситуация
– Какие свойства сложения и умножения вы знаете из начальной школы? Вы умеете записывать их буквенными выражениями? (Ответы детей).
Вычислить устно
Формула равенства, которая является правилом записи для вычисления любого значения.
Запишите в тетрадь ответы. Теперь внимание на слайд «Проверь себя» (4 слайд).
проверь себя
104 см 2.
350 км
82 М.
50 км/ч
6 ч
3. Сообщение темы и цели урока
– И так, тема сегодняшнего урока «Законы арифметического действия» (6 слайд).
— Запишите тему урока в тетрадь.
— Что нового нам предстоит узнать на уроке? (Вместе с детьми формируют мишени урока).
Применение формул при решении задач
Формулы периметра и квадратных фигур, пути
4.
Изучение нового материала.
Сколько учеников в классах 11 d и 12m?
Как узнать ответ? Если до d+m или до M+D результат изменится?
Какой вывод сделаем?
В вазе лежат 5 груш, 7 бананов и 3 яблока. Могу ли я узнать весь плод?
— Смотрим на экран. (7 слайдов) .
Законы сложения
Равенство
Пример
Движение
а + b = b + а
7 + 3 = 3 + 7
Объединение
(А + В) + С = А + (В + С)
(48 + 3) + 12 = (48 + 12) + 3 = 63
Вы видите законы сложения, записанные в алфавите и примерах.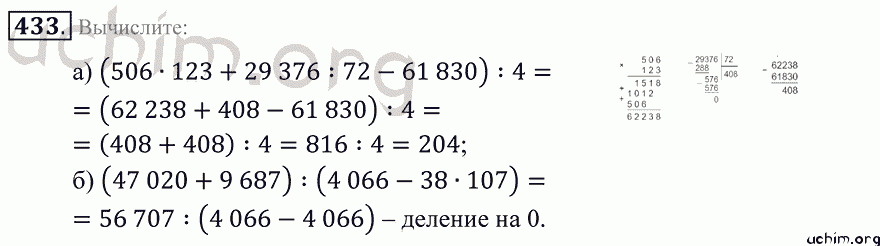
(Разбор примеров).
Отображение на доске 27+148+13=188
124+371+429+346=800+470=1270
А теперь попробуй
Молодец!
Ответить на вопросы
Да
Один учащийся с колонкой
Учащийся работает на других досках в тетрадях
83346+140458+ =
107888+32012+213355=
70+90+130+10=
5427+6328+10023+612=
5.Физминутка
Закрой глаза, расслабь тело,
Представь — Ты птица, ты вдруг прилетела!
Сейчас в океане дельфин плывет,
Сейчас в саду яблоки поспелые созрели.
Налево, направо, по сторонам посмотрел,
Открыл глаза, и снова за дело!
Выполнение учителем
6. Первичная проверка знаний усвоения материала (работа с учебником)..
№ 213 рассмотрим, устно 214
На досках посчитаем удобным способом
5*328*12 756*25*4
50*(346*2) 8*(956*125)
7. Контроль и самопроверка знаний (самостоятельная работа).
Вариант 1.
Вариант 2.
Выполнить индивидуально и пройти проверку, оценки к следующему занятию
8. Легкое задание
РТ, 212, 214
9. Из условий перестановки
5 …
Из перестановки множителей…
Чтобы умножить разницу в числе, нужно… Какие выводы вы сделали на уроке?
Всем спасибо за урок. Пока
Сегодня на уроке:
A. Узнал(а) ……
Q. Понравилось….
C. Не понравилось…
D. Было сложно для меня…
Формула крыс
S = Vt.
Периметр прямоугольника
Р = 2 (А + В)
Квадратный прямоугольник
S = АВ.
Пройденный путь
2. Реквизитная таблица
1) а = 8см
дюйм =13 см
2) v = 70кМ/ в.
t = 5.с.
3) а = 17м.
б = 24.м.
4) S = 300кМ
t = 6.с.
5) S = 420кМ
V = 70.кМ/ в.
С = ?
С = ?
Р = ?
В = ?
т = ?
Рассчитать
83346+140458+ =
107888+32012+213355=
7893+456342+300758126+319+434+551=
70+90+130+10=
5427+6328+10023+612=
Рассчитать удобным способом
5*328*12 756*25*4
50*(346*2) 8*(956*125)
Самостоятельная работа
А)25∙4∙86 б)176+24+8 в)4∙5∙333
Д) (977+23)∙49 д)(202-102)∙87
6.
Продолжить предложение
От перестановки слагаемых…
Если к сумме двух составляющих добавить третий член, то…
От перестановки множителей…
Если произведение двух множителей умножить на третий множитель, тогда…
Чтобы умножить сумму на число, нужно…
1. Формулы Велли
S = Vt.
Периметр прямоугольника
P = 2(A + Б)
Квадратный прямоугольник
S = AB.
Пройденный путь
2. Реквизитная таблица
1) а = 8см
дюйм =13 см
2) v = 70кМ/ в.
t = 5.с.
3) а = 17м.
б = 24.м.
4) S = 300кМ
t = 6.с.
5) S = 420кМ
V = 70.кМ/ в.
С = ?
С = ?
Р = ?
В = ?
т = ?
Рассчитать
83346+140458+ =
107888+32012+213355=
7893+456342+300758126+319+434+551=
70+90+130+10=
5427+6328+10023+612=
Рассчитать удобным способом
5*328*12 756*25*4
50*(346*2) 8*(956*125)
Самостоятельная работа
А)25∙4∙86 б)176+24+8 в)4∙5∙333
Д) (977+23)∙49д)(202-102)∙87
6.
Продолжить предложение
От перестановки слагаемых…
Если к сумме двух составляющих добавить третий член, то…
От перестановки множителей…
Если произведение двух множителей умножить на третий множитель, то…
Чтобы умножить сумму на число, нужно…
§ 13. Законы арифметических действий — учебник по математике 5 класс (Зубарева, Мордкович)
Краткое описание:
Чтобы успешно справляться с решением различных математических выражений и уравнений, а особенно формул, выраженных в алфавитном порядке, когда искомых несколько, необходимо знать основные законы арифметических действий. Они создаются на основе повторяющихся ситуаций, связанных с математическими действиями, и представляют собой неизменные правила, помогающие нам решать математические задачи и справляться с разными примерами по математике.
С некоторыми законами арифметических действий вы уже познакомились ранее и использовали при решении выражений.
Это, например, закон движения сроков — когда сроки разрешены, их сумма остается неизменной. Такие законы могут быть изображены в алфавитном порядке или озвучены в предложении устно. Как есть законы сложения, так есть и законы умножения. Действия, которые производятся с ними, различны, но правила их совершения одинаковы. Но правила меняются, когда дело доходит до смешивания действий сложения и умножения в одном выражении. Действие умножения является более сильным и первым по порядку выполнения, как и действие, записанное в скобках. В выражении 5 10 + 6 (4 + 7) сначала нужно перемножить первые два числа между собой, вычислить сумму в скобках и умножить ее на число перед скобками, и только потом подсчитать сумму получившиеся числа. Также правильным будет при раскрытии скобок каждое число умножить на число, стоящее перед скобками, а затем вычислить их сумму. Вы можете использовать любые варианты при решении различных выражений. Предлагаем перейти к материалу учебника и Подробнее рассмотреть этот материал на примерах, закрепив свои знания различными выражениями и уравнениями.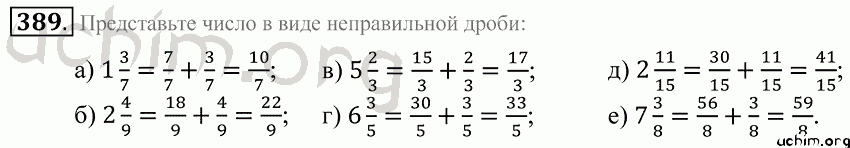
Цель: Проверить сформированность умений производить расчеты по формулам; Познакомить детей с подвижными, комбинированными и распределительными законами арифметического действия.
- ввести алфавитную запись законов сложения и умножения; Учить применять законы арифметических действий для упрощения вычислений и буквенных выражений;
- развивать логическое мышление, умственные способности, волевые навыки, математическую речь, память, внимание, интерес к математике, практичность;
- облегчают уважительное отношение друг к другу, чувство партнерства, доверия.
Тип занятия: Комбинированное.
- проверка ранее полученных знаний;
- подготовка учащихся к изучению нового материала
- заявление о новом материале;
- восприятие и ознакомление учащихся с новым материалом;
- первичное закрепление исследуемого материала;
- подведение итогов урока и домоводство.
Оборудование: компьютер, проектор, презентация.
План:
1. Организационный момент.
2. Проверить ранее изученный материал.
3. Изучение нового материала.
4. Первичная проверка усвоения знаний (работа с учебником).
5. Контроль и самопроверка знаний (самостоятельная работа).
6. Подведение итогов урока.
7. Отражение.
Во время занятий
1. Организационный момент
Учитель: Добрый день, дети! Начнем наш урок со стихотворения — помощь. Обратите внимание на экран. (1 слайд) . Приложение 2. .
Математика, друзья,
Нужен абсолютно всем.
На уроках работай прилежно,
И успех тебя ждёт.
2. Повторение материала
Повторяем пройденный материал. Я приглашаю студента к экрану. Задание: Соедините с помощью указки записанную формулу с ее названием и ответьте на вопрос, который еще можно найти с помощью этой формулы. (2 слайда).
Открой блокнот, подпиши номер, классная работа. Обратите внимание на экран. (3 слайда).
Работаем устно по следующему слайду. (5 слайдов).
12 + 5 + 8 25 10 250 – 50 200 – 170 30 + 15 45:3 15 + 30 45 – 17 28 25 4
Задача: найти значение выражений. (У экрана работает один ученик.)
— Что интересного заметили при решении примеров? На какие примеры стоит обратить особое внимание? (Ответы детей. )
Проблемная ситуация
— Какие свойства сложения и умножения вы знаете из начальной школы? Вы знаете, как записать их, используя буквенные выражения? (Ответы детей).
3. Изучение нового материала
— И так, тема сегодняшнего урока «Законы арифметического действия» (6 слайд).
— Запишите тему урока в тетрадь.
— Что нового нам предстоит узнать на уроке? (Вместе с детьми формируют мишени урока).
— Смотрим на экран. (7 слайдов) .
Вы видите законы сложения, записанные в алфавите и примерах. (Разбор примеров).
— Следующий слайд (8 слайд).
Разбираем законы умножения.
— А теперь познакомимся с очень важным распределительным законом (9 слайд).
— Подвести итоги. (10 слайдов).
— Зачем нужно знать законы арифметических действий? Придут ли они на дальнейшее обучение, при изучении каких предметов? (Ответы детей.)
— Запишите законы в тетрадь.
4. Крепежный материал
— Откройте учебник и устно найдите № 212 (A, B, D).
№ 212 (Б,ж,з,з) письменно на доске и в тетрадях. (Чек об оплате).
— устно работаем над числом 214.
— Выполняем задание № 215. Какой закон используется при решении этого числа? (Ответы детей).
5. Самостоятельная работа
— Запишите ответ в карточку и сравните свои результаты с соседом по парте. А теперь внимание на экран. (11 слайдов). (Проверить самостоятельную работу).
6. Результат урока
— Внимание на экране. (12 слайдов). Закончите предложение.
Оценки за урок.
7. Домашнее задание
§13, № 227, 229.
8. Рефлексия
Решение дробей 5-го класса через Island Math Stories: Part 901 Charter School: Part 15
Стеф Примиани, директор STEM, и Алисия Куомо, стажер по политике городского образования Университета Брауна
Комбинируйте 3/4 и 1/2.
Рене съела 3/4 пакета попкорна. Затем Мария съедает 1/2 пакета попкорна. Сколько всего попкорна съели Рене и Мария?
Обе задачи требуют одинаковых навыков нахождения эквивалентных дробей для объединения двух чисел с разными знаменателями. Но вопрос о попкорне дает реалистичный контекст почему.
«Обучение через решение задач можно описать как перевернутое по сравнению с обучением решению задач — с проблемой (задачами), представленной в начале урока, и навыками, возникающими в результате работы с проблемой (задачами)». 1
Описательная структура вопроса-проблемы предлагает учащимся создать модель с метками. В модели дискретных дробей учащиеся разбивают, чтобы найти эквивалентную дробь:
В модели числовых линий история попкорна более явно визуализируется как последовательность событий, последний скачок которой представляет собой сумму:
Создавая модель для объединения частей попкорна, учащиеся изучают процедуру нахождения эквивалентных частей. Кроме того, они сразу узнают один реалистичный контекст, в котором могут применяться математические навыки, и учащиеся могут легче замечать закономерности в типах задач, чтобы использовать более эффективные стратегии и решать все более сложные сценарии.
В разговорном интервью 2006 года профессор математики и писатель Джон А. Ван де Валле подчеркнул необходимость того, чтобы во всех американских классах был нормирован проблемно-ориентированный подход , основанный на идеях студентов , а не лекция под руководством учителя. Когда учитель читает лекцию по принципу «покажи и расскажи», Ван де Валле утверждает, что студенты сосредоточены на направлениях и правилах, а не на математических концепциях.
С проблемным учащемуся некуда обратиться, кроме своих собственных идей, связанных с проблемой. В результате вместо того, чтобы искать правила, учащиеся пытаются разобраться в релевантных идеях, заложенных в проблеме или задании .
Для меня также чрезвычайно важно учитывать, что каждый подход каждый день говорит студентам. Благодаря замечательным объяснениям под руководством учителя учащиеся часто рассматривают математику как набор правил, которые часто сбивают с толку и не имеют большого значения… В классе, основанном на задачах, учащиеся… сталкиваются с самым основным фактом математики: математика имеет смысл. Кроме того, они осознают, что именно они способны понимать математику. 1
20-минутный протокол Math Stories представляет собой ориентированный на учащихся подход, который делает именно то, что предлагает Ван де Валле: заставляет учащихся самостоятельно решать сложные задачи в реалистичных условиях. Как учителя могут использовать контекст в Math Stories и во время основного учебного блока? Почему контекст имеет значение в подходе, ориентированном на студента?
Часть видения Ван де Валле заключается в том, что математика не в способности идентифицировать типы задач и применять простые алгоритмы. Скорее, решение математических задач не является рутинным.
Определения решения проблем варьируются в зависимости от учебного плана, но по сути это нестандартных вопросов, которые можно решать с использованием более чем одной стратегии . «Изучение нескольких стратегий может помочь учащимся увидеть разные идеи и подходы к решению проблем и может позволить учащимся мыслить более гибко, когда сталкиваются с проблемой, не имеющей очевидного решения».
Последовательность математических рассказов для 5-го класса состоит примерно из 70 задач. Это тщательно продуманный прогресс, который начинается с обзора концепций 4-го класса, а затем через пару месяцев учащиеся переходят к стандартам дробей 5-го класса, используя все четыре операции. Как правило, в месяц предлагается 10-13 задачек, что дает учителям возможность гибко пересматривать сложные типы задач и пересматривать концепции.
Ключевым моментом в задаче на ежедневный рассказ является то, что она представляет собой математическую задачу в контексте . Предоставление контекста имеет решающее значение для поддержки учащихся в осмыслении и гибком решении проблем. Кроме того, сюжетные задачи помогают учащимся развивать навыки в трех областях, которые RAND (огромная беспристрастная исследовательская корпорация) считает необходимыми для развития навыков:
- Представительство
- Обоснование
- Обобщение
В то время как учащиеся могут быть подготовлены к определению типа задачи на явном уроке и следованию знакомой процедуре, в Math Stories учащимся не предоставляется никакой информации, кроме задачи на рассказ. Как предполагает Ван де Валле, такая структура невмешательства заставляет учащихся думать о том, какую информацию они уже знают и что от них требуется решить. Теоретически это звучит здорово, но в классах у учащихся разные потребности, они все еще развивают метакогнитивные навыки и часто быстро просматривают задачи и полагаются на простые алгоритмы.
Как научить учащихся внимательно читать задачки?
Контрольный список
Список вопросов может помочь учащимся в тщательном прочтении задачки на известную и неизвестную информацию. Информационная служба What Works (WWC) финансируется Институтом педагогических наук (IES) через Министерство образования США и является огромным ресурсом исследований в области образования. Вот примерный список подсказок WWC:
Моделирование самоконтроля и размышлений
Учителя должны демонстрировать, как использовать подсказки, подобные перечисленным выше, чтобы рассуждать с самим собой на протяжении всего процесса решения проблемы – при чтении рассказа, выборе стратегии решения и проверке твоя работа. Учащиеся учатся на примере, как думать вслух при решении сюжетной задачи. Вот пример самоконтроля студента из WWC, адаптированный к Math Stories. Учащийся задает и отвечает на последовательность вопросов, одинаковую независимо от типа задачи:
Пример задачи
5 друзей планируют разделить 3 пиццы поровну. Один из друзей больше не может прийти на ужин. Насколько больше пиццы получат друзья, если пиццу разделят только 4 человека, а не 5 человек?
Решение*
Ученик: Сначала я спрашиваю себя: «О чем эта история и что мне нужно выяснить?» Я вижу, что задача дала мне общее количество пиццы и два разных сценария распределения общего количества пиццы. Я знаю, что «насколько больше» требует от меня сравнить или вычесть разницу между тем, сколько пиццы получает каждый друг в каждом сценарии.
Я спрашиваю себя, «Сталкивался ли я с такой проблемой раньше?» Когда я вспоминаю задачи, которые мы решали, я вспоминаю задачу, в которой друзья делили сковороду с пирожными. Я помню, что нам пришлось разделить все на количество друзей, чтобы получить порцию каждого друга. Это похоже на похожую проблему, но мне придется разделить дважды, потому что есть два сценария, а затем сравнить.
Прежде чем продолжить, я задаюсь вопросом: «Какие шаги я должен предпринять, чтобы решить эту проблему?» Похоже, мне нужно разделить общее количество пиццы на количество друзей для каждого сценария.
4 друга: 3/5 пиццы на человека
5 друзей: 3/4 пиццы на человека
Проблема заключается в том, чтобы спросить меня, «насколько больше» пиццы получают друзья, когда разделяется только 4 человека вместо 5. Я знаю, что когда я сравниваю или нахожу разницу, я могу использовать вычитание. Но у меня должны быть одинаковые единицы для вычитания.
Я могу использовать свою модель:
Чтобы написать уравнение:
Итак, разница 3/20. Каждый из друзей получает на 3/20 пиццы больше, когда их всего 4, по сравнению с тем, когда их 5.
Наконец, я спрашиваю себя: «Имеет ли этот ответ смысл, когда я перечитываю задачу?» Мне кажется, что 3/20 — это ответ, потому что это разница между размером порции для 5 и 4 друзей. 3/20 — это небольшое число по сравнению с размерами порций. (Я знаю, что 3/10 — это то же самое, что 0,3 или 3%, а 3/20 — еще меньше!) Это имеет смысл, потому что задача состоит в том, чтобы найти разницу: если я заберу одного друга, это немного изменит количество пиццы. получит каждый человек.
Поддержка незнакомого языка и контекста
Безусловно, учащиеся будут сталкиваться с незнакомым языком и контекстом на формальных экзаменах, с которыми им придется бороться без помощи учителя или сверстников. Однако, как утверждает WWC: «Цель обеспечения того, чтобы учащиеся понимали язык и контекст задач, не в том, чтобы сделать задачи менее сложными. Вместо этого это позволяет учащимся сосредоточиться на математике в задаче, а не на необходимости изучать новые базовые знания или язык. Главный момент заключается в том, что учащиеся должны понять проблему и ее контекст, прежде чем пытаться ее решить». По этой причине учителям важно предвидеть, когда пятиклассникам в их классе могут потребоваться дополнительные разъяснения, особенно изучающим английский язык. Вот пример, адаптированный из WWC с использованием сюжетных задач Math Stories:
Персонализация задач по истории
WWC и другие исследования показывают, что учащиеся более вовлечены и могут найти связь с реальными приложениями математики, когда задачи по истории персонализированы. Учителя должны быть осторожны, чтобы не делать этого постоянно — ученики должны привыкнуть думать о сценариях за пределами своей зоны комфорта. Но иногда включение имен учеников, любимые тенденции, такие как бейблейды, и приглашение ученых придумывать свои собственные сценарии могут повысить вовлеченность. Каждая задача на историю в Math Stories основана на стандартах, поэтому можно легко заменить содержание на содержание, имеющее отношение к вашему классу, при этом продолжая обучать ключевым понятиям.