Решеба по матем языку 5 класс: Решебник по математике 5 класс Герасимов, ГДЗ 1-2 часть

Содержание

ГДЗ По Математике 5 Класс Номер 49 – Telegraph

>>> ПОДРОБНЕЕ ЖМИТЕ ЗДЕСЬ <<<

ГДЗ По Математике 5 Класс Номер 49

ГДЗ (готовое домашние задание из решебника) на Номер №49 по учебнику Математика . 5 класс . Учебник для общеобразовательных организаций / С .М . Никольский, М .К, Потапов, Н .Н . Решетников, А .В . Шевкин .

Убедись в правильности решения задачи вместе с ГДЗ по Математике за 5 класс Герасимов В .Д ., Пирютко О .Н ., Лобанов А .П . часть 1 . Ответы сделаны к книге 2019 года от Образование и воспитание . 49 .

ГДЗ 5 класс Математика Никольский, Потапов, Решетников Номер №49 . Задача №49 , ГДЗ по математике за 5 класс к учебнику Никольского .

Подробный решебник (ГДЗ ) по Математике за 5 (пятый ) класс — готовый ответ глава 1 . упражнение — 49 . Авторы учебника: Герасимов, Пирютко, Лобанов . Издательство: Образование и воспитание 2019 .

ГДЗ по математике за 5 класс позволит ученику разобраться в алгоритмах решения задач и примеров, а заботливые родители смогут самостоятельно Решебник по математике – это тот сборник, который облегчит жизнь не только юному ученику, но и его заботливым родителям!

Подробный решебник по математике для 5 класса , авторов Герасимов, Пирютко, 2019-2020 . ГДЗ ко всем заданиям учебника на Решеба . Издание подготовлено группой педагогов, которые постарались облегчить участь учащихся 5 класса, часами бьющихся над «домашкой» . .

ГДЗ по математике 5 класс Никольский . авторы: Никольский С .М ., М .К . Потапов, Н .Н . Решетников . ГДЗ — Готовые Домашние Задания .

ГДЗ по математике 5 класс Никольский задание — 49 . Подробное решение задание № 49 по математике для учащихся 5 класса , авторов Никольский, Потапов, Решетников, Шевкин 2019-2020 .

Готовые домашние задания по математике 5 класса под авторством Герасимов В .Д ., Пирютко О .Н . и Лобанов А .П . 2019-2020 . Любой школьник сможет сам подготовиться к уроку, сделав домашнюю работу при помощи нашего гдз , проверив правильность написанных им номеров . .

Решебник, готовые домашние задания (ГДЗ ) по математике для учащихся 5 класса, авторов Герасимов В .Д ., Пирютко О .Н ., Лобанов А .П . ГДЗ в решебнике Герасимова по математике за 5 класс (1-2 часть) 2019 года помогут как родителям, так и ученикам .

Видео решения задачи №49 по Математике 5 класс автора Виленкин Н .Я . Если ищете ГДЗ по Математике за 5 класс по учебнику Виленкина Н .Я ., то ответы в . .
Решение задания номер 49 . ГДЗ , математика , 6 класс — Зубарева, Мордкович — онлайн решебник .

Упражнение 49, Начертите отрезок АВ, длина которого равна 8 см 9 мм . Отметьте на нём точку С так, чтобы СВ = 3 см 4 мм . ГДЗ решебник и ответы 5 класс , Математика, Мерзляк, Полонский, Якир, Учебник .

Проверяй домашнее задание по математике за 5 класс по сборнику ГДЗ . Все решения задач снабжены подробным пояснениями .

ГДЗ по математике за 5 класс Никольский, это сборник ответов, разделённый на четыре главы . Все упражнения соответствуют принятым стандартам и расположены так же ГДЗ к задачам на смекалку по математике за 5-6 классы Шарыгин И .Ф . можно посмотреть здесь . Номера задач .

ГДЗ (готовое домашние задание из решебника) на Номер №49 по учебнику Математика . 5 класс . Учебник для общеобразовательных организаций / С . М . Никольский, М .К, Потапов, Н .Н . Решетников, А .В . Шевкин .

Видео решения задачи №49 по Математике 5 класс автора Виленкин Н . Я . Если ищете ГДЗ по Математике за 5 класс по учебнику Виленкина Н .Я ., то ответы в . .
Решение задания номер 49 . ГДЗ , математика , 6 класс — Зубарева, Мордкович — онлайн решебник .

ГДЗ Лол По Русскому Языку 5
ГДЗ По Русскому 5 Класс Тесты
Решебник По Белорусскому Языку 7 Валочка 2020
ГДЗ По Контурным Картам 7 Класс Дрофа
Биология Десятый Класс Углубленный Уровень Пономарева ГДЗ
Решебник 5 Класс Мерзляк Ответы
ГДЗ По Англ Яз 8 Класс
ГДЗ По Английскому Шестой Класс Дули
ГДЗ По Геометрии Атанасян Седьмой
ГДЗ По Математике Бунимович Кузнецов
ГДЗ Английский 5 Класс Enjoy English
Решебник 5 Ру
Решебник По Английскому Rainbow English
Решебник По Немецкому 11 Класс Воронина
ГДЗ Чуракова 3 Класс Рабочая Тетрадь
ГДЗ По Геометрии Рабочая Тетрадь Глазков
ГДЗ Громцева Физика 8
ГДЗ По Математике М К Потапов
ГДЗ По Англ 5 Афанасьева Михеева
ГДЗ Колягин 11 Класс Алгебра И Начала
ГДЗ Окружающий Мир Впр Волкова
Решебник По Английскому Безкоровайная
ГДЗ По Английскому 6 Класс Деревянко
ГДЗ 9 Кл Шмелев
Решебник По Беларуская Мова 8
Решебник По Географии 8 Класс Учебник Алексеев
ГДЗ По Истории 1 Часть Торкунова
Физика Комолова ГДЗ
Решебник По Атанасяну 11 Класс
Решебник Английский Третий Класс Рабочая
Решебник По Английскому Языку Тесты
ГДЗ По Английскому 10 Класс Спотлайт Тетрадь
ГДЗ Обществознание 6 Класс Учебник Боголюбова
ГДЗ Аверин Рабочая
ГДЗ По Алгебре 10 Задачник 2
ГДЗ По Алгебре 10 Й Класс Колягин
Решебник По Украинскому Языку 6
ГДЗ Английский 10 Перевод Текстов
ГДЗ По Биологии 10 Класс Учебник Сивоглазов
ГДЗ Моро 2 Класс Видео
ГДЗ По Англ Яз Быкова
ГДЗ Путина Английский 7
ГДЗ По Алгебре 10 11 Начала
ГДЗ От Путина Мордкович
Дидактические Алгебра Мерзляк ГДЗ
Решебник Математика Пирютко 6
ГДЗ По Русскому Языку 5 Разумовская Учебник
ГДЗ 3 Кл
ГДЗ По Матеше 6 Класс
ГДЗ По Математике 6 Класс Мерзляк 37

ГДЗ По Алгебре Номер 24 8 Класс

ГДЗ По Алгебре 10 Мордкович 2004

Гдз Перспектива Математика 1

Гдз Геометрия 7 9 Класс Атанасян

ГДЗ Матем Петерсон 2 Класс

ГДЗ Математика 5 класс Учебник Никольский, Потапов, Решетников, Шевкин

ГДЗ Математика 5 класс Учебник Никольский, Потапов, Решетников, Шевкин — решебник с ответами

Перейти к содержанию

Search for:

Приложение для Android

Курс подготовки к ОГЭ

Курс подготовки к ЕГЭ

Авторы: Никольский С. М., Потапов М.К., Решетников Н.Н., Шевкин А.В.

Издательство: Просвещение

Тип: Учебник

ГДЗ по Математике для 5 класс Никольского к учебнику поможет ребенку покорить трудную дисциплину. В начале средней школы учебная программа еще не очень сложная, но даже отличники нередко испытывают сложности с ее усвоением. Однако с ГДЗ ребенок сможет самостоятельно выбраться из затруднительного положения.
Решебник поможет разобраться со всеми проблемами по предмету, правильно выполнить домашние задания и качественно подготовиться к самостоятельным работам. Кроме того, работа со сборником формирует у ребенка ответственность, ведь бездумно списывать нельзя.

Выберите номер упражнения

123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244245246247248249250251252253254255256257258259260261262263264265266267268269270271272273274275276277278279280281282283284285286287288289290291292293294295296297298299300301302303304305306307308309310311312313314315316317318319320321322323324325326327328329330331332333334335336337338339340341342343344345346347348349350351352353354355356357358359360361362363364365366367368369370371372373374375376377378379380381382383384385386387388389390391392393394395396397398399400401402403404405406407408409410411412413414415416417418419420421422423424425426427428429430431432433434435436437438439440441442443444445446447448449450451452453454455456457458459460461462463464465466467468469470471472473474475476477478479480481482483484485486487488489490491492493494495496497498499500501502503504505506507508509510511512513514515516517518519520521522523524525526527528529530531532533534535536537538539540541542543544545546547548549550551552553554555556557558559560561562563564565566567568569570571572573574575576577578579580581582583584585586587588589590591592593594595596597598599600601602603604605606607608609610611612613614615616617618619620621622623624625626627628629630631632633634635636637638639640641642643644645646647648649650651652653654655656657658659660661662663664665666667668669670671672673674675676677678679680681682683684685686687688689690691692693694695696697698699700701702703704705706707708709710711712713714715716717718719720721722723724725726727728729730731732733734735736737738739740741742743744745746747748749750751752753754755756757758759760761762763764765766767768769770771772773774775776777778779780781782783784785786787788789790791792793794795796797798799800801802803804805806807808809810811812813814815816817818819820821822823824825826827828829830831832833834835836837838839840841842843844845846847848849850851852853854855856857858859860861862863864865866867868869870871872873874875876877878879880881882883884885886887888889890891892893894895896897898899900901902903904905906907908909910911912913914915916917918919920921922923924925926927928929930931932933934935936937938939940941942943944945946947948949950951952953954955956957958959960961962963964965966967968969970971972973974975976977978979980981982983984985986987988989990991992993994995996997998999100010011002100310041005100610071008100910101011101210131014101510161017101810191020102110221023102410251026102710281029103010311032103310341035103610371038103910401041104210431044104510461047104810491050105110521053105410551056105710581059106010611062106310641065106610671068106910701071107210731074107510761077107810791080108110821083108410851086108710881089109010911092109310941095109610971098109911001101110211031104110511061107110811091110111111121113111411151116111711181119112011211122112311241125112611271128112911301131113211331134113511361137113811391140114111421143114411451146114711481149115011511152115311541155115611571158115911601161116211631164116511661167116811691170117111721173117411751176117711781179118011811182118311841185118611871188118911901191119211931194119511961197119811991200120112021203120412051206120712081209121012111212121312141215

Adblock
detector

Стратегии изучения математики для изучающих английский язык (ELL)

Математику иногда считают «универсальным языком», поскольку она основана на абстрактных понятиях, таких как числа и формы. И в этом есть доля правды! В конце концов, два человека, говорящие на разных языках, могут решить одну и ту же математическую задачу и получить одно и то же решение. Тем не менее, язык необходим для обучения математике, поскольку математика неразрывно связана с языком, на котором она преподается.

Владение любым языком зависит от двух факторов: понимания языка и производства языка . Когда дело доходит до обучения математике учащихся ELL, мы можем внимательно изучить уроки и подумать: «Какова языковая нагрузка в данный момент? Понимание или производство?» Затем мы можем использовать целевые стратегии для развития академического языка, а также для углубления понимания математики.

Учащиеся, изучающие английский язык, несут другую когнитивную нагрузку, когда они также изучают математику. Ниже приведены стратегии ELL для математики, которые облегчают когнитивную нагрузку учащихся, чтобы они могли демонстрировать математическое понимание, в то время как вы сохраняете строгость на уроке.

Примечание о языке: мы используем общую фразу изучающий английский язык вместе с аббревиатурой ELL, но мы также признаем, что это несовершенная номенклатура. Учащиеся, изучающие английский язык, не могут четко соответствовать одному ярлыку.

ELL Strategies for Math: Language Comprehension

1: Использование процедур, которые разбирают текстовые задачи

Словесные задачи представляют собой особенно сложную проблему для учащихся, изучающих английский язык. Они достаточно сложны для студентов, которые уже продвинулись в своем развитии английского языка! Словесные задачи требуют, чтобы читатель разобрал большое количество нематематической лексики, такой как имена, предметы, профессия и места.

Обучение математике всегда будет включать текстовые задачи, так как именно так можно сформулировать сложные математические ситуации. Такие стратегии, как «Три прочтения» , «С каждым разом все сильнее и яснее» и «Сравни и соедини », помогают проанализировать контекст проблемы и помочь учащимся сосредоточиться на одном аспекте языка за раз.

2: Сосредоточьтесь на математическом словаре

Изучение математики , поэтому гораздо больше, чем изучение математического словаря. Тратьте время на слова.

Для многоязычных учащихся словарный запас иногда может стать входом в математику. У учащихся могут быть существующие представления о таких словах, как продукт, время, и один, например, , и, обсуждая их, вы объединяете идеи как по языку, так и по математике. Ваши ученики будут помогать вам изучать другие языки, поскольку вы помогаете им изучать математику, симбиотические отношения.

Заранее проведите словарный запас как по математической лексике, так и по нематематической лексике, которая появляется в текстовых задачах, с которыми учащиеся будут сталкиваться на уроке. Обучение словарному запасу включает в себя больше, чем просто повторение определений. Это может включать в себя словарные игры, чтение математических книг и использование таких инструментов, как банки слов.

3: Связь со знакомыми контекстами
Что могло бы заинтересовать ваших учеников, независимо от языка? Подумайте о том, какими видами спорта они занимаются, какую музыку слушают, какие сериалы смотрят, какие блюда едят, какие праздники отмечают (и это лишь некоторые из них). Если вы можете опираться на культурные знания ваших учеников, вы можете открыть пути для их вовлечения, даже когда язык служит временным барьером.
Ищите способы изменить контекст текстовых задач и возможные мосты между математикой, которую они понимают, и содержанием, которое вы пытаетесь преподавать. Позиционируйте своих учеников как математически компетентных, независимо от того, насколько хорошо они могут сформулировать свои рассуждения на английском языке. Если можете, позвольте им составить свои собственные текстовые задачи! Тогда вы узнаете больше о том, что им знакомо.
ELL Strategies for Math: Language Production
4: Использование рамок предложений
Рамки предложений позволяют учащимся практиковаться в разговорной речи, но могут помочь им чувствовать себя менее запуганными. Они предлагают эшафот студентам, которые понимают математические идеи, но застревают в английской грамматике. Эшафот распространяется на студентов, чей родной язык английский, но, тем не менее, им трудно сформулировать математические идеи.
Используя фреймы предложений в классе, вы также способствуете расширению словарного запаса (см. Стратегия 2: Сосредоточьтесь на математическом словарном запасе). Это дает учащимся четкие контексты, в которых можно практиковать словарь, а сам словарь может быть частью структуры предложения, например, «Этот многоугольник (является/не является) четырехугольником, потому что _____».
Ищите рамки предложений, которые относятся как к уроку, так и к содержанию. Профессиональное обучение математике HMH включает в себя множество примеров, подобных приведенным ниже:
_____ (является/не является) _____, потому что _____.
Я могу сделать вывод, что _____.
Хотя _____ и _____ оба имеют _____, они разные, потому что _____.
Если _____, то _____ будет _____.
_____ является многоугольником, потому что _____ и _____.
5: Создайте пространство для общения с низкими ставками
Важно, чтобы учащиеся могли опробовать идеи вслух в среде с низкими ставками, прежде чем их попросят поделиться со всем классом. Ищите способы, с помощью которых учащиеся, которые еще мало участвуют, могут присоединиться к разговору. Например:
Задавайте вопросы, на которые учащиеся могут ответить с помощью жестов или рисунков.
Предоставьте учащимся рамки предложений, чтобы помочь им выразить свои мысли на английском языке.
Предложите учащимся попрактиковаться в обмене своими идеями в обсуждениях с партнерами по более низким ставкам или в небольших группах, прежде чем их попросят поделиться со всем классом.
Нет необходимости уменьшать сложность урока математики, даже если вы должны думать о сложности языка. Включите процедуры и структуры, которые помогут учащимся участвовать в дискуссиях и делиться своими идеями. Планируя обучение, задавайте себе вопросы, подобные приведенным ниже примерам, чтобы помочь учащимся участвовать в процессе:
Чьи идеи я буду записывать?
Как студенты будут выражать свои идеи?
Какие визуальные модели могут использовать учащиеся для выражения своих идей?
Когда я предоставлю рамки предложений?
Когда на уроке у учащихся есть время для самостоятельного мышления и обсуждения с партнером или небольшой группой?
По возможности поощряйте учащихся думать, писать и участвовать в математических разговорах на любом доступном им языке. Неразумно ставить перед вами задачу выучить другой язык, но давно прошли те времена, когда вам приходилось смотреть все слово за словом в словаре. Переводите письма с помощью Google Translate или, если в вашей школе есть возможность, поищите обучающее программное обеспечение, доступное на нескольких языках.
6: Используйте инструменты, визуальные модели и манипуляции
Важно помнить, что барьером является язык, не обязательно знания. Эти стратегии — не просто хорошая практика для многоязычных учащихся. Все учащиеся с рабочим зрением получают пользу от визуального обучения, и то же самое относится к физическому обучению с помощью манипуляций. Математика уникальна тем, как часто и насколько гибко она может использовать визуальные и физические модели. Тем не менее, когда учащийся говорит на нескольких языках, модели могут превратиться из лучших практик в критические математические каркасы.
При цифровом обучении грань между визуальными и физическими моделями стирается. На самом деле, для многих студентов цифровые модели особенно полезны. Некоторые учащиеся чувствуют себя более комфортно при использовании инструментов, когда они могут делать это самостоятельно и, возможно, анонимно.
Когда дело доходит до арифметики, учащиеся могут рисовать вычисления, используя алгоритмы и модели, которые работают, но являются новыми для вас. Арифметика попадает в эту серую зону между процедурной математикой и концептуальной математикой и, как таковая, подвержена региональным различиям.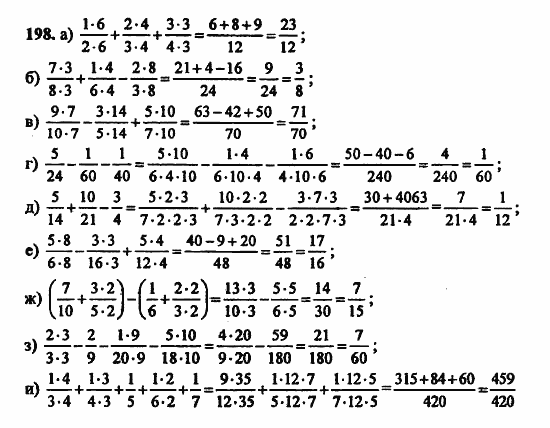 Только посмотрите, как «выглядит» дивизия для венесуэльского, американского и французского студента:
Как правило, учащиеся должны показать вам, что они знают. И прислушивайтесь к различиям! При сравнении различных способов деления (или умножения, сложения или вычитания) чисел, наряду с другими возможными культурными различиями, такими как способ записи чисел или рисование графиков, можно вести богатую дискуссию.
7: Сотрудничество с коллегами
Эта стратегия, возможно, является самой важной из всех и выходит за рамки простой помощи в языковом производстве. Это также помогает с пониманием; на самом деле, это помогает практически во всем! Только вы знаете роли в вашем сообществе, школе или округе. Есть ли услуги переводчика? Связи школы и сообщества? Преданные учителя английского языка для развития? Спросите своих коллег, что доступно, и используйте это!
Не забывайте и об инструкторах ELA. Неважно, в каком классе вы преподаете. Если вы преподаете на английском языке, то невозможно полностью отделить математический контент от английского. У нас нет «левого полушария» и «правого полушария», у нас есть просто мозг. Навыки, которые приходят в результате обучения чтению и письму на языке, также улучшают математические способности, и таким образом преподаватели ELA в вашей школе или округе могут внести ценный вклад в ваш класс.
Как помочь учащимся ELL в изучении математики
Поддерживая учащихся, изучающих английский язык, на уроках математики, мы часто не знаем, связана ли проблема с языковыми или математическими потребностями. Тем не менее, важно постоянно думать об активах, а не о дефиците. Класс, который в совокупности говорит на нескольких языках, — это культурная золотая жила!
***
Благодаря компонентам на испанском языке, многоязычным семейным письмам и руководствам по ELL математические решения HMH разработан с учетом многоязычных учащихся.
Связанные материалы
Алисса Фуллер
Преподаватель по математике; Дизайнер учебного процесса, HMH
20 октября 2022 г.
Д-р Кэри Снейдер
Руководитель писательской группы NGSS, доцент Портлендского государственного университета
12 октября 2022 г.
Дженнифер Прескотт
Форма Участник
07 октября 2022 г.
Объяснение ответов по математике: как помочь учащимся объяснить свое мышление
Вы когда-нибудь просили учащегося объяснить свой ответ по математике и получали пустой взгляд, быстрое изменение ответа или ответ: « I просто сделал это в своей голове» ? Честно говоря, каждый год мои ученики почти так начинают учебный год. Но благодаря целенаправленному обучению я могу заставить даже тех учеников с пустым взглядом объяснять свои ответы полными предложениями с математическим словарем к концу года.
Хотите посмотреть, как я это делаю? Продолжайте читать мои лучшие советы, чтобы ваши ученики объяснили свои ответы по математике.

В этот пост включены партнерские ссылки, если вы хотите приобрести упомянутые книги по профессиональному развитию.
1. Разговоры о числах
Разговоры о числах — отличный способ улучшить чувство чисел, заставить учащихся думать о математике по-новому и, конечно же, помочь им объяснить свои ответы. Если вы не знакомы с числовыми сообщениями, они имеют следующий формат:
Учитель размещает задачу или серию задач на диаграмме.
Учащиеся решают задачу в уме.
Учитель призывает учеников дать ответы и записывает все полученные ответы.
Учитель призывает учащихся объяснить, как они получили ответы.

Учащиеся делятся всеми стратегиями, которые они использовали для получения правильного ответа, которые учитель записывает и перефразирует по мере необходимости.
Этот учебный инструмент является мощным, поскольку учащиеся регулярно объясняют, как они получили свои ответы, и они регулярно слушают математические рассуждения и объяснения других учащихся.
Дополнительная литература: Number Talks by Sherry Parrish
2. Постановка задачи + запись или публикация стратегий и объяснений учащихся
Я использовал эту стратегию в своей комнате в течение многих лет, чтобы помочь своим ученикам обдумывать, решать и объяснять текстовые задачи. В основном, я ставлю словесную проблему или ситуацию. Мы читаем и обсуждаем проблему вместе, следя за тем, чтобы у всех учащихся была точка доступа или точка входа (в основном способ начать решение проблемы).
Студенты самостоятельно решают задачу, пока я хожу по комнате, создавая последовательность, чтобы поделиться работой студентов и объяснениями, которые затем проецируются на документ-камеру для просмотра всеми студентами. Видеть и слышать работы, мысли и объяснения других учеников очень полезно для всех моих учеников.
Дополнительная литература: Нажмите здесь, чтобы узнать больше об этой стратегии.
Если вам нужны текстовые задачи, чтобы решить задачу дня в вашем классе, нажмите здесь, чтобы увидеть мою задачу дня для 5-го класса (скоро будет 4-й класс).
3. Основы предложений
Основы предложений — отличный способ поддержать учащихся, особенно тех, кому трудно объяснить свои ответы или свое мышление. Вот мои основные предложения для объяснения ответов по математике.
Мой ответ… Я понял это…
Мой ответ… Чтобы получить ответ, я…
Мое решение… Я пришел к этому решению…
Чтобы получить ответ, я…
Сначала я…, Потом я…, Далее я…, Наконец, я…
Для начала я…

Первый шаг, который я сделал, был…
Эта проблема напомнила мне о…, поэтому я…
Я заметил…, поэтому я…
Я решил сложить/вычесть/умножить/поделить, потому что проблема…
Щелкните здесь или на изображении, чтобы загрузить копию этих основ предложений, которые помогут вашим учащимся объяснить свое математическое мышление. Их можно дать учащимся, чтобы они вклеили их в интерактивную математическую тетрадь в рамках урока по использованию стеблей. Их также можно превратить в якорную диаграмму.

Я также использую эти два примера, когда представляю основы предложения и рассказываю о том, как их использовать. Один из примеров объясняет ответ на текстовую задачу, а другой объясняет ответ на вычислительную задачу. Они находятся в той же загрузке, ссылка на которую приведена выше.
4. Обсуждение или обмен мнениями Ежедневно
Если учащиеся не рассказывают о том, как они решили проблему, или не объясняют свою работу, то, скорее всего, они не смогут написать об этом. Я ежедневно использую в своем классе «покажи и поговори» / «думай в паре», чтобы мои ученики говорили о математике.
В моем классе мы ежедневно обмениваемся устными объяснениями, а затем также записываем наши объяснения по крайней мере раз в неделю. Для этой цели я использую свой интерактивный блокнот с задачами по математике.
У меня есть задача по одному слову для каждого стандарта, поэтому я легко могу выполнять ее каждую неделю. Тот факт, что они размещены в наших интерактивных математических тетрадях, делает их отличным инструментом, к которому учащиеся могут обращаться.
Нажмите здесь, чтобы увидеть интерактивные задачи по математике, которые есть в моем магазине.
5. Моделируйте и перефразируйте
Когда вы обсуждаете математику со своими учениками, регулярно моделируйте, используя математический словарь для объяснения ответов. Если они не будут регулярно слышать правильный математический язык и словарный запас, то они не смогут использовать их сами.
В дополнение к моделированию перефразируйте ответы учащихся по мере необходимости, чтобы обеспечить ясность и точность. Вот какой язык вы можете использовать, когда перефразируете:
Я думаю, вы говорите… Это правильно?
Итак, ты… а потом ты… Верно?
Можете ли вы еще раз рассказать мне, как вы ________?
Можете ли вы повторить, как вы это сделали, но попробуйте использовать слова ___________ и ____________?
6.
Примеры для наставников
Мы постоянно используем тексты для наставников в наших обычных инструкциях по письму, и они так же хорошо помогают учащимся объяснять и писать по математике. Используйте примеры математических объяснений наставника, чтобы помочь учащимся увидеть то, что вы ожидаете, и помочь им сформулировать свои собственные объяснения.

Вот несколько способов собрать или создать примеры наставников для математических объяснений:
Создайте свои собственные примеры.
Используйте выпущенные примеры оценки состояния.
Поделиться текущими или предыдущими работами учащихся (с разрешения).
Щелкните здесь, чтобы загрузить два примера наставника, приведенные в Совете №3, которые показывают учащимся, как использовать основы предложений.
7. Концептуальное переобучение операций
Одна из основных причин, по которой учащиеся не могут объяснить свою работу по математике, заключается в том, что у них нет концептуального понимания того, что они делают. На самом деле я трачу довольно много времени на «обучение на уровне класса», возвращаясь к 4-му или даже 3-му классу и переучивая концепцию концептуальным способом. Иногда я немного отстаю в своем темпе, но могу ускориться позже, когда мои ученики намного быстрее осваивают навыки уровня своего уровня.
Концептуальное обучение операциям действительно помогает моим ученикам объяснить свои ответы, потому что они точно знают, почему они складывают, вычитают и т. д.
Чтобы узнать больше о том, как я делаю это с ситуациями по сравнению с ключевыми словами, нажмите здесь.
8. Word Bank
Я обнаружил, что мои ученики с трудом объясняли, почему они решили выполнить ту или иную операцию. Им очень помогло создание банка слов математических фраз для каждой операции. Вот пример:

Нажмите здесь, чтобы получить копию этого плаката по математике. Есть три версии, и каждая версия увеличивается в разнообразии и сложности.
Мне пришлось моделировать это несколько раз, прежде чем они смогли сделать это самостоятельно. Чтобы смоделировать это, я спрашивал студентов, какая из фраз лучше всего описывает, почему они выбрали эту операцию. Затем я бы попросил их сказать мне, почему эта фраза совпадает. После этого я моделировал то, что они сказали, в 1-2 предложениях, используя контекст слова «проблема» и фразу из таблицы.
Вот пример: я умножил, потому что мешков с конфетами было равных групп. Кроме того, проблема заключалась в запросе суммы, поэтому мне нужно было объединить равные группы . Пакеты были группами, и количество конфет в каждом пакете было одинаковым.
9. Разнообразие задач для объяснения: вычисления и текстовые задачи
Мои ученики практикуются в объяснении как вычислительных задач, так и текстовых задач. Обычно я начинаю с объяснения того, как они решили вычислительную задачу, а затем перехожу к объяснению текстовых задач. Если они не могут объяснить шаги, которые они предприняли для решения вычислительной задачи, то объяснение того, как и почему они решили задачу со словами, вероятно, станет для них огромной проблемой.
10. Объяснения партнеров
Еще один способ помочь учащимся, когда они только учатся объяснять свои ответы, используя сложную лексику и математический язык, — использовать объяснения партнеров. Попросите партнеров решить проблему или задачу вместе, а затем вместе объясните свой ответ. Вы даже можете дать им два разных цветных карандаша или маркера, чтобы они написали объяснения. Это позволит вам быстро проверить, какие партнеры предоставляют какую информацию в окончательном объяснении.
11. Задайте наводящие вопросы: Что вы сделали в первую очередь? Следующий?
Когда ваши ученики затрудняются, задавайте открытые вопросы, чтобы помочь им в объяснении. Вот некоторые из моих вопросов:
Что вы сделали в первую очередь?
Что ты сделал дальше?
Что заставило тебя это сделать?
Зачем ты это сделал?
Откуда вы знаете, что ваш ответ правильный?
Откуда ты это знаешь?
Какой математический словарь мы можем включить в наше объяснение?

Вопросы такого типа помогут учащимся подумать о своем мышлении и дадут им словесную практику с объяснением. И помните из совета № 4, если учащиеся не могут вербализовать свои объяснения, то, скорее всего, они не смогут их написать.
12. Встроить в математические центры.
Самый простой способ попрактиковать это — попросить их выбрать одну задачу или проблему, которую они решили для объяснения. Вы можете делать по одному на математический центр или по одному в день.
12. Регулярно говорите о математике в классе.
Лучший способ (оставленный напоследок) научить ваших учеников объяснять свои ответы по математике — это регулярно использовать и продвигать математические разговоры в классе. Я планирую написать новый пост на эту тему в будущем, но вы можете ознакомиться с этим предложением по дальнейшему чтению, если вам интересно узнать об этом сейчас.
Дополнительная литература: Преднамеренная беседа: как структурировать и вести продуктивные математические дискуссии
Помощь в переходе от устных объяснений к письменным
Вот мои основные стратегии, которые помогут учащимся перейти от устных объяснений к письменным.
1.) Пока учащийся объясняет свои мысли или свой ответ, записывайте основные ключевые слова, которые они произносят, в своего рода банк слов. Затем перескажите ученику, что вы слышали от него, и указывайте на каждое слово, когда вы его произносите. Наконец, попросите их записать свои мысли, используя некоторые или все ключевые слова, которые вы для них записали.

2.) Иногда мне приходится поддерживать сложность задач. Если я хочу, чтобы мои ученики действительно научились объяснять свои ответы, им должно быть достаточно комфортно с математикой, которую они выполняют. Для многих учеников работа над объяснением ответов при работе над сложной задачей на уровне класса может оказаться слишком сложной. Сначала помогите им научиться объяснять свои ответы с помощью навыков повторения, а затем перенести это в навыки и задачи уровня своего класса.
Я надеюсь, что эти предложения помогут вашим ученикам, когда они будут объяснять ответы и свои математические действия, а также размышлять над этими ответами.
No related posts.