Ответы по математике 5 класс сферы: ГДЗ Математика Бунимович 5 класс

Входная контрольная работа по математике 5 класс УМК «Сфера»

Входная контрольная работа Математика, 5 класс

Вариант 1.

1. Вычислите:

а) 1357 + 764 ; б) 316 – 128;

в) 340 · 205; г) 655 200 : 13 ;

2. Решите задачу:

В первый день бригада собрала 46 т картофеля, что в 2 раза меньше, чем во второй день. Сколько всего тонн картофеля было собрано за эти дни?

1. Решите уравнение: x – 18 = 42.

1. Решите задачу:

От одной станции в противоположных направлениях отправились два электропоезда. Скорость одного электропоезда равна 63 км/ч, а другого – 57 км/ч. Какое расстояние будет между ними через 2 часа?

1. Решите задачу:

Найдите площадь прямоугольника АВСD, если длина стороны АВ

равна 5 см, а длина стороны BС на 2 см больше.

Входная контрольная работа

Математика, 5 класс

Вариант 2.

1. Вычислите:

а) 1283+ 675; б) 246 – 178;

в) 280 · 305; г) 729 000 : 18 ;

2. Решите задачу:

В одной пачке 84 листа цветной бумаги, и в ней в 3 раза больше, чем во второй. Сколько всего листов цветной бумаги в двух пачках?

3. Решите уравнение: 39 – x =11.

4. Решите задачу:

Из пункта А в пункт В, расстояние между которыми равно 60 км,

одновременно выехали велосипедист и мотоциклист. Велосипедист едет

со скоростью 12 км/ч, а мотоциклист – 60 км/ч. На сколько часов позже велосипедист приедет в пункт В, чем мотоциклист?

5.Решите задачу:

Найдите площадь прямоугольника АВСD, если сторона АВ=10 м, а

сторона ВС в 2 раза меньше.

Входная контрольная работа

Математика, 5 класс

Вариант № 3

1.Вычислите:

а) 2147 + 739; б) 223 – 168;

в) 260 · 805; г) 54 900 : 18 ;

2. Решите задачу:

Учебник стоит 305 р., а ручка на 196 р. дешевле. Купили учебник и три

ручки. Сколько стоит покупка?

3.Решите уравнение: y 27 48

4. Решите задачу:

С одной пристани в противоположных направлениях отправились два катера. Скорость первого катера равна 23 км/ч, а второго – 37 км/ч. Какое расстояние будет между ними через 2 часа?

5.Решите задачу:

Ширина прямоугольника 16 мм, и она на 4 мм меньше длины.

Вычислите периметр и площадь прямоугольника.

Входная контрольная работа

Математика, 5 класс

Вариант № 4

1.Вычислите:

а) 3528 + 289; б) 328 – 179;

в) 150 · 607 г) 48 700 : 25 ;

2. Решите задачу:

Справочник стоит 280 р., а ручка на 176 р. дешевле. Купили справочник и две ручки. Сколько стоит покупка?

3.Решите уравнение: y 7 

4. Решите задачу:

С двух пристань навстречу друг другу отправились два катера. Скорость первого катера равна 24 км/ч, а второго – 32 км/ч. Какое расстояние будет между ними через 3 часа?

5.Решите задачу:

Ширина прямоугольника 25 мм, и она на 6 мм меньше длины.

Вычислите периметр и площадь прямоугольника.

Открытый урок по математике «Геометрические тела и их изображение». 5-й класс

Тип урока: изучение нового материала.

УМК: Математика. Арифметика. Геометрия. 5 класс: учеб. для общеобразоват. учреждений / Е.А.Бунимович и др. Рос.акад. наук, Рос. Акд. образования, изд-во «Просвещение». — М.:Просвещение, 2013.

Цель урока:

• Познакомить учащихся с такими телами, как цилиндр, конус, шар;
• Сформулировать представление о многогранниках;
• Научить распознавать многогранники и их элементы по проекционному чертежу;
• Рассмотреть применение многогранников в различных сферах жизни.

Задачи урока:

• Формирование пространственных представлений учащихся;
• Развитие умения наблюдать, рассуждать по аналогии;
• Развитие интереса к предмету через использование информационных технологий.

Цели урока:

• образовательная – обобщение и развитие знаний обучающихся о геометрических телах группы многогранников и их свойствах, формирование навыка применения полученных знаний в жизненных ситуациях.
• развивающая – развитие логического мышления, познавательного интереса к предмету, самостоятельности; развитие навыка целеполагания, читательских компетенций, учить сравнивать и обобщать изучаемые факты и понятия; учить анализировать ответы товарищей, понимать свои ошибки.
• воспитательная  – формирование морально-этической стороны личности, эстетического сознания, научной эстетики; тренировка стрессоустойчивости.

Задачи:

• применять знания о многогранниках, уметь выделять данный тип из многообразия геометрических тел, определять их общие свойства, читать их пространственные изображения и рисовать их на плоскости;
• умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи; понимать смысл поставленной задачи;
• слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, интегрироваться в группу сверстников и строить продуктивное взаимодействие, воспитывать ответственность и аккуратность;
• развивать умение анализировать, сравнивать, обобщать, делать выводы, самостоятельно ставить цели, развивать внимание, формировать коммуникативную компетенцию учащихся;
• выбирать способы решения задач в зависимости от конкретных условий; рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности.

Планируемые результаты обучения:

• Предметные: различать многогранники из многообразия геометрических тел; верно  использовать в речи термины: геометрическое тело, многогранник, поверхность, грань, ребро, перспектива; находить составные части многогранников, определять их число, читать пространственные изображения.
  Слушать собеседника и вести диалог; работать в паре и группе; излагать и аргументировать свою точку зрения; оценивать себя и товарищей.
• Личностные: формирование познавательных интересов, интеллектуальных и творческих способностей обучающихся; самостоятельность в приобретении новых знаний и практических умений; креативность мышления, инициатива, находчивость, активность при решении математических задач; воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения.
• Метапредметные: умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни; овладение навыками самостоятельного приобретения новых знаний, организации учебной деятельности, постановки целей, планирования, самоконтроля и оценки результатов своей деятельности, умениями предвидеть возможные результаты своих действий.

Ход урока

1. Организационный момент. СЛАЙД 1

Проверить готовность класса к уроку, настроить учащихся на деловой ритм.

— Ребята! Я рада вас видеть сегодня на уроке в хорошем настроении.

Посмотрите друг другу в глаза, улыбнитесь, глазками пожелайте товарищу хорошего рабочего настроения на уроке.

— Я вам желаю сегодня хорошей работы.

2. Актуализация опорных знаний.

Ребята, отгадайте ребусы. СЛАЙД 2-5

Геометрия

Сторона

Фигура

Вершина

— Правильно. 

— А  как,  вы,  думаете,  почему  именно  эти  слова я зашифровала?

— Молодцы, мы начинаем изучать новую главу, в ней представлен геометрический материал.

— Ребята, у вас на столах представлены геометрические фигуры. Разделите их на две группы.

• По какому признаку вы разделили фигуры? (плоские и объемные или фигуры на плоскости и фигуры в пространстве)
• Какие фигуры мы уже рассматривали на уроках математики в этом учебном году и хорошо с ними знакомы? (многоугольники).

—  Как вы думаете, ребята, о чём мы будем говорить сегодня на уроке? (о пространственных фигурах или геометрических телах)

3. Постановка целей и задач урока

• Сегодня на уроке мы будем изучать «Геометрические тела». Все геометрические тела обладают неповторимым совершенством и красотой. Сегодня на уроке мы узнаем и увидим много интересного.

— А что бы вы хотели узнать о них и чему научиться на уроке? (Знать название и свойства, составные элементы этих тел, уметь их распознавать, обозначать)
(СЛАЙД 6 Тема урока и задачи)

4. Первичное усвоение новых знаний.

Нас окружает множество предметов, но математиков интересуют лишь форма предметов и их размеры, поэтому вместо предметов они рассматривают геометрические тела. Вы, конечно, знаете уже некоторые геометрические тела, как они называются? СЛАЙД 7(изображение фигур)

Интересно происхождение названий геометрических тел. Выяснять, почему они так называются, будут следующие ученики ФИ (планшет, компьютер, энциклопедия) Работа с научным текстом, самостоятельное добывание знаний.

Заполните таблицу. (СЛАЙД 8)

Название	Что обозначает
КОНУС
ЦИЛИНДР
ШАР
СФЕРА
ПИРАМИДА

Для того чтобы больше узнать о геометрических телах мы воспользуемся учебником. Работать будете самостоятельно. Источником знаний у вас будет учебник,
а путеводителем для вас послужит рабочая карта урока.

Откройте учебники с. 186. Прочитайте фрагмент 1-2 с карандашом в руках.

Отмечаем на полях учебника значками в соответствии с обозначениями:

Прием «Инсерт» (СЛАЙД 9)

Чтение текста с пометками

+ я это знал

— я этого не знал

! это меня удивило

? хотел бы знать подробнее

Обсуждаем кратко и заполняем таблицу рабочей карты.

Задание 1. Заполните таблицу в соответствии с заданием, данным в первом столбце

Напишите общее название для всех пространственных фигур
Напишите название каждой фигуры в отдельности
Укажите основные характеристики поверхности каждой фигуры (из каких плоских фигур состоит)
Отметьте знаком «+» фигуры, поверхность которых состоит не только из плоских фигур
Приведите примеры объектов, чей вид напоминает данную фигуру
Дайте названия группам фигур и сформулируйте определение соответствующих понятий

Самопроверка по слайду (верные ответы отмечают +, количество + переносят в оценочный лист) СЛАЙД 10

«Тела вращения» СЛАЙД 11

Задание 2.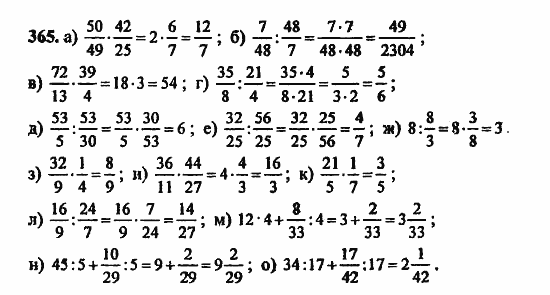 Среди геометрических тел, изображенных на рисунке, выберите многогранники и запишите их номера:__________________

Взаимопроверка слайд  (верные  ответы  отмечают  +, количество + переносят в оценочный лист)

СЛАЙД 12

Задание 3. Подпишите названия выделенных элементов многогранника.

Взаимопроверка — доска (верные ответы отмечают +, количество + переносят в оценочный лист).

Итак, ребята, сделаем вывод.

Вершины — это точки.

Ребра — отрезки, соединяющие эти точки (вершины).

Грани — это многоугольники.

УСТНО. Возьмите модели квадрата и треугольника.

1. Давайте посчитаем, чему равно количество вершин и сторон у многоугольника? (ОНИ МЕЖДУ СОБОЙ РАВНЫ)
2. Возьмите модели куба и пирамиды. Чему равно число вершин и число граней у многогранника?

(ОНИ МЕЖДУ СОБОЙ МОГУТ БЫТЬ НЕРАВНЫМИ).

ВЫВОД: у многоугольника столько же вершин, сколько сторон, а у многогранника число вершин и число граней не обязательно одинаково.

5. Закрепление новых знаний и способов действий.

Ребята, давайте поупражняемся в подсчёте граней, рёбер, вершин многогранников. Обратить внимание, что

Вершины — это точки.

Ребра — отрезки, соединяющие эти точки (вершины).

Грани — это многоугольники.

Задание 4. Рассмотрите рисунок 10.2 учебника. Охарактеризуйте каждый многогранник по плану. Каждый ряд определяет по две фигуры.

План	а)	б)	в)	г)	д)	е)
Число граней и их форма
Число ребер
Число вершин

 
— Сделайте вывод о соответствии числа вершин и числа сторон.

Ответы детей. Ещё раз обратить внимание вершины — точки, рёбра — отрезки, грани — многоугольники.

Физкультминутка

Вы, наверное, устали?
Ну, тогда все дружно встали.
Вверх ладошки! Хлоп! Хлоп!
По коленкам – шлёп, шлёп!
По плечам теперь похлопай!
Мы осанку исправляем
Спинки дружно прогибаем
Вправо, влево мы нагнулись,
До носочков дотянулись.
Плечи вверх, назад и вниз.
Улыбайся и садись!

— Открываем учебник № 673 стр. 188, проверка по слайду.

Задание 5. А теперь обратная работа, зная количество граней, определите фигуру. Тренажёр № 242 с 104. ВЗАИМОПРОВЕРКА (ответы за доской).

Задание 6. Пришло время самим сделать многогранник. У вас на столах есть деревянные палочки, пластилин. Используйте все свои знания и фантазию, сделайте каркасную модель одного из многогранников. В этом вам поможет рис 10. 2 на странице 186.

Выставка моделей.

— А теперь проверим, как усвоили тему урока.

Тест на закрепление.

Продолжите уточняющие вопросы, запишите вывод в тетради. (Работаем с текстовыделителями)

1. Правильно ли я понял, что все пространственные фигуры, с которыми мы познакомились на уроке называют (геометрическими телами).
2. Правильно ли я понял, что геометрические тела делятся на две группы: (многогранники  и тела вращения).
3. Правильно ли я понял, что поверхность многогранника состоит из (многоугольников).
4. Правильно ли я понял, что поверхность каждого геометрического тела разбивает пространство на (внутреннюю и внешнюю области).
5. Правильно ли я понял, что поверхностью шара называется (сфера).

При наличии времени выполнить проверку. Ответы за доской.

6. Подведение итогов.

— Сегодня мы с вами на уроке познакомились с предметами, которые окружают нас в повседневной жизни.

— Назовите наиболее часто встречающиеся вам многогранники (куб, конус, шар, пирамида, цилиндр).

— В реальной жизни приведите примеры многогранников?

СЛАЙД 8.

Где нам может пригодиться знание о геометрических телах?

Сегодня на уроке
Вы искали и творили,
Знания новые открыли,
Научились их применять,
Теперь задания легко вам выполнять!

— Большое спасибо всем за работу на уроке!

7. Рефлексия. Ассоциативный куст.

Выделить в каждом столбике нужное.

«Для меня сегодняшний урок…»

Урок	Я на уроке	Итог урока
Интересно	Работал	Понял материал
Скучно	Отдыхал	Узнал больше, чем знал
Безразлично	Помогал другим	Не понял

8. Домашнее задание.

Рубрика «Вопросы и задания» №1,2. Кроссворд.

ОЦЕНКИ ЗА РАБОТУ

9. Список использованной литературы.

1. Математика. Арифметика. Геометрия, 5 класс: книга для учителей, ведущих преподавание по учебным комплектам «Математика, 5» под редакцией Е.А.Бунимович, Г.В.Дорофеева (М.: Просвещение, 2010).
2. Справочник по математике.
3. Энциклопедия Кирилла и Мефодия. Электронная версия.

10. Интернет-ресурсы.

1. http: //nips. riss-telecom. ru/poli/
2. http: //www. uchportal. ru
3. http://festival. 1 september.ru/articles/503254/
4. http://www.ikt.oblcit.ru/8/perestoronina/urok
5. http://www.openclass.ru/node/2084
6. http://nips.riss-telecom.ru/poli/

Объяснение урока: Объемы сфер

В этом объяснении мы научимся находить объемы сфер и решать задачи, в том числе ситуации из реальной жизни.

Напомним, что в формулах вычисления площади и длины окружности мы встречали специальная математическая константа 𝜋(=3,14159…). Мы произносить эту греческую букву так же, как слово пирог , и важно помнить что оно просто представляет собой число, для которого мы иногда используем более простые приближения 3.14 или 227. Ввиду этого, может быть, и неудивительно, что мы встречаем 𝜋 снова, когда мы переходим к трехмерной задаче вычисления объем шара.

Формула: Объем сферы

Объем 𝑉 сферы радиусом 𝑟 определяется выражением формула 𝑉=43𝜋𝑟.

Поскольку 43 и 𝜋 — это просто числа, это означает, что пока мы знаем радиус сферы, мы всегда можем применить эту формулу, чтобы найти ее объем. Давайте начнем с рассмотрения примера с диаграммой.

Пример 1. Нахождение объема сферы по ее радиусу

Определите объем сферы, дав ответ с точностью до двух знаков после запятой. места.

Ответ

Из диаграммы видно, что сфера имеет радиус 6,3 см. Ссылаясь на формулу 𝑉=43𝜋𝑟, где 𝑉 — объем и 𝑟 — радиус сферы, можно заменить 𝑟=6,3 в правую часть, чтобы получить 𝑉=43×𝜋×(6,3)=1047,394…. 

Следовательно, объем сферы, округленный до двух знаков после запятой, равен 1‎ ‎047,39. Поскольку радиус был указан в сантиметрах, это объем в кубических сантиметрах; в объем сферы 1‎ ‎047.39см ³ до двух знаков после запятой места.

Обратите внимание, что, поскольку 𝜋 — бесконечное десятичное число, мы обычно имеем чтобы округлить ответ, показанный на нашем калькуляторе. По этой причине некоторые вопросы требуют ответы должны быть даны с точки зрения 𝜋. А также быть более аккуратным, чтобы выразить, эти ответы имеют то преимущество, что они точны.

Пример 2. Вычисление объема сферы в единицах Пи

Сфера имеет диаметр 18 см. Работайте над объемом сферы, давая свой ответ с точки зрения 𝜋.

Ответ

Здесь нам дан диаметр сферы, 18 см, что в два раза больше радиус. Теперь вспомним формулу 𝑉=43𝜋𝑟, где 𝑉 — объем сферы, а 𝑟 — радиус. Чтобы применить эту формулу для расчета объема, нам сначала нужно вычислить радиус, поэтому мы уменьшите диаметр вдвое, чтобы получить 𝑟=18÷2=9. Затем, заменив 𝑟 в формуле имеем 𝑉=43×𝜋×9.

Обратите внимание, что поскольку радиус 9, кратно знаменателю, 3, мы можем разложить 9 как 9×9 и переупорядочить выражение на правая часть до 43×9×𝜋×9.

Затем это упрощается до 4×3×𝜋×9=4×3×𝜋×81=4×3×81×𝜋=972𝜋.

Нет необходимы дальнейшие вычисления, потому что этот ответ кратен 𝜋. Поскольку диаметр дан в сантиметрах, объем шара должен быть 972 см ³ .

Формула объема сферы содержит только две переменные, 𝑉 и 𝑟. Это означает, что если нам дан объем шара, то мы можем всегда работайте в обратном направлении, чтобы найти его радиус. После того, как мы определили радиус, при необходимости мы можем удвойте это значение, чтобы получить диаметр. В следующем примере показано, как изменить формулу для решения этого типа проблемы.

Пример 3. Нахождение диаметра сферы по ее объему

Найдите диаметр сферы, объем которой равен 113,04 см ³ . (Брать 𝜋=3,14).

Ответ

Сначала вспомним формулу для вычисления объема 𝑉 сферы из радиус 𝑟: 𝑉=43𝜋𝑟.

Объем 𝑉=113,04 вместе с приближением 3,14 для 𝜋. Подставляя оба этих значения в формулу, получаем 113,04=43×3,14×𝑟, что упрощается до 113,04=31475×𝑟.

Умножение обеих сторон на 75 дает нам 8478=314×𝑟,, а деление на 314 дает нам 27=𝑟.

Чтобы найти 𝑟, нам нужно взять кубические корни из обеих частей: √27=√𝑟, так 3=𝑟, что совпадает с 𝑟=3.

Единицей объема является кубический сантиметр, поэтому радиус выражается в сантиметрах. Удвоение стоимости радиуса, находим, что диаметр сферы равен 6 см.

Обратите внимание, что в приведенном выше примере мы подставили значение для 𝑉, объем сферы, в формулу 𝑉=43𝜋𝑟, а затем переставить чтобы найти значение радиуса, 𝑟. Альтернативный подход заключается в перестановке формула, чтобы сделать 𝑟 предметом, а затем заменить 𝑉 напрямую. Здесь мы обрисовываем в общих чертах, как получить эту формулу для радиуса в с точки зрения объема.

Начиная с исходной формулы 𝑉=43𝜋𝑟 и переписывая правую часть, чтобы включить знаки умножения, мы имеем 𝑉=43×𝜋×𝑟.

Умножая обе части на 3, мы получаем 3𝑉=4×𝜋×𝑟, и деля на 4𝜋 дает 3𝑉4𝜋=𝑟.

Наконец, возьмем кубические корни с обеих сторон: что является нашей формулой для радиуса. Если бы мы подставили 𝑉=113,04 в этой формулы вместе с приближением 3.14 для 𝜋, то мы получили бы 𝑟=3, то же значение радиуса, что и в предыдущем пример.

Формула: Радиус сферы при заданном ее объеме

Радиус 𝑟 сферы объемом 𝑉 определяется выражением формула 𝑟=3𝑉4𝜋.

При разрезании сферы плоскостью, проходящей через ее центр, пересечение сфера и плоскость называется большим кругом . Другой способ думать об этом состоит в том, что большой круг сферы — это круг, который делит сферу ровно пополам, образуя два полушария. Это означает, что радиус большого круга будет также радиусом сферы (а также каждого полушария).

Мы можем использовать информацию о больших кругах для расчета объема соответствующего сферы или полушария. (Обратите внимание, что, поскольку объем полушария ровно вдвое меньше объема соответствующей сферы, мы можем настроить выражение 43𝜋𝑟 для объем сферы радиусом 𝑟 до 23𝜋𝑟 для объема полушария радиуса 𝑟.)

Пример 4: Расчет объема полушария

Рассчитайте объем полушария, давая ответ с точностью до двух десятичных знаков места.

Ответ

Диаграмма включает большой круг с радиусом 8,3 м. А теперь вспомните формулу 𝑉=43𝜋𝑟, где 𝑉 — объем сфера, а 𝑟 — ее радиус. Так как радиус большого круга также радиус соответствующей сферы, затем подставив 𝑟=8,3 в формулы, мы имеем, что объем этой сферы 𝑉=43×𝜋×(8,3)=2395,095…. 

Чтобы вычислить объем вышеприведенного полушария, мы делим этот ответ на 2, что дает 1197,547…. Радиус большого круга был указан в метрах, поэтому полушарие должно иметь объем. 1‎ ‎197,55 м ³ округлить до двух знаков после запятой места.

Описанный выше метод легко адаптировать для нахождения других частей сферы. За Например, если нас попросят найти объем трети сферы радиуса 𝑟, мы можно принять выражение 43𝜋𝑟 для объема сферы радиус 𝑟 и умножьте его на 13. Это говорит нам, что объем трети сферы радиуса 𝑟 равен 13×43𝜋𝑟=49𝜋𝑟.

Наконец, мы иногда встречаем вопросы с реальным контекстом, которые даются как слово задачи, без схем. В таких случаях важно внимательно прочитать вопрос и выяснить именно то, что нас просят найти. Сделав это, мы должны быть в состоянии применить формулу, возможно, более одного раза, чтобы получить наш ответ.

Пример 5. Решение текстовой задачи с объемами сфер

Металлическая сфера радиусом 14,1 см была расплавлена ​​и разделена на 4 равные части. сферы. Найдите радиус одной из меньших сфер, давая ответ на вопрос ближайший сантиметр.

Ответ

Наш первый шаг — определить общий объем металла в исходной сфере. Отзывать что объем 𝑉 сферы радиуса 𝑟 определяется выражением формула 𝑉=43𝜋𝑟. Применяя эту формулу с 𝑟=14,1, получаем 43×𝜋×(14,1)=11742,104….

Разделив этот общий объем на 4, мы вычисляем объем каждой меньшей сферы как 2935.526… см ³ .

Затем мы применяем формулу к одной из меньших сфер, используя объем для работы соответствующий радиус: 2935,526…=43×𝜋×𝑟.

Умножая обе части на 3, получаем 8806,578…=4×𝜋×𝑟, и деление на 4𝜋 дает 700,805…=𝑟.

Наконец, мы берем кубические корни с обеих сторон, чтобы получить 𝑟=8,882…, что дает ответ 9 при округлении до ближайшего сантиметра. Следовательно, длина радиус одной из меньших сфер равен 9 см.

Давайте закончим повторением некоторых ключевых понятий из объяснения.

Ключевые точки

• Объем 𝑉 сферы радиуса 𝑟 определяется формулой формула 𝑉=43𝜋𝑟.
• Поскольку формула содержит только две переменные, 𝑉 и 𝑟, если нам дан объем сферы, мы всегда можем вернуться к найдите его радиус (или диаметр).
• Большой круг сферы — это круг, который делит сферу ровно пополам, образуя два полушария. Большой круг и соответствующая ему сфера имеют один и тот же центр и радиус.
• Формулу можно использовать для нахождения объема полушария или других частей сфере, в том числе в реальных вопросах, представленных в виде текстовых задач.

5.5.5: Цилиндры, конусы и сферы

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

36047

• Иллюстративная математика
• Ресурсы OpenUp

Урок

Найдем объем фигур.

Упражнение \(\PageIndex{1}\): Регулировка сферы

Четыре ученика вычислили объем сферы радиусом 9 сантиметров и получили четыре разных ответа.

• Хан думает, что это 108 кубических сантиметров. 9{3}\пи\). Каково значение \(r\) для этой сферы? Объясните откуда вы знаете.

  Упражнение \(\PageIndex{3}\): Пробел в информации: Неизвестные размеры

  Ваш учитель даст вам либо карту задач , либо карту данных . Не показывайте и не читайте свою карточку своему партнеру.

  Если учитель дает вам карточку с задачами :

  1. Молча прочитайте свою карточку и подумайте, какая информация вам нужна, чтобы ответить на вопрос.
  2. Попросите вашего партнера предоставить конкретную информацию, которая вам нужна.
  3. Объясните, как вы используете информацию для решения проблемы.
     Продолжайте задавать вопросы, пока у вас не будет достаточно информации для решения проблемы.
  4. Поделитесь карточкой с проблемой и решите проблему самостоятельно.
  5. Прочтите карту данных и обсудите свои рассуждения.

  Если ваш учитель дает вам карту данных :

  1. Прочитайте вашу карту молча.
  2. Спросите своего партнера «Какая конкретная информация вам нужна?» и подождите, пока они запросят информацию у .
     Если ваш партнер запрашивает информацию, которой нет на карточке, не делайте за него расчеты. Скажите им, что у вас нет этой информации.
  3. Прежде чем делиться информацией, спросите: « Зачем вам эта информация? » Выслушайте рассуждения вашего партнера и задайте уточняющие вопросы.
  4. Прочитать карту проблем и решить проблему самостоятельно.
  5. Поделитесь картой данных и обсудите свои рассуждения.

  Сделайте здесь паузу, чтобы учитель мог просмотреть вашу работу. Попросите у учителя новый набор карточек и повторите задание, поменявшись ролями со своим партнером.

  Упражнение \(\PageIndex{4}\): Правильная подгонка

  Рисунок \(\PageIndex{2}\)

  Цилиндр диаметром 3 сантиметра и высотой 8 сантиметров наполнен водой. Решите, какие фигуры, описанные здесь, если таковые имеются, могут удержать всю воду из цилиндра. Объясните свои рассуждения.

  1. Конус высотой 8 сантиметров и радиусом 3 сантиметра.
  2. Цилиндр диаметром 6 сантиметров и высотой 2 сантиметра.
  3. Прямоугольная призма длиной 3 сантиметра, шириной 4 сантиметра и высотой 8 сантиметров.
  4. Сфера радиусом 2 сантиметра.

  Готовы ли вы к большему?

  Измученная жаждой ворона хочет поднять уровень воды в цилиндрическом сосуде, чтобы она могла дотянуться до воды клювом.

  • Контейнер имеет диаметр 2 дюйма и высоту 9 дюймов.
  • Уровень воды в настоящее время составляет 6 дюймов.
  • Ворона может добраться до воды, если она находится на расстоянии 1 дюйма от верха контейнера.

  Чтобы поднять уровень воды, ворона кладет в емкость шарообразные камешки. {3}\приблизительно 33,51\)).

  Практика

  Упражнение \(\PageIndex{5}\)

  Шарик мороженого имеет диаметр 3 дюйма. Какой высоты должен быть рожок для мороженого того же диаметра, чтобы в него поместилось все мороженое?

  Упражнение \(\PageIndex{6}\)

  Рассчитайте объем следующих фигур с заданной информацией. Для первых трех вопросов дайте каждый ответ как в терминах \(\pi\), так и с помощью \(3.14\) для аппроксимации \(\pi\). Не забудьте включить единицы измерения.

  1. Сфера диаметром 6 дюймов
  2. Цилиндр высотой 6 дюймов и диаметром 6 дюймов
  3. Конус высотой 6 дюймов и радиусом 3 дюйма
  4. Как связаны между собой эти три тома?

  Упражнение \(\PageIndex{7}\)

  Раздатчик надувных шариков с монетоприемником имеет большую стеклянную сферу, в которой находится множество сферических шариков. Большая стеклянная сфера имеет радиус 9 дюймов. Каждый надувной шарик имеет радиус 1 дюйм и находится внутри дозатора.

  No related posts.