Презентация на тему «Отрезок. Длина отрезка» 5 класс | Презентация к уроку по математике (5 класс) на тему:
Слайд 1
ОТРЕЗОК. ДЛИНА ОТРЕЗКА. Леонова Е.Д. 5 классСлайд 2
ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ ТОЧКА ЛИНИЯ ОТРЕЗОК ТОЧКА ОТРЕЗОК
Слайд 3
Читают « Отрезок АВ» Точки А и В — концы отрезка Обозначают АВ или ВА
Слайд 4
АВ = 1 см (длина отрезка АВ равна 1 см) На MN помещается три отрезка АВ MN = 3 см. На EF помещается четыре отрезка АВ EF = 4 см. РК = 17 мм Измерить отрезок означает подсчитать сколько единичных отрезков в нем помещается
Слайд 5
Если на отрезке АВ отметить точку С , то длина отрезка равна сумме длин отрезков АС и СВ АВ = АС + СВ Два отрезка называют РАВНЫМИ, если они совпадают при наложении. Пишут: АВ = CD Равные отрезки имеют равные длины Длину отрезка АВ называют РАССТОЯНИЕМ между точками А и В.
Слайд 6
Если конец первого отрезка совпадает с концом второго отрезка, конец второго отрезка совпадает с концом третьего отрезка и т. д., то отрезки образуют ЛОМАНУЮ Являются ли следующие фигуры ломаными? (Если нет , то почему?)
д., то отрезки образуют ЛОМАНУЮ Являются ли следующие фигуры ломаными? (Если нет , то почему?)
Слайд 7
ЗАМКНУТЫЕ ЛОМАННЫЕ
Слайд 8
Отрезок ВС на 3 см меньше отрезка АВ, длина которого равна 8 см. найдите длину отрезка АС. Задача
Слайд 9
Имеем: ВС = 8 – 3 = 5 (см) АС = АВ + ВС. Отсюда АС = 8 + 5 = 13 (см) Ответ: 13 см. Решение:
Слайд 10
Известно, что МК = 24 см, NP = 32 см, МР = 50 см. Найдите длину отрезка NK . Задача
Слайд 11
MN = MP – NP M N = 50 – 32 = 18 (см) NK = MK – MN NK = 24 -18 = 6 (см) Ответ: 6 см. Решение:
Слайд 12
Испокон веков люди пользовались такой естественной мерой длины, как шаг . Многие народы применяли меру длины дальность полета стрелы . Большие расстояния измеряли дневными переходами . Также использовали «измерительные приборы», которые были под рукой: дюйм, ладонь, пядь, локоть, фут, косая сажень и т.д. МЕРЫ ДЛИНЫ В СТАРИНУ
Слайд 13
Практическая работа. Когда нет измерительного прибора, расстояние можно измерять «голыми руками». Для этого полезно знать: а) расстояние между концами большого и указательного пальцев, когда они раздвинуты; б) ширину своей ладони; в) расстояние между концами раздвинутых среднего и указательного пальцев; г) длину своего указательного пальца; д) расстояние между концами большого пальца и мизинца, когда они широко расставлены. Задание 1) Измерьте с помощью линейки размеры своей руки. 2) Измерьте рукой ширину парты. 3) Проверьте полученный результат с помощью линейки
Для этого полезно знать: а) расстояние между концами большого и указательного пальцев, когда они раздвинуты; б) ширину своей ладони; в) расстояние между концами раздвинутых среднего и указательного пальцев; г) длину своего указательного пальца; д) расстояние между концами большого пальца и мизинца, когда они широко расставлены. Задание 1) Измерьте с помощью линейки размеры своей руки. 2) Измерьте рукой ширину парты. 3) Проверьте полученный результат с помощью линейки
Слайд 14
? 1.Сколько существует отрезков, концами которых являются две данные точки? 2.Как обозначают отрезок? 3.Какие вы знаете единицы длины? 4.Объясните,что означает измерить длину отрезка? 5.Каким свойством обладает длина отрезка? 6.Какие отрезки называют равными? 7.Какой из двух неравных отрезков считают большим? 8.Что называют расстоянием между точками А и В? 9.Что называют длиной ломаной?
§3. Отрезок. Длина отрезка (Страницы 8,9,10,11)
Главная › 5 класс › Математика › Рабочая тетрадь по математике 1 часть Мерзляк Полонский Якир 5 класс ПОВТОРЯЕМ ТЕОРИЮ16.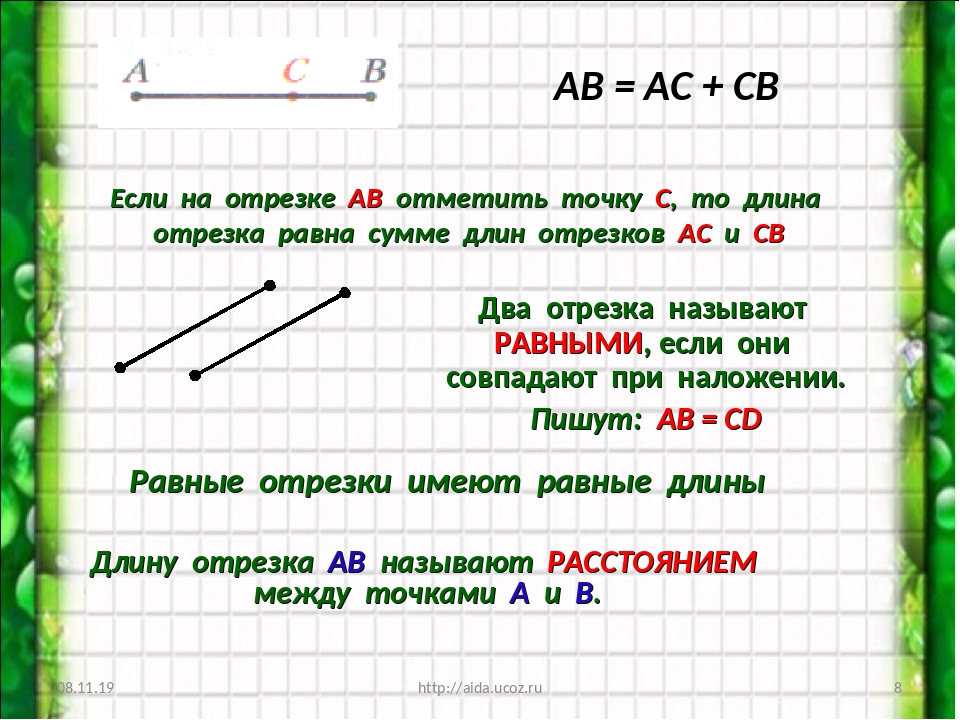 Заполните пропуски.
Заполните пропуски.
1) Точка и отрезок являются примерами геометрических фигур.
2) Измерить отрезок означает подсчитать, сколько единых отрезков в нем помещается.
3) Если на отрезке АВ ометить точку С, то длинна отрезка АВ равна сумме длин отрезков АС +СВ
4) Два отрезка называют равными, если они совпадают при наложении.
5) Равные отрезки имеют равные длины.
6) Расстоянием между точками А и В называют длину отрезка АВ.
17. Обозначьте отрезки, изображенные на рисунке, и измерьте их длины.
AB, ВC, СD, АD, АС, ВD
19. Запишите все отрезки, изображенные на рисунке. 20. Начертите отрезки СК и АD так, чтобы СК=4 см 6 мм, АD=2 см 5 мм.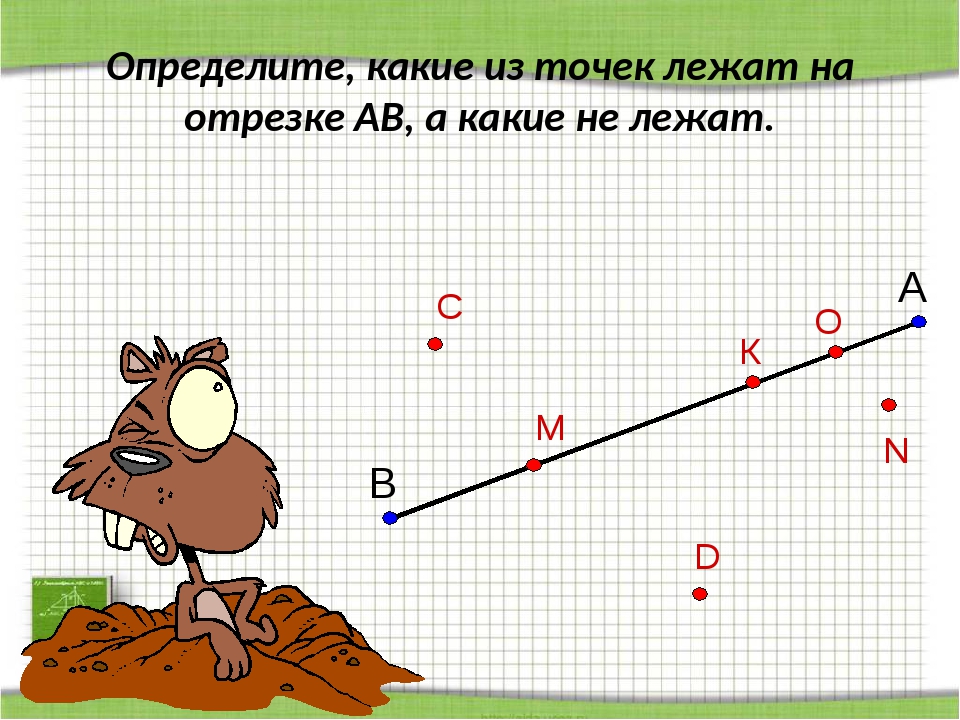 21. Начертите отрезок ВЕ, длина которого равна 5 см 3 мм. Отметьте на нем точку А так, чтобы ВА = 3 см 8 мм. Какова длина отрезка АЕ?
21. Начертите отрезок ВЕ, длина которого равна 5 см 3 мм. Отметьте на нем точку А так, чтобы ВА = 3 см 8 мм. Какова длина отрезка АЕ?АЕ=ВЕ-ВА= 5 см 3 мм — 3см 8мм = 1 см 5мм
22. Выразите данную величину в указанных единицах измерения. 23. Запишите звенья ломаной и измерьте их длины (в миллиметрах). Вычислите длину ломаной. 24. Отметьте точку В, расположенную на 6 клеток левее и на 1 клетку ниже точки А; точку С, расположенную на 3 клетки правее и на 3 клетки ниже точки В; точку D, расположенную на 7 клеток правее и на 2 клетки выше точки С. Соедините последовательно отрезками точки А, В, С и D.Образовалась ломаная АВСD, состоящая из 3 звеньев.
25. Вычислите длину ломаной, изображенной на рисунке.а) 5*36 = 180 мм
б) 3*28 = 84 мм
в) 10*10+15*4 = 160 мм
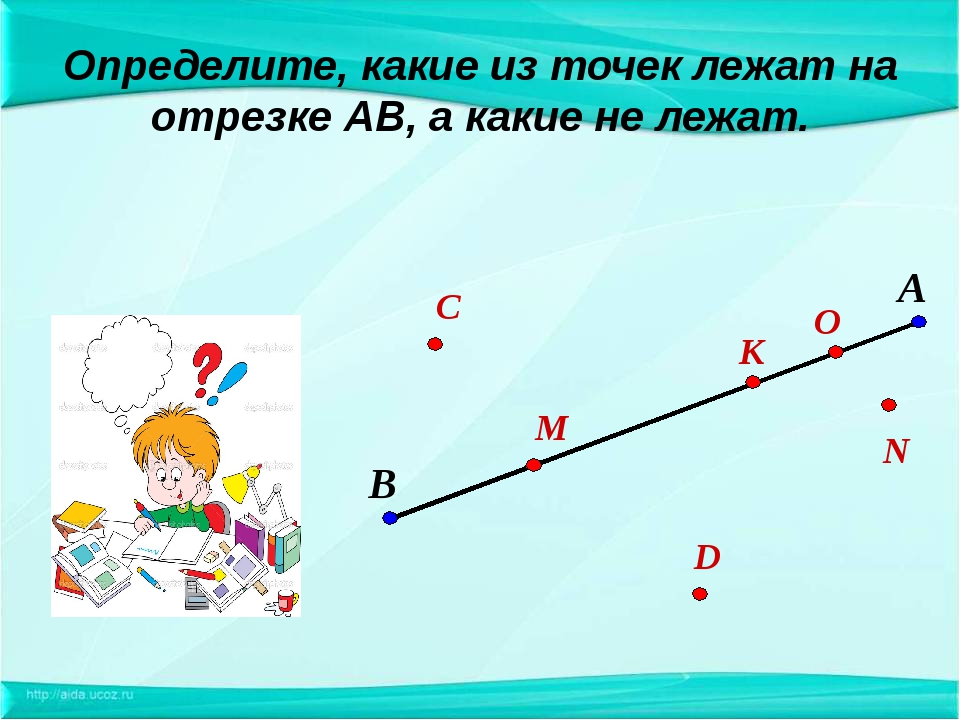 Постройте ломаную DСЕК так, чтобы DС=18 мм, СЕ=37 мм, ЕК=26 мм. Вычислите длину ломаной. 27. Известно, что АС=17 см, ВD=9см, ВС=3 см. Вычислите длину отрезка АD. 28. Известно, что МК=KN=NP=PR=RT=3 см. Какие еще равные отрезки есть на этом рисунке? Найдите их длины.
Постройте ломаную DСЕК так, чтобы DС=18 мм, СЕ=37 мм, ЕК=26 мм. Вычислите длину ломаной. 27. Известно, что АС=17 см, ВD=9см, ВС=3 см. Вычислите длину отрезка АD. 28. Известно, что МК=KN=NP=PR=RT=3 см. Какие еще равные отрезки есть на этом рисунке? Найдите их длины.10 точек
30. Начертите, не отрывая карандаша от бумаги, фигуры, изображенные на рисунке. По каждой линии можно проводить карандашом только один раз.§2. Цифры. Десятичная запись натуральных чисел — стр. 5-7§4. Плоскость. Прямая. Луч — стр. 12-14
Сохраните или поделитесь с одноклассниками:
Видеоурок по математике 5 класс тема Отрезок Длина отрезка Треугольник
00:04:12Обнаружено блокирование рекламы на сайте
Для существования нашего сайта необходим показ рекламы. Просим отнестись с пониманием и добавить сайт в список исключений вашей программы для блокировки рекламы (AdBlock и другие).
Просим отнестись с пониманием и добавить сайт в список исключений вашей программы для блокировки рекламы (AdBlock и другие).
04:12
Треугольник — это фигура, состоящая из трех отрезков, соединяющих три точки, не лежащие на одной прямой.
Следующие уроки
04:45
05:20
PPT — 10’5 сегментов в кругах Презентация PowerPoint | бесплатно для просмотра
PowerShow. com — ведущий веб-сайт для обмена презентациями и слайд-шоу. Независимо от того, является ли ваше приложение бизнесом, практическими рекомендациями, образованием, медициной, школой, церковью, продажами, маркетингом, онлайн-обучением или просто для развлечения, PowerShow.com — отличный ресурс. И, что лучше всего, большинство его интересных функций бесплатны и просты в использовании.
com — ведущий веб-сайт для обмена презентациями и слайд-шоу. Независимо от того, является ли ваше приложение бизнесом, практическими рекомендациями, образованием, медициной, школой, церковью, продажами, маркетингом, онлайн-обучением или просто для развлечения, PowerShow.com — отличный ресурс. И, что лучше всего, большинство его интересных функций бесплатны и просты в использовании. Вы можете использовать PowerShow.com, чтобы найти и загрузить примеры онлайн-презентаций PowerPoint ppt практически на любую тему, которую вы можете себе представить, чтобы вы могли узнать, как улучшить свои собственные слайды и презентации бесплатно.Или используйте его, чтобы найти и загрузить высококачественные презентации PowerPoint ppt с практическими рекомендациями и иллюстрированными или анимированными слайдами, которые научат вас делать что-то новое, также бесплатно. Или используйте его для загрузки собственных слайдов PowerPoint, чтобы вы могли поделиться ими со своими учителями, классом, студентами, руководителями, сотрудниками, клиентами, потенциальными инвесторами или всем миром.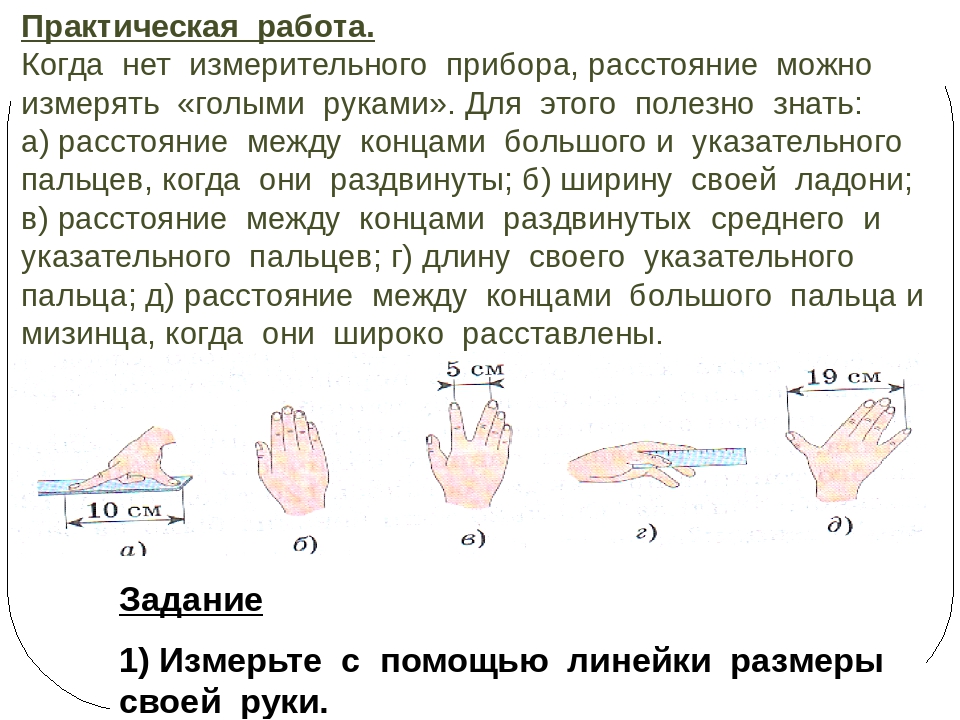
За небольшую плату вы можете получить лучшую в отрасли конфиденциальность в Интернете или публично продвигать свои презентации и слайд-шоу с высокими рейтингами. Но в остальном это бесплатно. Мы даже преобразуем ваши презентации и слайд-шоу в универсальный формат Flash со всей их оригинальной мультимедийной красотой, включая анимацию, эффекты перехода 2D и 3D, встроенную музыку или другой звук или даже видео, встроенное в слайды. Все бесплатно. Большинство презентаций и слайд-шоу на PowerShow.com можно бесплатно просматривать, многие даже можно бесплатно загрузить. (Вы можете выбрать, разрешить ли людям загружать ваши оригинальные презентации PowerPoint и слайд-шоу из фотографий за плату или бесплатно или вовсе.) Зайдите на PowerShow.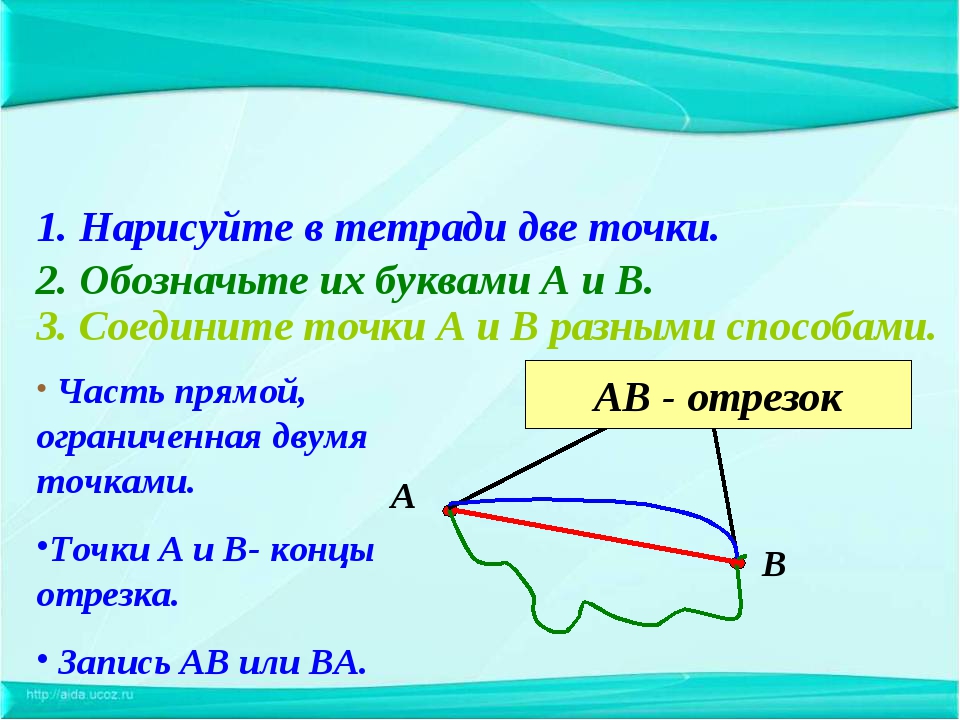
презентации бесплатно. Или используйте его, чтобы найти и загрузить высококачественные презентации PowerPoint ppt с практическими рекомендациями и иллюстрированными или анимированными слайдами, которые научат вас делать что-то новое, также бесплатно. Или используйте его для загрузки собственных слайдов PowerPoint, чтобы вы могли поделиться ими со своими учителями, классом, студентами, руководителями, сотрудниками, клиентами, потенциальными инвесторами или всем миром.Или используйте его для создания действительно крутых слайд-шоу из фотографий — с двухмерными и трехмерными переходами, анимацией и музыкой на ваш выбор — которыми вы можете поделиться со своими друзьями в Facebook или в кругах Google+. Это тоже бесплатно! За небольшую плату вы можете получить лучшую в отрасли конфиденциальность в Интернете или публично продвигать свои презентации и слайд-шоу с высокими рейтингами. Но в остальном это бесплатно.
 Мы даже преобразуем ваши презентации и слайд-шоу в универсальный формат Flash со всей их оригинальной мультимедийной красотой, включая анимацию, эффекты перехода 2D и 3D, встроенную музыку или другой звук или даже видео, встроенное в слайды.Все бесплатно. Большинство презентаций и слайд-шоу на PowerShow.com можно бесплатно просматривать, многие даже можно бесплатно загрузить. (Вы можете выбрать, разрешить ли людям загружать ваши оригинальные презентации PowerPoint и слайд-шоу из фотографий за плату или бесплатно или вовсе.) Зайдите на PowerShow.com сегодня — БЕСПЛАТНО. Здесь действительно каждый найдет что-то для себя!
Мы даже преобразуем ваши презентации и слайд-шоу в универсальный формат Flash со всей их оригинальной мультимедийной красотой, включая анимацию, эффекты перехода 2D и 3D, встроенную музыку или другой звук или даже видео, встроенное в слайды.Все бесплатно. Большинство презентаций и слайд-шоу на PowerShow.com можно бесплатно просматривать, многие даже можно бесплатно загрузить. (Вы можете выбрать, разрешить ли людям загружать ваши оригинальные презентации PowerPoint и слайд-шоу из фотографий за плату или бесплатно или вовсе.) Зайдите на PowerShow.com сегодня — БЕСПЛАТНО. Здесь действительно каждый найдет что-то для себя! Сферический сегмент | MATHalino
Сферический сегмент — это твердое тело, ограниченное двумя параллельными плоскостями через сферу. С точки зрения сферической зоны, сферический сегмент — это твердое тело, ограниченное зоной и плоскостями оснований зоны.
Свойства сферического сегмента
- Основания сферического сегмента — это сечения, образованные параллельными плоскостями.
 Радиусы нижней и верхней частей обозначены буквами a и b соответственно. Если либо a, либо b равно нулю, сегмент имеет одно основание. Если и a, и b равны нулю, твердое тело — это вся сфера.
Радиусы нижней и верхней частей обозначены буквами a и b соответственно. Если либо a, либо b равно нулю, сегмент имеет одно основание. Если и a, и b равны нулю, твердое тело — это вся сфера. - Если одна из параллельных плоскостей касается сферы, сформированное таким образом твердое тело представляет собой сферический сегмент одного основания .2 (3R — h) $ ( хорошо! )
Отметим также, что объем сегмента сферы высотой h и радиусами a и b равен объему сферы радиуса h / 2 плюс сумма объемов двух цилиндров с высотой h / 2 и радиусы которых равны a и b соответственно.
Площадь сегмента | eMathZone
Сегмент — это часть круга, отрезанная прямой линией, не проходящей через центр.2} = 3,1415 \ times 225 = 706,5 $$ кв. См
Площадь большого сегмента $$ = $$ площадь круга $$ — $$ площадь малого сегмента
$$ = 706,5 — 20,4 = 686,1 $$ квадрат см.(b) Площадь сегмента, если заданы высота и длина хорды сегмента:
Пусть $$ r = $$ радиус окружности
$$ h = $$ высота сегмента
$$ c = $$ длина хордыОтметим, что $$ ODB $$ — прямоугольный треугольник; гипотенуза равна $$ OB = r $$, а две другие стороны равны $$ OD = r — h $$ и $$ BD = c / 2 $$
$$ \, следовательно, $$ по теореме Пифагора$$ {\ left ({\ frac {c} {2}} \ right) ^ 2} + {\ left ({r — h} \ right) ^ 2} = {r ^ 2} $$
$$ {\ left ({\ frac {c} {2}} \ right) ^ 2} + {r ^ 2} — 2rh + {h ^ 2} = {r ^ 2} $$
$$ {\ left ({ \ frac {c} {2}} \ right) ^ 2} — 2rh + {h ^ 2} = 0 $$Решая относительно $$ r $$, $$ c $$ и $$ h $$, получаем следующие формулы:
$$ r = \ frac {{{{\ left ({\ frac {c} {2}} \ right)} ^ 2} + {h ^ 2}}} {{2h}} $$ — (1)
$$ h = r \ pm \ sqrt {{r ^ 2} — {{\ left ({\ frac {c} {2}} \ right)} ^ 2}} $$ — (2)
$$ c = 2 \ sqrt {h \ left ({2r — h} \ right)} $$ — (3)Примечание:
$$ r + \ sqrt {{r ^ 2} — {{\ left ({\ frac {c} {2}} \ right)} ^ 2}} $$ дает высоту основного сегмент
$$ r — \ sqrt {{r ^ 2} — {{\ left ({\ frac {c} {2}} \ right)} ^ 2}} $$ дает высоту меньшего сегментаПриводится множество формул для определения приблизительной площади сегмента.


 Радиусы нижней и верхней частей обозначены буквами a и b соответственно. Если либо a, либо b равно нулю, сегмент имеет одно основание. Если и a, и b равны нулю, твердое тело — это вся сфера.
Радиусы нижней и верхней частей обозначены буквами a и b соответственно. Если либо a, либо b равно нулю, сегмент имеет одно основание. Если и a, и b равны нулю, твердое тело — это вся сфера.