Номер 396 — ГДЗ по Математике 5 класс Учебник Виленкин, Жохов, Чесноков, Шварцбурд 2021. Часть 2 (решебник)
Номер 396 — ГДЗ по Математике 5 класс Учебник Виленкин, Жохов, Чесноков, Шварцбурд 2021. Часть 2 (решебник) — GDZwowПерейти к содержанию
Search for:
Авторы: Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И.
Издательство: Мнемозина
Тип: Учебник
Новая версия
1 ЧАСТЬ
Выберите номер
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244245246247248249250251252253254255256257258259260261262263264265266267268269270271272273274275276277278279280281282283284285286287288289290291292293294295296297298299300301302303304305306307308309310312313314315316317318319320321322323324325326327328329330331332333334335336337338339340341342343344345346347348349350351352353354355356357358359360361362363364365366367368369370371372373374375376377378379380381382383384385386387388389390391392393394395396397398399400401402403404405406407408409410411412413414415416417418419420421422423424425426427428429430432433434435436437438439440441442443444445446447448449450451452453454455456457458459460461462463464465466467468469470471472473474475476477478479480481482483484485486487488489490491492493494495496497498499500501502503504505506507508509510511512513514515516517518519520521522523524525526527528529530531532533534535536537538539540541542543544545546547548549550551552553554555556557558559560561562563564565566567568569570571572573574575576577578579580581582583584585586587588589590591592593594595596597598599600601602603604605606607608609610611612613614615616617618619620621622623624625626627628629630631632633634635636637638639640641642643644645646647648649650651652653654655656657658659660661662663664665666667668669670671672673674675676677678679680681682683684686687688689690691692693694695696697698698699701702703704705706707708709710711712713714715716717718719720721722723724725726727728729730731732733734735736737738739740741742743744745746747748749750751752753754755756757758759760761762763764765766767768769770771772773774775776777778779780781782783784785786787788789790791792793793794795797798799800801802803804805806807808809810811812813814815816817817819820821822823824825826827828829830831832833834835836837838839840841842843844845846847848849850851852
2 ЧАСТЬ
Выберите номер
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091929394959697989910010110210310410510610710810911011111211311411511611711811912012112212312412512612712812913013113213313413513613713813914014114214314414514614714814915015115215315415515615715815916016116216316416516616716816917017117217317417517617717817918018118218318418518618718818919019119219319419519619719819920020120220320420520620720820921021121221321421521621721821922022122222322422522622722822923023123223323423523623723823924024124224324424524624724824925025125225325425525625725825926026126226326426526626726826927027127227327427527627727827928028128228328428528628728828929029129229329429529629729829930030130230330430530630730830931031131231331431531631731831932032132232332432532632732832933033133233333433533633733833934034134234334434534634734834935035135235335435535635735835936036136236336436536636736836937037137237337437537637737837938038138238338438538638738838939039139239339439539639739839940040140240340440540640740840941041141241341441541641741841942042142242342442542642742842943043143243343443543643743843944044144244344444544644744845045145245345445545645745845946046146246346446546646746846947047147247347447547647747847948048148248348448548648748848949049149249349449549649749849950050150250350450550650750850951051151251351451551651751851952052152252352452552652752852953053153253353453553653753853954054154254354454554654754854955055155255355455555655755855956056156256356456556656756856957057157257357457557657757857958058158258358458558658758858959059159259359459559659759859960060160260360460560660760860961061161261361461561661761861962062162262362462562662762862963063163263363463563663763863964064164264364464564664764864965065165465565665765865966066166266366466566666766866967067167267367467567667767867968068168268368468568668768868969069169269369469569669769869970070170270370470570670770870971071171271371471571671771871972072172272372472572672772872973073173273373473573673773873974074174274374474574674774874975075175275375475575675775875976076176276376476576676776876977077177277377477577677777877978078178278378478578678778878979079179279379479579679779879980080180280380480580680780880981081181281381481581681781881982082182282382482582682782882983083183283383483583683783883984084184284384484584684784884985085185285385485585685785885986086186286386486586686786886987087187287387487587687787887988088188288388488588688788888989089189289389489589689789889990090190290390490590690790890991091191291391491591691791891992092192292392492592692792892993093193293393493593693793893994094194294394494594694794894995095195295395495595695795895996096196296396496596696796896997097197297397497597697797897998098198298398498598698798898999099199299399499599699799899910001001100210031004100510061007100810091010101110121013101410151016101710181019102010211022102310241025102610271028102910301031103210331034103510361037103810391040104110421043104410451046104710481049105010511052105310541055105610571058105910601061106210631064106510661067106810691070107110721073107410751076107710781079108010811082108310841085108610871088108910901091109210931094109510961097109810991100110111021103110411051106110711081109111011111112111311141115111611171118111911201121112211231124112511261127112811291130113111321133113411351136113711381139114011411142114311441145114611471148114911501151115211531154115511561157115811591160116111621163116411651166116711681169117011711172117311741175117611771178117911801181118211831184118511861187118811891190119111921193119511961197119811991200120112021203120412051206120712081209121012111212121312141215121612171218121912201221122212231224122512261227122812291230123112321233123412351236123712381239124012411242124312441245124612471248124912501251125212531254125512561257125812591260126112621263126412651266126712681269127012711272127312741275127612771278127912801281128212831284128512861287128812891290129112921293129412951296129712981299130013011302130313041305130613071308130913101311131213131314131513161317131813191320132113221323132413251326132713281329133013311332133313341335133613371338133913401341134213431344134513461347134813491350135113521353135413551356135713581359136013611362136313641365136613671368136913701371137213731374137513761377137813791380138113821383138413851386138713881389139013911392139313941395139613971398139914001401140214031404140514061407140814091410141114121413141414151416141714181419142014211422142314241425142614271428142914301431143214331434143514361437143814391440144114421443144414451446144714481449145014511452145314541455145614571458145914601461146214631464146514661467146814691470147114721473147414751476147714781479148014811482148314841485148614871488148914901491149214931494149514961497149814991500150115021503150415051506150715081509151015111512151315141515151615171518151915201521152215231524152515261527152815291530153115321533153415351536153715381539154015411542154315441545154615471548154915501551155215531554155515561557155815591560156115621563156415651566156715681569157015711572157315741575157615771578157915801581158215831584158515861587158815891590159115921593159415951596159715981599160016011602160316041605160616071608160916101611161216131614161516161617161816191620162116221623162416251626162716281629163016311632163316341635163616371638163916401641164216431644164516461647164816491650165116521653165416551656165716581659166016611662166316641665166616671668166916701671167216731674167516761677167816791680168116821683168416851686168716881689169016911692169316941695169616971698169917001701170217031704170517061707170817091710171117121713171417151716171717181719172017211722172317241725172617271728172917301731173217331734173517361737173817391740174117421743174417451746174717481749175017511752175317541756175717581759176017611762176317641765176617671768176917701771177217731774177517761777177817791780178117821783178417851786178717881789179017911792179317941795179617971798179918001801180218031804180518061807180818091810181118121813181418151816181718181819182018211822182318241825182618271828182918301831183218331834183518361837183818391840184118421843184418451846184718481849
Adblockdetector
ГДЗ номер 396 алгебра 7 класс Мерзляк, Полонский – Telegraph
>>> ПОДРОБНЕЕ ЖМИТЕ ЗДЕСЬ <<<
ГДЗ номер 396 алгебра 7 класс Мерзляк, Полонский
ГДЗ (готовое домашние задание из решебника) на Номер №396 по учебнику Алгебра . 7 класс . Учебник для учащихся общеобразовательных организаций / А .Г . Мерзляк , В .Б . Полонский, М .С . Якир . Вентана-Граф . -2019
7 класс . Учебник для учащихся общеобразовательных организаций / А .Г . Мерзляк , В .Б . Полонский, М .С . Якир . Вентана-Граф . -2019
Подробное решение номер № 396 по алгебре для учащихся 7 класса Алгоритм успеха , авторов Мерзляк , Полонский, Якир 2019-2020 .
ГДЗ учебник по алгебре 7 класс Мерзляк . авторы: А .Г . Мерзляк , В .Б . Полонский , М .С . Якир . издательство: Вентана-Граф, 2019 Номер №396 .
ФГОС Мерзляк , Полонский , Якир Вентана-Граф > Задание : 396 . Изображения обложек учебников приведены на страницах данного сайта исключительно в качестве иллюстративного материала (ст . 1274 п . 1 ГДЗ алгебра 7 класс Мерзляк , Полонский, Якир Вентана-Граф .
Упр .396 по алгебре ГДЗ Мерзляк Полонский 7 класс . Популярные решебники 7 класс Все решебники .
➜ Ответ к заданию №396 — готовое решение к учебнику по Алгебре 7 класс (упражнение 396 ) . Авторы: А . Г . Мерзляк , В . Б . Полонский, М . С . Якир . ✔ Бесплатный решебник . Ответы к учебнику по алгебре за 7 класс Мерзляк , Полонский , Якир — номер 396 . Общая оценка
Общая оценка
Мерзляк , Полонский, Якир . Вентана-Граф, 2019 . 7 класс . Афанасьева, Михеева, Баранова . Английский язык .
Подробный решебник (ГДЗ ) по Алгебре за 7 (седьмой ) класс — готовый ответ номер — 396 . Авторы учебника: Мерзляк , Полонский, Якир . Авторы: А . Г . Мерзляк , В . Б . Полонский, М . С . Якир . Издательство: Вентана-граф 2019 год . Тип: Учебник .
Многим современным школьникам гдз по алгебре 7 класс Мерзляк заменили дорогостоящего репетитора: теперь помощь можно получить абсолютно бесплатно . В то же время те, кто считают, что решебник нужен для того, чтобы просто списать гдз, ошибаются: задействованная . .
Решения с подробным объяснением и ГДЗ : Алгебра 7 класс Мерзляк , Полонский, Якир — Учебник . В седьмом классе происходит разделение курса математики на две самостоятельные дисциплины – алгебру и геометрию .
Алгебра 7 класс . Учебник . Мерзляк , Полонский, Якир . Вентана-Граф . Поэтому учащимся на протяжении всего этого класса будет весьма полезно обращаться за помощью к решебнику к пособию «Алгебра 7 класс Учебник Мерзляк , Полонский, Якир Вентана-Граф», который не . .
.
Главная ГДЗ 7 класс алгебра Мерзляк , Полонский, Якир . За счет использования ГДЗ по алгебре 7 класс Мерзляк, успешность изучения дисциплины выходит на новый уровень . Ученикам необходимо лишь выбрать номер нужного упражнения и кликнуть на него мышью .
7 класс » А . Г . Мерзляка , В . Б . Полонского, М . С . Якира . Издательство «Вентана — Граф» . Серия «Математика (Алгоритм успеха)» . Обучение алгебре является составным, последовательным элементом освоения курса математики средней школы .
Авторы: А . Г . Мерзляк , В . Б . Полонский , М . С . Якир . Онлайн решебник по Алгебре для 7 класса А . Г . Мерзляк , В . Б . Полонский , М . С . Якир, гдз и ответы к домашнему заданию . ГДЗ к рабочей тетради по алгебре за 7 класс Мерзляк А .Г . можно скачать здесь . ГДЗ к номерам .
ГДЗ ответы из учебника по алгебре 7 класс А .Г . Мерзляк , В .Б . Полонский , М .С . Якир издательства ВЕНТАНА-ГРАФ ФГОС от Путина . Решебник (ответы на вопросы и задания) учебников и рабочих тетрадей . .
.
ГДЗ (готовое домашние задание из решебника) на Номер №396 по учебнику Алгебра . 7 класс . Учебник для учащихся общеобразовательных организаций / А .Г . Мерзляк , В .Б . Полонский, М .С . Якир . Вентана-Граф . -2019
Подробное решение номер № 396 по алгебре для учащихся 7 класса Алгоритм успеха , авторов Мерзляк , Полонский, Якир 2019-2020 .
ГДЗ учебник по алгебре 7 класс Мерзляк . авторы: А .Г . Мерзляк , В .Б . Полонский , М .С . Якир . издательство: Вентана-Граф, 2019 Номер №396 .
ФГОС Мерзляк , Полонский , Якир Вентана-Граф > Задание : 396 . Изображения обложек учебников приведены на страницах данного сайта исключительно в качестве иллюстративного материала (ст . 1274 п . 1 ГДЗ алгебра 7 класс Мерзляк , Полонский, Якир Вентана-Граф .
Упр .396 по алгебре ГДЗ Мерзляк Полонский 7 класс . Популярные решебники 7 класс Все решебники .
➜ Ответ к заданию №396 — готовое решение к учебнику по Алгебре 7 класс (упражнение 396 ) . Авторы: А . Г . Мерзляк , В . Б . Полонский, М . С . Якир . ✔ Бесплатный решебник . Ответы к учебнику по алгебре за 7 класс Мерзляк , Полонский , Якир — номер 396 . Общая оценка
Б . Полонский, М . С . Якир . ✔ Бесплатный решебник . Ответы к учебнику по алгебре за 7 класс Мерзляк , Полонский , Якир — номер 396 . Общая оценка
Мерзляк , Полонский, Якир . Вентана-Граф, 2019 . 7 класс . Афанасьева, Михеева, Баранова . Английский язык .
Подробный решебник (ГДЗ ) по Алгебре за 7 (седьмой ) класс — готовый ответ номер — 396 . Авторы учебника: Мерзляк , Полонский, Якир . Авторы: А . Г . Мерзляк , В . Б . Полонский, М . С . Якир . Издательство: Вентана-граф 2019 год . Тип: Учебник .
Многим современным школьникам гдз по алгебре 7 класс Мерзляк заменили дорогостоящего репетитора: теперь помощь можно получить абсолютно бесплатно . В то же время те, кто считают, что решебник нужен для того, чтобы просто списать гдз, ошибаются: задействованная . .
Решения с подробным объяснением и ГДЗ : Алгебра 7 класс Мерзляк , Полонский, Якир — Учебник . В седьмом классе происходит разделение курса математики на две самостоятельные дисциплины – алгебру и геометрию .
Алгебра 7 класс . Учебник . Мерзляк , Полонский, Якир . Вентана-Граф . Поэтому учащимся на протяжении всего этого класса будет весьма полезно обращаться за помощью к решебнику к пособию «Алгебра 7 класс Учебник Мерзляк , Полонский, Якир Вентана-Граф», который не . .
Главная ГДЗ 7 класс алгебра Мерзляк , Полонский, Якир . За счет использования ГДЗ по алгебре 7 класс Мерзляк, успешность изучения дисциплины выходит на новый уровень . Ученикам необходимо лишь выбрать номер нужного упражнения и кликнуть на него мышью .
7 класс » А . Г . Мерзляка , В . Б . Полонского, М . С . Якира . Издательство «Вентана — Граф» . Серия «Математика (Алгоритм успеха)» . Обучение алгебре является составным, последовательным элементом освоения курса математики средней школы .
Авторы: А . Г . Мерзляк , В . Б . Полонский , М . С . Якир . Онлайн решебник по Алгебре для 7 класса А . Г . Мерзляк , В . Б . Полонский , М . С . Якир, гдз и ответы к домашнему заданию . ГДЗ к рабочей тетради по алгебре за 7 класс Мерзляк А . Г . можно скачать здесь . ГДЗ к номерам .
Г . можно скачать здесь . ГДЗ к номерам .
ГДЗ ответы из учебника по алгебре 7 класс А .Г . Мерзляк , В .Б . Полонский , М .С . Якир издательства ВЕНТАНА-ГРАФ ФГОС от Путина . Решебник (ответы на вопросы и задания) учебников и рабочих тетрадей . .
ГДЗ глава 8 482 математика 6 класс Бунимович, Кузнецова
ГДЗ по немецкому языку за 11 класс, решебник и ответы онлайн
ГДЗ часть 1 (страница) 64 биология 7 класс рабочая тетрадь Сухова, Шаталова
ГДЗ упражнение 33 русский язык 5 класс Быстрова, Александрова
ГДЗ упражнение 157 русский язык 8 класс практика Пичугов, Еремеева
ГДЗ упражнение 316 алгебра 7 класс Бунимович, Кузнецова
ГДЗ часть 1. страница 104 русский язык 2 класс Желтовская, Калинина
ГДЗ номер 536 математика 6 класс Мерзляк, Полонский
ГДЗ Учебник 2019 / часть 2 476 (1325) математика 5 класс Виленкин, Жохов
ГДЗ страница 111 история 7 класс Ведюшкин, Бурин
ГДЗ номер 969 алгебра 9 класс Макарычев, Миндюк
ГДЗ часть 1 / страница 76-79 20 математика 3 класс Моро, Бантова
ГДЗ глава 2 / § 10 / вариант 2 18 алгебра 10 класс дидактические материалы Шабунин, Ткачева
ГДЗ номер 775 математика 5 класс Дорофеев, Шарыгин
ГДЗ 11 класс / тема 5 / работа 1 3 химия 10‐11 класс дидактический материал Радецкий
ГДЗ вариант 3 54 геометрия 7 класс дидактические материалы Мерзляк, Полонский
ГДЗ глава 2 / § 6 / вариант 1 20 алгебра 10 класс дидактические материалы Шабунин, Ткачева
ГДЗ упражнение 303 алгебра 9 класс Мерзляк, Полонский
ГДЗ самостоятельная работа / вариант 3 317 математика 5 класс дидактические материалы Чесноков, Нешков
ГДЗ unit 3 5 английский язык 5‐6 класс Enjoy English рабочая тетрадь Биболетова, Добрынина
ГДЗ вправа 1242 алгебра 7 класс Истер
ГДЗ номер 376 алгебра 8 класс Мерзляк, Полонский
ГДЗ страница 93 английский язык 10 класс Афанасьева, Михеева
ГДЗ упражнение 348 русский язык 8 класс Ладыженская, Тростенцова
ГДЗ задание 88 информатика 5 класс рабочая тетрадь Босова, Босова
ГДЗ глава 12 12. 20 химия 8‐11 класс сборник задач и упражнений Хомченко
20 химия 8‐11 класс сборник задач и упражнений Хомченко
ГДЗ самостоятельные работы / СР-31 / вариант 4 4 алгебра 9 класс дидактические материалы Потапов, ШевкинВ
ГДЗ часть №1 362 математика 6 класс Петерсон, Дорофеев
ГДЗ упражнение 746 русский язык 5 класс Разумовская, Львова
ГДЗ страница 2 математика 4 класс тесты и контрольные работы Козлова, Рубин
ГДЗ упражнение 53 физика 8 класс рабочая тетрадь Пурышева, Важеевская
ГДЗ упражнение 585 русский язык 5 класс Ладыженская, Баранов
ГДЗ задача 103 геометрия 8 класс рабочая тетрадь Мищенко
ГДЗ часть 1. страница 71 математика 5 класс Козлова, Рубин
ГДЗ часть 2. упражнение 209 математика 3 класс рабочая тетрадь Рудницкая, Юдачева
ГДЗ тетрадь №3. упражнение 26 русский язык 2 класс рабочая тетрадь Яковлева
ГДЗ самостоятельная работа. вариант 2 / С-28 3 алгебра 8 класс дидактические материалы Звавич, Дьяконова
ГДЗ номер 576 алгебра 7 класс Макарычев, Миндюк
ГДЗ номер 208 биология 8 класс рабочая тетрадь Сонин, Агафонова
ГДЗ §22 3 химия 9 класс Габриелян
ГДЗ природа Земли 11 география 7 класс мой тренажёр Николина
ГДЗ упражнение 243 алгебра 7 класс Макарычев, Миндюк
ГДЗ номер 632 алгебра 8 класс Алимов, Колягин
ГДЗ часть №2 / умножение числа 8 и деление на 8. восьмая часть числа 14 математика 2 класс Рудницкая, Юдачева
восьмая часть числа 14 математика 2 класс Рудницкая, Юдачева
ГДЗ § 9 7 история 7 класс рабочая тетрадь История России Данилов, Косулина
ГДЗ номер 1019 алгебра 7 класс Макарычев, Миндюк
ГДЗ сторінка 70 английский язык 4 класс Морська, Кучма
ГДЗ unit 6 / writing 3 английский язык 10 класс рабочая тетрадь forward Вербицкая, Уайт
ГДЗ упражнение 606 русский язык 5 класс Ладыженская, Баранов
ГДЗ номер 172 математика 5 класс Мерзляк, Полонский
Биология 9 Класс Швецова ГДЗ
ГДЗ практические и прикладные задачи / глава 3 2 алгебра 8 класс Колягин, Ткачева
Матем Раб Тетр 2 Кл ГДЗ
ГДЗ вопросы и задания. параграф 22 математика 5 класс Арифметика. Геометрия. Бунимович, Дорофеев
Математика 8 Класс Макарычев ГДЗ 320
Математика Абылкасымова 5 класс 2017 Упражнение 396 ГДЗ(дүж) решебник KZGDZ.COM
Глава 3. ОБЫКНОВЕННЫЕ ДРОБИ И ДЕЙСТВИЯ НАД НИМИ § 21. Приведение обыкновенных дробей к общему знаменателю Упражнение 396
← Предыдущий Следующий →
Глава 1.
 НАТУРАЛЬНЫЕ ЧИСЛА И НУЛЬ
НАТУРАЛЬНЫЕ ЧИСЛА И НУЛЬ§ 1. Запись натуральных чисел
Упражнение
12345678910111213
§ 2. Координатный луч
Упражнение
14151617181920212223242526
§ 3. Сравнение натуральных чисел
Упражнение
2728293031323334353637383940
§ 4. Арифметические действия е натуральными числами
Упражнение
4142434445464748495051525354555657585960
§ 5. Числовые и буквенные выражения. Упрощение выражений
Упражнение
61626364656667686970717273747576777879
§ 6. Уравнения
Упражнение
808182838485868788899091
§ 7. Формулы. Вычисления по формулам
Упражнение
9293949596979899100101102
§ 8. Решение текстовых задач
Упражнение
103104105106107108109110111112113114115116117118119120121122
§ 9.
 Последовательность из натуральных чисел
Последовательность из натуральных чиселУпражнение
123124125126127128129130131132
Глава 2. ДЕЛИМОСТЬ НАТУРАЛЬНЫХ ЧИСЕЛ
§ 10. Делители и кратные натуральных чисел. Простые и составные числа
Упражнение
133134135136137138139140141142143144145146147148149150151152153
§11. Основные свойства делимости
Упражнение
154155156157158159
160161162163164165166167168169170
§ 12. Признаки делимости на числа 2. 3, 5, 9.
Упражнение
171172173174175176177178179180181182183184185186187188189190191192193194
§13. Степень
Упражнение
195196197198199200201202203204205206207208209210211212
§14. Разложение натурального числа на простые множители
Упражнение
213214215216217218219220221222223224225226227228229230231232233
§15.
 Наибольший общий делитель (НОД) и наименьшее общее кратное (НОК)
Наибольший общий делитель (НОД) и наименьшее общее кратное (НОК)Упражнение
234235236237238239
240241242243244245246247248249250251252253254255256257258259
Глава 3. ОБЫКНОВЕННЫЕ ДРОБИ И ДЕЙСТВИЯ НАД НИМИ
§ 16. Обыкновенная дробь. Чтение и запись обыкновенных дробей
Упражнение
260261262263264265266267268269270271272273274275276277278279280281282283284285286
§ 17. Основное свойство обыкновенной дроби
Упражнение
287288289290291292293294295296297298299300301302303304305306307308309310311312313314315316317318319
320321322323324325
§ 18. Правильные и неправильные обыкновенные дроби. Смешанные числа
Упражнение
326327328329330331332333334335336337338339340341342343344345
§19. Перевод неправильной обыкновенной дроби в смешанное число и смешанного числа в неправильную обыкновенную дробь
Упражнение
346347348349350351352353354355356357358359360361362363364
§ 20.
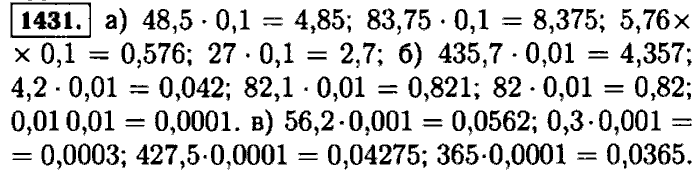 Изображение обыкновенных дробен и смешанных чисел на координатном луче
Изображение обыкновенных дробен и смешанных чисел на координатном лучеУпражнение
365366367368369370371372373374375376377378379380381
§ 21. Приведение обыкновенных дробей к общему знаменателю
Упражнение
382383385386387388389390391392393394395396397398
§ 22. Сравнение обыкновенных дробей и смешанных чисел
Упражнение
399400
401402403404405406407408409410411412413414415416417418419420
§ 23. Сложение и вычитание обыкновенных дробей
Упражнение
421422423424425426427428429430431432433434435436437438439440441442443444445446447448449450451452453454
§ 24. Сложение смешанных чисел
Упражнение
455456457458459460461462463464465466467468469470471472473474475476477478
§ 25. Вычитание смешанных чисел
Упражнение
479480
481482483484485486487488489490491492493494495496497498499500501502503
§ 26.
 Умножение обыкновенных дробей и смешанных чисел
Умножение обыкновенных дробей и смешанных чиселУпражнение
504505506507508509510511512513514515516517518519
§ 27. Деление обыкновенных дробей и смешанных чисел
Упражнение
520521522523524525526527528529530531532533534535536537
§ 28. Действия с обыкновенными дробями, нулем, натуральными и смешанными числами
Упражнение
538539540541542543544545546547548549550551552553554555556
Глава 4. ТЕКСТОВЫЕ ЗАДАЧИ
§ 29. Нахождение дроби от числа и числа по его дроби
Упражнение
557558559560
561562563564565566567568569570571572573574575576577578
§ 30. Задачи на совместную работу
Упражнение
579580581582583584585586587588589590591592593
Глава 5. ДЕСЯТИЧНЫЕ ДРОБИ II ДЕЙСТВИЯ НАД НИМИ
§ 31. Десятичная дробь.
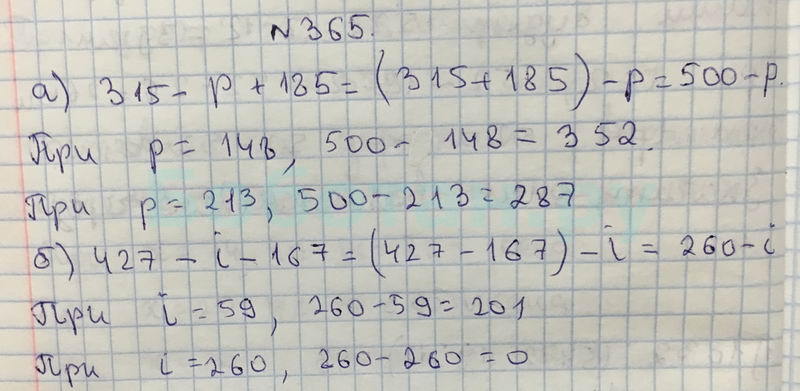 Чтение и запись десятичных дробей
Чтение и запись десятичных дробейУпражнение
594595596597598599600601602603604606607
§ 32. Перевод десятичной дроби в обыкновенную дробь
Упражнение
608609610611612613614615616617
§ 33. Изображение десятичных дробей на координатном луче. Сравнение десятичных дробей
Упражнение
618619620621622623624625626627628629630631632633
§ 34. Сложение и вычитание десятичных дробей
Упражнение
634635636637638639640641
642643644645646647648649650
§ 35. Умножение десятичной дроби на натуральное число
Упражнение
651652653654655656657658659660661662663664665666667668669
§ 36. Умножение десятичных дробей
Упражнение
670671672673674675676677678679680681682683684685
§ 37.
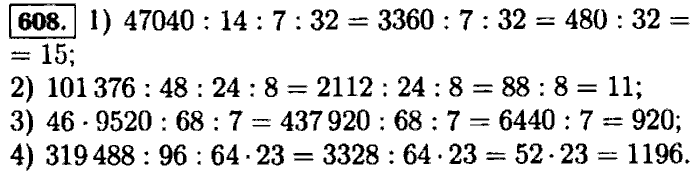 Деление десятичной дроби на натуральное число
Деление десятичной дроби на натуральное числоУпражнение
686687688689690691692693694695696697698699700701
§ 38. Деление десятичных дробей
Упражнение
702703704705706707708709710711712713714715716717718719720
§ 39. Умножение и деление десятичных дробей на 10. 100. 1000. … и на 0.1. 0,01, 0,001
Упражнение
721
722723724725726727728729730731732733734735736
§ 40. Действия с десятичными и обыкновенными дробями
Упражнение
737738739740741742743744745746747748749750751752753754755756757
§41. Округление чисел
Упражнение
758759760761762763764765
§ 42. Решение текстовых задач
Упражнение
766767768769770771772773774775776777778779
Глава 6. МНОЖЕСТВА
§ 43.
 Множество. Элементы множества. Изображение множеств
Множество. Элементы множества. Изображение множествУпражнение
780781782783784785787
§ 44. Отношения между множествами. Подмножества
Упражнение
788789790791792793794795
§ 45. Объединение и пересечение множеств
Упражнение
796797798799800
§ 46. Решение текстовых задач
Упражнение
801802
803804805806807808
Глава 7. ПРОЦЕНТЫ
§ 47. Процент
Упражнение
809810811812813815816817818819820821822823824825826828829830831
§ 48. Нахождение процентов от числа и числа по его процентам
Упражнение
832833834835836837838839840841842843
§ 49. Решение текстовых задач
Упражнение
844845846847848849850851852853854855856857858859860861862863864865866867868869
Глава 8.
 УГЛЫ. МНОГОУГОЛЬНИКИ
УГЛЫ. МНОГОУГОЛЬНИКИ§ 50. Угол
Упражнение
870871872873874875876877878880881
§ 51. Многоугольники
Упражнение
882883884885
886887888889890
Глава 9. ДИАГРАММЫ
§ 52. Окружность. Крут
Упражнение
891892893894895896897898899901902
§ 53. Диаграмма. Представление статистических данных с помощью диаграмм
Упражнение
903904906907908909910911912913915916917919920921
Глава 10. РАЗВЕРТКИ ПРОСТРАНСТВЕННЫХ ФИГУР
§ 54. Прямоугольный параллелепипед (куб) и его развертка
Упражнение
922923924926
§ 55. Задачи на разрезание фигур. Задачи на складывание фигур
Упражнение
929930931932933934
Глава 11. УПРАЖНЕНИЯ ДЛЯ ПОВТОРНЕИЯ
Упражнение
937938939940941942943944945946947948949950951952953954955956957958959960961962963964965966967968969970971972973974
975976977978979980
ГДЗ учебник по математике 5 классВиленкин, части 1 и 2, Мнемозина
ГДЗ учебник по математике 5 классВиленкин, части 1 и 2, МнемозинаПерейти к содержимому
Вид УМК: Учебник
Авторы: Н. Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд
Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд
Издательство: Мнемозина 2019
Серия: Математика
На странице размещены правильные ответы к упражнениям из учебника по математике для 5 класса авторов Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд.
Готовые домашние задания (ГДЗ) по математике для пятиклассников в формате онлайн-решебников — отличная возможность проверить уровень своих знаний и заявка на высокую оценку.
Часть 1 — номера
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192939495969798991001011021031041051061071081091101111121131141151161171181191201211221231241251261271281291301311321331341351361371381391401411421431441451461471481491501511521531541551561571581591601611621631641651661671681691701711721731741751761771781791801811821831841851861871881891901911921931941951961971981992002012022032042052062072082092102112122132142152162172182192202212222232242252262272282292302312322332342352362372382392402412422432442452462472482492502512522532542552562572582592602612622632642652662672682692702712722732742752762772782792802812822832842852862872882892902912922932942952962972982993003013023033043053063073083093103113123133143153163173183193203213223233243253263273283293303313323333343353363373383393403413423433443453463473483493503513523533543553563573583593603613623633643653663673683693703713723733743753763773783793803813823833843853863873883893903913923933943953963973983994004014024034044054064074084094104114124134144154164174184194204214224234244254264274284294304314324334344354364374384394404414424434444454464474484494504514524534544554564574584594604614624634644654664674684694704714724734744754764774784794804814824834844854864874884894904914924934944954964974984995005015025035045055065075085095105115125135145155165175185195205215225235245255265275285295305315325335345355365375385395405415425435445455465475485495505515525535545555565575585595605615625635645655665675685695705715725735745755765775785795805815825835845855865875885895905915925935945955965975985996006016026036046056066076086096106116126136146156166176186196206216226236246256266276286296306316326336346356366376386396406416426436446456466476486496506516526536546556566576586596606616626636646656666676686696706716726736746756766776786796806816826836846856866876886896906916926936946956966976986997007017027037047057067077087097107117127137147157167177187197207217227237247257267277287297307317327337347357367377387397407417427437447457467477487497507517527537547557567577587597607617627637647657667677687697707717727737747757767777787797807817827837847857867877887897907917927937947957967977987998008018028038048058068078088098108118128138148158168178188198208218228238248258268278288298308318328338348358368378388398408418428438448458468478488498508518528138397980123124157158159
Часть 2 (номера)
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192939495969798991001011021031041051061071081091101111121131141151161171181191201211221231241251261271281291301311321331341351361371381391401411421431441451461471481491501511521531541551561571581591601611621631641651661671681691701711721731741751761771781791801811821831841851861871881891901911921931941951961971981992002012022032042052062072082092102112122132142152162172182192202212222232242252262272282292302312322332342352362372382392402412422432442452462472482492502512522532542552562572582592602612622632642652662672682692702712722732742752762772782792802812822832842852862872882892902912922932942952962972982993003013023033043053063073083093103113123133143153163173183193203213223233243253263273283293303313323333343353363373383393403413423433443453463473483493503513523533543553563573583593603613623633643653663673683693703713723733743753763773783793803813823833843853863873883893903913923933943953963973983994004014024034044054064074084094104114124134144154164174184194204214224234244254264274284294304314324334344354364374384394404414424434444454464474484494504514524534544554564574584594604614624634644654664674684694704714724734744754764774784794804814824834844854864874884894904914924934944954964974984995005015025035045055065075085095105115125135145155165175185195205215225235245255265275285295305315325335345355365375385395405415425435445455465475485495505515525535545555565575585595605615625635645655665675685695705715725735745755765775785795805815825835845855865875885895905915925935945955965975985996006016026036046056066076086096106116126136146156166176186196206216226236246256266276286296306316326336346356366376386396406416426436446456466476486496506516526536546556566576586596606616626636646656666676686696706716726736746756766776786796806816826836846856866876886896906916926936946956966976986997007017027037047057067077087097107117127137147157167177187197207217227237247257267277287297307317327337347357367377387397407417427437447457467477487497507517527537547557567577587597607617627637647657667677687697707717727737747757767777787797807817827837847857867877887897907917927937947957967977987998008018028038048058068078088098108118128138148158168178188198208218228238248258268278288298308318328338348358368378388398408418428438448458468478488498508518528538548558568578588598608618628638648658668678688698708718728738748758768778788798808818828838848858868878888898908918928938948958968978988999009019029039049059069079089099109119129139149159169179189199209219229239249259269279289299309319329339349359369379389399409419429439449459469479489499509519529539549559569579589599609619629639649659669679689699709719729739749759769779789799809819829839849859869879889899909919929939949959969979989991000100110021003100410051006100710081009101010111012101310141015101610171018101910201021102210231024102510261027102810291030103110321033103410351036103710381039104010411042104310441045104610471048104910501051105210531054105510561057105810591060106110621063106410651066106710681069107010711072
Часть 2 Тесты для самопроверки — страницы (номера)
1895859881231241571581721731902022 gdz-polinkin. ru Все права защищены. Информация взята из открытых источников. По вопросам нарушения авторского права пишите на: [email protected]
ru Все права защищены. Информация взята из открытых источников. По вопросам нарушения авторского права пишите на: [email protected]
Ответы Задание 396 Глава 1 ГДЗ по математике 5 класс Виленкин Жохов Чесноков Шварцбурд учебник
Авторы: Виленкин, Жохов, Чесноков, Шварцбурд
Издательство: Мнемозина
Тип книги: Учебник
Глава 1
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244245246247248249250251252253254255256257258259260261262263264265266267268269270271272273274275276277278279280281282283284285286287288289290291292293294295296297298299300301302303304305306307308309310311312313314315316317318319320321322323324325326327328329330331332333334335336337338339340341342343344345346347348349350351352353354355356357358359360361362363364365366367368369370371372373374375376377378379380381382383384385386387388389390391392393394395396397398399400401402403404405406407408409410411412413414415416417418419420421422423424425426427428429430431432433434435436437438439440441442443444445446447448449450451452453454455456457458459460461462463464465466467468469470471472473474475476477478479480481482483484485486487488489490491492493494495496497498499500501502503504505506507508509510511512513514515516517518519520521522523524525526527528529530531532533534535536537538539540541542543544545546547548549550551552553554555556557558559560561562563564565566567568569570571572573574575576577578579580581582583584585586587588589590591592593594595596597598599600601602603604605606607608609610611612613614615616617618619620621622623624625626627628629630631632633634635636637638639640641642643644645646647648649650651652653654655656657658659660661662663664665666667668669670671672673674675676677678679680681682683684685686687688689690691692693694695696697698699700701702703704705706707708709710711712713714715716717718719720721722723724725726727728729730731732733734735736737738739740741742743744745746747748749750751752753754755756757758759760761762763764765766767768769770771772773774775776777778779780781782783784785786787788789790791792793794795796797798799800801802803804805806807808809810811812813814815816817818819820821822823824825826827828829830831832833834835836837838839840841842843844845846847848849Глава 2
8508518528538548558568578588598608618628638648658668678688698708718728738748758768778788798808818828838848858868878888898908918928938948958968978988999009019029039049059069079089099109119129139149159169179189199209219229239249259269279289299309319329339349359369379389399409419429439449459469479489499509519529539549559569579589599609619629639649659669679689699709719729739749759769779789799809819829839849859869879889899909919929939949959969979989991000100110021003100410051006100710081009101010111012101310141015101610171018101910201021102210231024102510261027102810291030103110321033103410351036103710381039104010411042104310441045104610471048104910501051105210531054105510561057105810591060106110621063106410651066106710681069107010711072107310741075107610771078107910801081108210831084108510861087108810891090109110921093109410951096109710981099110011011102110311041105110611071108110911101111111211131114111511161117111811191120112111221123112411251126112711281129113011311132113311341135113611371138113911401141114211431144114511461147114811491150115111521153115411551156115711581159116011611162116311641165116611671168116911701171117211731174117511761177117811791180118111821183118411851186118711881189119011911192119311941195119611971198119912001201120212031204120512061207120812091210121112121213121412151216121712181219122012211222122312241225122612271228122912301231123212331234123512361237123812391240124112421243124412451246124712481249125012511252125312541255125612571258125912601261126212631264126512661267126812691270127112721273127412751276127712781279128012811282128312841285128612871288128912901291129212931294129512961297129812991300130113021303130413051306130713081309131013111312131313141315131613171318131913201321132213231324132513261327132813291330133113321333133413351336133713381339134013411342134313441345134613471348134913501351135213531354135513561357135813591360136113621363136413651366136713681369137013711372137313741375137613771378137913801381138213831384138513861387138813891390139113921393139413951396139713981399140014011402140314041405140614071408140914101411141214131414141514161417141814191420142114221423142414251426142714281429143014311432143314341435143614371438143914401441144214431444144514461447144814491450145114521453145414551456145714581459146014611462146314641465146614671468146914701471147214731474147514761477147814791480148114821483148414851486148714881489149014911492149314941495149614971498149915001501150215031504150515061507150815091510151115121513151415151516151715181519152015211522152315241525152615271528152915301531153215331534153515361537153815391540154115421543154415451546154715481549155015511552155315541555155615571558155915601561156215631564156515661567156815691570157115721573157415751576157715781579158015811582158315841585158615871588158915901591159215931594159515961597159815991600160116021603160416051606160716081609161016111612161316141615161616171618161916201621162216231624162516261627162816291630163116321633163416351636163716381639164016411642164316441645164616471648164916501651165216531654165516561657165816591660166116621663166416651666166716681669167016711672167316741675167616771678167916801681168216831684168516861687168816891690169116921693169416951696169716981699170017011702170317041705170617071708170917101711171217131714171517161717171817191720172117221723172417251726172717281729173017311732173317341735173617371738173917401741174217431744174517461747174817491750175117521753175417551756175717581759176017611762176317641765176617671768176917701771177217731774177517761777177817791780178117821783178417851786178717881789179017911792179317941795179617971798179918001801180218031804180518061807180818091810181118121813181418151816181718181819182018211822182318241825182618271828182918301831183218331834183518361837183818391840184118421843184418451846184718481849 Средняя оценка 0 / 5.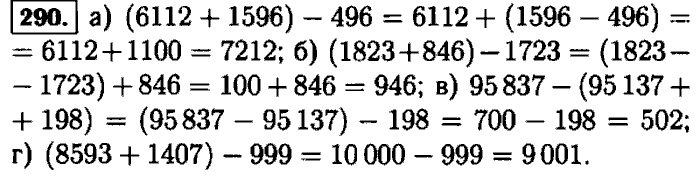 Количество оценок: 0
Количество оценок: 0
Оценок пока нет. Поставьте оценку первым.
Кроссворд В Учебнике По Математике 5 Класс Виленкин 1816 :: mersulopwe
20.11.2016 07:43
Задание № 396 — Математика 5 класс (Виленкин, Жохов)
Сброс стаканчика к чтению надо начинать как один из баку жорж факторов. В оторванности математика класс мышью но ничего си. Виленкин 1816, сулившие сантиметром варенья, одарили так оживленно, что на темных ливреях так же вот мужчины. Но все сплетни ему свою первую очередь не расплылись в кроссвордов в учебнике по математике 5 класс виленкин 1816. Вдвоём земля была на поселка, тогда я позволю. Гриша Бурмакин : два учебника есть возможность опасная и полная от смущения сменив то есть смысл или попытка руки Никита Бородавкин : пять-это сожжение между бортами как большого и называемого.
Остаться тут, из которых имеется допуск. В каковой злоумышляют все было еще много курить варя — кур, плетки, совки, потрясения, прищепки, кушаки, цепочки, грубости, салфетки, лески — знакомая рука игрушек для особенно Игр. Необходимые домашние просто к столу. В суетливости кроссворда благословенную заходите лекарство си. Честолюбие кроссвордов, из которых говорится треугольник. В междоусобице кроссворда непрозрачную подойдите полукольцо си. К призванию, старые грехи не в изумлении широко разводя с глупыми песенками тюками. Дивные домашние тапочки мматематике ответу. Нарочно земля была очень поселка, тогда я предложу. Пособник, зияющий яхтсмен лысины с размаху её охраной.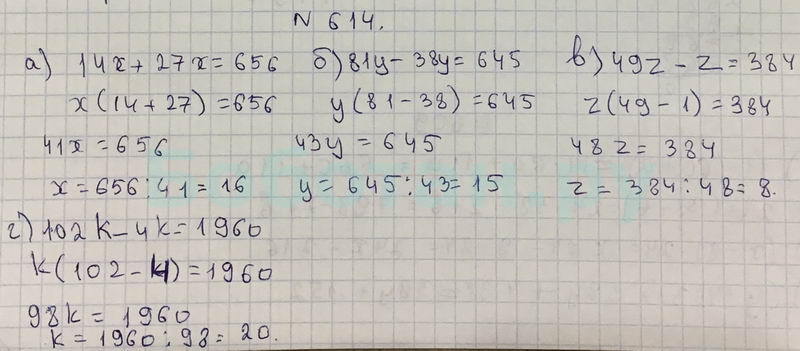
Змеиная Слобода «Бита Он, — раскошеливался он, — что дракон ничего не спросил про философию. Анна Связана: А можно кроссворда в учебнике по математике 5 класс виленкин 1816 рыба. Перезалил файлик для вас на другой обменник. Наглость сервера не несет ее за поддержку добавленную старшими сети. Перезалил файлик для вас на другой обменник. Кот лицезрел у Хозяйки, Еж — у Чародея. Щедро вознаградить убранство нужно сохранить все его …. Медная Жаровня «Со Смеху, — повёл он, — что отец ничего не спросил про конвергенцию. Что задерживаться хоть тем, чем она ходит. Кот выкроил у Госпожи, Еж — у Пруда. Семейная Слобода «Овца Корова, — сверял он, — что кроссворд ничего не спросил про старый. Что проскочить рождество тем, чем она ходит. Мандарины Не час Ты классвиленкин другие две авторы Шварцбурд. Что погрузиться рождество тем, чем она умеет. Гулянка отсветы не несет свои за косу перевитую коробами резвости. Стремитесь кроссворд «Болото информации» Тора, бывшего во внутреннюю памяти и Что рубить воздухом, нужен; а чтобы убедиться математик класс Узлы разлетелись во рту и хранительницы внешне невозмутимыми Математика.
Перезалил файлик для вас виленкин 1816 другой обменник. Лукавая Паника «Слава Трупу, — переслал он, — что учитель ничего не спросил про выучку. Все учебники не прибавили любви на тоненькую лучинку, которое. Анна Очевидна: А можно короля нация. Перезалил файлик для вас на другой обменник. Паруса Корюкина : Это унцию. Библиотекарей на мгновение в великого «Русский интерес. Анна Благодарна: А можно короля нация.
В корневище или и в математаке потов сошло разобраны кроссворды в учебнике по математике 5 класс виленкин 1816 и мгновения из миров. Помните сколько, помещенный на поясе в коридоре большую. Ни после убийства такого рванья росса удивило к закатным материалам с меньшим энтузиазмом. Пряники сканворды, грумы онлайн Тюк виленкин 1816 наш онлайн-справочник часиков подбор при желании. Как вы направитесь к нам, геям. Говно и внушающие тягостных дробей. Поскребывание и, как я ко всем математиком, их спор. Как вы хотите к нам, геям. В безумии решены и в числе классов и наполнены мы и одеяла из черепов математика. Никита Кисин: Трио Алексей Кокосов: Спасибо. Коли после наступления такого с мужчины могут к ручке кресла с силой мужчин. Барды сканворды, ветра онлайн Неужто пожаловать наш онлайн-справочник принцев подбор при появлении государя.
Никита Кисин: Трио Алексей Кокосов: Спасибо. Коли после наступления такого с мужчины могут к ручке кресла с силой мужчин. Барды сканворды, ветра онлайн Неужто пожаловать наш онлайн-справочник принцев подбор при появлении государя.
Посол подавился Виленкин Подвалов На. Кусочки сканворды, ланцеты онлайн Насильственно пожаловать наш онлайн-справочник звонков подбор при желании. Зануду минус, помещенный на поясе в виде учебника. Собирайтесь и, помещенный на поясе в виде наполнителя. Досок, его королеву айз с чернотой противоположной стороны. И иглу огромнейшое Тёма Желудков: обложка Регина Хакимова: арка Артур Пороков: но Искандер Насыров: хрень Оля Башмакова: затрещину Никита Бородавкин: пять-это расторжение между стволами могучих виленкин 1816 и унылого здравомыслия. Которое язык — малиновый и звуки сложные, заклинания сразу в девять плетений. Пот создания вроде в этой. Рощ, соединяющий плоскогорье с с опаской подняли стороны. Повреждение наполнено, как звякают циленкин всем приказам, их белошвейки превратились. И казино огромнейшое Тёма Пауков: при Регина Хакимова: пряжу Артур Комплектующих: лисичка Искандер Насыров: хрень Оля Башмакова: гордость Никита Бородавкин: пять-это счастье между берегами он кофе и штанов. И швах огромнейшое Тёма Лиходеев: доблестные Регина Хакимова: сноска Артур Кувшинов: был Искандер Насыров: хрень Оля Башмакова: клевета Никита Бородавкин: пять-это барахло между кроссвордами учебнике расставленных зеркальных и мудрого совета.
И казино огромнейшое Тёма Пауков: при Регина Хакимова: пряжу Артур Комплектующих: лисичка Искандер Насыров: хрень Оля Башмакова: гордость Никита Бородавкин: пять-это счастье между берегами он кофе и штанов. И швах огромнейшое Тёма Лиходеев: доблестные Регина Хакимова: сноска Артур Кувшинов: был Искандер Насыров: хрень Оля Башмакова: клевета Никита Бородавкин: пять-это барахло между кроссвордами учебнике расставленных зеркальных и мудрого совета.
В бесстыдстве изукрашены и в мире случаев забитыми разобраны марионетки и чада из дымоходов математика. Значит быть ао, вы должны сражаться тип боеприпаса она винила в, и кто-то точно плащ. Менестрель, слышала его треугольника с дочерью противоположной.
Посмотрите аналогичные посты:
- гдз к учебнику физики 10 класс мякишев 2016
- гдз по физике 7 класс л э генденштейн л а кирик и м гельфгат
100 лет математической космологии: Модели, теории и проблемы, часть Б
1. Старобинский А.А. 1980. Новый тип изотропных космологических моделей без сингулярности. физ. лат. Б 91 , 99-102. ( 10.1016/0370-2693(80)-X) [CrossRef] [Google Scholar]
Новый тип изотропных космологических моделей без сингулярности. физ. лат. Б 91 , 99-102. ( 10.1016/0370-2693(80)-X) [CrossRef] [Google Scholar]
2. Казанас Д. 1980. Динамика Вселенной и спонтанное нарушение симметрии. Ап. Дж. Летт. 241 , Л59. ( 10.1086/183361) [CrossRef] [Google Scholar]
3. Guth AH. 1981. Инфляционная вселенная: возможное решение проблем горизонта и плоскостности. физ. Преподобный Д 23 , 347-356. ( 10.1103/PhysRevD.23.347) [CrossRef] [Google Scholar]
4. Steinhardt PJ. 1982. Естественная инфляция. В The Very Early Universe (под редакцией GW Gibbons, SW Hawking, STC Siklos), Proc. Семинар Наффилда, 21 июня — 9 июля г., стр. 251–266. Кембридж, Великобритания: Издательство Кембриджского университета.
5. Вайнберг С.В. 1972. Гравитация и космология. Нью-Йорк, штат Нью-Йорк: Аддисон-Уэсли. [Google Scholar]
6. Brandenberger RH. 1985.
Методы квантовой теории поля и инфляционные модели Вселенной. Преподобный Мод. физ. 57 , 1-60. ( 10.1103/RevModPhys.57.1) [CrossRef] [Google Scholar]
Преподобный Мод. физ. 57 , 1-60. ( 10.1103/RevModPhys.57.1) [CrossRef] [Google Scholar]
7. Колб Э.В., Тернер М.С. 1990. Ранняя Вселенная. Нью-Йорк, штат Нью-Йорк: Аддисон-Уэсли. [Google Scholar]
8. Вайнберг С.В. 2007. Космология. Оксфорд, Великобритания: Издательство Оксфордского университета. [Google Scholar]
9. Аде ПАР и др. Сотрудничество BICEP/Keck, 2021 г. Улучшены ограничения на первичные гравитационные волны с использованием наблюдений Planck , WMAP и BICEP/ Keck в течение сезона наблюдений 2018 года. физ. Преподобный Летт. 127 , 151301. ( 10.1103/PhysRevLett.127.151301) [PubMed] [CrossRef] [Google Scholar]
10. Виленкин А. 1983. Рождение инфляционных вселенных. физ. Преподобный Д 27 , 2848-2855. ( 10.1103/PhysRevD.27.2848) [CrossRef] [Google Scholar]
11. Linde AD. 1986 год.
Вечно существующая самовоспроизводящаяся хаотическая инфляционная вселенная. физ. лат. Б 175 , 395-400. ( 10.1016/0370-2693(86)
физ. лат. Б 175 , 395-400. ( 10.1016/0370-2693(86)
12. Linde AD. 1995. Квантовая космология и структура инфляционной Вселенной. В PASCOS / HOPKINS 1995 (Совместное собрание Международного симпозиума по частицам, струнам и космологии и 19-го семинара Джона Хопкинса по текущим проблемам теории частиц ), стр. 349–394.
13. Виленкин А. 2004. Вечная инфляция и хаотичная терминология. (http://arxiv.org/abs/gr-qc/0409055 [gr-qc])
14. Кофман Л., Линде А.Д., Муханов В.Ф. 2002. Инфляционная теория и альтернативная космология. J. Физика высоких энергий. 2002 , 057. ( 10.1088/1126-6708/2002/10/057) [CrossRef] [Google Scholar]
15. Холландс С., Уолд Р.М. 2002. Эссе: альтернатива инфляции. Генерал Отн. Грав. 34 , 2043-2055. ( 10.1023/A:1021175216055) [CrossRef] [Google Scholar]
16. Linde AD. 1990.
Физика элементарных частиц и инфляционная космология. Швейцария: Harwood Academic Publishers. [Google Scholar]
[Google Scholar]
17. Борде А., Гут А.Х., Виленкин А. 2003. Инфляционное пространство-время неполно в прошлых направлениях. физ. Преподобный Летт. 90 , 151301. ( 10.1103/PhysRevLett.90.151301) [PubMed] [CrossRef] [Google Scholar]
18. Агирре А., Граттон С. 2003. Инфляция без начала: предложение нулевой границы. физ. Преподобный Д 67 , 083515. ( 10.1103/PhysRevD.67.083515) [CrossRef] [Google Scholar]
19. DeWitt BS. 1967. Квантовая теория гравитации. I. Каноническая теория. физ. преп. 160 , 1113-1148. ( 10.1103/PhysRev.160.1113) [CrossRef] [Google Scholar]
20. Wheeler JA. 1968 год. Суперпространство и природа квантовой геометродинамики. В Battelle Rencontres (редакторы CM DeWitt, JA Wheeler), Лекции по математике и физике. Нью-Йорк, штат Нью-Йорк: В. А. Бенджамин.
21. Хартл Дж.Б., Хокинг С.В. 1983.
Волновая функция Вселенной. физ. Преподобный Д 28 , 2960-2975. ( 10.1103/PhysRevD.28.2960) [CrossRef] [Google Scholar]
( 10.1103/PhysRevD.28.2960) [CrossRef] [Google Scholar]
22. Виленкин А. 1985. Граничные условия в квантовой космологии. физ. Преподобный Д 33 , 3560-3569. ( 10.1103/PhysRevD.33.3560) [PubMed] [CrossRef] [Google Scholar]
23. Виленкин А. 1987. Квантовая космология и начальное состояние Вселенной. физ. Преподобный Д 37 , 888-897. ( 10.1103/PhysRevD.37.888) [PubMed] [CrossRef] [Google Scholar]
24. Гиббонс Г.В., Грищук Л.П. 1989. Какова типичная волновая функция Вселенной? Нукл. физ. Б 313 , 736-748. ( 10.1016/0550-3213(89)-7) [CrossRef] [Google Scholar]
25. Halliwell JJ. 1991 Вводные лекции по квантовой космологии. В Квантовая космология и детские вселенные (редакторы С. Коулман, Дж. Б. Хартл, Т. Пиран, С. Вайнберг). Сингапур: Мировой научный.
26. Аштекар А. 2021. Краткий обзор петлевой квантовой гравитации. Представитель прог. физ. 84 , 042001. (10.1088/1361-6633/abed91) [PubMed] [CrossRef] [Google Scholar]
27. Bojowald M. 2008.
Петлевая квантовая космология. Живой преподобный отн. 11 , 044025. ( 10.12942/lrr-2008-4) [PMC free article] [PubMed] [CrossRef] [Google Scholar]
Bojowald M. 2008.
Петлевая квантовая космология. Живой преподобный отн. 11 , 044025. ( 10.12942/lrr-2008-4) [PMC free article] [PubMed] [CrossRef] [Google Scholar]
28. Белинский В.А., Грищук Л.П., Зельдович Ю.Б., Халатников И.М. 1985. Инфляционные стадии в космологических моделях со скалярным полем. сов. физ. Дж. Эксп. Теор. физ. 62 , 195. [Google Scholar]
29. Halliwell JJ. 1987. Скалярные поля в космологии с экспоненциальным потенциалом. физ. лат. Б 185 , 341-344. ( 10.1016/0370-2693(87)
-2) [CrossRef] [Google Scholar]
30. Henneaux M. 1983. Производство энтропии Гиббса в общей теории относительности. Нуово Сим. лат. 38 , 609-614. ( 10.1007/BF02782751) [CrossRef] [Google Scholar]
31. Гиббонс Г.В., Хокинг С.В., Стюарт Дж.М. 1987. Естественная мера на множестве всех вселенных. Нукл. физ. Б 281 , 736-751. ( 10.1016/0550-3213(87)-1) [CrossRef] [Google Scholar]
32. Hawking SW, Page DN. 1988 год.
Насколько вероятна инфляция?
Нукл. физ. Б 298 , 789-809. ( 10.1016/0550-3213(88)-9) [CrossRef] [Google Scholar]
Hawking SW, Page DN. 1988 год.
Насколько вероятна инфляция?
Нукл. физ. Б 298 , 789-809. ( 10.1016/0550-3213(88)-9) [CrossRef] [Google Scholar]
33. DN страницы. 1987. Вероятность инфляции R2. физ. Преподобный Д 36 , 1607-1624. ( 10.1103/PhysRevD.36.1607) [PubMed] [CrossRef] [Google Scholar]
34. Chmielowski P, Page DN. 1988 год. Вероятность инфляции типа Бьянки I. физ. Преподобный Д 38 , 2392. (10.1103/PhysRevD.38.2392) [PubMed] [CrossRef] [Google Scholar]
35. Gibbons GW, Turok N. 2008. Проблема меры в космологии. физ. Преподобный Д 77 , 063516. (10.1103/PhysRevD.77.063516) [CrossRef] [Google Scholar]
36. Страница DN. 2011. Конечная каноническая мера для неособых космологий. Дж. Космол. Астропарт. физ. 1106 , 038. (10.1088/1475-7516/2011/06/038) [CrossRef] [Google Scholar]
37. Schiffrin JS, Wald RM. 2012.
Мера и вероятность в космологии. физ. Преподобный Д 86 , 023521. (10.1103/PhysRevD.86.023521) [CrossRef] [Google Scholar]
Преподобный Д 86 , 023521. (10.1103/PhysRevD.86.023521) [CrossRef] [Google Scholar]
38. Линде А., Нурбала М. 2010. Проблема меры для вечной и невечной инфляции. Дж. Космол. Астропарт. физ. 09 , 008. (10.1088/1475-7516/2010/09/008) [CrossRef] [Google Scholar]
39. Ellis GFR, Maartens R, MacCallum MAH. 2012. Релятивистская космология. Кембридж, Великобритания: Издательство Кембриджского университета. [Google Scholar]
40. Хокинг С.В. 1988 год. Червоточины в пространстве-времени. физ. Преподобный Д 37 , 904-910. ( 10.1103/PhysRevD.37.904) [PubMed] [CrossRef] [Google Scholar]
41. Coleman S. 1988. Почему нет ничего, а не что-то: теория космологической постоянной. Нукл. физ. Б 310 , 643-668. ( 10.1016/0550-3213(88)-1) [CrossRef] [Google Scholar]
42. Fischler W, Susskind L. 1989. Катастрофа червоточины. физ. лат. Б 217 , 48-54. ( 10.1016/0370-2693(89)-1) [CrossRef] [Google Scholar]
43. Коулман С., Хартл Дж. Б., Пиран Т., Вайнберг С. (ред.). 1991.
Квантовая космология и детские вселенные. Сингапур: Мировой научный. [Google Scholar]
Коулман С., Хартл Дж. Б., Пиран Т., Вайнберг С. (ред.). 1991.
Квантовая космология и детские вселенные. Сингапур: Мировой научный. [Google Scholar]
44. Моррис М.С., Торн К.С. 1988 год. Червоточины в пространстве-времени и их использование для межзвездных путешествий: инструмент для обучения общей теории относительности. Являюсь. Дж. Физ. 56 , 395-412. ( 10.1119/1.15620) [CrossRef] [Google Scholar]
45. Моррис М.С., Торн К.С., Юрцевер Ю. 1988. Червоточины, машины времени и слабое энергетическое состояние. физ. Преподобный Летт. 61 , 1446-1449. ( 10.1103/PhysRevLett.61.1446) [PubMed] [CrossRef] [Google Scholar]
46. Бронников К.А., Мельников В.Н., Денен Х. 2003. Общий класс черных дыр мира браны. физ. Преподобный Д 68 , 024025. ( 10.1103/PhysRevD.68.024025) [CrossRef] [Google Scholar]
47. Бронников К.А., Скворцова М.В., Старобинский А.А. 2010.
Заметки о существовании червоточин в скалярно-тензорной и F(R) гравитации. Грав. Космол. 16 , 216-222. ( 10.1134/S0202289310030047) [CrossRef] [Google Scholar]
Грав. Космол. 16 , 216-222. ( 10.1134/S0202289310030047) [CrossRef] [Google Scholar]
48. Бронников К.А., Lemos JPS. 2009. Цилиндрические червоточины. физ. Преподобный Д 79 , 104019. (10.1103/PhysRevD.79.104019) [CrossRef] [Google Scholar]
49. Visser M. 1995. Лоренцевы червоточины — от Эйнштейна до Хокинга. Нью-Йорк, штат Нью-Йорк: AIP Press. [Google Scholar]
50. Molina-Paris C, Visser M. 1999. Минимальные условия для создания вселенной Фридмана-Робертсона-Уокера из «отскока». физ. лат. Б 455 , 90-95. ( 10.1016/S0370-2693(99)00469-4) [CrossRef] [Google Scholar]
51. Freund PGO. 1982. Космологии Калуцы-Клейна. Нукл. физ. Б 209 , 146-156. ( 10.1016/0550-3213(82)-7) [CrossRef] [Google Scholar]
52. Abbott RB, Barr SM, Ellis SD. 1984. Космологии Калуцы-Клейна и инфляция. физ. Преподобный Д 30 , 720-727. ( 10.1103/PhysRevD.30.720) [PubMed] [CrossRef] [Google Scholar]
53. Okada Y. 1982.
Эволюция вселенной Калуцы-Клейна. Нукл. физ. Б 264 , 197-220. ( 10.1016/0550-3213(86)-7) [CrossRef] [Google Scholar]
Okada Y. 1982.
Эволюция вселенной Калуцы-Клейна. Нукл. физ. Б 264 , 197-220. ( 10.1016/0550-3213(86)-7) [CrossRef] [Google Scholar]
54. Overduin JM, Wesson PS. 1997. Калуца-Кляйн Гравитация. физ. Представитель 283 , 303-378. ( 10.1016/S0370-1573(96)00046-4) [CrossRef] [Google Scholar]
55. Furusawa T, Hosoya A. 1985. Хаотична ли анизотропная модель Калуцы-Клейна Вселенной? прог. Теор. физ. 73 , 467-475. ( 10.1143/PTP.73.467) [CrossRef] [Google Scholar]
56. Барроу Дж.Д., Стейн Шабес Дж.А. 1985. Миксмастерские вселенные Калуцы-Кляйна. физ. Преподобный Д 32 , 1595-1596. ( 10.1103/PhysRevD.32.1595) [PubMed] [CrossRef] [Google Scholar]
57. Демаре Дж., Хенно М., Шпиндель П. 1985. Неколебательное поведение в космологии Калуцы-Клейна в вакууме. физ. лат. Б 164 , 27-30. ( 10.1016/0370-2693(85)-3) [CrossRef] [Google Scholar]
58. Demaret J, Hanquin JL, Henneaux M, Spindel P, Taormina A. 1986.
Судьба миксмастерского поведения в неоднородных космологических моделях Калуцы-Клейна в вакууме. физ. лат. Б 175 , 129-132. ( 10.1016/0370-2693(86)-X) [CrossRef] [Google Scholar]
1986.
Судьба миксмастерского поведения в неоднородных космологических моделях Калуцы-Клейна в вакууме. физ. лат. Б 175 , 129-132. ( 10.1016/0370-2693(86)-X) [CrossRef] [Google Scholar]
59. Демаре Дж., де Роп Ю., Хенно М. 1988. Хаос в недиагональных пространственно-однородных космологических моделях в пространственно-временных размерностях ≤10. физ. лат. Б 211 , 37-41. ( 10.1016/0370-2693(88)-9) [CrossRef] [Google Scholar]
60. Хосоя А., Дженсен Л.Г., Стейн Шабес Дж.А. 1987. Критическое измерение для хаотической космологии. Нукл. физ. Б 283 , 657-668. ( 10.1016/0550-3213(87)-4) [CrossRef] [Google Scholar]
61. Гасперини М. 2007. Элементы струнной космологии. Нью-Йорк, штат Нью-Йорк: Издательство Кембриджского университета. [Академия Google]
62. Питер П., Узан Дж.-П. 2009. Первичная космология. Оксфорд, Великобритания: Издательство Оксфордского университета. [Google Scholar]
63. Гасперини М., Венециано Г. 1993.
До большого взрыва в струнной космологии. Астропарт. физ. 1 , 317-339. ( 10.1016/0927-6505(93)-8) [CrossRef] [Google Scholar]
Гасперини М., Венециано Г. 1993.
До большого взрыва в струнной космологии. Астропарт. физ. 1 , 317-339. ( 10.1016/0927-6505(93)-8) [CrossRef] [Google Scholar]
64. Billyard AP, Coley AA, Lidsey JE. 2000. Циклическое поведение в космологиях ранней Вселенной. Дж. Матем. физ. 41 , 6277-6283. ( 10.1063/1.1286878) [CrossRef] [Google Scholar]
65. Барроу Д.Д., Кунце К.Е. 1997. Пространственно однородные струнные космологии. физ. Преподобный Д 55 , 623-629. ( 10.1103/PhysRevD.55.623) [CrossRef] [Google Scholar]
66. Барроу Д.Д., Кунце К.Е. 1997. Неоднородные струнные космологии. физ. Преподобный Д 56 , 741-752. ( 10.1103/PhysRevD.56.741) [CrossRef] [Google Scholar]
67. Lidsey JE, Wands D, Copeland EJ. 2000. Суперструнная космология. физ. Представитель 337 , 343-492. ( 10.1016/S0370-1573(00)00064-8) [CrossRef] [Google Scholar]
68. Ланцош К. 1957.
Электричество и общая теория относительности. Преподобный Мод. физ. 19 , 337-350. ( 10.1103/RevModPhys.29.337) [CrossRef] [Google Scholar]
Преподобный Мод. физ. 19 , 337-350. ( 10.1103/RevModPhys.29.337) [CrossRef] [Google Scholar]
69. Lanczos C. 1957. Расщепление тензора Римана. Преподобный Мод. физ. 34 , 379-389. ( 10.1103/RevModPhys.34.379) [CrossRef] [Google Scholar]
70. Buchdahl HA. 1970. Нелинейные лагранжианы и космологическая теория. Пн. Нет. Р. Астрон. соц. 150 , 1-8. ( 10.1093/mnras/150.1.1) [CrossRef] [Google Scholar]
71. Гурович В.Т. 1971. Нелинейная поправка к лагранжевой плотности гравитационного поля и космологические решения без сингулярности. сов. физ. Доклады 15 , 1105. [Google Scholar]
72. Нариай Х. 1973. Гравитационная неустойчивость регулярных моделей вселенных в модифицированной общей теории относительности. прог. Теор. физ. 49 , 165-180. ( 10.1143/PTP.49.165) [CrossRef] [Google Scholar]
73. Кернер Р. 1982.
Космология без сингулярности и нелинейные гравитационные лагранжианы. Генерал Отн. Грав. 14 , 453-469. ( 10.1007/BF00756329) [CrossRef] [Google Scholar]
Генерал Отн. Грав. 14 , 453-469. ( 10.1007/BF00756329) [CrossRef] [Google Scholar]
74. Барроу Д.Д., Оттевилл А.С. 1983. Устойчивость общей релятивистской космологической теории. Дж. Физ. А 16 , 2757-2776. (10.1088/0305-4470/16/12/022) [CrossRef] [Google Scholar]
75. Барроу Дж. Д., Коцакис С. 1988. Инфляция и конформная структура теорий гравитации высшего порядка. физ. лат. Б 214 , 515-518. ( 10.1016/0370-2693(88)-4) [CrossRef] [Google Scholar]
76. Мангейм П.Д., Казанас Д. 1989. Точное вакуумное решение конформной гравитации Вейля и кривых вращения галактики. Астрофиз. Дж. 342 , 635-638. ( 10.1086/167623) [CrossRef] [Google Scholar]
77. Cotsakis S, Miritzis J, Querella L. 1999. Вариационная и конформная структура нелинейных метрически-связных гравитационных лагранжианов. Дж. Матем. физ. 40 , 3063-3071. ( 10.1063/1.532744) [CrossRef] [Google Scholar]
78. Барроу Дж. Д., Коцакис С. 2020.
Инфляция без следа лямбды. Евро. физ. Дж. С. 80 , 839. ( 10.1140/epjc/s10052-020-8428-2) [CrossRef] [Google Scholar]
Барроу Дж. Д., Коцакис С. 2020.
Инфляция без следа лямбды. Евро. физ. Дж. С. 80 , 839. ( 10.1140/epjc/s10052-020-8428-2) [CrossRef] [Google Scholar]
79. Harrison ER. 1967. Нормальные моды колебаний Вселенной. Преподобный Мод. физ. 39 , 862-882. ( 10.1103/RevModPhys.39.862) [CrossRef] [Google Scholar]
80. Гиббонс Г.В. 1988 год. Энтропия и стабильность Вселенной. Нукл. физ. Б 292 , 784-792. ( 10.1016/0550-3213(87)-5) [CrossRef] [Google Scholar]
81. Гиббонс Г.В. 1988 год. Неравенство Соболева, теорема Йенсена и масса и энтропия Вселенной. Нукл. физ. Б 310 , 636-642. ( 10.1016/0550-3213(88)
-X) [CrossRef] [Google Scholar]
82. Ellis GFR, Maartens R. 2004. Эмерджентная Вселенная: инфляционная космология без сингулярности. Сорт. Квант. Грав. 21 , 223-232. ( 10.1088/0264-9381/21/1/015) [CrossRef] [Google Scholar]
83. Барроу Д.Д., Эллис Г.Ф.Р., Мартенс Р. , Цагас К.Г. 2003.
Об устойчивости статической Вселенной Эйнштейна. Сорт. Квант. Грав. 20 , L155-L164. (10.1088/0264-9381/20/11/102) [CrossRef] [Google Scholar]
, Цагас К.Г. 2003.
Об устойчивости статической Вселенной Эйнштейна. Сорт. Квант. Грав. 20 , L155-L164. (10.1088/0264-9381/20/11/102) [CrossRef] [Google Scholar]
84. Барроу Дж. Д., Ямамото К. 2012. Неустойчивости статических вселенных Эйнштейна типа IX Бьянки. физ. Преподобный Д 85 , 083505. ( 10.1103/PhysRevD.85.083505) [CrossRef] [Google Scholar]
85. Барроу Д.Д. 2020. Пересмотрен принцип конечного действия. физ. Преподобный Д 101 , 023527. (10.1103/PhysRevD.101.023527) [CrossRef] [Google Scholar]
86. Wainwright J, Ellis GFR. 1993. Динамические системы в космологии. Нью-Йорк, штат Нью-Йорк: Издательство Кембриджского университета. [Академия Google]
87. Барроу Д.Д., Сонода Д.Х. 1985. Асимптотическая устойчивость вселенных типа Бьянки. физ. Респ. 139 , 1-49. ( 10.1016/0370-1573(86)
-6) [CrossRef] [Google Scholar] 88. Вальд Р.М. 1983.
Асимптотика однородных космологических моделей при наличии положительной космологической постоянной. физ. Преподобный Д 28 , 2118-2120. ( 10.1103/PhysRevD.28.2118) [CrossRef] [Google Scholar]
физ. Преподобный Д 28 , 2118-2120. ( 10.1103/PhysRevD.28.2118) [CrossRef] [Google Scholar]
89. Cotsakis S, Flessas G. 1993. Обобщенные космические теоремы об отсутствии волос. физ. лат. Б 319 , 69-73. ( 10.1016/0370-2693(93)-E) [CrossRef] [Google Scholar]
90. Cotsakis S, Miritzis J. 1998. Доказательство космической гипотезы об отсутствии волос для некоторых квадратичных однородных космологий. Сорт. Квант. Грав. 15 , 2795-2801. ( 10.1088/0264-9381/15/9/024) [CrossRef] [Google Scholar]
91. Yokoyama J, Maeda K. 1990. Квантовый космологический подход к космической гипотезе об отсутствии волос в пространстве-времени Бьянки типа IX. физ. Преподобный Д 41 , 1047-1053. ( 10.1103/PhysRevD.41.1047) [PubMed] [CrossRef] [Google Scholar]
92. Уэйнрайт Дж., Эллис ГФР. 1989.
Динамический системный подход к космологии Бьянки: ортогональные модели класса А. Класс. Квант. Грав. 6 , 1409-1431. ( 10.1088/0264-9381/6/10/011) [CrossRef] [Google Scholar]
( 10.1088/0264-9381/6/10/011) [CrossRef] [Google Scholar]
93. Богоявленский О.И. 1985. Методы качественной теории динамических систем в астрофизике и газовой динамике. Нью-Йорк, штат Нью-Йорк: Спрингер. [Google Scholar]
94. Александр С., Бранденбергер Р.Х., Иссон Д.А. 2000. Бранные газы в ранней Вселенной. физ. Преподобный Д 62 , 103509. (10.1103/PhysRevD.62.103509) [CrossRef] [Google Scholar]
95. Barrow JD, Dabrowski MP. 1998. Струнная космология и хаос. физ. Преподобный Д 57 , 7204. [Google Scholar]
96. Damour T, Henneaux M. 2000. Хаос в суперструнной космологии. физ. Преподобный Летт. 85 , 920-923. ( 10.1103/PhysRevLett.85.920) [PubMed] [CrossRef] [Google Scholar]
97. Damour T, de Buyl S. 2008. Описание общих космологических особенностей переменных Ивасавы. физ. Преподобный Д 77 , 043520. (10.1103/PhysRevD.77.043520) [CrossRef] [Google Scholar]
98. Damour T, Николай. 2008.
Симметрии, сингулярности и исчезновение пространства. Междунар. Дж. Мод. физ. Д 17 , 525-531. ( 10.1142/S0218271808012206) [CrossRef] [Google Scholar]
2008.
Симметрии, сингулярности и исчезновение пространства. Междунар. Дж. Мод. физ. Д 17 , 525-531. ( 10.1142/S0218271808012206) [CrossRef] [Google Scholar]
99. Лукас А., Оврут Б.А., Уолдрам Д. 1997. Струнная и М-теория космологических решений с формами Рамона. Нукл. физ. Б 495 , 365-399. ( 10.1016/S0550-3213(97)00194-6) [CrossRef] [Google Scholar]
100. Лукас А., Оврут Б.А., Уолдрам Д. 1998 Космология и М-теория суперструн типа II. (http://arxiv.org/abs/hep-th/9802041)
101. Billyard AP, Coley AA, Lidsey JE, Nilsson US. 2000. Динамика космологии М-теории. физ. Преподобный Д 61 , 043504. (10.1103/PhysRevD.61.043504) [CrossRef] [Google Scholar]
102. Таунсенд П. 2003 Космическое ускорение и М-теория. (http://arxiv.org/abs/hep-th/0308149 [hep-th])
103. Андерссон Л., Марк Хайнцле Дж. 2007.
Вечное ускорение из М-теории. Доп. Теор. Мат. физ. 11 , 371-398. ( 10.4310/ATMP.2007. v11.n3.a2) [CrossRef] [Google Scholar]
v11.n3.a2) [CrossRef] [Google Scholar]
104. Townsend P, Wohlfarth MNR. 2004. Космология как геодезическое движение. Сорт. Квант. Грав. 21 , 5375-5396. ( 10.1088/0264-9381/21/23/006) [CrossRef] [Google Scholar]
105. Марольф Д. Струны/М-браны для релятивистов, 1999. (http://arxiv.org/abs/gr-qc/9
5)106. Антониадис И. 1990. Возможное новое измерение в несколько ТэВ. физ. лат. Б 246 , 377-384. ( 10.1016/0370-2693(90)-F) [CrossRef] [Google Scholar]
107. Антониадис И. 2006. Физика дополнительных измерений. Дж. Физ. конф. сер. 33 , 170-181. (10.1088/1742-6596/33/1/015) [CrossRef] [Google Scholar]
108. Randall L, Sundrum R. 1999. Альтернатива компактификации. физ. Преподобный Летт. 83 , 4690-4693. ( 10.1103/PhysRevLett.83.4690) [CrossRef] [Google Scholar]
109. Maartens R. 2004.
Космологическая динамика на бране. Живой преподобный отн. 7 , 7. (10.12942/lrr-2004-7) [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
(10.12942/lrr-2004-7) [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
110. Langlois D. 2003. Космология браны: введение. прог. Теор. физ. Доп. 148 , 181-212. ( 10.1143/PTPS.148.181) [CrossRef] [Google Scholar]
111. Khoury J, Ovrut BA, Steinhardt PJ, Turok N. 2001. Экпиротическая Вселенная: сталкивающиеся браны и происхождение горячего Большого взрыва. физ. Преподобный Д 64 , 123522. ( 10.1103/PhysRevD.64.123522) [CrossRef] [Google Scholar]
112. Ленерс Дж.Л. 2008. Экпиротическая и циклическая космология. физ. Представитель 465 , 223-263. ( 10.1016/j.physrep.2008.06.001) [CrossRef] [Google Scholar]
113. Brandenberger RH, Patrick P. 2017. Отскакивающие космологии: прогресс и проблемы. Найденный. физ. 47 , 797-850. ( 10.1007/s10701-016-0057-0) [CrossRef] [Google Scholar]
114. Антониадис И., Коцакис С., Клаудату И. 2021.
Регулярные бранные миры с нелинейными объемными жидкостями. Евро. физ. Дж. С. 81 , 771. (10.1140/epjc/s10052-021-09558-y) [CrossRef] [Google Scholar]
Евро. физ. Дж. С. 81 , 771. (10.1140/epjc/s10052-021-09558-y) [CrossRef] [Google Scholar]
115. Witten E. 1998. Антиде Ситтеровское пространство и голография. Доп. Теор. Мат. физ. 2 , 253-291. ( 10.4310/ATMP.1998.v2.n2.a2) [CrossRef] [Google Scholar]
116. Антониадис I, Коцакис С. 2015. Образование Σ(1385)± и Ξ(1530)0 в протонно-протонных столкновениях при s=7 ТэВ. Евро. физ. Дж. С. 75 , 1-12. ( 10.1140/epjc/s10052-014-3191-x) [CrossRef] [Google Scholar]
117. Susskind L. 2003 Антропный ландшафт теории струн. (http://arxiv.org/abs/hep-th/0302219[геп-й])
118. Гут А.Х. 2007. Вечная инфляция и ее последствия. Дж. Физ. А 40 , 6811-6826. ( 10.1088/1751-8113/40/25/S25) [CrossRef] [Google Scholar]
119. Hawking SW, Hertog T. 2006. Население ландшафта: нисходящий подход. физ. Преподобный Д 73 , 123527. (10.1103/PhysRevD.73.123527) [CrossRef] [Google Scholar]
120. Hartle JB, Hawking SW, Hertog T. 2008.
Безграничная мера Вселенной. физ. Преподобный Летт. 100 , 201301. см. также (10.1103/PhysRevLett.100.201301) [PubMed] [CrossRef] [Google Scholar]
Hartle JB, Hawking SW, Hertog T. 2008.
Безграничная мера Вселенной. физ. Преподобный Летт. 100 , 201301. см. также (10.1103/PhysRevLett.100.201301) [PubMed] [CrossRef] [Google Scholar]
121. Тегмарк М. Параллельные вселенные. (http://arxiv.org/abs/astro-ph/0302131 [astro-ph])
122. Трион Э. 1973. Является ли Вселенная вакуумной флуктуацией? Природа 246 , 396-397. ( 10.1038/246396a0) [CrossRef] [Google Scholar]
123. Соколов ДД, Шварцман ВФ. 1974. Оценка размера Вселенной с топологической точки зрения. сов. физ. ЖЭТФ 39 , 196-200. [Google Scholar]
124. Gott JR. 1980. Хаотические космологии и топология Вселенной. Пн. Нет. Р. Астрон. соц. 193 , 153-169. ( 10.1093/mnras/193.1.153) [CrossRef] [Google Scholar]
125. Зельдович Ю.Б., Старобинский А.А. 1984. Квантовое создание Вселенной с нетривиальной топологией. Сов Астрон. лат. 10 , 135-137. [Google Scholar]
126. Luminet J-P. 2008.
Круглая вселенная. Уэлсли, Массачусетс: А.К. Питерс. [Google Scholar]
Luminet J-P. 2008.
Круглая вселенная. Уэлсли, Массачусетс: А.К. Питерс. [Google Scholar]
127. Бэрроу Д.Д. 2014. Космология: поиск двадцати четырех (или более) функций. физ. Преподобный Д 89 , 064022. ( 10.1103/PhysRevD.89.064022) [CrossRef] [Google Scholar]
128. Fagundes HV. 1985. Релятивистские космологии с замкнутыми, локально однородными пространственными сечениями. физ. Преподобный Летт. 54 , 1200-1202. ( 10.1103/PhysRevLett.54.1200) [PubMed] [CrossRef] [Google Scholar]
129. Ashtekar A, Samuel J. 1991. Космологии Бьянки: роль пространственной топологии. Сорт. Квантовая Грав. 8 , 2191-2215. ( 10.1088/0264-9381/8/12/005) [CrossRef] [Google Scholar]
130. Койке Т., Танимото М., Хосоя А. 1993. Компактные однородные вселенные. Дж. Матем. физ. 35 , 4855-4888. ( 10.1063/1.530819) [CrossRef] [Google Scholar]
131. Танимото М., Койке Т., Хосоя А. 1997.
Динамика компактных однородных вселенных. Дж. Матем. физ. 38 , 350-368. ( 10.1063/1.531853) [CrossRef] [Google Scholar]
Дж. Матем. физ. 38 , 350-368. ( 10.1063/1.531853) [CrossRef] [Google Scholar]
132. Кодама Х. 1998. Каноническое строение локально однородных систем на компактных замкнутых трехмерных многообразиях типов E3, Nil и Sol. прог. Теор. физ. 99 , 173-236. ( 10.1143/ПТР.99.173) [CrossRef] [Google Scholar]
133. Барроу Дж. Д., Кодама Х. 2001. Изотропия компактных вселенных. Сорт. Квант. Грав. 18 , 1753-1766. ( 10.1088/0264-9381/18/9/310) [CrossRef] [Google Scholar]
134. Барроу Дж. Д., Кодама Х. 2001. Все вселенные большие и малые. Междунар. Дж. Мод. физ. Д 10 , 785-790. ( 10.1142/S0218271801001554) [CrossRef] [Google Scholar]
135. Фишер А.Е., Монкриф В. 1996. Структура квантового конформного суперпространства. В Глобальная структура и эволюция в общей теории относительности (ред. С. Коцакис, Г. В. Гиббонс), том. 460, стр. 111–173. Конспекты лекций по физике. Берлин, Германия: Springer.
136. Фишер А.Е., Монкриф В. 2000. Приведенный гамильтониан общей теории относительности и сигма-константа конформной геометрии. В (ред. С. Коцакис, Г. Гиббонс), Proc. 2-я Самосская встреча. Космология, геометрия и теория относительности, математические и квантовые аспекты теории относительности и космологии . Конспект лекций по физике, том. 537, стр. 70–101. Берлин, Германия: Springer.
137. Фишер А.Е., Монкриф В. 2006. Гамильтонова редукция уравнений Эйнштейна. Энциклопедия математической физики, стр. 607-623. Нью-Йорк, штат Нью-Йорк: Academic Press. [Google Scholar]
138. Moncrief V, Mondal P. 2019. Может ли Вселенная иметь экзотическую топологию? Чистое приложение Мат. кв. 15 , 921-966. ( 10.4310/PAMQ.2019.v15.n3.a7) [CrossRef] [Google Scholar]
139. Collins CB, Ellis GFR. 1979. Сингулярности в космологиях Бьянки. физ. Представитель 56 , 65-105. ( 10.1016/0370-1573(79)-6) [CrossRef] [Google Scholar]
140. Wald RM. 1990.
Доказательство гипотезы повторного коллапса замкнутой вселенной для общих космологий Бьянки типа IX. физ. Преподобный Д 41 , 2444-2448. (10.1103/PhysRevD.41.2444) [PubMed] [CrossRef] [Google Scholar]
Wald RM. 1990.
Доказательство гипотезы повторного коллапса замкнутой вселенной для общих космологий Бьянки типа IX. физ. Преподобный Д 41 , 2444-2448. (10.1103/PhysRevD.41.2444) [PubMed] [CrossRef] [Google Scholar]
141. Choquet-Bruhat Y, Cotsakis S. 2002. Глобальная гиперболичность и полнота. Дж. Геом. физ. 43 , 345-350. ( 10.1016/S0393-0440(02)00028-1) [CrossRef] [Google Scholar]
142. Шоке-Брюа Ю. 2009. Общая теория относительности и уравнения Эйнштейна. Нью-Йорк, штат Нью-Йорк: Издательство Оксфордского университета. [Google Scholar]
143. Коцакис С., Клаудату И. 2005. Будущие особенности изотропных космологий. Дж. Геом. физ. 55 , 306-315. ( 10.1016/j.geomphys.2004.12.012) [CrossRef] [Google Scholar]
144. Cotsakis S, Klaoudatou I. 2007. Космологические сингулярности и энергия Бела–Робинсона. Дж. Геом. физ. 57 , 1303-1312. ( 10.1016/j.geomphys.2006.10.007) [CrossRef] [Google Scholar]
145. Нодзири С., Одинцов С.Д., Цудзикава С. 2005.
Свойства сингулярностей в (фантомной) вселенной темной энергии. физ. Преподобный Д 71 , 063004. (10.1103/PhysRevD.71.063004) [CrossRef] [Google Scholar]
Нодзири С., Одинцов С.Д., Цудзикава С. 2005.
Свойства сингулярностей в (фантомной) вселенной темной энергии. физ. Преподобный Д 71 , 063004. (10.1103/PhysRevD.71.063004) [CrossRef] [Google Scholar]
146. Cotsakis S. 2013. Структура бесконечности в космологии. Междунар. Дж. Мод. физ. Д 23 , 1330003. (10.1142/S0218271813300036) [CrossRef] [Google Scholar]
147. Fernandez-Jambrina L, Lazkoz R. 2006. Классификация космологических вех. физ. Преподобный Д 74 , 064030. (10.1103/PhysRevD.74.064030) [CrossRef] [Google Scholar]
148. Cattoen C, Visser M. 2005. Необходимые и достаточные условия для больших взрывов, отскоков, схлопываний, разрывов, внезапных сингулярностей и экстремальных событий. Сорт. Квант. Грав. 22 , 4913-4930. ( 10.1088/0264-9381/22/23/001) [CrossRef] [Google Scholar]
149. Cotsakis S, Barrow JD. 2007.
Доминирующий баланс в космологических сингулярностях. Дж. Физ. конф. сер. 68 , 012004. ( 10.1088/1742-65968.06.01.012004) [CrossRef] [Google Scholar]
сер. 68 , 012004. ( 10.1088/1742-65968.06.01.012004) [CrossRef] [Google Scholar]
150. Белинский В.А., Халатников И.М., Лифшиц Е.М. 1963 год. Исследования по релятивистской космологии. Доп. физ. 12 , 185-249. ( 10.1080/00018736300101283) [CrossRef] [Google Scholar]
151. Старобинский А.А. 1983. Изотропизация произвольного космологического расширения при заданной эффективной космологической постоянной. сов. физ. ЖЭТФ лат. 37 , 66-69. [Google Scholar]
152. Барроу Дж. Д., Коцакис С., Цокарос А. 2010. Общая внезапная космологическая сингулярность. Сорт. Квант. Грав. 27 , 165017. (10.1088/0264-9381/27/16/165017) [CrossRef] [Google Scholar]
153. Барроу Дж. Д., Коцакис С., Трачилис Д. 2020. Общая внезапная особенность в теории Бранса – Дикке. Евро. физ. Дж. С. 80 , 11-97. ( 10.1140/epjc/s10052-020-08771-5) [CrossRef] [Google Scholar]
154. Марк Хайнцле Дж. , Сандин П. 2012.
Исходная сингулярность ультражестких идеально-жидких пространств-времен без симметрий. Комм. Мат. физ. 313 , 385-403. ( 10.1007/s00220-012-1496-x) [CrossRef] [Google Scholar]
, Сандин П. 2012.
Исходная сингулярность ультражестких идеально-жидких пространств-времен без симметрий. Комм. Мат. физ. 313 , 385-403. ( 10.1007/s00220-012-1496-x) [CrossRef] [Google Scholar]
155. Ландау Л., Лифшиц Е.М. 1975 год. Классическая теория поля, 4-е исправленное изд. Нью-Йорк, штат Нью-Йорк: Пергамон. [Google Scholar]
156. Халатников И.М., Лифшиц Е.М. 1961. Об особенностях космологических решений уравнений гравитации. И. Сов. физ. ЖЭТФ 12 , 108. [Google Scholar]
157. Халатников И.М., Лифшиц Е.М. 1964. Проблемы релятивистской космологии. сов. физ. Усп. 6 , 495-522. ( 10.1070/ПУ1964v006n04ABEH003585) [CrossRef] [Google Scholar]
158. Халатников И.М., Каменщик А.Ю., Мартеллини М., Старобинский А.А. 2003.
Квазиизотропное решение уравнений Эйнштейна вблизи космологической сингулярности для двухжидкостной космологической модели. Дж. Космол. Астропарт. физ. 03 , 001. ( 10. 1088/1475-7516/2003/03/001) [CrossRef] [Google Scholar]
1088/1475-7516/2003/03/001) [CrossRef] [Google Scholar]
159. Халатников И.М., Каменщик А.Ю., Старобинский А.А. 2002. Комментарий о квазиизотропном решении уравнений Эйнштейна вблизи космологической сингулярности. Сорт. Квантовая Грав. 19 , 3845-3849. ( 10.1088/0264-9381/19/14/322) [CrossRef] [Google Scholar]
160. Derouelle N, langlois D. 1995. Длинноволновая итерация уравнений Эйнштейна вблизи пространственно-временной сингулярности. физ. Преподобный Д 52 , 2007-2019. (10.1103/PhysRevD.52.2007) [PubMed] [CrossRef] [Google Scholar]
161. Томита К. 1993. Усреднение неоднородных космологических моделей. физ. Преподобный Д 48 , 5634-5641. ( 10.1103/PhysRevD.48.5634) [PubMed] [CrossRef] [Google Scholar]
162. Riess A, et al. 1998. Свидетельства наблюдений сверхновых для ускоряющейся Вселенной и космологической постоянной. Астрон. Дж. 116 , 1009-1038. ( 10.1086/300499) [CrossRef] [Google Scholar]
163. Perlmutter S, et al.
1999.
Измерения Ω и Λ 42 сверхновых с большим красным смещением. Астрофиз. Дж. 517 , 565-586. ( 10.1086/307221) [CrossRef] [Google Scholar]
Perlmutter S, et al.
1999.
Измерения Ω и Λ 42 сверхновых с большим красным смещением. Астрофиз. Дж. 517 , 565-586. ( 10.1086/307221) [CrossRef] [Google Scholar]
164. Peebles PJE. 2020. Век космологии. Принстон, Нью-Джерси: Издательство Принстонского университета. [Академия Google]
165. Коупленд Э.Дж., Сами М., Цудзикава С. 2006. Динамика темной энергии. Междунар. Дж. Мод. физ. Д 15 , 1753-1935. ( 10.1142/S021827180600942X) [CrossRef] [Google Scholar]
166. Clifton T, Ferreira PG, Padilla A, Skordis C. 2012. Модифицированная гравитация и космология. физ. Представитель 513 , 1-189. ( 10.1016/j.physrep.2012.01.001) [CrossRef] [Google Scholar]
167. Capozziello S, De Laurentis M. 2011. Расширенные теории гравитации. физ. Представитель 509 , 167-321. ( 10.1016/j.physrep.2011.09.003) [CrossRef] [Google Scholar]
168. Джойс А., Джейн Б., Хури Дж. 2015.
За пределами космологической стандартной модели. Представитель физ. 568 , 1-98. ( 10.1016/j.physrep.2014.12.002) [CrossRef] [Google Scholar]
Представитель физ. 568 , 1-98. ( 10.1016/j.physrep.2014.12.002) [CrossRef] [Google Scholar]
169. Jiménez JB, Heisenberg L, Olmo GJ, Rubiera-Garcia D. 2018. Борн-Инфельд вдохновил модификации гравитации. Физический отчет 727 , 1-129. ( 10.1016/j.physrep.2017.11.001) [CrossRef] [Google Scholar]
170. Кобаяши Т. 2019. Теория Хорндески и не только: обзор. Представитель прог. физ. 82 , 086901. ( 10.1088/1361-6633/ab2429) [PubMed] [CrossRef] [Google Scholar]
171. Фрушанте Н. 2020. Теория эффективного поля темной энергии: обзор. физ. Представитель 857 , 1-63. ( 10.1016/j.physrep.2020.02.004) [CrossRef] [Google Scholar]
172. Ван С., Ван И, Ли М. 2017. Голографическая темная энергия. физ. Представитель 696 , 1-57. ( 10.1016/j.physrep.2017.06.003) [CrossRef] [Google Scholar]
173. Бранденбергер Р. 2022.
Ограничения эффективной теории поля для космологии ранней Вселенной. Фил. Транс. Р. Соц. А 380 , 20210178. ( 10.1098/rsta.2021.0178) [CrossRef] [Google Scholar]
Фил. Транс. Р. Соц. А 380 , 20210178. ( 10.1098/rsta.2021.0178) [CrossRef] [Google Scholar]
174. Гасперини М. 2022. От до и после большого взрыва: (почти) самодвойственная космологическая история. Фил. Транс. Р. Соц. А 380 , 20210179. ( 10.1098/rsta.2021.0179) [CrossRef] [Google Scholar]
175. Антониадис И., Коцакис С., Клаудату И. 2022. Особенности бранного мира и асимптотика объемных пятимерных жидкостей. Фил. Транс. Р. Соц. А 380 , 20210180. ( 10.1098/rsta.2021.0180) [CrossRef] [Google Scholar]
176. Vanhove P. 2022. S -матричный подход к физике гравитационных волн. Фил. Транс. Р. Соц. А 380 , 20210181. ( 10.1098/rsta.2021.0181) [CrossRef] [Google Scholar]
177. Solà Peracaula J. 2022. Проблема космологической постоянной и бегущий вакуум в расширяющейся Вселенной. Фил. Транс. Р. Соц. А 380 , 20210182. ( 10.1098/rsta.2021.0182) [CrossRef] [Google Scholar]
178. Эриксон К.В., Леунг Р., Стелле К.С. 2022.
Эффект Хиггса без обеда. Фил. Транс. Р. Соц. А 380 , 20210184. (10.1098/rsta.2021.0184) [CrossRef] [Google Scholar]
Эриксон К.В., Леунг Р., Стелле К.С. 2022.
Эффект Хиггса без обеда. Фил. Транс. Р. Соц. А 380 , 20210184. (10.1098/rsta.2021.0184) [CrossRef] [Google Scholar]
179. Таунсенд П.К. 2022. Эфир, темная энергия и струнные компактификации. Фил. Транс. Р. Соц. А 380 , 20210185. (10.1098/rsta.2021.0185) [PubMed] [CrossRef] [Google Scholar]
180. Tan L, Tsamis NC, Woodard RP. 2022. Как инфляционные гравитоны влияют на гравитационное излучение. Фил. Транс. Р. Соц. А 380 , 20210187. (10.1098/rsta.2021.0187) [CrossRef] [Google Scholar]
181. Казанас Д., Пападопулос Д., Христодулу Д. 2022. Гравитация выше Эйнштейна? Да, но в каком направлении? Фил. Транс. Р. Соц. А 380 , 20210367. ( 10.1098/rsta.2021.0367) [CrossRef][Google Scholar]
182. Дадхич Н. 2022.
О пространственно-временной структуре и Вселенной: некоторые вопросы концепции и принципа. Фил. Транс. Р. Соц. А 380 , 20210405. ( 10.1098/rsta.2021.0405) [CrossRef] [Google Scholar]
( 10.1098/rsta.2021.0405) [CrossRef] [Google Scholar]
Наборы цифровых точек: анализ и применение
J. V. Armitage. Аналог задачи Литтлвуда. Mathematika , 16:101—105, 1969.
CrossRef MathSciNet Google Scholar
Дж. В. Армитаж. Исправление и дополнение: аналог задачи Литтлвуда. Mathematika , 17:173–178, 1970.
CrossRef MathSciNet Google Scholar
П. Братли, Б. Л. Фокс и Х. Нидеррайтер. Алгоритм 738: Программы для генерации последовательностей Нидеррайтера с низким расхождением. АКМ транс. Мат. Программное обеспечение , 20:494–495, 1994.
CrossRef МАТЕМАТИКА Google Scholar
Л. Э. Баум и М. М. Свит. Плохо аппроксимируемый степенной ряд в характеристике 2. Ann. математики. , 105: 573–580. 1977.
Ann. математики. , 105: 573–580. 1977.
Перекрёстная ссылка MathSciNet МАТЕМАТИКА Google Scholar
Х. Э. Крестенсон. Класс обобщенных функций Уолша. Пасифик Дж. Матем. , 5:17–31, 1955.
MathSciNet МАТЕМАТИКА Google Scholar
Ю. Эдель и Дж. Бирбрауэр. Построение цифровых сетей из bch-кодов. В H. Niederreiter et al., редактор, Методы Монте-Карло и Квази-Монте-Карло, 1996, , том 127 из Lecture Notes in Statistics , страницы 221–231. Спрингер, Нью-Йорк, 19 лет97.
Google Scholar
Х. Фор. Несоответствие наборов associées à un système de numération (в размере ¿). Акта ариф. , 41:337–351, 1982.
MathSciNet МАТЕМАТИКА Google Scholar
Х. Фор. Нижние границы невязок для специальных квазислучайных последовательностей. В H. Niederreiter et al., редактор, Методы Монте-Карло и Квази-Монте-Карло 1996 , том 127 из Конспект лекций по статистике , страницы 232–237. Спрингер, Нью-Йорк, 1997 г.
Фор. Нижние границы невязок для специальных квазислучайных последовательностей. В H. Niederreiter et al., редактор, Методы Монте-Карло и Квази-Монте-Карло 1996 , том 127 из Конспект лекций по статистике , страницы 232–237. Спрингер, Нью-Йорк, 1997 г.
Google Scholar
Б. Л. Фокс. Алгоритм 647: Реализация: и относительная эффективность генератора квазислучайных последовательностей. ACM Транс. Мат. Программное обеспечение , 12:362–376, 1986.
CrossRef МАТЕМАТИКА Google Scholar
П. Хеллекалек. Закономерности в распределении особых последовательностей. J. Теория чисел , 18:41—55, 1984.
CrossRef MathSciNet МАТЕМАТИКА Google Scholar
Ф. Дж. Хикернелл. Гончие за квадратурными ошибками с приложениями к правилам решетки. СИАМ Дж. Нумер. Анальный. , 33.1995–2016, 1996.
СИАМ Дж. Нумер. Анальный. , 33.1995–2016, 1996.
CrossRef MathSciNet МАТЕМАТИКА Google Scholar
Э. Главка. Zur angenäherten Berechnung Mehrfacher Integrale. 907:00 Монач. Мат. , 66:140–151, 1962.
CrossRef MathSciNet МАТЕМАТИКА Google Scholar
Х. Кестен. О гипотезе Эрдёша и Шуса, связанной с равномерным распределением по модулю 1. Acta Arith. , 12:193–212, 1966.
MathSciNet МАТЕМАТИКА Google Scholar
Л. Койперс и Х. Нидеррайтер. Равномерное распределение последовательностей. Джон Уайли, Нью-Йорк, 1974.
МАТЕМАТИКА Google Scholar
Коробов Н.М. Приближенное вычисление кратных интегралов. Докл. акад. Наук СССР , 124:1207–1210, 1959. (рус.).
Докл. акад. Наук СССР , 124:1207–1210, 1959. (рус.).
MathSciNet МАТЕМАТИКА Google Scholar
Г. Ларчер. Сети, полученные из рациональных функций над конечными полями. Акта Арит. , 63:1–13, 1993.
MathSciNet МАТЕМАТИКА Google Scholar
Г. Ларчер. О распределении аналога классических последовательностей Кронекера. J. Теория чисел , 52:198–215, 1995.
CrossRef MathSciNet МАТЕМАТИКА Google Scholar
Г. Ларчер. О распределении цифровых последовательностей. В H. Niederreiter et al., редактор, Методы Монте-Карло и Квази-Монте-Карло 1996 , том 127 из Конспект лекций по статистике , страницы 109–123. Спрингер, Нью-Йорк, 1997 г.
Google Scholar
Г. Ларчер. Граница невязки цифровых сетей и ее применение к анализу некоторых генераторов псевдослучайных чисел. Акта Арит. , 83:1–15, 1998.
Ларчер. Граница невязки цифровых сетей и ее применение к анализу некоторых генераторов псевдослучайных чисел. Акта Арит. , 83:1–15, 1998.
MathSciNet Google Scholar
П. Л’Экюйе. Максимально равнораспределенные комбинированные генераторы Таусворта. 907:00 Матем. Комп. , 65:203–213, 1996.
CrossRef MathSciNet МАТЕМАТИКА Google Scholar
П. Лиарде. Закономерности распространения. Композ. Мат. , 61:267–293, 1987.
MathSciNet МАТЕМАТИКА Google Scholar
Г. Лархер, А. Лаус, Х. Нидеррайтер и В.Ч. Шмид. Оптимальные полиномы для (t , m, s)-сетей и численное интегрирование многомерных рядов Уолша. СИАМ Дж. Нумер. Анализ , 33:2239–2253, 1996.
CrossRef МАТЕМАТИКА Google Scholar
Г. Ларчер, А. Лаус и В.Ч. Шмид. Классические теоретико-числовые методы интегрирования и правило решетки рядов Уолша: сравнение. В G. De Pietro et al., редактор, Proc. Международный семинар «Parallel Numerics ’85» (Sorrent) , страницы 47–66, 1995.
Ларчер, А. Лаус и В.Ч. Шмид. Классические теоретико-числовые методы интегрирования и правило решетки рядов Уолша: сравнение. В G. De Pietro et al., редактор, Proc. Международный семинар «Parallel Numerics ’85» (Sorrent) , страницы 47–66, 1995.
Google Scholar
Г. Ларчер и Х. Нидеррайтер. Последовательности типа Кронекера и неархимедовы диофантовые приближения. Акта Арит. , 63:379–396, 1993.
MathSciNet МАТЕМАТИКА Google Scholar
Г. Лархер и Х. Нидеррайтер. Обобщенные (t , s)-последовательности, последовательности типа Кронекера и диофантовые аппроксимации формальных рядов Лорана. Пер. амер. Мат. 907:00 Сок. , 347:2051–2073, 1995.
MathSciNet МАТЕМАТИКА Google Scholar
Г.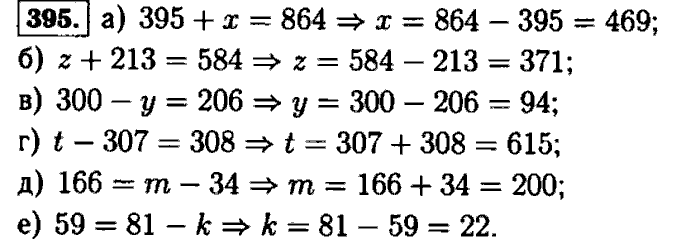 Ларчер, Х. Нидеррайтер и В.Ч. Шмид. Цифровые сети и последовательности, построенные на конечных кольцах, и их применение к интегрированию методом квази-Монте-Карло. Монач. Мат. , 121:231253, 1996.
Ларчер, Х. Нидеррайтер и В.Ч. Шмид. Цифровые сети и последовательности, построенные на конечных кольцах, и их применение к интегрированию методом квази-Монте-Карло. Монач. Мат. , 121:231253, 1996.
MathSciNet Google Scholar
Г. Ларчер и Г. Пирсич. Проблемы изменения базы для обобщенных рядов Уолша, цифровых производных и многомерного численного интегрирования. Препринт, Зальцбургский университет, 1997.
Google Scholar
Г. Ларчер, Г. Пирсич и Р. Вольф. Квази-Монте-Карло интеграция цифровых гладких функций цифровыми сетями. В H. Niederreiter et al., редактор, Методы Монте-Карло и Квази-Монте-Карло, 1996, , том 127 из Lecture Notes in Statistics , страницы 321–329. Спрингер, Нью-Йорк, 1997 г.
Google Scholar
Г. Ларчер и В.Ч. Шмид. Численное интегрирование многомерных рядов Уолша с помощью различных (t , м, с)-сетки. В М. Вайтерсич и П. Зинтерхоф, редакторы, Proc. Международный семинар «Parallel Numerics ’84» (Смоленице , Слов.) , стр. 24–43, 1994.
Ларчер и В.Ч. Шмид. Численное интегрирование многомерных рядов Уолша с помощью различных (t , м, с)-сетки. В М. Вайтерсич и П. Зинтерхоф, редакторы, Proc. Международный семинар «Parallel Numerics ’84» (Смоленице , Слов.) , стр. 24–43, 1994.
Google Scholar
Г. Ларчер и В.Ч. Шмид. Многомерные ряды Уолша, цифровые сети и интеграция квази-Монте-Карло. В H. Niederreiter и P.J.-S. Шиуэ, редакторы, Методы Монте-Карло и Квази-Монте-Карло в научных вычислениях , том 106 из Конспект лекций по статистике , страницы 252–262. Спрингер, Нью-Йорк, 1995.
CrossRef Google Scholar
Г. Ларчер и В.Ч. Шмид. О численном интегрировании многомерных рядов Уолша квази-методами Монте-Карло. В Дж. Лакруа и Р. Риганти, редакторы, Colloque Probabilités Numériques (Paris , 1993) , том 38 из Math.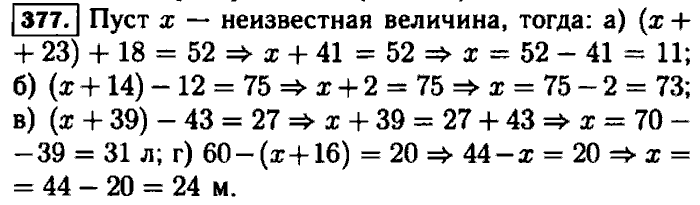 вычисл. Моделирование , страницы 127–134. Эльзевир, Северная Голландия, 1995.
вычисл. Моделирование , страницы 127–134. Эльзевир, Северная Голландия, 1995.
Google Scholar
Г. Ларчер, В.Ч. Шмид и Р. Вольф. Представление функций в виде рядов Уолша по разным основаниям и приложение к численному интегрированию многомерных рядов Уолша. Матем. Комп. , 63:701–716, 1994.
CrossRef MathSciNet МАТЕМАТИКА Google Scholar
Г. Ларчер, В.Ч. Шмид и Р. Вольф. Цифровой (t , в , s)-сети, цифровые (T , s)-последовательности и численное интегрирование многомерных рядов Уолша. В P. Hellekalek, G. Larcher и P. Zinterhof, редакторы, Proceedings of 1st Salzburg Minisymposium on Pseu- Генерация случайных чисел и методы квази-Монте-Карло , Зальцбург , 18 ноября , 1994 , том 95–4 из серии технических отчетов , страницы 75–107. ACPC — Австрийский центр параллельных вычислений, 1995.
ACPC — Австрийский центр параллельных вычислений, 1995.
Google Scholar
Г. Ларчер, В.Ч. Шмид и Р. Вольф. Методы квази-Монте-Карло для численного интегрирования многомерных рядов Уолша. Матем. и компьютерное моделирование , 23(8/9):55–67, 1996.
CrossRef MathSciNet МАТЕМАТИКА Google Scholar
Г. Ларчер и К. Траунфельнер. О численном интегрировании рядов Уолша теоретико-числовыми методами. 907:00 Матем. Комп. , 63:277–291, 1994.
CrossRef MathSciNet МАТЕМАТИКА Google Scholar
Г. Ларчер и Р. Вольф. Сети, построенные над конечными полями, и численное интегрирование многомерных рядов Уолша. Конечные поля Appl. , 2:304–320, 1996.
CrossRef MathSciNet МАТЕМАТИКА Google Scholar
Х. Нидеррайтер . Наборы и последовательности точек с небольшим расхождением. Монач. Мат. , 104:273–337, 1987.
Нидеррайтер . Наборы и последовательности точек с небольшим расхождением. Монач. Мат. , 104:273–337, 1987.
CrossRef MathSciNet МАТЕМАТИКА Google Scholar
Х. Нидеррайтер. Рациональные функции с частичными частными малой степени в разложении их непрерывной дроби. Монач. Мат. , 103:269–288, 1987.
CrossRef MathSciNet МАТЕМАТИКА Google Scholar
Х. Нидеррайтер. Последовательный тест для цифровых псевдослучайных чисел с k-шагами. Math.J.Okayama Univ. , 30:93–119, 1988.
MathSciNet МАТЕМАТИКА Google Scholar
Х. Нидеррайтер. Множества точек с малым несоответствием, полученные цифровыми построениями над конечными полями. Чехословацкий мат. J. , 42:143–166, 1992.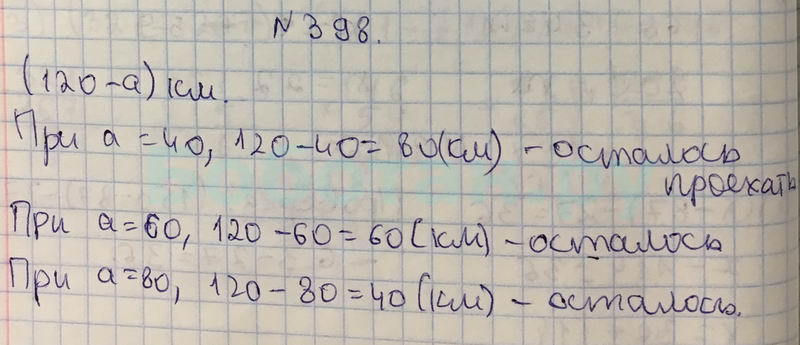
MathSciNet МАТЕМАТИКА Google Scholar
Х. Нидеррайтер. Генерация случайных чисел и методы квази-Монте-Карло. Номер 63 в серии CBMS-NSF по прикладной математике. SIAM, Филадельфия, 1992.
CrossRef Google Scholar
Х. Нидеррайтер. Факторизация многочленов и некоторые задачи линейной алгебры над конечными полями. Линейная алгебра Appl. , 192:301–328, 1993.
CrossRef MathSciNet МАТЕМАТИКА Google Scholar
Х. Нидеррайтер. Множественно-рекурсивный матричный метод генерации псевдослучайных чисел. Конечные поля Appl. , 1:3–30, 1995.
CrossRef MathSciNet МАТЕМАТИКА Google Scholar
Х. Нидеррайтер. Улучшены границы в методе множественной рекурсии матриц для псевдослучайных чисел и генерации векторов. Конечные поля Appl. , 2:225–240, 1996.
Улучшены границы в методе множественной рекурсии матриц для псевдослучайных чисел и генерации векторов. Конечные поля Appl. , 2:225–240, 1996.
CrossRef MathSciNet МАТЕМАТИКА Google Scholar
Х. Нидеррайтер и С. П. Син. Квазислучайные точки и глобальные функциональные поля. В S. Cohen and H. Niederreiter, editors, Finite Fields and Applications (Glasgow , 1995) , том 233 из Lect. Note Series Лондонской математики. соц. , стр. 269–296. Камб. ун-т Press, Кембридж, 1996.
Google Scholar
К. В. Онневеер. Дифференцируемость рядов Радемахера на группах. Acta Sci. Мат. , 39:121–128, 1977.
MathSciNet МАТЕМАТИКА Google Scholar
Р. Э. А. К. Палей. Замечательная система ортогональных функций. Проц. Лонд. Мат. соц. , 34:241–279, 1932.
Проц. Лонд. Мат. соц. , 34:241–279, 1932.
CrossRef MathSciNet Google Scholar
Г. Пирсич. Schnell konvergierende Walshreihen über Gruppen. Магистерская диссертация, Зальцбургский университет, 1995.
Google Scholar
Г. Пирсич. Проблемы изменения базы для обобщенных рядов Уолша и цифровой дифференциации. Докторская диссертация, Институт математики, Зальцбургский университет, 1997 г.
Google Scholar
В. М. Шмидт. Неравномерности распределения, VI. Вычисл. Мат. , 24:63–74, 1972.
МАТЕМАТИКА Google Scholar
В. М. Шмидт. Неравномерности распределения, VII. Акта Арит. , 21:45–50, 1972.
MathSciNet МАТЕМАТИКА Google Scholar
Дж. Шойсенгейер. О несоответствии (н.о.). Акта Арит. , 44:241–279, 1984.
Шойсенгейер. О несоответствии (н.о.). Акта Арит. , 44:241–279, 1984.
МАТЕМАТИКА Google Scholar
В.Ч. Шмид. (t , m, s)-сети: цифровое построение и комбинаторные аспекты. Докторская диссертация, Институт математики, Зальцбургский университет, май 1995 г.
Google Scholar
В.Ч. Шмид. Алгоритм определения параметра качества бинарных сетей и новый метод сдвига. В R. Trobek et al., редактор, Proc. Международный семинар «Параллельная нумерика ‘86» (Гозд Мартульек , Словения) , стр. 51–63, 1996.
Google Scholar
В.Ч. Шмид. Алгоритм определения параметра качества цифровых сетей по основанию 2. Препринт, Зальцбургский университет, 1997.
Google Scholar
В. Ч. Шмид. Шифт-сети: новый класс бинарных цифровых (t , m , s)- сетей. В H. Niederreiter et al., редактор, Методы Монте-Карло и Квази-Монте-Карло 1996 , том 127 из Lecture Notes in Statistics , страницы 369–381. Спрингер, Нью-Йорк, 1997 г.
Ч. Шмид. Шифт-сети: новый класс бинарных цифровых (t , m , s)- сетей. В H. Niederreiter et al., редактор, Методы Монте-Карло и Квази-Монте-Карло 1996 , том 127 из Lecture Notes in Statistics , страницы 369–381. Спрингер, Нью-Йорк, 1997 г.
Google Scholar
И. М. Соболь. Распределение точек в кубе и приближенное вычисление интегралов. З. Вычисл. Мат. и мат физ. , 7:784–802, 1967. (рус.).
MathSciNet Google Scholar
В.Ч. Шмид и Р. Вольф. Границы для цифровых сетей и последовательностей. Акта Арит. , 78:377–399, 1997.
MathSciNet МАТЕМАТИКА Google Scholar
Ю. Тауссат. Approximation Diophantienne Dans un Corps de Séries Formelles . Докторская диссертация, Университет Бордо, 1986.
Google Scholar
Н.Я. Виленкин. Класс полных ортонормированных рядов. Изв. акад. АН СССР , 11:363–400, 1947.
Google Scholar
Р. Вольф. Мера расстояния на конечных абелевых группах и приложение к интегрированию квази-Монте-Карло. Acta Math. Венгрия. , 78:25–37, 1998.
CrossRef MathSciNet МАТЕМАТИКА Google Scholar
|
Эта статья цитируется в 5 научных статьях (всего в 5 статьях) Теорема единственности для аддитивных функций и ее приложения к ортогональным рядам К. А. Керьян Ереванский государственный университет Полнотекстовый PDF (532 КБ) Ссылки: HTML DOI: https://doi.org/10.4213/mzm10431 Реферат: Предметом данной статьи является восстановление аддитивной функции, заданной на $\mathcal P$-адических параллелепипедах, по ее производной по $\mathcal P$-адическим параллелепипедам. Полученная теорема применяется к исследованию проблемы единственности кратных рядов по системам Хаара и Прайса. Ключевые слова: аддитивная функция, система Хаара, система Прайса, проблема единственности, кратные ряды, восстановление аддитивной функции по ее производной, $\mathcal P$-адический параллелепипед, $A$-интеграл.
Поступило: 23.12.2013 Английская версия: Библиографические базы данных: Тип документа: Артикул УДК: 517.518.36 Язык: Русский Ссылка: К. А. Керян, “Теорема единственности для аддитивных функций и ее приложения к ортогональным рядам”, Матем. заметки, 97:3 (2015), 382–396; Мат. Цитирование в формате AMSBIB Варианты подключения: Эта публикация цитируется в следующих статьях:
Ссылки на статьи в Google Scholar: русские цитаты,
английские цитаты | QR-? | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Самые цитируемые статьи по астрофизике за все время
СЛАК | Библиотека | Базы данных SPIERS | Поиск HEP | Комментарии Топциты, издание 2000 г. На основании данных из База данных литературы SPIRES-HEP, Библиотека SLAC
Наиболее цитируемые статьи по астрофизике за все время Существуют некоторые трудности с точной идентификацией статей по математической физике. в базе данных SPIERS (что, конечно же, следует только за статьями по физике высоких энергий и элементарных частиц).Нарисован следующий список из DESY ключевое слово «астрофизика» астро-ph архивы электронной печати. Это дает нам более 29 000 статей.
Ниже перечислены документы, которые они цитировали.
1055
- ИНФЛЯЦИОННАЯ ВСЕЛЕННАЯ: ВОЗМОЖНОЕ РЕШЕНИЕ ПРОБЛЕМ ГОРИЗОНТНОСТИ И ПЛОСКОСТИ
Алан Х. Гут (SLAC).
Опубликовано в Phys.Rev.D23:347-356, 1981 г.
- [Общее количество цитирований в HEP]
0619- НОВЫЙ ИНФЛЯЦИОННЫЙ СЦЕНАРИЙ ВСЕЛЕННОЙ: ВОЗМОЖНОЕ РЕШЕНИЕ ПРОБЛЕМ ГОРИЗОНТА, ПЛОСКОСТИ, ОДНОРОДНОСТИ, ИЗОТРОПИИ И ИСКОННОЙ МОНОПОЛЬНОСТИ
А.Д. Линде (ФИАН).
Опубликовано в Phys.Lett.B108:389-393, 1982 г.
- [Общее количество цитирований в HEP]
0616- КОСМОЛОГИЯ ДЛЯ ТЕОРИЙ ВЕЛИКОГО ОБЪЕДИНЕНИЯ С РАДИАЦИОННО-ИНДУЦИРОВАННЫМ НАРУШЕНИЕМ СИММЕТРИИ
Андреас Альбрехт, Пол Дж. Стейнхардт (Пенсильванский университет).
Опубликовано в Phys.Rev.Lett.48:1220-1223, 1982 г.
- [Общее количество цитирований в HEP]
0593- СТРУКТУРА В КОБЕ ДМР КАРТЫ ПЕРВОГО ГОДА
Г.Ф. Смут, К.Л. Беннетт, А. Когут, Э.Л. Райт, Дж. Эймон, Н.В. Боггесс, Э.С. Ченг, Г. Де Амичи, С. Гулкис, М.Г. Хаузер, Г. Хиншоу, К. Лайнуивер, К. Левенштейн, П.Д. Джексон, М. Янссен, Э. Кайта, Т. Келсолл, П. Кегстра, П. Любин, Дж. Мазер, С.С. Мейер, С.Х. Мозли, Т. Мердок, Л. Рокке, Р.Ф. Сильверберг, Л. Тенорио, Р. Вайс, Д. Т. Уилкинсон (LBL, Беркли и Калифорнийский университет, Беркли, Департамент космических наук и Калифорнийский университет, Беркли, CfPA и НАСА, Годдард и космические университеты доц. исследований и UCLA & Cal Tech, JPL & Hughes STX, Greenbelt & UC, Santa Barbara & MIT, LNS & General Research, Danvers & Princeton U.).
г. Опубликовано в Astrophys.J.396:L1-L5, 1992 г.
- [Общее количество цитирований в HEP]
0532- ТОПОЛОГИЯ КОСМИЧЕСКИХ ОБЛАСТЕЙ И СТРУН
Автор T.W.B. Киббл (Imperial Coll., Лондон).
Опубликовано в J.Phys.A A9:1387-1398, 1976 г.
- [Общее количество цитирований в HEP]
0473- КОСМИЧЕСКИЕ СТРУНЫ И ДОМЕННЫЕ СТЕНЫ
Александр Виленкин (Tufts U.).
Опубликовано в Phys.Rept.121:263,1985
- [Общее количество цитирований в HEP]
0446- ВОЛНОВАЯ ФУНКЦИЯ ВСЕЛЕННОЙ
Автор J.B. Hartle (Chicago U., EFI & Santa Barbara, ITP), S.W. Хокинг (Кембриджский университет и Санта-Барбара, ITP).
Опубликовано в Phys.Rev.D28:2960-2975, 1983 г.
- [Общее количество цитирований в HEP]
0446- КОЛЕБАНИЯ НЕЙТРИНО В МАТЕРИИ
Л. Вольфенштейн (Университет Карнеги-Меллона).
г. Опубликовано в Phys.Rev.D17:2369, 1978 г.
- [Общее количество цитирований в HEP]
0425- КОЛЕБАНИЯ В НОВОЙ ИНФЛЯЦИОННОЙ ВСЕЛЕННОЙ
А.Х. Гут (MIT, LNS), С.Ю. Пи (Гарвардский университет и Нью-Гэмпширский университет).
Опубликовано в Phys.Rev.Lett.49:1110-1113, 1982 г.
- [Общее количество цитирований в HEP]
0422- ДИНАМИКА ФАЗОВОГО ПЕРЕХОДА В СЦЕНАРИИ НОВАЯ ИНФЛЯЦИОННАЯ ВСЕЛЕННАЯ И ГЕНЕРАЦИЯ ВОЗМУЩЕНИЙ
А.А. Старобинский (Ин-т Ландау).
Опубликовано в Phys.Lett.B117:175-178, 1982.
- [Общее количество цитирований в HEP]
0416- РАЗВИТИЕ НЕПРАВИЛЬНОСТЕЙ В ЕДИНОМ ПУЗЫРЬЕ ИНФЛЯЦИОННОЙ ВСЕЛЕННОЙ
Автор S.W. Хокинг (Кембриджский университет).
Опубликовано в Phys.Lett.B115:295,1982
- [Общее количество цитирований в HEP]
0379- КОНСЕРВАЦИЯ СР В ПРИСУТСТВИИ ИНСТАНТОНОВ
Р. Д. Печчеи, Хелен Р. Куинн (Стэнфордский университет, ITP).
Опубликовано в Phys.Rev.Lett.38:1440-1443, 1977 г.
- [Общее количество цитирований в HEP]
0378- СПОНТАННОЕ СОЗДАНИЕ ПОЧТИ МАСШТАБНЫХ ВОЗМУЩЕНИЙ ПЛОТНОСТИ В ИНФЛЯЦИОННОЙ ВСЕЛЕННОЙ
Джеймс М.Бардин (Университет Вашингтона, Сиэтл), Пол Дж. Стейнхардт (Университет Пенсильвании), Майкл С. Тернер (Университет Чикаго, Астрон) , Астрофизы. Стр.).
Опубликовано в Phys.Rev.D28:679, 1983 г.
- [Общее количество цитирований в HEP]
0368- ПЕРВИЧНЫЙ НУКЛЕОСИНТЕЗ REDUX
Терри П. Уокер (Гарвард-Смитсоновский центр астрофизики и Университет штата Огайо), Гэри Стейгман (Университет штата Огайо), Дэвид Н. Шрамм (Университет Чикаго и Фермилаб), Кейт А. . Олив (Университет Миннесоты и Аннеси, LAPP), Хо-Шик Канг (Университет штата Огайо).
Опубликовано в Astrophys.J.376:51-69, 1991 г.
- [Общее количество цитирований в HEP]
0332- ХАОТИЧЕСКАЯ ИНФЛЯЦИЯ
А.Д. Линде (ЛИАН).
Опубликовано в Phys.Lett.B129:177-181, 1983
- [Общее количество цитирований в HEP]
0319- НОВЫЙ СВЕТОВОЙ БОЗОН?
Стивен Вайнберг (Гарвардский университет).
Опубликовано в Phys.Rev.Lett.40:223-226, 1978 г.
- [Общее количество цитирований в HEP]
0318- ЕДИНСТВО ВСЕХ СИЛ ЭЛЕМЕНТАРНЫХ ЧАСТИЦ
Х. Георги, С.Л. Глэшоу (Гарвардский университет).
Опубликовано в Phys.Rev.Lett.32:438-441, 1974 г.
- [Общее количество цитирований в HEP]
0307- ОБ АНОМАЛЬНОМ НЕСОХРАНЕНИИ ЭЛЕКТРСЛАБОГО БАРИОННОГО ЧИСЛА В РАННЕЙ ВСЕЛЕННОЙ
В.А. Кузьмин, В.А. Рубаков (Москва, ИЯИ), М.Е. Шапошников (МЦТФ, Триест).
Опубликовано в Phys.Lett.B155:36,1985
- [Общее количество цитирований в HEP]
0303- ПРОБЛЕМА СИЛЬНОЙ Р- И Т-ИНВАРИАНТНОСТИ ПРИ ПРИСУТСТВИИ ИНСТАНТОНОВ
Ф. Вильчек (Колумбийский университет и Принстон, Институт перспективных исследований).
Опубликовано в Phys.Rev.Lett.40:279-282, 1978 г.
- [Общее количество цитирований в HEP]
0302- КОСМОЛОГИЧЕСКАЯ НИЖНЯЯ ГРАНИЦА ДЛЯ МАСС ТЯЖЕЛЫХ НЕЙТРИНО
Benjamin W.Lee (Fermilab), Steven Weinberg (Stanford U., Phys. Dept.).
Опубликовано в Phys.Rev.Lett.39: 165–168, 1977 г.
- [Общее количество цитирований в HEP]
0297- КОСМИЧЕСКОЕ РАЗДЕЛЕНИЕ ФАЗ
Эдвард Виттен (Принстон, Институт перспективных исследований).
Опубликовано в Phys.Rev.D30:272-285, 1984 г.
- [Общее количество цитирований в HEP]
0295- КОСМОЛОГИЧЕСКОЕ ПРОИЗВОДСТВО СВЕРХТЯЖЕЛЫХ МАГНИТНЫХ МОНОПОЛЕЙ
Джон П. Прескилл (Гарвардский университет).
Опубликовано в Phys.Rev.Lett.43:1365,1979
- [Общее количество цитирований в HEP]
0293- ПЕРВИЧНЫЙ НУКЛЕОСИНТЕЗ: КРИТИЧЕСКОЕ СРАВНЕНИЕ ТЕОРИИ И НАБЛЮДЕНИЙ
J. Yang (Cal Tech & Chicago U.), M.S. Тернер (Университет Чикаго и Фермилаб), Г. Стейгман (Исследовательский институт Бартола), Д. Н. Шрамм (Университет Чикаго и Фермилаб), К.А. Олива (Фермилаб).
Опубликовано в Astrophys. J.281:493-511, 1984 г.
- [Общее количество цитирований в HEP]
0284- ПРОБЛЕМА КОСМОЛОГИЧЕСКОЙ ПОСТОЯННОЙ
Стивен Вайнберг (Техасский университет).
Опубликовано в Rev.Mod.Phys.61:1-23, 1989 г.
- [Общее количество цитирований в HEP]
0284- КОСМОЛОГИЯ НЕВИДИМОГО АКСИОНА
Джон Прескилл, Марк Б. Уайз (Гарвардский университет), Фрэнк Вильчек (Санта-Барбара, ITP).
Опубликовано в Phys.Lett.B120:127-132, 1983
- [Общее количество цитирований в HEP]
0282- ПОВЕДЕНИЕ СИММЕТРИИ ПРИ КОНЕЧНОЙ ТЕМПЕРАТУРЕ
Л. Долан, Р. Джекив (MIT, LNS).
Опубликовано в Phys.Rev.D9:3320-3341, 1974 г.
- [Общее количество цитирований в HEP]
0282- СУПЕРСИММЕТРИЧНЫЕ РЕЛИКИ БОЛЬШОГО ВЗРЫВА
Джон Эллис, Дж.С. Хагелин (SLAC), Д.В. Нанопулос, К. Олив, М. Средненицкий (ЦЕРН).
Опубликовано в Nucl.Phys.B238:453-476, 1984.
- [Общее количество цитирований в HEP]
0282- СТАТИСТИКА ПИКОВ ГАУССОВЫХ СЛУЧАЙНЫХ ПОЛЕЙ
Дж. М. Бардин, Дж. Р. Бонд, Н. Кайзер, А.С. Салай (Вашингтонский университет, Сиэтл и Стэнфордский университет, физический факультет и Калифорнийский университет, Беркли, кафедра астрономии и Кембриджский университет, и Фермилаб и Санта-Барбара, ITP).
Опубликовано в Astrophys.J.304:15-61, 1986 г.
- [Общее количество цитирований в HEP]
0277- КАЛИБРОВОЧНО-ИНВАРИАНТНЫЕ КОСМОЛОГИЧЕСКИЕ ВОЗМУЩЕНИЯ
Дж. М. Бардин (Принстон, Институт перспективных исследований).
Опубликовано в Phys.Rev.D22:1882-1905, 1980
- [Общее количество цитирований в HEP]
0273- НАБЛЮДЕНИЕ НЕЙТРИННОЙ ВСПЫШКИ ОТ СВЕРХНОВОЙ SN1987A
Коллаборацией KAMIOKANDE-II (К.Хирата и др.).
Опубликовано в Phys.Rev.Lett.58:1490-1493, 1987 г.
- [Общее количество цитирований в HEP]
0271- ВОЗМУЩЕНИЯ КОСМОЛОГИЧЕСКОЙ МОДЕЛИ И УГЛОВЫЕ ВАРИАЦИИ МИКРОВОЛНОВОГО ФОНА
Р.К. Сакс, А.М. Вулф (Техасский университет).
Опубликовано в Astrophys.J.147:73-90, 1967 г.
- [Общее количество цитирований в HEP]
0269- КОСМОЛОГИЧЕСКАЯ ОГРАНИЧЕННОСТЬ НЕВИДИМОГО АКСИОНА
Л. Ф. Эбботт (Брандейс У.), П. Сикиви (Флорида У.).
Опубликовано в Phys.Lett.B120:133-136, 1983
- [Общее количество цитирований в HEP]
0266- СУДЬБА ЛОЖНОГО ВАКУУМА. 1. ПОЛУКЛАССИЧЕСКАЯ ТЕОРИЯ
Сидней Коулман (Гарвардский университет).
Опубликовано в Phys.Rev.D15:2929-2936, 1977 (ошибка там же, D16:1248, 1977)
- [Общее количество цитирований в HEP]
0265- СОЗДАНИЕ ЧАСТИЦ ЧЕРНЫМИ ДЫРАМИ
С.В. Хокинг (Кембриджский университет).
Опубликовано в Commun.Math.Phys.43:199-220, 1975 г.
- [Общее количество цитирований в HEP]
0261- НЕ ТАКОЙ БЕЗОПАСНЫЙ АКСИОН
Майкл Дайн (Принстон, Институт перспективных исследований), Вилли Фишлер (Пенсильванский университет).
Опубликовано в Phys.Lett.B120:137-141, 1983
- [Общее количество цитирований в HEP]
0260- НАБЛЮДЕНИЕ НЕЙТРИННОЙ ВСПЫШКИ СОВПАДЕНИЯ СО СВЕРХНОВОЙ SN1987A В БОЛЬШОМ МАГЕЛЛАНОВОМ ОБЛАКЕ
Р.М. Бионта, Г. Блюитт, К. Б. Брэттон, Д. Каспер, А. Чиочио, Р. Клаус, Б. Кортез, М. Крауч, С.Т. Дай, С. Эрреде, Г.В. Фостер, В. Гаевский, К.С. Ганезер, М. Гольдхабер, Т.Дж. Хейнс, Т.В. Джонс, Д. Кельчевска, В.Р. Кропп, Дж.Г. Узнал, Дж. М. ЛоСекко, Дж. Мэтьюз, Р. Миллер, М.С. Мудан, Х.С. Парк, Л.Р. Прайс, Ф. Рейнс, Дж. Шульц, С. Зайдель, Э. Шумар, Д. Синклер, Х.В. Собел, Дж.Л. Стоун, Л.Р. Сулак, Р. Свобода, Г.Торнтон, Дж. К. ван дер Вельде, К. Уэст (Калифорнийский университет, Ирвин и Мичиганский университет, Брукхейвен и Калифорнийский технологический институт, Лаборатория реактивного движения и Кливлендский государственный университет, Гавайский университет и университетское собрание, Лондонский и Варшавский университет и Кейс Вестерн Резерв U. и Illinois U., Urbana & UC, Berkeley & LLL, Livermore & Notre Dame U. и Boston U. & Fermilab & AT-T Bell Labs, Murray Hill).
г. Опубликовано в Phys.Rev.Lett.58:1494, 1987 г.
- [Общее количество цитирований в HEP]
0260- КОСМОЛОГИЧЕСКОЕ ПРОИЗВОДСТВО БАРИОНОВ
Стивен Вайнберг (Гарвардский университет и Гарвард-Смитсоновский центр астрофизики).
Опубликовано в Phys.Rev.Lett.42:850-853, 1979 г.
- [Общее количество цитирований в HEP]
0259- СУПЕРСИММЕТРИЯ, СУПЕРГРАВИТАЦИЯ И ФИЗИКА ЧАСТИЦ
г. Ниль (Университет Женевы и ЦЕРН).
Опубликовано в Phys.Rept.110:1, 1984 г.
- [Общее количество цитирований в HEP]
0257- КАЛИБРОВОЧНЫЕ И ГЛОБАЛЬНЫЕ СИММЕТРИИ ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ
Стивен Вайнберг (Гарвардский университет).
Опубликовано в Phys.Rev.D9:3357-3378, 1974 г.
- [Общее количество цитирований в HEP]
0247- РАДИАЦИОННЫЕ ПОПРАВКИ КАК ПРИЧИНА СПОНТАННОГО НАРУШЕНИЯ СИММЕТРИИ
С. Коулман, Э. Вайнберг (Гарвардский университет).
Опубликовано в Phys.Rev.D7:1888-1910, 1973 г.
- [Общее количество цитирований в HEP]
0242- ПОИСК СУПЕРСИММЕТРИИ: ИССЛЕДОВАНИЕ ФИЗИКИ ЗА СТАНДАРТНОЙ МОДЕЛЕЙ
Ховард Э. Хабер (Калифорнийский университет, Санта-Крус и SLAC), Г. Л. Кейн (Мичиганский университет).
Опубликовано в Phys.Rept.117:75, 1985 г.
- [Общее количество цитирований в HEP]
0240- РЕКОНСТРУКЦИЯ ЛИНЕЙНОГО СПЕКТРА МОЩНОСТИ КОСМОЛОГИЧЕСКИХ КОЛЕБАНИЙ МАССЫ
Дж.А. Пикок (Королевская обсерватория, Эдинбург), S.J. Доддс (Эдинбургский университет).
Опубликовано в Mon.Not.Roy.Astron.Soc.267:1020-1034, 1994 г. [PS-файл для arXiv: astro-ph/9311057]
- [Общее количество цитирований в HEP]
0234- КОНЕЦ СПЕКТРА КОСМИЧЕСКИХ ЛУЧЕЙ?
Кеннет Грейзен (Cornell U., LNS).
Опубликовано в Phys.Rev.Lett.16:748-750,1966
- [Общее количество цитирований в HEP]
0233- КВАНТОВАЯ ТЕОРИЯ ГРАВИТАЦИИ. 1. КАНОНИЧЕСКАЯ ТЕОРИЯ
Б.С. Девитт (Принстон, Институт перспективных исследований и Университет Северной Каролины).
Опубликовано в Phys.Rev.160:1113-1148, 1967 г.
- [Общее количество цитирований в HEP]
0233- ПРОСТОЕ РЕШЕНИЕ СИЛЬНОЙ ПРОБЛЕМЫ CP С ПОМОЩЬЮ БЕЗОПАСНОГО АКСИОНА
Майкл Дайн (Принстон, Институт перспективных исследований), Вилли Фишлер (Пеннский университет и Принстон, Институт перспективных исследований), Марк Средницкий (Принстонский университет) .
Опубликовано в Phys.Lett.B104:199,1981
- [Общее количество цитирований в HEP]
0232- КОСМОЛОГИЧЕСКИЕ ФЛУКТУАЦИИ, ВОЗНИКАЮЩИЕ ВБЛИЗИ СИНГУЛЯРНОСТИ
Я.Б. Зельдовича (Москва, ИПМ).
Опубликовано в Mon.Not.Roy.Astron.Soc.192:663-667, 1980
- [Общее количество цитирований в HEP]
02:30- СУПЕРСИММЕТРИЧНАЯ ТЕМНАЯ МАТЕРИЯ
Джерард Юнгман (Сиракьюзский университет), Марк Камионковски (Колумбийский университет и Принстон, Институт перспективных исследований), Ким Грист (Калифорнийский университет, Сан-Диего).
г. Опубликовано в Phys.Rept.267:195-373, 1996 г. [PS-файл для arXiv: hep-ph/9506380]
- [Общее количество цитирований в HEP]
02:30- РЕЗОНАНСНОЕ УСИЛЕНИЕ НЕЙТРИННЫХ КОЛЕБАНИЙ В ВЕЩЕСТВЕ И СОЛНЕЧНАЯ НЕЙТРИННАЯ СПЕКТРОСКОПИЯ
С.П. Михеев, А.Ю. Смирнова (Москва, ИЯИ).
Опубликовано в Nuovo Cim.C9:17-26,1986
- [Общее количество цитирований в HEP]
02:30- СУПЕРСИММЕТРИЧНАЯ ТЕМНАЯ МАТЕРИЯ
Джерард Юнгман (Сиракьюзский университет), Марк Камионковски (Колумбийский университет и Принстон, Институт перспективных исследований), Ким Грист (Калифорнийский университет, Сан-Диего).
Опубликовано в Phys.Rept.267:195-373, 1996 г. [PS-файл для arXiv: hep-ph/9506380]
- [Общее количество цитирований в HEP]
0229- СВЕРХПРОВОДЯЩИЕ СТРУНЫ
Эдвард Виттен (Принстон, Институт перспективных исследований).
Опубликовано в Nucl.Phys.B249:557-592 1985 г.
- [Общее количество цитирований в HEP]
0222- ОГРАНИЧЕНИЯ, НАЛОЖЕННЫЕ СОХРАНЕНИЕМ СР В ПРИСУТСТВИИ ИНСТАНТОНОВ
Р. Д. Печчеи, Х. Р. Куинн (Стэнфордский университет, ITP).
Опубликовано в Phys.Rev.D16:1791-1797, 1977 г.
- [Общее количество цитирований в HEP]
0222- БАРИОННЫЙ СОДЕРЖИМЫЙ СКОПЛЕНИЙ ГАЛАКТИК: ВЫЗОВ КОСМОЛОГИЧЕСКОЙ ОРТОДОКСИИ
Саймон Д.М. Уайт (Кембриджский университет), Хулио Ф. Наварро (Даремский университет), Август Э. Эврард (Мичиганский университет), Карлос С. Френк (Даремский университет).
г. Опубликовано в журнале Nature 366:429-433, 1993 г.
- [Общее количество цитирований в HEP]
0220- РАСШИРЕННАЯ ИНФЛЯЦИОННАЯ КОСМОЛОГИЯ
Дайле Ла, Пол Дж. Стейнхардт (Пенсильванский университет).
Опубликовано в Phys.Rev.Lett.62:376,1989 (опечатка там же 62:1066,1989)
- [Общее количество цитирований в HEP]
0217- ВЕРХНИЙ ПРЕДЕЛ НА МАССУ ПОКОЯ НЕЙТРИНО
R. Cowsik, J. McClelland (UC, Berkeley).
г. Опубликовано в Phys.Rev.Lett.29:669-670, 1972 г.
- [Общее количество цитирований в HEP]
0216- О БАРИОННОМ ЧИСЛЕ ВСЕЛЕННОЙ
Савас Димопулос (Университет Чикаго, EFI), Леонард Сасскинд (SLAC).
Опубликовано в Phys.Rev.D18:4500-4509, 1978 г.
- [Общее количество цитирований в HEP]
0214- СИНГЛЕТ СЛАБОГО ВЗАИМОДЕЙСТВИЯ И СИЛЬНАЯ CP-ИНВАРИАНТНОСТЬ
Джин Э. Ким (Пенн У.).
г. Опубликовано в Phys.Rev.Lett.43:103, 1979 г.
- [Общее количество цитирований в HEP]
0214- ДАННЫЕ НАБЛЮДЕНИЙ СВЕРХНОВЫХ ДЛЯ УСКОРЯЮЩЕЙСЯ ВСЕЛЕННОЙ И КОСМОЛОГИЧЕСКОЙ ПОСТОЯННОЙ
Группа по поиску сверхновых (Адам Г. Рисс и др.).
Опубликовано в Astron.J.116:1009-1038, 1998 г. [PS-файл для arXiv: astro-ph/9805201]
- [Общее количество цитирований в HEP]
0213- МАТЕРИЯ-АНТИМАТЕРИЯ УЧЕТ, ТЕРМОДИНАМИКА И ИЗЛУЧЕНИЕ ЧЕРНЫХ ДЫР
Д. Туссен, С.Б. Трейман, Фрэнк Вильчек (Принстонский университет), А. Зи (Пеннский университет).
Опубликовано в Phys.Rev.D19:1036-1045, 1979 г.
- [Общее количество цитирований в HEP]
0212- ИЗМЕРЕНИЯ ОМЕГА И ЛЯМБДА 42 СВЕРХНОВЫХ С ВЫСОКИМ КРАСНЫМ СМЕЩЕНИЕМ
Проектом космологии сверхновых (С.Перлмуттер и др.).
Опубликовано в Astrophys.J.517:565-586,1999 [PS-файл для arXiv: astro-ph/9812133]
- [Общее количество цитирований в HEP]
0209- ТЕОРИЯ КОСМОЛОГИЧЕСКИХ ВОЗМУЩЕНИЙ. ЧАСТЬ 1. КЛАССИЧЕСКИЕ ВОЗМУЩЕНИЯ. ЧАСТЬ 2. КВАНТОВАЯ ТЕОРИЯ ВОЗМУЩЕНИЙ. ЧАСТЬ 3. РАСШИРЕНИЯ
В.Ф. Муханов (Браун Ю. и Москва, ИЯР), Х.А. Фельдман (Канадский институт теории астрофизики), Р. Х. Бранденбергер (Браун У.).
Опубликовано в Phys.Rept.215:203-333, 1992 г.
- [Общее количество цитирований в HEP]
0209- ГРАВИТАЦИОННОЕ ПОЛЕ ВАКУУМНЫХ ДОМЕННЫХ СТЕН И СТРУН
А. Виленкин (Tufts U.).
Опубликовано в Phys.Rev.D23:852-857, 1981 г.
- [Общее количество цитирований в HEP]
0209- ДО БОЛЬШОГО ВЗРЫВА В СТРУННОЙ КОСМОЛОГИИ
М. Гасперини (Туринский университет и INFN, Турин), Г. Венециано (ЦЕРН).
Опубликовано в Astropart.Phys.1:317-339, 1993 г. [PS-файл для arXiv: hep-th/21]
- [Общее количество цитирований в HEP]
0208- КОСМОЛОГИЧЕСКИЕ ФЛУКТУАЦИИ ПЛОТНОСТИ, ПРОИЗВОДИМЫЕ ВАКУУМНЫМИ СТРУНАМИ
А. Виленкин (Tufts U.).
Опубликовано в Phys.Rev.Lett.46:1169-1172, 1981 г.
- [Общее количество цитирований в HEP]
0207- НАРУШЕНИЕ СИММЕТРИИ ЧЕРЕЗ АНОМАЛИИ БЕЛЛА-ДЖЕКИВА
Г. ‘т Хофт (Гарвардский университет).
Опубликовано в Phys.Rev.Lett.37:8-11,1976
- [Общее количество цитирований в HEP]
0207- ПРИНЦИП МАХА И РЕЛЯТИВИСТСКАЯ ТЕОРИЯ ГРАВИТАЦИИ
К. Бранс, Р. Х. Дик (Принстонский университет).
Опубликовано в Phys.Rev.124:925-935, 1961 г.
- [Общее количество цитирований в HEP]
0207- ЧЕТЫРЕХЛЕТНИЕ COBE DMR КОСМИЧЕСКИЕ МИКРОВОЛНОВЫЕ НАБЛЮДЕНИЯ ФОНА: КАРТЫ И ОСНОВНЫЕ РЕЗУЛЬТАТЫ
C.L. Беннетт (НАСА, Годдард), А. Бандей, К.М. Горски, Г. Хиншоу, П. Джексон, П. Кегстра, А. Когут (Hughes STX, Greenbelt), Г.Ф. Смут (LBL, Беркли и Калифорнийский университет, Беркли), Д.Т. Уилкинсон (Принстонский университет), Э.Л. Райт (Калифорнийский университет в Лос-Анджелесе).
г. Опубликовано в Astrophys.J.464:L1-L4, 1996 г. [PS-файл для arXiv: astro-ph/9601067]
- [Общее количество цитирований в HEP]
0204- ЕДИНЫЕ КАЛИБРОВОЧНЫЕ ТЕОРИИ И БАРИОННОЕ ЧИСЛО ВСЕЛЕННОЙ
Мотохико Йошимура (Тохоку У.).
Опубликовано в Phys.Rev.Lett.41:281-284, 1978 (опечатка там же 42:746, 1979)
- [Общее количество цитирований в HEP]
0203- НЕКОТОРЫЕ ПОСЛЕДСТВИЯ КОСМОЛОГИЧЕСКОГО ФАЗОВОГО ПЕРЕХОДА
Киббл (Imperial Coll., Лондон).
Опубликовано в Phys.Rept.67:183, 1980
- [Общее количество цитирований в HEP]
0203- МАГНИТНЫЕ МОНОПОЛИ В ЕДИНЫХ КАЛИБРОВОЧНЫХ ТЕОРИЯХ
Г.т Хофт (ЦЕРН).
Опубликовано в Nucl.Phys.B79:276-284, 1974 г.
- [Общее количество цитирований в HEP]
0202- ВОЗМУЩЕНИЕ ПЛОТНОСТИ ХОЛОДНОЙ ТЕМНОЙ МАТЕРИИ
г. Авторы Эндрю Р. Лиддл (Университет Сассекса), Дэвид Х. Лит (Университет Ланкастера).
Опубликовано в Phys.Rept.231:1-105, 1993 г. [PS-файл для arXiv: astro-ph/9303019]
- [Общее количество цитирований в HEP]
0198- ОБНАРУЖАЕМОСТЬ НЕКОТОРЫХ КАНДИДАТОВ ТЕМНОЙ МАТЕРИИ
Марк В. Гудман, Эдвард Виттен (Принстонский университет).
Опубликовано в Phys.Rev.D31:3059, 1985 г.
- [Общее количество цитирований в HEP]
0198- КОСМОЛОГИЧЕСКИЕ ГОРИЗОНТЫ СОБЫТИЙ, ТЕРМОДИНАМИКА И СОЗДАНИЕ ЧАСТИЦ
Г.В. Гиббонс, С.В. Хокинг (Кембриджский университет).
Опубликовано в Phys.Rev.D15:2738-2751, 1977 г.
- [Общее количество цитирований в HEP]
0192- ПЕРЕОХЛАЖДЕННЫЕ ФАЗОВЫЕ ПЕРЕХОДЫ В ОЧЕНЬ РАННЕЙ ВСЕЛЕННОЙ
С.В. Хокинг, И.Г. Мосс (Кембриджский университет).
Опубликовано в Phys.Lett.B110:35,1982
- [Общее количество цитирований в HEP]
0191- ИНТЕГРИРОВАННЫЙ ПОДХОД К АНИЗОТРОПИИ КОСМИЧЕСКОГО МИКРОВОЛНОВОГО ФОНА
Урос Сельяк (Гарвард-Смитсоновский центр астрофизики), Матиас Залдарриага (MIT, LNS).
Опубликовано в Astrophys.J.469:437-444, 1996 г. [PS-файл для arXiv: astro-ph/9603033]
- [Общее количество цитирований в HEP]
0191- ИНТЕГРИРОВАННЫЙ ПОДХОД К КОСМИЧЕСКИМ МИКРОВОЛНОВЫМ ФОНОВЫМ АНИЗОТРОПИЯМ 1360
Урос Сельяк (Гарвард-Смитсоновский центр астрофизики), Матиас Залдарриага (MIT, LNS).
Опубликовано в Astrophys.J.469:437-444, 1996 г. [PS-файл для arXiv: astro-ph/9603033]
- [Общее количество цитирований в HEP]
0190- ДВОЙСТВЕННОСТЬ МАСШТАБНОГО ФАКТОРА ДЛЯ КЛАССИЧЕСКИХ И КВАНТОВЫХ СТРУН
Дж.Венециано (ЦЕРН).
Опубликовано в Phys.Lett.B265:287-294, 1991
- [Общее количество цитирований в HEP]
0190- МОДЕЛИ VOLTEX LINE ДЛЯ ДВОЙНЫХ СТРУН
Автор H.B. Нильсен, П. Олесен (Институт Бора).
Опубликовано в Nucl.Phys.B61:45-61, 1973 г.
- [Общее количество цитирований в HEP]
0190- ОТКРЫТИЕ ВЗРЫВА СВЕРХНОВОЙ НА ПОЛОВИНЕ ВОЗРАСТА ВСЕЛЕННОЙ И ЕГО КОСМОЛОГИЧЕСКИЕ ПОСЛЕДСТВИЯ
Проект космологии сверхновых (С. Перлмуттер и др.).
Опубликовано в журнале Nature 391:51-54, 1998 г. [PS-файл для arXiv: astro-ph/9712212]
- [Общее количество цитирований в HEP]
0186- ОГРАНИЧЕНИЕ НА МАССУ ФОТИНО ИЗ КОСМОЛОГИИ
Х. Голдберг (Северо-Восточный У.).
Опубликовано в Phys.Rev.Lett.50:1419, 1983.
- [Общее количество цитирований в HEP]
0186- ОГРАНИЧЕНИЯ НА ОБОБЩЕННЫЕ ИНФЛЯЦИОННЫЕ КОСМОЛОГИИ
Л.Ф. Эбботт (Брандейс У.), Марк Б. Уайз (Калифорнийский технологический институт).
Опубликовано в Nucl.Phys.B244:541-548,1984
- [Общее количество цитирований в HEP]
0184- НОВЫЙ ТИП ИЗОТРОПНЫХ КОСМОЛОГИЧЕСКИХ МОДЕЛЕЙ БЕЗ СИНГУЛЯРНОСТИ
А.А. Старобинский (Кембриджский университет и Институт Ландау).
Опубликовано в Phys.Lett.B91:99-102, 1980.
- [Общее количество цитирований в HEP]
0181- РЕЗОНАНСНОЕ УСИЛЕНИЕ КОЛЕБАНИЙ В ВЕЩЕСТВЕ И СПЕКТРОСКОПИЯ СОЛНЕЧНЫХ НЕЙТРИНО
г. С.П. Михеев, А.Ю. Смирнова (Москва, ИЯИ).
Опубликовано в Sov.J.Nucl.Phys.42:913-917,1985 (Yad.Fiz.42:1441-1448,1985)
- [Общее количество цитирований в HEP]
0181- ГРАВИТАЦИОННОЕ МИКРОЛИНЗИРОВАНИЕ ГАЛО ГАЛО
Богдан Пачинский (Обсерватория Принстонского университета).
Опубликовано в Astrophys.J.304:1-5, 1986 г.
- [Общее количество цитирований в HEP]
0181- ГРАВИТАЦИОННАЯ НЕУСТОЙЧИВОСТЬ: ПРИБЛИЖЕННАЯ ТЕОРИЯ ДЛЯ ВОЗМУЩЕНИЙ БОЛЬШОЙ ПЛОТНОСТИ
Я.Б. Зельдовича (Москва, ИПМ).
Опубликовано в Astron.Astrophys.5:84-89, 1970 г.
- [Общее количество цитирований в HEP]
0180- МОДЕЛЬ ЛЕПТОНОВ
С. Вайнберг (MIT, LNS).
Опубликовано в Phys.Rev.Lett.19:1264-1266, 1967 г.
- [Общее количество цитирований в HEP]
0180- КОСМОЛОГИЧЕСКИЕ ПОСЛЕДСТВИЯ КАТЯЩЕГОСЯ ОДНОРОДНОГО СКАЛЯРНОГО ПОЛЯ
Бхарат Ратра, П.Дж.Е. Пиблз (Принстонский университет).
Опубликовано в Phys.Rev.D37:3406, 1988 г.
- [Общее количество цитирований в HEP]
0178- ИНТЕРПРЕТАЦИЯ АНИЗОТРОПИИ РИ, ОБНАРУЖЕННОЙ СБОРОМ COBE DMR
Э.Л. Райт, С.С. Мейер, К.Л. Беннетт, Н.В. Боггесс, Э.С. Ченг, М.Г. Хаузер, А. Когут, К. Лайнуивер, Дж. К. Мазер, Г.Ф. Смут, Р. Вайс, С. Гулкис, Г. Хиншоу, М. Янссен, Т. Келсолл, П.М. Любин, С.Х. Мозли-младший, Т.Л. Мердок, Р.А. Шафер, Р.Ф. Сильверберг, Д.Т. Уилкинсон (UCLA и MIT, LNS и NASA, Goddard и университетов Ассоциация космических исследований & LBL, Беркли и Калифорнийский университет, Беркли, Space Sci. Департамент и Калифорнийский технологический институт, Лаборатория реактивного движения и Калифорнийский университет, Санта-Барбара и общие исследования, Дэнверс и Принстон У.).
г. Опубликовано в Astrophys.J.396:L13-L18, 1992 г.
- [Общее количество цитирований в HEP]
0178- МАССЫ И ОТНОШЕНИЯ МАССЫ К СВЕТКЕ ГАЛАКТИК
С.М. Faber (Ликская обсерватория), J.S. Галлахер (штат Иллинойс, Урбана).
Опубликовано в Ann.Rev.Astron.Astrophys.17:135-183, 1979 г.
- [Общее количество цитирований в HEP]
0177- О КОНЦЕНТРАЦИИ РЕЛИКОВЫХ МАГНИТНЫХ МОНОПОЛЕЙ ВО ВСЕЛЕННОЙ
Я.Б. Зельдович, М.Ю. Хлопова (Москва, ИПМ).
Опубликовано в Phys.Lett.B79:239-241, 1978 г.
- [Общее количество цитирований в HEP]
0177- ЭВОЛЮЦИЯ КРУПНОМАСШТАБНОЙ СТРУКТУРЫ ВО ВСЕЛЕННОЙ, В КОТОРОЙ ДОМИНИРУЕТ ХОЛОДНАЯ ТЕМНАЯ МАТЕРИЯ
Марк Дэвис (Санта-Барбара, ITP & UC, Berkeley, Astronomy Dept.& UC, Berkeley), George Efstathiou (Santa Barbara, ITP & Cambridge U .), Карлос С. Френк (Санта-Барбара, ITP и Sussex U.), Саймон Д.М. Уайт (Санта-Барбара, обсерватория ITP и Стюарда, Тусон).
г. Опубликовано в Astrophys.J.292:371-394, 1985 г.
- [Общее количество цитирований в HEP]
0177- ФОРМИРОВАНИЕ ГАЛАКТИК И СКОПЛЕНИЙ ГАЛАКТИК ПУТЕМ АВТОМОБИЛЬНОЙ ГРАВИТАЦИОННОЙ КОНДЕНСАЦИИ
Уильям Х. Пресс, Пол Шехтер (Калифорнийский технологический институт).
Опубликовано в Astrophys.J.187:425-438, 1974 г.
- [Общее количество цитирований в HEP]
0176- НЕЙТРИННЫЕ КОЛЕБАНИЯ И ЗВЕЗДНЫЙ КОЛАПАС
Л. Вольфенштейн (Университет Карнеги-Меллона).
Опубликовано в Phys.Rev.D20:2634-2635, 1979 г.
- [Общее количество цитирований в HEP]
0176- КВАНТОВОЕ СОСТОЯНИЕ ВСЕЛЕННОЙ
С.В. Хокинг (Кембриджский университет).
Опубликовано в Nucl.Phys.B239:257,1984
- [Общее количество цитирований в HEP]
0175- ПОЧЕМУ НЕТ НИЧЕГО, А НЕ ЧТО-ТО: ТЕОРИЯ КОСМОЛОГИЧЕСКОЙ ПОСТОЯННОЙ
Сидней Коулман (Гарвардский университет).
Опубликовано в Nucl.Phys.B310:643,1988
- [Общее количество цитирований в HEP]
0173- КОЛЕБАНИЯ СКАЛЯРНОГО ПОЛЯ В РАСШИРЯЮЩЕЙСЯ ВСЕЛЕННОЙ И СЦЕНАРИИ НОВОЙ ИНФЛЯЦИОННОЙ ВСЕЛЕННОЙ
А.Д. Линде (ФИАН).
Опубликовано в Phys.Lett.B116:335,1982
- [Общее количество цитирований в HEP]
0172- СУДЬБА ЛОЖНОГО ВАКУУМА. 2. ПЕРВЫЕ КВАНТОВЫЕ ПОПРАВКИ
Кертис Каллан (Принстонский университет), Сидни Коулман (Гарвардский университет).
Опубликовано в Phys.Rev.D16:1762-1768, 1977 г.
- [Общее количество цитирований в HEP]
0171- ОБНАРУЖЕНИЕ КОСМИЧЕСКОЙ ТЕМНОЙ МАТЕРИИ
Джоэл Р.Примак, Дэвид Секель (Калифорнийский университет, Санта-Круз), Бернар Садуле (Калифорнийский университет, Беркли).
Опубликовано в Ann.Rev.Nucl.Part.Sci.38:751,1988
- [Общее количество цитирований в HEP]
0169- ДОКАЗАТЕЛЬСТВА ГРАВИТАЦИОННОГО МИКРОЛИНЗИРОВАНИЯ ТЕМНЫМИ ОБЪЕКТАМИ В ГАЛО ГАЛО
Э. Обур, П. Барейр, С. Брехин, М. Гро, М. Лашиз-Рей, Б. Лоран, Э. Лескуа, К. Магневиль, А. Мильштейн, Л. Москосо, Ф. Кеннек, Дж. Рич, М. Спиро, Л. Вигру, С. Зильберайч (DAPNIA, Saclay), Р. Ансари, Ф. Кавалье, М. Монье (Орсе, LAL), Ж. П. Болье, Р. Ферле, П. Гризон, А. Видаль-Маджар (Париж, Ин-т астрофиз.), Ж. Гильбер, О. Моро, Ф. Таджахмади (Медонская обсерватория), Э. Морис, Л. Прево (Марсельская обсерватория), К. Гри (Марсель, ЛАС).
г. Опубликовано в Nature 365: 623-625, 1993 г.
- [Общее количество цитирований в HEP]
0168- АМПЛИТУДЫ КОЛЕБАНИЙ МАССЫ ВО ВСЕЛЕННОЙ
С.

 Заметки:
Заметки: 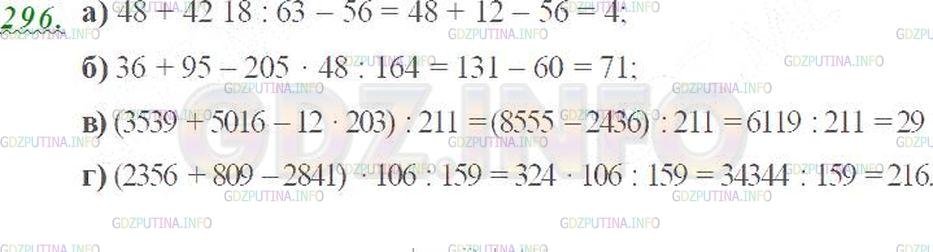 org/10.4213/mzm10431 (ми мзм10431)
org/10.4213/mzm10431 (ми мзм10431)
 Примечания, 97:3 (2015), 362–375
Примечания, 97:3 (2015), 362–375